Imaging conical intersection dynamics during azobenzene photoisomerization by ultrafast X-ray diffraction

Significance

Vibronic coherences are unique features that emerge in the decisive moments of photochemistry and photophysics. Here we demonstrate how X-ray diffraction can access fundamental information about these coherences. This is enabled by recent developments at free-electron lasers, working toward temporal resolution and single-molecule accessibility of scattering-based measurements. Time-resolved diffraction patterns of the isomerization of azobenzene are simulated. The process is monitored in time via the momentum-space signal, with a special focus on the mixed elastic/inelastic scattering from coherences. We give practical ideas on how this relatively weak contribution to the signal can potentially be retrieved. A direct connection to the real-space movie of the conical intersection dynamics is made, enabling the observation of quantum coherences that direct chemical processes.

Abstract

X-ray diffraction is routinely used for structure determination of stationary molecular samples. Modern X-ray photon sources, e.g., from free-electron lasers, enable us to add temporal resolution to these scattering events, thereby providing a movie of atomic motions. We simulate and decipher the various contributions to the X-ray diffraction pattern for the femtosecond isomerization of azobenzene, a textbook photochemical process. A wealth of information is encoded besides real-time monitoring of the molecular charge density for the cis to trans isomerization. In particular, vibronic coherences emerge at the conical intersection, contributing to the total diffraction signal by mixed elastic and inelastic photon scattering. They cause distinct phase modulations in momentum space, which directly reflect the real-space phase modulation of the electronic transition density during the nonadiabatic passage. To overcome the masking by the intense elastic scattering contributions from the electronic populations in the total diffraction signal, we discuss how this information can be retrieved, e.g., by employing very hard X-rays to record large scattering momentum transfers.

Diffraction signals reveal the momentum transfer experienced by an incident photon through interference with one or more scatterers. Traditionally, X-ray diffraction is used to determine the structure of crystalline matter. A momentum-space image, provided by the scattered photons, is recorded, allowing for the reconstruction of the real-space crystal structure. Diffraction patterns are dominated by the Bragg peaks, arising from the interaction of multiple scatterers in a long-range crystalline order. The relevant material quantity is the electronic charge density, from which the X-ray photons elastically scatter.

The advent of free-electron X-ray light sources (1, 2) has added two game-changing ingredients to diffraction experiments. The first is a peak brilliancy that can exceed third-generation synchrotron sources by nine orders of magnitude (3). The high number of photons in the beam allows for a significant reduction of the sample size, while still achieving the necessary ratio of scattered photons per object to record diffraction patterns. Structure determination of nanocrystals (4, 5), aligned gas-phase molecular samples (6), and macromolecular structures (7, 8) were reported. Attempts toward imaging single molecules at free-electron lasers were made (9), although some challenges remain (8). The second ingredient is temporal resolution, enabled by subfemtosecond pulse durations (1 fs = $10^{-15}$ s), also available from tabletop setups through, e.g., high harmonic generation (10) or laser-driven plasma sources (11). Time-resolved diffraction movies can monitor the electronic charge density evolution during a chemical process (12–19). A complementary technique is ultrafast electron diffraction, where the X-rays are replaced by bright electron pulses that scatter from the total (nuclear + electronic) charge density (20–24).

Diffraction from matter in nonstationary states, such as molecules undergoing a chemical transformation, involves physical processes that go beyond elastic scattering from instantaneous snapshots of the electronic ground state density. This is especially true for excited molecules, being in a time-evolving superposition of many-body states. Inelastic scattering from different electronic states (25–27), as well as electronic and vibrational coherences (27–30), contributes to the signal.

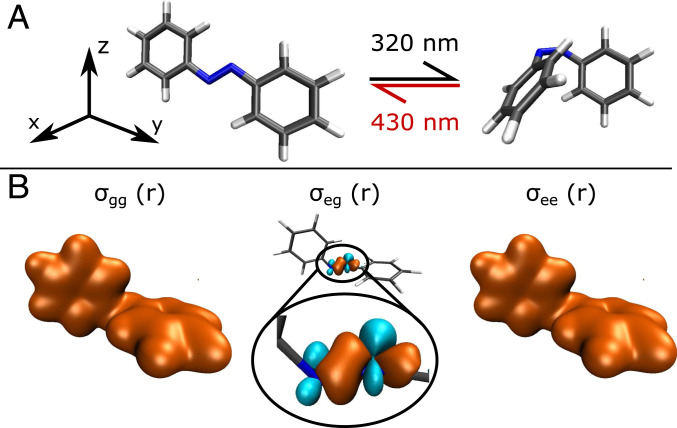
Here we study theoretically the diffractive imaging of vibronic coherences that emerge at conical intersections (CoIns). These are regions of degeneracy in electronic potential energy surfaces (PESs), where the movement of electrons and nuclei become strongly coupled, enabling ultrafast radiationless relaxation channels back to the ground state (31, 32). Processes like the primary event of vision (33) or the outcome of photochemical reactions (23), among many others, are determined by the occurrence and properties of CoIns. A textbook example of CoIn dynamics is the optical switching between cis and trans azobenzene (Fig. 1A): azobenzene can be switched selectively on a femtosecond timescale between both isomers (34–36) with high quantum yield, it exhibits interesting photophysics like a violation of Kasha’s rule (37, 38), and it has found broad application as the photoactive unit in switching the activity of pharmaceutical compounds (39) or neurons (optogenetics) (40). There is a large body of experimental and theoretical literature on azobenzene, and the previous references are by no means exhaustive. For a deeper overview of scientific progress about azobenzene photophysics, we refer the reader to ref. 38 and section 8 of its supplement.

Fig. 1.

Molecular structures and electron densities of azobenzene. (A) Isomerization scheme with the (Left) trans and (Right) cis geometry. Both processes can be selectively achieved with high quantum yield. In this work, we simulate the $\mathit{\text{cis}}\to \mathit{\text{trans}}$ process. (B) Real-space electronic densities at a structure close to the CoIn at 90° of CNNC torsion, with the ground state (96 electrons; Left), the transition state (1 electron; Middle), and the excited state (96 electrons; Right) density.

Three-vibrational-mode PESs for the photoisomerization of azobenzene were reported in ref. 41. The nuclear space consists of the carbon–nitrogen–nitrogen–carbon (CNNC) torsion angle and the two CNN bending angles between the azo unit and the benzene rings. CNNC torsion is the reactive coordinate that connects the cis and trans minima at 0° and 180°, respectively, while the two CNN angles are responsible for the symmetry breaking that leads to the minimum energy CoIn seam (41). We perform nuclear wave packet simulations of the $\mathit{\text{cis}}\to \mathit{\text{trans}}$ isomerization, yielding the total nuclear + electronic molecular wave function. Using the quantum-electrodynamical formalism for time-resolved diffraction signals developed in refs. 27 and 42, we follow the isomerization via its diffraction snapshots. The focus of this paper is on the coherence contributions to the diffraction signal and their distinctly different shapes and magnitudes compared to the other contributions. This results in a real-space movie of the molecular transition charge density at the CoIn.

Dissecting the Diffraction Signal into Pathways

We follow the derivation of the single-molecule time-resolved X-ray diffraction (TXRD) in refs. 27 and 42, using electronic $r$ and nuclear $R$ degrees of freedom. The single-molecule diffraction signal allows us to circumvent the domination of sharp Bragg peaks and retrieve the continuous patterns from individual molecules. An incident photon is scattered from the molecular electron density $\widehat{\sigma }\left(\mathbf{\text{q}}\right)$, i.e., the Fourier transform of the real-space density $\widehat{\sigma }\left(\mathbf{r}\right)$. The scattering vector $\mathbf{q}={\mathbf{k}}_s-{\mathbf{k}}_p$ represents the momentum transfer between the incident and scattered photon with wave vectors ${\mathbf{k}}_p$ and ${\mathbf{k}}_s$. Although $\widehat{\sigma }\left(\mathbf{\text{q}}\right)$ is a single-body electron operator, it acts in the joint nuclear + electronic space. Therefore, it depends on $R$ as well and remains an operator in the nuclear space after taking its matrix elements in the electronic subspace, i.e., $\widehat{\sigma }\left(\mathbf{\text{q}},\mathbf{\text{R}}\right)$. We expand the total time-dependent molecular wave function $\psi \left(\mathbf{r},\mathbf{R},t\right)$ in the adiabatic basis

$$\psi \left(\mathbf{r},\mathbf{R},t\right)=\sum _i{c}_i\left(t\right){\chi }_i\left(\mathbf{R},t\right)\phi \left(\mathbf{r},\mathbf{R}\right),$$ [1]

where ${\chi }_i\left(\mathbf{R},t\right)$ is the normalized nuclear wave packet in the adiabatic electronic state ${\phi }_i\left(\mathbf{r},\mathbf{R}\right)$, and $c_i$ is the electronic state amplitude. Eq. 1 is an exact representation which does not invoke the adiabatic approximation and can be similarly formulated in, e.g., a diabatic basis.

The one-molecule TXRD signal of a sample with $N$ noninteracting molecules reads (27)

$$S_1\left(\mathbf{q},T\right)\propto N\int dt|{\mathbf{E}}_{\mathbf{p}}\left(t-T\right){|}^2{\tilde{S}}_1\left(\mathbf{q},t\right),$$ [2]

with the delay time $T$, the X-ray probe pulse envelope ${\mathbf{E}}_{\mathbf{p}}\left(t-T\right)$, and time-dependent molecular response ${\tilde{S}}_1\left(\mathbf{q},t\right)$. Using two electronic states (a ground state $g$ and an excited state $e$), as we do it in our azobenzene Hamiltonian, ${\tilde{S}}_1\left(\mathbf{q},t\right)$ reads

$$\begin{array}{ccc}\hfill {\tilde{S}}_1\left(\mathbf{q},t\right)& ={\rho }_{gg}\left(t\right)\langle {\chi }_g\left(t\right)\left|{\widehat{\sigma }}_{gg}^{†}{\widehat{\sigma }}_{gg}\right|{\chi }_g\left(t\right)\rangle \hspace{1em}\hfill & \hfill \left(\mathrm{i}\right)\\ \hfill & \hspace{1em}+{\rho }_{ee}\left(t\right)\langle {\chi }_e\left(t\right)\left|{\widehat{\sigma }}_{ee}^{†}{\widehat{\sigma }}_{ee}\right|{\chi }_e\left(t\right)\rangle \hspace{1em}\hfill & \hfill \left(\mathrm{i}\mathrm{i}\right)\\ \hfill & \hspace{1em}+{\rho }_{gg}\left(t\right)\langle {\chi }_g\left(t\right)\left|{\widehat{\sigma }}_{ge}^{†}{\widehat{\sigma }}_{eg}\right|{\chi }_g\left(t\right)\rangle \hspace{1em}\hfill & \hfill \left(\mathrm{i}\mathrm{i}\mathrm{i}\right)\\ \hfill & \hspace{1em}+{\rho }_{ee}\left(t\right)\langle {\chi }_e\left(t\right)\left|{\widehat{\sigma }}_{eg}^{†}{\widehat{\sigma }}_{ge}\right|{\chi }_e\left(t\right)\rangle \hspace{1em}\hfill & \hfill \left(\mathrm{i}\mathrm{v}\right)\\ \hfill & \hspace{1em}+2\mathcal{R}\left[{\rho }_{eg}\left(t\right)\langle {\chi }_e\left(t\right)\left|{\widehat{\sigma }}_{ee}^{†}{\widehat{\sigma }}_{eg}\right|{\chi }_g\left(t\right)\rangle \right.\hspace{1em}\hfill & \hfill \left(\mathrm{v}\right)\\ \hfill & \hspace{1em}+\left.{\rho }_{eg}\left(t\right)\langle {\chi }_e\left(t\right)\left|{\widehat{\sigma }}_{eg}^{†}{\widehat{\sigma }}_{gg}\right|{\chi }_g\left(t\right)\rangle \right],\hfill \end{array}$$ [3]

where ${\rho }_{gg}$ and ${\rho }_{ee}$ are the electronic state populations, ${\rho }_{eg}$ is the coherence magnitude, and we write $\widehat{\sigma }=\widehat{\sigma }\left(\mathbf{q}\right)$ for brevity. Terms i and ii in Eq. 3 represent elastic scattering from the electronic ground and excited state, respectively, and use the state densities ${\widehat{\sigma }}_{ii}$ ($i=e,g$). They can also include inelastic contributions from vibrational coherences. Terms iii and iv describe inelastic scattering from these two states using the transition densities ${\widehat{\sigma }}_{eg}$. The last term (v) in Eq. 3, spanning lines five and six, represents scattering from vibronic coherences. It contains the nuclear wave packet of the two different states in $bra$ and $ket$, and its amplitude is given by the coherence magnitude ${\rho }_{eg}$. The latter process is of mixed elastic/inelastic nature and thus only detectable with a broadband detector, which is usually the case for XRD detectors. This detection bandwidth must be sufficient to cover the energy splitting of the wave packet overlap between the electronic states.

There are a few important points to note. First, as can be seen from Eq. 3, scattering does not simply occur from charge densities but from expectation values over products of charge density operators $⟨{\sigma }^{†}\sigma ⟩$ (in the limit of impulsive diffraction, where both interactions occur at the same time). This means that the real-space molecular structure may not be simply reconstructed from the inverse Fourier transform (${\mathcal{F}}^{-1}$) of the diffraction pattern, an issue that is related to the well-known phase problem in diffraction. According to the convolution theorem

$${\mathcal{F}}^{-1}\left[\widehat{\sigma }\left(\mathbf{q}\right)\widehat{\sigma }\left(\mathbf{q}\right)\right]=\widehat{\sigma }\left(\mathbf{r}\right)*\widehat{\sigma }\left(\mathbf{r}\right)\hspace{0.17em}\ne \hspace{0.17em}\widehat{\sigma }\left(\mathbf{r}\right)\widehat{\sigma }\left(\mathbf{r}\right),$$ [4]

the inverse Fourier transform does not yield the product of real-space densities but their convolution. This is called the Patterson function (43), often used in crystallography, that gives correlations between atomic or intermolecular distances rather than the real-space geometry. Additionally, the phase problem can be solved for successful real-space reconstruction, e.g., by oversampling (44–46) or by anomalous diffraction (47) in the resonant limit.

The second point to note is that Eq. 3 is exact and contains all contributions to the signal. This requires us to explicitly calculate $\widehat{\sigma }\left(\mathbf{\text{q}},\mathbf{\text{R}}\right)$ across the nuclear space, which can be a demanding task. Many theoretical frameworks use the independent atom model, where the total density of the molecule $\alpha$ is constructed by assigning form factors $f_a$ to each atom $a$ and summing over them:

$${\sigma }_{\alpha }\left(\mathbf{q}\right)=\sum _a\left|f_a\left(\mathbf{q}\right)\right|e^{i{\mathbf{q}\mathbf{R}}_a}.$$ [5]

This approximation can be helpful in describing elastic scattering or population dynamics (24, 48–50) but misses the coherence term in Eq. 3, which is our main focus. These have never been singled out from diffraction patterns, which allow for a direct observation of quantum coherences that determine the fundamental mechanisms of chemical reactions. For this purpose, we follow the complete formulation in Eq. 3 and compute $\widehat{\sigma }\left(\mathbf{\text{q}},\mathbf{\text{R}}\right)$ across the considered nuclear space (Materials and Methods and Eq. 9).

The third point connects to the structure factor that is responsible for the emergence of Bragg peaks. Diffraction patterns are usually recorded on an organized molecular assembly, i.e., a crystal. In these cases, the two scattering events in the diffraction signal (Eq. 3) do not occur from the electron density of a single molecule but from two different molecules $\alpha$ and $\beta$. Multiplication of two $\widehat{\sigma }\left(\mathbf{q}\right)$ from different molecules then contains the structure factor given by

$$F_{\mathbf{q}}=\sum _{\alpha }\sum _{\alpha \ne \beta }{e}^{-i\mathbf{q}\cdot \left({\mathbf{r}}_{\alpha }-{\mathbf{r}}_{\beta }\right)}.$$ [6]

The long-range, intermolecular order of the sample is thus the dominating contribution, and it is the primary information commonly extracted from diffraction experiments. Scattering from single molecules, as given by Eq. 3 and as investigated here, is conceptually different.

Azobenzene Quantum Dynamics

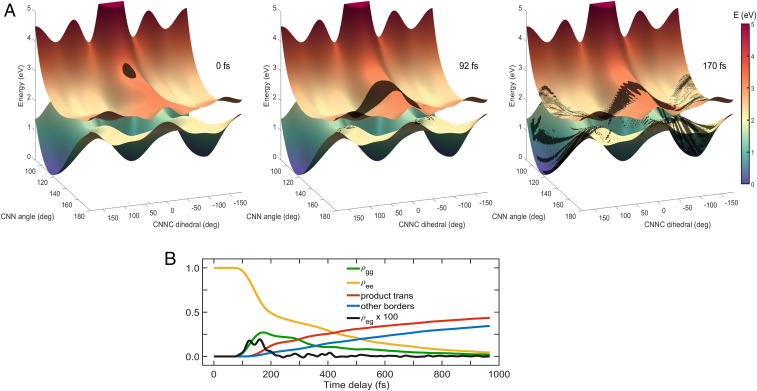
Our effective Hamiltonian for azobenzene $\mathit{\text{cis}}\to \mathit{\text{trans}}$ isomerization is based on the PESs reported in ref. 41, which includes three nuclear degrees of freedom. The first nuclear coordinate is the CNNC dihedral angle that captures the torsion between the two benzene rings. The trans geometry is located at 180° of torsion and the cis minimum close to 0°. The other two degrees of freedom are the CNN bending angles between the azo unit and the two respective carbon rings, where both the cis and trans minima are located between 115° and 120°. The two electronic states are the ground state S₀ and the $n{\pi }^{*}$ S₁ state, involving electronic excitation of a nitrogen lone-pair electron. The two potential minima at the cis (CNNC = 0°) and trans (CNNC = $\pm$180°) geometry in S₀ are separated by a 1.5-eV barrier. Barrierless isomerization is possible in S₁ with a CoIn located between the minima, where the electronic states become very close in energy with a significant nonadiabatic coupling. For the $\mathit{\text{cis}}\to \mathit{\text{trans}}$ isomerization, the minimum energy CoIn is located at around CNNC = 94° and requires symmetry breaking between the CNN angles, where one angle is at 140°, while the other CNN angle remains around 115°. In fact, the coupling region extends from CNNC = 80° to 110°, thus representing a CoIn seam rather than a singular point, which is asymmetric with respect to the torsion. Calculating and storing the electronic densities $\widehat{\sigma }\left(\mathbf{\text{q}},\mathbf{\text{R}}\right)$ across $\mathbf{R}$ with an appropriate $\mathbf{q}$ resolution requires us to reduce the nuclear space to two dimensions. We therefore constructed a two-dimensional nuclear space by fixing one of the CNN angles at 116° and keeping the other angle and the CNNC torsion. The resulting PESs are drawn in Fig. 2 and capture the $\mathit{\text{cis}}\to \mathit{\text{trans}}$ reactive pathway with the symmetry breaking CNN coordinate leading to the minimum energy CoIn.

Fig. 2.

PESs and nuclear wave packet snapshots during photoisomerization. (A) PESs of the S₁ and S₀ electronic states in the two-dimensional nuclear space. The nuclear wave packet starts in S₁ at the cis structure (0° torsion), assuming impulsive excitation. It reaches the CoIn at around 90° torsion and 140° of CNN bending at 90 fs. A vibronic coherence emerges in the course of the nonadiabatic passage. The wave packet bifurcates, and in the S₀ state, significant parts have reached the trans geometry at 170 fs. Periodic boundary conditions are employed along torsion in the excited state, while absorbing the wave packet at 180° torsion in the ground state due to having reached the product minimum. The complete movie is provided as electronic supplement (Movie S1). (B) Electronic state populations and coherence magnitude during the process. The nuclear wave packet relaxes from S₁ (yellow) to S₀ (green). The amount that has reached the trans geometry is drawn in red. Other parts of the wave packet exit the nuclear grid at CNN angles larger than 180°, a process that is not further captured or investigated. The coherence magnitude becomes nonvanishing at the CoIn passage starting from around 90 fs, after which it stays significant for 100 fs and then slowly decays.

We perform exact nuclear wave packet dynamics on these adiabatic PESs by solving the time-dependent Schrödinger equation (Materials and Methods). Assuming impulsive excitation, the wave packet starts in S₁ at the cis geometry (Fig. 2A, Left) and is initially localized in both nuclear degrees of freedom. Within the first few femtoseconds, it evolves to higher CNN angles and starts to spread along the CNNC torsion (Fig. 2A, Middle). Around 90 fs, it reaches the CoIn region and starts to relax to S₀. A vibronic coherence emerges that is initially localized at the CoIn, visible through the wave packet overlap in the two states (Fig. 2A, Middle). The coherence magnitude, along with the population dynamics, is drawn in Fig. 2B. After evolving away from the CoIn, the wave packet and thus the vibronic coherence are no longer local in the CNN angle but exhibit a spread there as well. This delocalized structure is visible in Fig. 2A, Right, showing both the local coherence before and around the CoIn and the spreading in CNN thereafter. Around 170 fs, the first significant parts of the wave packet have reached the trans geometry. After reaching the product minimum, the wave packet is absorbed at CNNC = $\pm$180°, and the photochemical reaction is completed. As can be seen in Fig. 2B, the product yield represented by the red line emerges slightly before 200 fs and accumulates thereafter. Some parts of the wave packet exit the nuclear grid at CNN $\ge$ 180°, a process that is not further captured by our Hamiltonian and thus acts as a loss channel (blue line in Fig. 2B). The important part of the CoIn dynamics happens before 300 fs, with the subsequently highly delocalized wave packet slowly completing the relaxation before 1 ps. Absorbing the nuclear wave packet at CNNC = $\pm$180° is an artificial measure that prevents it from leaving the product minimum again. In reality, most of the nuclear wave packet will be trapped there by, e.g., vibrational relaxation to other modes not contained in our Hamiltonian. Wave packet recurrence to the CoIn region might still happen, a process that will influence the observed kinetics in Fig. 2B and especially the coherence magnitude ${\rho }_{eg}$. In the diffraction patterns, we focus on the first 300 fs, i.e., the period of the primary CoIn dynamics. Since the first major parts of the nuclear wave packet reach the product minimum at around 170 fs, recurrences to the CoIn region are not expected before 250 fs, and thus, the kinetics and diffraction patterns before 300 fs should be accurate, which is also the time where ${\rho }_{eg}$ exhibits the greatest magnitude.

To image this process by TXRD, we computed the state and transition electron densities across our two-dimensional nuclear space. Examples are depicted in Fig. 1B at a geometry that is in the vicinity of the CoIn (CNNC = 92°, CNN = 140°). The state densities ${\widehat{\sigma }}_{gg}\left(\mathbf{r}\right)$ and ${\widehat{\sigma }}_{ee}\left(\mathbf{r}\right)$ look very similar, with a total of 96 electrons contributing. The transition density ${\widehat{\sigma }}_{eg}\left(\mathbf{r}\right)$ is much smaller, with only one electron contributing. It is mainly located around the nitrogen atoms, corresponding to the $n{\pi }^{*}$ character of the excitation. This gives one reason why elastic scattering usually dominates the inelastic contributions. Since the terms in Eq. 3 consist of products of $\widehat{\sigma }\left(\mathbf{\text{q}},\mathbf{\text{R}}\right)$ operators, this relative strength gets further amplified. In smaller and/or lighter molecules, where fewer electrons contribute to the elastic scattering, the relative strength of inelastic and mixed contributions will be larger.

Diffraction Pattern Snapshots during Isomerization

In the following, we assume diffraction from an oriented molecule. This can be achieved (6), although not to a perfect degree, but is experimentally more demanding than a randomly oriented sample. This means that in any case, the diffraction patterns presented in the following are ideal cases that in reality will be not as clear. In ref. 51, we have compared oriented versus nonoriented molecules in the simulation of a spectroscopic signal that targets vibronic coherences. The signal was visible in the isotropic case as well since one of the spatial directions was dominating the others. Diffractive imaging of coherences, as presented here, may exhibit a similar behavior. For a randomly oriented molecular sample, rotational averaging of the presented data must be performed, where we expect the diffraction patterns to look not as clean but still exhibiting the key features. We examine different $\mathbf{q}$-space directions separately to distinguish between their contributions. The molecular axes are defined in Fig. 1A, with the $x$ axis perpendicular to the molecular plane of the trans geometry, the $y$ axis going through both carbon rings and the $azo$ unit, and the $z$ axis going only through one carbon ring.

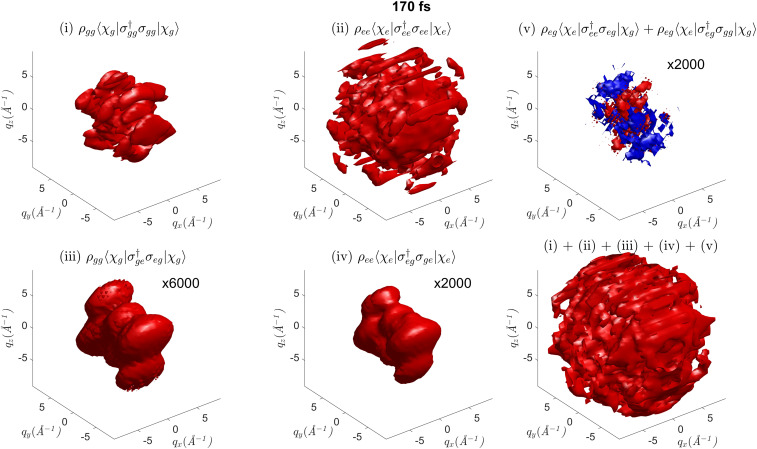
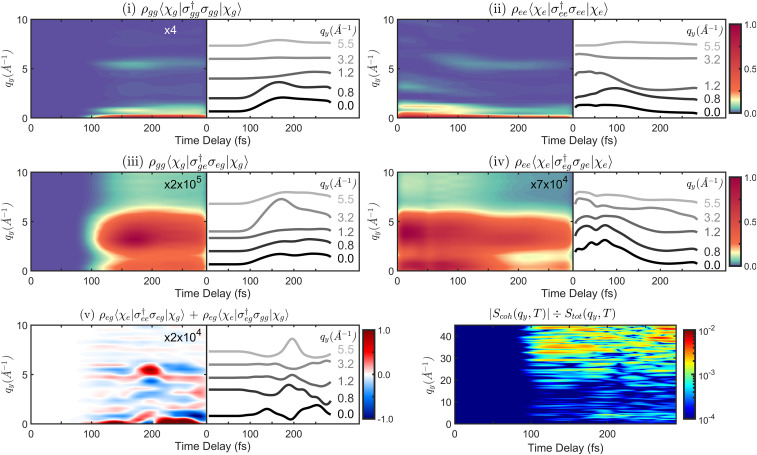
The complete three-dimensional diffraction pattern is presented in Fig. 3, dissected into the different contributions of Eq. 3 and labeled i through v accordingly. An exemplary snapshot at 170 fs is chosen because all contributions are nonvanishing there, while a complete movie is provided as electronic supplement (Movie S2). The two most interesting observations are the relative strengths of the individual terms and the distinct image of the coherence contribution. The dominant term is elastic scattering from the excited state ii since ${\rho }_{ee}$ is larger than ${\rho }_{gg}$ and ${\rho }_{eg}$ (compare populations in Fig. 2B). Ground state elastic scattering (term i) is weaker, although well visible. The inelastic scattering components (terms iii and iv) in Fig. 3 are around three orders of magnitude weaker than their elastic counterparts. This can be attributed to their scattering from the product of two transition density operators, each being around 100 times smaller than the state densities (1 electron versus 96 electrons). The coherence term v in Fig. 3, i.e., scattering from the vibronic coherence, is 2,000 times weaker than the total signal and equally strong as the inelastic scattering terms. In contrast to all other terms, the coherence scattering exhibits negative (blue) as well as positive (red) contributions. It also exhibits the most pronounced dynamic behavior (compare Movie S2) and will be discussed in the following.

Fig. 3.

The five contributions (i to v) to the X-ray diffraction pattern labeled according to Eq. 3 at 170 fs. The complete $\mathbf{q}$-space object is depicted, where $\mathbf{q}$ is the scattering vector of momentum transfer, and we assume an oriented molecule. Contribution i is elastic scattering from the electronic ground state S₀. Contribution ii is elastic scattering from the electronically excited state S₁. Contribution iii is inelastic scattering from S₀, scaled by a factor of 6,000. Contribution iv is inelastic scattering from S₁, scaled by a factor of 2,000. Contribution v is mixed elastic/inelastic scattering from vibronic coherences, scaled by a factor of 2,000. In contrast to the other terms, positive (red) and negative (blue) contributions are present. (Bottom Right) The total signal. The complete movie is provided as electronic supplement (Movie S2).

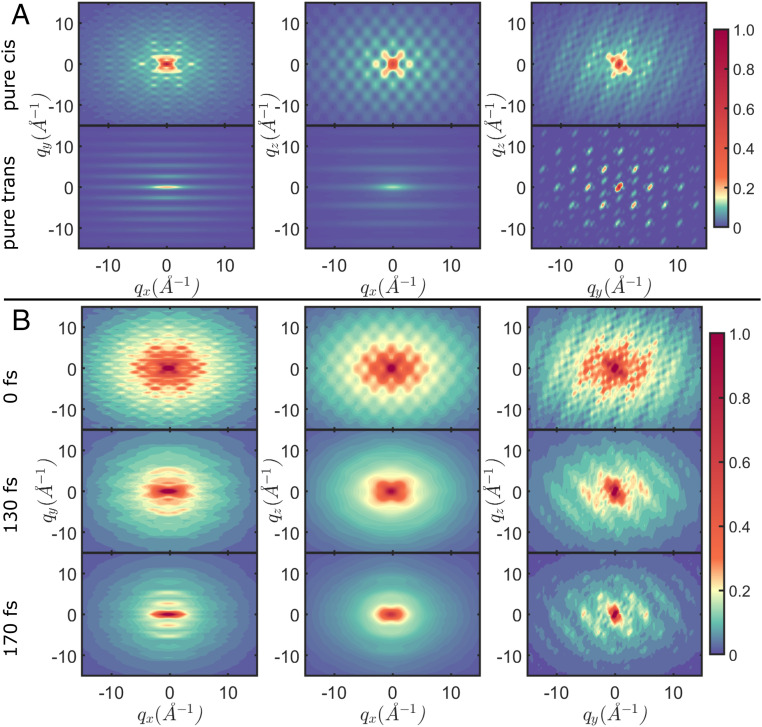
To get a better understanding of the diffraction patterns, two-dimensional projections obtained by integration over $q_x$, $q_y$, and $q_z$ are shown for the total signal in Fig. 4. For reference, this is done in Fig. 4A for the pure cis and trans geometries, without considering the nuclear wave packet. In all three planes, cis and trans exhibit distinctly different diffraction patterns. Snapshots at 0, 130, and 170 fs during the wave packet dynamics, and as calculated from Eq. 3, are depicted in Fig. 4B. At 0 fs, the pattern resembles the pure cis one because the wave packet starts here. This changes once major parts of the wave packet have moved away from the cis region toward the CoIn (130 fs). At 170 fs, where significant parts of the wave packet have reached the trans product minimum, the diffraction pattern exhibits the same features as the one for the pure trans geometry. In the ${\mathbf{q}}_x{\mathbf{q}}_y$ and ${\mathbf{q}}_x{\mathbf{q}}_z$ planes, the initially radial diffraction pattern changes to a vertically squeezed one with repeating peaks in vertical direction. In the ${\mathbf{q}}_y{\mathbf{q}}_z$ plane, the radial pattern narrows and exhibits peaks around 3 to 5 ${\AA }^{-1}$ of momentum transfer. This demonstrates how TXRD can monitor the photoisomerization in real time.

Fig. 4.

Two-dimensional diffraction patterns of the total signal (Eq. 3) in the ${\mathbf{q}}_{xy}$, ${\mathbf{q}}_{xz}$, and ${\mathbf{q}}_{yz}$ planes, while integrating over the respective other direction. The molecular axes are defined in Fig. 1(A. (A) Scattering from the pure cis (Top) and trans (Bottom) geometry. This is not observable, since spread of the nuclear wave packet is not accounted for, but serves as a reference. (B) Diffraction patterns at 0, 130, and 170 fs during the dynamics. The pattern at 0 fs resembles the pure cis geometry in A. A change in pattern is observed at 130 fs, where parts of the wave packet have passed the CoIn. At 170 fs, where a considerable amount of the wave packet has reached the product minimum, the diffraction pattern includes features from the pure trans pattern in A. The isomerization can be followed in real time. The complete movie is provided as electronic supplement (Movie S3).

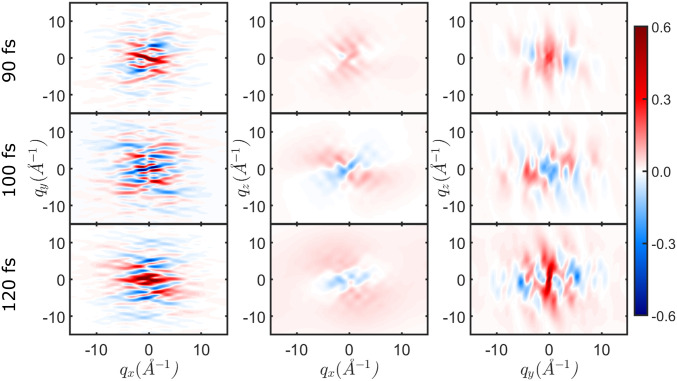
The evolution of the coherence term v in Eq. 3 in the two-dimensional projections is depicted in Fig. 5. It vanishes before 80 fs because the wave packet is purely in S₁, and there is no vibronic coherence yet. The latter emerges around 90 fs, when the CoIn is reached. The signal is strongest in the ${\mathbf{q}}_{xy}$ plane, with fast oscillations especially in ${\mathbf{q}}_y$ direction. During the CoIn dynamics, there occur phase changes in these oscillations, as can be seen when comparing the snapshots at 90, 100, and 120 fs in Fig. 5. These features are remarkably different from the total diffraction signal in Fig. 4.

Fig. 5.

Two-dimensional diffraction patterns of the coherence contribution (v in Eq. 3) in the ${\mathbf{q}}_{xy}$, ${\mathbf{q}}_{xz}$, and ${\mathbf{q}}_{yz}$ planes, while integrating over the respective other direction. The signal emerges at 90 fs, where a vibronic coherence builds up due to the CoIn passage. Phase changes between positive (red) and negative (blue) contributions can be observed in all three planes. The complete movie is provided as electronic supplement (Movie S4).

Time-Resolved Diffraction Traces

In the following, we present time-resolved traces of the diffraction pattern along ${\mathbf{q}}_y$. All observations discussed here can equally be made in ${\mathbf{q}}_x$ and ${\mathbf{q}}_z$. For the X-ray probe field, we use a 10-fs full width at half maximum of the intensity envelope. The population dynamics is much slower and can be observed with longer pulses as well (note though that we assume instantaneous scattering of both $\widehat{\sigma }$ interactions when deriving Eq. 2). The fast oscillations in the coherence contribution are captured by the 10-fs probe as well.

All contributions to the TXRD signal are presented in Fig. 6. The prominent features along ${\mathbf{q}}_y$ in ii are at 0, 1.2, 3.2, and 7.8 ${\AA }^{-1}$ momentum transfer. Between 50 and 120 fs, where the wave packet evolves away from the cis region and through the CoIn, the pattern changes. The 1.2 ${\AA }^{-1}$ feature decreases to 0.8 ${\AA }^{-1}$, the one at 3.2 ${\AA }^{-1}$ disappears, and a new one at 5.5 ${\AA }^{-1}$ emerges. The elastic ground state scattering (term i) vanishes before 90 fs as there is no wave packet in S₀. The main features are located at 0, 0.8, and 5.5 ${\AA }^{-1}$, similar to the S₁ pattern after 120 fs. This is not surprising, as ${\widehat{\sigma }}_{gg}\left(\mathbf{r},\mathbf{R}\right)$ and ${\widehat{\sigma }}_{ee}\left(\mathbf{r},\mathbf{R}\right)$ look very similar in real space (compare Fig. 1B), and the nuclear wave packet explores similar regions in $\mathbf{R}$. The inelastic scattering contributions iii and iv in Fig. 6 are much weaker. Their strongest feature shows up at 4 ${\AA }^{-1}$ instead of 0 ${\AA }^{-1}$, reflecting the inelastic nature of the scattering process. They are expected to be better visible in the total signal for chemical systems with fewer electrons.

Fig. 6.

Time-resolved diffraction signal (Eqs. 2 and 3) using a 10-fs full width at half maximum probe pulse. We display the ${\mathbf{q}}_y$ direction at $q_x$ = $q_z$ = 0, while similar observations can be made in all three directions. Signal contributions are scaled by the indicated factors and sorted similar to Fig. 3. Horizontal slices at characteristic ${\mathbf{q}}_y$ values are given next to each diffraction pattern. Contributions i and ii are elastic scattering from ground and excited state. Contributions iii and iv are inelastic scattering from ground and excited state. The elastic and inelastic S₀ signal contribution is zero before 100 fs due to no population and emerges after 100 fs with the wave packet relaxing to this state. In these four contributions, a distinct change in the diffraction pattern can be observed around 100 fs, where significant parts of the wave packet have left the cis side of the PES and evolve to the trans side. Contribution v is mixed elastic/inelastic scattering from the vibronic coherence (fifth term in Eq. 3). (Bottom Right) Ratio of the strength of the coherence contribution vs in the total signal, indicated with a logarithmic color scale. Being around ${\mathrm{10}}^4$ times weaker at low values of ${\overrightarrow{q}}_y$, it gets gradually stronger at higher values and is only ${\mathrm{10}}^2$ times weaker at ${\mathbf{q}}_y\simeq$ 40 ${\AA }^{-1}$.

Our nuclear wave packet simulations assume an initial optical excitation of 100% into S₁. Experimentally, this can require very high pulse intensities, where multiphoton absorption channels not only contribute but dominate. In reality, it is rather a small fraction that will be excited to S₁ to stay in the linear regime (18, 19). This means that unlike our simulations, the ground state diffraction contribution is not zero before 100 fs but more likely the dominating one. This does not affect the qualitative features in the excited state diffraction pattern, and especially in the coherence contribution that we focus on, but can add a large experimental background that needs to be addressed.

Isolating the Coherence Term

The coherence term, which emerges as a feature unique to the CoIn, is shown in Fig. 6. Again, it exhibits positive (red)/negative (blue) temporal oscillations at each $q_y$. The strongest features are at 0 and 5.5 ${\AA }^{-1}$. Ideally, one would like to isolate this feature from the total diffraction signal to record a $\mathbf{q}$-space movie of the CoIn dynamics. However, it is significantly weaker and masked by the elastic scattering, especially at low values of $q_y$. The situation improves when going to higher momentum transfer. To illustrate this, the ratio of the coherence term to the total signal is drawn in Fig. 6F with a logarithmic color scale. At $q_y\le$ 20 ${\AA }^{-1}$, this ratio is between 1 $\times 10^{-4}$ and 5 $\times 10^{-4}$, with an exception at 200 fs and 4 ${\AA }^{-1}$. At 30 ${\AA }^{-1}$ and above, the ratio goes up to 1 $\times 10^{-2}$, meaning that the coherence term is only 100 times weaker than the total signal here. This can be explained by the transition densities ${\widehat{\sigma }}_{eg}$ being more confined in $r$ space than the diagonal state densities (compare Fig. 1A), and thus having a wider spread in $\mathbf{q}$, which is a feature that can be generally expected in many molecules. Going to these momentum transfer amplitudes requires pulse energies between 30 and 40 keV. Currently, up to 25 keV are possible using superconducting accelerators at the European X-ray Free Electron Laser in Hamburg and the Stanford Linear Coherent Light Source (1).

Another tool that may be used to retrieve the coherence term is frequency-resolved detection. By frequency-dispersing the scattered photons, inelastic (Stokes and Anti-Stokes) contributions can be measured separately at different frequencies. In the single-scatterer case described by Eq. 2, the coherence term is a mixed elastic/inelastic process. This means that such separation is not straightforward, since one of the two photon amplitudes is scattered elastically and the other one inelastically. They thus arrive at the detector with different frequencies, and the coherence term can only be recorded by detecting both photons with a broadband detector. Separation of the coherence term could be achieved by measuring the total signal with a broadband detector and subsequently subtracting the purely elastic and purely inelastic events measured in a separate experiment with a frequency-resolved detection. Other possibilities entail stochastic covariance-based measurements (52, 53) or using entangled photons (54).

Frequency-resolved measurement to single out the coherence term can be more easily performed in the two-molecule diffraction signal (27, 42). This dominates when long-range molecular order is present in the sample and is not applicable in our example since the Hamiltonian for azobenzene isomerization was constructed for the gas phase, with no environmental influence. Nevertheless, the molecular response in the TXRD signal for the two-scatterer case reads (27, 42)

$$\begin{array}{cc}\hfill S_2\left(\mathbf{q},t\right)\propto F\left(q\right)\int & dt|{\mathbf{E}}_{\mathbf{p}}\left(t-T\right){|}^2\hfill \\ \hfill & \hspace{1em}|{\rho }_{gg}\langle {\chi }_g\left(t\right)|{\widehat{\sigma }}_{gg}|{\chi }_g\left(t\right)\rangle \hfill \\ \hfill & +{\rho }_{ee}\langle {\chi }_e\left(t\right)\left|{\widehat{\sigma }}_{ee}\right|{\chi }_e\left(t\right)\rangle \hfill \\ \hfill & +2\mathcal{R}\left[{\rho }_{eg}\langle {\chi }_e\left(t\right)\left|{\widehat{\sigma }}_{eg}\right|{\chi }_g\left(t\right)\rangle \right]{|}^2.\hfill \end{array}$$ [7]

The amplitude in Eq. 7 can be obtained by solving the phase problem. The only inelastic contribution in Eq. 7 is the coherence term in line four, and in this case it does not include elastic contributions. It can more easily be separated than in the one-scatterer case, although care has to be taken with the influence of the structure factor and the physics of CoIns with intermolecular interactions.

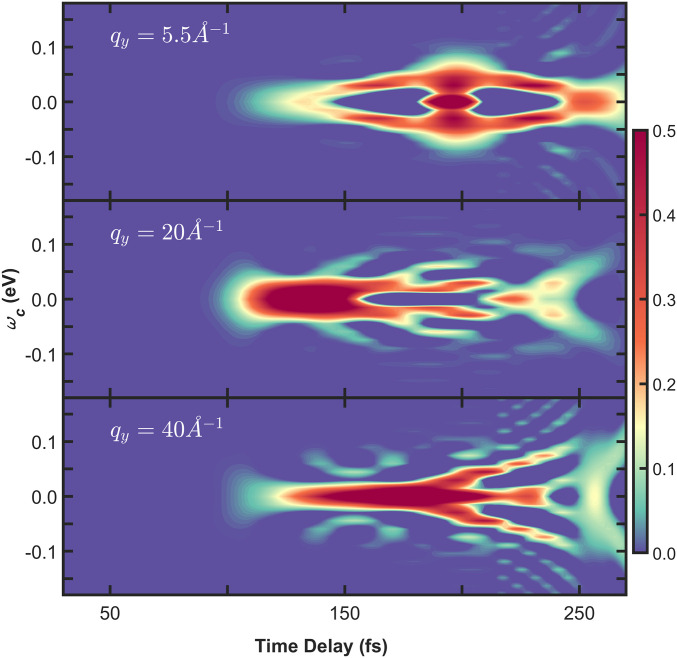
In ref. 51, we have introduced the Wigner time/frequency spectrogram of a spectroscopic signal that reveals detailed information about the coherence pathway on the molecular PES and the energetic distribution of the participating vibronic states. The diffraction image of the vibronic coherence in Fig. 6 (term v) similarly exhibits temporal oscillations with a certain frequency. In this case, it is not the energy splitting between the adiabatic states that is encoded but the phase evolution of the electronic transition density, from which the scattered photons are recorded. The Wigner spectrogram is given by

$$\begin{array}{cc}\hfill W\left(T_c,{\omega }_c\right)& \hspace{0.17em}=\hfill \\ \hfill \int \hspace{0.17em}\mathrm{d}\tau & S\left(T_c+\frac{\tau }{2}\right)\hspace{0.17em}S\left(T_c-\frac{\tau }{2}\right)\hspace{0.17em}{\mathrm{e}}^{-\mathrm{i}{\omega }_c\tau },\hfill \end{array}$$ [8]

where $S\left(T\right)$ is the signal trace at a specific ${\mathbf{q}}_y$. Three different spectrograms are shown in Fig. 7 for temporal signal traces at ${\mathbf{q}}_y=$ 5.5, 20, and 40 ${\AA }^{-1}$. They exhibit similar qualitative features. After emerging at 100 fs between 0 and 0.05 eV, a spread to higher ${\omega }_c$ values can be observed at 150 fs. The transient frequency by which the electronic transition density switches its phase during the nonadiabatic passage can be read from the spectrograms. Since all three spectrograms exhibit the same qualitative features, this connects well with our proposal to detect the coherence term at high momentum transfer without loss of detail. We stress that this information is not accessible by optical techniques, which detect (transition) dipoles and not the spatial profile of (transition) densities. Moreover, spectroscopic signals rely on the optical accessibility of states, which is subject to selection rules and dipole magnitudes. Scattering from electron densities by off-resonant X-ray diffraction is ubiquitously applicable.

Fig. 7.

Wigner representation (Eq. 8) of the coherence diffraction image in Fig. 6. For the spectrogram in Top, a temporal slice was taken from term (v) in Fig. 6 at 5.5 ${\AA }^{-1}$ momentum transfer. The spectrograms in Middle and Bottom were calculated from temporal traces at 20 and 40 ${\AA }^{-1}$ accordingly.

Real-Space Reconstruction

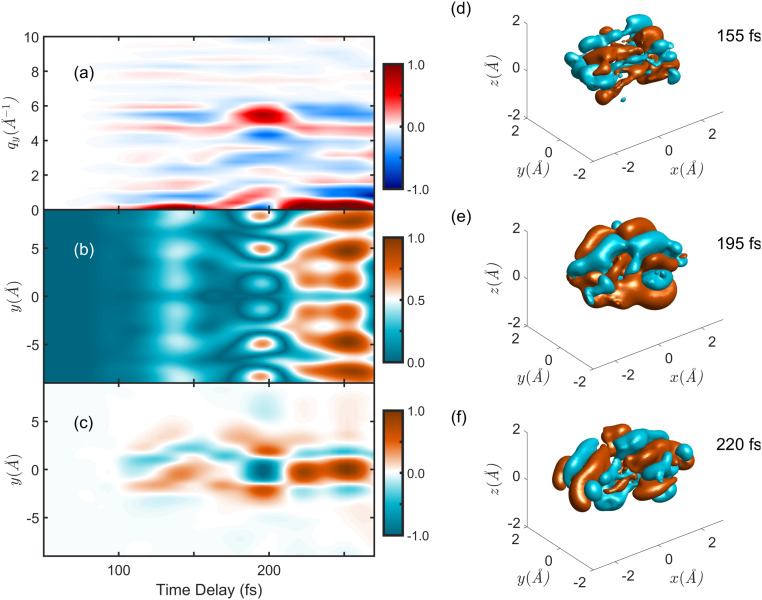
The ultimate goal of ultrafast photochemistry is to record movies of CoIn dynamics in real space. As mentioned above, the inverse Fourier transform of the diffraction image does not yield the real-space image. It yields the Patterson function (43), which shows correlations between atomic positions or interatomic distances rather than the full real-space molecular geometry. Additionally, for a correct inversion of the diffraction pattern, the phases of the photons that are lost upon measurement need to be recovered (47). Nevertheless, we can perform a naive inverse Fourier transform of the coherence term v and compare it to the real-space image that we have access to through simulations (although not experimentally observable and not given by the Patterson function). This is shown in Fig. 8, with the coherence term further noted as $S_{1,\left(\mathrm{v}\right)}\left(\mathbf{q},t\right)$, in Fig. 8A. Fig. 8B displays the naive inverse Fourier transform along ${\mathbf{q}}_y$, i.e., ${\mathcal{F}}^{-1}\left[{\tilde{S}}_{1,\left(\mathrm{v}\right)}\left(\mathbf{q},T\right)\right]$. The temporal oscillation pattern is preserved. In Fig. 8C, we compare this to the real-space picture of the transition density, which we have calculated by $⟨{\chi }_e\left(t\right)\left|{\sigma }_{ge}\left(\mathbf{r}\right)\right|{\chi }_g\left(t\right)⟩$, i.e., the expectation value of the real-space transition density across the nuclear space. Upon integration over $\mathbf{x}$ and $\mathbf{z}$, we get the time-resolved evolution of the transition density along $\mathbf{y}$. Again, the temporal oscillation pattern, i.e., the phase change of the electronic transition density during the CoIn dynamics, matches ${\tilde{S}}_{1,\left(\mathrm{v}\right)}\left(\mathbf{q},T\right)$ in Fig. 8A and ${\mathcal{F}}^{-1}\left[{\tilde{S}}_{1,\left(\mathrm{v}\right)}\left(\mathbf{q},t\right)\right]$ in Fig. 8B. This is also visible in the complete three-dimensional snapshots of $⟨{\chi }_e\left(t\right)\left|{\sigma }_{ge}\left(\mathbf{r}\right)\right|{\chi }_g\left(t\right)⟩$ in Fig. 8 D–F. Looking along $y$, the phase between positive (orange) and negative (teal) density changes from 155 to 195 fs and again to 220 fs. This matches the observations at these times in Fig. 8 A–C. Thus, by imaging the diffraction pattern of the vibronic coherence, fundamental information about the CoIn itself can be retrieved.

Fig. 8.

Transforming the q-space diffraction pattern to the real-space image. (A) Mixed elastic/inelastic scattering from the vibronic coherence (fifth term in Eq. 3). (B) Absolute value of the inverse Fourier transform of A along ${\mathbf{q}}_y$. (C) Real-space picture of the transition density $⟨{\chi }_e\left(t\right)\left|{\sigma }_{ge}\left(\mathbf{r},\mathbf{R}\right)\right|{\chi }_g\left(t\right)⟩$ along the $\mathbf{y}$ molecular axis, integrated over the nuclear space $\mathbf{R}$. The changes in phase between positive (orange) and negative (blue) are visible in both the ${\mathbf{q}}_y$ diffraction pattern, that is, the experimentally observable case, and the naive real-space reconstruction in B. (D–F) Snapshots of the transition density $⟨{\chi }_e\left(t\right)\left|{\sigma }_{ge}\left(\mathbf{r},\mathbf{R}\right)\right|{\chi }_g\left(t\right)⟩$ at 155, 195, and 220 fs. The transition density ${\sigma }_{ge}\left(\mathbf{r},\mathbf{R}\right)$ corresponds to an $n\pi *$ excitation from the nitrogen lone pair (compare Fig. 1B), and thus, the integral over the nuclear space shown here resembles this structure. The phase switch along $q_y$ that is observable here is reflected in the diffraction pattern and reconstruction. The complete movie is provided as electronic supplement (Movie S5).

Summary

We have simulated the TXRD for the $\mathit{\text{cis}}\to \mathit{\text{trans}}$ photoisomerization of azobenzene. Exact nuclear wave packet simulations, performed on high-level reduced-dimensional ab initio PESs, capture the complete (electronic and nuclear) many-body molecular wave function during the isomerization process. The latter involves a CoIn passage, where vibronic coherences emerge. These cause distinct features in the diffraction pattern, which we simulate by employing a rigorous quantum-electrodynamical framework.

Within 200 fs, the time-resolved diffraction signal changes from exhibiting pure cis isomer features to closely resembling the trans isomer. This clearly monitors the photochemical reaction process. The signal is dominated by elastic diffraction from the electronic S₁ and S₀ states. Mixed elastic/inelastic scattering from the vibronic coherence is significantly weaker, but its ratio can be amplified by two orders of magnitude when looking at high values of scattering momentum transfer. This requires very hard X-ray pulses above 20 keV, motivating further development at the large free-electron laser facilities. The high energy and short wavelengths needed to observe this contribution are currently readily available with electron diffraction (15, 23, 24). Scattering of electrons exhibits similar terms to the X-ray case and contains additional information due to scattering from nuclei. Electron diffraction analogs of the present study are being developed.

The momentum-space coherence contribution to the diffraction signal exhibits distinct temporal oscillations. These closely resemble the real-space evolution and phase modulation of the transition charge density during CoIn relaxation. Although this cannot be directly retrieved from the diffraction pattern, the fundamental physical information is encoded in this coherence term. Recording this feature will constitute a large step toward imaging movies of CoIn dynamics. This image goes beyond the accessibility of vibrational coherences by optical methods and will help in deciphering the basic mechanisms that direct photochemical reactions.

Materials and Methods

Ab Initio Quantum Chemistry.

The PES for azobenzene photoisomerization was reported in ref. 41 and mapped in a space of three nuclear degrees of freedom: the CNNC torsion (cis and trans minimum at 0° and $\pm$180°, respectively) and two CNN bending angles between the $azo$ unit and the two respective benzene rings. For the $\mathit{\text{cis}}\to \mathit{\text{trans}}$ direction, we fixed one of the CNN angles at 116°, while keeping the other angle and the CNNC torsion flexible. Both the educt and product minima, as well as the reactive CoIn pathway, are contained in this Hamiltonian. Quantum chemical calculations were performed using the multistate Restricted Active Space Self Consistent Field and the Second-Order Perturbation Theory Restricted Active Space modules of the MOLCAS8 program (55) and the “Atomic Natural Orbital Large Valence Double Zeta Polarized” (ANO-L-VDZP) basis set (56). An active space of 18 electrons in 16 orbitals was employed, including all $\pi$ and $\pi *$ orbitals and the two nitrogen lone pairs. The two involved excited states are the electronic ground state S₀ and the first excited state S₁ involving an $n\to \pi *$ excitation. A fitting function to obtain smooth surfaces from these calculations is given in ref. 41.

Nonadiabatic coupling matrix elements, accounting for the CoIn dynamics, were computed on the same level of theory, by displacing the molecular structure along the two internal coordinates at each grid point. They are nonvanishing in the region between CNNC = 80° to 110° and CNN = 133° and 147°. Instead of a single point, an extended CoIn seam is present with slight asymmetry in the CNNC torsion, and that is reached by symmetry breaking of the CNN angles.

Electronic Densities.

Following the electronic structure calculations, the state and transition densities ${\sigma }_{ij}\left(q,R\right)$ were evaluated in 2° increments in CNNC between 0° and 360° torsion and CNN bending between 80° and 180° (a total of 9,180 grid points). They were evaluated from the state specific charge density matrices $P_{rs}^{ij}$ according to

$${\sigma }_{ij}\left(\mathbf{q},\mathbf{R}\right)=\int dr{e}^{-i\mathbf{q}\cdot \mathbf{r}}\sum _{rs}{P}_{rs}^{ij}\left(\mathbf{R}\right){\varphi }_r^{*}\left(\mathbf{r},\mathbf{R}\right){\varphi }_r\left(\mathbf{r},\mathbf{R}\right),$$ [9]

using the basis set of atomic orbitals ${\varphi }_r\left(\mathbf{r}\right)$. Using the ANO-L-VDZP, there are a total of 246 ${\varphi }_r\left(\mathbf{r}\right)$ for azobenzene (14 for each nitrogen and carbon and 5 for each hydrogen). All 96 electrons of azobenzene contribute to the diagonal state densities ${\sigma }_{ii}$, while the transition density consists of one electron located in the nitrogen lone pairs (Fig. 1A).

Wave Packet Simulations.

Exact quantum dynamical simulations in the reduced-dimensional space of two reactive coordinates were performed by solving the time-dependent Schrödinger equation

$$i\hslash \frac{\partial }{\partial t}\psi =Ĥ\psi =\left[{\widehat{T}}_q+\widehat{V}\right]\psi .$$ [10]

on a spatial grid with 600 grid points in CNNC and 256 in CNN. The Chebychev propagation scheme (57) was used to numerically propagate the vibrational ground state wave function of S₀ after impulsive excitation to S₁ with a time step of 0.05 fs. The TXRD signal in Eqs. 2–3 was evaluated with a 1-fs time step. The kinetic energy operator ${\widehat{T}}_q$ in Eq. 10 is set up according to the G-Matrix formalism (58) in $M=2$ reactive coordinates $r$ and $s$ as described in ref. 59.

$${\widehat{T}}_q\simeq -\frac{{\hslash }^2}{2m}\sum _{r=1}^M\sum _{s=1}^M\frac{\partial }{\partial q_r}\left[G_{rs}\frac{\partial }{\partial q_s}\right]$$ [11]

with the G-Matrix computed via its inverse elements

$${\left(G^{-1}\right)}_{rs}=\sum _{i=1}^{3N}{m}_i\frac{\partial x_i}{\partial q_r}\frac{\partial x_i}{\partial q_s}.$$ [12]

In the S₁ state, periodic boundary conditions are employed along the CNNC torsion. A Butterworth filter (60) was used to absorb the nuclear wave packet at the borders in the CNN direction to prevent artifacts. In S₀ the filter was also employed at 0° and 360° of torsion, to absorb the parts of the wave packet that have reached the product minimum.

Data Availability.

All study data are included in the article and SI Appendix.