Graphical abstract
Keywords: SARS-CoV-2, COVID-19, Origin, Epidemics, Viral invasion, Herd immunity
Abstract
A virus that can cause a global pandemic must be highly adaptive to human conditions. Such adaptation is not likely to have emerged suddenly but, instead, may have evolved step by step with each step favored by natural selection. It is thus necessary to develop a theory about the origin in order to guide the search. Here, we propose such a model whereby evolution occurs in both the virus and the hosts (where the evolution is somatic; i.e., in the immune system). The hosts comprise three groups – the wild animal hosts, the nearby human population, and farther-away human populations. The theory suggests that the conditions under which the pandemic has initially evolved are: (i) an abundance of wild animals in the place of origin (PL0); (ii) a nearby human population of low density; (iii) frequent and long-term animal-human contacts to permit step-by-step evolution; and (iv) a level of herd immunity in the animal and human hosts. In this model, the evolving virus may have regularly spread out of PL0 although such invasions often fail, leaving sporadic cases of early infections. The place of the first epidemic (PL1), where humans are immunologically naïve to the virus, is likely a distance away from PL0. Finally, this current model is only a first attempt and more theoretical models can be expected to guide the search for the origin of SARS-CoV-2.
1. Introduction
The pandemic coronavirus disease 2019 (COVID-19) is caused by the virus severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). By now, the number of scientific reports has been astounding, covering almost all aspects of COVID-19 [1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11], [12], [13], [16], [14], [15]. Among the questions, the origin may be the most intriguing and controversial one. Where, when, and how did the pandemic originate? Although these questions are flooding the public domains, few seem to realize how loaded these questions are. The popular concept of the origin of SARS-CoV-2 is a non-evolutionary one. The idea is to search for animals that harbor the human SARS-CoV-2; a successful find would then define the place of origin. According to this logic, one could conclude that Bronx Zoo in New York City is the place of origin, as some wild animals there are known to harbor the same SARS-CoV-2 strain as in humans [17]; however, the transmission is more likely from humans to these animals, not the other way around. Thus, the origin needs to be defined conceptually before one starts looking for it.
The analyses of previous epidemics, like the SARS of 2002–2003, do offer a guide to trace the origin. There have been many models on the spillover of the viral pathogens from the animal hosts to humans [18], [19], [20], [21], [22]. For example, Plowright et al. [22] proposed detailed ecological models attempting to define the parameters that permit cross-species transmissions to happen. The number of parameters is very large including the viral shedding rate, infection intensity, pathogen pressure, pathogen survival, host immunity, and a host of other parameters.
These models are mainly concerned with the ecological conditions under which the spillover takes place. The origin of a pandemic is, however, about how these ecological conditions come into existence. Here, we introduce a co-evolutionary genetic model for the evolution of SARS-CoV-2 in the incipient stage of the pandemic. We assume that many of the ecological parameters such as the shedding rate, infection intensity, and host immunity are genetically (or epigenetically) defined. The task is then to see whether the new alleles can be fixed and, if it cannot be fixed, whether it can be maintained in the population long enough for other mutants to emerge.
Our model incorporates elements common to many epidemics that include HIV, influenza A, and SARS [23], [24], [25], [26], [27], [28]. Briefly, for a viral strain in wild animals to acquire the multiple changes necessary for the high infectiousness in humans, there must be an evolutionary mechanism that can confer a selective advantage in each step of the evolution. By this mechanism, a string of slight improvements adds up to a complex trait in the spirit of the “blind watchmaker” [29]. For example, the SARS virus of 2002–2003 has 5 non-synonymous changes in the receptor-binding domain (RBD) of the S protein vis-à-vis their putative ancestor found it the wild animals [27], [30].
In this view, the “origin of SARS-CoV-2” should be an evolutionary process that would take some time to complete. In fact, there may be several distinct evolutionary processes—the evolution of the viral genome in wild animal hosts and the further evolution in humans. Furthermore, the immune responses in the animal hosts and humans add further complexities. The development of immunity can be considered somatic evolution of the immune system [31], [32]. These processes happen on a short time scale relative to the evolutionary processes of the germline.
Finally, a companion study by Ruan et al. [33] on the founder population size concludes that outbreaks are often started by 5–10 infected travelers. Hence, once SARS-CoV-2 has evolved in its place of origin (PL0 for short), the fully evolved strain may easily spread elsewhere by a few travelers. The epidemics erupt outside of (rather than within) PL0 because the outside populations have not gained the host immunity.
2. The outline of the model
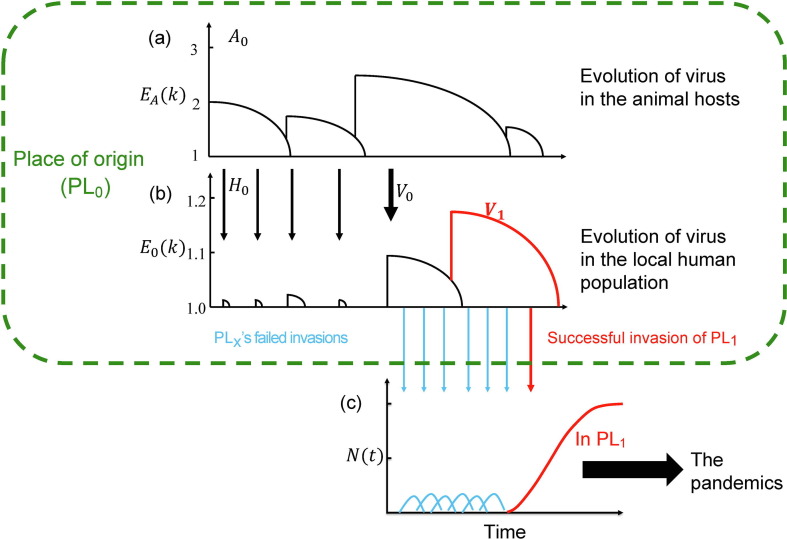
Fig. 1 is a model tracing the early evolution of SARS-CoV-2 in PL0 that eventually unleashes the global pandemic. As stated, the model, although a strictly theoretical construct, is based on observations reported for earlier epidemics of HIV, influenza A, and SARS [23], [24], [25], [26], [27], [28]. The terms and symbols central to this model are summarized in Table 1 . In PL0, there should be an abundance of wild animals in which the virus has evolved step-by-step over a prolonged period of time. Such a place, possibly a wildlife reserve or a remote countryside, might generally have a local human population (referred to as H 0) of low density.
Fig. 1.
A model for the origin and early evolution of the epidemics. (a, b) The evolution of the virus in the place of origin (PL0; inside the green box). (c) The invasion outside of PL0.
Table 1.
Definition of symbols and terms.
| Items | Meaning |
|---|---|
| Subscript | 0 = place of origin; 1 = place of first epidemic |
| Locale | PL0 = place of origin with wild animals and local human population PL1 = place of the first epidemic PLx = places of failed invasion by the virus prior to the first epidemic |
| Host population |
H0 = the human population in PL0 A0 = the collection of wild animal populations in PL0 |
| Viral strain |
V0 = the first viral strain from the animal hosts that can sustain itself in H0 long enough to acquire adaptive mutations V1 = the first viral strain that evolves from V0 to attain high infectiousness in H0 |
| Infectiousness |
k = the number of individuals each carrier can infect in a defined time period with mean and variance of E(k) and V(k) E(k; t) = E(k) may vary with time as the hosts develop immunity E0(k) is E(k) with the subscript designating the H0 population EA(k) is E(k) with the subscript designating the A0 population |
| Number of infected individuals |
N(t) at time t. N(0) is the initial number of infection u = the probability of ultimate extinction when N(t) = 0 for some t = time of infection until extinction = the cumulative number of infections across generations |
| Immunity | z controls the rate of developing immunity in the host population as a function of time |
We model the infectiousness of the virus in both the animal hosts and humans. As in the companion study [33], the infectiousness is expressed by the distribution of k, which is the number of individuals a carrier will infect in a time period (see below). The population dynamics of the virus depends on the distribution of k, in particular, its mean (E(k)) and variance (V(k)). E(k) is closely related, but not identical, to the key epidemiological parameter R 0 [33]. The population size of the virus at time t is N(t), defined as the number of infected individuals in the host population.
Fig. 1a depicts the evolution of the virus in animal hosts (referred to as A 0). Here, the hosts may be a species (say, of bats) or more than one species of wild animals among which the virus circulates. The infectiousness is expressed as EA(k) where A denotes the wild animals. EA(k) would increase when the virus acquires an adaptive mutation and would decrease as the host develops the herd immunity. The process depicted in Fig. 1a is in the evolutionary time scale and only the most recent events are shown. Also, EA(k) is>1 as a virus with EA(k) ≤ 1 would be quickly eliminated (see below).
In Fig. 1b, the spread of the virus from the animal hosts to H 0 is depicted. As the virus evolves, it may have invaded H 0 multiple times (indicated by thin arrows) but failed to trigger an epidemic. Because natural selection has been continuously working in the animal hosts (but not in humans), higher infectiousness in the wild animal hosts than in H 0 is expected. Hence, E 0(k) > 1 is rare and failed invasions should be common (E 0(k) denotes the viral infectiousness in H 0). The failed invasions may nevertheless cause the gradual build-up of herd immunity in H 0. Thus, the trend of E 0(k) in H 0 goes down, similar to that in the animal hosts.
The crucial step for the virus to infect humans is the emergence of a proto-human virus, as shown by the thick arrow in the middle of Fig. 1b. This proto-human strain, V 0, has an E 0(k) > 1 albeit unlikely to be much larger. For that reason, V 0 may sustain the infection in H 0 long enough to acquire new mutations for further enhancement of infectiousness in humans. The duration of the infection and the total number of infections will be the crux of the theory developed in this study. We shall designate the first new strain selected for the spread in humans as V 1 (shown by the red line). Over a period of time, herd immunity would develop in H 0 to suppress V 1, which is thus expected to appear and then disappear from H 0.
Fig. 1c portrays the invasion of the virus outside of PL0 by tracking the viral population size changes (N(t)). Outside of PL0, V 1 (or even V 0) would be more infectious than in H 0 as those other populations are immunologically naïve. Nevertheless, many invasions may have failed (blue arrows in Fig. 1c) before the first epidemic appears. The probability of failed invasions can be calculated. The failed invasions may leave a few sporadic cases dated before the onset of the global pandemic. Eventually, V 1 would trigger the first epidemic (the red arrow and red line of Fig. 1b and c) in a place referred to as PL1. In this view, PL1 and PL0 are likely some distance apart since populations adjacent to PL0 may have a degree of herd immunity as well.
Finally, given the small number of infections needed to start an outbreak of COVID-19 [33], it would be inevitable that a global pandemic will ensure (big solid arrow, Fig. 1c).
3. Results
3.1. Model predictions of the long-term co-existence of virus and hosts
We track the viral population size, N(t), as the virus evolves to cope with the herd immunity of the hosts. N(0) is the viral population size at the time of invasion and is equivalent to I 0 of Ruan et al.’s [33] study. Since every infected individual is assumed to have identical behavior, we present the results for N(0) = 1. For a viral invasion, the probability of ultimate extinction is denoted by . If the extinction probability is u with N(0) = 1 (i.e., ), then the probability would be un when N(0) = n. In humans, the viral generation time is assumed to be 4 days [5] as in Ruan et al.’s study [33].
3.1.1. A partial model with constant E(k) when there is no host immunity
We first consider a partial model with neither host immunity nor viral evolution and, thus, with constant E(k). Viral invasion of the host population would fail when all infected individuals fail to infect others (i.e., k = 0) in any generation. This could happen if E(k) is smaller, or at least close to 1. In Table 2 (also Tables S1–S4 online), we show the probability of ultimate extinction (u) for N(0) = 1 under various distributions of k (power law, Poisson, and binomial). Analytically, u is the smallest non-negative root of the following equation:
| (1) |
where pk is the probability distribution of k. If k follows the Poisson distribution, we can obtain its extinction probability by the following equation:
Table 2.
The ultimate extinction probability of invading viruses under various E(k) and V(k).
|
E(k) |
||||||
|---|---|---|---|---|---|---|
| 1 | 1.5 | 2 | 3 | 4 | 5 | |
| Power law distribution with V(k) = 10E(k) | ||||||
| N(0) = 1 | 1.0 | 0.90 | 0.78 | 0.63 | 0.51 | 0.41 |
| N(0) = 3 | 1.0 | 0.72 | 0.47 | 0.25 | 0.13 | 0.07 |
| N(0) = 5 | 1.0 | 0.58 | 0.29 | 0.10 | 0.03 | 0.01 |
| Poisson distribution with V(k) = E(k) | ||||||
| N(0) = 1 | 1.0 | 0.42 | 0.20 | 0.06 | 0.02 | 0.007 |
| Binomial distribution with V(k) = E(k)/2 | ||||||
| N(0) = 1 | 1.0 | 0.24 | 0.087 | 0.017 | 0.004 | 0.001 |
Hence,
| (2) |
where Lambert W is the Lambert W function [34]. The detailed derivations for the power law distribution are shown in the Supplementary information online.
Eq. (1) shows the dependence of the extinction probability on the distribution of k. In this study, k follows three different distributions (power law, Poisson, and binomial distribution) with E(k) ranging from 1 to 5. As shown in Table 2, the probability of extinction is very high if N(0) = 1 under the power law distribution. If E(k) = 2, 78% of the invasions would fail. Even if E(k) is 4.5 as is observed in COVID-19, the chance of failure is still around 45%. In infections with E(k) < 2, the probability of failed infections would be higher than 80%. Note that, given the same E(k), the chance of failure is generally lower if V(k) decreases. For example, if V(k) = E(k) as in the Poisson distribution, the probability of failure with E(k) = 4.5 would only be about 1%.
Fig. 2 a–c show 50 replicates of the changes in N(t) as a function of time when E(k) ranges between 1.05 and 1.5. It appears that the population would either go extinct in the first few generations or escape extinction by continuing to grow in size. In particular, when N(t) reaches 100, a successful epidemic would be certain. Thus, the virus would either disappear or cause an epidemic in this non-evolutionary model.
Fig. 2.
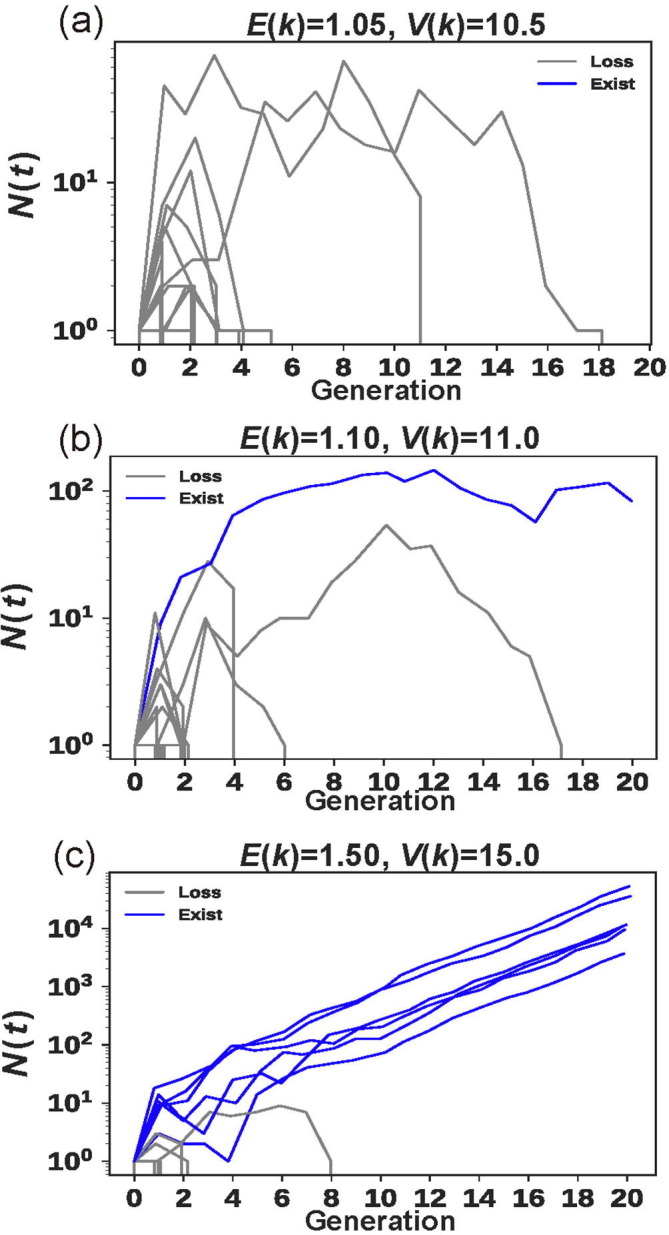
The changes in N(t) over time with constant E(k). (a–c) Fifty replicates of the changes in N(t) as a function of time when V(k) = 10E(k) where E(k) is 1.05, 1.1, or 1.5, respectively. Here k follows a power law distribution. Note that, when N(t) reaches 100, the epidemic would be certain.
3.1.2. The full model with host immunity and continual viral evolution
As the virus and the host cannot coexist in the long run under constant E(k), we consider a more realistic scenario in which the host would develop immunity to suppress the virus and the viral genome would evolve to evade the suppression. This scenario would be analogous to an evolutionary arms race, but note that the (somatic) evolution in the host happens in the immune system [31], [32]. For that reason, the arms race has the dynamics much faster than the germline coevolution [35], [36], [37].
In modeling this arms race, the host would repress the E(k) of the virus to below 1 and the virus may acquire adaptive mutations to drive E(k) above 1. In the previous study [33], we let the distribution of k follow different distributions, in particular, the Poisson distribution with V(k) = E(k) and the power law distribution (in this case, we let V(k) = 5E(k)). Unless held back by a new adaptive mutation in the viral genome, we assume that the herd immunity will decrease E(k) as specified below:
| (3) |
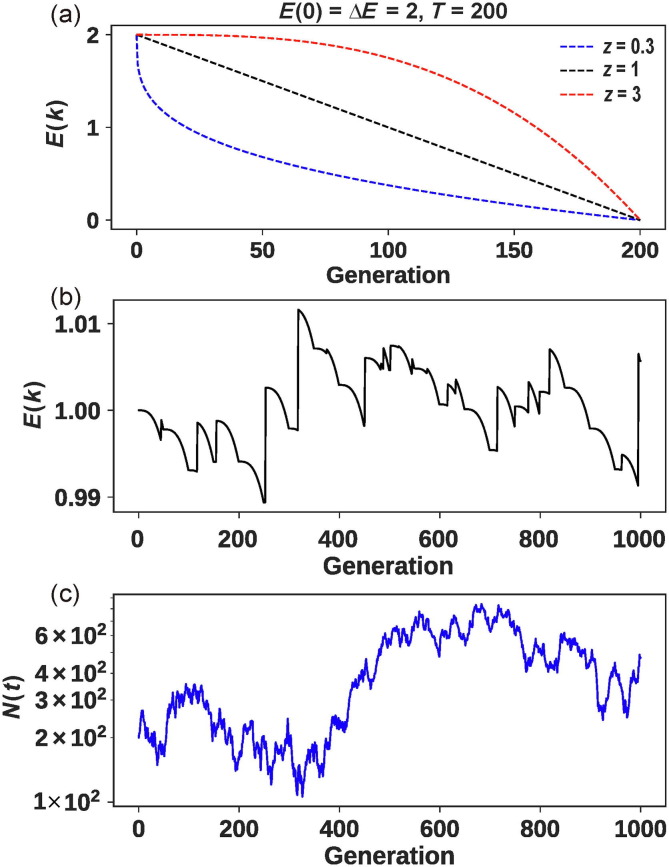
where is the initial E(k), is the E(k) at generation t, T is the time required to reduce E(k) by ΔE. The parameter z determines the curvature of E(k) over time as shown in Fig. 3 a. When z = 1, E(k) declines linearly over time. When z > 1, E(k) declines slowly in the beginning but the decline gradually speeds up yielding a convex shape as shown in red in Fig. 3a. This pattern may be seen when the virus invades an immunologically naïve population. In such a population, the herd immunity slowly builds up but accelerates later on. The opposite is seen with z < 1 whereby the herd immunity is high in the beginning and E(k) decreases rapidly. The decline in E(k) slows down when most individuals in the population have acquired immunity, hence giving rise to the concave appearance shown in blue in Fig. 3a. This pattern may apply to the repeated failed invasions of the virus as the later rounds of invasions would encounter strong immunity as they enter the host population.
Fig. 3.
The evolution of the virus in the host. (a) The decline of E(k) as a function of time due to the build-up of host immunity, according to Eq. (3). The rate of decline depends on whether the host has some immunity from previous viral invasions that failed. (b) An example of the evolution of the infectiousness (E(k)) in animal hosts over 1000 generations. Each jump is due to the emergence of an adaptive mutation in the virus. The parameters: U = 0.02, T = 1/U, = 1, ΔE = 0.005, z = 3, and m = 0.005. (c) The corresponding population size (N(t)) changes under the parameters of (b). Here, k follows a power-law distribution with V(k) = 5E(k).
For each new adaptive mutation, the E(k) will increase as follows:
| (4) |
where is infectivity gain. Unless otherwise specified, we assume follows the exponential distribution with mean equal to m. Here, we assume the accumulation of adaptive mutations follows the Poisson process with the average rate of U. For a long-term persistence in animal (or human) hosts, the decline of E(k) by herd immunity should be held back by a new adaptive mutation. During the time gap waiting for a new adaptive mutation (~1/U), the decline of E(k) is m approximately. A simple way to satisfy this condition is to let T = 1/U, ΔE = . In this case, the expected infectivity of the virus in the hosts (A 0 or H 0) is now a function of time.
| (5) |
where is the number of adaptive mutation at time t, is the infectivity gain of a particular adaptive mutation, and is the quotient (i.e., the integer part of the ratio of t to T). Note that the value in humans (i.e., E 0(k)) is much lower than the corresponding in wild animals (i.e., EA(k)) because the infectiousness (E(k) and V(k)) evolves in the wild animals. For example, the viral RBD possesses an exceptionally high affinity for angiotensin-converting enzyme 2 (ACE2) only in the species where the virus is found originally [27], [30], [38], [39].
When the host develops the herd immunity against the viral strain that has a non-zero probability of long-term persistence (i.e., E(k) > 1), those persistent cases would now go extinct eventually. However, the infection would last much longer than the invasions with E(k) < 1. With an initial population size N(0) = 1, we denote the duration between the initial infection and extinction as T inf. The total number of infected individuals summed over all generations is designated as N inf:
| (6) |
where is the infected cases at generation t. Note is never greater than the population size of H 0, but N inf can be larger since it is a cumulative count. N inf, positively correlated with T inf, would determine the probability of new adaptive mutations in the viral strain, which will then overcome the herd immunity.
3.2. Modeling the evolution in the wild animals of PL0
For the evolution of the virus in the animal host as sketched in Fig. 1a, their long-term existence is likely the outcome of an evolutionary arms race. Fig. 3b shows an example where each viral mutation that increases the infectiousness is countered by the immune response of the host. Each response by the host is further countered by another viral mutation that increases the infectiousness (Eq. (5)). The viral population thus waxes and wanes over a long time span (Fig. 3c). The example is only a demonstration that realistic parameter values can indeed lead to the long-term coevolution between the virus and the immune system of the host. The parameter space conducive for co-existence is large, especially when V(k) decreases much faster than E(k). We should add that a simple condition for the long-term existence of virus is for E(k) to approach 1 and V(k) to approach 0 as t increases. In other words, the number of infected individuals in the population would stay constant over generations, thus giving the virus plenty of time to acquire new adaptive mutations.
3.3. Modeling the viral evolution in H0 at PL0
The main challenge is to explain how a highly infectious strain like SARS-CoV-2 could have evolved in humans. Given that humans are expected to develop immunity as the virus evolves step by step, neither side should have such an overwhelming advantage over the other in the arms race. In contrast, human populations elsewhere are immunologically naïve; hence, the high infectiousness is plausible outside of PL0.
In PL0, the virus would likely infect the local human population regularly. However, the infection is usually unsustainable since the contagion has been selected in the animal hosts, not in humans. The failed invasions nevertheless could elicit a degree of herd immunity in H 0 [40]. A crucial event would then be the emergence of a rare strain that happens to be moderately infectious in humans, referred to as V 0. It would seem unlikely that V 0 could be so infectious as to trigger a global pandemic in humans. Instead, we assume that V 0 only needs to sustain the infection long enough to acquire advantageous mutations for further evolution in human populations.
In Fig. 4 , we show the invasion of V 0 with a very modest E(k) of 1.1. Such a strain would succeed in the invasion with a probability of <5% (Table 2). Furthermore, when the host population evolves the immunity, E(k) would drop below 1, leading to the virus’s eventual extinction. Fig. 4 presents the distribution of T inf and N inf in the process of invasion-to-extinction.
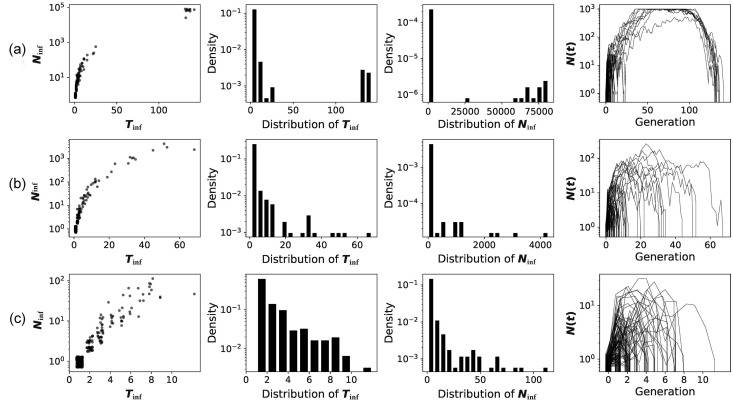
Fig. 4.
The distribution of and after viral invasion. A virus (i.e., N(0) = 1) with initial E(k) = 1.1 invades human population (population size is 1000). The distribution of k follows a power law distribution with V(k) = 5E(k). is the duration between the initial infection and ultimate extinction. Ninf is the total number of infected individuals summed over all generations. Due to the prior build-up of herd immunity, E(k) will decrease at 3 different rates (z = 3, 1, or 0.3) as shown in (a–c), respectively. For each parameter set, 300 repeats are simulated. Each repeat is portrayed by a thin line in the last panel.
Fig. 4a is most interesting as and both show a bi-modal distribution. V 0 either dies out by generation 30 or sustains the invasion for >130 generations. The reason for this bimodal distribution is that ~95% of the invasions with E(k) = 1.1 would fail, which corresponds to the rapidly failed cases. The remaining 5% would become extinct when the host population develops herd immunity, which takes another 100 generations in this simulation. In this process, would be either <100 or >60,000. Only in the latter cases would N inf be large enough to yield adaptive mutations for the virus to overcome the immune suppression (see Supplementary information online for the probability of acquiring mutations). The fourth panel of Fig. 4a shows that, for about 50 generations, V 0 is found in almost every individual in H 0.
While Fig. 4a shows the infection of V 0 has only a 5% chance of sustaining the infection, the chance by the 10th infection would be 40% (~ (1–0.9510)). However, since the immunity would develop gradually, this simple calculation may not be valid. In later invasions, the probability of failure could become higher. With this consideration, the virus would generally disappear by generation 50 (Fig. 4b) and, in later infections, the invasion may all fail by generation 10 (Fig. 4c). In other words, V 0 may have few chances to invade the human population. If the invasion fails, the human host would be immunologically vigilant, thus thwarting subsequent attempts. Although we let k follow power law distribution with V(k) = 5E(k) here, the same pattern can be obtained with larger or smaller V(k) (Figs. S1 and S2 online).
In this model, the arms race between the invading virus and the human host is a long drawn-out battle in PL0. Each new mutation that may allow the virus to invade the human population from the animal hosts would usually fail. The failed virus would need another new mutation to start another round of battle. The biological characteristics of PL0 are, therefore, (i) a place with a high density of wild animals (in particular, bats), (ii) a local low-density human population (such that the invasions usually fail), (iii) long-term coexistence and frequent contacts between the animal and human populations, and (iv) a level of herd immunity in the animal and human hosts. All these conditions are conducive for the virus to accumulate many mutations step-by-step toward the high infectiousness necessary for the pandemic outside of PL0.
3.4. The spread of V1 from PL0 to PL1 — the first epidemic
The conditions in PL0 should allow a V 0 strain to sustain itself in H 0 long enough to acquire beneficial mutations that are adaptive specifically in humans. For simplicity, we assume that a V 1 strain carrying the first beneficial mutation is capable of triggering an epidemic (if V 1 fails to establish itself, the next adaptive mutation would create a V 2 strain and, if it fails too, there may be a V 3 and so on). Note that V 1 would be repressed by the cumulative herd immunity in H 0 but V 1 should have a chance of spreading outside of PL0.
In Fig. 1c, once V 1 succeeds in spreading to an immunologically naïve population in PL1, the pandemic would be a near certainty since no population outside of PL0 is immune to the virus. Ruan et al.’s study [33] shows that the epidemics in many countries are initiated by 5–10 travelers into the region. Hence, the spread to PL1 should be likely once SARS-2-CoV-2 is fully evolved in PL0. With E(k) = 4.5 and 5 carriers, Table 2 shows the probability of invasion failure to be < 2% (~0.455 = 1.8%).
4. Discussion
In light of the previous models for viral epidemics [18], [19], [20], [22], we propose the current model which has several key features: First, viral adaptation to the new human host requires many evolutionary steps. This assumption has been validated for other viral pathogens [23], [24], [25], [26], [27], [28], [30]. Previous models have also pointed out that cross-species transmissions evolve mainly over the time scale of millions of years [21]. Thus, host-switching like other complex adaptations is a multi-step process. Second, the onset of an epidemic is highly unpredictable [18] and this current model has built a mathematical framework to address the stochasticity. Third, the multi-step evolution often leads to a stasis between the host and the pathogen, rather than a global pandemic. The current model proposes to separate the place of origin and places of epidemics by geography.
As the virus evolves, failed invasions prior to the first epidemic in PL1 seem likely (blue arrows of Figs. 1b and 2). We shall refer to places of possible earlier invasions as PLx where sporadic cases of COVID-19 may be found. Such failed invasions would be most informative about the early stages of the pandemic, if the genomic sequences can be obtained and examined. There have been multiple reports of such a possibility in France [41], Japan, and various parts of the US. These reports have often been discredited without further investigations that can definitively rule in, or rule out, SARS-CoV-2's involvement. In particular, patterns of traveling to PLx’s may offer a clue of PL0, where the local human population should show a degree of immunity to SARS-CoV-2. Some researchers [40] appear to suggest candidate PL0 sites to be where humans come in frequent contact with bats. Given the existence of a large reservoir of coronaviruses in wild bats, people in the countryside with a sizable bat population may show some immunity to the viruses [1], [40]. At present, the closest strain isolated in wild animals is 10% divergent from the genome of SARS-CoV-2 [6], [42], a distance estimated to take 30–300 years to evolve (Jian Lu, unpublished results). At present, we are still far from finding the origin of this pandemic.
In the popular view, the “first” SARS-CoV-2 corresponds to one of the strains circulating in humans. An extension of this view is that the place of origin is the same as PL1. This extension is problematic. In the Guns, Germs and Steel, Diamond [43] has documented many instances that pathogens spread to the places where they encounter low resistance (such as smallpox in the Aztec populations). The geographical separation between the place of origin of any taxon (not just virus) and the site of proliferation has led Gould et al. to the explanation of “punctuated equilibrium” [44]. The fossil records in the place of origin may be continual but few; in contrast, their abundance at the site of the outbreak would appear to suddenly come out of nowhere. For a recent example, the widely discussed “Spanish flu” of 1918 broke out in the war zone but most likely originated in Kansas [45], [46]. In short, if PL0 is the same as PL1, which is widely assumed, then the origin and evolution of SARS-CoV-2 must be very unusual. A theory for such an unusual origin is thus needed.
Like many other evolutionary questions on the origin, where, when, and how SARS-CoV-2 becomes fully evolved will remain an intriguing question. We suggest the question be about the early evolution of SARS-CoV-2, rather than about the “origin”. The former implies a process whereas the latter seems to mean a single time point. This distinction is important as seen in the earlier debates on the “origin” of dogs [47] and new species in environments [48].
Conflict of interest
The authors declare that they have no conflict of interest.
Acknowledgments
Acknowledgments
This work was supported by the National Natural Science Foundation of China (31730046, 91731000, 31900417, and 81972691), Guangdong Basic and Applied Basic Research Foundation (2020B1515020030, 2019A1515010708), and the National Key Research and Development Project of China (2020YFC0847000). We thank Drs. Yaping Zhang, Jian Lu, Xuemei Lu, Suhua Shi, Weiwei Zhai, Jianzhi George Zhang, Bingjie Chen, Zheng Hu, and Jindong Zhao for comments and suggestions.
Author contributions
Chung-I Wu and Yongsen Ruan designed the study and constructed the theoretical framework. Yongsen Ruan did the simulation with the help of Chung-I Wu. Yongsen Ruan and Chung-I Wu wrote the manuscript. All authors interpreted the findings, revised the manuscript, and approved the final version for publication.
Biographies

Yongsen Ruan, Postdoctoral Fellow, School of Life Sciences, Sun Yat-sen University. He is interested in theoretical population genetics and specialized in computational biology and mathematical modeling.

Chung-I Wu, Professor, School of Life Sciences, Sun Yat-sen University. He is an evolutionary biologist and a member of the Academia Sinica. For the past 30 years, he has been a professor at the University of Chicago and the head of the Department of Ecology and Evolution (1998–2008). From 2008 to 2014, he served as the director of the Beijing Institute of Genomics of the Chinese Academy of Sciences. In 2004, he cooperated with Guoping Zhao and other domestic experts to reveal the evolutionary dynamics of the SARS virus. He has also accomplished a series of work on the origin and evolution of SARS-CoV-2.
Footnotes
Supplementary materials to this article can be found online at https://doi.org/10.1016/j.scib.2020.12.020.
Appendix A. Supplementary data
The following are the Supplementary data to this article:
References
- 1.Andersen K.G., Rambaut A., Lipkin W.I. The proximal origin of SARS-CoV-2. Nat Med. 2020;26:450–452. doi: 10.1038/s41591-020-0820-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ferretti L., Wymant C., Kendall M. Quantifying SARS-CoV-2 transmission suggests epidemic control with digital contact tracing. Science. 2020;368:eabb6936. doi: 10.1126/science.abb6936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Li R., Pei S., Chen B. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2) Science. 2020;368:489–493. doi: 10.1126/science.abb3221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Liu Y., Gayle A.A., Wilder-Smith A. The reproductive number of COVID-19 is higher compared to SARS coronavirus. J Travel Med. 2020;27:taaa021. doi: 10.1093/jtm/taaa021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wölfel R., Corman V.M., Guggemos W. Virological assessment of hospitalized patients with COVID-2019. Nature. 2020;581:465–469. doi: 10.1038/s41586-020-2196-x. [DOI] [PubMed] [Google Scholar]
- 6.Zhang T., Wu Q., Zhang Z. Probable pangolin origin of SARS-CoV-2 associated with the COVID-19 outbreak. Curr Biol. 2020;30:1346–1351.e2. doi: 10.1016/j.cub.2020.03.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zhou P., Yang X.L., Wang X.G. A pneumonia outbreak associated with a new coronavirus of probable bat origin. Nature. 2020;579:270–273. doi: 10.1038/s41586-020-2012-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Boni MF, Lemey P, Jiang X. Evolutionary origins of the SARS-CoV-2 sarbecovirus lineage responsible for the COVID-19 pandemic. Nat Microbiol. 2020;5:1408–1417. doi: 10.1038/s41564-020-0771-4. [DOI] [PubMed] [Google Scholar]
- 9.Liu Y.X., Zhang C., Huang F.M. Elevated plasma levels of selective cytokines in COVID-19 patients reflect viral load and lung injury. Natl Sci Rev. 2020;7:1003–1011. doi: 10.1093/nsr/nwaa037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Tang X.L., Wu C.C., Li X. On the origin and continuing evolution of SARS-CoV-2. Natl Sci Rev. 2020;7:1012–1023. doi: 10.1093/nsr/nwaa036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Korber B, Fischer WM, Gnanakaran S. Tracking changes in SARS-CoV-2 spike: evidence that D614G increases infectivity of the COVID-19 virus. Cell. 2020;182:812–827. doi: 10.1016/j.cell.2020.06.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wu C.I., Poo M.M. Moral imperative for immediate release of 2019-nCoV sequence data. Natl Sci Rev. 2020;7:719–720. doi: 10.1093/nsr/nwaa030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.He X, Lau EHY, Wu P. Temporal dynamics in viral shedding and transmissibility of COVID-19. Nat Med. 2020;26:672–675. doi: 10.1038/s41591-020-0869-5. [DOI] [PubMed] [Google Scholar]
- 14.Wen H, Liu F, Huang M, et al. A proposal for clinical trials of COVID-19 treatment using homo-harringtonine. Natl Sci Rev 2121;8:nwaa257. [DOI] [PMC free article] [PubMed]
- 15.Gu J., Yan H., Huang Y. Comparing containment measures among nations by epidemiological effects of COVID-19. Natl Sci Rev. 2020;7:1847–1851. doi: 10.1093/nsr/nwaa243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhou Y.G., Fu B.Q., Zheng X.H. Pathogenic t-cells and inflammatory monocytes incite inflammatory storms in severe COVID-19 patients. Natl Sci Rev. 2020;7:998–1002. doi: 10.1093/nsr/nwaa041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Halfmann P.J., Hatta M., Chiba S. Transmission of SARS-CoV-2 in domestic cats. N Engl J Med. 2020;383:592–594. doi: 10.1056/NEJMc2013400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Geoghegan J.L., Duchene S., Holmes E.C. Comparative analysis estimates the relative frequencies of co-divergence and cross-species transmission within viral families. PLoS Pathog. 2017;13 doi: 10.1371/journal.ppat.1006215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Geoghegan J.L., Holmes E.C. Predicting virus emergence amid evolutionary noise. Open Biol. 2017;7 doi: 10.1098/rsob.170189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Parrish C.R., Holmes E.C., Morens D.M. Cross-species virus transmission and the emergence of new epidemic diseases. Microbiol Mol Biol Rev. 2008;72:457–470. doi: 10.1128/MMBR.00004-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Plowright R.K., Becker D.J., McCallum H. Sampling to elucidate the dynamics of infections in reservoir hosts. Philos Trans R Soc Lond B Biol Sci. 2019;374:20180336. doi: 10.1098/rstb.2018.0336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Plowright R.K., Parrish C.R., McCallum H. Pathways to zoonotic spillover. Nat Rev Microbiol. 2017;15:502–510. doi: 10.1038/nrmicro.2017.45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lemey P., Rambaut A., Pybus O.G. HIV evolutionary dynamics within and among hosts. Aids Rev. 2006;8:125–140. [PubMed] [Google Scholar]
- 24.Sharp P.M., Hahn B.H. Origins of HIV and the aids pandemic. Cold Spring Harb Perspect Med. 2011;1 doi: 10.1101/cshperspect.a006841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Watanabe Y., Ibrahim M.S., Suzuki Y. The changing nature of avian influenza A virus (H5N1) Trends Microbiol. 2012;20:11–20. doi: 10.1016/j.tim.2011.10.003. [DOI] [PubMed] [Google Scholar]
- 26.Webster R.G., Bean W.J., Gorman O.T. Evolution and ecology of influenza A viruses. Microbiol Rev. 1992;56:152–179. doi: 10.1128/mr.56.1.152-179.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Cui J., Li F., Shi Z.L. Origin and evolution of pathogenic coronaviruses. Nat Rev Microbiol. 2019;17:181–192. doi: 10.1038/s41579-018-0118-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hu B., Zeng L.P., Yang X.L. Discovery of a rich gene pool of bat SARS-related coronaviruses provides new insights into the origin of SARS coronavirus. PLoS Pathog. 2017;13 doi: 10.1371/journal.ppat.1006698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Dawkins R. The blind watchmaker. London: Longman Scientific & Technical; 1986.
- 30.Wu K., Peng G., Wilken M. Mechanisms of host receptor adaptation by severe acute respiratory syndrome coronavirus. J Biol Chem. 2012;287:8904–8911. doi: 10.1074/jbc.M111.325803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Flajnik M.F., Kasahara M. Origin and evolution of the adaptive immune system: genetic events and selective pressures. Nat Rev Genet. 2010;11:47–59. doi: 10.1038/nrg2703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Simon A.K., Hollander G.A., McMichael A. Evolution of the immune system in humans from infancy to old age. Proc Biol Sci. 2015;282:20143085. doi: 10.1098/rspb.2014.3085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ruan Y., Luo Z., Tang X. On the founder effect in COVID-19 outbreaks – how many infected travelers may have started them all? Natl Sci Rev. 2021;8:nwaa246. doi: 10.1093/nsr/nwaa246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Corless R.M., Gonnet G.H., Hare D.E.G. On the lambertw function. Adv Comput Math. 1996;5:329–359. [Google Scholar]
- 35.Ruan Y., Wang H., Chen B. Mutations beget more mutations-rapid evolution of mutation rate in response to the risk of runaway accumulation. Mol Biol Evol. 2020;37:1007–1019. doi: 10.1093/molbev/msz283. [DOI] [PubMed] [Google Scholar]
- 36.Milholland B., Dong X., Zhang L. Differences between germline and somatic mutation rates in humans and mice. Nat Commun. 2017;8:15183. doi: 10.1038/ncomms15183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Blokzijl F., de Ligt J., Jager M. Tissue-specific mutation accumulation in human adult stem cells during life. Nature. 2016;538:260–264. doi: 10.1038/nature19768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wan Y., Shang J., Graham R. Receptor recognition by the novel coronavirus from Wuhan: an analysis based on decade-long structural studies of SARS coronavirus. J Virol. 2020;94:e00127–20. doi: 10.1128/JVI.00127-20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Shang J., Ye G., Shi K. Structural basis of receptor recognition by SARS-CoV-2. Nature. 2020;581:221–224. doi: 10.1038/s41586-020-2179-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Graham R.L., Baric R.S. SARS-CoV-2: combating coronavirus emergence. Immunity. 2020;52:734–736. doi: 10.1016/j.immuni.2020.04.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Deslandes A., Berti V., Tandjaoui-Lambotte Y. SARS-CoV-2 was already spreading in france in late december 2019. Int J Antimicrob Agents. 2020;55 doi: 10.1016/j.ijantimicag.2020.106006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Xiao K., Zhai J., Feng Y. Isolation of SARS-CoV-2-related coronavirus from malayan pangolins. Nature. 2020;583:286–289. doi: 10.1038/s41586-020-2313-x. [DOI] [PubMed] [Google Scholar]
- 43.Diamond J.M. Norton; New York: 2005. Guns, germs, and steel: the fates of human societies. [Google Scholar]
- 44.Gould S.J., Eldredge N. Punctuated equilibrium comes of age. Nature. 1993;366:223–227. doi: 10.1038/366223a0. [DOI] [PubMed] [Google Scholar]
- 45.Barry J.M. The site of origin of the 1918 influenza pandemic and its public health implications. J Transl Med. 2004;2:3. doi: 10.1186/1479-5876-2-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Crosby AW, Societies ACoL. America's forgotten pandemic: the influenza of 1918. Cambridge: Cambridge University Press; 2003.
- 47.Wang G.D., Shao X.J., Bai B. Structural variation during dog domestication: insights from gray wolf and dhole genomes. Natl Sci Rev. 2019;6:110–122. doi: 10.1093/nsr/nwy076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.He Z., Li X., Yang M. Speciation with gene flow via cycles of isolation and migration: insights from multiple mangrove taxa. Natl Sci Rev. 2019;6:275–288. doi: 10.1093/nsr/nwy078. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.