A Bayesian approach to improving spatial estimates of prevalence of COVID-19 after accounting for misclassification bias in surveillance data in Philadelphia, PA

Highlights

• •Surveillance data obtained by public health agencies for COVID-19 are biased.
• •Bayesian approaches can be used to adjust for misclassification bias in surveillance data.
• •Misclassification alone does not explain spatial heterogeneity in COVID-19.

Abstract

Surveillance data obtained by public health agencies for COVID-19 are likely inaccurate due to undercounting and misdiagnosing. Using a Bayesian approach, we sought to reduce bias in the estimates of prevalence of COVID-19 in Philadelphia, PA at the ZIP code level. After evaluating various modeling approaches in a simulation study, we estimated true prevalence by ZIP code with and without conditioning on an area deprivation index (ADI). As of June 10, 2020, in Philadelphia, the observed citywide period prevalence was 1.5%. After accounting for bias in the surveillance data, the median posterior citywide true prevalence was 2.3% when accounting for ADI and 2.1% when not. Overall the median posterior surveillance sensitivity and specificity from the models were similar, about 60% and more than 99%, respectively. Surveillance of COVID-19 in Philadelphia tends to understate discrepancies in burden for the more affected areas, potentially misinforming mitigation priorities.

1. Introduction

While responding to public health emergencies, exemplified by the COVID-19 outbreak 2019-20, public health authorities rely upon accurate surveillance for cases. As with most communicable diseases, it is expected that COVID-19 disease would be heterogeneously distributed in the population. Factors such as poverty, crowding, and access to resources may affect the transmission networks through which infections spread (Patel et al., 2020). As such, public health surveillance programs need to tailor their approaches to identifying cases based upon this heterogeneity in a manner that balances the need to capture all cases while ensuring the highest-risk groups have access to testing. Yet given strapped budgets and insufficient resources, it is understandable that a surveillance program may ultimately not be tailored based on community attributes alone. This is compounded by imperfections in diagnostic tests (Yap et al., 2020). The consequence of this is imperfect case detection: i.e. misclassification of infected as uninfected and vice versa.

Broadly speaking, there are two processes that can drive this. First, agencies that conduct public health surveillance (in the U.S., state and local health departments) may not be aware of true COVID-19 cases in the population; in other words, suboptimal sensitivity in that these cases can be considered “false negatives” in terms of surveillance. These unreported cases may arise from both symptomatic and asymptomatic individuals. For those who are symptomatic, limited testing capacity of the health department – especially early in any epidemic – gives priority to some occupations and demographics (CDC, 2020a). Even for individuals tested (with a positive result) reporting delays may mean that at any given time surveillance data are incomplete. For those who are asymptomatic – by one estimate around 1 in 3 persons (Oran and Topol, 2020) – they likely would not seek health care, and thus not be tested becoming “false negatives” in surveillance. Relatedly, should sufficient testing capacity be reached and a priority approach is no longer needed, social, structural, and spatial disparities may mean that some individuals are unable – or unwilling – to engage with the healthcare system and consequently are also unknown to the health department (Patel et al., 2020). The second process that can drive imperfect case detection relates to the characteristics of the diagnostic test itself: the polymerase chain reaction-based assay in use in the U.S. (CDC, 2020b). Among individuals who obtain a diagnostic test for SARS-CoV-2, the virus that causes COVID-19 disease, imperfect assay sensitivity and specificity may lead to both false negative and false positive test results (Yap et al., 2020). We have evidence that this is indeed the case in Philadelphia (Burstyn et al., 2020). Thus, even in a perfect system that captures all infected for testing, there may still be misclassification of COVID-19 diagnoses.

We sought to understand the potential for bias in COVID-19 spatial surveillance data for Philadelphia, PA, while considering imperfect case detection. The expected result is that the health department will be better equipped to direct resources to the areas at greatest risk. In order to do this, we conducted a Bayesian uncertainty analysis to estimate the plausible under- or over-counting occurring in the community using only data that are known to the health department, a marker of community deprivation, preexisting knowledge about the prevalence of COVID-19, and accuracy of laboratory testing. From the outset, we do not claim that we are able to fully recover the truth – existing data in situ cannot reveal this – and in order to understand the magnitude of bias we must proceed by sacrificing identifiability of statistical models (Lash et al., 2009). Ours is rather an attempt to move beyond the common practice of ignoring such misclassification, as noted by others (Shaw et al., 2018).

2. Methods

2.1. Data sources

Deidentified, aggregated datasets representing COVID-19 cases in Philadelphia, Pennsylvania by ZIP code were retrieved June 10, 2020 from OpenDataPhilly (City of Philadelphia, 2020a). These data captured SARS-CoV-2 testing throughout the city, both positive and negative test results, and are inclusive of all tests to this date. Any tests conducted by a private or public laboratory were required to be reported to the City of Philadelphia per their regulations (City of Philadelphia, 2020b). Therefore, these data represented surveillance counts of total number of tests, positive and negative, by ZIP code up to the date retrieved. There are 47 populated ZIP codes in Philadelphia; at least one test was conducted in each. As such, no ZIP codes were excluded from analysis. To ensure correct linkage with other aggregated data (i.e., from the U.S. Census, see below) we used a cross-walk from ZIP codes to ZIP Code Tabulation Areas (UDS Mapper, 2020); for simplicity, we will continue to refer to these geographic units as “ZIP codes”.

The total population size for each ZIP code was obtained from the 2018 American Community Survey 5-year estimates, the most recent available. Area deprivation index (ADI) has previously been implicated as a correlate of disease testing and reported cases of COVID-19 in several cities across the U.S. (Bilal et al., 2020). Goldstein et al. (manuscript under review) demonstrate that catchment in a healthcare system is function of ADI, further cementing the importance of using a marker of community deprivation in engagement with the health care system. ADI for each ZIP code was operationalized as a Z-score composite of 2018 American Community Survey 5-year estimates of education, employment, income and poverty, and household composition where a higher score indicates greater deprivation (Messer et al., 2006). Conceptually, we believe that ADI captures the hypothesized factors that may lead to differential testing for COVID-19 by ZIP code during the pandemic, and thus being captured in surveillance data, as well as heterogeneity in prevalence of the infection.

2.2. Estimating prevalence and spatial distribution of COVID-19

For each ZIP code i, aggregated counts of positive test results (Y_i*) obtained from the OpenDataPhilly divided by the underlying population size (N_i) served as the observed estimates of COVID-19 period prevalence throughout Philadelphia. The relationship between the observed estimates and true prevalence (r_i) of COVID-19 is a function of the sensitivity (SN_i) and specificity (SP) of the surveillance process. Rather than attempting to deconstruct the surveillance process into its constituent parts, which is both complex and nebulous, we assume an overall measure of program accuracy. We allowed sensitivity to vary by ZIP code as we hypothesized the implementation of the testing program differed throughout the city resulting in select individuals not being tested. Conversely, we utilized a single measure of specificity citywide, as once individuals are in fact tested, we do not expect ZIP code differences in false diagnoses. Further details on their operationalization are provided in the Statistical Analysis section.

While ZIP code serves as our geographic unit of analysis, it is important to note that communicable diseases do not follow arbitrary mail delivery boundaries (unless, for example, a river served as a boundary and it was impossible to cross it). As such, a priori we anticipated spatial autocorrelation in the data, and utilized Moran's I (empirical Bayes rate modification) and spatial correlograms to test this hypothesis. Choropleth maps were created to depict the spatial patterning of COVID-19 throughout the city. Our focus on ZIP codes as the unit of analysis is due to its utility to health departments when publicly releasing data, such as maps of COVID-19 for a given jurisdiction: it is the smallest geographical identifier allowed through the U.S. Health Insurance Portability and Accountability Act (Code of Federal Regulations, 2000).

2.3. Statistical analysis

We employed a Bayesian modeling approach to determine the posterior distribution of true prevalence of COVID-19 by ZIP code in Philadelphia, accounting for potential bias in the surveillance process. We modeled several quantities simultaneously to consider the disease surveillance process Eqs. 1–(4). We assumed that the observed cases $Y_i^{*}$in each ZIP code were the sum of the observed infected if truly infected $Y_i^t$and the observed infected if not truly infected $Y_i^f$as

$$Y_i^{*}=Y_i^t+Y_i^f$$ (1)

The number of true positive SARS-CoV-2 infected cases in ZIP code i based on ZIP code surveillance was specified as

$$Y_i^t\sim Binom\left(S{N}_i,Y_i\right)$$ (2)

where SN_i is the varying sensitivity of the surveillance process and Y_i is the unknown number of true positive SARS-CoV-2 infected cases in the ith ZIP code. The number of false positive SARS-CoV-2 tests in ZIP code i based on ZIP code surveillance was specified as

$$Y_i^f\sim Binom\left(1-SP,N_i-Y_i\right)$$ (3)

where SP is the specificity of the surveillance process and population size is N_i. Finally, the number of true positive SARS-CoV-2 infected cases in ZIP code i based on true prevalence r_i and population size N_i was specified as

$$Y_i\sim Binom\left(r_i,N_i\right)$$ (4)

The quantity Y_i is unknown and must be predicted from the model. This specification was adapted from the work of Burstyn, Goldstein, and Gustafson Burstyn et al., 2020). Two models (Eqs. 5 and (6) were explored to model the true prevalence r_i of COVID-19 in a given ZIP code i allowing for various parameter specifications:

$$logit\left(r_i\right)={\eta }_0+{\eta }_1*AD{I}_i+u_i(model\#1)$$ (5)

$$r_i\sim Unif\left(a=0,b=0.1\right)\left(model\#2\right)$$ (6)

Model #1 (Eq. 5) specifies that the logit of true prevalence was conditional on the background rate η₀, the effect η₁ of ADI, and unstructured random effects u_i, where u_i ~ Norm(μ = 0, σ² = 1/τ_u) and τ_u is the precision of the random effect. Model #2 (Eq. 6) eschews conditioning on ADI and places a prior directly on true prevalence.

The models are completed with specification of all the prior distributions for the parameters. For Eq. 5, the logit of true prevalence of COVID-19 when ADI is equal to the citywide mean received a prior of η₀ ~ Norm(μ = −3.5, σ² = 0.25), which corresponds to a prior 3% prevalence with an approximate standard deviation of 2%. It has been difficult to elucidate an informative prior on prevalence for Philadelphia due to a variety of factors, including non-random sampling, biased tests, and heterogeneous outbreaks. Thus, our best estimate was informed by a neighboring jurisdiction in Delaware that conducted sewage-based PCR testing of the most populous and urban county in the state and estimated 3% prevalence (Wilson, 2020). The effect of ADI on the logit of true prevalence received a prior of η₁ ~ Norm(μ = 0.04, σ² = 0.0016), which was informed by effect estimates obtained from regressing ZIP code aggregated cases of COVID-19 by ADI (Bilal et al., 2020). We used a weakly informative prior τ_u ~ Gamma(κ = 1, θ = 0.1) for the precision of the exchangeable random effects. For Eq. 6, the prior r_i ~ Unif(a = 0, b = 0.1) was set directly on true prevalence, corresponding to a minimum and maximum prevalence of 0% and 10%, respectively. These bounds represent our reasonable extremes for the true prevalence of COVID-19 in any ZIP code in Philadelphia during our study period based on a seroprevalence study across multiple cities (Havers et al., 2020). The varying probability of observed cases of COVID-19 if truly infected received an informative beta distribution, SN_i ~ Beta(α = 14.022, β = 9.681). This corresponded to a median sensitivity of 59% with 5- and 95-percentiles of 42% and 75%, respectively. The probability of testing negative for COVID-19 if not truly infected received an informative beta distribution, SP ~ Beta(α = 100, β = 3.02). This corresponded to a median specificity of 95% with 5- and 95-percentiles of 94% and 99%, respectively. Since the accuracy of the surveillance program was unknown in the study area, we assumed that surveillance performed no better than the accuracy of the diagnostic test alone which has an estimated sensitivity between the 70 and 90% range and near perfect specificity (Yap et al., 2020), and allowed a fairly wide range of plausible values, allowing the data to inform where SN_i and SP are likely distributed. Full model details may be found in Appendix 1 in the Supplemental Materials.

Heuristically, our models relate the observed prevalence to the true prevalence, r_i, through the sensitivity and specificity of the surveillance process, where the observed prevalence p_i = SN_ir_i + (1-SP)(1-r_i). In other words, the observed prevalence is the sum of the observed infected if infected (true positives; defined in Eq. 2) and the observed infected if not infected (false positives; defined in Eq. 3), divided by number of residents in each ZIP code.

2.3.1. Simulation study

Given the non-identifiability of our models and potential influence of prior specifications, we conducted a simulation study where the true sensitivity and specificity of the surveillance program, as well as the true prevalence in each ZIP code were known. Full details may be found in Appendix 2 in the Supplemental Materials. Briefly, we considered two choices of priors for η₀ – Norm(μ = −3.5, σ² = 0.5) and Norm(μ = 0, σ² = 2.71) for models conditioned on ADI (i.e., Eq. 5) – and two choices of priors for SN_i – Beta(α = 14.022, β = 9.681) and Unif(a = 0.25, b = 0.75) for both models (i.e., Eqs. 5 and 6) – and tested the model performance across 9 combinations of true mean prevalence (1%, 3%, and 5%) and surveillance program mean sensitivity (30%, 50%, 70%). We found that our analysis required at least some informative priors on η₀, which are justified in context of COVID-19. Consequently, some may view our efforts as an uncertainty or bias analysis rather than true adjustment for misclassification, although we intuit, based on previous experience (Burstyn et al., 2020), that some learning about true prevalence and misclassification parameters was possible.

For both our main analysis and simulation study, Bayesian modeling occurred in Just Another Gibbs Sampler via the r2jags package. Five chains were run for 50,000 iterations, discarding the first 5,000 samples for burn-in, and trimming to every 10th iteration. Diagnostics included kernel density visualizations of the posterior distributions and traceplots. A parameter was considered to have converged if its Gelman-Rubin statistic was less than 1.2. Posterior estimates are provided as the median with accompanying 95% credible intervals (CrI). The posterior distribution of $Y_i$ enabled a calculation of citywide true prevalence r = $\sum Y_i/\sum N_i$. All computational codes are available to download from https://doi.org/10.5281/zenodo.4116290.

3. Results

3.1. Naïve analysis

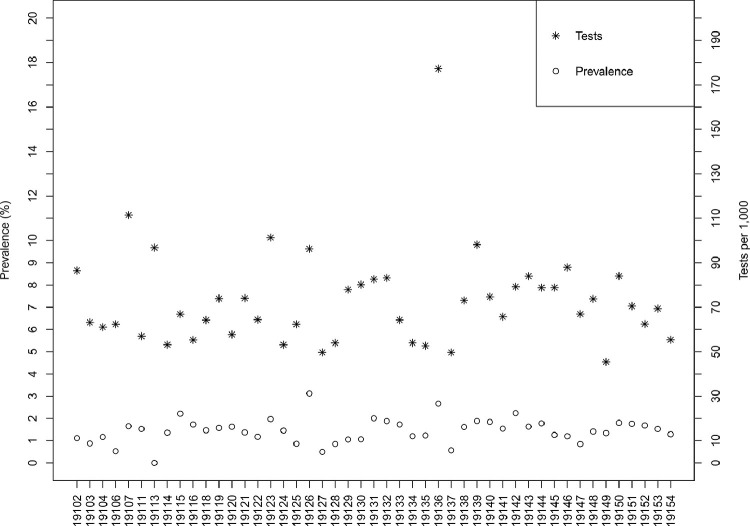
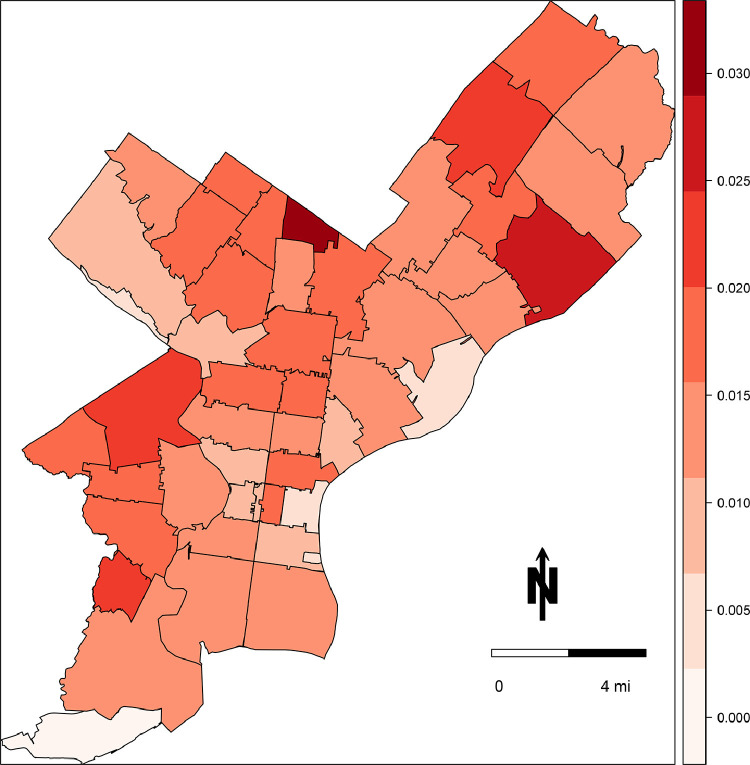
As of June 10, 2020, there were 111,497 documented tests in Philadelphia, of which 23,941 (21%) were classified by the laboratory as positive for SARS-CoV-2. With a total population more than 1.5 million, this translates to a testing rate of 71 tests per 1,000 individuals and an observed prevalence of 1.5%, assuming a negligible number of repeat tests per individual. Testing and observed prevalence varied by ZIP code, with a range of 45–177 tests per 1000 individuals and the observed prevalence of 0% to 3.1% (Fig. 1 ). Observed positive tests per capita exhibited weak spatial dependency across the city (Moran's I = 0.10, p = 0.08); the total number of tests per capita did not appear to be spatially autocorrelated (Moran's I = 0.01, p = 0.3). The choropleth map in Fig. 2 demonstrates heterogeneity in observed prevalence of COVID-19 across the city, with highest burden in 19126 (3.1%) and 19136 (2.7%), and the lowest burden in 19106 (0.5%), 19127 (0.5%), and 19113 (0%).

Fig. 1.

Distribution of estimates of SARS-CoV-2 testing and prevalence by ZIP code in Philadelphia, PA, reported by the Philadelphia Department of Public Health as of June 10, 2020.

Fig. 2.

Choropleth map of the estimates of COVID-19 prevalence by ZIP code in Philadelphia, PA, reported by the Philadelphia Department of Public Health as of June 10, 2020.

3.2. Simulation study

The full results of the simulation study may be found in Appendix 2 of the Supplemental Material. Modeling prevalence conditioned on ADI under the prior specifications for ${\eta }_0$ ~ Norm(μ = -3.5, σ² = 0.5) and a Beta prior on SN_i resulted in posterior distributions all centered around 3% prevalence, while modeling prevalence conditioned on ADI under the prior specifications for ${\eta }_0$ ~ Norm(μ = 0, σ² = 2.71) resulted in posterior distributions spanning unrealistic values of hypothesized prevalence. Placing the prior directly on prevalence, r_i ~ Unif(a = 0, b = 0.1), resulted in posterior distributions that were markedly narrower than the prior and that largely captured the true prevalence in their credible intervals. Results were robust to the alternative specification SN_i ~ Unif(a = 0.25, b = 0.75). The two approaches that used informative priors on prevalence, that is, ${\eta }_0$ =  Norm(μ = -3.5, σ² = 0.25) and r_i ~ Unif(a = 0, b = 0.1), appeared to have comparable performance when true prevalence was 3% or higher and true sensitivity was at least 50% on average. Based on the results of the simulations, we used the informative priors η₀ ~ Norm(μ = -3.5, σ² = 0.5) for the model conditioned on ADI and SN_i ~ Beta(α = 14.022, β = 9.681) for both models.

3.3. Bayesian adjusted analysis

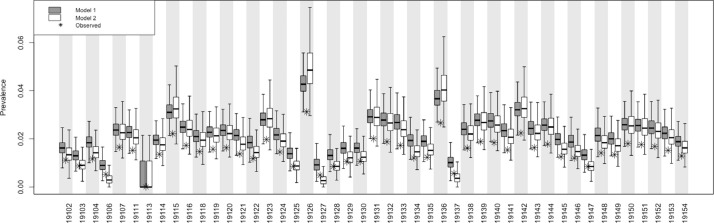
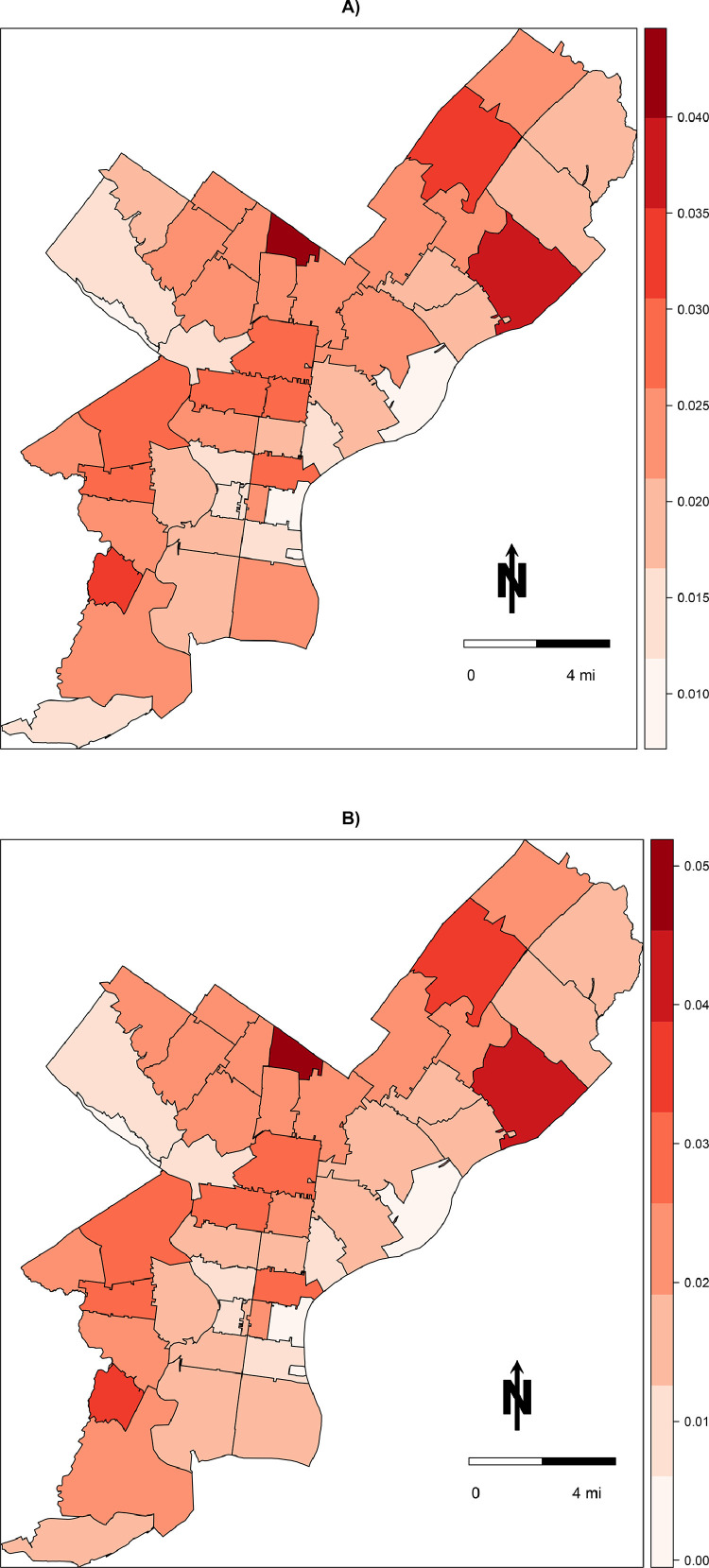
All models demonstrated good mixing of chains (Supplemental Material, Appendices 3 and 4) and all models successfully converged with parameter-specific Gelman-Rubin statistics uniformly <1.2. Fig. 3 depicts the ZIP code level posterior estimates for the two models alongside the observed prevalence estimates obtained from surveillance data. Qualitatively, the models tended to yield similar posterior distributions when the observed prevalence was around 2%. In ZIP codes with lower observed prevalence, the model conditioned on ADI (model #1; Eq. 5) tended to have higher posterior values compared to the model with the prior placed directly on true prevalence (model #2; Eq. 6), whereas in ZIP codes with greater prevalence, model #1 tended to have lower posterior values compared to model #2. In other words, the model conditioned on ADI had posterior distributions of prevalence values that were more similar to the prior.

Fig. 3.

Posterior distributions of estimated (boxplots) and observed (asterisks) prevalence of COVID-19 by ZIP code in Philadelphia, PA.

3.3.1. Model #1 conditioned on ADI

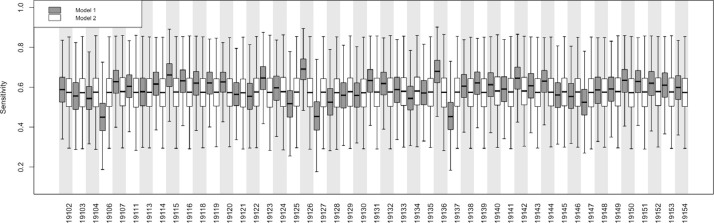
After accounting for bias in the surveillance data, the posterior citywide true prevalence was 2.3% (95% CrI: 2.1%, 2.6%). As with the naïve estimates, we observed heterogeneity in the posterior prevalence proportions throughout the city, with a low of 0.9% (95% CrI: 0.5%, 1.7%) in ZIP code 19106 to a high of 4.2% (95% CrI: 3.4%, 5.4%) in ZIP code 19126. Overall posterior surveillance sensitivity and specificity were 58.9% (95% CrI: 42.1%, 75.9%) and 99.8% (95% CrI: 99.7%, 100%), respectively. Sensitivity varied across ZIP codes from a low of 45.0% (95% CrI: 27.6%, 65.7%) in ZIP code 19106 to a high of 69.1% (95% CrI: 53.7%, 83.1%) in ZIP code 19126 (Fig. 4 ).

Fig. 4.

Posterior distributions of COVID-19 surveillance sensitivity by ZIP code in Philadelphia, PA for model #1 conditioned on the area deprivation index (ADI) and model #2 not conditioned on ADI. See text for details.

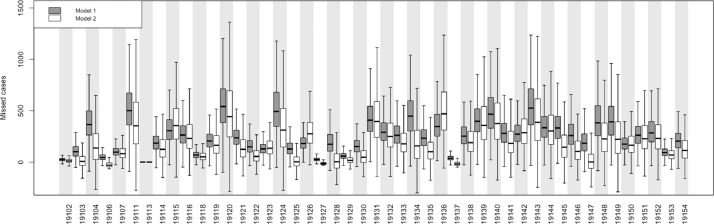
Posterior prevalence of COVID-19 demonstrated a heterogenous distribution throughout the city (Fig. 5 a) and were similar in patterning to the observed prevalence estimates (Fig. 2) albeit scaled up in magnitude. Certain ZIP codes appeared more likely to have bias than others (Fig. 6 ), with ZIP code 19120 (observed prevalence of 1.6%, posterior prevalence of 2.4%) having the greatest anticipated number of missed cases in the city at 541 (95% CrI: 161, 1,138). Posterior distributions for other parameters may be found in Appendices 3 and 4 in the Supplemental Material.

Fig. 5.

Choropleth map of medians of posterior distributions of COVID-19 prevalence by ZIP code in Philadelphia, PA for A) model #1 conditioned on the area deprivation index (ADI) and B) model #2 not conditioned on ADI. See text for details.

Fig. 6.

Bias in the surveillance data of COVID-19 by ZIP code in Philadelphia, PA for model #1 conditioned on the area deprivation index (ADI) and model #2 not conditioned on ADI. See text for details. Missed cases (number of people) is the difference between the posterior median expected count (number of people) and the surveillance observed count (number of people).

3.3.2. Model #2 not conditioned on ADI

After accounting for bias in the surveillance data, the posterior citywide true prevalence was 2.1% (95% CrI: 1.8%, 2.6%), with a low of 0.3% (95% CrI: 0.01%, 0.9%) in ZIP code 19127 to a high of 4.9% (95% CrI: 3.5%, 7.6%) in ZIP code 19126. Overall posterior surveillance sensitivity and specificity were slightly lower than model #1: 57.6% (95% CrI: 37.0%, 76.4%) and 99.6% (95% CrI: 99.4%, 99.8%), respectively. As compared to model #1, sensitivity was less heterogeneous across ZIP codes (Fig. 4).

Posterior prevalence of COVID-19 were again heterogenous throughout the city yet only slightly differed from the patterning depicted in model #1 (Fig. 5b). As with model #1, certain ZIP codes appeared more likely to have bias than others, although there was greater uncertainty in the posterior distributions in model #2 (Fig. 6).

4. Discussion

In this investigation we observed that 1) the prevalence of COVID-19 in the community is likely underestimated based on posterior sensitivity of surveillance, 2) this underestimation is heterogenous by ZIP code in the city, 3) false diagnoses play a minimal role in overall reported cases based on near perfect posterior specificity. It is critical that public health have the best possible data to plan and respond to public health crises as they unfold, rather than relying upon statistical adjustment, such as ours. But if empirical estimates of accuracy of surveillance are not possible to obtain (as is the case early in any epidemic) decisions that are enshrined in policy must account for likely bias informed from analyses such as ours, rather than either pretending that surveillance data are perfect, or making qualitative unarticulated judgements about the extent of bias in the data (as is regrettably commonplace in epidemiology). Resources were limited during the early pandemic including testing kits, healthcare personnel, and personal protective equipment (CDC, 2020a, 2020c, 2020d). Any deviation between the surveillance of true cases of COVID-19 and reported cases can impact allocation of these precious resources in terms of when and where they are most needed. A key consideration of health departments is where known cases are occurring as they distribute resources depends upon this geospatial surveillance. For example, examining Fig. 2, which depicted the prevalence of COVID-19 cases based purely on known cases to the health department, one may reach different conclusions as to the magnitude of the outbreak compared to Fig. 5, which depicted the estimate of true prevalence.

Accurate estimates for true prevalence of COVID-19 for a given jurisdiction has been an area of great interest to the public health community but are still difficult to obtain: even our analysis required an informative prior, which should be defensible. Fortunately, historical data that justify informative priors are beginning to emerge from ongoing multi-faceted surveillance efforts, such as studies of seroprevalence surveys. In a study of residual blood specimens obtained from commercial laboratories across ten geographic sites in the U.S., age- and sex-standardized seroprevalence of SARS-CoV-2-specific antibodies, which would indicate current or past infection, were reported as high as 6.9% (95% confidence interval: 5.0, 8.9%) in the New York City metropolitan area to as low as 1.0% (95% confidence interval: 0.3, 2.4%) in the San Francisco Bay area (Havers et al., 2020). The Philadelphia metropolitan area had a seroprevalence of 3.2% (95% confidence interval: 1.7, 5.2%) and is in line with our citywide posterior prevalence. The authors estimated that in Philadelphia there were 6.8 infections per 1 reported case. It is important to note that the specimens obtained from the laboratories did not reflect a random sample of the population: these were individuals who sought healthcare for specific reasons, which may have biased the estimates reported by Havers et al. Testing the sewage for presence of the viral genetic material has been one innovative solution to address some of these concerns (Peccia et al., 2020). One such application at the county level noted a prevalence near 3%: 15 times the number of cases captured via surveillance at the time (Wilson, 2020).

Our analysis found one Philadelphia ZIP code in particular that was alarming: 19126. In consultation with the health department, we determined this particular ZIP code contained three nursing homes (personal communication, Philadelphia Department of Public Health). Congregant settings can serve as an ideal environment for respiratory disease transmission. In a study among residents of a large homeless shelter in Boston, 36% (n = 147) had a positive polymerase chain reaction assay, suggesting active infection (Baggett et al., 2020). A large outbreak at a single location could in fact drive the reported positive tests in surveillance data from a single ZIP code. Thus, we emphasize that methodological work such as ours requires knowledge of the surveillance and demographic processes to interpret the data.

Further complicating case detection has been concerns with the diagnostic test that is employed by health departments in the U.S. Among those tested, imperfect accuracy of the laboratory assay can make the difference between a false positive based on the clinical findings that are attributable to another cause, or a false negative based on lack of clinical findings consistent with COVID-19. As such, testing has crucial implications on surveillance so that we can formulate a more informed response to the pandemic. Despite the rapid development and deployment of various laboratory testing platforms by multiple parties, including nucleic acid testing and serological assays, limited data exist on the accuracy of these platforms (Yap et al., 2020). A limited body of existing research has suggested suboptimal sensitivity (in the range of 60-80% is likely realistic); the consequence of which is a large number of false negative test results. That is, individuals who may have SARS-CoV-2 infection, the virus that causes COVID-19 disease, are not always being correctly diagnosed via the PCR test, and subsequently, not reported to public health authorities, thereby potentially spreading the infection to susceptible individuals.

Additionally, and central to our research question, the availability and distribution of diagnostic tests has not been equitable (Bilal et al., 2020). The Centers for Disease Control and Prevention advises a priority-based approach to testing for the SARS-CoV-2 virus, the etiologic agent, based on age, occupation, and morbidity (CDC, 2020a). Indeed, this has been adopted and adapted in Philadelphia through a 4-tier testing prioritization approach (Vital Strategies, 2020). Until sufficient tests are available and anyone who seeks testing can be tested, disparities will persist. This includes asymptomatic persons who wish to be tested: by one estimate, at least 30% of total cases (and as high as 45%) may be asymptomatic (Oran and Topol, 2020). Thus, any analysis of historical secondary data needs to take into account potential proxies of testing prioritization, such as the area deprivation index we have used. Indeed, from our perspective this motivates the application of model #1, which conditioned true prevalence on ADI, as a preferred model.

There have been other efforts – both Bayesian and frequentist – to quantify and adjust for misclassification of infectious diseases captured through a surveillance process. Vaccine effectiveness studies may be biased by not taking into account underreporting and changing case definitions for pertussis, a reportable respiratory disease commonly called whooping cough (Goldstein et al., 2016). Specifically, they observed that sensitivity of surveillance varied from a low of 18% to a high of 90% depending upon assumptions about the amount of underreporting of true cases in the city. This had the consequence of biasing estimates of vaccine effectiveness between 32 to 95%. In a study of bias in Lyme disease surveillance, Rutz et al. noted that misclassification of disease resulted in an underestimation of probable and confirmed cases by 13% (Rutz et al., 2019). Principle reasons for this misclassification were similar to our hypotheses about COVID-19 surveillance: inaccurate diagnosis, complex surveillance resulting in missed cases, and incomplete reporting. A study by Bihrmann et al. examined misclassification of paratuberculosis in cattle, and whether this diagnostic error impacted spatial surveillance of the disease (Bihrmann et al., 2016). Although they observed meaningful nondifferential misclassification of the disease (diagnostic test sensitivity ~50%), after adjusting in prevalence modeling, this did not impact the observed spatial patterning suggesting the misclassification was homogenous across geographies.

We acknowledge the following limitations and strengths to this work. First, our measures of surveillance sensitivity and specificity may not be directly actionable. That is, we are unable to identify clearly where in the process the greatest bias is introduced in the data. For example, it may be that the diagnostic test has been sufficiently refined to leave only a trivial number of false negative and positive cases, and that the priority testing approach is solely responsible for the missed cases. Unfortunately, we cannot make any conclusions about the individual steps in the surveillance process. Second, we make a strong assumption that our models were correctly specified lest our results could be biased. Third and relatedly, our models were dependent upon an informative prior for true prevalence, yet our prior was based on non-Philadelphia data, because as far as we know, more directly applicable data were not available. The simulations provided a level of re-assurance that even with a miss-specified model or prior, reasonable approximation of true prevalence was still possible. Nevertheless, an important feature of our Bayesian modeling approach is the flexibility to test these various scenarios once improved surveillance data and prior knowledge become available. Our approach is also readily adaptable to other locales and time periods. By simply swapping in the reported surveillance data and estimates of true prevalence and the ADI effect, this analysis can be recreated for any jurisdiction, or updated for real-time analysis.

In conclusion, biases in surveillance of COVID-19 in Philadelphia tend to understate discrepancies in burden for the more affected areas, potentially leading to bias in setting priorities. Patient healthcare may be jeopardized if resources are incorrectly allocated as a result of this inaccuracy and subsequent failure to identify plausible worst-case scenario as is desirable for risk management. Our hope is that the improved maps in this study that account for surveillance inaccuracies can aid the Philadelphia Department of Public Health better direct resources to the areas at greatest risk. Beyond this jurisdiction, we have demonstrated a generalizable method that can be used for other locales responding to epidemics and dealing with imperfect surveillance data.

Declaration of Competing Interest

The authors have no conflicts to declare.