Continuous Learning in Model‐Informed Precision Dosing: A Case Study in Pediatric Dosing of Vancomycin

Abstract

Model‐informed precision dosing (MIPD) leverages pharmacokinetic (PK) models to tailor dosing to an individual patient’s needs, improving attainment of therapeutic drug exposure targets and thus potentially improving drug efficacy or reducing adverse events. However, selection of an appropriate model for supporting clinical decision making is not trivial. Error or bias in dose selection may arise if the selected model was developed in a population not fully representative of the intended MIPD population. One previously proposed approach is continuous learning, in which an initial model is used in MIPD and then updated as additional data becomes available. In this case study of pediatric vancomycin MIPD, the potential benefits of the continuous learning approach are investigated. Five previously published models were evaluated and found to perform adequately in a data set of 273 pediatric patients in the intensive care unit. Additionally, two predefined simple PK models were fitted on separate populations of 50–350 patients in an approach mimicking clinical implementation of automated continuous learning. With these continuous learning models, prediction error using population PK parameters could be reduced by 2–13% compared with previously published models. Sample sizes of at least 200 patients were found suitable for capturing the interindividual variability in vancomycin at this institution, with limited benefits of larger data sets. Although comprised mostly of trough samples, these sparsely sampled routine clinical data allowed for reasonable estimation of simulated area under the curve (AUC). Together, these findings lay the foundations for a continuous learning MIPD approach.

Study Highlights.

• WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

☑ Precision dosing is expected to improve patient outcomes, however, models developed in one patient population may perform poorly when translated to a new patient population. Continuous learning has been proposed as a strategy to improve model‐informed precision dosing (MIPD) by tailoring a model to the intended use population as more data become available.

• WHAT QUESTION DID THIS STUDY ADDRESS?

☑ This study assessed the potential benefits of implementing continuous learning and investigated the minimum amount of additional data required to produce a tailored model in a pediatric vancomycin intensive care population.

• WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

☑ This work shows that even simple prespecified models tailored to an organization match or outperform the predictive performance of external models, and that, for pediatric vancomycin, the benefits of increasingly large data sets over 200 patients is minimal.

• HOW MIGHT THIS CHANGE CLINICAL PHARMACOLOGY OR TRANSLATIONAL SCIENCE?

☑ Rather than creating increasingly complex or niche models from large and multi‐institutional data sets, MIPD models could be tailored to the intended population using an automated continuous learning approach.

Pharmacokinetic (PK) models have been brought to the point of care, aided by development and deployment of software tools that allow clinicians to estimate their patients’ PK parameters and simulate dosing regimens. ¹ , ² , ³ Preliminary studies suggest that this model‐informed precision dosing (MIPD) facilitates attainment of therapeutic targets, reduces drug‐induced adverse events, and improves clinical outcomes. ⁴ , ⁵ , ⁶ However, MIPD requires a model that adequately describes patient PKs for the drug of interest in the intended population, or that at least adapts appropriately to newly collected drug concentration data. Naive application of a previously published model could introduce bias or imprecision in dose selection. Developing a new model or validating existing models for each new patient population requires a sufficiently large prior data set collected from a sufficiently diverse group of patients and ideally from multiple institutions, and is time‐consuming. ¹ , ¹⁸ These efforts could delay implementation of MIPD in a particular clinical site, which comes with its own risks of drug overexposure or underexposure.

We have previously proposed a “continuous learning” approach ⁷ that iteratively refines a PK model to the MIPD population. This approach begins with selecting an initial model, either a “fit‐for‐purpose” model taken from the literature or developed from existing retrospective data, then implementing this model at the point of care. As clinical data become available through this routine clinical use, this model is then updated to better describe the MIPD population. Application of this continuous learning approach requires answering several unknowns. First, it is unclear how much improvement in prediction accuracy and bias can be attained by tailoring a model to a specific institution’s patient population. Second, it is not known how much additional clinical data is required to create a sufficiently predictive “continuous learning” model that outperforms models developed in external populations.

Here, we present a case study of the continuous learning approach in the application of MIPD to vancomycin dosing at a pediatric intensive care unit of a large urban research hospital. Vancomycin presents an important application of MIPD; it is listed by the World Health Organization (WHO) as an essential medicine, ⁸ there is considerable interindividual variability (IIV) in vancomycin PK, and rapid attainment of therapeutic exposure levels is associated with improved clinical outcomes, whereas overexposure is associated with nephrotoxicity. ⁹ , ¹⁰ , ¹¹ In this retrospective case study, we investigate the performance benefit of continuous learning models with simple, predefined model structures. Simple models such as these would allow more automated model development at smaller, non‐research institutions that may not routinely collect broad panels of biomarkers, and that may not have access to trained pharmacometricians. We compare the performance of these continuous learning models with five previously published pediatric vancomycin PK models, selected to represent the “standard of care” in MIPD. We examine how continuous learning model predictive performance improves with increasing sample size, and confirm that data collected through routine clinical care allows for adequate description of the full shape of the PK curve. Together, these experiments aim to validate the continuous learning approach, a critical first step toward implementing an automated or semi‐automated continuous learning model prospectively.

METHODS

Study approval

A waiver for informed consent was granted by the University of California, San Francisco (UCSF)’s Institutional Review Board (approval #17‐23274) because this retrospective review of deidentified data was assessed to involve no more than minimal risk to the subjects.

Patient data collection

Data for model fitting and model evaluation were collected retrospectively from routine clinical care of pediatric patients treated with intravenous vancomycin using the InsightRX precision dosing platform at the intensive care unit (ICU) of UCSF Benioff Children’s Hospital between March 2018 and May 2020. These data described vancomycin dose administration times, dose amounts and infusion rates; the collection times and measured values of serum creatinine (SCR) levels collected during or within a week prior to treatment with vancomycin; the collection times and measured quantities of vancomycin serum levels; patient age; total body weight; height; and sex. Patients between the ages of 51 days and 21 years and who had at least one vancomycin serum level recorded were included for analysis. Drug levels drawn during or within 15 minutes after infusion were excluded from analysis (n = 15). Patients for whom data appeared to be mistakenly entered (e.g., implausible patient weights) were removed from analysis (n = 4). Patients for whom medication administration times or quantities were ambiguous were removed from analysis (n = 4). The infusion duration was missing for one dose for one patient, and was imputed as being of the same duration as all other medication administrations during that treatment course. The final data set comprised of 673 individual patients, 11,403 doses, and 2,839 drug levels.

Population pharmacokinetic model training

Patient records were randomly assigned into an evaluation population (n = 323) and a model training population (n = 350). From this model training population, patient records were further randomly sampled to create one data set of 200 patients, one data set of 100 patients, and 5 data sets of 50 patients each (Figure 1 ). Randomization was performed with replacement such that each of these data sets contained each individual patient a maximum of one time, but such that one patient could be included in any number of these data sets.

Figure 1.

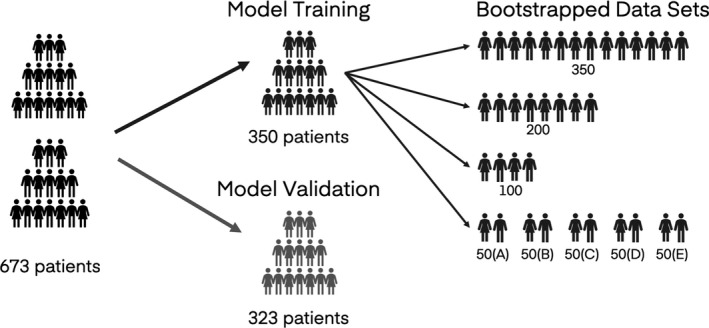
Diagram depicting creation of evaluation and model training data sets. Patients were randomly assigned to either the evaluation data set or the model training data set. Patients in the model training data set were then further randomly sampled to create additional subsampled data sets of 200, 100, or 50 patients. Sampling was performed such that each patient was included in each subsampled data set no more than once, but such that one patient could be included in more than one of the subsampled data sets.

Two linear population pharmacokinetic (PopPK) models were predefined using prior knowledge of vancomycin PKs to define an expected model structure and covariate model. The first PopPK model was a one‐compartment model (M1), parametrized with CL and V, and the second PopPK model was a two‐compartment model (M2), parametrized with CL, V, V2, and Q. PK parameters were scaled allometrically according to total body weight (WT; kg). There is broad agreement within the literature regarding covariates predictive of pediatric vancomycin PKs, with published models typically reporting creatinine clearance, SCR, postmenstrual age, postnatal age, and/or weight as statistically significantly improving model specification. Because vancomycin is primarily cleared renally, creatinine clearance and SCR were considered as covariates. SCR was more commonly included as a covariate in pediatric vancomycin studies ¹² , ¹³ , ¹⁴ , ¹⁵ vs. CR clearance, ¹⁶ and therefore SCR (mg/dl) was selected as a covariate acting on clearance. A variety of covariate models have been reported for SCR in pediatric vancomycin PK, including a power model ¹² , ¹³ and an exponential model. ¹⁴ , ¹⁵ A power model was implemented for ease of interpretation. Because a relatively high proportion of patients (30.9%) in this study were under the age of 1 year, a maturation factor based on postmenstrual age (weeks) was included in the clearance term using previously published covariate values. ¹⁷ Because this factor approaches 1 in older children, age (in years) was also included as a covariate using a power model. All covariates were allowed to vary over time. AGE and postmenstrual age were calculated at the time of each dose, vancomycin level, or other observation. All SCR and weight measurements collected during the treatment course were included. During ordinary differential equation integration, time‐varying covariates were handled with next‐observation carried backward. Based on these expected relationships, the following covariate models were used:

$$\text{TVCL}={\theta }_{\text{CL}}·{\left(\frac{\text{WT}}{70}\right)}^{0.75}·{\left(\frac{1}{\text{SCR}}\right)}^{{\theta }_{\text{SCR}}}·{\left(\frac{\text{AGE}}{7}\right)}^{{\theta }_{\text{AGE}}}·\left(\frac{{\text{PMA}}^{3.33}}{{\text{PMA}}^{3.33}+55.4^{3.33}}\right)$$

$$\text{TVV}={\theta }_V·\left(\frac{\text{WT}}{70}\right)$$

$$\text{TVV}2={\theta }_{V2}·\left(\frac{\text{WT}}{70}\right)$$

$$\text{TVQ}={\theta }_Q·{\left(\frac{\text{WT}}{70}\right)}^{0.75}$$

Model structure for explaining variability was also based on a review of typical practices for describing vancomycin PKs. IIV was included on CL and V for M1, and on CL, V, V2, and Q for M2. Correlation between ${\eta }_{\mathit{CL}}$ and ${\eta }_V$ was included for both models. A combined proportional and additive error model was used for both models. Other sources of variability, such as intrapatient variability, were not included in surveyed literature models, and were therefore not included in these predefined models.

NONMEM version 7.4.3 (GloboMax LLC, Hanover, MD) was then used to estimate the model parameters for these two predefined models using each of the eight subsampled data sets described in Figure 1 , resulting in 16 trained models. Following successful minimization, the covariance step was performed to assess the precision of the estimates. No further adjustments were made to model structure or covariate structure.

Population pharmacokinetic model evaluation

Model predictive performance was evaluated in the evaluation population data set. Here, predictive performance was defined as the ability of the tool to predict the next vancomycin level for the patient given all the data available prior to that level. These calculations were performed using the prospective evaluation (proseval) command in Perl‐speaks‐NONMEM. ¹⁸ , ¹⁹

A literature review was conducted to identify PopPK models describing vancomycin PK in pediatric patients, and five appropriate models were identified, summarized in Table 1 . The predictive performance of these models was evaluated in the evaluation population data set using the same method described above. The Le model ¹³ was used for MIPD of the patients included in this study; of the pediatric vancomycin models available at the time of the initial pilot MIPD period at this institution, it was the model developed in the largest patient population.

Table 1.

Literature models describing pediatric vancomycin pharmacokinetics selected for evaluation and comparison

Properties	Units	Avedissian	Colin	Kloprogge	Lamarre	Le
Citation		Avedissian et al. (2017)	Colin et al. (2019)	Kloprogge et al. (2019)	Lamarre, Lebel and Ducharme (2000)	Le et al. (2014)
Model structure		1 compartment, linear	2‐compartment, linear	2‐compartment, linear	2‐compartment, linear	1‐compartment, linear
Development population		Pediatric, ICU	Pooled data from 14 pediatric and adult studies	Pediatric	Pediatric	Pediatric
Patients	n	250	2,554	616	78	138
Vancomycin levels	n	658	8,300	4,137	256	712
Age	Years
Median (range)		9.8	(0.46–101)	(0.003–21.2)	7 (0.01–18)	6.1
Interquartile range		3.2–14.0				(2.2–12.2)
Mean (SD)			5.1
Weight	kg
Median (range)		30	(0.42–160)	0.742–95	25 (0.93–74)	22.2
Interquartile range		15.0–50.0				(13.2–37.9)
Mean (SD)				19
SCR	mg/dl
Median (range)			(0.15–9.75)	(0.057–10.1)		0.37
Interquartile range					(0.30–0.50)
Mean (SD)			0.44	0.54 (0.28)
Data handling		Excluded patients (n = 3) with SCR above the following age‐based thresholds at the start of vancomycin therapy: <2 years, 0.5 mg/dL; 2–12 years, 1 mg/dL; 12 + years, 1.3 mg/dL	Missing values for height or SCR were imputed with the median value for that study, or from an age‐matched national study in that population.	Excluded patients with samples > 48 hours after a dose. Assumed samples collected within 1.5 hours after the start of infusion were collected prior to drug administration instead.	Assumed troughs were collected 15 minutes prior to start of infusion and peak samples were collected 1 hour after.	Patients were included only if they had at least one peak sample and one trough sample, and n ≥ 3 samples overall.

SCR, serum creatinine; ICU, intensive care unit; SD, standard deviation.

Area under the curve estimation and simulation

Simulations were performed in NONMEM using the Kloprogge model. ¹² “True” area under the PK curve (AUC) was calculated for simulated patients, and drug concentrations were extracted with sampling schemes matching those in the original evaluation data set. The continuous learning models and the literature models were then each used to estimate the AUC over a 24‐hour interval at the time of each simulated drug concentration using the estimated individual PK parameters.

Statistics and error metrics

The difference between predicted values and measured values were described using root mean square error (RMSE) and mean percent error (MPE). To better understand the variability in these metrics, RMSE and MPE were calculated for 5,000 bootstrapped samples of 300 of the 323 patients in the model validation data set (Figure 1 ). The average, 2.5th percentile, and 97.5th percentile was determined for these bootstrapped samples, and overlap of the 2.5th−97.5th interval between models was compared to assess statistical significance. Analysis of data files generated by NONMEM and Perl‐speaks‐NONMEM was performed in R version 3.6.2. ²⁰ Nonparametric tests, such as the Wilcoxon rank sum test, were used to compare distributions that were not normally distributed.

RESULTS

Patients and data collection

Patient characteristics for the model training and evaluation data sets are shown in Table 2 . The model fitting population comprised of 350 patients and 1,549 vancomycin levels (average: 4.4 per patient) and the evaluation population comprised of 323 patients and 1,290 vancomycin levels (average: 4.0 per patient). Very few samples (~ 1%) were peak samples, defined here as collected within 2 hours after the end of infusion (Figure S1 ). No statistically significant differences between the evaluation population were found for the covariates listed (Wilcoxon rank sum hypothesis test P > 0.1).

Table 2.

Summary of data used for model training and model evaluation

Parameter	Units	Model training population	Model evaluation population
Patients	n	350	323
Vancomycin levels	n	1,549	1,290
Doses	n	6,154	5,249
Levels per patient median, (range)	n	2 (1–38)	2 (1–49)
Peak samples	n (%)	16 (1.0%)	15 (1.2%)
Level value, median (range)	mg/L	11 (1–56)	11 (0–60)
Percent male	%	60.6	57.0
Age, median (range)	years	3.5 (0.2–20.5)	3.85 (0.2–20.2)
Weight, median (range)	kg	12.25 (2.1–110.6)	15.1 (2.7–160.7)
SCR at treatment start, median (range)	years	0.3 (0.1–9.4)	0.3 (0.1–9)

SCR, creatinine.

Model training

The predefined one‐compartment and two‐compartment models were each trained on the eight subsampled data sets described in Figure 1 . Parameter estimates for the resulting eight one‐compartment models and eight two‐compartment models are summarized in Tables 3 , 4 , respectively. The number of patients in the data set used to fit the model is indicated in the name of each model. For example, M1‐100 is the one‐compartment model trained on 100 patients. For both model structures, there was reasonably good agreement and relatively low standard error in the parameters for the models developed on 200 patients and 350 patients. Although all 16 models minimized successfully, the covariance step could not be completed for 3 of the 5 one‐compartment models developed on 50 patients (M1‐50(A), M1‐50(D), and for M1‐50(E)) and for 3 of the 5 two‐compartment models developed on 50 patients (M2‐50(A), M2‐50(B), and M2‐50(C)). The models fit on the 100‐patient and 50‐patient data sets differed more substantially from the models developed on the larger data sets. This variability was particularly pronounced for the two‐compartment model, for which six thetas and four etas were estimated, compared to four thetas and two etas for the one‐compartment model.

Table 3.

Model parameters for one‐compartment continuous learning models

	Unit	M1‐350	M1‐200	M1‐100	M1‐50(A)	M1‐50(B)	M1‐50(C)	M1‐50(D)	M1‐50(E)
N patients		350	200	100	50	50	50	50	50
N samples		1,549	814	452	249	208	243	178	314
N cmt		1	1	1	1	1	1	1	1
${\theta }_{\text{CL}}$	L/hr	3.98 (6.1%)	3.8 (9.5%)	3.53 (9.9%)	3.96	4.15 (15%)	3.32 (13%)	3.76	3.56
${\theta }_V$	L	87.7 (7.7%)	93.8 (11%)	80.1 (11%)	83.5	64.8 (20%)	76.1 (18%)	87	73
${\theta }_{\text{SCR}}$		0.648 (7.7%)	0.682 (12%)	0.679 (10%)	0.64	0.589 (21%)	0.766 (12%)	0.641	0.579
${\theta }_{\text{AGE}}$		0.0622 (36%)	0.0435 (66%)	0.0617 (59%)	0.0661	0.0814 (60%)	0.0486 (110%)	0.009	0.009
Prop.	%	0.261 (3.1%)	0.259 (4.4%)	0.284 (5.7%)	0.308	0.272 (5.1%)	0.242 (8.7%)	0.291	0.293
Add.	mg/L	1.68 (55%)	1.79 (67%)	2.08 (83%)	0.0105	0.477 (190%)	1.72 (160%)	0.0105	1.48
${\eta }_{\text{CL}}$		0.384 (4.3%)	0.368 (6.7%)	0.427 (7.4%)	0.344	0.424 (16%)	0.406 (12%)	0.453	0.381
${\eta }_{\text{CL}}\sim {\eta }_V$		0.626 (3.5%)	0.578 (5%)	0.866 (4.1%)	0.835	0.631 (8.7%)	0.388 (14%)	0.512	0.266
${\eta }_V$		0.555 (11%)	0.554 (17%)	0.487 (13%)	0.457	0.403 (16%)	0.561 (21%)	0.717	0.429

Values shown are estimates with the relative standard error (RSE) expressed in parentheses. Missing RSE values indicate the covariance step could not be performed in NONMEM.

SCR, serum creatinine; N _cmt, number of compartments in the training data set; N _patients, number of patients in the training data set; N _samples, number of vancomycin serum levels in the training data set.

Table 4.

Model parameters for two‐compartment continuous learning models

	Unit	M2‐350	M2‐200	M2‐100	M2‐50(A)	M2‐50(B)	M2‐50(C)	M2‐50(D)	M2‐50(E)
N patients		350	200	100	50	50	50	50	50
N samples		1549	814	452	249	208	243	178	314
N cmt		2	2	2	2	2	2	2	2
${\theta }_{\text{CL}}$	L/hr	3.4 (0.54%)	2.7 (12%)	2.95 (10%)	3.8	3.67	3.06	2.68 (180%)	1.2 (63%)
${\theta }_V$	L	65.5 (8.9%)	66 (8.5%)	54.7 (15%)	60.8	28.3	69.4	41.7 (88%)	56.9 (14%)
${\theta }_{\text{SCR}}$		0.658 (0.85%)	0.727 (11%)	0.645 (11%)	0.58	0.474	0.773	0.76 (180%)	0.914 (29%)
${\theta }_{\text{AGE}}$		0.0854 (6.0%)	0.0715 (44%)	0.0975 (34%)	0.0611	0.0853	0.039	0.0786 (17%)	0.0473 (280%)
${\theta }_{V2}$	L	109 (2.8%)	459 (39%)	135 (59%)	28.8	28.5	26.6	38.5 (0.8%)	5870 (160%)
${\theta }_Q$	L/hr	1.23 (5.2%)	1.86 (17%)	1.69 (21%)	0.958	1.69	0.661	1.28 (1.4%)	2.63 (36%)
Prop.	%	0.264 (0.61%)	0.262 (3.7%)	0.314 (4.7%)	0.297	0.267	0.233	0.262 (0.48%)	0.286 (4.9%)
Add.	mg/L	1.13 (2.0%)	1.02 (74%)	0.544 (150%)	0.0105	0.0105	1.52	1.29 (9.1%)	0.605 (92%)
${\eta }_{\text{CL}}$		0.422 (90%)	0.468 (8.3%)	0.463 (9.7%)	0.403	0.546	0.444	0.314 (8.9%)	0.523 (31%)
${\eta }_{\text{CL}}\sim {\eta }_V$		0.868 (16%)	0.878 (5%)	0.939 (8.1%)	0.969	1	0.585	0.322 (88%)	0.524 (23%)
${\eta }_V$		0.493 (160%)	0.508 (14%)	0.572 (21%)	0.577	0.95	0.733	0.392 (16%)	0.253 (22%)
${\eta }_{V2}$		1.86 (26%)	1.01 (38%)	2.16 (130%)	0.271	0.00316	0.00316	0.147 (34%)	1.97 (180%)
${\eta }_Q$		0.926 (3.5%)	0.899 (22%)	0.386 (27%)	1.26	1.49	1.38	1.73 (23%)	0.707 (32%)

Values shown are estimates with the relative standard error (RSE) expressed in parentheses. Missing RSE values indicate the covariance step could not be performed in NONMEM.

SCR, serum creatinine; N _cmt, number of compartments in the training data set; N _patients, number of patients in the training data set; N _samples, number of vancomycin serum levels in the training data set.

Model evaluation

The predictive capacity of these 16 simple models and of 5 models taken from the literature were evaluated on a holdout data set of 323 patients, and error was assessed using RMSE (Figure 2a,b ) and MPE (Figure 2c,d ). For each patient, the first vancomycin level was predicted using population estimates (Figure 2a,c ). Subsequent levels were predicted prospectively, using the first n −1 levels to estimate the individual’s PK parameters, and then using these parameters to predict the nth level (Figure 2b,d ). Statistical significance was determined by overlap of the 2.5th–97.5th percentiles of bootstrapped samples (Figure S2 ).

Figure 2.

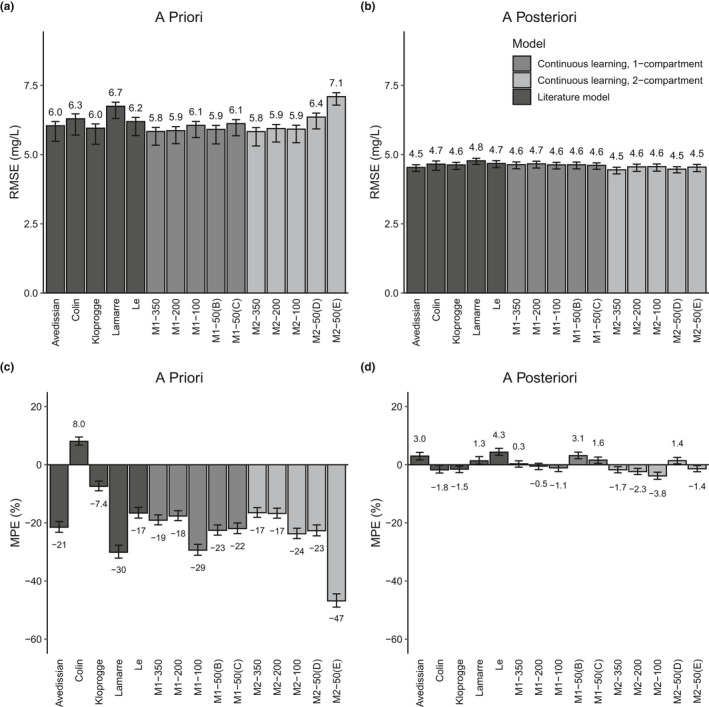
Root mean squared error (RMSE) and mean percent error (MPE) for the population estimate for the first vancomycin level and for the prospective prediction using MAP Bayesian estimation of patient parameters for subsequent levels. Bars indicate the average value of bootstrapped samples, and error bars indicate the 2.5th and 97.5th percentile of bootstrapped samples. The six models for which the covariance step could not be estimated (see Tables 3 , 4 ) have been excluded, for clarity.

Four of the previously published models selected for evaluation produced similarly precise predictions, with population prediction RMSE values between 6.0 and 6.3 mg/L (Figure 2a ). The Lamarre model produced statistically significantly less precise predictions a priori. Four of these literature models showed a persistent bias toward predicting higher levels than observed for population estimates (MPE ranging from −7.4% to −30%), whereas the Colin model a priori predictions were, on average, lower than the observed levels (MPE: 8.0%; Figure 2c ). Of these five models, the Kloprogge model, which was developed in a comparatively densely sampled population of 616 pediatric patients, showed the lowest error and bias in population estimates for the patients in this study. Differences among the five literature models shrank for predictions of subsequent levels, with RMSE ranging between 4.5 and 4.8 mg/L and MPE ranging between −1.8% and 4.3%.

The one‐compartment continuous learning model developed on 350 patients (M1‐350) showed a 3–13% reduction in RMSE compared with the literature models for the population estimate of the first vancomycin level (RMSE: 5.8 mg/L), however, bias was larger than that of 3 of the literature models (19%). The one‐compartment model developed on 200 patients (M1‐200) performed very similarly (RMSE: 5.9 mg/L, MPE: 18%). The one‐compartment model developed on 100 patients (M1‐100) showed a considerable increase in bias (29%), although RMSE for this model was still similar to the RMSE calculated for the models from the literature. Consistent with the high variability between model parameters for the five 50‐patient models (Table 3 ), the predictive performance of the 50‐patient models showed considerable variability in error and high bias (RMSE: 5.9–6.4 mg/L; MPE: −21 to −39%). All one‐compartment models, regardless of the size of the data set used to train the models, showed similar error and bias for a posteriori prediction of levels (RMSE: 4.6 to 4.7 mg/L; MPE: −1.3% to 2.9%).

The 2‐compartment model developed on 350 patients (M2‐350) also produced a 3–13% reduction in RMSE compared with the literature models, and prediction bias was slightly but not significantly less than that of M1‐350 (−17% vs. −19%). As seen with the one‐compartment model, reducing the training population sample size to 200 patients resulted in very little change in predictive capability. The 50‐patient data sets showed considerable variability in error and bias (RMSE: 5.9–7.1 mg/L; MPE: −9.2%–47%). All two‐compartment models performed similarly for prediction of levels after the first (RMSE: 4.4–4.6 mg/L; MPE: −4.1–1.3%).

AUC estimation

Vancomycin dosing guidelines emphasize the ratio of AUC over 24 hours to minimum inhibitory concentration as the primary PK/pharmacodynamic predictor of vancomycin activity. For optimal AUC‐guided MIPD, consideration must be given not only to the ability of a model to predict a trough level, but also to its ability to describe the full shape of a PK curve. Because the data available in this study were collected during routine clinical care, and because peak samples are not routinely collected at this institution (Figure S1 ), we were concerned that the continuous learning models, especially those implementing one‐compartment kinetics, would not be able to capture the full PK curve. Misspecification of the PK curve would result in erroneous and/or biased AUC estimates. The gold standard for estimating AUC is noncompartmental analysis, however, this approach requires densely sampled serum concentrations. Instead, simulated “true” AUC estimates were compared with AUC estimates produced by each of the literature models and the continuous learning models (Figure 3 ). The Kloprogge model was selected for creating the simulated data set and simulated “true” AUC values because it was (i) a two‐compartment model, and vancomycin PK is most commonly found to be described by two compartments, (ii) developed in a more densely sampled data set than the other models under consideration (6.7 samples per patient; Table 1 ), and (iii) described the patients in this population well (Figure 2 ). For clarity, the models developed in 50 patients have been excluded, because their predictive performance and the precision of their parameter estimates was not acceptable (Figure 2 , Tables 3 , 4 ). Statistical significance of differences was assessed by comparing overlap of the 2.5th–97.5th percentiles of the RMSE and MPE of bootstrapped AUC estimates (detailed in Figure S3 ).

Figure 3.

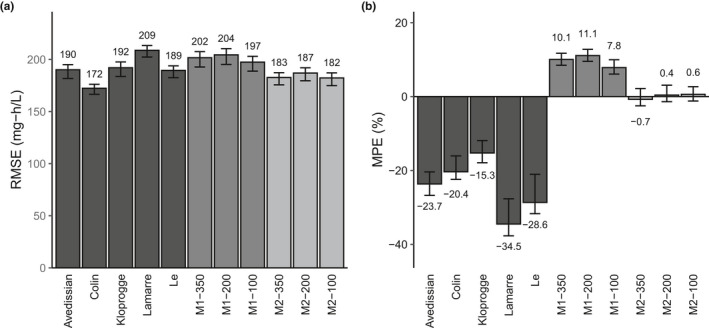
Estimation of area under the curve (AUC) for simulated concentration‐time curves. (a) Root mean squared error (RMSE) and (b) mean percent error (MPE) for AUC estimates for the literature models, one‐compartment (M1) and two‐compartment (M2) continuous learning models for data simulated using the Kloprogge model. Bars indicate the average value of bootstrapped samples and error bars indicate the 2.5th and 97.5th percentile of bootstrapped samples. AUC calculation error is expressed relative to the simulated “true” AUC.

The literature models estimated AUC with RMSE ranging from 172–209 mg‐h/L (Figure 3a ) and MPE ranging from −34.5% to −15.3% (Figure 3b ). There was no clear improvement in AUC estimation between the one‐compartment models (Avedissian and Le) and the two‐compartment models (Colin, Kloprogge, and Le). The two‐compartment continuous learning models estimated AUC with significantly lower error (RMSE: 182–187 mg/L) compared to the one‐compartment continuous learning models (RMSE: 197–204 mg/L), and with significantly lower bias than the one‐compartment continuous learning models (MPE: 0.4–−0.7% vs. 7.8–11%). There were no appreciable benefits in developing models on larger data sets. The Colin model produced the most precise estimates of AUC, although was not statistically significantly different from two two‐compartment continuous learning models (M2‐350 and M2‐100), which showed significantly less bias.

DISCUSSION

The benefits of MIPD hinge on models that are sufficiently predictive of patient PKs. The research presented here supports the continuous learning approach, finding that literature models vetted for their applicability to a particular patient population performed acceptably well, but that prediction precision and bias could be improved by tailoring models to the hospital’s patient population.

Development of PopPK models is a lengthy, iterative process that requires considerable expertise and training. ¹⁸ , ²¹ In this study, simple predefined models developed in the same patient population for which they were intended to be used were found to outperform or match the predictive capacity of previously published models that were developed according to a more conventional and time‐consuming process. It should be noted that the literature on vancomycin PK is relatively rich, ¹⁴ , ²² , ²³ and the prespecified model structure was therefore well‐informed. MIPD of less well‐described drugs may be better enabled by the use of alternative strategies, such as reducing the weight of the model priors during patient PK parameter estimation. ⁷ For some drugs, there is poor consensus in the literature regarding which covariates are statistically significant predictors of PKs. For these applications, continuous learning may need to be expanded to include a systematic covariate selection process. Still, there are a number of other drugs well‐positioned for MIPD that could benefit from the continuous learning strategy presented here. ²⁴ , ²⁵

There appears to be limited gains in predictive performance from fitting a continuous learning model on > 200 patients, with the models fit on 350 patients and 200 patients performing similarly in prediction error and bias. Consistent with this finding, the models from the literature trained on at least 200 patients (Avedissian: 250, Colin: 2,554, and Kloprogge: 616) generally showed better predictive performance than those of models fit on fewer than 200 patients (Lamarre: 78, and Le: 138). The estimates for model parameters for the 350‐patient models and the 200‐patient models showed relatively good agreement, although the precision of the estimates improved with additional data. Although predictive performance benefits were slight, users may feel more confident implementing models with narrower confidence intervals around the population parameters. The model validation performed here provides evidence that fitting models on large data sets collected across multiple facilities (e.g., Colin model) does not necessarily translate to models that are more transferable to new patient populations. This model validation study also did not find evidence that more niche models are necessarily better for MIPD; whereas the Avedissian model was developed specifically to describe pediatric patients in the ICU such as those patients included in this study, it did not outperform the Kloprogge model, which was developed to describe a more general pediatric patient population. These findings may not transfer readily to other drugs in a clinical MIPD setting. For example, drugs with higher IIV than vancomycin may require larger data sets for continuous learning model fitting. Drugs with more complex model structures or more complex covariate structures would also likely require larger patient data sets. It is also possible that other institutions may have more or less IIV.

Differences between model predictive performance for the models evaluated here were more pronounced for predictions made using population estimates compared with predictions made after vancomycin levels were available. Accurate population estimate predictions are a crucial component of MIPD. Prior work suggests that reaching PK targets within the first 24–48 hours of vancomycin therapy is associated with improved clinical outcomes ⁹ , ¹⁰ , ²⁶ and has been recommended as part of the updated guidelines for vancomycin therapy. ²³ Compared with the application of models developed external to an institution, the continuous learning approach may allow for better estimation of how the “average” patient treated at that institution will respond prior to the availability of therapeutic drug monitoring levels. These improvements in PopPK predictions could facilitate earlier attainment of exposure targets.

One potential limitation in training models using data collected over the course of clinical care is that the samples collected are predominantly trough samples, limiting examples from which a model may learn how to describe peak concentrations. This capability is particularly important for drugs like vancomycin, for which the AUC is the primary consideration for guiding dosing decisions. ²³ However, in simulated patients, the continuous learning models performed on par with or better than the literature models at estimating the true AUC for these simulated patients. The more biased AUC estimates produced by the Kloprogge model was unanticipated, but may arise from the individual PK parameter estimates being based on less informative observations (i.e., predominantly trough samples) relative to the data that informed the model priors. It should be noted that these AUC estimates are not predicted AUCs but estimated using all data available for each simulated patient. Still, together, these data show that models trained using the continuous learning approach on data collected during routine clinical care adequately estimate AUC. Furthermore, AUC‐guided MIPD strategies allow for less reliance on trough sampling and more random sampling, which may further improve the data available for continuous learning approaches.

In this paper, we validated the ability of the continuous learning approach to improve upon the MIPD standard of care (i.e., models taken from the literature), both in terms of model predictive capacity and ability to estimate AUC. We also studied minimum data requirements before acceptably predictive continuous learning models could be produced. However, there remain important continuous learning implementation questions. From a regulatory perspective, prospective continuous learning implementation must satisfy applicable regulatory standards. ²⁷ From a technical perspective, prospective implementation of continuous learning will also require implementation of controls to prevent overfitting or model drift. ²⁸ , ²⁹ , ³⁰ Although some approaches have been proposed for managing these concerns in a healthcare context, additional work will be required to extend and validate these methods for nonlinear mixed effects models. From a clinical perspective, the reasons for why, how, and when continuous learning models change over time must be explainable and communicated clearly to the clinicians using MIPD at the point of care. ³¹

It will be interesting to examine further what the sources of variability better explained by a continuous learning institution‐tailored model might be. These sources could include obesity rates or other comorbidities present in the population treated at this institution, typical comedications administered at this institution, or sampling practice and assay error magnitudes in this institution. The continuous learning framework presented here could also be extended to investigate the impact of pharmacogenomics on PKs and pharmacodynamics in a variety of drugs. As genetic testing becomes a more routine component of patient care, single‐nucleotide polymorphism or other genetic information could be added to existing PK models through the continuous learning process. It will be important to investigate the potential benefits of continuous learning using a more sophisticated model development process that would evaluate covariate model structures in more detail; still it is promising that such simple models as examined here perform well. The work described here provides an early case study of the continuous learning approach in pediatric vancomycin MIPD, and the applicability of these findings to other drugs and patient populations will be exciting future directions.

Funding

No funding was received for this work.

Conflict of Interest

J.H.H., D.M.H.T., J.D.F., S.G., and R.J.K. are employees and stockholders of InsightRX. All other authors declared no competing interests for this work.

Author Contributions

J.H.H. wrote the manuscript. S.G., R.J.K., and J.H.H. designed the research. J.H.H., R.J.K., J.D.F., S.S.L. performed the research. S.G., R.J.K., J.H.H., and D.M.H.T. analyzed data.

Supporting information

Figure S1

Figure S2

Figure S3

SupplementaryMaterial S1

SupplementaryMaterial S2