Mechanisms of Premature Ventricular Complexes Caused by QT Prolongation

Abstract

QT prolongation, due to lengthening of the action potential duration in the ventricles, is a major risk factor of lethal ventricular arrhythmias. A widely known consequence of QT prolongation is the genesis of early afterdepolarizations (EADs), which are associated with arrhythmias through the generation of premature ventricular complexes (PVCs). However, the vast majority of the EADs observed experimentally in isolated ventricular myocytes are phase-2 EADs, and whether phase-2 EADs are mechanistically linked to PVCs in cardiac tissue remains an unanswered question. In this study, we investigate the genesis of PVCs using computer simulations with eight different ventricular action potential models of various species. Based on our results, we classify PVCs as arising from two distinct mechanisms: repolarization gradient (RG)-induced PVCs and phase-2 EAD-induced PVCs. The RG-induced PVCs are promoted by increasing RG and L-type calcium current and are insensitive to gap junction coupling. EADs are not required for this PVC mechanism. In a paced beat, a single or multiple PVCs can occur depending on the properties of the RG. In contrast, phase-2 EAD-induced PVCs occur only when the RG is small and are suppressed by increasing RG and more sensitive to gap junction coupling. Unlike with RG-induced PVCs, in each paced beat, only a single EAD-induced PVC can occur no matter how many EADs in an action potential. In the wide parameter ranges we explore, RG-induced PVCs can be observed in all models, but the EAD-induced PVCs can only be observed in five of the eight models. The links between these two distinct PVC mechanisms and arrhythmogenesis in animal experiments and clinical settings are discussed.

Significance

QT prolongation promotes early afterdepolarizations (EADs) in the single cell and ventricular arrhythmias in the heart. It is widely accepted that EADs can propagate in tissue to generate premature ventricular complexes (PVCs) as arrhythmia triggers, but there is little experimental evidence to support this. Here, we used computer simulations of different ventricular action potential models of various species to investigate the genesis of PVCs and the mechanistic links between EADs and PVCs. We identified two mechanisms of PVCs: repolarization-gradient-induced PVCs and EAD-induced PVCs, which exhibit distinctly different behaviors. The mechanistic insights from our study provide a better understanding of the links between QT prolongation, EADs, and arrhythmogenesis, which may help to identify effective therapeutic targets.

Introduction

Early afterdepolarizations (EADs) are abnormal depolarizations during the plateau or repolarizing phase of an action potential (AP) in cardiac myocytes (1, 2, 3). EADs have been widely demonstrated experimentally in single cells and tissue and thus are considered a major cause of arrhythmias (4, 5, 6, 7, 8, 9), particularly in long QT syndrome (LQTS) and heart failure. It has been hypothesized that EADs cause arrhythmias via the following three scenarios: 1) lengthening AP duration (APD) regionally to result in a tissue substrate for unidirectional conduction block and thus the formation of reentry, 2) resulting in premature ventricular complexes (PVCs) that serve as triggers for reentry formation, and 3) causing repetitive firings to result in sustained focal arrhythmias. In the latter two scenarios, the PVCs or the focal arrhythmias are believed to be triggered by EADs or result from EAD propagation in tissue. In other words, similar to normal AP propagation (10, 11, 12, 13, 14), it is believed that EADs can also propagate from the EAD-prone region to a normal region as long as the source-sink effect is favorable. Although this paradigm is widely accepted, little experimental evidence is available to support it, and the exact mechanistic links between EADs and PVCs have not been well established.

In early experimental studies, two distinct types of EADs were observed in Purkinje fibers (15, 16, 17, 18). For example, Damiano and Rosen (15) showed that in isolated canine Purkinje fibers, at an extracellular potassium (K⁺) concentration of 4 mM, EADs occurred at membrane potentials of −3 to −30 mV, with amplitudes being 2–30 mV. Because these EADs occurred during phase 2 of the APs, they are called phase-2 EADs. At a K⁺ concentration of 2 mM, EADs occurred at much more negative membrane potentials (−50 to −70 mV) with larger amplitudes. These EADs are called phase-3 EADs because they occurred during phase 3 of the APs. Damiano and Rosen observed that the phase-2 EADs did not induce triggered APs (aka PVCs), whereas the phase-3 EADs did. Other experimental studies of Purkinje fibers also show similar observations (19,20).

Experimental studies in ventricular tissue have also been carried out to link phase-2 EADs with PVCs. Yan et al. (21,22), using rabbit and canine left ventricular wedge preparations and microelectrode recordings, observed phase-2 EADs in the endocardial layer and triggered responses (aka PVCs) in the epicardial layer in the same paced beat. Although these studies provide direct evidence for the association between phase-2 EADs and PVCs, a causal link between phase-2 EADs and PVCs is still missing. Liu and Laurita (23) also used a canine left ventricular wedge preparation and optical mappings and observed that “Interestingly, the breakthrough site of triggered activity always occurred where local repolarization gradients were largest, not where APD was longest or shortest.” In other words, the triggered beat did not originate from the region of the longest APD (the M-cell or the endocardial region) where EADs are more likely to occur. Other optical mapping studies (24,25) have also shown similar results that the triggered beats always originate from the steep APD gradient region, not from where APD is the longest. Although phase-2 EADs were present in these studies, it cannot be established that the triggered beats are caused by the phase-2 EADs based on the recordings alone.

In addition to the experimental observations in Purkinje fibers and ventricular tissue, another important observation is that EADs observed in isolated ventricular myocytes are almost exclusively phase-2 EADs, as detailed in our previous study (26). The EADs observed in computer simulations of many AP models are also phase-2 EADs (see statistical results in our previous study (26), as well as EADs shown in many other computer simulations (27, 28, 29, 30, 31)). This raises a key question: are phase-2 EADs causally linked to PVCs in cardiac tissue? Answering this question is of great importance because it not only can reveal the mechanisms by which PVCs arise but can also be helpful in identifying novel therapeutic targets.

In a previous study (25), we used a rabbit ventricular AP model to show that phase-2 EADs were either suppressed or confined in heterogeneous tissue, and PVCs emerged in tissue because of a tissue-scale dynamical instability caused by the repolarization gradient (RG) and enhanced I_Ca,L. However, because that study’s conclusion was drawn only from a rabbit ventricular AP model, it is not clear whether that result is generalizable to other species or other AP models. Moreover, our previous study did not reveal whether or how phase-2 EADs and PVCs are causally related. In this study, we carried out simulations of single cells and one-dimensional (1D) cables using ventricular AP models of different species, including guinea pig, rabbit, canine, and human, to investigate the mechanisms of PVCs and the causal links between EADs and PVCs under conditions of QT prolongation. We simulated a total of eight AP models and scanned wide ranges of parameters. Despite large differences in EAD and PVC behaviors among the AP models, we can classify the PVCs into two broad mechanisms: RG-induced PVCs and phase-2 EAD-induced PVCs. The RG-induced PVCs are promoted by increasing RG, whereas the EAD-induced PVCs occur only when RG is small. Interestingly, phase-2 EADs play almost no role in the first mechanism but are required in the second mechanism. PVCs in the second mechanism occur in narrow bands of parameters. We propose two scenarios of arrhythmogenesis based on the two mechanisms of PVC genesis and discuss their implications for clinical arrhythmias.

Methods

AP models

The following ventricular AP models were used in this study: 1) the 1994 Luo and Rudy (LRd) guinea pig ventricular AP model (32,33), 2) the 2004 Shannon et al. (SB) rabbit ventricular AP model (34), 3) the 2004 Hund and Rudy (HRd) canine ventricular AP model (35), 4) the 2004 ten Tusscher et al. (TP04) human epicardial ventricular AP model (36), 5) the 2010 Grandi et al. (GB) human epicardial ventricular AP model (37), 6) the 2011 O’Hara et al. (ORd) human endocardial ventricular AP model (38), and 7) the 2019 Tomek et al. (ToRORd) human endocardial ventricular AP model (39), which is modified from the ORd model. The original codes for the AP models were downloaded from the authors’ websites and incorporated into our own C++ and CUDA codes for simulation. For convenience, we have listed the maximum conductance of the major currents in Table S1 and plotted the I/V curves for I_Ca,L in Fig. S1 for the seven models we used in this study. We also simulated the simple 1991 Luo and Rudy (LR1) guinea pig ventricular AP model (40) to gain better mechanistic insights for PVC genesis. To generate EADs in the LR1 model, we modified the following time constants: τ_d → 0.3τ_d, τ_f → 0.5τ_f, and τ_x → 6τ_x. We set G_K = 1 mS/cm² and G_K1 = 0.4 × 0.6047 mS/cm² as control and varied G_K and G_si to generate EADs and PVCs.

Single-cell model

Single-cell simulations were carried out for EADs. The governing ordinary differential equation for voltage (V) is

$$\frac{dV}{dt}=-\frac{I_{ion}+I_{stim}}{C_m},$$ (1)

where C_m = 1 μF/cm² and I_ion is the total ionic current density. I_stim is the stimulus current density, which is a short pulse. Repolarization failure (RF) was defined if the voltage remains depolarized in the whole duration of the simulation, which was 5 s.

1D cable model

1D cable simulations were carried out for the genesis of PVCs. The governing partial differential equation for voltage (V) in the 1D cable is

$$\frac{\partial V}{\partial t}=-\frac{I_{ion}+I_{stim}}{C_m}+D\frac{{\partial }^{2}V}{\partial x^2},$$ (2)

where D = 0.0005 cm²/ms is the diffusion constant which gives rise to a typical conduction velocity around 0.4 m/s, depending on the specific AP model. I_stim was the same as in the single-cell simulations. No-flux boundary conditions were used. The length of the cable is 200 cells with the cell length Δx = 0.015 cm. RG was modeled by setting heterogeneous G_Ks or G_Kr in the cable as detailed further below.

Initial conditions and pacing protocols

The initial condition is the same as in the original code of each model downloaded from the repository site of the original authors. The durations and strengths of the stimulation pulses are also the same as in the original code of each model. A single pacing stimulus was applied at t = 100 ms to elicit an AP to observe EADs and RF. For the 1D cable, all cells were given the same initial conditions as those for the single-cell simulations. A single pacing stimulus was applied simultaneously to all cells in the cable at t = 100 ms to observe PVCs. The simulation duration for each simulation (or parameter set) is 5 s for both single-cell and 1D cable simulations.

Note that the stimulus is applied simultaneously to all cells in the cable instead of one end of the cable. The main reason is that to closely compare the single-cell behaviors with the genesis of PVCs in the cable, the cells in the cable are stimulated in the same way with the same initial conditions as for the single cells. If the pacing is applied at one end, the cells in the cable are stimulated via the diffusive current, which is different from the external stimulus. Moreover, conduction in the cable results in different conditions at the moments of excitation for different cells. On the other hand, the heart is a three-dimensional (3D) organ in which the conduction is along one direction, and the cells in the direction perpendicular to the direction of conduction are excited almost simultaneously, such as the cells in the endocardial layer. Therefore, the simultaneous pacing protocol is physiologically relevant. Nevertheless, we compared pacing from one end with simultaneous pacing, and the results only differ slightly (see Fig. S5).

LQTS conditions

We simulated three types of LQTS: LQTS type 1 (LQT1), LQTS type 2 (LQT2), and LQTS type 3 (LQT3). For LQT1, I_Ks was removed by setting the maximum conductance G_Ks = 0. For LQT2, I_Kr was removed by setting the maximum conductance G_Kr = 0. Note that these are the most extreme conditions of LQTS, such as in the transgenic rabbit models of LQTS (41). For LQT3, the late sodium current I_NaL was increased. For consistency, we added the I_NaL formulation from the HRd model (35) to all models. The maximum conductance G_NaL = 0.0065 mS/μF was used in the original HRd model, and we increased G_NaL by 10 times to G_NaL = 0.065 mS/μF to model LQT3, which gives rise to a peak I_NaL between 1 and 1.5 pA/pF depending on the specific AP model. The APs for control and under the three LQTS conditions are shown in Fig. S2 for the seven AP models.

Parameter settings

Besides altering the maximum conductance to model different LQTS conditions, we also altered the maximum conductance of other ionic currents to elicit EADs in the single cell and PVCs in the 1D cable. We used α to denote the fold change of a parameter from its value in the original model. For example, α(P_Ca) indicates that the maximum conductance of I_Ca,L is α-fold of that in the original model, and thus, α(P_Ca) = 1 corresponds to the maximum I_Ca,L conductance being the control value.

We carried out two types of simulations. In the first type, we scanned α(P_Ca) and α(G_Kr) (LQT1) or α(G_Ks) (LQT2 and LQT3) for EADs and RF in the single cell (Fig. 1) and PVCs in the 1D cable (Fig. 2). The 1D cable (see Fig. 2 H) was divided into two equal regions (100 cells each), a long APD region and a short APD region, by setting G_Ks (LQT2 and LQT3) or G_Kr (LQT1) differently in the two regions. Other parameters were uniform throughout the whole cable. We denoted the change in G_Ks or G_Kr as α(G_Ks) or α(G_Kr) in the long APD region and the change in G_Ks or G_Kr as β(G_Ks) or β(G_Kr) in the short APD region [β(G_Ks) ≥ α(G_Ks) or β(G_Kr) ≥ α(G_Kr) was used to maintain the long and short APD regions].

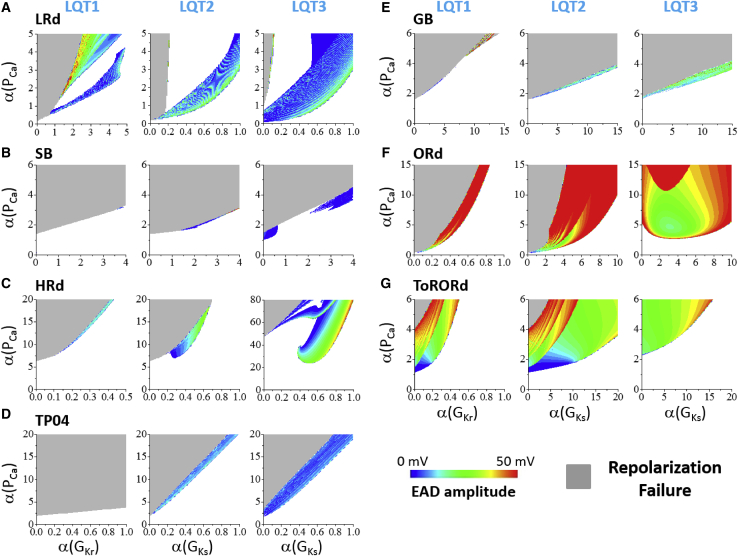
Figure 1.

Phase diagrams showing AP behaviors in an uncoupled myocyte under different LQTS conditions. Phase diagrams for AP behaviors under three LQTS conditions (LQT1, LQT2, and LQT3) for seven ventricular AP models are shown. For each panel, the y axis is fold change in P_Ca and the x axis is fold change in G_Kr (LQT1) or G_Ks (LQT2 and LQT3). The white region is normal repolarization, the gray region is RF, and the colored region is the AP exhibiting EADs. The EAD amplitude is indicated by the color scale. (A) LRd model is shown. (B) SB model is shown. (C) HRd model is shown. (D) TP04 model is shown. (E) GB model is shown. (F) ORd model is shown. (G) ToRORd model is shown. To see this figure in color, go online.

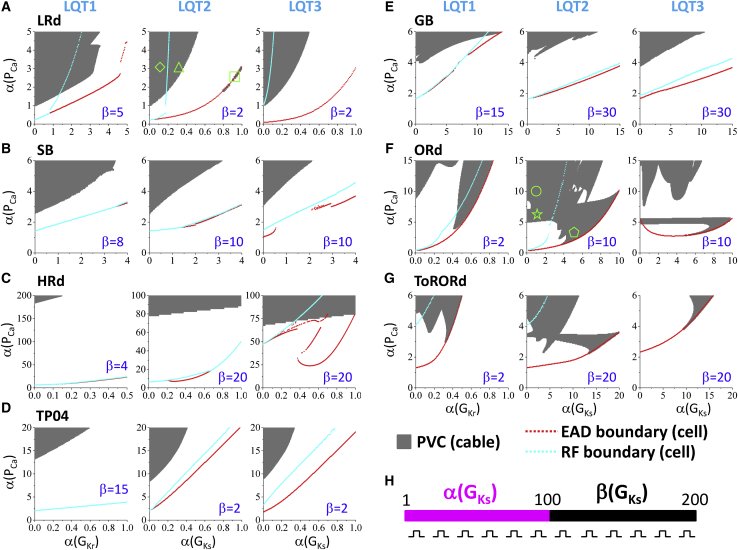
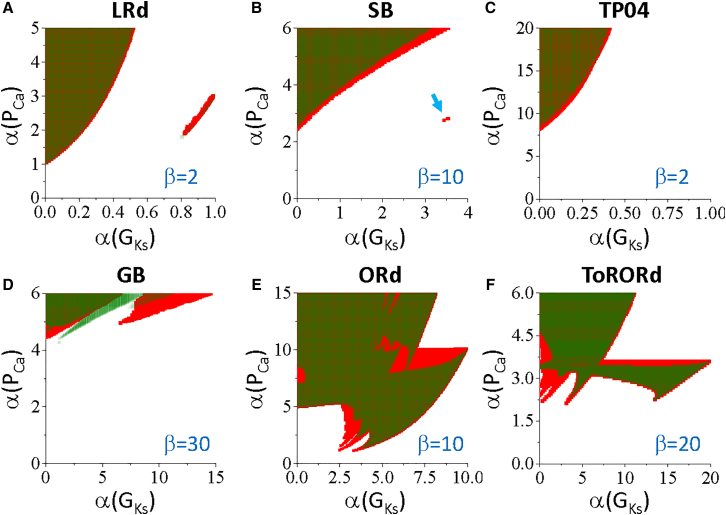
Figure 2.

Effects of I_Ca,L and RG on PVC genesis under different LQTS conditions. Phase diagrams plotting PVC regions for the seven ventricular AP models are shown. The y axis and x axis are the same as in Fig. 1. Gray region is where PVCs are observed in the 1D cable. The red dotted lines are the single-cell EAD boundaries, and the cyan dotted lines are the single-cell RF boundaries taken from Fig. 1. β-values, marked on each panel, are the fold change of G_Kr (LQT1) or G_Ks (LQT2 and LQT3) in the short APD region as indicated in (H). (A) LRd model is shown. (B) SB model is shown. (C) HRd model is shown. (D) TP04 model is shown. (E) GB model is shown. (F) ORd model is shown. (G) ToRORd model is shown. (H) A schematic plot of the 1D cable model is given. The cable length is 200 cells, which was paced simultaneously by a single stimulus applied at t = 100 ms. The RG was simulated by setting the maximal G_Ks (or G_Kr for LQT1) in the first half (α-fold) differently from the second half (β-fold) of the cable. α ≤ β so that the APD in the first half of the cable is longer than that in the second half. Note that RF can occur much more easily in the single cell than in tissue because of the existence of RG (RF in the 1D cable is observed only inside the gray region). To see this figure in color, go online.

In the second type of simulation, we randomly draw the maximum conductances of the major currents from the assigned intervals to search for EADs and RF in the single cell and PVCs in the 1D cable. This type of parameter setting allows us to explore PVC genesis in a high-dimensional parameter space and perform parameter sensitivity analyses. In the 1D cable, G_Ks was set differently in the two regions of the cable to generate RG. We first randomly draw a β(G_Ks) value for the short APD region. We then draw another random number ξ uniformly distributed in [0,1] and set α(G_Ks) = ξβ(G_Ks). By choosing α(G_Ks) and β(G_Ks) this way, they are independent, and α(G_Ks) ≤ β(G_Ks) is always satisfied. β(G_Ks) is set as 0.5- to 2-fold of the values labeled on the panels of LQT2 in Fig. 2. The conductance of other currents is uniform in the cable, in the range of 0.5- to 2-fold of the control values except that α(G_Ca,L) was set as in the same ranges as in Fig. 2. Details of the specific parameter intervals are shown in Table S2. For each AP model, 60,000 random parameter sets (or simulations) were carried out in both the single cell and the 1D cable.

Parameter sensitivity analyses

We performed parameter sensitivity analyses for EADs, RF, and PVCs using the logistic regression method proposed by Morotti and Grandi (42). Note that the parameters in our simulations were uniformly distributed in the assigned intervals.

Numerical methods

Simulations were carried out using a forward Euler method with a fixed time step. For the single cells, Δt = 0.01 ms was used. For the 1D cable, Δx = 0.015 cm and Δt = 0.01 ms were used. All the models were programed in CUDA C++, and simulations were performed on NVIDIA Tesla K80 GPU cards (NVIDIA, Santa Clara, CA).

Results

EAD and RF properties in uncoupled myocytes

Fig. 1 shows the single-cell AP behaviors (including normal repolarization, EADs, and RF) under the conditions of the three types of LQTS for different α(P_Ca) and α(G_Kr) in LQT1 or α(G_Ks) in LQT2 and LQT3. These diagrams are called phase diagrams. In general, as expected, EADs and RF were promoted by increasing the maximum conductance of the inward currents and/or decreasing the maximum conductance of the outward currents. EADs have more difficulty occurring under the conditions of LQT1. There are almost no EADs observed in the SB and TP04 models. There are very small EAD regions in the HRd and GB models. However, EADs occur in much wider ranges of parameters under the conditions of LQT2 and LQT3 than that of LQT1 for all models. This indicates that I_Ks may play a significant role in EAD genesis (3). In the LRd, ORd, and ToRORd models, EADs occur more easily, and their amplitudes are larger. In the parameter intervals used (see Table S2), the EADs in all the AP models are phase-2 EADs (see Fig. S3 for the histograms of EAD takeoff potential measured using the randomly drawn parameter sets). No phase-3 EADs were observed.

Cellular EADs and tissue RG in the genesis of PVCs

Fig. 2 shows the phase diagrams from the 1D cable simulations under the three types of LQTS as described in Methods. In each panel, the gray region is where PVCs occur, the red dotted line is the lower boundary of EAD, and the cyan dotted line is the lower boundary of RF in the single cell replotted from the corresponding panels in Fig. 1. For all models, the threshold for PVCs is above the EAD boundary and decreases as α(P_Ca) and RG increase (PVCs tend to occur at the upper-left regions of the phase diagrams). Unlike EADs in the single-cell simulations, we did not observe any major differences in phase diagram characteristics between the three types of LQTS. For most of the models and LQTS conditions, PVCs occur substantially above the EAD and RF boundaries. However, PVCs can occur at the EAD boundary in the ORd model (Fig. 2 F), the ToRORd model (Fig. 2 G), and under the LQT2 condition of the LRd model (middle panel of Fig. 2 A). PVCs are very difficult to generate in the HRd model (Fig. 2 C), and we needed to use a much larger α(P_Ca) (a 100-fold increase or more) to observe PVCs. Because of this, we did not perform any additional simulations with the HRd model.

Note that we used very different β-values for different AP models and different LQTS conditions for the phase diagrams. This is mainly because of the different responses of the APs to G_Ks or G_Kr (see Fig. S2). For example, for the SB model or the ORd model, blocking I_Ks only changes APD slightly, and thus, a very large β-value is needed to result in a large enough RG for PVC genesis. The requirement of different β-values for different models and LQTS cases can also be found in Figs. 5, S6, and S7. Changing the β-value changes the PVC boundary and structure of the phase diagram, but the PVC region will be always above the single-cell EAD boundary. For example, if we reduce the β-value from 10 to 5 under LQT2 conditions with the ORd model, the phase diagram becomes more complex, exhibiting more islands of PVC regions, but still remains above the single-cell EAD boundary (see Fig. S4). Also note that as described in Methods, in the 1D cable simulations shown in Fig. 2, we applied the stimulus simultaneously to all cells in the cable instead of pacing from one end of the cable. If we pace the cable from one end of the cable, it only exhibits a small effect on the phase diagrams. For example, we show the phase diagrams of the LRd model for three pacing protocols in Fig. S5. The phase diagrams only differ slightly among the three pacing protocols.

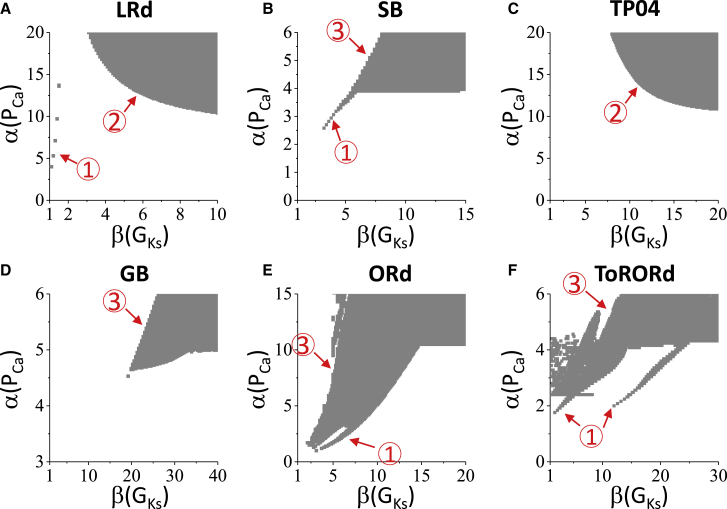
Figure 5.

Effects of increasing G_Ks in the short APD region on PVC genesis. 1D cable simulations under the conditions of LQT2 are shown. For all models, α(G_Ks) = 1 and β(G_Ks) ≥ 1. Gray regions are where PVCs occur in the 1D cable. The circled numbers “1,” “2,” and “3” mark different types of responses to the change of α(P_Ca) and β(G_Ks) as discussed in the main text. (A) LRd model is shown. (B) SB model is shown. (C) TP04 model is shown. (D) GB model is shown. (E) ORd model is shown. (F) ToRORd model is shown. To see this figure in color, go online.

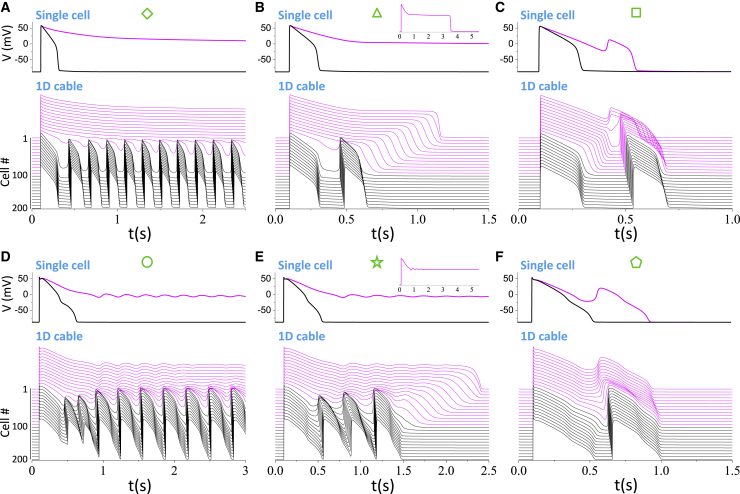
Fig. 3, A–C show three examples (marked by symbols in Fig. 2 A) from the LRd model under the LQT2 condition. When the RG is large (diamond, Fig. 3 A), sustained PVCs occur because RF occurs in the long APD region. Close to the border of the PVC region (triangle, Fig. 3 B), cells repolarize in the long APD region, and a single PVC occurs. There can also be more PVCs depending on the exact RG and α(P_Ca). Note that in both cases, no EADs occur in the long APD region (see also the single-cell APs in the upper panels). In the third example (square, Fig. 3 C), the RG is small, and a single PVC occurs, which is directly associated with the EAD present in the long APD region. Note that the parameters for observing this type of PVCs are at the same location of the single-cell boundary of EADs (the gray dots overlap with the red dotted line in the LQT2 case in Fig. 2 A). Fig. 3, D–F show examples from the ORd model under LQT2 (symbols marked in Fig. 2 F). The PVC behaviors are similar to those shown in Fig. 3, A–C. Note that in Fig. 3 E, RF occurs in the single cell for the parameters in the long APD region, but repolarization occurs in the cable in the long APD region because of cell coupling. This same scenario occurs in a wide range of parameters (e.g., the no-PVC regions above the RF boundaries as well as the PVC regions close to the lower PVC boundaries in Fig. 2) for all the AP models simulated in this study.

Figure 3.

Examples of PVC behaviors in 1D cables. Upper panel: APs from an isolated single cell with the parameters in the long APD region (magenta) and the short APD region (black). Lower panel: 3D plots of time-space-voltage from the 1D cable. Magenta is the long APD region, and black is the short APD region. (A–C) The LRd model is shown. The symbols above the panels correspond to those marked on the middle panel in Fig. 2A (the LQT2 case of the LRd model) to indicate their locations in the phase diagram. Diamond (A): α(P_Ca) = 3 and α(G_Ks) = 0.1. Triangle (B): α(P_Ca) = 3 and α(G_Ks) = 0.3. The long AP in the single cell repolarizes at t = 3.55 s (see inset). Square (C): α(P_Ca) = 2.4 and α(G_Ks) = 0.905. (D–F) ORd model is shown. The symbols above the panels correspond to those marked on the middle panel in Fig. 2F (the LQT2 case of the ORd model) to indicate their locations in the parameter space. Circle (D): α(P_Ca) = 10 and α(G_Ks) = 1. Star (E): α(P_Ca) = 6 and α(G_Ks) = 1. The long AP in the single cell fails to repolarize for the entire duration of simulation (see inset). Pentagon (F): α(P_Ca) = 2.5 and α(G_Ks) = 5. To see this figure in color, go online.

The source-sink effects on PVC genesis

One important condition for AP conduction is source-sink effects, which implies that it is safer for the AP to propagate when the gap junction conductance is reduced (10, 11, 12, 13, 14). For the same reason, reducing gap junction conduction promotes phase-3 EAD or delayed afterdepolarization (DAD) induced PVCs (43). To investigate the effects of gap junction coupling on PVC genesis shown in the AP models, we carried out the same simulations as in Fig. 2 under the LQT2 condition with a fivefold reduced diffusion constant (Fig. 4). Fig. 4 shows that reducing the gap junction conductance indeed expands the regions exhibiting PVCs for all models. The effects are small for the LRd, SB, and TP04 models but relatively larger for the GB, ORd, and ToRORd models.

Figure 4.

Effects of gap junction coupling on PVC genesis. Phase diagrams for control diffusion constant (D = 0.0005 ms/cm², half-transparent olive) and for reduced diffusion constant (D = 0.0001 ms/cm², red) are given. These simulations were using the LQT2 parameters for each model. (A) LRd model is shown. (B) SB model is shown. (C) TP04 model is shown. (D) GB model is shown. (E) ORd model is shown. (F) ToRORd model is shown. The arrow in (B) highlights the occurrence of a small region of EAD-induced PVCs promoted by reduction of D in the SB model. To see this figure in color, go online.

We then altered the source-sink conditions by shortening the APD in the short APD region. Fig. 5 shows the simulation results for the LQT2 condition of the six models. We fixed α(G_Ks) = 1 but increased β(G_Ks) from 1, at which the cable is homogeneous. The responses of the AP models to β are complex but can be roughly summarized into three types. The first type of response is that PVCs occur when β is relatively small, marked as type “1” in the panels in Fig. 5. This response is suppressed by increasing β. The second type of response is that a larger β needs a smaller I_Ca,L conductance (α(P_Ca)) to generate PVCs, marked as type “2” in the panels, mainly observed in the LRd (Fig. 5 A) and TP04 (Fig. 5 C) models. The third type of response is that as α(P_Ca) increases, a larger β is needed for PVCs to occur, marked as type “3” in the panels in Fig. 5. Although the responses are different for different AP models, one thing in common is that for all AP models, PVCs always occur by increasing β and α(P_Ca) (right-upper regions of the phase diagrams). Note that the β-values needed to observe PVCs are very different for different AP models, which is one of the reasons that led us to choose very different β-values for different AP models and LQTS conditions in Fig. 2. We did the same simulations for LQT2 with α(G_Ks) = 0 (see Fig. S6) and for LQT1 with α(G_Kr) = 0 (see Fig. S7), which show the same responses.

Key determinants of PVC genesis

To investigate the major parameters affecting PVC genesis, we performed simulations in which we randomly varied the maximum conductance of the major ionic currents for EADs or RF in the single cell and PVCs in the 1D cable (see Table S2 for the assigned parameter intervals). For each AP model, we performed 60,000 simulations, i.e., 60,000 random parameter sets. We then investigated the correlations of these conductances with the occurrence of EADs and RF in a single cell and PVCs in tissue.

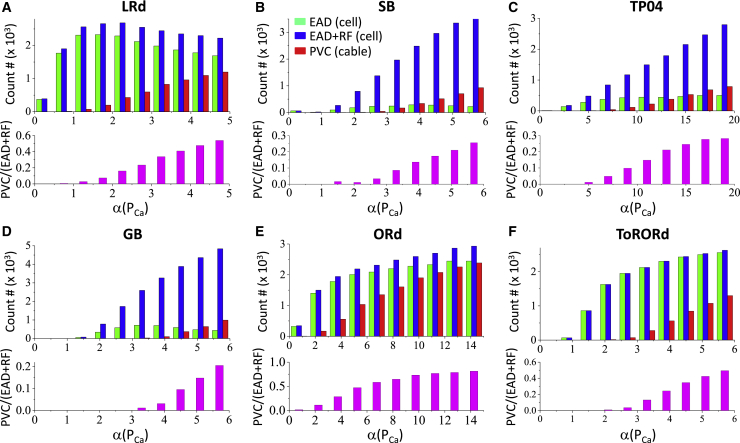
The most important current for PVC genesis in tissue is I_Ca,L. Fig. 6 shows the effects of I_Ca,L conductance on EADs, RF, and PVCs for the six AP models. We plotted histograms of the event counts for parameter sets exhibiting EADs (green bars) and exhibiting EADs or RF (blue bars) in the single cell. We also plotted histograms for the parameter sets generating PVCs in the 1D cable on the same panel. In general, increasing α(P_Ca) increases the occurrences of EADs and RF in the single cell and PVCs in the 1D cable. The ratio of the cases exhibiting PVCs in the cable versus the cases exhibiting either EADs or RF in the single cell (lower panel for each model) increases as α(P_Ca) increases. This indicates that increasing α(P_Ca) exhibits a much stronger effect in tissue to promote PVCs than in a single isolated cell to promote EADs or RF. We detected the minimal α(P_Ca) values required to observe EADs or RF in the single cell and those required to observe PVCs in the 1D cable from the 60,000 random parameter sets, shown in Table 1. The α-values vary widely among the AP models, but for all the AP models, the minimal α(P_Ca) threshold for PVCs is substantially higher than that for EADs or RF, with the ratio (α_PVC/α_EAD) ranging from around 2.3-fold to more than 16-fold for the six AP models.

Figure 6.

Effects of I_Ca,L on PVC genesis analyzed using a random population of ionic conductances. For each AP model, 60,000 random parameter sets were simulated for both the single cell and the 1D cable as detailed in Methods. A histogram is plotted to count the numbers of conductance parameter sets that exhibit the corresponding events. The x axis (α(P_Ca)) is divided into 10 bins for each histogram. Because we used uniform random numbers to draw parameters, each bin thus contains the same number of parameter sets, i.e., 6000. Green bar: events for EADs occurring in the isolated single cell. Blue bar: events for either EADs or RF occurring in the isolated single cell. Red bar: events for PVCs occurring in the 1D cable. The lower panel in magenta shows the ratio of cases exhibiting PVCs in the cable versus the cases exhibiting either EADs or RF in the isolated single cell (the magenta bar is the ratio of the red bar over the blue bar). (A) LRd model is shown. (B) SB model is shown. (C) TP04 model is shown. (D) GB model is shown. (E) ORd model is shown. (F) ToRORd model is shown. To see this figure in color, go online.

Table 1.

The Minimal Values of the Maximum I_Ca,L Conductance Required for the Occurrence of EADs in the Single Cell and for the Occurrence of PVCs in the 1D Cable for the AP Models

Model	αEAD	αPVC	αPVC/αEAD
LRd	0.033	0.533	16.152
SB	0.106	1.229	11.594
TP04	1.235	4.820	3.903
GB	1.245	3.003	2.412
ORd	0.251	1.246	4.964
ToRORd	0.880	2.077	2.360

Data were from the same simulations as for Fig. 6. α_EAD, occurrence of EADs in the single cell; α_PVC, occurrence of PVCs in the 1D cable.

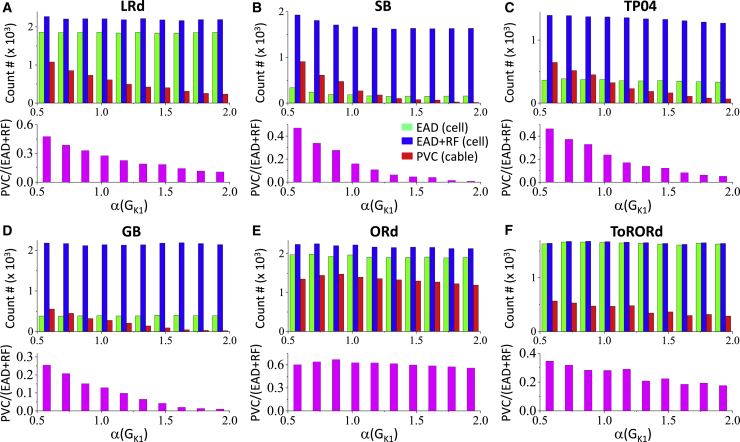
I_K1 is another current that plays an important role in the genesis of PVCs in tissue. Fig. 7 shows the effects of I_K1 conductance on the occurrence of EADs, RF, and PVCs, plotted in the same manner as Fig. 6. For all models, changing G_K1 has no or little effect on the occurrence of EADs or RF in the single cell but can have a large effect on PVC in the cable. Namely, increasing G_K1 suppresses PVCs in all the models (although this effect is much smaller in the ORd model, most likely because of its small value of G_K1; see Table S1 for G_K1-values for different models).

Figure 7.

Effects of I_K1 on PVC genesis analyzed using a random population of ionic conductances. The simulations and histograms are the same as described in Fig. 6, but with I_K1 being the x axis parameter. (A) LRd model is shown. (B) SB model is shown. (C) TP04 model is shown. (D) GB model is shown. (E) ORd model is shown. (F) ToRORd model is shown. To see this figure in color, go online.

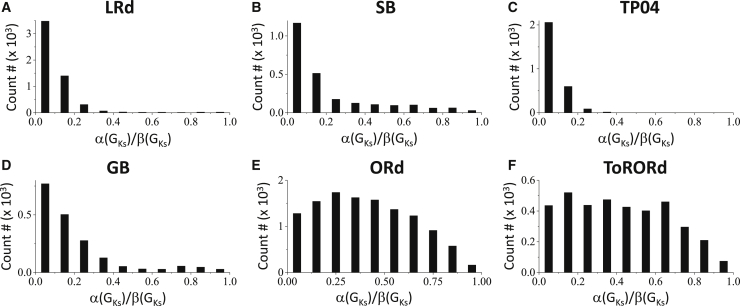
Fig. 8 shows the effects of RG on the genesis of PVCs for the six AP models. The tissue is homogeneous when α(G_Ks) = β(G_Ks), and the RG increases as α(G_Ks)/β(G_Ks) decreases. The likelihood of PVC occurrence increases as the RG increases for all models. The LRd, SB, TP04, and GB models exhibit very strong dependence on RG, whereas the ORd and ToRORd models exhibit weaker dependence on RG.

Figure 8.

Effects of RG on PVC genesis analyzed using a random population of ionic conductances. The histograms show the numbers of parameter sets exhibiting PVCs as a function of the ratio α(G_Ks)/β(G_Ks), a measure of the RG magnitude. The cable is homogeneous when α(G_Ks)/β(G_Ks) = 1 and becomes more heterogeneous for smaller α(G_Ks)/β(G_Ks).

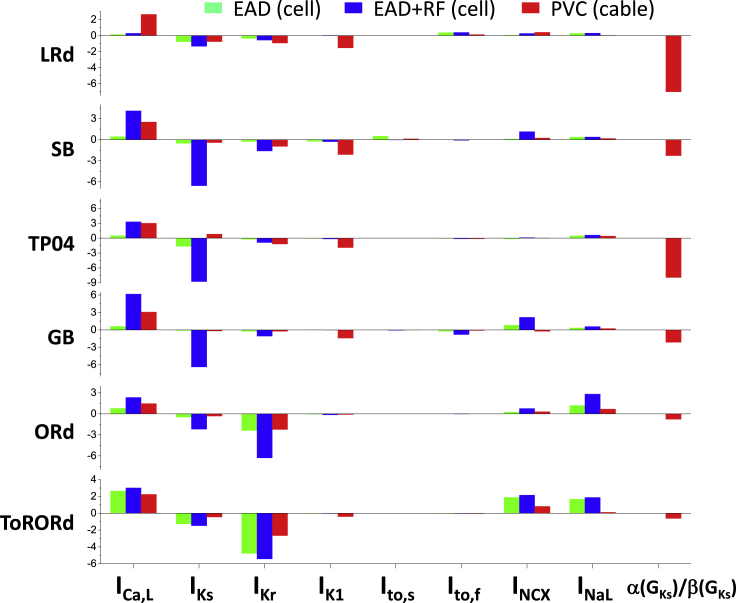
Parameter sensitivity analyses were carried out in previous studies to quantify the contributions of different ionic currents on APD and the occurrence of EADs in single myocytes (42,44, 45, 46). To show the dependence of the occurrence of PVCs on conductance of different ionic currents and tissue heterogeneities, we performed logistic regression analyses to quantify the sensitivity of the occurrence of EADs, RF, and PVCs to the maximum conductance of the ionic currents and RG, summarized in Fig. 9. The maximum I_Ca,L conductance exhibits a strong positive correlation with the occurrence of PVCs in tissue for all the AP models. It also shows a strong positive correlation with the occurrence of RF but a much weaker correlation with the occurrence of EAD in a single cell for most of the AP models. These correlation properties can be clearly seen in Fig. 6. The maximum I_Ks conductance exhibit a strong negative correlation with the occurrence of RF for all models and a strong correlation with the occurrence of EADs for some models. However, it exhibits a much weaker correlation with the occurrence of PVCs in the cable for all models (note: the TP04 model even shows a positive correlation). The maximum I_Kr conductance exhibits much stronger effects for the ORd and ToRORd models than other models in both the single cell and the cable. The maximum I_K1 conductance exhibits a very weak or almost no correlation with the occurrence of EADs and RF for all models but a strong negative correlation with the occurrence of PVCs (except for the ORd model), which is also clearly seen in Fig. 7. The effects of I_to are small for all models. Both I_NCX and I_NaL exhibit stronger single-cell effects than their effects in tissue. Finally, agreeing with the results shown in Fig. 8, for all models, the occurrence of PVCs negatively correlates with α(G_Ks)/β(G_Ks) (note: α(G_Ks)/β(G_Ks) is negatively correlated with RG, and thus, RG is positively correlated with the occurrence of PVCs), with the LRd and TP04 models exhibiting the strongest correlations. Note that the large variabilities in parameter sensitivities (the regression coefficients) to a specific ionic current among different AP models reflect the difference in the maximum conductance of the ionic currents, the kinetics, and the mathematical formulations in the AP models, but they could also be enhanced by the different parameter ranges used in the simulations. Nonetheless, the regression shows that I_Ca,L, I_K1, and RG play very important roles in PVC genesis in tissue.

Figure 9.

Sensitivity of EADs and RF in a single cell and PVCs in a 1D cable to the maximum conductance of different ionic currents and RG. Color bars are the logistic regression coefficients for EADs and RF in the single cell and PVCs in the 1D cable. The data sets were from the same simulations as for Figs. 6, 7, and 8. To see this figure in color, go online.

Mechanistic insights from the simple LR1 model

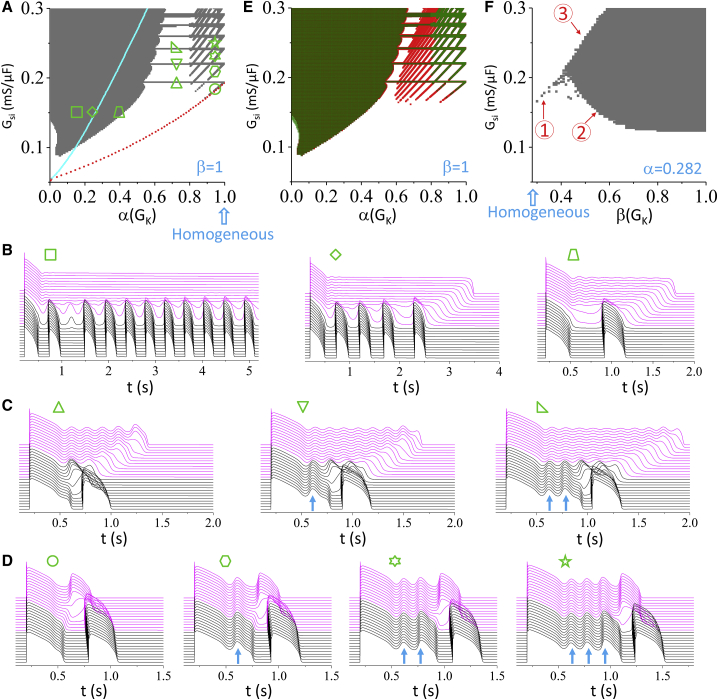
Based on the simulations of the detailed AP models, we can identify key ionic currents and RG as important determinants for PVC genesis. However, PVC behaviors and responses to the parameters still differ substantially. To better understand the mechanisms of PVC genesis as well as the roles of EADs and RG, we used the simple LR1 AP model (40). The model includes three time-dependent currents, I_Na, I_si, and I_K. I_si is called slow inward current in the LR1 model, which corresponds to I_Ca,L in the other models. To observe EADs, we modified the model by speeding up the I_si kinetics and slowed the kinetics of I_K (see Methods for parameter changes from the original model). We performed the same simulations of the single cell as in Fig. 1 for EADs and RF, which are shown in Fig. S8. Fig. 10 shows the 1D cable simulation results for PVCs, which are summarized and compared with those of other models as follows:

• 1)Fig. 10 A shows a phase diagram plotted in the same way as in Fig. 2. The gray regions are where PVCs occur in the 1D cable, and the red dotted line is the EAD boundary in the single cell. The PVCs always occur above the EAD boundary of the isolated single cell, agreeing with all the AP models in Fig. 2.
• 2)The majority of the PVCs in the phase diagram are potentiated by increasing the maximum conductance (G_si) and tissue RG (the left gray region in Fig. 10 A), which agrees with the observations in all the models and for almost all LQTS types shown in Fig. 2. In Fig. 10 B, we plotted the voltage recorded from the cable for G_si = 0.15 mS/μF and different α(G_K). When α(G_K) is small, the long APD region fails to repolarize, and the PVCs become sustained firings. As the α(G_K) increases, the long APD region can successfully repolarize, and one or multiple PVCs occur. If α(G_K) is increased further, eventually no PVCs occur. These PVC behaviors are the same as in Fig. 3, A, B, D, and E.
• 3)In the upper-right region of the phase diagram in Fig. 10 A, there are horizontal bars of PVC regions. The fact that these bars are horizontal implies that they are independent of RG. As shown in our previous study with the rabbit AP model (25), the PVCs in these bars are a special case occurring at the cable boundaries, and therefore, they do not depend on RG. We can see such bars in the ORd and ToRORd models (e.g., in the LQT3 case in Fig. 2 F and the LQT2 case in Fig. 2 G). Although these bars do not depend on RG, they depend sensitively on G_si and occur at narrow bands of G_si. Space-time plots of voltage show that only a single PVC occurs (Fig. 10 C), and as G_si increases, a jump from a lower bar to a higher bar is associated with the addition of an EAD to the short APD region. The PVC is always associated with the last EAD in the short APD region.
• 4)In the upper-right region of the phase diagram in Fig. 10 A, there are tilted belts of PVC regions. Note that these belts meet the horizontal bars when the cable is almost homogeneous, i.e., α ≈ β. This is also the case in the ORd and ToRORd models (see Fig. 2, F and G). The belts and bars exhibit a 1:1 relationship. The lowest belt meets the EAD boundary of the single cell. This type of belts is seen in the LRd model under the condition of LQT2 (Fig. 2 A), the ORd model (Fig. 2 F), and the ToRORd model (Fig. 2 G). Similarly, space-time plots of voltage show that only a single PVC occurs (Fig. 10 D), and as G_si increases, a jump from a lower belt to a higher one is associated with the addition of an EAD to the cable (both long and short APD region). Again, the PVC is always associated with the last EAD in the long APD region. The EAD-induced PVCs shown in Fig. 3, C and F from the LRd and ORd models are also from the belt regions.
• 5)Fig. 10 E plots the phase diagram with the control diffusion constant (half-transparent olive) overlapped with the one with reduced gap junction coupling (red), corresponding to Fig. 4. Reducing gap junction conductance by five times expands the RG-induced PVC region only slightly but significantly increases the region of EAD-induced PVCs. In other words, the EAD-induced PVCs are more sensitive to gap junction coupling than the RG-induced PVCs. This can explain the different responses to the gap junction coupling shown in Fig. 4, i.e., the genesis of PVCs is more sensitive to gap junction coupling in the AP models that are more prone to EADs (such as the ORd and ToRORd models) than in the ones that are less prone to EADs (such as the TP04 model).
• 6)Fig. 10 F shows the effects of increasing the G_K in the short APD region, corresponding to Fig. 5. We observed three responses as marked by “1,” “2,” and “3” in the phase diagram, which are the same responses shown in Fig. 5. Fig. S9 shows examples of behaviors crossing these boundaries. For boundary “3,” when the maximum I_si (I_Ca,L) conductance is large (Fig. S9 A), repolarization fails in the entire cable above the boundary. Increasing β causes repolarization in the short APD region, allowing both EAD-induced and RG-induced PVCs to occur. When the maximum I_si (I_Ca,L) conductance is smaller (Fig. S9 B), repolarization occurs in both long and short APD regions, but the RG is too mild for PVCs to occur. Increasing β (and thus RG) first promotes EAD-induced PVCs and then suppresses the PVCs (crossing boundary “1”). For boundary “2,” RG is already large in the left of the boundary but still not large enough for PVCs to occur (Fig. S9 C). Increasing β causes the APD to become even shorter in the short APD region and promotes RG-induced PVCs.

Figure 10.

PVC genesis in the LR1 model. (A) PVC regions (gray) from the 1D cable and the lower EAD boundary (red dotted line) and RF boundary (cyan dotted line) from a single cell are shown, plotted in the same manner as for Fig. 2. (B) 3D plots of time-space-voltage showing RG-induced PVCs are given. G_si = 0.15 mS/μF, from left to right (also indicated by the symbols in A): α(G_K) = 0.15, α(G_K) = 0.25, and α(G_K) = 0.42. (C) 3D plots of time-space-voltage showing EAD associated PVCs from the horizontal bars are given. Upward arrows mark the EADs in the short APD region occurring before the PVC. α(G_K) = 0.7, from left to right (also indicated by the symbols in A): G_si = 0.194 mS/μF, G_si = 0.22 mS/μF, and G_si = 0.242 mS/μF. (D) 3D plots of time-space-voltage showing EAD-induced PVCs from the tilted belts are given. α(G_K) = 0.95, from left to right (also indicated by the symbols in A): G_si = 0.184 mS/μF, G_si = 0.2085 mS/μF, G_si = 0.229 mS/μF, and G_si = 0.247 mS/μF. (E) Effects of gap junction coupling on PVC genesis are shown. Overlap of the PVC regions under control conditions (replot of A in half-transparent olive) and reduced gap junction coupling (red) is shown, plotted in the same way as in Fig. 4. (F) Effects of varying G_K in the short APD region on PVC genesis are shown, plotted in the same manner as in Fig. 5. To see this figure in color, go online.

Remarkably, all the PVC behaviors and their responses to parameter changes seen in the detailed models are present uniquely in the LR1 model. This indicates that although the detailed models have increased physiological details (such as more types of ionic currents and intracellular Ca²⁺ cycling), the underlying mechanisms of PVC can be well captured by the simple LR1 AP model.

Discussion

In this study, we carried out computer simulations of single-cell and 1D cable models to investigate the mechanisms of PVC genesis and their relationship to cellular phase-2 EADs caused by APD prolongation. We used eight ventricular AP models and simulated three types of LQTS conditions, as well as populations of random parameter sets. Our major findings can be summarized as follows. In all the AP models, we only observed phase-2 EADs in the isolated single cell in the parameter ranges simulated in this study (Fig. S3). Although different PVC behaviors occur in different models, we can broadly classify them into two mechanisms: RG-induced PVCs and phase-2 EAD-induced PVCs. The RG-induced PVCs are promoted by increasing RG without requiring EADs and are insensitive to gap junction coupling. The phase-2 EAD-induced PVCs are more sensitive to gap junction coupling, occurring when EADs are present in the long APD region and RG is mild. The key determinants of PVC genesis are I_Ca,L and I_K1 conductance and RG. Although the physiologically detailed AP models contain experimentally calibrated ionic current formulations and Ca²⁺ cycling dynamics, all of the fundamental PVC mechanisms can be well described by the simple LR1 model, indicating that the underlying PVC mechanisms revealed in this study are generic.

Mechanisms of PVCs caused by QT prolongation

There are several existing known mechanisms of PVC genesis in cardiac diseases (43,47), such as propagation of phase-3 EAD-induced triggered activities, DAD-induced triggered activities, and phase-4 depolarizations (pacemakers), as well as phase-2 reentry in Brugada syndrome. Here, we confine our discussion to PVC genesis under the conditions of QT prolongation. A hallmark of QT prolongation is the propensity for EADs to occur, and thus, EADs have been considered as arrhythmia triggers by propagating as PVCs in tissue. However, no convincing experimental evidence exists to support this widely believed hypothesis. In this study, we used computer simulations of eight AP models over wide ranges of parameters to investigate the mechanisms of PVC genesis due to QT prolongation. Although the specific requirements of and responses to parameter changes for PVC genesis are different for different AP models, the PVCs across all these models can be broadly classified into two mechanisms: RG-induced PVCs and phase-2 EAD-induced PVCs.

For the RG-induced PVCs, the presence of EADs is not required. Instead, the requirements are a large RG and a strong I_Ca,L. A larger RG requires a smaller I_Ca,L to elicit PVCs. The RG-induced PVCs are insensitive to gap junction coupling but require a strong enough sink in the short APD side. The number of PVCs after a paced beat depends on RG and I_Ca,L, ranging from a single PVC to multiple PVCs in a short burst to sustained firing indefinitely. This mechanism of PVCs was also observed in several previous simulation studies (25,48, 49, 50, 51). As shown in these previous studies (25,48), the RG-induced PVCs are caused by a tissue-scale dynamical instability promoted by increased RG and enhanced I_Ca,L, and are not related to single-cell EADs.

On the other hand, for the EAD-induced PVCs, the presence of EADs is required. Importantly, a maximum of only one PVC can occur after each paced beat, which is always associated with the last EAD on the long APD side. In contrast to the RG-induced PVCs, the EAD-induced PVCs tend to occur when the RG is small. It is more sensitive to gap junction coupling and suppressed by increasing the sink in the short APD side. RG-induced PVCs were observed in all AP models as long as the RG and I_Ca,L were large enough, but EAD-induced PVCs were only observed in a subset of the AP models (LR1, LRd, ORd, and ToRORd). As shown in Fig. 1, EADs occur more easily and the EAD amplitudes are large in these AP models. Moreover, this type of PVCs occurs only when the parameters are narrowly matched, forming discrete bars and belts in the phase diagrams. Although EADs are required for this mechanism, we argue that these PVCs are actually not a result of phase-2 EAD propagation as widely thought and that they are also a tissue-scale phenomenon related to dynamical instabilities, the details of which need to be revealed in future studies.

There are experimental recordings to support both PVC mechanisms identified by our simulations. In the optical mapping study by Liu and Laurita (23), D-sotalol was used to induce an LQT2-like phenotype and ATX-II to induce an LQT3-like phenotype in canine ventricular tissue. They demonstrated that RG was much larger under LQT3 than both control and LQT2 conditions (the maximal RG was 3.6 ms/mm under normal control and 43.92 ms/mm under LQT3). Because of the large RG in LQT3, PVCs occurred much more easily than in control and LQT2. They also observed that PVCs always originated from where the RG was the steepest. In another study by Maruyama et al. (24) using optical mapping, E-4031 and low [K⁺]_o and [Mg²⁺]_o were used to prolong APD and induce PVCs in rabbit hearts. They also observed that with a substantially increased RG, multiple PVCs could repetitively originate from the same steep RG site before the long APD region repolarized (see Fig. 7 A in Maruyama et al. (24)). These observations by Liu and Laurita (23) and by Maruyama et al. (24) agree well with the RG-induced PVC mechanism shown in our simulations. Evidence for the EAD-induced PVC mechanism has also been demonstrated in optical mapping experiments in several studies (see Fig. 4 in Maruyama et al. (24) and Fig. 2 in Huang et al. (25)), in which the PVCs were clearly linked to an EAD on the long APD side.

Roles of EADs in the genesis of PVCs

It is well known that phase-3 EADs or their triggered activities can propagate in cardiac tissue to give rise to PVCs once the source-sink conditions are satisfied (43), similar to the propagation of sinus rhythm originating from the sinoatrial node or DAD-induced triggered activity. However, whether phase-2 EADs can result in PVCs remains in debate. Because the vast majority of the EADs observed in experiments of ventricular myocytes as well as in computer AP models are phase-2 EADs, understanding how phase-2 EADs are linked to PVCs is necessary. In this study, we show that under the conditions of QT prolongation, PVCs can be induced by RG without the presence of EADs or by phase-2 EADs. However, the phase-2 EAD-induced PVCs exhibit different features from the phase-3 EAD-induced PVCs. First, the existence of phase-2 EADs may not necessarily lead to PVCs no matter how big the EAD area is (see Fig. 5 in Huang et al. (25) for a direct demonstration of this point). On the other hand, for phase-3 EADs, PVCs always occur as long as the EAD area is large enough to overcome the sink effect. Second, the phase-2 EAD-induced PVCs only occur when the parameters are properly matched (see Fig. 10 A). This implies that the genesis of phase-2 EAD-induced PVCs is not a simple propagation of EADs as in the case of phase-3 EAD-induced PVCs. Certain tissue-scale conditions need to be satisfied (e.g., the RG cannot be too small or too large), and both the EAD amplitude and takeoff potential are also important. Note that phase-3 EADs or their triggered activity exhibit lower takeoff potentials and larger amplitudes than phase-2 EADs. Third, although multiple phase-2 EADs can occur in an AP, only one PVC can occur in a single pacing beat. Although our study demonstrated that the occurrence of phase-2 EADs does not guarantee the occurrence of PVCs, phase-2 EADs still play an important role in the genesis of PVCs under the condition of QT prolongation.

Model-dependent differences

Although we can observe all the PVC behaviors or mechanisms in the simple LR1 model, the details of these behaviors differ substantially between the more sophisticated AP models. In the TP04, GB, and HRd models, we only observed RG-induced PVCs. In the SB and LRd models, we can observe both mechanisms, but the EAD-induced PVCs are rare. In the ORd, and ToRORd models, we also observed both mechanisms, and the EAD-induced PVCs were observed in a much wider range of parameter settings than with TP04, GB, and HRd. Note that EADs in general occur much more easily with large EAD amplitudes for the ORd and ToRORd models, which may explain why the EAD-induced PVCs are also easier to generate in these models. Because the ToRORd model is based on the original ORd model, it is not surprising that they exhibit similar behaviors.

The reason that the ORd model is more prone to EADs and PVCs may be as follows. The AP of the ORd model is much more triangulated and also has a much lower I_K1 conductance compared to other models. Moreover, I_Ca,L recovers much faster during the plateau phase (38), with the peak I_Ca,L being even higher during EADs than during the normal AP excitation (29,52). AP triangulation is known to be prone to EADs (53), and based on our results, reduced I_K1 and increased I_Ca,L are key factors for the PVC genesis in tissue. Because each AP model is developed based on their specific experimental data sets, the ionic currents are weighted differently in different models, often by a significant factor. Therefore, different models can exhibit very different responses to the same channel blocker (54) (see Fig. S2 for the different responses of the seven AP models to the same blocker). One way to interpret this is to consider this variability as physiological diversity between cells or between individuals (30,55, 56, 57). On the other hand, some of these differences may be due to the caveats of the models themselves. For example, in our simulations the HRd canine ventricular AP model requires an extremely high I_Ca,L conductance (more than 100 times the control value) for PVCs to occur. Experimental studies have shown that PVCs can occur in canine hearts under drug-induced LQTS without a substantial increase in I_Ca,L (7,21,23). Therefore, certain caveats may exist in the HRd model that require an unrealistically high I_Ca,L conductance for PVCs to occur.

Implications for arrhythmogenesis in clinical settings

Increasing RG as a risk factor for arrhythmogenesis in patients is widely known. For example, in a mapping study of LQTS patients (58), Vijayakumar et al. showed that RGs were much larger in LQTS patients than in normal subjects. Moreover, the symptomatic patients in that study exhibited larger RGs than the asymptomatic patients. In another clinical study, Kirchhof et al. (59) showed that patients who developed torsade de pointes exhibit a much larger T-wave amplitude than those who did not develop torsade de pointes. A higher T-wave amplitude directly correlates to a larger RG. Many other studies use the interval between the peak and the end of the T-wave to quantify the RG throughout the heart, and have shown that this metric can be a promising risk predictor for arrhythmias or sudden cardiac death (60, 61, 62).

Traditionally, QT prolongation is thought to be arrhythmogenic through the trigger-substrate paradigm as follows. QT prolongation increases RG, which can act as a tissue substrate for unidirectional conduction block (58). QT prolongation also results in EADs, which somehow propagate as PVCs. These PVCs propagate toward the increased RG region and undergo functional conduction block to form a reentrant arrhythmia. However, conflicting data to this hypothesis also exist, as it is well known that QT-prolongation-induced RG increase may also suppress EADs because of the increased source-sink effect. In other words, although increasing RG enhances the tissue substrate, it may simultaneously suppress the triggers, thereby suppressing arrhythmias. This does not agree well with the clinical observation that increasing RG increases the risk of arrhythmias and sudden cardiac death.

Based on our simulations, we propose two scenarios of QT-prolongation-induced arrhythmogenesis via each of the two mechanisms of PVC genesis. The first scenario is via the mechanism of RG-induced PVCs; as shown in our previous simulations in which we describe a mechanism called R from T (25,51,63), these PVCs propagate unidirectionally from the RG region. When the RG region is small, they maintain as target wave PVCs without inducing reentry (see Fig. 7 in (63). or Fig. 8 in (51) for an example of this scenario). As shown in our simulations, those PVCs can manifest as a singlet, a doublet, a triplet, or an episode of nonsustained focal VT. If RF occurs in the RG region, sustained focal VT may occur. However, when the RG region is large enough, reentry can form, resulting in sustained reentrant VT or VF. In this manner, the R-from-T mechanism is able to generate both focal and reentrant arrhythmias in which there is no clear distinction between trigger and substrate because both arise from the same cause, the increased RG.

The second scenario of QT-prolongation-induced arrhythmogenesis results from the EAD-induced PVCs. One can assume that there is naturally a distribution of large and small RG regions in the heart. An EAD-induced PVC can be generated from the small RG region, which then propagates toward the large RG region. If the large RG region is not steep enough to generate RG-induced PVCs but steep enough for unidirectional conduction block and to avoid its own EAD-induced PVC, then that initial PVC could be blocked to form reentry. In our previous study, we called this the R-to-T mechanism (51). Under this scenario, only singlets of PVCs can be observed before the occurrence of reentrant VT and VF. In this mechanism, the trigger and substrate are clearly distinct entities, matching the well-known traditional trigger-substrate mechanism of arrhythmogenesis.

Both scenarios can theoretically occur in the human hearts, which agrees with the observation that increasing RG results in an increased risk of arrhythmias. However, the RG-induced PVC mechanism is a more robust mechanism that can result in the full range of rich PVC patterns seen in clinical LQTS.

Limitations

There are several limitations of this study to be mentioned. APD lengthening and increasing I_Ca,L (such as under β-adrenergic stimulation) bring in more Ca²⁺ into the cell, which increases the SR Ca²⁺ load and thus SR Ca²⁺ release. This can affect Ca²⁺-dependent inactivation of I_Ca,L and other Ca²⁺-dependent currents that affect the APD and the genesis of EADs (3,64). This can also cause spontaneous SR Ca²⁺ releases (oscillations) to promote EADs (8,65, 66, 67, 68, 69, 70). In the AP models simulated in this study over a wide range of parameters, the EADs are caused by reactivation of I_Ca,L. However, it is possible that spontaneous Ca²⁺ release induced EADs may occur in certain parameter regimes for some of the models. For example, with the SB model, we observed a biphasic distribution of the EAD takeoff potentials (see Fig. S3 B), and the EADs in the higher takeoff potential group are caused by spontaneous Ca²⁺ oscillations. However, the PVCs generated using this model are mainly via the RG-induced PVC mechanism (Fig. 2), indicating that the spontaneous SR Ca²⁺ releases induced EADs in this model may not play a significant role in PVC generation. In addition to the large increase of I_Ca,L, we also increased the SR Ca²⁺ uptake rates in these models (simulating β-adrenergic stimulation), but we did not observe spontaneous SR Ca²⁺ release induced EADs except in the SB model (we showed the takeoff potential histograms in Fig. S10 for the uptake rates being three times of their control values and did not observe any characteristic difference in the histograms from those for the control uptake rates shown in Fig. S3). The reason that spontaneous SR Ca²⁺ release occurs in the SB model may be that the SR Ca²⁺ release in the SB model is described by a four-state RyR gating model regulated by cytosolic and SR Ca²⁺, but in other models, such as the ORd model, it is directly controlled by I_Ca,L. Therefore, major modifications of these AP models may be needed to result in spontaneous SR Ca²⁺ release induced EADs to investigate their roles in the genesis of PVCs.

We explored a very wide range of parameters for each AP model without calibrating the APs with experimental data. Some of the parameters could be far off from the physiological ranges. As we discussed above, some of the requirements may be due to the caveats in the AP models, such as in the HRd model. However, our goal was to reveal the potential mechanisms of PVC genesis caused by QT prolongation, and we showed that although the parameters required for PVC genesis are vastly different for different AP models, the underlying mechanisms shown in the models are consistent with the two mechanisms. Ideally, one may calibrate the APs with experimental data (39,56,71) first and then apply stresses, such as β-adrenergic stimulation, to investigate whether these mechanisms of PVCs can still occur under physiological conditions.

We only applied a single beat with a fixed initial condition for each parameter set for the simulations in this study. However, the genesis of PVCs in the real heart occurs when the heart is continuously beating, and thus, continuous pacing may be needed to allow the system to reach the steady state using a periodic pacing protocol or a pacing protocol simulating the heart rate variabilities. Because of the large numbers of cable simulations needed to catch the sensitive responses (such as the narrow belts shown in the phase diagrams), it is unrealistic to pace many beats because of limited computational resources. Moreover, continuous pacing can induce heart rate dependent spatiotemporal repolarization dynamics in both the single cell and the cable (63,72), it also becomes difficult to compare the single-cell results with the cable results to reveal the role of the cellular EADs in the genesis of PVCs. Nevertheless, although the phase diagrams shown in this study may be different for different initial conditions, we believe that the two mechanisms of PVCs identified in this study still apply. Further studies using continuous pacing protocols with different pacing rates are needed to reveal the roles of heart rate and its variabilities in the genesis of PVCs.

We used a simple parameter setting to model RG in the 1D cable, but the causes of RG could be much more complex, which may affect the genesis of PVCs. Moreover, a real heart is a 3D organ which can exhibit much more complex structural and electrophysiological heterogeneities. These tissue-scale properties will also impact the PVC genesis. Nevertheless, we believe that the two PVC mechanisms identified in this study are generic and applicable to the complex tissue-scale environments in the real heart.

Conclusions

Based on our simulations of multiple ventricular AP models in different species, we conclude that under the conditions of QT prolongation, PVCs can be generated by two mechanisms, which we categorize as RG-induced PVCs and phase-2 EAD-induced PVCs. The RG-induced PVCs are promoted by increasing RG without requiring the presence of EADs, but the EAD-induced PVCs occur only with a small RG and are suppressed by increasing RG. Both types of PVCs have been observed in optical mapping experiments and may be responsible for arrhythmogenesis in clinical LQTS.

Editor: Eric Sobie.