COVID-19 outbreak in Wuhan demonstrates the limitations of publicly available case numbers for epidemiological modeling

Abstract

Epidemiological models are widely used to analyze the spread of diseases such as the global COVID-19 pandemic caused by SARS-CoV-2. However, all models are based on simplifying assumptions and often on sparse data. This limits the reliability of parameter estimates and predictions.

In this manuscript, we demonstrate the relevance of these limitations and the pitfalls associated with the use of overly simplistic models. We considered the data for the early phase of the COVID-19 outbreak in Wuhan, China, as an example, and perform parameter estimation, uncertainty analysis and model selection for a range of established epidemiological models. Amongst others, we employ Markov chain Monte Carlo sampling, parameter and prediction profile calculation algorithms.

Our results show that parameter estimates and predictions obtained for several established models on the basis of reported case numbers can be subject to substantial uncertainty. More importantly, estimates were often unrealistic and the confidence/credibility intervals did not cover plausible values of critical parameters obtained using different approaches. These findings suggest, amongst others, that standard compartmental models can be overly simplistic and that the reported case numbers provide often insufficient information for obtaining reliable and realistic parameter values, and for forecasting the evolution of epidemics.

1. Introduction

Epidemiological models are essential tools in public health as they facilitate assessments and forecasts of the spread of infectious diseases. This has been for instance demonstrated for influenza (Yang et al., 2015), dengue (Reich et al., 2016), Ebola (Shaman et al., 2014), Zika (Chowell et al., 2016), and – most recently – COVID-19 (Ferguson et al., 2020, Boldog et al., 2020). These assessments and forecasts are the basis for political decision making (Doms et al., 2018) and therefore of vital importance.

The spectrum of mathematical modeling approaches in epidemiology ranges from relatively simple ordinary differential equation (ODE) models (Kermack et al., 1927, Hethcote, 2000, Brauer and Castillo-Chavez, 2012), partial differential equation (PDE) models (Chalub and Souza, 2011, Lotfi et al., 2014), stochastic differential equation (SDE) models (Dargatz et al., 2006, Greenwood and Gordillo, 2009, Allen, 2010), continuous-time discrete-state Markov chain (CTMC) models (Allen, 2010, Britton, 2010, Isham, 2007), to complex agent-based models (Epstein and Axtell, 1996, Bruch and Atwell, 2015). While ODE, PDE and SDE models provide descriptions at the population level, agent-based models are centered around formulations of the properties and dynamics of individuals. Some models explicitly account for space (usually in terms of countries, regions and/or cities) to capture spreading. Furthermore, models for the infection spread are usually combined with models of testing and reporting strategy to link them to the observed case number (Birrell et al., 2011).

The choice of the modeling approach depends on the purpose of the study, the availability of information about the underlying disease and population, and the amount and quality of experimental data. Yet, all these models rely on parameter values that need to be extracted from the literature or estimated from given data. The parameters of epidemiological models in many studies are inferred using frequentist and Bayesian parameter estimation methods. Frequentist methods often rely on parameter optimization for obtaining point estimates and profile likelihoods for uncertainty analysis (Brookhart et al., 2002). Bayesian methods exploit sampling strategies such as Markov chain Monte Carlo (MCMC) methods (Weidemann et al., 2014, Birrell et al., 2011) or variational inference (Chatzilena et al., 2019). Also flexible emulator based methods based, e.g. on Gaussian process, have been applied (Farah et al., 2014). For applications in which competing hypotheses are available, the parameter estimation is often complemented by model selection. Established model selection measures include the Akaike Information Criterion (AIC) (Akaike, 1973), the Bayesian Information Criterion (BIC) (Schwarz, 1978), or Bayes factors (Kass and Raftery, 1995).

In this study, we exploit state-of-the-art parameter estimation and model selection approaches to perform an analysis of the COVID-19 outbreak in Wuhan, China. The first cases of COVID-19 were reported on December 30, 2019 and the Chinese Center for Disease Control and Prevention confirmed the isolation of a novel virus on January 7, 2020 (Gralinski and Menachery, 2020). Already by January 27, there were 1590 confirmed cases which include severe cases and 85 cumulative death cases in Wuhan, and several exported confirmed cases to Cambodia, Canada, France, Japan, Malaysia, Nepal, Republic of Korea, Singapore, Thailand, United States of America, and Vietnam (World Health Organization, 2020). As SARS-CoV-2 spread quickly, the Director-General of World Health Organisation (WHO) declared the flood of infections caused by SARS-CoV-2 a global pandemic on March 11 (Tedros, 2020).

Our study complements other modeling efforts (Shao and Shan, 2020, Chen et al., 2020, Li et al., 2020a, Ming et al., 2020, Read et al., 2020, Koo et al., 2020, Neher et al., 2020, Li et al., 2020b, Zhao et al., 2020b, Tian, 2020, Liu et al., 2020a, Nordt and Herdener, 2020, Jenny et al., 2020) by considering multiple established model topologies, observables, parameter estimation and model selection approaches. To recapitulate the situation in the beginning of the pandemic, we limit the use of prior knowledge to a minimum. This highlights challenges, e.g. the limited information content of case numbers and the dependence on proper model topology, but also opportunities for quantitative modeling in epidemiology.

2. Results

2.1. Observable selection and parameter identifiability

For this study, we considered the case numbers reported by the Health Commission of Hubei Province (2020) and Wuhan Municipal Health Commission (2020). These case numbers were particularly relevant for the analysis of the early transmission dynamics and the planning of interventions. Accordingly, these data were the basis of several modeling studies on the dynamics of COVID-19 epidemic (see e.g. Tian, 2020, Zhao et al., 2020a, Wang et al., 2020, Ming et al., 2020, Roosa et al., 2020, Zhao et al., 2020b, Peng et al., 2020, Li et al., 2020b). Here, we used the time interval from January 9 to February 9, as afterwards the definition of a positive test changed (Chinese Center for Disease Control and Prevention, 2020), which limits the comparability.

The Chinese Center for Disease Control and Prevention provides time-resolved information on:

• •Reported number of infected individuals: $y_I\left(t\right)$
• •Reported number of recovered individuals: $y_R\left(t\right)$
• •Reported number of deceased individuals: $y_D\left(t\right)$
• •Reported cumulative number of infected individuals: $y_T\left(t\right)=y_I\left(t\right)+y_R\left(t\right)+y_D\left(t\right)$

The reported number of deceased individuals is probably most accurate, yet the overall reliability of the measurement and the distribution of the errors is unknown. As in the literature different combinations of these observables are used for model parameterization, we consider here the following fitting scenarios:

• •O1: Observations of $y_T$ and $y_D$.
• •O2: Observations of $y_I$ and $y_D$.
• •O3: Observations of $y_I$, $y_R$ and $y_D$.

As different studies considered different aspects of the data, we first asked which scenario is most suited to determine the parameters of the infection process.

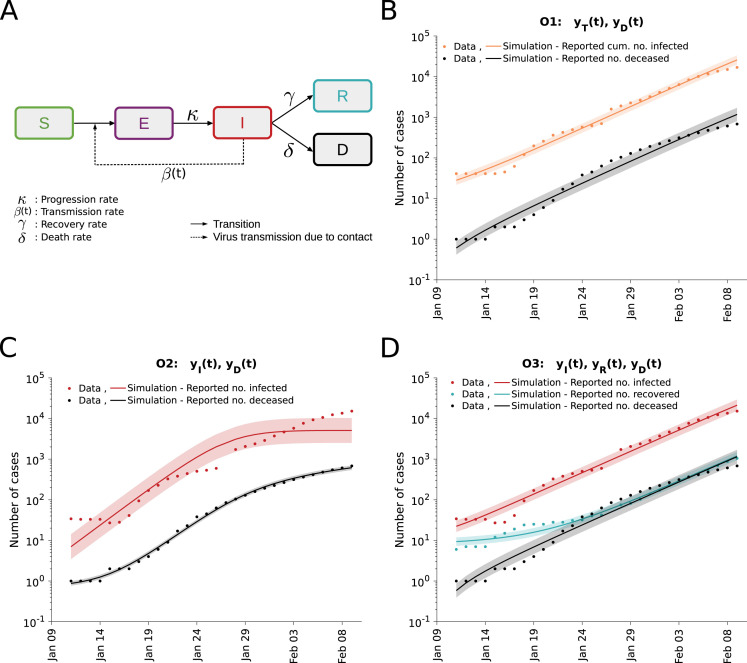
To address this question, we employed a classical deterministic Susceptible–Exposed–Infectious–Recovered–Deceased (SEIRD) model (Capasso, 1993). This compartmental model describes the size of the susceptible ($S$), exposed ($E$), infectious ($I$), recovered ($R$) and deceased ($D$) subgroups (Fig. 1A). The time-dependence of the subgroup sizes is governed by the ODEs:

$$\frac{dS}{dt}=-\beta \frac{SI}{N}S\left(0\right)=N_S$$

$$\frac{dE}{dt}=\beta \frac{SI}{N}-\kappa \cdot EE\left(0\right)=N_E$$

$$\frac{dI}{dt}=\kappa E-(\gamma +\delta )II\left(0\right)=N_I$$

$$\frac{dR}{dt}=\gamma IR\left(0\right)=N_R$$

$$\frac{dD}{dt}=\delta ID\left(0\right)=N_D$$

in which $\beta$ is the average number of contacts per person per time which result in an infection, $\kappa$ is the rate at which exposed individuals become infectious, $\gamma$ is the rate at which infectious individuals recover, $\delta$ is the rate at which infectious individuals decease, and $N=S\left(t\right)+E\left(t\right)+I\left(t\right)+R\left(t\right)+D\left(t\right)$ is the overall population size. Note that the inverse of the rate $\kappa$ is the average incubation time $T_E={\kappa }^{-1}$. The initial conditions for the different state variables are given by $N_S$, $N_E$, $N_I$, $N_R$ and $N_D$. The initial conditions are usually non-zero and might be inferred along with the unknown model parameters as shown in Peng et al., 2020, Tsay et al., 2020, Tang et al., 2020. We applied the simplifying assumption that all infectious individuals are observed.

Fig. 1.

Analysis of different observable combinations. (A) Schematic of the SEIRD model. (B,C,D) Fitting results for observation scenarios O1, O2, and O3 assuming log-normally distributed measurement noise. The simulation for the maximum likelihood estimate (line) and interval for $+∕-$ one standard deviation of the inferred noise level (shaded area) is depicted. The upper bound for the inverse of the rate constants was set to 182 days and for the initial conditions to 1000 individuals.

For all observable scenarios we performed a maximum likelihood estimation assuming normally as well as log-normally distributed measurement noise with unknown standard deviations (see Materials and Methods). All parameters were assumed to be unknown with conservative bounds (Table 4), similar to various recent publications (Roda et al., 2020, Bertozzi et al., 2020, Tang et al., 2020, Peng et al., 2020). The multi-start local optimizations converged (Supplementary Figure S1A) and the simulations with the maximum likelihood estimates achieved a good agreement with the observed data (Fig. 1B–D and Supplementary Figure S1C–E). This confirms the findings of other research groups showing that the SEIRD model is sufficient to fit the observed case numbers of the COVID-19 outbreak in Wuhan. The comparably low noise levels inferred for the number of deceased individuals confirms our expectation that these observations are most reliable. Model selection based on AIC and BIC indicated a strong support for log-normally distributed measurement noise (Supplementary Figure S1B). For this choice, the residual distribution is consistent with the theoretically expected on Supplementary Figure S2, which indicated that the statistical model is appropriate.

Table 4.

Model parameters. Nominal values, lower bounds, upper bounds, priors and units for the model parameters. The nominal values are only used for model parameters which are not fitted.

	Name	Fitted	Nominal value	Lower bound	Upper bound	Prior	Unit
Parameters of transition rates	${\beta }_0$	Yes	-	$10^{-5}$	$10^5$	log-uniform	day−1
	${\xi }_0$	Yes	-	0.0038	16.63	log-uniform	day−1
	$\kappa$	Yes	-	0.0038	16.63	log-uniform/-normal	day−1
	$\gamma$	Yes	-	0.0038	16.63	log-uniform/-normal	day−1
	$\nu$	Yes	-	0.0038	16.63	log-uniform	day−1
	$\delta$	Yes	-	0.0038	16.63	log-uniform/-normal	day−1
	$\rho$	Yes	-	0.0038	16.63	log-uniform	day−1
	$\Delta$	Yes	-	0.0038	16.63	log-uniform	-
	$T_C$	No	13	-	-	-	day
	$k$	Yes	-	0.0038	16.63	log-uniform	day−1
Total and initial number of people	$N$	No	$9\times 10^6$	-	-	-	#
	$N_E$	Yes	-	$10^{-1}$	$10^3$	log-uniform	#
	$N_A$	Yes	-	$10^{-1}$	$10^3$	log-uniform	#
	$N_I$	Yes	-	$10^{-1}$	$10^3$	log-uniform	#
	$N_R$	Yes	-	$10^{-1}$	$10^3$	log-uniform	#
	$N_{R^{\prime }}$	Yes	-	$10^{-1}$	$10^3$	log-uniform	#
	$N_D$	Yes	-	$10^{-1}$	$10^3$	log-uniform	#
Noise level	${\sigma }_T^2$	Yes	-	$10^{-3}$	$10^3$	log-uniform	#
	${\sigma }_I^2$	Yes	-	$10^{-3}$	$10^3$	log-uniform	#
	${\sigma }_R^2$	Yes	-	$10^{-3}$	$10^3$	log-uniform	#
	${\sigma }_D^2$	Yes	-	$10^{-3}$	$10^3$	log-uniform	#

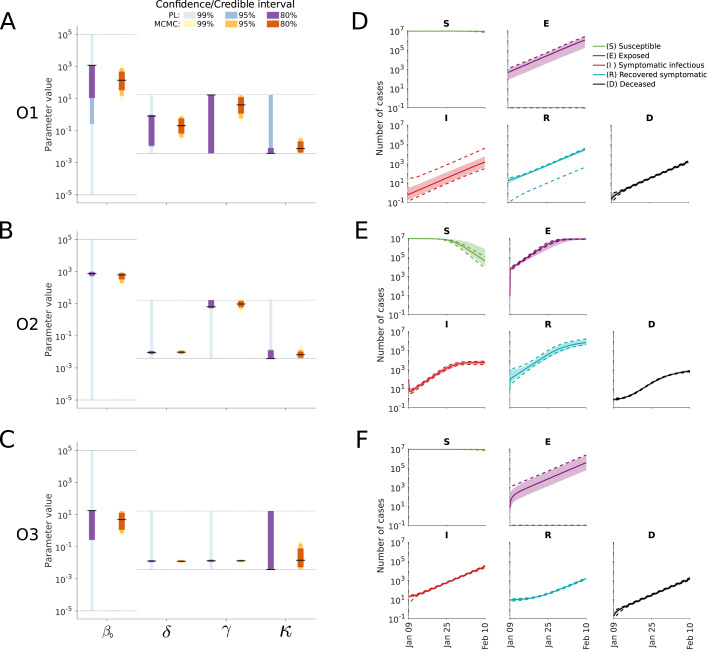
For an in-depth analysis of the impact of the choice of observables, we performed uncertainty analysis using frequentist and Bayesian methods using bounded log-uniform priors (Fig. 2). This analysis revealed several well-known problems, e.g. that the estimates of the transmission rate $\beta$ and the progression rate $\kappa$ are subject to substantial uncertainties (see also previous studies (Tuncer and Le, 2018, Roda et al., 2020, Roosa and Chowell, 2019)). Furthermore, profile likelihood calculation and MCMC sampling showed that for the case of an upper bound for the inverse of the rate constants of 182 days and for the initial conditions of 1000 individuals, O3 provides improved parameter identifiability and decreased parameter uncertainties compared to O1 and O2 (Fig. 2A–C). This was to be expected as O3 uses three observables ($I$, $R$ and $D$) while O1 and O2 use two observables (and a subset of the information encoded in O3). Overall, the results were robust to changes in the bounds of the rates and for the initial conditions (Supplementary Figures S3, S4 and S5).

Fig. 2.

Uncertainty quantification for the different observable combinations. (A–C) Parameter confidence/credibility intervals obtained using profile calculation and MCMC samples. The gray lines indicate the employed parameter boundaries. (D–F) Posterior of state variables obtained by MCMC sampling. Medians (line) and 99% confidence (dashed lines) / credibility intervals (area) are indicated. The upper bound for the inverse of the rate constants was set to 182 days and for the initial conditions to 1000 individuals.

As in some studies a subset of rates and initial conditions is fixed to specific values, we analyzed the impact of the choices on the estimates of the remaining parameters. We observed that while the maximum likelihood estimates remained mostly similar for different plausible choices, the confidence intervals are altered substantially (Supplementary Figures S3, S4 and S5). Subsequently, we analyzed the impact of fixing the initial number of exposed individuals $N_E$ for model O3. Here, we found that the estimates of the remaining parameters to be sensitive to the choice of $N_E$. This was particularly relevant for the progression rate $\kappa$, for which implausible confidence intervals were obtained for a range of values of $N_E$ (Supplementary Figure S6). This is critical as it implies that fixing the initial value of this compartment (for which usually only unreliable estimates are available), can bias the complete analysis. The selected bounds as well as indicating which parameters are estimated for the subsequent analyses in the manuscript are shown in Table 4. Interestingly, the large parameter uncertainties for O1 and O2 are only partially reflected in the prediction uncertainties (Fig. 2D–F) due to a strong parameter correlation (Supplementary Figures S7, S8 and S9).

The most critical observation was that the parameter estimates are not realistic, independently of the selected initial / estimated conditions, and that the credibility intervals derived from the MCMC samples are too narrow. The 99%-credibility intervals for O1, O2 and O3 suggested that $\kappa$ is in the interval of [0.39, 4.28] $\times 10^{-2}$ days⁻¹. This would imply an incubation period of [23.4, 257.6] days. This is not consistent with the estimates reported by the WHO which indicate a median incubation time of 5–6 days (World Health Organization, 2020), which have been confirmed by several other studies (Chen et al., 2020, Li et al., 2020b, Koo et al., 2020, Jenny et al., 2020, Neher et al., 2020). Similar inconsistencies are observed for the basic reproduction number. Not only the Bayesian parameter estimates for bounded log-uniform priors are off, but also the maximum likelihood estimates. However, in contrast to narrow 99%-credibility intervals computed from MCMC samples, the 99%-confidence intervals derived from profile likelihoods are broad and cover realistic values. This indicates that parameters estimates derived from case numbers can be unrealistic and their reliability should be carefully assessed using different approaches.

In addition to the parameters, several model predictions are unrealistic and implausible. This includes high numbers of exposed individuals for O1. Given the estimated parameters of the transmission process, these estimate numbers of exposed individuals at the initial time point of our simulation could not have been reached. This implies that the estimated rate constants and initial conditions are inconsistent in this setup. As the consistency of the model and its parameters is essential, this needs to be assessed and ensured.

As the information encoded in the number of reported cases alone appeared insufficient to infer realistic and identifiable parameter estimates, we complemented it in the following with log-normal priors for the incubation period, death rate and recovery rate as specified in the Materials and Methods section. The parameters of the prior of the incubation time are derived from the work of Backer et al. (2020), which is based on the infections among travelers from Wuhan. While the parameters of the priors of the death and recovery rates are derived from the work of Zhou et al. (2020). We tested the sensitivity of the results with respect to the parameters by considering a range of values for the scale parameter. This revealed that plausible estimates of the incubation period $T_E$ are already obtained for weak priors, whereas plausible estimates for the death and recovery rates required strong priors (Supplementary Figure S10). For the subsequent analysis, we set the scales of the priors according to the reliability of the parameters provided in the respective publications. As O3 with these priors achieves plausible estimates, i.e. the parameter confidence intervals cover values reported in the literature (Read et al., 2020, Jenny et al., 2020, Peng et al., 2020), we considered for the following sections this setup with priors in the model fitting (Fig. 3A).

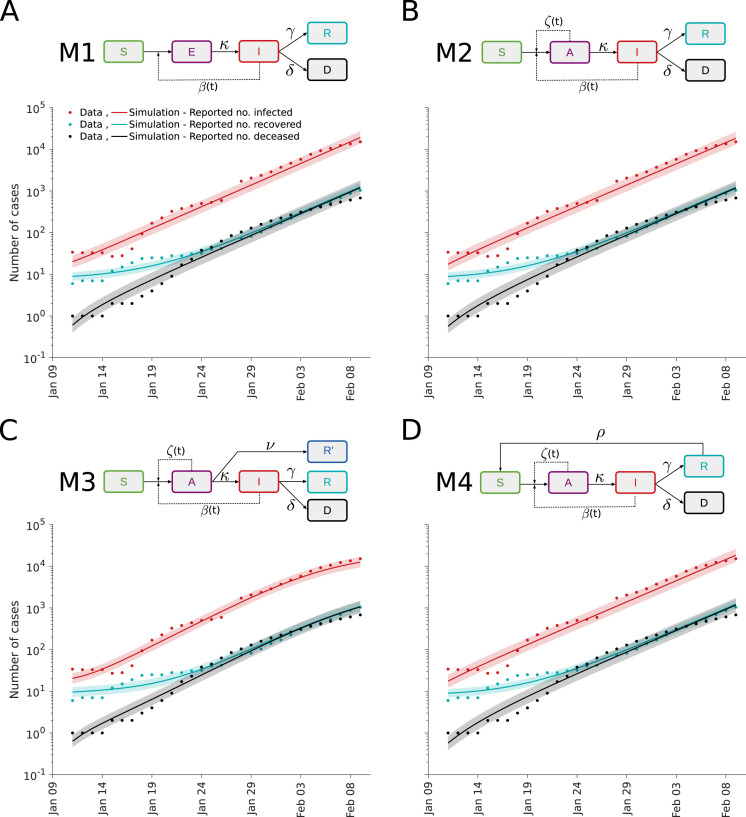
Fig. 3.

Fit for different epidemiological models. (A–D) Illustration of model structures (top) and model-data comparison (bottom). The simulation for the maximum likelihood estimate (line) and interval for $+∕-$ one standard deviation of the inferred noise level (shaded area) is depicted.

2.2. Analysis of transmission process

The SEIRD model with the priors for the incubation period, the death rate and the recovery rates provides a reasonable description of the case numbers reported for Wuhan (Fig. 3A). Yet, this widely used model disregards the observation that patients are asymptomatic (European Centre for Disease Prevention and Control, 2020a). These patients can be infectious but are more difficult to detect. To study the impact of asymptomatic patients, we consider besides the basic SEIRD model (M1) also two alternative epidemiological models:

• •M2: A SAIRD model considering asymptomatic individuals ($A$) with transmission rate $\zeta$ and symptomatic individuals ($I$) with transmission rate $\beta$. The asymptomatic individuals are assumed to become symptomatic.
• •M3: A SAIRD model similar to M2, which allows for the direct recovery of asymptomatic patients. The recovered asymptomatic patients ($R^{\prime }$) are assumed to remain unreported.

We assume that the reported number of infected individuals corresponds to the number of symptomatic patients ($I$). Accordingly, the reported number of recovered individuals is assumed to count only previously symptomatic individuals.

As a further model extension, we consider the possibility of waning immunity. Some studies suggested that the infection with SARS-CoV-2 does not necessarily induce a long-lived antibody response (Amanat and Krammer, 2020, Long et al., 2020), while others found antibody responses 4 months after infection (Gudbjartsson et al., 2020). To address this, we consider:

• •M4: A SAIRD model similar to M2, which allows recovered individuals ($R$) to become susceptible ($S$) with rate $\rho$.

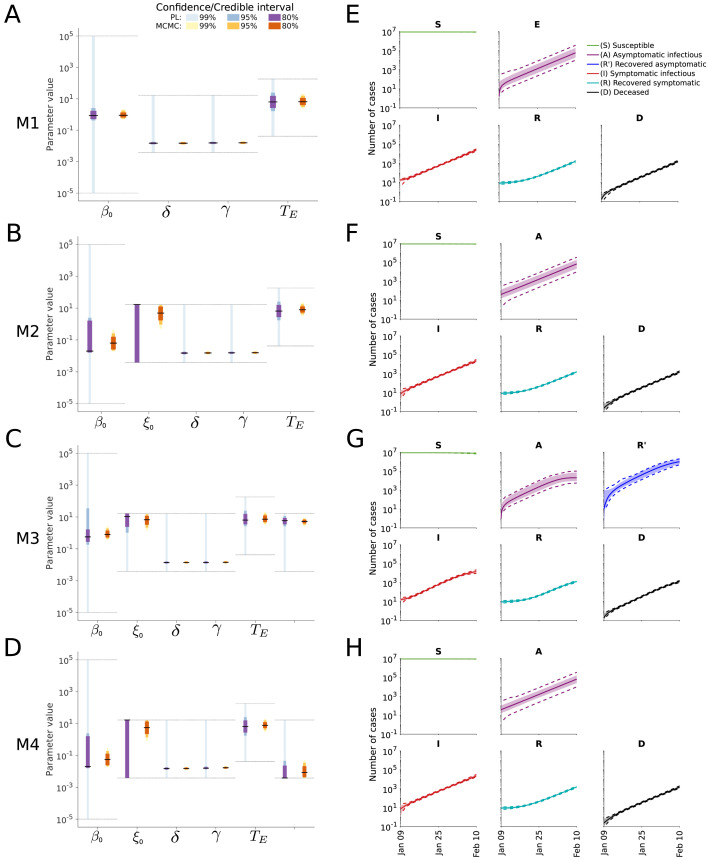
The parameters of models M1–M4 were estimated using multi-start local optimization. The simulations of models M1 to M4 for the respective maximum a posterior estimate show a reasonable agreement with the data (Fig. 3). Interestingly, while the simulations for M1, M2 and M4 are similar, the simulation for M3 shows an early saturation (Fig. 3C). The reason is that the initial number of unobserved recovered patients (which can also be interpreted as immune patients) is estimated to be very high, which does not appear to be plausible.

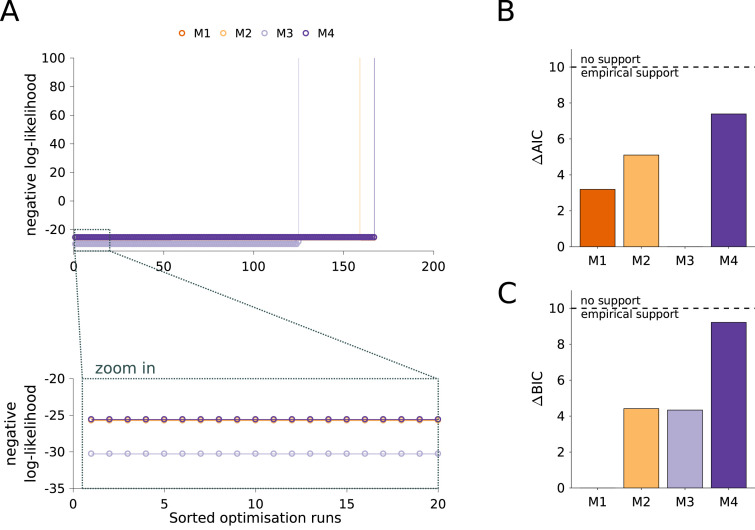
As the fitting results for all models were highly reproducible (Fig. 4A), we considered the values of the likelihood function and evaluated the AIC and BIC for model selection (Fig. 4B,C). First of all, we observed that although M4 is more complex than M1 and M2, it does not achieve a better likelihood value (Fig. 4A, zoom in). This suggests that recovered individuals are not again becoming susceptible in the considered time frame. However, when taking into account the AIC and BIC values, for which differences of 10 are considered substantial (Burnham and Anderson, 2002), we cannot reject M4. As all models achieved a relatively similar fit, M1 to M3 appeared to be suitable descriptions and the ranking differs for AIC and BIC. This confirms the limited information content of the case numbers as there is clear evidence for the relevance of asymptomatic cases.

Fig. 4.

Analysis of model structure. (A) Waterfall plots for the 200 multi-start runs. The optimization runs are sorted by increasing negative log-likelihood value. The lower panel shows a magnification of the best 20 starts. (B) Differences in AIC with respect to the lowest value indicate M3 as the most plausible model. (C) Differences in BIC with respect to the lowest value indicate M1 as the most plausible model. Black dashed line in (B) and (C) depicts a change of 10 units considered as a rejection threshold (Burnham and Anderson, 2002).

To assess the uncertainty of the parameter estimates and predictions, we computed the profile likelihoods and performed MCMC sampling (Fig. 5A–D). The results indicate that the parameter uncertainties for M2–M4 are larger than for M1, but that most parameters are well determined. The profile likelihoods yield overall more conservative estimates than the sampling (Supplementary Figures S11, S12, S13 and S14). The predictions of the state variables based on the sampling suggest low uncertainties of all model states (Fig. 5E–H) while still having large parameter uncertainties as a result of correlations between parameters (Supplementary Figures S11, S12, S13 and S14). In particular for M3 this appears unrealistic as there are so far no reports about a large number of immune individuals (Fig. 5G).

Fig. 5.

Uncertainty quantification for different model structures. (A–D) Confidence/credibility intervals for the model parameters obtained using profile calculation and MCMC sampling. The gray lines indicate the employed parameter boundaries. (E–H) Confidence/credibility intervals for the state variables obtained using prediction profile likelihood calculation and MCMC sampling. Medians (line) and 99% confidence (dashed lines) / credibility intervals (area) are indicated.

2.3. Analysis of intervention effect

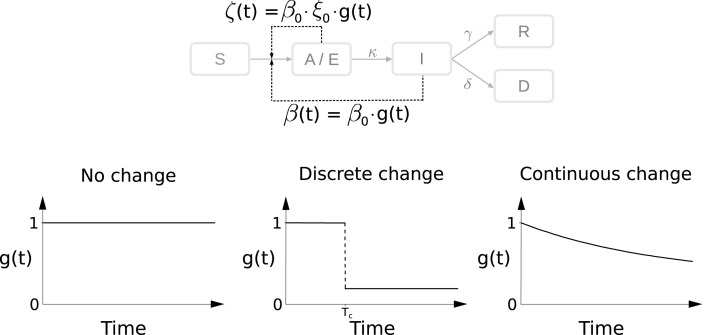
A key question in many recent studies is how much interventions such as compulsory masks and social contact restrictions, as well as the rising public awareness impact the transmission rate of SARS-CoV-2. To study how well this question can be assessed based on early case report data, we considered three simple scenarios:

• •No change of the transmission rate.
• •Discrete change in the transmission rate due to the compulsory masks introduced by the government in Wuhan on January 22 and substantially increasing contract restrictions.
• •Continuous change in the transmission rate due to rising public awareness and a broad spectrum of interventions.

These scenarios are illustrated in Fig. 6 and a detailed mathematical description is provided in the Materials and Methods section.

Fig. 6.

Modeling intervention strategies. Schematic of distinct intervention effects influencing $\beta$ and $\zeta$. $T_C$ denotes the time at which an intervention is performed.

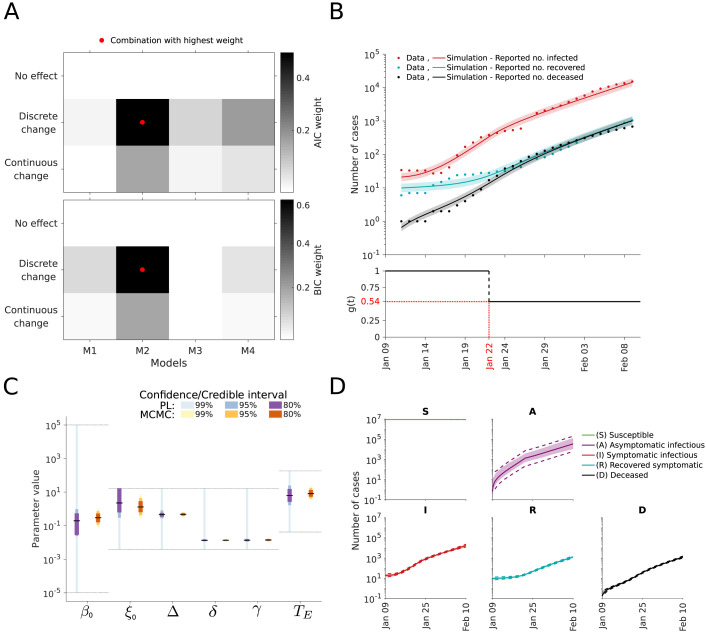
As the result of the analysis of the infection dynamics carried out in the previous section was inconclusive, we considered model M1 to M4. For all 12 combinations of model structures and intervention effects, we performed parameter estimation and uncertainty analysis. The assessment of the model selection criteria provided support for a discrete change in the transmission rate on January 22 (Fig. 7A). The resulting model provides an accurate description of the data and suggests that the transmission rate dropped by around 46% (Fig. 7B). Moreover, the residual distribution is consistent with the theoretically expected (Supplementary Figures S15). The uncertainty estimates for the decrease ($\Delta$) depend heavily on the analysis approach. While MCMC sampling yields a 99% credibility interval from 32.2 to 63.67%, the profiles suggests a much broader regime (Fig. 7C and Supplementary Figure S16). Accordingly, the reported case number for the early outbreak were not sufficient for an accurate assessment of all model parameters. Despite the parameter uncertainties, the states seem to be relatively well determined (Fig. 7D).

Fig. 7.

Analysis of intervention effects. (A) Model selection using AIC weights (top) and BIC weights (bottom). (B) Best model fit (top) and estimated intervention effect (bottom). The simulation for the maximum likelihood estimate (line) and interval for $+∕-$ one standard deviation of the inferred noise level (shaded area) is depicted. (C) Confidence/credibility intervals for the model parameters obtained using profile calculation and MCMC sampling. The gray lines indicate the employed parameter boundaries. (D) Confidence/credibility intervals for the state variables obtained using prediction profile likelihood calculation and MCMC sampling. Medians (line) and 99% confidence (dashed line) / credibility intervals (area) are indicated.

3. Discussion

Pandemics pose a global challenge and show the importance of model-based forecasting. Forecasts influence the political decision-making process and have a significant impact on our society. Minimizing model uncertainties and properly evaluating them is therefore crucial. Yet, many publications are still only using reported case number and/or omit an identifiability and uncertainty analysis (Li et al., 2020a, Ming et al., 2020, Maier and Brockmann, 2020, Read et al., 2020, Zhao et al., 2020b, Barbarossa et al., 2020, Salim et al., 2020, Berk and Kadyrov, 2020). Here, we demonstrated that both aspects are problematic.

Our analysis of the COVID-19 outbreak in Wuhan demonstrates that the parameterization of epidemiological models can result in incorrect parameter estimates and predictions. Surprisingly, even Bayesian uncertainty analysis using MCMC sampling with bounded log-uniform priors as well as informative priors on the incubation time, death and recovery rates, resulted in an underestimation of the indeterminacy and provided inaccurate predictions. In principle this could be caused by (i) problems in the parameter estimation, (ii) unsuitable statistical data model, (iii) poor data quality, (iv) low information content of the data, and (v) inadequate process descriptions. Yet, we ensured the reliability and reproducibility of the fitting results (by even comparing multiple methods) and confirmed the appropriateness of the noise data (by considering multiple noise models and evaluating residual distributions). This indicates that (i)-(iii) do not cause the observed problems. In our opinion the concrete reasons are:

• (1)The models considered here and used in various other publications are too simple to obtain meaningful parameter estimates during the early phase of the COVID-19 epidemic. They neglect for instance particularities of the process (e.g. a large number of asymptomatic cases (Nishiura et al., 2020)), the stochastic nature of the process (He et al., 2020, Halloran et al., 2008), the heterogeneity of the population (e.g. the age structure (Wu et al., 2020)), and time-dependent testing and reporting protocols (Chinese Center for Disease Control and Prevention, 2020). As the parameter estimates depend on the model characteristics, such simplifications can result in biased estimates and predictions.
• (2)The case report data provide only limited information about the process, in particular the distribution of inter-event times are difficult of reconstruct, which is also discussed in multiple other studies (Zhao et al., 2020b, Roosa et al., 2020, Chowell, 2017, Ahmetolan et al., 2020, Anastassopoulou et al., 2020, Mukandavire et al., 2020, Liu et al., 2020b).

Besides parameter estimation, the aforementioned limitations of case numbers were observed in the model selection process. The data did, for instance, not allow to unravel that a large number of the asymptomatic cases is not detected. Yet, the data still contained information that allowed to detect the effect of government restrictions.

The problems we encountered in this study have in parts been described for other models. In particular, practical and structural identifiability has been reported in several publications which used case report data (Chowell, 2017, Roosa et al., 2020, Mukandavire et al., 2020, Zhao et al., 2020b, Tuncer and Le, 2018, Roda et al., 2020). In contrast, bias in parameter estimates and inappropriateness of confidence intervals – which is caused by unsuitability of the model – is rarely discussed.

Fortunately, the problems can be addressed by refining the models and by incorporating additional information. Already the incorporation of details of the disease progression provides substantially improved estimates and predictions (Giordano et al., 2020). In addition, parameter priors can be used to incorporate information which is not contained in case numbers. Yet, – as we demonstrate above – the priors have to be chosen appropriately, as the results can be very sensitive to them. Furthermore, while literature-based priors are used in many manuscripts (Khailaie et al., 2020), we hypothesize that it would be better to use information about individual cases for parameter estimation and model selection. In particular the date of the onset of symptoms, the date of the positive test, and the date of recovery/death for individuals is highly relevant. These data are being collected and analyzed (Backer et al., 2020, Lauer et al., 2020, Zhou et al., 2020, Wölfel et al., 2020), but should in the future be shared much earlier. Furthermore, randomized testing would be required, ideally using antibody tests to determine the fraction of completely asymptomatic patients. Such studies are usually not possible during an initial phase of a pandemic but are now on the way (Bayerisches Staatsministerium für Wissenschaft und Kunst., 2020).

This study does not offer new insights into the COVID-19 pandemic. However, it pinpoints important pitfalls and showcases the relevance of the underlying assumptions and the available data. Furthermore, it demonstrates that even a proper uncertainty analysis using state-of-the-art frequentist or Bayesian approaches does not ensure that the true parameters and dynamics are captured within the uncertainty bounds. While we demonstrate this aspect here for deterministic compartmental models – which are the basis of many modeling studies for COVID-19 and beyond – it certainly holds also for other modeling approaches. Similarly, model-free studies are based on assumptions, data and statistical models, rendering them subject to at least the same limitations.

4. Materials and methods

4.1. Data

The study is based on official reports on the total number of cases and the numbers of infected individuals, recovered individuals and deceased individuals. From January 11 to 20, the reports were made available by the Wuhan Municipal Health Commission (2020). Afterwards, the reports were organized by the Health Commission of Hubei Province (2020). All these data are publicly available on the respective webpages. The complete data sets used in this study are listed in Table 1.

The exact population size in the city of Wuhan in the period under consideration is not precisely known due to Chinese New Year. In this study we assume a population size of 9 million which was mentioned by the mayor of Wuhan, Zhou Xianwang (Business Insider, Ashley Collman, 2020).

Table 1.

Number of total, infected, deceased and recovered cases in Wuhan, China. Missing data in the official reports are indicated by “-”.

Date	Total	Infected	Recovered	Deceased
January 9	–	–	–	–
January 10	–	–	–	–
January 11	41	34	6	1
January 12	41	33	7	1
January 13	41	33	7	1
January 14	41	33	7	1
January 15	41	27	12	2
January 16	45	28	15	2
January 17	62	41	19	2
January 18	121	94	24	3
January 19	198	169	25	4
January 20	258	227	25	6
January 21	363	326	28	9
January 22	425	380	28	17
January 23	495	441	31	23
January 24	572	502	32	38
January 25	618	533	40	45
January 26	698	593	42	63
January 27	1590	–	–	85
January 28	1905	1726	75	104
January 29	2261	2050	82	129
January 30	2639	2377	103	159
January 31	3215	2884	139	192
February 1	4109	3714	171	224
February 2	5142	4653	224	265
February 3	6384	5768	303	313
February 4	8351	7621	368	362
February 5	10117	9272	431	414
February 6	11618	10606	534	478
February 7	13603	12360	698	545
February 8	14982	13497	877	608
February 9	16902	15177	1044	681

4.2. Mathematical models

We considered four different deterministic compartmental models for the description of the transmission process. The state variables of the models are the number of individuals with particular characteristics and the notations can be found in Table 2.

Table 2.

State variables of the mathematical models.

Name	Description
$S$	Susceptible
$E$	Exposed but not infectious
$A$	Asymptomatic and infectious
$I$	Symptomatic and infectious
$R$	Recovered with previously symptomatic progression
$R^{\prime }$	Recovered with previously asymptomatic progression
$D$	Deceased

The models allow for various processes which result in the transitions of individuals between compartments (see Fig. 3). A description of the rates is provided in Table 3. For the time-dependence of the transmission rates $\beta$ and $\zeta$,

$$\beta \left(t\right)={\beta }_0\cdot g\left(t\right)\text{and}\zeta \left(t\right)={\beta }_0\cdot {\xi }_0\cdot g\left(t\right),$$

we considered three scenarios:

Table 3.

Rates in the mathematical models.

Name	Process	Description
$\beta \left(t\right)$	$S+I$$\to$$E∕A$	(Time-dependent) transmission rate for symptomatic
$\zeta \left(t\right)$	$S+A$$\to$$E∕A$	(Time-dependent) transmission rate for asymptomatic
$\kappa$	$E∕A$$\to$$I$	Progression rate (= $T_E^{-1}$ for incubation time $T_E$)
$\gamma$	$I$$\to$$R$	Recovery rate for symptomatic case
$\nu$	$A$$\to$$R^{\prime }$	Recovery rate for asymptomatic case
$\delta$	$I$$\to$$D$	Death rate
$\rho$	$R$$\to$$S$	Rate at which immunity wanes

• •No change: $g\left(t\right)=1$
• •Discrete change: $g\left(t\right)=\left\{\begin{array}{cc}1\hfill & \text{for }t\le T_C\hfill \\ 1-\Delta \hfill & \text{otherwise}\hfill \end{array}\right)$
• •Continuous change: $g\left(t\right)=e^{-kt}$

The function $g\left(t\right)$ describes the reduction of the transmission rates compared to baseline at $t=0$, with $g\left(0\right)=1$ for all scenarios. The parameters for the discrete change are the time point $T_C$ and the relative reduction $\Delta$, and for the continuous change we have the decay rate $k$. The parameter ${\xi }_0=\frac{{\zeta }_0}{{\beta }_0}$ denotes the relative difference between the transmission rates of the symptomatic individuals ($\beta \left(t\right)$) and asymptomatic individuals ($\zeta \left(t\right)$).

The ODEs governing the dynamics of the different compartmental models are provided in Table 5. We decided to initialize the model on January 9, which is when the virus was first detected (European Centre for Disease Prevention and Control, 2020b), defining $t=0$. As on January 22 the wearing of masks became mandatory, we set for the scenario of a discrete reduction of $\beta$ for $T_C=13$ days.

The state variables of the model were linked to the observed case numbers using observation functions. The observation functions for the total number of cases ($y_T$) as well as for the number of infected ($y_I$), recovered ($y_R$) and deceased ($y_D$) people are provided in Table 5. As the reported numbers are subject to unknown measurement noise, we considered two error models:

• •
  Additive normally distributed measurement noise:

  $${\overline{y}}_{T,k}=y_T\left(t_k\right)+{\epsilon }_{T,k},{\epsilon }_{T,k}\sim \mathcal{N}(0,{\sigma }_T^2)$$

  $${\overline{y}}_{I,k}=y_I\left(t_k\right)+{\epsilon }_{I,k},{\epsilon }_{I,k}\sim \mathcal{N}(0,{\sigma }_I^2)$$

  $${\overline{y}}_{R,k}=y_R\left(t_k\right)+{\epsilon }_{R,k},{\epsilon }_{R,k}\sim \mathcal{N}(0,{\sigma }_R^2)$$

  $${\overline{y}}_{D,k}=y_D\left(t_k\right)+{\epsilon }_{D,k},{\epsilon }_{D,k}\sim \mathcal{N}(0,{\sigma }_D^2)$$
• •
  Multiplicative log-normally distributed measurement noise:

  $${\overline{y}}_{T,k}=y_T\left(t_k\right)\cdot {\epsilon }_{T,k},{\epsilon }_{T,k}\sim log\mathcal{N}(0,{\sigma }_T^2)$$

  $${\overline{y}}_{I,k}=y_I\left(t_k\right)\cdot {\epsilon }_{I,k},{\epsilon }_{I,k}\sim log\mathcal{N}(0,{\sigma }_I^2)$$

  $${\overline{y}}_{R,k}=y_R\left(t_k\right)\cdot {\epsilon }_{R,k},{\epsilon }_{R,k}\sim log\mathcal{N}(0,{\sigma }_R^2)$$

  $${\overline{y}}_{D,k}=y_D\left(t_k\right)\cdot {\epsilon }_{D,k},{\epsilon }_{D,k}\sim log\mathcal{N}(0,{\sigma }_D^2)$$

The observation time points $t_k$, $k=1,\dots ,32$, are the days listed in Table 1, and the measurements (as indicated with the superscript $m$) are the respective case numbers. The distribution parameters ${\sigma }_T$, ${\sigma }_I$, ${\sigma }_R$ and ${\sigma }_D$ were considered as unknown.

In the following the parameters of the transition rates, the total and initial number of people in different compartments, and the parameters of the noise distribution are inferred. A comprehensive list of all model parameters and implemented constraints is provided in Table 4. The boundaries of the search space were chosen very conservatively to indicate the initial knowledge gap about SARS-CoV-2 and COVID-19.

Table 5.

Mathematical models. ODEs for the transmission dynamics, initial conditions and observations functions are defined for all considered model structures. As some models consider only a subset of the state variables, some rows are empty.

	SEIRD model (M1)	SAIRD model (M2)	SAIRRD model (M3)	SAIRDS model (M4)
Infection dynamics	$\frac{dS}{dt}=-\beta \frac{SI}{N}$	$\frac{dS}{dt}=-\beta \frac{SI}{N}-\zeta \frac{SA}{N}$	$\frac{dS}{dt}=-\beta \frac{SI}{N}-\zeta \frac{SA}{N}$	$\frac{dS}{dt}=-\beta \frac{SI}{N}-\zeta \frac{SA}{N}+\rho R$
	$\frac{dE}{dt}=\beta \frac{SI}{N}-\kappa E$
		$\frac{dA}{dt}=\beta \frac{SI}{N}+\zeta \frac{SA}{N}-\kappa A$	$\frac{dA}{dt}=\beta \frac{SI}{N}+\zeta \frac{SA}{N}-(\kappa +\nu )A$	$\frac{dA}{dt}=\beta \frac{SI}{N}+\zeta \frac{SA}{N}-\kappa A$
	$\frac{dI}{dt}=\kappa E-(\gamma +\delta )I$	$\frac{dI}{dt}=\kappa A-(\gamma +\delta )I$	$\frac{dI}{dt}=\kappa A-(\gamma +\delta )I$	$\frac{dI}{dt}=\kappa A-(\gamma +\delta )I$
	$\frac{dR}{dt}=\gamma I$	$\frac{dR}{dt}=\gamma I$	$\frac{dR}{dt}=\gamma I$	$\frac{dR}{dt}=\gamma I-\rho R$
			$\frac{d{R}^{\prime }}{dt}=\nu A$
	$\frac{dD}{dt}=\delta I$	$\frac{dD}{dt}=\delta I$	$\frac{dD}{dt}=\delta I$	$\frac{dD}{dt}=\delta I$
Initial conditions	$S\left(0\right)=N-N_E-N_I-N_R-N_D$	$S\left(0\right)=N-N_A-N_I-N_R-N_D$	$S\left(0\right)=N-N_A-N_I-N_R-N_{R^{\prime }}-N_D$	$S\left(0\right)=N-N_A-N_I-N_R-N_D$
	$E\left(0\right)=N_E$
		$A\left(0\right)=N_A$	$A\left(0\right)=N_A$	$A\left(0\right)=N_A$
	$I\left(0\right)=N_I$	$I\left(0\right)=N_I$	$I\left(0\right)=N_I$	$I\left(0\right)=N_I$
	$R\left(0\right)=N_R$	$R\left(0\right)=N_R$	$R\left(0\right)=N_R$	$R\left(0\right)=N_R$
			$R^{\prime }\left(0\right)=N_{R^{\prime }}$
	$D\left(0\right)=N_D$	$D\left(0\right)=N_D$	$D\left(0\right)=N_D$	$D\left(0\right)=N_D$
Observables	$y_T=I+R+D$	$y_T=I+R+D$	$y_T=I+R+D$	$y_T=I+R+D$
	$y_I=I$	$y_I=I$	$y_I=I$	$y_I=I$
	$y_R=R$	$y_R=R$	$y_R=R$	$y_R=R$
	$y_D=D$	$y_D=D$	$y_D=D$	$y_D=D$

4.3. Parameter estimation

To infer the unknown model parameters we used frequentist and Bayesian approaches. These approaches considered the conditional probability $p\left(\mathcal{D}\right|\theta )$ of the data $\mathcal{D}$ given the parameters $\theta$, also known as likelihood. For additive normally distributed measurement noise the likelihood function is

$$p\left(\mathcal{D}\right|\theta )=\prod _{i\in \mathcal{I}}\prod _{k=1}^{32}\frac{1}{\sqrt{2\pi }{\sigma }_i}exp\left\{-\frac{1}{2}{\left(\frac{{\overline{y}}_{i,k}-y_i\left(t_k\right)}{{\sigma }_i}\right)}^2\right\},$$

and for multiplicative log-normally distributed measurement it is

$$p\left(\mathcal{D}\right|\theta )=\prod _{i\in \mathcal{I}}\prod _{k=1}^{32}\frac{1}{\sqrt{2\pi }{\sigma }_i{\overline{y}}_{i,k}}exp\left\{-\frac{1}{2}{\left(\frac{log\left({\overline{y}}_{i,k}\right)-log\left(y_i\left(t_k\right)\right)}{{\sigma }_i}\right)}^2\right\}.$$

The set of considered observables is encoded by $\mathcal{I}$ and differs for the scenarios O1 to O3: ${\mathcal{I}}_{\text{O1}}=\{T,D\}$, ${\mathcal{I}}_{\text{O2}}=\{I,D\}$, and ${\mathcal{I}}_{\text{O3}}=\{I,R,D\}$. In addition to the case reports, we also incorporated knowledge available before the parameter estimation. For Bayesian approaches this was done by defining prior distributions. These prior distributions are mostly log-uniform with conservative upper and lower bounds, meaning that the distribution over the log-transformed parameter values is flat. For $\kappa$ we include in parts of the study information about the incubation period (Backer et al., 2020), given by a log-normal prior:

$$p\left(\kappa \right)=\frac{1}{\sqrt{2\pi }{\sigma }_{\kappa }\kappa }exp\left\{-\frac{1}{2}{\left(\frac{log\left(\kappa \right)-log\left(\hat{\kappa }\right)}{{\sigma }_{\kappa }}\right)}^2\right\},\text{with}\hat{\kappa }={(6.4\text{[day]})}^{-1}\text{ and }{\sigma }_{\kappa }=0.3.$$

For $\delta$ and $\gamma$ we include in parts of the study information about the mean death and mean recovery time (Zhou et al., 2020), given by a log-normal prior:

$$p\left(\delta \right)=\frac{1}{\sqrt{2\pi }{\sigma }_{\delta }\delta }exp\left\{-\frac{1}{2}{\left(\frac{log\left(\delta \right)-log\left(\hat{\delta }\right)}{{\sigma }_{\delta }}\right)}^2\right\},\text{with}\hat{\delta }={(18.5\text{[day]})}^{-1}\text{ and }{\sigma }_{\delta }=0.15,$$

and

$$p\left(\gamma \right)=\frac{1}{\sqrt{2\pi }{\sigma }_{\gamma }\gamma }exp\left\{-\frac{1}{2}{\left(\frac{log\left(\gamma \right)-log\left(\hat{\gamma }\right)}{{\sigma }_{\gamma }}\right)}^2\right\},\text{with}\hat{\gamma }={\left(22\text{[day]}\right)}^{-1}\text{ and }{\sigma }_{\gamma }=0.1.$$

For the frequentist approaches the available estimates of $\kappa$, $\delta$ and $\gamma$ are treated as data points.

Remark

For the parameter estimation we consider the log-transformed parameter values. For the log-transformed parameters, the log-uniform prior become effectively a uniform prior. This renders the frequentist and the Bayesian approaches comparable, namely, the maximum likelihood and the maximum a posteriori estimates coincide.

4.3.1. Maximum likelihood and maximum a posteriori estimates

To determine the maximum likelihood and the maximum a posteriori estimates, we minimized the negative log-likelihood function and negative log-posterior function, respectively. As these optimization problems are non-linear and non-convex, we used multi-start local optimization. The starting points for the local optimizations were generated using latin hypercube sampling. Local optimization was performed using the interior point algorithm implemented in the MATLAB function lsqnonlin.m, which exploits the least-squares like structure of the optimization problems. To facilitate convergence, we computed the gradients of the residuals via forward sensitivity equations. The convergence of the global optimization was assessed using waterfall plots.

For each of the 18 considered combinations of compartment model, noise model, observable scenario and intervention scenario, we performed 200 local optimizations. For all combinations at least 15 runs converged to the observed global optimum. This suggested that the results are highly reliable.

4.3.2. Frequentist uncertainty analysis

To evaluate the (frequentist) parameter and prediction confidence intervals we used profile likelihoods (Raue et al., 2009, Kreutz et al., 2013). The profile likelihoods were computed using the MATLAB toolbox Data2Dynamics (Raue et al., 2015). This toolbox implements optimization-based methods with adaptive step-size selection as well as fast integration-based methods (Hass et al., 2016). To ensure the robustness of the results, the consistency of the outcomes was checked and confirmed.

The profile likelihoods were used to derive the (finite sample) confidence intervals and to assess practical identifiability (Raue et al., 2009). For a significance level $\alpha$, the bounds of the confidence interval were determined as the smallest and largest parameter values for which the profile likelihood stays above the threshold defined by the $\alpha$th-percentile of the ${\chi }^2$-distribution (Meeker and Escobar, 1995). We used the ${\chi }^2$-distribution with one degree of freedom which yields the so called point-wise confidence intervals. We note that for practically identifiable parameters (as termed (Raue et al., 2009)), the confidence intervals can still be rather wide.

4.3.3. Bayesian uncertainty analysis

To evaluate the (Bayesian) parameter and prediction credibility intervals we used Markov chain Monte Carlo sampling (Ballnus et al., 2017). The parameter posterior distribution was sampled using the Adaptive Metropolis algorithm implemented in the MATLAB toolbox PESTO (Stapor et al., 2018). The methods are self-tuning and provided good convergence properties. Convergence after burn-in was assessed using the Geweke test (Geweke, 1992). The parameter samples were used to generate samples for the model states and observables.

The samples of parameters and predictions were used to derive the credibility intervals. For a credibility level $\alpha$, the bounds of the credibility interval were determined as the $100\alpha ∕2$- and the $100(1-\alpha ∕2)$-percentile of the respective sample. This procedure yields the so called equal-tailed interval.

4.4. Model selection

We considered competing hypotheses on the dynamics of the infection process, the effect of the intervention and the noise distribution. Each of the resulting models was assessed using the Akaike information criterion (AIC),

$${\mathrm{AIC}}_j=-2logp\left(\mathcal{D}\right|{\hat{\theta }}^{\left(j\right)})+2n_{\theta }^{\left(j\right)},$$

and the Bayesian information criterion (BIC),

$${\mathrm{BIC}}_j=-2logp\left(\mathcal{D}\right|{\hat{\theta }}^{\left(j\right)})+log\left(n_{\mathcal{D}}\right)n_{{\theta }^{\left(j\right)}},$$

in which $j$ is the model index, ${\hat{\theta }}^{\left(j\right)}$ is the maximum likelihood estimate for the $j$th model, and $n_{{\theta }^{\left(j\right)}}$ is the number of parameter of the $j$th model. The number of independent data points is denoted by $n_{\mathcal{D}}$. The parameter priors are treated as data points, therefore included in $n_{\mathcal{D}}$. AIC and BIC account for the likelihood of the data and penalize model complexity. Low AIC and BIC values are favorable. We consider a difference of 10 between AIC/BIC values of different models as substantial (Burnham and Anderson, 2002).

For analysis and visualization we also evaluated the AIC and BIC weights (Burnham and Anderson, 2002). The AIC weight for the $j$th model is defined as

$$w_{\mathrm{AIC},j}=\frac{exp\{-\frac{1}{2}({\mathrm{AIC}}_j-{\mathrm{AIC}}_{min})\}}{\sum _{j^{\prime }}exp\{-\frac{1}{2}({\mathrm{AIC}}_{j^{\prime }}-{\mathrm{AIC}}_{min})\}},\text{with}{\mathrm{AIC}}_{min}≔\underset{j^{\prime }}{min}{\mathrm{AIC}}_{j^{\prime }},$$

and provides the weight of evidence in favor of the $j$th model being the actual best model in terms of the Kullback–Leibler Information (assuming that the true model is in the considered set). The BIC weight for the $j$th model is defined as

$$w_{\mathrm{BIC},j}=\frac{exp\{-\frac{1}{2}({\mathrm{BIC}}_j-{\mathrm{BIC}}_{min})\}}{\sum _{j^{\prime }}exp\{-\frac{1}{2}({\mathrm{BIC}}_{j^{\prime }}-{\mathrm{BIC}}_{min})\}},\text{with}{\mathrm{BIC}}_{min}≔\underset{j^{\prime }}{min}{\mathrm{BIC}}_{j^{\prime }},$$

and provides an approximation to the Bayesian posterior probability of the $j$th model. AIC and BIC weights are between 0 and 1, and a high value indicates a strong support.

4.5. Implementation and availability

The model formulation, parameter estimation and profile likelihoods were performed in the MATLAB toolbox Data2Dynamics (https://github.com/Data2Dynamics/d2d) (Raue et al., 2015). Outliers in the computed prediction profiles arising from calculation errors were corrected subsequently. The calculation of parameter confidence intervals and MCMC sampling was carried out using the MATLAB toolboxes PESTO (https://github.com/ICB-DCM/PESTO) (Stapor et al., 2018) and AMICI (https://github.com/ICB-DCM/AMICI) (Fröhlich et al., 2017a, Fröhlich et al., 2017b). For numerical integration Data2Dynamics and AMICI rely on the SUNDIALS solver CVODES (Serban and Hindmarsh, 2005).

The complete implementation (including the respective version of the used toolboxes) and data are available on ZENODO ( https://doi.org/10.5281/zenodo.4457194). This includes the MATLAB code as well as the specification of the parameter estimation problems as PEtab files (Schmiester et al., 2020) (with the model in SBML format Hucka et al. (2003)).

CRediT authorship contribution statement

Elba Raimúndez: Visualization, Formal analysis, Methodology, Software, Writing - original draft, Writing - review & editing. Erika Dudkin: Visualization, Formal analysis, Software, Writing - original draft, Writing - review & editing. Jakob Vanhoefer: Methodology. Emad Alamoudi: Resources. Simon Merkt: Resources, Software. Lara Fuhrmann: Resources. Fan Bai: Conceptualization, Resources. Jan Hasenauer: Conceptualization, Writing - original draft, Writing - review & editing, Supervision.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following is the Supplementary material related to this article.

MMC S1

This e-component contains all Supplementary Figures.