Rational policymaking during a pandemic

Abstract

Policymaking during a pandemic can be extremely challenging. As COVID-19 is a new disease and its global impacts are unprecedented, decisions are taken in a highly uncertain, complex, and rapidly changing environment. In such a context, in which human lives and the economy are at stake, we argue that using ideas and constructs from modern decision theory, even informally, will make policymaking a more responsible and transparent process.

The COVID-19 pandemic exposes decision problems faced by governments and international organizations. Policymakers are charged with taking actions to protect their population from the disease while lacking reliable information on the virus and its transmission mechanisms and on the effectiveness of possible measures and their (direct and indirect) health and socioeconomic consequences. The rational policy decision would combine the best available scientific evidence—typically provided by expert opinions and modeling studies. However, in an uncertain and rapidly changing environment, the pertinent evidence is highly fluid, making it challenging to produce scientifically grounded predictions of the outcomes of alternative courses of action.

A great deal of attention has been paid to how policymakers have handled uncertainty in the COVID-19 response (1–6). Policymakers have been confronted with very different views on the potential outbreak scenarios stemming from divergent experts’ assessments or differing modeling predictions. In the face of such uncertainty, policymakers may respond by attempting to balance the alternative perspectives, or they may fully embrace one without a concern that this can vastly misrepresent our underlying knowledge base (7). This tendency to lock on to a single narrative—or more generally, this inability to handle uncertainty—may result in overlooking valuable insights from alternative sources, and thus in misinterpreting the state of the COVID-19 outbreak, potentially leading to suboptimal decisions with possibly disastrous consequences (2, 8–10).

This paper argues that insights from decision theory provide a valuable way to frame policy challenges and ambitions. Even if the decision-theory constructs are ultimately used only informally in practice, they offer a useful guide for transparent policymaking that copes with the severe uncertainty in sensible ways. First, we outline a framework to understand and guide decision-making under uncertainty in the COVID-19 pandemic context. Second, we show how formal decision rules could be used to guide policymaking and illustrate their use with the example of school closures. These decision rules allow policymakers to recognize that they do not know which of the many potential scenarios is “correct” and to act accordingly by taking precautionary and robust decisions, that is, that remain valid for a wide range of futures and keep options open (11). Third, we discuss directions to define a more transparent approach for communicating the degree of certainty in scientific findings and knowledge, particularly relevant to decision-makers managing pandemics.

Decision under Uncertainty

The Policymaker’s Problem(s).

The decision-making problem faced by a high-level government policymaker during a crisis like the COVID-19 pandemic is not trivial. In the first stage, when a new infectious disease appears, the policymaker may attempt to contain the outbreak by taking early actions to control onward transmission (e.g., isolation of confirmed and suspected cases and contact tracing). If this phase is unsuccessful, policymakers face a second-stage decision problem that consists of determining the appropriate level, timing, and duration of interventions to mitigate the course of clinical infection. These interventions may include banning mass gatherings, closing schools, and more extreme “lockdown” restrictions.

While these measures are expected to reduce the pandemic’s health burden by lowering the peak incidence, they also impose costs on society. For instance, they may have adverse impacts on mental health, domestic abuse, and job loss at a more personal level. Moreover, there are societal losses due to the immediate reduced economic activity coupled with a potentially prolonged recession and adverse impacts on longer-term health and social gradients. Policymakers must thus promptly cope with a complex and multifaceted picture of direct and indirect, proximal and distal, health, and socioeconomic trade-offs. In the acute phase of the pandemic, the trade-off between reducing mortality and morbidity and its associated socioeconomic consequences may seem relatively straightforward. Still, once out of this critical phase, most trade-offs are difficult and costly. How should the policymaker decide when and how to introduce or relax measures in a justifiable way, not just from a health and economic perspective but also politically? The answer critically depends on the prioritization and balance of potentially conflicting objectives (12).

Scientific Evidence and the Role of Modeling.

Scientific knowledge is foundational to the prevention, management, and treatment of global outbreaks. Some of this evidence can be summarized in pandemic preparedness and response plans (at both international and national levels) or might be directly obtained from panels of scientists with expertise in relevant areas of research, such as epidemiologists, infectious disease modelers, and social scientists. An essential part of the scientific evidence comes from quantitative models (13). Quantitative models are abstract representations of reality that provide a logically consistent way to organize thinking about the relationships among variables of interest. They combine what is known in general with what is known about the current outbreak to produce predictions to help guide policy decisions (14).

Epidemiological models (e.g., refs. 15 and 16) have been used to guide decision-making by assessing what is likely to happen to the transmission of the virus if policy interventions—either independently or in combination—were put in place. Such public health-oriented models are particularly useful in the short term to project the direct consequences of policy interventions on the epidemic trajectory and to guide decisions on resource allocations (17). As the measures put in place also largely affect the economic environment, decision-makers must, at least implicitly, confront trade-offs in the health- and nonhealth-related economic consequences. To weigh these trade-offs necessarily requires more than epidemiological models. For example, health policy analysis models, such as computable general equilibrium models, are used to simultaneously estimate the direct and indirect impacts of the outbreak on various aspects of the economy, such as labor supply, government budgets, or household consumption (18). More recent integrated assessment models combine economics and epidemiology by incorporating simplified epidemiological models of contagion within stylized dynamic economic frameworks. Such models address critical policy challenges by explicitly modeling dynamic adjustment paths and endogenous responses to changing incentives. They have been used to investigate the optimal policy response or alternative macroeconomic policies’ effectiveness to the economic shocks due to the COVID-19 pandemic (19–22). However, these different modeling approaches do not formally incorporate uncertainty; instead, they treat it ex-post, for example using sensitivity analyses.

Uncertainty.

Decisions within a pandemic context have to be made under overwhelming time pressure and amid high scientific uncertainty, with minimal quality evidence and potential disagreements among experts and models. In the COVID-19 outbreak, there was uncertainty about the virus’s essential characteristics, such as its transmissibility, severity, and natural history (3, 23, 24). This state of knowledge translates into uncertainty about the system dynamics, which renders uncertain the consequences of alternative policy interventions such as closing down schools or wearing masks in public. At a later stage of the pandemic, information overload becomes an issue, making it more difficult for the decision-maker to identify useful and good-quality evidence. The consequence is that, given the many uncertainties they are built on, no single model can be genuinely predictive in the context of an outbreak management strategy. Yet, if their results are used as insights providing potential quantitative stories among alternative ones, models can offer policymakers guidance by helping them understand the fragments of information available, uncover what might be going on, and eventually determine the appropriate policy response. The distinction between three layers of uncertainty—uncertainty within models, across models, and about models—can help the policymaker understand the extent of the problem (25–28).

Uncertainty within models reflects the standard notion of risk: uncertain outcomes with known probabilities. Models may include random shocks or impulses with prespecified distributions. It is the modeling counterpart to flipping coins or rolling dice in which we have full confidence in the probability assessment.

Uncertainty across models encompasses both the unknown parameters for a family of models or more discrete modeling differences in specification. Thus, it relates to unknown inputs needed to construct fully specified probability models. In the COVID-19 context, this corresponds, for example, to the uncertainty of some model parameters, such as how much transmission occurs in different age groups or how infectious people can be before they have symptoms. Existing data, if available and reliable, can help calibrate these model inputs. An additional challenge for the policymaker is the proliferation of modeling groups, researchers, and experts in various disciplines (epidemiology, economics, and other social sciences). Each of these provides forecasts and projections about the disease’s evolution and/or its socioeconomic consequences. This uncertainty across models and their consequent predictions may be difficult to handle by policymakers, especially as one approach is not necessarily superior to another but simply adds another perspective (29). There is no single “view.” Analysis of this form of uncertainty is typically the focal point of statistical approaches. Bayesian analyses, for instance, confront this via the use of subjective probabilities, whereas robust Bayesians explore sensitivity to prior inputs. Decision theory explores the ramifications of subjective uncertainty, as there might be substantial variation in the recommendations across different models and experts, reflecting other specific choices and assumptions regarding modeling type and structure.

Finally, as models are, by design, simplifications of more complex phenomena, they are necessarily misspecified, at least along some dimensions. For instance, they might not mention certain variables that matter, which modelers are or are not aware of, or they may be limited in the scope of functional relationships considered, unknown forms of specification and measurement errors, and so forth. Consequently, there is also uncertainty about the models’ assumptions and structures. It might sometimes be challenging, even for experts, to assess the merits and limits of alternative models and predictions.* This is what we mean in our reference to uncertainty about models.

How to Make Rational Decisions under Uncertainty?

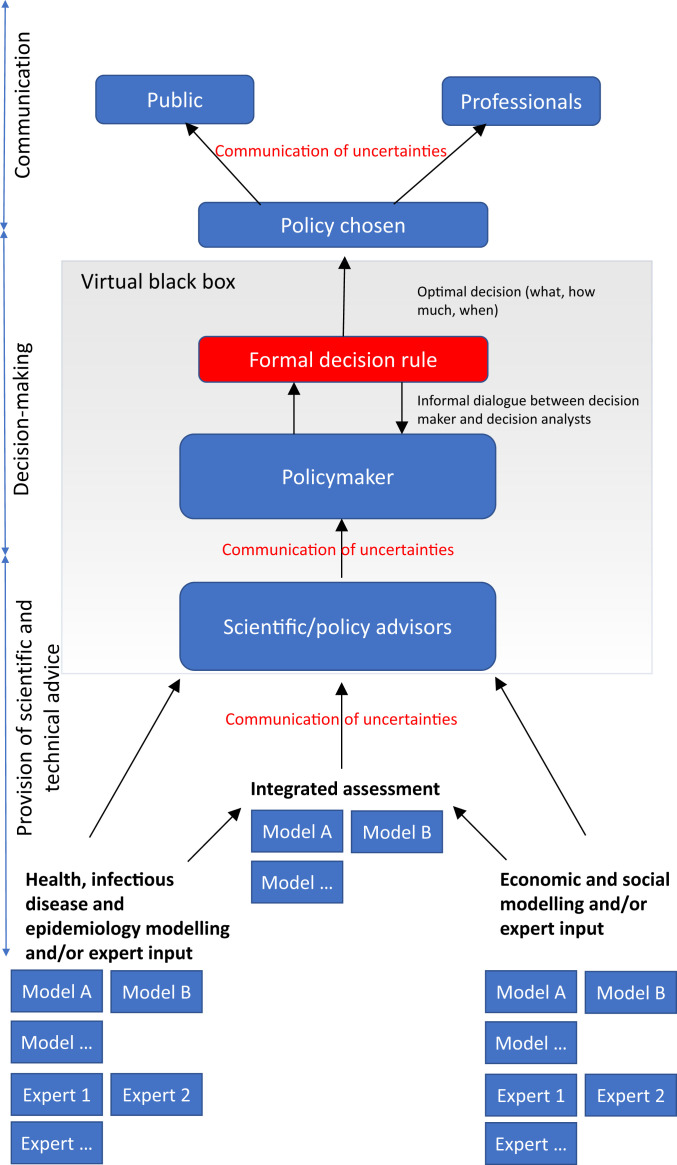
Now that we have characterized the elements of the decision problem under uncertainty (Fig. 1), the question remains on how to make the best possible decision. In other words, how should the policymaker proceed to aggregate the different (and usually conflicting) scientific findings, model results, and expert opinions—which are all uncertain by construction and by lack of reliable data—and ultimately determine policy? Insights from modern decision theory are of the most significant value at this stage. They propose normative guidelines and “rules” to help policymakers make the best, that is, the most rational, decision under uncertainty.

Fig. 1.

Overview of the decision problem under uncertainty.

How Can Formal Decision Rules Be Useful?

The formal decision rules proposed by decision theorists are powerful, mathematically founded^† tools that relate theoretical constructs and choice procedures to presumably observable data. Making a decision based on such rules is equivalent to complying implicitly with a set of general consistency conditions or principles governing human behavior. During a crisis such as the COVID-19 pandemic, using decision theory as a formal guide will lend credibility to policymaking by ensuring that the resulting actions are coherent and defensible. To illustrate how decision theory can serve as a coherence test (31), imagine the case of a policymaker trying to determine what the best response to the current pandemic is. The decision-makers can make up their minds by whatever mix of intuition, expert advice, imitation, and quantitative model results they have available and then check their judgment by asking whether they can justify the decision using a formal decision rule. Conceptually, it can be seen as a form of dialogue between the policymakers and decision theory, in which an attempt to justify a tentative decision helps to clarify the problem and, perhaps, leads to a different conclusion (32). Used this way, formal decision rules may help policymakers clarify the problem they are dealing with, test their intuition, eliminate strictly dominated options, and avoid reasoning mistakes and pitfalls that have been documented in psychological studies (e.g., confirmation bias, optimism bias, representativeness heuristic, prospect theory, etc.) (33).

Finally, because committees might investigate how decisions were taken during the crisis, for example about how lockdown measures were implemented and lifted, policymakers are held to account for the actions they took. A formal decision model can play an essential role in defending one’s choice and generating ex-post justifiability. For example, it could help a policymaker who had to decide which neighborhoods to keep under lockdown and which not to explain the process that led to such decisions to citizens who might think they have not been treated fairly.

Which Decision Rule to Follow?

As decision theory proposes a variety of different rules for decision-making under uncertainty, the call for using decision theory begs the question, Which rules to follow? The answer depends, in our opinion, on the society or organization in question. Decision theory should offer a gamut of models, and the people for whom decisions are made should find acceptable the model that is considered to “provide a justification” for a given decision. Thus, the answer ultimately depends on the policymakers’ characteristics, for example which conditions or behavioral principles they want to comply with, how prudent they want the policy to be, or what answer their constituency expects to receive. In Fig. 2, we present a simple example of school closures’ decision problem during the COVID-19 pandemic. We use this to demonstrate how distinct quantitative model outputs (some of which represent “best guesses” while others represent “reasonable worst-case”^‡ possibilities) can be combined and used in formal decision rules, and what the resulting recommendations in terms of policy responses are.

Fig. 2.

Case study. School closures and their length during the COVID-19 pandemic (see refs. 52–69). Details are provided in SI Appendix.

The policymaker’s problem consists in finding the right balance between protecting the health and preventing economic and social disruptions by choosing whether and for how long to keep schools closed, given the scarce scientific evidence and the disagreement that may exist across model projections, possibly leading to significantly different policies.

The decision rules that we present differ primarily in how they handle probabilities. According to the Bayesian view, which holds that any source of uncertainty can be quantified probabilistically, the policymaker should always have well-defined probabilities about the impacts of the measures taken. If they rely on quantitative model outputs or expert advice to obtain different estimates, then they should attach a well-defined probability weight to each of these and compute an average. Thus, in the absence of objective probabilities, the decision-makers have their own subjective probabilities to guide decisions.

However, it may not always be rational to follow this approach (34–37). Its limitation stems from its inability to distinguish between uncertainty across models (which has an epistemic nature and is due to limited knowledge or ignorance) and uncertainty within models (which has an aleatory nature and is due to the intrinsic randomness in the world). In the response to the COVID-19 outbreak, the Bayesian approach requires the policymaker to express probabilistic beliefs (about the impact of a policy, about the correctness of a given model, etc.), without being told which probability it makes sense to adopt or being allowed to say “I don’t know.” Because of the disagreements that may exist across different model outputs, or expert opinions, another path may be to acknowledge one’s ignorance and relax the assumption that we can associate precise probabilities to any event. Modern decision theory proposes decision rules in line with this non-Bayesian approach. The axiomatic approach on which it is founded serves as an essential guide in understanding the merits and limitations of alternative ways to confront uncertainty formally. While we do not see this theory as settling on a single recipe for all decision problems, it adds important clarity to the rationale behind alternative decision rules.

Discussion

The decision rules presented in Fig. 2 are fully compatible with normative interpretations and could be particularly useful to design robust policies in this COVID-19 pandemic context. They assume that policymakers cope with uncertainty without reducing everything to risk, a pretension that tacitly presumes better information than they typically have. When exploring alternative courses of action, policymakers are necessarily unsure of the consequences. In such a context, sticking to the Bayesian expected utility paradigm not only requires substantive expertise (in weighting the pros and cons of alternative models) but also overshadows the policymaker’s reaction to the variability that may exist across models. While we focus, in Fig. 2, on a subset of decision rules, which can be checked for logical consistency, it should be clear, however, that other criteria, such as minmax regret (38), also exist and have been used in some applied contexts (39, 40). As mentioned above, we believe that a decision criterion is also a matter of personal preferences, which should somehow be aggregated over the different individuals for whom the decisions are made. Thus, the examples used in this paper are inevitably subjective, too.

We recognize the challenges in using decision theory when the decision-making process itself is complicated and many participants are involved with potentially different incentives. Nevertheless, we also see value to its use in less formal ways as guideposts to prudent decision-making and as a sensible way of framing the uncertainties in the trade-offs that policymakers are presented with.

In this example, the decision problem setup has been deliberately kept to minimal complexity to focus on the decision theory aspects. In particular, the set of actions is here limited to a single intervention (the duration of the school closure). In reality, the decision problem would, of course, require a much higher dimensional space (e.g., selective local closures, school dismissal, etc.), the interaction with other social distancing measures, or the ability to integrate start and stop times. Along the same lines, time constraints, learning, and dynamic considerations have been assumed away for the sake of tractability. In reality, it should be clear that the existence of deadlines could restrict which actions are feasible so that different sets of actions may correspond to different timings.

Similarly, as time passes, experts learn more about virus transmission and disease dynamics, which ultimately leads them to update their projections. Different “updating rules” allow incorporating such new information into the decision-making process. Our general message is the same as the one concerning the decision rules: The decision-maker should make her choice of the updating rule and be able to justify her decision based on this rule and the conditions that it does or does not satisfy. Finally, for expositional simplicity, we also abstracted from concerns about model misspecification, while recognizing this to be an integral part of how decision-makers should view the alternative models or perspectives that they confronted.

Concluding Remarks

During a period of crisis, policymakers, who make decisions on behalf of others, may be required to provide a protocol that suggests a decision-theoretic model supporting their decisions. Decision theory can contribute to a pandemic response by providing a way to organize a large amount of potentially conflicting scientific knowledge and providing rules for evaluating response options and turning them into concrete decision-making.

In this paper, we have highlighted the importance of quantitative modeling to support policy decisions [the same recommendation has also been made in other public health contexts (40)]. This use of models is common in different macroeconomic settings, including the assessments of monetary and fiscal policies. Some may see quantitative modeling as problematic because it requires seemingly arbitrary subjective judgments about the correctness of the different model specifications, leading them to prefer qualitative approaches. Even qualitative methods cannot escape the need for subjective inputs, however. Restricting scientific inputs to be only qualitative limits severely potentially valuable inputs into prudent policymaking. Instead, we argue in favor of using quantitative models and data, including explicit information about our underlying knowledge’s limits. We propose decision rules that incorporate the decisionmaker’s confidence in her subjective probabilities, thus rendering the decision-making process based on formal quantitative rules both robust and prudent.

In practical terms, ensuring that policy options are in line with formal decision rules could be achieved by having a decision analyst in the group of advisors to nurture a dialogue between policymakers and decision theory. This dialogue could clarify the trade-offs and encourage a more sanguine response to the uncertainties present when assessing the alternative courses of action and result in an improved policy outcome (31, 41).

To make the decision-making process under uncertainty more efficient, we also suggest acknowledging and communicating the various uncertainties transparently (42). For example, illustrating, quantifying, and discussing the multiple sources of uncertainty may help policymakers better understand their choices’ potential impact. To this aim, modelers should provide all information needed to reconstruct the analysis, including information about model structures, assumptions, and parameter values. Moreover, the way uncertainty around these choices affects model results needs to be accurately communicated, such as systematically reporting uncertainty boundaries around the estimates provided (43). Scientific and policy advisors would then need to synthesize all this information (32)—coming from diverse sources across different disciplines, possibly of different quality—to help policymakers turning it into actionable information for decisions, while making sure the complete range of uncertainty (including within and across models) is clearly reported and understood properly (44, 45).

One possible way to go is to enhance standardization by developing and adopting standard metrics to evaluate and communicate the degree of certainty in key findings. While several approaches have been proposed (46), insights could, for example, be gained from the virtues and the shortcomings of the reports of the Intergovernmental Panel on Climate Change (47). Another way is to develop further communication and collaboration between model developers and decision-makers to improve the quality and utility of models and the decisions they support (48).

Finally, while policymakers are responsible for making decisions, they are also responsible for communicating to professionals and the public. The way individuals respond to advice and measures selected is as vital as government actions, if not more (3). Communication should thus be an essential part of the policy response to uncertainty. In particular, government communication strategies to keep the public informed of what we [do not (49)] know should balance the costs and benefits of revealing information (how much, and in what form) (50).

As government strategies have been extensively debated in the media and models have become more scrutinized, one lesson learned from the COVID-19 management experience may be that policymakers and experts must increase their approaches’ transparency. Using the constructs from decision theory in policymaking, even in an informal way, will help ensure prudent navigation through the uncertainty that pervades this and possibly future pandemics. Being open about the degree of uncertainty surrounding the scientific evidence used to guide policy choices and allowing for the assumptions of the models used or for the decision-making process itself to be challenged is a valuable way of retaining public trust (51). At the same time, it is essential to counteract what is too often displayed by self-described experts who seek to influence policymakers and the public by projecting a pretense of knowledge that is likely to be false.

Materials

Supplementary information is included in SI Appendix, Methods Supplement to Figure 2.

Data Availability.

There are no data underlying this work.