Design of Biologically Active Binary Protein 2D Materials

Abstract

Ordered two-dimensional arrays such as S-layers^1,2 and designed analogues^3–5 have intrigued bioengineers,^6,7 but with the exception of a single lattice formed with flexible linkers,⁸ they are constituted from just one protein component. For modulating assembly dynamics and incorporating more complex functionality, materials composed of two components would have considerable advantages.^9–12 Here we describe a computational method to generate co-assembling binary layers by designing rigid interfaces between pairs of dihedral protein building-blocks, and use it to design a p6m lattice. The designed array components are soluble at mM concentrations, but when combined at nM concentrations, rapidly assemble into nearly crystalline micrometer-scale arrays nearly identical (based on TEM and SAXS) to the computational design model in vitro and in cells without the need for a two-dimensional support. Because the material is designed from the ground up, the components can be readily functionalized, and their symmetry reconfigured, enabling formation of ligand arrays with distinguishable surfaces which we demonstrate can drive extensive receptor clustering, downstream protein recruitment, and signaling. Using AFM on supported bilayers and quantitative microscopy on living cells, we show that arrays assembled on membranes have component stoichiometry and structure similar to arrays formed in vitro, and thus that our material can impose order onto fundamentally disordered substrates like cell membranes. In sharp contrast to previously characterized cell surface receptor binding assemblies such as antibodies and nanocages, which are rapidly endocytosed, we find that large arrays assembled at the cell surface suppress endocytosis in a tunable manner, with potential therapeutic relevance for extending receptor engagement and immune evasion. Our work paves the way towards a synthetic cell biology, where a new generation of multi-protein macroscale materials is designed to modulate cell responses and reshape synthetic and living systems.

One Sentence Summary:

Design of a two component protein array enables robust formation of complex large scale ordered biologically active materials

Genetically programmable materials that spontaneously co-assemble into ordered structures following mixture of two or more components are far more controllable than materials constitutively forming from one component; they offer control over assembly onset in ambient conditions, thereby enabling rigorous characterization and components manipulations which lend the system to a wide variety of applications.^9,13 Most previously described 2D protein materials, such as S-layers^14,15 and de-novo designed arrays, primarily involve single protein components which spontaneously self-assembly, complicating characterization and repurposing for specific tasks.^3,16–21 A two component array has been generated by flexibly linking Strep-tag to one homo-oligomer, and mixing with the tetrameric dihedral streptavidin,⁸ but due to the flexibility, the structure of the designed material was not fully specifiable in advance, and since both building-blocks have dihedral symmetry, the array has identical upper and lower surfaces. A de-novo interface design between rigid domains that is stabilized by extensive noncovalent interactions would provide more control over atomic structure and a robust starting point for further structural and functional modulation.

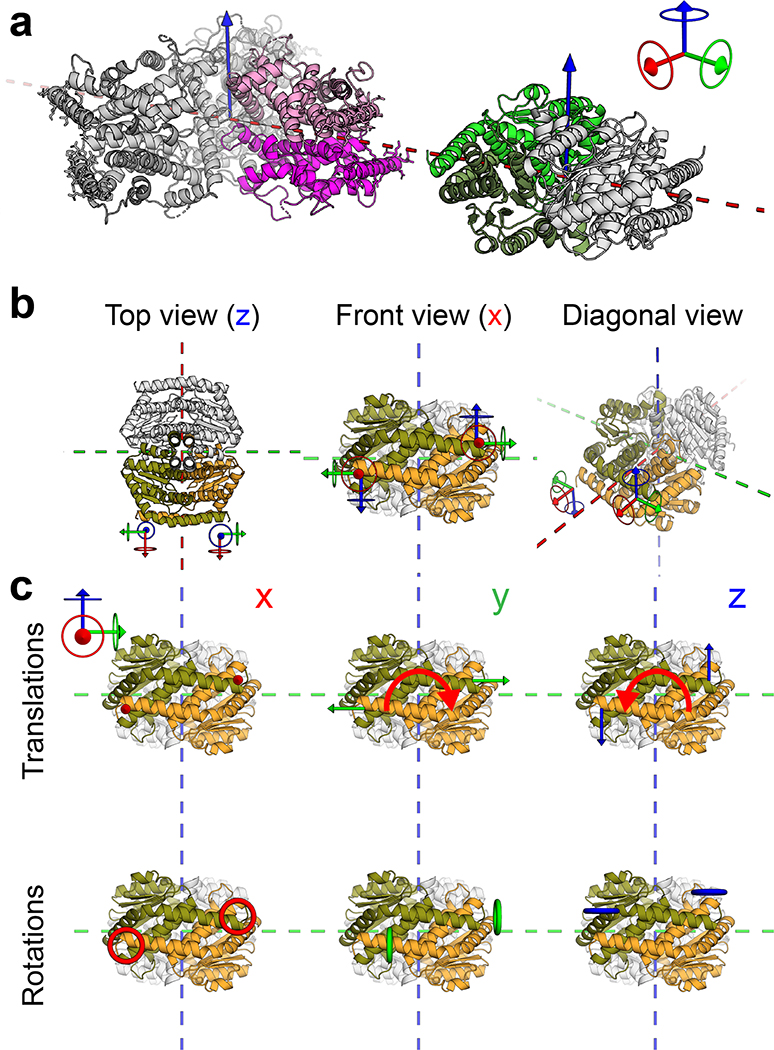
We set out to generate two component 2D arrays by designing interfaces between two different dihedral protein building-blocks (BBs).^10,22 There are 17 distinct plane symmetry groups that define 2D repetitive patterns, but a broader set of unique geometries are available using 3D objects; 33 distinct planar geometries can be generated by combining two objects.¹⁵ The BBs can be either cyclic or dihedral homooligomers oriented in space such that their highest order rotation symmetry (C_x: xÎ{2,3,4,6}) is perpendicular to the plane. We chose a subset of the 17 plane symmetry groups (p3m1, p4m, p6m) that can be generated by designing a single additional interface between BBs with dihedral symmetry.^11,12 We chose to use objects with dihedral rather than cyclic symmetry for their additional in-plane 2-fold rotation axes (Fig. 1a, dashed lines) that intrinsically correct for any deviation from the design model which might otherwise result in out-of-plane curvature (see Extended Data Figure 1 for further discussion). This higher symmetry comes at a cost in the number of degrees of freedom (DOF) available for a pair of objects to associate: while cyclic components are constrained in a plane to 4 DOFs, for dihedrals the only DOFs are the lattice spacing and discrete rotations of the BBs (the dihedral axes of the two components must be aligned). For example, figure 1a shows a two component 2D lattice generated by placing D3 and D2 BBs on the C3 and C2 rotation centers of the p6m(*632) symmetry group such that their in-plane C2 axes coincide (see SI video S1 for illustration of the docking process). We sampled 2D arrays in the p3m1[D3-D3], p4m[D4-D4, D4-D2], and p6m[D6-D3, D6-D2, D3-D2] groups built from 965 dihedral BBs available in the PDB²³ with D2, D3, D4 and D6 symmetry and x-ray resolution better than 2.5Å. For each group, all pairs of dihedral BBs were placed with their symmetry axes aligned to those of the group, and the lattice spacing (Fig. 1a, middle) and the discrete rotations (Fig. 1a, left) were sampled to identify arrangements with contact regions greater than 400 sq Å and composed primarily of aligned helices. The amino acid sequences at the resulting interfaces between the two building blocks were optimized using Rosetta combinatorial sequence design²⁴ to generate low energy interfaces with a hydrophobic center surrounded by polar residues.²⁵

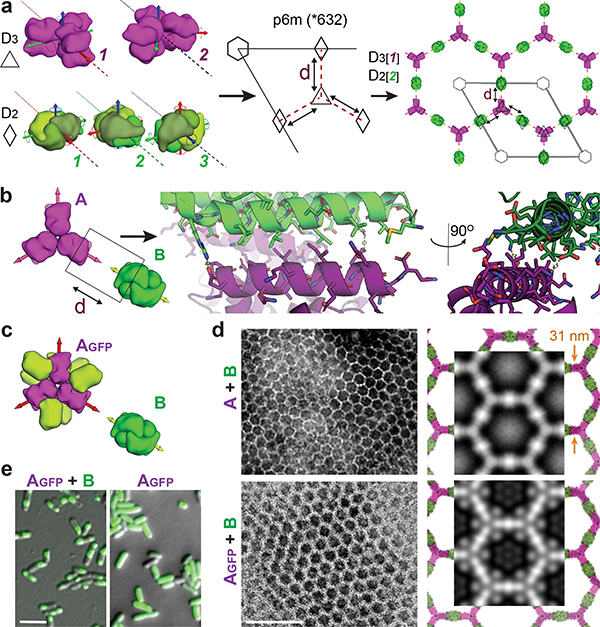
Figure 1. Design strategy and in vivo assembly characterization.

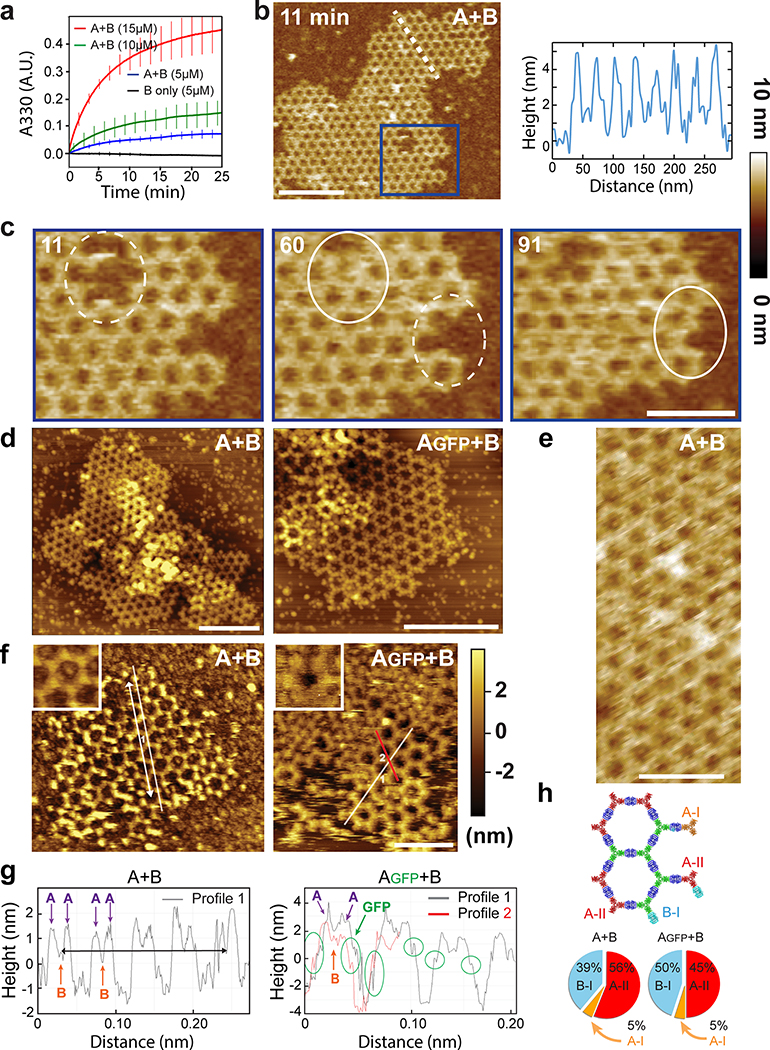
(a) Left panel: example for valid building blocks (BBs) orientations - one BB symmetry axis must align with a plane reflection axis (dashed line). Middle: top view of the p6m symmetry operators and the lattice spacing degree of freedom (dashed line, d); Right: a possible p6m array configurations using D₃ and D₂ BBs, dashed lines indicate on the direction BBs slide into contact. (b) Left to right: Top view BBs configuration; in-plane closer view of the Hetero-interface residues configuration; 90° rotated view perpendicularly to the plane. (c) Model of A genetically fused to GFP (Agfp). (d) Negative stain TEM images of 2D arrays formed in E. coli coexpressing A+B (top left panel) and Agfp+B (bottom left panel). Right panel: corresponding averaged images superimposed with design model (A - magenta, B - green, GFP omitted). (e) Confocal microscopy imaging of cells expressing Agfp (right panel) or Agfp+B (left panel). Scale bars: (d) 100 nm, (e) 5μm.

We selected forty-five of the lowest energy designs (2 - p3m1, 10 - p4m, and 33 - p6m) with high shape complementarity and few buried polar groups not making hydrogen bonds (Fig. 1b), and co-expressed the proteins in E coli after mRNA optimization (Methods, Fig. S1, S2, and Tables S1, S2).^29–31 Cells were lysed, soluble and insoluble fractions were separated. Insoluble fractions containing both proteins by SDS-Page were examined by negative stain electron microscopy (EM), and design #13 displayed the clearest hexagonal lattice (Fig. 1d, top left panel; see Fig. S3, and Table S3 for other designs). Design #13 belongs to the p6m symmetry group and is composed of D3 and D2 homooligomers (hereon referred to as components A and B, respectively). The computational design model and the averaged EM density match closely (Figure 1d, top right panel), suggesting that the designed interface drives assembly of the intended array geometry.

To determine whether co-assembly occurs in cells or after lysis, we genetically fused superfolder green fluorescent protein (GFP) to the N-terminus of component A (Agfp) (Fig. 1c). GFP-fusion did not affect array assembly (Fig. 1d), and consistent with the design model, the added GFP resulted in the appearance of additional density near the trimeric hubs. In cells expressing both Agfp and B, but not Agfp alone, GFP fluorescence was concentrated in patches, suggesting that array assembly occurs in cells (Fig. 1e).

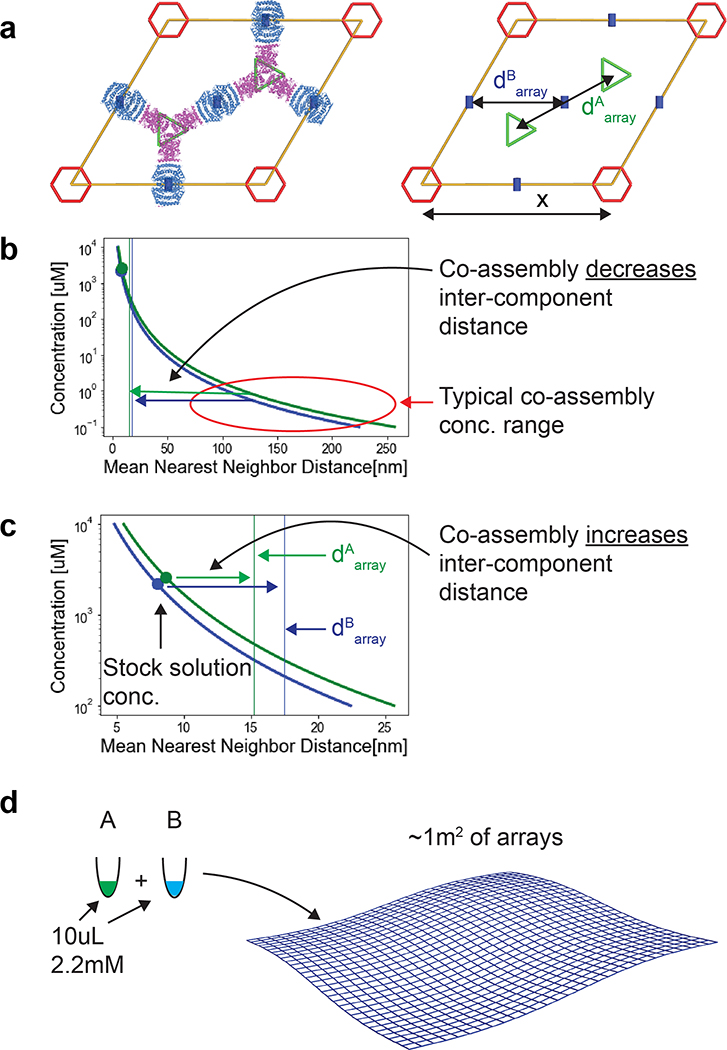
An advantage of two-component materials is that if the isolated components are soluble, co-assembly can in principle be initiated by mixing.⁹ This is important for unbounded (i.e. not finite in size) crystalline materials which typically undergo phase separation as they crystallize, complicating their usage in solution. A measure of binary system quality is the ratio between the maximum concentration at which both components are individually soluble to the minimum concentration at which they co-assemble when mixed; the higher this ratio, the easier to prepare, functionalize, and store the components in ambient conditions. To evaluate the components’ Self-Assembly and the system Co-Assembly ratio (SACAr), we separately expressed and purified the A and B components. Following stabilization of both components by evolution guided design,²⁶ we found that both components could be stored individually at concentrations exceeding 2 mM at room temperature and for durations longer than 3 month (see methods and Tables S5, S6, Fig. S4, S5 for CD results, and Extended Data Figure 4a for SAXS of the individual components) without aggregation, but rapidly assembled into the 2D array when mixed at concentrations as low as ~10 nM. Thus for this system SACAr > 10⁵; a value so high that upon assembly from stock solutions at mM concentrations the distance between each component increases (within the plane) to about twice the estimated mean nearest neighbor distance (see Extended Data Figure 2 for further discussion)²⁷, and the solution instantaneously jellifies (SI video S2).

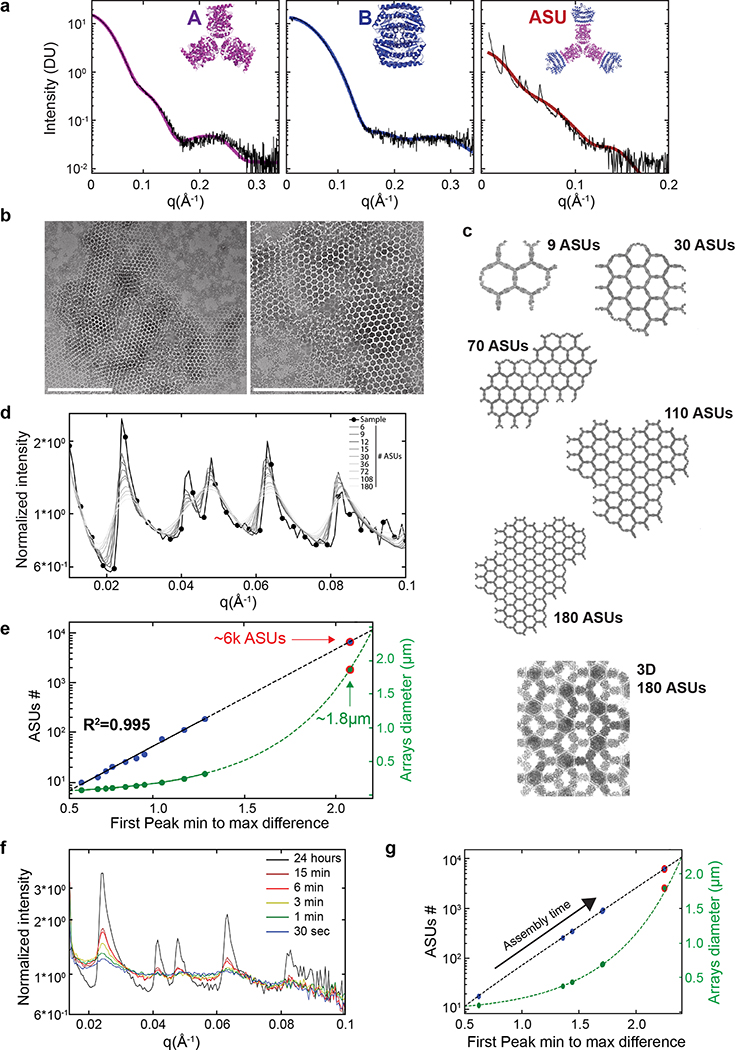
Upon mixing the two purified proteins in vitro at equimolar concentrations, even larger and more regular hexagonal arrays were formed compared to in vivo assembly in bacteria (Fig. 2a,c vs. Fig. 1d). The arrays survive transferring to the TEM grid and incubation with negative stain despite being only ~4 nm thick (see design model and AFM cross section in Extended Data Figures 5b and 9c–d), suggesting a considerable in-plane strength. No assembly was observed with either component alone (see Extended Data Figure 4a and 5a for SAXS and light scattering, respectively, and Fig. S6 for TEM). Array density is closely superimposable on the design model, with the outlines of both components evident (Fig. 2b), suggesting the structure of the material is very close to the model. We then used SAXS to probe array structure in solution (Fig. 2e and Extended Data Figure 5). Scattering rings appear in SAXS spectra at Bragg peaks consistent with P6 symmetry, and unit cell spacing of 303Å (Table S7), in close agreement with the designed 2D array model (310Å), and AFM data (315Å) (Extended Data Figure 5f,g), but not with a 3D stacked arrangement (inset in Fig. 2e, and Extended Data Figure 4c). The agreement between the experimental SAXS profiles and theoretical profiles computed from the design model increases with increasing numbers of subunits (Extended Data Figure 4c–e), suggesting that arrays are at least 1.8μm in diameter in solution. Some array stacking with a discrete number of symmetry preserving packing arrangements was observed in EM (Fig. 2c). Based on the solution SAXS results and further structural analysis we attribute these observations to EM sample preparation processing conditions (see Extended Data Figure 3 for further discussion).

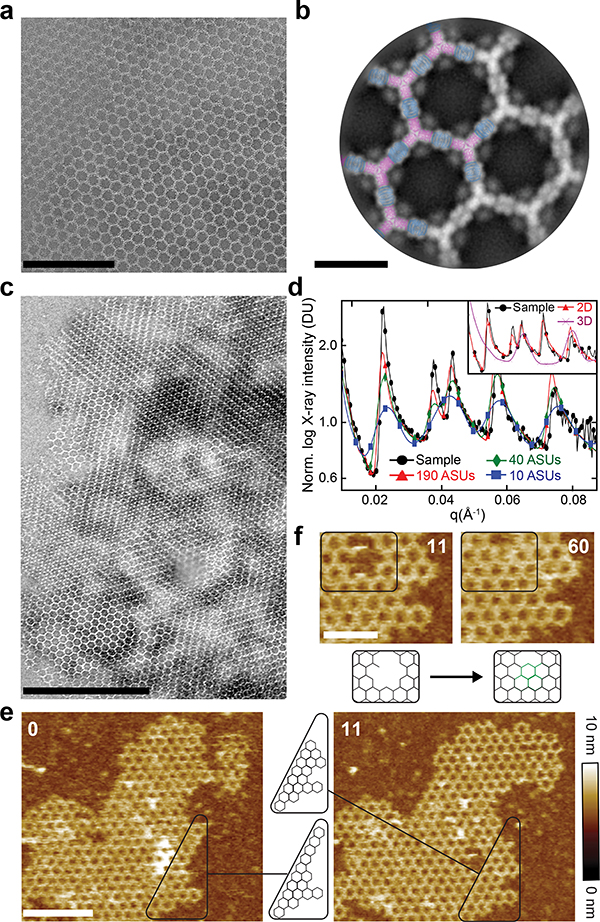
Figure 2. Structure of in vitro assembled arrays.

(a) Negative stain TEM of monolayered Agfp+B array. (b) Computational model (A - magenta, B - blue) overlayed on averaging of (a) (gray), GFP density is evident near A. (c) Negative Stain EM of micron-scale arrays. (d) SAXS profile of overnight assembly of A and B (black) versus calculated profiles from atomic models of various sheet dimensions have near identical peaks spacing and positions. Inset: SAXS profiles for the measured sample (black), 2D (red) and 3D (magenta) models. (e) AFM imaging of array growth on mica showing assembly (black box) spanning a number of unit cells. (f) Close up of (e) showing healing of lattice vacancy defects (black box). Elapsed time: minutes. Scale bars: (a) 200 nm; (b) 20 nm; (c) 500nm; (e) 200 nm; (f) 200 nm.

We then investigated the kinetics and assembly mechanism in vitro by mixing the two components and monitoring growth in solution by light scattering and SAXS, and on a substrate by AFM (Fig. 2f and Extended Data Figures 4, 5). Upon mixing the two components at micromolar concentrations, lattice assembly in solution occurred in minutes with concentration-dependent kinetics (Extended Data Figure 5a). SAXS indicated rapid growth of the arrays to 0.4 μm in diameter within the first 2 min after mixing the components (at 10 μM) and at 0.7 μm within 6 min (Extended Data Figure 4f,g and methods). The hexagonal lattice could be readily visualized by AFM, and the pathway of assembly assessed by in situ AFM imaging at different time points (Fig. 2e; Extended Data Figure 5b–c). The designed 2D material exhibited self-healing: cracked edges reform (Fig. 2e, upper right corner) and point defects and vacancies in the interior of the lattice evident at early time points were filled in at later time points (Fig. 2f; Extended Data Figure 5c). To determine whether the rate-limiting step in growth is initiation or completion of hexagonal units, we counted the numbers of each of the possible edge states in a set of AFM images. A units bound to two B units — designated A-II sites — comprise the most stable edge sites, while A units with just one neighboring B unit — designated A-I sites — were the least stable, occurring far less often than exposed B-I sites (Extended Data Figure 5h). The results imply that attachment of a B unit to an A-I site to create a (most) stable A-II site is rate limiting during assembly (see Extended Data Figure 5.d, f, and g for quantitative analysis).

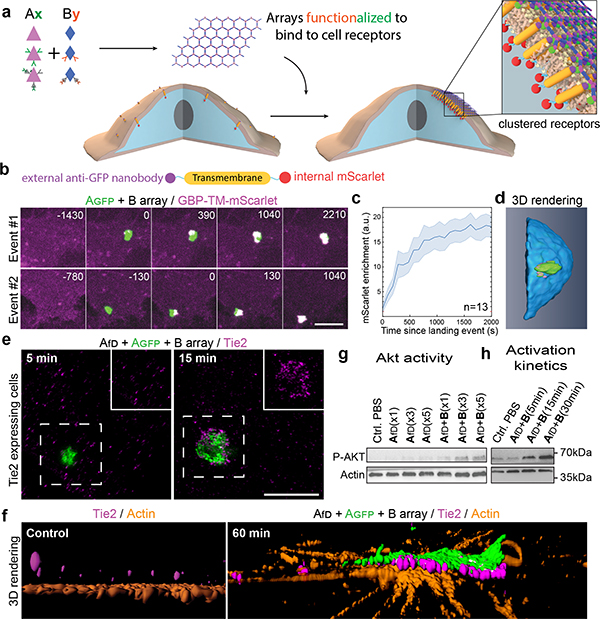
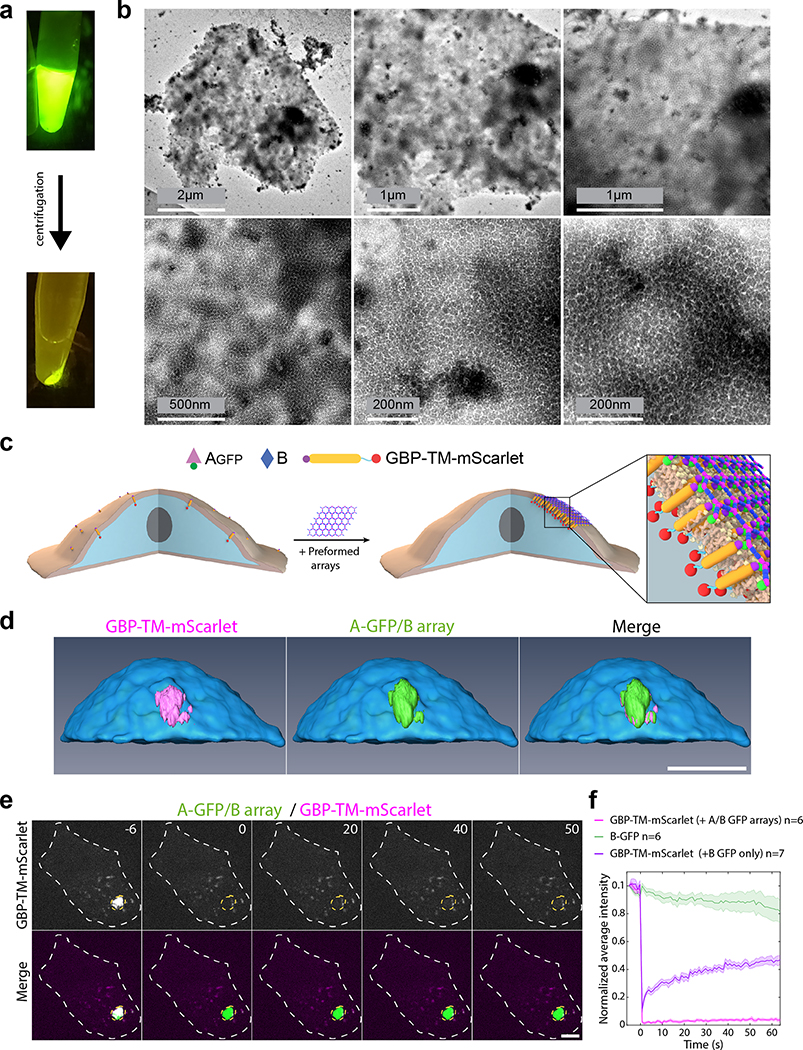
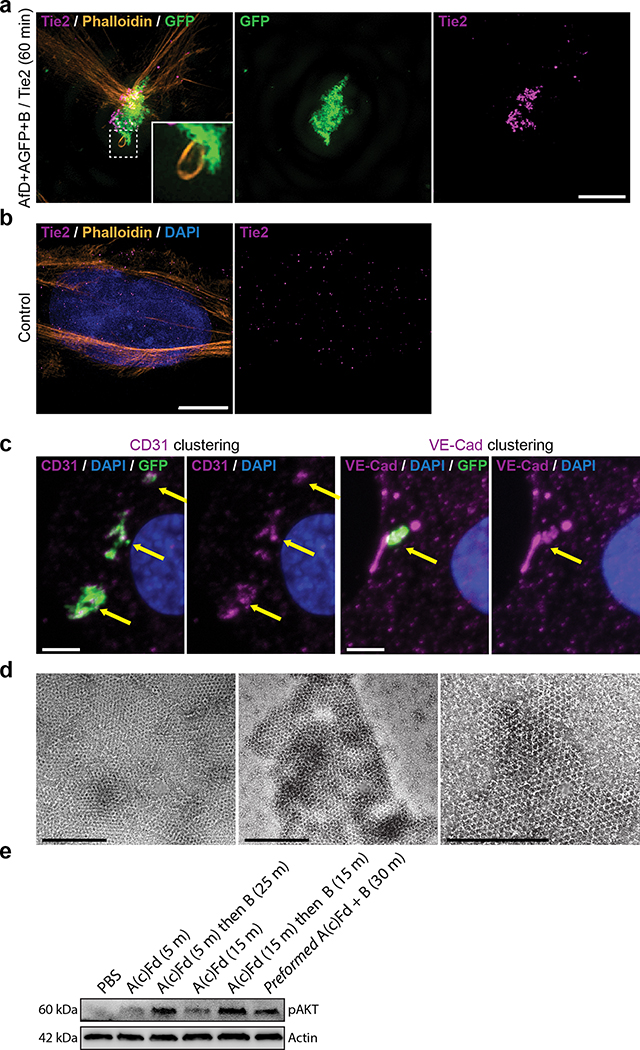
We next investigated if preformed arrays could cluster transmembrane receptors on living cells (Fig. 3). In contrast to antibodies, extensively used to crosslink cell surface proteins, arrays provide an extremely high density of attachment sites in a regular 2D geometry. To quantitatively measure clustering, we stably expressed a model receptor composed of a transmembrane segment (TM) fused to an extracellular GFP nanobody (GBP, GFP Binding Peptide)²⁸ and an intracellular mScarlet (noted GBP-TM-mScarlet) in fibroblasts (Fig. 3a). In the absence of arrays, the mScarlet signal was diffused, but when a preformed Agfp+B array landed onto the cells, mScarlet clustered under the array in ≈20 min (Fig. 3b,c, SI video S3, see also Fig. 3d, video S4 and Extended Data Figure 6 for 3D reconstructions and EM validation that purified arrays retain hexagonal order). Fluorescence Recovery After Photobleaching (FRAP) showed that clustered receptors remain stably associated with the arrays (Extended Data Figure 6e–f and video S5). To determine if the patterned and highly multivalent interactions between arrays cell surface receptors can induce a downstream biological signal, we targeted the Tie-2 receptor. Using the SpyCatcher-SpyTag (SC-ST) conjugation system,²⁹ we fused a ligand for the Tie-2 receptor, the F domain of the angiogenesis promoting factor Ang1, to A_SC, a modified A component having SpyCatcher genetically fused to its N-terminus (the resulting fusion is noted Afd). Pre-assembled arrays displaying Ang1 and GFP (Afd+Agfp+B), induced clustering of endogenous Tie-2 receptors on Human Umbilical Vein Endothelial Cells (HUVECs; Fig. 3e; see also Extended Data Figure 7 for further examples, controls, and TEM characterization). Clustering kinetics were comparable to GBP-TM-mScarlet (Fig. 3h). Because the amount of arrays was adjusted to ensure a small number (0–2) of labeled arrays per cell, the effects of large scale receptor clustering on downstream effectors could be investigated in detail. Super-resolution microscopy revealed extensive remodeling of the actin cytoskeleton underneath the Tie-2 clusters after 60 min (Fig. 3f), which could reflect adherens junction formation (Extended Data Figure 7c). The Ang1 arrays, but not the individual functionalized array component, induce AKT signaling (Fig. 3g, h), showing that the arrays can have biological activities beyond those of their components.

Figure 3. Dynamics of array-induced receptor clustering and biological activation.

(a) Array functionalization by genetic or post-translational fusions. (b) 3T3 cells expressing GBP-TM-mScarlet (GBP: anti-GFP nanobody; TM: transmembrane domain) were incubated with preformed Agfp+B arrays, and mScarlet clustering was monitored by confocal microscopy. (c) Quantification of the effects seen in (b). (d) 3D rendering of an array binding event. (e-h) Tie2 receptor clustering induced by preformed Afd+Agfp+B arrays (fD: F domain of angiopoietin). (e) Tie2 receptors were imaged 5 or 15 minutes after binding of arrays to cells. Insets: high-magnification of the dashed area, omitting the array signal. (f) 3D reconstruction in the absence of arrays (left panel) or 60 minutes post array-binding (right panel) showing the alignment between array and clustered Tie2. (g) Effect of array-induced Tie2 clustering on p-AKT activation. fD monomer concentration: x1/x3/x5: 17.8/53.4/89 nM respectively. (h) Dynamics of Tie2 activation. Scale bars: (b) 3 μm; (e) 2.5 μm.

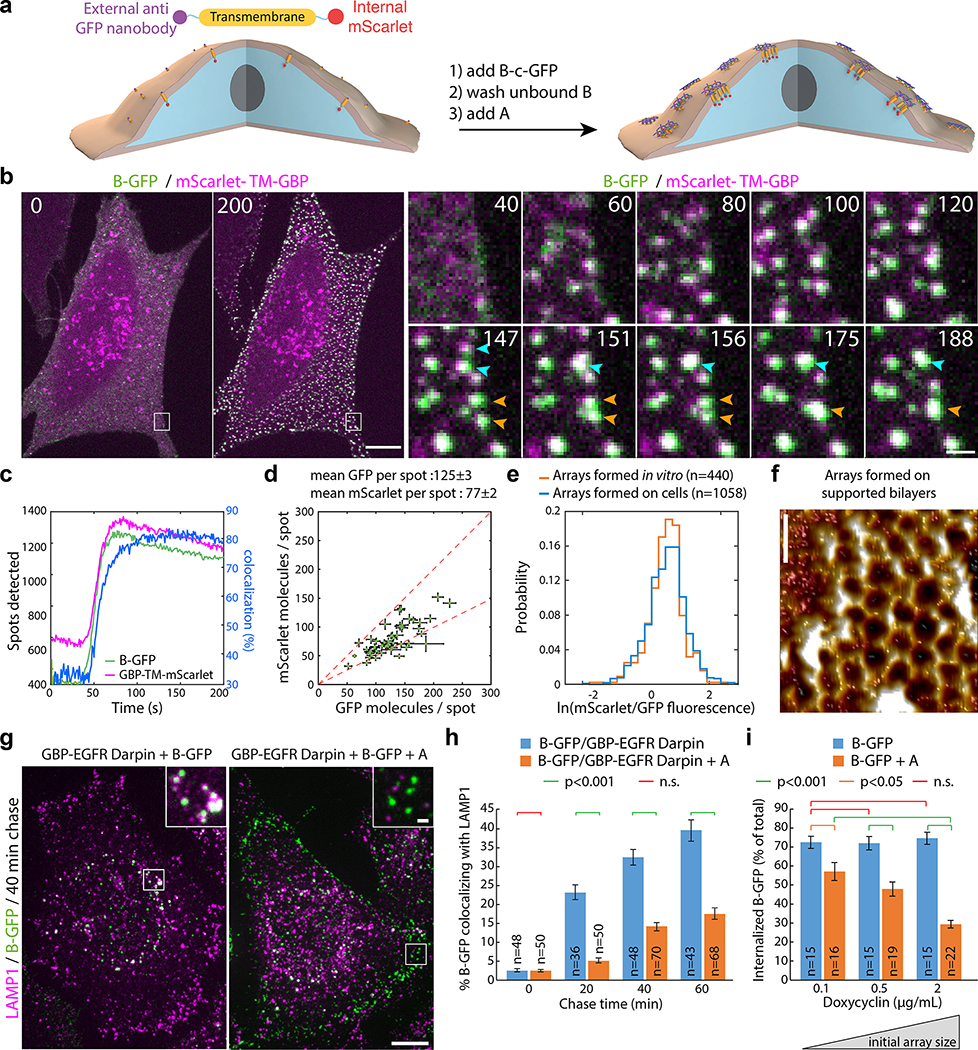
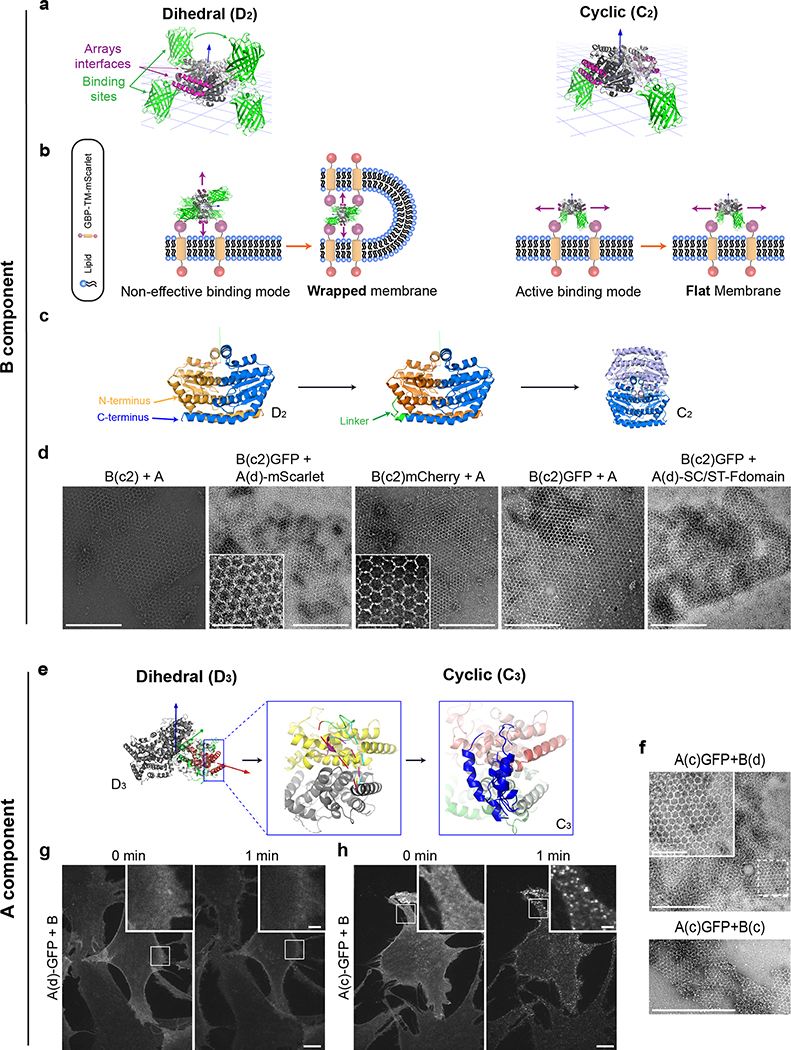
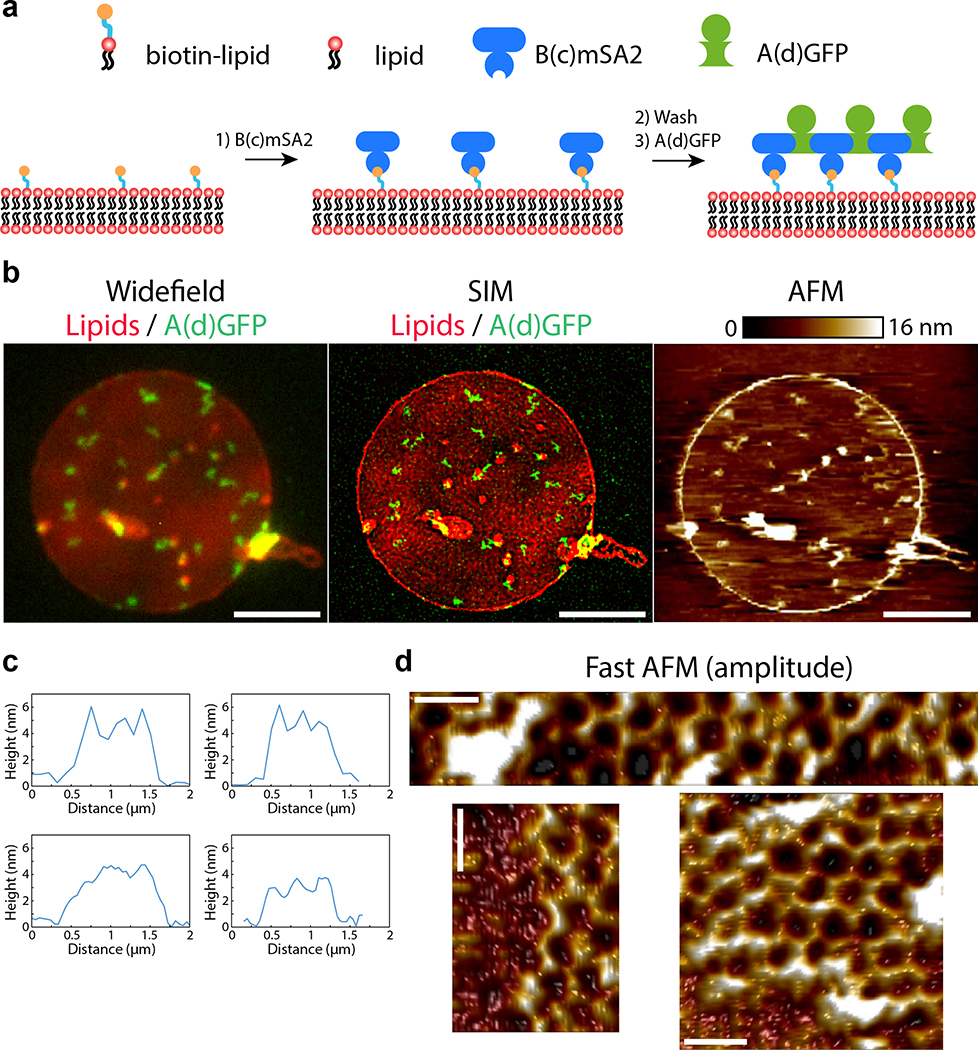
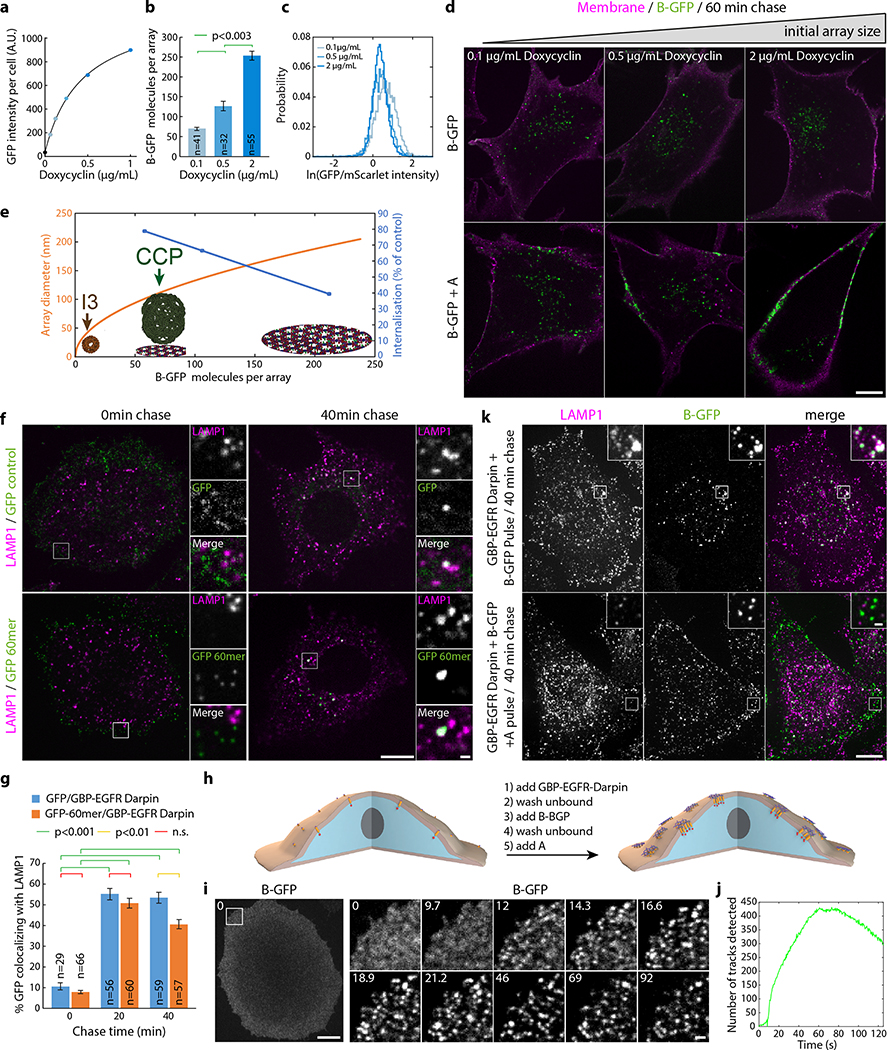
Taking advantage of the two-component nature of the material, we sought to speed up assembly kinetics and homogeneity of clustering by first saturating membrane receptors with one component, then triggering assembly with the second (Fig. 4a). Dihedral building blocks were not suited for this task, likely because cell membranes can wrap around their symmetrical two sides displaying an equal number of binding sites, thereby blocking assembly (Extended Data Figure 8 and Fig. S7 for further discussion). Hence, we devised cyclic pseudo-dihedral versions of each component (referred to as A(c), B(c); Extended Data Figure 8, Fig. S7, and Tables S8, S9). AFM characterization revealed that arrays grown on supported lipid bilayers by first tethering one cyclic component then adding the other leads to formation of 2D hexagonal arrays nearly identical to those formed in solution (Fig. 4f, Extended Data Figure 9 and methods). Likewise, this two-step procedure using cyclic components led to array formation on cells expressing GBP-TM-mScarlet (Fig. 4a–d and Extended Data Figure 8f).

Figure 4. Large arrays assembled on cells block endocytosis.

(a) GBP-TM-mScarlet-expressing 3T3 cells were incubated with B(c)gfp then A and imaged by confocal microscopy. (b) Upon addition of A, foci positive for B(c)gfp / mScarlet appear, which eventually fuse (arrows). (c) Quantification of effects seen in (b). (d) Number of GFP and mScarlet molecules per array plotted per cell (mean±SEM; n=8972 arrays in N=50 cells). Dash red: boundary ratios for 1:1 or 2:1 B(c)gfp/GBP-TM-mScarlet ratio, depending on the number of GBP-TM-mScarlet bound per B(c)gfp dimer. (e) mScarlet/GFP fluorescence intensity ratio histograms of B(c)gfp/A(d)mScarlet arrays, either preformed or assembled on cells (n=1058 arrays in N=12 cells / n=440 preformed arrays). (f) AFM imaging of arrays assembled as in (a), but on supported bilayers. Lookup table corresponds to [0–410] pm amplitude. (g) EGF receptors (EGFR) on HeLa cells were clustered using A, B(c)gfp, and GBP-EGFR-Darpin, a fusion binding both GFP and EGFR. After 40min, cells were processed for LAMP1 immunofluorescence and confocal imaging (maximum-intensity z-projections; insets: single planes). (h) Quantification of the effects seen in (g)(n: number of cells). Statistics: ANOVA1 (p<0.001) followed by Tukey test. (o) 3T3 cells expressing GBP-TM-mScarlet under Doxycyclin control were treated with increasing doses of Doxycyclin to control the initial size of arrays, then treated as in (a) and internalization was quantified after 60 min. Statistics: ANOVA1 (p<0.001) followed by Tukey test. Scale bar: 10 μm (b-left, g), 1 μm (b-right, g inset) and 50 nm (k).

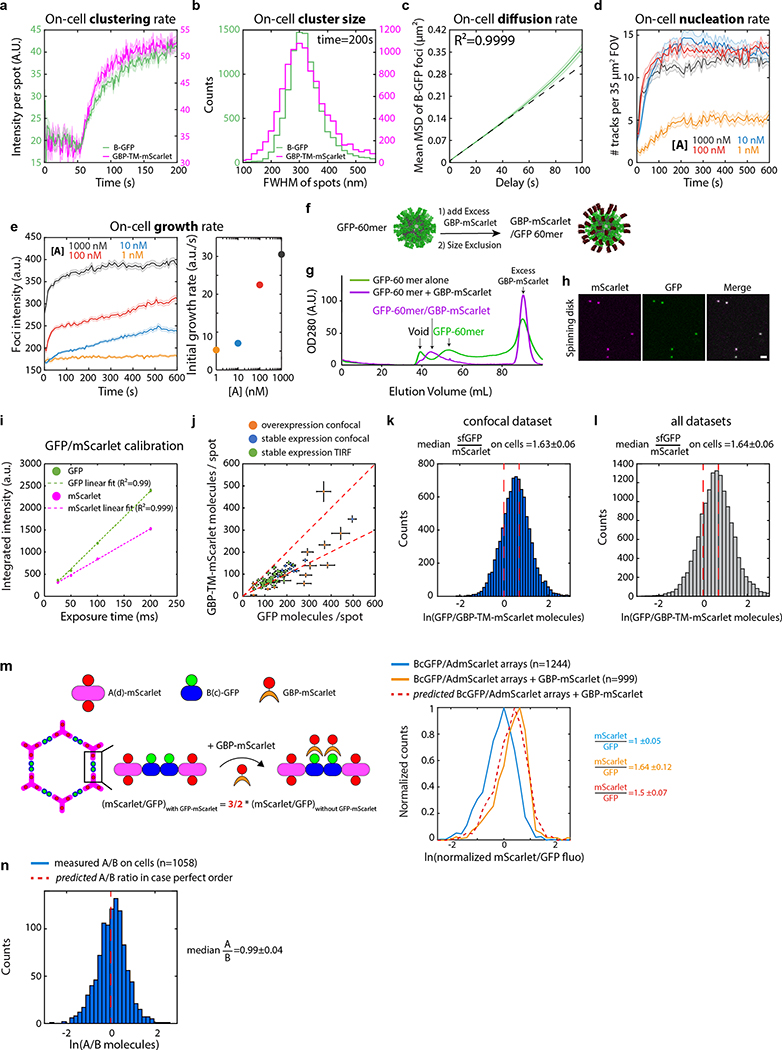
Array formation on cells was fast (≃20s) and colocalizing mScarlet patches appeared synchronously with GFP-positive patches, indicating simultaneous receptor clustering (Fig. 4b–c; SI video S6). These diffraction-limited arrays eventually stop growing, likely due to the lack of available transmembrane-anchored B(c)gfp. Instead, they slowly diffuse (D=0.0005 μm²/s, Extended Data Figure 10.c), and some eventually merge into larger arrays (Fig. 4b arrows, 4c for quantification and SI video S6). Receptor clustering by array assembly onto cells was faster than with preformed arrays (Fig. 3c versus Fig. 4c), synchronized (Fig. 4b, d) homogenous (all arrays have similar size; see Extended Data Figure 10b) and elicited downstream signaling (Extended Data Figure 7e). On cell assembly dramatically improved clustering synchronization compared to preformed arrays: all clusters in Extended Data Figure 10b appeared within ≃15s, compared to 980±252s (mean±SEM) for Fig. 3c. As expected, the concentration of A affected both the nucleation rate and the growth rate of arrays: higher concentrations of A increased nucleation and initial growth rate, but growth rate decays faster over time likely due to the saturation of all available B components (Extended Data Figure 10d–e).

Each diffraction-limited array contained on average 125±3 GFP and 77±2 mScarlet molecules (Fig. 4d; Extended Data Figure 10.f–i and Supplementary methods). The GFP/mscarlet ratio per array was remarkably similar within the same cell and between cells, suggesting that all arrays are virtually identical within the cell population and that the number of clustered receptors scales with array size (Fig. 4d and Extended Data Figure 10j–l). The median GFP/mscarlet ratio (1.63±0.06) is within the expected [1 2] range, corresponding to either 1 or 2 GBP-TM-mScarlet bound per B(c)gfp dimer (Extended Data Figure 10k). Array size can be tuned both by varying the concentration of A at a given receptor density (Extended Data Figure 10e) and/or by varying the cell surface density of GBP-TM-mScarlet via a doxycycline-inducible promoter (Extended Data Figure 11b,c; the latter does not alter receptor clustering efficiency).

We then investigated if arrays assembled on membranes and on cells retain the lattice order. Fast AFM revealed that arrays assembled on supported bilayers are similar to those formed in solution: 2D, single layered and ordered (Fig. 4f, Extended Data Figure 9c–d). The mScarlet/GFP fluorescence ratio of B(c)gfp / A(d)mScarlet arrays was remarkably similar between arrays assembled in vitro or onto cells, suggesting comparable degree of order (1.45±0.07 for in vitro versus 1.48±0.06 for cells, Fig. 4e; see also Extended Data Figure 8d for EM verification of the order of preformed B(c)gfp / A(d) mScarlet arrays and Extended Data Figure 10m and methods for further controls of the fluorescence ratio analysis). Similarly, direct measurement of the A/B ratio of arrays assembled on cells revealed a ratio of 0.99±0.04, closely consistent with the designed structure (Extended Data Figure 10n and Supplementary methods).

Following ligand-induced oligomerization, numerous receptors, such as the Epidermal Growth Factor Receptor (EGFR), are internalized by endocytosis and degraded in lysosomes as a means to downregulate signaling. Similarly, EGFR oligomerization by antibodies and nanobodies^30,31 targeting different epitopes induce rapid EGFR endocytosis and lysosomal degradation. This uptake is not specific to small oligomers, as large 3D clusters, such as those induced with our 60-mer nanocages³² functionalized with EGFR binders, are also rapidly internalized and routed to lysosomes (Extended Data Figure 11f–g). This phenomenon has been proposed to lower the efficiency of immunotherapy in in vivo models.³³ We thus wondered if the 2D geometry and large size of our material compared to clathrin coated vesicles could modulate endocytosis. Functionalizing array components with EGFR binders enabled EGFR clustering in HeLa cells with similar fast kinetics as GBP-TM-mScarlet (Extended Data Figure 11h–j). However, while endogenous EGFR bound to dimeric B(c)gfp was rapidly internalized and routed to lysosomes, clustering EGFR by addition of A quantitatively inhibited this effect (Fig. 4g–h and Extended Data Figure 11k for split channel images). Similarly, functionalizing arrays with the Notch ligand DLL4 allowed Notch clustering on U2OS cells with a similar endocytic block (Supplementary figures S8–9). The extent of this endocytosis inhibition can be tuned by modulating array size using our inducible system (Fig. 4i and Extended Data Figure 11d).

Several lines of evidence suggest that our designed material assembles in a similar way on cells as it does in vitro. First, AFM showed that assembly of the two components on supported lipid bilayers, using a protocol very similar to that used for on cell assembly, generates single layer arrays with the hexagonal lattice structure nearly identical to those formed in solution (compare fig 4f with fig 2a and Extended Data Figures 5,9). Second, the remarkable homogeneity in the growth rate and size distribution of the arrays assembled on cells resembles ordered crystal growth more than random aggregation. Third, the distribution of the ratio of fluorescence intensities of the two fluorescently labeled array components on cells is the same for preformed arrays: disorganized aggregates would be expected to have a wide range of subunit ratios. Fourth, the A/B ratio of arrays generated on cells is close to 1, consistent with the array structure and again not expected for a disorganized aggregate. While these results suggest that the overall 2D array geometry and subunit stoichiometry are preserved when the arrays assemble on a cell membrane, it will be useful to measure the array defect frequency when technology for structural determination on cells sufficiently improves. This caveat notwithstanding, these results highlight the power of quantitative light microscopy to translate structural information from defined in vitro reconstituted systems to the much more complex cellular membrane environment.

Our studies of the interactions of the designed protein material with mammalian cells provides new insights into cell biology of membrane dynamics and trafficking. We observe a strong dependence of endocytosis on array size and on the geometry of receptor binding domain presentation: arrays roughly the size of clathrin coated pits almost completely shut down endocytosis, while smaller arrays, and nanoparticles displaying large numbers of receptor binding domains are readily endocytosed (Extended Data Figure 11e). Mechanistically, this endocytic block likely relates to the increased curvature free energy and/or membrane tension and further investigations of this phenomenon may shed light on the mechanisms of cellular uptake. From the therapeutics perspective, the ability to shut down endocytosis without inducing signaling, as in our EGFR binding arrays, could help extending the efficacy of signaling pathway antagonists, which can be limited by turnover due to endocytosis. Furthermore, the ability to assemble designed protein around cells opens up new approaches for reducing immune responses to introduced cells, for example for type I diabetes therapy.

The long range almost-crystalline order, tight control over the timing of assembly, and the ability to generate complexity by functionalizing array components differentiate this designed two-dimensional material from naturally occurring and previously designed protein 2D lattices and opens many avenues for exploration. The stepwise assembly approach offers a fine level of control to cluster receptors compared to pre-assembled materials or aggregates: the receptor density in the clusters is fixed and the fluorescence intensity of the array component can be directly converted into the absolute number of receptors being clustered. Together with the localization of activation to regions underneath the arrays this should facilitate investigation of the molecular events downstream of receptor clustering. Imposition of a predetermined order onto transmembrane proteins could open up new approaches to structure determination. Furthermore, these binary biopolymers and methods to generate new ones, provide novel tools and paradigms for the emerging field of engineered living materials,³⁴ where combinations of programmable cells produce building blocks of de-novo binary scaffolds to continuously regenerate or remodel their extracellular structure and function in response to environmental cues. We expect the methodology developed here, combined with the rapid developments in de novo design of protein building-blocks and quantitative microscopy techniques, will open the door to a future of programmable biomaterials for synthetic and living systems.

Methods:

Computational design.

Crystal structures of 628 D2, 261 D3, 63 D4, and 13 D6 dihedral homooligomers with resolution better than 2.5Å were selected from the Protein Data Bank (PDB)²³ to be used as building blocks (BBs). Combinatorial pairs of BBs were selected such that they afford the two rotation centers required in a selected subset of plane symmetries (P3m1 [C3-C3], p4m [C4-C4, C4-C2], p6m [C6-C2, C6-C3, C3-C2]). The highest-order rotation symmetry axis of each BB was aligned perpendicular to the plane and an additional 2-fold symmetry axis was aligned with the plane symmetry reflection axis. Preserving these constraints allows positioning the D2, D3, D4, and D6 BBs in 6, 2, 2, and 2 unique conformations, respectively, and results in a total of ~2.6M unique docking trajectories. In a first iteration Symmetric Rosetta Design²⁴ was applied to construct the BBs dihedral homooligomers, position them in the correct configuration in space and slide them into contact, along the plane symmetry group reflection axes. Docking trajectories are discarded if clashing between BBs are detected, if a fraction greater than 20% of contact positions (residues belonging to one BB within 10Å of their partner BB residues) do not belong to a rigid secondary structure (helix/beta sheet), or if the surface area buried by the formation of the contact is lower than 400Ų. These initial filtering parameters narrow the number of potential design trajectories to approximately 1% of the original trajectories number. In a second iteration, the selected docks (BBs pairs contact orientation) are regenerated by Symmetric Rosetta Design, slide into contact and retract in steps of 0.05Å to a maximum distance of 1.5Å. For each position, layer sequence design calculations, implemented by a Rosetta script,²⁵ are made to generate low-energy interfaces with buried hydrophobic contacts that are surrounded by hydrophilic contacts. Designed substitutions not substantially contributing to the interface were reverted to their original identities. Resulting designs were filtered based on shape complementarity (SC), interface surface area (SASA), buried unsatisfied hydrogen bonds (UHB), binding energy (ddG), and number of hydrophobic residues at the interface core. A negative design approach that includes an asymmetric docking is used to identify potential alternative interacting surfaces. Designs that exhibit a non-ideal energy funnel are discarded as well. Forty-five best scoring designs belonging to p3m1: 2, p4m: 10, and p6m: 33, were selected for experiments. Protein monomeric stabilization was done to the D2 and D3 homooligomers of design #13 using the PROSS server (see Fig. S4, S5 and Table S5).²⁶ Pyrosetta³⁵ and RosettaRemodel³⁶ were used to model and generate linkers to render the D2 and D3 working homooligomers into C2 and C3 (cyclic pseudo-dihedral) homooligomers (see Extended Data Figure 8, Fig. S7 and Tables S8, S9 for details and further discussion). Linkers for non-structural fusions, i.e., optical labels and binding sites such as spyTag/spyCatcher, were not modeled computationally. All Rosetta scripts used are available upon request.

Expression construct generation.

Genes encoding for the 45 pairs were initially codon optimized using DNAWorks v3.2.4³⁷ followed by RNA ddG minimization of the 50 first nucleotides of each gene using mRNAOptimiser³⁸ and Nupack3.2.2 programs (Fig. S1).³⁹ For screening in an in-vivo expression setup, bicistronic constructs were cloned (GenScript®) in pET28b+ (kanamycin resistant), between NcoI and XhoI endonuclease restriction sites and separated by an intergenic region ‘TAAAGAAGGAGATATCATATG’. For the working design, separately expressing constructs were prepared by polymerase chain reaction (PCR) from sets of synthetic oligonucleotides (Integrated DNA Technologies) to generate linear DNA fragments with overhangs compatible with a Gibson assembly⁴⁰ to obtain circular plasmids. Additional labels (His tag, sfGFP, mCherry, mScarlet, spyTag, spyCatcher, mSA2,⁴¹ and AVI tag) were either genetically fused by a combination of PCR and Gibson processes or through post expression conjugation using the spyTag spyCatcher system²⁹ or biotinylation.⁴² Note that the variant of GFP used throughout the paper, on both A/B components and the 60-mer nanocages is sfGFP (referred to as GFP in the text for simplicity).

The transmembrane nanobody construct (Fig. 3–4) consists of an N-terminal signal peptide from the Drosophila Echinoid protein, followed by (His)₆-PC tandem affinity tags, a nanobody against GFP²⁸ (termed GBP for GFP Binding Peptide), a TEV cleavage site, the transmembrane domain from the Drosophila Echinoid protein, the VSV-G export sequence^43,44 and the mScarlet protein⁴⁵. The protein expressed by this construct thus consists of an extracellular antiGFP nanobody linked to an intracellular mScarlet by a transmembrane domain (named GBP-TM-mScarlet in the main text for simplicity). This custom construct was synthesized by IDT and cloned into a modified pCDNA5/FRT/V5-His vector, as previously described⁴⁶ for homologous recombination into the FRT site. A version without the mScarlet (GBP-TM) was similarly derived. We also modified the backbone to allow Doxycycline-inducible expression by first replacing the EF1a promoter by Tet promoter, then by making the backbone compatible with the MXS chaining system⁴⁷ and ligating in the CMV::rtTA3 bGHpA cassette.

For the GBP-mScarlet and GBP-EGFR-Darpin fusions, we modified a pGEX vector to express a protein of interest fused to GBP downstream of the Gluthatione S transferase (GST) purification tag followed by TEV and 3C cleavage sequences. We then cloned mScarlet and a published Darpin against EGFR⁴⁸ (clone E01) into this vector, which thus express GST-3C-TEV-GBP-mScarlet and GST-3C-TEV-GBP-EGFR-Darpin fusions, respectively.

Protein expression and purification.

Unless stated otherwise, all steps were performed at 4°C. Protein concentration was determined either by absorbance at 280nm (NanoDrop 8000 Spectrophotometer, Fisher Scientific), or by densitometry on coomassie-stained SDS page gel against a BSA ladder.

For initial screening of the 45 designs for A and B, bicistronic plasmids were transformed into BL21 Star (DE3) E. coli. cells (Invitrogen) and cultures grown in LB media. Protein expression was induced with 1 mM isopropyl β-d-1-thiogalactopyranoside (IPTG) for 3 hours at 37°C or 15 hours at 22°C, followed by cell lysis in Tris-buffer (TBS; 25 mM Tris, 300 mM NaCl, 1 mM dithiothreitol (DTT), 1 mM phenylmethylsulfonyl fluoride (PMSF), and lysozyme (0.1mg/ml) using sonication (Fisher Scientific) at 20W for 5min total ‘on’ time, using cycles of 10s on, 10s off. Soluble and insoluble fractions were separated by centrifugation at 20,000 × g for 30 minutes and protein expression was screened by running both fractions on SDS-PAGE (Bio-Rad) (see Fig. S3) and for selected samples also by negative stain EM. All subsequent experiments done on separately expressed components were performed on (His)6-tagged proteins. Following similar expression protocols (22°C/15 hours) cultures were resuspended in 20mM supplemented Tris-buffer and lysed by microfluidizer at 18k PSI (M-110P Microfluidics, Inc.). The soluble fraction was passed through 3ml of nickel nitrilotriacetic acid agarose (Ni-NTA) (Qiagen), washed with 20 mM imidazole, and eluted with 500 mM imidazole. Pure proteins with the correct homooligomeric conformation were collected from a Superose 6 10/300 GL SEC column (GE Healthcare) in Tris-buffer (TBS; 25 mM Tris, 150 mM NaCl, 5% glycerol). Separately expressed components were kept at a concentration of ~200 μM at 4°C.

SpyTag-spyCatcher conjugation was done by mixing a tagged protein and the complementary tagged array component at a 1.3:1 molar ratio, overnight incubation (~10 hours) at 4°C followed by Superose 6 10/300 GL SEC column purification to obtain only fully conjugated homooligomers. Sub-loaded conjugation was done at tag:array protein 0.17:1 molar ratio and used as is. Biotinylation of AVI-tagged components was performed with BirA as described in [⁴²] and followed by Superose 6 10/300 GL SEC column purification. In-vitro array assembly was induced by mixing both array components at equimolar concentration.

GFP-tagged 60-mer nanocages were expressed and purified as previously.³² GBP-mScarlet was expressed in E. coli BL21 Rosetta 2 (Stratagene) by induction with 1 mM IPTG in 2X YT medium at 20°C overnight. Bacteria were lysed with a microfluidizer at 20kPsi in lysis buffer (20 mM Hepes, 150 mM KCl, 1% TritonX100, 5% Glycerol, 5 mM MgCl₂, pH 7.6) enriched with protease inhibitors (Roche Mini) and 1 mg/ml lysozyme (Sigma) and 10 μg/ml DNAse I (Roche). After clarification (20,000 rpm, Beckman JA 25.5, 30min 4°C), lysate was incubated with Glutathione S-sepharose 4B resin (GE Healthcare) for 2 h at 4°C and washed extensively with (20mM Hepes, 150mM KCl, 5% glycerol, pH7.6), and eluted in (20mM Hepes, 150mM KCl, 5% glycerol, 10mM reduced glutathione, pH7.6). Eluted protein was then cleaved by adding 1:50 (vol:vol) of 2 mg/mL (His)₆ -TEV protease and 1 mM/0.5 mM final DTT/EDTA overnight at 4°C. The buffer of the cleaved protein was then exchanged for (20mM Hepes, 150mM KCl, 5% Glycerol, pH 7.6) using a ZebaSpin column (Pierce), and free GST was removed by incubation with Glutathione S-sepharose 4B resin. Tag-free GBP-mScarlet was then ultracentrifuged at 100,000 × g for 5 min at 4C to remove aggregates. GBP-mScarlet was then incubated with GFP-60mer nanocages,³² followed by size exclusion chromatography (see Microscope calibration), which further removed the TEV protease from the final mScarlet-GBP/GFP-60mer.

GBP-EGFR-Darpin was expressed similarly as GBP-mScarlet, except that lysis was performed using sonication, lysate clarification was performed at 16,000 rpm in a Beckman JA 25.5 rotor for 30min at 4°C). After TEV cleavage buffer was exchanged for (20mM Hepes, 150mM KCl, 5% Glycerol, pH 7.6) by dialysis, free GST and TEV proteases were removed by sequential incubation with Glutathione S-sepharose 4B resin and Ni-NTA resin. Tag-free GBP-EGFR-Darpin was then flash frozen in liquid N₂ and kept at −80°C.

Delta-like ligand 4 (DLL4) was prepared from a fragment of the human Delta ectodomain (1–405) with a C-terminal GS-SpyTag-6xHis sequence (Table S7). The protein was purified by immobilized metal affinity chromatography from culture medium from transiently transfected Expi293F cells (Thermo Fisher), then further purified to homogeneity by size exclusion chromatography on a Superdex 200 column in 50 mM Tris, pH 8.0, 150 mM NaCl, and 5% glycerol, and flash frozen before storage at −80°C. DLL4 was conjugated to the SpyCatcher tagged A homooligomers (Asc) at 1.5:1 molar ratio of DLL4 to Asc. The Asc-st-DLL4 conjugate was purified by size exclusion chromatography on a Superose 6 column. The Asc-st-DLL4-jf646 conjugate was produced by coupling of 1.5 μM Asc-st-DLL4 to excess Janelia Fluor 646 SE (Tocris) overnight at 4°C in 25 mM HEPES, pH 7.5, 150 mM NaCl. The labeled Asc-st-DLL4 was then purified by desalting on a P-30 column (Bio-Rad). The final molar ratio of JF646 to Asc-st-DLL4 was 5:1.

Negative-stain electron microscopy.

For initial screening of coexpressed designs insoluble fractions were centrifuged at 12,000g for 15 min and resuspended in Tris-buffer (TBS; 25mM Tris, 300mM NaCl) twice prior to grid preparation. Samples were applied to glow-discharged EM grids with continuous carbon, after which grids were washed with distilled, deionized water, and stained with 2% uranyl formate. EM grids were screened using an FEI Morgagni 100 kV transmission electron microscope possessed of a Gatan Orius CCD camera. For the working design EM grids were initially screened using the Morgagni. Micrographs of well-stained EM grids were then obtained with an FEI Tecnai G2 Spirit transmission electron microscope (equipped with a LaB6 filament and Gatan UltraScan 4k × 4k CCD camera) operating at 120 kV and magnified pixel size of 1.6 Å. Data collection was performed via the Leginon software package.⁴⁹ Single-particle style image processing (including CTF estimation, particle picking, particle extraction, and two-dimensional alignment and averaging) was accomplishing using the Relion software package.⁵⁰

UV-vis Kinetics characterization of in vitro assembly.

Arrays formation kinetics was determined by turbidity due to light scattering, monitored by absorption at 330 nm wavelength, using an Agilent Technologies (Santa Clara, CA) Cary 8454 UV-Vis spectrophotometer. Absorption spectrum at wavelengths range of 190 nm to 1100 nm was acquired every 5 seconds for 25 minutes immediately following an initial blanking. Absorption curves at 330nm were constructed of measurements of blank samples (buffer: 25 mM Tris-HCl, 150 mM NaCL, 5% glycerol, and 500 mM imidazole) as control, B components at 5 μM, and A+B mixtures (5, 10 or 15 μM). Curves were acquired for three experimental replicates for each experimental condition (two for blank control). Curves were processed as follows: the respective initial value (first time point) was first subtracted from each curve to account for initial background; then, a non-linear offset was applied by subtracting the averaged curve of the blank measurements from each and all the other curves. Extended Data Figure 5a shows the average absorption of each group of samples and standard deviation (n=3 experimental replicates). All data was processed using python Dataframe and Numpy packages.

Protein stabilization characterization.

Far-ultraviolet Circular Dichroism (CD) measurements were carried out with an AVIV spectrometer, model 420. Wavelength scans were measured from 260 to 195 nm at temperatures between 25 and 95 °C. Temperature melts monitored absorption signal at 220 nm in steps of 2 °C/min and 30 s of equilibration time. For wavelength scans and temperature melts a protein solution in PBS buffer (pH 7.4) of concentration 0.2–0.4 mg/ml was used in a 1 mm path-length cuvette.

SAXS Experiments.

Small angle X-ray scattering data were collected at the SIBYLS beamline at the Advanced Light Source in Berkeley California.⁵¹ Components A and B were measured independently and as a mixture in 25 Tris, 150 NaCl and 5% glycerol. Imidazole was added to the mixture in a stepwise fashion after A and B were mixed 1:1. These solutions were prepared 24 hours prior to collection. Before collection samples were placed in a 96 well plate. Each sample was presented to the X-ray beam using an automated robotics platform. The 10.2keV monochromatic X-rays at a flux of 10¹² photons per second struck the sample with a 1 × 0.3mm rectangular profile that converged at the detector to a 100μm × 100μm spot. The detector to sample distance was 2 m and nearly centered on the detector. Each sample was exposed for a total of 10 seconds. The Pilatus 2M detector framed the 10 second exposure in 300ms frames for a total of 33 frames. No radiation damage was observed during exposures.

Components A and B were independently collected at 4 concentrations (40, 80, 120, 160 μM). No concentration dependence was observed so the 160 μM, highest signal, SAXS measurement was fully analyzed using the Scatter program developed by Rambo et al at SIBYLS and the Diamond Light Source. SAXS profiles were calculated using the FOXS⁵² and compared to the measured data with excellent agreement χ² < 1 for hexameric A and tetrameric B (Extended Data Figure 4a). No further processing was conducted as the agreement between calculated SAXS from the model and the experiment was sufficient to verify close agreement of the atomic model.

The mixture of components A and B were measured at 4 concentrations as well (0.5, 2, 5, and 10 μM). The scattering profiles all had peaks (Fig. S2e and Extended Data Figure 4a, d, f) at q spacings as indicated in Table S7. The scattering can be described in several ways according to scattering theory. In crystalline systems the diffraction intensity is the convolution of the lattice and the asymmetric unit within the lattice.⁵³ Below we will distinguish the peaks as a diffraction component and the asymmetric unit as the scattering component. A very good match of Bragg spacings with the diffraction observed comes from calculating a P6 lattice with a 303Å spacing as shown in Table S7 (compared to 315Å spacing measured by AFM and 310Å predicted by the design model). The calculation was done using a CCP4 script based on the “unique” command which generates a unique set of reflection given a symmetry and distances.⁵⁴

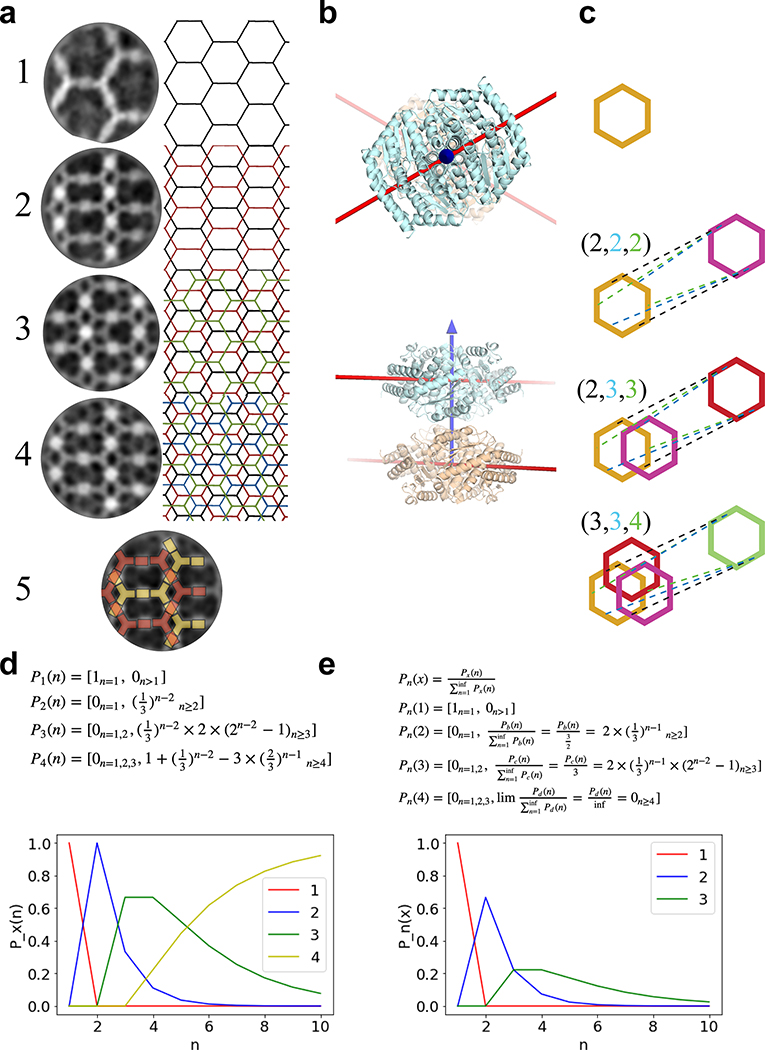
The measured SAXS profile was also matched by calculations of the SAXS from atomic models (Fig. 2e and Extended Data Figure 4c). Atomic model sheets were created by increasing the number of Asymmetric Units (ASUs) defined as 12 monomers: 6 belonging to the A Hexamer and 6 to 3 halves of the surrounding B tetramers (see Extended Data Figure 4a rightmost panel). Array counting 10, 13, 17, 21, 26, 31, 37, 75, 113, and 188 ASUs along the P6 lattice were used for SAXS profiles modeling using FOXS. The calculated SAXS profiles have diffraction peaks placed in agreement with the measured data. As per scattering theory⁵⁵ the diffracting from the lattice increased relative to the scattering from the asymmetric unit as the sheet size increased. The diffraction to scattering ratio in the measured profiles are larger than those in all calculated profiles indicating that the sheets are larger in solution than the largest models we created.

We utilized the trend in the ratio of the diffraction to scattering from the models to estimate the size of the sheets observed in solution. All calculations and the experimental SAXS profiles were scaled by the underlying scattering. The higher the angle, the smaller the contribution of the diffraction, so the highest angle experimental signal with sufficient signal to noise was used (0.1 < q < 0.15Å) for this scaling all profiles relative to one another. Once scaled, the ASU was divided through all scattering curves where the ASU is as defined above. By dividing through, the exponential decay of the scattering profile was removed and yielded a set of peaks that oscillate about a constant background which was further normalized so as to oscillate about a value of one (Fig. 2e and Extended Data Figure 4d) over a useful q range between 0.01 < q < 0.1 Å^-1. The intensity difference between the first minimum and first maximum peak from all calculated profiles was tabulated and the trend was fit to the number of ASUs (x) using two simple formulas: 1) exponential form: k1*exp^k2*x+k3 [k1=2.2, k2=3.5,k3=−1.6], 2) polynomial form: k1*x^k2+k3 [k1=64.5, k2=4.3,k3=8.9]. A reasonable fit was obtained for the exponential form as shown in Extended Data Figure 4e. Extrapolating from this fit, the average array consists of 6000 ASUs (2000 using the polynomial fit) and assuming a circular array shape it average size would be 1.8μm in diameter (1.05 using the polynomial fit).

Time resolved SAXS measurements were obtained for mixtures at 10μM at several time points ranging from 30 sec to 15 min. Each measurement was collected from a separate well to avoid accumulated damage to the samples. SAXS profiles were scaled (including the overnight SAXS profile to which a fit was obtained) and the ASU was divided. The min to max peaks distance was calculated and scaled for all profiles to agree with the values obtained for the common sample (the overnight sample the fit was obtained for in Extended Data Figure 4e). The exponential fit above was then applied to estimate the transient dimensions at each time point obtained by the SEXS measurement (Extended Data Figure 4f, g).

Cell Culture:

Flp-In NIH/3T3 cells (Invitrogen, R76107) were cultured in DMEM (Gibco, 31966021) supplemented with 10% Donor Bovine Serum (Gibco, 16030074) and Pen/Strep 100units/ml at 37°C with 5% CO₂. Cells were transfected with Lipofectamine 2000 (Invitrogen, 11668). Stable transfectants obtained according to the manufacturer’s instructions by homologous recombination at the FRT were selected using 100 μg/mL Hygromycin B Gold (Invivogen, 31282–04-9). HeLa cells were cultured in DMEM supplemented with 10% Fetal Bovine Serum and Penicillin-streptomycin 100units/ml at 37°C with 5% CO₂.

Human Umbilical Vein Endothelial Cells (HUVECs) (Lonza, Germany) were grown on 0.1% gelatin-coated 35mm cell culture dish in EGM2 media (20% Fetal Bovine Serum, 1% penicillin-streptomycin, 1% Glutamax (Gibco, catalog #35050061), 1% ECGS (endothelial cell growth factors), 1mM sodium pyruvate, 7.5mM HEPES, 0.08mg/mL heparin, 0.01% amphotericin B, a mixture of 1x RPMI 1640 with and without glucose to reach 5.6 mM glucose in final volume). HUVECs were expanded till passage 4 and cryopreserved.

ECGS was extracted from 25 mature whole bovine pituitary glands from Pel-Freeze biologicals (catalog # 57133–2). Pituitary glands were homogenized with 187.5 mL ice cold 150 mM NaCl and the pH adjusted to pH4.5 with HCl. The solution was stirred in a cold room for 2 hours and centrifuged at 4000 RPM at 4C for 1 hour. The supernatant was collected and adjusted to pH7.6. 0.5g/100 mL streptomycin sulfate (Sigma #S9137) was added, stirred in the cold room overnight and centrifuged 4000 RPM at 4C for 1 hour. The supernatant was filtered using a 0.45 to 0.2-micrometer filter.

The HUVEC cells were expanded till P8, followed by 16hrs starvation with DMEM low glucose media prior to protein scaffold treatment. The cells were then treated with desired concentrations of protein scaffolds in DMEM low glucose media for 30 min or 60 min. Cells were cultured at 37C, 5% CO₂, 20% O₂.

U2OS cells (ATCC, HTB-96) were cultured in DMEM (Corning) supplemented with 10% fetal bovine serum (Gemini) and 1% Pen/Strep (Gibco) at 37°C with 5% CO₂. U2OS cells expressing Notch1-Gal4 or FLAG-Notch1-EGFP chimeric receptors⁵⁶ were maintained as for parental cell lines, and additionally were selected on 50 μg/mL hygromycin B (Thermo) and 15 μg/mL blasticidin (Invitrogen). Expi293F (Thermo Fisher) cells were cultured in Expi293 medium (Thermo Fisher) on an orbital shaker at 125 rpm at 37°C with 5% CO₂.

Fluorescent Microscopy of in vivo assemblies in bacteria.

Glycerol stocks of E. coli strain BL21(DE3) having the single cistronic Agfp and the bicistronic Agfp+B were used to grow overnight cultures in LB medium + KAN at 37°C. To avoid GFP signal saturation, leaky expression only was used by allowing culture to remain at 37°C another 24 hours before spotted onto a 1% agarose-LB-KAN pad. Agarose pads were imaged using the Leica SP8X confocal system to obtain bright and dark field images.

Characterization of array-induced protein relocalization and array growth dynamics on cells

All live imaging of NIH-3T3 cells (Figs 3a–d, 4a–e,g–h, and Extended Data Figures 6, 8, 10, and 11) was performed in Leibovitz’s L-15 medium (Gibco, 11415064) supplemented with 10% Donor Bovine Serum and HEPES (Gibco, 1563080, 20mM) using the custom spinning disk setup described below. For protein relocalization by preformed arrays experiments, GBP-TM-mScarlet expressing NIH/3T3 cells were spread on glass-bottom dishes (World Precision Instruments, FD3510) coated with fibronectin (Sigma, F1141, 50μg/ml in PBS), for 1 hour at 37°C then incubated with 10μl/mL of preformed arrays. Cells were either imaged immediately (Fig. 3b–c) or incubated with the arrays for 30 minutes (Fig. 3). Preformed arrays were obtained by mixing equimolar amounts (1μM) of Agfp mixed with B in the presence of 0.5M Imidazole overnight at RT in a 180 μl total volume. This solution was then centrifuged at 250,000 × g for 30 minutes at 4°C and resuspended in 50 μl PBS. For assembly on the surface of cells (Fig. 4), spread cells were incubated with B(c)gfp (1μM in PBS) for 1 minute, rinsed in PBS, and imaged in serum/HEPES-supplemented L-15 medium. A was then added (0.2μM in serum/HEPES-supplemented L-15 medium) during image acquisition.

For the formation of arrays, the A and B components are mixed in equimolar concentration. For example, to generate Asc-st-DLL4 + Agfp + B arrays, components are mixed in molar ratios of (4:1:5). For DLL4/Notch1 array experiments, U2OS cells stably expressing Notch1-Gal4 or Notch1-EGFP chimeric receptors⁵⁶ grown in culture medium +2 μg/mL doxycycline were transferred to coverslip bottom dishes for 18–24 hr (MatTek), and then incubated at 4°C or 37°C for 15–30 min (unless otherwise indicated). For Figure S8, Notch1-EGFP cells were treated with specified pre-formed Asc-stDLL4-jf646+BmCherry array material diluted to 0.5 μM in culture medium (or mock treated) for 15 min at specified temperature and washed in 3× with ice cold PBS. Treated (or mock treated) cells were then incubated at 4°C or 37°C for >60 min in Fluorobrite (Gibco) culture medium. For Figure S8, Notch1-Gal4 cells were treated in two steps, first with 0.5 μM Adll4 in ice cold culture medium, washed 3× in ice cold PBS before second treatment with Agfp+B mixed at 0.5 μM each immediately before a 60 min incubation, 3× ice cold PBS wash, and imaged in DMEM. After array treatment, cells were imaged at either 37°C (Fig. S8c; Fig. S9b,d) or at 15°C (Fig. S9a,c).

In situ AFM characterization.

Array growth and dynamics at molecular resolution were characterized by mixing both components at equimolar concentration (7μM) and immediately injecting the solution into the fluid cell on freshly cleaved mica. All in-situ AFM images were collected using silicon probes (HYDRA6V-100NG, k=0.292 N m-1, AppNano) in ScanAsyst Mode with a Nanoscope 8 (Bruker). To minimize damage to the structural integrity of the arrays during AFM imaging, the applied force was minimized by limiting the Peak Force Setpoint to 120 pN or less.³⁴ The loading force can be roughly calculated from the cantilever spring constant, deflection sensitivity and Peak Force Setpoint.

Correlative SIM/AFM characterization on supported bilayers

Arrays were assembled on supported bilayers (Fig. 4f and also Extended Data Figure 9) in a manner mimicking assembly on cells (see above and also Fig. 4a). Supported bilayers were formed according to the method of Chiaruttini and colleagues.⁵⁷ Briefly, a lipid mixture (1mg/ml lipids in chloroform, 47.5% POPC, 47.5% DOPE, 5% DSPE-PEG(2000)-Biotin, 0.2% Rhodamine-PE, all from Avanti Polar Lipids) was used to form GUVs in [5 mM Hepes 300 mM Sucrose pH 7.5] in a Nanion Vesicle Prep Pro. GUVs were then diluted 1:1 (vol:vol) in 20 mM Hepes 150 mM KCl pH 7.5. A clean-room grade coverslip (Nexterion, Schott, #1.5, 25 ×75 mm) was surface-activated under pure oxygen in a plasma cleaner (PlasmaPrep2, GaLa instruments) then assembled into a peelable flow chamber using a top 22×22 mm standard glass coverslip and a custom Silicon insert (SuperClear Silicone Sheet 40° shore A, 0.5 mm thickness, Silex Silicon, 25×75 mm insert with a 12×35mm hole precisely cut with a Graphtec CE6000 cutting plotter). GUVs were burst onto the activated glass surface, and, after extensive washing with [20 mM Hepes, 150 mM KCl, pH 7.6], the glass surface was quenched with PLL-PEG (SuSoS, 1 mg/ml in 10 mM Hepes, pH 7.6) for 5 minutes, before further washing with [20 mM Hepes, 150 mM KCl, pH 7.6]. A solution of B(c)mSA2 (200 nM in 20 mM Hepes, 150 mM KCl, pH 7.6) was then flowed in and incubated for 1 min before extensive washes in (20 mM Hepes, 150 mM KCl, pH 7.6). Then, a solution of A(d)gfp (20 nM in 20 mM Hepes, 150 mM KCl, 500 mM Imidazole, pH 7.6) was flowed in and incubated for 5 min. Flow cell was then washed extensively with [20 mM Hepes, 150 mM KCl, pH 7.6], and sample fixed with 0.25 % glutaraldehyde (weight:vol, EMS) in PBS for 5 min and 4 % Paraformaldehyde (weight:vol, EMS) in PBS for 5 min. Fixatives were then removed by extensive washing in [20 mM Hepes, 150 mM KCl, pH 7.6]. The top 22×22 mm coverslip was then carefully removed, leaving the insert in place in order to hold a volume of imaging buffer (20 mM Hepes, 150 mM KCl, pH 7.6). This allowed simultaneous super-resolution Structured Illumination Microscopy (SIM) imaging through the bottom coverlip, and AFM imaging from the top of the open chamber (Extended Data Figure 9).

Correlative AFM/SIM imaging was performed by combining a Bioscope Resolve system (Bruker, Santa Barbara, CA, USA) with a home-made SIM system.⁵⁸ The fields of view of the two microscopes were aligned so that the AFM probe was positioned in the middle of the field of view of the SIM microscope. A brightfield image of the “shadow” of the AFM cantilever was used to precisely align the AFM probe with the SIM lens. To acquire structured illumination microscopy images, a ×60/1.2 NA water immersion lens (UPLSAPO 60XW, Olympus) focused the structured illumination pattern onto the sample, and the same lens was also used to capture the fluorescence emission light before imaging onto an sCMOS camera (C11440, Hamamatsu). The wavelengths used for excitation were 488 nm (iBEAM-SMART-488, Toptica) for the protein arrays and 561 nm (OBIS 561, Coherent) for the lipid bilayers. Images were acquired using custom SIM software described previously.⁵⁸

AFM images were acquired in Fast Tapping imaging mode using Fastscan-D probes (Bruker), with a nominal spring constant of 0.25 N/m and a resonant frequency of 110 kHz. Images were recorded at scan speeds ranging between 2 and 10 Hz and tip-sample interaction forces between 100 and 200 pN. Large scale images (20 × 20 μm) were used to register the AFM with the SIM fields of view and small (500 × 500 nm) scans were performed in order to resolve the structure of the arrays. Raw AFM images were first order fitted with reference to the lipid bilayer. Amplitude images were inverted and a lowpass filter was applied to remove excess noise. For the high magnification scans, amplitude images are presented as movement of the arrays on the lipid bilayer does not affect the resolution of these images to the same extent as that of topography images. Amplitude data is helpful in visualising features and the shape of the sample, however note that the z- scale in amplitude images indicates the amplitude error and thus is not representative of the height of the sample.

Protein extraction and Western blot analysis

Cells were lysed directly on the plate with lysis buffer containing 20 mM Tris-HCl pH 7.5, 150 mM NaCl, 15 % Glycerol, 1% Triton x-100, 1 M ß-Glycerolphosphate, 0.5 M NaF, 0.1 M Sodium Pyrophosphate, Orthovanadate, PMSF and 2% SDS. 25 U of Benzonase Nuclease (EMD Chemicals, Gibbstown, NJ), and 100x phosphatase inhibitor cocktail 2. 4x Laemli sample buffer (900 μl of sample buffer and 100 μl β-Mercaptoethanol) is added to the lysate then heated (95°C, 5mins). 30 μl of protein sample was run on SDS-PAGE (protean TGX pre-casted gradient gel, 4%−20%, Bio-rad) and transferred to the Nitro-Cellulose membrane (Bio-Rad) by semi-dry transfer (Bio-Rad). Membranes are blocked for 3h with 5% BSA (P-AKT) or 1h with 5% milk (β-Actin) corresponding to the primary antibodies and incubated in the primary antibodies overnight at 4°C. The antibodies used for western blot were P-AKT(S473) (Cell Signaling 9271, 1:2000), β-Actin (Cell Signaling 13E5, 1:1000). The membrane incubated with P-AKT was then blocked with 5% milk prior to secondary antibody incubation. The membranes were then incubated with secondary antibodies anti-rabbit IgG HRP conjugate (Bio-Rad) for 2hrs and detected using the immobilon-luminol reagent assay (EMP Millipore). For gel source data of the various Western Blots displayed in this paper, see Supplementary Figure S10.

Cell (immuno)staining

For Fig. 3e–f and Extended Data Figure 7, cells were fixed in 4 % paraformaldehyde in PBS for 15 min, washed with PBS (3×5mins) and blocked for 1h in 3 % BSA (Fisher bioreagents CAS 9048–46-8) and 0.1% Triton X-100 (Sigma 9002–93-1). The cells were then incubated in primary antibody overnight, washed with PBS (3×5 min), incubated with the secondary antibody in 3% BSA and 0.1% Triton X-100 for 1hr, washed (4×10 mins, adding 1 μg/ml DAPI in 2nd wash), mounted (Vectashield, VectorLabs H1400) and stored at 4°C. The antibodies for immunostaining were anti-Tie2 (Cell Signaling AB33, 1:100); CD31 (BD Biosciences 555444, 1:250); VE-cadherin (BD Biosciences 555661, 1:250); Alexa 647-conjugated secondary antibody (Molecular Probes) and Phalloidin conjugated with Alexa Fluor 568 (Invitrogen A12380, 1:100).

Alternatively, for Fig. 4g–h and Extended Data Figure 11k, HeLa cells spreaded on fibronectin-coated glass bottom dishes and treated with A/B were fixed in 4 % paraformaldehyde in PBS for 20min, permeabilized with 0.05 % saponin (Sigma) in PBS for 5 min, then washed in PBS, then in PBS-1 % BSA for 5min, then in PBS. Cells were then incubated with anti LAMP1 antibodies (Developmental Studies Hybridoma Bank, clone H4A3 1:500) in PBS-1% BSA for 20min, then washed thrice in PBS, then incubated with anti-mouse F(ab’)2-Alexa647 (Invitrogen) secondary antibodies at 1:500 in PBS-1%BSA for 20 min. Cells were then washed thrice in PBS. Imaging was performed in PBS instead of mounting medium to avoid squashing the cells, thereby biasing the array/lysosome colocalization.

Alternatively, to label cell membranes of fixed NIH/3T3 cells expressing GBP-TM-mScarlet (Fig. 4i and Extended Data Figure 11d) Alexa 633-wheat germ agglutinin (Thermofisher, 1:1000 in PBS for 1 min). Fixation and imaging in PBS were performed as above.

Endocytic block

To evaluate the endocytic block affecting clustered EGF receptors (Fig. 4g–h), HeLa cells were plated on glass-bottom dishes (World Precision Instruments, FD3510) coated with fibronectin (Sigma, F1141, 50 μg/ml in PBS), for 2 hour at 37°C DMEM-10% serum, then serum-starved overnight in DMEM-0.1 % serum. Cell were then incubated with 20 ug/mL GBP-EGFR-Darpin in DMEM-0.1% serum for 1min at 37°C, then washed in DMEM-0.1 % serum, then incubated with 0.5 μM B(c)gfp in DMEM-0.1 % serum for 1min at 37°C, then washed in DMEM-0.1% serum, then 0.5 μM A in DMEM-0.1 % serum was added (or not) for 1 min at 37°C. Cells were then chased for a varying amount of time in DMEM-0.1 % serum at 37°C before fixation, immunofluorescence against LAMP1 (see above), and spinning disk confocal imaging followed by unbiased automated image quantification (see below).

Alternatively, for Extended Data Figure 11f–g, cells were treated with GBP-EGFR-Darpin as above, then 100 pM of GFP-60mer nanocages was added in DMEM-0.1 % serum for 1 min at 37°C prior to chasing in DMEM-0.1 % serum at 37°C, fixation, LAMP1 immunofluorescence and imaging/quantification. Control in this case was the unassembled trimeric building block of the GFP-60mer.

To quantitatively measure the internalization of GFP-positive arrays as a function of their size (Fig. 4h–i), we could not use the colocalization with LAMP1 as above, as the GBP-TM-mScarlet construct is not routed to lysosomes upon endocytosis (presumably routed to recycling endosomes). We thus relied on a membrane marker and quantified the amount of signal at the plasma membrane versus inside the cell. Experimentally, stable NIH/3T3 cells expressing GBP-TM-mScarlet under Doxycycline (Dox)-inducible promoter were treated with varying doses of Doxycycline for 24h, then cells were spread on fibronectin-coated coverslips for 1h as above, then incubated with 0.5 μM B(c)gfp in serum-supplemented DMEM medium for 1 min at 37°C, rinsed in PBS, then 0.5 μM unlabelled A was added (or not) serum-supplemented DMEM medium for 1min at 37°C. After a 60min chase in serum-supplemented DMEM medium at 37°C, cells were briefly incubated with Alexa-633-coupled Wheat Germ Agglutinin to label cell membranes, then cells were fixed, imaged by spinning disk confocal microscopy and images were processed for automated image analysis (see below).

Flow cytometry

To measure the density of active GBP-TM-mScarlet at the surface of cells as a function of the expression level of this construct (Extended Data Figure 11a), stable NIH/3T3 cells expressing GBP-TM-mScarlet under Doxycycline-inducible promoter were treated with varying doses of Doxycycline for 24h, then cells were incubated with 1μM purified GFP in serum/HEPES-supplemented L-15 medium for 1min at RT, then wash in PBS-1mM EDTA, then trypsinized and resuspended in serum/HEPES-supplemented L-15 medium. GFP-fluorescence per cell was then measured by Flow cytometry in an iCyt Eclipse instrument (Sony) using a 488 nm laser. Data analysis was performed using the supplier’s software package.

Imaging

TIRF imaging of array assembled onto cells (Fig. 4d and Extended Data Figure 11k) was performed on a custom-built TIRF system based on a Nikon Ti stand equipped with perfect focus system, a fast Z piezo stage (ASI), an azimuthal TIRF illuminators (iLas2, Roper France) modified to have an extended field of view (Cairn) and a PLAN Apo 1.45 NA 100X objective. Images were recorded with a Photometrics Prime 95B back-illuminated sCMOS camera run in pseudo global shutter mode and synchronized with the azimuthal illumination. GFP was excited by a 488nm laser (Coherent OBIS mounted in a Cairn laser launch) and imaged using a Chroma 525/50 bandpass filter mounted on a Cairn Optospin wheel. System was operated by Metamorph. This microscope was calibrated to convert fluorescence intensity into approximate molecule numbers (see Extended Data Figure 10 and Supplemental Materials chapter (“Microscope calibration and comparison between preformed arrays and arrays made on cells”).

For fast imaging of array formation (Fig 4, and Extended Data Figures 8, 10, and 11), receptor recruitment by preformed arrays (Fig. 3b–d and Extended Data Figure 6), quantitative imaging of the endocytic block effect (Fig 4, Extended Data Figure 11), calibrated molecular ratios (Fig 4 and Extended Data Figure 10), and Fluorescence Recovery After Photobleaching (FRAP; Extended Data Figure 6), imaging was performed onto a custom spinning disk confocal instrument composed of Nikon Ti stand equipped with perfect focus system, a fast Z piezo stage (ASI) and a PLAN Apo Lambda 1.45 NA 100X (or Plan Apo Lambda 1.4 60X) objective, and a spinning disk head (Yokogawa CSUX1). Images were recorded with a Photometrics Prime 95B back-illuminated sCMOS camera run in pseudo global shutter mode and synchronized with the spinning disk wheel. Excitation was provided by 488, 561 or 630nm lasers (all Coherent OBIS mounted in a Cairn laser launch) and imaged using dedicated single bandpass filters for each channel mounted on a Cairn Optospin wheel (Chroma 525/50 for GFP and Chroma 595/50 for mCherry/mScarlet and Chroma ET655lp for WGA-637 and Alexa 647). FRAP was performed using an iLAS2 galvanometer module (Roper France) mounted on the back port of the stand and combined with the side spinning disk illumination path using a broadband polarizing beamsplitter mounted in a 3D-printed fluorescence filter cube. To enable fast 4D acquisitions, an FPGA module (National Instrument sbRIO-9637 running custom code) was used for hardware-based synchronization of the instrument, in particular to ensure that the piezo z stage moved only during the readout period of the sCMOS camera. Temperature was kept at 37°C using a temperature control chamber (MicroscopeHeaters.Com, Brighton UK). System was operated by Metamorph. This microscope was also calibrated to convert fluorescence intensity into approximate molecule numbers (see Extended Data Figure 10 and Supplemental Materials chapter (“Microscope calibration and comparison between preformed arrays and arrays made on cells”).

Imaging of immunofluorescence experiments depicted in Fig. 3e–f, on GE DeltaVision OMX SR super-resolution microscope using 60x objective and OMX software and Imaris software. The images in Extended Data Figure 7 were taken in Nikon A1R confocal microscope using 60x objective.

Notch/DLL4 datasets (Figures S8 and S9) were collected using a 100X/1.40NA oil immersion objective on a Spectral Applied Research Aurora Borealis-modified Yokagawa CSU-X1 spinning disk confocal microscope (Nikon Ti), equipped with a 5% CO-₂ temperature-controlled chamber (OkoLab). For Figure S9, images for the “cold” condition were acquired at 15°C (Figure S9). Images in Figure S8 and those in Figure S9 for “warm” condition images were acquired at 37°C. GFP fluorescence was excited with a 488 nm solid state laser at 60 mW, mCherry fluorescence was excited with a 561 nm solid state laser at 60 mW, and JF646 fluorescence was excited with a 642 nm solid state laser at 60 mW (each selected with an AOTF). Fluorescence emission was detected after passage through a 405/488/561/642 Quad dichroic beamsplitter (Semrock). Fluorescence from excitation at 488 nm was detected after passage through a 525/50 nm emission filter (Chroma), fluorescence from excitation at 561 nm was detected using a 625/60 nm emission filter (Chroma), and fluorescence from excitation at 642 nm was detected using 700/75 (Chroma). Images in Figure S8 were collected with a sCMOS (Hamamatsu Flash4.0 V3), and those in Figure S9 with a cooled CCD camera (Hammamatsu, ORCA-ER), both controlled with MetaMorph software (Molecular Devices). Data were collected as Z-series optical sections on a motorized stage (Prior Proscan II) with a step-size of 0.25 microns, and are displayed as maximum Z-projections. For side view (Fig. S9), an optical xz slice was computed after deconvolution of the z-stack using the adaptive-bind algorithm of the Autoquant software.

Statistics

Unless stated otherwise, measurements are given in mean ± SEM. No randomization methods were used in this study. No blind experiments were conducted in this study. Statistical analyses were performed using GraphPad Prism 8 or SigmaStat 3.5 with an alpha of 0.05. Normality of variables was verified with Kolmogorov-Smirnov tests. Homoscedasticity of variables was always verified when conducting parametric tests. Post-hoc tests are indicated in their respective figure legends.

Image processing

Unless stated otherwise, images were processed using Fiji⁶⁰ /ImageJ 1.52d, Imaris, OMERO⁶¹ and MATLAB 2017b (Mathworks) using custom codes available on request. Figures were assembled in Adobe Illustrator 2019 and videos were edited using Adobe Premiere pro CS6.

Spatial drift during acquisition was corrected using a custom GPU-accelerated registration code based on cross correlation between successive frames. Drift was measured on one channel and applied to all the channels in multichannel acquisitions.

For live quantification of mScarlet recruitment by preformed Agfp+B arrays (Fig. 3c), the array signal was segmented using a user-entered intensity threshold (bleaching is minimal so the same threshold was kept throughout the video) and the mean mScarlet intensity was measured within this segmented region over time after homogenous background subtraction. The local mScarlet enrichment is then computed as the ratio between this value and the mean mScarlet intensity after background subtraction of a region of the same size but not overlapping with the array.

For 3D reconstruction (Fig. 3d and Extended Data Figure 6d), confocal z-stack of cells (Δz=200nm) were acquired, and cell surface was automatically segmented in 3D using the Fiji plugin LimeSeg developed by Machado and colleagues.⁶² 3D rendering was performed using Amira software.

For analysis of FRAP data of GBP-TM-mScarlet clustered by preformed Agfp+B arrays (Extended Data Figure 6e–f), since the GFP signal was used to set the area to bleach for mScarlet, we segmented the GFP signal using an intensity threshold and measured the intensity of the mScarlet signal in this region over the course of the experiment (pre-bleach and post bleach). This is justified as our FRAP setup only bleaches mScarlet (and not GFP), and the photobleaching of GFP due to imaging is limited (about 20% during the time course of the acquisition, see Extended Data Figure 6). Background was then homogeneously subtracted using a ROI outside the array as a reference, and Intensity was then normalized using the formula:

$$I_{norm}(t)=\frac{I\left(t\right)}{I_{prebleach}}$$

with I(t), the mean intensity at time point t; I_prebleach the intensity before bleaching (averaged over six time points). As a control that binding of Agfp alone (that is, not in an array) does not affect fluorescence recovery of GBP-TM-mScarlet (meaning that the array does not recover because all the GBP-TM-mScarlet is trapped by the Agfp+B array), we performed FRAP experiments of GBP-TM-mScarlet in cells incubated with Agfp alone. As expected, we found that it recovers (Extended Data Figure 6f).

For live quantification of array assembly and growth on cells (Fig. 4c–d, Extended Data Figure 10d, and 11j), Bgfp and mScarlet foci were first automatically detected in each frame by 2D Gaussian fitting using the Fiji Plugin Thunderstorm⁵⁹. Then, to objectively address the colocalization between Bgfp and mScarlet foci, we used an object based method⁶³, where two foci are considered colocalized if the distance between their fluorescent centroids is below 200nm, which is close to the lateral resolution of the microscope. To measure the GFP and mScarlet fluorescence of colocalizing foci over time (Fig. 4c) the trajectories of Bgfp foci were first tracked using the MATLAB adaptation by Daniel Blair and Eric Dufresne of the IDL particle tracking code originally developed by David Grier, John Crocker, and Eric Weeks (http://site.physics.georgetown.edu/matlab/index.html). Tracks were then filtered to keep only GFP-tracks that were found to colocalize with a mScarlet foci (that is if distance between GFP and a mScarlet fluorescence centroids is below 200nm) and that had at least 150 timepoints. Foci intensity was then measured by measuring the maximum intensity in a 4-pixel diameter circle centered on the fluorescence centroid after background subtraction. Then, for each time point, the fluorescence of all the Bgfp foci present in this time point, and their corresponding mScarlet foci, was averaged (Extended Data Figure 10a). To evaluate the array nucleation rate, we down sampled our dataset into a series of small regions of interest of equal size (35μm²) in regions of the cells where the membrane was in focus (>14 regions per concentration of A). We then tracked all Bgfp foci as above in each region. We then averaged the number of tracks present per region over time (Extended Data Figure 10d). The intensity over time of each array was then measured as above and averaged across all arrays and all FOVs (Extended Data Figure 10e left panel). The average initial velocity was then measured on these curves to generate the right panel of Extended Data Figure 10e.

For Mean Square Displacement (MSD) analysis (Extended Data Figure 10c), the MSD of segments of increasing duration (delay time t) was computed (MSD(t) = < (Δx)² > + <(Δy)² >) for each GFP-positive track using the MATLAB class MSD Analyzer⁵⁸ (n = 2195 tracks in N=3 cells). We then fitted the first 30 points weighted mean MSD as a function of delay time to a simple diffusion model captured by the function MSD (t) = 4D_eff t with D_eff the effective diffusion rate (R²=0.9999; D_eff=0.0005 μm²/s).

For automated quantification of the colocalization between GFP-positive arrays and LAMP1 staining (Fig. 4h), the raw data consisted of 3D confocal stacks (Δz=200nm) of cells in both channels (GFP/LAMP1). We first automatically segmented the GFP channel by 2D gaussian fitting using Thunderstorm⁵⁹ as above for each z-plane. To automatically segment the LAMP1 channel, we could not use 2D gaussian fitting, as the signal is not diffraction limited, so instead we relied on unbiased intensity thresholding set at the mean plus two standard deviations of the signal’s intensity distribution in the brightest z-plane after homogenous background subtraction. This intensity threshold was kept constant across all z-planes of the same cell, but could vary between cells depending on the strength of the staining in each cell. We then scored each GFP-positive spot as colocalized if its fluorescence centroid was contained within a LAMP1-positive segmented region. The percentage of colocalization is then computed as:

$$\mathrm{\%}ofcolocalization=\frac{\sum colocalizingparticles}{\sum totalparticles}\times 100$$

This measurement was then averaged for all z-planes of a given cell, and this average percentage of colocalization per cell was averaged between different cells and compared between conditions. Quantitatively similar values of the percentage of colocalization were obtained if the analysis was performed in 3D (using our previously described method)⁶⁴ rather than in 2D then averaged across the cell, or conversely, if the percentage of colocalization per z-plane was summed rather than averaged, indicating that data are not biased due to some z-plane having less GFP-positive spots than others (data not shown).

For automated quantification of the colocalization between GFP-positive nanocages and LAMP1 staining (Extended Data Figure 11f–g), we used a similar approach as the one described above to quantify the array/LAMP1 colocalization, except that the planes corresponding to the ventral side of the cell were excluded, as we noticed that nanocages had a tendency to stick to the dish, and thus when seeing a nanocage on the ventral plane of the cell, we could not know if it was bound to the cell surface, but not internalized, or simply stuck onto the dish. In addition, in this case, we expressed the percentage of colocalization as the fraction of signals that do colocalize, that is:

$$\mathrm{\%}ofcolocalization=\frac{\sum Intensitycolocalizingparticles}{\sum Intensitytotalparticles}\times 100$$

Indeed, as 60-mer are internalized, they accumulate in lysosomes, which thus display more signal than isolated 60-mer. Using a particle-based calculation would thus not be accurate.

For automated quantification of the fraction of GFP-positive arrays associated with WGA-positive plasma membranes (Fig. 4i and Extended Data Figure 11d), the raw data consisted of 3D confocal stacks (Δz=200nm) of cells in both channels (GFP/WGA). To automatically segment the membrane channel, we used an unbiased intensity threshold set at the mean plus one standard deviation of the WGA signal intensity distribution in the brightest plane after homogeneous background subtraction. We then measured the intensity of the GFP channel either for each z-plane in the entire cell, or within the membrane segmented regions. To avoid noise, we measured GFP intensities only above an intensity threshold set automatically to the mean plus two standard deviations of the GFP signal intensity distribution in the brightest plane (after homogenous background subtraction). We then scored for each z-plane the percentage of internalized signal as the fraction of the total signal not associated with membrane, that is:

$$\mathrm{\%}ofinternalizedsignal=\frac{{Integratedintensity}_{wholecell}-{Integratedintensity}_{membrane}}{{Integratedintensity}_{wholecell}}\times 100$$

This measurement was then averaged for all z-planes of a given cell, and this average percentage of colocalization per cell was averaged between different cells and compared between conditions.

Extended Data

Extended Data Figure 1. Dihedral building blocks inherent advantage for planar assemblies.

(a) Model of two dihedral homooligomers, a D₃ hexamer (left panel, four monomers in gray and a pair of monomers constituting a single interface are colored in purple and magenta) and a D₂ tetramer (right panel, two monomers in gray, with a pair of jointly interfacing monomers colored in green shades). Both components are positioned such that their highest order rotation symmetry axis is perpendicular to the plane (blue arrows) and an additional 2-fold (C₂) in plane rotation symmetry axis of each component is aligned with the other component in plane C₂ symmetry axis (red dashed line). (b) Top, front, and diagonal view of the D₂ homooligomer showing the symmetric nature of the interface. Due to the C₂ rotation symmetry of the interface (within each building block) it can be considered as two smaller interfaces, this is illustrated by the two diagrams showing the rotated origin. (c) At each monomeric interface (each monomeric interface constitutes exactly half of the full contact area between two interacting homooligomer) there are 6 ways for the interacting monomer pairs two deviate from the predicted, designed, conformation. These are the 6 Degrees Of Freedom (DOFs) between each two free objects in a 3D space, and could be classified to 3 translational and 3 angular DOFs. In (c) the six panels decompose the six DOFs to show the outcome of local deviations at the monomeric interface on the homooligomeric interface geometry. It shows that due to the dihedral homooligomers C₂ symmetry alignment all angular deviations (lower row) and cell spacing (this is the distance between the components and illustrated here with red arrows, upper left panel) are being counterweighted, as a result those would not propagate along the symmetric assembly. The remaining two translation DOFs, orthogonal to the cell spacing (two rightmost upper panels) would result in an in-plane twist (red curved arrow) that if too large may hinder correct propagation.

Extended Data Figure 2. Designed component solubility Nearest Neighbor (NN) model vs. assembled array geometry.

(a) Unit cell description. In the p6m plane symmetry unit cell there are exactly 2 C₃ rotation centers (green triangles) and 3 C₂ rotation centers (1 fully within the unit cell and 4 halves, blue small rectangles); for illustration purposes the design model is overlaid on top of the unit cell diagram. Unit cell length is X=31 nm, and the distance between each two nearest A components or B components is denoted by d^A_array and d^B_array, respectively, and are equal to ~15nm and 17.5nm, respectively. (b) Mean Nearest Neighbor distance in nm as a function of component concentrations. Based on the law of distribution of the nearest neighbor in a random distribution of particles we derive the average inter particle distance for a given component concentration, d^A_NN and d^B_NN (Chandrasekhar, S. Stochastic Problems in Physics and Astronomy. Rev. Mod. Phys. 15, 1–89 (1943)). The mean distance is given by $D=0.55396\cdot n^{-\frac{1}{3}}$ where $n=\frac{N}{V\cdot Nd}$, N is the number of monomers, V is volume in nm³, and Nd is the number of monomers in each homooligomer: 6 and 4 for D₃ and D₂, respectively. The vertical lines show the components distance upon assembly (d^A_array and d^B_array). Typically in our work co-assembly is initiated at components concentration around 5μM and below (range indicated by the red ellipse). The graph shows that under these concentrations the co-assembly process brings the components much closer to each other, as indicated by the two horizontal arrows. (c) NN mean distance of components stored at high concentration {D3:[2.6μM,d^A_NN=8.7nm], D2:[2.2μM,d^B_NN=8.0nm], see Table S6} is shown with a full circle markers to the left of the vertical lines thus in these concentrations d^A_NN< d^A_array and d^B_NN< d^B_array. This situation is interesting because here co-assembly practically draws the components apart, somewhat analogous to the ice/water expansion anomaly, and is substantially different from the typical process that occurs in one-component materials that assemble around a nucleation center (we note that the components are drawn apart only within the plane, unlike the situation in ice). This unique phenomenon stems from the designable system properties: interface orthogonality, components stabilization, and sparse assembly geometry. (d) Illustration of stock solution volumes required to generate a total of 1m² of arrays. We note that in current processes multiple μm scale arrays or smaller are formed.

Extended Data Figure 3. Arrays ordered stacking.

(a) In multiple TEM images either single or stacks of arrays are observed. Averaging the apparently indistinguishable conformations (four left panels) and pattern illustration of each (right four panels) revealed that in all cases arrays interact through a single contact point shown in the lowest panel (number 5, middle) which illustrates the lattice packing arrangements diagram on top of a.2. This diagram shows that those contact points are all between the vertical faces of the B component. Because the B component alone is soluble at mM concentrations (Table S6 and Extended data Figure 2c) we assume that the stacking is an artifact of TEM grid preparation and that array assembly in solution proceeds solely in two dimensions (This is shown later by solution SAXS in Fig 2d, and Extended data Figure 4). (b) Interacting B components from different arrays share the vertical rotation axis and are rotated around that axis by 60°, top and bottom panels show the alignment geometry from top and side views, respectively. (c) Assuming this observation defines the way the system predominantly performs means that hexagon belonging to vertically interacting arrays can interact in three different ways, all including that similar B-B interaction at exactly two contact points, rendering those three interaction options to be energetically equivalent. Thus, we assume that when arrays interact all three possible options have the same probability. When an array is added to a single array all three contacting options will result in a similar outcome (panel a.2 and c.2). When a third and fourth layers are added, three different outcomes could be obtained (panels a and c 2–4). (d) Definition: The probabilities to observe a certain pattern given the number of arrays in a stack. This analysis supports the assumption that given a hexagonal lattice is observed only a single layer is layered. (e) Definition: Given a pattern observation, the probability the observed pattern comprises a certain number of arrays. Again, observing a hexagonal array means that only a single array is layered, while observing a square lattice does not mean that only 2 layers are stacked, even though that is the situation with the highest probability. This also shows that an observation of pattern (4) does not provide any information about the number of stacked layers. The equations above each panel describe the different probability distributions.

Extended Data Figure 4. SAXS analysis.

a) Left and middle panels: Components A and B SAXS measurements (black curves) analyzed using the Scatter program and SAXS profiles (magenta and blue for components A and B model (shown in insets), respectively) calculated using FOXS (Schneidman-Duhovny, D., Hammel, M., Tainer, J. A. & Sali, A. FoXS, FoXSDock and MultiFoXS: Single-state and multi-state structural modeling of proteins and their complexes based on SAXS profiles. Nucleic Acids Res. 44, W424–W429 (2016)) and demonstrating excellent agreement (A: χ²=0.18, B: χ²=0.20) and no concentration dependence. Right panel: A+B mixture SAXS measurement (black curves) and ASU scattering profile (brown). Bragg peaks shown in the A+B SAXS data correlate with the p6 symmetry model and spacing of 303 Angstrom (see Table S8) in close agreement with TEM data and design model. The ASU model (top right panel corner) comprises 12 monomers, 6 belonging to a single A component (D₃ hexamer in magenta) and 6 more belonging to 3 halves of the B component (half of a D₂ tetramer in blue). b) Negative stain TEM assembly validation for the components used for the SAXS experiments demonstrating the local expected order. c) Array models with increasing size, increasing number of ASUs, and 3D crystal model of stacked arrays as inferred from TEM analysis shown in Extended data Figure 3d. Scattering profiles of array models consisting of an increasing number of ASUs ([6, 9, 12, 15, 30, 36, 72, 108, 180] gray scale intensity corresponds to ASUs #) and selected models are shown in (c). A+B mixture SAXS measurement profile (as shown in (a) right panel) is shown as a black curve and circle markers demonstrating close agreement between the computational design model of the p6 array and structures formed in solution. e) Interpolation of measured arrays ASUs number and dimensions (assuming circular arrays) based on the fit to the models’ SAXS profiles intensity difference between the first peak minimum and maximum (see method) suggesting that in solution (unsupported) the two components form 2D arrays which constitute about 6,000 ASUs (tera-Da scale flat assembly) and are 1.8 μm in diameter. f) SAXS profiles collected directly following the mixture of array components at time points ranging from 30 sec to 15 min. Each measurement was collected from a separate well to avoid accumulated damage to the samples. It is notable that within the first 30 seconds following components mixture at 10μM, distinctive Bragg peaks emerge. Based on the computational model analysis (panels (e) and (g)) these newly formed arrays constitute only a few hexagons; however, this suggests that SAXS measurements enable a thorough kinetics study and construction of phase diagrams of macroscale 2D binary systems. Scale bars: (b) 500 nm

Extended Data Figure 5. In vitro assembly kinetics and AFM edge analysis.

(a) Kinetics of array formation in solution monitored by light scattering, (mean ± SD; n=3 experimental replicates; see methods for details). (b-h) AFM characterization of arrays on freshly cleaved mica substrates in fluid cell from a solution containing components at equimolar concentrations of 7μM. Arrays were assembled from A+B components or Agfp+B as indicated. (b) Left panel: height section profile along the white dashed line of an AFM image of growing A+B arrays (right panel). Note that this picture is the same as the one in Fig. 2e, reproduced here for convenience. (c) Close up of the area in blue in (b) showing healing of lattice vacancy defects and growth (dashed to solid white circles). Elapsed time in minutes. Note that the left and middle pictures are the same as the ones in Fig. 2f, reproduced here for convenience. (d) Structural comparison of A+B arrays (left panel) and Agfp+B arrays (right panel). To extract the unit cell length, we further processed five images of arrays assembled from A+B components and fives images of arrays assembled from Agfp+B components. Five pixels width gaussian blur filter was applied to smooth the images (low pass filter) and a cross section along the crystal lattice direction was used to assess the length of every five unit cells. A+B and Agfp+B arrays unit cell length and standard deviation are calculated to be 31.51 ± 0.41nm (n=14) and 31.57 ± 0.53nm (n=20), respectively. (e) High magnification detail of a A+B array. (f-g) Edge analysis based on our ability to characterize edge states. By comparing arrays formed from A+B components (left panels) vs. arrays formed from Agfp+B components (right panel). By analysing the profile along crystal lattice directions (indicated with white lines in (f) and as the white or red curves in (g) a measurable signal for the GFP fusions or the lack of it, can be measured. Lattice edge state analysis for the co-assembly of Agfp units and B units assume the images capture equilibrium distributions of edge sites and are based on ΔG(i - j) = -kTln(p_i/p_j). We assume equilibrium states because assembly kinetics is significantly faster (see panel a and Extended Data Figures 4f,g) than the experimental setup. This is further supported by the set of images in fig. 2e–f and panel c above where we follow the dynamics of a single array at time points ranging from “zero” to 91 minutes which demonstrate mostly defects healing, and reshaping. For the edge state statistics we analysed 9 and 2 images for the A+B pair in liquid and air, respectively, and 6 and 3 images for the Agfp+B pair in liquid and air, respectively. The calculated free energy differences between different edge states: ΔG(A_GFP-II - A_GFP-I) = −5.5 kJ/mol, ΔG(B-1 - A_GFP-I) = −5.2 kJ/mol, and ΔG(A_GFP-II - B) = −0.3 kJ/mol. Unit cell spacing, the distance between the centers of each two hexagons, is calculated by measuring the distance over a number of unit cells (white arrow in (f left panel) corresponding to the black arrow in (g left panel)). The arrow length is estimated at 215nm and unit cell spacing at 315Å (see methods) in close agreement with the design model 310Å). (h) Lattice edge state statistics. Scales bar: (b,d) 200nm, (c,e-f) 100nm

Extended Data Figure 6. Preformed arrays cluster transmembrane proteins in stable assemblies.

(a-b) Preformed arrays clusters characterization. (a) 2D arrays formed in-vitro by mixing Agfp+B in equimolar concentration (5uM) in buffer (25mM Tris-HCl, 150mM NaCl, 5% glycerol) supplemented with 500mM imidazole followed by overnight incubation at room temperature in eppendorf tube (total volume of 200μL). After polymerisation, solution is centrifuged, supernatant is discarded, and pellet is resuspend the same buffer. (b) Negative stain TEM images of the resuspended array pellet (10-fold dilution, see methods). (c-d) Clustering of transmembrane proteins by preformed arrays. (c) principle of the experiment: NIH/3T3 cells expressing GBP-TM-mScarlet are incubated with Agfp+B arrays for 30min leading to clustering of the mScarlet construct. This is the same scheme as in Fig. 3a reproduced here for clarity. (d) After incubation with preformed arrays, live cells are processed for imaging by spinning disk confocal microscopy. 3D z-stacks are acquired (11 μm, Δz=0.2 μm) and processed for 3D reconstruction. Note that the intracellular mScarlet protein signal overlaps perfectly with the extracellular GFP signal of the array. (e-f) mScarlet constructs clustered by the arrays are not dynamic. (e) Cells were incubated with Agfp+B arrays for 1 hour at 37°C, then the mScarlet signal was bleached and its fluorescence recovery monitored. The GFP signal was used to delineate the bleaching area. (f) Quantification of the effect seen in a (see methods). The mScarlet signal (magenta curve) does not recover, suggesting that GBP-TM-mScarlet molecules are stably trapped by the Agfp+B array. As a control that binding of Agfp alone (that is, not in an array) does not affect fluorescence recovery of GBP-TM-mScarlet (meaning that the array does not recover because all the GBP-TM-mScarlet is trapped by the Agfp+B array), we also performed FRAP experiments of GBP-TM-mScarlet in cells incubated with Agfp alone (purple curve). As expected, these recovers. Scale bars: (d) 12 μm; (e) 6 μm.

Extended Data Figure 7. Tie2 receptor clustering and CD31/VE-Cad recruitment.

(a,b) Clustering of Tie2 receptors. Imaging of cells incubated for 60min with GFP-positive arrays functionalized with the F domain of the angiogenesis promoting factor Ang1 (a,c), or not (b), then fixed and processed for immunofluorescence with Tie2 antibodies (a,b), CD31 (c, left two panels) or VE-CAD (c, right two panels) antibodies. Note that Tie2 signal is dramatically reorganized and colocalizes with the array (compare a and b). (c) Recruitment of CD31 and VE-Cad under the F domain array (arrows), together with the extensive Actin remodeling (Fig. 3f and inset to a left panel), suggests that the structure induced by the array is a precursor to adherens junction. (d) Negative stain TEM validation of arrays formation using pre-functionalized components AscstfD+BcGFP (A component with a genetically fused spyCatcher peptide fused to spyTag-fDomain (see Table S10 for sequences), and cyclic B component with genetically fused GFP). (e) Assembly of Tie2 cluster via on-cell assembly of arrays is as potent at inducing AKT signalling as preformed arrays. The A(c)fD alone elicits much less AKT phosphorylation alone than when assembled into arrays by the B subunits on cells. Assembly here is done sequentially as in Figure 4 by first incubating with A(c)fD followed by extensive washing of unbound A(c)fD, then by adding the B subunit. As a reference, cells were treated with preformed A(c)Fd+B arrays. Induction of phospho AKT is similar between A(c)fD+B arrays assembled on cells or pre assembled. Scale bars: (a,b,c) 2.5 μm, (d) 500nm.

Extended Data Figure 8. Component desymmetrization.

(a-d) B-component desymmetrization. (a) left panel: model of the B component dihedral homooligomer (gray, with the arrays forming interfaces in purple) with GFP fusions (green), blue arrow pointing towards a perpendicular direction to the plane. Right panel: model of a cyclic B component with only two GFP fusions both facing to one vertical direction, note the purple region remain unchanged. (b) Left panel: illustration of the consequences of the binding of a dihedral homooligomer to a flat surface like a lipid bilayer through GFP/GBP interactions: array interfaces are either blocked or facing a direction which is not parallel to the plane. This thereby may induce membrane wrapping and assembly block because propagation interfaces are facing the membrane. Right panel: Ideal binding conformation with the purple arrows indicating the propagation direction when a cyclic component binds to the same membrane. This does not induce any membrane remodelling. (c) schematics of the linker insertion protocol. In the D₂ dimer, C- and N-terminal ends are adjacent (left panel, arrows pointing on the terminals). A linker is designed to connect the two (middle panel) resulting in approximately twice as big a monomer which forms a C₂ homooligomer (right panel). (d) negative stain EM images of arrays made of B(c) or B(c)gfp and various A components. (e-h) A component desymmetrization. (e) Left panel: A component dihedral (D₃) model, two monomers (colored green to red) and red arrow pointing on the designed array interface direction. Middle panel: Various fragments build between the C-term of one monomer to different positions near the N-term of the second monomer. Right panel: Model of the cyclic A components with the new linkers indicated in blue, note that again arrays interfaces remain unchanged. (f) negative stain EM screening for hexagonal assemblies. Top panel shows cyclic A components genetically fused to GFP (A(c)gfp) with dihedral B components, while in the bottom panel both components are cyclic. (g-h). Cyclisation of the A component enables array assembly on cells. Stable NIH/3T3 cells constitutively expressing GBP-TM-mScarlet were incubated with 1μM A(d)gfp (g) or 1μM A(c)gfp (h), rinsed in PBS, then 1μM unlabelled B was added and cells were imaged by spinning disk confocal microscopy. Images correspond to a single confocal plane of the GFP channel. On the contrary to dihedral A, cyclic A enables rapid array assembly on cells, as seen by the characteristic appearance of diffraction limited, GFP-positive spots (see inserts and also Fig. 4 and main text). See also figure S7 in the supplemental material for additional discussion, rationale of component desymmetrization, and computational protocol. Scales Bars: (d) 500 nm (100 nm in inserts); (g,h) 10 μm, 2 μm for insets.

Extended Data Figure 9. Correlative SIM/AFM of arrays assembled onto supported bilayers.

(a) Design of the assay (see also methods): a supported lipid bilayer containing 5% biotinylated lipids and 0.2% fluorescent lipids is formed onto a glass coverslip in a flow cell. B(c)mSA2 (200 nM) is then injected into the chamber to bind to biotinylated lipids. After washing the excess of unbound B, A(d)gfp (20nM) is injected into the chamber. After assembly for 5 min, the chamber is extensively washed and the sample fixed. The top lid of the chamber is then removed, and the sample is imaged by Super-resolution structured illumination microscopy (SIM) imaging from the bottom and atomic force microscopy (AFM) from the top. This correlative imaging allows one to find the arrays by light microscopy, before increasing the magnification to determine their degree of order by AFM. Note that the sequential mode of assembly used here is conceptually identical to the assembly of arrays onto cells (Fig. 4). Indeed, the cyclic B component (B(c)) is used to anchor the array to the membrane via its monovalelent functionalization moiety (mSA2 here compared to GFP on cells), and assembly can only happen on the membrane, as there is no free B(c)mSA2 in solution. Accordingly, arrays assembled onto supported bilayers by this method are very similar to arrays assembled on cells when imaging with diffraction-limited microscopy (see b, left panel). (b) Low magnification image of arrays assembled as above obtained by correlative Widefield microscopy (left panel), SIM super resolution microscopy (middle panel) and AFM (right panel). Super-resolution imaging indicates that arrays appearing as diffraction-limited spots by widefield microscopy can actually be somewhat elongated structures. This is in remarkable agreement with our observation that arrays assembled on cell membranes can fuse post-assembly (Fig. 4b and Fig. 4c for quantification). This further confirms that assembly on supported bilayers and on cells are similar. (c) Examples of topography in the image presented in the b-right panel. Note that height measured by AFM is uniform at about 3–4 nm, confirming 2D growth. (d) High-magnification images of arrays seen in (c) by fast AFM, demonstrating high hexagonal order of the polymer onto supported bilayers (see methods; Note that the bottom right panel is identical to Fig. 4f, reproduced here for convenience). Lookup table corresponds to amplitude between 0 and 455, 475 and 410 pm for the top, bottom left and bottom right panels, respectively. From b-d, we conclude that the height and the size of the lattice on membranes is exactly as expected from the design model (Fig. 1), the EM imaging of arrays assembled in solution (Fig. 2a–c and Fig. Extended data Figure 8), the SAXS measurements of arrays assembled in solution (Fig. 2e and Extended data Figure 4) and the AFM measurements on mica substrates (Fig. 3 and Extended data Figure 5). This confirms that assembly on membranes leads to ordered arrays and also validates that our quantitative light microscopy measurements (Fig. Extended data Figure 10 and Fig. 4e) are a valid proxy for bulk order evaluation. Scale bars: 5 μm (b) 50 nm (d).

Extended Data Figure 10. Array dynamics and order in cell membranes.

(a-e) Automated quantification of array assembly on cells. (a) Stable NIH/3T3 cells constitutively expressing GBP-TM-mScarlet were incubated with 1μM B(c)gfp, rinsed in PBS, then 0.2μM unlabelled A was added and cells were imaged by spinning disk confocal microscopy. Upon addition of A, numerous foci positive for extracellular B(c)gfp and intracellular mScarlet appear, (see Figure 4b for representative images). (b) Size distribution (Full Width Half Maximum, FWHM) of the GFP- and mScarlet-positive spots generated in (a) at t=200sec imaged by TIRF microscopy (n=8972 arrays in N=50 cells). (c) Arrays assembled onto cells slowly diffuse at the cell surface. B(c)gfp foci at the cell surface were then automatically tracked, and the Weighted mean Square Displacement (MSD) was plotted as a function of delay time (Green solid line; n = 2195 tracks in N=3 cells, lighter area: SEM). Dashed black line: linear fit reflecting diffusion (R²=0.9999; D_eff=0.0005 μm²/s). (d-e) NIH/3T3 cells constitutively expressing GBP-TM-mScarlet were incubated with 0.5 μM B(c)gfp, rinsed in PBS, then the indicated of unlabelled A was added and array dynamics was automatically measured by spinning disk confocal microscopy. (d) array nucleation rate per Field of View (FOV). (e) Middle panel: array intensity (equivalent to array size) over time (see methods; Mean+/−SEM). Right panel, initial growth rate of arrays as a function of the concentration of A. Number of FOVs analysed for left panel: 1 nM=16, 10 nM=14, 100 nM=18, 1000 nM=17; number of tracks analysed for middle and right panels: 1 nM=373, 10 nM=425, 100 nM= 599, 1000 nM= 639). Increasing the concentration of A leads to an increase of both the nucleation rate and the initial growth rate. However, higher concentrations of A led to a faster drop in the growth rate, most likely due to the saturation of all B components by A components. The inflection in the 100nM and 1000nM curves corresponds to the transition from array growth to array fusion (see also Fig. 4b, c, Extended data Figure 11j), which is less clear at 10nM. Note that the final intensity of the arrays (i.e. their size) depends on the concentration of A. (f-i) Establishment of a 1:1 GFP/mScarlet calibration standard. (f) Purified GFP-60mer nanocages were mixed with an excess of purified GBP-mScarlet, then submitted size exclusion chromatography to isolate GFP-60mer nanocages saturated with GBP-mScarlet. (g) Chromatogram comparing the size exclusion profile of either the GFP-60mer alone, or the GFP-60mer +GBP-mScarlet mix. The high molecular weight peak of assembled 60-mer nanocages is further shifted to high molecular weight due to the extra GBP-mscarlet molecules, but is still not overlapping with the void of the column. (h) Spinning disk confocal imaging of GFP/GBP-mScarlet nanocages purified as in (g) onto a glass coverslip. Fluorescence is homogenous and there is perfect colocalization between the GFP and mscarlet channels Scale bar: 1 μm. (i) Mean+/−SEM fluorescence in both GFP and mScarlet channels of GFP/GBP-mScarlet nanocages as a function of microscope exposure time, showing that the instrument operates in its linear range ( number of particles analysed: 25ms: n=167; 50ms n=616; 100ms: n=707 and 200ms: n=1086). Similar results were obtained for TIRF microscopy. Exposure for all calibrated experiments in this paper is 50ms. Note that the variant of GFP used throughout the paper, on both B and the nanocages is sfGFP (referred to as GFP for simplicity). (j-l) The clustering ability of arrays scales with array size and does not depend on the microscopy technique used. To explore a wide range of expression levels of GBP-TM-mScarlet, we measured the average number of GFP and mScarlet molecules per array in NIH/3T3 cells expressing GBP-TM-mScarlet either stably or transiently, leading occasionally to some highly overexpressing cells. To verify that our evaluation of the clustering efficiency, that is the GFP/mScarlet ratio, was not affected by the microscopy technique, we imaged cells with two calibrated microscopes (Total Internal Reflection Fluorescence (TIRF) microscopy and Spinning disk confocal (SDC) microscopy). As can be seen in j, all cells fall along the same line, suggesting a similar GFP/mScarlet ratio independently on the expression level or the microscopy technique. (overexpression imaged by spinning disk (SDC): n=12 cells; overexpression imaged by TIRF: n=15 cells; stable expression imaged by TIRF: n=50 cells, this last dataset corresponds to Fig. 4d, reproduced here for convenience). (k-l) Histogram of the GFP/mScarlet ratio (in molecules) by pooling for all cells in the TIRF dataset (k; n=8972 arrays in N=50 cells; corresponds to Fig. 4d), or for all dataset pooled (l; n=14074 arrays in N=77 cells). Dash red lines: theoretical boundary GFP/mScarlet ratios for either a 1:1 B(c)GFP : GBP-TM-mScarlet ratio, in case both GFPs of the B(c)gfp dimer are bound to GBP, or a 2:1 ratio, in case only one GFP of the B(c)gfp dimer is bound to GBP. Irrespective of the technique used, the median GFP/mScarlet ratio at 1.64(m) left: Principle of the experiment: preformed B(c)gfp/A(d)mScarlet arrays are incubated with or without a two-fold molar excess of GBP-mScarlet over B(c)gfp prior to centrifugation to remove unassembled components and excess GBP-mScarlet, and their fluorescence analyzed by spinning disk confocal microscopy. Right panel: histogram of mScarlet/GFP fluorescence intensity ratio for the indicated arrays, normalized by the median ratio of the sample without GBP-mScarlet. The fluorescence ratio increases by the amount predicted by the structure, suggesting that the fluorescence ratio is a bona fide proxy for bulk order. See also Fig. Extended data Figure 8d for EM verification of the order of B(c)gfp/A(d)mScarlet arrays. (n) Evaluation of the A/B ratio in terms of molecules in arrays assembled on cells with Bgfp and AmScarlet taking into account FRET between GFP and mScarlet (see methods; n=1058 arrays in N=12 cells). The ratio is nearly identical to the ideal 1:1 ratio suggesting that arrays made on cells have the same level of order as those made in vitro.

Extended Data Figure 11. Control of Array size, and 2D/3D EGFR clustering.

(a-e) Array size controls the extent of their endocytosis block. (a) Measurement of the surface density of GBP-TM-mScarlet as a function of GBP-TM-mScarlet expression levels. Stable NIH/3T3 cells expressing GBP-TM-mScarlet under Doxycycline (Dox)-inducible promoter where treated with increasing doses for Dox for 24h, then briefly incubated with purified GFP and the amount of immobilized GFP per cell was assessed by flow cytometry (mean fluorescence per cell, n>4000 cells/sample). (b-c) Cells as in (a) were incubated with 1μM B(c)gfp, rinsed in PBS, then 0.2μM unlabelled A was added and cells were imaged by spinning disk confocal microscopy. The average number of B(c)gfp molecules per array was then estimated (mean±SEM, b), as well as the GFP/mScarlet intensity ratio (c). Number of spots/cells analyzed, respectively: 0.1 μg/mL Dox: 4602/41; 0.5 μg/mL Dox: 2670/32; 2 μg/mL Dox: 6439/55. Dox induction increases the number of B(c)gfp, meaning array size can be modulated by controlling receptor density at the cell surface. Clustering activity scales accordingly. (d) cells as in (b) were treated with increasing doses of Dox for 24h, then incubated with 0.5μM B(c)gfp, rinsed in PBS, then 0.5μM unlabelled A was added (or not). After 60min, cells were briefly incubated with Alexa-633-coupled Wheat Germ Agglutinin to label cell membranes, then cells were fixed and imaged by spinning disk confocal microscopy. Images correspond to single confocal planes. Images correspond to quantification displayed in Fig. 4i. (e) Graphical summary illustrating the extent of the endocytic block (d) as a function of the initial mean number of B(c)gfp per array (see b). For reference, the apparent diameter of arrays as a function of their B(c)gfp content, the size of 60mer nanocages (I3) and Clathrin Coated Pits (CCP) are also figured. (f-g) Clustering of EGFR into a 3D spherical geometry does not induce endocytic block. (f) Endogenous EGF receptors (EGFR) on HeLa cells were clustered using GBP-EGFR-Darpin and either 3D icosahedral nanocages functionalized with GFP, or trimeric GFP unassembled building block as a control. After varying chase time, cells were fixed, processed for immunofluorescence with anti-LAMP1 antibodies and imaged by spinning disk confocal microscopy. Images correspond to single confocal planes, and side panels correspond to split-channel, high-magnification of the indicated regions. (g) Automated quantification of the colocalization between GFP and LAMP1 in the samples described in (f). n indicates number of cells analysed per condition. Statistics were performed using an ANOVA1 test followed by Tukey’s post-hoc test (p<0.001). There is very little (if any) endocytic block for EGF receptors clustered with the 60mer nanocages as the percentage of colocalization is similar between control GFP timers and GFP 60mer icosahedron. (h-k) Clustering of EGF receptors via arrays induces endocytic block. (h) Experiment scheme: Serum starved HeLa cell were incubated with 20ug/mL GBP-anti EGFR Darpin in DMEM-0.1% serum, then washed in DMEM-0.1% serum, then incubated with 0.5μM B(c)gfp in DMEM-0.1% serum, then washed in DMEM-0.1% serum, then 0.5μM A in DMEM-0.1% serum is added. Cells are then either imaged live (i) or incubated in DMEM-0.1% serum for 40 minutes before fixation and processing for immunofluorescence using anti-LAMP1 antibodies (k). (i) Addition of A induces rapid clustering of EGFR, in a similar fashion to the GBP-TM-mScarlet construct (see Fig. 4b). (j) Automated quantification of the number of tracks of arrays as a function of time reveals that the dynamics of array formation is fast and quantitatively similar to the GBP-TM-mScarlet construct (compare with Fig. 4c). This suggests that the fast kinetics seen in Fig. 4a–c are not due to the properties of this single-pass synthetic model receptor, but are rather a property of the arrays themselves. (k) EGF receptors on HeLa cells were clustered (or not) as in h. Cells were then fixed and processed for immunofluorescence using LAMP1 antibodies and imaged by spinning disk confocal microscopy. After 40 min chase, unclustered EGFR extensively colocalizes with lysosomal marker LAMP1, while clustered EGFR stays at the plasma membrane, suggesting that array-induced 2D clustering of EGFR inhibits its endocytosis. Images correspond to maximum-intensity z-projections across entire cells (insets correspond to single confocal planes). Images correspond to split channels of Figure 4g. EGFR clustering did not trigger EGF signaling, presumably because the distance between receptors in the cluster is longer than within EGF-induced dimers (data not shown). Scale bars: 10 μm (d,f, i-left panel and k) and 1 μm (f,k insets and i-right panel).

Data Availability Statement

Rosetta build, Rosetta build database, and all scripts used in this work are available upon request