Performance of molecular crystals in conversion of light to mechanical work

Significance

Over recent years, the increased reporting on mechanically responsive molecular crystals has accumulated an extensive library of organic crystalline materials with diverse nature-like energy-transduction mechanisms. While the chemistry behind the underlying molecular transformations is elaborate, these single crystals' work-producing capacity remains underexplored due to the need for customized testing setups suitable for delicate organic microstructures. Using a simple setup, we lay out a set of performance metrics by which we characterize the light-driven actuation in azobenzene crystals as an exemplary chemical class of dynamic molecular crystals. This work may guide the quantification of responsive molecular crystals' actuation potential and act as an invitation to ramp up interdisciplinary interest to further develop this class of materials into controlled all-organic actuating elements.

Abstract

Dynamic molecular crystals have recently received ample attention as an emerging class of energy-transducing materials, yet have fallen short of developing into fully realized actuators. Through the trans–cis surface isomerization of three crystalline azobenzene materials, here, we set out to extensively characterize the light-to-work energy conversion of photoinduced bending in molecular crystals. We distinguish the azobenzene single crystals from commonly used actuators through quantitative performance evaluation and specific performance indices. Bending molecular crystals have an operating range comparable to that of microactuators such as microelectromechanical systems and a work-generating capacity and dynamic performance that qualifies them to substitute micromotor drivers in mechanical positioning and microgripping tasks. Finite element modeling, applied to determine the surface photoisomerization parameters, allowed for predicting and optimizing the mechanical response of these materials. Utilizing mechanical characterization and numerical simulation tools proves essential in accelerating the introduction of dynamic molecular crystals into soft microrobotics applications.

A machine is a system of controllable integrated parts which utilizes input energy to perform a predetermined task. The active, work-generating component within a machine is an actuating element composed of responsive, dynamic material. To fabricate precise and controllable structures, engineers have typically resorted to rigid actuator materials. However, within the context of robotics, soft smart materials have the unique capacity to host elements of sensing, actuation, and feedback into a single light body, which allows for added autonomous functionalities (1, 2). Light-driven actuation is particularly advantageous because of its noninvasive and remote activation, targeted manipulation, and complete control over the input energy (3). Various reported approaches for light-driven actuation include photothermal effects, radiation pressure (4), photostrictive effects (5), photochemical reactions (6), and photoinduced phase transitions (7, 8). Photoresponsive functionalities have been extensively integrated into soft polymer-based materials through functionalization or doping with photoreactive molecules, such as azobenzenes and, to a lesser extent, diarylethenes, stilbenes, and anthracenes (9–13). The softness of these materials generally contributes to larger multiplanar deformations compared to hard materials. However, the resultant motions introduce infinite degrees of freedom, and, unless deformation directors are introduced (14, 15), attaining control over their response posits significant practical challenges. Compared to the amorphous nature of polymers, the ordered structures of dynamic molecular crystals allow for anisotropic properties and a direction-dependent mechanical response that is easier to model and control. These features are thought to be important in soft microrobotics and qualify such adaptive crystals to function as single-component actuating elements.

Photodimerization of anthracenes (16), linkage photoisomerizations (17), and trans–cis photoisomerization of azobenzenes (18) are all photoswitching mechanisms that lead to the deformation of the crystal lattice, mostly at the irradiated surface of the crystal. With sufficiently slender crystals, the induced tensile, compressive, or shear strain is translated into directional mechanical displacements that vary between bending (19), twisting (20), and coiling (21). Exploring the mechanical response of these organic materials has been approached almost entirely from a chemical perspective. It is driven by attempts to find or design new structures with optimal properties. However, property optimization is not possible without a comprehensive understanding of the full potential of a material. Before any actuator material is considered for a particular application, its performance must be evaluated according to criteria that determine its suitability for the task at hand (22). Appropriate metrics include motion specifications, force and work output, cyclability, and efficiency, as well as material mechanical properties, among other parameters. These performance indices can be used to establish quantitative and systematic benchmarking of molecular crystals’ actuating capacity, independent of the underlying chemistry and structure. The values can be compared against typically used actuators to guide their consideration and selection in early engineering design and rapid device prototyping.

Given the reported potential of azobenzene crystals as a typical subcategory of photodynamic crystals capable of fairly rapid and reversible response (19, 23–26), we set out to quantitatively characterize the light-driven bending of three representative azobenzene crystals in order to define their performance as actuating elements. Due to the previously overlooked interference of the ultraviolet (UV) light with force sensors, which prevents direct force measurement, a custom setup was built, where suitably fabricated polydimethylsiloxane (PDMS) micropillars of varying stiffness were used as loads to determine the performance of the crystals. Universal static and dynamic performance indices for bending crystals were established and compared to those of commercially available actuators by using global property diagrams. Finally, a finite element analysis (FEA), applied to model the photobending behavior of one of the materials, provided a robust model that deepened our understanding of the mode of actuation and provided the means to optimize and predict the mechanical response from any bendable dynamic crystal.

Results and Discussion

Synthesis of Azobenzene Single Crystals and Force Measurement Setup.

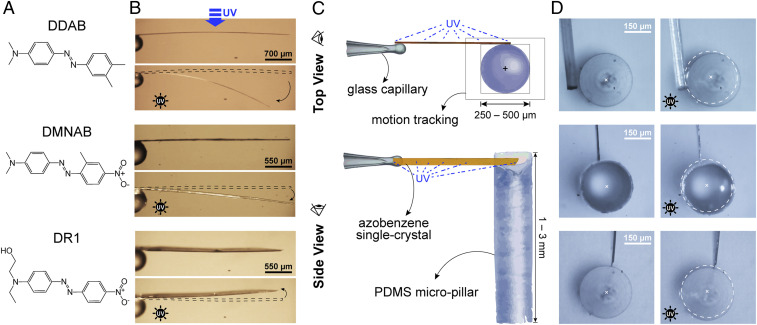
Three substituted azobenzenes—namely, N-ethyl-N-(2-hydroxyethyl)-4-(4-nitrophenylazo)aniline (“Disperse Red 1”; DR1) (19), 3ʹ,4ʹ-dimethyl-4-(dimethylamino)azobenzene (DDAB) (23), and 4ʹ-(dimethylamino)-2-methyl-4-nitroazobenzene (DMNAB) (Fig. 1A)—were crystallized to obtain slender, long planks (SI Appendix, Fig. S1). Five single crystals of each compound were separated and tested under identical conditions. Each crystal was affixed onto a glass capillary at one end to form a cantilever. Upon irradiating their (001) or $\left(00\overline{1}\right)$ face with UV light, the crystals bent reversibly due to photoinduced trans–cis isomerization at their surface (Fig. 1B). The compressive or tensile surface strains generated by the molecular transformation cause the structure to bend toward or away from the light, respectively, as the isomerization continues and propagates into the crystal. DR1 crystals bend toward the light, while DDAB and DMNAB crystals bend away from it. Since the trans–cis isomerization is reversible, once the irradiation is switched off, crystals of DR1 and DMNAB quickly recover their original straight shape under visible light due to the conversion of the cis isomer to the trans one. In contrast, crystals of DDAB require a much longer time to return to their original shape, and the recovery can be accelerated thermally.

Fig. 1.

Azobenzene photoresponse and its force generation measured by a customized setup. (A) Chemical structures of the azobenzene compounds. (B) Photoresponse of the fixed azobenzene single crystals (the crystals correspond to the compounds in A; the direction of light irradiation is from the top for all crystals). (C) Cartoon showing the force-measurement setup used to track the deflection of the PDMS micropillar tips. (D) Displacement of the micropillar tips bent by azobenzene single crystals upon irradiation.

The generated motion of the free end of each crystal can be used to displace objects and exert a force against a load. A set of PDMS micropillars of varying stiffness (250 to 500 µm in diameter and 1 to 3 mm in length) was fabricated (SI Appendix, Fig. S2) and used to gauge the force-generating capacity of all crystals and to evaluate their performance (Fig. 1C and SI Appendix, Table S1). Each crystal was made to bend against a series of micropillars of increasing stiffness (0.6 to 12 mN⋅m⁻¹) until minimal displacement of the pillars was observed (Fig. 1D and Movie S1). At that point, the force by which the crystal impinges on the pillar has reached its maximum and is counterbalanced by the stiffness of the pillar. The height-to-diameter aspect ratio of the micropillars was maintained above five, such that it was safe to ignore the shear contribution to the total deformation and attribute the entire displacement to bending (27). By tracking the motion of the displaced pillars, the force exerted by the crystal tip on each pillar can be determined as

$$F=k\mathit{\text{δ}},$$ [1]

where k is the stiffness of the micropillar calculated using a Young’s modulus for PDMS, E_PDMS = 2.6 MPa (28), and δ is the displacement of the pillar’s tip. The maximum force output, F_max, is reached at the force needed to block any further displacement of the actuator against the load (“blocking force”).

Understanding the Basics: Static Performance.

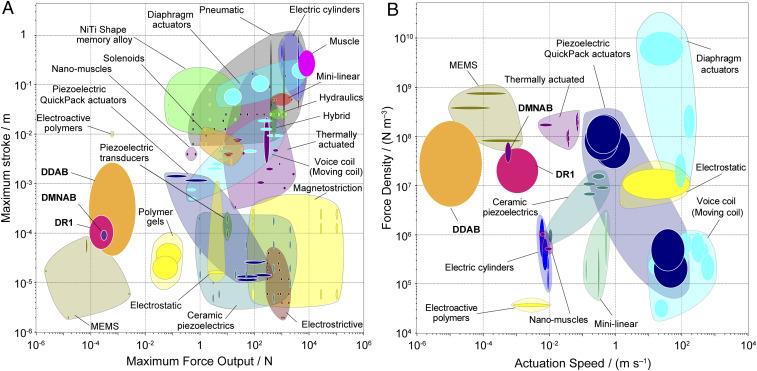
Typically, the maximum force output and maximum free stroke are used as actuator specifications, and they describe the static performance of an actuator when it is completely restrained or entirely free, respectively. Crystals of the three azobenzene materials studied here exhibit maximum strokes ranging from 0.048 to 2.7 mm between 1% and 100% of their original length and generate forces between 0.084 and 4.4 mN (SI Appendix, Table S2). These parameters are coplotted in Fig. 2A with those of standard actuator classes retrieved from an actuator database (SI Appendix, Table S3). Macroactuators such as pneumatic and hydraulic actuators and electric cylinders exhibit large strokes and output forces, as compared to the microsized azobenzene crystals and microelectromechanical systems (MEMS) devices. In terms of their maximum stroke, the azobenzene single crystals conveniently spread between hard materials with short strokes and soft materials with larger strokes. Generally, the more rigid materials exhibit shorter strokes that are around 10% of their initial lengths, while softer polymeric, elastomeric, and biological materials exhibit deformations over 100 times their original length. Similarly, rigid actuator materials based on ceramics, hard metals, and alloys such as magnetostrictive, piezoelectric, electrostrictive, and electrostatic actuators exhibit larger force outputs than soft actuators such as polymer gels and electroactive polymers whose resistance to deformation is low. The force output of these crystals is only comparable to those of MEMS and some soft actuators, like polymer films and gels. The displacement occurs along the weak bending axis, which decreases the pushing capacity of the crystal tip against a load, particularly in long crystals, as compared to the generally uniaxial displacement in other actuator classes. Some applications require moderate strokes and high force output, particularly positioning, object manipulation, precision, high-resolution, and high-dynamics tasks. Biomedical endoscopy, optical scanning, and laser communication are among the applications that require larger deformations rather than high force outputs (29).

Fig. 2.

Static performance indices. Actuator maximum stroke versus maximum force output (A) and actuator force density versus actuation speed (B) for the three photoresponsive azobenzene materials (DDAB, DMNAB, and DR1) studied here, coplotted with the same attributes for the main actuator classes. The opaque bubbles represent the range of performance indices values of a particular material, while the translucent envelopes group materials that belong to the same actuator class.

Given the small size of the azobenzene crystals used here and the wide range of sizes among the actuator classes showcased, the analysis of the normalized attributes allows for a better comparison of the performance capacities of these actuator families. Here, we use scale-invariant metrics through normalizing these properties by the volume. These metrics, such as force density, often called “property densities,” can be useful when selecting actuator materials for applications with space constraints. Fig. 2B shows that azobenzene single crystals are capable of force densities that are significantly higher than many actuators and are similar to the much smaller MEMS-based devices, thermal actuators, and some piezoelectric materials. High force densities indicate that these crystals can outperform many actuators in the same size range.

The response time (the time needed to reach a maximum stroke) is another critical actuation property that determines the maximum frequency of actuation when cycled. Given that the actuators presented have maximum strokes that are over three orders of magnitude apart, comparing their response times becomes unsuitable. Instead of the response time, here, we consider the actuation speed of the unrestrained response to evaluate each actuator’s capacity to generate displacement per unit time in the absence of a load (Fig. 2B). By considering the maximum actuation speed and the maximum stroke of a material, one can estimate the minimum response time. The actuation speed of the azobenzene crystals ranges between 0.0012 and 4.6 mm⋅s⁻¹ (SI Appendix, Table S2). The slowest response is that of DDAB crystals, with an average response time to reach maximum displacement of 120 s (15 s to reach 80% of the maximum actuation), as compared to 0.28 and 0.18 s for DR1 and DMNAB, respectively. The response time and recovery time for DR1 and DMNAB crystals are on the same order; however, DDAB crystals take much longer to recover fully, a process that can be assisted thermally or by irradiating the opposite crystal face. While the irradiation conditions can influence the response time and the recovery time for these crystals, optimal conditions (SI Appendix) were chosen under which the crystals performed best while maintaining a reversible response and intact crystal structures. The shortest response time reported for a photoresponsive molecular crystal is 25 µs for a single crystal of cyclopentene derivative with a 6-min recovery time (30); however, the possible contribution of laser-radiation pressure to the deformation has not been considered in interpreting this result. Diarylethene and azopyridine crystals that exhibit photobending have considerably longer response times, between 35 ms and 5 s, with a recovery ranging between 0.5 s and 20 min (31–33). Other crystals, such as some anthracenes and benzoxazole derivatives, have even longer response times, ranging between 18 and 44 s, and recovery times within 1.2 to 15 min (20, 34, 35). Typically, organic crystals that respond to light by a photosalient effect (photoinduced jumping) or a phase transition exhibit rapid bending or violent jumping within 5 ms to 33 s. However, this often leads to drastic compromise on the integrity of their crystal structures (36, 37). The speed of displacement by these crystals is comparable to that of MEMS-based devices, thermal actuators, and piezoelectric and electroactive actuators, despite the latter being electrically driven and is often resorted to for fast responses.

Performance under Dynamic Loading.

Generally, actuators are used in dynamic configurations and conditions. Throughout actuation, internal and external factors affect the interaction of the actuator with its environment and result in a continuous change in the loading, displacement, and energy flow. The dynamic performance of actuators can be evaluated by indicators such as work, power, frequency, and efficiency (38). To evaluate the actuator’s effective force and capacity to perform work, the maximum work output, W_out, is defined as the maximum amount of energy transferred by a force:

$$W_{\text{out}}=F·r,$$ [2]

where F is the effective generated force, and r is the displacement or the resultant stroke. With free, unrestrained motion, the maximum stroke produces no force and, hence, no work, while with a heavily restrained actuator, the displacement is null, and so is the work output. The maximum power output, P_out, of an actuator is the amount of work produced, W_out, per unit time (Eq. 3). It is also a measure of energy transduction, which reflects on the capacity of the material to function as a smart actuator and sensor simultaneously.

$$P_{\text{out}}=\hspace{0.17em}\frac{W_{\text{out}}}{t}=\frac{F_{\text{max}}·r}{t}.$$ [3]

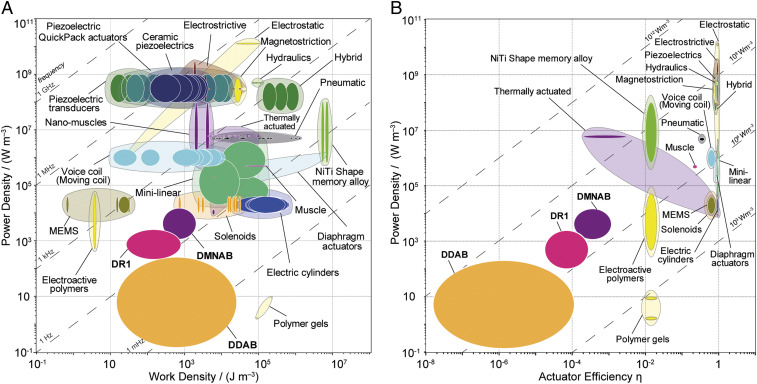
Fig. 3A shows the power density plotted against the work density of the azobenzene crystals, among other actuators. The lines of slope +1 connect actuators that have the same maximum achievable frequency, which is directly dependent on the response time as well as the recovery time. While the azobenzene single crystals have a work density of 0.17 to 24 kJ⋅m⁻³, which is comparable to that of piezoelectric materials, the latter operate at much higher frequencies and are, therefore, high-power-delivering actuators. The contour lines in Fig. 3A show that DR1, DMNAB, and DDAB crystals appear to operate at frequency ranges similar to those of muscles, solenoids, and some shape-memory alloys. High power density allows for the miniaturization of devices where space is constrained—for example, in technologies for wearable devices. While electrically driven actuator materials rank highest, azobenzene crystals report power densities between 0.14 × 10⁴ and 1.5 × 10⁴ W⋅m⁻³, similar to electroactive polymers, MEMS-based devices, and some thermal actuators.

Fig. 3.

Dynamic performance indices. Actuator power density versus work density (A) and actuator power density versus energy efficiency (B) for the three photoresponsive azobenzene materials (DDAB, DMNAB, and DR1) coplotted with the same attributes for the main actuator classes. The opaque bubbles represent the range of values of performance indices of a particular material, while the translucent envelopes group materials that belong to the same actuator class. The contour lines link together classes of actuators that have the same maximum operational frequency (A) or input power per unit volume (B).

Actuator efficiency becomes particularly relevant when the actuator must operate cyclically and is defined as the ratio of mechanical power output to power input during a complete actuation cycle:

$$\eta =\frac{P_{\mathrm{out}}}{P_{\mathrm{in}}}=\frac{P_{\mathrm{mechanical}}}{P_{\mathrm{irradiation}}}.$$ [4]

Most light-driven actuators (LDAs) have low energy-conversion efficiency, typically in the range of 10⁻¹⁰ to 10⁻⁵% (39), especially when compared to hydraulic (40 to 55%), electric (75 to 80%), and magnetic actuators (<80%) (40). The loss of energy due to the dissipation of heat or the small thermal expansion in photothermally driven actuators explains the low efficiency of LDAs. Photoactuation that takes the form of bending generates high stresses that accumulate at the base of the structure when used to push against loads, which also reduces the efficiency of converting the transformations in the material to mechanical motion (41). While efficiencies on the order of at least 1% are needed to manipulate macroscopic objects and avoid extensively powerful irradiations, low efficiency in LDAs is not a limiting factor in the actuation of microscopic objects, given the moderate input powers required to generate the small output forces needed. Typically, azobenzene-functionalized photoactuation, although robust and chemically stable, has low efficiencies on the order of 10⁻¹⁶% (42). Some polymeric and bilayer photoactuators can achieve a photomechanical response with a high energy-conversion efficiency of up to 5 × 10⁻³% (43) and 8 × 10⁻³ to 10⁻²% for some polyvinylidene fluoride (44) and poly(N-isopropylacrylamide) (45) actuators, respectively. The three azobenzene crystalline materials studied here have energy-conversion efficiencies of 10⁻⁶ to 0.1%, with DR1 reaching efficiencies as high as 0.01 to 0.1% and outperforming most reported LDAs in the same size category.

Numerical Solutions to Experimental Problems: FEA.

Through simple mathematical modeling of the photobending behavior of azobenzene single crystals, the actuation mechanism can be modulated and controlled by specific irradiation parameters. Thereby, the quantitative behavior of any crystal under specified irradiation conditions can be predicted without having to resort to experimental analysis. The bending crystal can be modeled as a cantilever with two layers, where the actuation relies on the mismatch between the photoinduced strain in the active layer (isomerized cis layer) and the inactivity of the second layer (nonisomerized trans layer). The maximum displacement can then be determined by using the Stoney equation (46) and can be expressed as:

$${\delta }_{\max }=\kappa \frac{L^2}{2}=\frac{6E_{\mathrm{t}}{E}_{\mathrm{c}}{t}_{\mathrm{t}}{t}_{\mathrm{c}}\left(t_{\mathrm{t}}+t_{\mathrm{c}}\right)L^2{\epsilon }_{\max }}{2\left(E_{\mathrm{t}}^2{t}_{\mathrm{t}}^4+E_{\mathrm{c}}^2{E}_{\mathrm{c}}^4+2E_{\mathrm{t}}{E}_{\mathrm{c}}{t}_{\mathrm{t}}{t}_{\mathrm{c}}\left(2t_{\mathrm{t}}^2+2t_{\mathrm{c}}^2+3t_{\mathrm{t}}{t}_{\mathrm{c}}\right)\right)},$$ [5]

where κ is the curvature of the crystal, L is the length of the crystal, ε_max is the maximum photoinduced surface strain, E is the Young’s modulus, t is the thickness, and the subscripts t and c denote the trans substrate and the cis isomerized layer, respectively. The effective Young’s modulus of an irradiated crystal, which is essential to understand the effect of the actuation on the flexibility of the crystal, can also be calculated while accounting for the isomerized layer and its mechanical properties (46):

$$E_{\mathrm{eff}}=\frac{E_{\mathrm{c}}^2{t}_{\mathrm{c}}^4+E_{\mathrm{t}}^2{t}_{\mathrm{t}}^4+2E_{\mathrm{t}}{E}_{\mathrm{c}}{t}_{\mathrm{t}}{t}_{\mathrm{c}}\left(2t_{\mathrm{t}}^2+2t_{\mathrm{c}}^2+3t_{\mathrm{t}}{t}_{\mathrm{c}}\right)}{\left(E_{\mathrm{c}}{t}_{\mathrm{c}}+E_{\mathrm{t}}{t}_{\mathrm{t}}\right)t^3},$$ [6]

where t is the total thickness of the crystal.

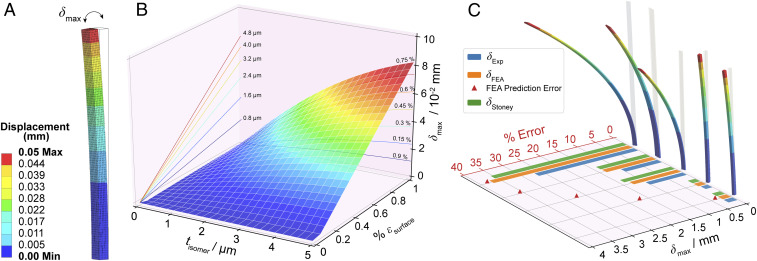
Given that the azobenzene trans–cis isomerization is not a single-crystal-to-single-crystal transformation, the photoinduced surface strain cannot be simply determined through conventional diffraction methods. Similarly, it is difficult to experimentally determine the depth of propagation of the isomerization into the irradiated surface of the crystal. Therefore, we resorted to FEA through numerical simulations to extract the photoisomerization parameters for DDAB single crystals and build a simplified mathematical model that can be solved analytically. The FEA method is a numerical approach that breaks down a system into small, finite elements through a particular space discretization, which results in a set of simultaneous algebraic equations that are assembled to model the entire system. Otherwise, this exercise would require the solution of ordinary and partial differential equations that are analytically unobtainable. The long-range order, well-defined edges and faces, and homogeneity in mechanical properties of these crystals allow for easier and more accurate modeling compared to other soft materials. A DDAB single crystal was subject to five irradiation cycles for 2 min each and was left to recover fully between each cycle. The mean of the maximum deflections from all cycles was determined to be 50 µm. Using the Ansys static structural model, the partially isomerized single crystal was then modeled as a trans–cis bilayer microcantilever and the photogenerated cis layer as a homogeneous thin film of varying thickness (Fig. 4A and SI Appendix, Fig. S3). The photoinduced strain was replicated through thermal strain induced by a temperature change in the thin-film layer only. Young’s moduli for the trans and cis substrates of 1.7 and 2.6 GPa, respectively, and a Poisson’s ratio estimate of 0.3 were used to define the mechanical properties of the generated model (25). Fig. 4B shows the three-dimensional (3D) surface plot that explains how varying the strain and the thickness of the thin film representing the isomerized cis layer affects the total displacement of the modeled crystal. The response surface was then numerically optimized under constraints of 0.1 to 1% for strain in dynamic molecular crystals (47), an isomerization depth of at least 300 nm in DDAB crystals (25), and the experimentally obtained value for displacement.

Fig. 4.

Finite element analysis (FEA) of the bending of a single DDAB crystal. (A) Ansys-simulated and meshed model crystal color-coded by displacement from the initial position. (B) A 3D surface plot of the change in maximum displacement with respect to the depth of the isomerization and the surface strain of the model crystal. (C) The accuracy of the numerically solved model in predicting the maximum displacement of five different DDAB single crystals.

The trans–cis isomerization depth was determined to be up to 4.9 ± 0.5 µm, with a respective photoinduced surface strain of around 0.6 ± 0.05% along the crystal’s longest axis. The maximum displacement of the model crystal was also calculated by using the Stoney equation (Eq. 5) and compared with the FEA results for different isomerization parameters (SI Appendix, Fig. S4). The results closely match those obtained numerically, particularly for lower strains. The effective Young’s modulus of the entire crystal, E_eff = 1.94 GPa, was also calculated. Finally, five random DDAB single crystals subject to the same irradiation conditions as the model crystal were used to validate the FEA model and the Stoney equation calculations of the maximum displacement in comparison to experimental data (Fig. 4C and SI Appendix, Table S4). The FEA predictive model was able to estimate the crystals’ mechanical response to irradiation with an average error of 25%, where the highest errors were for the crystals with the highest displacement. The accuracy of this model is contingent upon the assumption that after prolonged exposure to irradiation, the photoisomerized layer is converted entirely to the cis isomer with a defined depth and that there is no slip at the boundary between the isomerized cis layer and the trans crystal body. After determining and validating the trans–cis surface isomerization parameters for DDAB crystals, it is now possible to predict, with a certain degree of accuracy, the response of any random DDAB crystal with a defined geometry. Establishing such models and control over these structures allows for their incorporation in simulations that play an essential role in robotics design and accelerates their integration in applications and devices.

Performance-Based Recommendations for Potential Applications.

A thorough characterization of the actuating performance of single crystals of three different photoresponsive azobenzenes was conducted, which allowed for a direct comparison of the performance of these typical photomechanical crystals with a wide variety of conventional actuators. While only three representative compounds were chosen here, an identical procedure to extract performance indices could be applied to other dynamic crystals, including other thermoresponsive and mechanoresponsive subclasses. These measurables unveil the true capacity of these unique, organic materials en route to their application as work-generating elements. The graphical presentation of the performance indices aids in highlighting the opportunities where the potential lies for new or substitute materials to be further considered and improved. The results indicate that the performance of the three azobenzene crystals is closest to microactuators such as MEMS, and further analysis that focuses on that size range could be insightful. After considering the performance indices reported here, it becomes clear that the photoresponsive azobenzene crystals can be used in several microscale applications. Their performance is comparable to that of small microdrivers and electromagnetic micromotors, as well as to some positioning and mechanical gripping systems. The force output of these microdevices is typically in the range of 5 to 20 mN, with a maximum stroke of 20 µm to 20 mm and a response time up to 30 ms (48). They are common in minimally invasive diagnostics and surgery, microrobotic elements and medical devices, handling of semiconductors, spatially controlling optical components, and cell-manipulation tools. Microfluidic applications in medical technology and, more increasingly, in chemistry and biotechnology require small and lightweight actuating structures with fast response times. Microvalves, for example, are typically based on piezoactuation and pneumatic actuation, where the response time is around 0.5 s with micronewton-per-meter work output and resultant strokes around 50 to 100 µm (49). The photoresponse of the azobenzene single crystals can also be used in an oscillatory fashion to create active micromixers that generate turbulence between laminar flows in microchannels and can withstand a blocking-flow pressure of up to 17 MPa. While these potential applications of dynamic molecular crystals remain primarily unexplored, more interdisciplinary works that take advantage of engineering design processes and numerical modeling and simulation tools are crucial to promote the rapid prototyping and accelerate the advancement of this class of materials.

Materials and Methods

Experimental details on the crystallization of DDAB, DMNAB, and DR1; the determination of the photomechanical response; the fabrication of the PDMS micropillars for use as a force measurement setup; and the FEA conducted through an Ansys simulation can be found in SI Appendix.

Data Availability.

All study data are included in the article and/or supporting information.