Abstract
Motivation
Advances in experimental and imaging techniques have allowed for unprecedented insights into the dynamical processes within individual cells. However, many facets of intracellular dynamics remain hidden, or can be measured only indirectly. This makes it challenging to reconstruct the regulatory networks that govern the biochemical processes underlying various cell functions. Current estimation techniques for inferring reaction rates frequently rely on marginalization over unobserved processes and states. Even in simple systems this approach can be computationally challenging, and can lead to large uncertainties and lack of robustness in parameter estimates. Therefore we will require alternative approaches to efficiently uncover the interactions in complex biochemical networks.
Results
We propose a Bayesian inference framework based on replacing uninteresting or unobserved reactions with time delays. Although the resulting models are non-Markovian, recent results on stochastic systems with random delays allow us to rigorously obtain expressions for the likelihoods of model parameters. In turn, this allows us to extend MCMC methods to efficiently estimate reaction rates, and delay distribution parameters, from single-cell assays. We illustrate the advantages, and potential pitfalls, of the approach using a birth–death model with both synthetic and experimental data, and show that we can robustly infer model parameters using a relatively small number of measurements. We demonstrate how to do so even when only the relative molecule count within the cell is measured, as in the case of fluorescence microscopy.
Availability and implementation
Accompanying code in R is available at https://github.com/cbskust/DDE_BD.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
The dynamics of intracellular processes are determined by the structure and rates of interactions between different molecular species. However, stochasticity and limitations of experimental methods make it difficult to infer the characteristics of these interactions from data. On the single-cell level, different molecular species can occur in small number, correlate with phenotype, and localize within different parts of the cell. The resulting dynamics can thus be highly variable over time, and across the population. Averaging over such fluctuations can lead to inaccurate representations of the underlying biology (Cai et al., 2006), and inference methods therefore need to account for stochasticity within individual cells, and variability across the population (Kaern et al., 2005; Kepler and Elston, 2001; Raj and van Oudenaarden, 2008; Smith and Grima, 2018).
Different statistical approaches have been developed to fit stochastic models to data from single-cell assays, offering a window into the dynamical processes within individual cells (Bergmann et al., 2016; Boys et al., 2008; Choi et al., 2017; Daigle et al., 2012, 2015; Poovathingal and Gunawan, 2010; Zechner et al., 2014; Zimmer et al., 2015). Among these, Bayesian methods have been particularly promising. To apply Bayesian techniques, one typically assumes a model for the network of interactions, postulates a prior over model parameters, and uses experimental data to determine a posterior and estimates of unknown parameters (Boys et al., 2008; Choi and Rempala, 2012; Choi et al., 2017; Golightly and Wilkinson, 2005). However, Bayesian approaches can suffer from the curse of dimensionality (Blum et al., 2013), and are thus difficult to implement directly when the number of parameters is high, or the network of interactions is large. The problem is exacerbated when the system is not fully observed, as here one must marginalize over the unobserved components of the system.
One way to circumvent this problem is to replace uninteresting or unobserved reactions with time delays (Barrio et al., 2013; Bel et al., 2009; Gomez et al., 2016; Korenčič et al., 2012; Leier et al., 2014). For instance, the production of regulator proteins requires on the order of minutes: Production involves transcription, translation and post-translational steps such as protein folding, oligomerization and maturation (Golding et al., 2005; Kaern et al., 2005). Rather than model each step individually (Fritz et al., 2014; Megerle et al., 2008), one can describe protein production by an effective, random delay that represents a sequence of noisy biochemical processes with fluctuating completion times (McAdams and Shapiro, 1995). Related approaches have been used to derive effective low-dimensional models for oscillations induced by chain delays (Barrio et al., 2006; Chen et al., 2015; Hussain et al., 2014; Mather et al., 2009), and in cases where transcription oscillates stochastically between on and off states (Lewis, 2003).
The theory of stochastic systems with random delays is well-understood (Gupta et al., 2014; Gupta and Rawlings, 2014). The Gillespie algorithm, Langevin equations and mean-field models can be extended to systems with distributed delays, allowing for efficient sampling at small, intermediate, or high molecule counts, respectively (Brett and Galla, 2013; Gupta et al., 2014; Schlicht and Winkler, 2008). However, using such models involves a compromise: Adding delay can lead to other challenges, as the resulting models are typically non-Markovian. In particular, this complicates the derivation of parameter likelihood functions, making such models more difficult to analyze and use for parameter inference (Calderazzo et al., 2019; Heron et al., 2007). Thus, developing a general inference framework for biochemical reaction networks with distributed delays that works even when molecule counts are low remains a challenging open problem. Important progress has been made for certain delay stochastic differential equations (Heron et al., 2007), and delay linear noise approximations (Calderazzo et al., 2019). These approaches rest on the assumption that molecule counts are high enough to allow delay stochastic differential equations to accurately capture system dynamics (Gupta et al., 2014). However, one must frequently deal with low molecule counts when using imaging data obtained from fluorescent imaging of single cells.
To address this problem, we describe a systematic way to derive likelihoods for the parameters in common biochemical reaction models that include delays. These results allow us to extend MCMC methods to efficiently estimate reaction rates, and delay distribution parameters from single-cell assays even when molecular counts are low. We illustrate the advantages and limitations of our approach using a delay birth/death process, which provides a simple model of gene expression. Our method is robust: It allows us to recover the mean delay even when the delay distribution is misspecified. When only a relative measure of molecule count is available, such as a fluorescence trace, delay parameters can be accurately estimated if the dilution rate can be estimated separately. Our method performs well on experimental data: We show that given the dilution rate of YFP (yellow fluorescent protein) estimated directly from observed cell growth rates, we can infer the time delay of the synthesis of YFP from multiple cell trajectories measured using quantitative time-lapse microscopy. Our approach therefore provides a robust basis for the development of hierarchical networks inference methods that can be used to characterize biochemical processes across cellular populations.
2 Materials and methods
2.1 Derivation of the likelihood function
Following Boys et al. (2008) we consider a biochemical reaction network consisting of u species, and v reactions, . Reaction Rk is given by
where the pkj and qkj are the stoichiometric coefficients. Reaction Rk is equipped with rate constant θk and reaction initiation propensity , where represents the number of molecules of each chemical species at time t.
Suppose that at least one reaction , once initiated, requires a random time to complete. Let and denote times at which this reaction initiates and completes, respectively. We call the (random) delay associated with reaction . We assume that delayed reactions only change the state of the system upon completion, and do not consider consuming reactions (Anderson, 2008; Cai, 2007). For instance, production of a given protein starts with the initiation of transcription, but the number of mature proteins in the system changes only after transcription, translation and post-translational steps result in a fully functional protein. We leave the case of delayed consuming reactions, which change the system state at both their initiation and completion, for future work.
Let ηk be the measure supported on that describes the delay distribution associated with reaction Rk. We assume, for the sake of simplicity, that these distributions do not depend on time or the state of the system, and that each ηk depends on a vector of parameters . In this setting, Schlicht and Winkler (2008) have proven the existence of reaction completion propensities defined by
| (1) |
where denotes the trajectory of the chemical reaction network from time 0 to time T. These completion propensities may be understood intuitively by conditioning on the present. Suppose that a reaction of type k completes at time t. Conditioned on this event, ηk describes the probability distribution for the initiation time t – s of this reaction. On the level of propensities, one therefore computes fk by convolving hk with the delay distribution ηk.
The completion propensities fk define the effective rates of reactions at time t, and allow us to write the likelihood of the parameters for an observed sequence of completed reactions in a form analogous to the case without delays (Boys et al., 2008). Integrating the completion propensities in time, define
where is the vector of reaction rate constants and is the collection of parameters that define all of the delay measures, ηk. If the state, of the chemical reaction network is known for all , then the likelihood function for the set of delay parameters Δ and the vector of rate constants θ is given by
| (2) |
Here ni denotes the total number of reactions that complete over the time interval , and for , we denote the reaction that completes within using the pair , where reaction completes at time tij. Details of the derivation are provided in the Supplementary Methods.
When sampling trajectories of a biochemical reaction network, the ‘forward’ view of delayed chemical kinetics is typically used: When a delayed reaction initiates, a (random) completion time is drawn, and the change in the system is postponed until the future time at which the reaction completes. In contrast, we obtain the likelihood function in Eq. (2) by adopting a ‘backward’ view of delayed chemical kinetics: We assume that we know only the reaction completion times, and treat the corresponding unobserved reaction initiation times that occurred in the past as random quantities. This backward view is useful for the inference problem because reaction initiation times are typically not observed experimentally. By contrast, sampling algorithms such as the Gillespie algorithm typically adopt a ‘forward’ approach, where once a reaction is initiated and recorded, the corresponding reaction completion time is random.
2.2 Approximate likelihood given observations at discrete times
Assume now that we only observe the system, y(t), at a discrete set of times, , yielding a vector of measurements . These observations can be used to approximate the exact likelihood given by Eq. (2) using a τ-leaping approach (Gupta and Rawlings, 2014). First we replace the propensities, fk, defined in Eq. (1) with approximate propensities, that are constant between observations. We obtain by averaging fk over and interpolating hk linearly between measurements (see Supplementary Methods for details):
where , and Δk denotes the vector of parameters that define the measure ηk as before. Note that we do not discretize the delay distributions.
Our formula for is valid whenever the delay measure ηk is defined by a probability density function. For reactions that do not involve delay (that is, when ηk is a Dirac-delta measure at zero), our formula for reduces to
Using the the likelihood in Eq. (2) can be approximated by (Gupta et al., 2014):
| (3) |
where and rki denotes the number of reactions of type k whose completion has been observed in the interval . When the approximation in Eq. (3) is valid (for instance when the reaction rates are constant between observations), then conditioned on system history up to time i, the number of reactions of type k that have been completed within follows a Poisson distribution with mean .
2.3 Statistical inference of model parameters using discrete-time data
We next describe an MCMC algorithm for obtaining the posterior distribution over the model parameters, (), using the approximate likelihood given in Eq. (3) and prior distributions over the unknown parameters. Bayes’ Theorem and Eq. (3) allow us to express the posterior distribution over model parameters given the observed data as:
| (4) |
Here and are priors over the rate and delay parameters, respectively. The prior can be chosen depending on the delay distributions. We used gamma distributions for because the support of each θk is positive. Moreover, for mass action kinetics the propensity function is separable, so that , and hence the gamma distribution defines a conjugate prior (Wilkinson, 2011).
Samples from the posterior distribution given by Eq. (4) can be generated given complete trajectories of all species (i.e. ) using Gibbs sampling (Choi and Rempala, 2012; Smith and Roberts, 1993). In order to sample θ and Δ from their conditional posterior distributions, we use the Metroplis-Hastings algorithm (Tierney, 1994). However, sampling θ and Δ from their conditional posterior distributions requires knowledge of the number of completed reactions, rki. Crucially, the discrete-time measurements y(i), , do not uniquely determine the number of completed reactions between observations. We thus need to sample the number of completed reactions rki during each step of Gibbs sampling. To do so, we use the block updating method described by Boys et al. (2008) to sample the number of completed reactions of each type during each time interval given the observed system states y(i) and , using the Metropolis-Hastings algorithm with a random walk. For the proposal distributions of the number of reactions, we use the Skellam distribution (Boys et al., 2008; Johnson and Kotz, 1985). Since we formulate the posterior in Eq. (4) using an approximate likelihood that reflects a τ-leaping approach, we do not consider the specific times at which reactions have been completed during each time interval but only the total number of completed reactions (see Supplementary Methods for details).
The following algorithm can then be used to generate samples from the approximate posterior distribution given by Eq. (4).
Initialize values for the reaction rates θ, parameters for the delay distributions, Δ and reaction counts rki for the hidden trajectory. Use gamma priors for the rates, θk.
Sample, in order, θk, , from the conditional posterior distribution, given all other rate constants, , delay parameters Δ and reaction numbers. If y(t) and θk are separable in the propensity function , then sample θk from the gamma posterior distribution. Otherwise, use the Metropolis-Hastings algorithm.
Sample, in order, Δkl, and , from the conditional posterior, given θ and for all , using the Metropolis-Hastings algorithm since the conditional posterior does not follow a known distribution.
Sample rki for all and , given θ, Δ and the observed trajectory, , using the block updating method.
Repeat steps 2–4 until convergence is achieved.
In the Supplementary Methods we provide expressions for all the likelihoods, and illustrate the algorithm in the case of a stochastic birth–death process with delayed birth.
2.4 Measurement of YFP level and cell area of individual cells
We tested our algorithm using experimental data from our previous work (Cheng et al., 2017). Specifically, the was cloned to a medium copy-number plasmid, which was later transformed into E.coli JS006A strain which was, in turn, derived from the JS006 strain (Stricker et al., 2008) by introducing a constitutively expressing AraC into the genome. To measure single-cell YFP expression, we cultured the cells in a custom-designed microfluidic device, mounted on a Nikon Eclipse Ti Microscope. Phase contrast and YFP images were taken every 1 min. Background YFP was first recorded for 12 min, then the medium was switched to include 2% ARA to trigger YFP expression. After the experiment, phase-contrast images were segmented and analyzed using custom Matlab code (https://github.com/alanavc/rodtracker). We analyzed results of two experimental runs. The fluorescence is considerably lower in the second experiment which is likely due to the differences in the heights of the PDMS chip, and conditions of the excitation light bulb between the two experiments.
2.5 Relating fluorescence and molecular count
To estimate the fluorescence signal per YFP molecule (γ), we measured how the YFP signal of a mother cell is partitioned among two daughter cells. To measure the partitioning during a decreasing phase of the fluoresce signal we followed (Rosenfeld et al., 2005). We used a genetic circuit with PBAD -lacI and Plac/ara-sfyfp, which forms an incoherent feedforward loop and thus generates a single pulse of YFP (Cheng et al., 2017). Specifically, during the decreasing phase after reaching the peak of the pulse, total YFP signals from a mother cell before a cell division and from two daughter cells after the cell division were measured.
3 Results
3.1 Delay is estimated accurately and precisely with sufficient data
We first tested whether our algorithm can be used to identify the mean, and variance, , of the delay distribution, as well as the reaction rates of a delayed, stochastic birth–death process:
| (5) |
In the generative model, we used gamma distributed delay in the birth reactions, assuming that creation of protein is the result of a chain of exponentially distributed monomolecular reaction steps (Barrio et al., 2013; Leier et al., 2014), approximable by a gamma distribution (Bel et al., 2009; Calderazzo et al., 2019; Heron et al., 2007). We generated 500 sample trajectories from the model given by Eq. (5) using the delayed Gillespie algorithm (Gupta et al., 2014), and subsampled each trajectory by recording the molecular count at evenly spaced intervals (Fig. 1a). A considerable number of molecules was produced before the mean delay time (6 min) due to variability of reaction delays (Fig. 1a inset). Therefore, using either the earliest detectable signal, or a threshold to estimate delay can lead to biased estimates of the mean delay, .
Fig. 1.
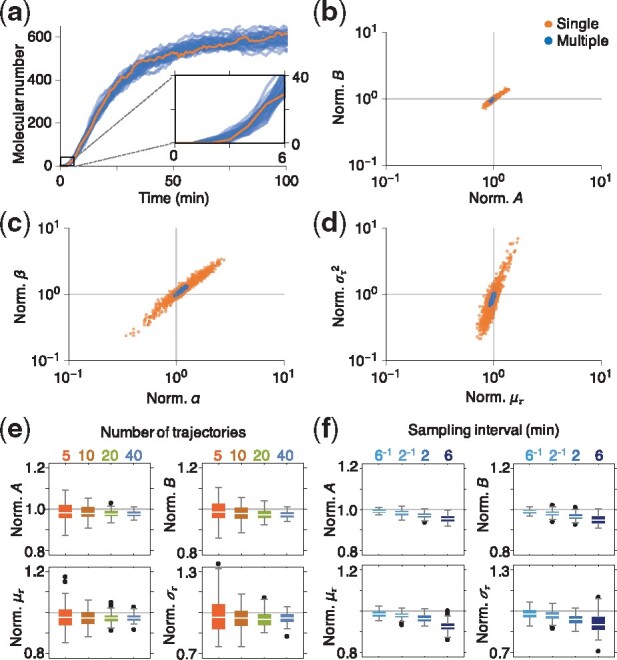
Estimation of the delay distributions using multiple trajectories is accurate and precise. (a) Simulated trajectories of a delayed stochastic birth–death process (Eq. 5) with rate parameters A = 30 min–1, B = 0.05 min–1 and delay , i.e. min and min2. We assumed that . Trajectories used for inference were sampled at 1 min intervals. (b–d) MCMC generated samples from the posterior distributions over parameters using a single trajectory (orange) or 40 trajectories (blue). While the rate parameters, A, B, can be estimated well using a single trajectory (b), estimation of the delay requires multiple trajectories (c and d). Here, the sample values were normalized by dividing with the true parameter values. (e) Box plots of 100 posterior means using an increasing number of trajectories. Subsets of between 5 and 40 trajectories were chosen randomly and repeatedly from a set of 500 simulations. Estimates were normalized by dividing by the true parameter values. (f) Increased sampling rate leads to more accurate estimation. Note that sparser measurements, at intervals of 2 and 6 min, still allowed for reasonably accurate and precise estimates of all parameters, as long as a sufficient number of trajectories was used (40 in this case). (Color version of this figure is available at Bioinformatics online.)
We inferred the two production and degradation rates, A, B, as well as the delay distribution parameters, using the MCMC algorithm described in the Section 2 and Supplementary Methods. Although we used non-informative priors for all parameters, the reaction rates could be accurately estimated from a single subsampled realization of the process (orange trajectory in Fig. 1a, and posterior distribution in Fig. 1b). However, the posterior distribution over the delay parameters revealed a strong correlation between the two (Fig. 1c), making the delay mean and variance difficult to estimate concurrently (Fig. 1d). Increasing the number of sampled trajectories in the estimation to 40 resulted in a precise estimate of all parameters (Fig. 1b–d). The precision of posterior mean estimates increased with the number of trajectories used for estimation (Fig. 1e). Furthermore, as we increased the sampling rate, the approximate likelihood (Eq. 3) became more accurate, and, as a result, the accuracy of estimates improved (Fig. 1f). We thus expect that a sufficient number of trajectories and a sufficiently high sampling rate are needed for precise and accurate estimation, respectively. More data (i.e. a larger number of trajectories/a higher sampling rate) is needed as the noise level of the system increases (see Supplementary Fig. S1 for details). However, with a sufficiently large number of trajectories, even sparsely sampled data can provide reasonably accurate estimates of all model parameters. This is true even when the time between observations equals the mean delay time (Fig. 1f).
3.2 Mean delay can be estimated when the underlying time delay distribution is misspecified
We next asked whether delay mean and variance can be estimated even when the delay distribution is misspecified. To do so we generated sample trajectories with delays that followed a beta and inverse gamma distribution with equal mean and variance (see Fig. 2a). While the gamma distribution assumed in the estimation algorithm has infinite support and decays exponentially, the beta distribution has compact support, while the inverse-gamma distribution has a heavy tail.
Fig. 2.
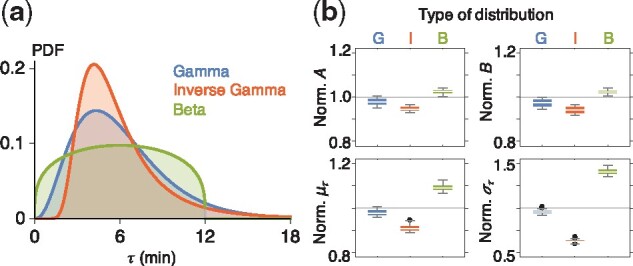
The mean, but not the variance of the delay can be accurately and precisely estimated when the delay distribution is misspecified. (a) Three types of delay distributions: , Inverse- and . For all distributions and . (b) A box plot of 100 posterior mean estimates. As in Fig. 1, parameters were estimated using 40 sample trajectories randomly and repeatedly chosen from a set of 500 trajectories generated assuming one of the three delay distributions shown in panel (a). Here the estimates were normalized by dividing with their true values
Given sufficiently many observed trajectories, our algorithm provided accurate and precise estimates of the rates, and mean delay (Fig. 2b). However, the estimate of delay variance, was biased when the delay distribution was misspecified, with a systematic underestimate when the true delay followed an inverse-gamma distribution, and overestimate when the true delay followed a beta distribution.
3.3 With relative molecular level measurements estimation of delay requires separate estimates of dilution rate
Frequently we cannot measure the actual molecular count within a cell directly. For instance, measurements of fluorescence reporter intensity are approximately proportional to the absolute species number, but the proportionality constant cannot always be determined precisely, and hence estimates of molecular number from such measurements can be noisy (Cai et al., 2006; Rosenfeld et al., 2005, 2006; Yu et al., 2006).
We next asked how such errors in the estimates of absolute protein numbers affect delay distribution inference. To address this question we scaled the sample trajectories in Figure 1a to mimic a twofold error in the estimate of the proportionality constant used to convert fluorescence to molecular counts. Such scaling changes the mean and the variance of the signal differently (Fig. 3a) distorting the level of intrinsic fluctuation, as measured by the coefficient of variation. In turn, a mis-scaling can lead to biases in estimation of all parameters including the mean, and variance, of the delay (Fig. 3b). Thus inaccurate measurements of molecular levels can distort delay estimates.
Fig. 3.
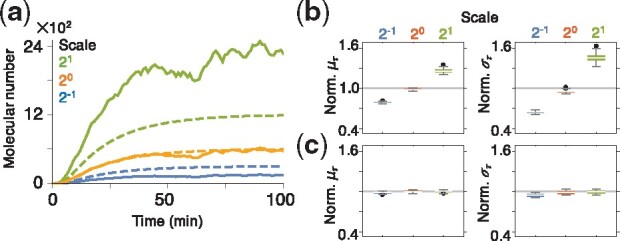
Measurements of dilution rate allow for accurate estimation when only relative molecular levels measurements are available. (a) The average (dashed) and variance (solid) of the 500 simulated trajectories in Figure 1a, scaled by 0.5, 1 and 2. The average and variance of the scaled trajectories were scaled by different amounts (blue and green). (b) Using scaled trajectories to estimate delays leads to large biases. Here, we show box plots based of 100 posterior means, each estimated using 40 subsampled trajectories. (c) When the dilution rate, B, is known, the delay distribution can be accurately and precisely estimated even with incorrectly scaled data. (Color version of this figure is available at Bioinformatics online.)
Advances in lapse imaging techniques are making it easier to estimate cell growth rates, and resulting dilution rates, B, directly (Megerle et al., 2008; Norman et al., 2013; Taheri-Araghi et al., 2015). We therefore assumed next that the dilution rate, B, can be estimated separately, and set to their true value. Once we did so we were able to accurately and precisely estimate delay distribution parameters, even with incorrectly scaled data (Fig. 3c). This indicates that identifying the timescale of the birth–death process by correctly estimating the dilution rate, B, can overcome biases due to incorrectly scaled data. Thus our algorithm can be used to effectively infer delays even when only relative molecular levels are known, or when the conversion of fluorescence to protein counts is not accurate.
Furthermore, we found that having access to a separate estimate of the dilution rate, B, can resolve unidentifiability issue when only partial data is available. For instance, as their number increases, cells in microfluidic traps can become crowded and their growth can slow as a result (Delarue et al., 2016; Volfson et al., 2008). To ensure measurements under minimal strains on the cells, sometimes we use only the initial fluorescence measurements before crowding can impact gene expression (e.g. the first 25 min in Fig. 1a). The initial part of the fluorescence trajectory, before saturation, but after YFP maturation, is approximately linear with slope . As a consequence only A/B is identifiable from data. However, if the dilution rate, B, can be estimated separately, the growth rate, A, can be estimated even from partial data (Supplementary Fig. S2). Importantly, the delay parameters, and can also be accurately estimated from partial data (Supplementary Fig. S2). We therefore conclude that a separate measurement of the dilution rate, B, allows for successful estimation of time delays from limited, and misscaled data.
3.4 Estimation of time delay in transcriptional and translational regulation
We next tested our algorithm on experimental data obtained using time-lapse fluorescence microscopy. As protein synthesis is not instantaneous, there can be considerable delay between gene activation and the formation of functional proteins (Fig. 4a). To estimate this delay, we used a PBAD reporter-only circuit, which we constructed previously by placing a YFP gene under control of the PBAD promoter in E.coli (Cheng et al., 2017). In this circuit the addition of Arabinose (ARA) promotes the rapid activation of AraC, which promotes the constitutive transcription of YFP (Fritz et al., 2014; Megerle et al., 2008). Once the translated YFP protein matures, it generates a fluorescence signal. YFP synthesis rate is not strongly affected by cell growth (Austin et al., 2006; Fritz et al., 2014; Megerle et al., 2008). On the other hand, as cells grow, YFP is diluted. As YFP is a relatively stable protein (Andersen et al., 1998), and is not enzymatically degraded in this system, dilution is the main reason for the decrement in protein number within a cell. Thus, the dynamics of YFP concentration, which is determined by time delayed constitutive synthesis and linear degradation, is well described by Eq. (5).
Fig. 4.
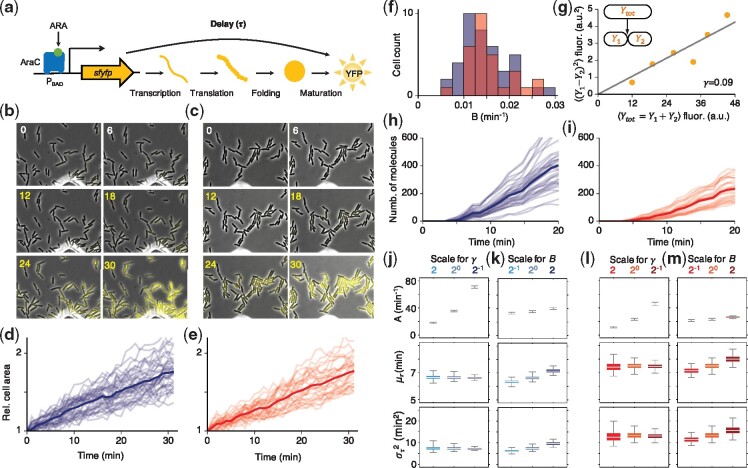
Robust estimation of the time delay distribution of YFP synthesis after induction. (a) When ARA is added to the media, AraC promotes the synthesis of YFP. The synthesis process involves transcription, translation, protein folding and maturation which result in a delay between YFP gene activation, and the observation of the fluorescence signal generated by mature YFP. (b, c) Time-lapse images of YFP expression from two independent experiments, performed previously (Cheng et al., 2017). At 12 min after measurement was started, 2% ARA was added to the media, promoting the constitutive transcription of YFP. (d, e) The lineage of each cell was identified via manual segmentation of images, and the change in individual cell areas was tracked [39 cells in (d) and 29 cells in (e)]. When a mother cell divided into two daughter cells, the area of the mother cell was added to the area of the daughter cell. (f) We estimated dilution rates by fitting an exponential function to the cell growth data. The average dilution rate of the 39 cells from the first, and the 29 cells from the second experiment are 0.015 ± 0.005 and 0.016 ± 0.005 min–1, respectively. (g) A conversion constant from YFP signal level to the number of YFP molecules (γ) was estimated by measuring the binomial error in partition of total YFP signal () at cell division to two daughter cells (Y1 and Y2). The constant γ was estimated as described in the text. (h, i) We estimated YFP molecule number per unit area by dividing the total fluorescence level of each individual cell (b, c) with its total area (d, e), and with the estimated scaling factor γ (g). (j–m) Using our inference algorithm with these trajectories, and fixing the dilution rate at the estimated value, B = 0.015, we obtained 104 posterior samples for the remaining parameters (j, l). Due to the higher molecular numbers in (h) than (i), the estimated birth rate, A and delay variance, were higher and lower, respectively, in (j) than (l): 35.4 ± 0.4 and 23.1 ± 0.5, and 7.4 ± 0.7 and 13.4 ± 1.4. However, the estimated mean delay time, was similar in the two cases: 6.6 ± 0.1 min (j) and 7.5 ± 0.2 min (l). Estimation of the delay mean and variance was robust to the twofold change in γ (j and l) and B (k and m)
Previously, we performed, and reported on, two independent experiments using time-lapse fluorescence microscopy to measure the YFP trajectories from individual cells in a growing population after induction (Fig. 4b and c) (Cheng et al., 2017). In both experiments, the fluorescence signal from matured YFP was recorded from each cell at 1 min intervals. After measuring background fluorescence levels for 12 min, we added 2% ARA to the media to promote YFP synthesis (Fig. 4b and c). We tracked the total fluoresce signal in each cell (Fig. 4b and c), to obtain a timeseries of YFP molecule number within a unit area. To do so we first tracked changes in area of individual cells using time–lapse images (Fig. 4d and e). When a cell divided, the area of a mother cell was added to the area of a daughter cell. By fitting the observed volume growth trajectories to an exponential function, we estimated the dilution rates of individual cells in the population (Fig. 4f), which were consistent with previous estimates (Megerle et al., 2008).
Next, we estimated the fluorescence signal per YFP molecule (γ) by estimating the ratio between the square difference of measured fluorescence between two daughter cells () and the measured fluorescence of a mother cell () (Fig. 4g). This approach is based on the assumption that proteins from the mother cell are partitioned independently, and without bias between the two daughter cells [see Rosenfeld et al. (2005, 2006) for details]. Then, by dividing the intensity of the total fluoresce signal in each cell (Fig. 4b and c) by our estimate of and the cell’s area (Fig. 4d and e), we obtained an estimate of the timecourse of YFP molecules per unit area for each of 39 cells in the first, (Fig. 4h) and 29 cells in the second experiment (Fig. 4i).
In neither experiment did the YFP signal saturate before the end of the experiment, and we thus only obtained partial trajectories in both cases. To address this problem, we fixed the dilution rate, B = 0.015 (Fig. 4f) which we estimated from the observed rate of growth and division while estimating the remaining parameters, A, and from the partial trajectories. The difference in the total fluorescence levels between the two experiments (Fig. 4h and i) resulted in a higher estimated production rate, A, in the first experiment (Fig. 4j). Without investigating further, we could not tell whether this difference in production rates was real, or whether discrepancies in the experimental setup caused a difference in the strengths of the recorded signal.
Despite the difference in the inferred rates, the estimated mean delay times, were similar: 6.6 ± 0.1 min (Fig. 4j) and 7.5 ± 0.2 min (Fig. 4l), in the first and second experiment, respectively. The estimated time delay is similar to the time to maturation of YFP variant VENUS () measured using real-time monitoring of a single molecule (Yu et al., 2006), supporting the accuracy of our algorithm.
The inferred proportionality constant, (Fig. 4g) depends on the camera setting, and can vary between experiments (Fig. 4h and i). We thus examined the impact of varying the constant γ on the estimated parameters. Even in the presence of a twofold change in γ, the estimates of delay mean, and variance, changed little (Fig. 4j and l). Thus our conclusions about the robustness of the inference algorithm when the dilution rate is known extend to experimental data (Fig. 3c). Furthermore, as the dilution rate, B, can differ between cells (Fig. 4f), we also investigated the sensitivity of our inference method to changes in the exact value of this constant. Even a twofold change in the dilution, resulted in only a small changes in the estimate of mean delay time, (%; see Fig. 4k and m), providing a further indication that our approach is robust.
4 Conclusion
We have introduced a principled approach to extending Bayesian inference techniques that allows for parameter estimation in biochemical reaction networks with delays. We have shown that the method can be used to estimate both reaction rates and delay distribution parameters from experimentally obtainable observation of gene regulatory networks. Although the method has some limitations, we have shown that they can be addressed by proper experimental design.
We considered a simple birth–death process with a small number of parameters in order to understand the advantages and limitations of the proposed method. Nevertheless, our approach is scalable: The derivation of the likelihood function for the different parameters, and the experimental design principles we discussed can be extended to systems with many biochemical species, multiple delays and complex dynamics. Examples include networks of interacting birth–death processes with nonlinear delayed protein synthesis, and systems that oscillate due to delayed negative feedback loops (Chen et al., 2015; Cheng et al., 2017). Importantly, replacing unobserved or uninteresting reaction pathways with time delays in large biochemical reaction networks can significantly reduce the number of model parameters. We thus expect that an equivalent algorithm to the one we presented can then be used to infer rates and characterize delays in the resulting reduced networks. The identifiability of time delay in more complex models is a challenge that we will address in future work.
When molecular counts are sufficiently high, chemical master equations can be approximated by analytically tractable reductions such as delay stochastic differential equation (SDEs), and linear noise approximations (LNAs) (Brett and Galla, 2013; Gupta et al., 2014; Kim et al., 2014; Thomas et al., 2012). Previous work has leveraged these approximations for Bayesian parameter inference. Specifically, Heron et al. (2007) have developed a Bayesian algorithm using SDE models containing distributed delay, with particular emphasis on oscillations generated by delayed negative feedback loops (Monk, 2003). Recently, a filtering approach based on LNAs has been developed to infer distributed delays (Calderazzo et al., 2019). An interesting avenue for future research is to develop hybrid models, and combine our method with previous SDE or LNA approaches to gain both in computational speed and accuracy.
While delay distributions were difficult to infer from a single trajectory, a relatively small number of trajectories allowed for efficient inference of all parameters. An important caveat is that when we used multiple cell trajectories for inference, we assumed that all recorded cells were identical. Thus, our algorithm at present does not take into account cell-to-cell variability in YFP expression due to differences in growth rates, plasmid copy numbers, asymmetric partition of proteins at division and other factors. In particular, heterogeneity in ARA uptake rates is known to cause considerable cell-to-cell variation in time delay (Megerle et al., 2008). However, the 2% ARA in the media we used in our experiments was sufficiently high to ensure that uptake occurred rapidly, and minimized cell-to-cell variability. This at least partly justifies our assumption that cell-to-cell differences in time delay are mainly due to measurement, and intrinsic noise. Indeed, our estimates of time delay are consistent with those obtained using real-time monitoring of a single molecule (Yu et al., 2006). The robust performance of our method with relatively small number of measurements suggests that it can be extended to hierarchical models which take into account cell-to-cell variability and extrinsic noise sources (Zechner et al., 2014).
The delayed reactions we have treated in this work are of the non-consuming type: The system state only changes upon reaction completion. It would be interesting to extend our inference methodology to handle consuming reactions (delayed reactions that alter system state at both initiation and completion). Forward Gillespie-like algorithms that generate sample paths have been developed in this context (Anderson, 2008; Cai, 2007). However, it is challenging to rigorously derive both likelihoods and SDE reductions for systems that include consuming reactions, because initiation and completion for such reactions are not independent. Path integral approaches may shed light on these challenges (Brett and Galla, 2015).
In sum, we have presented a method to characterize reduced models of biochemical networks with delays. Our approach is flexible, and the robustness of the method suggests that it can be extended to more complex biochemical reaction networks, and hierarchical models allowing us to shine a light on complex processes within cells, and populations.
Supplementary Material
Acknowledgements
We thank Alan Veliz-Cuba and Mehdi Sadeghpour for valuable comments.
Funding
This work was supported by the National Institutes of Health grant RO1 GM117138 (M.R.B., K.J., W.O.), by National Science Foundation grants DMS 1662305 (K.J.), DMS 1662290 (M.R.B.) and DMS 1816315 (W.O.), by DBI-1707400 (K.J.), by a Korea University Grant (B.C.), by the National Research Foundation of Korea grants NRF-2017R1D1A3B03031008 (B.C.) and NRF-2016 RICIB 3008468 (J.K.K.), by EWon fellowship (J.K.K.) and by Welch Foundation grant C-1729 (M.R.B.).
Conflict of Interest: none declared.
Contributor Information
Boseung Choi, Department of National Statistics, Korea University Sejong Campus, Sejong 30019, Korea.
Yu-Yu Cheng, Department of Biochemistry, University of Wisconsin-Madison, Madison, WI 53706, USA.
Selahattin Cinar, Department of Mathematics, University of Houston, Houston, TX 77204, USA.
William Ott, Department of Mathematics, University of Houston, Houston, TX 77204, USA.
Matthew R Bennett, Department of Biosciences, Rice University, Houston, TX 77005, USA; Department of Bioengineering, Rice University, Houston, TX 77005, USA.
Krešimir Josić, Department of Mathematics, University of Houston, Houston, TX 77204, USA; Department of Biosciences, Rice University, Houston, TX 77005, USA; Department of Biology and Biochemistry, University of Houston, Houston, TX 77204, USA.
Jae Kyoung Kim, Department of Mathematical Sciences, Korea Advanced Institute of Science and Technology, Daejeon 34141, Korea.
References
- Andersen J.B. et al. (1998) New unstable variants of green fluorescent protein for studies of transient gene expression in bacteria. Appl. Environ. Microbiol., 64, 2240–2246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson D.F. (2008) A modified next reaction method for simulating chemical systems with time dependent propensities and delays (vol 127, art no 214107, 2007). J. Chem. Phys., 128, 109903–109903-1. doi: 10.1063/1.2899331. [DOI] [PubMed] [Google Scholar]
- Austin D.W. et al. (2006) Gene network shaping of inherent noise spectra. Nature, 439, 608.. [DOI] [PubMed] [Google Scholar]
- Barrio M. et al. (2006) Oscillatory regulation of hes1: discrete stochastic delay modelling and simulation. PLoS Comput. Biol., 2, e117.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrio M. et al. (2013) Reduction of chemical reaction networks through delay distributions. J. Chem. Phys., 138, 104114.. [DOI] [PubMed] [Google Scholar]
- Bel G. et al. (2009) The simplicity of completion time distributions for common complex biochemical processes. Phys. Biol., 7, 016003.. [DOI] [PubMed] [Google Scholar]
- Bergmann F.T. et al. (2016) Piecewise parameter estimation for stochastic models in COPASI. Bioinformatics, 32, 1586–1588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blum M.G. et al. (2013) A comparative review of dimension reduction methods in approximate Bayesian computation. Stat. Sci., 28, 189–208. [Google Scholar]
- Boys R.J. et al. (2008) Bayesian inference for a discretely observed stochastic kinetic model. Stat. Comput., 18, 125–135. [Google Scholar]
- Brett T., Galla T. (2015) Generating functionals and Gaussian approximations for interruptible delay reactions. Phys. Rev. E Stat. Nonlinear Soft Matter Phys., 92, doi: 10.1103/PhysRevE.92.042105. [DOI] [PubMed] [Google Scholar]
- Brett T., Galla T. (2013) Stochastic processes with distributed delays: chemical Langevin equation and linear noise approximation. Phys. Rev. Lett., 110, 250601.. [DOI] [PubMed] [Google Scholar]
- Cai L. et al. (2006) Stochastic protein expression in individual cells at the single molecule level. Nature, 440, 358.. [DOI] [PubMed] [Google Scholar]
- Cai X. (2007) Exact stochastic simulation of coupled chemical reactions with delays. J. Chem. Phys., 126, 124108.. [DOI] [PubMed] [Google Scholar]
- Calderazzo S. et al. (2019) Filtering and inference for stochastic oscillators with distributed delays. Bioinformatics, 35, 1380–1387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y. et al. (2015) Emergent genetic oscillations in a synthetic microbial consortium. Science, 349, 986–989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng Y.-Y. et al. (2017) The timing of transcriptional regulation in synthetic gene circuits. ACS Synthetic Biol., 6, 1996–2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi B., Rempala G.A. (2012) Inference for discretely observed stochastic kinetic networks with applications to epidemic modeling. Biostatistics, 13, 153–165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi B. et al. (2017) Beyond the Michaelis-Menten equation: accurate and efficient estimation of enzyme kinetic parameters. Sci. Rep., 7, 17018.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daigle B.J. et al. (2012) Accelerated maximum likelihood parameter estimation for stochastic biochemical systems. BMC Bioinformatics, 13, 68.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daigle B.J. Jr. et al. (2015) Inferring single-cell gene expression mechanisms using stochastic simulation. Bioinformatics, 31, 1428–1435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delarue M. et al. (2016) Self-driven jamming in growing microbial populations. Nat. Phys., 12, 762.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fritz G. et al. (2014) Single cell kinetics of phenotypic switching in the arabinose utilization system of E. coli. PLoS One, 9, e89532.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golding I. et al. (2005) Real-time kinetics of gene activity in individual bacteria. Cell, 123, 1025–1036. [DOI] [PubMed] [Google Scholar]
- Golightly A., Wilkinson D.J. (2005) Bayesian inference for stochastic kinetic models using a diffusion approximation. Biometrics, 61, 781–788. [DOI] [PubMed] [Google Scholar]
- Gomez M.M. et al. (2016) The effects of time-varying temperature on delays in genetic networks. SIAM J. Appl. Dyn. Syst., 15, 1734–1752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta A., Rawlings J.B. (2014) Comparison of parameter estimation methods in stochastic chemical kinetic models: examples in systems biology. AIChE J., 60, 1253–1268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta C. et al. (2014) Modeling delay in genetic networks: from delay birth–death processes to delay stochastic differential equations. J. Chem. Phys., 140, 204108–204101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heron E.A. et al. (2007) Bayesian inference for dynamic transcriptional regulation; the hes1 system as a case study. Bioinformatics, 23, 2596–2603. [DOI] [PubMed] [Google Scholar]
- Hussain F. et al. (2014) Engineered temperature compensation in a synthetic genetic clock. Proc. Natl. Acad. Sci. USA, 111, 972–977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson N., Kotz S.I. (1985) Distributions in Statistics: Discrete Distributions V. 3. John Wiley & Sons, New York, NY. [Google Scholar]
- Kaern M. et al. (2005) Stochasticity in gene expression: from theories to phenotypes. Nat. Rev. Genet., 6, 451.. [DOI] [PubMed] [Google Scholar]
- Kepler T.B., Elston T.C. (2001) Stochasticity in transcriptional regulation: origins, consequences, and mathematical representations. Biophys. J., 81, 3116–3136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim J.K. et al. (2014) The validity of quasi-steady-state approximations in discrete stochastic simulations. Biophys. J., 107, 783–793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korenčič A. et al. (2012) The interplay of cis-regulatory elements rules circadian rhythms in mouse liver. PLoS One, 7, e46835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leier A. et al. (2014) Exact model reduction with delays: closed-form distributions and extensions to fully bi-directional monomolecular reactions. J. R. Soc. Interface, 11, 20140108.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis J. (2003) Autoinhibition with transcriptional delay: a simple mechanism for the zebrafish somitogenesis oscillator. Curr. Biol., 13, 1398–1408. [DOI] [PubMed] [Google Scholar]
- Mather W. et al. (2009) Delay-induced degrade-and-fire oscillations in small genetic circuits. Phys. Rev. Lett., 102, 068105.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McAdams H.H., Shapiro L. (1995) Circuit simulation of genetic networks. Science, 269, 650–656. [DOI] [PubMed] [Google Scholar]
- Megerle J.A. et al. (2008) Timing and dynamics of single cell gene expression in the arabinose utilization system. Biophys. J., 95, 2103–2115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monk N.A. (2003) Oscillatory expression of hes1, p53, and nf-κb driven by transcriptional time delays. Curr. Biol., 13, 1409–1413. [DOI] [PubMed] [Google Scholar]
- Norman T.M. et al. (2013) Memory and modularity in cell-fate decision making. Nature, 503, 481.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poovathingal S.K., Gunawan R. (2010) Global parameter estimation methods for stochastic biochemical systems. BMC Bioinformatics, 11, 414.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raj A., van Oudenaarden A. (2008) Nature, nurture, or chance: stochastic gene expression and its consequences. Cell, 135, 216–226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenfeld N. et al. (2005) Gene regulation at the single-cell level. Science, 307, 1962–1965. [DOI] [PubMed] [Google Scholar]
- Rosenfeld N. et al. (2006) A fluctuation method to quantify in vivo fluorescence data. Biophys. J., 91, 759–766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlicht R., Winkler G. (2008) A delay stochastic process with applications in molecular biology. J. Math. Biol., 57, 613–648. [DOI] [PubMed] [Google Scholar]
- Smith A.F., Roberts G.O. (1993) Bayesian computation via the Gibbs sampler and related Markov Chain Monte Carlo methods. J. R. Stat. Soc. Ser. B (Methodological), 55, 3–23. [Google Scholar]
- Smith S., Grima R. (2018) Single-cell variability in multicellular organisms. Nat. Commun., 9, 345.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stricker J. et al. (2008) A fast, robust and tunable synthetic gene oscillator. Nature, 456, 516.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taheri-Araghi S. et al. (2015) Cell-size control and homeostasis in bacteria. Curr. Biol., 25, 385–391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas P. et al. (2012) The slow-scale linear noise approximation: an accurate, reduced stochastic description of biochemical networks under timescale separation conditions. BMC Syst. Biol., 6, 39. doi: 10.1186/1752-0509-6-39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tierney L. (1994) Markov chains for exploring posterior distributions. Ann. Stat., 22, 1701–1728. [Google Scholar]
- Volfson D. et al. (2008) Biomechanical ordering of dense cell populations. Proc. Natl. Acad. Sci. USA, 105, 15346–15351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilkinson D.J. (2011) Stochastic Modelling for Systems Biology, 2nd edn. CRC Press. [Google Scholar]
- Yu J. et al. (2006) Probing gene expression in live cells, one protein molecule at a time. Science, 311, 1600–1603. [DOI] [PubMed] [Google Scholar]
- Zechner C. et al. (2014) Scalable inference of heterogeneous reaction kinetics from pooled single-cell recordings. Nat. Methods, 11, 197.. [DOI] [PubMed] [Google Scholar]
- Zimmer C. et al. (2015) Exploiting intrinsic fluctuations to identify model parameters. IET Syst. Biol., 9, 64–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.