Abstract
Epidemics may pose a significant dilemma for governments and individuals. The personal or public health consequences of inaction may be catastrophic; but the economic consequences of drastic response may likewise be catastrophic. In the face of these trade-offs, governments and individuals must therefore strike a balance between the economic and personal health costs of reducing social contacts and the public health costs of neglecting to do so. As risk of infection increases, potentially infectious contact between people is deliberately reduced either individually or by decree. This must be balanced against the social and economic costs of having fewer people in contact, and therefore active in the labor force or enrolled in school. Although the importance of adaptive social contact on epidemic outcomes has become increasingly recognized, the most important properties of coupled human-natural epidemic systems are still not well understood. We develop a theoretical model for adaptive, optimal control of the effective social contact rate using traditional epidemic modeling tools and a utility function with delayed information. This utility function trades off the population-wide contact rate with the expected cost and risk of increasing infections. Our analytical and computational analysis of this simple discrete-time deterministic strategic model reveals the existence of an endemic equilibrium, oscillatory dynamics around this equilibrium under some parametric conditions, and complex dynamic regimes that shift under small parameter perturbations. These results support the supposition that infectious disease dynamics under adaptive behavior change may have an indifference point, may produce oscillatory dynamics without other forcing, and constitute complex adaptive systems with associated dynamics. Implications for any epidemic in which adaptive behavior influences infectious disease dynamics include an expectation of fluctuations, for a considerable time, around a quasi-equilibrium that balances public health and economic priorities, that shows multiple peaks and surges in some scenarios, and that implies a high degree of uncertainty in mathematical projections.
Author summary
Epidemic response in the form of social contact reduction, such as has been utilized during the ongoing COVID-19 pandemic, presents inherent tradeoffs between the economic costs of reducing social contacts and the public health costs of neglecting to do so. Such tradeoffs introduce an interactive, iterative mechanism that adds complexity to an infectious disease system. Consequently, infectious disease modeling typically has not included dynamic behavior change that must address such a tradeoff. Here, we develop a theoretical strategic model that introduces lost or gained economic and public health utility through the adjustment of social contact rates with delayed information. This model produces an equilibrium, a point of indifference where the tradeoff is neutral, and at which a disease will be endemic for a long period of time. Under small perturbations, this model exhibits complex dynamic regimes, including oscillatory behavior, runaway exponential growth, and eradication. These dynamics suggest that for epidemic responses that rely on social contact reduction, secondary waves and surges with accompanied business and school re-closures and shutdowns may be expected, and that accurate projection under such circumstances is unlikely.
Introduction
Adapting to a changing landscape of risk during an infectious disease epidemic may pose a significant dilemma for a susceptible individual or for a governing body responsible for the health of susceptible individuals. On the one hand, changing behavior (e.g. through social distancing) can reduce the reproduction number (R0) of an epidemic and save many from death or morbidity [1, 2]. On the other hand, behavior change can reduce an individual’s ability to make a living or, for a group of people, can hamper or cause a recession in the economy through decreased production, sales, and investment and increased unemployment, inflation, and debt [3]. This dilemma introduces a behavior change trade-off for the decision-maker, a balancing act between epidemiological interests and economic interests.
There is growing interest in the role of behavior in infectious disease dynamics (see Funk et al., 2010 [4] for a general review). Behavior relevant to epidemic outcomes is known to change in response to perceived risk during epidemics (e.g. measles-mumps-rubella (MMR) vaccination choices [5], condom purchases in HIV-affected communities [6], and social distancing in influenza outbreaks [7] and during the ongoing COVID-19 pandemic [8]). Although behavior is difficult to measure, quantify, and predict [9], modelers have adopted a variety of strategies to investigate its role in epidemic outcomes. These strategies include agent-based modeling [10], network structures that model behavior as a social contagion process [11] or that replace central nodes when sick [12], and game theoretic descriptions of rational choice under changing incentives, as in the case of vaccination [7, 13, 14]. A common approach to incorporating behavior into epidemic models is to track co-evolving dynamics of behavior and infection [11, 15–17].
In epidemic response policy, it is typical to think of behavior change as an exogenously-induced intervention without considering associated incentives for the individual or the collective. Due to the interactive relationship between behavior and epidemic dynamics, adaptive behavior should instead be thought of as endogenous to an infectious disease system because it is, in part, a consequence of the prevalence of the disease, which in turn responds to changes in behavior [9, 18]. An epidemic system with adaptive behavior responds to the conditions it itself creates, and is thus a complex, adaptive system [19], subject to the properties and tendencies of such systems.
The interaction between behavioral incentives and epidemic dynamics introduces a negative feedback into the epidemic system. In an important early expansion of Kermack and McKendrick’s seminal Susceptible-Infectious-Removed (SIR) model [20], Capasso and Serio built a self-iterative epidemic model by making the transmission parameter (β) a negative function of the number of infected because “in the presence of a very large number of infectives the population may tend to reduce the number of contacts per unit time.” [21] A negative feedback such as this may lead to an endemic equilibrium [22]. This happens because, at low levels of prevalence, the cost of behavior change to avoid disease relative to the risk of infection may not be justified, even though the collective, public benefit in the long-term may be greater. Conversely, as prevalence increases, the probability of infection also increases, thus increasing incentives to adopt protective behavior [13]. If responses are based on outdated information, a negative feedback between prevalence and social contact can produce sustained oscillations in time-series data [23].
Such periodicity (i.e. multi-peak dynamics) has long been documented empirically in epidemiology [24, 25]. Periodicity can be driven by seasonal contact rate changes (e.g. when children are in school) [26], seasonality in the climate or ecology [27], sexual and social behavior change [23, 28], and host immunity cycling through new births of susceptibles or a decay of immunity over time. Some papers in nonlinear dynamics have studied delay differential equations in the context of epidemic dynamics and found periodic solutions as well [29]. Although it is atypical to include delay in modeling, delay is an important feature of epidemics. Delays of information acquisition, behavioral response, scientific investigation, and those inherent in natural biological processes can affect epidemic outcomes. In the ongoing COVID-19 pandemic, for example, there have been delays in the international recognition of the outbreak [30], delays in the identification of the virus, delays in the acquisition of reliable information on suspected and confirmed cases [31], and delays in the development and deployment of competent diagnostics [32].
Although infectious disease modelers have begun to incorporate adaptive behavior into their models, few studies in the literature capture the competing economic and public health incentives that drive delayed behavioral responses in both individual and group settings during epidemics [33, 34]. Here we develop a theoretical model using both discrete and continuous time and both SIR and SIS compartmental epidemic structures. The model, which is designed to be strategic rather than tactical (sensu Holling [35]), is adjusted on the principle of endogenous behavior change through an adaptive social-contact rate that can be thought of as either individually motivated or institutionally imposed. We introduce a novel utility function that motivates the population’s effective contact rate at a particular time period. This utility function is based on information about the epidemic size that may not be current. This leads to a time delay in the contact function that increases the complexity of the population dynamics of the infection. Results from the discrete-time model show that the system approaches an equilibrium in many cases, although small parameter perturbations can lead the dynamics to enter qualitatively distinct regimes. The analogous continuous-time model retains periodicities for some sets of parameters, but numerical investigation shows that the continuous time version is much better behaved than the discrete-time model. This behavior is similar to that in models of ecological population dynamics, and a useful mathematical parallel can be drawn between these systems.
Model specifications
SIS
To represent endogenous behavior change, we start with the classical discrete-time susceptible-infected-susceptible (SIS) model [20], which, when incidence is relatively small compared to the total population [36, 37], can be written in terms of the recursions
| (1) |
| (2) |
| (3) |
where at time t, St represents the number of susceptible individuals, It the infected individuals, and Nt the number of individuals that make up the population, which is assumed fixed in a closed population. We can therefore write N for the constant population size. Here γ, with 0 < γ < 1, is the rate of removal from I to S due to recovery. This model in its simplest form assumes random mixing, where the parameter b represents a composite of the average contact rate and the disease-specific transmissibility given a contact event. In order to introduce human behavior, we substitute for b a time-dependent bt, which is a function of both b0, the probability that disease transmission takes place on contact, and a dynamic social contact rate ct whose optimal value, , is the number of contacts per unit time that maximize utility for the individual. is determined at each time t as in economic epidemiological models [34], namely
| (4) |
where represents the optimal contact rate, defined as the number of contacts per unit time that maximize utility for the individual. Here, is a function of the number of infected in the population according to the perceived risks and benefits of social contacts, which we model as a utility function. We assume that there is a constant utility independent of contact, a utility loss associated with infection, and a utility derived from the choice of number of daily contacts with a penalty for deviating from the choice of contacts which would yield the most utility.
This utility function is assumed to take the form
| (5) |
Here U represents utility for an individual at time t given a particular number of contacts per unit time c, α0 is a constant that represents maximum potential utility achieved at a target contact rate . The second term, , is a concave function that represents the penalty for deviating from . The third term, , is the cost of infection (i.e. morbidity), α2, multiplied by the probability of infection over the course of the time unit. The time-delay Δ represents the delay in information acquisition and the speed of response to that information. We note that can be approximated by
| (6) |
when is small and We thus assume is small, that is, prevalence is low, and approximate U(c) in Eq 5 using Eq 6. Eq 5 assumes a strictly negative relationship between number of infecteds and contact.
We assume an individual or government will balance the cost of infection, the probability of infection, and the cost of deviating from the target contact rate to select an optimal contact rate , namely the number of contacts, which takes into account the risk of infection and the penalty for deviating from the target contact rate. This captures the idea that individuals trade off how many people they want to interact with versus their risk of becoming infected, or that authorities want to reopen the economy during a pandemic and have to trade off morbidity and mortality from increasing infections with the need to allow additional social contacts to help the economy restart. This optimal contact rate can be calculated by finding the maximum of U with respect to c from Eq 5 with substitution from Eq 6, namely
| (7) |
Differentiating, we have
| (8) |
which vanishes at the optimal contact rate, c*, which we write as to show its dependence on time. Then
| (9) |
which we assume to be positive. Therefore, total utility will decrease as It increases and also decreases. Utility is maximized at each time step, rather than over the course of lifetime expectations. In addition, Eq 9 assumes a strictly negative relationship between number of infecteds at time t − Δ and . While behavior at high degrees of prevalence has been shown to be non-linear and fatalistic [38, 39], in this model, prevalence (i.e., ) is assumed to be small, consistent with Eq 6.
We introduce the new parameter , so that
| (10) |
We can now rewrite the recursion from Eq 2, using Eq 4 and replacing ct with as defined by Eq 10, as
| (11) |
When Δ = 0 and there is no time delay, f(⋅) is a cubic polynomial, given by
| (12) |
SIR
For the susceptible-infected-removed (SIR) version of the model, we include the removed category and write the (discrete-time) recursion system as
| (13) |
| (14) |
| (15) |
where Rt = N − It − St, with b0 the baseline contact rate and specified by Eq 10. With bt = b, say, and not changing over time, Eqs 13–15 form the discrete-time version of the classical Kermack-McKendrick SIR model [20]. The inclusion of the removed category entails that is the only equilibrium of the system Eqs 13–15; unlike the SIS model, there is no equilibrium with infecteds present. In general, since includes the delay Δ, the dynamic approach to is expected to be quite complex. Numerical analysis of this SIR model shows strong similarity between the SIS and SIR models for several hundred time steps before the SIR model converges to . In the section “Numerical Iteration and Continuous-Time Analog” we compare the numerical iteration of the SIS (Eq 11) and SIR (Eqs 13–15) and integration of the continuous-time (differential equation) versions of the SIS and SIR models.
Analytical results
Equilibria
To determine the dynamic trajectories of (11) without time delay, we first solve for the fixed point(s) of the recursion (11) (i.e., value or values of I such that f(It+1) = It = It−Δ). That is, we solve
| (16) |
From Eq 16, it is clear that I = 0 is an equilibrium as no new infections can occur in the next time-step if none exist in the current one. This is the disease-free equilibrium denoted by . Other equilibria are the solutions of
| (17) |
namely
| (18) |
We label the solution with the + sign I* and the one with the − sign . I* > 0 but I* ≤ N if 4αγ/Nb0 ≤ 0, which is impossible under our assumptions that α and γ are positive. Hence I* is not feasible. Further, under these same conditions, , and if
| (19) |
It is important to note that under these conditions is an equilibrium of the recursion (11) for any Δ ≥ 0. Recall that for the SIR version of this model the only equilibrium is .
Stability of the equilibria
Assessing global asymptotic stability in epidemic models is an important task of mathematical epidemiology [40, 41]. The three equilibria of the SIS recursion (11) are qualitatively different. corresponds to a disease-free population; I* is greater than N and is therefore not feasible; is the only positive feasible equilibrium if (this is equivalent to R0 > 1, where ) and is, therefore, the most interesting for the asymptotic stability behavior of the epidemic. Mathematical stability analysis of recursion (11) is complicated because of the delay term Δ. However, from (11), if , the disease-free equilibrium is locally unstable, and in this case is indeed feasible.
Local stability of in (18) is discussed in detail in S1 Appendix. First, in the absence of delay (i.e., Δ = 0), is locally stable if , and the condition for this to hold when is legitimate is
| (20) |
If inequalities (20) and hold, then is locally stable. However, even if both of these inequalities hold, the number of infecteds may not converge to . It is well known that iterations of discrete-time recursive relations, of which (12) is an example (i.e., with Δ = 0), may produce cycles or chaos depending on the parameters and the starting frequency I0 of infecteds.
Numerical iteration and continuous-time analog
We begin with numerical analysis of the discrete-time SIS recursion (11), which includes the delay parameter Δ. Local stability properties of the equilibrium state , with , are shown in the Appendix under the assumption , which also entails that the disease-free equilibrium is locally unstable. In the recursion (11), the number of infecteds at time t will not, in general, be integers, but can be interpreted as the expected number of infected in the population. Further, the dynamics of It under such a recursion can be very sensitive to the starting condition I0, the size of the time delay Δ, and the parameters: and α. The local stability of , namely whether It converges to from a starting number of infecteds close to , may tell you little about the actual trajectory of It from other starting conditions.
Table 1 reports an array of dynamic trajectories without delay (Δ = 0) for some choices of parameters. In seven cases, I0 = 1, and in two cases the numerical iteration of Eq 12 was initiated with I0 ≠ 1. The first three rows show three sets of parameters for which the equilibrium values of are very similar but the trajectories of It are different: a two-point cycle, a four-point cycle, and apparently chaotic cycling above and below . In all of these cases, . Clearly the dynamics are sensitive to the target contact rate in these cases. The fourth and eighth rows show that It becomes unbounded (tends to + ∞) from I0 = 1, but a two-point cycle is approached if I0 is close enough to in these cases. For the parameters in the ninth row, if I0 is close enough to there is damped oscillation into : here . In the case marked *, is locally stable and with a large enough initial number of infecteds, there is damped oscillatory convergence to . In the case marked **, with I0 = 1 the number of infecteds becomes unbounded, but in this case, is locally unstable (), and starting from I0 close to a stable two-point cycle is approached. S5 Fig is a bifurcation diagram for recursion (11) with Δ = 0 and the other parameters from the first three lines of Table 1. As increases, first there is convergence to , then period doubling to chaos and finally passage to negative infinity.
Table 1. Some results for dynamics of infection with Δ = 0.
| Parameters | Equilibrium | |||||
|---|---|---|---|---|---|---|
| N | b0 | γ | α | Dynamics | ||
| 250 | 0.1 | 0.1 | 0.2 | 0.1 | 240.371 | I0 = 1: two-point cycle 110.436, 339.564 |
| 250 | 0.1 | 0.1 | 0.205 | 0.1 | 240.799 | I0 = 1: four-point cycle above and below |
| 250 | 0.1 | 0.1 | 0.209 | 0.1 | 241.115 | I0 = 1: apparent chaos around |
| 250 | 0.5 | 0.1 | 0.1 | 0.1 | 227.639 |
I0 = 1: becomes unbounded. I0 = 226: converges to two-point cycle. |
| 250 | 0.115 | 0.1 | 0.1 | 0.1 | 203.375 | I0 = 1: overshoots , then decreases to |
| 350 | 0.1 | 0.1 | 0.1 | 0.1 | 290.839 | I0 = 1: overshoots , then decreases to |
| 1,000 | 0.1 | 0.1 | 0.1 | 0.1 | 900.000 | I0 = 1: damped oscillation to |
| 1,100 | 0.1 | 0.1 | 0.1 | 0.1 | 995.119 |
I0 = 1: It becomes unbounded I0 = 990: damped oscillation to |
| 10,000 | 0.05 | 0.08 | 0.0015 | 0.375 | 35.718 | I0 = 1: monotone convergence to |
Stability analysis of the SIS model is more complicated when Δ ≠ 0, and in S1 Appendix we outline the procedure for local analysis of the recursion (11) near . Local stability is sensitive to the delay time Δ as can be seen from the numerical iteration of (11) for the specific set of parameters shown in Table 2. Some analytical details related to Table 2 are in S1 Appendix.
Table 2. The effect of the delay, Δ, on dynamics of infecteds*.
| Δ | Outcome |
|---|---|
| 0 | Monotone convergence to |
| 1 | Damped oscillation to |
| 2 | locally unstable; I0 < 72 bounded oscillation; I0 > 73 unbounded oscillation |
| 3 | locally unstable; collapse (−∞) |
| 4 | locally unstable; collapse (−∞) |
* In all cases, N = 10, 000, b0 = 0.05, γ = 0.08, , α = 0.375, . I0 = 1 unless stated.
The fifth and sixth rows of Table 1 exemplify another interesting dynamic starting from I0 = 1. It becomes larger than (overshoots) and then converges monotonically down to ; in each case . For the parameters in the seventh row, there is oscillatory convergence to from I0 = 1 (), while in the last row there is straightforward monotone convergence to . The dependence of the dynamics for recursion (11) on the delay Δ and target contact rate is illustrated for Δ = 0, 1, 2 in S6 Fig. The bifurcation diagram for each Δ shows the shift, summarized in Table 2, from convergence to period doubling, chaos, and negative infinity, which occurs for smaller values of as Δ increases.
A continuous-time analog of the discrete-time recursion (11), in the form of a differential equation, substitutes dI/dt for It+1 − It in (11). We then solve the resulting delay differential equation numerically using the VODE differential equation integrator in SciPy [42, 43] (source code available at https://github.com/yoavram/SanJose). Using the parameters in Table 2, Figs 1–4 compare the effect of the parameters on the trajectories of the discrete-time and continuous-time SIS model specified in (11). The number of time steps used in the computations illustrated in these figures is less than 250 in each case. In Fig 1 the delay ranges from Δ = 0 to Δ = 5, while in Fig 2 the delay is Δ = 2 and Figs 3 and 4 have delay Δ = 3. In the supplementary material S1–S4 Figs, the discrete-time and continuous-time recursions of the SIR model are compared for short and much longer durations.
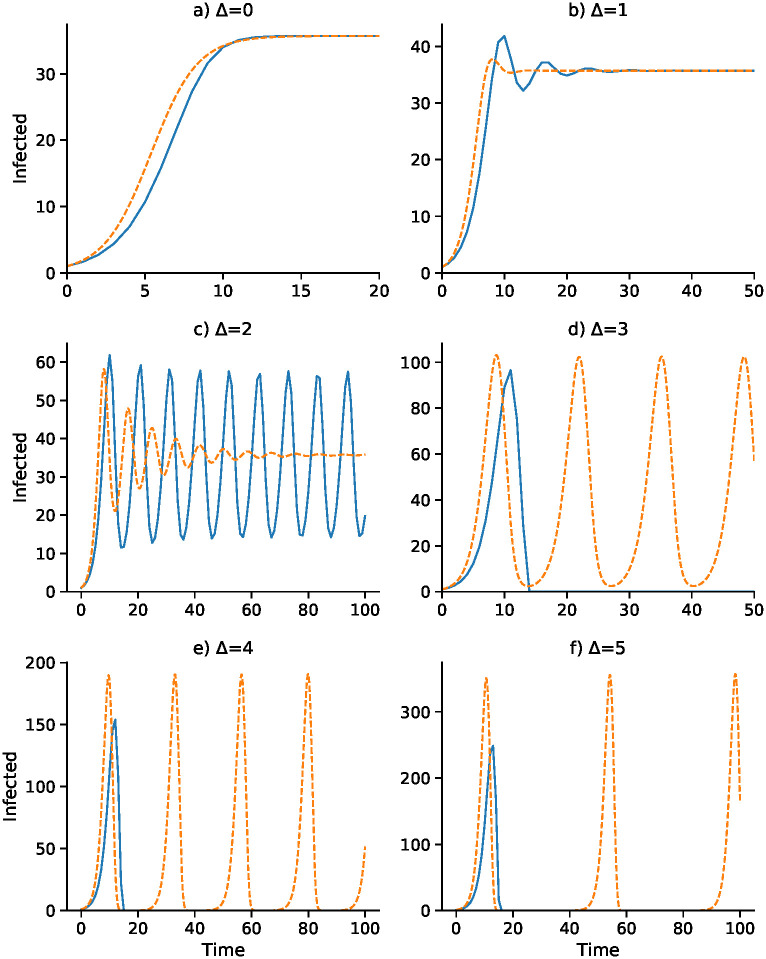
Fig 1. Discrete-time SIS (blue) and continuous-time SIS (orange) dynamics for delays Δ = 0 to Δ = 5.
N = 10, 000, b0 = 0.05, γ = 0.08, , α = 0.375, and I0 = 1. Here the epidemic equilibrium is .
Fig 4. Effect of removal rate γ on dynamics with delay Δ = 3.
Discrete- and continuous-time results are in blue and orange, respectively. Other parameters as in Fig 1 with I0 = 1.
Fig 2. Effect of initial number of infecteds I0 on the dynamics for delay Δ = 2.
Discrete- and continuous-time results are in blue and orange, respectively. Other parameters as in Fig 1. As in Fig 1, .
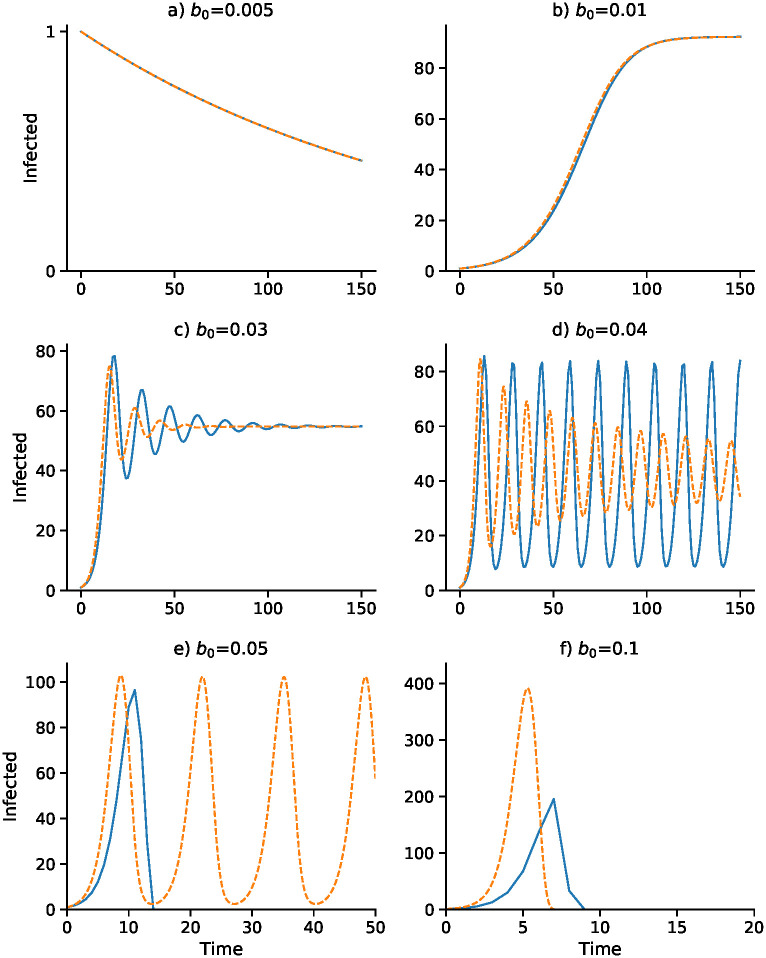
Fig 3. Effect of baseline contact rate b0 on dynamics with delay Δ = 3.
Other parameters as in Fig 1 with I0 = 1. Discrete- and continuous-time results are in blue and orange, respectively. Note that α changes with b0 as α = b0 α2/2α1: (A) α = 0.0375; (B) α = 0.075; (C) α = 0.225; (D) α = 0.3; (E) α = 0.375; (F) α = 0.75.
In Fig 1, with no delay (Δ = 0) and a one-unit delay (Δ = 1), the discrete and continuous dynamics are very similar, both converging to . However, with Δ = 2 the differential equation oscillates into while the discrete-time recursion enters a regime of inexact cycling around , which appears to be a state of chaos. For Δ = 3 and Δ = 4, the discrete recursion “collapses”. In other words, It becomes negative and appears to go off to −∞; in Fig 1, this is cut off at I = 0. The continuous version, however, in these cases enters a stable cycle around . It is important to note that in Fig 1 for each panel the initial frequency was I0 = 1 infected individual. For Δ = 2, for example, with an initial value of I0 higher than about 73, instead of the inexact cycle, which is approached for smaller values of I0, the discrete recursion goes off and becomes negatively unbounded. This dependence of the dynamics on I0 is illustrated for Δ = 2 in Fig 1, where the continuous-time version of the SIS model (11) oscillates into . Two expanded views of the inexact cycling seen for I0 = 1 in Fig 1 are presented in S7 Fig.
Figs 3 and 4 focus on a delay of Δ = 3 and show the dependence of the discrete- and continuous-time dynamics on parameters b0 and γ, respectively. For b0 increasing from 0.005 to 0.05 the pattern of trajectories from I0 = 1 is remarkably similar to that for γ decreasing from 0.75 to 0.1. First, both converge to , then both converge to , then there is stable oscillation into . For b0 = 0.04 and γ = 0.2, however, the continuous trajectory enters a stable cycle while the discrete trajectory cycles inexactly around . For higher values of I0, however, the discrete-time trajectory may become unbounded. Finally, for b0 = 0.05 and γ = 0.75, the discrete-time trajectory goes to −∞, but is shown stopped at 0, while the continuous case develops a stable cycle.
The discrete- and continuous-time trajectories for the SIR model (13–15) were studied with the same parameters as used in Figs 1–4. Each computation is presented twice: first, for the same length of time as the SIS discrete- and continuous-time in Figs 1–4, and second, for up to 5,000 time units. The trajectories are shown in the Supplementary material, where S1–S4 Figs show short and longer run times. For the longer run times, as expected, in both discrete-time and continuous-time versions of the SIR model, there are eventually no infecteds. Comparing the short-run and long-run figures, the former are not good predictors of the latter in the SIR setting. The short-run behavior of the discrete-time model usually involves a great deal of cycling, which is difficult to see on the longer time scales. S8 Fig compares the SIR and SIS dynamics for the model in Fig 2A with I0 = 1 (see also S7 Fig), with panels A and B illustrating the short term and panels C and D the longer term dynamics. Panels A and B appear to show convergence to , but in panels C an D, after about 500 time units, both discrete- and continuous-time versions show the number of infected declining to zero.
It is worth noting that if the total population size of N decreases over time, for example, if we take N(t) = Nexp(−zt), with , then the short-term dynamics of the SIS model in (11) begins to closely resemble the SIR version. This is illustrated in S9 Fig, where are, as in S8 Fig, the same as in Fig 2A. With N decreasing to zero, both S and I will approach zero in the SIS model, which explain its apparent similarity to the SIR model.
Discussion
This simple epidemic model with adaptive social contact produces two possible equilibria, one with zero infecteds, where the disease is eradicated, and one between zero and N, the population size, where the disease is endemic. These equilibria are locally stable under different conditions. Dynamics produced by this model are complex and subject to regime shifts across thresholds in the initial conditions and parameter settings. These dynamics include damped oscillation to the equilibrium, periodic oscillation, chaotic oscillation, and regression to positive or negative infinity. Our stability analysis is carried out in the neighborhood of the equilibria. Although global asymptotic stability analysis of some epidemic models has been possible [29, 40, 41], the inclusion of the delay Δ seems to make global analysis extremely difficult in general [29].
Our model makes a number of simplifying assumptions. We assume that all individuals in the population will respond in the same fashion to government policy and that governments or individuals choose a uniform contact rate according to an optimized utility function, which is homogeneous across all individuals in the population. This contact rate will, in practice, vary across the population according to a variety of drivers including, but not limited to, disease state, cultural and religious practices, political affiliation, housing density, occupation, risk tolerance, and age. Finally, we assume that the utility function is symmetric around the optimal number of contacts so that increasing or decreasing contacts above or below the target contact rate, respectively, yield the same reduction in utility. These assumptions allowed us to create the simplest possible model that includes adaptive behavior trade-offs and time delay.
Convergence to an endemic equilibrium when economic and public health trade-offs are included in an epidemic model is consistent with both theory [22] and other models [33]. Our results show certain parameter sets can lead to limit-cycle dynamics, consistent with other behavior change models [23, 44] and negative feedback mechanisms with time delays [45, 46]. This is because the system is reacting to conditions that were true in the past, but not necessarily true in the present. The time scale and the meaning of the delay, Δ, can influence the qualitative dynamics of the epidemic and, under certain conditions, can lead to a stable cyclic epidemic even in the continuous-time version of our model. We note that these distinct dynamical trajectories as seen in our computational experiments come from a purely deterministic recursion. This means that oscillations and even erratic, near-chaotic dynamics and collapse in an epidemic may not necessarily be due to seasonality, complex agent-based interactions, changing or stochastic parameter values, demographic change, host immunity, or socio-cultural idiosyncrasies. In our discrete-time model, there is the added complexity that the non-zero equilibrium may be locally stable but not attained from a wide range of initial conditions, including the most natural one, namely a single infected individual.
This dynamical behavior in number of infecteds can result from mathematical properties of a simple deterministic system with homogeneous endogenous behavior change, similar to complex population dynamics of biological organisms [47]. The mathematical consistency with population dynamics suggests a parallel in ecology, that the indifference point for human behavior functions in a similar way to a carrying capacity in ecology, below which a population will tend to grow and above which a population will tend to shrink. For example, the Ricker Equation [48], commonly used in population dynamics to describe the growth of fish populations, exhibits similar complex dynamics and qualitative state thresholds. These ecological models are typically structured mathematically in discrete time, while continuous time models are more commonly used in modeling epidemics. There is no a priori reason to prefer the continuous time framework over that in discrete time. It is not clear which strategic approach is more realistic as transmission from an infected to a susceptible individual may happen at anytime, but epidemiologists do tend to frame their thinking in discrete time-steps of days and weeks.
Observed epidemic curves of many transient disease outbreaks typically inflect and go extinct, as opposed to this model that may oscillate perpetually or converge monotonically or cyclically to an endemic disease equilibrium. Including institutional and public efforts that are further incentivized to eradicate, rather than to optimize short-term utility trade-offs, would alter the dynamics to look more like real-world epidemic curves. Beyond infectious diseases that remain endemic to society, outbreaks may also flare up once or multiple times, such as the double-peaked outbreaks of SARS in three countries in 2003 [49], and surges in fluctuations in COVID-19 cases globally in 2020 [50]. There may be many causes for such double-peaked outbreaks, one of which may be a lapse in behavior change after the epidemic begins to die down due to decreasing incentives [11], as represented in our simple theoretical model. This is consistent with findings that voluntary vaccination programs suffer from decreasing incentives to participate as prevalence decreases [51, 52]. A recent analysis [53] that incorporated epidemic-like transmission of sentiment opposed to vaccination against an infection found that the transient dynamics of the anti-vaccine sentiment could induce complex dynamics of the disease epidemic. However, this analysis did not incorporate a time delay in the manifestation of the anti-vaccine sentiment. The relation between the spread of the sentiment and of the infection is, therefore, somewhat different from that seen here between an adaptive contact rate and the epidemic dynamics.
One of the responsibilities of infectious disease modelers is to predict and project forward what epidemics will do in the future in order to better assist in the proper and strategic allocation of preventative resources. However, there are limits to the power and precision of such modeling. In our model, allowing for adaptive behavior change leads to a system that is qualitatively sensitive to small differences in values of key parameters. These parameters are very hard to measure precisely; they change depending on the disease system and context and their inference is generally subject to large errors. Further, we don’t know how policy-makers weight the economic trade-offs against the public health priorities (i.e., the ratio between α1 and α2 in our model) to arrive at new policy recommendations. Geographic and/or cultural variation in our parameter (and concomitant variation in the delay Δ) are likely to affect how epidemic dynamics are affected by such trade-offs.
In our model, complex dynamic regimes occur more often when there is a time delay. If behavior change arises from fear and fear is triggered by high local mortality and high local prevalence, such delays are biologically inherent because death and incubation periods are lagging epidemiological indicators. Lags, whether social, environmental, or biological, mean that people can respond inappropriately to an unfolding epidemic crisis, but they also mean that people can abandon protective behaviors prematurely as conditions improve. Developing approaches to reduce lags or to incentivize protective behavior throughout the duration of any lag introduced by the natural history of the infection (or otherwise) should be a priority in applied research. Policy-makers should also consider the benefit of the long-term utility of early-stage overreaction to outbreaks and consider overriding short-term incentives. In light of the COVID-19 crisis, understanding endogenous delayed behavior change and economic incentives is of crucial importance to outbreak response and epidemic management. We anticipate further developments along these lines that could incorporate long incubation periods and other delays, recognition of asymptomatic transmission, influential heterogeneous drivers, and meta-population dynamics of simultaneous, connected epidemics.
Supporting information
Conditions are given for various values of the delay time Δ and the parameters in Table 2.
(PDF)
Parameters are the same as in Fig 1. Panels A–F represent shorter times and G–L longer times. For Δ = 3, 4, 5, the discrete-time trajectories are stopped at I = 0, as they go off to −∞. The continuous-time cases all converge to zero infecteds.
(TIF)
Discrete-time (blue) and continuous-time (orange) trajectories are similar to the SIS graphs. Parameters as in Fig 2. Panels A–D represent shorter time and E–H longer times.
(TIF)
Discrete-time (blue) and continuous-time (orange) trajectories are similar to the SIS graphs in Fig 3. Parameters as in Fig 3. Panels A–F represent shorter times and G–L longer times.
(TIF)
Note the compression of the cycles seen in Fig 4 and the earlier decline to zero infecteds. Panels A–E represent shorter times and F–J longer times. Parameters as in Fig 4.
(TIF)
The dotted horizontal line delineates the total population size (N = 250). Dynamics exhibit convergence to the endemic equilibrium (including monotonic, overshooting, and damped oscillation) and period doubling to chaos, followed by passage to negative infinity.
(TIF)
Dynamics progress from convergence to chaos to negative infinity. As Δ increases, transitions between dynamic regimes begin at smaller values of .
(TIF)
(A): Return map showing more than one It+1 value for each value of It. (B): Comparing the “elliptical” dynamics in part (A) with continuous-time damped oscillation (orange) to equilibrium . Other parameters as in Fig 2. This figure is the same as Fig 2A.
(TIF)
Note the apparent approach to in panels A and B. Both discrete-time and continuous-time trajectories eventually approach R = N for longer times as in panel C.
(TIF)
This uses the same parameters as in Fig 2 but sets N = N(t) = exp(−zt), where with γ = 0.08, b0 = 0.05, . Note the similarity to S8 Fig, panels A and B.
(TIF)
Acknowledgments
The authors thank Kaleda Krebs Denton and W. Brian Arthur for helpful comments on an earlier draft of the manuscript.
Data Availability
All relevant data are within the manuscript and its Supporting information files.
Funding Statement
This research was supported in part by the Morrison Institute for Population and Research Studies (morrisoninstitute.stanford.edu) (MWF), by Israel Science Foundation grants 552/19 and 3811/19 (isf.org.il) (YR), and by a Graduate Research Fellowship from the National Science Foundation #2015160091 (nsf.gov) (RFA). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Bauch CT, Galvani AP. Social factors in epidemiology. Science. 2013;342(6154):47–49. 10.1126/science.1244492 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Ferguson N. Capturing human behaviour. Nature. 2007;446(7137):733–733. 10.1038/446733a [DOI] [PubMed] [Google Scholar]
- 3. Eichenbaum MS, Rebelo S, Trabandt M. The macroeconomics of epidemics National Bureau of Economic Research. 2020. [Google Scholar]
- 4. Funk S, Salathe M, Jansen VAA. Modelling the influence of human behaviour on the spread of infectious diseases: a review. Journal of The Royal Society Interface. 2010;750:1247–1256. 10.1098/rsif.2010.0142 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Reluga TC, Bauch CT, Galvani AP. Evolving public perceptions and stability in vaccine uptake. Mathematical Biosciences. 2006;204(2):185–198. 10.1016/j.mbs.2006.08.015 [DOI] [PubMed] [Google Scholar]
- 6. Ahituv A, Hotz VJ, Philipson T. The responsiveness of the demand for condoms to the local prevalence of AIDS. Journal of Human Resources. 1996; p. 869–897. 10.2307/146150 [DOI] [Google Scholar]
- 7. Reluga TC. Game theory of social distancing in response to an epidemic. PLoS Computational Biology. 2010;6(5):e1000793 10.1371/journal.pcbi.1000793 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Lewnard JA, Lo NC. Scientific and ethical basis for social-distancing interventions against COVID-19. The Lancet Infectious Diseases. 2020;. 10.1016/S1473-3099(20)30190-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Funk S, Bansal S, Bauch CT, Eames KT, Edmunds WJ, Galvani AP, et al. Nine challenges in incorporating the dynamics of behaviour in infectious diseases models. Epidemics. 2015;10:21–25. 10.1016/j.epidem.2014.09.005 [DOI] [PubMed] [Google Scholar]
- 10.Bobashev GV, Goedecke DM, Yu F, Epstein JM. A hybrid epidemic model: combining the advantages of agent-based and equation-based approaches. In: Simulation Conference, 2007 Winter. IEEE; 2007. p. 1532–1537.
- 11. Epstein JM, Parker J, Cummings D, Hammond RA. Coupled contagion dynamics of fear and disease: mathematical and computational explorations. PLoS One. 2008;3(12):e3955 10.1371/journal.pone.0003955 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Scarpino SV, Allard A, Hébert-Dufresne L. The effect of a prudent adaptive behaviour on disease transmission. Nature Physics. 2016;12(11):1042 10.1038/nphys3832 [DOI] [Google Scholar]
- 13. Cornforth DM, Reluga TC, Shim E, Bauch CT, Galvani AP, Meyers LA. Erratic Flu Vaccination Emerges from Short-Sighted Behavior in Contact Networks. PLoS Computational Biology. 2011;7(1):e1001062 10.1371/journal.pcbi.1001062 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Reluga TC, Galvani AP. A general approach for population games with application to vaccination. Mathematical Biosciences. 2011;230(2):67–78. 10.1016/j.mbs.2011.01.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Funk S, Gilad E, Watkins C, Jansen VAA. The spread of awareness and its impact on epidemic outbreaks. Proceedings of the National Academy of Sciences. 2009;106(16):6872–6877. 10.1073/pnas.0810762106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Wang Z, Andrews MA, Wu ZX, Wang L, Bauch CT. Coupled disease–behavior dynamics on complex networks: A review. Physics of Life Reviews. 2015;15:1–29. 10.1016/j.plrev.2015.07.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Metz JAJ, Diekmann O. The Dynamics of Physiologically Structured Populations vol. 68 of Lecture Notes in Biomathematics. Berlin: Springer-Verlag; 1986. [Google Scholar]
- 18. Arthur RF, Gurley ES, Salje H, Bloomfield LS, Jones JH. Contact structure, mobility, environmental impact and behaviour: the importance of social forces to infectious disease dynamics and disease ecology. Philosophical Transactions of the Royal Society B: Biological Sciences. 2017;372(1719):20160454 10.1098/rstb.2016.0454 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Holland JH. Hidden order: How adaptation builds complexity. Basic Books. 1995. [Google Scholar]
- 20. Kermack WO, McKendrick G. A contribution to the mathematical theory of epidemics In: Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. vol. 115 The Royal Society; 1927. p. 700–721. [Google Scholar]
- 21. Capasso V, Serio G. A generalization of the Kermack-McKendrick deterministic epidemic model. Mathematical Biosciences. 1978;421:43–61. 10.1016/0025-5564(78)90006-8 [DOI] [Google Scholar]
- 22. Philipson T. Economic epidemiology and infectious diseases. Handbook of Health Economics. 2000;1:1761–1799. 10.1016/S1574-0064(00)80046-3 [DOI] [Google Scholar]
- 23. d’Onofrio A, Manfredi P. Information-related changes in contact patterns may trigger oscillations in the endemic prevalence of infectious diseases. Journal of Theoretical Biology. 2009;256(3):473–478. 10.1016/j.jtbi.2008.10.005 [DOI] [PubMed] [Google Scholar]
- 24. Hethcote HW, Levin SA. Periodicity in epidemiological models In: Applied Mathematical Ecology. Springer; 1989. p. 193–211. [Google Scholar]
- 25. Hethcote HW, Yorke JA. Gonorrhea transmission dynamics and control. vol. 56 Springer; 2014. [DOI] [PubMed] [Google Scholar]
- 26. Fine PE, Clarkson JA. Measles in England and Wales—I: an analysis of factors underlying seasonal patterns. International Journal of Epidemiology. 1982;11(1):5–14. 10.1093/ije/11.1.5 [DOI] [PubMed] [Google Scholar]
- 27. Bouma MJ, Pascual M. Seasonal and interannual cycles of endemic cholera in Bengal 1891–1940 in relation to climate and geography In: The Ecology and Etiology of Newly Emerging Marine Diseases. Springer; 2001. p. 147–156. [Google Scholar]
- 28. Althouse BM, Hébert-Dufresne L. Epidemic cycles driven by host behaviour. Journal of The Royal Society Interface. 2014;11(99):20140575 10.1098/rsif.2014.0575 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Busenberg SN, Cooke KL. Periodic solutions of delay differential equations arising in some models of epidemics In: Applied Nonlinear Analysis. Elsevier; 1979. p. 67–78. [Google Scholar]
- 30. Gu E, Li L. Crippled community governance and suppressed scientific/professional communities: A critical assessment of failed early warning for the COVID-19 outbreak in China. Journal of Chinese Governance. 2020:1–18. [Google Scholar]
- 31. Kretzschmar ME, Rozhnova G, Bootsma M, van Boven M, van de Wijgert J, et al. Impact of delays on effectiveness of contact tracing strategies for COVID-19: a modelling study. The Lancet Public Health. 2020;5(8):452–459. 10.1016/S2468-2667(20)30157-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Sharfstein JM, Becker SJ, Mello MM. Diagnostic testing for the novel coronavirus. Journal of the American Medical Association. 2020;323(15):1437–1438. 10.1001/jama.2020.3864 [DOI] [PubMed] [Google Scholar]
- 33. Perrings C, Castillo-Chavez C, Chowell G, Daszak P, Fencihel EP, Finnoff D, et al. Merging economics and epidemiology to improve the prediction and management of infectious disease. EcoHealth. 2014;11:464–475. 10.1007/s10393-014-0963-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Fenichel EP, Castillo-Chavez C, Ceddia MG, Chowell G, Parra PAG, Hickling GJ, et al. Adaptive human behavior in epidemiological models. Proceedings of the National Academy of Sciences. 2011;108(15):6306–6311. 10.1073/pnas.1011250108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Holling CS. The strategy of building models of complex ecological systems. Systems Analysis in Ecology. 1966; p. 195–214. 10.1016/B978-1-4832-3283-6.50014-5 [DOI] [Google Scholar]
- 36. Keeling MJ, Rohani P. Modeling infectious diseases in humans and animals. Princeton University Press; 2008. [Google Scholar]
- 37. Finkenstädt BF, Grenfell BT. Time series modelling of childhood diseases: a dynamical systems approach. Journal of the Royal Statistical Society: Series C (Applied Statistics). 2000;49(2):187–205. [Google Scholar]
- 38. Auld MC. Choices, beliefs, and infectious disease dynamics. Journal of Health Economics. 2003;22(3):361–377. 10.1016/S0167-6296(02)00103-0 [DOI] [PubMed] [Google Scholar]
- 39. Bonds MH, Keenan DD, Leidner AJ, Rohani P. Higher disease prevalence can induce greater sociality: a game theoretic coevolutionary model. Evolution. 2005;59(9):1859–1866. 10.1111/j.0014-3820.2005.tb01056.x [DOI] [PubMed] [Google Scholar]
- 40. Buonomo B, d’Onofrio A, Lacitignola D. Global stability of an SIR epidemic model with information dependent vaccination. Mathematical Biosciences. 2008;216(1):9–16. 10.1016/j.mbs.2008.07.011 [DOI] [PubMed] [Google Scholar]
- 41. Li MY, Muldowney JS. Global stability for the SEIR model in epidemiology. Mathematical Biosciences. 1995;125(2):155–164. 10.1016/0025-5564(95)92756-5 [DOI] [PubMed] [Google Scholar]
- 42. Virtanen P, Gommers R, Oliphant TE, Haberland M, Reddy T, Cournapeau D, et al. SciPy 1.0: fundamental algorithms for scientific computing in Python. Nature Methods. 2020;17(3):261–272. 10.1038/s41592-019-0686-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Zulko. Scipy-based delay differential equation (dde) solver. https://pypi.org/project/ddeint; 2019.
- 44. Wang W. Epidemic models with nonlinear infection forces. Mathematical Biosciences & Engineering. 2006;3(1):267 10.3934/mbe.2006.3.267 [DOI] [PubMed] [Google Scholar]
- 45. May RM. Time-delay versus stability in population models with two and three trophic levels. Ecology. 1973;54(2):315–325. 10.2307/1934339 [DOI] [Google Scholar]
- 46. Beddington JR, May RM. Time delays are not necessarily destabilizing. Mathematical Biosciences. 1975;27(1-2):109–117. 10.1016/0025-5564(75)90028-0 [DOI] [Google Scholar]
- 47. May RM. Simple mathematical models with very complicated dynamics. Nature. 1976;261(5560):459 10.1038/261459a0 [DOI] [PubMed] [Google Scholar]
- 48. Ricker WE. Stock and recruitment. Journal of the Fisheries Board of Canada. 1954;11(5):559–623. 10.1139/f54-039 [DOI] [Google Scholar]
- 49. Wallinga J, Teunis P. Different epidemic curves for severe acute respiratory syndrome reveal similar impacts of control measures. American Journal of Epidemiology. 2004;1606:509–516. 10.1093/aje/kwh255 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.World Health Organization (WHO). Coronavirus disease (2019): situation report, 155. https://apps.who.int/iris/handle/10665/332855.
- 51. Geoffard PY, Philipson T. Rational epidemics and their public control. International Economic Review. 1996; 37(3): 603–624. 10.2307/2527443 [DOI] [Google Scholar]
- 52. Bauch CT, Galvani AP, Earn DJD. Group interest versus self-interest in smallpox vaccination policy. Proceedings of the National Academy of Sciences of the United States of America. 2003;100(18):10564–10567. 10.1073/pnas.1731324100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Mehta RS, Rosenberg NA. Modeling anti-vaccine sentiment as a cultural pathogen. Evolutionary Human Science. 2020;2:e21 10.1017/ehs.2020.17 [DOI] [PMC free article] [PubMed] [Google Scholar]