Luminescent Surfaces with Tailored Angular Emission for Compact Dark-Field Imaging Devices

Abstract

Dark-field microscopy is a standard imaging technique widely employed in biology that provides high image contrast for a broad range of unstained specimens¹. Unlike bright-field microscopy, it accentuates high spatial frequencies and can therefore be used to emphasize and resolve small features. However, the use of dark-field microscopy for reliable analysis of blood cells, bacteria, algae, and other marine organisms often requires specialized, bulky microscope systems, and expensive additional components, such as dark-field-compatible objectives or condensers^2,3. Here, we propose to simplify and downsize dark-field microscopy equipment by generating the high-angle illumination cone required for dark field microscopy directly within the sample substrate. We introduce a luminescent photonic substrate with a controlled angular emission profile and demonstrate its ability to generate high-contrast dark-field images of micrometre-sized living organisms using standard optical microscopy equipment. This new type of substrate forms the basis for miniaturized lab-on-chip dark-field imaging devices, compatible with simple and compact light microscopes.

In contrast to bright-field microscopy, which primarily relies on variations in optical absorption within the specimen to create image contrast, dark-field microscopy exploits the scattering of incident light from localized variations in refractive index^2–5. For weakly scattering materials, this approach provides a significant improvement in signal-to-noise ratio. This is particularly useful for specimens that display little or no absorption and allows for imaging of weakly scattering biological samples^6–9 and metallic nanoparticles^10–12. Since dark-field microscopy is based on the rejection of incident and reflected unscattered light, only light that is scattered by the sample’s features contributes to the image. In essence, dark-field microscopy emphasizes high spatial frequency components associated with small features in the specimen morphology and in some imaging scenarios can provide resolution beyond the diffraction limit^13–15.

In a typical dark-field microscope, light is incident on the sample at oblique polar angles (measured with respect to the sample surface normal) that are larger than the objective’s maximum light collection angle θ_max, given by the objective’s numerical aperture NA = n sin θ_max^{[4, 5, 16]}. Consequently, only light that is scattered by the sample into a cone of apex angle 2θ_max centered around the microscope’s optical axis is collected. A typical dark-field microscope requires a specialized filter cube and dedicated objectives or condensers, which permit shaping of the incident light cone^{2, 3, 16}. Dark-field objectives usually have a smaller numerical aperture than comparable bright-field objectives to ensure that specularly-reflected light is not collected^{2, 3}. However, a smaller numerical aperture results in a reduced spatial resolution.

In the last few years, newly developed plasmonic-based approaches^17–20 have opened up new paths to overcoming the equipment complexity and size limitations of conventional dark-field microscopy. In these methods, evanescent surface plasmon waves are not captured in the far-field, which results in a dark background, but can be scattered into propagating far-field modes by objects within the surface plasmon field, which consequently appear bright. These techniques have clear advantages compared to classic dark-field imaging devices, but they are not free of limitations. First, they rely on elaborate data analysis for the reconstruction of an image from scans of the sample surface¹⁷, including deconvolution and noise reduction algorithms²⁰. Second, they involve additional complex optical components^17–19, which significantly increase the size of the whole imaging system and limit widespread implementation.

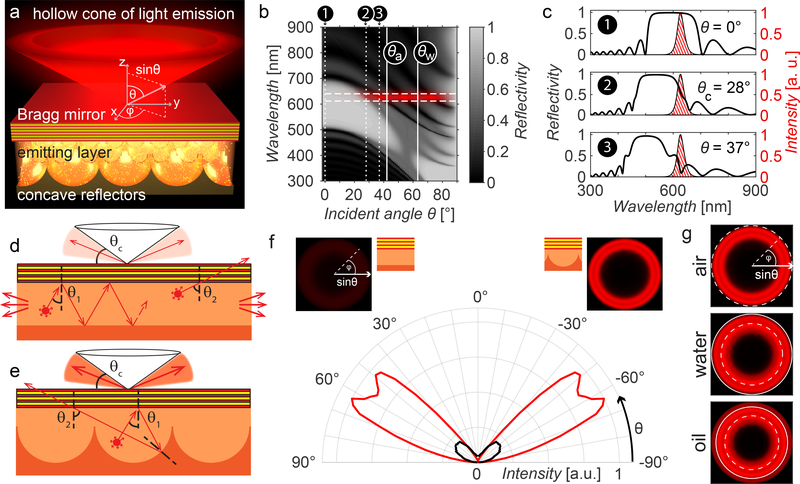
Here, we propose to simplify and miniaturize dark-field microscopy instrumentation by integrating the dark-field light source into the sample substrate. We introduce a luminescent micro-patterned photonic surface with a controlled angular emission profile. This novel type of substrate forms the basis for miniaturized lab-on-chip dark-field microscopy devices that are compatible with simple and compact light microscopes. The light emitted by the substrate is confined to high polar angle ranges due to the interplay between three different structural components: (1) a flat Bragg mirror that by its spectrally selective and angle-dependent transmission characteristics determines the surfaces’ angular emission profile; (2) a light-emitting layer beneath the Bragg reflector, which in our system is composed of light-emitting cadmium selenide/cadmium sulphide (CdSe/CdS) core-shell quantum dots (QDs)²¹ dispersed in a poly(methyl methacrylate) matrix; (3) a micro-patterned bottom reflector underneath the light-emitting layer to recycle light into propagation angle ranges that are transmitted by the Bragg reflector (Fig. 1a). The design is inspired by colour mixing structures found in the wing scales of Papilio butterflies^{22, 23} and builds on recent findings on how to enhance the underlying optical effects in bio-inspired materials²⁴. We call this dark-field imaging technique, which relies on the unique light-emission characteristics of the substrate, “substrate luminescence-enabled dark-field” imaging (short SLED).

Figure 1: The concept of substrate luminescence-enabled dark-field imaging.

a) 3D schematics of the device design. b) Grey-scale encoded reflectivity of a Bragg mirror with a reflection band centred at 585nm as a function of light incidence angle and wavelength. Solid white vertical lines mark the critical angles θ_a and θ_w beyond which total internal reflection occurs if the upper medium is air or water. The spectral emission range of the QDs is marked with horizontal dashed white lines; the red overlay represents the angle ranges at which emitted light can escape from the Bragg reflector. c) Selected spectra from (b) at incidence angles θ = 0°, θ_c = 28° (where the Bragg reflector exhibits a reflectivity of 50% for the QD’s spectral emission range), and θ = 37°, marked by dotted lines in (b). The QD emission spectrum is represented as the red-hatched area. d) Schematic depicting a possible optical path of a light beam emitted by a QD in the case of a flat bottom reflector. If the light is emitted at an angle θ₁ for which it is reflected by the Bragg mirror, the beam will keep bouncing between the two reflective surfaces, until it escapes at the sample edge. For a higher incidence angle θ₂ light can couple out. e) In the case of a bottom reflector patterned with semi-spherical cavities, the light emitted at an angle θ₁ can – through scattering from the patterned bottom surface – reach an incident angle θ₂ large enough to transmit through the Bragg reflector. f) Simulated angular emission profiles comparing the angle-dependent intensity of light emitted by a substrate with flat bottom reflector (black) and a substrate with a micro-patterned bottom reflector (red). The insets show visualizations of the emitted light intensity and colour as a function of the angle of incidence onto the Bragg reflector, which increases from 0º at the images’ centre to 90º at the edges. g) Emission profiles in air, water, and oil. The dashed line corresponds to an output angle of 90˚ in air, while the solid line corresponds to 90˚ in water.

To evaluate the potential of this substrate design for integrated dark-field microscopy devices, we first investigated the surface’s optical performance theoretically. A custom-made optical modelling environment developed in MATLAB allows us to study the optical behaviour and interplay of individual structural components. The system’s Bragg reflector is modelled with 13 layers of titanium dioxide (TiO₂, refractive index $n_{\mathrm{T}\mathrm{i}{\mathrm{O}}_2}=2.2$) and silicon dioxide (SiO₂, $n_{\mathrm{S}\mathrm{i}{\mathrm{O}}_2}=1.49$) to match the structure and parameters that were subsequently realized experimentally; its reflection characteristics are found using Rouard’s technique²⁵. By tuning the layer thicknesses in the Bragg reflector, the spectral position of its reflection band is matched to the experimentally determined emission spectrum of the QDs, which only permits light to escape at large polar angles. In other words, the light emitted by the QDs is reflected back into the polymer matrix, unless its propagation angle (with respect to the Bragg reflector’s surface normal) is larger than a critical angle θ_C and smaller than the critical angles of total internal reflection θ_A for air and θ_W for water as the imaging medium (Fig. 1b, c). This angle is determined by the design of the Bragg reflector and the emission wavelength of the quantum dots. The luminescent substrate thus channels all light into a hollow emission cone with minimum and maximum apex angle defined by the Bragg mirror’s reflection band.

We used a custom 3D ray-tracing code to model the light propagation within the QD-doped polymer medium between the Bragg reflector and the concave reflectors forming the gold-coated micro-patterned bottom surface, taking into account the spectrally varying refractive index and absorption coefficient of gold²⁶. We made the assumption that the concentration of QDs was small enough to not affect the refractive index of the PMMA layer. Combining wave optics-based modelling (Rouard’s technique²⁵) to establish the interactions of light with the Bragg reflector and geometrical optics-based approaches (ray-tracing) to approximate light propagation within the semi-spherical cavities, we obtained an estimate of the optical response of the complete structure composed of Bragg reflector, light-emitting QDs, and micro-patterned metallic bottom surface. A comparison of the theoretical emission characteristics of two different designs, one with a patterned and one with a flat gold bottom surface, indicates that the micro-patterns drastically amplify the intensity of light emitted at high angles. In a structure with a flat reflecting bottom surface, most of the emitted light is coupled out from the substrate’s side edges (Fig. 1d). On the contrary, substrates featuring concave, hemispherical cavities recycle the majority of light reflected by the Bragg mirror, until it impinges on the Bragg reflector at an angle larger than θ_C, at which point the light escapes (Fig. 1e). Therefore, light can exit from the top of the surface after multiple reflections from the micro-patterned surface. This redistribution of light into incidence angle ranges for which the Bragg reflector is transmissive enables a much more intense wide-angle illumination compared to a flat gold bottom surface for identical QD excitation strength (Fig. 1f). Finally, optical modelling helps us to design the Bragg-filter’s reflection band so that the substrate’s angular emission profile forms a hollow emission cone located in any desired polar angle range. To use the substrates for dark-field microscopy with common bright-field objectives, the emission angle range should be located outside of the objective’s numerical aperture. As expected, the emission profile depends on the medium above the device. We based our design on three media common in optical microscopy, air, water, and oil, as well as on the numerical aperture of the high NA objectives commonly available to validate this proposed concept experimentally (Fig. 1g).

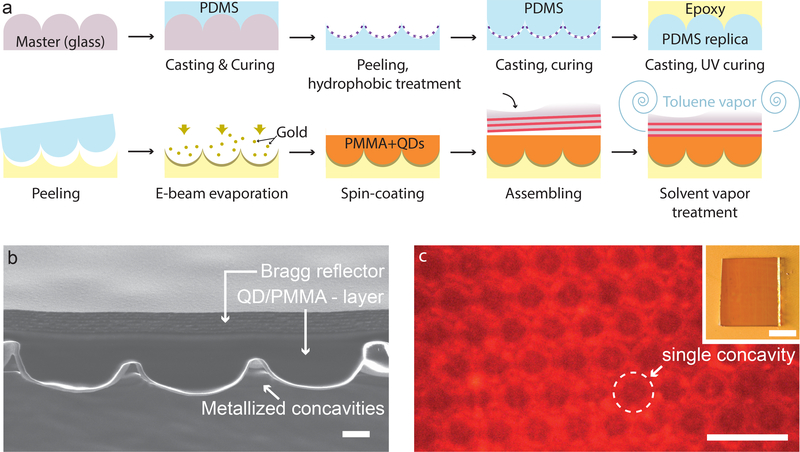
To experimentally demonstrate the proposed substrate luminescence–enabled dark-field imaging technique, we developed a repeatable fabrication technique to create surfaces with various controlled light emission profiles (Fig. 2a). The structure’s optical properties can be altered by modifying the design parameters: First, changing the QD type or mixing different QDs together allows for adjustment of the emission spectrum. Second, the thickness of individual oxide layers in the Bragg reflector can be varied to modify the angular emission profile associated with a specific spectral emission range. Finally, the geometry of the micro-patterned bottom reflector can also be modified to change the angular distribution of the emitted light intensity within the angle range for which the Bragg reflector allows light to transmit.

Figure 2: The fabricated SLED surface.

a) Schematic of the manufacturing procedure. The patterned epoxy substrate was obtained by a three-step replica moulding procedure, consisting in casting PDMS on a glass master, PDMS casting on PDMS, and epoxy casting on the PDMS replica. Then, the SLED surface was assembled by adding the metal reflector, QDs and Bragg reflector on top of the patterned epoxy. b) Cross-sectional SEM view of the SLED device showing the patterned bottom surface, the QD-doped PMMA layer and the Bragg reflector; scale bar: 1μm. c) Top view of the complete device obtained by fluorescence microscopy with the microscope’s focus plane on the bottom reflector; scale bar: 10μm. Inset shows a macroscopic top-view of the assembled SLED surface; scale bar: 1mm.

A cross-section of a representative sample obtained by scanning electron microscopy (SEM) shows the micro-scale concavities filled with the QD-containing polymer matrix topped off by the Bragg reflector (Fig. 2b). Based on our theoretical investigations, the Bragg reflector was designed to have a bandgap centred at 585nm to achieve a hollow emission cone with the large apex angle needed for dark-field imaging, while still allowing us to characterize the surface’s optical properties using high NA objectives. A laser diode with an emission wavelength of λ = 405nm (CW, output power 5mW, Sony) was used to excite the QD’s in the sample, resulting in light emission in the red spectral range (Fig. 2c).

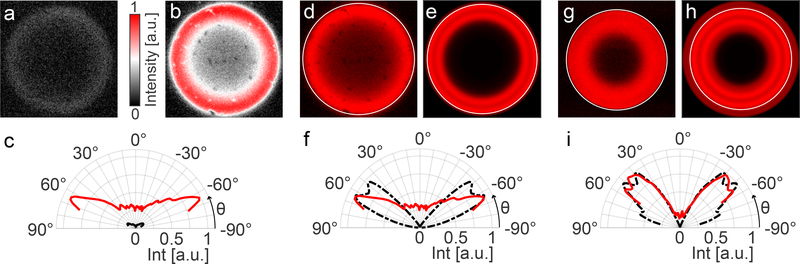
We evaluated our concept of enhancing the surface’s emission characteristics using micro-patterned bottom structures by comparing the emission resulting from a device with a flat gold reflector at the bottom with the emission from a design with a micro-patterned reflective bottom surface. Both samples were excited with the laser diode at an incident power of < 5mW at the surface of the sample. The sample with the patterned bottom surface shows a significantly higher emission intensity and signal-to-noise ratio compared to the substrate with a flat bottom reflector (Fig. 3a–c), in excellent agreement with the optical modelling (Fig. 1f). Furthermore, the surfaces’ emission profiles in air and in immersion oil match the predicted optical response in these media (Fig. 3d–i). The experimental data is truncated at higher angles due to the limited numerical aperture of the microscope objectives (marked by the white ring in Figs. 3d, e, g, h). We also note that the experimentally obtained angular emission profile in air deviates from the predictions at lower angles (Fig. 3f). We speculate that this escape of light from the Bragg reflector at lower angles is indicative of scattering defects in the Bragg reflector layers.

Figure 3: Optical characteristics of the light-emitting surfaces.

a, b) Comparison of the emission profile of substrates with a flat bottom reflector (a) and micro-patterned reflecting bottom surface (b). c) Polar plot comparing the two specimens’ angular emission profile extracted as an average of radial emission patterns from (a) and (b). The red and black curves represent data from the samples with patterned and flat bottom reflectors, respectively. d) Experimentally determined emission profile for a sample with patterned bottom reflector in air imaged with a 100x objective (NA = 0.95). The objective’s numerical aperture is marked with the white circle. e) Corresponding modelling results for a Bragg reflector centred at 585nm. f) Polar plot extracted from (d, red) and (e, black). g) Experimentally determined emission profile for a sample with patterned bottom reflector in immersion oil imaged with a 100x objective (NA = 1.3). h) Corresponding modelling results for a Bragg reflector centred at 585nm. i) Polar plot extracted from (g, red) and (h, black).

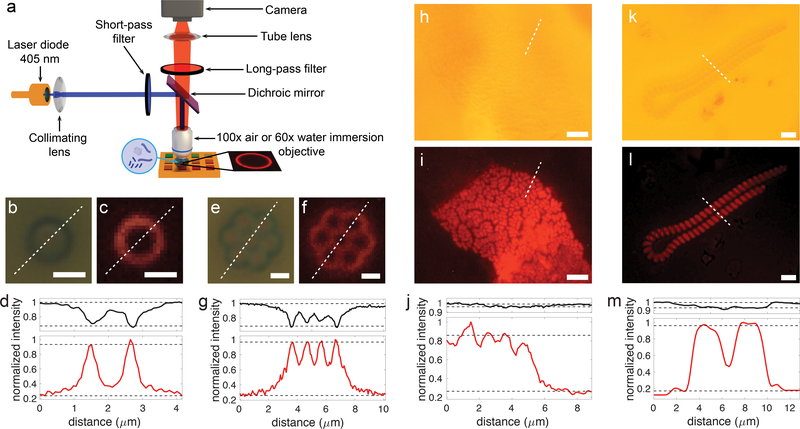
To demonstrate the utility of the proposed luminescent surfaces for dark-field microscopy, we imaged colloids and biological samples with low refractive index contrast (Fig. 4). The Bragg reflector was designed to obtain optimal optical performances for use with a 100x air objective (NA = 0.9) and a 60x water-immersion objective (NA = 1.0) (Fig. 4a). Images obtained with standard bright-field microscopy and with the SLED approach are compared to demonstrate the ability of our substrates to provide high-contrast images for specimen with little absorption and low refractive index contrast (Fig. 4b–i). First, using the 100x air objective, 1-μm polystyrene colloids were imaged in both bright-field and with SLED (Fig. 4b–g). Images obtained by SLED show the reciprocal intensity profile to one obtained by bright-field microscopy, hence demonstrating the dark-field character of our approach. The image contrast, calculated as the difference between the maximum and minimum image intensity values divided by their sum, was significantly improved when the colloids were imaged with SLED (Fig. 4d, g). While bright-field illumination resulted in a contrast of 0.20 ± 0.01 (mean ± std. dev.), SLED illumination provided a contrast of 0.60 ± 0.02.

Figure 4: Application of the SLED surfaces to image colloids and marine micro-organisms.

a) Schematics of the optical setup used for imaging. In the case of biological samples, a drop of water containing the micro-organisms is deposited on the SLED surface and imaged using an immersion lens. SLED measurements rely on exposure of the substrate with blue light from a laser diode. Bright-field images and SLED images together with corresponding intensity profiles (black lines – bright-field, red lines – SLED) extracted along the white dashed lines are shown in b-d) for a single colloid, e-g) for a colloid cluster, h-j) for a colony of E. coli bacteria in water, and k-m) for micro-algae in sea water. Scale bars: 1μm (c, d, e, f), 5μm (h, i), 10μm (k, l). The dashed black lines in (d), (g), (j), and (m) indicate the levels used to determine the image contrasts specified in the main text. These levels are chosen based on image dimensions so that 5% of the intensity values lie above and below for the images of colloids and 15% for the images of bacteria and micro-algae, which generously accounts for camera noise levels. Based on these thresholds, standard deviations of the bright-field and SLED contrast values stated in the main text result from at least 5 (single colloid) and more than 15 (bacteria and micro-algae) discrete values above and below the upper and lower intensity thresholds.

Second, a drop of water containing marine micro-organisms or Escherichia coli (short E. coli) was positioned on top of the light-emitting surface and imaged with the water immersion lens (Fig. 4f–i). In the case of biological samples, which due to weak absorption and low refractive index contrast in water are difficult to image with bright-field illumination, the contrast improvement obtained with SLED is even more striking. For the E. coli sample, bright-field illumination only provided a contrast of 0.021 ± 0.003, while SLED light enabled an image contrast of 0.57 ± 0.02. The contrast enhancement when imaging marine micro-organisms (Fig. 4k–m) was similarly high; SLED illumination resulted in a contrast of 0.76 ± 0.03, while for bright-field light it was only 0.040 ± 0.004. Hence, SLED illumination permits the visualization of sub-micron features in weakly or non-absorbing specimen with low refractive index difference to the surrounding medium, which cannot be easily imaged using bright-field microscopy and standard numerical contrast enhancement techniques (see supplementary information, Fig. S4).

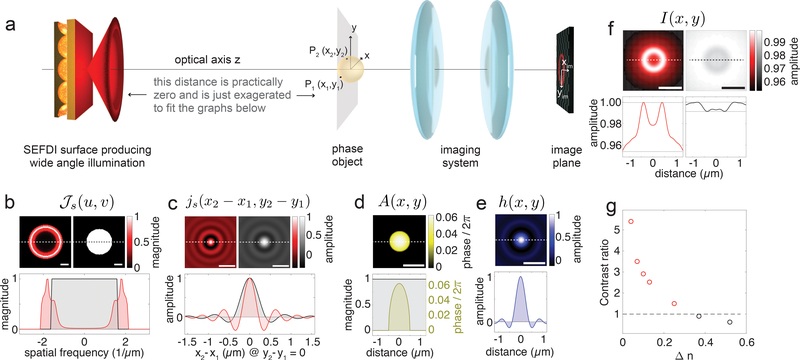
The imaging characteristics of the SLED substrate in combination with a standard light microscope can be modelled in the theoretical framework of imaging with partially coherent, quasi-monochromatic light pioneered by Hopkins²⁷ and educationalised elegantly by Born & Wolf²⁸, and Goodman²⁹. We describe the microscope setup as consisting of the SLED light source transilluminating a pure phase object, which is imaged by the objective and tube lens onto a CCD array (Fig. 5a). Focussing on the capacity to achieve image contrast, we neglect the imaging system’s magnification and regard it as a simple space-invariant 4f-system, which simplifies the problem’s mathematical complexity without compromising any contrast comparison. The source’s coherence properties can be quantified through the mutual intensity that is incident on the object. For quasi-monochromatic illumination originating from a large uniform spatially incoherent source, such as the SLED surfaces, the source’s mutual intensity spectrum ${\mathcal{J}}_s\left(u,v\right)$, is proportional to its angular emission profile (Fig. 5b)^27,28. Here, the spatial frequencies are $u=\frac{n}{{\lambda }_0}\sin \theta \cos \phi$ and $v=\frac{n}{{\lambda }_0}\sin \theta \sin \phi$, where n is the refractive index of the surrounding medium, while θ and φ are the polar and azimuthal angles marked in Fig. 1a. Furthermore, the normalized mutual intensity j_s in the object plane (Fig. 5c) is proportional to the Fourier transform of ${\mathcal{J}}_s\left(u,v\right)$ and only depends on the space coordinate differences of any two object points (x₁,y₁) and (x₂,y₂), i.e. j_s(x₁,x₂,y₁,y₂) = j_s(x₁ − x₂,y₁ − y₂). Finally, the normalized spatial intensity distribution I(x_im,y_im) in the image of a pure phase object with complex amplitude transmission function A(x,y) (Fig. 5d) imaged through a space-invariant 4f-system with amplitude transfer function h (Fig. 5e) is given by

$$I\left(x_{\text{im}},y_{\text{im}}\right)=\underset{\begin{array}{c}\text{Illuminated}\\ \text{area}\end{array}}{\iiint }{j}_s\left(x-x^{\prime },y-y^{\prime }\right)A(x,y)A^{*}\left(x^{\prime },y^{\prime }\right)h\left(x_{\text{im}}-x,y_{\text{im}}-y\right)h^{*}\left(x_{\text{im}}-x^{\prime },y_{\text{im}}-y^{\prime }\right)\text{d}x\text{d}y\text{d}{x}^{\prime }\text{d}{y}^{\prime }$$

Figure 5: Modelling to compare image formation with SLED illumination and bright-field illumination.

a) Schematics showing the sequence of optical elements in the imaging experiments. From left to right: SLED surface – phase object – 4f-imaging system, schematically represented by two lenses – image plane, where the camera is positioned. b) The angular spectrum ${\mathcal{J}}_{\mathrm{s}}\left(\mathrm{u},\mathrm{v}\right)$, where u,v are the spatial frequencies. The graphs on the top show ${\mathcal{J}}_{\mathrm{s}}$ for the SLED surface (left) and for bright-field illumination through a water objective with numerical aperture 1.0 (right); scale bar – 1/μm. The bottom graph displays normalized magnitudes of ${\mathcal{J}}_{\mathrm{s}}$ for the SLED surface (red) and bright-field illumination (black) acquired along the dashed lines in the top graphs. c) The complex degree of mutual spatial coherence j_s(x₂ − x₁,y₂ − y₁) for the SLED surface (left) and the bright-field illumination (right). The bottom graph displays normalized magnitudes of j_s(x₂ − x₁,0) for the SLED surface (red) and bright-field illumination (black) acquired along the dashed lines in the top graphs. d) Phase map of the complex amplitude transmission function A(x,y) of a transparent spherical particle with refractive index 1.37 for light of 630nm wavelength. The bottom yellow graph shows the phase profile along the dashed line in the top map. The black line represents the absolute value of the object’s amplitude transmission function. e) Amplitude spread function of the imaging system as a 2D map and a profile taken along the white dashed line in the map. f) SLED image and bright-field image of the phase object with corresponding profiles shown below. Scale bars in (c-f) – 1μm. g) Contrast ratio used as a metric to compare image contrast obtained with SLED light and with bright-field illumination as a function of refractive index difference Δn between phase object and surrounding medium. For Δn ≤ 0.3 SLED illumination provides better contrast then bright-field light (corresponding data points marked in red).

The four-dimensional integration in the object coordinates x, y and x’, y’ runs over the whole illuminated area (for a detailed derivation see supplementary information). Images of a spherical pure phase object akin to the experimentally imaged colloids but with significantly smaller refractive index contrast (diameter - 1μm, refractive index - 1.37) for SLED illumination and for bright-field light are shown in Fig. 5f. These modelling results show that the partially coherent light field emitted by the SLED surfaces enables imaging of phase objects analogous to dark-field illumination by translating phase disturbances at the object plane into intensity contrast at the image plane. Especially for transparent objects with weak refractive index difference to the surrounding medium, such as bacteria, cells, or marine micro-organisms, this technique enables enhanced contrast as compared to standard bright-field imaging (Fig. 5g). The emission characteristics of SLED surfaces are akin to the light fields achieved with a dark-field condenser in Köhler’s illumination for which it can be shown that the illumination does not cause image aberrations²⁸. Consequently, only the microscope objective and tube lens contribute to aberrations. The resolution obtained with SLED illumination is comparable to the resolution in bright-field light.

In conclusion, we show that luminescent surfaces with tailored angular emission profiles can be generated by using processes that allow for control of the structures’ composition and micro-morphology. The theoretical modelling of the surface’s optical characteristics, complemented and confirmed by our experimental work, demonstrate the potential of the proposed substrate design to enable a novel type of dark-field microscopy, which we have termed “substrate luminescence-enabled dark-field” imaging (short SLED). This approach facilitates dark-field imaging with simple and compact light microscopes that are not equipped with dark-field components. Preliminary experiments suggest that a surface with an area of 25×25mm² can be designed to exhibit up to ten different spectrally and angularly distinct emission profiles. Such multi-spectral emitter surfaces could be used with a wide variety of light-collection equipment available on the market. Randomly rough surfaces as the bottom reflector could be a viable alternative to the concave microstructures presented here, provided their roughness is well controlled (see supplementary information, Fig. S3). In this study, light emission from the QDs was achieved using a low-budget laser diode, however, electrical excitation of the QDs could greatly enhance this approach, and could be implemented with minor design changes of the device.^{30, 31} Combining electrical excitation with the use of a mixture of QDs, for spectral multiplexing could open new avenues toward the design of a fully integrated on-chip simultaneous dark-field and multi-spectral imaging device.³²

Methods

Fabrication of micro-patterned bottom reflectors

A glass master covered with convex hexagonally-packed semi-spheres with a diameter of 4.6μm was fabricated by Papierfabrik Louisenthal GmbH. A first moulding step was performed by casting polydimethylsiloxane (PDMS) Sylgard 184® from Dow Corning after mixing the elastomer base and the curing agent in a weight ratio 10:1. After curing for 3 hours at 70°C, the PDMS was carefully peeled off from the master, revealing the inverted structure (hexagonally-packed semi-spherical concavities). To perform PDMS double-casting, the elastomer master was plasma-etched with oxygen for 10 seconds before being left for a minimum of 3 hours in a desiccator with a few drops of Aquapel® Glass Treatment on a glass slide. This commercial fluorinated compound increases the hydrophobicity of the PDMS elastomer to enable PDMS double-casting. Then, a new mixture of Sylgard 184® was casted on the treated PDMS master and cured for 3 hours at 70°C. It could be easily peeled off from the initial PDMS master and preserves the geometry of the structure, creating an imprint as on the initial glass master. Last, high-temperature resistant optical epoxy OG142–87 from Epotek® was cast on the final PDMS mould cured under UV light for 3 hours and easily peeled off to obtain a hard micro-patterned sample covered with hexagonally-packed semi-spherical concavities. The temperature resistance of the epoxy is an important factor for the next fabrication step of electron-beam evaporation of a gold coating that involves working at high temperature (about 100°C), where other common polymers start expanding, affecting the quality of the thin film deposited on it. The PDMS masters were reused up to 8 times without any noticeable degradation of the micro-structure. The Aquapel®-fluorinated PDMS master could be reused without any further treatment for PDMS double-casting, even a month after its first replication.

Electron-beam evaporation of gold on the patterned epoxy

Patterned epoxy samples were coated with a 15 nm thick seed layer of titanium and 200 nm of gold by e-beam evaporation. All deposition materials were purchased from Kurt J. Lesker®. The deposition was performed with an e-beam evaporator AJA ATC, in the clean room of the Exploratory Materials Laboratory (EML) of the Microsystems Technology Laboratories (MTL) at MIT. The deposited thickness was determined with a Dektak® 150 mechanical surface profilometer and through SEM cross-section imaging.

Spin-coating of the quantum dot polymer matrix

Poly(methyl methacrylate) (PMMA, average molecular weight 15,000 g/mol determined by GPC) and toluene (anhydrous 99.8%) were purchased from Sigma-Aldrich® and used without any further purification. The quantum dots (QD) were synthesized in the Bawendi group at the MIT Department of Chemistry following the recipe reported by Coropceanu et al.²¹. The photoluminescence emission peak of the QDs in solution was located at a wavelength of 630 nm. PMMA powder was mixed at 25wt.% in toluene and stirred until fully dissolved. The solution was then filtered, and added to a vial containing dry QDs to obtain 5wt.% of QDs in the PMMA-toluene solution. The mixture was stirred for a few minutes, until the QDs were fully dispersed. Using a spin coater (Laurell Technologies® WS-650MZ-23NPP), 200μL of the final solution was spin-coated on the gold patterned surface at 2000 rpm, until the solvent fully evaporated and the colour of the film did not change anymore.

Bragg reflector fabrication by electron-beam evaporation and assembly

Titania (TiO₂) and silica (SiO₂) used for the deposition were purchased from Kurt J. Lesker®. The e-beam evaporation was performed on the same equipment used for the deposition of gold on the patterned surface. Bragg reflectors were obtained by alternating 13 layers of TiO₂ and SiO₂, always starting and finishing with a TiO₂ layer, as it is the higher refractive index material. The Bragg reflectors can be deposited directly on top of the PMMA/QDs-covered metal bottom reflectors. Alternatively, they can be formed on thin glass coverslips. The coverslips can then be cut and assembled with the QD/PMMA coated bottom reflectors by putting them in physical contact – with the Bragg reflector side on the PMMA film – and fusing them in a toluene environment for approximately an hour. Thicknesses and refractive indices of the constituent layers in the multilayer reflectors were measured using a custom-made ellipsometer. In addition, the thicknesses were confirmed via profilometry performed with a Dektak® 150 mechanical surface profilometer and through SEM cross-section imaging. For our samples, the refractive indices were 2.2±0.02 for TiO₂ and 1.49±0.01 for SiO₂.

Optical characterization setup

All optical measurements were performed on an Olympus® BX51 optical microscope. Images were acquired with a RGB Allied Vision Technologies® Prosilica GT camera mounted on the microscope’s imaging port. A high NA oil immersion lens (Olympus UPlanFL 100x / 1.30 oil) and a regular air objective (UMPlanFl 100x / 0.95) in conjunction with a Bertrand lens were used to image the samples’ angular emission profiles. The excitation source was a Sony® SLD3236VF laser diode, used with a Thorlabs® ITC4005 laser controller. The beam created by the laser diode was collimated through a 30mm focal length lens and its position and angle was controlled with two adjustable 45° mirrors before coupling it into the optical microscope. A customized microscope filter cube consisting of a short-pass filter ( < 450nm, Thorlabs® FESH0450), a long-pass dichroic mirror ( > 425nm, Thorlabs® DMLP425R) and a long-pass filter ( > 570nm, Thorlabs® FGL570) was also used. The standard excitation power used to excite the QDs was < 5mW to avoid heating and intensity variation of the laser diode. In addition, some tests were run with an excitation power up to 20mW without witnessing any photo-bleaching of the QDs. A 60x water immersion lens (Olympus (LUMPlanFl N 60x / 1.00 w) was used for the imaging of marine micro-organisms and bacteria.

Optical Modelling

Modelling of the emission characteristics of the sample geometries with spherical concavities, flat surfaces, and randomly rough surfaces with a Gaussian height distribution was performed using a custom Matlab code. This code allows to calculate the reflection and transmission characteristics of the top Bragg reflector based on Rouard’s method²⁵, while employing ray tracing to model light propagation within the structures and reflection of the bottom gold surface (taking into account the wavelength-dependent refractive indices and absorption coefficients of gold²⁶). To assess the emission characteristics of the different geometries we generated 100,000 rays of random position and direction within the volume enclosed by the Bragg filter and the bottom gold reflectors. We assumed incoherent superposition of different rays emitted from the surface in the same angular direction, i.e. adding their intensities, since we expect no phase relation between light that is emitted fluorescently from different points within the cavity structures. The number of 100,000 rays was chosen after testing for selected geometries that the resulting emission profiles had converged to the same result as for modelling runs with 150,000 and 200,000 rays. The theoretical modelling of image formation with partially coherent light is described in detail in the supplementary information.