CaliPro: A Calibration Protocol That Utilizes Parameter Density Estimation to Explore Parameter Space and Calibrate Complex Biological Models

Abstract

Introduction

Mathematical and computational modeling have a long history of uncovering mechanisms and making predictions for biological systems. However, to create a model that can provide relevant quantitative predictions, models must first be calibrated by recapitulating existing biological datasets from that system. Current calibration approaches may not be appropriate for complex biological models because: 1) many attempt to recapitulate only a single aspect of the experimental data (such as a median trend) or 2) Bayesian techniques require specification of parameter priors and likelihoods to experimental data that cannot always be confidently assigned. A new calibration protocol is needed to calibrate complex models when current approaches fall short.

Methods

Herein, we develop CaliPro, an iterative, model-agnostic calibration protocol that utilizes parameter density estimation to refine parameter space and calibrate to temporal biological datasets. An important aspect of CaliPro is the user-defined pass set definition, which specifies how the model might successfully recapitulate experimental data. We define the appropriate settings to use CaliPro.

Results

We illustrate the usefulness of CaliPro through four examples including predator-prey, infectious disease transmission, and immune response models. We show that CaliPro works well for both deterministic, continuous model structures as well as stochastic, discrete models and illustrate that CaliPro can work across diverse calibration goals.

Conclusions

We present CaliPro, a new method for calibrating complex biological models to a range of experimental outcomes. In addition to expediting calibration, CaliPro may be useful in already calibrated parameter spaces to target and isolate specific model behavior for further analysis.

Electronic supplementary material

The online version of this article (10.1007/s12195-020-00650-z) contains supplementary material, which is available to authorized users.

Introduction

As part of a systems biology approach, mathematical and computational modeling can interrogate biological theories and provide context to better understand complex phenomena across multiple scales. In particular, the explosion of data from genomics, transcriptomics, proteomics and metabolomics coupled with the introduction of data from new cytometry and imaging techniques have revealed an opportunity for systems modeling approaches to predict and reveal mechanistic relationships between various biological agents.3,8,11,12,28,29,39,40,42,50–52,60 However, before making useful predictions, a model must be able to replicate particular experimental outcomes and/or temporal dynamics of the related biological system.

Model calibration is the process of altering model inputs, e.g. initial conditions and parameters, until model outputs satisfy one or more biologically-related criteria. Often, these criteria include matching model outputs to experimental data across time. For simple models with relatively few parameters, calibration can be trivial. However, complex models often face a more difficult calibration process for three reasons. First, the number of parameters in these models can be large. Second, initial parameter estimates can be discovered via experimental studies (or other models) but still may contain a large degree of uncertainty. For example, if a parameter estimate is derived from multiple studies, estimates could vary greatly between them and a modeler will understandably have less confidence in the true value of this parameter. Third, some parameters are, by construction, intended to represent a group of biological processes. If a process(es) is modeled more phenomenologically, then parameter values may be very difficult, if not impossible, to measure directly via experiments.

A large body of work covers the calibration of complex models to biological data (see Read et al.45 for a thorough review of various calibration techniques in biological modeling). Popular calibration algorithms such as simulated annealing,6 genetic algorithms,26,59 gradient descent7 and others23,25 leverage the power of optimization schemes to refine parameter space in an iterative fashion. As Read et al. acknowledge, many, if not all, of these calibration techniques use a single metric (often called an ‘objective function’) to define the difference between experimental and simulated outcomes. The general aim is to minimize these differences across each iteration. However, not all models can or should be fit to experimental data through the minimization of a single metric for each outcome.

In fact, new experimental technologies (e.g., single-cell measurements, flow cytometry, advanced imaging) have allowed for the identification of greater biological variability, often across scales ranging from genomic to population-level information. In fact, many experimental techniques now allow for the observation of greater biological variability. For example, at the genetic scale, advanced imaging techniques, single cell sequencing and mass cytometry have catalyzed the Human Cell Atlas Project,46 an effort to map the variability across every human cell type. Additionally, the introduction of functional assay screening22 and targeted immunotherapy strategies18 within cancer precision medicine have embraced heterogeneity across the population and provide a path toward patient-specific clinical therapies.

In response, mathematical and computational models have been built to address questions from fields as diverse as cell-signaling,54 wound healing,47 sepsis15 and drug treatment in tuberculosis,41 among many others. As systems biology approaches attempt to reveal sources of variability, models must first be able to recapitulate biological variance and therefore should not be fit to a median trend line or a single metric. By calibrating to and thereby capturing a distribution of outcomes, modeling can assess and provide explanations of variability between individuals, species or other modelled biological agents.

Bayesian calibration approaches are a collection of calibration techniques that utilize Bayesian statistics to leverage information about the distribution of model outputs, information about the distribution of parameters and assumptions that relate model parameters to outputs.1,4,17,21,33,38,43,49,57,62 Sample Importance Resampling (SIR) is one example of a Bayesian calibration approach that draws a large number of parameter combinations from a prior parameter distribution, executes the model to create simulation outcomes, then uses outcomes to estimate a likelihood for each parameter set compared to the experimental data. The approach requires resampling from the original parameter space with replacement, where likelihood values are assigned as sampling weights.48 This approach, refined and modified over the years 16,43,44,55 has yielded success in calibrating models for which the distribution of both parameter values and experimental outcomes can be sufficiently derived from available data.

However, if the distribution of values within experimental datasets or model parameters cannot be approximated, Bayesian calibration approaches may not be the best strategy. Furthermore, some models should be calibrated with an emphasis on finding a robust parameter space—defined as a continuous region of parameter space wherein the vast majority of model runs will pass within the bounds of experimental data for the particular outcomes of interest—instead of a single global optimum or a vast parameter space wherein some areas are weighted more than others. Finding a robust parameter space for a complex biological model is often a user-intensive process that, when performed manually, can take weeks due to a lack of automated protocols. Here, we describe a calibration protocol, CaliPro, that quickly identifies a robust parameter space where a range of distinct and biologically reasonable simulation results are represented when both model parameter and experimental data distributions cannot be approximated. We highlight the ability of CaliPro to identify a robust parameter space for multiple model types, including simple, complex, deterministic and stochastic biological models. We apply this approach to a variety of model types to show the flexibility of this protocol to calibrate different types of systems to multiple datasets.

Methods

Defining the Appropriate Use for CaliPro

Many traditional model-fitting techniques and strategies discover the global, or local, optimum within the outcome landscape. These techniques belong to a class of optimization procedures called metaheuristics.5 Unlike these procedures, CaliPro is an empirical approach that is not guaranteed to find the single global, or even local, optimum as it is commonly defined.

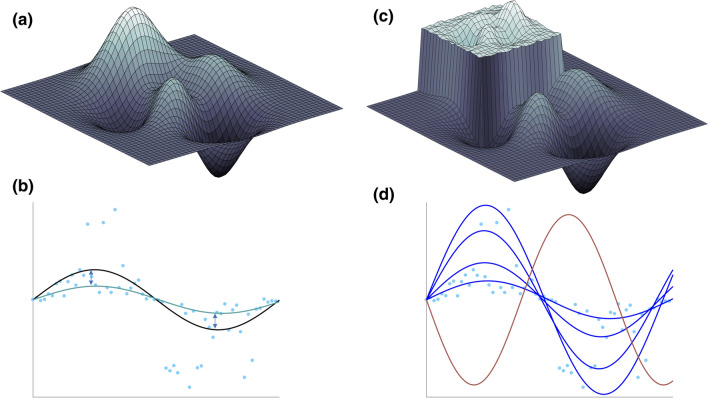
Both hill-climbing (a heuristic procedure 9) and simulated annealing (a metaheuristics process 6) algorithms will find the global optimum of a smooth, peaked landscape (Figs. 1a and 1b) given ample time and computational resources. However, if a modeler wishes to fit to only the median of the data, they may potentially ignore important events that cause a higher or lower response. Models do have the potential to elucidate this behavior when properly calibrated to the entire range of experimental outcomes.2 If the modeler seeks to identify model simulations that fit within the range of the experimental data (blue simulation lines in Fig. 1d), the outcome space (Fig. 1c) becomes very difficult, if not impossible, for these algorithms to evaluate. As the model simulations either fall within the elevated region, or far below it, this binary classification of model simulations does not provide a heuristic or meta-heuristic process with enough information to estimate the next parameter combination decision. Figures 1c and 1d outlines one such theoretical case where CaliPro can calibrate the model, by embracing the binary classification of model simulation outcomes and represent the full range of experimental outcomes.

Figure 1.

Calibrating a model to a range of plausible outcomes requires a new calibration approach. (Panel a and b) panel a represents an example of a smooth model outcome landscape defined by a biologically relevant hypercube of parameter space. Each (x, y, z) point in this hypothetical 3D mapping of outcome space is defined by a single set of parameter inputs. (b) The teal curve represents a single model outcome within the full landscape in (a), that is, the teal curve corresponds to a single (x, y, z) point in (a). The blue dots are available experimental datasets, and the black curve represents a hypothetically known optimal for fitting the model to that experimental data (this corresponds to the white peak in a). Ultimately, in the situation outlined by panel a and b, the modeler seeks to minimize the difference (shown as arrows) between the simulation and median line by defining an objective function and using either hill-climbing or simulated annealing (or another similar technique) to select the next parameter combination. (Panel c and d) If the optimal within outcome space is a set of simulations that encompass various aspects of the experimental data, the landscape in (a) looks much more like the landscape in (c). Here, the optimum is now an elevated region of space that may include many outcomes. Panel d now includes a set of simulations (shown in royal blue) that reasonably recapitulate different aspects of the experimental data and each individual simulation maps to different points on the elevated region in (c). One failed simulation (shown in red) does not reasonably portray the experimental data (light blue dots), and would map to the lower regions in outcome space in (c).

We envision the use of CaliPro in situations such as those shown in Fig. 1 but, more specifically, for calibration to meet three criteria: (1) the termination of model calibration is not a single parameter set that can recapitulate one aspect of the experimental dataspace (such as the median), but rather a set of parameter ranges that represent a continuous and robust parameter space able to recapitulate the broad range of outcomes captured within the experimental data. (2) The objective function cannot be easily defined as many model simulations may lie within the experimental dataspace and those that lie outside of that dataspace may not necessarily provide an optimization procedure with information for its next parameter choice. (3) The distribution of experimental outcomes is indistinguishable, or should not be approximated. CaliPro provides a method for which models with these criteria can be calibrated to experimental data that might encompass a broad range of outcomes but whose distribution might not be easily distinguished.

General Overview of CaliPro

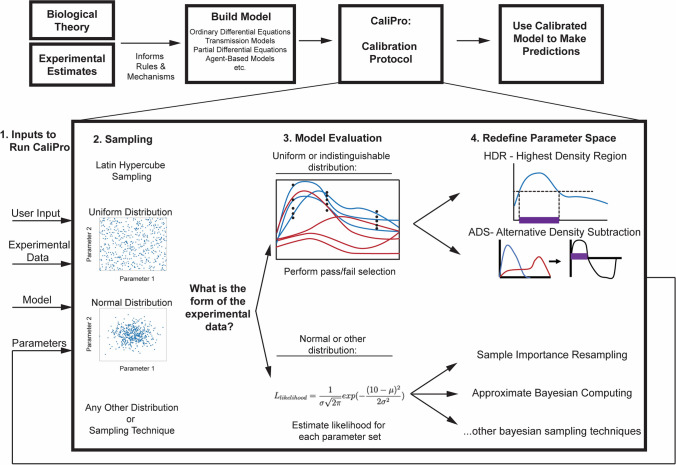
CaliPro is utilized following a model building process, when a modeler already has (1) a model in hand and (2) a series of datasets that exhibit behavior that the model is partially designed to replicate. Figure 2 displays the general overview process of CaliPro. Step 1 of Fig. 2 shows the multiple data types that are input to CaliPro.

Figure 2.

Overview of CaliPro. The model building process begins by incorporating biological theory and experimental estimates to inform rules, mechanisms, and model structure. Once the model is built, there is (an often prolonged) period of calibration, wherein the model outcomes and general behavior are compared to a set of experimental outcomes across time to identify the best fit. Here, we have provided a protocol, called CaliPro, for calibrating complex biological models. This begins with Step 1: Inputs. Several inputs including the experimental data, the model itself, and the model parameters—given as a range of initial values for each parameter. Step 2: Sampling. Here, we utilize an Latin Hypercube Sampling (LHS) scheme (see Ref. 34 for an in-depth review of LHS and uncertainty/sensitivity analysis) where each parameter is sampled uniformly or normally, but sampling could be performed using any sampling scheme (Sobol sampling, Monte Carlo, etc.). Step 3: Model Evaluation. At this stage in the calibration process, the modeler will execute the model for each of the parameter combinations created via sampling parameter space, and begin to evaluate the model by comparing it to the experimental data. If the form of the experimental data can be approximated by a likelihood, or the modeler is comfortable assigning a distribution to the experimental data, they should proceed with Bayesian calibration approaches such as Sample Importance Resampling, approximate Bayesian computing or other techniques. However, if the modeler cannot distinguish a distribution for experimental datasets, or if that distribution is uniform at each timepoint, then we suggest narrowing the parameter space via our CaliPro techniques. Still as part of the model evaluation in step 3, the modeler chooses a pass set definition (Supplementary Material: Box 1) to identify a subset of model simulations that they consider the pass run set (blue simulation lines). All other runs constitute the fail run set (red simulation lines). Step 4: Redefine Parameter Space. Transitioning from evaluating the model, the modeler creates two density plots for each parameter, one for the pass parameter set and the other for the fail parameter set (blue, red lines density plot lines, respectively) across the original parameter range (the x-axis) for each parameter. Like any other density plot, the y-axis represents the probability density function. If a modeler prefers, the y-axis could be transformed to become a percentage (normalized from 0 to 100). The modeler then narrows the parameter ranges using either Highest Density Region (HDR) or Alternative Density Subtraction (ADS) selection (see more on these approaches in methods). Each parameter will be sampled again from this new parameter subrange (purple bounded region identified on the x-axis) at Step 2 in an iterative fashion. Steps 2–4 are repeated until the termination criteria (Supplementary Material: Box 1) has been met. At this point, the modeler has a well-calibrated model.

Determining initial parameter ranges can be a difficult process as even parameters discovered via experimental studies (or other models) may contain uncertainty as to their exact value(s). However, by examining multiple values from the literature, the modeler should assign the widest range that are biologically feasible, which includes all previous estimates that have been derived. It is also important to note that some parameters are fairly well-constrained, either biologically or by design, and are thus easier to assign an initial range. Following initial parameter range assignment, in Step 2 the modeler performs a stratified sampling of the parameter space using such algorithms as Latin Hypercube Sampling (LHS), Sobol sampling, Monte Carlo, etc. The model is then executed for each of the parameter combinations.

Step 3 in Fig. 2, Model Evaluation, is a crucial step. If the experimental datasets for calibration at each timepoint can be approximated as a distribution (Gaussian, Poisson, or otherwise) we suggest following Bayesian calibration approaches by creating a likelihood to compare model parameters and simulation outcomes with the experimental data. Subsequently, there are many techniques to refine parameter space, including SIR. However, should the experimental data be uniform or indistinguishable, then we suggest specifying a pass set definition (Supplementary Material: Box 1). This is a user-intensive step of CaliPro, as the pass set definition is entirely up to the modeler. Within CaliPro this model evaluation step can also be automated and defined computationally a priori. Model simulations that satisfy the pass set definition are gathered together into one matrix and thereby constitute a pass run set (Supplementary Material: Box 1). All model runs that do not satisfy the pass set definition are placed within the fail run set (Supplementary Material: Box 1).

Next, CaliPro creates two density plots for each parameter within the pass and fail parameter sets (Supplementary Material: Box 1) to display the regions of parameter space that are more inhabited by the pass or fail run set (Step 4 in Fig. 2). Once the density plots have been created, the initial parameter ranges can be refined using one of two methods (Step 4 in Fig. 2, methods below). Following parameter range refinement, these parameters will be sampled again in an iterative fashion. Steps 2–4 will be repeated until the termination criteria (Supplementary Material: Box 1) is met.

Highest Density Region Estimation to Identify Parameter Subranges

Calculating the highest density region (HDR) is one approach to summarize a probability distribution. HDR satisfies the following criteria: (1) the region that summarizes the probability distribution must occupy the smallest possible volume in the sample space and (2) every point within the region has a probability density larger than every point outside the region.27 HDR is defined by letting f(x) be the density function of random parameter X. Then the $100\left(1-\alpha \right)\%$ HDR is the subset $R\left(f_{\alpha }\right)$ of the sample space for parameter X such that $R\left(f_{\alpha }\right)=\left\{x:f\left(x\right)\ge f_{\alpha }\right\}$where $f_{\alpha }$ is the largest constant such that $Pr\left(X\in R\left(f_{\alpha }\right)\right)\ge 1-\alpha$.27 A modeler specifies α, which represents the size of the region, as a percentage of the density function, f(x).

We apply this method to the distribution created by the pass parameter set across a one-dimensional parameter space, for each parameter (Step 4 in Fig. 2). When used within the CaliPro pipeline, HDR serves to refine parameter space by identifying subranges within each individual parameter range toward the region that has the highest density of simulations that satisfy the pass set definition. While HDR can identify several disjoint regions for multimodal distributions, within the CaliPro pipeline, if disjoint regions are identified, the parameter range for the next iteration will be bounded by the minimum value and the maximum value across the disjoint regions.

Alternative Density Subtraction to Identify Parameter Subranges

Another option for narrowing the initial parameter range of each parameter is Alternative Density Subtraction (ADS). ADS leverages information from the probability density of both the pass parameter set and fail parameter set across each parameter range. ADS is defined by letting p(x) be the density function of the pass parameter set for the random parameter X and by letting d(x) be the density function of fail runs for the same random parameter X. Then ADS is the subset of the sample space of X such that $\left\{x:p\left(x\right)-d\left(x\right)\ge 0\right\}$.

When used within the CaliPro pipeline (Step 4 in Fig. 2), ADS refines parameter space by identifying regions within each individual parameter range that have a higher density of simulations that satisfy the pass set definition than those that fail to satisfy the pass set definition. If disjoint regions are identified, the parameter range for the following iteration will be bounded by the minimum value and the maximum value across the disjoint regions.

Computational Platform

CaliPro can be implemented within any programming language. In the examples we list below, we have implemented CaliPro in R (version 3.5.3) and Matlab (R2016) environments. R packages used include plyr, dplyr and tidyr for data organizing and reformatting. We used ggplot2 and scales for plotting and hdrcde to identify highest density regions when that option was exercised within CaliPro.

On our lab website (webpage address: http://malthus.micro.med.umich.edu/CaliPro), we provide a directory that includes all Matlab scripts for running a fully automated version of CaliPro, including model execution of the predator–prey model example described below. We suggest modelers wishing to utilize the CaliPro framework use these scripts as a starting point for their own implementation. Additionally, all equations are listed in the Supplementary Material.

Results

To show how to apply CaliPro, we provide four examples of model formulations with datasets for calibration. We show that CaliPro is model agnostic and works well for these types of model structures: ordinary differential equations (ODEs) (deterministic, continuous) and agent-based models (stochastic, discrete). The number and type of experimental datasets will likely differ for potential CaliPro users: therefore, we also illustrate this diversity in our examples.

Example 1: CaliPro Finds Parameter Ranges That Satisfy a Predator–Prey Test Problem

We first test CaliPro using a classic ODE system of deterministic population dynamics: a predator–prey (or Lotka-Volterra) model. The Lotka-Volterra model is a two-equation model that was developed independently by Lotka (1925) and Volterra (1926) to represent predator–prey interactions across time and has been studied in thousands of papers since its first publication.

The model has two state variables (H(t) and L(t) as a vector of values corresponding to each time point) and several parameters that represent predator and prey interactions across time. H(t) represents the number of prey per time, L(t) represents the number of predators per time, $\alpha$ represents reproduction rate constant of prey, $\beta$ is the rate constant of predation, $\sigma$ is the death rate of predators and $\delta$ is the reproduction rate constant of predators:

$$\frac{\text{d}H}{\text{d}t}=\alpha H\left(t\right)-\beta H\left(t\right)L\left(t\right)$$

$$\frac{\text{d}L}{\text{d}t}=-\sigma L\left(t\right)+\delta H\left(t\right)L\left(t\right)$$

At this point, a modeler could calibrate this model to a single trend line for each of the two species using traditional calibration techniques (e.g. least square regression). However, we use this model to test whether CaliPro can identify a parameter space that satisfies a range of experimental outcomes. For simplicity, we built a small test problem using a synthetic experimental dataset that has a range of outcome values at each time point. To build this synthetic experimental dataset, we selected a narrow range of values for each of the four parameters in the model (Table 1—synthetic data range). Then, we simulated the model 500 times, sampling from this narrow parameter space. The minimum and maximum value of those 500 simulations for 21 timepoints are shown as black data points in Fig. 3 and make-up our synthetic experimental dataset. These synthetic experimental data points serve as the data for calibration within this test-case CaliPro example.

Table 1.

Initial Parameter Ranges and Calibrated Parameter Ranges for the predator–prey test case problem

Parameters	Synthetic data range	First iteration range	CaliPro final range
Alpha	0.5–0.7	0.1–0.9	0.53–0.66
Beta	0.02–0.035	0.01–0.1	0.03–0.042
Sigma	0.6–0.9	0.1–0.99	0.7–0.88
Delta	0.02–0.03	0.001–0.1	0.02–0.027

For each of the four parameters, the first iteration range was assigned to be much larger than the range of parameters used to create the synthetic dataset. Following five CaliPro iterations, the final sampling space was satisfactorily close to the synthetic data range, with 98% of model realizations lying with the minimum and maximum bounds of experimental datasets

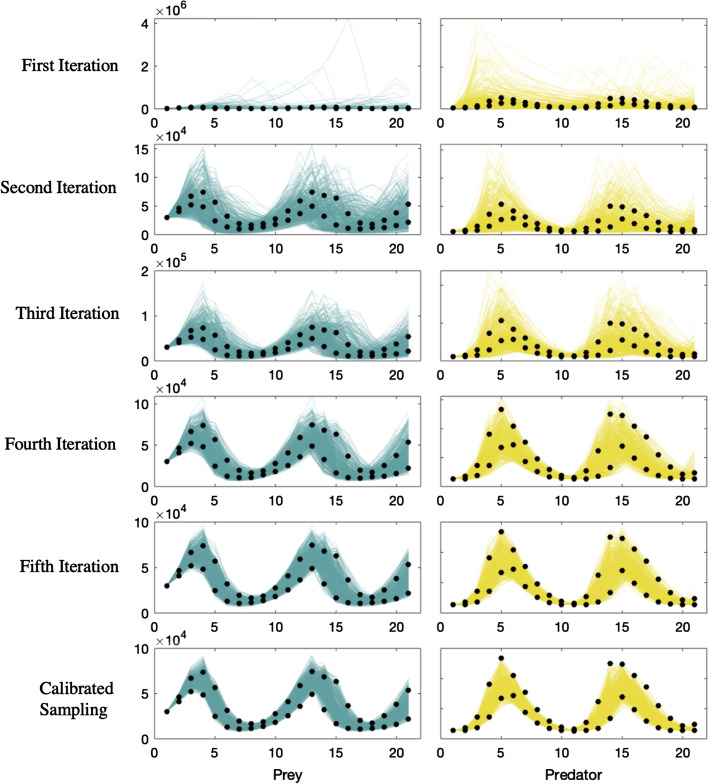
Figure 3.

Example 1—predator–prey model: CaliPro identifies best fit parameter space using HDR. Prey (blue) and predator (gold) model simulation populations overlaid on synthetic experimental data (black data points) at each timepoint (minimum and maximum values shown). Termination criteria: 90% of runs must belong to pass run set. Pass set definition: (Iterations 1 and 2) Simulation values, at each timepoint, lie within the range bounded by two times the maximum experimental data point and half the value of the minimum experimental data point for each species. (Iterations 3–6) For each time point, the simulation value must fall within the 1.25 times the maximum experimental data point and the value of the minimum experimental data point divided by 1.25 for both predator and prey. In the final iteration, 98% of the 500 simulations belong to the pass run set, exceeding our termination criteria.

Beginning with CaliPro to calibrate this model, we sample from our initial parameter range: a larger range of values for each parameter that encompass the smaller range used to create the synthetic experimental dataset (Table 1—first iteration range). Figure 3 (top row) shows the predator (gold) and prey (blue) outcomes following this initial sampling of parameter space. As part of the CaliPro process, we define a termination criterion that 90% of runs must belong to pass run set. Additionally, we outline a pass set definition where simulation values must fall within ranges bounded by two times the maximum experimental data point and one-half of the value of the minimum experimental data for both predator and prey populations for every time point. This pass set definition was selected because it encapsulates the synthetic experimental data while ensuring there are enough simulations within the pass run set to inform the next iteration. Altogether, a given model simulation must satisfy each of those criteria (above the minimum, but below the max for each of the 21 timepoints for each species) in order to belong within the pass run set. If even one simulation value does not reside within this range for one time point in one species, the simulation is designated as part of the fail run set. Following initial sampling, < 1% of the 500 model simulations satisfy the pass set definition, so we narrow this parameter space using the HDR method with a coverage of 0.85 as described in ‘Methods’. The second iteration in Fig. 3 reveals the results of sampling this parameter space, wherein ~ 35% of runs are now classified as part of pass run set.

Now, there may be modeling instances wherein the termination criteria for CaliPro could be satisfied following the results of this second iteration, as the model outcomes do capture the full spread of experimental outcomes and generally capture the behavior of the experimental data across both predator and prey (Fig. 3, second iteration). However, the goal is to identify a more refined parameter space for this test problem as the range of outcomes is slightly too broad for our satisfaction.

We continue using CaliPro via iteration, but reformulate our pass set definition to be stricter than the previous iterations (see Matlab files for automated implementation at http://malthus.micro.med.umich.edu/CaliPro) since our pass parameter set is sufficiently large. Now, we impose a new pass set definition specifying a narrower range for both predators and prey for every time point. We use HDR again to narrow the parameter space following iteration 2 and resample this space 500 times. Following the third iteration, 16% of the 500 model simulations satisfy the new pass set definition. We narrow and resample parameter space three more times before our termination criteria is met (see Fig. 3). Out of 500 total model simulations at the final iteration, 98% of model simulations belong to the pass run set. Figure 3 shows model outcomes against the synthetic experimental dataset; and Fig. 4 displays the iterative refining of the parameter space for each parameter in this model. We display the pass and fail parameter density plots for each parameter at each iteration in Fig. 4. These parameter density plots reveal where, across the range of sampled values, the majority of simulations did or did not satisfy the pass set definition. For example, in the initial sampling of the $\delta$ parameter range in column 4 of Fig. 4, the runs that satisfy the pass set definition clearly reside along the region bounded between 0 and 0.04. Through iteratively defining the next parameter range for sampling (the purple range band along a portion of the x-axis on each subplot in Fig. 4), we satisfy our termination criterion that 90% of the runs satisfy the pass set definition by iteration 6. CaliPro is able to find a range of values for each parameter that satisfies our test problem of relatively simple predatory–prey dynamics (Table 1).

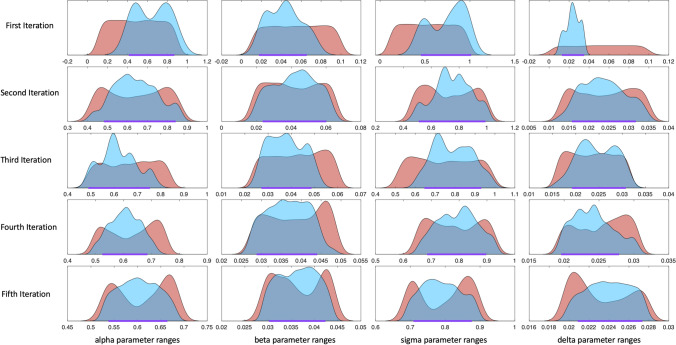
Figure 4.

Example 1—parameter density plots at each CaliPro iteration. The density plots for pass (blue) and fail (red) parameter sets are shown for each parameter (columns) and at each iteration (rows). Ranges along the x-axis where the pass parameter density is larger than the fail parameter density suggest regions in parameter space where simulations are more likely to satisfy the pass set definition. The purple range band along the x-axis of each density plot denotes the region of parameter space identified by HDR (HDR coverage set at 0.85) that will become the parameter range for sampling in the next iteration. 6th iteration is not shown as sampling from the purple band along the x-axis in the fifth iteration results in a calibrated parameter space.

Example 2: CaliPro Identifies Parameter Ranges for ODE Granuloma Lesion Model within Non-human Primate Lung

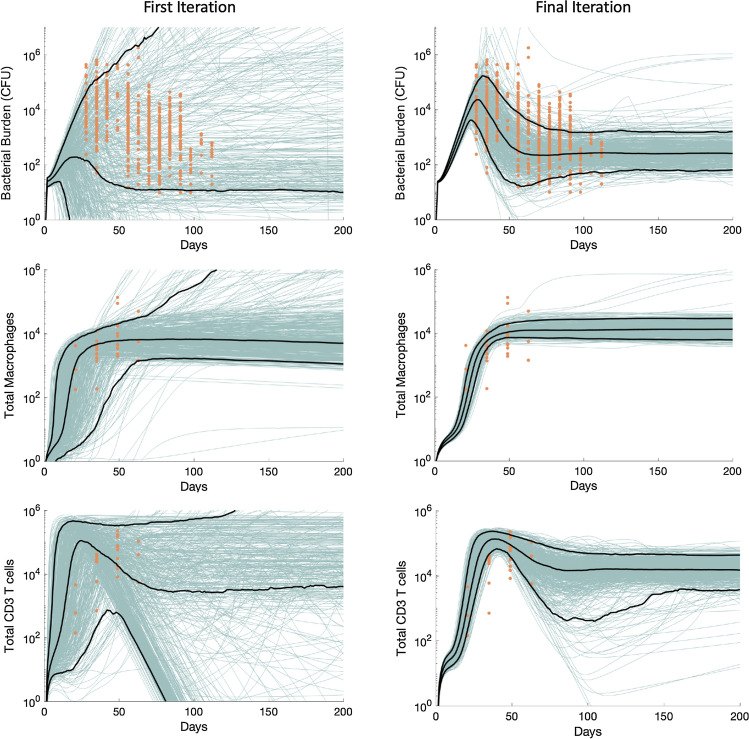
For a larger example, we apply CaliPro to a system of 16 non-linear ODEs (see Supplementary Material) that capture bacterial, T cell, macrophage and cytokine dynamics within a single granuloma lesion that forms within a non-human primate (NHP) lung as an immune response to infection with Mycobacterium tuberculosis.61 As a roughly spherical mass of immune cells acting to contain bacteria to a local region within the lung, the granuloma is typically a few millimeters in size and is the hallmark of tuberculosis. We use CaliPro to explore parameter space of this more detailed non-linear ODE model with 108 parameters and identify parameter ranges that replicate NHP single granuloma experimental datasets.

Unlike Example 1 above, in this example we calibrate this system of ODEs to three separate experimental datasets, rather than a synthetic dataset, shown as orange data points across time in Fig. 5. There are 628 data points in the bacterial burden dataset and 26 data points in the T cell and macrophage dataset. Each separate data point represents experimental data generated on outcomes from an individual NHP granuloma. Thus, while these datasets are not strictly temporal in nature, since the data are gathered at the time of NHP necropsy, the outcomes taken together can be treated as a single dataset, although it is a collection of data.

Figure 5.

Example 2—Single Granuloma ODE: CaliPro identifies calibrated parameter space using ADS. 500 model simulations are shown (blue lines) overlaid on experimental data (orange data points) for bacterial numbers (Bacterial Burden), total numbers of CD3+ T cells and total numbers of macrophages. The 5th, 50th, and 95th percentiles of model simulations are shown as black lines. Termination criteria: 75% of runs must belong to pass run set. Pass set definition: (all Iterations) Simulation values, at each timepoint, lie within the range bounded by an order of magnitude above the maximum experimental data point and an order of magnitude below the value of the minimum experimental data point for each experimental dataset. Additionally, for days 90–200, the simulation value for bacterial numbers cannot eclipse 36,000. In the final iteration, 91% of the 500 simulations belong to the pass run set, exceeding our termination criteria.

We begin the CaliPro process on this system by defining our initial parameter range of values for 80 of the 108 parameters in the model. We determined initial parameter ranges by examining experimental values from literature as well as other previous models.13,14,20,24,35,56,60,63,64 It is important to note that values of some parameters were fairly well-constrained (e.g. extensive data in the literature gives rates of bacterial killing) while others are less so. The remaining 28 parameters are death or decay rates, ratios or weights for scaling, or other parameters that are constrained by the biology and are therefore not varied. We specify the pass set definition such that the simulations must fall within the range bounded by an order of magnitude on either side of the minimum and maximum experimental data point for every time point across each of the three experimental outcomes. The experimental data range includes over four orders of magnitude, therefore our pass set definition was selected because it encapsulates the general behavior of the experimental datasets we are using for calibration, and will not remove simulations that are within the same order of magnitude as experimental data points. Additionally, we know that the long-term behavior of bacterial numbers in granulomas is fairly stable without intervention,30–32 so we set an upper bound at 36,000 bacteria for days 90–200. If the simulation value for bacterial numbers eclipses this bound within those days, the simulation is immediately assigned as part of the fail run set. We sample this initial parameter space to create 500 model simulations and show the simulation outcomes overlaid with experimental data (Fig. 5). Of this sampling, only 6.8% of the runs satisfy the pass set definition. We then use ADS to narrow the parameter space and resample, finding that 46.8% of the runs satisfy the pass set definition during the second iteration. We iterate this process until the final iteration yields 91% of the total model runs belong to the pass run set, which is above our termination criterion of 75%. Additionally, the simulation outcomes are consistent with other information about this biological system: we know that bacterial levels of individual granulomas should peak prior to day 50, and should stabilize after day 100, whereas T cell and macrophage cell numbers should increase until they stabilize or drop around day 75.32 Thus, CaliPro is able to simultaneously calibrate a complex, non-linear ODE system to a series of diverse experimental outcomes and calibration goals.

Example 3: CaliPro Identifies Continuous Parameter Space for a Transmission Model of Infectious Disease without Assigning Likelihoods or Informative Priors

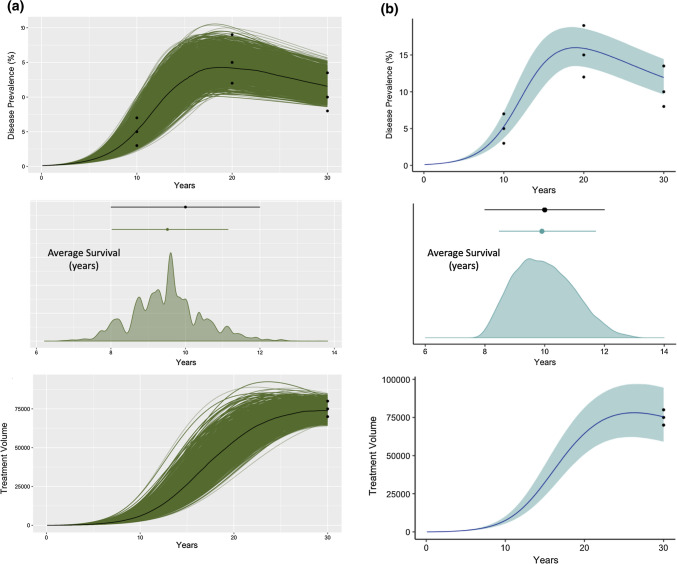
In a review of Bayesian calibration approaches, Menzies et al.38 present an ODE model of a generic sexually-transmitted disease that includes six state variables, representing non-susceptible, susceptible, early diseased, late diseased, treated, and dead populations. Eleven parameters govern the rates of transmission between these populations, and the model is evaluated for 30 years. See Menzies et al. for a model schematic and further model details.38 The equations for this model are available in Supplementary Material.

Additionally, the authors present three sets of “calibration targets”, or experimental datasets that are used to calibrate the model—disease prevalence, treatment volume, and average survival in years. Menzies et al. assign functions to approximate likelihoods of modeled outcomes to the original datasets and use an SIR technique to probe parameter space and calibrate the model to these targets (calibration technique and results recreated herein—Fig. 6a). However, as Menzies et al. point out, care must be taken when deciding to approximate likelihoods, define summary statistics, or assign distributions to experimental outcomes.38 Additionally, we suggest that any approximations or estimations derived from low sample sizes may introduce unnecessary assumptions into the calibration process.

Figure 6.

Example 3—disease transmission: SIR and CaliPro calibrations. (a) We recreated the results of Menzies et al.38 by using SIR to calibrate the ODE transmission model (individual model simulations shown as green lines and median trend line shown in black) to three experimental outcomes: disease prevalence, average survival (in years), and treatment volume. The average survival graph also shows the posterior distribution of average survival across all the parameter combinations. Experimental data are shown as black data points. (b) Model simulation and experimental outcomes following CaliPro using HDR. The 5th–95th percentile is represented by the blue region (50th percentile—dark blue line). Termination criteria: 75% of runs must belong to pass run set. Pass set definition: (iterations 1–3) For each time point, simulation values lie within 1.25 times the maximum experimental data point and 0.75 times the value of the minimum experimental data point for all calibration targets. (Iteration 4) Changed the lower bound of pass set definition to be an exact match to the experimental data at each timepoint.

Therefore, in this example, we use CaliPro to calibrate their ODE model to the same calibration targets, but do not impose likelihoods nor assume any prior known distributions of the experimental datasets. Unlike Menzies et al., and in an effort to further test CaliPro, we set our initial parameter range to create a parameter space that is uninformative—we uniformly sampled each of the seven varied parameters according to an LHS scheme. These initial parameter ranges were assigned to the widest values that Menzies et al. selected when they sampled with normal (or beta) parameter distributions. We generated 500,000 samples within this uninformative parameter space.

Of these samples, we outline a pass set definition as simulations that include average survival, treatment volume, and disease prevalence outcomes within the range bounded by 75% of the minimum and 125% of the maximum experimental data point for every experimental time point across each of the three outcomes. This pass set definition was selected because it encapsulates the general behavior of the calibration targets. Following each iteration, we refine parameter space by defining the new parameter ranges for each parameter using HDR with a coverage of 0.75 of the density created by the pass parameter set. After the first iteration, subsequent samplings generated 10,000 simulations (fewer samples were necessary to identify the pass run set). Following the third iteration, the distribution of the pass parameter set was trending toward the minimum values of the calibration target data for average survival time. Thus, we adjusted the lower bound of our pass set definition to be an exact match to the experimental data at each timepoint for the fourth iteration. After four iterations, 97% of model simulations satisfy the parameter set definition. Figure 6 shows the 95% confidence interval and median line of all the simulations in the calibrated parameter space. CaliPro is able to calibrate this model to the calibration targets outlined by Menzies et al. despite an uninformative prior and without assigning a likelihood function to the datasets. We propose that CaliPro is a useful calibration tool for a situation where the modeler is unable to assign priors or likelihoods (e.g. small sample sizes).

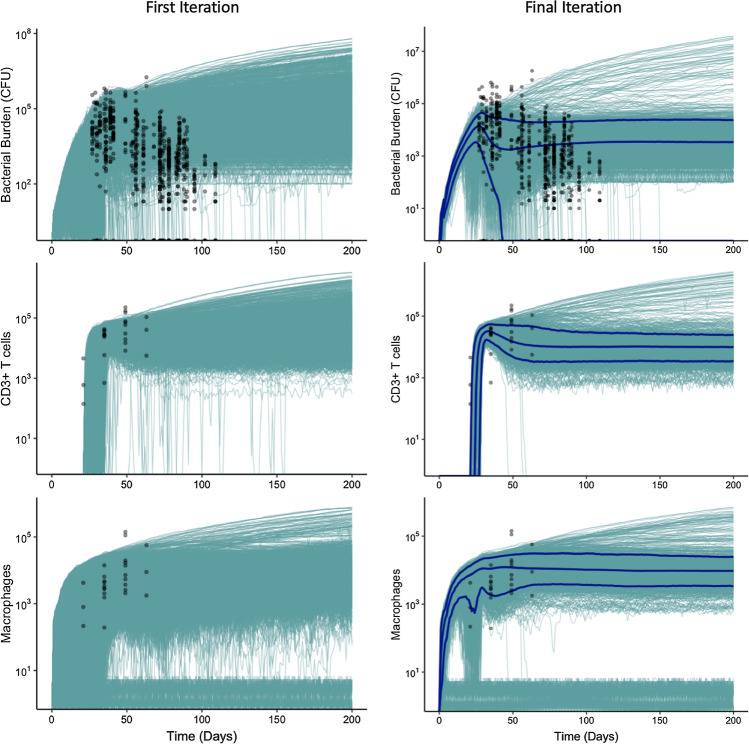
Example 4: CaliPro Successfully Calibrates Stochastic Models: Using an Agent-Based Model of Granuloma Outcomes as an Example

While CaliPro displays a promising ability to identify robust parameter space for ODE models of varying complexity, stochastic models are notoriously difficult to calibrate.38 We posit that CaliPro is agnostic to model formulation and therefore unbothered by new complexities that stochastic models raise in traditional calibration settings. Thus, we apply CaliPro to a stochastic agent-based model of granuloma formation, GranSim.

GranSim is a two-dimensional hybrid agent-based model of granuloma formation during Mycobacterium tuberculosis infection. GranSim captures the environmental, cellular, and bacterial dynamics at the site of infection across molecular, cellular, and tissue-scale events. The spatial environment of this model is a 4 mm by 4 mm section of lung tissue. Agents (cells) populate this environment and constitute various immune cells as well as bacteria. The cells interact with one another across time according to rules that dictate movement, speed, proliferation, and change of phenotype. Chemokines and cytokines also exist on the lattice, but are represented as continuous values instead of individual agents, making the model a hybrid formulation. As an established model, GranSim has been modified and calibrated across 15 years extensively to data from the NHP model of tuberculosis13,14,20,36,37,53,60,64 and see GranSim website for more details: http://malthus.micro.med.umich.edu/GranSim). Herein, we present a single calibration effort of this model using CaliPro.

Our data for single granuloma formation is the same as the experimental data we used to calibrate the granuloma ODE model (example 2). However, for this calibration, we use bacterial numbers as the primary measure to sort pass and fail simulations, then use the immune response metrics (T cell and macrophage counts) and visual confirmation of granuloma formation (via agent-based model snapshots) as validation measures. This adds a new spatial criterion that must be met in addition to the temporal dataset criteria.

For comparison, we select the initial parameter ranges to be the same as a previous manual calibration effort performed in the lab—where 52 of 131 parameters in GranSim are varied within reasonable bounds according to values from literature and previous versions of the model.13,14,60,64 We sampled this parameter space 1000 times according to an LHS scheme with three replicates each to create 3000 unique in silico granulomas (Fig. 7). For the first iteration, we specified the pass set definition to include simulations where total bacterial numbers in the simulation were less than the maximum experimental value (36000) at day 85. This pass set definition was selected because we wanted to isolate the simulations whose bacterial values decreased after peaking near day 40. After the first iteration, 62% of the runs satisfy the pass set definition. We refine the parameter space using the ADS method and resample to create another set of 3000 granulomas. At iteration 2, we redefined our pass set definition so that simulations must have less than 10⁴ bacteria at day 175—an additional criterion that was implemented so that simulation bacterial numbers remain stable across time. Of the 3000 simulations, 67.5% satisfy this new pass set definition. Again, we refined the parameter space using ADS, and resampled. However, this time 83% of simulations satisfy the pass set definition, eclipsing our preset termination criteria of 75%. As a validation step, we checked the immune response of these calibrated simulations to ensure the majority fell within the bounds created by the T cell and macrophage experimental data (Fig. 7). NHP granulomas have a distinct formation and, while there is variation, there are generally well-accepted spatial structures.10,32 So, as a secondary validation step, we manually inspected screenshots of the agent-based model to ensure that they recapitulated known granuloma spatial characteristics. This introduces modeler bias, however, as with most experimental studies, these kinds of assumptions and decisions are necessary. We are currently working on a way to automate visual discrimination of both simulated and experimental granulomas. Thus, CaliPro is able to calibrate a complex, stochastic and discrete hybrid model to a set of diverse experimental outcomes, calibration goals, and validation datasets.

Figure 7.

Example 4—agent-based model: CaliPro finds calibrated parameter space using ADS. Model simulations (blue lines) and experimental data (black data points representing total bacterial numbers, total Macrophage cell counts, and total CD3+ T cell counts) across time in days. The 5th, 50th, and 95th percentiles of model simulations are shown as dark blue lines for the final iteration. In simulations where bacterial burden sterilizes, the macrophage count drops below 10. Termination criteria: 75% of runs must belong to pass run set. Pass set definition: (Iteration 1) Simulations with total bacterial numbers less than the maximum experimental value (36,000) at day 85. (Iteration 2 and 3) Simulations with total bacterial numbers less than 10⁴ at day 175.

Discussion

Increasingly, mathematical and computational models are utilized to interrogate complex biological systems, provide context to understand interactions, and make predictions. Model calibration is a crucial step that ensures models reasonably portray biological complexities in the real system and can thus make reliable inferences or predictions of future system state(s). However, traditional calibration approaches are not always appropriate for complex biological models due to one of two drawbacks: 1) many calibration approaches minimize an objective function in order to recapitulate only a single aspect of the experimental data (such as a median trend) or 2) Bayesian calibration techniques require specification of parameter priors and likelihoods of experimental data which cannot always be confidently assigned if there are low numbers of experimental samples or if distributions across samples are indistinguishable. As such, we have developed CaliPro, an iterative calibration protocol that utilizes parameter density estimation to refine model parameter spaces and to calibrate models to temporal biological datasets.

By assigning model simulations to a pass or fail run set upon each sampling of parameter space, CaliPro provides an automated framework through which the goals of calibration are clearly defined and standardized. Further, as the definition of pass vs. fail is a user-intensive step, the roles of both modelers’ expertise and biologists’ intuitions are more explicitly integrated into CaliPro. As such, specifying a pass set definition is perhaps the most crucial step in CaliPro. However, it can easily be defined by considering the acceptable criteria under which the modeler might be satisfied when calibration is considered complete. For example, there may be multiple calibration goals, as we outlined in Example 2, where model simulations must match the general dynamics outlined by the three separate experimental datasets. Additionally, by imposing an upper-bound for bacterial numbers at later time points, we explicitly integrated the intuition of the biology into the calibration process. We believe that CaliPro’s incorporation of explicit definitions of intuition are an important contribution of this method that is typically overlooked within other calibration procedures.

Relatedly, the modeler can toggle the pass set definition according to bounds defined by the datasets available. If the datasets are sparse or are estimated across a wide range of studies, then a modeler can assign a pass set definition that is more lenient. Conversely, if a modeler is certain that datasets represent an absolute maximum or minimum value that could ever be observed experimentally, then the modeler should define a very strict adherence to dataset(s). Like others,2 we tend to subscribe to the notion that a model likely captures more biological variability than the heterogeneity observed from the naturally limited sample sizes procured from experimental datasets.

If CaliPro fails to identify a robust calibrated parameter space, the user should evaluate their input prior to attempting other methods of calibration. Primarily, we suggest evaluating the pass set definition. This is a crucial step within CaliPro, and as our results section shows, iteration successions do not require the same pass set definition. In general, we have found the number of CaliPro iterations should have an inverse relationship with the leniency of the pass set definition. Thus, the pass set definition should become more strictly aligned with the experimental datasets as CaliPro progresses through iterations.

The method of refining the model parameter space is another user input that can dictate the success of calibration. HDR more quickly narrows parameter space between iterations. If the range of experimental data is very narrow, HDR may be the correct choice (such as the predator–prey model and transmission ODE model examples). However, if the range of experimental data varies greatly within one time point, ADS might be the more appropriate choice. In general, we suggest that modelers use ADS as this method accounts for information from all aspects of parameter space (pass and fail sets) whereas HDR only includes information from a subset of space (only pass sets).

While we have shown that CaliPro works for both stochastic and deterministic models, CaliPro may not be the correct approach for every calibration situation. For example, there is a vast literature of calibration solutions targeted at recapitulating just one dynamic in a mathematically rigorous manner. Further, CaliPro is only able to identify a parameter space where system outcomes recapitulate the dynamics of the experimental dataset. In the predator–prey model (Example 1), it is well-known that the system can exhibit chaotic behavior.58 However, because the synthetic experimental dataset for that example does not exhibit this chaotic behavior, CaliPro does not identify a parameter space that captures that system behavior. More generally, when applying CaliPro to any modeling system, CaliPro is unlikely to find behavior that exists outside the ranges of calibration datasets, and thus may “miss” potentially interesting behaviors that could be predictions of the model for other parameter ranges.

Additionally, if the modeler is comfortable specifying likelihood functions to relate the model and experimental datasets in-hand, we suggest employing one of the suites of Bayesian calibration approaches, such as SIR. Further, in our experience, calibrating agent-based models that exhibit oscillations (such as agent-based models of predator–prey dynamics) with CaliPro is a difficult task. Identifying the pass run set in such a situation is complicated as the timing of the oscillations may differ between model simulation and experimental data, resulting in a failed run even when frequency and peak-to-trough values of simulations and experiments are identical. For agent-based models that exhibit oscillations, one could perform a Fourier transform on simulation outcomes and compare to experimental data within the frequency domain to evaluate the model as one solution.

In addition to enabling models to reasonably approximate biological processes, we believe a great strength of CaliPro is the potential to extend beyond the calibration protocol itself. In particular, the parameter density plots (as we showed in Fig. 4) that are created for the pass and fail parameter sets within every iteration provide a large amount of information to the modeler. In general, we advise using the parameter density plots as a quick and easy method to identify and focus on certain behavior in the model. For example, if a subset of runs exhibit interesting behavior near the end of a simulation, the modeler can consider this subset the pass run set and then compare the parameter densities of the pass parameter set to those of the fail parameter set—those that do not exhibit the behavior. Moreover, after the final iteration, when the model has been calibrated to the experimental datasets, a modeler could use the parameter density plots (Fig. 4) in order to identify the ideal prior distribution of each parameter (instead of uniform or normal) for future model simulations. Finally, beyond the scope of this paper—but an important consideration for any calibration or modeling process—we believe the parameter density plots offer a possible method for identifying highly correlated parameters by isolating parameters whose density plots are near identical across model behavior (see Reference 19 for an excellent framework to address parameter identifiability).

Electronic supplementary material

Below is the link to the electronic supplementary material.

Abbreviations

ODE

Ordinary differential equation

LHS

Latin hypercube sampling

HDR

Highest density region

ADS

Alternative density subtraction

SIR

Sample importance resampling

TB

Tuberculosis