Refining all-atom protein force fields for polar-rich, prion-like, low complexity intrinsically disordered proteins

Abstract

Significant efforts in the last decade have given us highly accurate all-atom protein force fields for molecular dynamics (MD) simulations of folded and disordered proteins. These simulations, complemented with experimental data, provide new insights into molecular interactions that underlie the physical properties of proteins, especially for intrinsically disordered proteins (IDPs) for which defining the heterogeneous structural ensemble is hugely challenging by experiments alone. Consequently, the accuracy of these protein force fields is of utmost importance in order to ensure reliable simulated conformational data. Here, we first assess the accuracy of current state-of-the-art force fields for IDPs (ff99SBws and ff03ws) applied to disordered proteins of low amino acid sequence complexity that can undergo liquid-liquid phase separation. Based on a detailed comparison of NMR chemical shifts between simulation and experiment on several IDPs, we find that regions surrounding specific polar residues result in simulated ensembles with exaggerated helicity when compared to experiment. To resolve this discrepancy, we introduce residue-specific modifications to the backbone torsion potential of three residues (Ser, Thr, Gln) in the ff99SBws force field. The modified force field, ff99SBws-STQ, provides a more accurate representation of helical structure propensity in these LC domains without compromising faithful representation of helicity in a region with distinct sequence composition. Our refinement strategy also suggests a path forward for integrating experimental data in the assessment of residue-specific deficiencies in the current physics-based force fields and improve these force fields further for their broader applicability.

Graphical Abstract

Introduction

Intrinsically disordered proteins (IDPs) and regions (IDRs) are biologically functional without adopting a single well-defined folded structure.¹ They are present in a significant fraction in the proteome of all organisms^1–3 and participate in essential physiological and pathological functions including stress response⁴ and signaling.⁵ They are also involved in cell regulation and various neurodegenerative diseases such as amyotrophic lateral sclerosis (ALS) and frontotemporal dementia (FTD) through the formation of protein aggregates.⁶ IDPs are also involved in cellular liquid-liquid phase separation (LLPS), which underlies the formation of some membraneless organelles^7,8 and may serve as precursors for pathogenic aggregates.^9,10 Many IDPs can contain partial secondary structures, including helices^11,12 and β-sheet structures,^13,14 that can contribute to their intermolecular interactions and self-assembly processes. Therefore, accurately probing these transient secondary structures in experiments and simulations is essential for understanding the underlying molecular mechanisms of protein assembly in LLPS.

Experimental techniques such as X-ray crystallography and cryogenic electron microscopy (cryo-EM) can resolve folded protein structures down to angstrom-scale but are unable to provide detailed spatiotemporal information on the equilibrium structural ensembles of disordered proteins because these techniques and sample preparations quench and/or cannot observe the heterogeneous nature and rapid interconversion between a large number of microstates.¹⁵ Nuclear magnetic resonance (NMR) in solution has provided a wealth of information on the local structural and dynamical properties of IDPs to generate important insights into their biological function. It is often helpful to combine NMR data with molecular modeling techniques to generate conformational ensembles consistent with the experimental observables such as chemical shifts and J-coupling to obtain atomic details obscured by averaging.^16–20 It is also highly desirable to obtain the necessary information on IDP properties directly from physics-based all-atom transferable force fields without requiring any experimental input on the system of interest. Such models can provide unprecedented details on the structural and dynamical properties as well as atomic interactions responsible for the observed behavior.^21,22 This can be critical in establishing IDP sequence-structure/motions-function relationships and provide hypotheses for experimental work.²³

With the rapid development of computer hardware and advanced sampling techniques to conduct molecular dynamics (MD) simulations based on atomistic protein force fields over the past decade, it became apparent that improvements in their accuracy and transferability were necessary to realize the potential for molecular simulations to serve as a “computational microscope.”^24,25 Progressive efforts in the last 10–15 years have resulted in significant improvements in the accuracy of all-atom protein force fields beginning with a substantial step forward on achieving secondary structure balance and thereby demonstrating true transferability in terms of their application to proteins of different structural classes.^26–29 The empirical approach by Best and Hummer to use helical propensity data on a short peptide,²⁶ Ac-(AAQAA)₃-NH₂, to achieve such secondary structure balance also demonstrated that the potential energy functions only needed fine-tuning as opposed to a significant reparameterization as in previous force field development efforts.

This strategy to modify only backbone-torsion-potentials yielded many improved force field variants, marked by a symbol ‘*’ next to their name, such as ff03*, ff99SB*, charmm22*.^26,30 In these force fields, modifications on backbone torsion potentials were applied uniformly to all amino acids (except proline and glycine) and was not tuned to capture any residue-specific biases in the force field. Since then, several studies have taken additional steps to make residue-specific corrections to side-chain³¹ and backbone³² torsion potentials, as well as more elaborate bottoms-up parameterization of energy function parameters,^33–36 resulting in highly accurate protein force fields.

The use of these optimized force fields has been especially fruitful for studying IDPs by overcoming challenges of using the experimental techniques alone.^37–40 At the same time, the flat conformational energy landscapes of IDPs can make conformational ensembles more sensitive to systematic errors in the model. Therefore, simulations of IDPs have been used successfully for evaluating the remaining deficiencies of these force fields and providing roadmaps for their continued improvement.⁴¹ For example, the unfolded states of proteins remained too collapsed in the force fields tuned for secondary structure balance alone (such as ff03*), which was also corroborated by available experimental data from single-molecule FRET and SAXS.⁴² Some improvements in preventing unfolded state collapse were visible by changing the water model (TIP4P/2005)⁴³ in protein simulations while trying to improve the temperature cooperativity of the helix-coil transition and the associated solvation effects. The new protein force fields, marked by symbol ‘w’ for an improved water model TIP4P/2005 (ff03w and ff99SBw), provided significant improvement in protein-protein interactions but only modest success in capturing IDP dimensions.⁴⁴ Based on the accumulated evidence from other studies, protein-water interactions were scaled (strengthened)⁴⁵ to model the size of solvated disordered proteins accurately with force fields suffixed by ‘ws’ such as ff03ws and ff99SBws.⁴⁶ Our previous work based on these optimization strategies has leveraged the force field improvements to probe the secondary structure, single-chain configurations, and contact formation of IDPs and demonstrated their applicability to reproduce the structure and dynamics of unfolded proteins accurately. ^47–50,

At this point, it is instructive to ask if there are areas of concern about the applicability of these refined force fields for IDPs. The recent surge of interest in biomolecular LLPS and the underlying atomic interactions responsible for stabilizing the protein-rich condensed phase has motivated us to look at low complexity (LC) IDPs⁵¹ in which a few amino acid types dominate their composition, and at prion-like domains, named for their polar-rich residue sequence composition that resembles the composition of yeast prion proteins.⁵² These LC IDPs present new challenges in conducting accurate simulations as any minor deficiencies in particular amino acid types that dominate the sequence composition can propagate additively. Therefore, we believe that LC protein sequences are useful benchmarks to assess the accuracy of current state-of-the-art all-atom force fields.

Methods

All-atom MD simulations were conducted on 44-residue fragments from the disordered regions of FUS LC (FUS LC_0–43, FUS LC_37–97, FUS LC_41–84, FUS LC_77–120, FUS LC_120–163), TDP-43 CTD (TDP-43_310−350),RNA Pol II CTD heptads (RNA Pol II_1927−1970), and hnRNPA2 LC (hnRNPA2_190−233, hnRNPA2_265−308). The length of the peptides was chosen, such that sampling the conformational space of the protein is computationally tractable. The GROMACS 4.6.7 MD engine⁵³ was used for simulations, with PLUMED 2.2.4 plugin.⁵⁴ Simulations were conducted using different variants of Amber force fields as specified in the text (see SI Tables S2–S4), using the original and modified versions of ff03ws and ff99SBws⁴⁶ which includes TIP4P/2005 explicit water molecules.⁴³ Production simulations were conducted using replica exchange molecular dynamics (REMD)⁵⁵ in a well-tempered ensemble (WTE),^56,57 a type of metadynamics method.⁵⁸ This combination is known as parallel tempering in the well-tempered ensemble (PT-WTE) and is useful for reducing the number of replicas required to explore the conformational space efficiently. Temperature is held constant for each replica using Langevin dynamics as a thermostat with a friction constant of 1 ps⁻¹ and a time step of 2 fs. Electrostatic interactions are calculated using the particle-mesh Ewald method⁵⁹ up to fourth order with a real-space cutoff distance of 1.0 nm. A 1.0 nm cutoff distance is used for the van der Waals interactions. For each protein, a random protein structure is generated and solvated in a truncated octahedron box with a face-to-face distance of 6.5 nm. The system is initially equilibrated for 100 ps at each temperature used for parallel tempering. In our simulations, 16 replicas at temperatures ranged from 300 to 500 K are constructed. Differences in temperatures between the replicas are determined such that the exchange acceptance probability is about 30%. The positions and velocities of the thermally equilibrated system are then used as the initial configuration of the PT-WTE simulations. WTE was applied using Gaussian functions of width σ_i = 750 kJ/mol added at a τ_G =20 ps interval, with a bias factor of γ = (T +ΔT)/ΔT = 36 and initial hill height of 2.5 kJ/mol. Chemical shifts and helical propensities in these simulations are calculated using the SPARTA+ algorithm⁶⁰ and secondary structure is computed using DSSP.⁶¹ Experimental secondary structure propensities were also be derived from NMR secondary chemical shifts by using the δ2d software.⁶² RMSD (root-mean-squared deviation) from experimental chemical shifts (see SI text) was calculated as (x_sim − x_expt)²/N where N is the number of residues sampled, x_sim is the simulated chemical shifts from SPARTA+ and x_expt is the NMR chemical shifts. For each peptide, two residues from each terminus and residues missing from experimental data are not included in the analysis. RMSD is calculated for each residue type based on the chemical shift differences between simulations and experiments. The relevant input files can be downloaded at https://bitbucket.org/jeetain/all-atom_ff_refinements.

Results and Discussion

We conduct parallel tempering (PT) MD simulations in a well-tempered ensemble (WTE)⁵⁶ to enhance conformational sampling (see Methods) with two suitable force fields for IDPs (ff03ws and ff99SBws) on a set of prion-like domains including domains from TDP-43, Fused in Sarcoma (FUS), and hnRNPA2, as well as the C-terminal heptad repeat domain of RNA Polymerase II (RNA Pol II),.^47,48,50,63 Similar to our previous work, we use 44-residue fragments of these proteins to reduce the computational cost associated with simulations of full-length proteins using a multi-replica approach necessary to obtain converged equilibrium properties. We use the lowest temperature (300 K) replica for all the analyses presented in this paper.

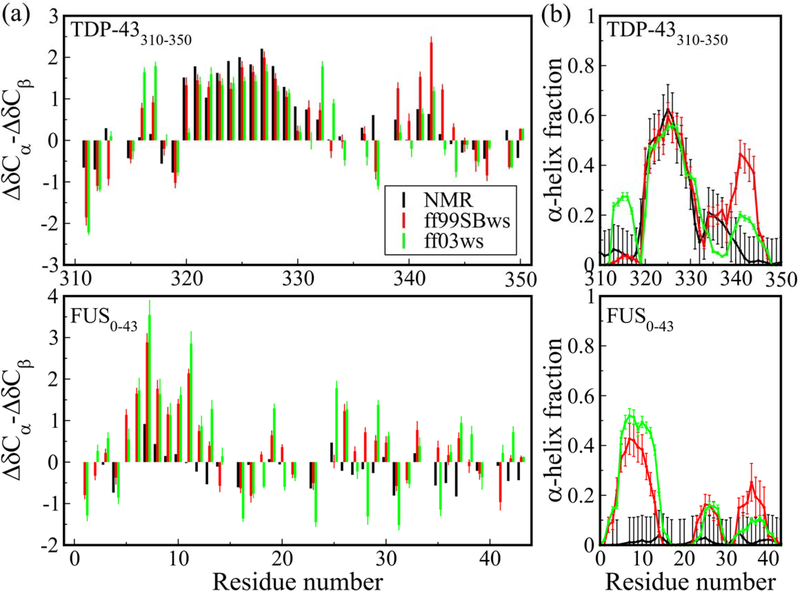
First, we focus on the results of two protein fragments, TDP-43_310–350 and FUS LC_0–43, as an example of IDPs where NMR data suggest partial helical structure and complete disorder, respectively. We calculate the chemical shifts from the simulated ensembles using the SPARTA+ algorithm⁶⁰ and subtract the sequence-based random-coil values from the Poulsen webserver⁶⁴ to compute secondary chemical shifts, which can be used to infer secondary structure populations. Figure 1a shows an excellent agreement between the simulation and experimental data in the helix-forming region (ΔδC_ɑ-ΔδC_β values, a well-established metric of helical (positive values) or sheet (negative values) computed by calculating the difference between the C_ɑ and C_β observed chemical shifts and those expected for a completely random coil disordered protein) at residues 321–330 in TDP-43_310–350, an alanine rich region embedded in the LC domain.¹² However, in the case of FUS LC_0–43, simulation data suggests the formation of helical structures in the N-terminal region, residues 6–13, which is not supported by the experimental data.^22,65 We also compute the secondary structure propensities from the simulation data directly using the DSSP algorithm⁶¹ and compare these to the predicted values based on the experimental NMR chemical shift data using the δ2d webserver⁶² (Fig. 1b). Again, we see excellent agreement between simulation and experiment regarding the presence of partial helicity in the alanine-rich segment of TDP-43, but apparent overpopulation of helix in several regions of the polar rich FUS LC. Overall, both the force fields display similar behavior with some minor differences.

Figure 1.

(a) Chemical shifts ΔδC_α − ΔδC_β and (b) α-helix propensities of TDP-43_310−350 and FUS₀₋₄₃ using all-atom force fields ff99SBws and ff03ws, compared to experimental results. Chemical shifts are calculated from protein structure using SPARTA+ algorithm. Secondary structures are assigned by DSSP. Experimental values of secondary structure propensities are calculated from NMR chemical shifts using the δ2D program.

Robustelli et al. had shown a similar behavior for ff03ws on other IDPs with various partially populated secondary structures and proposed a new force field to provide a better representation of folded and disordered proteins.³³ We also conducted additional simulations using their ff99SB-disp force field.³³ These data are shown in supporting information (SI) Fig. S1. Consistent with previous findings that partial helical structures may be underpopulated in ff99SB-disp³³, simuations with ff99SB-disp show underpopulation of helix in TDP-43_310–350 while lower overall helicity for the disordered FUS LC_0–43. However, it is interesting that the simulated ensemble using ff99SB-disp also populates ɑ-helical structures, like ff03ws and ff99SBws, in the N-terminal part of FUS LC_0–43 which are not present in the experimental data.

The analysis above clearly suggests that further fine-tuning of the current state-of-the-art force fields is needed to make them suitable for low-complexity sequences such as FUS LC_0–43. The observed overpopulation of helical structures in the case of FUS LC_0–43 is most likely related to the presence of specific amino acids for which the balance in helical and extended structures is not optimal. In our previous work, we had used the Lifson-Roig helix growth parameter (w) to assess residue-level helical propensities with a model Ala-based host-guest peptide that helped us identify residues with significant deviations from the experiment and propose refinements.⁶⁶ Moving forward, it will be useful to develop a strategy that can take advantage of the available NMR data on the sequences of interest and does not require us to interpret the secondary structure propensities in terms of a helix-coil transition model in the context of a host-guest peptide.

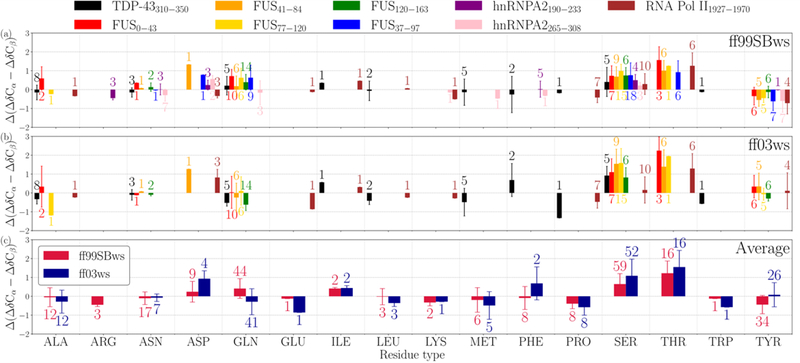
Here, we calculate the differences between the secondary chemical shifts between the simulation and experimental data, Δ(ΔδC_ɑ-ΔδC_β) = (ΔδC_ɑ-ΔδC_β)_sim - (ΔδC_ɑ-ΔδC_β)_expt, for each residue in a variety of IDPs for which NMR data are available. We selected many peptide fragments from a set of prion-like IDPs such as FUS LC, TDP-43 CTD, hnRNPA2 LC, RNA Pol II C-terminal domain for the proposed comparison (SI Table S1). These LC protein sequences are mainly composed of polar and aromatic amino acids with a low occurrence of nonpolar aliphatic amino acids. The Δ(ΔδC_ɑ-ΔδC_β) data are shown in Fig. 2 as a for each residue type and each simulated peptide (Fig 2a,b) and the average over all the peptides with the two force fields (Fig 2c). We find that the residues Ser and Thr in ff99SBws and ff03ws, and Gln in ff99SBws, which constitute a significant fraction of the amino acid composition in these sequences, deviate significantly from the experimental values. The positive Δ(δC_ɑ-δC_β) values reflect the overpopulation of helical structures in these residues. Numerically, the average deviations for threonine are the most significant (~ +1.0 ppm) followed by serine (~ +0.5 ppm) and glutamine (~ +0.3 ppm) in ff99SBws. Also, the observed deviations in different sequences (Fig. 2a,b) may reveal sequence-dependence to some degree, but the overall trend is qualitatively consistent.

Figure 2.

Deviation of chemical shifts Δ(ΔδC_α −ΔδC_β) (in ppm) in simulations from NMR ¹³C chemical shifts. (a) and (b) shows Δ(ΔδC_α −ΔδC_β) of each peptide from ff99SBws and ff03ws simulations, respectively. (c) shows the average of all peptides in the same force field. Error bars are the standard deviations among the sampled residues. Annotated numbers next to the bar are the number of the residues of that type present in the chosen peptide(s).

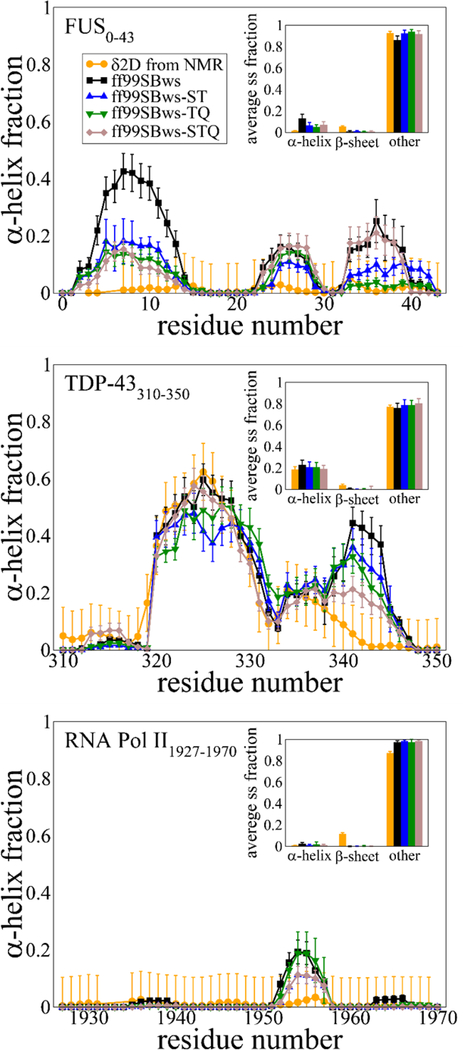
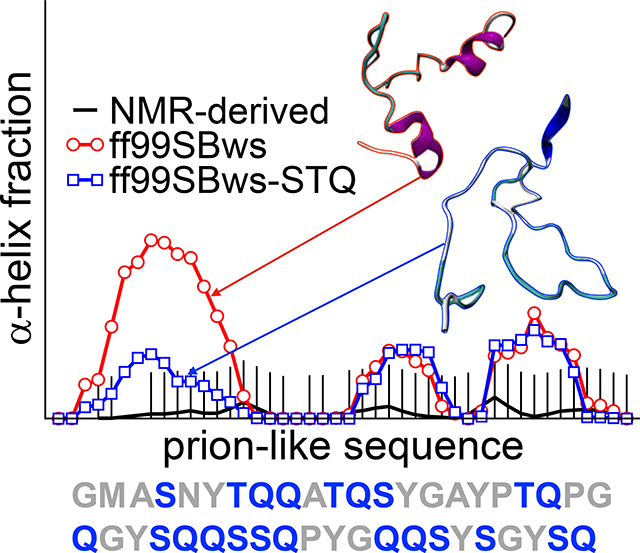
Based on the analysis above, we decided to test the effect of changes in the backbone torsion potential parameters of three amino acids (Ser, Thr, and Gln, referred hereafter as STQ group) in ff99SBws. Best and Hummer proposed the following form for the backbone dihedral angle ψ correction: V₁(ψ;k_ψ,δ_ψ) = k_ψ[1+cos(ψ −δ_ψ)], where k_ψ and δ_ψ are the magnitude and phase offset of V₁, respectively. For ff99SBws, k_ψ = 2.0 kJ/mol and δ_ψ =105.4° are used to correct the intrinsic bias toward β-sheet structures for the ff99SB force field.²⁶ After testing for various values, we find that a reduction in k_ψ from 2.0 kJ/mol to 1.0 kJ/mol is sufficient and appropriate to shift the bias away from helical configurations. To make a broader assessment on how changes in the potential parameters for the STQ residues affect the observed secondary structure propensities, we tested several combinations of the modified residues (S, T, ST, TQ, STQ; Figure 3) for three peptides from our dataset, FUS LC₀₋₄₃, TDP-43_310−350, and RNA Pol II_1927−1970. We conduct PT-WTE simulations for these three peptides with variants of the ff99SBws force field, where the suffix letter(s) represent the amino acids for which the k_ψ is modified. For example, in the case of ff99SBws-ST, torsion potential is changed for Ser and Thr residues.

Figure 3.

Secondary structure propensities of (a) FUS₀₋₄₃, (b) TDP-43_310−350, and (c) RNA Pol II_1927−1970. Error bars for DSSP values are deviations between 10-ns segments in the simulation trajectories. Error bars for δ2d population per residue are 0.1 (10%).

The Δ(ΔδC_ɑ- ΔδC_β) comparison between the ff99SBws and its new variants are shown in the SI Fig. S2 for ST, TQ, and STQ. We note that a change in only one of the residue types (S or T) k_ψ is not sufficient to observe any meaningful differences from the ff99SBws force field (Table 1). For force field variants with two or more residues k_ψ modified, we find that the deviations consistent with overly helical simulations are reduced for FUS LC_0–43 but are minimally affected for TDP-43_310–350 and RNA Pol II_1927–1970. For reference, an additional comparison between ff99SBws, ff99SBws-STQ, and ff99SB-disp force fields is presented in SI Fig. S3, showing that ff99SB-disp does not fully capture the balance of partial helical structure in these sequences. To quantify the overall differences on the whole sequence, we computed the root mean squared deviation (RMSD) between the simulation and experimental data and report it in Table 1. The RMSD values highlight the benefits of applying the proposed residue-specific changes for all the peptides, but this is especially true for the FUS LC. We also confirm that these changes do not negatively impact the observed Δ( ΔδC_ɑ- ΔδC_β) behavior of other neighboring residues.

Table 1:

Root-mean-squared deviation (RMSD) of simulated ΔδC_α – ΔδC_β (in ppm) from NMR ¹³C chemical shifts of three IDPs for ff99SBws, modified ff99SBws variants (S,T,ST,TQ,STQ) (this study), and ff99SB-disp.

	FUS0–43	TDP-43310–350	RNA Pol II1927–1970
ff99SBws	0.90 ± 0.11	0.64 ± 0.09	0.68 ± 0.11
ff99SB-disp	0.90 ± 0.11	0.78 ± 0.07	0.74 ± 0.11
ff99SBws-S	0.86 ± 0.10
ff99SBws-T	0.98 ± 0.13
ff99SBws-ST	0.64 ± 0.07	0.71 ± 0.08	0.74 ± 0.08
ff99SBws-TQ	0.62 ± 0.08	0.66 ± 0.06	0.71 ± 0.10
ff99SBws-STQ	0.54 ± 0.07	0.51 ± 0.04	0.74 ± 0.08

To visualize the local structural changes, we also calculate the secondary structure propensities from the simulated ensembles using the DSSP algorithm for these different force field variants and compare it with experimental values derived from chemical shifts using δ2D method (Fig. 3). For FUS LC_0–43, the modified force fields (ST, TQ, and STQ) significantly reduce the helicity in the N-terminal region as compared to the ff99SBws. The helical fraction at all residue positions is below 20%, which we believe may be at or close to the detection limit for interpretation of the NMR data using methods based on chemical shifts such as δ2D given the possibility of many different low population states with different structures making up the conformational ensemble. For TDP-43_310−350, we do not observe a significant change in the helical population in the previously identified region (residues 321–330) among different force fields, a considerable decrease in helicity (from 40% to 20%) is observed between residues 340–345. The latter (STQ) helps improve the agreement with the experiment, which is different than what is seen in the case of ff99SB-disp that shows reduced helicity everywhere for this peptide (SI Fig. S3). RNA Pol II_1927−1970 shows relatively little changes in the observed behavior presumably since it is almost entirely disordered, which was already captured well in the ff99SBws force field.

To check if inter-residue contacts are affected by the changes in the force field parameter, we compute contact maps for FUS_0–43 and TDP-43_310–350, as shown in SI Fig. S4 and S5. As expected, a significant reduction in helical contacts (i,i+4) is observed, but otherwise, the contacts are relatively similar between the structural ensemble generated based on ff99SBws and ff99SBws-STQ. We note that the changes in the peptide dimensions due to the STQ dihedral corrections are relatively small (SI Fig. S6), and therefore, not expected to lead to significant changes in the formation of non-local intramolecular contacts.

To assess the convergence of our simulation data in terms of secondary structure propensity, we also plot residue-level secondary structure as a function of simulation time for each replica moving through the temperature space (SI Fig. S7 and S8). These data highlight many transitions between different states and the transient nature of populated structures, which ultimately contributes to the convergence of the estimated propensities reported in the paper.

We also check the performance of these new parameters with an additional test case, which is commonly employed to test the suitability of dihedral corrections, i.e., (AAQAA)₃ peptide. As shown in SI Fig. S9, there is a small reduction in the helical propensity of this peptide, but the overall results are still consistent with the NMR data.

We believe that the changes proposed here should improve the accuracy of the force field in general, but more work is needed to see if certain sequences containing STQ residues do not show improvement in agreement with experimental observables compared to the ff99SBws model. Nonetheless, we note that many recent studies have proposed force fields with residue-specific torsion and nonbonded parameters to improve their accuracy with a particular focus on IDPs. It is possible to incorporate some of these changes in our proposed force field further to improve the resulting IDP properties of arbitrary sequences, but significant work is needed to test the combination of parameters that will yield an optimal behavior. We plan to focus on this in our future work.

Conclusion

In conclusion, our proposed residue-type specific modifications on backbone torsion potentials of ff99SBws improved the accuracy of all-atom simulation of low-complexity IDPs (FUS₀₋₄₃, TDP-43_310−350, and RNA Pol II_1927−1970) in terms of their agreement with the ¹³C NMR chemical shifts, and hence secondary structure propensities. In this study, we adjusted the torsion potential correction parameter for three polar amino acids (S, T, and Q) to illustrate a promising path for all-atom force field optimization for IDPs using NMR spectroscopy data. Most importantly, the new force field (ff99SBws-STQ) is still transferable and does not require any experimental input while simulating a specific protein system of interest. We expect that ff99SBws-STQ will provide a more accurate description of the structural and dynamical properties of IDPs involved in the formation of biomolecular condensates via LLPS and become an indispensable model for future simulations of the many disordered proteins rich in polar residues.