Temperature-Dependent Kinetic Isotope Effects in R67 Dihydrofolate Reductase from Path-Integral Simulations

Abstract

Calculation of temperature-dependent kinetic isotope effects (KIE) in enzymes presents a significant theoretical challenge. Additionally, it is not trivial to identify enzymes with available experimental accurate intrinsic KIEs in a range of temperatures. In the current work, we present a theoretical study of KIEs in the primitive R67 dihydrofolate reductase (DHFR) enzyme and compare with experimental work. The advantage of R67 DHFR is its significantly lower kinetic complexity compared to more evolved DHFR isoforms. We employ mass-perturbation-based path-integral simulations in conjunction with umbrella sampling and a hybrid quantum mechanics–molecular mechanics Hamiltonian. We obtain temperature-dependent KIEs in good agreement with experiments and ascribe the temperature-dependent KIEs primarily to zero-point energy effects. The active site in the primitive enzyme is found to be poorly preorganized, which allows excessive water access to the active site and results in loosely bound reacting ligands.

Introduction

Enzymes are flexible biological macromolecules that greatly accelerate chemical reactions relative to the uncatalyzed reaction in aqueous media.^1,2 The source of the catalytic effect in enzymes is multifaceted, but much of the catalytic power of enzymes may be ascribed to preorganization of the charge distribution in active sites, which preferentially stabilizes the transition state (TS).^1,2 The many aspects of the catalytic effect in enzymes have been studied extensively using both experimental and theoretical methods.³⁻¹¹

An important tool in studying enzymatic reactions is kinetic isotope effects (KIE). KIE is a very sensitive tool for studying enzyme reaction mechanisms as KIE can provide insights into reaction kinetics,¹²⁻¹⁴ dynamics in the active site,¹⁵⁻¹⁸ solvent effects,^19,20 and TSs.²¹⁻²³ KIEs explore the change in the rate of a reaction upon isotopic substitution and can provide direct information regarding changes in bonding during the chemical event. Specifically, primary KIEs are the indicator for atoms that are directly involved in bond making or breaking at the TS, while secondary KIEs indicate the location of the TS along a reaction coordinate.²⁴ Another useful and characteristic property is the temperature dependence of KIE as it provides valuable information regarding the interplay between catalytic site dynamics and mechanisms.²⁵⁻²⁷ The temperature dependence of KIEs in enzymes has been studied extensively in recent decades;¹¹ however, the source of the temperature dependence is controversial. The presence of temperature-independent KIEs has been interpreted as an indicator of quantum mechanical tunneling and the ability of enzymes to reach so-called tunneling-ready states.²⁸⁻³³ It has been suggested that the coupled protein motions on the ps–fs timescale might reduce the barrier height^6,34−36 or promote tunneling by modulating the potential energy barrier along the chemical reaction coordinate [e.g., donor–acceptor distances (DAD)].³⁷⁻⁴² Some studies suggest that fast protein motions couple to the tunneling-ready conformation and directly modulate the width of the activation barrier and hence the reaction rate.^37,43−46 It has also been proposed that slower millisecond conformational fluctuations may be involved in driving the chemical step of the reaction.⁴⁷⁻⁵¹

Dihydrofolate reductase (DHFR) has been used as a prototype protein to study enzyme kinetics and dynamics,^49,52−62 and in particular E. coli DHFR (ecDHFR) has been widely used.^{42,47,48,62−67} Experimental and theoretical studies on wild-type (WT) ecDHFR have shown varying degrees of KIE temperature-dependence, depending on the methods applied.^{16,30,35,51,62−65,68−73} Kohen and co-workers showed significant variation in the temperature dependence of the KIE for mutant forms of the enzyme.^16,30,70,71 This was ascribed to the effect of mutations on the enzyme dynamics, and especially on the DAD motion.⁷⁴⁻⁷⁸ Here, the temperature independence of the KIEs was proposed to originate from tightly distributed DADs at the TS (e.g., in WT ecDHFR), which is thought to be optimized for hydrogen tunneling and does not change significantly with temperature. In contrast, temperature-dependent KIEs have been suggested to be a consequence of a loose active site where the TS is composed of a wide range of DADs at thermal equilibrium, and therefore, the distribution of DADs is temperature-sensitive. In contrast, an experimental and computational study of standard ecDHFR and heavy ecDHFR (isotopically labeled) suggested that the fast enzyme vibrations are not electronically coupled to the bond activation but found stronger coupling at lower temperatures below 20 °C.⁷⁹ In spite of the numerous experimental and theoretical studies of ecDHFR, no consensus have emerged as to the role of temperature dependence of KIE and tunneling. Part of this lies in the complex kinetic scheme in ecDHFR.^68,80 Theoretical studies attempting to compute the temperature-dependent KIEs in ecDHFR have also been published,^{11,39,81−86} yet this remains a challenge.⁸⁴ Hence, it would be helpful to test theoretical methods for enzymes where the kinetics is simpler and the rate-limiting step is unmasked.

Experimental studies on the primitive R67 DHFR revealed temperature-dependent KIEs. These studies suggested that the primitive enzyme is poorly preorganized and requires significant gating of its DAD prior to the reaction, resulting in significant temperature dependence.^87,88 The advantage of studying R67 DHFR is its simple kinetic scheme, with measured KIEs that are nearly free of kinetic complexity.

In the present study, we compute the KIEs for primitive R67 DHFR to investigate the correlation between the KIEs, their temperature dependence, DAD distribution, and active site preorganization and dynamics. The current study complements earlier experimental work on this enzyme. Here, we employ quantum mechanics–molecular mechanics (QM/MM), in conjunction with classical molecular dynamics and quantum path-integral (PI) methods, to understand the temperature dependence of KIEs in R67 DHFR.

Methods

System Preparation

Initial Michaelis complexes were constructed using the X-ray crystal structures of plasmid-encoded DHFR, that is, R67 (2rk1),⁸⁹ with bound folate and the oxidized cofactor NADP⁺. The activated ternary complex of R67 DHFR exists as a homo-tetramer at physiological pH which dissociates into dimers at low pH values. We used the monomeric R67 (2rk1) from the Protein Data Bank, and the coordinates were replicated with 222 symmetry to obtain the tetrameric protein (Figure 1A). We note that R67 monomer consists of 78 amino acids after cleavage of the highly disordered 20 terminal amino acid long tail in the crystal structure.⁹⁰⁻⁹³ His62 imparts a crucial role in maintaining the tetrameric form of the enzyme as it forms a hydrogen bond with Ser59 in another monomer.⁹⁴⁻⁹⁶ Therefore, the protonation state of His62 was set to neutral to maintain the H-bond between His62 and Ser59, otherwise, it dissociates into dimers.⁹⁴⁻⁹⁶ The missing coordinates for the p-ABA-Glu tail of DHF were modeled using Discovery Studio (Biovia, Inc.), and the substrate N5 position was protonated.⁹⁷⁻⁹⁹ Furthermore, the protonation states of all titratable amino acid residue side chains were adjusted to pH 7, and the protonation states of the other His residues (either neutral tautomeric forms or positively charged forms) were determined based on the hydrogen bonding patterns of the local environment. The HBUILD facility in the program CHARMM was employed to add missing hydrogen atoms in the protein.^100,101 The effect of buffer charges and the overall negative charge of the ternary complex were modeled by the addition of 25 sodium ions and 19 chloride ions, to yield a net neutral system. The ionic concentration here mimics experimental conditions⁸⁸ and effectively screens the charges in the system.

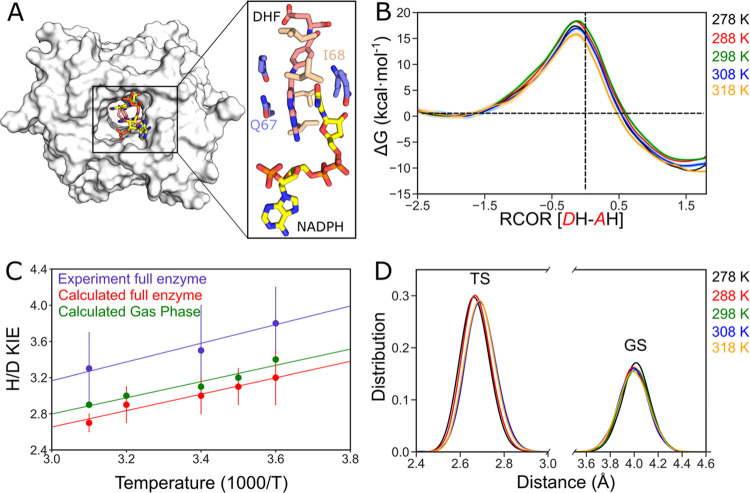
Figure 1.

(A) Schematic representation of R67 DHFR shown as surface and ligands shown as sticks in the active site pore. A subset of the active site is shown in the enlarged version of the ligands and some active site residues. (B) Classical free-energy profile for the hydride transfer reaction catalyzed by R67 DHFR at different temperatures. The error bars are shown as highlighted regions around the solid lines. (C) Computed H/D KIEs for the R67 catalyzed hydride transfer reaction. Red and green points represent calculated KIEs in the enzyme and gas phase (with AM1-SRP parameterization), respectively, while blue points are experimental^87,88 KIEs. (D) Distribution of distances calculated between donor and acceptor atoms from ground state (GS) and TS trajectories. Colors: black, red, green, blue, and orange represent energies at temperatures 278, 288, 298, 308, and 318 K, respectively. The color-temperature notation also applies to (B).

Simulation Details

The potential energy surface in the present study is described by a hybrid QM/MM Hamiltonian,^102,103 where the catalytically active QM region is treated with a modified AM1 semiempirical Hamiltonian¹⁰⁴ denoted AM1-specific reaction parameter (AM1-SRP).¹⁰⁵ This Hamiltonian was designed to reproduce high-level calculations for an assortment of electronic and thermodynamic properties for reactions involving various nicotinamide and pterin derivatives.¹⁰⁶ Moreover, a ribose puckering correction surface was also included in the Hamiltonian, wherein the potential energy corrections and gradients are calculated on a grid (termed mAM1-SRP).¹⁰⁷ The QM region includes significant fragments of DHF and NADPH (69 atoms in total), which are proximal to the reaction center and is expected to be large enough,¹⁰⁸ whereas the MM region contains the remaining ligand atoms, the entire protein, water molecules, and salt. The water molecules were represented by the three-point charge TIP3P model.¹⁰⁹ The QM/MM boundary was treated with the generalized hybrid orbital¹¹⁰ method. The interactions between the QM and MM region were treated by electrostatic embedding. A detailed QM/MM partitioning scheme and a thorough description of the development of mAM1-SRP are provided elsewhere.^106,107,111 The MM region here was treated with the all-atom CHARMM36 force field.^111−114 The Michaelis complex was solvated with a pre-equilibrated cubic water box of dimensions ca. 65 × 65 × 65 ų. Periodic boundary conditions were employed, and long-range electrostatic interactions were accounted for using the Ewald QM/MM summation technique (64 × 64 × 64 fast Fourier transform grid, κ = 0.340 Å^–1).¹¹⁵ The QM/MM calculations were performed using the SQUANTM module in CHARMM.¹⁰³ The system was first minimized and subsequently heated up gradually to 298 K for 25 ps, followed by equilibration at the same temperature for 1 ns. The equilibration run was performed in the isothermal–isobaric (NPT) ensemble at 1 atm, and the target temperature was controlled by the extended constant pressure/temperature method^116,117 and a Hoover thermostat.¹¹⁸ The leapfrog integration scheme¹¹⁹ was used to propagate the equations of motions, and the SHAKE algorithm¹²⁰ was applied to constrain all MM bonds involving hydrogen atoms, allowing a time step of 1 fs. During the initial stages of the equilibration, we applied several nuclear Overhauser effect restraints on key hydrogen bond interactions between the ligands and the surrounding residues, as well as within the protein. The classical free-energy profiles for hydride transfers at different temperatures (278–318 K) were obtained using the umbrella sampling (UM) technique.¹²¹ The antisymmetric reactive stretch (ζ_asym) reaction coordinate was used to describe the hydride transfer.^122,123 ζ_asym is the difference between the lengths of the breaking C4N–H and forming H–C6 bonds. The reaction coordinate was discretized and divided into 16 evenly spaced regions, or “sampling windows,” ranging from −2.0 to 1.5 Å. Each sampling window was subjected to an appropriate harmonic restraint, which keeps ζ_asym in the desired region, and an umbrella potential [roughly the negative of the potential of mean force (PMF)] as a function of ζ_asym. The cumulative simulation time per window was 500 ps, and the statistics for the reaction coordinate were sorted into bins of width 0.01 Å. PMF profiles were computed using the weighted histogram analysis method.^124,125

To account for nuclear quantum effects, we employed PI simulations within the framework of the quantized classical path (QCP) approach^126,127 with staging sampling (SQCP).^128−130 In this approach, SQCP quantum simulations correct the classical UM simulations, and we term this combined PI and UM technique PI–UM. To calculate the KIE, we employed the mass free-energy perturbation (FEP) version of SQCP termed PI-FEP/UM.^129,131,132 The SQCP simulations were employed on 6120 classical configurations of the hydride transfer reaction, combined with 100 PI steps per classical step. Each quantized atom was described by 32 beads (hydrogen isotopes: ¹H, ²H, and neighboring heavy atoms). Thus, ∼20 million QM/MM energy calculations are needed for the reaction at one temperature. In total, we calculated KIEs at five different temperatures from 278 to 318 K with increments of 10 K. To estimate the standard errors in the computed KIEs, the combined PI simulation data at a given state were divided into 10 separated blocks, each treated independently. The standard uncertainties (±1σ) were determined from these 10 blocks, and the total averages for both the PI–UM and the PI-FEP/UM methods were computed.¹³² All PI-simulation used the abovementioned QM/MM potential. All simulations were performed using the CHARMM program^100,101 with a parallel version that efficiently distributes integral calculations for the quantized beads.

Gas-Phase Calculations

Temperature-dependent KIEs were computed in the gas phase with the AM1-SRP Hamiltonian using models for protonated dihydrofolate and NADPH (6-CH₃-H₃pterin⁺ and CH₃-H₂nic, respectively).¹⁰⁶ The reactant and TSs were geometry optimized and characterized using frequency calculations. The KIEs were computed within the harmonic approximation. All gas-phase calculations employed the Gaussian 16 program.¹³³

Results and Discussion

We obtained the classical mechanics PMF profiles at 278, 288, 298, 308, and 318 K for the catalyzed hydride transfer from NADPH to H₃folate⁺ (N5-protonated DHF) in the R67 DHFR, as shown in Figure 1B. The classical activation free energies for the R67 catalyzed reaction, ΔG^‡, at the abovementioned temperatures are obtained as 17.4 ± 0.5, 18.4 ± 0.5, 18.4 ± 0.4, 17.0 ± 0.6, and 15.7 ± 0.6 kcal/mol, respectively. The addition of nuclear quantum effects using PI–UM (i.e., SQCP) to the hydride transfer further reduces the barrier for this reaction by 2–3 kcal/mol,¹⁰⁶ and the corresponding quantum corrected free energies are calculated as 15.6 ± 0.6, 16.2 ± 0.5, 15.7 ± 0.5, 14.2 ± 0.6, and 13.6 ± 0.6 kcal/mol, respectively. The quantum corrected PMF at 298 K underestimates the experimental free-energy barrier by ∼1.8 kcal/mol (∼1.3 s^–1 translates into 17.3 kcal/mol using Eyring’s equation),^90,94 which might be a result of the pABA-Glu tail flexibility, which impacts the reaction barrier as seen previously.^91,134 Interestingly, we observe temperature-dependent free energies for the hydride transfer reaction in R67 DHFR, which is in accordance with the kinetic data obtained at different temperatures.¹³⁵ Although, our simulated activation free energies underestimate the experimental values at temperatures 298, 308, 318 K, the results follow the overall experimental trend.¹³⁵ The correlation coefficient between temperature and experimental activation free energies is calculated as R = 0.97, while our simulated results yield R = 0.92 with slopes of −0.06 and −0.05 for the correlation curves, respectively (Figure S1).

Further by employing mass-perturbation PI simulations (PI-FEP/UM with SQCP), we incorporated nuclear quantum effects for both light (H) and heavy (D) isotopes in the hydride transfer reaction. The quantum corrected ratios of phenomenological rates were computed, and using these ratios, H/D KIEs are plotted in Figure 1C. The temperature-dependent KIEs for R67 DHFR in this work are in good agreement with the experimentally obtained trend^87,88 although the values are slightly underestimated from the calculations (Figure 1D). As a comparison, we also compute the gas-phase KIEs within the standard harmonic approximation (no tunneling correction) for the hydride transfer between the reacting fragments CH₃-H₂nic and 6-CH₃-H₃pterin⁺.¹⁰⁶ These values are slightly higher than the simulated PI-FEP/UM values due to the harmonic approximation. The similar experimental and computational values and trends suggest that the temperature dependence observed in these KIEs originates mainly from zero-point energy effects.

To explore the correlation between the DAD and KIEs, we calculated the distance between the C4N atom in the nicotinamide ring and the C6 atom of DHF (DAD) in R67 DHFR at the GS and TSs and plotted their distribution in Figure 1D. The evolution of DADs from GS to TS provided in Supporting Information (Figure S2) shows a smooth decrease in the DADs, suggesting sufficient overlap between adjacent sampling windows. We observe that in all of the GS trajectories, the DAD distribution is centered around ∼4.0 ± 0.1 Å. These DADs are longer when compared to its evolved counterpart (ecDHFR DAD = ∼3.6 ± 0.1 Å),^{75,77,136−139} suggesting that the more evolved enzyme is better preorganized. Therefore, R67 DHFR requires significant reorganization to bring the reactants together to a reactive state. Turning to the TS, we note the narrow distribution of DADs, with the major population situated at a distance of ∼2.65 ± 0.06 Å. At higher temperatures, the distributions shift slightly toward larger DAD, suggesting that the TS complexes are subject to thermal sampling. Overall, we ascribe this to the loose and solvent-exposed active site of R67 DHFR, where the amplitude of the oscillatory dynamics is higher, and thermally activated sampling of the DAD gives rise to temperature-dependent KIEs.

Comparison of the active site environment of several DHFR isoforms provides a rationale for how these enzymes have evolved to preorganize their active site. We recently emphasized the critical role of the catalytic M20 loop in DHFR,^140,141 building on earlier work by Rod and Brooks.^142,143 The highly evolved ecDHFR and human DHFR have a tightly bound M20 loop that packs against the pterin ring conducive for the chemical reaction.¹⁴⁴ The M20 loop preorganizes the active site by introducing a hydrophobic environment near the substrate N5 atom to increase its basicity, as well as a water pocket near the C4-keto group for effective charge screening.^140,141 The hydrophobic amino acids in the M20 loop effectively sequester the solvent molecules from the substrate N5 atom which otherwise would suppress the substrate basicity. The M20 loop is also suggested to play a role in the protonation of the substrate N5.¹⁴²

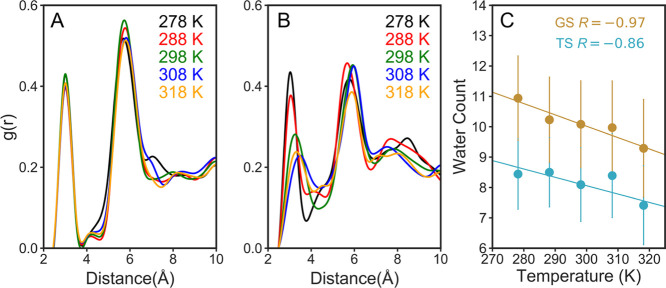
The characteristic difference between these two variants is that ecDHFR possesses an intrinsically floppy loop that can adopt multiple states, whereas loop motion in hsDHFR is controlled by hinges. For catalysis, both these variants adopt a fully closed and catalytically competent state, which is inaccessible to bulk water. The active site hydration is crucial for the charge screening as well as in determining the substrate N5 pK_a, as evident from recent studies.^140,141,143 Therefore, we calculated the radial distribution function (RDF) between the substrate N5 atom and water oxygens to study the active site hydration. We note a sharp peak near N5 within hydrogen bonding distance (∼3.0 Å) for all GS complexes (Figure 3A), suggesting a highly ordered water molecule. However, this solvation peak shifts slightly to a greater distance (∼3.5 Å) for TS complexes at higher temperatures (298.15–318.15 K), as shown in Figure 2B. In addition, the second solvation peak at ∼5.5–6.0 Å becomes less prominent in the TS when compared to the GS complexes, indicating exclusion of water near the substrate at higher temperatures. Moreover, we calculated the number of water molecules in the substrate vicinity (within 6 Å from three atoms in the reacting cluster: NADPH:C4, DHF:C6, and DHF:N5) to quantify the active site hydration in R67 DHFR. We note nearly 9–11 water molecules in GS and ∼8 for TS trajectories. Overall, we see a greater penetration of water molecules (Figure S3A,C) in the substrate proximity for R67 DHFR and, perhaps the reason for smaller N5 pK_a.^140,141,143 In contrast, the evolved counterparts (ecDHFR and human DHFR) have ∼3 water molecules situated farther (∼6.0 Å) from the N5 atom^41,141,145 as the M20 loop provides a hydrophobic environment near N5 and increases its pK_a by 6 units relative to solution.^{140,141,143,146} We also calculated the number of water molecules in the first solvation shell for the reacting atoms showing one water molecule interacting with N5 (Table S1), although we note differences only in the second solvation shell.

Figure 3.

(A) RMSF of Cα of R67 at different temperatures. The top and bottom panels represent RMSF at GS and TS, respectively. (B) Schematic representation of R67 DHFR shown as cartoons and substrate-cofactor shown as sticks in the active site pore. The red color in the cartoon representation depicts highly flexible regions that correspond to high RMSF values. The roman numbers designate the number of the monomers in R67 DHFR.

Figure 2.

RDF between DHF N5 and water oxygen for (A) GS and (B) TS trajectories. Colors: black, red, green, blue, and orange in (A,B) represent RDF at temperatures 278, 288, 298, 308, and 318 K, respectively. (C) Correlation between temperature and water count in GS and TS trajectories colored tan and cyan, respectively. The correlation coefficient was calculated using linear regression analysis.

Interestingly, we note anticorrelation between hydration number and temperature for both GS and TS complexes with correlation coefficients of 0.97 and 0.86, respectively (Figure 2C). Furthermore, we find good correlation between the hydration number and the activation free energies at different temperatures both in GS (R = 0.74) and TS (R = 0.71) complexes (Figure S3B), illustrating the impact of solvation on the free-energy barriers. The relationship between the solvent exposure and reduced catalytic rates has also been reported for thermophilic tmDHFR.^147−150 This infers that active site water is detrimental to the enzyme activity and in R67 DHFR, the active site is porous, solvent exposed, with a poorly preorganized active site, which requires significant reorganization for efficient catalysis. This reorganization requires thermal activation including the removal of water from the active site.

As a final point, we studied the dynamics of R67 DHFR by calculating root mean square fluctuations (RMSF) of the Cα atom positions. Unsurprisingly, we note a slight gradual increase in the thermal fluctuation of Cα when moving from lower to higher temperatures. The higher thermal fluctuations are noted mostly for the flexible loops of the enzyme and some of which are in the proximity (>4 Å) of the substrate and cofactor. The residues K32 and K33, which interact predominantly with the DHF pABA-Glu tail and adenosine binding domain of NADPH, also show higher thermal fluctuations (4–5 Å), suggesting overall loose binding of the ligands in the active site.

Conclusions

In the current work, we presented a theoretical study of KIEs in the primitive R67 DHFR enzyme and compared the results with the experimental work. We employed mass-perturbation-based PI simulations in conjunction with UM and a hybrid QM/MM Hamiltonian. We obtained that temperature-dependent KIEs are in quite good agreement with experiments. We ascribe the temperature-dependent KIEs mainly to zero-point energy effects. We identified a poorly preorganized active site in the primitive enzyme, which allows excessive water access to the active site and results in loosely bound reacting ligands. The significance of preorganization, that is, creating a hydrophobic environment near the active site has been reported earlier for various enzymes and is also evident from our previous studies. The exposure of the active site to solvent due to mutations, poor preorganization or protein flexibility, has profound effect on the enzyme activity. Studies of enzymes such as DHFR,^140,141,150 glycerol-3-phosphate-dehydrogenase,¹⁵¹ triosephosphate isomerase,¹⁵² peraoxonase,¹⁵³ and organophosphatase¹⁵⁴ have shown that penetration of solvent molecules to the active site is detrimental to catalytic activity. In fact, these enzymes might have evolved to exclude solvent from the active site cage, and this is crucial for their activity.¹⁴¹

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.0c10318.

• Number of water molecules within 3 Å of reacting atoms, correlation between temperature and quantum corrected activation free energies for hydride transfer reactions at different temperatures, evolution of DADs going from GS to TS, and the number of water molecules in substrate proximity and their correlation with quantum corrected activation free energies (PDF)

The authors declare no competing financial interest.