Spatially Controlled Octahedral Rotations and Metal–Insulator Transitions in Nickelate Superlattices

Abstract

The properties of correlated oxides can be manipulated by forming short-period superlattices since the layer thicknesses are comparable with the typical length scales of the involved correlations and interface effects. Herein, we studied the metal–insulator transitions (MITs) in tetragonal NdNiO₃/SrTiO₃ superlattices by controlling the NdNiO₃ layer thickness, n in the unit cell, spanning the length scale of the interfacial octahedral coupling. Scanning transmission electron microscopy reveals a crossover from a modulated octahedral superstructure at n = 8 to a uniform nontilt pattern at n = 4, accompanied by a drastically weakened insulating ground state. Upon further reducing n the predominant dimensionality effect continuously raises the MIT temperature, while leaving the antiferromagnetic transition temperature unaltered down to n = 2. Remarkably, the MIT can be enhanced by imposing a sufficiently large strain even with strongly suppressed octahedral rotations. Our results demonstrate the relevance for the control of oxide functionalities at reduced dimensions.

The ubiquitous electron–lattice coupling in perovskite oxides enables us to tune their functionalities by virtue of structural engineering.¹⁻¹⁰ In addition to the well-established strain approach, engineering of the oxygen octahedral rotations (OOR) has been recognized as another effective tool since both the electronic bandwidth and magnetic exchange interaction in oxides are sensitive to the changes of the M–O–M (M, transition metal ion) bond angle.³⁻¹⁰ At the interface between two perovskites, the corner-shared octahedral network has to rearrange to maintain the connectivity, known as the octahedral proximity effect.³ Such an effect is usually confined within several unit cells (uc) and rapidly decays away from the interface,³⁻¹⁰ in contrast to the long-range effect up to tens of nanometers for strain engineering.^1,2 By forming short-period superlattices (SLs), the interfacial OOR coupling can be extended throughout the entire film, thus creating novel structural phases with distinct properties from the individual components.^7,11,12 Importantly, the OOR can be manipulated in SLs by designing the relative thickness ratio of the component layers or selectively utilizing a tilt-control layer, offering extra tuning “knobs”.^7,9,12 However, when the layer thickness is reduced down to a few uc in SLs, a dimensional effect comes into play and usually reduces the bandwidth.¹³⁻¹⁹ The competition between the OOR and dimensional effects remains rarely explored^20,21 but is crucial for the rational control over oxide functionalities at the atomic scale.

Rare-earth nickelates RNiO₃ have received continuous attention not only because of their puzzling physics but also for the potential to design “Mottronics” devices.^22,23 Except for R = La, RNiO₃ displays a sharp metal–insulator transition (MIT) which can be systematically tuned by changing rare-earth cations. Concurrent with the MIT, a structural transition from orthorhombic (Pbnm) to monoclinic (P2₁/c) symmetry occurs due to the breathing distortions of the NiO₆ octahedra. This MIT is accompanied by a paramagnetic to antiferromagnetic transition for R = Pr and Nd, although the transitions are well separated for the smaller rare-earth ions. The mechanism for this temperature-driven MIT has been a long-standing debate.²⁴⁻³⁰ Recently, resonant inelastic X-ray scattering spectroscopy revealed a negative charge transfer energy and oxygen ligand holes (L) in NdNiO₃ (NNO),³¹ supporting a theoretically predicted bond disproportionation scenario.²⁵ The ground state is then described as alternatively arranged Ni 3d⁸ and Ni 3d⁸L² sites, which are associated with the breathing mode of the NiO₆ octahedra.³⁰ The two inequivalent Ni–O bonds can also account for the peculiar antiferromagnetic order at low temperatures.²² More recently, the intimate competition between the two main structural distortions in RNiO₃, namely, the breathing mode and the OOR, has been unveiled by first-principles calculations, where a certain magnitude of OOR can trigger the breathing mode and induce the MIT.²⁹

RNiO₃ at reduced dimensions is of interest as a planar orbital order, similar to high-temperature superconducting cuprates, has been predicted.^32,33 Aside from the orbital control, an emergent antiferromagnetic order, competing electronic phases, and enhanced charge-order propensity have been reported in artificially confined RNiO₃ heterostructures.^13,15,34,35 Herein, the combined effects of the OOR and spatial confinement on the MIT were studied in NNO/SrTiO₃ (STO) SLs via digitally varying the NNO layer thickness, n in the uc. We observed a nonmonotonic variation of the MIT temperature (T_MIT) as a function of n because of the competition between the OOR and dimensional crossover. On the other hand, the antiferromagnetic transition temperature (T_N) is found to be mainly controlled by the Ni–O–Ni bond angle and Ni–O bond length but insensitive to the dimensional reduction. The distinct response of the MIT and the antiferromagnetic transition to dimensionality offers great opportunities to engineer novel phases in nickelate SLs.

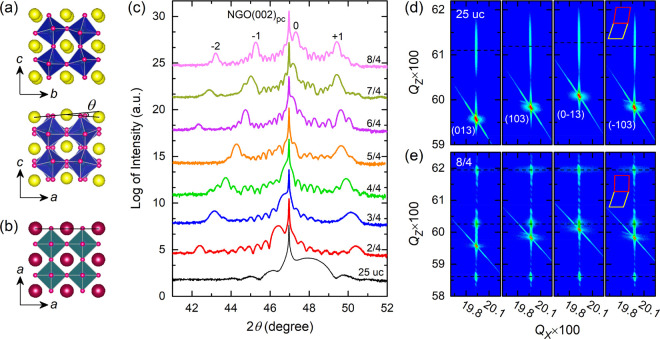
The NNO/STO SLs, n/4, were fabricated on (001)_pc-oriented (pc, pseudocubic) NdGaO₃ (NGO) substrates by means of pulsed laser deposition monitored with reflection high-energy electron diffraction (RHEED) (Figure S1). We set the STO layer thickness to 4 uc and the repetition number of the NNO/STO bilayer to 10. Bulk NNO is orthorhombic at room temperature showing an OOR pattern of a⁺b^–b^– in Glazer notation (Figure 1a). Hereafter, we use the pseudocubic indices for NNO and NGO, with a, b, and c corresponding to the [001], [11̅0], and [110] axes of the orthorhombic lattice. According to first-principles calculations, the combination of out-of-phase and in-phase rotations can drive antipolar displacements of the A-site cations to optimize the oxygen coordination,³⁶ as visualized from the projection along the b axis of NNO. In this work, we used the A-site displacements as a relative measure of the OOR considering the high accuracy in determining Nd³⁺ positions from scanning transmission electron microscopy (STEM).^7,9,37 Unlike orthorhombic NNO, STO is cubic without any OOR and A-site displacements (Figure 1b). The symmetry mismatch at the heterointerface is expected to alter the OOR in the near-interface region of NNO and tune its properties.^3,5Figure 1c shows the high-resolution θ–2θ X-ray diffraction (XRD) scans around the NGO(002)_pc peak for SLs with varied n. The presence of satellite peaks and thickness fringes for all SLs attests to their abrupt interfaces and smooth surfaces. Atomic force microscopy further confirms the terraced surface (Figure S2). As n reduces, the main peak gradually shifts to lower angles because of the increasing contribution from the compressively strained STO layer. Reciprocal space mappings (Figure 1d,e) reveal a change in crystal symmetry from orthorhombic in the NNO single film to tetragonal in the 8/4 SL. An analogous structural change has also been reported in SrRuO₃ films grown on STO when scaling down the thickness below a critical value.³⁸ The tetragonal phase is ascribed to the suppressed OOR along the in-plane axes as evidenced by STEM and half-order XRD measurements.^5,38,39 For the SLs with smaller n, the RSMs show the same features as the 8/4 SL (Figure S3). Given the fact that XRD measurements provide spatially averaged structural information over the samples, we performed atomically resolved STEM measurements to reveal more delicate changes of the OOR within the NNO/STO SLs.

Figure 1.

Structural characterization of NNO/STO SLs. Schematic lattice structure of NNO (a) and STO (b). The royal blue and dark cyan octahedra and yellow, wine, and magenta spheres represent NiO₆, TiO₆, Nd, Sr, and O, respectively. (c) High-resolution XRD θ–2θ scans around the NGO(002)_pc peak for the NNO/STO SLs with varied n. RSMs around pseudocubic (013), (103), (01̅3), and (1̅03) reflections measured from the 25-uc NNO single film (d) and the 8/4 SL (e). The schematic insets show the shear distortion of the pseudocubic lattice.

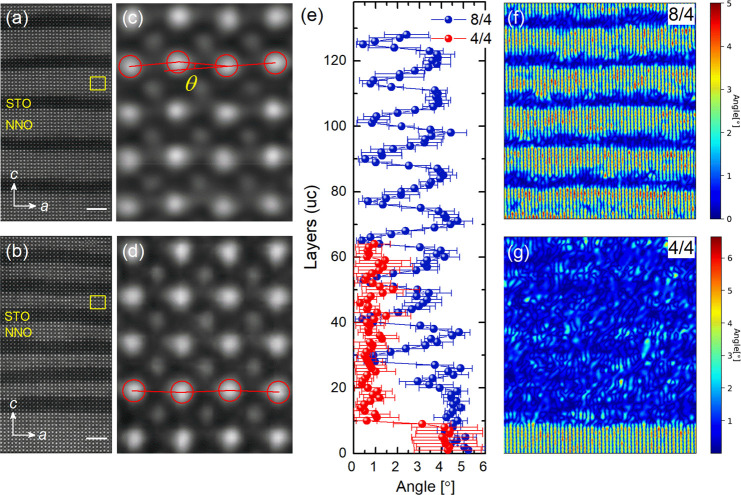
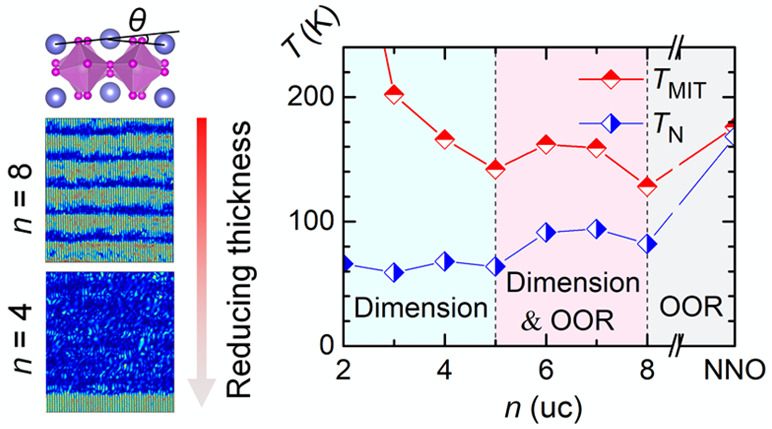
Figure 2a,b shows the high-angle annular dark field (HAADF)-STEM images of the 8/4 and 4/4 SLs, respectively. Due to the large difference in atomic numbers between the Sr and the Nd atoms, the NNO and STO layers can be readily identified from the Z-contrast images as well as the electron energy loss spectroscopy (EELS) color maps (Figure S4). Figure 2c,d shows the enlarged images of the NNO layer in the corresponding SLs to highlight the displacements of Nd³⁺. We define θ as the deviation of the angle between three successive Nd³⁺ cations along the a axis from 180°. Note that θ scales with the OOR.^7,9,37 We find that the 8/4 SL shows pronounced antipolar displacements of Nd³⁺, which becomes negligible in the 4/4 SL. The quantified measure of θ is carried out along the growth direction as summarized in Figure 2e. A clear modulation of θ is observed in the 8/4 SL. The noninterfacial region of NNO shows a maximum θ of ∼4.0 ± 0.5° which decays in the vicinity of the interface. For the 4/4 SL, we observe a uniform θ of ∼0.5° throughout the SL. Therefore, the coherence length of the interfacial OOR coupling is around ∼2 uc on the NNO side, which is comparable to those of the SrIrO₃/STO and La_0.7Sr_0.3MnO₃/STO interfaces.^21,40Figure 2f,g shows the cross-sectional mapping of θ. The modulated θ in the 8/4 SL is in sharp contrast with the nearly homogeneous distribution of θ in the 4/4 SL. The almost quenched A-site antipolar displacement indicates a⁰a⁰c^– for the 4/4 SL.⁴¹ This means the OOR along the in-plane axes is further quenched by reducing the NNO layer thickness.

Figure 2.

STEM characterization of OOR in NNO/STO SLs. STEM-HAADF images of NNO/STO SLs with n = 8 (a) and n = 4 (b). Scale bar, 2 nm. The corresponding enlarged images are shown in (c) and (d) to highlight the A-site antipolar displacements. The deviation angle θ is defined as described in the main text. (e) Layer-resolved deviation angle θ. Cross-sectional mapping of θ in the SLs with n = 8 (f) and n = 4 (g).

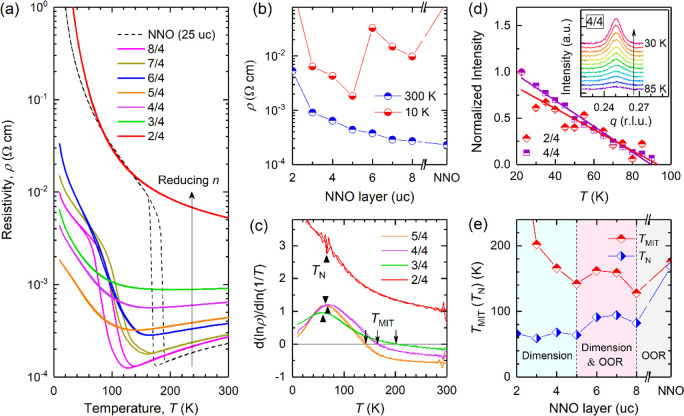
The modifications to the structural ordering within the NNO/STO SLs are expected to cause significant variations to the transport properties. Figure 3a shows the temperature dependent resistivity curves of the NNO/STO SLs as well as a 25-uc thick NNO film for reference. The resistivities at 300 K [ρ(300 K)] and 10 K [ρ(10 K)] are plotted against n in Figure 3b. At first glance, as n is reduced, ρ(300 K) gradually increases whereas ρ(10 K) shows a nonmonotonic variation. As we will discuss below, the monotonic increase of ρ(300 K) is related to the reduced dimensions as well as the increasing disorders, while the complex evolution of ρ(10 K) is due to the competition between the OOR and the dimensionality effect. The NNO film undergoes a sharp MIT as the temperature decreases below 176 K, which is 24 K lower than the bulk value (∼200 K) because of the tensile strain.^2,22,42 The resistivity shows a change of 4 orders of magnitude across the MIT, indicative of the high crystallinity and optimal oxygen stoichiometry of the film.^42,43 In the 8/4 SL T_MIT drastically decreases to 128 K. Also, the low-temperature insulating state is suppressed as manifested by the sharp decline of ρ(10 K) shown in Figure 3b. This is related to the suppression of orthorhombic distortions as evidenced by the RSM results in Figure 1d,e. The suppressed OOR along the in-plane axes stretches the Ni–O–Ni bond and boosts the bandwidth as revealed by X-ray absorption spectroscopy (XAS).^9,10 Note that the transition hysteresis is similar to the NNO single film, which implies that the percolation behavior across the MIT is not interrupted in the n = 8 SL.²² However, the thermal hysteresis is markedly weakened upon reducing n from 8 to 6 uc. Meanwhile, the T_MIT gradually increases from 128 to 162 K accompanied by a rise of ρ(10 K). This is ascribed to the dimensionality effect which stabilizes the insulating phase by blocking the interlayer electron hopping.¹⁴⁻¹⁷ As a result, the region with coexisting metallic and insulating phases gradually vanishes.¹⁷ Most strikingly, as n is further reduced, we observe an unexpected decline of T_MIT from 162 K at 6 uc to 142 K at 5 uc, concurrent with a sudden drop of ρ(10 K). The result is somewhat counterintuitive since the dimensionality effects are expected to raise the T_MIT continuously by promoting the insulating state.¹⁷ We suggest the delicate changes of OOR in the SLs to be responsible for this anomaly. As n is reduced below a critical thickness (∼6 uc), the OOR of the SLs changes to a⁰a⁰c^– by quenching the in-plane OOR given the limited coherence length of the interfacial OOR coupling.^3,21,40 The quenched in-plane octahedral tilting can suppress the breathing mode instabilities in NNO and then weaken the MIT.²⁹ Upon decreasing n below 5 uc, the OOR of the SLs should be virtually unchanged, and the dominated dimensionality effects dramatically increase the T_MIT (Figure 3c). To gain further insights into the thickness-dependent MIT, we fit the metallic resistivity of the SLs with n ≥ 3 using the power law ρ = ρ₀ + AT^α, where the parameter A is determined by the strength of the electron scattering.⁴⁴ The power-law exponent α is found to increase from α = 1.0 ± 0.1 for n ≥ 5 to α = 1.90 ± 0.01 for n = 4 and end up with α = 3.14 ± 0.01 for n = 3 (Figure S5). The departure from a linear scaling in perovskite nickelates has been ascribed to a joint effect of epitaxial strain and oxygen vacancies.⁴⁴ Considering the fact that all SLs are coherently strained to the NGO substrate, the larger α for n = 3, 4 is probably due to the increasing amounts of oxygen vacancies with ultrathin NNO layers. This can also contribute to the enhanced resistivity and T_MIT by creating local disproportionation of NiO₆ octahedra.⁴⁵ The n = 2 SL exhibits insulating behavior in the entire temperature range measured. The temperature dependent resistivity curve can be well fitted with the two-dimensional variable range hopping conduction model (Figure S6), attesting to the dimensional crossover.³⁵ Note that the effect of disorder should not play a dominant role in the low-temperature insulating states for the SLs with n > 2. Otherwise we would have seen a monotonic increase of ρ(10 K) with reducing n.

Figure 3.

Thickness-dependent MITs in NNO/STO SLs. (a) Temperature dependent resistivity (ρ–T) curves of NNO/STO SLs with varied n, along with a 25-uc-thick NNO single film for comparison. (b) Resistivities at 300 and 10 K as a function of n. (c) d(ln ρ)/[d ln(1/T)] vs T plots for the SLs with n = 2, 3, 4, and 5. T_MIT and T_N, marked by the arrow and triangle, are defined as the temperature of the upturn in the ρ–T curve and the peak in the d(ln ρ)/[d ln(1/T)] vs T plot during the cooling process. (d) Temperature dependent integrated intensity of the q = (1/4, 1/4, 1/4)_pc reflection measured for SLs with n = 2 and 4 using RMD. The linear fitting is used to extract the onset temperature of the antiferromagnetic order. The inset shows the isothermal rocking curves around the q = (1/4, 1/4, 1/4)_pc reflection taken from the SL with n = 4. The measurements were performed from 30 to 85 K with a step of 5 K. (e) Phase diagram of NNO/STO SLs as a function of n. Here T_N is derived from the resistivity measurements.

The altered OOR should also have a profound impact on the antiferromagnetic transitions of the SLs. Here, the peak position of the d(ln ρ)/[d ln(1/T)] vs T plot has been used to track T_N in RNiO₃.^2,46 As shown in Figure 3e, T_N nearly coincides with T_MIT for the NNO single film, while they are well separated for all SLs. The decoupling of MIT and spin ordering has also been reported for other RNiO₃-based heterostructures and SLs with different boundary conditions.^2,9,47,48 The suppressed OOR along in-plane axes leads to a decrease of T_N from ∼168 K for the 25-uc NNO film to ∼82 K for the n = 8 SL, following the trend in the bulk RNiO₃ phase diagram.²² As n decreases from 8 to 6 uc, T_N hardly changes due to the slightly altered OOR in this thickness range. Remarkably, the further blocking of the in-plane OOR reduces T_N from ∼91 K to ∼64 K as n decreases from 6 to 5 uc. This drop of T_N is not substantial given the relatively small change of the absolute Ni–O–Ni bond angle. It is interesting to note that T_N remains nearly constant for n ≤ 5 in contrast to a rapidly increasing T_MIT (Figure 3c). For the insulating SL with n = 2, the antiferromagnetic transition is manifested as an anomaly around ∼68 K of the d(ln ρ)/[d ln(1/T)] vs T curve, corresponding to a kink visualized from the enlarged resistivity curve (Figure S7). This resembles RNiO₃ with small rare-earth ions.⁴⁶ X-ray resonant magnetic diffraction (RMD) measurements were performed for the SLs with n = 4 and 2 (Figure 3d and Figure S7). The observation of the specific q = (1/4, 1/4, 1/4)_pc reflection ascertains the presence of antiferromagnetic order in the SLs even with 2-uc NNO. The integrated peak intensity linearly decreases with increasing temperature, different from NNO single films which follow the mean field model.^2,48 Such abnormal temperature dependence is in line with that reported for short-period NNO/NdAlO₃ SLs, which has been ascribed to the enhanced spin fluctuations in two-dimensional systems.⁴⁸ The linear extrapolations give onset temperatures of ∼93 K for n = 2 and ∼90 K for n = 4 SL. The values are ∼30 K higher than those derived from resistivity measurements. Such a discrepancy arises because the RMD and derivative of resistivity characterize different stages of the antiferromagnetic transition. While RMD probes the onset of antiferromagnetic domains, the deflection point from the d(ln ρ)/[d ln(1/T)] plot marks the percolation threshold. For two-dimensional systems, the percolation occurs when the volume fraction of the antiferromagnetic insulating phase reaches 50%.⁴⁹ Importantly, the RMD results strengthen the conclusion that T_N in SLs with n ≤ 5 is stable against further reducing n down to 2 uc.

Taken together, the results suggest that T_N is mainly governed by the Ni–O–Ni bond angle and insensitive to the dimensional crossover in NNO/STO SLs. The argument is supported by the report on NNO/NdAlO₃ SLs, where a thickness-independent T_N of ∼150 K is observed even with a 2-uc thick NNO layer.⁴⁸ The quasi-two-dimensional antiferromagnetic order preserved in RNiO₃ is also consistent with previous observations in LaNiO₃/LaAlO₃ SLs, where an emergent antiferromagnetic order was probed in the otherwise paramagnetic LaNiO₃ when the layer thickness was reduced to 2 uc.¹³

To address the effects of varied tetragonal distortions on the MITs, we compared the MITs of NNO/STO SLs with n = 5 grown on (001)_pc-NGO (a_pc = 3.858 Å), (001)-(LaAlO₃)_0.3(Sr₂AlTaO₆)_0.7 (LSAT, a = 3.868 Å), and (001)-STO (a = 3.905 Å) substrates. RSM measurements confirm their fully strained states and identical tetragonal symmetry (Figure S8). The SLs grown on NGO and LSAT show very similar behavior, although the one on LSAT shows slightly higher T_MIT and T_N (Figure 4a,d). By contrast, the greater tetragonal distortion imposed by the STO substrate gives rise to substantially increased T_MIT and T_N, as well as an enhanced resistivity jump across the MIT. To understand the varied MIT behaviors, the electronic structure was studied using XAS performed at O K- and Ni L-edges. Figure 4b shows the O K-edge prepeak which arises from the strong covalency between the Ni 3d and O 2p states. The peak position is determined by the charge transfer energy.^23,48,51 By taking the SL grown on NGO as a reference, the prepeak shifts ∼25 meV and ∼95 meV to lower energies for the SLs grown on LSAT and STO, respectively (Figure 4e). Such a red shift of the O K-edge prepeak can be assigned to an increasing charge transfer energy when the SL is subjected to a larger in-plane tensile strain.^2,52Figure 4c shows XAS at the Ni L-edge taken at 40 K, well below T_MIT. Both the Ni L₂- and L₃-edges split into two peaks, resembling bulk RNiO₃.^51,53 We define ΔE as the energy separation of the two Ni L₃ peaks given the well-defined double-peak feature. ΔE increases from 1.27 eV on NGO to 1.29 eV on LSAT and then to 1.45 eV on STO (Figure 4f). The trend is in line with that of bulk RNiO₃ upon reducing the ion radius of R, indicating that the charge transfer energy and breathing distortions of NiO₆ octahedra increase with a.^51,53 Our results suggest that robust MITs can be triggered by imposing a large tetragonal distortion to NNO/STO SLs, albeit with strongly suppressed OOR.

Figure 4.

MITs in NNO/STO SLs with varied tetragonal distortions. (a) ρ–T curves of the n = 5 SLs grown on various substrates. T_MIT and T_N are marked by arrows and triangles, respectively. (b) XAS spectra of the prepeak of the O K-edge at 300 K. (c) XAS spectra of the Ni L-edge at 40 K. ΔE is the splitting energy of the double peaks of the Ni L₃ edge. (d–f) Summary of the T_MIT, T_N, and energy shift of the O K-edge prepeak relative to the SL grown on NGO, as well as ΔE as a function of the in-plane lattice constant, a.

To summarize, the OOR of NNO/STO SLs evolves from a modulated to uniform pattern as we reduce the layer thickness of NNO. The altered OOR profoundly influences the MIT and the antiferromagnetic transition. We observe a reduced T_MIT and T_N, together with a weakened insulating ground state as the OOR is suppressed. The dimensionality effect also plays a role in the MIT which raises T_MIT by reducing the effective bandwidth. However, T_N is closely linked to the modifications of the crystal structure and is insusceptible to the dimensional crossover. Our results illustrate that the delicate interplay between the spatial confinement and the interfacial OOR coupling can be utilized to engineer novel electronic phases at the atomic level.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.0c03850.

• Materials and Methods section and supplementary Figures S1–S8 including RHEED intensity profile and patterns, AFM images, RSMs, STEM images and EELS mappings, fittings of the metallic resistivity, enlarged view of the ρ−T curve, and RMD measurements (PDF)

Author Contributions

B.C. synthesized the samples and conducted the basic structural characterizations and transport measurements. N.G. and D.J. performed the STEM measurements and analyses under the supervision of J.V. R.J.G. performed the RMD measurements. B.C. performed the XAS measurements assisted by J.H.L. and C.P. B.C., N.G., M.S., M.B., M.H., G.R., and G.K. discussed the results. B.C. and G.K. conceived the project and wrote the manuscript with inputs from all authors.

The authors declare no competing financial interest.