Coronavirus disease 2019 (COVID-19): survival analysis using deep learning and Cox regression model

Abstract

Coronavirus (COVID-19) is one of the most serious problems that has caused stopping the wheel of life all over the world. It is widely spread to the extent that hospital places are not available for all patients. Therefore, most hospitals accept patients whose recovery rate is high. Machine learning techniques and artificial intelligence have been deployed for computing infection risks, performing survival analysis and classification. Survival analysis (time-to-event analysis) is widely used in many areas such as engineering and medicine. This paper presents two systems, Cox_COVID_19 and Deep_ Cox_COVID_19 that are based on Cox regression to study the survival analysis for COVID-19 and help hospitals to choose patients with better chances of survival and predict the most important symptoms (features) affecting survival probability. Cox_COVID_19 is based on Cox regression and Deep_Cox_COVID_19 is a combination of autoencoder deep neural network and Cox regression to enhance prediction accuracy. A clinical dataset for COVID-19 patients is used. This dataset consists of 1085 patients. The results show that applying an autoencoder on the data to reconstruct features, before applying Cox regression algorithm, would improve the results by increasing concordance, accuracy and precision. For Deep_ Cox_COVID_19 system, it has a concordance of 0.983 for training and 0.999 for testing, but for Cox_COVID_19 system, it has a concordance of 0.923 for training and 0.896 for testing. The most important features affecting mortality are, age, muscle pain, pneumonia and throat pain. Both Cox_COVID_19 and Deep_ Cox_COVID_19 prediction systems can predict the survival probability and present significant symptoms (features) that differentiate severe cases and death cases. But the accuracy of Deep_Cox_Covid_19 outperforms that of Cox_Covid_19. Both systems can provide definite information for doctors about detection and intervention to be taken, which can reduce mortality.

Introduction

Coronaviruses problem is one of the most serious problems, that faces the world [1]. Coronaviruses were first discovered in the 1930s, but only animals were infected with it. Human coronaviruses were discovered in the 1960s. Coronaviruses have taken many phases of mutation; it started as the common cold in 1960s, till reaching the current form with respiratory effects. A novel coronavirus was reported as the cause of a cluster of cases of pneumonia in Wuhan, a city in China's Hubei Province, at the end of 2019. It spread exponentially, leading to an epidemic across China, followed by several cases across the world in other countries. The World Health Organization (WHO) identified the disease COVID-19 in February 2020, which stands for coronavirus disease 2019 [2]. Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) is a virus that causes COVID-19; previously, and it was referred to as 2019-nCoV. Because of the increase in mortality due to COVID-19 and the increase in the speed of its spread, many methods have been developed to reliably predict patient survival based on symptom data and specific clinical parameters.

Artificial intelligence is now needed in order to help expert epidemiologists. AI provides a useful tool, that can help in computing risk factor, classification, even drug analysis, and finally responding to crisis according to health data specialists. Because of the increase in COVID-19 patients and the lack of equipment to receive all patients, a hard choice is taken. The necessary medical care is applied only to patients with more probability to survive. Calculating the probability to survive and the effect of each feature like symptoms in our case on survival probability is done using survival analysis.

Survival analysis is a model for time until a certain “event”. Time-to-event data encounters several research challenges such as censoring, symptoms (features) correlations, high-dimensionality, temporal dependencies, and difficulty in acquiring sufficient event data in a reasonable period of time [3]. There are many current literature techniques for conducting this sort of survival study. Among them, the Cox Proportional Hazards Model (Cox) [4] which is a Regression models that is commonly used in survival analysis [5].

Survival analysis methods can work with specific problems, with a data type that waits for the event to occur. Cox regression is the most appropriate method to deal with this kind of data. Occasionally, the basic assumptions of the model, for example, non-proportionality for the Cox model, are not true. The choice of an appropriate model varies depending on the complexity and features that affect the suitability of the model [6], in model building. Data-driven approaches are robust. A long-range regression analysis of COVID-19 using immunological, epidemiological, and seasonal effects on US data is going to be done out to 2025 [7].

The implementation of the designated dataset in its original form in this research led to the appearance of some trammels such as high collinearity and convergence, so autoencoder deep neural network is implemented to solve such problems. To predict the survivability analysis, Cox regression is implemented in two situations: the first is called Cox_Covid_19, and the second is called Deep_Cox_Covid_19. Cox_Covid_19 implements Cox regression on the original dataset, while Deep_Cox_Covid_19 implements autoencoder deep learning before Cox regression to solve the problems associated with the dataset.

Our main objective in this paper is to define the main features affecting the survival probability for COVID-19 with the aid of the most suitable machine learning algorithm. This information can help doctors in taking the right decision about each patient’s case according to the available treatment and medical instruments. The principal contributions of this research could be summarized as the following:

• At first, finding the survival probability for each patient.

• At second, finding the impact of each feature on survival probability by calculating p value for each feature. The p value is an indication of the impact of each feature on survival.

• Enhancing Cox_COVID_19 system by applying deep neural network, for increasing accuracy, presenting a new system called Deep_ Cox_COVID_19.

• Finally, a comparison between Cox_COVID_19 and Deep_ Cox_COVID_19 is provided in terms of concordance, accuracy, precision, and recall.

The paper is organized as follows: The related work is presented in Sect. 2. Then, the proposed system design and implementation are introduced in Sect. 3. Section 4 introduces the results and discussion. Finally, the conclusion is discussed in the last section.

Related work

Up to now, the 2019 novel coronavirus pneumonia (COVID-19) is one the greatest public health problems that faced the world throughout its history. Worldwide, as of 2:00 a.m. CEST, 14 Apr 2020, 1,980,704 confirmed cases of COVID-19 have been reported to the WHO, including 67,666 deaths [2]. One of the earliest applications of data mining techniques was in medical fields in which it can accurately predict and diagnose diseases and improve medical decision-making. Many researchers have focused on conducting work in COVID_19 application and experimental application of medical datasets for scientific purposes.

Khan et al. [8] for accelerated failure time models, developed variable selection approaches consisting of a group of algorithms based on a combination of the Dantzig selector and the Buckley-James method, two frequently used techniques in the field of variable selection for survival analysis. Additionally, Khan et al. [9] proposed new approaches to variable selection for censored results, based on optimized AFT models using regularized weighted least squares. A mixture of L₁ and L₂ standard penalties under two proposed elastic net type approaches is used by the regularized technique. The two proposed methods are also expanded by incorporating censoring observations into their model optimization structures as constraints.

XGBoost machine learning algorithm predictive modelling is presented by Yan et al. [10]. Their methodology is able to predict mortality risk for COVID-19 dataset. The proposed model defined that lactic dehydrogenase (LDH), lymphocyte and high-sensitivity C-reactive protein (hs-CRP) are the key features for differentiating between critical patients from the two classes. Xiang et al. [11] present an algorithm for determining COVID-19 biomarker for earlier diagnosis based on IBM SPSS statistics 22.0 (New York, USA) software for statistical analysis, the Wilcoxon signed-rank test for data comparison between two groups. They found that using serum urea, CREA, CysC, DBIL, CHE, and LDH can be used to differentiate severely COVID-19 cases from non-severe COVID-19 cases.

In addition of using many parametric models, but the best was chosen by Bayesian information criterion (BIC) as presented by Mollazehi et al. [12]. The authors apply their algorithm on COVID-19 dataset for patients in Singapore to predict the recovery time from COVID-19 in Singapore between 23 January and 13 March 2020. Nemati et al. [13] introduced an approach that was applied on 1,182 COVID-19 cases and was based on several statistical methods to evaluate survival characteristics. By using various ML and statistical analysis approaches, the discharge-time prediction of COVID-19 cases was assessed. The findings show that in this analysis the Gradient Boosting survival model outperforms other models of patient survival.

A semi-supervised learning method based on the Cox and AFT models is presented by Liang et al. [14] applied on DLBCL (2002), DLBCL (2003), lung cancer and AML to overcome small sample size and censored data that limit accuracy. The semi-supervised model of learning can substantially increase the predictive performance of Cox and AFT models in the survival study. Lee et al. [15] presented algorithms based on cause-specific version of the Cox Proportional Hazards Model (cs- Cox) and DeepHit applied in breast cancer dataset for handling competing risks. Moreover, Ranganath et al. [16] presented a heterogeneous data types that occur in the electronic health record based on baseline Framingham risk score deep survival analysis.

Material and methods

Survival analysis is a time till event analysis. Cox regression is one of the most commonly methods in survival analysis. Here, we used an autoencoder deep neural network to improve performance. In this section, all methods that we used in this paper and different types of survival analysis methods are presented.

Survival analysis models

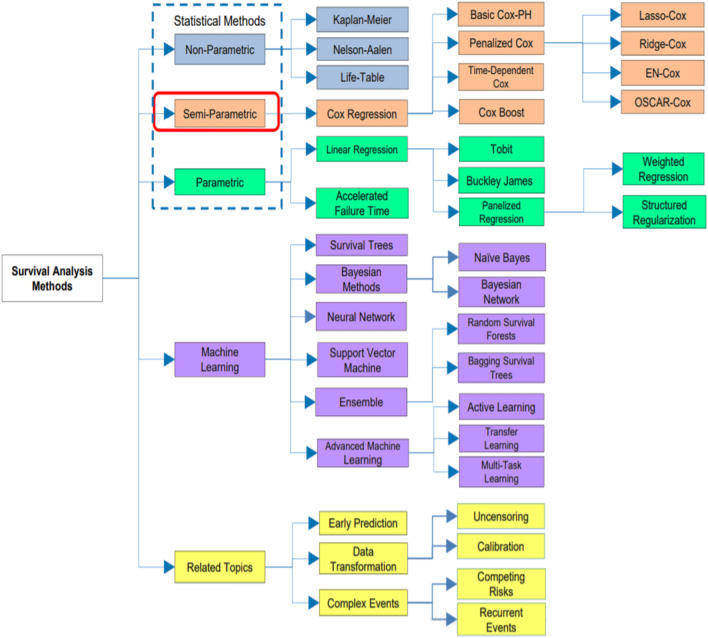
Survival analysis models [17, 18] are categorized to parametric, nonparametric and semi-parametric models, as shown in Fig. 1 [18]. For the parametric model, it isn’t suitable for normal distribution in which negative values can be found. The parametric model assumes that the survival time follows a known distribution. Methods of parametric model are such as Tobit, Buckley-James, Penalized regression and Accelerated Failure Time. For the semi-parametric model, even if the regression parameters are known, the distribution of the survival time is still unknown. It isn’t a fully parametric or a fully nonparametric. Methods of the semi-parametric model are such as Cox model, Regularized Cox, CoxBoost and Time-Dependent Cox. For the nonparametric model, it is difficult to understand and gives unreliable estimates but more efficient when the appropriate theoretical distributions aren’t known. Methods of nonparametric model are such as Kaplan–Meier, Nelson-Aalen and Life-Table.

Fig. 1.

[18]: Taxonomy of survival analysis methods

Cox regression method

Cox regression [19] method is a statistical method that is used often in medical research, for predicting the survival time for different patients. Cox Regression method is used for predicting the degree of effect of different features upon survival which is called hazard rate. Cox regression method is considered as an example of semi-parametric models.

The hazard function $h\left(t\right)$ can be used to express the Cox model. Shortly, the probability of dying at time t is provided by the hazard function. It can be estimated as follows:

$$h\left(t\right)=h_0\left(t\right)\times \text{exp}\left(b_1{x}_1+b_2{x}_2+\cdots +b_n{x}_n\right)$$ 1

where the survival time is expressed by “t”. The hazard function $h\left(t\right)$ is determined using “n covariates” $(x_1,x_2,\dots ,x_n)$. The impact of covariates is measured using the coefficients $(b_1,b_2,\dots ,b_n)$. “$h_0$” is the baseline hazard.

Autoencoder deep neural network

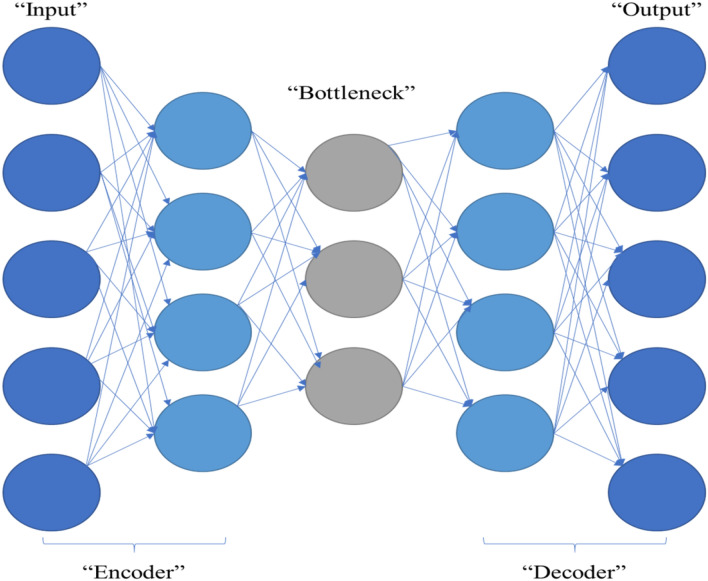
Autoencoder is an unsupervised artificial neural network. An autoencoder is a neural network that can efficiently encode data then reshaping and reconstructing the data back from the encoded representation, removing noise from the data that can affect the performance of the prediction model. Figure 2 shows the layers of the used autoencoder neural network.

Fig. 2.

Autoencoder components

Figure 2 shows the autoencoder components:

• Encoder In this step, reducing the input dimensions and compressing the input data into an encoded representation is the main goal.

• Bottleneck This layer contains the lowest possible dimensions of the input data; the compressed representation of the input is presented in this layer.

• Decoder In this step, the data are reconstructed from the encoded version to extract a new representation of data, that is as close to the original input as possible and removing noise.

• Reconstruction loss This is the method for measuring the performance of our decoder and how close the new representation to the original input.

Proposed survival analysis system

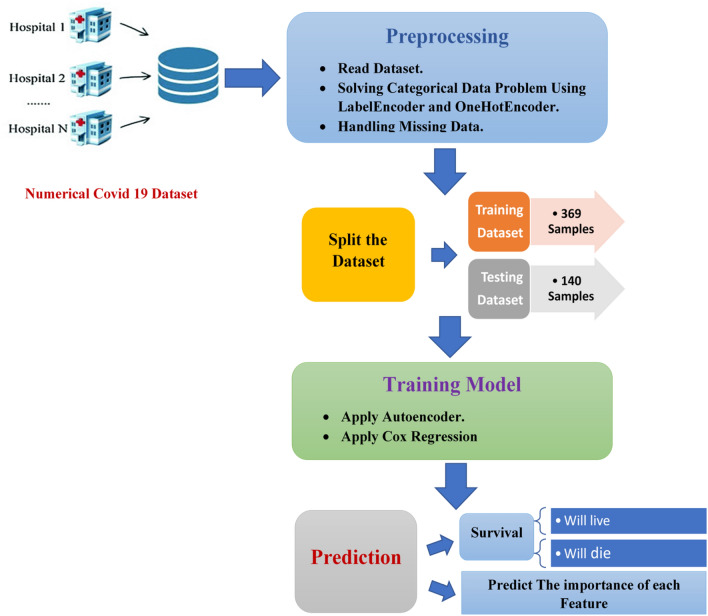
The two systems proposed in this paper are Deep_Cox_COVID_19 and Cox_COVID_19. Both systems are used to define significant symptoms (features) that differentiate between sever and death cases. Cox_COVID-19 is based on Cox regression to predict the survival probability. Deep_Cox_COVID_19 is a combination of deep neural network which is autoencoder and Cox regression method to predict the survival probability. The system is made up of three major stages as shown in Fig. 3:

• Data preprocessing in this paper contributes reading COVID_19 dataset, then solving categorical data problems, and handling missing data. After reading the dataset, there were some categorical to be handled such as gender and country, Labelencoder is applied to solve the categorical problem of gender feature, and onehotencoder for handling the categorical problem of country feature. Finally, handling missing data are done by searching for non-numeric values and replacing them with the mean of the column where they belong.

• The second stage is the training model. It starts with splitting the dataset to training and testing subsets. Then for Cox_COVID_19 model it is all about applying Cox regression for predicting survival probability. For Deep_Cox_COVID_19 model, it starts with applying autoencoder to reconstruct features and then applying Cox regression for survival analysis.

• The last stage is to predict survival, whether alive or dead, and the importance of each feature.

• The steps for Cox_COVID_19 are shown in the following pseudocode.

Fig. 3.

Proposed survival analysis system architecture

Input

Hospital’s dataset

Trigger

At the start of the proposed survival analysis system architecture

Output

Predict the importance of each feature

Steps

1. Import libraries

2. Read datasets

3. Set X as the set of features

4. Set Y as the set that contains duration till death

5. Set event as whether dead or alive.

6. Randomly split dataset into Training_Dataset and Testing_Dataset

7. Randomly split Training_Dataset into X_train and Y_train

8. Randomly split Testing_Dataset into X_test and Y_test

9. Apply Autoencoder

10. Apply COX Regression to predict the survival probability.

11. Compute concordance to rank model.

12. Predict the most important features affecting mortality.

13. Compute accuracy and precision.

14. The steps for Deep_Cox_COVID_19 are shown in the following pseudocode.

Input

Hospital’s dataset

Trigger

At the start of the proposed survival analysis system architecture

Output

Predict the importance of each feature

Steps

• 14Import libraries
• 15Read datasets
• 16Set X as the set of features
• 17Set Y as the set that contains duration till death
• 18Set event as whether dead or alive.
• 19Randomly split dataset into Training_Dataset and Testing_Dataset
• 20Randomly split Training_Dataset into X_train and Y_train
• 21Randomly split Testing_Dataset into X_test and Y_test
• 22Input for the neural network: X_train as a training subset and X_test as a testing subset.
• 23Set epochs = 100
• 24Randomly initialize the weights and the parameters of the network.
• 25For each i ∈ epochs Do
• 26Compute the output according to the parameters.
• 27Compute errors using the validation subset X_test.
• 28Update weights and parameters.
• 29End for
• 30Set Train_features as the reduced representation of X_train using the neural network.
• 31Set Test_features as the reduced representation of X_test prediction using the neural network.
• 32Apply Autoencoder
• 33Apply COX Regression to predict the survival probability.
• 34Compute concordance to rank model.
• 35Predict the most important features affecting mortality.
• 36Compute accuracy and precision.

Results

In this section, a dataset description, validation, and the findings of adding an autoencoder deep neural network to a Cox regression model are presented.

Dataset set

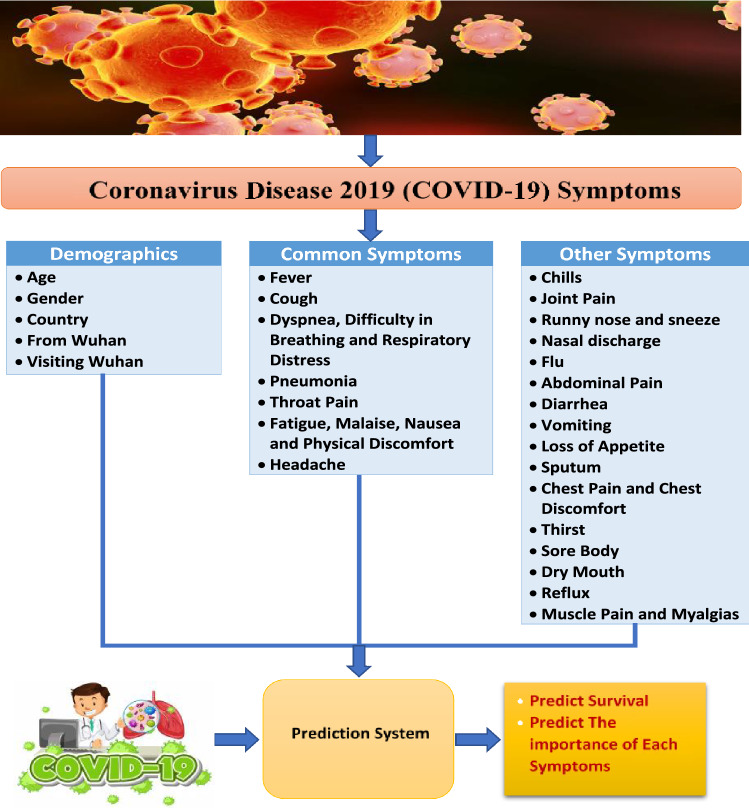
In this study, a clinical dataset for COVID-19 patients is used [20]. This dataset consists of 1085 patients, and as features, it has an id for each patient, reporting date, summary, location, country, gender, age, symptom, hospital visit, exposure_Start, exposure_end, visiting Wuhan, from Wuhan, death and recovered. The symptoms can be divided into demographics symptoms, common symptoms and other symptoms and all shown in Fig. 4. The demographics symptoms are age, gender, country, from Wuhan and visiting Wuhan. The common symptoms are like fever, cough, pneumonia, headache and throat pain. The other symptoms are like chills, joint pain, thirst, flu and reflux.

Fig. 4.

Characteristics of patients

For each patient, if died, the date of death is shown in the summary column and if alive it means till the date of the dataset downloaded. So, the duration till death or being alive is calculated. For patients with no symptom’s information, they were removed from the dataset and for patients with no gender information, they were removed from the dataset leaving the information for only 509 patients.

For the train subset, there are 36 samples that have died, and the other 333 sample that are still alive. For the test subset, there are 10 samples that have died and the other 130 are still alive.

The features that are used in this system, age, gender, and different symptoms. The information about the used dataset after removing patients that don’t have enough information is shown in Table 1.

Table 1.

COVID-19 clinical dataset description

Dataset	Target variables		Symptoms (Features)			Training samples	Testing samples
	Classes	Duration
COVID-19 dataset [20]	Two classes: death or alive	Time to the event of death or life	29			369	140
			Demographics	Common	Other
			5	7	17

Characteristics of the 509 patients

COVID-19 features can be categorized into demographics and symptoms. According to common protocols all over the world, symptoms can be categorized into common symptoms with most patients and other symptoms. Figure 4 shows different characteristics for patients with COVID-19.

Validation

To rank the model, concordance index [21, 22] is used. The concordance index is like measuring accuracy in classification problems but in survival analysis. Concordance is used as a rating of how well the model is. Concordance maximum value is one. The closer the concordance to one, the better the model is. Equation 2 [21] shows the mathematical expression for concordance index:

$$c=\frac{1}{\left|\epsilon \right|}\sum _{{\epsilon }_{\mathit{ij}}}{1}_{f\left(x_i\right)<f\left(x_j\right)}$$ 2

where “$\left|\epsilon \right|$” is the number of edges in the order graph, and $f\left(x_i\right)$ is the predicted survival time for an item “$i$”.

Cox_COVID_19 model has a concordance of 0.923 out of 1 for training and 0.896 out of 1 for testing, so it is a very good Cox model. Deep_Cox_COVID_19 improved the performance as it has a concordance of 0.983 for training and 0.999 for testing.

For accuracy [23], it can be defined as the percentage of right predictions that could be done by machine learning model. Formally, accuracy can be defined using Eq. 3 [21]:

$$\text{CA =}\frac{\text{Number}\text{. of correct classified samples}}{\text{Total number of samples}}=\frac{\text{TP + TN}}{\text{TP + FN + TN + FP}}$$ 3

where

“TP”: True positives; “TN”: True negatives; “FP”: False positives, and “FN”: False negatives.

Precision Precision is the ratio of correctly predicted positive observations to the total predicted positive observations.

$$\text{Precision = TP / (TP + FP)}$$ 4

Experimental results

Cox_COVID_19 results

For each feature, the percentage of each occurrence in the dataset, p value, and coefficient are computed. The p value is used with each feature for testing the null hypothesis that the coefficient is equal to zero (no effect). For a predictor to have a lower p value (that can be less than 0.05), it means that it has a big impact on your model, and any changes in the predictor's value will lead to changes in the response variable. A positive coefficient indicates a worse prognosis, and a negative coefficient indicates a protective effect of the variable with which it is associated. The features are categorized into demographics and symptoms; the symptoms are categorized into common symptoms and other symptoms according to common protocols all over the world. Table 2 shows that age, muscle pain, pneumonia all have p value which is less than 0.05 and throat pain has a p value that is higher than 0.05 but still very small. So that age, pneumonia, muscle pain and throat pain are the most important factors affecting mortality.

Table 2.

Features’ percentage and P value

Symptom (Feature)			Percentage in dataset	P value	Coefficient
Demographics	Age		–	9.835E-15	0.1121
	Gender	Male	61.69%	0.2095	− 0.4998
		Female	38.31%
Common symptoms	Cough		29.86%	0.937	− 0.0807
	Fever		46.56%	0.8287	− 0.1853
	High fever		0.4%	0.9712	− 8.5365
	Muscle pain		2.4%	0.0453	2.7147
	Joint pain		1.8%	0.9524	− 8.4264
	Throat pain		8.3%	0.06003	2.5466
	Pneumonia		36.7%	0.0119	2.9523
	Respiratory distress		0.2%	0.9864	− 6.4765
	Dyspnoea		1.4%	0.9909	− 2.636
	Difficulty in breathing		3.14%	0.1446	1.7397
	Malaise		5.5%	0.9396	− 6.7776
	Fatigue		2.16%	0.1021	2.3038
Other symptoms	Running nose		3.14%	0.9355	− 7.9937
	Flu		0.59%	0.9781	− 7.0568
	Chest pain		0.59%	0.9656	− 8.5042
	Sputum		2.16%	0.9559	− 7.3175
	Dry mouth		0.2%	0.9798	− 8.5962
	Thirst		0.2%	0.9866	− 6.4765
	Abdominal pain		0.2%	0.9975	− 1.9189
	Vomiting		1.18%	0.9715	− 6.2568
	Diarrhea		1.96%	0.9702	− 5.7918
	Loss of appetite		0.39%	0.9682	− 9.2821
	Chills		2.95%	0.9386	− 8.4315
	Sore body		0.2%	0.9933	− 3.9594
	Reflux		0.2%	0.9945	− 3.4291
	Nausea		0.79	0.9774	− 6.3657
	Headache		3.73%	0.9505	− 6.2049

Bold values indicated best results

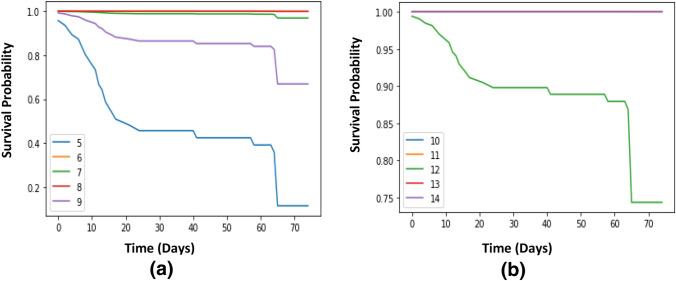
The main contribution for Cox_COVID_19 model is to predict the survival probability overtime. Figure 4 shows the survival probability for fifteen patients’ overtime that are chosen as examples for predicting survival probability.

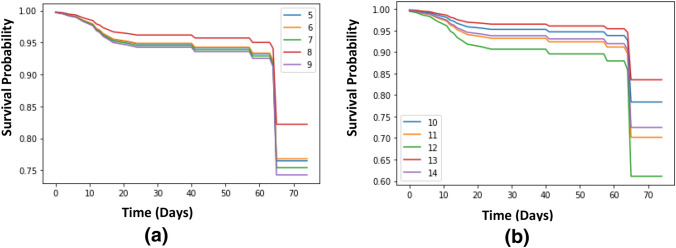
Survival probability for randomly ten patients using Cox_COVID_19 is shown in Fig. 5a. It is shown that patient 6 and patient 8 have a survival probability up to one over the whole time, patient 7 has a survival probability that is close to one, patient 9 has a probability of surviving, that is decreasing to be close to 0.7, and patient 5 has a probability that is decreasing overtime till reaching less than 0.1. Survival probability for another randomly five patients using Cox_COVID_19 is shown in Fig. 5b. For Fig. 6a, survival probability for the first randomly five patients using Deep_Cox_COVID_19 is presented. Figure 6b shows the survival probability for the second randomly five patients using Deep_Cox_COVID_19.

Fig. 5.

a, and b: Survival curve for randomly 10 patients using Cox_COVID_19

Fig. 6.

a, and b: Survival curve for randomly 10 patients using Deep_Cox_COVID_19

Improving Cox_COVID_19 system using deep learning

The implementation of the designated dataset in its original form in this research led to the appearance of some trammels such as high collinearity and convergence, so autoencoder deep neural network is implemented to solve such problems by reconstructing features presenting a new system called Deep_Cox_COVID_19. After comparing results, it is shown that Deep_Cox_COVID_19 system outperforms Cox_COVID_19 system in terms of concordance, accuracy and precision. Table 3 shows the internal construction of the autoencoder, we built in this paper. It consists of one layer with 31 nodes for the input layer, of one layer with 31 nodes as an encoder, one layer with 30 nodes as bottleneck and finally the decoder to reconstruct data, with one layer and 31 nodes.

Table 3.

Autoencoder construction

	Input layer	Encoder	Bottleneck	Decoder	Reconstruction loss	Activation function
Number of layers	1	1	1	1	binary_crossentropy	Relu
Number of nodes	31	31	30	31	–	–

Loss functions are used to determine the error between the prediction of our model and the actual target variable, the used reconstruction loss function in this paper is binary_crossentropy. An activation function is the function used to predict the output based on the input, and the used activation function in this paper is Rectified Linear Unit (ReLU). ReLU can be considered as a linear function in which the input will be directly outputted if it is positive; otherwise, it will output zero. For several forms of neural networks, it has become the default activation feature because it is easier to train a model that uses it and often achieves better performance.

Cox regression [17] is used to predict the probability of survival for each patient. For evaluating the accuracy of the model, a threshold is used. So that, the patients with a probability for survival higher than the threshold, they are the closest to survive, and patients with a probability for survival lower than the threshold, they are the furthest to survive. Table 4 shows a comparison between Cox_COVID_19 system and Deep_Cox_COVID_19 system. It is shown in Table 4 that, for Cox_COVID_19 system, the best accuracy of the test subset is up to 95.71%, with a threshold up to 0.1 and accuracy for the train subset up to 93.5%. The best accuracy with the train subset is 96.21%, with a threshold up to 0.3 and accuracy with the test subset up to 95.71%. As shown in the results below, Deep_Cox_COVID_19 system always gives better accuracy for both test and train subsets with all subsets.

Table 4.

Survival function accuracy for proposed system with different thresholds

Threshold	Cox_COVID_19		Deep_Cox_COVID_19
	Accuracy
	Train (%)	Test (%)	Train (%)	Test (%)
0.1	93.5	95.71	95.12	95.71
0.15	93.5	95	95.39	95.71
0.2	93.77	95	95.93	95.71
0.3	93.77	92.9	96.21	95.71
0.45	93.31	91.4	96.21	95

Bold values indicated best results

As shown in Table 5, Deep_Cox_COVID_19 system always gives better precision for both test and train subsets with all subsets.

Table 5.

Survival function precision for proposed system

Threshold	Cox_COVID_19		Deep_Cox_COVID_19
	Precision
	Train (%)	Test (%)	Train (%)	Test (%)
0.1	100	100	100	100
0.15	92.9	80	100	100
0.2	93.3	80	100	100
0.3	81	50	100	100
0.45	77.8	41.7	81.5	80

Bold values indicated best results

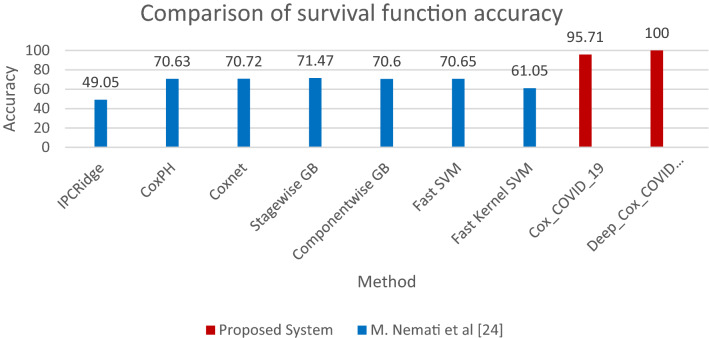
A comparison between our proposed system (Cox_COVID_19, and Deep_Cox_COVID_19) results and different algorithms (IPCRidge, CoxPH, Coxnet, Stagewise GB, Componentwise GB, Fast SVM, and Fast Kernel SVM) [24] applied on the clinical dataset for COVID-19 is presented in Table 6. The results show the proposed system achieves higher survival function accuracy as shown in Fig. 7.

Table 6.

Comparison of survival function accuracy for proposed systems and other algorithms

Author(s)	Algorithm	Accuracy (%)	Dataset
Nemati et al. [24]	IPCRidge	49.05	Open-access COVID- 19 epidemiological data [25]
	CoxPH	70.63
	Coxnet	70.72
	Stagewise GB	71.47
	Componentwise GB	70.60
	Fast SVM	70.65
	Fast Kernel SVM	61.05
Proposed system	Cox_COVID_19 (Cox regression method)	95.71	Novel Corona Virus 2019 Dataset-Kaggle [20]
	Deep_Cox_COVID_19	100

Bold values indicated best results

Fig. 7.

Survival function accuracy for proposed system and other algorithms

A comparison between our Cox_COVID_19 results and another algorithm applied on the same clinical dataset for COVID-19 is presented in Table 7.

Table 7.

Comparison of proposed system and previous studies for features affecting the mortality

Author(s)	Algorithm	Key features		Results
		Feature	Percentage
Yan, Zhang et al. [10]	XGBoost machine learning algorithm	Male	58.7%	Male, fever, cough, fatigue, dyspnoea, lactic dehydrogenase (LDH), lymphocyte and high-sensitivity C-reactive protein (hs-CRP) are the key features for differentiating between critical patients from the two classes
		Fever	49.9%
		Cough	13.9%
		Fatigue	3.7%
		Dyspnoea	2.1%
Shuai Zhang et al. [26]	Univariable Cox regression Model	Age, years	–	Age, male, fever, cough, weakness, severely ill, any and hypertension are the most important factors affecting the mortality
		Male	60%
		Fever	66.67%
		Cough	70%
		Weakness	53.33%
		Severely ill	96.67%
		Any	70%
		Hypertension	53.33%
Cox_COVID_19 prediction system	Cox regression method	Age	–	Age, fever, cough, pneumonia, muscle pain and throat pain are the most important factors affecting the mortality
		Male	61.69%
		Fever	46.56%
		Pneumonia	36.7%
		Cough	29.86%
		Throat Pain	8.3%

Conclusion

The results show that age, muscle pain, and pneumonia all have p value that is less than 0.05 and throat pain has a p value that is higher than 0.05 but still very small. So that, age, pneumonia, muscle pain and throat pain are the most important factors affecting the mortality. For evaluating the accuracy of the model, a threshold is used. So that the patients with a probability for survival higher than the threshold, they are the closest to survive, and patients with a probability for survival lower than the threshold, they are the furthest to survive. The best result for Cox_COVID_19 is when the threshold up to 0.1 with a training accuracy up to 93.5% and a testing accuracy up to 95.71%. Deep_Cox_COVID_19 shows better results with all threshold values, but the best result was when the threshold was up to 0.3 with a training accuracy up to 96.21% and a testing accuracy up to 95.71%. An autoencoder deep neural network is implemented to solve problems like high collinearity and convergence presenting Deep_Cox_COVID_19 system. Deep_Cox_COVID_19 system outperforms Cox_COVID_19 in terms of concordance, accuracy and precision.