Statistical Approaches to Candidate Biomarker Panel Selection

Abstract

The statistical analysis of robust biomarker candidates is a complex process, and is involved in several key steps in the overall biomarker development pipeline (see Fig. 22.1, Chap. 19). Initially, data visualization (Sect. 22.1, below) is important to determine outliers and to get a feel for the nature of the data and whether there appear to be any differences among the groups being examined. From there, the data must be pre-processed (Sect. 22.2) so that outliers are handled, missing values are dealt with, and normality is assessed. Once the processed data has been cleaned and is ready for downstream analysis, hypothesis tests (Sect. 22.3) are performed, and proteins that are differentially expressed are identified. Since the number of differentially expressed proteins is usually larger than warrants further investigation (50+ proteins versus just a handful that will be considered for a biomarker panel), some sort of feature reduction (Sect. 22.4) should be performed to narrow the list of candidate biomarkers down to a more reasonable number. Once the list of proteins has been reduced to those that are likely most useful for downstream classification purposes, unsupervised or supervised learning is performed (Sects. 22.5 and 22.6, respectively).

The statistical analysis of robust biomarker candidates is a complex process, and is involved in several key steps in the overall biomarker development pipeline (see Chap. 19). Initially, data visualization (Sect. 22.1, below) is important to determine outliers and to get a feel for the nature of the data and whether there appear to be any differences among the groups being examined. From there, the data must be pre-processed (Sect. 22.2) so that outliers are handled, missing values are dealt with, and normality is assessed. Once the processed data has been cleaned and is ready for downstream analysis, hypothesis tests (Sect. 22.3) are performed, and proteins that are differentially expressed are identified. Since the number of differentially expressed proteins is usually larger than warrants further investigation (50+ proteins versus just a handful that will be considered for a biomarker panel), some sort of feature reduction (Sect. 22.4) should be performed to narrow the list of candidate biomarkers down to a more reasonable number. Once the list of proteins has been reduced to those that are likely most useful for downstream classification purposes, unsupervised or supervised learning is performed (Sects. 22.5 and 22.6, respectively).

The statistical analysis of proteomics data to identify candidate biomarkers and ultimately, the development of predictive models is a complex, multi-step and iterative process. Candidate biomarker selection requires involvement by dedicated statisticians and bioinformaticians with in-depth knowledge of experimental design, insight about how experimental data was generated, as well as a grasp of the types of data structures that the proteomics experiment generated. For these reasons, analysts should be involved in the biomarker study design from the very beginning. Doing so also allows them to obtain a better understanding of the resultant data and any nuances associated with them. Further, they can also assist with experimental details to ensure that the proper analyses can be performed at the end of the experiment. Such an appreciation of the data obtained helps drive strategies for handling outliers or missing data, the pre-processing approaches frequently necessary when working with omics data, and the appropriate selection of hypothesis tests for analyzing the data.

The goal of learning methods is to classify the samples into two or more groups based on a subset of proteins that are most useful for distinguishing between the groups. This subset of proteins is commonly referred to as candidate biomarkers for the classification. The result of supervised learning is a variable importance list that ranks those proteins which are most likely to separate one group of interest from another. This variable importance list is ordered by each protein’s ability to discriminate one group from another. In order for a classification task to generalize samples outside the initial discovery samples, some sort of resampling needs to be employed (Sect. 22.7). Resampling techniques can be as simple as setting aside a separate sample set to validate the performance of classification algorithm, or cross-validation techniques where some of the discovery data are left out of the training and are instead used for the testing the trained model. Additionally, methods exist for assessing the ability of a supervised learning algorithm to correctly classify samples from each of the groups of interest. Examining the prediction success or receiver operating characteristic (ROC) curves gives the user a feel for how well the classification algorithm performs (Sect. 22.8). Ideally, the classification algorithm should be able to predict class identity just as well on the training dataset as the testing dataset for a biomarker panel that can be used to distinguish one group from another.

The end result of the biomarker discovery pipeline mentioned above is a list of candidate biomarkers that can be used to distinguish a future sample as belonging to a particular group. However, the experimentation/data analysis process does not end with the creation of a predictive model. This is just the initial discovery phase where a candidate biomarker panel has been identified, and subjected to qualification using independent quantitative proteomics measurements. The next phase is the verification phase, wherein the same biomarker panel has to prove a successful predictor in an independent dataset. This step is critical to the survival of a biomarker panel for further study, by demonstrating the ability of said biomarker panel to generalize to additional samples. Once the biomarker panel has been verified in an independent dataset, further downstream steps can be taken to Validate (Chap. 19: Introduction), produce, and market a diagnostic test based on the discovered biomarker panel.

22.1. Data Inspection/Visualization

Proteomics data typically have a high degree of variability, due both to biological variability from one sample to another and technical variability relating to the technology used, as well as to inherent differences between proteins (e.g., isoforms and post-translational modifications). In addition, proteomics experiments are frequently performed on small sample sizes (less than ten samples per group). The resultant data typically contains over 1000 variables, which results in a wide data set - one that has small n (sample size) and large p (number of variables).

The first step in working with any data set should be data inspection and/or data visualization. This process involves checking the data for consistency of type, examining the dataset for missing values or outliers, as well as graphically displaying the data to better understand the nature and behavior of the various observations.

22.1.1. Data Consistency

Checking the data for consistency involves examining the values present for each individual variable. If the data is supposed to be numeric, one should check that all the values are actually numbers, and that there are no textual strings present. Bioplex cytokine assay data frequently are returned from the instrument with values such as “OOR<“. It is up to the data analyst to determine what this value represents (while it is an actual value, but it is below the limit of detection of the instrument), and what to replace this value with. We will discuss data replacement in following sections. An example of this is presented in Table 22.1. If the data is supposed to be positive values only, do any of the columns have negative values? This can be easily checked simply by calculating the minimum for all variables. Another way to check data consistency is to make sure that the data is matched correctly by subject, if matching is mentioned in the study design. Matching is a statistical technique where members of one group are “matched” to members of another group with regards to possibly confounding variables in order to minimize the effect the confounder has on the treatment effect. If the study design suggests that individuals will be matched for gender and age, then the data analyst should verify that males are matched with males, females are matched with females, and individuals with a similar age are matched to other individuals within that same age range. If any data consistency issues are present, they should be corrected before any type of analysis is performed. Doing so often involves communication with the PI as well as with the technical staff that generated the dataset.

Table 22.1.

Sample of initial data file

Sample No.	IP-10	MIP-1a	TNF-a	VEGF	TRAIL
1	36800.84	718.23	28017.48	44634.68	21562.09
2	13247.18	2675.18		−10569.1	5360.15
3	2682.51	OOR >	5006.67	2790.2	1359.8
4	10.28	5.4	18.75	9.04	1.9
5	3.34	1.57	5.33	3.37	2.39
6	0	*5.80	*7.11	167.62	OOR <

Table 22.1 demonstrates several examples of data inconsistencies. For instance, the last value in the IP-10 column is a 0. This was a value that was initially missing, but the researcher changed all missing values to 0 for that cytokine. MIP-1a has two issues. The first is a value of “OOR >“ (out of range positive) when a numeric value is expected. The second is a value of *5.80 when a strict numeric is expected. The analyst needs to best determine how to handle such instances, often in consultation with the lab performing the experiment or the PI of the project. TNF-a has a true missing value as well as an “*” that needs to be dealt with. VEGF has a negative value when only positive values are possible. Thus, further investigation is needed as to why the negative value is present. Lastly, TRAIL has a value of “OOR <“ (out of range negative) that needs to be properly handled.

22.1.2. Missing Values/Outlier Detection

Dealing with missing values and outliers presents many challenges for the data analyst. Frequently, basic science experimentalists will replace a missing value with a value of 0. This value of 0 can have many different definitions. For instance, a value of 0 might indicate a plausible, real value, but one that fell below the detection limit of the instrument. Instead of placing a value for that particular data point, a researcher might opt to call it a 0. How the analyst handles a 0 value depends on the true meaning of that 0 value. In other situations, the researcher might opt to replace a missing value with a 0 value. This is done because some software packages are unable to handle missing values, and the researcher thinks missing values make the dataset look ugly. Thus, it is important to determine if any such substitutions have been made within a given dataset. If multiple 0 values are observed, the PI or research technician should be consulted to determine the true meaning of these 0 values.

Common ways to deal with missing values include simply leaving those samples out of the data analysis, data imputation, or choosing analysis methods that ignores missing values (such as those mentioned in Sects. 22.6.2, 22.6.3, and 22.6.4). Several methods exist for data imputation, which will be discussed in the following section.

Another common issue in proteomics data sets, as well as other omics data sets, is the presence of outliers. Outliers are individual data points, large or small, that lie further from the majority of the data than would ordinarily be expected and can have an exaggerated influence on the fit of a given algorithm. An outlier may indicate a bad data point: one that results from improper coding, or possibly an experiment gone awry. Outliers heavily influence descriptive statistics such as the mean, as well as impacting the types of hypothesis testing that can validly/reliably be performed on the data. Thus, their detection is an important step in the analysis pipeline. A simple method for detecting outliers is the creation of a boxplot, discussed in the next section, which will graphically display the absence/presence of any outliers. Specifically, a data value is often said to be an outlier if it lies further away from the mean or median of the dataset than ± 1.5*IQR (interquartile range). If the outlier is the result of improper data entry, its value should be easily corrected. If the outlier is the result of an experiment gone awry, then the value should be removed from the dataset and treated as a missing value. If, however, the cause of the outlier cannot be attributed to either of those two instances, the value must remain in the dataset and appropriate procedures should be utilized downstream, i.e. ones that are robust to the presence of outliers.

22.1.3. Graphical Methods

Many types of graphical methods exist to display proteomics data. These include histograms, boxplots, scatterplots, and quantile-quantile plots (also known as q-q plots), among others. Plots can tell one about the presence of outliers within the data, about possible relationships amongst variables within the dataset, about the validity of certain hypothesis test assumptions (such as whether the data is normally distributed), or about possible differences between groups.

Histograms arrange the data points into bins of equal width, where the height of each bar represents the number or proportion of data points that lie within each bin. Histograms are useful for determining whether there are outliers within the data (are there single bins which are separated by many empty bins from the rest of the data?), as well as giving a feel for the shape/distribution of the data. One can visually determine if the data is symmetric (possibly normally distributed) or skewed (not normally distributed). A skewed distribution is one that is not symmetrical, but rather has a long tail in one direction. Example histograms are presented in Fig. 22.1. These histograms represent Bioplex cytokine assay values for IP-10 for patients with Dengue Fever (DF) and Dengue Hemorrhagic Fever (DHF), taken from our NIAID Clinical Proteomics Center Dengue Fever (CPC) project (see Chap. 20 for description). These histograms represent data that is highly skewed, as the shape of the histogram is not symmetric, but rather shifted towards the left. In addition, outliers are present within the DHF subjects as there are three bins that are separated from the rest of the data.

Fig. 22.1.

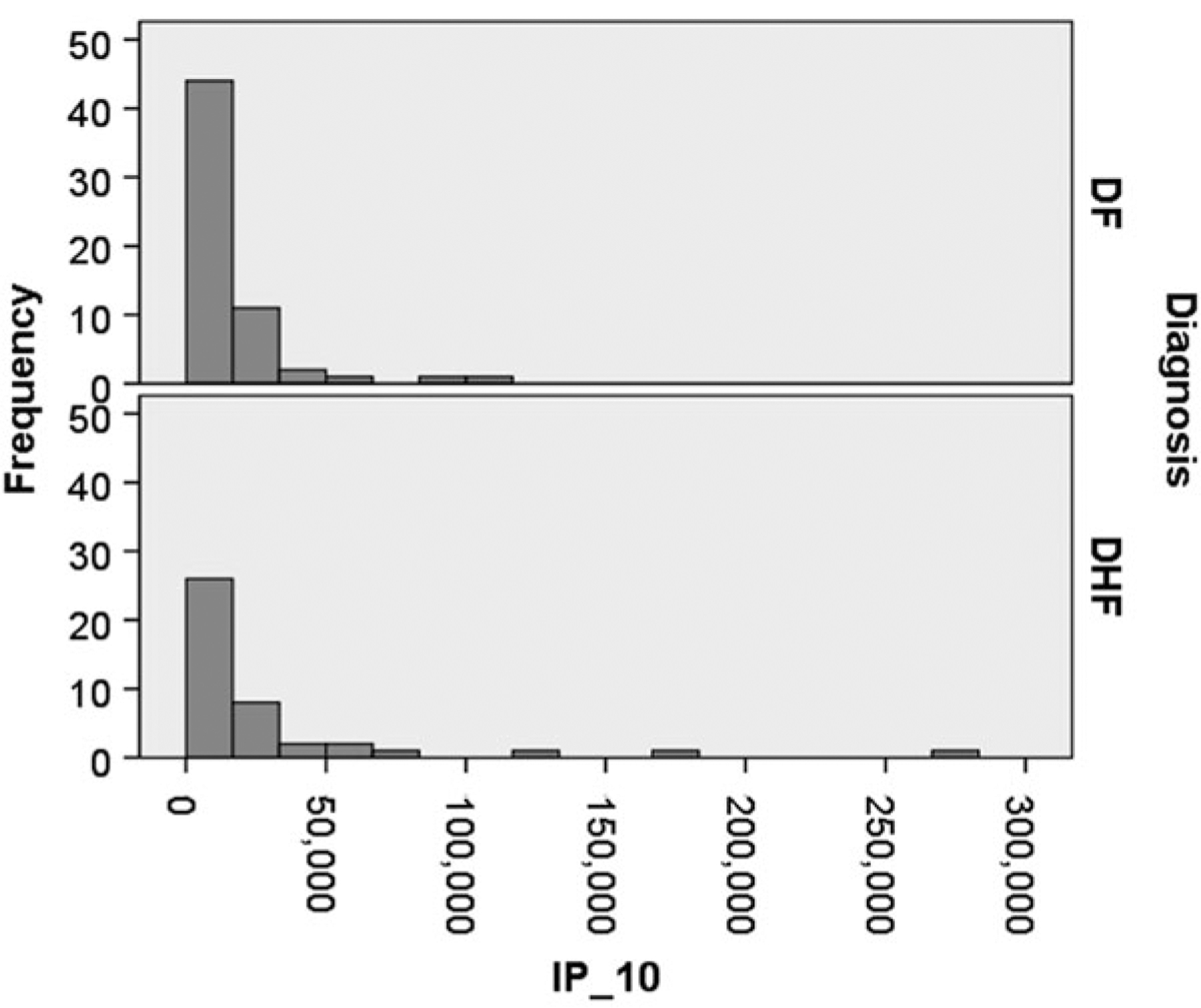
Histograms for IP_10 Cytokine data. Dengue Fever is on the top; Dengue Hemorrhagic Fever is on the bottom

Boxplots show the shape of the distribution, the central value of a dataset, and the variability within the dataset, by displaying the median, the interquartile range (IQR), as well as any potential outliers. As the name implies, the graphs have a box shape. The middle 50 % of the data is displayed within the central rectangle, the median value is frequently displayed as a line within the central rectangle, and whiskers are displayed above and below the central rectangle, representing the range up to some multiple of the IQR away from the median. The upper hinge (edge) of the box indicates the 75th percentile of the data, and the lower hinge (edge) of the box indicates the 25th percentile of the data. In addition, individual outliers are displayed usually as stars or circles on the plot. If no outliers are present, the ends of the whiskers represent the largest and smallest value within a dataset. An example of a boxplot is presented in Fig. 22.2. Like histograms, boxplots can be used to assess the distribution of a given dataset. For data that is symmetric (and thus possibly normally distributed), the median line will lie roughly in the center of the rectangle. In addition, the whisker above the rectangle will be roughly the same length as the whisker below the rectangle. For skewed data (and thus data that is probably not normally distributed), the median line will lie much closer to the top or bottom of the rectangle than the middle, and the whiskers above and below the rectangle will not be the same length. Boxplots can also be used to examine if there are differences between two or more groups by looking for overlapping rectangles when multiple boxplots are drawn on the same plot.

Fig. 22.2.

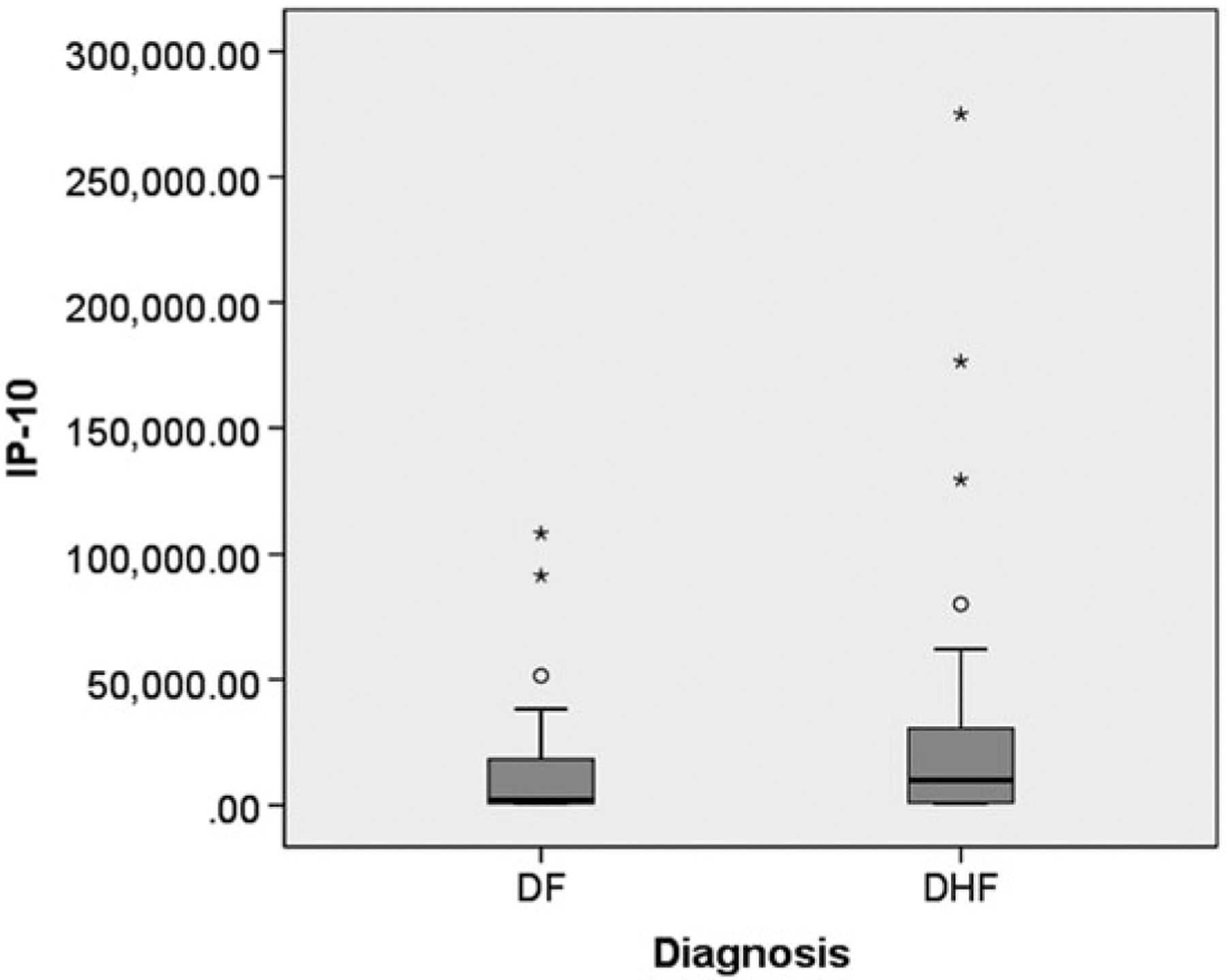
Boxplots for IP_10 Cytokine data. Dengue Fever is on the left; Dengue Hemorrhagic Fever is on the right

The example in Fig. 22.2 represents IP-10 Bioplex cytokine assay data for the Dengue Fever project (the same as is shown for the histogram in Fig. 22.1). The value of IP-10 for patients with Dengue Fever (DF) is shown in the left boxplot, and the value of IP-10 for patients with Dengue Hemorrhagic Fever (DHF) is shown in the right boxplot. Both of these groups have outliers, which are represented by the circles and the stars (figure created using SPSS v20). In addition, both of the boxplots represent data that is skewed as the median line is not in the middle of the rectangle. The whisker above both boxes is also much longer than the whisker below each box.

A scatterplot is a graphical representation of how two different variables relate to each other. The values for one variable are plotted along the x-axis, while the values for another variable are plotted along the y-axis. Scatterplots are useful for detecting a correlation between two variables, as well as if there appears to be some sort of functional relationship between the two variables. If the two variables are correlated, there will be an obvious trend in the location of the dots on the scatterplot. Scatterplots can be used to determine if the functional relationship is a linear one, a quadratic one, a logarithmic one, or one of many different types of functions. This is extremely useful if some sort of modeling is to be done later on.

Another mechanism for aiding with determining whether the dataset is normally distributed is the q-q plot. The q-q plot is a special scatterplot. As the name implies, it is one that uses the quantiles of the data to create the plot. Along the x axis are the quantiles of the experimental data. Along the y axis are the quantiles of a specified distribution that has the same mean and standard deviation as the experimental data. The specified distribution is a normal distribution if the assumption of normality is being assessed. If all the data points lie on the line y = x, then the experimental data perfectly matches data that is normally distributed. If however, there is deviation away from such a straight line, some amount of skewness is present.

Figure 22.3a, b represent q-q plots for the IP-10 Bioplex cytokine assay data discussed above. The shape of both of these plots is very non-linear, which indicates again that the data is highly skewed. Ideally, we would like all of the points to lie on the straight diagonal line which would mean the experimental data exactly follows a normal distribution.

Fig. 22.3.

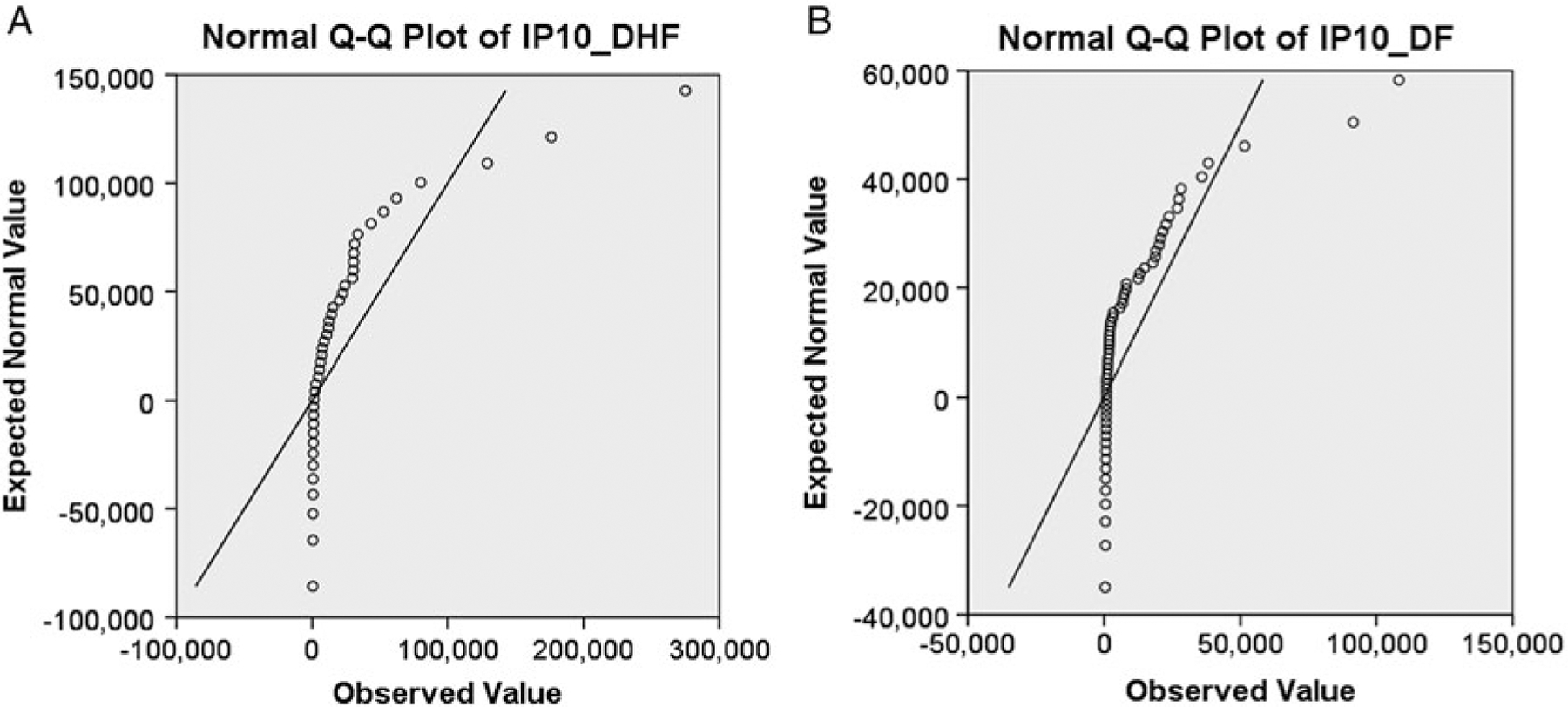
(a) Q-Q plot of IP-10 cytokine data for Dengue Hemorrhagic Fever, (b) Q-Q plot of IP-10 cytokine data for Dengue Fever

22.2. Pre-processing

Data pre-processing methods refer to the addition, deletion, or transformation of the proteomics data in some fashion before downstream analysis is performed. Pre-processing of the data is a critical step to ensure that the results obtained from statistical testing are both valid as well as correct. How the data is pre-processed can sometimes have a dramatic effect on the output of the model creation process. Some procedures, such as classification and regression trees (Sect. 22.6.2) are fairly insensitive to data pre-processing, while other methods such as logistic regression are not [18]. Pre-processing includes dealing with outliers and missing values through techniques such as imputation as well as normalizing or transforming the dataset to meet hypothesis testing and/or modeling assumptions.

22.2.1. Missing Values/Imputation

Missing values within a dataset present an important, and often overlooked, challenge to downstream data analysis. The reasons for the missing data might bias the results, so the underlying mechanism needs to be considered when determining the most appropriate method for handling missing values. Rubin [25] defines three types of mechanisms that cause data to be missing: data missing completely at random, data missing at random, and data missing not at random. Data missing completely at random means the missing values are truly just randomly missing (and thus ignorable). What this means is that there is no relationship between the value that is missing and either the observed variables or the unobserved parameters of interest. This is the easiest mechanism for a data value to be missing and results in unbiased data analysis. Data missing at random (but not completely) happens when the probability of a missing value depends on some observed values but does not depend on any data that has not been observed (or the group assignment). Unfortunately, missing at random has a somewhat confusing name as it does not mean missing completely at random which is what the name implies. Data that is missing not at random means the probability of a missing value depends on the variable that is missing. This type of “missingness” is often a result in survey analysis where the respondent fails to answer a question because of the nature of the question (i.e. income level).

Some analytic techniques (such as those that deal with repeated measurements on the same sample) require that there are no missing values. Several methods exist that will allow the end user to overcome missing data. The first is to simply remove the sample which resulted in the incomplete data. While this is the simplest approach, it is often not preferred since the sample size (which is often small to begin with) will be reduced. Other methods include some form of data imputation, where missing values are substituted with appropriate imputed values. Common imputation methods include single imputation methods such as data replacement with a set value, data replacement with a mean or median, simple regression, as well as model-based methods such as multiple imputation and maximum likelihood [19].

List-wise deletion can occur in one of two ways: complete case elimination as mentioned above or pairwise deletion. List-wise deletion results in removing an entire observation from the dataset. The advantage of this method is that it is simple, and one can compare the results of one variable to that of another as the dataset is the same for all variables. The disadvantages include a reduction in the power of the analysis since the size of the dataset has been reduced, and that the loss of generality that downstream analysis is not based on all the information collected. Pairwise deletion involves just removing the data that is missing for a given variable, and leaving that subject in the analysis of other variables where information is present. The advantages of pairwise deletion are that this method uses all the data that has been collected for the analysis of a given variable as well as keeps as many cases/samples as possible. The disadvantage is that it becomes difficult to compare the results from one variable to another as the same samples were not used to generate all results.

Single imputation methods are fairly straightforward. For cytokine data, replacement of character data (such as OOR > or OOR<) is often done with ten times the largest value observed in the dataset or one tenths the lowest value observed within the dataset, respectively. This is because the definition of OOR > is “Out-of-Range High” which means that a numeric value should exist for that data point, but said value is above the detection range of the instrument. The approach is similar for OOR < values. Imputation using the mean or median value replaces any missing value for a given variable with either the average or the median value for that variable. The disadvantages to using this method are that the overall variability for that variable will be reduced and the correlation/covariance estimates are also weakened. Simple regression involves replacing the missing data with that obtained from fitting a regression equation to the remaining data. This method works well if there is more than one variable of interest. The advantage of this method is that it uses information from all the data that is obtained. The disadvantages are that the overall measure of variability within the dataset has been diminished as well as that the model fit and correlation estimates will likely be better than had a value been initially obtained.

Model-based imputation methods include multiple imputation and maximum likelihood. This method does not impute any data, but rather uses each cases available data to compute maximum likelihood estimates [9]. The maximum likelihood estimate of a parameter is the value of the parameter that is most likely to have resulted in the observed data. The likelihood is computed separately for those cases with complete data on some variables and those with complete data on all variables. These two likelihoods are then maximized together to find the estimates. Like multiple imputation, this method gives unbiased parameter estimates and standard errors. One advantage is that it does not require the careful selection of variables used to impute values that multiple imputation method requires. An additional imputation method is K-nearest neighbors (KNN) imputation [1]. With this technique, the k nearest neighbor algorithm is utilized where proteins behave as the neighbors and the distance between proteins is based on the correlation between two proteins.

22.2.2. Normalization

The most common form of data pre-processing is what is commonly known as normalizing (or standardizing) the data. This process centers and rescales the data. To center the data for a given variable, each value has the overall variable mean subtracted from the original value. To scale the data variable, the centered data is then divided by the standard deviation of each data variable. Centering results in the data variable having a mean of zero, and scaling results in the variable having a standard deviation of one. Normalizing the data is commonly done to improve the numeric stability of some classification techniques. Support Vector Machine modeling (Sect. 22.6.5) is one technique that requires the data to be normalized before analysis. Principal Component Analysis is another technique that benefits from centering and scaling the data. The downside to centering and scaling data is that the data are no longer in their original units, so it is sometimes challenging to interpret the normalized computer output. However, simple arithmetic manipulations can make the model fit into the original scale.

22.2.3. Transformations

Data transformations are frequently used when the data appear skewed. The most common forms of data transformations are the logarithmic transformation, the square root transformation, or the inverse transformation. Many statistical hypothesis tests have an underlying assumption that the data be normally distributed, the variances be equal (homoscedasticity), or both. Biological data, which are often skewed, frequently do not meet these assumptions. Data transformations often make the assumptions more valid. To perform a data transformation, simply take the logarithm (any base will do as long as the chosen base is consistent from one data value to another) of every entry for a given variable. Likewise, the square root of the data value or the inverse can be taken as well. The goal is to help transform the proteomic data into a dataset that is not skewed or one that has similar variance between two or more groups of interest. Both of these concepts are important assumptions for parametric testing mentioned in Sect. 22.3.1. Once the transformation has been applied to every data point, the transformed data should be used for downstream analysis. It is important to check whether the transformation helped make the data appear more normally distributed. Valid methods for examining normality of the data include checking boxplots as well as q-q plots, both of which were described in Sect. 22.1.3. If the data contain multiple groups (such as Dengue Fever vs Dengue Hemorrhagic Fever, or Chagas disease with cardiomyopathy versus Chagas disease without cardiomyopathy, Chap. 20), each group should be assessed for symmetry individually. The logarithmic transformation frequently works well for intensity data (such as that from 2D gel or cytokine experiments) while the square root transformation works well for count data.

22.3. Hypothesis Testing

While exploratory techniques are an important component to guide investigators to promising hypotheses about mechanisms and structure, the classical techniques for inference such as hypothesis testing and confidence interval construction provide a useful and generally accepted metric for validating or rejecting hypotheses of interest. Built on the classical adversarial construction of proof against a null hypothesis of no discovery, hypothesis testing provides researchers with a way to summarize and quantify evidence that is generally invariant across most fields of science. Statistical hypothesis tests falls into two categories: parametric and nonparametric. As mentioned above in Sect. 22.2.3, parametric tests require extra assumptions for their validity. These assumptions are that the data come from a simple random sample, are normally distributed, and also that the variances are homogeneous. If the normality or variance assumptions are violated, parametric tests are not appropriate for a dataset. Nonparametric techniques have no assumptions about the distribution of the data. However, they do require randomness of the data and independence of the samples.

22.3.1. Parametric Tests

Parametric tests include one sample t-tests, two-sample t-tests, paired t-tests, and multiple versions of analysis of variance (ANOVA). One-sample t-tests are the most simplistic form of a hypothesis test. They are used when researchers want to determine whether a parameter (such as the mean) of a variable matches that of one that was published. The null hypothesis is that the mean of the obtained variable is equal to the published or hypothesized value, and the alternative hypothesis is that the mean of the observed variable is not equal to the null value. This type of test is most often used when a researcher is new to a specific technique or instrument, and they want to check that they are performing the experiment properly or that they have used the correct settings for an instrument. As the name implies, the values of only one condition are being measured. In other words, only a control sample is examined.

The two-sample t-test is an extension of the one sample t-test. Instead of just one group being compared to some known value, the objective of a two-sample t-test is to look for differences between two groups: typically a control sample and an infected sample. Here, the two samples should be sampled independently from each other. This means that the samples are not matched or related in some fashion. An additional assumption for the two-sample t-test to be valid is that the variance of group 1 (i.e. controls) is similar to the variance of group 2 (e.g. Infected). If this assumption is violated, there is a version to control for unequal variances, called Welch’s correction, which can be used instead. For either form of the t-test, each group needs to be checked for normality to meet that assumption. Thus, one should check to see if the controls samples are normally distributed and one should separately check to see if the infected/treated samples are also normally distributed. If either group violates the normality assumption, a parametric test may not be appropriate. However, a transformation should typically be attempted before reverting to a nonparametric test. If the transformation is applied to one group, that same transformation must be applied to all other groups. The transformed data should then be checked for normality. If the transformed data helps the samples look more normally distributed, then the transformed data should be analyzed via the student’s t-test (not the raw data). For the Dengue Fever example data, the data was transformed using log base 2. This data was then analyzed via the Welch’s correction for the two-sample t-test. The results indicate that 107 protein spots are differentially abundant between the DF & DHF samples at a significance level of 0.05. These 107 spots will be the input for the examples in Sects. 22.6.2, 22.6.3, 22.6.4, 22.6.5, 22.6.6, and 22.6.7.

Paired t-tests are similar to two-sample t-tests; however, instead of the two samples being independent, they are required to be dependent (matched). This means that they have either been matched to account for possible confounding factors such as on age, gender, race, etc. or that the sample is from the same patient over time, such as a pre- and post- measurement after the administration of some drug. Just as the previous t-tests had the assumption that the data be normally distributed, the paired t-test does as well. However, when checking for normality with paired data, the difference between groups is assessed instead of the normality of each group separately. This is because the formula for the test statistic is based on the difference instead of each group individually. Thus, to determine if the data is normally distributed for paired data, the pre measurement would be subtracted from the post measurement and that value would be plotted on a q-q plot.

Analysis of Variance (ANOVA) techniques are used when there are more than two groups being compared or there are multiple factors being investigated. There are many forms of ANOVA, including one-way ANOVA (three or more groups being compared at once), two-way ANOVA (at least two factors with at least two levels each), and repeated measures or mixed-model ANOVA (in which at least one factor has multiple measurements on the same individual over time). The basic premise for ANOVA is that instead of mean values being considered, the amount of variability both within a group and also between groups is being compared. For one-way ANOVA, a single null hypothesis is examined: whether there is a difference among multiple different group means. For two-way ANOVA, multiple null hypotheses are examined: whether there is a difference due to the first factor; whether (typically) there is a difference due to the second factor; and whether there is an interaction between the first and second factor.

Unlike with t-tests where you immediately can conclude if group 1 is significantly different from group 2 based on the observed p-value, with ANOVA all that is known based on the initial results of running the hypothesis test is that at least one group differs from the others within a given factor. Post-hoc tests, such as Tukey’s or Dunnett’s tests, can be used to determine exactly where the differences lie. Tukey’s post-hoc test compares all levels of a factor to each other. Dunnett’s test, on the other hand, compares each level to a control level only.

For example, if you are comparing a control strain of a disease to an attenuated strain to a virulent strain, the initial results of a one-way ANOVA will tell you that at least one of the strains is different from the others, but the exact differences will not be able to be determined. Running Tukey’s test will compare control to attenuated, control to virulent, and attenuated to virulent to allow one to possibly conclude that control is different from virulent only. Dunnett’s test, on the other hand, would only compare control to attenuated and also control to virulent, but will not compare attenuated to virulent (which may not be a hypothesis of interest for some studies).

22.3.2. Nonparametric Tests

Nonparametric tests include chi-square tests, the Mann-Whitney test, the Wilcoxon Signed Rank test, and the Kruskal-Wallis test. All of these tests do not require the data to have a specific shape. Because of the lack of assumptions, nonparametric tests should only be used if the data are highly skewed or the variances are not homogeneous between groups. Whereas the test statistic for a parametric test is based on the actual data value, a test statistic for a nonparametric test is based on the ranks of the data instead. As a result, if data meets the assumptions for using a parametric test, such a test should be preferred over a nonparametric equivalent.

22.3.3. Multiple Hypothesis Corrections

When dealing with proteomics experiments, and other “omics” experiments as well, instead of just testing one protein at a time, researchers typically examine many (often hundreds or thousands) of hypotheses at a time. Doing so increases the probability of false positives: that is, incorrectly rejecting a null hypothesis when no difference between groups exists. This is a serious problem in many basic science experiments, and needs to be dealt with accordingly. The method for correcting the number of false positives, and bringing number of false positives back to a more reasonable level, is known as multiple hypothesis corrections. There are two methods for controlling the false positive rate when one is testing multiple hypotheses simultaneously. They are known as the Family Wise Error Rate (FWER) and False Discovery Rate (FDR) corrections.

The FWER is the probability of wrongly rejecting any of the null hypotheses. The most common FWER correction is the Bonferroni correction [21], although Tukey’s test corrects for FWER in the ANOVA setting. FWER corrections are considered to be conservative methods for controlling for multiple hypothesis tests, and frequently results in no proteins remaining significantly differentially abundant in a proteomics experiment.

FDR, on the other hand, seeks to control the proportion of false positives among the complete set of rejected null hypotheses (rather than the probability of any false positives). The most common FDR method is the Benjamini-Hochberg method [2]. FDR procedures allow for more potential false positives than FWER methods, but they have increased power when compared to FWER methods. As a result, FDR methods are less conservative than FWER methods, and usually result in more proteins being significantly differentially abundant between two groups.

22.4. Feature Reduction

A major problem in mining large datasets is the “curse of dimensionality”: that is, model efficacy decreases as more variables are added. In many omics experiments, we not only want to learn about which genes/proteins are different from one group to another, but we would like to build a predictive model to determine possible biomarkers for things such as a disease progression or diagnosis. However, as more and more variables are added to the model, the computational time increases and the information gained becomes minimal. Feature reduction aims to decrease the number of input variables to the model; it moderates the effect of the curse of dimensionality by removing irrelevant or redundant variables or noisy data. Feature reduction has the following positive effects: speeding up processing time of the algorithm, enhancing the quality of the data, increasing the predictive power of the algorithm, and making the results more understandable.

22.4.1. Hypothesis Testing Results

One technique for reducing the dimension of the variables to be included in predictive analysis is to eliminate those variables which show no variable-wise significant difference between groups without adjustment for multiple testing. This means some form of hypothesis test has been run on the dataset, and the insignificant variables (p-value > 0.05) are removed. Frequently in omics data analysis, removing only those variables with a p-value > 0.05 still results in a large (greater than 100) variables of interest. In this case, a more restrictive p-value cut-off is used for the downstream analysis.

22.4.2. Significance Analysis of Microarrays (SAM)

Significance analysis of microarrays (SAM) is a widely used permutation-based approach to identify differentially expressed genes when assessing statistical significance using false discovery rate (FDR) adjustment in high dimensional datasets [23]. SAM can be applied to proteomics data since protein abundance microarrays are high-throughput technology capable of generating large quantities of proteomics. SAM algorithm is a great tool comparing t statistic with multiple hypothesis testing adjustments to determine which hypothesis to reject to minimize the number of false positives and negatives by permuting the columns of the protein abundance. Resampling method (permutation) can be used to estimate p values to avoid the joint distribution of the test statistics. Two sample t-test procedures require parametric Gaussian assumptions. There are attractive points to SAM using multiple testing procedures, that it does not rely on the parametric assumptions and it does not involve any complex estimation procedures. SAM uses the permutation methods (default 100 times) to estimate FDR and computes a modified t-statistics which measures the strength of the relationship between protein abundance and disease outcome. It also accounts for feature-specific fluctuations in signals and adjusts for increasing variation in features with low signal-to-noise ratios. Data are presented as a scatter plot of expected (x-axis) vs observed (y-axis) relative differences between group, where significant deviations that exceed a threshold from expected relative differences are identified and considered “significant”. The solid line indicates the relative difference expression of group is identical, but the dotted line drawn at threshold delta value. The delta was chosen by minimal cross-validation errors. The high rank features of SAM results are marked red color (induced protein) and green color (suppressed protein). For our CPC aspergillosis study, the 110 spots among total 655 spots in 2D-gel data are selected for differentiating case vs. control by 100 permutations and FDR as 5 % for delta = 0.35. The Microsoft Excel add-in SAM package can be used with specific option filtering. There are several options, for example, multi-class, two-class paired, and two-class unpaired response types using the t-test, Wilcoxon test, and analysis of variance test. The limitation of SAM procedure is that this approach is a univariate version approach and not allowed to consider the correlated structure between features like a multivariate regression modeling. An example of a SAM result for aspergillosis data is shown in Fig. 22.4.

Fig. 22.4.

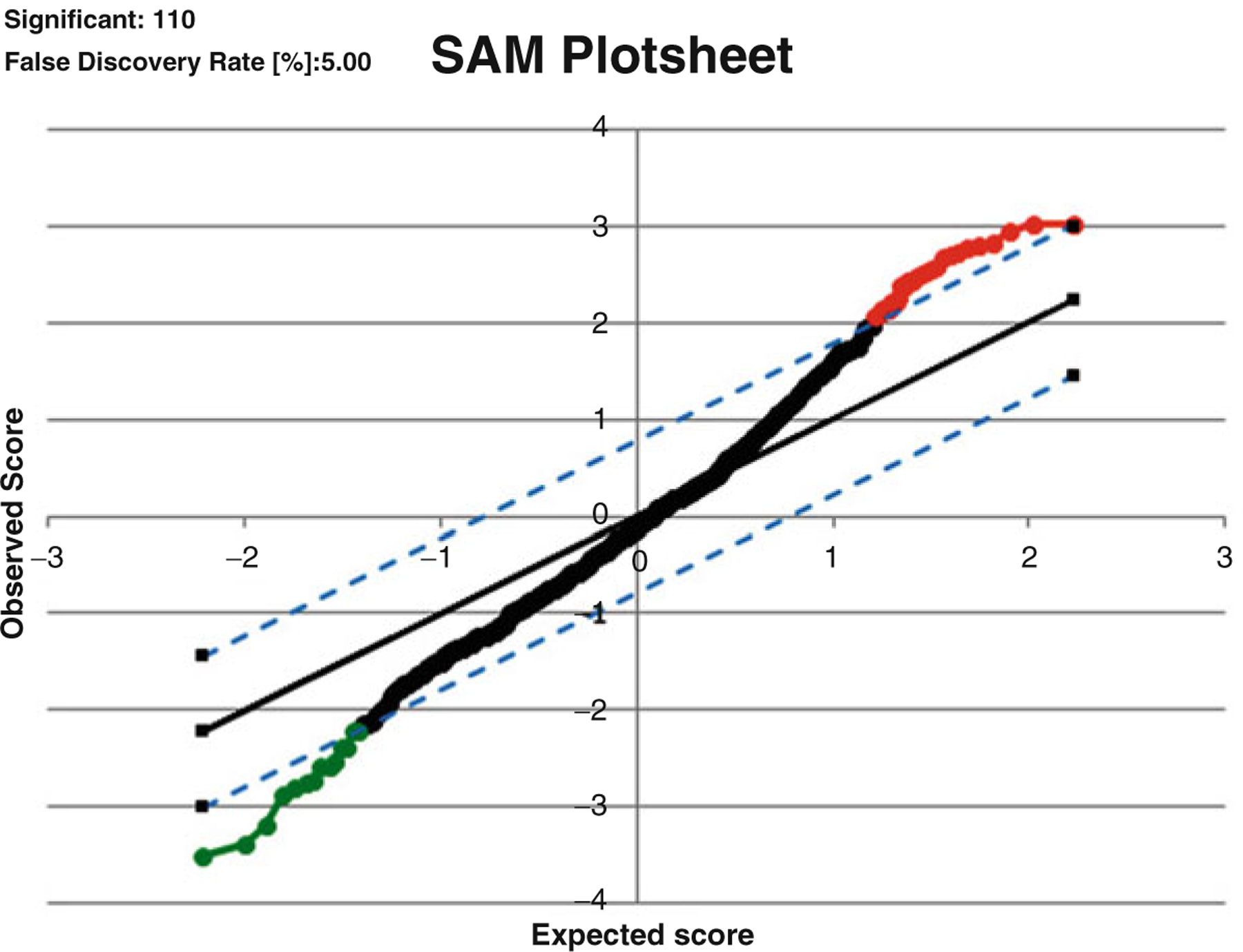
SAM result for Aspergillosis dataset

22.4.3. Fold-Change

Fold Change refers to the values for the control samples being divided by the obtained values for the treated samples. If this results in a value less than one, then the inverse value is taken and a negative sign is added. Thus, the value for fold changes range from -infinity to −1, and then also from 1 to + infinity. A fold-change cut-off value of ±2 is frequently used in proteomics experiments when looking for differential expression. Proteins with an absolute fold-change greater than 2 are thought to be differentially abundant between groups of interest. Thus, only proteins that exhibit such characteristics are considered for downstream analysis. The fold-change cut-off is sometimes increased (to 2.5 or 3) if the number of proteins that have such a fold-change is large.

22.4.4. PCA

Principal component analysis (PCA) is useful for the classification as well as compression of a dataset. The main goal of PCA is to decrease the dimensionality of the dataset by finding a new set of variables, called principal components that represent the majority of the information present within the original dataset. The information is related to the variation present within the original dataset and is calculated by the covariance among the original variables. The number of important principal components is typically smaller than the initial number of variables in the dataset. This new variable space will reduce the complexity and noise within the dataset and reveal hidden characteristics within the data. The principal components are uncorrelated (orthogonal) with each other and are also ordered by the total fraction of information about the original dataset they contain. The first principal component accounts for as much of the variability in the original dataset as possible, and each subsequent component accounts for as much of the remaining variability as possible. The process for determining the principal components is one based on covariance eigenvalues and eigenvectors. The results are presented in the form of scores (projections of the eigenvectors) and loadings (eigenvalues).

22.5. Unsupervised Learning

Machine learning falls into two categories of methods: those that are considered to be unsupervised, and those that are considered to be supervised. The primary difference between the two methods is what is assumed to be known at the start of the process. For unsupervised learning, the “truth” is not assumed to be known, nor is it used in the process. “Truth”, in our context, is knowing which group a sample belongs to. In an experiment distinguishing between Dengue Fever and Dengue Hemorrhagic Fever, the “truth” would be which patients have Dengue Fever, and which patients have Dengue Hemorrhagic Fever. For supervised methods, the “truth” is required for each algorithm. Hierarchical clustering, K-means clustering, and PCA are all examples of unsupervised learning methods.

22.5.1. Hierarchical Clustering

Hierarchical clustering seeks to group available data into clusters by the formation of a dendrogram. Hierarchical clustering is based on two key principles: (1) Members of each cluster are more closely related to other members of that cluster than they are to members of another cluster, and (2) Elements in different clusters are further apart from each other than they are from members of their own cluster. The process by which samples are grouped into clusters is determined by a measure of similarity between the objects. Various measures of similarity exist, including Euclidean distance, Manhattan (city-block) distance, and Pearson correlation. Euclidean distance is the most commonly used measure of similarity for proteomics experiments, but it is sensitive to outliers within the data. The Manhattan distance requires that the data be standardized before use. The Pearson correlation is a similarity measure that is scale invariant, but it is not as intuitive to use as the other measures of similarity.

Not only must one measure the similarity (distance) between two data points, but one must also determine how to measure the distance between two clusters. This distance can be calculated in at least three ways as: (1) the minimum distance between any two objects in the different clusters; (2) the maximum distance between any two objects in the different clusters; or (3) the average distance between all objects in one cluster and all objects in the other cluster. In addition to measures of similarity and distance, one can build the dendrogram either via top-down (divisive) methods or bottom-up (agglomerative) methods. For divisive methods, the process is reversed with each object first belonging to its own cluster. Figure 22.5 represents the results of hierarchical clustering on the Dengue Fever dataset. The input data is the log2 transformed 2D gel data using only the 107 spots that were significantly different based on the t-test analysis. As the reader can see, this dataset is challenging. Ideally, the DF subjects should cluster with the DHF subjects. Unfortunately, there is some amount of overlap between the diseases as the clusters are not solely one disease or the other.

Fig. 22.5.

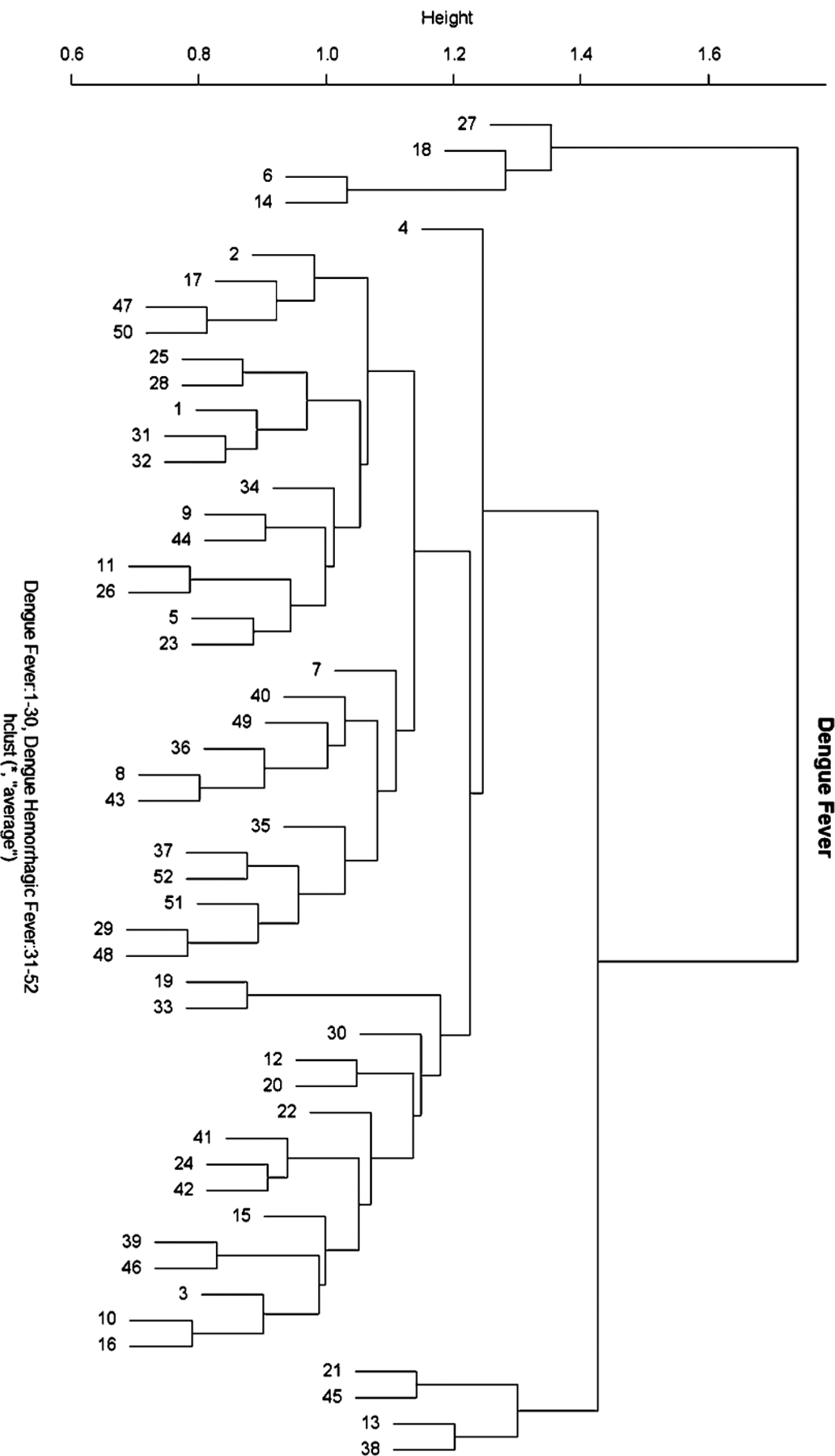
Hierarchical clustering of Dengue Fever study. Subjects labeled 1–30 are subjects with Dengue Fever; Subjects labeled 31–52 are subjects with Dengue Hemorrhagic Fever

22.5.2. K-means Clustering

K-means clustering is similar to hierarchical clustering; however, instead of obtaining n clusters at the end, the data samples are grouped into a pre-specified number, k < n, clusters. The goal of k-means clustering is to partition the data into k subsets which are significantly different from each other. K-means clustering is most useful when the user knows a-priori the number of clusters that the data should belong to, i.e. if the data samples come from control, attenuated, and virulent strains of a disease, one would expect three clusters to be created. Methods do exist, however, to aid the user in estimating the appropriate number of clusters. With both k-means clustering and hierarchical clustering, the user has the ability to examine in a graphical fashion how similar different groups of data are, and whether there are some proteins that will enable one to easily discriminate one group (i.e., control) from another group (i.e., infected).

22.5.3. PCA

As mentioned above in Sect. 21.4.4, PCA is used to identify patterns in the data. PCA expresses data in such a way that it highlights differences and similarities between both groups and samples within each group. In a data set with many correlations, an ordination technique is needed to look at overall structure of the available data. PCA is based on linear correlation between the data values, and transforms the original variables into new, uncorrelated variables. Consider m observations (e.g., protein abundance levels) on n variables (e.g., conditions/individuals). This results in an m x n data matrix. PCA reduces the dimensionality of the data matrix by identifying r new variables, where r < n. Each new variable, r, is a principal component (PC). Each PC is a linear combination of the original n variables.

To perform PCA, start with the m x n matrix of protein abundance data: m rows correspond to proteins (expression levels), n columns correspond to conditions/individuals. Apply data standardization, such as the logarithmic transformation or scaling and centering the data such that the mean value is 0 and the standard deviation is 1. Calculate the covariance matrix of the dataset, C. Find the eigenvectors and eigenvalues of the matrix C. Create n new variables, PC_n, that are linear functions of the original n observations:

$$\begin{gathered} {\text{PC}}_1={\text{a}}_{11}{\times }_1+{\text{a}}_{12}{\times }_2+\dots +{\text{a}}_{1\text{n}}{\times }_{\text{n}} \\ {\text{PC}}_2={\text{a}}_{21}{\times }_1+{\text{a}}_{22}{\times }_2+\dots +{\text{a}}_{2\text{n}}{\times }_{\text{n}} \\ {\text{PC}}_{\text{n}}={\text{a}}_{\text{n}1}{\times }_1+{\text{a}}_{\text{n}2}{\times }_2+\dots +{\text{a}}_{\text{nn}}{\times }_{\text{n}} \end{gathered}$$

The coefficients above (referred to as “loadings”), a_nn, represent the linear correlation between the original variables, x_n, and the PC_n. The coefficients are chosen to satisfy three requirements: (1) the variance of PC_n is as large as possible; (2) all values of PC_n are uncorrelated; and (3) sum across rows = 1 (a₁₁×₁ + a₁₂×₂ + … + a₁₁×_n = 1). Thus, the end result of PCA is that the data has been transformed so it is expressed in terms of the patterns between samples and groups.

22.6. Supervised Learning/Classification

Machine learning is the study of how to build systems that learn from experience. It is a subfield of artificial intelligence and utilizes theory from cognitive science, information theory, and probability theory. Machine learning usually involves a training set of data as well as a test set of data. These are both from the same dataset, and the system is “trained” using the training data, and then run on the test data to classify it, and test the model? There are two types of machine learning algorithms: supervised and unsupervised learning. In unsupervised learning, we simply have a set of data points. We do not know classes associated with these data points. In supervised learning, we also know which classes the training data belong to. Machine learning has recently been applied in the areas of medical diagnosis, bioinformatics, stock market analysis, classifying DNA sequences, speech recognition, and object recognition.

22.6.1. Logistic Regression

The main objective of logistic regression is to model the relationship between a set of continuous, categorical, or dichotomous variables and a dichotomous outcome that is modeled via the logit function. Whereas typical linear regression seeks to regress one variable onto another (typically continuous data), logistic regression seeks to model via a probability function of a binary outcome. Logistic regression is the method used when the outcome is a “yes/no” response versus a continuous one. Traditionally, such problems were solved by ordinary least squares regression or linear discriminant analysis. However, these approaches were found to be less than optimal due to their strict assumptions (normality, linearity, constant error variance, and continuity for ordinary least squares regression and multivariate normality with equal variances and covariances for discriminant analysis). A logistic regression equation takes the form:

$$\text{ln}\left[\frac{p}{\left(1-p\right)}\right]=\alpha +{\sum }_{j=1}^k\beta j\text{Xj}+\text{e}$$

where p is the probability that event Y occurs P(Y = 1), p/(1 − p) is the odds ratio, and ln [p/(1 − p)] is the log odds ratio (the logit).

Thus, logistic regression is the method used for a binary, rather than a continuous outcome. The logistic regression model does not necessarily require the assumptions of some other regression models, such as the assumption that the variables are normally distributed in linear discriminant analysis. Maximum likelihood estimation is used to solve for the logistic regression equation estimates. Recent techniques such as penalized shrinkage and regularization estimation, and also lasso-type regularization logistic regression models have been developed to improve prediction accuracy in classification.

One of the advantages of using logistic regression is that there is assumed to be a linear association between the feature and response variables. However, one has the ability to add logarithmic transformations or squares of data to increase the performance of the model. One of the key disadvantages of logistic regression is that the method does not accommodate missing values. Additionally, logistic regression is unable to deal with variables that are highly correlated, except when using the lasso or ridge penalties. Lastly, including variables that are not important features can hinder (decrease) the performance of the model. For this reason, logistic regression cannot be used as an additional feature selection technique. It can, however, be used in combination with other feature selection techniques.

22.6.2. CART

Classification and regression trees (CART, [3]) are a nonparametric method for building decision trees to classify data. CART is highly useful for our applications because it does not require initial variable selection. The three main components of CART are creating a set of rules for splitting each node in a tree, deciding when a tree is fully grown, and assigning a classification to each terminal node of the tree [22]. Decision trees, such as CART, have a human readable split at each node which is a binary response of some feature in the data set. The basic algorithm for building the decision tree seeks some feature of the data which splits it (here into two groups) maximizing the difference between the classes contained in the parent node. CART is a recursive algorithm which means that once it has decided on an appropriate split resulting in two child nodes, the child nodes then become the new parent nodes, and the process is carried on down the branches of the tree. CART can use cross validation techniques to determine the accuracy of the decision trees.

To build a decision tree, the following need to be determined: (1) which variable should be tested at a node, (2) when should a node be declared a terminal node and further splitting stop, and (3) if a terminal node contains objects from different classes, how should the class of a terminal node be determined? The process for doing so is listed below.

1. Start with splitting a variable at all of its split points. Sample splits into two binary nodes at each split point.

2. Select the best split in the variable in terms of the reduction in impurity (heterogeneity).

3. Repeat steps 1 & 2 for all variables at the root node.

4. Assign classes to the nodes according to a rule that minimizes misclassification costs.

5. Repeat steps 1–5 for each non-terminal node.

6. Grow a very large tree T_max until all terminal nodes are either small or pure or contain identical measurement vectors.

7. Prune and choose final tree using cross validation.

Some of the advantages of CART are that it can easily handle data sets which are complex in structure, it is extremely robust and not very effected by outliers, and it can use a combination of both categorical and continuous data. Missing data values do not pose any obstacle to CART as it develops alternative split points for the data that can be used to classify the data when there are missing values. Additionally, variables used within the CART framework are not required to meet any distributional assumptions (such as being normally distributed or having equal variances within groups). CART can also handle correlated data.

CART also has several disadvantages. CART tends to overfit data, so one should plan to trim (prune) the model so that it can be most useful. Unfortunately, how much to prune the data/tree is one of personal choice. Many software implementations of CART have automatic pruning as an option. The tree structures within CART may be unstable. This means that even small changes in the sample data can result in a drastically different tree. Lastly, while the tree is optimal at each individual split, it might not be globally optimal.

CART was run on the Dengue Fever example data mentioned in prior sections of this chapter. Namely, the log2 transformed data from the 107 significant 2D gel spots was used as input to the CART algorithm. Tenfold cross-validation was selected since the sample size is fairly small (less than 30 subjects within each class). Figure 22.6a shows the representation of the Classification Tree that was produced that is best able to discriminate DF from DHF samples. Figure 22.6b shows the variable importance for the CART model. Table 22.2a shows the prediction success for the training data and Table 22.2b shows the prediction success for the testing data. Figure 22.7 shows the ROC Curves for both the training and testing datasets. The blue curve represents the training data, and the red curve represents the testing data. The AUC for the training data is 0.90 and the AUC for the testing data is 0.47.

Fig. 22.6.

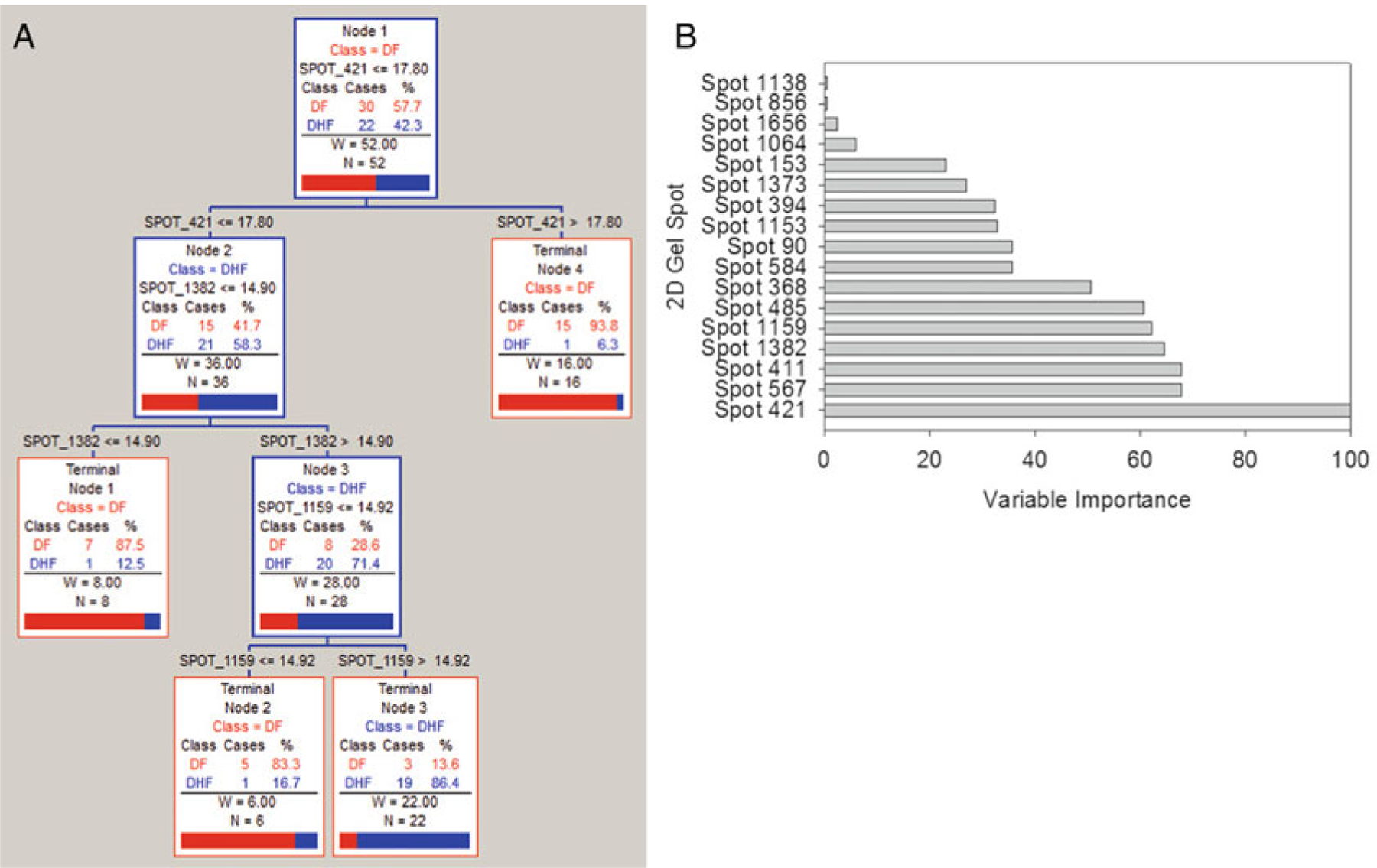
(a) CART tree for DF vs DHF comparison, (b) Variable importance for the CART model

Table 22.2.

(a) Prediction success for the training data, (b) Prediction success for the testing

A Class	Total	Prediction
		DF (n = 30)	DHF (n = 22)
DF	30	27	3
DHF	22	3	19
Total	52	Correct = 90 %	Correct = 87 %
B Class	Total	Prediction
		DF (n = 30)	DHF (n = 22)
DF	30	15	15
DHF	22	15	7
Total	52	Correct = 50 %	Correct = 32 %

Fig. 22.7.

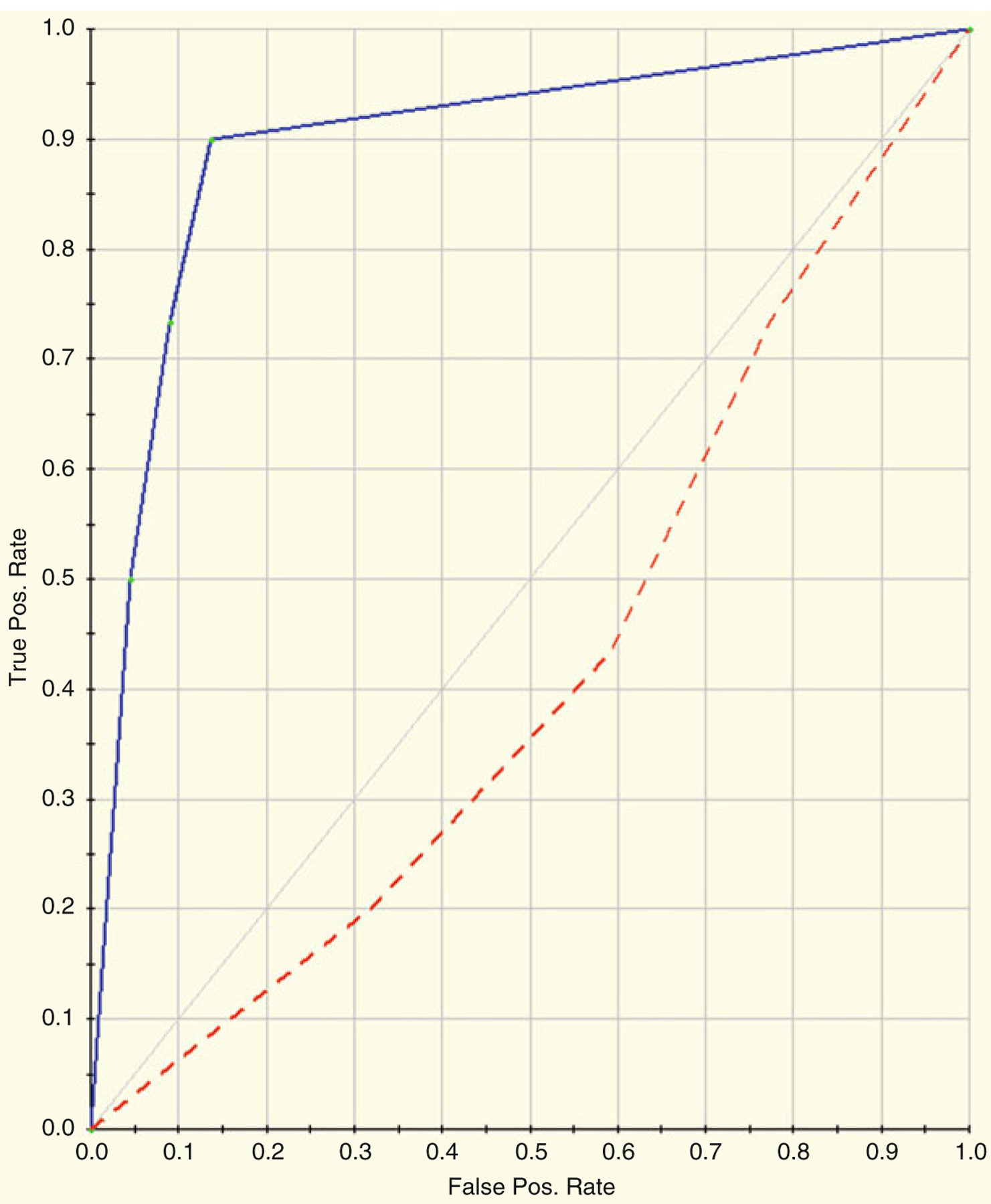
ROC Curves for both the training and testing datasets. The blue curve represents the training data, and the red curve represents the testing data. The AUC for the training data is 0.90 and the AUC for the testing data is 0.47

22.6.3. RF

Random Forests (RF), developed by L. Breiman [4], offers several unique and extremely useful features which include built-in estimation of prediction accuracy, measures of feature importance, and a measure of similarity between sample inputs. RF improves upon classical decision trees such as CART while still keeping many of the appealing properties of tree methods. Decision trees are known for their ability to select the most informative descriptors among many and to ignore the irrelevant ones. By being an ensemble of trees, RF inherits this attractive property and exploits the statistical power of ensembles. The RF algorithm is very efficient, especially when the number of descriptors is very large. This efficiency over traditional CART methods arises from two general areas. The first is that CART requires some amount of pruning of the tree to reach optimal prediction strength; RF, however, does not do any pruning, which reduces performance time. Second, RF uses only a small number of descriptors to test the splitting performance at each node instead of doing an exhaustive search, as does CART.

RF thus builds many trees and determines the most likely splits based upon a comparison within the ensemble of trees. The procedure makes use of both a training dataset and a test dataset. It proceeds as follows: First, a sample is bootstrapped from the training dataset. Then, for each bootstrapped sample, a classification tree is grown. Here, RF modifies the CART algorithm by randomly selecting from a subset of the descriptors, instead of choosing the best split among all samples and variables. This means that at each node, a user defined number of variables are examined to determine the best split/variable amongst that list. This number is typically small, on the order of five to ten variables to choose from. At each node of the tree, a separate list of variables is considered. This procedure of creating trees is repeated until a sufficiently large number of trees have been computed, usually 500 or more.

In practice, some form of cross-validation technique is used to test the prediction accuracy of any computational technique. RF performs a bootstrapping cross-validation procedure in parallel with the training step of its algorithm. This method allows some of the data to be left out at each step, and then used later to estimate the accuracy of the classifier after each instance (i.e. tree) has been completed.

The advantages of RF are that high levels of predictive accuracy are delivered automatically, and there are only a few control parameters to experiment with. Additionally, RF works equally well for classification situations as well as regression situations. RF is the most resistant to overfitting of the models discussed in this chapter. This means the algorithm typically generalizes well for new data. RF is a quick algorithm, which means it creates results rapidly even with thousands of potential predictors. This is because RF does not use all variables at each level of the tree building process. RF does not require prior feature reduction, as it can perform variable selection during the tree building process. RF also has the ability to handle missing values. There are only a couple disadvantages to RF. First, the algorithm can overfit some datasets that are extremely noisy. Additionally, the classifications created by RF can be difficult to interpret as the splits are not listed in the results file (i.e., the user does not know what value of a variable to classify as one group versus the other group). The results list only the important variables that can be used to distinguish one group from another.

Figures 22.8 and 22.9 and Table 22.3 depicts the results of running RF on the Dengue Fever data using a default of 500 trees. Figure 22.8 shows the resultant variable importance for the top twenty most important spots. Table 22.3 shows the prediction success for the models. Figures 22.8 and 22.9 shows the ROC curve for the data. The AUC for the ROC is 0.77.

Fig. 22.8.

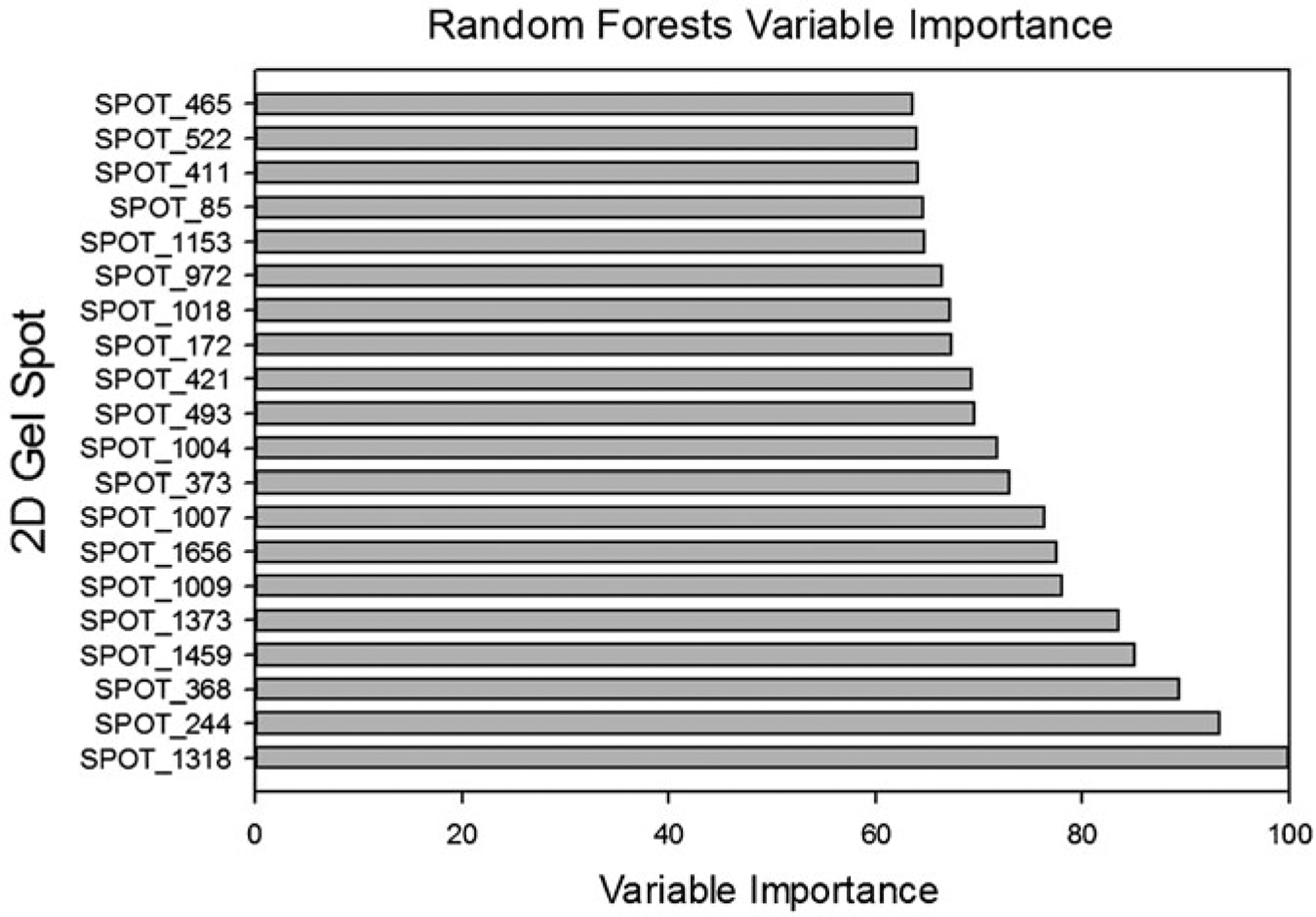
Random forests variable importance for the top 20 most important spots

Fig. 22.9.

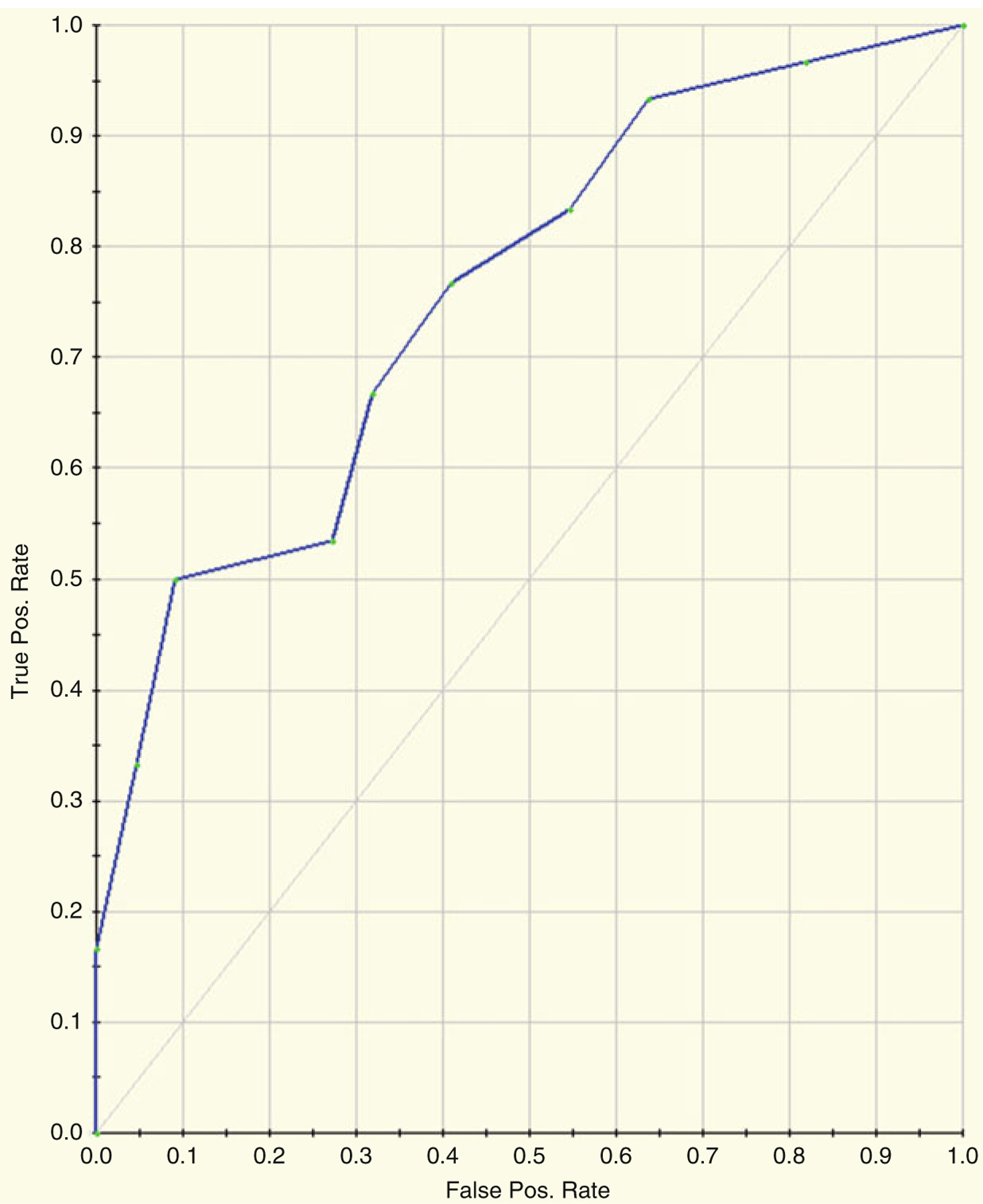
ROC curve for the data. The AUC for the ROC is 0.77

Table 22.3.

Prediction success for the models

Class	Total	Prediction
		DF (n = 11)	DHF (n = 41)
DF	30	10	20
DHF	22	1	21
Total	52	Correct = 33 %	Correct = 95 %

22.6.4. MARS

Multivariate Adaptive Regression Splines (MARS) is a robust nonparametric modeling approach for feature reduction and model building [12]. MARS is a multivariate regression method that can estimate complex nonlinear relationships using a sequence of spline functions of the predictor variables. Regression splines seek to find thresholds and breaks in relationships between variables and are very well suited to identifying changes in the behavior of individuals or processes over time. The basic concept behind regression splines is to model using potentially discrete linear or nonlinear functions of given analytes over differing intervals. The resulting piecewise curve, referred to as a spline, is represented by basis functions within the model.

MARS builds models of the form

$$f\left(x\right)=\sum _{i=1}^k{c}_i{B}_i\left(x\right).$$

Each basis function B_i(x) takes one of the following three forms: (1) a constant, there is just one such term, the intercept; (2) a hinge function, which has the form max(0,x − const) or max(0,const − x). MARS automatically selects variables and values of those variables for knots of the hinge functions; or (3) a product of two or more hinge functions. These basis functions can model interactions between two or more variables.

This algorithm has the ability to search through a large number of candidate predictor variables to determine those most relevant to the classification model. The specific variables to use and their exact parameters are identified by an intensive search procedure that is fast in comparison to other methods. The optimal functional form for the variables in the model is based on regression splines called basis functions.

MARS uses a two-stage process for constructing the optimal classification model. The first half of the process involves creating an overly large model by adding basis functions that represent either single variable transformations or multivariate interaction terms. The model becomes more flexible and complex as additional basis functions are added. The process is complete when a user-specified number of basis functions have been added. In the second stage, MARS deletes basis functions in order of least contribution to the model until the optimum one is reached. By allowing for the model to take on many forms as well as interactions, MARS is able to reliably track the very complex data structures that are often present in high-dimensional data. By doing so, MARS effectively reveals important data patterns and relationships that other models often struggle to detect. Missing values are not a problem because they are dealt with via nested variable techniques. Cross-validation techniques are used within MARS to avoid over-fitting the classification model, and randomly selected test data can also be used to avoid the issue as well. The end result is a classification model based on single variables and interaction terms which will determine class identity. Thus, MARS excels at finding thresholds and breaks in relationships between variables and as such is very well suited for identifying changes in the behavior of individuals or processes over time.

Some of the advantages of MARS are that it can model predictor variables of many forms, whether continuous or categorical, and that it can tolerate large numbers of input predictor variables. As a nonparametric approach, MARS does not make any underlying assumptions about the distribution of the predictor variables of interest. MARS is also a relatively fast algorithm, which means you can get results for large datasets in under a minute. In addition, like CART and RF, MARS also has the ability to handle missing values within a dataset so that imputation techniques are not necessary.

MARS also has several disadvantages. The algorithm performs in such a fashion that the results are easily overfit to a specific dataset. While MARS allows interactions terms to appear in the model, such interaction terms are extremely difficult to interpret biologically. In addition, confidence intervals for predictive variables cannot be calculated directly.

Table 22.4 and Figs. 22.10 and 22.11 show the results of running MARS on the log2 transformed Dengue Fever dataset. The model was created using tenfold cross-validation and allowed for 107 potential basis functions to be included. Table 22.4a shows the variable importance; Table 22.4b shows the prediction success rates for the training data; Figure X + 2: 6C shows the prediction success rates for the testing data; and Figure X + 2: 6D shows the ROC curves for the training and testing data. The blue curve represents the training data and the red curve represents the testing data. The AUC for the training data is 1.0 and the AUC for the testing data is 0.63.

Table 22.4.

(a) MARS prediction success rates for the training data, (b) MARS prediction success rates for the testing data

A Class	Total	Prediction
		DF (n = 29)	DHF (n = 23)
DF	30	29	1
DHF	22	0	22
Total	52	Correct = 97 %	Correct = 100 %
B Class	Total	Prediction
		DF (n = 32)	DHF (n = 20)
DF	30	20	10
DHF	22	12	10
Total	52	Correct = 67 %	Correct = 45 %

Fig. 22.10.

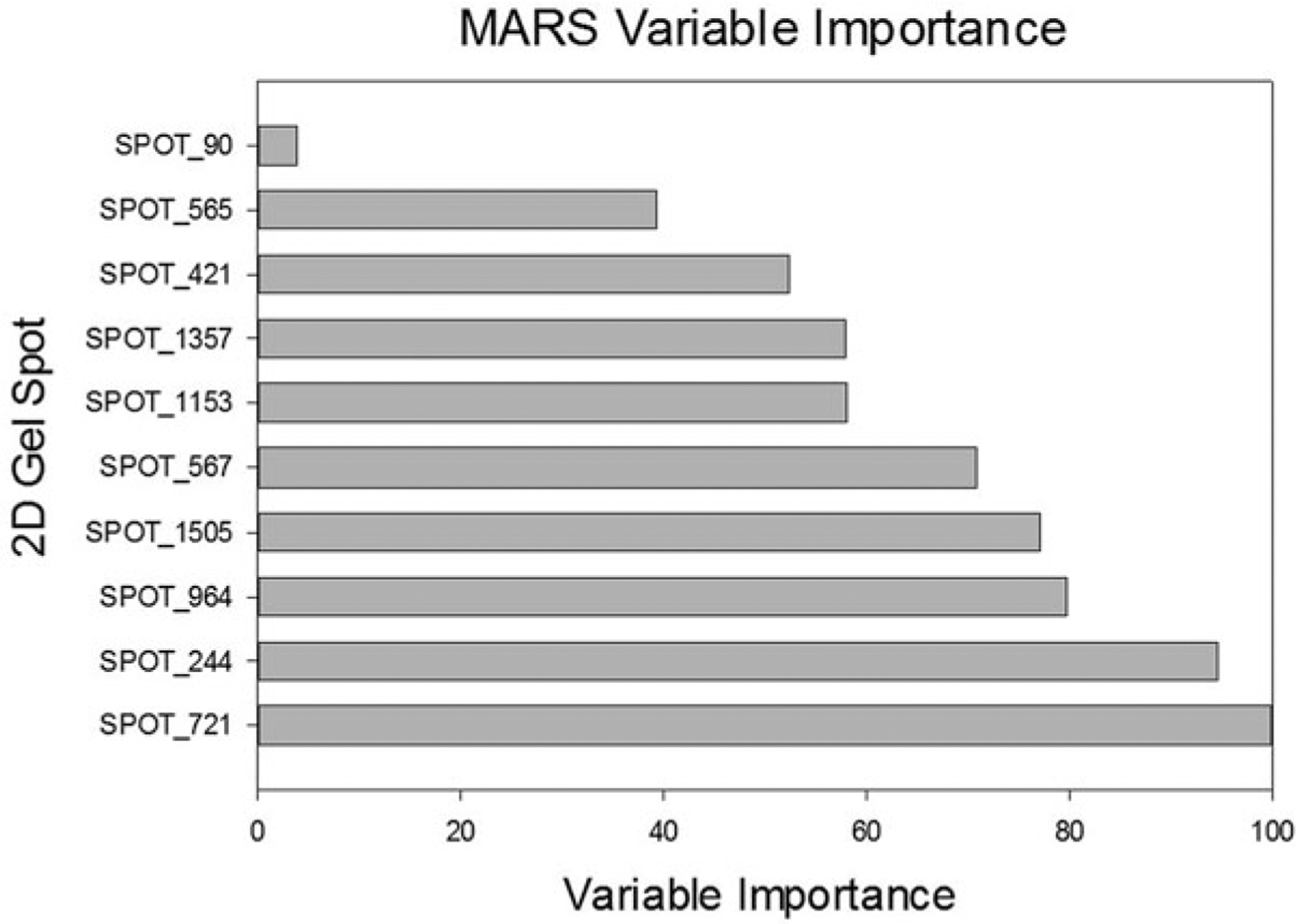
MARS variable importance

Fig. 22.11.

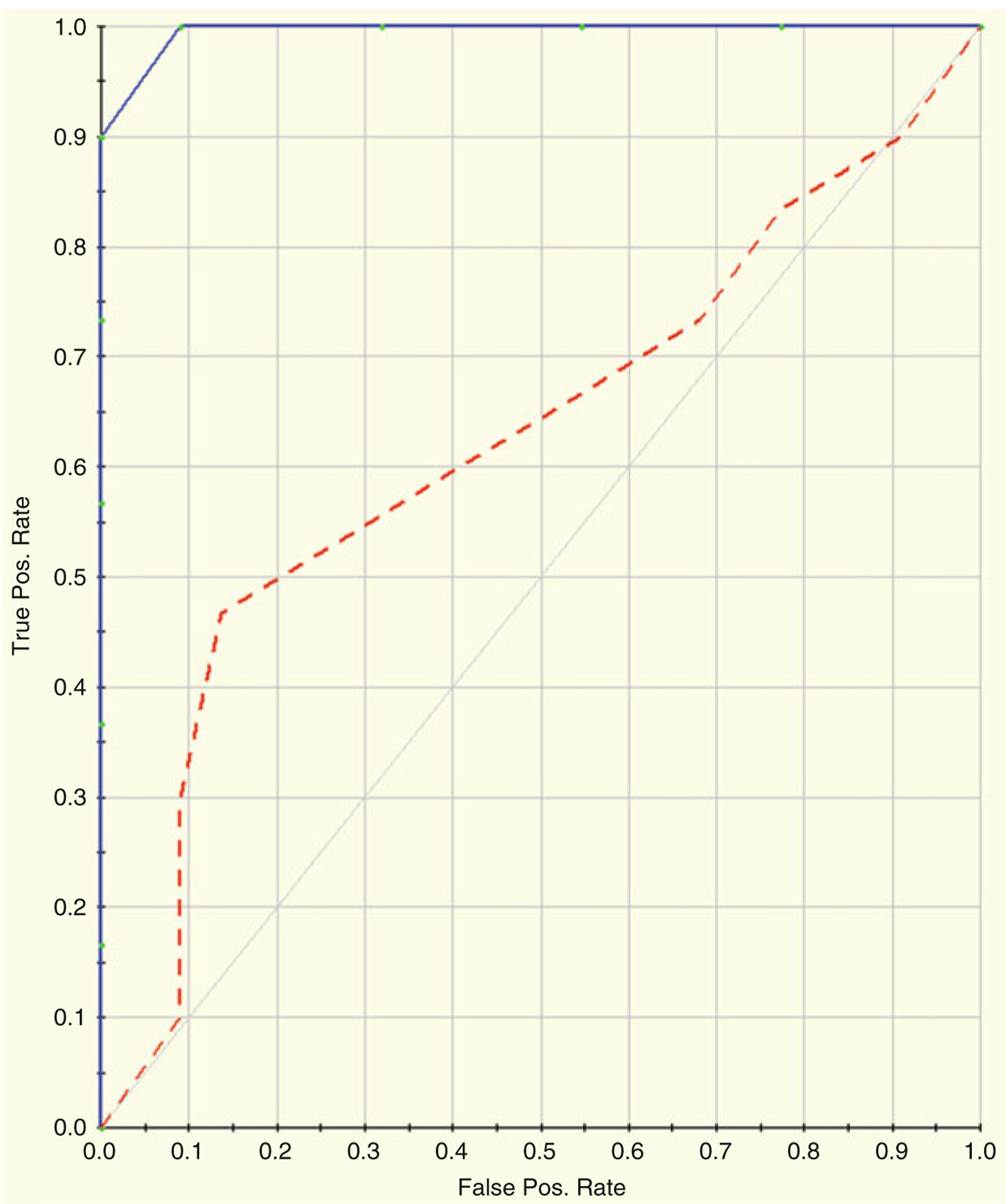
ROC curves for the training and testing data. The blue curve represents the training data and the red curve represents the testing data. The AUC for the training data is 1.0 and theAUC for the testing data is 0.63

22.6.5. SVM

Support vector machines (SVMs) are based on simple ideas that originated in the area of statistical learning theory [16]. SVMs apply a transformation to highly dimensional data to enable researchers to linearly separate the various features and classes. As it turns out, this transformation avoids calculations in high dimension space. The popularity of SVMs owes much to the simplicity of the transformation as well as their ability to handle complex classification and regression problems. SVMs are trained with a learning algorithm from optimization theory and tested on the remainder of the available data that were not part of the training dataset [6]. The main aim of support vector machines is to devise a computationally effective way of learning optimal separating parameters for two classes of data.

SVMs project the data into higher dimensional space where different classes or categories are linearly or orthogonally separable by locating a hyperplane (basically, a line or surface that linearly separates data) within the space of data points that can separate multiple classes of data. SVMs also maximize the width of a band separating the data from the hyperplane so that the linear separation is optimal. SVMs use an implicit mapping of the input data, commonly referred to as Φ, into a highly dimensional feature space defined by some kernel function. The learning then occurs in the feature space, and the data points appear in dot products with other data points [20]. One particularly nice property of SVMs is that once a kernel function has been selected and validated, it is possible to work in spaces of any dimension. Thus, it is easy to add new data into the formulation since the complexity of the problem will not be increased by doing so.

The advantage of SVMs is that they are not data-type dependent. This means that categorical as well as quantitative data can be analyzed together. SVMs are also not dimension dependent. They have the ability to map the data into higher dimensions in order to find a dimension where the data appear to separate into different groups. Additionally, there are various kernel functions that can be used to map the input data into the feature space, the most popular being the radial basis function (or Gaussian) kernel. SVMs also can be used to classify more than just two groups at a time.

There are several disadvantages to using SVMs. Most notably, SVMs are seen as “black box” algorithms and thus fewer researchers are willing to use them because they do not fully understand the algorithm. Additionally, SVMs have an extensive memory requirement because of the quadratic programming necessary to complete the transformation to higher order dimensions. Thus, the SVM algorithm can be very slow in the testing phase. The choice of the kernel function is subjective, which means that choosing one kernel function over another will possibly result in a different classification. Lastly, the data needs to be normalized (scaled and centered) before using the algorithm.

22.6.6. TreeNet

Sometime CART algorithm build non smooth step function classification boundary which leads the variance of it is large and unstable results, so alternative ensemble classification modeling is needed to improve accuracy by increasing randomness through resampling methods. If in the binary classification, a fitting model misclassifies those observations, that model can be applied again, but with extra weight given to the observations misclassified. Then, after a large number of fitting attempts, each with difficult-to-classify observations given relatively more weight, overfitting can be reduced if the fitted values from the different fitting attempts are combined. Boosting is a weak learning algorithm which combines the outputs from many weak classifiers to produce a powerful classifier [15]. A stochastic gradient-boosted model (TreeNet) is a generalized tree boosting that produces an accurate and effective off-the-shelf procedure for data mining [10]. The algorithm generates thousands of small decision trees built in a sequential error-correcting process to converge to an actual model. At each iteration, a subsample of the training sample is drawn at random without replacement from the full training sample to improve robustness to outliers-contaminated data. The variance of the individual base learner is increased at each iteration, but the correlations between the estimates are decreased at different iterations, therefore the variance of the combined model would be reduced. TreeNet performs consistently well in predictive accuracy across many different kinds of data while maintaining the ability to train the model quickly comparing to one CART classifier. The variable importance measure in percentage scale provides how the variables contribute to predictions on the classification. TreeNet graph provides relative influence of each variable and root mean square (RMS) error, a measure of the differences between values predicted by a model and the values actually observed, to assess the power of the model. TreeNet model is also a black box approach how classifiers are complex and hard to interpret the results unlike general probabilistic framework to reach a particular answer and the weak classifiers are too complex, which can lead to over-fitting. Treenet algorithm requires no prior knowledge needed about weak learner, and is easy to run quickly.

22.6.7. Generalized Path Seeker (GPS) Based on AIC and BIC

The comparisons of penalized-regression methods in binary response and logistic regression such as the ridge penalty (α∑β_i².), lasso penalty (α∑|β_i|), and elastic net (combined α∑|β_i| + (1 − α) ∑β_i²) were conducted. The ridge regression can only shrink the coefficients, but the lasso regression can do both shrink and variable selection on the coefficients. The elastic net regression can identify the group effect where strongly correlated features tend to be in the model together. The corresponding log-likelihood function of β (L) is given by

$$\text{L}=\text{log}L\left(\beta \right)=Y^{T}X\beta -\sum \text{log}\left(1+\text{exp}\left(x_i\beta \right)\right).$$

The coefficient vector β that minimizes the penalized log-likelihood is β = argmin_β∈Rp − ∑(y_i log p_i + (1 − y_i) log(1 − p_i)) + Penalty (β), where p_i = P(y = 1|x). To estimate the coefficient, we perform generalized path seeker (GPS), a high speed lasso-style regression from Friedman [11] to regularize regression. GPS demonstrates the regularized regression based on the generalized elastic net family of penalties. The efficient least angle regression (LARS) algorithm of Efron et al. [8] finds the entire regularization paths in an iterative way with the computational effort. For a binary outcome variable and the logistic regression models, the lasso estimator is estimated by penalizing the negative log-likelihood with the L₁-norm through the absolute constraint of regression coefficients like α||β||₁ = α∑|β_i|.

The Akaike information criterion (AIC) is given by

$$\text{AIC}=-2\text{ln}(\text{L})+2(\text{p}+1),$$

where L is the binomial log-likelihood for the model, and p is number of covariates estimated in the model.

The Bayesian information criterion (BIC) is given by

$$\text{BIC}=-2\text{ln}(\text{L})+\text{ln}(\text{n})\times (\text{p}+1),$$

where n is the samples size, and p is defined as those variables in AIC.

Among the models having different number of covariates, the one yielding the smallest AIC and BIC values is selected as the optimal model. In AIC and BIC, the binomial log-likelihood may be viewed as a measure of the goodness-of-fit of a model with the number of parameters functioning as a penalty for model complexity. The complexity penalty α term is chosen by AIC or BIC criterion to evaluate the negative log-likelihood. The elastic net, α||β||₁ + (1 − α)||β||²₂, combines the L₁ and L₂ penalizing terms and possesses a grouping effect, i.e., in a set of variables that have high pairwise correlations, the elastic net groups the correlated variables together. Lasso and elastic net are especially well suited to wide data, meaning data with more predictors than observations in linear regression model. The regularization model outputs provide piece-wise linear regression path plots along with cross validation to identify important predictors. This procedure is applicable for variable selection for the parametric linear components. If the parametric assumptions are not satisfied, we need nonparametric approach like MARS model beyond linearity of features related to disease outcomes.

Figures 22.12 and 22.13 and Tables 22.5a, b depict the results of running GPS on the Dengue Fever data using tenfold cross-validation. Figure 22.12 shows the resultant variable importance for the top twenty most important spots. Table 22.5a shows the prediction success for the training data; Table 22.5b shows the prediction success for the testing data. Figure 22.13 shows the ROC curve for the data. The blue curve represents the training data; the red curve represents the testing data. The AUC for the training ROC is 1.0; the AUC for the testing data is 0.92.

Fig. 22.12.

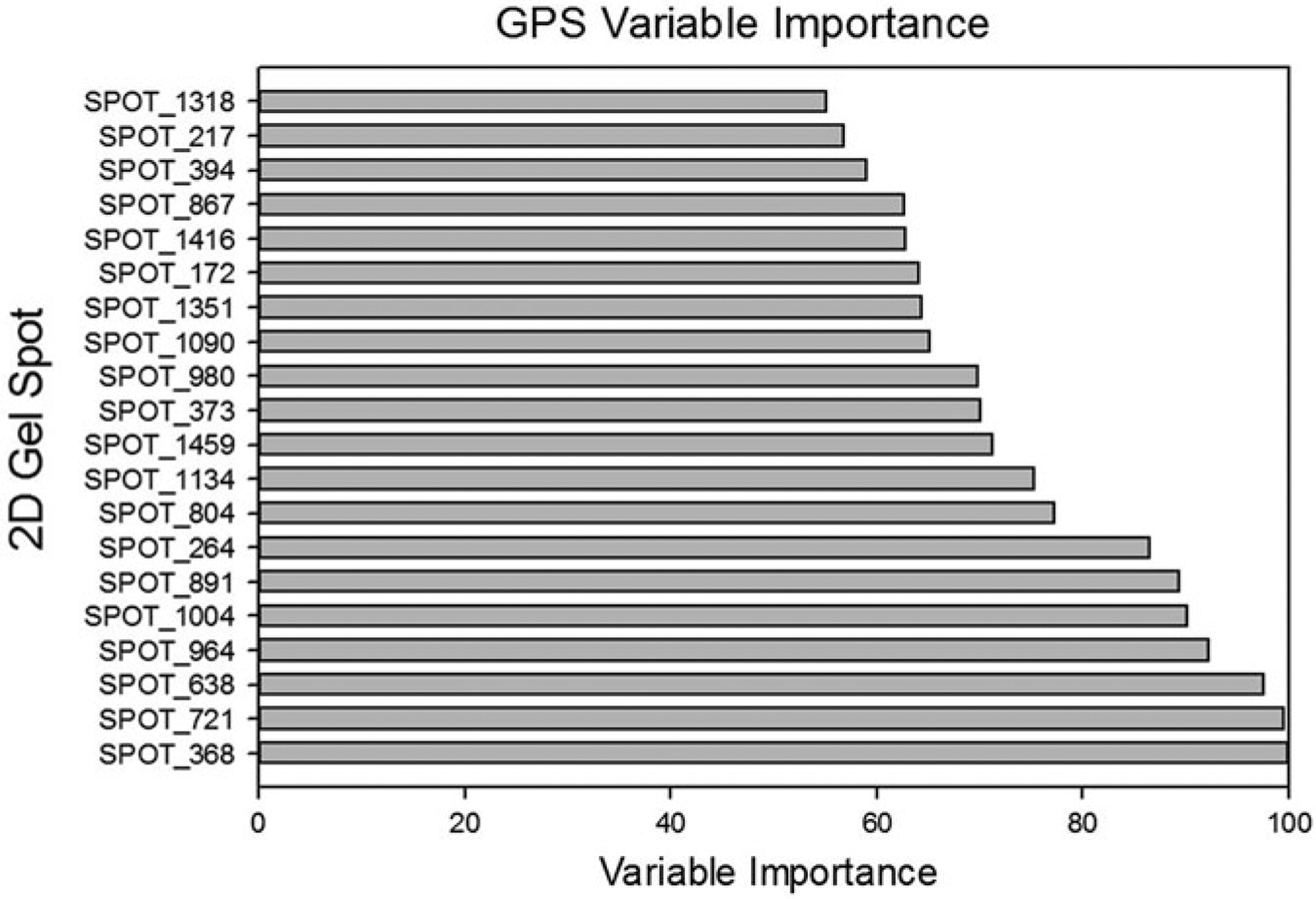
GPS variable importance for the top 20 most important spots

Fig. 22.13.

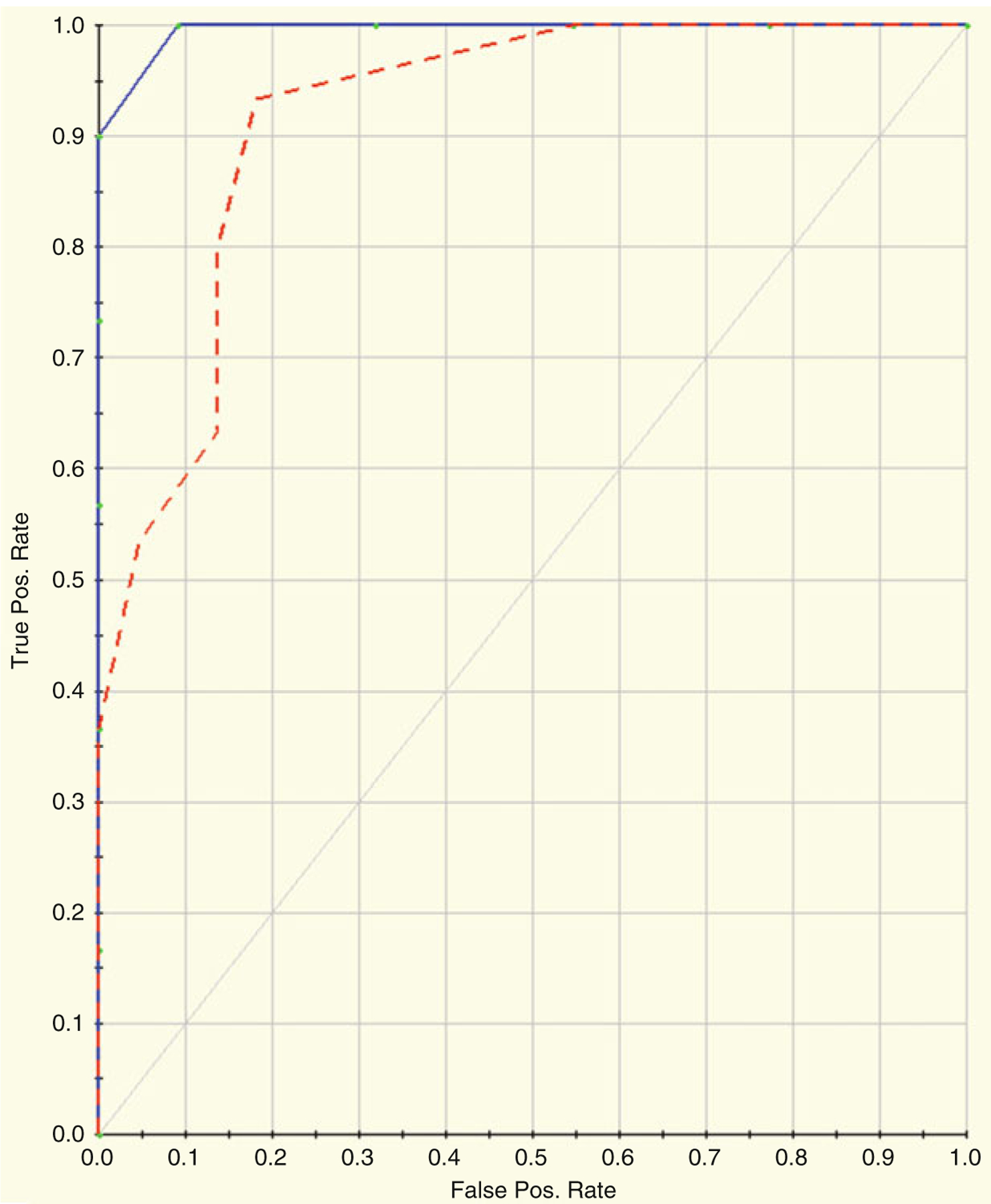
ROC curve for the data. The blue curve represents the training data; the red curve represents the testing data. The AUC for the training ROC is 1.0; the AUC for the testing data is 0.92

Table 22.5.

(a) Prediction success for the training data, (b) Prediction success for the testing data

A Class	Total	Prediction
		DF (n = 31)	DHF (n = 21)
DF	30	30	0
DHF	22	1	21
Total	52	Correct = 100 %	Correct = 95 %
B Class	Total	Prediction
		DF (n = 27)	DHF (n = 25)
DF	30	24	6
DHF	22	3	19
Total	52	Correct = 80 %	Correct = 86 %

22.7. Resampling Techniques

22.7.1. Training/Testing Sets

A key concept in machine learning is the creation of a predictive model based on a training dataset, and then assessing the ability of the model to perform on an independent testing dataset (mentioned in Sect. 22.6). Ideally, the training data should be collected separately from the testing data. This can mean that discovery samples are used for the training data and validation samples are used for the testing data. Another way to create training and testing datasets is to set aside some of the training data to be used instead for the testing data. If the study contains more than 60 samples in a given group, this is the preferred method for machine learning algorithms. How much of the training data to set aside for the testing data is up to the user. Frequently, 70–80 % of the dataset samples are retained for the training of the predictive model, with the additional 20–30 % being set aside to test the model performance. For the majority of the work performed by the Clinical Proteomics Center, the analysis was performed by using cross-validation techniques (mentioned below in G.3).

22.7.2. Bootstrapping

Bootstrap resampling [7] is a general method for inference that has been applied to a variety of statistical problems too difficult to solve analytically. The standard nonparametric bootstrap resampling treats the population data as a sample and samples with replacement repeatedly to produce an approximation to a statistic’s sampling distribution. As a result, reliable confidence intervals and hypothesis tests are easily calculated, often with properties superior to standard parametric techniques. In predictive modeling, bootstrap resampling has been found to “smooth” out discontinuities in many fitting algorithms. The resulting model is typically less variable without a substantial increase in bias.

22.7.3. CV/k-fold CV

CV gives an accurate and robust indication of how well an algorithm can make new predictions [17]. CV is an important technique for avoiding testing hypotheses that may be inferred from the data, but don’t actually exist. CV is appropriate for each of the classification methods we will discuss. One well-accepted method for cross validation is termed “k-fold” CV. Here the full dataset is divided into k subsets and the holdout method, where a set amount of data is withheld from the analysis, is repeated k times. Each time, one of the k subsets is used as the test set and the remaining subsets are used as the training sets. The average error across all trials is then computed to assess the predictive power of the classification technique used. The advantage of the k-fold CV method is that many combinations of training set vs. test set trials are used to calculate an average predictive error; so this method provides an estimate of an algorithm’s predictive power that is much less dependent upon the initial selection of members for the training set.

22.8. Model Diagnostics/Performance/Quality Assessment

In practice, it is often customary for a supervised classification to be conducted using several modeling approaches. The investigators then examine the model performance using a variety of criteria, as well as look for convergence of informative features. A widely accepted approach in model evaluation is to evaluate the area under the receiver operating characteristic (ROC) curve [14].

22.8.1. Receiver-Operating Characteristic (ROC) Curves/AUC

For a given technique, multiple models are frequently created. One method used to evaluate and compare the various models is by ROC curves [24]. An ROC curve is a graphical plot of the sensitivity vs. 1-specificity of a binary classifier system as its discrimination threshold is varied. This is an equivalent representation of a plot of the fraction of true positives vs. the fraction of false positives. The assumption is that the samples on each side of the binary classifier are from a separate population, and the ROC curve is a graphical presentation of the validity of this assumption. The area under the ROC curve (AUC) measurements indicate the ability of a model to discriminate amongst the outcome groups. Figures 22.7, 22.9, and 22.11 show the ROC curve for the Dengue Fever study comparing DF vs. DHF.

For the choice of regularization parameter, information criterion such as cross validation, generalized cross validation (GCV), Akaike information criterion (AIC) and Bayesian information criterion (BIC) can be used. Generalized cross-validation can be viewed as an approximation to cross-validation,

$$GCV=\frac{1}{n}\sum _{i=1}^n{\left[\frac{\left[y-f\left(x_i\right)\right]}{\left(1-\frac{k}{n}\right)}\right]}^2,$$

where n is the number of observations, y is dependent variable x is the independent variable (s), and k is the effective number of parameter or degree of freedom in the model. The effective degrees of freedom is the means by which the GCV error functions puts a penalty on adding variables to the model. The effective degrees of freedom is chosen by the modeler. The GCV can be used to rank the variables in importance. To rank the variables in importance, the GCV is computed with and without each variable in the model.

22.8.2. Deviance/Residual Plots

Model checking is an important procedure to check for assessing model adequacy in multiple linear or logistic regression. Often the interest is to assess the linear or non-linear association of binary responses on features. The logistic regression model assumes that the logit of the outcome is a linear combination of features. When model assumptions are not satisfied, we have problems, the confidence intervals of the coefficients are wide and the statistical tests are incorrect and inefficient. We examine whether our model has all of the relevant predictors and if the linear association of them is appropriate.

Next, we evaluate the partial residual plot as a diagnostic graphical tool for identifying the nonlinear relationship between the logit of the disease outcome and features for additive models. A partial residual plot (Fig. 22.14) is a scatterplot of the partial correlation of each independent with the dependent outcome after removing the linear effects of the other independent features in the model. The log-likelihoods ratio test statistic is twice the difference in log-likelihoods of linear and nonlinear of each feature. For each feature, we also examine the log-likelihood ratio-test p-values comparing the negative binomial log likelihood (i.e., deviance $d_i=2\left[y_i\text{log}\left(\frac{y_i}{{\widehat{p}}_i}\right)+\left(n_i-y_i\right)\text{log}\left(\frac{n_i-y_i}{n-{\widehat{p}}_i}\right)\right]$) between the full model and the reduced model. After performing log-likelihoods ratio test on nonlinear models with smaller p-value less than 0.05, it is preferable to use a non-parametric fit like MARS model. An example of partial residual plot of lymphocytes clinical data for Dengue data is shown in Fig. 22.14. It shows the non-linearity of lymphocytes to logit of the Dengue Hemorrhagic Fever.

Fig. 22.14.

Partial residual plot

In proteomic studies, some proteins could not be accurately measured, so they lead measurement error problems. It is well known that ignoring measurement error in covariate leads to biased estimate of the covariate effects. There are a number of measurement error models reported in the literature [5, 13].

Measurement error in the predictors, lack-of-fit error (under-fitting and over-fittings), and error due to omitting relevant important predictors can cause poor performance when building models, especially in terms of reproducibility of the training model into test data. Statistical methods include the random effects in linear mixed effect models could quantify between variation, within variation and unwanted noise variation. Therefore, the model performance estimators should be evaluated from a test set. We need to perform an examination process of similarity between training and test set samples for reproducibility of the model. We observed that verification sample variations in aspergillosis are much larger than in the qualification sample ones. We know that the final optimal classification model can be used to predict the probability of new data being in the disease group in the training samples. The final classification model could be optimized in terms of minimal noise in the predictors and response.