Accelerating availability of clinically-relevant parameter estimates from Thromboelastogram point-of-care device

Abstract

Background:

Modeling approaches offer a novel way to detect and predict coagulopathy in trauma patients. A dynamic model, built and tested on thromboelastogram (TEG) data, was used to generate a virtual library of over 160,000 simulated RapidTEGs. The patient-specific parameters are the initial platelet count, platelet activation rate, thrombus growth rate, and lysis rate (P(0), k1, k2, and k3, respectively).

Methods:

Patient data from both STAAMP (n=182 patients) and PAMPer (n=111 patients) clinical trials were collected. A total of 873 RapidTEGs were analyzed. 116 TEGs indicated maximum amplitude (MA) below normal and 466 TEGs indicated lysis percent above normal. Each patient’s TEG response was compared against the virtual library of TEGs to determine library trajectories having the least sum-of-squared error versus the patient TEG up to each specified evaluation time ∈ {3, 4, 5, 7.5, 10, 15, 20 minutes}. Using 10 nearest-neighbor trajectories, a logistic regression was performed to predict if the patient TEG indicated MA below normal (< 50 mm), lysis percent 30 minutes after MA (LY30) greater than 3%, and/or blood transfusion need using the parameters from the dynamic model.

Results:

The algorithm predicts abnormal MA values using the initial 3 minutes of RapidTEG data with a median AUC of 0.95, and improves with more data to 0.98 by 10 minutes. Prediction of future platelet and packed red blood cell transfusion based on parameters at 4 and 5 minutes, respectively, provides equivalent predictions to the traditional TEG parameters in significantly less time. Dynamic model parameters could not predict abnormal LY30 or future fresh frozen plasma transfusion.

Conclusions:

This analysis could be incorporated into TEG software and workflow to quickly estimate if the MA would be below or above threshold value within the initial minutes following a TEG, along with an estimate of what blood products to have on hand.

Level of Evidence:

Therapeutic/Care Management: Level IV: Prospective/retrospective study using historical controls or having more than one negative criterion.

Study Type:

Diagnostic Test

Introduction

In the United States, trauma is the leading cause of death for individuals 46 and younger¹. This growing burden presents many practical challenges in the Emergency Room and Intensive Care Unit (ICU), especially for patients with impaired coagulation. Approximately 33 percent of trauma patients develop coagulopathy, representing an opportunity for improved personalized and timely protocol-based mitigation². Included in these protocols, targeted fluid resuscitation with specific blood products can help coagulopathic patients by restoring necessary components for coagulation^{3, 4, 5}. Increasingly, viscoelastic assays, such as the thromboelastogram or TEG (Haemonetics; Braintree, MA), are used in emergent situations where coagulopathy might be of concern⁴. TEG-informed resuscitation protocols can correct impairments in coagulation and have been shown to improve in-hospital and 28-day survival compared to conventional coagulation assay (CCA)-based protocols, which result in more products being transfused³. Since faster point-of-care results in faster patient-specific transfusion decisions, research on expediting TEG results could help save patients’ lives and optimize resource use.

Currently, the quickest TEG assay is the RapidTEG. The RapidTEG activates both intrinsic and extrinsic clotting pathways and decreases time until results are reported, at the cost of decreasing information obtained from the time until activation parameter (R). Parameters reported with a RapidTEG include R (time until activation), TEG ACT (Activated Clotting Time, transformation of R), K (time until 20 mm clot strength is reached), alpha angle (angle between horizontal and tangent line to TEG curve, indicating speed of clot formation), MA (maximum amplitude, traditionally associated with maximum clot strength), LY30 (% decrease in TEG amplitude 30 minutes after MA, associated with clot lysis), and other less common parameters. While R, TEG ACT, K, and alpha angle are determined within minutes of starting a RapidTEG and give information on ability to form a clot, MA and LY30 take much longer and inform clot strength and lysis⁶. Time to maximum amplitude (TMA) can exceed 20 minutes, and LY30 isn’t determined until 30 minutes after MA is reached. Low MA (MA < 50 mm) has been shown to indicate either low platelet count or function^{4, 6}. High LY30 (> 3%) is indicative of abnormally high fibrinolysis. Some protocols call for platelet transfusions for low MA or dosing tranexamic acid to patients with high LY30⁴. Therefore, knowing these parameters sooner would expedite treatment decisions.

To address the time delay before results are available, multiple sources have tested and reported a correlation between TEG amplitude at early times and MA^{7, 8, 9}. Early times tested include 5 and 10 minutes after R is reached. This simple correlation could give an earlier estimate of clot strength to clinicians, as low MA has been strongly linked to increased mortality. The present work aims to develop a mechanistic relationship, rather than simple correlation, that characterizes MA using as little as 3 minutes of TEG data. In addition to MA, the feasibility of early prediction of transfusion need was also assessed.

Methods

We use RapidTEG data to parametrize a personalized mathematical model that captures changes in TEG amplitude over the duration of the test. Model parameters are tested for their ability to inform patient coagulation status before the outputs from the RapidTEG would be reported.

RapidTEG and Transfusion Data

RapidTEGs were collected from subjects enrolled in the Study of Tranexamic Acid during Air Medical Prehospital transport (STAAMP¹⁰, total enrollment 994 subjects) and Prehospital Air Medical Plasma (PAMPer^{11, 12}, total enrollment 523 subjects) clinical trials. The present study evaluates only patients seen at the University of Pittsburgh Medical Center (UPMC) Healthcare System. From a source population of 293 patients with 1044 TEGs, we extract 873 TEGs from 182 STAAMP patients (n=609 TEGs) and 111 PAMPer patients (n=264 TEGs) of sufficient quality for further analysis. This filtering process is outlined in detail in the Supplementary Material: Figure S1–S6. For the 873 TEGs, average TMA, MA, and LY30 in this dataset are 18.7(±5.6) minutes, 58.7 (±10.8) mm (SD: 10.8), and 1.4% (±5.8%), respectively. For each TEG, a determination was made whether there was insufficient coagulation (MA < 50 mm, n=116) or excessive lysis (LY30 > 3%, n=466). Full transfusion data (platelets, red blood cells, plasma, and cryoprecipitate) were available from medical records for all PAMPer subjects. However, only 102 of those subjects had a baseline TEG available.

Dynamic Model

Inspired by highly-detailed, mechanistic models of the clotting cascade ^{13, 14, 15, 16, 17, 18}, we developed an early indicator of coagulopathy coupling a simplified mathematical model of TEG response and an algorithm for rapidly estimating key TEG parameters and transfusion needs. While a simplified model sacrifices mechanistic complexity, it is biologically-inspired and fits RapidTEG data well¹⁹. The three states defined in this model are (1) effective free platelets, P(t), (2) activated platelets, P_a(t), and (3) thrombus, T(t). We coin the term effective free platelets to designate circulating platelets physiologically ready for activation, which is a subset of the circulating platelet pool. In 25 random STAAMP patients with simultaneous RapidTEG and platelet counts, we found a strong correlation between effective platelet count estimated by the model and platelet counts (r = 0.66). In this three-state model, the time evolution of each state is defined by a separate differential equation: platelets can be activated, which drives thrombus formation, and then thrombus is broken down through the process of lysis (Figure 1 and Eq. 1, 2 and 3):

$$\frac{\text{dP}\left(\text{t}\right)}{\text{dt}}=-{\text{ k}}_1\text{P}\left(\text{t}\right)$$ Eq. 1

$$\frac{{\text{dP}}_{\text{a}}\left(\text{t}\right)}{\text{dt}}={\text{k}}_1\text{P}\left(\text{t}\right)-{\text{k}}_2{\text{P}}_{\text{a}}{\left(\text{t}\right)}^2$$ Eq. 2

$$\frac{\text{dT}\left(\text{t}\right)}{\text{dt}}={\text{k}}_2{\text{P}}_{\text{a}}{\left(\text{t}\right)}^2-{\text{k}}_3\text{T}\left(\text{t}\right)$$ Eq. 3

Figure 1:

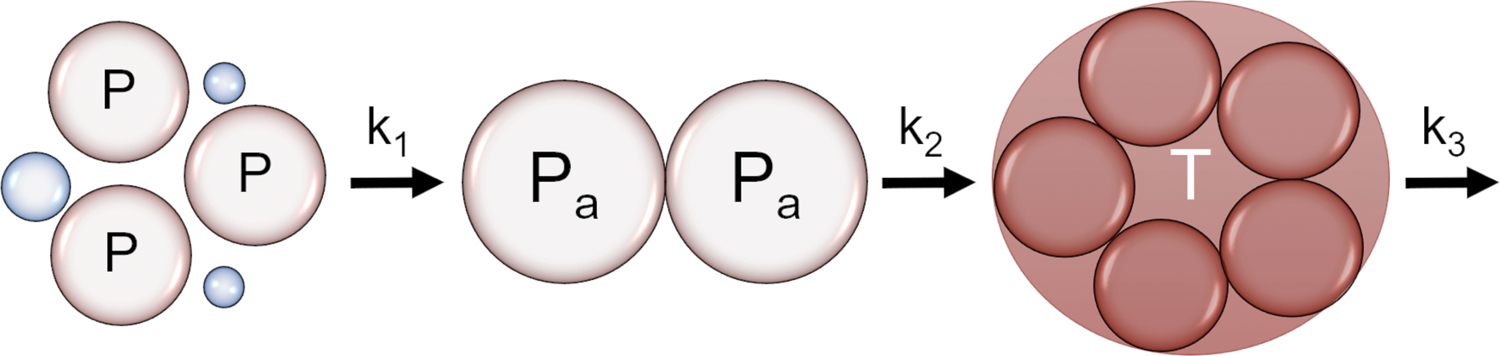
Visual representation of the dynamic model relating the free platelets (P) with the activation at a rate of k₁, activated platelets (P_a) with clotting rate of k₂, and thrombus (T) with a lysis rate of k₃.

There is an initial effective free platelet number P(0) that characterizes the initial P(t) state. As platelets are activated, they are lost from the P(t) state and added to the activated platelet state, P_a(t) at a rate of k₁. As thrombus forms, activated platelets are then lost to the thrombus state, T(t), with a squared dependence upon P_a(t) and a rate of k₂. Initially, a linear dependence was tested, however, the squared dependence resulted in improved fits across all TEG data. The thrombus state is broken down with a lysis rate k₃. The resulting four model parameters include the initial effective free platelet number P(0), platelet activation rate (k₁), thrombus growth rate (k₂), and lysis rate (k₃). Further, parameter k₁ was fixed based on initial RapidTEG data, using a scaled value of the inverse of the time until 4 mm in amplitude was reached (t₄) resembling the TEG’s R parameter, as shown in Equation 4:

$${\text{ k}}_1=\frac{1.1}{{\text{ t}}_4}$$ Eq. 4

This relationship was found to quite robust across the entire set of TEGs. The other TEG-specific parameters (P(0), k₂, k₃) were estimated for each RapidTEG by minimizing the sum of squared error between the upper half of the TEG tracing and the model state T(t) (Eq. 3).

RapidTEG Virtual Library

We examined whether partial RapidTEG data could be used to predict full RapidTEG trajectories. We first created the RapidTEG virtual library, a set of over 167,000 reference RapidTEG trajectories, by varying parameters P(0), k₁, k₂, and k₃ over a range of plausible values determined from fits of the dynamic model to TEG data. The range of TEG trajectories in the virtual library covers a wide range of possible TEG shapes that have been observed by clinicians and in our dataset. The advantage of a virtual library is that it allows, given an actual partial RapidTEG tracing, very rapid identification of similar partial trajectories from the virtual library. Since each simulated trajectory has been creating using a set of parameters, matching these partial trajectories associates the RapidTEG tracing with sets of parameters corresponding to these similar simulated trajectories. Specifically, using the library of simulated RapidTEGs and the individual patients’ RapidTEGs, the following steps were performed:

1. Apply a window of time (the initial 3, 4, 5, 7.5, 10, 15 or 20 minutes) to both the RapidTEG data and simulated RapidTEGs from the virtual library.

2. Compute sum-of-squared error (SSE) between a subject’s RapidTEG and the library trajectories over the specified time window (3, 4, 5, 7.5, 10, 15 or 20 minutes). This quantifies of how close each entry in the library is to the TEG being tested.

3. For each RapidTEG and each window of time, select the nearest 10 parameter sets (P(0), k₁, k₂, k₃) representing simulated trajectories with the smallest SSE over each time window. The design choice of 10 nearest neighbors is user dependent and the basis for this decision is supported in Supplementary Material: Figure S7, and Table S1.

4. Use, over each time window, the 10 parameter sets along with SSE to project the entire RapidTEG trajectory and predict occurrence of low MA, high LY30, and transfusion need.

Predicting MA and LY30

We evaluated whether dynamic model parameters could predict MA as a continuous output, and whether this prediction improved with increasing information (i.e., more time) from the TEG trajectory. Using dynamic model parameters from the 10-nearest neighbors fit to each partial TEG trajectory as predictors, a linear regression model was developed to predict MA. Fit quality was assessed using the R-squared value.

When trying to predict coagulopathy defined by TEG outputs (MA<50mm or LY30≥3%) using dynamic model parameters, step 4 of the algorithm was achieved using four logistic regression (LR) models using 10 nearest-neighbor parameter sets from the virtual library to predict each of the four outcomes (normal or low MA; normal or high lysis) for each window of RapidTEG data (first 3, 4, 5, 7.5, 10, 15 or 20 minutes). LR models were developed (n=585 TEGs) and tested (n=288 TEGs), where development and test groups had equal incidence of low MA or high LY30. To screen parameters to include in the multivariate models, univariate LR was first performed, and significant parameters (p<0.05) were retained. To further test the robustness of the prediction accuracy associated with changes in the randomized splits of this smaller dataset, a three-fold cross validation process was conducted. This three-fold cross validation process includes; randomly splitting the data into three sets of n=291 TEGs, training on two sets, testing on the third, then repeating the process so that each set is tested once, and recording the performance of each fold. Performance is measured by taking the area under the curve (AUC) of the receiver operating characteristic (ROC) curve of all three folds. This procedure is repeated 100 times. By combining the 100 random splits, a distribution of 300 different AUCs were obtained for each of the time points tested (3, 4, 5, 7.5, 10, 15, or 20 minutes). LR performance is traditionally evaluated using only AUC reported on the test sets^{20, 21}. Results were compared with the LR prediction of the instantaneous amplitude at the last time point seen by the algorithm (3, 4, 5, 7.5, 10, 15, or 20 minutes), as well as an additional comparison combining the model parameters with the amplitude in an additional combined LR model. Differences between means of the distributions of AUCs were tested using the Student’s t-test.

Predicting Transfusion Administration

Traditional RapidTEG parameters and dynamic model parameters were used separately to predict transfusions within 24 hours of admission and 24 hours after the start of a baseline TEG (Supplementary Material: Figure S8). A distinctly marked time zero (baseline) TEG was only available for 102 subjects. Cryoprecipitate was administered in small subset of subjects (n=12), thus models predicting cryoprecipitate transfusion were not considered.

We developed logistic regression (LR) models to predict transfusions using dynamic model parameters associated with outcome from univariate analysis for each window of data (3, 4, 5, 7.5, 10, 15 or 20 minutes). LR models were also built using standard TEG parameters (R, MA, K, alpha, LY30) from the full tracing. The same validation approach was used for all statistical models. Results were compared with the LR prediction of the instantaneous amplitude at the last time point seen by the algorithm (3, 4, 5, 7.5, 10, 15, or 20 minutes), as well as an additional comparison when combining model parameters with amplitude in an additional combined LR model. Results for all time windows and for all three of these models are presented in Supplementary Material: Figure S9.

Results

At the time of this study, 994 subjects had been enrolled in STAAMP. A total of 523 subjects were enrolled in PAMPer (completed 2017). Within the subset of subjects enrolled at the University of Pittsburgh with available TEG data, and after eliminating incomplete or discontinuous TEGs, 84 percent of TEGs remained (293 subjects, n=873 TEGs). Discontinuous or incomplete TEGs removed included TEGs that were stopped early (<1000 seconds), had excessively low amplitudes (i.e. flat lines), or large jumps between data points (the full procedure for removing TEGs can be found in Supplementary Material: Procedure for removing discontinuous TEGs, Figure S2–S6). The split between STAAMP and PAMPer was 182 subjects with n=609 TEGs, and 111 patients with n=264 TEGs, respectively. Trial treatment assignment and outcomes are yet to be presented for the STAAMP trial. Subject characteristics from this subset are presented in Table 1. The table shows that the combination of both clinical trials and how this results in expanded diversity in the population (specifically for ISS and PAMPer versus STAAMP), The two studies have similar demographics.

Table 1:

Patient demographics and in-hospital mortality information available from University of Pittsburgh Medical Center. SD: standard deviation. ISS: Injury Severity Score.

	STAAMP	PAMPer	Total
Total Patients (n)	182	111	293
Females	43 (24%)	26 (23%)	69 (23%)
Caucasian	132 (73%)	72 (65%)	204 (70%)
Black	12 (6.6%)	7 (6.3%)	19 (6.5%)
Not Caucasian or Black	32 (29%)	38 (21%)	70 (24%)
Average Age ± SD	41 ± 18	45 ± 18	43 ± 18
Average ISS ± SD	13.5 ± 10.9	20.0 ± 13.1	16.1 ± 12.2
Blunt Injury	150 (82%)	96 (86%)	246 (84%)
Penetrating Injury	32 (18%)	15 (14%)	47 (16%)
In-Hospital Mortality	21 (12%)	25 (23%)	46 (16%)

Dynamic Model Performance

The dynamic model produced very good fits to RapidTEGs, with mean absolute error per point across all TEGs of 0.24 mm. Model performance over the full trajectories can be demonstrated by comparing the average per point error (or residual error) at all time points. An example fit to a RapidTEG, is shown in Figure 2A. A plot of the per point residual error for the top half of all TEGs is shown in Figure 2B, with 2 standard deviations at each point outlined by the grey envelope. The analysis shows how the average per point error is low, with 2 standard deviations resulting in smaller than ± 3 mm of error at any time point. Dynamic model fits have a tendency to overshoot data in the first minute of the TEG trajectory. This tendency represents an expected structural shortcoming of a highly simplified ODE model and an inability to capture data with observed delay. However, overall the performance is still acceptable, and to highlight when the model fails to capture data, we show the highest SSE TEGs in the Supplemental Material: Figure S10.

Figure 2:

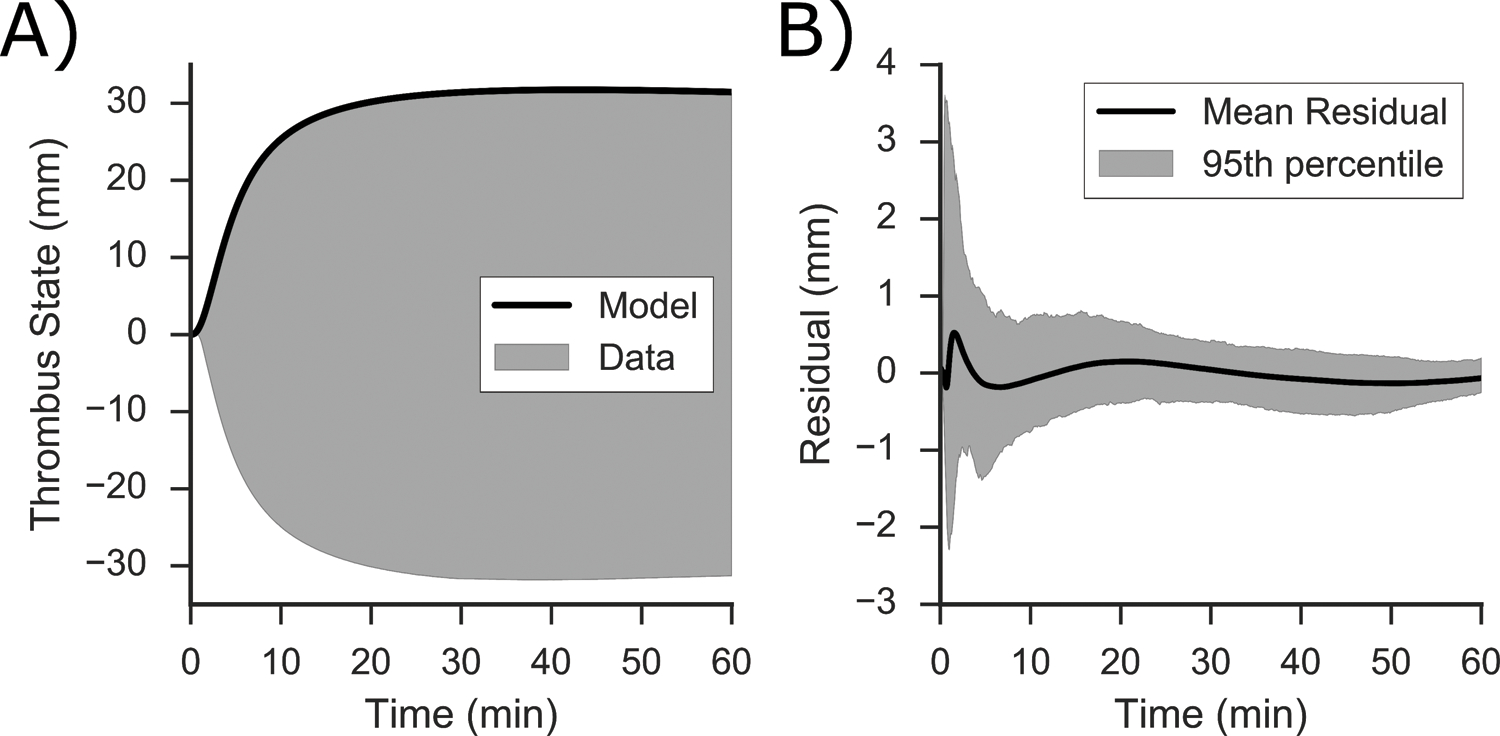
A) Representative RapidTEG (in grey) with the model fit shown (in black), B) Residual error (in mm) between the model and the top half the fitted TEG averaged at each time point of all 873 RapidTEGs (in black), the range (in grey) outlines the 95th percentile of the residual error.

Predicting TEG Output

Linear regression results for predicting MA are shown in Table 2. Dynamic model parameters P(0), k₁, k₂, and k₃, as well as SSE proved significant in predicting MA from partial trajectories. Increasing R² values with increasing length of partial trajectories was observed, confirming increased predictive ability with time, as expected.

Table 2:

Model parameters (P(0), k1, k2, k3) along with the addition to sum of squared error (SSE) showing the significance for predicting maximum amplitude (MA) of the TEG, as calculated by linear regression.

Time (mins)	Parameters and Significance	R2
3	P(0)**, k1**, k2**, k3**, SSE*	0.477
4	P(0) **, k1**, k2**, k3**, SSE**	0.512
5	P(0) **, k1**, k2**, k3**, SSE**	0.596
7.5	P(0) **, k1**, k2**, k3**	0.681
10	P(0) **, k1**, k2**, k3**	0.727
15	P(0) **, k1**, k2**, k3**, SSE**	0.830
20	P(0) **, k1**, k2**, k3**, SSE**	0.866

P-value codes:

^*:< 0.01

^**:< 0.0001.

Figure 3 shows how AUC increases with additional data (longer time windows) for predicting MA<50mm; median AUC is 0.90 with three minutes of data collected using our algorithm (P). In general, this figure also shows that accuracy using the amplitude alone (A) out-predicts the model parameters. However, the combined model (PA, using the amplitude along with our model parameters), the AUC using 3, 4 and 5 minutes is boosted above the accuracy of either (P or A) predicted alone, with a median AUC of 0.95 with only 3 minutes of data. Regression gave inaccurate and insignificant predictive results for LY30>3%, with AUC’s near 0.5 for all time points, except a small improvement at 20 minutes to a median AUC of 0.66. Full lysis predictions are shown in Supplementary Material: Figure S11. These results are unsurprising because lysis contributes to long time-scale TEG response, so an algorithm’s ability to estimate LY30 from the initial minutes of data is expected to be poor and improve slightly with more data.

Figure 3:

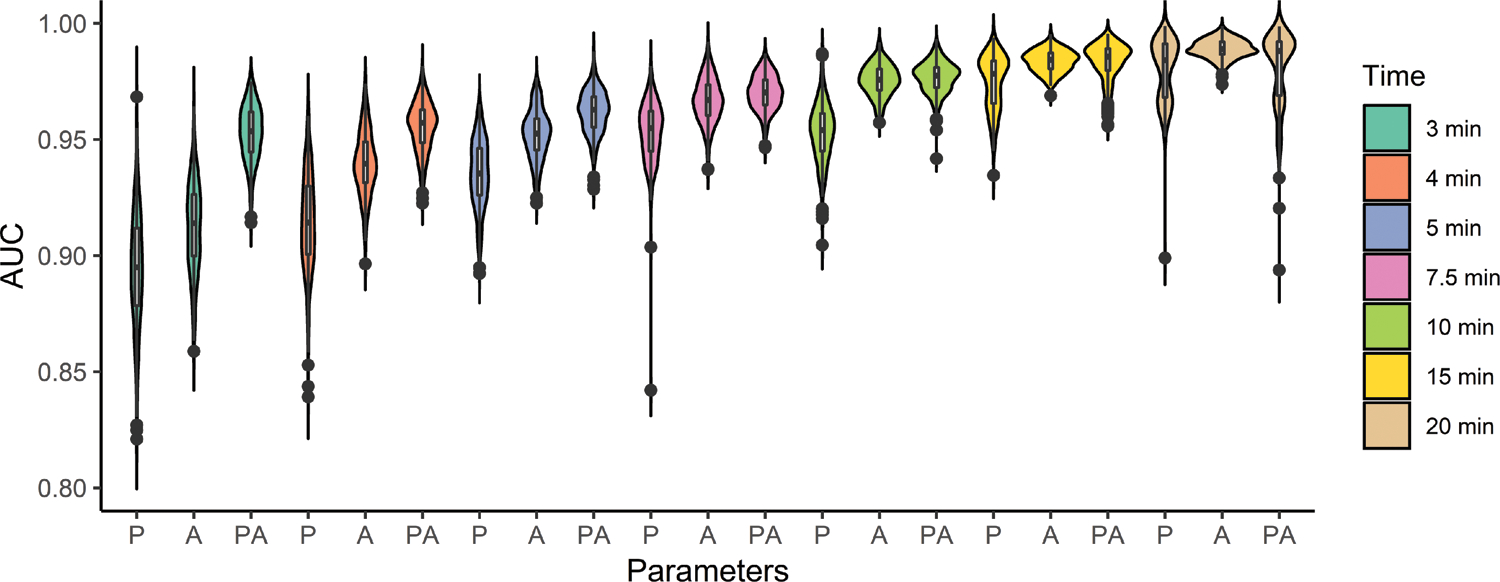
Ability of dynamic model parameters from partial trajectories to predict MA<50mm at different time points (X = 3, 4, 5, 7.5, 10, 15, or 20 minutes), using model parameters (PX), amplitude at X (AX), and the combination (PAX). Plots show the AUC from the ROC of the LR in the test set versus amount of TEG data used (in minutes) using the 10 nearest neighbor parameter sets as selected by the algorithm.

Predicting Transfusion Administration

Of the 102 PAMPer subjects with an initial RapidTEG and transfusion data, 67 subjects (65.7%) received PRBC and 30 subjects (29.4%) received PLT during their hospital stay. Of this subset of RapidTEGs, 29 of the 102 RapidTEGs exhibited low MA. In univariate analysis, the only traditional TEG parameter predictive of transfusion administration in the 24 hours post-enrollment was MA, and it was also predictive of PRBC and PLT administration in the 24 hours following the initial TEG. Figure 4 compares the performance of dynamic model parameters computed from partial TEG tracings (P), instantaneous amplitude (A), and the combination of the two (PA) to full TEG data for predicting PLT and PRBC transfusion administration. The ability to predict PRBC transfusion from partial TEG data (Figure 4A) is lower than the ability to predict platelet transfusion, as determined by consistently lower AUCs than Figure 4B. The PLT transfusion predictions are statistically equal to the performance using full TEG parameters by 10 minutes, arguing this would provide a noninferior prediction. Dynamic parameters approach the accuracy of TEG data to predict PRBC administered within 24 hours post enrollment with an AUC slightly lower than that of the full TEG tracing as determined by Wilcoxon tests between distributions and the full TEG parameter predictions. Neither full TEG tracings nor dynamic model parameters have the ability to predict PRBC administered 24 hours after the TEG was obtained. When comparing the instantaneous amplitude (A) ability to predict transfusion, there were small improvements observed in AUCs for PRBC predictions at 3 minutes (median AUC: 0.6). Predicting Fresh Frozen Plasma (FFP) transfusion with our method proved to be significantly less accurate than using the traditional TEG parameters as shown in the Supplementary Material: Figure S12.

Figure 4:

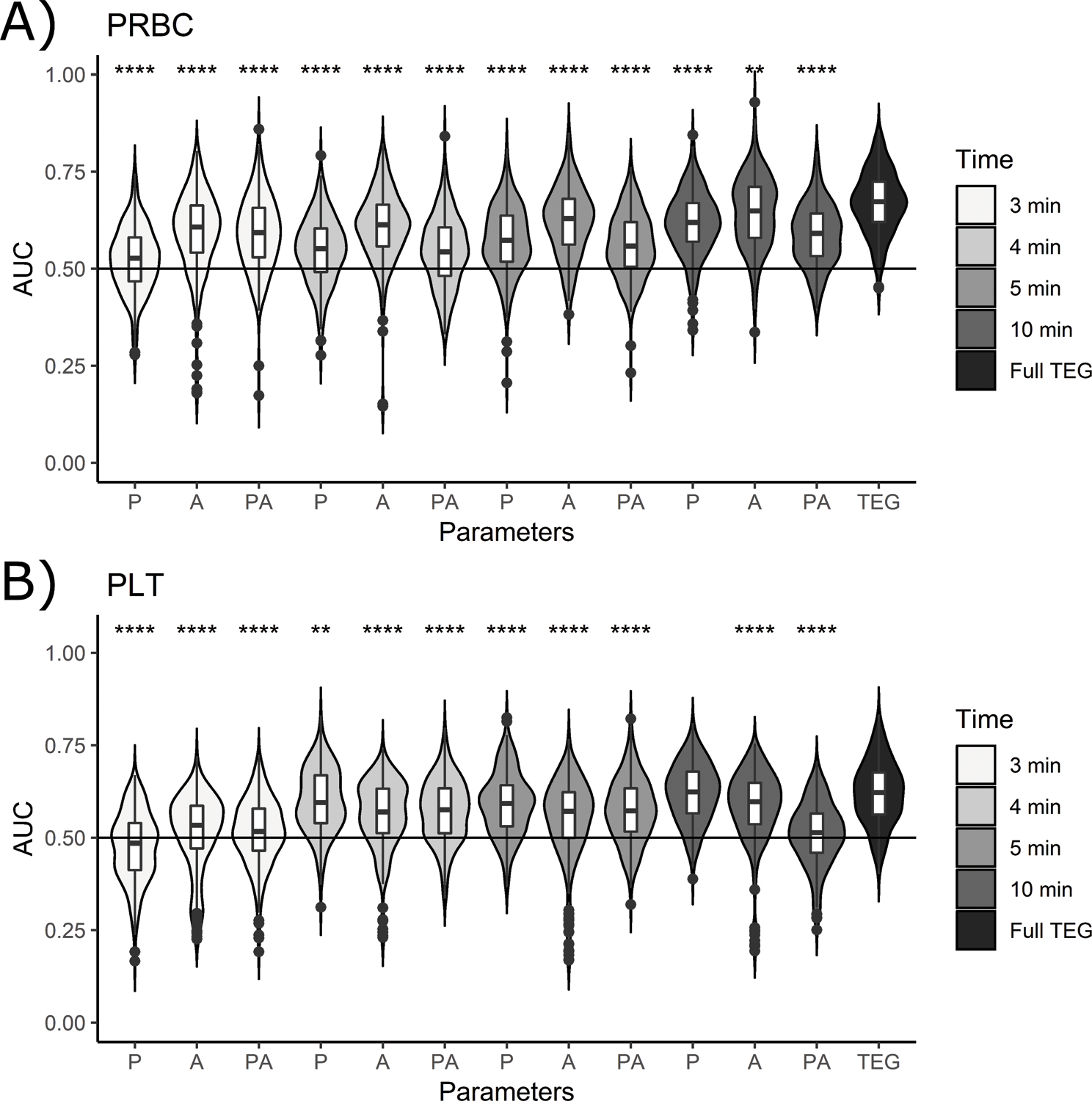
Accuracy (AUC of the ROC) of multiple predictions of transfused blood products using the 10 KNN parameters (P), the instantaneous amplitude (A), and the combination of both (PA) at 3, 4, 5, and 10 minutes, and additionally using traditional (full) TEG predictions (labeled TEG), for: A) PRBC within 24 hours of enrollment, and C) PLT within 24 hours of enrollment. Lines are drawn at 50 percent accuracy to emphasize the points where estimates lose their clinical utility. P-value codes: **: < 0.01, ***: < 0.001, ****: < 0.0001.

Discussion

When hemostasis cannot be established easily, having fast point-of-care options could offer improved resource utilization – choosing the right treatment at the right time. To address this problem, our work examined the performance of a faster point-of-care assessment of specific coagulation challenges. By implementing a simple dynamic model of coagulation, as observed in the ex vivo TEG, valuable clinical information can be extracted with high AUC.

We calibrated a simple model – while still capturing some mechanistic information – in available clinical data. More detailed models of the clotting cascade have been developed ^{13, 14, 15, 16, 17, 18}, some expanding on Jones and Mann ^{13, 14, 15, 16} and others looking at multiscale integration of dynamics and the physical forces into discrete models ^{17, 18}. While these models capture detailed mechanistic information, including clotting factors and other physiological considerations, it would be challenging to obtain reliable and unique estimates of model parameters in these complex descriptions. Our simplified mechanism trades off complexity for identifiability of model parameters to provide a small number of sensitive parameters that capture TEG response.

Even though our model captures TEG data, it is still too simple to identify exact deficits in the coagulation cascade. However, compared to the published simple correlations between amplitude at initial time points and MA, this work represents a step towards a physiologically motivated approach. Where RapidTEGs are available, the opportunity for direct translation to patient-specific recommendations from this work is motivated by the AUCs of our predictions within the initial minutes of data collection. For a more in depth comparison over the different time points, the ROC curves, precision-recall curves, a sensitivity and specificity comparison, and a parameter versus MA analysis are shown in Supplementary Material: Figures S13–S15, respectively.

Only three minutes of TEG data were needed to predict MA problems with AUC at or above 0.90 with model parameters alone. Adding instantaneous amplitude results in a boosted AUC of 0.95. These accuracies increase with more data, until reaching an AUC of 0.99 at 15 minutes. With this method, quick preliminary analysis and outputs of MA projected above or below the (50 mm) threshold would decrease time until patient-specific treatment decisions can be made. Providing an initial estimate from our algorithm to clinicians would outpace all other available point-of-care coagulation assays. Furthermore, when the time until MA can be over 30 minutes, any advanced notice of low MA is expected to improve clinical outcomes. The risks associated with making clinical treatment decisions using an initial estimate, versus waiting for the full TEG, would have to be further analyzed through a prospective clinical trial to verify the safety and utility in the clinical workflow.

There are limitations to our method. For the prediction of transfusions, we were limited by the small number of patients with transfusion data (n=102). Thus, although we are confident in the reported accuracy of the determination that subjects did or did not receive blood products, the generalizability of this work may be limited. Once the clinical trials conclude, we plan to add additional transfusion data to mitigate this limitation. Many current trauma protocols call for the administration of fixed ratios of red blood cell units and platelets, thus leaving little room for personalizing transfusional support, which is reasonable in subjects bleeding profusely. Our method more appropriately targets fewer extreme cases where transfusional needs are not immediately apparent or when patients develop a coagulopathic phenotype. Our current algorithm is unable to detect lysis problems or need of plasma (FFP) transfusion. Although the former is not surprising, it suggests modifications of the algorithm using longer time windows, possibly combined with a dataset enriched for patients with high lysis. Other approaches would be to use a more refined mesh for the remaining parameters or perform a simpler (1 parameter) optimization. This type of improvement may result in more comprehensive early profiling of coagulation, and thereby potentially improved coagulopathy identification. As for the deficiencies in the prediction accuracy of different transfusions in both the TEG and model parameters, this limitation could also be mitigated by increasing sample size.

Moving forward, improvements could be made to the dynamic model. First, as additional analytes and assays become available in the clinic, such as fibrinogen level and thrombin generation assays, models could be modified to explicitly include appropriate dynamics. Additional model structures are also being tested by our group to accurately simulate other variants of thromboelastic assays, beyond the RapidTEG. Ideally, it would be best to compute optimal fit parameters in real-time, as the TEG is generated. Currently, this patient-fitting optimization routine is not sufficiently rapid, reliably identifiable, or guaranteed to converge, motivating the use of a concrete algorithm: relying on a virtual library that can input data during collection and map a range of parameter space that ultimately provides useful predictions. As computational power becomes increasingly available, it may become possible to directly estimate optimal ranges of dynamic parameters with minimal delay. In the absence of these additional resources however, improvements could be made to the virtual library by including potentially more targeted discretization of the parameters generating the virtual library. This involves deeper analysis of parameter distributions from optimization, and testing additional discretization.

Overall, the impact of this proposed algorithm in the clinic lies in accurate and fast predictions of coagulopathy and transfusion need directly or through MA, a clinical parameter that currently guides standard of care transfusion protocols. One could envision embedding the algorithm presented here into point-of-care viscoelastic hardware or on a website where clinicians upload a photo of a TEG in-progress, thereby providing early prediction of coagulopathy and clinical decision support only minutes after initiating the assay.

Supplementary Material

Supplemental Data File (.doc, .tif, pdf, etc.)

Figure S1: Diagram showing the filtering of TEG data for analysis.

Figure S2: Examples of TEG data removed for containing < 1000 seconds of data.

Figure S3: Examples of TEG data removed for averaging < 1 mm.

Figure S4: Examples of TEG data removed for averaging < 5 mm and MA < 7 mm.

Figure S5: Examples of TEG data removed with negative jumps of magnitude less than the maximum jump in the data.

Figure S6: Examples of TEG data removed with large negative jumps and the maximum jump between two data points > 2.5 mm.

Figure S7: Plot showing the error metrics versus the number of top fits (KNN), guiding choice of 10 KNN.

Table S1: Model parameters that are significant for predicting maximum amplitude of the TEG (MA), as calculated by stepwise logistic regression.

Figure S8: Accuracy (AUC of the ROC) of predictions of transfused blood products using the 10 KNN for the model parameters at 3, 4, 5, and10 minutes, and using traditional TEG predictions (labeled: TEG), for: A) PRBC within the 24 hours after the TEG, and B) PLT within the 24 hours after the TEG. Lines are drawn at 50 percent accuracy to emphasize the points where estimates lose their clinical utility. P-value codes: **: < 0.01, ***: < 0.001, ****: < 0.0001 comparing all distributions to the distribution generated using TEG parameters.

Figure S9: The full set of model parameters (P), instantaneous amplitude (A), and combined (PA) are shown at all time points (3, 4, 5, 7.5, 10, 15, 20 minutes). For predicting transfusion of PRBC, PRBC 24 hours after baseline TEG, PLT, and PLT 24 hours after baseline TEG, from top to bottom, respectively. P-value codes: **: < 0.01, ***: < 0.001, ****: < 0.0001.

Figure S10: The worst 4 fit TEGs using the dynamic model optimization defined in the methods. Showing A) the worst fit patient TEG, B) second worst fit patient TEG, C) third worst fit patient TEG, and D) fourth worst fit patient TEG, as measured by the sum of squared error (SSE).

Figure S11: Plot showing the distribution of the AUCs predicting high lysis (LY30≥3%) from using model parameters (P), instantaneous amplitude (A), and both (PA), at all time points (3, 4, 5, 7.5, 10, 15, 20 minutes.

Figure S12: Plot showing the distribution of the AUCs predicting FFP transfusion from using model parameters (P), instantaneous amplitude (A), and both (PA), at all time points (3, 4, 5, 7.5, 10, 15, 20 minutes, along with the prediction using TEG parameters (MA, TMA, alpha, k, R, TEGACT, LY30). P-value codes: **: < 0.01, ***: < 0.001, ****: < 0.0001. All distributions have means significantly less than the TEG parameter prediction of plasma transfusion need.

Figure S13: Plot of the A) Receiver Operating Characteristic (ROC) curves and the B) Precision vs. Recall curve from the LR using the following features: the model parameters (P(0), k1, k2, k3), the Sum of Squared Error (SSE) between the simulation and data up the time the test is performed (3, 4, 5, 7.5, 10, 15, 20 minutes), and instantaneous amplitude at 3, 4, 5, 7.5, 10, 15, 20 minutes. Thus, totaling the number of features used in the predictions as six.

Figure S14: Plot of the sensitivity (left) and specificity (right) versus the specified time window (3, 4, 5, 7.5, 10, 15 or 20 minutes) used in the algorithm. In the legend, the different cutoff values used to distinguish patients with MA problem or not from their predicted risk from the LR are shown by the different colors.

Figure S15: Plot showing the dynamic parameters versus the actual MA from 3 minutes of data, with the colors showing the predictions. Points in black were predicted above the clinical threshold and points in grey were predicted below the clinical threshold. The four plots show the four different parameters (P0 – top left, k1 – top right, k2 – bottom left, and k3 – bottom right).