Toward human intervention-free clinical diagnosis of intracranial aneurysm via deep neural network

Summary

Intracranial aneurysm (IA) is an enormous threat to human health, which often results in nontraumatic subarachnoid hemorrhage or dismal prognosis. Diagnosing IAs on commonly used computed tomographic angiography (CTA) examinations remains laborious and time consuming, leading to error-prone results in clinical practice, especially for small targets. In this study, we propose a fully automatic deep-learning model for IA segmentation that can be applied to CTA images. Our model, called Global Localization-based IA Network (GLIA-Net), can incorporate the global localization prior and generates the fine-grain three-dimensional segmentation. GLIA-Net is trained and evaluated on a big internal dataset (1,338 scans from six institutions) and two external datasets. Evaluations show that our model exhibits good tolerance to different settings and achieves superior performance to other models. A clinical experiment further demonstrates the clinical utility of our technique, which helps radiologists in the diagnosis of IAs.

Highlights

• •GLIA-Net is a deep learning method for the clinical diagnosis of IAs
• •It can be applied directly to CTA images without any laborious preprocessing
• •A clinical study demonstrates its effectiveness in assisting diagnosis
• •An IA dataset of 1,338 CTA cases from six institutions is publicly released

The bigger picture

Intracranial aneurysms (IAs) are enormous threats to human health with a prevalence of approximately 4%. The rupture of IAs usually causes death or severe damage to the patients. To enhance the clinical diagnosis of IAs, we present a deep learning model (GLIA-Net) for IA detection and segmentation without laborious human intervention, which achieves superior diagnostic performance validated by quantitative evaluations as well as a sophisticated clinical study. We anticipate that the publicly released data and the artificial intelligence technique would help to transform the clinical diagnostics and precision treatments of cerebrovascular diseases. They may also revolutionize the landscape of healthcare and biomedical research in the future.

Intracranial aneurysm (IA) diagnosis on CTA images is laborious and time consuming in clinical routine. By combining global risk prediction with local IA recognition, the proposed GLIA-Net can robustly and efficiently assist radiologists in clinical practice without any pre- or postprocessing. The state-of-the-art performance has been validated via a multi-cohort dataset, which has been publicly released to democratize deep learning algorithms for biomedical research.

Introduction

The diagnosis and treatment of intracranial aneurysms (IAs) are important and difficult in clinical assessment. As reported, the prevalence of IAs in the general population can be up to 6%,¹ and the rupture of IAs is always associated with severe morbidity and mortality.² According to statistics, 80% of nontraumatic subarachnoid hemorrhages are caused by the rupture of IAs,^3,4 and most of the nontraumatic subarachnoid hemorrhages will result in death or dismal prognosis.^5,6 However, the small size of IAs and low-intensity contrast to normal vessels in medical image scans makes even subspecialty-trained radiologists need to check up to hundreds of image slices carefully for one patient. Moreover, individual radiologists may not make consistent assessments, also emphasizing the diagnostic difficulties. Aiming to improve the diagnosis, delicately developed algorithms for the detection of IAs from computed tomography angiography (CTA) and magnetic resonance angiography (MRA) have been proposed over the past several decades.7, 8, 9, 10 Although digital subtraction angiography (DSA) is still the gold standard for diagnosing IAs, CTA has been proved to be able to diagnose IAs in most situations11, 12, 13, 14 and is a non-invasive, time-saving, and cost-effective technique with usually wider availability.¹⁵ Besides, compared with MRA, CTA is a faster, widely available diagnostic technique that costs less and has higher image resolution.

The essential role of clinical diagnosis is to detect IAs and generate three-dimensional (3D) segmentation. Despite the rapid development of biomedicine, radiologists still need to make great efforts in the manual detection of IA lesions from medical images, and with highly limited computer assistance. Conventional automatic or semi-automatic segmentation methods for IAs have been proposed during the past few years.^16,17 However, they are quite sensitive to different device settings and require a lot of laborious pre and post operations.

Offering an alternative solution, recent advances in deep learning have shown great potential for medical image interpretation, which promises to assist radiologists and clinicians to speed up and improve the clinical diagnosis. Inspired by the development of deep learning on segmentation for natural image interpretation, several deep neural networks, such as U-Net,¹⁸ V-net,¹⁹ 3D U-Net,²⁰ and P-Net,²¹ have been validated successfully on biomedical datasets recently. Such successes stimulate an upsurge of research interest in deep-learning-based biomedical applications, including the diagnosis of IAs.^7,8 Nevertheless, current deep learning models for IA image interpretation seldom consider the inherent characteristics of biomedical data and still need human interventions like brain extraction or bone removal, which highly depend on the human and device resources in different institutions. Besides, the training datasets of these models are pretty small, comprising no more than a few hundreds of aneurysms. Given that the training data are usually collected from a single institution, it is hard to guarantee the generalization capability of the learned models when facing a large, multi-institutional cohort.

To take a step further in the diagnosis of IAs, we first investigated all the difficulties in achieving IA segmentation from medical images. The difficulties are listed as follows. Medical images for IA diagnosis are typically quite large (over 500 pixels in all the three dimensions) and it is difficult to identify the 3D structural lesion regions from just a single 2D image. Besides, patients may undergo thorough examinations that cover not only the head region but also the neck or lung/heart region, which increases the size of the original CTA scans. However, processing 3D images directly has been impossible for such a large image size so far because of the limited computation resources. Besides, the size of IAs is generally small compared with the whole image, making it hardly possible to down-sample the image to meet the computation resource requirement as the aneurysms may be lost.

There are some methods that were designed to deal with the huge amount of data in medical images. Some methods directly use 2D or 2.5D segmentation methods.22, 23, 24 Kong et al.²⁵ used a recurrent neural network (RNN) to encode information among several 2D slices, but these methods only work well for large object segmentation, such as cardiac and kidney partition. As a compromise between 3D feature requirement and limited computation resource, some methods use the 3D patching strategy, which clips a small cube as an input sample.^20,26 Such 3D methods can extract local shape information very well but raise another problem: the global structure information is lost in clipped patches. This can be ignored in some applications like tumor detection in pathology slices but is very important for the lesions that have a global position tendency in the body, like IAs. Although there are some works considering that multi-level feature fusion can achieve a plausible effect on targets with different sizes,^27,28 they still adopt the whole image as input, which means they cannot accommodate such huge CTA images in one glance. Some medical imaging models do consider the location information,29, 30, 31 but they just directly use the coordinate values without delicately extracting and representing the location information, thus they are closely attached to the data they use.

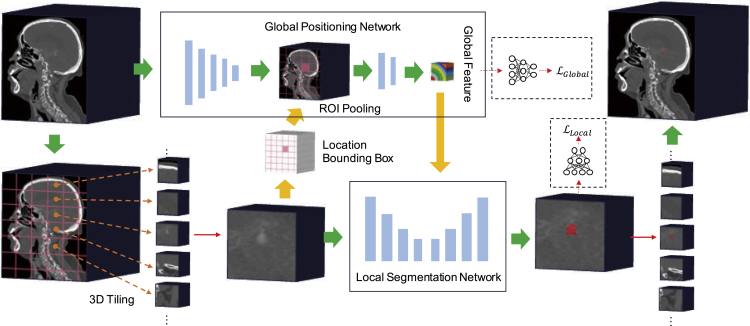
Based on these considerations, in this paper, we propose a strategy to adopt global structure information in the normal 3D patching segmentation network. Our model is called the Global Localization-based IA Network (GLIA-Net). The overview of our model is shown in Figure 1. This method can be used in any 3D sliding-cube convolution tasks, especially for those requiring strong global position information. Besides, we propose a strategy to design spatial variant losses for annotated pixels. This is to consider the annotation inconsistency on the lesion edges.³² We use CTA images because they have a short examination period in emergency treatment and are more economical to obtain in many countries. The segmentation model in this work does not need any pre- or postprocessing procedures with human intervention, like brain extraction or bone removal, and can also work on CTA images containing neck or lung regions without any advanced accessory equipment or medical software. The internal dataset in this work contains 1,338 CTA images with 1,489 IAs from six different institutions, which guarantees the generalization ability of the model. Compared with the existing deep learning models, GLIA-Net achieves a target-wise recall rate of 82.1 (78.2–86.0, 95% confidence interval [CI]) on the internal test set with 4.38 (2.91–5.85, 95% CI) false-positive IAs per case, and a voxel-wise segmentation average precision (AP) of 61.9 (59.4–64.4, 95% CI), showing superior diagnostic performance. To further validate the clinical feasibility of our model, a clinical experiment has also been conducted.

Figure 1.

The workflow of our GLIA-Net model in IA segmentation

The original CTA image is directly used as the global image. A 3D tiling method is adopted and generates many local images. The model consists of two parts: (1) global positioning network, which analyzes the global image and gives a risk distribution map roughly to the (2) local segmentation network, which uses the local images to generate voxel-wise segmentation results. The final segmentation map is constructed from all the local image patches.

Results

Data

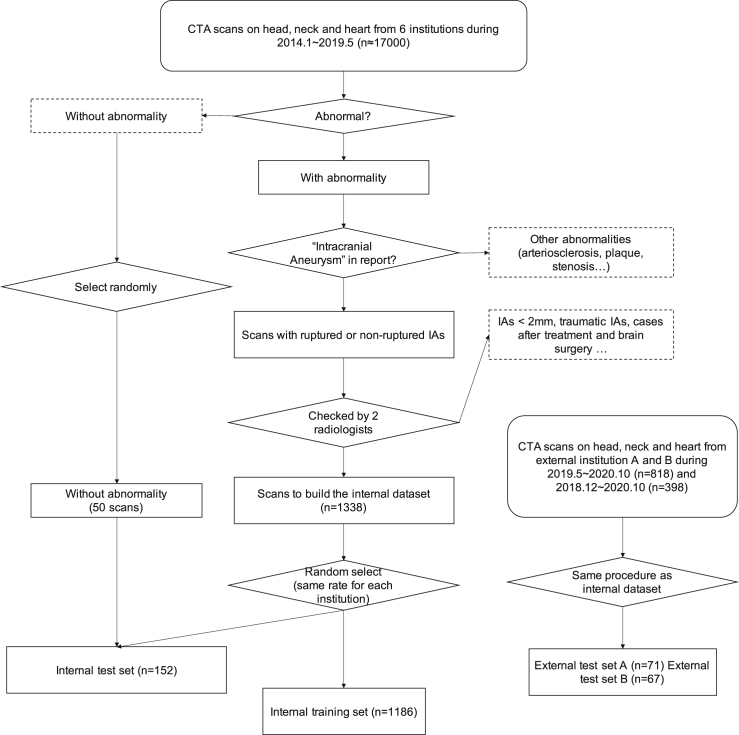
The large variety of IAs' positions, shapes, and sizes makes them hard to identify. Thus, a large dataset with different but complementary aspects of patients is required for training and evaluation. We collected an internal dataset from six institutions (Guizhou Provincial People's Hospital, Affiliated Hospital of Zunyi Medical University, Tongren Municipal People's Hospital, Xingyi Municipal People's Hospital, The Second People's Hospital of Guiyang, The First People's Hospital of Zunyi) and two external datasets from two institutions (People's Hospital of Anshun City, Zhijin People's Hospital). The internal dataset contains 1,338 CTA images with 1,489 IAs, which contributes to a huge number of 699,266 512 × 512 2D image slides in total (approximately 174GB of disk space). The pipeline to build the dataset and the inclusion and exclusion criteria are shown in Figure 2.

Figure 2.

Flowchart of data selection and division

The n in the flowchart means the number of cases.

The images all contain the head region of the patients, some of which may also contain the neck or heart region. The data include non-ruptured ones and ruptured ones with subarachnoid hemorrhage or parenchymal hemorrhage. The CTA scans in the internal dataset were captured by 11 devices that belong to six equipment models (SIEMENS SOMATOM Definition AS+, SIEMENS SOMATOM Definition Flash, SIEMENS SOMATOM Force, NMS NeuViz 128, GE MEDICAL SYSTEMS Discovery CT, SIEMENS Sensation 64) from three manufactures (Siemens, Neusoft, and GE Healthcare). There are four different scan layer thicknesses (0.6 mm, 0.625 mm, 0.75 mm, and 1.0 mm). All the patients were in the head-first-supine (HFS) position during the examination with peak voltage between 70 and 140 kV, and tube current between 45 and 1,275 mA.

The CTA images were annotated by five clinicians and reviewed by two experienced CTA diagnosis radiologists with the associated clinical and personal information of the patients. The identified IAs were manually segmented on each slice by using the open-source annotation software ITK-SNAP.³³ The annotation was used as the ground truth standard both in training and evaluation, although it should be noted that there might be some bias or noise considering the vague boundary of IAs in CTA images and high inter-observer variability, which means they may not share the same labeling standard subconsciously.

The whole internal dataset was split into 1,186 cases for training and 152 cases for testing. The internal test set contains 50 negative cases (no IAs occur). We do not include negative cases in the training set, because the training already suffers from severe data imbalance as the IAs are small in the brain. We verified that all the positive CTA images distribute roughly equally for different institutions, ages, and genders in the internal training and test set. The training set was used to train the model and the test set was only used to evaluate the performance of our model, which means that the model could not see the images in the test set before the training is done.

To evaluate the generalization of our model, we also collected two external datasets from another two institutions that were not included in the internal dataset. The external test set A contains 71 (including 24 negatives) cases and the external test set B contains 67 (including 22 negatives) cases. The building process of these external datasets was the same as that in the internal dataset. The scans in the external dataset A were captured using one device, a Philips Ingenuity CT model, while those in the external dataset B were also captured using one device, a Philips Brilliance 64 model. These models were not included in the internal dataset. Slice thicknesses for the two external test sets are both 0.9 mm, which does not appear in the internal dataset either. The detailed dataset statistics can be viewed in Figure 3 and Table 1.

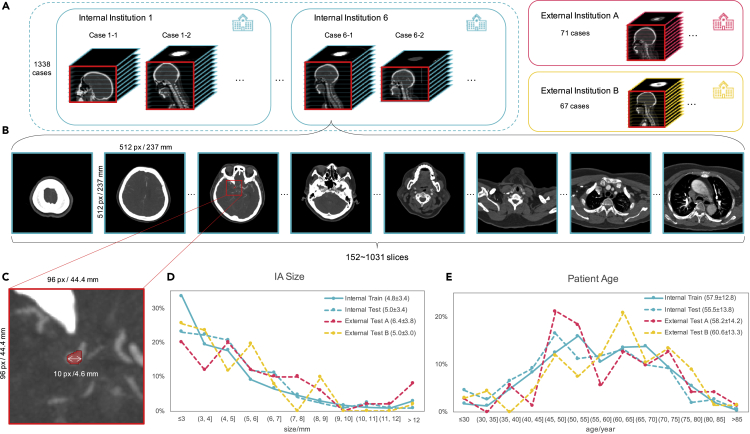
Figure 3.

Dataset illustration in this study

The IAs are typically tiny in the whole CTA images (about 1/1,000,000 in voxels), which makes the diagnosis a tough task.

(A) Our internal dataset contains 1,338 CTA cases (1,489 IAs) that were collected from six different institutions and the two external test set contains 71 and 67 cases (50 and 51 IAs) respectively. The CTA scans used in training were captured by 11 devices that belong to seven equipment models coming from three manufactures with four different scan layer thicknesses.

(B) Each case contains 152–1,310 image slices with a size of 512 × 512 resulting in a total of 699,266 slices, which may include neck and heart regions associated with the head region as they were collected from real clinical examinations.

(C–E) (C) IAs are typically tiny compared with the whole CTA scans. The presence of IAs was annotated by five clinicians and reviewed by two experienced CTA diagnosis radiologists with reference to the patients' clinical reports and personal information. We also show the histograms of (D) patient age distribution and (E) IA size distribution for the dataset, and the legend also shows the mean and SD.

Table 1.

Dataset statistics in detail

Dataset	No. of cases	No. of IAs	No. of cases that contain		Gender		No. of cases containing
			Ruptured IAs	Non-ruptured IAs	Male	Female	0 IA	1 IA	2 IAs	≥3 IAs
Internal training	1,186	1,363	474	712	508	678	0	1,043	119	24
Internal test	152	126	42	60	63	89	50	85	13	4
External test A	71	50	29	18	32	39	24	44	3	0
External test B	67	51	25	20	33	34	22	40	4	1

Performance evaluation

Our model uses a patching strategy to segment IAs across the whole original CTA scan (the global image) without bone removal or any other preprocessing. One CTA image is split into lots of small patches (the local image) and the network is applied on each patch at a time. At last, the results of all patches are combined to build the entire segmentation map. The segmentation network gives each voxel in the input 3D CTA patch a label that indicates whether it belongs to an IA or normal tissue. Our GLIA-Net consists of two components: (1) the global positioning network, which extracts the information of IA distribution in the global image; and (2) the local segmentation network, which is used to segment voxel-wise label in the current local image. The input to the local segmentation network keeps the original resolution, while that to the global positioning network is down-sampled to fit in the limited Graphics Processing Unit (GPU) memory. The major difference between our IA segmentation model and other segmentation models is that we use a global positioning network to equip our patch-based local segmentation network with global information that a normal segmentation model cannot access. The global information is not just conveyed by some simple features like the position coordinate, but with a deep neural feature from the global image. In the following, we will discuss the ability and performance of our model.

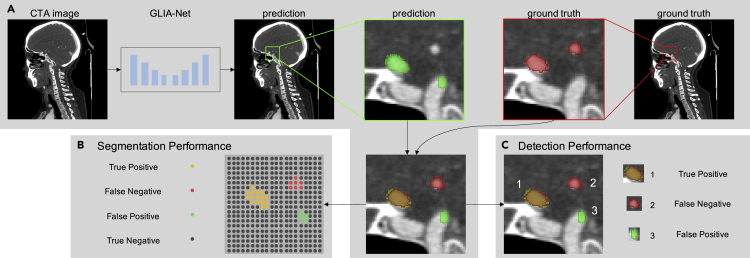
Considering most IAs are small compared with the whole brain area and our segmentation model needs to give prediction labels for each voxel in the image, which is harder than just a binary patient classification objective, we used multiple related metrics to evaluate the performance of our model. To begin with, the AUC (area under curve) value computed on the ROC (receiver operating characteristic) curve³⁴ and the AP value computed on the precision-recall curve³⁵ are considered to demonstrate the overall performance of a segmentation task, which considers all the probability thresholds on the output. Then, we set a fixed probability threshold of 0.5 in the following qualitative evaluations. The precision, recall, DSC (dice similarity coefficient),³⁶ and 95% HD (the 95th percentile Hausdorff distance)³⁷ values were calculated in this threshold. To show the stability of the tested models, we also show the 95% confidence interval (95% CI) of all evaluation metrics, which was summarized from five different runs for each experiment setting. The performance can be explained in two aspects: voxel-wise segmentation performance and target-wise detection performance (see Figure 4).

Figure 4.

Evaluation procedures for voxel-wise segmentation performance and target-wise detection performance

(A) Generation of the prediction map using our GLIA-Net and the ground truth map on which we perform the evaluation.

(B) Segmentation performance is calculated on every voxel in the image, which measures the shape and edge of predicted IAs.

(C) Detection performance is calculated on every IA in the prediction and ground truth maps, which measures the ability of our model to identify IAs in CTA images.

Our segmentation model was trained on the training set of our internal dataset (see also in the Experimental procedures and the Supplemental experimental procedures) and was tested on the internal test set and two external test sets.

We also compared our GLIA-Net with two deep learning models. First, we compared our GLIA-Net with the enhanced version of U-Net,¹⁸ which is also the baseline network of our local segmentation network. This deep learning network has been widely used in many segmentation tasks in the past few years and has shown great power compared with traditional models. In our experiment, we modified the original U-Net to a 3D version and replaced its original convolutions with residual blocks. Then, we compared our model with a state-of-the-art IA segmentation network called HeadXNet.⁸ This model can be regarded as the ultimate version of U-Net supported by the advanced feature extracting network SE-ResNeXt^38,39 and atrous spatial pyramid pooling.⁴⁰ We chose this network as a comparison because it showed great potential in IA segmentation and its ability was tested on clinical data. To compare consistently, all the models were trained on the same training dataset and used the same training procedure.

Segmentation performance

Every test image was split into hundreds of 3D patches with overlaps and was processed by our segmentation model. The patches that contain IAs are called positive patches and those containing no aneurysm are called negative patches. To focus on the positive patches both in training and evaluation of the model, positive patches were duplicated manually to match approximately the same number as negative patches. Next, we evaluated the segmentation performance of our model compared with other models. The evaluation results are shown in Table 2. Our GLIA-Net increased the segmentation performance by a large margin in almost all metrics on the internal test set and two external datasets. Note that all the tested models have a better performance on the external test set A than on the internal test set, which may be because that the IAs in the external test set A are easier to identify (with bigger average size, as shown in Figure 3D). On external test set B, the performance of our model is only slightly lower than that on the internal test set, while other models drop a lot, which verifies the generalization ability of our model. The precision-recall curve and the ROC curve of our model are shown in Figure S1.

Table 2.

Voxel-wise segmentation performance

Dataset	Model	Precision↑ (95% CI)	Recall↑ (95% CI)	DSC↑ (95% CI)	95% HD↓ (95% CI)	AUC↑ (95% CI)	AP↑ (95% CI)
Internal test	U-Net	14.0 (11.9–16.2)	71.3 (63.9–78.7)	23.2 (20.5–25.9)	19.6 (17.9–21.3)	98.8 (98.6–99.0)	17.5 (14.6–20.4)
	HeadXNet	16.2 (13.1–19.2)	55.6 (33.0–78.2)	23.2 (20.6–25.9)	15.9 (14.6–17.1)	98.2 (97.1–99.2)	25.0 (12.0–38.0)
	GLIA-Net (ours)	48.8 (44.5–53.0)	72.9 (66.9–78.9)	57.9 (56.4–59.5)	9.07 (7.84–10.3)	98.2 (97.6–98.8)	61.9 (59.4–64.4)
External test A	U-Net	23.9 (20.7–27.1)	71.0 (59.3–82.8)	35.3 (31.8–38.9)	19.5 (17.7–21.3)	97.9 (97.7–98.2)	30.2 (21.9–38.4)
	HeadXNet	27.1 (20.6–33.6)	52.7 (29.2–76.2)	32.4 (25.5–39.3)	15.6 (14.2–17.0)	96.2 (92.8–99.6)	32.1 (18.6–45.6)
	GLIA-Net (ours)	71.2 (65.2–77.3)	83.9 (82.2–85.7)	76.8 (73.7–79.9)	8.28 (7.05–9.52)	99.0 (98.8–99.1)	80.5 (78.6–82.3)
External test B	U-Net	6.54 (5.65–7.44)	43.6 (37.9–49.3)	11.3 (9.94–12.7)	21.0 (19.7–22.3)	86.9 (83.0–90.7)	6.86 (5.22–8.49)
	HeadXNet	14.8 (10.2–19.4)	32.6 (22.3–43.0)	18.1 (15.7–20.6)	15.9 (14.5–17.2)	86.1 (81.3–91.0)	14.3 (8.69–19.9)
	GLIA-Net (ours)	59.8 (54.7–64.8)	57.4 (43.0–71.8)	57.2 (50.5–64.0)	8.78 (7.79–9.76)	98.2 (97.2–99.2)	55.8 (44.0–67.6)

Values are given in units of % except for 95% HD, which is given in mm.

Detection performance

One of the aims of our model is to help clinicians find all the IAs hidden in the original CTA images. So, the performance of IA detection is also important. Unlike voxel-wise segmentation, target-wise detection is designed to point out where IAs exist, in which the IA shapes and sizes do not matter. Here, we set a standard to identify correct detection. First, we find out all the lesion regions in the segmentation map generated by the model and the ground truth label map. Then, if the center distance of any two lesion regions in the segmentation map and the ground truth map is smaller than the summation of their radiuses, we marked them matched. Then the matched and unmatched lesion regions can be used to calculate the following detection metrics, such as precision and recall.

The detection performance of our model and the comparison with other methods are shown in Table 3. Because U-Net and HeadXNet treat all patches from different parts of the CTA image in the same way, they may generate many false-positive predictions everywhere in the global image. Thanks to the global positioning network, our GLIA-Net not only reduced the false-positives a lot but also detected more IAs successfully. Specifically, our model detected 103 (98.5–108.3, 95% CI) IAs out of 126 in the internal test set, with only 4.38 (2.91–5.85, 95% CI) false-positive predictions per case. The performance on the external test sets are slightly lower, but still comparable with that on the internal test set.

Table 3.

Target-wise detection performance

Dataset	Model	TPs↑ (95% CI)	FPs↓ (95% CI)	FNs↓ (95% CI)	Recall↑ (95% CI)	FPs per case↓ (95% CI)
Internal test	U-Net	92.4 (89.0–95.8)	4.68k (3.72k–5.64k)	33.6 (30.2–37.0)	73.3 (70.6–76.0)	30.8 (24.5–37.1)
	HeadXNet	69.2 (45.1–93.3)	2.41k (1.21k–3.62k)	56.8 (32.7–80.1)	54.9 (35.8–74.1)	15.9 (7.96–23.8)
	GLIA-Net (ours)	103 (98.5–108)	666 (443–889)	22.6 (17.7–27.5)	82.1 (78.2–86.0)	4.38 (2.91–5.85)
External test A	U-Net	34.0 (30.6–37.4)	1.41k (1.07k–1.75k)	16.0 (12.6–19.4)	68.0 (61.2–74.8)	19.8 (15.0–24.7)
	HeadXNet	24.2 (15.9–32.5)	670 (335–1.01k)	25.8 (17.5–34.1)	48.4 (31.8–65.0)	9.44 (4.71–14.2)
	GLIA-Net (ours)	36.0 (33.9–38.1)	193 (127–259)	14.0 (11.9–16.1)	72.0 (67.7–76.3)	2.72 (1.79–3.65)
External test B	U-Net	31.8 (29.4–34.2)	3.08k (21.3k–4.02k)	19.2 (16.8–21.6)	62.4 (57.7–67.0)	45.9 (31.8–60.0)
	HeadXNet	24.8 (18.5–31.1)	1.64k (737–2.55k)	26.2 (19.9–32.5)	48.6 (36.3–60.9)	24.5 (11.0–38.0)
	GLIA-Net (ours)	36.6 (33.3–39.9)	296 (222–371)	14.4 (11.1–17.7)	71.8 (65.4–78.2)	4.42 (3.31–5.54)

The total number of true positive (TP), false-positive (FP), and false-negative (FN) predicted IAs are shown. The target-wise recall rate in the unit of % and the number of false-positive IAs per case are also given.

Results analysis

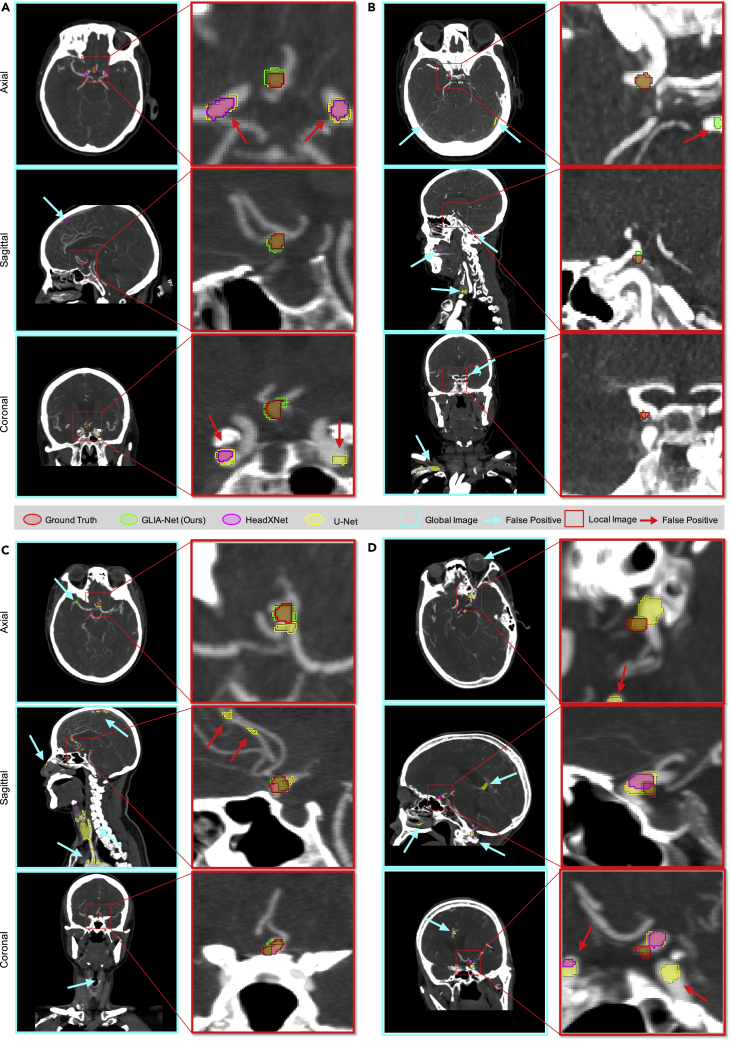
Besides the quantitative evaluations stated above and the ablation study of different parts of our GLIA-Net in Table S1 and Figure S1, we also show the visualization of four CTA images and the corresponding segmentation results predicted by our GLIA-Net and other methods in Figure 5. These examples were selected randomly from the internal test set. As shown in the figures, our model can identify IAs accurately even if they are ridiculously small compared with the whole CTA scan. With the help of our global positioning network, our GLIA-Net can reduce lots of false-negative predictions at low-risk regions where other models processing directly on local images often fail. Moreover, because the training is less affected by structures at low-risk regions, the true-positive predictions of our model are closer to the ground truth than other methods.

Figure 5.

Qualitative comparison with other models

Segmentation results of four CTA cases, (A), (B), (C), and (D), randomly selected from the internal test set. There are three perspectives (axial, sagittal, and coronal) for each 3D CTA case for better visualization. The CTA images are shown using 11-layer MIP (maximum intensity projection). The window width and window level of the CTA images are 600 and 200 Hounsfield Units. Because of the global positioning network, our GLIA-Net has much fewer false-positive predictions at low-risk regions where other methods often generate positive, including in-head (e.g., sagittal in [A] and axial in [B]) and out-of-head (e.g., coronal in [B] and sagittal in [C]) regions. Besides, the segmentation results of our model are also closer to the annotation compared with other models (e.g., local images in [C] and [D]). Better viewed in a high-resolution image.

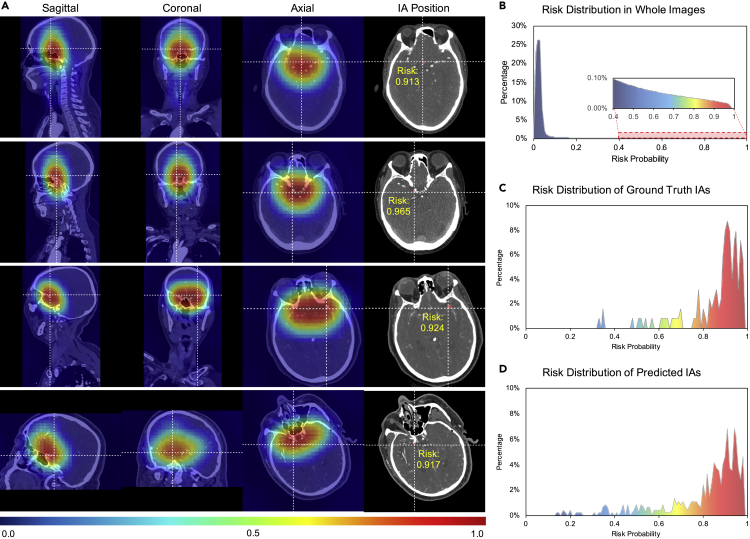
The global positioning network in our model can help the local segmentation network to learn global distribution information for the occurrence of IAs. This is important for current patch-based segmentation models on this task, which can only process one small local image clipped from the global image at a time and will lose the global structure information of the human body. To show the effectiveness of our global positioning network, we provide a visualization of its output global risk distribution map in Figure 6. The risk distribution map is built as follows. First, we collected the output probability from the final layer of our global positioning network for a small patch, which can represent the risk probability for this patch. Second, we collected the risk probabilities of all the tiled patches that can cover the whole global image. Finally, the value in each voxel in the probability distribution map was averaged by values of all the patches that contain this voxel. Because the small patches are tiled from the global image using the sliding-widow approach, we set the overlap of the sliding window to about 84% of the patch size to increase the resolution of the risk probability distribution map.

Figure 6.

Global probability distribution generalized by the global positioning network

(A) Four examples in four rows are randomly selected from the internal test set. Generated by the global positioning network, the probability distribution maps are shown in false color and displayed on top of the original CTA image. The first three columns are the sagittal, coronal, and axial perspectives. The final column shows the actual position of the IAs using crosshairs, together with the risk probability value at the target center.

(B–D) (B) The risk value distribution in whole CTA images, which summarizes all the voxels of cases in the internal test set. The percentages of high-risk regions are quite small in the whole scans. The risk value distributions of the center of (C) ground truth IAs and (D) predicted IAs by our GLIA-Net are summarized on all the IAs. Most IAs occurred in high-risk regions and our model estimates the IA risk distribution successfully.

Red regions in Figure 6 indicate higher possibilities to contain IAs and blue regions are the relatively safe areas. However, note that the IAs are generally too tiny to spot in the down-sampled global images, which means the heatmap does not point out exactly the location of IAs, but a risk distribution in the whole scan. Most parts in the image are predicted low-risk areas of IAs inferred by our model, while most IAs occurred in high-risk regions for both the ground truth and the prediction of our model. The results show that the global positioning network can perceive human structural knowledge in the global image and extract useful information that is not opposed to the local segmentation network. This is important because similar structures to the IAs in other parts of the body can affect the training and testing procedure a lot if only performed on the local image.

Clinical experiment

Besides the performance on voxel-wise segmentation and target-wise detection, we also want to explore the clinical utility of our model and find out how the model can help clinicians. We performed a clinical experiment to compare the accuracy and time spent by radiologists to segment IAs with and without the assistance of our model. Without the assistance, the clinicians needed to perform the judgment by themselves from the raw CTA images. With the assistance, both the raw CTA images and the prediction of our model were available for the clinicians to diagnose, in which they can identify whether the results generated by our model are correct or not.

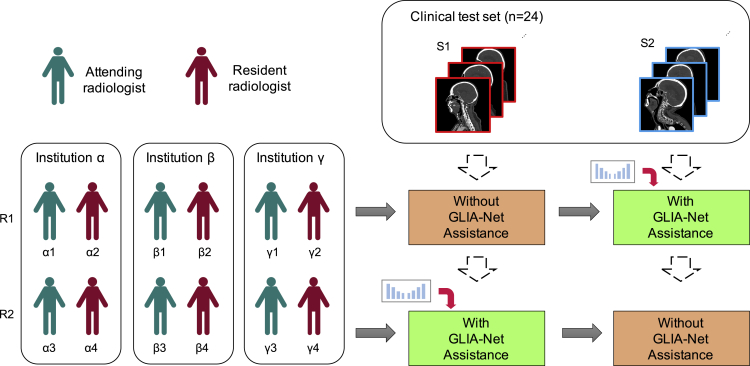
The design of our clinical experiment is shown in Figure 7. To simulate the real environment in clinical usage, we collected another 24 CTA scans from daily examinations in one of the internal institutions (Guizhou Provincial People's Hospital), of which 17 contain at least one IA and the others contain none. These CTA images were performed using our segmentation model in advance. The time spent only consists of the diagnosis and segmentation time by the clinicians without data-loading time. There were six resident radiologists and six attending radiologists from three institutions (Guizhou Provincial People's Hospital, The First Affiliated Hospital of Guizhou University of Traditional Chinese Medicine, and Renhuai City People Hospital) participating in this experiment. Only the raw CTA images and the prediction maps were accessible to these radiologists during the experiment, which means they could not refer to the patient identifications, clinical reports, treatment histories, or follow-up examinations. To avoid the bias of different clinicians and different study cases, we used a crossover experiment design. We split the radiologists into two groups, R1 and R2, both of which had six radiologists. The study cases were also grouped into S1 and S2 equally. The radiologists in R1 diagnosed S1 without the assistance of our model and diagnosed S2 with the assistance. On the contrary, the radiologists in R2 diagnosed S1 with the assistance and diagnosed S2 without it.

Figure 7.

Clinical study design

We use a crossover clinical study design in which six attending and six resident radiologists from three different institutions were split into R1 and R2, while 24 CTA cases were split into S1 and S2. The clinical test dataset was collected from daily examinations in one of the internal institutions, which is an independent validation dataset.

We developed a CTA viewing and annotation tool by ourselves to assist radiologists in the IA diagnosis procedure (see Figure S6), which is also used in the clinical experiment. The evaluation result is shown in Table 4. We show the result in three aspects: (1) case-wise, which is to indicate the diagnostic ability of the radiologist; (2) target-wise, which shows the performance to detect IA targets; (3) voxel-wise, which is to evaluate the segmentation result that radiologists know about the shape and size of the aneurysms. Most of the diagnosing metrics with the model's assistance are better than without it, especially on the time spent, target-wise recall rate, and case-wise sensitivity. Our model is more helpful for resident radiologists than attending radiologists. The diagnosing time and target-wise recall rate of radiologists have a statistically significant difference before and after model assistance (p value 0.02 and <0.01). We also give an evaluation for radiologists from different institutions without and with the assistance of our model (see Table S2). Although there are diagnosing differences among different institutions, which may be due to different diagnosis abilities of different institutions, all radiologists can benefit from our model consistently, which also indicates that our model can help radiologists with different diagnosing performance in clinical practice.

Table 4.

Diagnosing difference with and without the assistance of our model in our clinical study

		Time↓	Voxel-wise	Target-wise		Case-wise
			DSC↑ (95% CI)	Precision↑ (95% CI)	Recall↑ (95% CI)	Specificity↑ (95% CI)	Sensitivity↑ (95% CI)	ACC↑ (95% CI)
Model		25.8 (24.9–26.7)	30.1 (25.3–34.8)	19.3 (14.2–24.4)	85.8 (80.0–91.5)	38.9 (26.1–51.7)	96.2 (92.2–100)	79.2 (75.6–82.8)
Attending radiologist	without assist	132 (118–145)	57.9 (46.2–69.6)	91.7 (82.0–100)	68.8 (52.2–85.3)	100 (100–100)	80.6 (67.8–93.3)	86.1 (76.9–95.3)
	with assist	121 (107–135)	67.6 (58.8–76.4)	91.7 (82.0–100)	88.2 (79.1–97.3)	90.3 (79.1–100)	88.7 (79.8–97.6)	88.9 (79.7–98.1)
Resident radiologist	without assist	162 (150–175)	48.2 (29.0–67.4)	81.6 (68.3–94.9)	66.0 (48.1–83.9)	83.3 (63.0–100)	82.4 (68.5–96.3)	83.3 (72.4–94.2)
	with assist	143 (131–156)	54.4 (40.3–68.6)	88.4 (77.4–99.4)	84.7 (77.6–91.8)	100 (100–100)	84.9 (78.1–91.6)	88.9 (83.9–93.9)
All	without assist	147 (137–156)	53.1 (41.5–64.6)	86.6 (77.9–95.3)	67.4 (55.2–79.6)	91.7 (80.4–100)	81.5 (72.1–90.9)	84.7 (77.6–91.9)
	with assist	132 (123–142)	61.0 (51.9–70.1)	90.0 (82.6–97.4)	86.5 (80.6–92.3)	95.1 (88.9–100)	86.8 (81.1–92.4)	88.9 (83.7–94.1)
	p value	0.02	0.16	0.29	<0.01	0.31	0.19	0.19

Time is given in seconds. p value is computed on 12 radiologists. Other metrics are given in %. ACC, accuracy.

The clinical experiment verifies our model's clinical utility. Our model helps clinicians increase their diagnosis performance in almost all metrics and saves diagnosis time. We should also note that the radiologists in this clinical experiment only need to identify IAs, but the most common situation for radiologists is to examine a variety of diseases, in which case they may need more time, and the assistance of the model should also be very helpful.

Discussion

In this work, we collected a large IA segmentation dataset of CTA images with pixel-wise segmentation labels. Our internal dataset contains 1,338 CTA examinations consisting of 699,266 image slices and 1,489 IAs overall. Then we proposed a fully automatic segmentation technique that contains a global positioning network to provide global risk probability information and a patch-based local segmentation network to generate voxel-wise predictions. Our model can be directly used in different clinics and under different scan settings with no pre- or postprocessing procedure. The result shows that our GLIA-Net can identify over 80% of IA targets with only about four false-positives per case on the internal test set.

The improvement of our model can be explained by its global focus design. Different from most of the medical image segmentation networks directly transformed from those for natural images, our model makes use of the statistics of medical images as much as possible. Our design has several advantages in IA segmentation. First, the global positioning network combining with the patch-based local segmentation network leverages the full resolution of the CTA images without down-sampling the images to fit the memory limit. Otherwise, small targets like early-stage IAs or those tiny ones hiding in the corners of the brain may be lost. Second, such a global mechanism can provide local patches with a global location feature, which is important for many localization tasks such as identifying IAs in the brain, because such lesions have a strong tendency to locate in specific regions. Patch-based segmentation methods can work well for some segmentation tasks with subtle relation between the lesion region and its global position, such as segmentation on tumor pathology whole-slide images. However, IAs are related to the vascular network distributed in the brain, which makes the global position information important. Third, it is not rare for the brain CTA images to contain necks or even part of the lungs in real-world clinical applications. The global positioning network can be treated as an additional brain detection network, but it can give more information than just an object detection model and does not need additional annotations. Besides, a pyramid-weighted loss strategy was used in training, which can reduce the impact of the variability and uncertainty of expert labelers. The evaluation result shows that our technique is more capable in this IA segmentation task than other methods.

In clinical practice, the size of IAs also matters in the diagnosing procedure. Small IAs (such as smaller than 3mm) are relatively hard to identify, while large IAs are hardly missed. In our experiment, we also quantify this influence of IA sizes (see Table 5 and Figure S2). The experiment shows that the recall rate of IAs larger than 7 mm is about 20% higher than that of IAs smaller than 3 mm for our GLIA-Net. Although U-Net can achieve a compatible recall rate for targets smaller than 3 mm and larger than 7 mm, it generates over 30 false-positive predictions per case, which is not applicable for clinical usage. Our GLIA-Net can identify most of the aneurysms of different sizes while keeping the number of false-positive targets much smaller.

Table 5.

Detection performance for aneurysms with different sizes on the internal test dataset

Aneurysm Size (mm)	Metric	U-Net	HeadXNet	GLIA-Net
<3	recall↑	74.6 (70.0–79.2)	53.5 (33.6–73.5)	70.3 (64.1–76.5)
	FPs per case↓	35.9 (28.4–43.4)	15.6 (7.73–23.4)	5.22 (3.52–6.92)
3–7	recall↑	70.7 (67.3–73.8)	54.8 (36.0–73.7)	82.3 (77.8–86.7)
	FPs per case↓	36.5 (28.7–44.2)	18.2 (9.47–27.0)	5.05 (3.40–6.71)
>7	recall↑	91.8 (89.2–94.3)	67.1 (49.0–85.1)	90.6 (88.1–93.1)
	FPs per case↓	32.1 (24.6–39.7)	15.2 (8.31–22.2)	3.52 (2.32–4.72)

FPs per case is the number of false-positive targets predicted per case. The unit of the recall rate is %.

Although our GLIA-Net achieved promising results in IA segmentation and could assist radiologists and clinicians in their diagnosis, it also has some limitations. First, during the COVID-19 pandemic, performing a clinical study with more radiologists and larger clinical cases is much more difficult than usual. However, a continuous online validation enrolling more radiologists and more cases with the assistance of our model in clinical practice would better demonstrate the validity of our model in the future. Second, our model was only trained on CTA images. If other modalities, such as MRA images and DSA (the current gold standard for IA diagnosis), are adopted, the usage scope can be broader, and the accuracy may be higher.

The study of IA is important for the health of the public. In the future, beyond the identification and segmentation, predicting the rupture of IAs based on the knowledge of the location, size, and shape of IAs will be worth exploring. Therefore, GLIA-Net can not only assist clinicians in the diagnosis of IAs but can also encourage more implementations of artificial intelligence in healthcare.

Experimental procedures

Resource availability

Lead contact

Further information and requests for resources and materials should be directed to and will be fulfilled by the Lead contact, Feng Xu (feng-xu@tsinghua.edu.cn).

Materials availability

This study did not generate any materials.

Data and code availability

Original data have been deposited to our data server: http://39.98.209.108/seafile/d/34d94c4bc44a42fdb33d/. The internal and external datasets are only available for non-commercial purposes.

The GLIA-Net, together with the training and evaluation code generated during this study, are available at Github: https://github.com/MeteorsHub/GLIA-Net. The annotation tool used in the clinical study is also available at Github: https://github.com/MeteorsHub/MedLabelMe.

Methods

Deep learning usually uses artificial neural networks with millions and billions of parameters to fit a mathematical function to predict or describe a specific problem. The network needs a lot of training data to modify its parameters and generate outputs closer and closer to the real outputs using the gradient descent method. In our case, we used a deep neural network to segment every IA with different sizes, shapes, and locations in the large CTA image scans.

The whole pipeline of our method is shown in Figure 1. We use GLIA-Net (global positioning network) to segment IAs from CTA image scans. It takes the whole 3D CTA scan, called global image as input, which has a variant number of slices along the depth axis. GLIA-Net tiles many sub-images, or patches, from the global image with an overlap size to process, which are called the local images. GLIA-Net consists of two dataflow pathways: the global positioning network and the local segmentation network. The global positioning network is proposed to estimate the global probability distribution of IAs in the global image. The local segmentation network is focused on local images that are tiled from the global image and gives voxel-wise segmentation of the IA. During the training period, a global binary loss was added to the global positioning network and a local voxel-wise segmentation loss to the local segmentation network. Besides, we propose a pyramid-weighted loss that takes the variability and uncertainty of expert labelers into account in the loss design of the local segmentation network. The data preprocessing and network details are elaborated below and in the Supplemental experimental procedures.

Global positioning network

Because our GLIA-Net processes every local image patch one by one to segment IA, the global location information for the current patch will be lost if no additional global feature is adopted. Thus, a global positioning network is proposed to extract a global positioning feature and feed it to the local segmentation network. First, several 3D convolution blocks are applied to the global image input and extract a global feature map. This global feature map is expected to have global distribution information about how IAs locate in the brain and neighboring body parts. Then, a region-of-interest pooling layer⁴¹ is added to pool the feature map from the bounding box corresponding to the current local image location. The extracted global feature map for the current patch location is then reshaped to a fixed size by an adaptive maximum-pooling layer, and processed by another few 3D convolution blocks to generate the global location feature, which will be sent to the local segmentation network to assist in segmenting fine-scale targets.

In order to guide the global positioning network with an intermediate objective, we add a global feature classification cross-entropy loss. If there are any IA voxels in the current processing local patch, the global label is positive, otherwise negative. A 3D convolution layer, a global maximum-pooling layer, and a fully connected layer are added to the global position feature map, and a softmax cross-entropy loss is computed as the global positioning loss:

$${\mathcal{L}}_{Global}=-\left(z\ln \hat{z}+\left(1-z\right)\ln \left(1-\hat{z}\right)\right)$$

where $z$ and $\hat{z}$ are the ground truth label and the softmax probability prediction of the global positioning network output.

Local segmentation network

Our objective is the 3D segmentation of IA on CTA scans, which is a difficult segmentation task because the target region is quite small. So, our local segmentation network is applied to the local images under the original image resolution to avoid missing any small target. We modify U-Net¹⁸ to serve as our local segmentation network, which is an encoder-decoder structure. All the convolution and pooling layers are transformed into a 3D version, and we use residual network blocks⁴² to avoid gradient vanishing in our deep model. The encoder architecture consists of several levels of layers to extract image features in different scales. As for the decoder, we adopt transpose convolution layers to recover segmentation results step by step. Skip connections are used to link each layer level between the encoder and the decoder. The location feature extracted from the global positioning network is element-wise multiplied to all the skip connections before adaptive pooling layers to unify their shapes.

Because of the small target size compared with the input image, we use exponential logarithmic loss⁴³ that combines cross-entropy loss and dice loss for our local segmentation network:

$${\mathcal{L}}_{Local}={\omega }_{Dice}{\mathcal{L}}_{Dice}+{\omega }_{Cross}{\mathcal{L}}_{Cross}$$

where ${\omega }_{Dice}$ and ${\omega }_{Cross}$ are the weights for the dice loss and cross-entropy loss, respectively. The dice loss is used to minimize the shape difference of the segmentation output and the ground truth target:

$${\mathcal{L}}_{Dice}=E{\left(-\ln \frac{2y\hat{y}+\epsilon }{y+\hat{y}+\epsilon }\right)}^{{\gamma }_{Dice}}$$

where $E(\ast )$ is the function to compute the mean value for each voxel position. $y$ and $\hat{y}$ are the ground truth label and the probability prediction of the local segmentation network output. ${\gamma }_{Dice}$ is the parameter to control the nonlinearities of the loss function. $\epsilon$ is used as a smoothing factor.

Besides, we propose a pyramid weighting strategy for the cross-entropy loss. As mentioned above, the IAs are exceedingly small in the brain. This causes a problem for radiologists in the dataset annotation procedure: they may mark a precise IA position but with a relatively vague segmentation edge considering the few voxels in that region. In the meantime, human experts' annotation has high inter-observer variability,³² which means they may not share the same labeling standard on the lesion edges. To solve the label uncertainty problem for small segmentation regions (see details in Figures S3 and S5), we adopt a pyramid-weighted cross-entropy loss in our IA segmentation loss. The computation detail of the pyramid weight is shown in Figure S4. The weights of the loss for voxels near the center of IAs are high and those to the IA edges are low. In consideration of not affecting the size of the segmentation results of large targets, where the boundary is not the crucial component, we only compute pyramid weights for small targets less than 400 voxels, and the larger ones are set with a fixed weight. Then the loss function for cross-entropy is:

$${\mathcal{L}}_{Cross}=E\left({\omega }_p{\left(-\left(y\ln \hat{y}+\left(1-y\right)\ln \left(1-\hat{y}\right)\right)\right)}^{{\gamma }_{Cross}}\right)$$

where ${\omega }_p$ is the pyramid weight. To build the pyramid weights, we use minimum pooling with a 3 × 3 kernel to erode the label map step by step until the center of the region, and then sum up all the intermediate label maps. This training technique leads the network to focus on positive region locations with less attention to the lesion edges.

At last, we train our end-to-end model using a combined loss:

$${\mathcal{L}}_{Total}={\omega }_{Global}{\mathcal{L}}_{Global}+{\omega }_{Local}{\mathcal{L}}_{Local}$$

where ${\omega }_{Global}$ and ${\omega }_{Local}$ are the loss weights for global loss and local loss respectively.

Ethics approval and consent to participate

Ethical approval was obtained from the ethics committee at each institution. Informed consent was obtained from participants at each institution for ethical approval. In this study, a de-identification method was introduced to protect patient privacy by removing sensitive information (medical record number, account number, patient name, birthday, contact, address, etc.) manually from medical data.

Published: January 22, 2021