Quantifying Intracellular Particle Flows by DIC Object Tracking

Abstract

Label-free imaging techniques such as differential interference contrast (DIC) allow the observation of cells and large subcellular structures in their native, unperturbed states with minimal exposure to light. The development of robust computational image-analysis routines is vital to quantitative label-free imaging. The reliability of quantitative analysis of time-series microscopy data based on single-particle tracking relies on accurately detecting objects as distinct from the background, i.e., segmentation. Typical approaches to segmenting DIC images either involve converting images to those resembling phase contrast, mimicking the optics of DIC object formation, or using the morphological properties of objects. Here, we describe MATLAB based, single-particle tracking tool with a GUI for mobility analysis of objects from in vitro and in vivo DIC time-series microscopy. The tool integrates contrast enhancement with multiple modified Gaussian filters, automated threshold detection for segmentation and minimal distance-based two-dimensional single-particle tracking. We compare the relative performance of multiple filters and demonstrate the utility of the tool for DIC object tracking (DICOT). We quantify subcellular dynamics of a time series of Caenorhabditis elegans embryos in the one-celled stage by detecting birefringent yolk granules in the cytoplasm with high precision. The resulting two-dimensional map of oscillatory dynamics of granules quantifies the cytoplasmic flows driven by anaphasic spindle oscillations. The frequency of oscillations across the anterior-posterior (A-P) and transverse axes of the embryo correspond well with the reported frequency of spindle oscillations. We validate the quantitative accuracy of our method by tracking the in vitro diffusive mobility of micron-sized beads in glycerol solutions. Estimates of the diffusion coefficients of the granules are used to measure the viscosity of a dilution series of glycerol. Thus, our computational method is likely to be useful for both intracellular mobility and in vitro microrheology.

Significance

Differential interference contrast (DIC) time-lapse microscopy is widely used in cell and developmental biology as a label-free method involving minimal perturbation. Single-particle tracking tools specific to DIC microscopy are lacking. We have developed a computational tool for DIC object detection and tracking with a GUI and demonstrate its utility by tracking intracellular yolk granules in the crowded cytoplasm of one-celled Caenorhabditis elegans embryos. The frequency of the oscillatory flows of the granules compares well with that of spindle oscillation. Our method is also validated by tracking the Brownian motion of micron-sized beads to estimate the viscosity of solutions in vitro. This tool could have wider relevance for biophysical measurements of cellular mobility and subcellular mechanics.

Introduction

Label-free microscopy is widely used to study transparent cells and tissues. In particular, differential interference contrast (DIC) or Nomarski (1) and phase-contrast microscopy (2) are standard modes built into biological microscopes to generate image contrast using inherent features such as the anisotropy of refractive index and density. Although fluorescence microscopy offers the advantage of molecular specificity, the phototoxicity resulting from such an approach in live imaging can alter cell physiology (3). Because of the inherent advantages of reduced light exposure and minimal intervention in the sample, label-free in vivo microscopy combined with computational image analysis continues to be relevant. Image segmentation of phase-contrast images is relatively simpler because it involves distinguishing dark objects against a bright background. As a result, a wide variety of computational methods have been successfully developed to quantify cellular and subcellular objects in phase-contrast images (4, 5, 6, 7). Objects in DIC images, on the other hand, are represented as a combination of light and dark regions, giving a pseudo-three-dimensional effect, with a typically gray background. Segmentation of such images is more involved, with previous approaches relying on either converting them to “pseudophase” (8) or extracting low-level information such as gradient (9,10), shear direction (11,12), spatial filtering using “Mexican hat” kernels to denoise combined with region-max to segment (13), and brightness fluctuations (14). Although shape-specific methods have been successfully used for tracking the dynamics of filopodia (15) and microtubules (MTs) (14,16), they are limited in their utility. Some alternative methods to particle tracking include particle image velocimetry, which for example, has been used to quantify intracellular flows by occurring after yolk-granule mobility in DIC images (17), optical flow methods (18), and differential dynamic microscopy based on intensity fluctuation statistics in images (19) that have been used to measure ciliary beat frequencies in vivo (20). Although such methods are robust and work on in vivo data, ignoring the individual identity of objects potentially could result in missing out in changes in as a function of position or time. This in turn could lead to ignoring important local effects that might be functionally related to in vivo heterogeneity in mobility. The absence of a robust and general solution to detect intracellular structures in DIC at high particle densities has hindered further quantification of label-free images.

Caenorhabditis elegans embryos are ideal samples for in vivo computational imaging in DIC because they are optically transparent and lack pigments. DIC-microscopy-based mutational screens have been used to understand embryonic cell divisions (21) and spindle mechanics (22). Algorithms used to identify features in C. elegans embryos include a shortest path method to automatically identify embryo stages and quantify boundary dynamics during divisions (23,24). Similarly, active contours have been used to track spindle dynamics (25,26). The analysis of intracellular dynamics by segmentation-based approaches has been restricted to quantifying centrosome positional dynamics (22,27,28). At the same time, detailed theoretical models of the mechanics anaphase spindles and their oscillations in C. elegans based on molecular motors and MTs have been developed (29, 30, 31). However, a comparison between theoretical predictions and experiments continues to be limited by the methods available for noninvasive measurement of intracellular mechanics. Although label-free quantitative microscopy could address this need, it requires the development of methods for precise segmentation in a crowded environment from such images.

Here, we describe a DIC-object-tracking (DICOT) method that combines a novel filtering approach that we refer to as scaling of Gaussian (SoG). Combined with a distance-based, single-particle tracking approach, we employ it to analyze in vivo cytoplasmic flow dynamics in a one-cell C. elegans embryo and as a means of estimating viscosity from bead diffusion in glycerol solutions.

Materials and Methods

DIC segmentation and tracking

We implement multiple filters combined with automated threshold detection to segment objects in each frame, followed by a minimal distance tracking method to connect object and build tracks. As a first step, the user chooses one of the filters: Gaussian, difference of Gaussian (DoG), inverse Laplacian of Gaussian (iLoG), or an SoG. The SoG filter is calculated as a difference between a Gaussian function h_G with a filter of size k_size and a standard deviation σ and the following scaled mean:

$$h_{SoG}=h_G-\langle h_G\rangle \left(\lambda -\varphi \right),$$ (1)

where ϕ is the strength of the difference-based scaling by the mean and λ is a switch parameter typically set to 1 for DIC images. A value of λ = −1 is useful for dark objects against a bright background. The steps involved in the process of filtering and segmentation are described in the Algorithm Box (Supporting Materials and Methods) and Fig. 1. The filter is a modified Gaussian and comparable with a DoG filter because of the subtraction operation. Of the four user-provided inputs to SoG, two are easily determined by the user with λ = 1 for DIC images and the kernel size k_size estimated from the characteristic size of the objects, with the only free parameters being the standard deviation σ of the Gaussian and sensitivity (S) factor ϕ for scaling by the mean, which control the spread and height of the filter, respectively. The filter is implemented in MATLAB (The MathWorks, Natick, MA).

Figure 1.

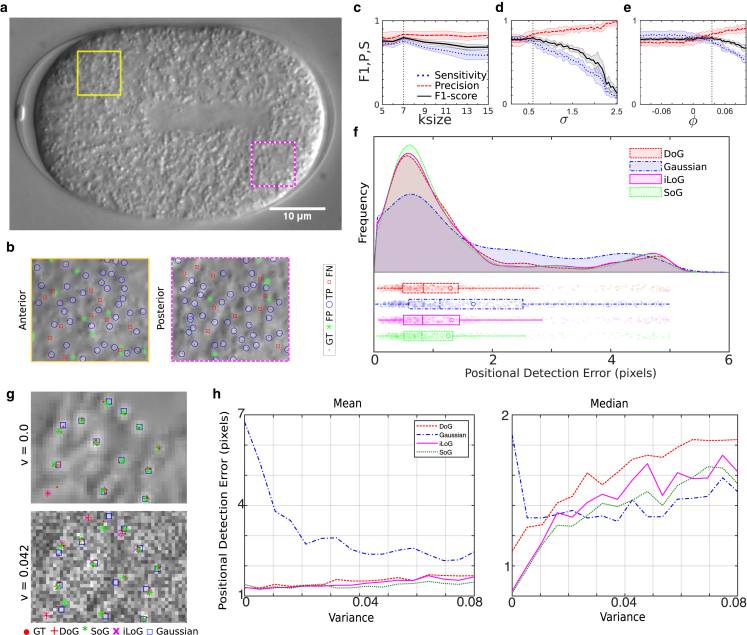
Detecting yolk-granules in a C. elegans embryo in DIC. (a) The yolk granules of a C. elegans embryo in the one-celled stage in DIC microscopy from the mid-plane are segmented using a novel scaling of Gaussian (SoG) method combined with automated thresholding. Scale bar, 5 μm. (b) The workflow is described using a representative region of interest (ROI) of the embryo image (box with dashed blue line from (a)); shown is a filtered image by convolving the image with an SoG filter (parameters: k_size = 9 and σ = 1.25), resulting in enhanced contrast; shown is a segmented image obtained by thresholding by a modified Otsu’s method; and centroids of detected objects (asterisk) are overlaid on the original image. To see this figure in color, go online.

The filtered image is contrast adjusted by scaling between the minimal and maximal values of the histogram and segmented by using the p^th root of the value output by Otsu’s method, τ. We find $\sqrt{\tau }$, i.e., p = 2, to be optimal for the objects we have tested.

Segmentation results in centroids of multiple granule (Fig. 1 b) that are connected to form tracks based on two input parameters: 1) search radius (r_s) to define the local neighborhood that depends on particle velocity, and 2) minimal time frames (T_min), which a track spans. The pair-wise distance d_j(Δt) between every j^th centroid in successive frames t and t + Δt are linked if the minimal distance is less than the search radius r_s. Centroids that do not form a part of any trajectory are treated as new start points. To avoid artifacts due to poor statistics, short tracks are eliminated if they span less than T_min number of frames. Image noise was simulated as multiplicative speckle noise with zero mean and increasing variance using the inbuilt function imnoise in MATLAB (The MathWorks), and the error of positional accuracy was tested by finding the distance between the ground truth (GT) and the automated detection in a representative frame from a DIC image time series of the C. elegans embryo.

Embryo time series

Multiple time series of C. elegans N2 embryos (N2_15, N2_18, and N2_20) were taken from a published database (http://www.ens-lyon.fr/LBMC/NematodeCell/2010/12/) reported by Valfort et al. (32). Typically 450 frames (Δt = 0.5 s) were analyzed by selecting a subset of frames corresponding to the onset of anaphase spindle oscillations.

Microscopy of bead suspensions in glycerol

Glycerol (99% GC; Sigma-Aldrich) solutions in water with increasing concentrations 0, 10, 20, 30 and 40% (vol/vol) were used to resuspend monodisperse polystyrene beads (National Institute of Standards and Technology Traceable Particle Size Standards; Bangs Laboratories, Fishers, IN) of a diameter of 1 μm. For diffusion measurements, the beads were diluted 1:100 (vol/vol) to get sufficient separation, so their mobility can be considered to be independent of crowding effects. The solution containing the bead suspension was flowed into a double-backed tape chamber (dimensions: 1 cm × 1 cm × 0.01 cm) sandwiched between a slide and a coverslip (Medicos Supplies, Pune, India). Samples were imaged using a 40× (NA 0.9 or 0.65 ELWD) lens on a Nikon Eclipse Ti-E inverted microscope (Nikon, Tokyo, Japan) at 30°C by a temperature control system (Okolab, Pozzuoli, Italy). Images were acquired every 0.5 s for 1 min with an Andor Clara2 CCD camera (Andor Technology, Belfast, UK).

Data analysis

The yolk granules were classified into four regions based on the apparent axis along which they were maximally displaced: anterior (A), posterior (P), or one of the transverse axes—transverse 1 (T1) or transverse 2 (T2). The x- and y-positions with time were used to calculate the distance from their respective origins in x (Δx) and y (Δy), and the distance was averaged for each region (Δy for the A-P axis and Δx for the T1-T2 axis). The frequency of oscillation was estimated using a fast Fourier transform. An average curve was estimated for each region as follows:

• 1)Shift the origin of the position time series of the yolk granules, r_j,t (where r is either the x- or y-position), with respect to their initial positions in x (Δx) and y (Δy), resulting in a new series $r_{j,t}^{\text{∗}}$:

$$i=0\{\begin{array}{ll}{r}_{j,t}^{\text{∗}}=\hfill & r_{j,t}-r_{j,1}\hfill \\ {\overline{r}}_{\left(i=0\right)}=\hfill & \frac{{\sum }_{j|t}{r}_{j,t}^{\text{∗}}}{n_{j|t}}\hfill \end{array},$$ (2)

• where n is the number of tracks at a given time point t and j represents the identity of the track.

• 2)Calculate the average time-series ${\overline{r}}_i$ for the i^th iteration by estimating the deviation of every particle from the average curve obtained at the previous iteration (i − 1), subtracting the mean deviation $\left(\langle \Delta r_{j,t}\rangle \right)$ and averaging over each track at a given time point (n_j|t) for all time points as follows:

$$i>0\{\begin{array}{ll}\Delta r_{j,t}=\hfill & r_{j,t}-{\overline{r}}_{i-1}\hfill \\ r_{j,t}^{\text{∗}}=\hfill & r_{j,t}-\langle \Delta r_{j,t}\rangle \hfill \\ {\overline{r}}_i=\hfill & \frac{{\sum }_{j|t}{r}_{j,t}^{\text{∗}}}{n_{j|t}}\hfill \end{array}.$$ (3)

• 3)Consider the curve to be the optimal average curve and stop the iteration when the global deviation across all tracks N is smaller than a threshold value δ:

$$i++,\text{iff}\{\frac{{\sum }_j^N\langle \Delta r_{j,t}\rangle }{N}\ge \delta .$$ (4)

We find the global deviation saturates for δ < 10⁻⁴ within 5–10 iterations. All data analysis was performed using a code written in MATLAB R2017b (The MathWorks).

Estimating the diffusion coefficient of bead mobility

The effective diffusion coefficient (D) of bead motility was estimated from a fit to the mean-square displacement (MSD) plot as a function of time interval (t) using methods described previously (33,34). The anomalous diffusion model MSD = 4 × D_eff × t^α was applied to the MSD data using a Levenberg-Marquardt nonlinear least-square routine implemented in both MATLAB (The MathWorks) and SciPy (Python 3.6) (35). The anomaly parameter α was found to be ∼1, indicating diffusion without drift or restriction.

As an alternative method to cross-check our estimates, we measured the diffusion coefficient of beads based on an approach originally described by Perrin (36). The displacement along the x (Δx) and y axes (Δy) for every successive step of each trajectory were plotted in a frequency histogram and fit to a standard Gaussian expression:

$$P\left(\Delta x\right)=\frac{1}{\sigma \sqrt{2\pi }t}{\text{exp}}^{-\Delta x^2/2{\sigma }^2},$$ (5)

where σ is the standard deviation for one-dimensional diffusion that is related to the diffusion coefficient (D) by σ = $\sqrt{2Dt}$.

The viscosity η was estimated from Stokes-Einstein relation D = k_BT/6πηr, where the radius of the beads (r) is 0.5 μm and $k_{B}T$ is the product of Boltzmann’s constant and temperature (K), taken as 4.1 pN-nm.

Code performance and availability

A typical time series with 450 frames of 450 × 300 pixels required 5–10 min to process with 200 particles per frame on a Linux Workstation with two Intel Xeon processors (2.20 GHz) and 64-GB RAM. The program has a GUI-based, user-friendly interface (Fig. S1) compatible with MATLAB2019b and higher (The MathWorks). The source code has been made OpenSource and can be accessed here: https://github.com/CyCelsLab/DICOT. Additionally, we have also released a command-line tool with the source code here https://github.com/CyCelsLab/DICOT_cmd, compatible with MATLAB2017b and higher (The MathWorks), to allow for rapid modifications of the program and the easy addition of new filters.

Results and Discussion

Testing the detection accuracy of intracellular granules in DIC images

The quality of single-particle tracking (SPT) depends on the accuracy of the object detection. To achieve high-accuracy tracking, we test multiple filtering approaches, Gaussian, inverse Laplacian of Gaussian (iLoG), difference of Gaussian (DoG), and the scaling of Gaussian (SoG). These filters are then combined with segmentation by thresholding based on Otsu’s method to detect objects in DIC images. The SoG filter scales a standard Gaussian filter (h_G) with the mean $\left(\langle h_G\rangle \right)$ and an S factor ϕ as follows:

$$h_{SoG}=h_G-\langle h_G\rangle \left(\lambda -\varphi \right).$$ (6)

When the image contains bright objects against a dark background, typical for both DIC and fluorescence, image λ is set to 1, whereas it is set to −1 for dark objects against a bright background (Fig. S3). The S factor ϕ is used to enhance the degree of contrast between the fore- and background. The SoG filter is a simpler version of the DoG filter h_DoG = h_G1(σ₁) − h_G2(σ₂), where h_G1 and h_G2 are two Gaussians, and σ₁ and σ₂ define the respective spread. For a DoG filter when σ₂ $\gg$ σ₁, the difference approximates SoG (Fig. S2). At the same time, the LoG filter, based on the second derivative of a Gaussian, can also be mapped to DoG under specific conditions of Gaussian filters (37) due in part to the fact that they are based on a Gaussian. However, the simplicity in using SoG scaling on a Gaussian by a scalar value by the use of a single S parameter ϕ and estimation of filter size from object size, as compared with multiple or derivatives of Gaussians, suggests a simplicity that could be more user-friendly for optimization in the analysis of diverse experimental data sets. The filtered images are thresholded based on a modified Otsu’s method (38), resulting in object detection.

The detection method appears to identify the majority of birefringent yolk granules in a DIC image time series of C. elegans embryos as identifiable by eye (Fig. 1 a). The enhanced contrast achieved by SoG filtering allows object segmentation by automated thresholding (Fig. 1 b). To quantify the extent of correctly detected yolk granules, we have used six randomly selected frames in the time series in two representative regions of interest (ROIs), one anterior and one posterior, to account for any spatial differences (Fig. 2 a; Fig. S4) and marked yolk granules manually to serve as the GT of detection (Fig. 2 b). The output from DICOT analysis was then classified based on the Euclidean distance of the granule coordinates (x-y-positions) detected by the algorithm to the “true coordinate” into the following classes.

Figure 2.

P of yolk-granule detection in DIC. (a) ROIs from the anterior (A) (line) and posterior (dashed line) regions of a DIC image time series of a C. elegans embryo were used to estimate (b) the ground truth (GT; solid circle) through manual annotation of granules and classify detections based on the algorithm as either true positives (open circle), detected by the algorithm, as well as manually false positives (asterisk), those identified by the algorithm but not manually, and false negatives (open square), those that were identified manually but the algorithm failed to detect. (c–e) The mean $\pm$ standard deviation (SD) from n = 6 ROIs measuring S (dotted line, Eq. 7), P (dashed line, Eq. 8), and the F1 score (solid line, Eq. 9) of detection are plotted to examine the effect of three different parameters input to DICOT, namely (c) the filter size k_size (with σ =0.5949, ϕ = −0.0354), (d) the standard deviation of the filter σ (k_size = 7), ϕ = 0.0354), and (e) the S factor ϕ (with σ = 0.5949, k_size = 7). The fixed values were taken from a systematic scan of all three parameters (Fig. S6) and are marked with a vertical dotted line. (f) Shown is the frequency distribution of the positional detection error in pixels based on filtering by either Gaussian (dash-and-dot line), inverted iLoG (solid line), DoG (dashed line), or SoG (dotted line) is plotted with (bottom) the box-plot representing the data scatter. Here, the following symbols have the described meaning: open circle, mean; midline, median; and whiskers, minimum and maximum. (g) The effect of multiplicative speckle noise on positional detection error was examined for a range of variance values of the noise function. Two representative images of variance 0 and 0.042 were filtered based on the optimal parameters for detection by filtering and segmentation based on either Gaussian (open circle), iLog (cross), DoG (plus sign), or SoG (asterisk) filters. The error is the distance from the GT (solid circle). (h) The mean (left) and median (right) positional detection error for increasing variance of noise ranging is plotted. To see this figure in color, go online.

True positives (TP)

The distance of the centroid identified by the algorithm lies within a threshold (τ_dist) distance of the interactively annotated point. A τ_dist of two pixels was chosen to account for human error while selecting centroid of granule.

False positives (FP)

Detections obtained from the algorithm at a distance to the GT greater than τ_dist are classified as false positives.

False negatives (FN)

All manual annotations that were not detected by the algorithm are classified as false negatives.

To quantify how well DICOT works at object detection, we estimate three variables: sensitivity (S), precision (P), and the F1 score. S is defined as the ratio of correct detections by the algorithm (TP) and all detections both true and false, as described by the following expression:

$$S=\frac{TP}{TP+FN}.$$ (7)

An alternative measure, P is the fraction of correctly classified detections out of total detections from the algorithm as given by the following:

$$P=\frac{TP}{TP+FP}.$$ (8)

Finally, the F1-score (F1) combines both measures of P and S as follows:

$$F1=\frac{2\times P\times S}{P+S}.$$ (9)

We find the S, P, and F1 are affected similarly by kernel size k_size and σ (Fig. 2, c and d), whereas ϕ < 0 is optimal for S and F1 but not P (Fig. 2 e). Increasing the filter size (k_size) results in reduced S, whereas P was maximal for values greater than six pixels, and the F1 score is optimal for k_size between five and seven pixels. Based on a comparison between manual detection (Fig. S5 a) with SoG, Gaussian, inverted LoG- and DoG-based image filters (Fig. S5, b–d) of qualitatively SoG are comparable with LoG and DoG filtering (Fig. S5 e). Evaluation of the P, S, and F1 score, compared for two different methods of scoring, suggests that the SoG and DoG are comparable in their performances (Fig. S6, a–c). In contrast, we find the statistics of positional detection error is the lowest for SoG compared with the other filtering methods tested in terms of mean, median, and outliers (Fig. 2 f). To avoid any biases, we scanned multiple parameters for each filter systematically across a range of comparable values and used those parameters that maximized the F1 score (Fig. S7, a–d). Although the error resulting from filtering by SoG, iLoG, and DoG is comparable, we find increasing “noise” in the image (Fig. S8) changes the positional detection error with SoG and iLoG, showing the smallest error and greater robustness compared with the other filters (Fig. 2, g and h). This suggests that our method is optimal for the analysis of in vivo time series of C. elegans embryos. We proceeded to track the granule mobility and quantify the flow in the cytoplasm.

Oscillatory dynamics of yolk granules at anaphase

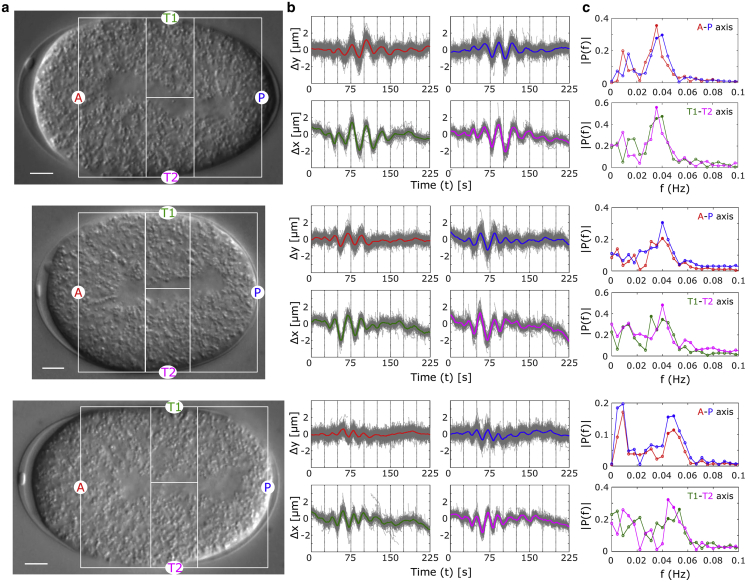
One-celled embryos of C. elegans in the anaphase experience cytoplasmic flows in the midplane driven by MT-motor interactions observed in terms of yolk-granule movement (31,39). This is driven by the oscillatory nature of the spindle movement, which has been quantified in previous work (25,26,31,32). Because yolk granules are thought to be passively mobile in the cytoplasm (22), our approach to particle tracking could provide a spatial map of this cytoplasmic mobility driven by spindle oscillations. We can successfully track multiple DIC image time series of the midplane of these embryos and classify them into anterior (A), posterior (P), or two transverse regions, T1 and T2 (Fig. 3 a; Video S1), because granules remain largely relatively restricted to a region of the embryo. The time-dependent displacement of granules along either the y axis for regions A and P, or along the x axis for T1 and T2, display oscillatory behavior that is captured by an average curve (Fig. 3 b) obtained by iterative optimization to individual trajectories (Fig. S9). The oscillations along the two axes A-P and T1-T2 are out of phase, as expected from spindle geometry and the incompressible nature of the cytoplasm. The dominant frequency of oscillation based on Fourier analysis of average trajectories along both axes is 40 mHz (Fig. 3 c). Our estimate is based on the statistics of ∼10² trajectories of yolk granules per cell. This estimate matches the reported oscillatory frequency of 40 mHz measured using pairs of centrosomes in each cell (25,26,32). Thus, our approach to yolk-granule tracking provides detailed spatiotemporal information and better statistics as compared with centrosome movement to understand the mechanics of cytoplasmic flows.

Figure 3.

In vivo microrheology of C. elegans yolk-granule mobility. (a) Three representative DIC image time series of the midplane of a C. elegans embryo taken from the Valfort et al. data set (32) (N2 embryo time-series N2_15, N2_18, and N2_20 taken from http://www.ens-lyon.fr/LBMC/NematodeCell/2010/12/) are marked to highlight the regions of the embryo in which yolk-granule mobility was analyzed: the anterior (A; red), posterior (P; blue), and two transverse regions, T1 (green) and T2 (magenta). Scale bar, 5 μm. (b) The change in position along x (Δx) across the transverse axes and in y (Δy) across the A-P axes of individual granules are plotted as a function of time (gray lines). Colored lines represent the mean profiles for the A (red), P (blue), T1 (green), and T2 (magenta) regions. (c) The probability of oscillatory frequencies, P(f), is plotted from mean distance-time data for A (red), P (blue), T1 (green), and T2 (magenta) regions (open circle). Solid circles indicate the dominant frequencies. For color references, please refer to the online edition. To see this figure in color, go online.

Video S1. C. elegans Embryos with Tracked Granules

The granules in a time series of C. elegans first embryonic division are tracked (blue dot - current position of granule, red line - trajectory of granules) using DIC tracking method. The time series have been described by Valfort et al. (32) (Image-Database). Scale: 5 μm; Δt: 0.5 s.

Microrheology of beads in glycerol solutions

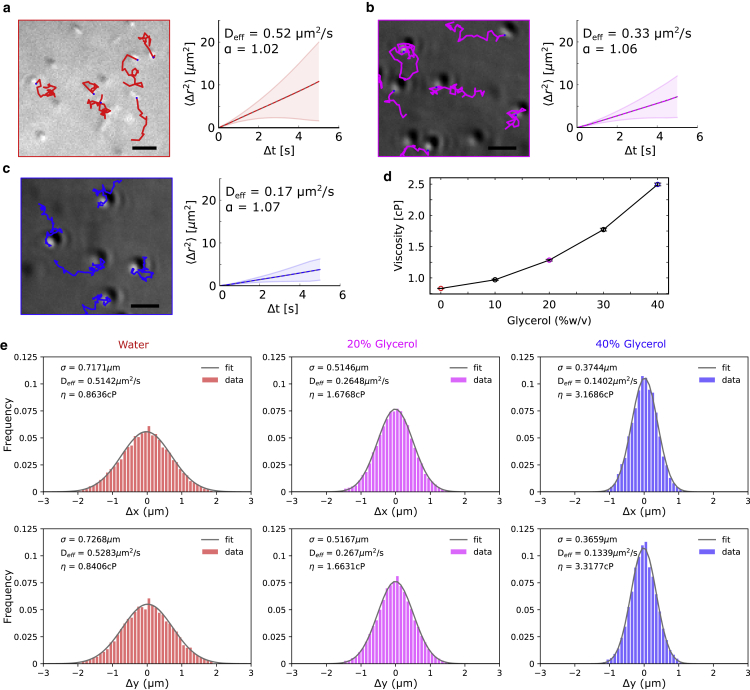
We test the accuracy of our approach to object tracking by quantifying the diffusive mobility of 1-μm polystyrene beads in multiple dilutions of glycerol solutions (0–40% v/v) from DIC image time series (Videos S2, S3, and S4). From the trajectories of the bead mobility, we estimated the MSD $\left(\langle r^2\rangle \right)$ as a function of time t of multiple beads and fit it to a model of diffusive mobility $\langle r^2\rangle$ = 4Dt^α (Fig. 4, a–c) as described in our previous work (34). The value of the anomalous diffusion exponent α obtained from fitting is ∼1, confirming that bead mobility is diffusive. The diffusion coefficient D is then used to estimate the viscosity η (Fig. 4 d) based on the Stokes-Einstein relation η = k_BT/D6πr, where r is the granule radius and k_BT the thermal energy scale. We also estimated the value of viscosity from the same trajectories by alternatively following a method originally described by Perrin (36) by fitting Gaussian functions to the one-dimensional displacement along x and y axes (Fig. 4 e). Both methods yield viscosity values that are consistent with published values (40) for glycerol solutions (Fig. S10). Thus, we believe our method can serve as a convenient tool for microrheology and mobility of label-free DIC imaging of micron-sized objects, both intracellular and in vitro.

Figure 4.

Microrheology of glycerol solutions from bead mobility. (a–c) 1-μm-diameter beads suspended in increasing concentrations of glycerol were imaged to measure the bead mobility. The beads were tracked (colored lines) and the MSD ± SD (line with gray area indicting SD) calculated. Track colors correspond to glycerol concentrations (%v/v) in water: (a) 0% (red), (b) 20% (magenta), and (c) 40% (blue). Scale bar, 2 μm. (d) Shown is the viscosity estimated from the diffusion of 1-μm-sized beads in solutions of glycerol concentrations ranging from 0 to 40%. Values represent mean $\pm$ SEM (n = 10 ROIs). (e) Histograms of the instantaneous displacement of beads in X and Y obtained from tracking were fitted to a standard Gaussian. The effective diffusion coefficient D was then estimated based on σ = $\sqrt{2Dt}$ from the Gaussian fit and the Stokes-Einstein relation used to estimate viscosity η. To see this figure in color, go online.

Video S2. Beads Diffusing in Water

A representative time series of 1 μm beads diffusing in water tracked (blue dot - current position of granule, red line - trajectory of granules, yellow numbers - particle identifier) using SoG filter. Scale: 10 μm; Δt: 0.5 s.

Video S3. Beads Diffusing in 20% Glycerol

A representative time series of 1 μm beads diffusing in 20% (w/v) glycerol tracked (blue dot - current position of granule, red line - trajectory of granules, yellow numbers - particle identifier) using SoG filter. Scale: 10 μm; Δt: 0.5 s.

Video S4. Beads Diffusing in 40% Glycerol

A representative time series of 1 μm beads diffusing in 40% (w/v) glycerol tracked (blue dot - current position of granule, red line - trajectory of granules, yellow numbers - particle identifier) using SoG filter. Scale: 10 μm; Δt: 0.5 s.

Conclusions

The yolk-granule mobility in C. elegans embryos demonstrated here suggests the frequency of oscillation of granules matches that of the spindle movement. Although it once more suggests the passive nature of yolk-granule mobility, it also provides a spatiotemporal readout of the forces that drive spindle motility. The previous estimates of the viscous drag acting on the spindles (22,41) and more recent measurements of the viscoelastic nature of the cytoplasm (42) suggest the relevance of such a tool for quantifying cytoplasmic flows. Combining the measurement of intracellular yolk-granule mobility with spindle movement could improve our understanding of the mechanobiology of asymmetric cell division. Indeed, the proliferation of deep-learning methods in cell image analysis, as exemplified by the effective use of U-nets for segmentation from bright-field images (43), suggests the approaches we describe in combination with learning approaches could further improve detection and analysis. Our implementation of the tool as a GUI with interactive parameter optimization as well as choice of multiple filters is likely to allow for use on multiple data sets. In conclusion, our approach represents a general method for segmentation and tracking of both in vitro and in vivo DIC microscopy data. In the future, this tool could improve our understanding of subcellular mechanics using label-free microscopy for cellular and developmental processes, not just limited to the C. elegans embryo.

Author Contributions

Y.K.J., R.C., and D.K. wrote the software. Y.K.J., D.K., and R.C. analyzed and validated it. Y.K.J. and C.A.A. performed the experiments. C.A.A. wrote the manuscript, supervised the project, and acquired the funding.

Editor: Jason Swedlow.