Abstract
Diffusion is a fundamental mechanism for protein distribution in cell membranes. These membranes often exhibit complex shapes, which range from shallow domes to elongated tubular or pearl-like structures. Shape complexity of the membrane influences the diffusive spreading of proteins and molecules. Despite the importance membrane geometry plays in these diffusive processes, it is challenging to establish the dependence between diffusion and membrane morphology. We solve the diffusion equation numerically on various static curved shapes representative for experimentally observed membrane shapes. Our results show that membrane necks become diffusion barriers. We determine the diffusive half-time, i.e., the time that is required to reduce the amount of protein in the budded region by one half, and find a quadratic relation between the diffusive half-time and the averaged mean curvature of the membrane shape, which we rationalize by a scaling law. Our findings thus help estimate the characteristic diffusive timescale based on the simple measure of membrane mean curvature.
Significance
Diffusion is an integral process for distributing proteins throughout biological membranes. These membranes typically have complex shapes and structures, often featuring elongated shapes such as tubes or necklace-like pearls. The diffusion process on these shapes is significantly different from the well-studied two-dimensional diffusion on a planar substrate. We use numerical simulations to study the characteristic diffusion time on different static membrane shapes, and we observe a slowing down of the diffusion dynamics on strongly curved shapes. Our results provide a simple relationship to estimate the characteristic diffusion timescale based on the membrane shape.
Introduction
Diffusion is a fundamental transport mechanism that plays a key role in many biological processes (1,2). For example, diffusion is the main mechanism for transport and mixing of components in primitive cells (3); it facilitates the formation of protein oligomers and lipid-protein assemblies associated with the metabolism and signaling in cells (4, 5, 6). It also allows the formation of protein gradients needed to establish cell polarity and trigger morphogenesis (7). Experiments have revealed that diffusion is a mechanism responsible for the fast spreading of macromolecules on the membrane surface (8). These observations are consistent with the fluid nature of biological membranes, which allows the displacement of anchored molecules and transmembrane proteins (9).
The transport of proteins and other molecules often occurs in membranes with complex shapes, which can be the result of biological process that require membrane deformation, such as endo- and exocytosis (10) or communication pathways for material transport between the Golgi apparatus and the endoplasmic reticulum, which require the formation of tube networks (11). The membrane shape is one of the factors that determine the distribution of diverse membrane inclusions such as transmembrane proteins. Theoretical models of biological membranes, in which the membrane was treated as a continuous surface, have proposed a coupling between the membrane curvature and the protein density (12). This coupling is the result of the interactions between the proteins and the membrane and is related to the intrinsic shape of the protein. The protein structure can induce a change in the spontaneous curvature of the membrane and modify its bending energy (13,14). Experiments have shown that transmembrane proteins with intrinsic curvature (such as potassium channels, KvAP, which resemble a cone) are enriched in highly curved nanotubes, whereas the water channel AQP0 (which resembles a cylinder) had the same density in a planar and in a tubular structure (15). Membrane curvature is also an important factor determining the distribution of transmembrane receptors at the highly curved leading edge of lamellipodia (16). Further, theoretical studies predicted a membrane-curvature-mediated attractive interaction between conical inclusions (17), leading to a higher density of proteins in a curved membrane.
Many effects can influence the diffusion dynamics on biological membranes, e.g., cytoskeletal barriers (18), molecular crowding (19), membrane fluctuations (20), and the considerable deformation of the plasma membrane revealed by electron microscopy (21). Theoretical estimates of the diffusion coefficient of molecules on a curved surface, mimicking the microvilli observed in plasma membranes, revealed a slower diffusion as compared with an ideal planar surface (22). The shape of the diffusing molecule can affect the magnitude of the diffusion coefficient, for which the Saffman-Delbrück theory (23,24) relates the diffusion coefficient with the viscosity of the surrounding media, the membrane thickness, and the size of the protein. This theory reveals a weak, logarithmic dependence with the protein size. Subsequent experimental studies suggested a stronger dependence between the molecule size and its diffusion coefficient (25) and also suggested a dependence between the diffusion coefficient of certain transmembrane proteins and surface tension (26). Moreover, a curvature-dependent diffusion coefficient can be obtained assuming that the membrane curvature induces changes of the membrane thickness (27). However, these results cannot be generalized to strongly curved membrane shapes.
It has been shown that the macroscopic shape of the membrane itself affects how proteins or molecules move. Experiments have revealed that the radius and length of tubes influence the time required to distribute proteins (28). The same observation was made by a theoretical approach in which the diffusion equation is solved on tubular shapes, which shows agreement with the equilibration time found in experiments (29). However, biological membranes may exhibit a variety of shapes that differ significantly from a cylindrical tube; e.g., membranes form pits in early stages of endocytosis, and nearly spherical vesicles joined with the surrounding membrane by a narrow neck at later stages (30,31). Membranes can also form concatenated buds joined by narrow bridges or necks (32, 33, 34). Numerical simulations of diffusion on pearled structures have shown that the pearled geometry, together with diffusion barriers created by certain proteins, is responsible for the sequestration of cargo in the buds (32). These results suggest that the membrane geometry has an important effect on the lateral diffusion of molecules and proteins (35, 36, 37).
The diffusion process on a curved two-dimensional surface depends on the local curvature and is thus more complex than diffusion on a flat surface. For small membrane deformations, theoretical studies have shown that an effective diffusion coefficient can be derived in terms of the surface curvature (38). A generalized theoretical treatment of the diffusion on an arbitrary surface gives a solution of the diffusion equation as an expansion around the solution on a flat surface. The coefficients are highly complex functions of the curvature, only simplified in cases in which the surfaces have constant Gaussian curvature (39), which in general is not the case for biological systems.
The wide range of shapes of biological membranes makes it challenging to obtain a generalized analytical solution for the diffusion equation on a generic surface. To understand how proteins diffuse on complex membrane shapes such as domes, tubes, and pearling structures, we develop a mathematical model for their diffusive dynamics on these static shapes. To decouple the effect of membrane morphology on diffusion-mediated protein distribution from the effects derived from protein-membrane curvature interactions (13,14,17,40), we make the following assumptions: the membrane shape is static, the proteins neither bind to nor unbind from the membrane, the proteins neither modify the membrane bending energy nor its shape (20), and we neglect the lipid-composition-mediated interaction between proteins (41). Together, this allows us to treat the protein species as a continuous field in space that diffuses on the fixed membrane shapes. The model is solved numerically, with the numerical simulations allowing us to describe the characteristic time it takes to diffuse away from a curved region and discuss the implications of the Gaussian and the mean curvature in terms of the half-time, i.e., the time required for the protein density to reduce by one half in the budded region.
Methods
Parameterization of the membrane
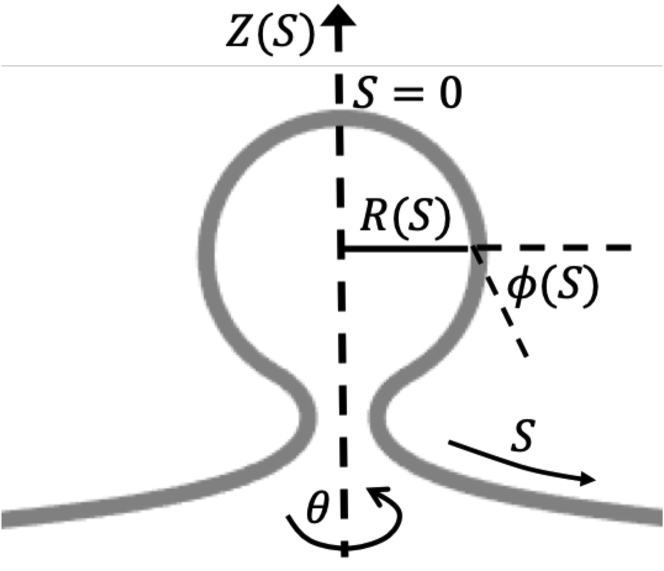
The membrane shapes that we consider here are axially symmetric. All shapes are parametrized by the arc length S measured along the curved surface and the tangent angle ϕ as shown in Fig. 1. In this geometry, the variables R(S), Z(S), and the membrane area A(S) satisfy the following differential equations:
| (1) |
| (2) |
and
| (3) |
where ( )′ . The mean curvature H of the membrane in the arc-length parameterization is given by (42)
| (4) |
Figure 1.
The membrane surface parameterization in axisymmetric coordinates, where S is the arc length measured along the membrane, R(S) is the radial coordinate, ϕ(S) is the angle that the curved membrane forms with respect to the horizontal R-axis, and Z(S) is the height of the membrane. The angle θ is the rotation around the symmetry axis.
Membrane geometry
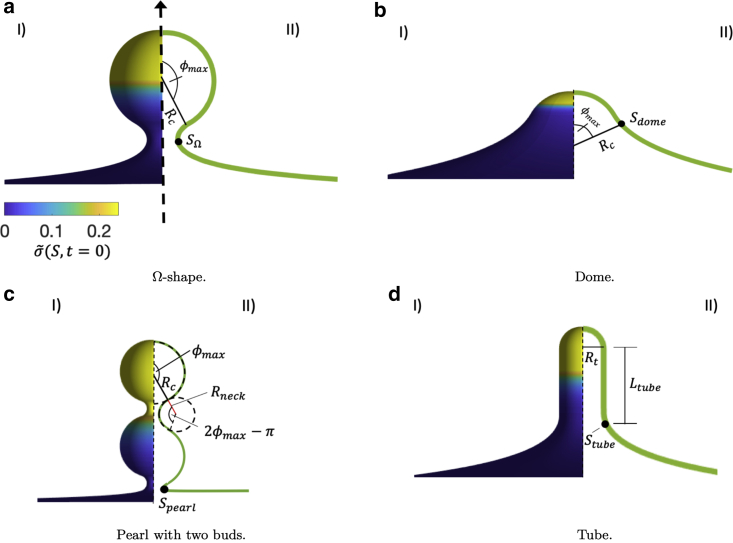
The membrane shapes that we consider here are shown in Fig. 2: an Ω-shape (Fig. 2 a), a dome shape (Fig. 2 b), pearled structures with different numbers n ∈ [2, 3, 4] of pearls (Fig. 2 c), and cylindrical tubes capped by a half sphere (Fig. 2 d). Each shape is composed of two regions: the inner budded region and the outer region. In the outer region, the principal curvature ϕ′ is given by
| (5) |
for all shapes to achieve a vanishing mean curvature. We define the principal curvature ϕ′ in Eq. 4 for the different shapes as follows.
Figure 2.
(a) (I) A membrane with an Ω-shape. The color bar represents the initial protein density (S,t = 0). (II) The budded region has a radius of curvature Rc, and the point at which the radial distance is minimal, SΩ, defines the budded area Abud. For the Ω-shape, ϕmax = 5π/6. (b) (I) A dome shape and the initial protein density is shown. (II) The dome region has a radius of curvature Rc and ϕmax = π/3. The dome area is given by the area of a spherical cap, Abud = (1 − cos(ϕmax)). (c) A pearled structure with two buds and the initial protein density is shown. (II) Each bud on the pearl has a radius of curvature Rc and ϕmax = 9π/10. The neck region has a radius of curvature Rneck. The area of the pearled structure is Abud = A(Spearl), at which the radial distance is minimal. (d) (I) A tube with the initial protein density is shown. (II) The tube has a radius Rt and a height Ltube measured from the bottom of the spherical cap to the tube rim. Stube = πRc/2 + Ltube, and the tube area is Abud = A(Stube). Initially, the total protein density mtot is the same for all shapes, and it is located at the top of the budding structures. The shapes are axially symmetric and represent shapes commonly observed in biological membranes. To see this figure in color, go online.
Dome and Ω shape
| (6) |
with ϕmax = π/3 for the dome shape (Fig. 2 b) and ϕmax = 5π/6 for the Ω-shape (Fig. 2 a). In the case of a dome shape, we consider the region with non-zero mean curvature as the budded region. For the case of an Ω-shape, we denote the membrane portion above the minimal neck radius as the budded region.
Pearl (n = 2)
| (7) |
where S1 = Rcϕmax, S2 = S1 + (2ϕmax − π)Rneck, S3 = S2 + (2ϕmax − π)Rc, and ϕmax = 9π/10 (Fig. 2 c). The radius of curvature of the neck region, Rneck, is set to Rneck = Rc/4. More pearls can be added to the shape by defining additional neck and bud regions.
Tube
| (8) |
The length Ltube is adjusted such that the dimensionless area of the budded region is equal to 1.
Diffusion equation
We assume that the density of a generic protein or molecule is described by a continuous field (42,43) in line with the continuous models of membranes (44,45), implying that the protein size is significantly smaller than the length scale associated with the membrane surface. The protein density depends on the arc length S and the time t, (S, t). The field (S, t) follows a diffusive dynamics on the different shapes shown in Fig. 2. The diffusion equation in the absence of sources and under axial symmetry is given by (42)
| (9) |
where D is the diffusion coefficient (19) and assumed to be constant. On a flat membrane, with ϕ = 0 and R = S, Eq. 9 is written as . On a curved surface, the diffusion equation (Eq. 9) contains an additional term , which depends both on the local curvature and the gradient of the protein density. Diffusion on a curved surface is, as such, different from the diffusion on a flat surface. The combined effect of curvature and protein distribution can in general not be captured in a single effective diffusion constant.
We write the diffusion equation (Eq. 9) in dimensionless form using the square root of the area of the budded region of the membrane, , as a characteristic length. Then the timescale is given by τ = Abud/D, and the dimensionless variables are , s = , r = , z = , a = , and σ = Abud . By introducing these scaling relations into Eq. 9, we obtain
| (10) |
where, for simplicity, we keep ( )′ . As an initial protein density, we consider = c(1 − tanh[5(a(s) − a0)]) for all membrane shapes, where there is a one-to-one correspondence between the arc length s and the area a(s), given by Eq. 3. The constants c and a0 are chosen such that σ(a(s = 0)) = 0.5 and mtot = 0.24, with mtot = the total amount of protein. The chosen functional dependence of aims to resemble a protein distribution that is localized in a particular membrane domain, as one would expect, e.g., on lipid rafts. The proteins are distributed nearly homogeneously at the top of the budding region, with a smooth transition to the protein-free part of the membrane, as illustrated in Fig. 2. As time proceeds, this initial density will diffuse over the entire membrane surface. The boundary condition imposed on the diffusion equation is such that there is no flux of protein at the boundaries of the spatial domain, i.e., σ′(s = 0) = 0 and σ′(s → ∞) = 0. In this case, the total amount of protein mtot is conserved over time because the proteins cannot escape from or flow through the membrane boundaries. Equation 10 is integrated numerically in time with a time step dt = 5 × 10−3 to obtain the spatio-temporal density profile on the membrane, using an implicit time discretization and a centered difference scheme to solve the spatial derivative of the protein density.
Results
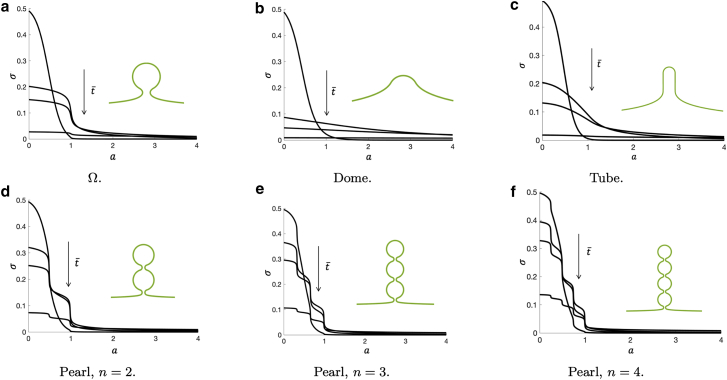
In Fig. 3, the protein density σ is shown as a function of the membrane area a at different points in time, = [1, 50, 100, 500]dt. These density profiles exhibit notable qualitative differences. The Ω-shape and the pearling structures exhibit a staircase-like protein profile in the budded region (a < 1), where the protein density approaches a nearly homogeneous distribution within the individual pearls. In contrast, neither the dome nor the tubular shape shows a step-like protein distribution at any point in time. Comparing dome or tubular shapes and Ω or pearl-like shapes at the latest time point, we find for the latter that the protein density in the budded region is much higher, indicating that the presence of narrow necks slows the diffusion of the proteins.
Figure 3.
Density profiles as a function of the membrane area a at different times, = [1, 50, 100, 500]dt, for (a) an Ω-shape, (b) a dome shape, (c) a tube, and (d)–(f) pearling structures with different number of pearls. In all simulations, the initial density is given by = c(1 − tanh(5(a(s) − a0))), where c and a0 are such that σ(a(s = 0), = 0) = 0.5 and mtot = 0.24. represents a nearly uniform protein distribution located at the top of the budding structure. As time proceeds, the initial protein density spreads over the membrane area, where the profiles are qualitatively different. In the case of the Ω- (a) and the pearling shapes (d–f), the protein density has a staircase-like profile along each of the pearls, indicating that the narrow necks prevent the profile from having a smoother transition. The overall effect of the membrane necks on the diffusion on buds and pearls is to slow down the exit of proteins from the budded structure. The corresponding shape is shown in the inset of each panel. To see this figure in color, go online.
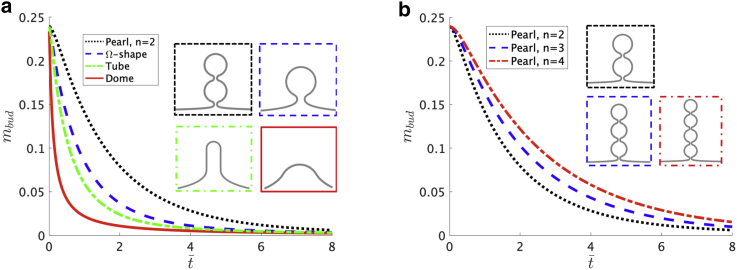
To characterize the effect of the membrane shape on the diffusive dynamics by a single parameter, we define the amount of protein in the budded region mbud = and determine how mbud evolves in time. In Fig. 4 a, we show the time evolution of mbud on the pearling structure with n = 2, the Ω-shape, the tube, and the dome shape. Our simulations show that, in accordance with the qualitative discussion of the density profiles in Fig. 3, the amount of protein in the budded region decreases faster in shapes that do not have narrow necks, such as the dome shape and the tube, whereas mbud decreases more slowly on the Ω-shape and the pearling structure. Additionally, Fig. 4 b shows mbud(t) for the different pearl-like structures with n = 2, 3, 4, for which we see that mbud decreases more slowly with a larger number of pearls.
Figure 4.
The total protein density on the budded region mbud = as a function of time for different membrane geometries. (a) mbud on the dome, tube, Ω, and pearl-like (n = 2) shapes is shown. Initially, all the proteins are localized at the upper part of the budding structure. (b) The effect of the number of pearls in the pearl-like structure on mbud is shown. The proteins exit the pearled region more slowly if the number of pearls, n, increases. The line style of the border surrounding each shape is the same as the corresponding mbud shown in the legend. To see this figure in color, go online.
The results in Fig. 4 highlight that the membrane shape influences both the temporal and spatial evolution of the protein distribution. To characterize the diffusion process by a single quantity, we define as the half-time, i.e., the time it takes for the total amount of proteins in the budded region to be reduced by 50%. On a flat membrane, the half-time is denoted as . The ratio > 1 on all budded membranes, indicating that diffusion on a flat surface is faster compared with diffusion on a curved surface.
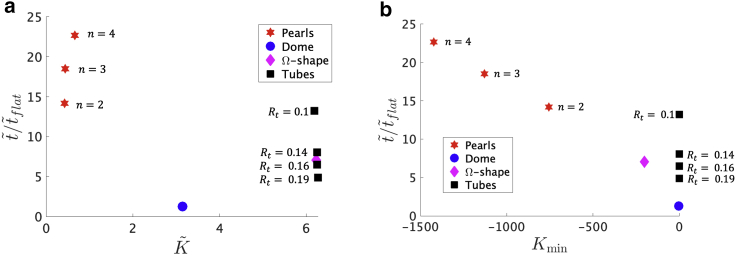
We aim at relating to the characteristics of the membrane shape, for which we consider the Gaussian curvature K averaged over the budded area ; the Gaussian curvature of the membrane neck, Kmin, i.e., where the membrane radius is minimal; and the mean curvature averaged over the budded area, . In addition to the Ω-shape, the pearled structures (with different numbers of buds), and the dome, we consider four tubes with different radii Rt ∈ [0.1, 0.14, 0.16, 0.19], where the tube height is set through the fixed dimensionless tube area a = 1.
In Fig. 5 a, we plot as a function of and observe that is not clearly correlated to the averaged Gaussian curvature . is similar for the tubes and the Ω-shape, but their is different. All the pearled structures, on the other hand, have a similar , but is also clearly different and up to five times larger with respect to in the tubes and in the Ω-shape. for the dome is clearly different from the of the tubes and the pearls. Additionally, the diffusion time on Ω-shapes is similar to the diffusion time on tubes. Fig. 5 b shows as a function of the minimal value of the Gaussian curvature, Kmin, which corresponds to the point along the arc length s at which the neck is smallest. The pearling shapes with a larger number of vesicles have a more negative Kmin. In contrast, the shapes in which the neck regions are absent, as in the domes and the tubes, have a close to zero Kmin. Fig. 5 b indicates that increases as the membranes have more constricted regions, which slow down diffusion.
Figure 5.
(a) The ratio as a function of the averaged Gaussian curvature . There is not a clear dependence between and across all the shapes considered. The tubes and the Ω-shape have a similar , which is larger than the of the pearled structures. The time , however, is clearly different, especially in the pearled structures, which also have a similar . (b) The ratio as a function of the minimal value of the Gaussian curvature along the arc length, Kmin, is shown for all the shapes considered. Kmin corresponds to the point where the neck joining the budded structure with the surrounding flat membrane is minimal, in the case of the pearls and the Ω-shape. In the tubes, Kmin corresponds to the tube rim, and in the dome, Kmin is the point beyond which the mean curvature vanishes. The values for the tube radii (Rt ∈ [0.1, 0.14, 0.16, 10.19]) are shown at the markers in (a) and (b), where the tube height is set through the fixed dimensionless tube area a = 1. To see this figure in color, go online.
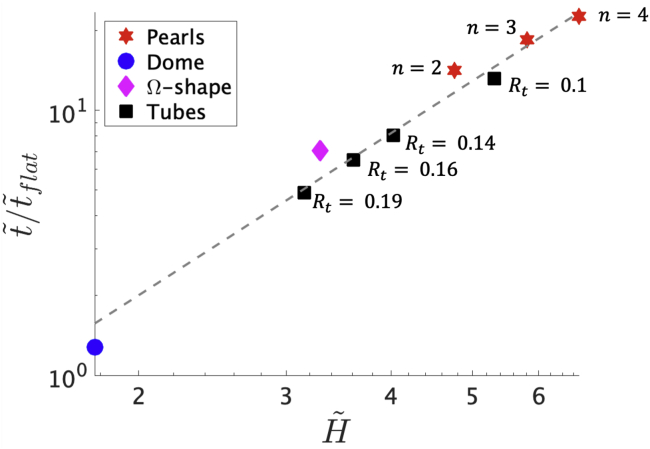
In Fig. 6, is shown as a function of the averaged mean curvature in logarithmic axis, where we find that . To understand the quadratic relation between the averaged mean curvature and , we turn to the diffusion equation (Eq. 10) for a cylinder, which is given by = σ″ as r = Rc with the cylinder radius Rc. We can then rewrite σ″ by using the membrane area as a variable to get σ″ = (2πRc)2 , where we have used Eq. 3 to relate the membrane area to the arc length. As a consequence, the diffusion equation can be expressed as . From these equations and using the fact that the mean curvature of a cylinder is 1/Rc, we obtain the scaling law , recovering the scaling relation found in the numerical simulations. Hence, a tube with larger curvature increases the exit time of proteins toward the flat surface (29). In Fig. 6, we can also notice that the diffusion on tubular shapes is slightly faster, i.e., lower , compared with pearling structures.
Figure 6.
The ratio as a function of the averaged mean curvature for each of the shapes considered, in logarithmic scale. The gray dashed line represents a fit , where m = 2.03 is the average of the slopes of the logarithmic relation between and , indicating that the exit time approximately follows a quadratic relation with respect to . However, some of the pearled structures do not follow the quadratic fit. This difference can be rationalized qualitatively, associating the tubes with a cylinder of infinite height and the shapes with spherical buds with a sphere. In these simpler geometries, the diffusion equation can be solved analytically, and an effective diffusion coefficient Deff can be defined. On a cylinder with the same radius of a sphere, Deff is larger as time proceeds, indicating that in cylindrical geometries, the diffusion is faster. Here, we observe that in general, is smaller in the tubes, indicating a faster diffusion with respect to the pearls and the Ω-shape. However, there are other effects that play an important role on the diffusion from these structures, such as the obstacles produced by the neck regions in the Ω-shape and the pearled structures. To see this figure in color, go online.
An analytic expression for cannot, in general, be derived. However, we can compare the effective diffusion constant on simpler shapes, specifically on an infinite cylinder and a sphere, with our numerical results, which capture the same essential features of the diffusion process. Holyst et al. found the following expressions for the effective diffusion constant Deff of a single particle diffusing on an infinite cylinder and a sphere, respectively: and (46), where R is the radius of the cylinder or the sphere. The effective diffusion constant is defined as Deff = <x2(t)>/4t, with <x2(t)> the mean-square displacement of the particle. In both cases, the diffusion constant is time dependent and decreases over time. Furthermore, the diffusion process is slowed down, i.e., Deff < D, for both the cylinder and the sphere, and the effective diffusion constant on a sphere is always smaller than the effective diffusion constant on a cylinder, if both shapes exhibit the same radius. From the relations for the effective diffusion coefficients on a sphere and a cylinder described above, we also notice that when t is large, → 0, indicating that diffusion ceases. This is a consequence of the finite surface of the sphere available for the diffusion of molecules (47). In the case of an infinite cylinder, this area is not bounded, and the effective diffusion coefficient has a finite value equal to at large t.
These analytical results indicate that the effective diffusion on a cylinder is faster than in a sphere as time proceeds and help us understand why is smaller in the tubes than in the dome and the pearled structures, as shown in Fig. 6. However, in the pearled structures, the diffusion is not limited to a single sphere because the proteins are free to diffuse outside each bud, though the process is slowed significantly. Finally, is a timescale at which all the effects mentioned above play an important role on the diffusion of proteins from the different shapes because a significant part of the initial protein density has exited the deformed regions and gone through the obstacles imposed by the membrane geometry.
Conclusions
In this work, we study the influence of characteristic shapes found in biological membranes—Ω-shaped buds, pearls, domes, and tubes—on the diffusion of a protein density field. The shapes considered have a strong influence on the density profiles obtained as time proceeds and also influence the characteristic time after which the proteins exit the budded region; the presence of narrow necks (pearls, Ω-shaped buds) prevents a fast decay of the total density on the budded structure as compared with the shapes for which such necks are absent (tubes, domes). To characterize the effect of the shape on diffusion more precisely, we have determined the averaged Gaussian and mean curvature for each shape. The time associated with proteins leaving the budded structures, , does correlate with the mean curvature, but not with the Gaussian curvature; whereas follows a quadratic relation with respect to , it does not show a clear dependence with respect to . However, a larger is associated with a more negative Gaussian curvature Kmin in the neck region. This indicates that constricted regions indeed delay the exit of proteins from curved membranes and also likely have implications during dynamic membrane budding by membrane inclusions (17) or protein coats (48,49), in which the neck region formed around a growing budded structure limits the diffusion of proteins. The static profiles considered here allowed us to isolate the effect of membrane shape on protein diffusion, but considering budding dynamics requires additional biophysical effects that modify the membrane energy and lead to a more complex protein flux. Some of these biophysical effects are protein-induced spontaneous curvature (33,42), protein crowding (50,51), mixing entropy (52), protein-protein interactions (53,54), membrane tension (55), membrane fluctuations (20), and protein recruitment (56,57).
The relations between , , and Kmin can help estimate relevant timescales related to the diffusive motion of proteins on complex membrane shapes. Our results suggest that the exit of proteins is strongly affected in elongated shapes such as the tubes and the pearled structures. These structures are observed in different biological contexts and in some cases can be reproduced by different experimental techniques. In addition, photobleaching provides a powerful technique to investigate the mobility of proteins inside cells (58) and in the membrane surface (59). This technique allowed to experimentally corroborate the recovery time predicted theoretically in tubular geometries (29) and motivates the use of theoretical models to predict diffusive behavior of proteins and molecules in more generic shapes.
Acknowledgments
The authors acknowledge funding from the Research Council of Norway (Project Grant 263056).
Editor: Ana-Suncana Smith.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2020.12.014.
Supporting Material
References
- 1.Kühn T., Ihalainen T.O., Timonen J. Protein diffusion in mammalian cell cytoplasm. PLoS One. 2011;6:e22962. doi: 10.1371/journal.pone.0022962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Cicuta P., Keller S.L., Veatch S.L. Diffusion of liquid domains in lipid bilayer membranes. J. Phys. Chem. B. 2007;111:3328–3331. doi: 10.1021/jp0702088. [DOI] [PubMed] [Google Scholar]
- 3.Mika J.T., Poolman B. Macromolecule diffusion and confinement in prokaryotic cells. Curr. Opin. Biotechnol. 2011;22:117–126. doi: 10.1016/j.copbio.2010.09.009. [DOI] [PubMed] [Google Scholar]
- 4.Javanainen M., Martinez-Seara H., Vattulainen I. Diffusion of integral membrane proteins in protein-rich membranes. J. Phys. Chem. Lett. 2017;8:4308–4313. doi: 10.1021/acs.jpclett.7b01758. [DOI] [PubMed] [Google Scholar]
- 5.Dix J.A., Verkman A.S. Crowding effects on diffusion in solutions and cells. Annu. Rev. Biophys. 2008;37:247–263. doi: 10.1146/annurev.biophys.37.032807.125824. [DOI] [PubMed] [Google Scholar]
- 6.Verkman A.S. Solute and macromolecule diffusion in cellular aqueous compartments. Trends Biochem. Sci. 2002;27:27–33. doi: 10.1016/s0968-0004(01)02003-5. [DOI] [PubMed] [Google Scholar]
- 7.Fradin C. On the importance of protein diffusion in biological systems: the example of the Bicoid morphogen gradient. Biochim. Biophys. Acta Proteins Proteom. 2017;1865:1676–1686. doi: 10.1016/j.bbapap.2017.09.002. [DOI] [PubMed] [Google Scholar]
- 8.Frye L.D., Edidin M. The rapid intermixing of cell surface antigens after formation of mouse-human heterokaryons. J. Cell Sci. 1970;7:319–335. doi: 10.1242/jcs.7.2.319. [DOI] [PubMed] [Google Scholar]
- 9.Dimova R., Aranda S., Lipowsky R. A practical guide to giant vesicles. Probing the membrane nanoregime via optical microscopy. J. Phys. Condens. Matter. 2006;18:S1151–S1176. doi: 10.1088/0953-8984/18/28/S04. [DOI] [PubMed] [Google Scholar]
- 10.Wu L.-G., Hamid E., Chiang H.-C. Exocytosis and endocytosis: modes, functions, and coupling mechanisms. Annu. Rev. Physiol. 2014;76:301–331. doi: 10.1146/annurev-physiol-021113-170305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Waterman-Storer C.M., Salmon E.D. Endoplasmic reticulum membrane tubules are distributed by microtubules in living cells using three distinct mechanisms. Curr. Biol. 1998;8:798–806. doi: 10.1016/s0960-9822(98)70321-5. [DOI] [PubMed] [Google Scholar]
- 12.Leibler S. Curvature instability in membranes. J. Phys. (Paris) 1986;47:507–516. [Google Scholar]
- 13.Callan-Jones A., Bassereau P. Curvature-driven membrane lipid and protein distribution. Curr. Opin. Solid State Mater. Sci. 2013;17:143–150. [Google Scholar]
- 14.Kralj-Iglic V., Svetina S., Zeks B. Shapes of bilayer vesicles with membrane embedded molecules. Eur. Biophys. J. 1996;24:311–321. doi: 10.1007/BF00180372. [DOI] [PubMed] [Google Scholar]
- 15.Aimon S., Callan-Jones A., Bassereau P. Membrane shape modulates transmembrane protein distribution. Dev. Cell. 2014;28:212–218. doi: 10.1016/j.devcel.2013.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Atilgan E., Wirtz D., Sun S.X. Morphology of the lamellipodium and organization of actin filaments at the leading edge of crawling cells. Biophys. J. 2005;89:3589–3602. doi: 10.1529/biophysj.105.065383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Auth T., Gompper G. Budding and vesiculation induced by conical membrane inclusions. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2009;80:031901–031911. doi: 10.1103/PhysRevE.80.031901. [DOI] [PubMed] [Google Scholar]
- 18.Blum J.J., Lawler G., Shin I. Effect of cytoskeletal geometry on intracellular diffusion. Biophys. J. 1989;56:995–1005. doi: 10.1016/S0006-3495(89)82744-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lippincott-Schwartz J., Snapp E., Kenworthy A. Studying protein dynamics in living cells. Nat. Rev. Mol. Cell Biol. 2001;2:444–456. doi: 10.1038/35073068. [DOI] [PubMed] [Google Scholar]
- 20.Reister E., Seifert U. Lateral diffusion of a protein on a fluctuating membrane. Europhys. Lett. 2005;71:859–865. [Google Scholar]
- 21.Adler J., Shevchuk A.I., Parmryd I. Plasma membrane topography and interpretation of single-particle tracks. Nat. Methods. 2010;7:170–171. doi: 10.1038/nmeth0310-170. [DOI] [PubMed] [Google Scholar]
- 22.Aizenbud B.M., Gershon N.D. Diffusion of molecules on biological membranes of nonplanar form. A theoretical study. Biophys. J. 1982;38:287–293. doi: 10.1016/S0006-3495(82)84560-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Saffman P.G., Delbrück M. Brownian motion in biological membranes. Proc. Natl. Acad. Sci. USA. 1975;72:3111–3113. doi: 10.1073/pnas.72.8.3111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Daniels D.R., Turner M.S. Diffusion on membrane tubes: a highly discriminatory test of the Saffman-Delbruck theory. Langmuir. 2007;23:6667–6670. doi: 10.1021/la0635000. [DOI] [PubMed] [Google Scholar]
- 25.Gambin Y., Lopez-Esparza R., Urbach W. Lateral mobility of proteins in liquid membranes revisited. Proc. Natl. Acad. Sci. USA. 2006;103:2098–2102. doi: 10.1073/pnas.0511026103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Quemeneur F., Sigurdsson J.K., Lacoste D. Shape matters in protein mobility within membranes. Proc. Natl. Acad. Sci. USA. 2014;111:5083–5087. doi: 10.1073/pnas.1321054111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Gov N. Diffusion in curved fluid membranes. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2006;73:041918. doi: 10.1103/PhysRevE.73.041918. [DOI] [PubMed] [Google Scholar]
- 28.Domanov Y.A., Aimon S., Bassereau P. Mobility in geometrically confined membranes. Proc. Natl. Acad. Sci. USA. 2011;108:12605–12610. doi: 10.1073/pnas.1102646108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Klaus C.J.S., Raghunathan K., Kenworthy A.K. Analysis of diffusion in curved surfaces and its application to tubular membranes. Mol. Biol. Cell. 2016;27:3937–3946. doi: 10.1091/mbc.E16-06-0445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lampe M., Vassilopoulos S., Merrifield C. Clathrin coated pits, plaques and adhesion. J. Struct. Biol. 2016;196:48–56. doi: 10.1016/j.jsb.2016.07.009. [DOI] [PubMed] [Google Scholar]
- 31.Avinoam O., Schorb M., Kaksonen M. ENDOCYTOSIS. Endocytic sites mature by continuous bending and remodeling of the clathrin coat. Science. 2015;348:1369–1372. doi: 10.1126/science.aaa9555. [DOI] [PubMed] [Google Scholar]
- 32.Buono R.A., Leier A., Otegui M.S. ESCRT-mediated vesicle concatenation in plant endosomes. J. Cell Biol. 2017;216:2167–2177. doi: 10.1083/jcb.201612040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Tsafrir I., Caspi Y., Stavans J. Budding and tubulation in highly oblate vesicles by anchored amphiphilic molecules. Phys. Rev. Lett. 2003;91:138102–138106. doi: 10.1103/PhysRevLett.91.138102. [DOI] [PubMed] [Google Scholar]
- 34.Yu Y., Granick S. Pearling of lipid vesicles induced by nanoparticles. J. Am. Chem. Soc. 2009;131:14158–14159. doi: 10.1021/ja905900h. [DOI] [PubMed] [Google Scholar]
- 35.Sukhorukov V.M., Bereiter-Hahn J. Anomalous diffusion induced by cristae geometry in the inner mitochondrial membrane. PLoS One. 2009;4:e4604. doi: 10.1371/journal.pone.0004604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kusters R., Kapitein L.C., Storm C. Shape-induced asymmetric diffusion in dendritic spines allows efficient synaptic AMPA receptor trapping. Biophys. J. 2013;105:2743–2750. doi: 10.1016/j.bpj.2013.11.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Byrne M.J., Waxham M.N., Kubota Y. The impacts of geometry and binding on CaMKII diffusion and retention in dendritic spines. J. Comput. Neurosci. 2011;31:1–12. doi: 10.1007/s10827-010-0293-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Faraudo J. Diffusion equation on curved surfaces. I. Theory and application to biological membranes. J. Chem. Phys. 2002;116:5831–5841. [Google Scholar]
- 39.Balakrishnan J. Spatial curvature effects on molecular transport by diffusion. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 2000;61:4648–4651. doi: 10.1103/physreve.61.4648. [DOI] [PubMed] [Google Scholar]
- 40.Reynwar B.J., Illya G., Deserno M. Aggregation and vesiculation of membrane proteins by curvature-mediated interactions. Nature. 2007;447:461–464. doi: 10.1038/nature05840. [DOI] [PubMed] [Google Scholar]
- 41.Reynwar B.J., Deserno M. Membrane composition-mediated protein-protein interactions. Biointerphases. 2008;3:FA117–FA124. doi: 10.1116/1.2977492. [DOI] [PubMed] [Google Scholar]
- 42.Agrawal A., Steigmann D.J. A model for surface diffusion of trans-membrane proteins on lipid bilayers. Z. Angew. Math. Phys. 2011;62:549–563. [Google Scholar]
- 43.Góźdź W.T. Diffusion of macromolecules on lipid vesicles. Langmuir. 2008;24:12458–12468. doi: 10.1021/la801767q. [DOI] [PubMed] [Google Scholar]
- 44.Helfrich W. Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. C. 1973;28:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 45.Lipowsky R. Coupling of bending and stretching deformations in vesicle membranes. Adv. Colloid Interface Sci. 2014;208:14–24. doi: 10.1016/j.cis.2014.02.008. [DOI] [PubMed] [Google Scholar]
- 46.Hołyst R., Plewczyński D., Burdzy K. Diffusion on curved, periodic surfaces. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1999;60:302–307. doi: 10.1103/physreve.60.302. [DOI] [PubMed] [Google Scholar]
- 47.Yoshigaki T. Theoretically predicted effects of Gaussian curvature on lateral diffusion of membrane molecules. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2007;75:041901–041917. doi: 10.1103/PhysRevE.75.041901. [DOI] [PubMed] [Google Scholar]
- 48.Antonny B. Membrane deformation by protein coats. Curr. Opin. Cell Biol. 2006;18:386–394. doi: 10.1016/j.ceb.2006.06.003. [DOI] [PubMed] [Google Scholar]
- 49.Dmitrieff S., Nédélec F. Membrane mechanics of endocytosis in cells with turgor. PLoS Comput. Biol. 2015;11:e1004538. doi: 10.1371/journal.pcbi.1004538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Stachowiak J.C., Schmid E.M., Hayden C.C. Membrane bending by protein-protein crowding. Nat. Cell Biol. 2012;14:944–949. doi: 10.1038/ncb2561. [DOI] [PubMed] [Google Scholar]
- 51.Liese S., Wenzel E.M., Carlson A. Protein crowding mediates membrane remodeling in upstream escrt-induced formation of intraluminal vesicles. Proc. Natl. Acad. Sci. USA. 2020;117:28614–28624. doi: 10.1073/pnas.2014228117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Flory P.J. Thermodynamics of high polymer solutions. J. Chem. Phys. 1942;10:51–61. [Google Scholar]
- 53.Alimohamadi H., Rangamani P. Modeling membrane curvature generation due to membrane⁻protein interactions. Biomolecules. 2018;8:120–145. doi: 10.3390/biom8040120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Tozzi C., Walani N., Arroyo M. Out-of-equilibrium mechanochemistry and self-organization of fluid membranes interacting with curved proteins. New J. Phys. 2019;21:093004. [Google Scholar]
- 55.Kozlov M.M., Chernomordik L.V. Membrane tension and membrane fusion. Curr. Opin. Struct. Biol. 2015;33:61–67. doi: 10.1016/j.sbi.2015.07.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Arroyo M., Walani N., Kaurin D. Onsager’s variational principle in soft matter: introduction and application to the dynamics of adsorption of proteins onto fluid membranes. In: Steigmann D., editor. Role of Mechanics in the Study of Lipid Bilayers. Volume 577. Springer; 2018. pp. 287–332. [Google Scholar]
- 57.Rojas Molina R., Liese S., Carlson A. Diffuso-kinetic membrane budding dynamics. Soft Matter. 2020 doi: 10.1039/d0sm01028f. [DOI] [PubMed] [Google Scholar]
- 58.White J., Stelzer E. Photobleaching GFP reveals protein dynamics inside live cells. Trends Cell Biol. 1999;9:61–65. doi: 10.1016/s0962-8924(98)01433-0. [DOI] [PubMed] [Google Scholar]
- 59.Yguerabide J., Schmidt J.A., Yguerabide E.E. Lateral mobility in membranes as detected by fluorescence recovery after photobleaching. Biophys. J. 1982;40:69–75. doi: 10.1016/S0006-3495(82)84459-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.