Intestinal villus structure contributes to even shedding of epithelial cells

Abstract

In the intestinal epithelium, proliferated epithelial cells ascend the crypts and villi and shed at the villus tips into the gut lumen. In this study, we theoretically investigate the roles of the villi on cell turnover. We present a stochastic model that focuses on the duration over which cells migrate the shortest paths between the crypt orifices and the villus tips, where shedding cells are randomly chosen from among those older than the shortest-path cell migration times. By extending the length of the shortest path to delay cell shedding, the finger-like shape of the villus would tightly regulate shedding-cell ages compared with flat surfaces and shorter projections; the villus allows epithelial cells to shed at around the same age, which limits them from shedding early or staying in the epithelium for long periods. Computational simulations of cell dynamics agreed well with the predictions. We also examine various mechanical conditions of cells and confirm that coordinated collective cell migration supports the predictions. These results suggest the important roles of the villi in homeostatic maintenance of the small intestine, and we discuss the applicability of our approach to other tissues with collective cell movement.

Significance

The intestinal villi are numerous finger-like structures covered by epithelial cells and projecting into the gut lumen. The villi are well known for expanding the gut surface area for efficient absorption; we suggest that they also contribute to tight regulation of cell turnover. The villi limit epithelial cells from shedding early or remaining in the epithelium for long periods by separating the villus tips, where cells shed, from the crypts, where cells are produced. Here, we propose even shedding of epithelial cells as another role of the villi and underline their physiological and pathophysiological importance.

Introduction

The small intestine owes most of its nutrient-absorptive surface area to the villi—numerous finger-like structures protruding into the lumen from the intestine’s wall covered by a single layer of cells, most of which are absorptive epithelial cells (1). The villi are 400–1000 μm tall in humans (2) and 150–400 μm tall in mice (3) and contribute an absorptive surface area ∼6.5 times greater than a simple cylindrical intestine of the same diameter and length would (4). Hence, the villous atrophy observed in conditions such as celiac disease or Crohn’s disease often severely hampers absorption (5,6).

The small intestine has the fastest cell turnover in the body. Its epithelial cells are renewed every 3–5 days by repeating cycles of cell proliferation, migration, and shedding (7, 8, 9). Each villus is surrounded by several invaginations called crypts. Intestinal stem cells at the crypt base divide with cell cycles of ∼12–24 h (10,11). Daughter cells differentiate within the crypts, then ascend the crypts, and then migrate to the nearest villus. Upon reaching the villus tip, the cells shed into the gut lumen. The small intestine is considered to maintain its homeostasis by replacing epithelial cells and filling its surface with fresh cells while keeping the total epithelial cell number constant (12). This continual renewal process enhances the assimilation and protection of the small intestine (13).

To elucidate cell turnover mechanisms in the small intestine, previous studies have explored cell proliferation and cell behavior in the intestinal crypts (14, 15, 16, 17, 18), driving forces of cell movement in the villus epithelium (19, 20, 21, 22) and cell-shedding processes at the villus tips (23,24). Furthermore, the influences of pathological factors, such as inflammation or infection, on cell motility in the epithelium or cell turnover of the small intestine have been investigated (25,26). On the other hand, to our knowledge, few studies have focused on the effects of the villus shape itself on normal cell turnover of the small intestine.

In this study, we theoretically investigate the roles of the villus on cell turnover and propose that its finger-like shape tightly regulates shedding-cell ages; the villus limits epithelial cells from shedding early or staying in the epithelium for prolonged periods. In the Methods, we provide some details of the three-dimensional (3D) surface and the two-dimensional (2D) plane cell-based dynamic models. In the Results, focusing on the time when cells migrate over the shortest paths between the crypt orifices and the cell-shedding sites, we begin by presenting a stochastic model that describes cell turnover of tissues with collective cell migration and examine the effects of the height or shape of the villus on the spread of shedding-cell ages. Using this model, we then numerically predict the distributions of shedding-cell ages for three structures with different shapes. Next, we computationally simulate the 3D surface cell-based model for three geometries and compare the results with the predictions of the stochastic model. Lastly, we build the simplified 2D plane cell-based model for two flat regions with different lengths and address the effects of active cell migration and different material properties of cells on shedding-cell age distributions. We also discuss the applicability of our approach to other tissues with collective cell movement.

Methods

3D surface cell-based model

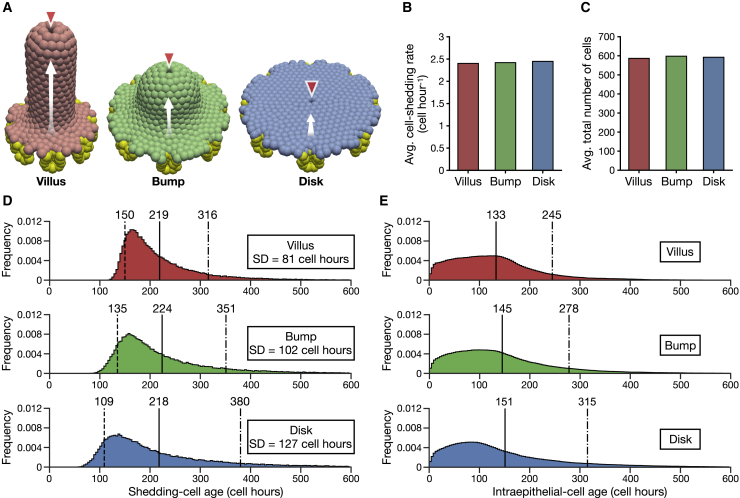
We performed computational simulations of a 3D surface cell-based model using an off-lattice overlapping sphere model developed by Mirams et al. (27). We constructed three geometries: Villus, Bump, and Disk, as shown in Fig. 3 A and Fig. S2. Times, in the model, are measured in cell hours, and units of space are cell diameters (CDs). The Villus has a finger-like shape, the Bump has a hemisphere-like shape, and the Disk has a flat circular surface. Sizes are scaled so that each structure has approximately the same cell number: 600 cells was chosen for a practicable simulation cost. Each structure is surrounded by eight crypts following the murine intestine (28). Each structure also has one shedding site at its tip or center. Cells proliferated in the crypts move over the surfaces and shed at the shedding sites. Because of the scaling for approximately the same cell number, the length of the shortest path from the crypt orifices to the shedding site is longest in the Villus, followed by the Bump and finally the Disk (Fig. S2).

Figure 3.

Simulations of the 3D surface cell-based model. (A) Given are snapshots of the Villus (left), Bump (middle), and Disk (right). Proliferative cells are colored yellow; the other colors indicate differentiated cells. Cells from the crypts move on the surfaces as indicated by the white arrows and are shed at the shedding sites marked by the red arrowheads. (B) Given is the average number of cells that shed per one cell hour. (C) Given is the average total number of cells in the structures. (D) Given are the shedding-cell age distributions of the Villus (top), Bump (middle), and Disk (bottom). Dashed lines, the early shedding-cell ages; solid lines, the average shedding-cell ages; dot-dash lines, the late shedding-cell ages. (E) Shown are the intraepithelial-cell or differentiated-cell age distributions of the Villus (top), Bump (middle), and Disk (bottom). The decreased frequency around age 0 is because proliferative cells account for the majority of the population. The solid lines represent the average intraepithelial-cell ages, and the dot-dash lines represent the old intraepithelial-cell ages. To see this figure in color, go online.

Cells are modeled as a set of nodes, each of which represents a cell center. The cells are free to move within the surfaces (29). Cells move according to interactions with neighboring cells, which are determined by whether two cell centers are within a certain interaction distance of 1.5 CDs (27); because the cells move, cell neighborhoods are updated in every time step. Elastic-cell-cell interaction drives local repulsive and attractive forces, and each cell experiences the Hookean linear spring forces that act along the vectors connecting neighboring cell centers (29). For simplicity, all springs are set with the same spring constant. The total force acting on cell i at time t is, therefore, the sum of all elastic forces coming from the springs of all neighboring cells j∈${\mathcal{M}}_i$(t) connecting to cell i at that time, given by the following:

$${\mathbf{F}}_i\left(t\right)=\mu \sum _{j\in {\mathcal{M}}_i\left(t\right)}{\hat{\mathbf{r}}}_{i,j}\left(t\right)\left(\Vert {\mathbf{r}}_{i,j}\left(t\right)\Vert -s_{i,j}\left(t\right)\right),$$ (1)

where μ is the spring constant, r_i,j(t) = r_j(t) − r_i(t) is the vector from the center of cell i to the center of cell j at time t, ${\hat{\mathbf{r}}}_{i,j}$(t) is the corresponding unit vector, and s_i,j(t) is the natural length of the spring connecting cells i and j at time t. The natural length is 1.0 CD for all cells unless cells i and j are a pair of dividing cells. When a cell divides, s_i,j(t) increases linearly from 0.3 CD to 1.0 CD over the first cell hour to represent cell growth (30). By making the simplifying assumption that internal terms are sufficiently small compared with dissipative terms (31), cell inertia is neglected, and we obtain the following first-order equation of motion for cell i:

$$\eta \frac{\text{d}{\mathbf{r}}_i}{\text{d}t}={\mathbf{F}}_i\left(t\right),$$ (2)

where r_i is the vector of the cell center i, and η is the drag coefficient representing the cell-substrate adhesion. We solve this equation numerically using the forward Euler method with a time step Δt sufficiently small to achieve numerical stability. Thus, the effective displacement of each cell center i within Δt is given by

$${\mathbf{r}}_i\left(t+\Delta t\right)={\mathbf{r}}_i\left(t\right)+\frac{1}{\eta }{\mathbf{F}}_i\left(t\right)\Delta t.$$ (3)

Proliferative and differentiated cells are determined by their locations. Cells located in the crypts behave as proliferative cells and so can divide. Cells outside the crypts are differentiated cells that cannot divide. Each cell has an individual cell age that increments every time step. Each proliferative cell is assigned to a randomly chosen cell division interval, after which it will supply a cell naturally into the surface. When a cell divides, a daughter cell is placed within the crypt surface with its center 0.3 CD away from the center of the mother cell in a randomly chosen direction (30). Their cell age is then reset to 0, and new division intervals are assigned. Cells moved outside the surface are returned to it perpendicularly in the next time step. Cells emerging from the crypts change into differentiated cells, which move across the surfaces and ultimately shed at the shedding sites.

When cell centers move above the threshold heights of the Villus or Bump or approach within a threshold distance of the Disk center, they are removed (27,32). Associated springs are removed at this time, and spring connections are not formed within the shedding sites. The shedding sites’ heights or diameters are chosen to give similar cell-shedding rates and shedding behavior among structures when equal cell proliferation rates are given. Cells are not removed other than at the shedding sites. Cell movement is, therefore, passively driven by mitotic pressure of the proliferative cells and by the negative pressure of cell shedding (29). The determination of other parameter values and dimensions is described in Supporting materials and methods, Appendix S7 a.

2D plane cell-based model

The 2D plane cell-based model is also an off-lattice overlapping sphere model. We built two flat rectangular geometries with different lengths: Long and Short, as shown in Fig. 4 A. Times are measured in cell hours and distances are measured in CDs. Both shapes have one crypt and one shedding site, and their dimensions are set to have ∼200 cells in total (Figs. S4, A and B). The mechanics of cell movement are the same as in the 3D model. We represent cell centers by nodes that are free to move within the surfaces. Cells are deemed neighbors if their centers are within the interaction distance of 1.5 CDs, and to allow for changes due to cell movement, cell neighborhoods are updated at every time step. The force on each cell is the sum of the forces due to interactions with neighboring cells, calculated as a Hookean linear spring force (Eq. 1). Again, the equation of motion and displacement of each cell center is expressed by Eqs. 2 and 3, μ is the spring constant connecting cells, η is the drag coefficient acting on cells, and the natural length of connecting springs is 1.0 CD except for cell division.

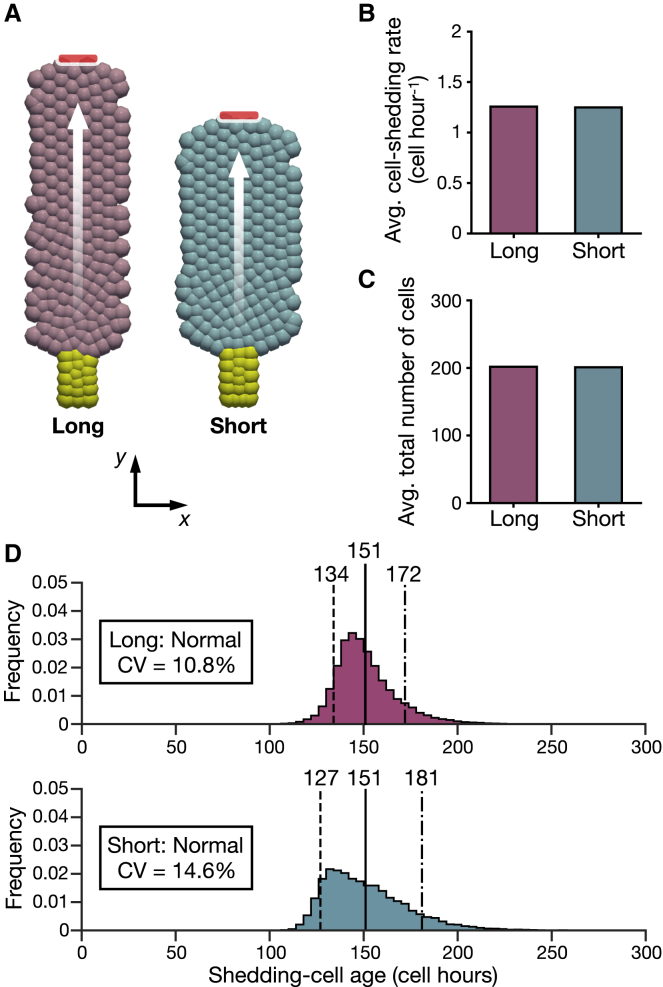
Figure 4.

Validation of the 2D plane cell-based model: normal results. (A) Given are snapshots of the Long (left) and Short (right). Proliferative cells are colored yellow; other colors are differentiated cells. Cells from the crypts move on the surfaces as indicated by the white arrows and shed at the shedding sites indicated by red markers. (B) Given is the average number of cells that shed per one cell hour. (C) Given is the average total number of cells in the models. (D) Shown are the shedding-cell age distributions of the Long (top) and Short (bottom). The dashed lines represent the early shedding-cell ages, the solid lines represent the average shedding-cell ages, and the dot-dash lines represent the late shedding-cell ages. To see this figure in color, go online.

Cells located in the crypts are proliferative, and the others are differentiated. Each cell has an age that increments from its birth. A proliferative cell divides when its cell age exceeds a randomly assigned division interval. At that moment when a cell divides, a daughter cell is placed 0.3 CD away from the center of the mother cell in a randomly chosen direction within the crypt surface, and the natural length of the spring increases linearly from 0.3 CD to 1.0 CD over the first cell hour. Then, their cell age is reset to be 0, and new division intervals are assigned. Cells pushed out of the surface return perpendicularly into the surface in the next time step. Differentiated cells move over the surfaces and shed at the shedding sites. Cells are removed when their centers exceed the threshold distances from the crypt orifices; neighboring cells lose the springs connecting with the removed cells. Both shapes have shedding sites of the same width to ensure similar cell-shedding behavior. Cells are not removed other than the shedding sites. Cell movement is, therefore, passively driven by mitotic pressure and negative pressure by cell shedding when an active migration force is not implemented.

In the 2D model, we also examined a case in which cells actively migrate. We introduced an additional active migration force acting on each cell (33), modifying Eq. 2 to

$$\eta \frac{\text{d}{\mathbf{r}}_i}{\text{d}t}={\mathbf{F}}_i\left(t\right)+\alpha \widehat{{\mathbf{e}}_{\mathbf{y}}},$$ (4)

where α is a constant representing the magnitude of the active migration force and $\widehat{{\mathbf{e}}_{\mathbf{y}}}$ is the unit vector in the direction from the crypt to the shedding site. We solve Eq. 4 numerically. Other parameter values and dimensions were determined as described in Supporting materials and methods, Appendix S7 b.

Results

Description of cell turnover by the stochastic model

In this section, we first present a stochastic model of cell turnover that focuses on the time when cells migrate over the shortest paths between the crypt orifices and the shedding sites. Next, we examine the effects of the height or shape of the villus on the spread of shedding-cell ages. We then compare the spread of shedding-cell ages among three structures with different shapes. Lastly, we conduct numerical calculations of the stochastic model for the three structures.

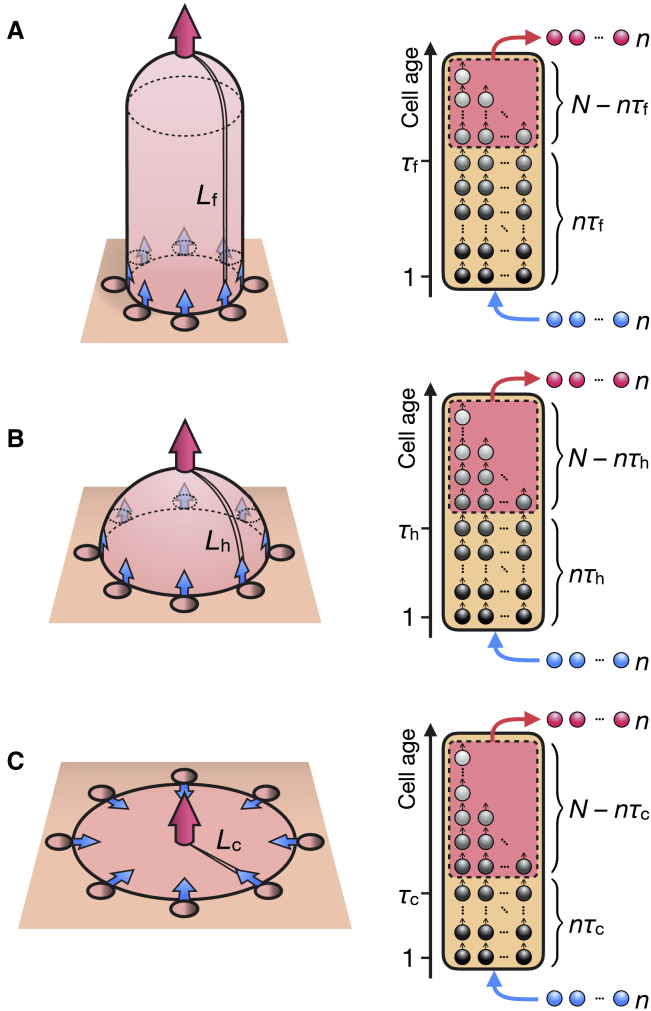
Fig. 1 A, left panel, shows the epithelium of the small intestine where a finger-like villus is surrounded by several crypts. Epithelial cells emerge from the crypts, enter and ascend the villus surface, and shed at the villus tip into the gut lumen. Here, we suppose that cells from the crypts directly enter the adjacent villus surface and that cells move collectively in the epithelium to the villus tip. Upon reaching the villus tip, cells are shed by anoikis, where neighboring cells expel those accumulated at the villus tip (23,34). The probability of cell shedding would, therefore, be constant regardless of cell ages or cell types. Furthermore, we do not consider the apoptosis that is occasionally observed outside the villus tip. Cells must hence migrate to the shortest path between the crypt orifices and the villus tip (L_f), as indicated by the double line, at least before shedding, and the shedding-cell age would at least exceed the time needed for cells to migrate over the shortest path (τ_f).

Figure 1.

Stochastic model of cell turnover. Left panels: given is the schematic description of the finger-like (A), hemispheric (B), and circular disk (C) structures of the epithelium. Cells enter the epithelium from the crypts (blue arrows) and shed from the tips or the center of the structures (red arrows). L_f, L_h, and L_c, as indicated by double lines, are the lengths of the shortest path between the crypt orifices and the shedding sites. Right panels: shown are the stochastic processes of cell turnover in respective structures. τ_f, τ_h, and τ_c are the cell migration times for the shortest paths of the respective structures. Each structure has a total of N cells in the epithelium and chooses n red-colored cells as the shedding cells from those aged above the shortest-path cell migration times, i.e., the cells surrounded by the dashed-line frames. After the remaining intraepithelial cells have incremented their ages by 1, n blue-colored cells of age 1 are supplied into the epithelium from the crypts. To see this figure in color, go online.

Fig. 1 A, right panel, illustrates the stochastic process of cell turnover of the finger-like villus at steady state. There are N cells, in total, in the epithelium. At each time step, n cells are randomly chosen to be the shedding cells from those aged over τ_f, intraepithelial-cell ages are incremented by 1, and n cells of age 1 are supplied from the crypts. N remains constant under these conditions. Therefore, the number of cells that cannot shed is nτ_f, the number of cells that can shed is N − nτ_f, and the probabilities that cells of age t can shed are as follows:

$$\{\begin{array}{cc}0,& \left(t\le {\tau }_{\text{f}}\right),\\ \frac{n}{N-n{\tau }_{\text{f}}}=p_{\text{f}},& \left(t>{\tau }_{\text{f}}\right).\end{array}$$ (5)

Thus, the probability of cell shedding at age t is given by

$$\{\begin{array}{cc}0,& \left(t\le {\tau }_{\text{f}}\right),\\ p_{\text{f}}{\left(1-p_{\text{f}}\right)}^{t-{\tau }_{\text{f}}-1},& \left(t>{\tau }_{\text{f}}\right),\end{array}$$ (6)

which has a geometric distribution when t > τ_f. Hence, the expected value of the shedding-cell age is T = N/n, and the standard deviation (SD) of the shedding-cell ages is given by (see Supporting materials and methods, Appendix S1)

$${\sigma }_{\text{f}}=\sqrt{\left(T-{\tau }_{\text{f}}\right)\left(T-{\tau }_{\text{f}}-1\right)}.$$ (7)

This expression shows that σ_f decreases as τ_f approaches T: the spread of shedding-cell ages decreases as the shortest-path cell migration time approaches the expected value of the shedding-cell age.

We then modeled the finger-like villus as a structure with a hemisphere atop a cylinder (Fig. S1 A) and examined how the villus height affects the spread of shedding-cell ages. We define the epithelial surface area as the total surface area surrounded by the crypts. When the height of the finger-like structure is varied while keeping a constant epithelial surface area, L_f lengthens, thereby τ_f increases as the overall villus height increases (see Supporting materials and methods, Appendix S2). Assuming that N and n are constant regardless of the villus height, making T the same, σ_f decreases as the villus height increases (Eq. 7). A taller finger-like villus hence reduces the spread of shedding-cell ages. Next, we discussed the effects of the villus shapes on the spread of shedding-cell ages, e.g., the villus with pointed tip has also been observed in vivo (3). Modeling the pointed villus as a cone for simplicity (Fig. S1 B), the conical structure has a longer length of the shortest path between the base and the tip of the structure than that of the finger-like structure for the same epithelial surface area (see Supporting materials and the methods, Appendix S3). The conical structure hence has a smaller spread of shedding-cell ages than the finger-like structure for the same values of N and n. The villi with more pointed tips can also decrease the spread of shedding-cell ages.

To further explore the roles of the finger-like shape of the villus on cell turnover, we then compare three structures—the finger-like, hemispheric, and circular disk structures as shown in Figs. 1 and S1, A, C, and D. All of the structures are surrounded by crypts, and cells shed at the tips or the center of the structures. When all structures have equal epithelial surface areas, the length of the shortest path always decreases in the order of the finger-like, hemispheric, and circular disk structures—L_f > L_h > L_c—independently of their scales (see Supporting materials and methods, Appendix S4). Thus, the shortest-path cell migration time also decreases in the same order: τ_f > τ_h > τ_c. Assuming that N and n are the same regardless of the structures, making T equal, the finger-like structure has the smallest spread of shedding-cell ages, followed by the hemispheric and circular disk structures, in that order (Eq. 7): σ_f < σ_h < σ_c. Here, σ_h and σ_c are the SDs of the shedding-cell ages of the hemispheric and circular disk structures, respectively. The finger-like structure shows more uniform shedding-cell ages than do the hemispheric and circular disk structures.

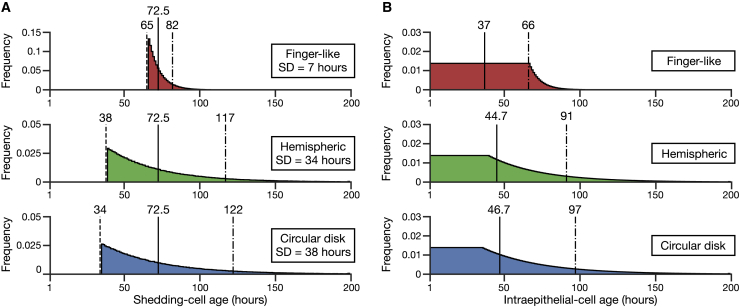
Finally, we performed numerical calculations on the stochastic model for the three structures: the finger-like, hemispheric, and circular disk structures. As shown in Table 1, we estimated parameter values using experimental results of the murine small intestine (see Supporting materials and methods, Appendix S5; (9,22)). All structures are set to have the same values of N and n but different shortest-path cell migration times. Fig. 2 A shows the shedding-cell age distributions. All structures have equal mean shedding-cell ages but differing SDs. For all three structures, the shedding-cell age is distributed geometrically, with the minimal shedding age being associated with the length of the shortest path from crypt to shedding zone. The minimal shedding age is greatest for the finger-like structure, followed by the hemispheric structure, then the circular disk structure. On the other hand, the finger-like structure has the youngest late shedding-cell age, indicated by the 90th percentile of each shedding-cell age distribution, followed by the hemispheric and circular disk structures, in that order. It is expected that the finger-like structure sheds nearly almost all of its cells within 100 h, which agrees with the observations of labeled cells in the murine intestine shedding within 5 days (7). Fig. 2 B shows the intraepithelial-cell age distributions. In all structures, the cell frequency is constant until the shortest-path cell migration time and then decreases. The finger-like structure has the lowest average intraepithelial-cell age, followed by the hemispheric structure and then the circular disk structure. Furthermore, the old intraepithelial-cell age, which is defined as the 90th percentile of each intraepithelial-cell age distribution, increases in the same order. We also confirmed that the SDs of shedding-cell ages and the average intraepithelial-cell ages obtained from the numerical calculation coincide with those calculated analytically (see Supporting materials and methods, Appendix S6). It is hence predicted that compared with the hemispheric or circular disk structures, the finger-like structure reduces the spread of the shedding-cell ages and limits cells from shedding early or staying in the epithelium for long periods.

Table 1.

Estimated parameter values of numerical calculations in the stochastic model

Symbol	Value	Description
N	1885	total number of cells in the epithelium
n	26 h−1	cell supply and shedding rates
τf	65 h	the shortest-path cell migration time of the finger-like structure
τh	38 h	the shortest-path cell migration time of the hemispheric structure
τc	34 h	the shortest-path cell migration time of the circular disk structure

Figure 2.

Numerical calculations of the stochastic model. (A) Shown are the shedding-cell age distributions of the finger-like (top), hemispheric (middle), and circular disk (bottom) structures. Dashed lines, the shortest-path cell migration times; solid lines, the average shedding-cell ages; dot-dash lines, the late shedding-cell ages. (B) Shown are the intraepithelial-cell age distributions of the finger-like (top), hemispheric (middle), and circular disk (bottom) structures. The solid lines represent the average intraepithelial-cell ages, and the dot-dash lines represent the old intraepithelial-cell ages. To see this figure in color, go online.

Investigation by the 3D surface cell-based model

To consider the effects of cell-cell interactions and the geometry of surfaces, we conducted computational simulations of the 3D surface cell-based model and examined whether the results agree with the predictions from the stochastic model. As shown in Fig. 3 A, we then constructed three geometries: Villus, Bump, and Disk. Their dimensions are chosen for approximately equal total cell numbers. All structures are also set to have the same numbers and sizes of crypts, which gives the same cell proliferation rates. Cells proliferated in the crypts move on the surfaces and shed at the tips or center of the structures. The length of the shortest path between the crypt orifices and the shedding sites is the longest in the Villus, followed by the Bump and Disk, in that order (Fig. S2).

The cell proliferation rates are set to be equal for all structures, and the equilibrium total cell numbers are uniform over time (Fig. S3 A); thus, all structures have approximately the same average cell-shedding rates (Fig. 3 B). The average total cell numbers are also approximately equal among structures (Fig. 3 C). The Villus and Disk show about the same average cell density, and the Bump has a lower density (Fig. S3 B), suggesting that not only the difference in the path length between the crypts and the shedding sites but also the geometrical feature, flat or curved, determines cell density. In addition, slight decreases in cell density from the crypts to shedding sites are shown (Fig. S3 C), which echoes the cell-density profiles in the lower villus region (22,35). Fig. 3 D shows the shedding-cell age distributions. In all geometries, the peak points of the distributions shift to the right of the respective minimal shedding-cell ages, and left tails appear. The shifts would be due to random cell motion caused by cell-cell interactions, which prevents cells from straight moving from the crypt orifices to the shedding sites (Video S1), and cells that migrate in the shortest times decrease. The average shedding-cell ages are approximately equal among structures, as indicated by the solid lines. On the other hand, the Villus has the smallest SD of the shedding-cell ages, followed by the Bump and then Disk. Dash and dot-dash lines in Fig. 3 D indicate the early and late shedding-cell ages that are defined as the 10th and 90th percentiles of the shedding-cell ages, respectively. The Villus has the oldest early shedding-cell ages, followed by the Bump and Disk, in that order. By contrast, the Villus has the youngest late shedding-cell ages, followed by the Bump and Disk, in that order. Fig. 3 E shows intraepithelial-cell age distributions. The average intraepithelial-cell age increases in the order of the Villus, Bump, and Disk. The old intraepithelial-cell age, indicated by the 90th percentile of each intraepithelial-cell age distribution, also increases in the same order. The results of the 3D model show the following compared with the Bump and Disk under equal cell proliferation rates and equal total cell numbers: the Villus reduces the spread of the shedding-cell ages and limits cells from shedding early or staying in the epithelium for prolonged periods. These results agreed well with the predictions of the stochastic model.

Video S1. The 3D surface cell-based model: villus, bump, and disk

Proliferative cells are colored yellow, and differentiated cells are colored white.

Validation of the 2D plane cell-based model

To promote generalization and examine various mechanical conditions of cells, we then built a simplified 2D plane cell-based model using the same framework as the 3D model. As shown in Figs. 4 A and S4 A, we considered two flat, rectangular geometries with one crypt and one shedding site at opposite ends. They differ in length: Long and Short. Cells increased in the crypts move toward the shedding sites.

We began by examining whether the 2D model shows similar results to the 3D model. Their dimensions and parameter values are determined for the same total cell numbers and same cell proliferation rates; ordered collective cell migration occurs in the upper parts of both shapes (Video S2). The equilibrium total cell numbers are constant over time (Fig. S4 C), and both shapes have approximately equal average cell-shedding rates (Fig. 4 B). The average total cell numbers are also approximately equal between the two shapes (Fig. 4 C). The Long has a higher average cell density than the Short (Fig. S4 D), and both show gradual decreases in cell density from the crypts to the shedding sites (Fig. S4 E). The shedding-cell age distributions, shown in Fig. 4 D, have the same average, but the Long has a narrower range than the Short. Considering the subsequent comparisons with distributions having largely different average shedding-cell ages, the spread of shedding-cell ages is compared using the coefficient of variations (CVs) in the 2D model. The Long has an older early shedding-cell age and younger late shedding-cell age than the Short. Moreover, the Long has a narrower intraepithelial-cell age distribution than the Short (Fig. S4 F). These results are similar to those of the 3D model, indicating that the stochastic model predictions are held for the 2D model. We hereinafter refer to the conditions or results of this section as normal.

Video S2. The normal condition in the 2D plane cell-based model: long and short

Proliferative cells are colored yellow, and differentiated cells are colored white.

Effects of active cell migration

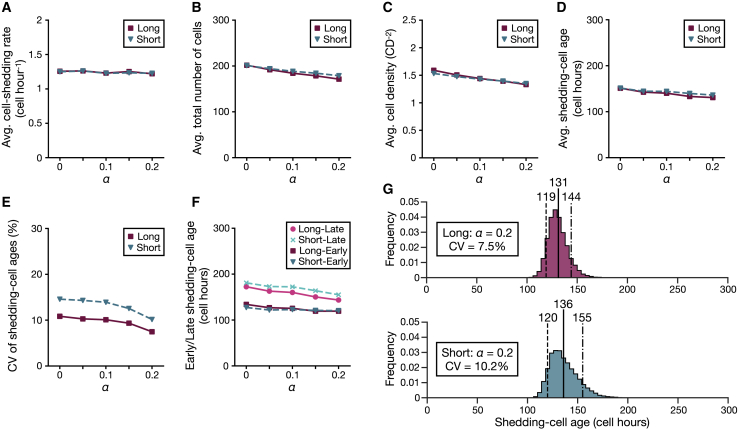
Although the renewal of the intestinal epithelium is considered to be driven by the mitotic pressure in the crypts (1,21), active cell migration of an actomyosin-dependent manner has also been proposed to occur in the upper part of the villus (19,22). We then simulated this effect in the 2D model by applying an active migration force in the y axis direction, as expressed by Eq. 4. Here, α is a constant representing the magnitude of the active migration force and varied between 0 and 0.2. The “normal” settings above are used for the other parameter values except for the crypt depth.

We regulate the crypt depth to achieve approximately equal proliferation rates for all conditions, and the average cell-shedding rates become about the same (Fig. 5 A). Increasing cell movement toward the shedding sites decreases the average total cell numbers (Fig. 5 B), average cell density (Fig. 5 C), and average shedding-cell ages (Fig. 5 D). Cell density increases toward the shedding sites as α increases (Fig. S5 A), which is similar to the cell-density profiles observed in the upper villus region (22). The decreased cell density near the crypts allows space for cells from the crypts and reduces noise due to displacements by cell proliferation in the crypts (Fig. S5 B; Video S3). This, in turn, decreases the CVs of shedding-cell ages for large α, and the Long has smaller CVs than the Short does for all α (Fig. 5 E). The differences between the early and late shedding-cell ages also decrease as α increases, and the Long has a narrower range of the shedding-cell ages than the Short does for all α (Fig. 5, F and G). In addition, the average and early shedding-cell ages of the Long fall slightly below those of the Short as α increases, which would be due to different cell motility between the Long and Short caused by the small difference in cell density depending on the shapes (Fig. 5 C). To conclude, active cell migration advances the shedding-cell ages and decreases their spread.

Figure 5.

Effects of active cell migration. The setting α = 0 gives the same outcome as the “normal” results. (A) Given is the average number of cells that shed per one cell hour. (B) Given is the average total number of cells in the models. (C) Given is the average cell density of the models. (D) Given is the average shedding-cell age. (E) Given is the CV of the shedding-cell ages. (F) Given are the early or late shedding-cell ages. (G) Shown are the shedding-cell age distributions of the Long (top) and Short (bottom) for α = 0.2. The dashed lines represent the early shedding-cell ages, the solid lines represent the average shedding-cell ages, and the dot-dash lines represent the late shedding-cell ages. To see this figure in color, go online.

Video S3. Active cell migration in the 2D plane cell-based model: long and short for α = 0.2

Proliferative cells are colored yellow, and differentiated cells are colored white.

Effects of different material properties of cells

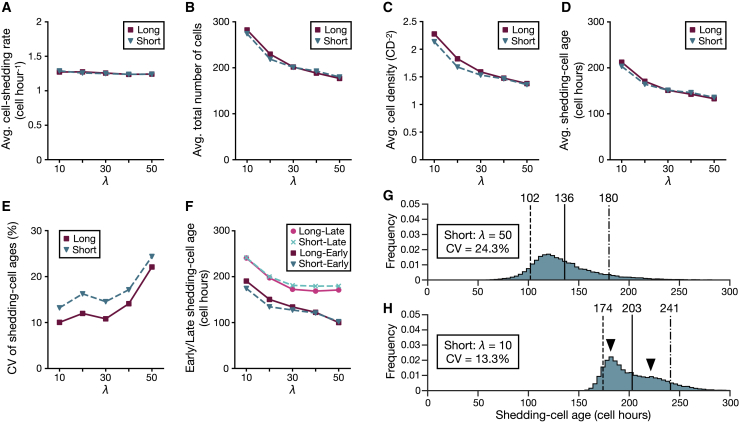
In the 3D model and in the normal configuration of the 2D model, we set parameter values of the spring constant (μ) and drag coefficient (η) to minimize cell rearrangements and achieve coordinated collective cell movements, as observed in the villus surface (7,22). However, different parameter values would alter cell behavior and affect shedding-cell age distributions. In the cell-based models, a parameter λ = μ/η relates to relaxation timescales at cellular levels (36) and collective cellular diffusion at tissue levels (31,37); a large value of λ corresponds with a short relaxation time and fast and long-distance propagation of internal stress. Here, we simulate the 2D model by fixing η = 1.0 and varying μ between 10 and 50 to examine the effects on cell turnover with different material states of cells. The settings of the normal configuration are used for the other parameter values except for the crypt depth.

The proliferation rates are set to be equal for all conditions, and the average cell-shedding rates are approximately the same (Fig. 6 A). The average total cell numbers (Fig. 6 B), average cell density (Fig. 6 C), and average shedding-cell ages (Fig. 6 D) decrease as λ increases. The cells crowd and move slowly with small λ, and they become sparse and move quickly for large λ (Video S4). Cells are densely packed near the crypts, which leads to a marked decrease in cell density from the crypts to the shedding sites for small λ, and the density approaches uniform for large λ (Fig. S6 A). The CVs of the shedding-cell ages show a tendency to increase as λ increases, and the Long has smaller CVs than the Short does for all λ (Fig. 6 E). The differences between the early and late shedding-cell ages are the smallest when λ = 30, and the Long has a narrower range of the shedding-cell ages than the Short for all λ (Fig. 6 F). In addition, as in the case of active cell migration, the slight differences in the average shedding-cell ages between the Long and Short would be attributed to different cell motility caused by their cell-density differences (Fig. 6 C). For large values of λ, young and old cells mix in the surfaces (Fig. S6 D), which would be due to the low cell density and effective propagation of cell-division-driven displacements, thus the shedding-cell ages are widely distributed (Figs. 6 G and S6 B). By contrast, small λ has gradual cell age distributions with little cell mixing in the surfaces (Fig. S6 D), which would be due to the short crypt depth (Table S2) and short-distance propagation of internal stress. However, small λ exhibits bimodal shedding-cell age distributions (Figs. 6 H and S6 C), which would be due to slight separation of population movement for wide channels caused by the high cell density and slow transportation of internal forces. This is supported by the results that a narrow channel shows a unimodal shedding-cell age distribution (see Supporting materials and methods, Appendix S8; Fig. S6 E; Video S5). When λ = 30, cells distribute within the surfaces in order of age (Fig. S6 D), and the shedding-cell ages do not exhibit dual modes (Fig. 4 D). Finally, large or small values of λ show wide and multimodal distributions of the shedding-cell ages under the same cell proliferation rates and the same model shapes; a moderate value of λ (=30) leads to coordinated collective cell migration and supports the stochastic model predictions.

Figure 6.

Effects of different material properties of cells. The results when λ = 30 are the same as the “normal” results. (A) Given is the average number of cells that shed per one cell hour. (B) Given is the average total number of cells in the models. (C) Given is the average cell density of the models. (D) Given is the average shedding-cell age. (E) Given is the CV of the shedding-cell ages. (F) Given are the early or late shedding-cell ages. (G and H) Shown are the shedding-cell age distributions of the Short for λ = 50 (G) and λ = 10 (H). The dashed lines represent the early shedding-cell ages, the solid lines represent the average shedding-cell ages, and the dot-dash lines represent the late shedding-cell ages. Arrowheads indicate the dual modes of the distribution. To see this figure in color, go online.

Video S4. Comparison of different material properties of cells in the 2D plane cell-based model: long and short for λ = 10 (left panels), and long and short for λ = 50 (right panels)

Proliferative cells are colored yellow, and differentiated cells are colored white.

Video S5. The narrow 2D plane cell-based model with λ = 10

Proliferative cells are colored yellow, and differentiated cells are colored white.

Discussion

The villi contribute most of the intestine’s luminal surface, which is essential for efficient absorption. Moreover, cell turnover renews the epithelial cells, maintaining the absorption and protection of the small intestine. Although both the villi and cell turnover are crucial for the physiology of the small intestine, how the villi affect cell turnover has not been well investigated. In this study, we used three mathematical models—the stochastic model, the 3D surface cell-based model, and the 2D plane cell-based model—to theoretically propose that the finger-like shape of the villus contributes to the tight regulation of cell turnover. We first presented a stochastic model that focuses on the duration over which cells migrate the shortest paths between the crypt orifices and the shedding sites. We suggested that tall or pointed villi both lengthen the length of the shortest path and extend its cell migration time, which reduces the spread of shedding-cell ages. We also predicted that compared with the hemispheric and circular disk structures, the finger-like structure has a longer shortest path, and thereby a longer cell migration time, and exhibits a narrower range of shedding-cell ages (Fig. 2 A). We then performed simulations of a 3D model for three geometries—Villus, Bump, and Disk—and obtained results similar to those predicted from the stochastic model: the Villus has a narrower range of shedding-cell ages, older early shedding-cell ages, and younger late shedding-cell ages than both the Bump and Disk (Fig. 3 D). Lastly, we conducted 2D model simulations for various mechanical conditions of cells. Active migration forces further advance the shedding-cell ages and reduce their spread (Fig. 5), suggesting that the active cell migration promotes cell turnover. We also showed that the shedding-cell age distributions are varied depending on the values of λ (Fig. 6) and that coordinated collective cell migration supports the predictions of the stochastic model.

We examined the effects of the villus height on cell turnover by the stochastic model. The villus height, for instance, differs among the sites of the small intestine in vivo (7): the duodenum has the tallest villi, followed by the jejunum and ileum, in that order. We also explored the effects of the geometrical difference on cell turnover using the hemispheric or circular disk structures (Fig. 1, B and C). For example, collective cell movement on a hemispheric surface is observed in the retina of teleost fish (38,39); cells from a ring-shaped stem-cell niche in the retinal periphery migrate collectively to the posterior side, which expands the eye size. In addition, cell movement on a circular disk structure is observed in the lobulus hepatis (40); cells produced near the portal triad in the lobular margin move toward the central vein during cell turnover. Observations of cell movement on tissues with different shapes would allow us to further explore the effects of surface shapes on cell turnover. Next, because the stochastic model focuses on the time over which cells move from the origin to their destination, it can be applied to various tissues with collective cell migration. The skin epidermis, for instance, grows from a single layer of proliferative cells at the base (41). Cells divide, differentiate, move outward, and shed from the skin surface. Epidermal cells of about the same age are placed side by side and shed about the same time, suggesting that the shortest-path cell migration times are close to the mean shedding-cell ages, and therefore, the spread of shedding-cell ages would be small (Eq. 7). Branch-like structures are observed in the epithelium of the lung, kidney, and mammary gland, and cells migrate collectively toward their tips during their morphogenesis (42). If their shapes are symmetric, that is all branches have equal lengths, we would obtain unimodal age distributions of cells reaching the tips of the branches. If they are asymmetric, that is branches differ in their length, there would be multiple shortest-path cell migration times, and the age of cells reaching the tips of the branches would be distributed multimodally. On the other hand, the stomach and large intestine have only randomly arranged crypts in their luminal surfaces, and cells proliferated in the crypts are considered to shed at the crypt orifices or luminal surfaces by anoikis (43,44), making it difficult to identify the shedding sites. Computational simulations would be useful to examine the shedding-cell age distributions of these tissues; the implementation of cell removal depending on cell-basal-membrane distances (45) or local cell density would not require identifying the shedding sites beforehand.

Although we used the cell migration speed, cell density, and cell-shedding rates that are independent of the height or shape of the structures in the stochastic model, they can vary with geometrical features or cell motility. First, experimental studies have indicated that geometrical constraints change collective cell behavior in vitro (46,47); cell populations move faster and more orderly in narrower geometries. Thus, strong geometrical constraints imposed by the thin shape of the villus would increase cell migration speed and lead to coordinated collective cell movement in the villus epithelium. Next, the cell-based models showed that the average cell density varies depending on the surface shapes (Figs. S3 B and S4 D), suggesting that the total cell numbers differ among structures with the same epithelial surface area. Then, the shedding-cell numbers are suggested to change with the local cell density in anoikis (48); higher cell density promotes cell shedding to maintain homeostatic cell numbers. Because cell shedding at the villus tips is considered to occur by anoikis (23,34), an increase in cell density in the upper villus region due to active cell migration (Fig. S5 A; (22)) would promote cell shedding. Finally, it has been suggested that cell extrusion frequency relates to inherent mechanical instability depending on the local curvature of the epithelium (49, 50, 51). Tight curvature of the villus tips would hence confer an advantage for cell shedding over flat surfaces, which would further promote cell shedding on the villus. These facts indicate that surface shapes, cell density, and cell behavior are involved in the regulation of cell turnover. In addition, the shortest-path cell migration times, the total cell numbers in the epithelium, and the cell supply and shedding rates would change among structures, and they would be related to each other; e.g., the shortest-path cell migration times would decrease, and the total cell numbers would increase as the cell supply and shedding rates increased. Furthermore, the stochastic model considers graded distributions of cell age in the epithelium, and the cell-based models owe cell-positional fluctuation only to cell division in the crypts. It has been indicated that cell-positional noise affects tissue renewal dynamics depending on the noise sources (52). The implementation of cell age fluctuation in our stochastic model and that of random or directional active cell motility in mechanical models would allow us to understand the effects of cell-positional exchange on cell turnover. Finally, the results of the cell-based models indicate that the material states of cells alter cell population behavior and affect shedding-cell age distributions (Fig. 6). Cellular mechanical properties such as cell stiffness are varied depending on the types or malignancy of cells (53), which would lead to different dynamics of cell turnover.

Conclusions

We have shown theoretical evidence that the finger-like shape of the villus contributes substantially to the tight regulation of cell turnover in the small intestine and have highlighted the significant roles of the villi in homeostatic maintenance of the small intestine. Our stochastic model suggested that the villus extends the cell migration time over the shortest path between the crypt orifices and the villus tips and decreases the spread of shedding-cell ages. Cell-based dynamic models supported the predictions of the stochastic model and indicated that collective cell behavior also affects the shedding-cell age distributions. Finally, based on the results in this study, we provide two predictions about the influences of the villi on pathophysiology of the small intestine. First, villous atrophy associated with inflammatory diseases (5) would disturb tightly regulated cell turnover maintained by the villi and allow inefficient old cells to remain longer in the intestinal epithelium, which exacerbates malabsorption. Second, compared with other digestive organs, the small intestine has overwhelmingly low risks of tumorigenesis and cancer metastasis from other malignancies (54,55). We suggest that the tight regulation of cell shedding by the villi decreases these risks by reducing old, mutable cells and by shedding mutant cells before their colonization of the intestinal epithelium. We expect that our study would help to explore physiological functions and disorders of the digestive organs, and our approach presented here would be useful to further understand various biological tissues with collective cell movement.

Author contributions

Y.K. performed the research and wrote the article.

Editor: Mark Alber.