Trajectory-based energy landscapes of gene regulatory networks

Abstract

Multistability and natural biological variability can result in significant heterogeneity within a cell population, leading to challenges in understanding and modulating cell behavior. Energy landscapes can offer qualitatively intuitive visualizations of cell phenotype and facilitate a more quantitative understanding of cellular dynamics, but current methods for landscape generation are mathematically involved and often require specific system properties (e.g., ergodicity or independent gene/protein probability distributions) that do not always hold. Here, we present a simple kinetic Monte Carlo-based method for landscape generation from a system of ordinary differential equations using only simulation trajectories initialized throughout the phase space of interest. The resulting landscape produces three quantitative features relevant to understanding cell behavior: stability (reflected by the depth or potential of landscape valleys), velocity (representing average directional movement on the landscape), and variance in velocity (indicative of landscape positions with heterogeneous movements). We applied this method to a genetic toggle switch, a core decision-making network in binary cellular responses, to elucidate effects of biologically relevant intrinsic and extrinsic cues. Intrinsic noise, such as stochasticity in transcription-translation and differences in cell cycle position, manifests through changes in valley width and position, reflecting increased population heterogeneity and more probabilistic cell fate transitions. The landscapes also capture the effect of an external inducer, revealing a quantitative correlation between the rate of cell fate transition and the energy barrier above a threshold inducer concentration determined by the permissivity of the valley. Further, in tracking dynamically changing landscapes under time-varying external cues, we unexpectedly found that an oscillatory inducer input can modulate cell fate heterogeneity and lead to periodic cell fate transitions entrained to the input frequency, depending on the intrinsic degradation rate of the switch. The landscape generation approach outlined herein is generalizable to other network topologies and may provide new quantitative insights into their dynamics.

Significance

Cellular noise is essential for adaptation and survival in dynamic environments, but this heterogeneity can also hinder therapeutic efficacy (e.g., in cancer) and robust cell engineering (e.g., in stem cell differentiation). Here, we present a simple method for energy landscape generation that requires only trajectories generated from an ordinary differential equation model. We use this approach to visualize and quantify the effects of key sources of noise on a gene regulatory network, generating, to our knowledge, new insights into the propagated effects of such heterogeneity on cell behavior. We further quantify how landscape dynamics change in the presence of an external cue and identify a strategy for achieving more uniform behaviors in an inherently nonoscillatory system: response entrainment using an oscillatory cue.

Introduction

Biological systems can be manipulated by different extrinsic cues, such as growth factors, cytokines, and mechanical stresses (1), but individual cells can show significant heterogeneity in their response to the same external cue (2) because of intrinsic variability (e.g., cell cycle position (3,4), differences in protein levels (5,6), and stochasticity in transcription-translation (7,8)). This phenomenon is often exacerbated by the presence of multiple steady states, leading to divergent cell fates. Conventional systems analysis techniques, such as bifurcation diagrams, can only capture multiple steady states in the context of deterministic multistability and are not designed to capture intrinsic variability and biological noise. Similarly, whereas stochastic simulations from an initial state can account for noise and multimodality (9), analysis of the resulting trajectories only provides local details in the neighborhood of the simulation trajectory and steady state. Such narrowly focused information is typically insufficient for biological systems, particularly when there are multiple stable steady states that are distributed across phase space; thus, a global picture is required to infer system characteristics such as the presence and robustness of all possible cell fates. Using these analyses can lead to omission of key features that determine cell behavior, posing a significant challenge in understanding biological systems, particularly in the context of noise and variability.

Energy landscapes offer an intuitive way of understanding the global behavior of systems with multiple steady states and different types of noise (10). This approach has been used in several biological contexts to understand cell decision making, most famously in the form of Waddington’s epigenetic landscape in visualizing embryonic development (11). In this qualitative depiction, undifferentiated cells can be thought of as a collection of balls that gravitate toward valleys with low potential (differentiated states), with their movements being dictated by the topography of the landscape and the noisiness of the system. The path of each individual cell can vary, depending on its initial state and inherent noise within the system, mirroring the heterogeneity in cell response and fate under the same external cue, as is often observed experimentally. Landscape formalisms have been used to understand several biological systems, including genetic switches (12, 13, 14), cell cycle progression (15), and cell differentiation processes (16,17). Initial approaches were based on stochastic simulations of systems that probabilistically transition between steady states, sampling the trajectories over long periods of time; although narrowly applicable, this method allowed the generation of a system landscape using the probabilities of the occurrence of each state in the phase space (18,19). Unfortunately, this approach requires the system to have ergodicity (i.e., the system has to be able to sample the entire phase space, given enough time, through noise-driven fluctuations). This can be unrealistic for faithfully representing biologically relevant systems. For example, cell differentiation processes often lead to one stable cell type and do not stochastically transition between different phenotypes. Subsequent approaches solving for the steady-state probability distributions (16,20) are more broadly generalizable but can be mathematically involved; formulating the chemical master equations or, alternatively, equations for mean and variance of each species to obtain the corresponding probability distributions is challenging, particularly for high-dimensional systems and different types of noise. This approach tends to be highly system specific and requires recalculation for any change in the system interactions. Because steady-state probability distributions are used, the resulting system landscape only shows dynamics in terms of perturbations from the steady state, which need not be the same as the dynamics of approaching steady state in higher-dimensional systems. Furthermore, these solutions assume and solve for independent probability distributions for all model variables (e.g., genes and proteins), even when analyzing highly interconnected and thus interdependent gene regulatory networks; although this allows for a mathematically simpler analysis, the approximation does not always accurately reflect the underlying biology.

Here, we present a simple kinetic Monte Carlo-based landscape generation methodology that captures both steady-state and intermediate dynamics of a biological system. From a system of ordinary differential equations (ODEs), the method initializes stochastic simulations at multiple randomly sampled starting conditions and tracks each cell throughout these simulations. The recorded trajectories are then used to generate the underlying landscape potential and flux without requiring ergodicity. The simplicity and extensibility of this method make it trivial to study model variations, such as additional species or time-varying cues, which would require significant reformulation of the chemical master equation or mean/variance-based equations. We applied our method to produce quantitative landscapes of a genetic toggle switch, a useful test bed because it is at the core of several important biological decision-making circuits involving cell fate decisions (21, 22, 23) and cell cycle regulation (5,24). For example, during cell cycle progression, both G1/S and G2/M transitions are each governed by a bistable toggle switch. In particular, the G1/S transition is modulated by a toggle switch involving the cyclin-dependent kinase CDK2 and its inhibitor p21. Studies involving this network have significantly advanced the understanding of heterogeneity in the quiescence-proliferation decision (i.e., whether a cell will divide or not), as well as factors affecting the duration of the G1 phase (5). The toggle switch is also a core topology during multiple stages of the stem cell developmental trajectory. Trophectoderm lineage determination, one of the first decisions made during fetal development, is governed by a toggle switch involving OCT4 and CDX2. Similarly, endoderm lineage determination is dictated by a Nanog-GATA6 toggle switch. Understanding the behavior of these core topologies has elucidated stem cell behavior in both in vivo development and in vitro differentiation (25).

For a minimal synthetic genetic toggle switch (26), the landscape shows steady-state details of the system, as predicted by the deterministic model; in addition, the effect of noise on system stability, as well as features of intermediate system dynamics, such as relative time to steady state, can be elucidated. Our methodology further allowed us to investigate the role of intrinsic variability among cells such as differing initial protein abundances, transcriptional bursting, and cell cycle position. We then studied the effect of extrinsic cues on the system, showing how both constant and time-dependent applications of an inducer influence the landscape. A constant input destabilizes the noninduced state while simultaneously reducing the potential barrier for transition to the induced state, eventually leading to cell transitions. This threshold is predicted by the velocity vectors in the noninduced valley corresponding to the permissivity of the valley. Further, the cell transition rate can be predicted from the corresponding potential barrier through transition-state theory. In contrast, oscillatory inputs cause the underlying system landscape to dynamically change and, at certain frequencies, entrain a toggle switch to have concerted periodic transitions tuned to the input frequency. This characteristic frequency is dependent on the system timescale, which in this case is the intrinsic degradation rate of the proteins. Overall, this study presents a simple and generalizable method for landscape generation to elucidate key biologically relevant effects of typical intrinsic and extrinsic cues on a gene regulatory network.

Materials and methods

Software

The ODE-based deterministic mathematical model was solved using the numerical stiff solver ode23s in MATLAB (The MathWorks, Natick, MA). The Gillespie algorithm for the stochastic model was programmed in C++. Histograms, videos, graphs, trajectories, and pseudoenergy landscapes were visualized using MATLAB. Additional graphs were generated using Microsoft Excel (Microsoft, Redmond, WA).

Energy landscape generation

We sampled initial conditions randomly from the entire phase space of interest and tracked the simulation until steady-state potentials converged; this time was determined by a deterministic simulation of our system for one parameter set and remained unchanged to allow reasonable comparisons across different parameter sets. We used the protein abundances sampled from these trajectories to construct a probability distribution (P) that was then converted into a pseudopotential energy surface (U = −ln(P)), which is plotted as a function of the variables of interest to obtain a potential energy surface. Further details are provided in the Supporting materials and methods.

Velocity calculation

We calculated the velocities of each trajectory by a finite time difference formula or by using the ODE expression $d\overline{x}/dt=f\left(\overline{x}\right)$. In a given discretized area of the phase space, we averaged the velocity of all trajectories that pass through the area and assigned this as the velocity at the center of the discretized area within the landscape, denoted by an arrow, the length of which is proportional to the logarithm of the magnitude of the velocity, and a circle, the radius of which is proportional to the logarithm of the associated coefficient of variation. Using a logarithmic scale for these components allows a better comparison between different points in the landscape that have disparate velocity magnitudes. Linear scales also tend to deemphasize details in regions with low velocities, particularly near unstable steady states, leading to a less informative visualization. Further details are provided in the Supporting materials and methods.

Stochastic gene expression

During each time step in the simulation, we sampled the state of each gene, checking whether it was bound or unbound by using the concentration of the inhibitory molecule. If the gene could produce protein (i.e., was unbound) and the Gillespie algorithm selected the protein production step, we then increased the number of proteins by a number sampled from a Poisson distribution, the mean of which corresponded to the mean burst size. If the gene was bound, then no proteins were produced. When there were multiple genes for the same protein (e.g., after DNA replication), we checked the binding state for both genes and updated the reaction propensities accordingly. MATLAB and C++ code used to generate landscapes for each case are provided in Data S1 (TrajectoryBasedLandscapes.zip).

Results and discussion

Generation of potential and velocity for an energy landscape

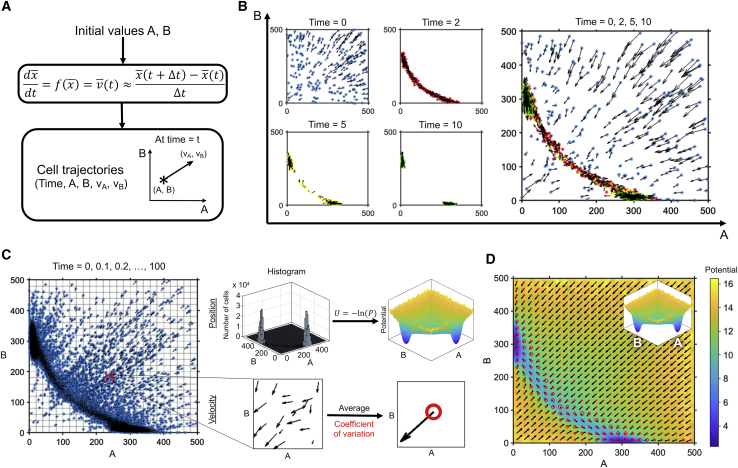
In molecular dynamics, the potential energy surface reflects the corresponding probability distribution of system states; a lower potential energy implies that the system has a higher probability of existing in that state during a simulation. Using this principle, we designed a set of simulations that capture the relative probabilities of the existence of a cell with a specified concentration of state variables (e.g., protein abundances). We sample initial conditions randomly from the entire phase space of interest (Fig. 1 A), thereby bypassing the requirement for ergodicity. The number of initial conditions is determined by a quantitative convergence analysis (27). We track the simulation and use the protein abundances sampled from these trajectories to construct a probability distribution (P) that is then converted into a pseudopotential energy, U = −ln(P) (Fig. 1, B and C). This allows us to generate a potential energy surface that is reflective of the corresponding probability distribution of system states.

Figure 1.

Generation of a potential energy landscape with velocities. (A) Schematic showing the generation of cell trajectories to obtain position and velocity within the phase space of interest is shown. (B) The scatter plots at different times show the abundances of A and B, as well as the velocities for 250 out of 10,000 cells used for the simulation. The plots are also shown as an overlay. (C) Conversion of the scatter plot to a potential energy landscape with velocities is shown. The combined scatter plot of A and B abundances and velocities sampled at different times is shown. The abundances are used to generate a 2D histogram that is then converted into a potential energy surface. The phase space is discretized, and the velocities within each gridded region are averaged to obtain the mean velocity and variance for that region. (D) Combined landscape with potential and flux for a genetic toggle switch is shown.

A valley on the landscape represents a region with low potential energy, where cells remain for a large amount of simulation time. Typically, this would correspond to a steady state, especially for systems in which the direction of motion can be inferred from the slope of the potential energy surface. However, some systems might have a temporary transition state that the system traverses before reaching a steady state. For example, lineage commitment for hematopoietic progenitors can pass through a temporary bipotent transition state before committing to a final cell fate (28). In a more extreme case, the cell cycle, which shows oscillatory behavior at steady state, requires the system to not stay at a fixed potential energy minimum within the generated landscape, but rather compels movement, depending on the velocity at each point on the landscape (15). Thus, potential energy alone does not provide a complete picture of the system; we require the velocity along the potential surface to make accurate conclusions about system behavior.

For a two-dimensional system, velocities on the landscape would simply be the time derivative calculated from the dynamic equations. However, for higher-dimensional systems, this becomes nontrivial because we do not necessarily possess (or cannot accurately represent) information about variables that are not the axes of the generated landscape. The time derivatives could be integrated out of the N-dimensional system to convert it into a two-dimensional system (15), particularly if the variable distributions are independent of each other, but this process tends to be nontrivial. Instead, we use a simpler method that involves determining the velocities of each cell at each point along the trajectory, either by calculating $d\overline{x}/dt=f\left(\overline{x}\right)$ or by using a simple finite time difference, $\left(\bar{x}\left(t+\Delta t\right)-\bar{x}\left(t\right)\right)/\Delta t$. Using this, we obtain the average velocity and coefficient of variation at each point within the phase space, shown as arrows (vectors) and circles at the base of each arrow, respectively (Fig. 1 C). The generated average velocities have good agreement with the deterministic velocities calculated using the rate equations, indicating that this method can be used to describe system velocity and direction of motion within a landscape (Fig. S1). Overall, this energy landscape with velocity overlays (Fig. 1 D) provides an intuitive visualization and quantitative understanding of biological systems, particularly those with nonlinearities, multistability, and stochasticity.

This technique is also applicable to higher dimensions. Given the use of simulation trajectories, the calculation of the potential energy function remains straightforward; however, the challenge is in depicting the result in an intuitive and meaningful manner. For a three-species system, the result can be visualized as a “potential object,” where the color at different coordinate positions represents the underlying potential energy (Fig. S2, A and B). For a more intuitive representation, dimension reduction techniques, such as principal component analysis, can be used to simplify N-dimensional trajectories (N > 2) into two-dimensional (2D) trajectories, which can then generate a traditional potential energy surface (Fig. S2 C).

Although we have used the Gillespie algorithm to account for the inherent noisiness and to generate cell trajectories, other simulation approaches, such as stochastic differential equations with a noise term or even deterministic methods, could be used to obtain a similar visualization. However, each method has limitations in terms of how accurately it would capture necessary system characteristics. For example, deterministically generated landscapes would only be able to account for differences in trajectories along the landscape due to initial protein abundances and would be unable to represent molecular, transcriptional, and other cellular noise usually present in these systems. Appropriate modeling choices can be made in generating the landscape to further simplify trajectory generation, depending on the biological features necessary for understanding system behavior.

Effect of intrinsic parameters on the landscape

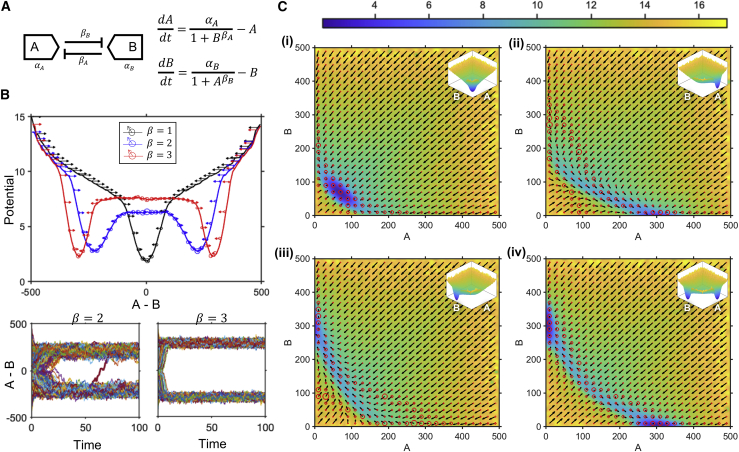
We chose to apply this method to a genetic toggle switch with two cross-antagonistic proteins, A and B, that bind to each other’s DNA and repress corresponding protein production. The simple toggle switch topology (Fig. 2 A) consists of two key parameters: α, the intrinsic production rate, and β, the cooperativity of repression. By increasing the latter, we observe that the system goes from being monostable to robustly bistable, as predicted from deterministic simulations of this toggle switch (Fig. 2 B, top; (26)). In addition, the generated landscapes provide details of the steady state and intermediate system dynamics. At β = 2, we observe that the system can stochastically switch between the two steady states (Fig. 2 B, bottom left). This is indicated by the presence of near-zero average velocities with high variances between the two basins, which implies that the individual cell velocities are nonzero and in opposite directions, facilitating cell transitions between the two valleys, even at steady state. As we go from β = 2 to β = 3, the system reaches steady state faster (indicated by the steeper gradient descent into the valleys) and has less variability associated with the stable steady states (indicated by the narrower width of the valleys); these phenomena are confirmed by the time series of the two conditions (Fig. 2 B, bottom).

Figure 2.

Energy landscapes of a genetic toggle switch showcasing both steady-state behavior and intermediate dynamics. (A) Schematic of the genetic toggle switch is shown. (B) One-dimensional (1D) representations of the system landscape for different cooperativities of repression (top) with temporal trajectories of each cell for β = 2 and β = 3 (bottom) are shown. (C) Pseudoenergy landscapes are shown for different rates of production of A and B: (i) α_A = 1, α_B = 1, (ii) α_A = 3, α_B = 1, (iii) α_A = 1, α_B = 3, (iv) α_A = 3, α_B = 3. Color bar indicates system potential.

By varying the intrinsic protein production rates (α), we obtain four qualitative states: 1) both OFF, 2) A ON, B OFF, 3) A OFF, B ON, and 4) both ON (Fig. 2 C). The fourth condition shows the existence of a bistable landscape. The two valleys, with velocity vectors converging into them, represent the stable steady states of the system; the point of zero average velocity with divergent velocity vectors in the region between the two valleys, represents the unstable steady state. The velocity vectors also indicate that the unstable steady state is a saddle node, as expected from deterministic stability analysis. In addition, the velocity vectors support the fact that the system is indeed bistable and does not have two states due to noise-induced bimodality. The latter would arise from stochastic switching between the two states, leading to the presence of a large number of zero average velocity vectors, with high variance in the region between the states, which is not the case here. Additionally, both steady-state valleys persist under a more deterministic regime, with an increased number of molecules in the system (Supporting materials and methods; Fig. S8). Taken together, these results show that our methodology can capture steady-state details (e.g., stability, variance, and stochastic switching), as well as intermediate dynamics (e.g., time to steady state), features that are typically missing from deterministic analyses as well as other methods of landscape generation.

Integration of intrinsic biological variability into the landscape

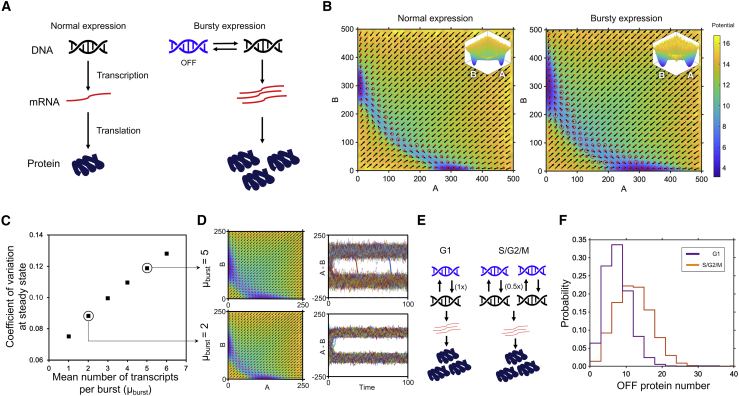
Biological systems often exhibit intrinsic variability due to noise in protein expression, potentially leading to heterogeneous responses under the same external cue (7). A major contributor to this intrinsic noise is transcriptional bursting, the rapid, stochastic generation of multiple mRNA molecules from a single DNA molecule (Fig. 3 A; (29)). In this process, a DNA molecule is thought to switch stochastically between two states: accessible (ON) or inaccessible (OFF) by the transcription machinery. When the DNA is ON, multiple transcripts are rapidly produced, depending on how long the gene is accessible and the probability of transcription machinery binding to the gene. In our simulations, we assume that this number of transcripts is given by a Poisson distribution (30), defined by the mean number of transcripts produced per burst or mean burst size (μ_burst). To provide a commensurate comparison, we scale the DNA ON time by μ_burst; this scaling ensures that the mean expression levels of the proteins remain the same, regardless of the mean burst size. Accounting for this additional process in our simulation, we observe an increase in the widths of both the stable valleys and the intermediate region, indicating that the system has more observed heterogeneity in protein levels throughout the simulation, even though the mean expression levels are unchanged (Fig. 3 B). This heterogeneity also increases with increasing mean burst size (Fig. 3 C). Burstiness can also decrease system stability by promoting stochastic switching between two steady states, particularly for genes with larger mean burst sizes (Fig. 3 D). This implies that systems with similar mean protein expression can still exhibit different biological behavior if they have different intrinsic noise in protein production, resulting in an irreversible decision when μ_burst is low and a more plastic outcome when μ_burst is high. Our analysis here has assumed Poissonian synthesis, but mRNA production is not always Poissonian and can change, depending on the promoter and gene (30,31). This can lead to differently shaped valleys, depending on the shape of the underlying distribution (Fig. S3). Nonetheless, the increase in variability due to burstiness and the subsequent consequences are likely to remain qualitatively applicable to other cases.

Figure 3.

Energy landscape of a genetic toggle switch showing the effect of bursty expression and cell cycle progression. (A) Schematic of conventional deterministic expression compared with stochastic bursty expression is shown. (B) Landscapes are shown of normal expression and bursty expression (mean burst size = 5 mRNA/protein per transcription-translation cycle) while keeping the net protein production rate constant. (C) Scatter plot showing the coefficient of variation at steady state for different mean burst sizes is shown. (D) Landscapes for genes with equal mean expression and different burst sizes shown alongside the single cell trajectories are shown. (E) Schematic showing the differences between transcription in G1 phase versus transcription in S/G2/M phases is shown. (F) Distributions are shown for the repressed protein at steady state when the cell is in the G1 phase or S/G2/M phases. The two distributions are statistically distinct, as assessed by the Kolmogorov-Smirnov test (p < 10⁻⁶).

An additional source of heterogeneity in genetically identical cells arises from the cell cycle position. After DNA replication (S/G2/M phases), cells halve their total transcription rate to maintain the same rate of protein synthesis compared with cells with a single copy of DNA (G1 phase). This has been shown in previous studies to be due to reduction in the time that each DNA copy spends in a transcriptionally accessible state (Fig. 3 E; (29)). This phenomenon leads to an increase in variance of the OFF protein and more leakiness of the system at steady state because of higher concentrations of the repressed protein (Fig. 3 F). The increased variance results in greater population heterogeneity and therefore heterogeneity in response to an external cue, even when considering a uniform population of cells in S/G2/M. Additionally, increased leakiness during S/G2/M in these cells makes them more susceptible to leaving the steady state under the same external cue. This could potentially be used to selectively target cells in the S/G2/M phase, as is generally preferred in cancer treatment to selectively kill actively dividing tumor cells while leaving nondividing normal cells unaffected.

Overall, these intrinsic factors can lead to significant variability, even within a genetically identical population, and potentially lead to incorrect biological interpretations, both qualitatively and quantitatively, when applied in an experimental setting. Thus, accounting for these intrinsic factors is important in establishing an accurate mechanistic understanding of the system and subsequently being able to engineer desired behaviors.

Effect of a constant external cue on the landscape

External cues, ranging from cytokine signals to mechanical forces to osmotic stress, can markedly influence the behavior of biological systems. These cues are generally experimentally tunable and can significantly change key features of the system landscape, including the number of valleys, depth of the valleys, and the paths accessible by cells. This can lead to dramatically different cell behaviors. Qualitative and quantitative insights into the effect of these cues, particularly in the context of biological variability, can help design better strategies for manipulating biological systems to produce desired behaviors, for example in designing more robust stem cell differentiation protocols.

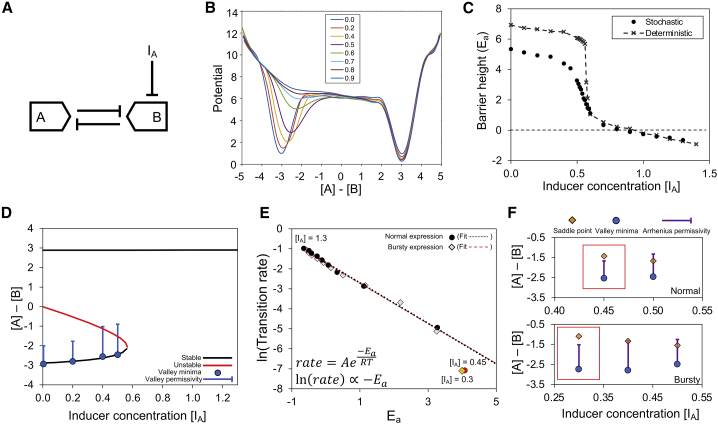
Chemical inducers are a class of external cues that commonly serve as inputs to synthetic biological circuits to produce the desired output. Many of these molecules regulate gene expression of a protein by disabling its repressor, usually by binding to the repressor and decreasing its affinity for its DNA binding site (Fig. 4 A). Increasing the effective inducer concentration biases the bistable system landscape toward the induced state by destabilization of the opposing node. This initially manifests as a reduction in valley depth and increased leakiness for the noninduced state, as well as a reduction in the transition barrier from the noninduced state to the induced state. This eventually leads to the disappearance of both the noninduced valley and the intermediate region, resulting in a monostable landscape with a single valley corresponding to the induced state (Fig. 4 B). This change in landscape is reversible with removal of the inducer; however, the reversibility in cell phenotype is dependent on whether the system can stochastically transition at steady state (Figs. S4 and S5).

Figure 4.

Effect of inducer on the toggle switch landscape. (A) Schematic shows the effect of inducer on the toggle switch. (B) Potential landscape as a function of the concentration difference between A and B for different inducer concentrations is shown. Concentration [X] of a component X is given by the number of molecules of X divided by the system Avogadro number (N_A = 100 in this case). (C) Effect of inducer on barrier height (activation energy) in the stochastic case compared with the deterministic case is shown. (D) Stability diagram of the toggle switch system with respect to inducer concentration overlayed with the valley minima and valley permissivity calculated from stochastic simulations, showcasing the ability of the stochastic system to transition at lower inducer concentrations, is shown. (E) Correlation between activation energy and transition rates for different inducer concentrations for normal expression (black circles) and bursty expression (gray diamonds) with linear fits to each (black dots and red dashes, respectively) is shown. The red circle and orange diamond are cases in which the correlation fails (overpredicts transition rate) for normal and bursty expression, respectively; these are for inducer concentrations of 0.45 and 0.3 for normal and bursty expression, respectively. The lowest simulated inducer concentrations that follow the correlation are 0.5 and 0.4 for normal and bursty expression, respectively, with the next points increasing in intervals of 0.1 up to a maximal inducer concentration of 1.3. (F) Graphs show the valley minima with valley permissivity and the saddle point for the normal and bursty expression cases showing failure of the Arrhenius correlation when the saddle point does not lie within the range of valley permissivity in the red boxes.

In a deterministic toggle switch, transitions to the induced state happen abruptly above a certain inducer concentration when the energy barrier for transition suddenly and dramatically decreases (Fig. 4 C). This threshold concentration also corresponds to the point in the stability diagram where the system undergoes a saddle node bifurcation, going from three steady states (two stable, one unstable) to one stable steady state (Fig. 4 D). However, when stochasticity is introduced within the system, the energy barrier for the transition process begins to decrease at a slightly lower inducer concentration and changes less abruptly compared with the deterministic case. This leads to a region within the phase space where there are noise-driven transitions that occur at lower inducer concentrations than the deterministic threshold. The presence of these transitions is better understood from the stability diagram and the variability due to stochastic noise at steady state, here referred to as valley permissivity. On the landscape, this is defined as the positive difference between the concentration at the valley minimum and the maximal achievable concentration away from the valley minimum at steady state due to stochastic variability without undergoing a transition. Specifically, transitions occur when the valley permissivity overlaps the saddle point (unstable steady state), allowing cells to transition to the induced state once they probabilistically cross this point (Fig. 4 D).

The presence of these noise-driven transitions has a twofold effect on cell behavior. First, there are induced transitions at lower inducer concentrations than predicted by the deterministic analysis, which could lead to incorrect inference of key biological parameters. Second, because of the probabilistic nature of these crossings, only a fraction of the cells can reach the induced state at these low inducer concentrations within a given time period, thus leading to a heterogeneous population, unless the time frame is long enough to allow all cells to transition. Cells that do not respond to a cue within the time frame of an experiment, because of stochasticity as described here, could be incorrectly perceived as a distinct phenotype. For example, this could be problematic in cancer chemotherapy or antibiotic treatment, in which constraints on drug dosing may lead to the incorrect conclusion that cells are drug resistant instead of stochastically nonresponsive but potentially treatable with a different treatment regimen.

In addition to quantitative insight on the presence or absence of transitions, these landscapes also provide information about the dynamics of transition. As per transition state theory, the natural logarithm of the transition rate is proportional to the energy barrier height as measured from the initial state (also referred to as activation energy, E_a). Specifically, this Arrhenius equation is $\ln \left(k\right)=-E_a/RT$, where k is the rate constant for a process, R is the gas constant, and T is absolute temperature. Indeed, we observe a strong correlation between the mean transition rate (i.e., inverse of the mean transition time as measured through stochastic simulations) and the energy barrier (Fig. 4 E). Notably, this relationship fails below a threshold inducer concentration, overpredicting the expected rates. By analyzing the landscapes, we found that this failure occurs when the saddle point is not within a certain relative concentration, here referred to as Arrhenius permissivity (Fig. 4 F), meaning that cells do not reach the saddle point at a sufficiently high frequency. On the landscape, the Arrhenius permissivity refers to the positive difference between the concentration at the valley minimum, [X]_min, and the concentration [X], whose steady-state probability relative to the valley minimum is given by the exponent of the negative of the transition energy barrier; in other words, [X] is defined by $P_{ss}\left(\left[X\right]\right)/P_{ss}\left({\left[X\right]}_{min}\right)=e^{-E_a}$, where P_ss refers to steady-state probability. In our simulations, steady state refers to the time after the transient approach to the stable steady states has been completed. Additionally, within this toggle switch system, [X] corresponded to the concentration for which the potential is ∼80% of the transition barrier energy. We also note that, by definition, the valley permissivity is greater than the Arrhenius permissivity. The former indicates whether stochastic transitions are possible, and the latter determines whether the transition rates follow the Arrhenius relationship.

The Arrhenius equation requires that, given sufficient time, the system must sample the entire phase space (or in the case of unidirectional reactions, the region between the initial state and the transition state) at a frequency inversely proportional to the exponent of the energy at each point. However, in our system, because of decreased Arrhenius permissivity at lower inducer concentrations, this does not remain true and thus leads to slower transitions. This is further validated by increasing Arrhenius permissivity by adding transcriptional bursting to the system (Fig. 4 E). We observe that the threshold inducer concentration in which the relationship fails now decreases and still corresponds to the case wherein the saddle point does not lie within the Arrhenius permissivity (Fig. 4 F).

Quantitative prediction of transition times and determining the point of failure can help design better experimental strategies with dynamic inputs to achieve desired cellular behavior. Stem cell differentiation strategies often involve treating cells with a series of different cues that direct them toward a particular fate. Determining the optimal exposure times for each cue is critical for specifying the differentiation trajectory and subsequently the final cell fate. Errors in this timing can lead to undesired excursions on the landscape and consequently undesired cell types. Given a functionally accurate model, this type of analysis can be used to suggest optimal time points for each cue while taking into consideration natural biological variability and stochasticity.

Effect of a time-dependent external cue on the landscape

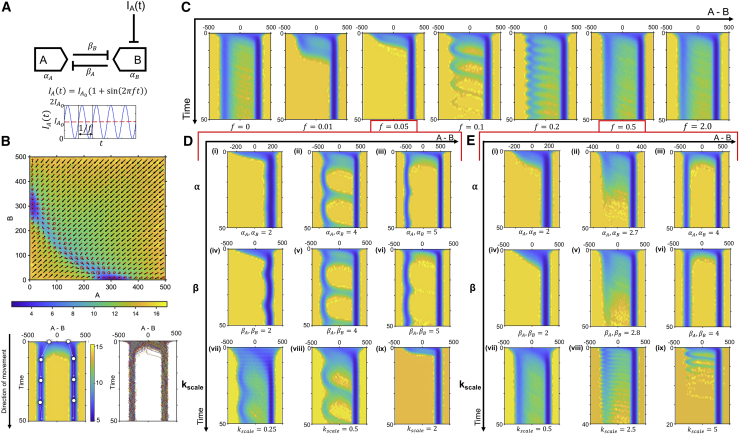
Biological circuits are often exposed to time-varying input signals. In many cases, these are oscillatory inputs with a characteristic amplitude and frequency, as seen in circuits regulated by the cell cycle (32), circadian rhythm (33), p53 signaling (34), and NF-κB signaling (35). To simulate this in our system, we used a sinusoidal inducer concentration $I_A\left(t\right)=I_{A_0}\left(1+\sin \left(2\pi ft\right)\right)$ with a characteristic amplitude $I_{A_0}$ and frequency f (Fig. 5 A). However, because of the highly dynamic nature of the inputs, the landscapes are not constant and instead change shape, depending on the instantaneous inducer concentration (Video S1). This makes interpreting the landscape using a simple 2D picture challenging and can lead to inaccurate conclusions about system behavior if done without representing the dynamic nature of these landscapes.

Figure 5.

Effect of sinusoidal inducer inputs on the toggle switch landscape. (A) Schematic showing the effect of inducer on a simple toggle switch landscape along with a description of the input sinusoidal inducer concentration is shown. Parameters used to generate the simulations are shown in the table. (B) 2D landscape of a toggle switch with I_A = 0.2 followed by the waterfall landscape depiction and time trajectories of the same system is shown. (C) Waterfall landscapes depicting the effect of different frequencies of inducer sine wave oscillation are shown. (D and E) Waterfall landscapes show the effect of system parameters α (i–iii), β (iv–vi), and k_scale (the time constant of the system; vii–ix) in inducing concerted transitions within the landscape at f = 0.05 (D) and f = 0.5 (E).

To visually encode this information, we generate “waterfall landscapes” that showcase snapshots of the one-dimensional (1D) landscape at each instant as a function of time (Fig. 5 B). In this depiction, each cell can be thought of as a ball starting at an initial condition from the top of the landscape and preferentially moving toward regions of lower potential while simultaneously rolling down the plot (much like an actual ball moving along a rivulet or waterfall). Although we lose some information by transforming a 2D (A,B) system to a 1D (A-B) system, this allows us to understand cellular decision making in the face of dynamically changing landscapes while still providing information about cell fate distributions, intrinsic noise, and differences in starting conditions, features that are not captured in a static landscape or the time trajectories of the system.

Interestingly, we observe that frequency of the oscillatory input can significantly change system response, even under constant amplitude of input (Fig. 5 C). For a fixed amplitude of $I_{A_0}=0.5$, we broadly observe three regimes of system behavior, depending on input frequency. At low but nonzero frequencies, the system is completely induced to a single stable steady state. At intermediate frequencies, the system exhibits periodic concerted transitions to the induced stable steady state corresponding to the frequency of inducer input. In this regime, a toggle switch system can be made to behave similar to an oscillatory system with a characteristic frequency. However, at higher frequencies, the system behavior is similar to a nonoscillatory input, and there do not appear to be concerted transitions. Biologically, these findings indicate that a toggle switch, a characteristically binary system, can be modulated to show different responses, depending on the frequency of an input signal. To our knowledge, this has not been reported in literature and presents interesting implications for biological systems governed by the toggle switch. For example, regulation of the p21-CDK2 biological switch by the oscillatory p53 signal (36) could lead to significant heterogeneity within a population, depending on the characteristic frequency of oscillation, with more uniformity at lower frequencies and more heterogeneity at higher frequencies, even when the amplitude remains the same. Additionally, this strategy of periodic inducer application may be useful in stem cell differentiation to produce a more homogeneous population in cases for which a desired inducer is cytotoxic at high, sustained concentrations (e.g., CHIR in cardiomyocyte differentiation (37)), but better tolerated in high-concentration pulses.

To better understand the dependence of system behavior on input frequency, we perform a parameter sensitivity analysis on f = 0.05 (Fig. 5 D), a frequency too low to elicit concerted transitions in the original simulations, and f = 0.5 (Fig. 5 E), a frequency too high to elicit concerted transitions. In the former case, we observe that increasing α and β by a small amount can restore concerted transitions to the system, whereas in the latter, changes in both parameters are unable to produce concerted transitions. An additional parameter is the characteristic time constant of the system that has been used in the scaling analysis for obtaining nondimensional ODEs, k_scale, which here is the intrinsic degradation rate constant of the proteins in the system. Decreasing this parameter (i.e., slowing down the kinetics of the system) results in concerted transitions for f = 0.05, whereas increasing this parameter (i.e., speeding up the system) does the same for f = 0.5. These results provide insight into the key requirements for these transitions to occur in a periodic manner. When the frequency is too low (f = 0.05), the amount of inducer in the system increases and stays greater than the mean for long periods of time (t = 20), leading the cells to be completely induced (Video S2). This can be counteracted by increasing the intrinsic production rate α within the system, which would then require longer time periods of high inducer concentration for complete induction. Similarly, increases in the cooperativity of repression β make the potential barrier between the two states higher, which again requires longer periods of high inducer for induction. These changes allow the system to have concerted transitions under low-frequency oscillatory inputs.

When the frequency is too high, the system is unable to react fast enough to the rapidly changing landscape and thus behaves similarly to a system with a constant inducer concentration (Video S3). This can be modified by increasing k_scale, which allows the system to react more quickly to the rapidly changing landscape, resulting in concerted transitions. This behavior is also seen at low frequencies if the system is slowed down by decreasing k_scale. Specifically, these concerted transitions are observed when the input frequency is such that it can periodically induce a subpopulation of cells from the opposing state and does not change significantly before at least part of the subpopulation of induced cells reaches the separatrix (Videos S4 and S5). In conclusion, there is a “Goldilocks” frequency range that is dependent on the system parameters that allows the system to respond with less heterogeneity.

Conclusions

This study presents a simple method for landscape generation to facilitate intuitive visualization and quantitative analysis of a gene regulatory network within the context of biologically relevant variability. Through this approach, we are able to identify, quantify, and better understand system dynamics; here, we used a well-studied genetic toggle switch as an exemplar for testing and validating our method, and we discovered unexpected behaviors such as system entrainment. The approach can be readily extended to analyze and visualize more complex two-dimensional systems, such as a self-activating toggle switch (Figs. S6 and S7), and even higher-dimensional systems using data reduction techniques (Fig. S2 C), potentially including comprehensive models parametrized with multiomics data to supplement purely data-driven approaches (38,39). Additionally, this type of analysis can be particularly useful in systems for which noise and heterogeneity within a given population create a barrier to forming an accurate understanding, posing significant challenges in modulation and prediction of behavior. For example, heterogeneity within a patient tumor underpins the presence of dormant cancer cells and drug-resistant subpopulations (40); these lead to significant difficulty in designing effective treatment regimens and predicting patient outcome. Similarly, heterogeneity within a cell population can lead to unintended variability in cell fate under an external cue, leading to difficulty in generating populations of a single cell type through differentiation or dedifferentiation without additional processing steps (41,42). Utilizing the framework developed herein can aid in including such effects more easily and facilitate the development of strategies to better predict and modulate cellular response.

Author Contributions

H.V., S.M.A., and C.A.S. designed the study, analyzed the data, and wrote the manuscript. H.V. performed the computational simulations.

Editor: Kevin Janes.

Supporting material

Data S1. TrajectoryBasedLandscapes.zip

Compressed folder with MATLAB code for visualization and C++ code for toggle switch trajectory generation