Characterization of the strain-rate–dependent mechanical response of single cell–cell junctions

Significance

Cell–cell junctions are essential components in multicellular structures and often experience strains of different magnitudes and rates. However, their mechanical behavior is currently underexplored due to the lack of techniques to quantitatively characterize junctional stress–strain relationships. We developed a polymeric microstructure to strain the mutual junction of a single cell pair while simultaneously recording the junction stress and observed previously unseen strain-rate–dependent junction responses. We showed that cytoskeleton growth could relax the stress buildup and prevent junction failure at low strain rates, while high strain rates led to synchronized junction failures at remarkably large strains (over 200%). We expect this platform and our biophysical understanding to form the foundation for the rate-dependent mechanics of cell–cell junctions.

Abstract

Cell–cell adhesions are often subjected to mechanical strains of different rates and magnitudes in normal tissue function. However, the rate-dependent mechanical behavior of individual cell–cell adhesions has not been fully characterized due to the lack of proper experimental techniques and therefore remains elusive. This is particularly true under large strain conditions, which may potentially lead to cell–cell adhesion dissociation and ultimately tissue fracture. In this study, we designed and fabricated a single-cell adhesion micro tensile tester (SCAµTT) using two-photon polymerization and performed displacement-controlled tensile tests of individual pairs of adherent epithelial cells with a mature cell–cell adhesion. Straining the cytoskeleton–cell adhesion complex system reveals a passive shear-thinning viscoelastic behavior and a rate-dependent active stress-relaxation mechanism mediated by cytoskeleton growth. Under low strain rates, stress relaxation mediated by the cytoskeleton can effectively relax junctional stress buildup and prevent adhesion bond rupture. Cadherin bond dissociation also exhibits rate-dependent strengthening, in which increased strain rate results in elevated stress levels at which cadherin bonds fail. This bond dissociation becomes a synchronized catastrophic event that leads to junction fracture at high strain rates. Even at high strain rates, a single cell–cell junction displays a remarkable tensile strength to sustain a strain as much as 200% before complete junction rupture. Collectively, the platform and the biophysical understandings in this study are expected to build a foundation for the mechanistic investigation of the adaptive viscoelasticity of the cell–cell junction.

Adhesive organelles between neighboring epithelial cells form an integrated network as the foundation of complex tissues (1). As part of normal physiology, this integrated network is constantly exposed to mechanical stress and strain, which is essential to normal cellular activities, such as proliferation (2–4), migration (5, 6), differentiation (7), and gene regulation (7, 8) associated with a diverse set of functions in tissue morphogenesis (9–11) and wound healing (9). A host of developmental defects or clinical pathologies in the form of compromised cell–cell associations will arise when cells fail to withstand external mechanical stress due to genetic mutations or pathological perturbations (12, 13). Indeed, since the mechanical stresses are mainly sustained by the intercellular junctions, which may represent the weakest link and limit the stress tolerance within the cytoskeleton network of a cell sheet, mutations or disease-induced changes in junction molecules and components in adherens junctions and desmosomes lead to cell layer fracture and tissue fragility, which exacerbate the pathological conditions (14–17). This clinical relevance gives rise to the importance of understanding biophysical transformations of the cell–cell adhesion interface when cells are subjected to mechanical loads.

As part of their normal functions, cells often experience strains of tens to a few hundred percent at strain rates of 10⁻⁴ to 1 s⁻¹ (18–21). For instance, embryonic epithelia are subjected to strain rates in the range of 10⁻⁴ to 10⁻³ s⁻¹ during normal embryogenesis (22). Strain rates higher than 0.1 s⁻¹ are often experienced by adult epithelia during various normal physiological functions (21, 23, 24), such as breathing motions in the lung (1 to 10 s⁻¹) (25), cardiac pulses in the heart (1 to 6.5 s⁻¹) (20), peristaltic movements in the gut (0.4 to 1.5 s⁻¹), and normal stretching of the skin (0.1 to 5 s⁻¹). Cells have different mechanisms to dissipate the internal stress produced by external strain to avoid fracture, often via cytoskeleton remodeling and cell–cell adhesion enhancement (26, 27). These coping mechanisms may have different characteristic timescales. Cytoskeleton remodeling can dissipate mechanical stress promptly due to its viscoelastic nature and the actomyosin-mediated cell contractility (17, 28–32). Adhesion enhancement at the cell–cell contact is more complex in terms of timescale. Load-induced cell–cell adhesion strengthening has been shown via the increase in the number of adhesion complexes (33–35) or by the clustering of adhesion complexes (36–39), which occurs on a timescale ranging from a few minutes up to a few hours after cells experience an initial load (28). External load on the cell–cell contact also results in a prolonged cell–cell adhesion dissociation time (40, 41), suggesting cadherin bonds may transition to catch bonds under certain loading conditions (42, 43), which can occur within seconds (44). With the increase in cellular tension, failure to dissipate the stress within the cell layer at a rate faster than the accumulation rate will inevitably lead to the fracture of the cell layer (45). Indeed, epithelial fracture often aggravates the pathological outcomes in several diseases, such as acute lung injuries (46), skin disorders (47), and development defects (48). It is generally accepted that stress accumulation in the cytoskeleton network (49, 50) and potentially in the cytoplasm is strain-rate–dependent (51). However, to date, there is a lack of understanding about the rate-dependent behavior of cell–cell adhesions, particularly about which of the stress-relaxation mechanisms are at play across the spectrum of strain rates. In addition, it remains unclear how the stress relaxation interplays with adhesion enhancement under large strains, especially at high strain rates which may lead to fracture, that is, a complete separation of mature cell–cell adhesions under a tensile load (45, 52, 53). Yet, currently, there is a lack of quantitative technology that enables the investigation of these mechanobiological processes in a precisely controlled manner. This is especially true at high strain rates.

To delineate this mechanical behavior, the cleanest characterization method is to directly measure stress dynamics at a single mature cell–cell adhesion interface. Specifically, just as a monolayer cell sheet is a reduction from three-dimensional (3D) tissue, a single cell–cell adhesion interface, as a reduction from a monolayer system, represents the smallest unit to study the rheological behavior of cellular junctions. The mechanistic understanding uncovered with this single unit will inform cellular adaptations to a more complex stress microenvironment in vivo and in vitro, in healthy and diseased conditions. To this end, we developed a single-cell adhesion micro tensile tester (SCAµTT) platform based on nanofabricated polymeric structures using two-photon polymerization (TPP). This platform allows in situ investigation of stress–strain characteristics of a mature cell–cell junction through defined strains and strain rates. With SCAµTT, we reveal some interesting biophysical phenomena at the single cell–cell junction that were previously not possible to observe using existing techniques. We show that cytoskeleton growth can effectively relax intercellular stress between an adherent cell pair in a strain-rate–dependent manner. Along with cadherin-clustering–induced bond strengthening, it prevents failure to occur at low strain rates. At high strain rates, insufficient relaxation leads to stress accumulation, which results in cell–cell junction rupture. We show that a remarkably large strain can be sustained before junction rupture (>200%), even at a strain rate as high as 0.5 s⁻¹. Collectively, the rate-dependent mechanical characterization of the cell–cell junction builds the foundation for an improved mechanistic understanding of junction adaptation to an external load and potentially the spatiotemporal coordination of participating molecules at the cell–cell junction.

Results

SCAµTT, a Single-Cell Adhesion Interface Mechanical Characterization Platform.

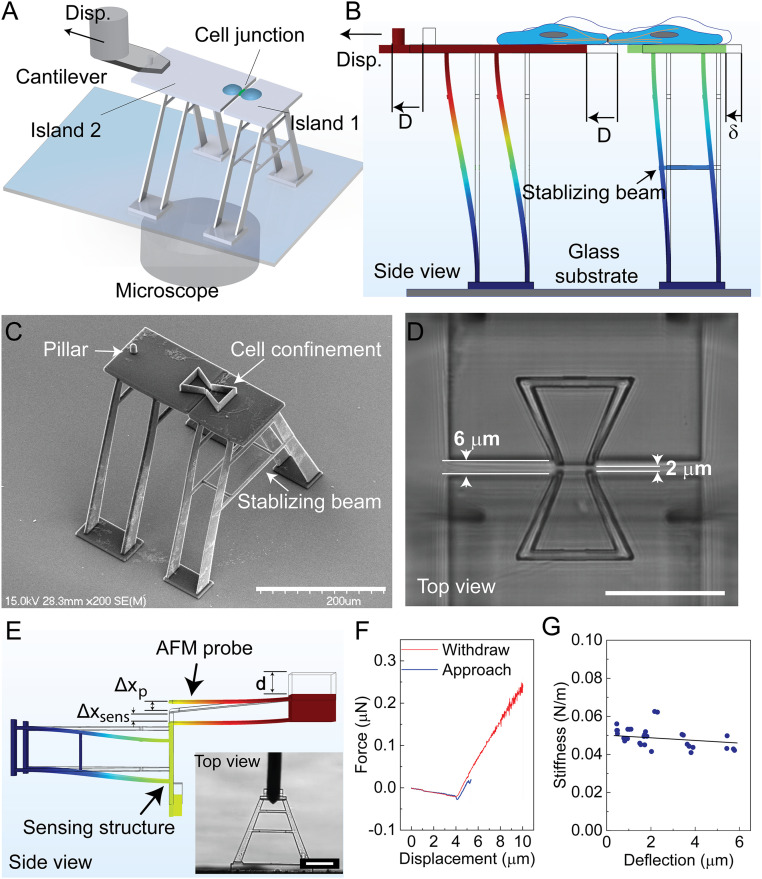
A microstructure has been designed and fabricated to interrogate the mechanical behavior of the cell–cell adhesion complex under large strains (Fig. 1A). This structure, fabricated from IP-S photoresist using TPP (54), consists of two movable islands on top of vertical “A-shaped” beams with well-calibrated stiffness. A pair of epithelial cells are deposited onto the movable islands with one on each side. The formation of a mature cell–cell junction between the cell pair mechanically couples the two islands. To interrogate the mechanical responses of the cell pair, we displace one of the islands (Island 2) using a nanopositioner from an atomic force microscope (AFM) system in a precisely controlled manner, while the other one (Island 1) is consequently displaced by the tensional force transmitted through the cell–substrate adhesion and the cell–cell junction. The coupling between the nanopositioner and Island 2 is facilitated by capturing the pillar structure on Island 2 using an engineered AFM probe in which a through-hole is drilled by focused ion beam (FIB) etching. The device is integrated on top of an inverted microscope for monitoring the displacement of the islands, from which the deformation of the supporting beams is determined based on digital image correlation (DIC). Island 1, therefore, functions as a force sensor that can be used to measure nano-Newton range forces by relating its displacement to the spring constant of the beam that supports it (Fig. 1B). A detailed illustration of the platform is shown in SI Appendix, Fig. S1.

Fig. 1.

A single cell–cell adhesion interface mechanical characterization platform. (A) A single cell pair with junctional contacts is formed on Islands 1 and 2. To apply mechanical strain to the cell–cell junction, an AFM-based manipulation system displaces Island 2. (B) The deflection of Island 1 (δ) under the applied displacement (D) is recorded to determine the force–displacement relationship. (C) Scanning electron microscopy (SEM) image of the structures fabricated on top of a glass substrate. The bowtie structures confine the cells on each island. (D) The two islands were spaced 6 µm apart to prevent attachment of the islands to each other, with a 2-µm gap between the cell-confining bowties to allow formation of the cell–cell junction. (E) To measure the stiffness, an AFM probe applies force to the structure until a displacement set point is achieved, and then retracts. The AFM records the applied force, P_AFM, and vertical displacement d. The vertical structure displacement, Δx_sens, and deflection of the AFM probe, Δx_p, are determined from the AFM output. The inset image shows the probe applying force onto the structure. (F) A representative force–displacement curve obtained at a maximum applied force of 294 nN is shown. (G) Sensing structure stiffness, k_sens, versus structure deflection, Δx_sens is plotted (n = 30). (Scale bars, 200 µm in C; 50 µm in D; 100 µm in E.)

Design, Fabrication, and Mechanical Characterization of the Sensing Structures.

The stiffness of the supporting beams was designed to be as close to the stiffness of the cell–cell junction (0.01 N/m to 0.5 N/m) (55) as possible to acquire the best balance between force-sensing resolution and applied strain to the cell–cell junction, with the ability to measure a force in the range of 0 to 50 nN at the junction (56, 57). Compared with horizontal beams, vertical beams offer greater control of their length, which allows for easy adaptation to this desired stiffness and offers better structural stability during the TPP fabrication process (SI Appendix, section 2 and Figs. S2 and S3). A set of vertical “A-shaped” beams were designed and fabricated considering different constraints in beam stiffness, beam stability, fabrication limitations, and imaging requirements (SI Appendix, section 2). To confine the migration of the deposited cells, a bowtie structure was designed and fabricated with one trapezoid on each island. The area of the trapezoid and the length of its opening edge were optimized to preserve the physiological conditions with an area large enough to sustain cell growth and an opening edge of 12 μm to facilitate junction formation at the interface between the two islands (56, 57) (Fig. 1C). The gap between the two movable islands, particularly between the bowtie opening where the junction forms, should be kept to a minimum to facilitate junction formation, but a gap distance of less than 2 μm leads to unwanted polymerization of the resin that tethers the two islands during the fabrication process. We increased the gap of the nonbowtie region to 6 μm to reduce the risk of attachment of the islands (Fig. 1D).

To measure the stiffness of the “A-shaped” beam structure, a tipless cantilever probe with a thermally tuned stiffness was used to apply force on an isolated sensing structure in phosphate-buffered saline (PBS) solution. Based on the displacement of the probe and the force measurement from the AFM probe, the deflection and subsequently the stiffness of the microstructure were determined (Fig. 1E and SI Appendix, section 3). For each measurement, the automated detection of the AFM was used to initiate contact between the probe and the structure. Once contact was established, a constant probe displacement rate was initiated to apply force on the structure until the force set point was achieved. The probe was then retracted until it was no longer in contact with the structure before beginning the process again. This produced the force–displacement curve, from which the stiffness of the beam can be extracted (Fig. 1F). The calculated beam stiffness was found to be 0.049 ± 0.005 N/m under liquid conditions (Fig. 1G), which is within the desired range. This stiffness value remains valid for a sensing beam deflection of ∼6 µm (i.e., a maximum force of 294 nN), displaying a large linear range. It is worth mentioning that the TPP printing parameters, including laser power and scan speed, can have a significant influence on the measured stiffness. Considering the resolution of DIC at a few tens of nanometers, this sensing beam stiffness can resolve the forces of a few cadherin bonds [∼40 pN for each cadherin bond (58)]. Furthermore, the elastic behavior of the sensing beam is confirmed with a stretch-and-release experiment showing negligible plastic deformation (SI Appendix, section 4 and Fig. S4).

Formation of Cell–Cell Adhesion Junctions on the Platform.

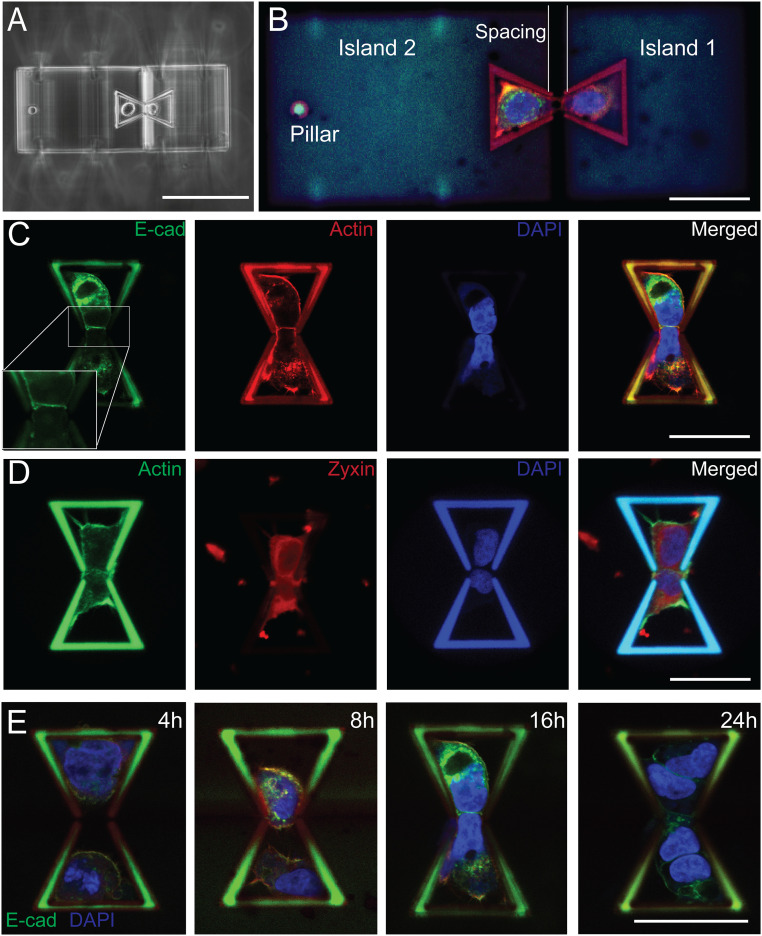
Cells were deposited into the bowtie structure using an Eppendorf single-cell isolation setup, which includes a pressure controller, a 3D manipulator, and microcapillary (59) (SI Appendix, section 5 and Fig. S5). To enhance cell attachment to the structure, fibronectin was used to coat the surface of the bowtie structure. As shown in Fig. 2A, a pair of A431 cells were successfully deposited and placed inside the bowtie structure. The cells expressed green fluorescent protein (GFP)-tagged E-cadherin (E-Cad) and were stained for F-actin and nucleus after being deposited and incubated for 16 h. A mature cell–cell junction, defined as the homeostatic state when E-Cad levels and distribution are stabilized at the cell–cell contact (60), is formed between the cell pair as indicated by the expression of GFP-tagged E-Cad, which bridges the gap between the two islands and mechanically couples them (Fig. 2 B and C). The immunofluorescence images of these cells on the structure suggest that the polymer material used in the TPP fabrication is biocompatible and allows for proper cell attachment and growth. Staining zyxin, a widely used mature focal adhesion protein marker (61), together with F-actin confirms that cells successfully form focal adhesions on the structure (Fig. 2D). To find the best time for mechanical characterization after cell deposition, a time-lapse study was performed (4, 8, 16, and 24 h). The results showed that cells do not form a mature junction before 16 h. However, they start proliferating after 24 h, resulting in more than two cells within each bowtie confinement (Fig. 2E). Therefore, prior to mechanical testing, cells were incubated for 16 h after cell deposition.

Fig. 2.

Cell–cell adhesion formation and cell growth on the scaffolds. (A) Phase-contrast image shows a pair of suspended A431 cells deposited onto the fabricated structure in the opposing bowtie confinement scaffolds. (B) The deposited cell pairs adhered onto the scaffold and started to form a cell–cell junction at the gap to couple the two movable islands. Cells expressing GFP-tagged E-Cad were stained for actin (red) and the nucleus (blue). (C) A431 cells expressing GFP-tagged E-Cad were imaged 16 h after deposition with actin (red) and nucleus (blue) staining. (D) Zyxin (red), actin (green), and nucleus (blue) were stained to visualize the formation of focal adhesion 16 h after deposition. (E) Time-lapse images show the junction formation process, with cells expressing E-Cad GFP stained for nucleus (blue) at 4, 8, 16, and 24 h. (Scale bars, 100 µm in A; 50 µm in B to E.)

Displacement-Controlled Mechanical Characterization of the Cell–Cell Junction.

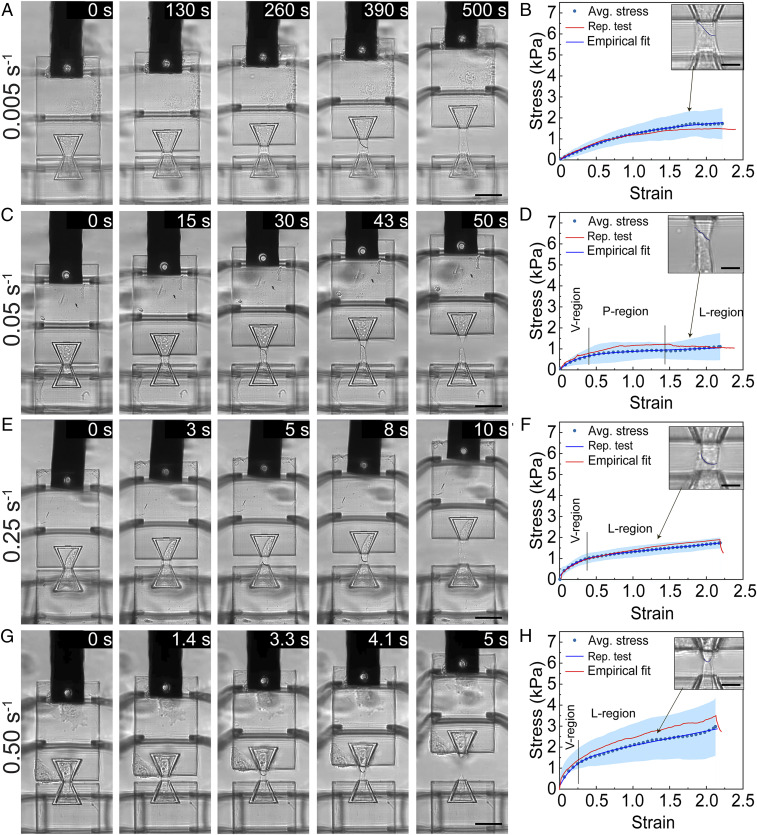
To interrogate the mechanical behavior of the cell–cell junction, we stretched the junction by displacing Island 2 at different rates. We examined four strain rates ranging from 0.005 s⁻¹ to 0.5 s⁻¹ and observed different modes of stress relaxation and cell–cell adhesion failure that are strongly strain-rate–dependent. We first stretched the cell pair at a strain rate of about 0.005 s⁻¹ (100 nm/s in displacement rate) and observed that none of the junctions failed at the end of the 50 μm displacement. A typical set of time-series images shows that there is no sign of rupture in the cell–cell junction (Fig. 3A). The stress–strain curve exhibits a typical viscoelastic behavior wherein the stress increases nonlinearly with a decreasing rate as the strain increases, and the cell pairs are elongated to a maximum strain of 221.8 ± 8.2% at a maximum stress of 1.72 ± 0.73 kPa (Fig. 3B). Under a strain rate of 0.05 s⁻¹, cell–cell junctions begin to show some signs of rupture through a gradual necking process seen in the time-series images and experience a maximum strain of 217.8 ± 10.0% and stress of 1.09 ± 0.63 kPa at the point of failure (Fig. 3 C and D). The stress–strain curve shows three different regions: a viscoelastic region, a plateau region (i.e., necking process), and a linear region up to failure at 217.8% strain. Among all the stretch tests performed under this strain rate (n > 20), 47% of them resulted in complete cell–cell adhesion rupture, indicating that 0.05 s⁻¹ may represent a critical strain rate beyond which stress accumulation induced by mechanical stretching outperforms stress relaxation. Similar observations can be made from a strain rate of 0.25 s⁻¹ with a less obvious plateau region, a higher stress level at failure, and more rapid and complete junction failure (Fig. 3 E and F). All stretch tests at the strain rate of 0.25 s⁻¹ resulted in complete junction rupture, in clear contrast to the 0.05 s⁻¹ strain rate. At a strain rate of 0.50 s⁻¹, the stress–strain curve starts with a viscoelastic region, followed by a linear region up to the rupture point. A stress level of 3.04 ± 1.36 kPa was observed at the failure point and junctions failed at 215.1 ± 37.4% strain (Fig. 3 G and H). The gradual disappearance of the plateau region from low strain rate to high strain rate tests suggests stress accumulation at high strain rate due to lagging and inadequate stress relaxation.

Fig. 3.

Displacement-controlled mechanical characterization of a single cell–cell junction at different strain rates. Representative image frames and the corresponding stress–strain curves are shown for stretch tests performed at strain rates of 0.005 s⁻¹ (A, B), 0.05 s⁻¹ (C, D), 0.25 s⁻¹ (E, F), and 0.50 s⁻¹ (G, H). For each strain rate tested, Island 2 was displaced by 50 μm. For B, D, F, and H, an average stress-strain curve (Avg. stress, dotted line) ± SD (blue region), a representative stress–strain curve (Rep. stress, red curve), and an empirical fit for the average stress (Empirical fit, blue curve) are shown. The insets for B, D, F, and H show the zoom-in images of the cell–cell junctions at the strains indicated by the arrows. In D, F, and H, the regions are marked with viscoelastic region (V-region), plateau region (P-region), and linear region (L-region). The average stress–strain curves in B, D, F, and H represent data from 11, 12, 7, and 7 stretch tests, respectively. (Scale bars, 50 µm in A, C, E, and G; 15 µm in the inset of B, D, F, and H.)

Our tensile tests demonstrate that the cell pair can withstand a remarkably large strain level before the cell–cell junction completely ruptures. This clearly contrasts with data obtained from suspended cell doublets without a mature cell–cell adhesion using dual micropipette aspiration (DPA), in which cadherin bonds rupture at small strain and low levels of stress (62). Under low strain rates, the cell–cell junction remains largely intact even when the strain is higher than 200%. Comparing with the 0.50 s⁻¹ strain rate, the lower maximum stress under the strain rate of 0.005 s⁻¹, at which cell–cell adhesion complexes remain largely intact, indicates the existence of another effective stress dissipation scheme inside cells. Considering the dynamic nature of cytoskeletons among all the intracellular structures, we speculate that the mechanical stress is dissipated via the remodeling and reorganization of their cytoskeletons. However, under high strain rates, the cell pair dissipates stress primarily through the dissociation of cell–cell adhesion complexes, and complete breakage occurs at a strain level of ∼200%. In addition, all failures occur at the cell–cell contact symmetrically through the rupture of the cell–cell adhesion complex, as observed from stretching tests at different strain rates (SI Appendix, Fig. S6 and Movies S1–S4). The image series of the tensile test (Fig. 3 A, C, E, and G) and the zoom-in images of the cell–cell adhesion region (Inset of Fig. 3 B, D, F, and H) show the decrease in length of the mutual cell junction until complete separation, suggesting intermediate bond dissociation accompanying the straining process, which leads to ultimate cell adhesion complex failure. The absence of asymmetrical failure, potentially at the cytoskeleton to cell membrane tether at one side of the cell pair, implies that the cell–cell adhesion complex represents the weakest link in the cytoskeleton–cell adhesion–cytoskeleton system. Moreover, the rupture of the cell–cell junction occurs in a gradual fashion at lower strain rates, like unzipping a zipper, with localized snap and retraction of the cytoskeleton near the failure point at the edge of the cell–cell contact.

A Mechanosensing Constitutive Model for the Viscoelastic Behavior of a Cell Pair.

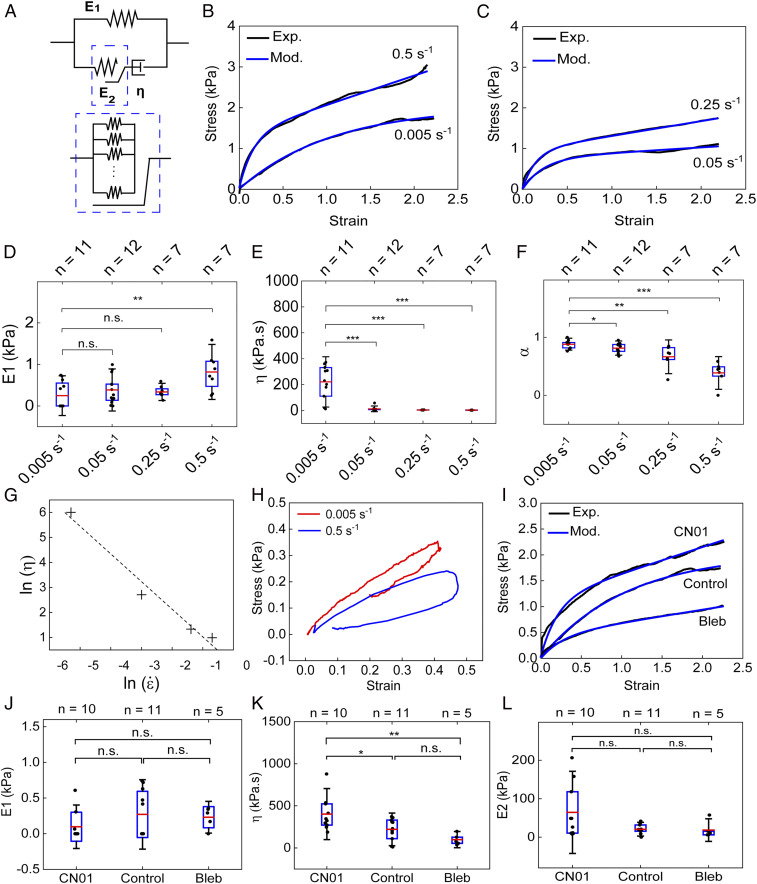
The stress–strain relationships from the four types of tensile tests of varied strain rates can be well fitted with an empirical exponential growth function plus a linear function: σ = −Ae^−Bε + Cε, supporting an overall viscoelastic behavior (Fig. 3 B, D, F, and H). Considering that the cell membrane deforms along with their intracellular components when a pair of cells are stretched, the standard linear solid (SLS) model (SI Appendix, Fig. S7A), consisting of a Maxwell branch and an elastic branch, is the simplest model that can effectively capture such a viscoelastic behavior. The SLS model has been widely used to model the mechanical responses of suspended cells, where the Maxwell branch represents the intracellular components while the elastic branch represents the plasma membrane (63). Since minimal deformation of the cell nuclei was observed even at a strain level as large as 200% in our tensile tests, we expect that the elastic element in the Maxwell branch is primarily contributed by the cytoskeleton. Although the SLS model can reproduce the general shape of the stress–strain relationships, it predicts that the elastic modulus of the spring in the Maxwell branch increases with the increase in the strain rate (SI Appendix, Fig. S7B). This prediction is in contradiction to the fact that cytoskeleton growth hardly occurs at high strain rates given the limited response time. Alternatively, we modified the SLS model by incorporating a mechanosensing component to account for the stress dissipation mediated by cytoskeleton remodeling (17, 64). As shown in Fig. 4A, the spring with Young’s modulus of E₁ represents the cell membrane, while the second spring with Young’s modulus of E₂ and the dashpot with the viscosity of η represent the elastic and viscous elements of intracellular components, respectively. The viscous component is contributed by the combined effect of cytoplasmic and cytoskeleton friction (51). The cytoskeleton of adherent cells constantly undergoes reorganization through dynamic assembly and disassembly to maintain its mechanical homeostasis in response to the tensile load. We expect that the elastic element of intracellular components is primarily contributed by the cytoskeleton, and E₂ can be considered as the collective moduli of all stress fibers that sustain the load and should be proportional to the number of individual stress fibers within the plane perpendicular to the stretching direction, as demonstrated by the inset in Fig. 4A. The value of E₂ should be collectively determined by the cell–cell junction length and cell–cell adhesion complex density. The continuous growth of the cytoskeleton is expected to lead to an increase in the resting length of the second spring, which could partially or even completely relax the passive stress (σ_S2) resulting from stretching:

$${\sigma }_{S2}=E_2\left({\epsilon }_{S2}-{\epsilon }_0\right)\text{,}$$ [1]

where ε_S2 and ε₀ are the total strain of the second spring and the strain resulting from the continuous growth of the cytoskeleton, respectively. We relate the cytoskeleton growth rate with the strain rate of the second spring through a model parameter α:

$${\dot{\epsilon }}_0=\alpha {\dot{\epsilon }}_{S2}\text{,}$$ [2]

where 0 ≤ α ≤ 1. When α = 0, ${\dot{\epsilon }}_0=0$, suggesting that the cytoskeleton does not grow at all, which corresponds to stretch with a very high strain rate. When α = 1, Eq. 2 reduces to ${\dot{\epsilon }}_0={\dot{\epsilon }}_{S2}$, indicating that the growth of the cytoskeleton is able to completely release the passive stress, which could occur under stretch with an extremely low strain rate. Therefore, α can be considered as an effective parameter to indicate the growth level of the cytoskeleton during the stretch test and thus the stress dissipation efficiency. The model predicts the following time-dependent relationship between stress (σ_tot) and strain (ε_tot):

$${\dot{\sigma }}_{tot}+\frac{(1-\alpha )E_2}{\eta }{\sigma }_{tot}=\left[E_1+(1-\alpha )E_2\right]{\dot{\epsilon }}_{tot}+\frac{(1-\alpha )E_1{E}_2}{\eta }{\epsilon }_{tot}\text{.}$$ [3]

Under a constant strain-rate condition, Eq. 3 yields

$${\sigma }_{tot}=E_1{\epsilon }_{tot}+\eta {\dot{\epsilon }}_{tot}\left[1-\text{exp}\left(-\frac{\left(1-\alpha \right)E_2}{\eta }\frac{{\epsilon }_{tot}}{{\dot{\epsilon }}_{tot}}\right)\right]\text{.}$$ [4]

As shown in Fig. 4 B and C, Eq. 4 is able to robustly capture the viscoelastic responses of cells under different strain rates. Fitting the stress–strain curves obtained in our stretch tests with Eq. 4 allows us to predict how E₁, (1 − α)E₂, and η vary with the strain rate.

Fig. 4.

Strain-rate–dependent and actomyosin-contractility–controlled viscoelastic behavior of the cell pair. (A) Diagram of the modified standard linear solid (MSLS) model that was used for fitting the experimental data. (B, C) The stress–strain curves obtained by applying stretch at different strain rates (0.005 s⁻¹, 0.5 s⁻¹, 0.25 s⁻¹, and 0.50 s⁻¹) were fitted using Eq. 4 according to the MSLS model. (D–F) Box plots comparing the values of E₁ (D), η (E), and α (F) obtained from fitting the stress–strain curves using Eq. 4 for different strain rates. (G) The predicted viscosity is plotted with respect to the strain rates in a log–log scale. (H) Hysteresis analysis is shown by recording the stress–strain relationship following a full cycle of application and release of tensile load on a cell pair at two strain rates (0.005 s⁻¹ and 0.50 s⁻¹). (I) The stress–strain curves obtained by stretching cells treated with CN01, Bleb, and DMSO control at a rate of 0.005 s⁻¹ are fitted using Eq. 4. (J–L) Box plots comparing the values of E₁ (J), η (K), and E₂ (L) obtained from fitting the stress–strain curves for cells treated with CN01 and Bleb using Eq. 4. For each box plot, the number of experiments is indicated on top of each graph. *P < 0.05, **P < 0.01, ***P < 0.001.

Our model predicts that E₁ is independent of the strain rate and has an average value of ∼1.2 kPa (Fig. 4D), which is consistent with previously reported values (51, 65). The viscosity η is predicted to monotonically decrease with the strain rate (Fig. 4E), suggesting that the cytoplasm is a shear-thinning material. Such a shear-thinning feature has been identified for the cytoplasm of several other types of cells previously (66, 67). Plotting the predicted viscosity against the strain rate in a logarithmic scale reveals that the mechanical behavior of the cytoplasm can be approximated as a power-law fluid following the Oswald equation, that is, η = $K{\dot{\epsilon }}^{(n-1)}$, with the exponent of n = −0.104 (Fig. 4G). In general, shear thinning is caused by flow-facilitated disentanglement of polymer chains, which is consistent with the expected enhanced alignment of cytoskeleton structures after cells are subjected to uniaxial stretching (68). Since the cells are expected to have similar cytoskeleton structures to start with, we can directly compare the stress dissipation efficiency mediated by the cytoskeleton growth by assuming that E₂ has the same value. The predicted decrease in α from low strain rate to high strain rate suggests that the stress dissipation efficiency decreases with strain rate as a result of reduced cytoskeleton growth (Fig. 4F). The predicted rate-dependent growth of the cytoskeleton is supported by the clear difference in the residual plastic strain after releasing the tensile load in our hysteresis tests (Fig. 4H). We stretched the cell pair under two different strain rates (0.005 s⁻¹ and 0.50 s⁻¹) to a strain level of about 40% and then completely released the mechanical load. The cell pair stretched under the strain rate of 0.005 s⁻¹ resulted in a plastic strain of ∼20%. However, less than 10% plastic strain is observed for the cell pair stretched under the strain rate of 0.50 s⁻¹, suggesting limited cytoskeleton growth under the high strain rate.

We next subjected the cell pair to cellular contractility modulators, RhoA Activator I CN01 and myosin II inhibitor blebbistatin (Bleb), to examine the impact of actomyosin activity on the mechanical behavior of the cell pair under mechanical stress. Stress–strain curves collected at a strain rate of 0.005 s⁻¹ show a clear contrast between samples treated with CN01, Bleb, and dimethyl sulfoxide (DMSO) control (SI Appendix, section 8 and Fig. S8). Specifically, CN01 raises the overall stress level compared with controls at the same strain, while Bleb reduces the stress accumulation (Fig. 4I). The stress–strain curves were then analyzed using the constitutive model. As expected, E₁ stays the same for all conditions (Fig. 4J). Enhancement of actomyosin contractility by CN01 significantly increases η and E₂, while Bleb reduces both of them (Fig. 4 K and L). The increase (decrease) in both η and E₂ by CN01 (Bleb) is consistent with the enhanced (reduced) stress fiber formation. It is worth mentioning that the stress increase induced by CN01 can be partially suppressed by subsequent addition of ROCK inhibitor, exhibiting a reverse effect on the contractility modulation, which can be captured dynamically by our SCAµTT platform (SI Appendix, Fig. S9). Collectively, our data support the idea that stress dissipation is facilitated by the actin filament growth during tensile loading conditions.

Cadherin Strengthening and Rupture under Rate-Dependent Stretch of Cell–Cell Junction.

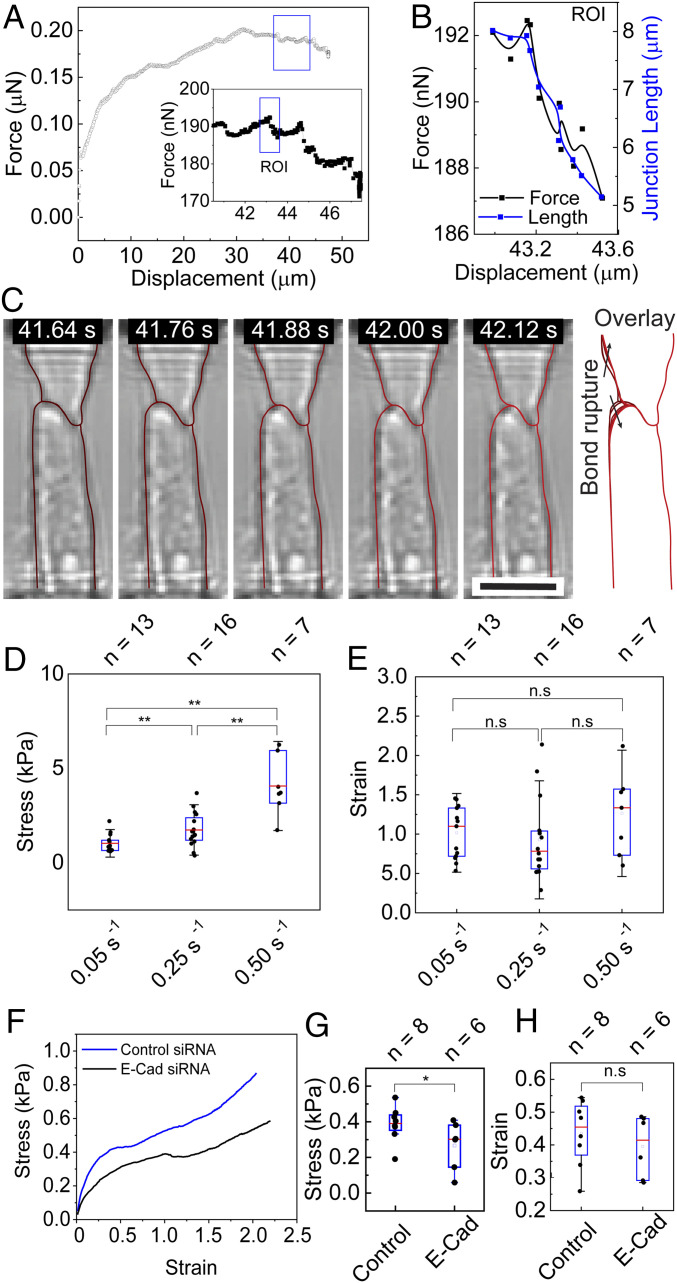
We attribute the observed necking process to the rupture of cell–cell adhesion bonds, which is most apparent under the intermediate strain rate. A few cadherin bonds are ruptured in discrete steps at the edge of the cell–cell junction, which corresponds to a small drop in the measured forces in the force–displacement curve (Fig. 5). To investigate the bond rupture, we selected a representative example of the stretch tests at the strain rate of 0.05 s⁻¹ with obvious regions of junction rupture followed by stiffening, which is represented by each drop and rise in the curve (Fig. 5A). The rupture of bonds releases the force in the stress fibers that were in direct connection with the bonds and locally relaxes the stretched cell membrane, consequently leading to a drop of the measured force. One representative region of interest (ROI) is plotted in Fig. 5B, in which a total force drop of 5 nN and a junction length reduction of ∼3 µm were observed for an ∼490-nm displacement (SI Appendix, section 10 and Fig. S10). Correspondingly, a total of 10 image frames were captured showing the snap and retraction of the cytoskeleton at the edge of the cell–cell junction (Fig. 5C), and each discrete snap motion corresponds to a small drop in force. Considering the strength of a single cadherin bond of around 40 pN (69), this decline is the result of rupturing about a few hundred cadherin bonds in each discrete event with a resolution of a few bonds.

Fig. 5.

Cadherin bond rupture exhibits rate-dependent behavior during strain-rate–controlled stretch. (A) A representative force–displacement curve obtained at a strain rate of 0.05 s⁻¹ is shown. Inset shows the zoom-in of the portions of the force–displacement curve indicated in the box. (B, C) The force–displacement curve (black curve) and junction length (blue curve) (B) within the ROI in the inset of (A) are shown, with the outline of each cell traced in corresponding frames (C). The overlay in (C) shows the change in cell–cell junction length and shape of each cell (dark red in the first frame and light red in the last frame). (D, E) Stress levels (D) and strain levels (E) at which the initiation of bond rupturing occurs for the tensile tests at different strain rates: 0.05 s⁻¹ (n = 13), 0.25 s⁻¹ (n = 16), and 0.50 s⁻¹ (n = 7). (F–H) Average stress–strain curves (F), as well as stress levels (G) and strain levels (H) at which the initiation of bond rupturing occurs, for tensile tests at 0.05 s⁻¹ on cells with E-Cad siRNA knockdown (n = 6) and control siRNA (n = 8). *P < 0.05. (Scale bars, 25 µm in C, Inset.)

The bond dissociation events also exhibit strong strain-rate dependency. First, at a very low strain rate, the absence of bond rupture may be attributed to cadherin strengthening. This is confirmed by the clustering of GFP-tagged E-Cad when the cell doublet is subject to low levels of strain (<100%) at the strain rate of 0.05 s⁻¹ (SI Appendix, Fig. S11). It has been observed that cadherin bond clustering in epithelial cells under tensile load occurs in a timescale of minutes, right in line with the time span of a low strain rate tensile test (about 10 min) (33). Second, the critical stress level at which cadherin bonds show initial signs of dissociation increases significantly with increasing strain rate (Fig. 5D). As shown in Fig. 5E, the initiation of bond rupture events occurs at similar strain levels of around 100% for all three strain rates. However, the critical stress is significantly higher for 0.50 s⁻¹ (4.04 kPa) compared with 0.5 s⁻¹ and 0.25 s⁻¹ (0.99 kPa and 1.72 kPa, respectively). Considering the time span of a few seconds for a tensile test at the strain rate of 0.50 s⁻¹, bond clustering may not be the main contributor to the observed increase in the critical stress. On the other hand, the observed increase in the strength of cadherin bonds agrees well with previous reports from single-molecule force microscopy studies of E-Cad bonds, which showed that the peak rupture force in E-Cad bonds increases logarithmically with the loading rate (69, 70). Knockdown of E-Cad by small interfering RNA (siRNA) resulted in a decrease in the overall stress level during the strain application (Fig. 5F). Analysis of the stress–strain curves of E-Cad knockdown cell pairs showed a significant decrease in the critical stress, as compared with controls using control siRNA (SI Appendix, section 12 and Fig. S12 and Fig. 5G). Interestingly, the strain levels at which cadherin bonds initiate unbinding remain unchanged with E-Cad knockdown (Fig. 5H). This may suggest that the reduction in the number of E-Cad bonds decreased the total tension within the cytoskeleton network and thus the stress level during stretching, while the remaining bonds still rupture at similar strain levels. Collectively, our results demonstrate that E-Cad adhesions regulate the load-bearing potential of the cell–cell junction under tensile load and play a major role in the rate-dependent strengthening of the cell–cell junction.

Discussion

In this study, we fabricated a polymeric microstructure using TPP for displacement application and force sensing to examine the rate-dependent mechanical behavior of a single cell–cell adhesion complex. To faithfully characterize the intricacy of the biophysical and biochemical response of an individual cell–cell adhesion interface under large strains, a functional technique needs to fulfill the following requirements. First, it should have a highly sensitive force-sensing component that allows easy quantification of pico- or nano-Newton forces. Second, it should have the capability to apply mechanical strain or stress in a controlled manner. Third, the testing can be conducted under physiologically relevant conditions, especially allowing the formation of mature cell–cell junctions and cell–extracellular matrix (ECM) adhesions. Although several techniques have been developed for the quantitative assessment of cell-generated forces, including traction force microscopy (TFM) (71), elastomer-based micropillar arrays (57), and 3D-printed microscaffolds (72, 73), they are restricted to static observations and unable to apply mechanical stimuli, not to mention strain-rate–controlled mechanical stretch. Techniques do exist to apply mechanical strain to a monolayer of cells, but the stress within individual cell–cell adhesions cannot be determined (52). Further, when a defined load is applied to individual cell–cell junctions in studies using AFM-based single-cell force spectroscopy (SCFS) (58, 74) and DPA (75, 76), it can only be carried out on isolated suspended cells in which mature intercellular junctions are yet to form, and the focus can only be placed on the separation of cadherin bonds while the effect of stress relaxation of the cytoskeleton and the cell–ECM interactions are inaccessible (62).

SCAµTT is a platform that allows in situ interrogation of the stress–strain characteristics of a mature cell–cell junction through defined strain and strain rate, promoting a paradigm shift in the mechanical characterization of cell–cell adhesions. Besides the capabilities discussed above, the throughput for mature cell–cell junction interrogation is also increased due to parallel sample preparation and testing, as the equipment for manipulating or stretching cells does not need to be used to hold cells in place during junction maturation. The presence of the mature cell–ECM junction allows for the application of large strains as in DPA, whereas the force sensitivity of the beams achieves force and displacement resolution comparable to SCFS (10 pN and 50 nm, respectively) (77). Besides its application in the mechanical characterization of single cell–cell junctions, SCAµTT can also be used to investigate the cytoskeleton mechanics and dynamics under controlled strains and/or strain rates, as well as in the study of the crosstalk between cell–cell adhesion and cell–ECM adhesion, by incorporating micropillar array-based TFM into our platform. These studies can be carried out not only on cell doublets but also on single cells and cell monolayers with minimal modification to the bowtie structure.

The ability of SCAµTT to quantify precisely the stress within a cell doublet at different strains enables us to decipher the strain-rate–dependent behavior of the cytoskeleton-junction system as part of the adaptive viscoelasticity of epithelial cell–cell junctions (78). The stress–strain relationship at different strain rates reveals multiple rate-dependent stress dissipation mechanisms orchestrated by the cytoskeleton and the cell–cell junction. We showed that the cytoplasm exhibits a passive shear-thinning viscoelastic behavior following the Oswald equation. This power-law relationship between strain rate and viscosity suggests that such a passive stress dissipation mechanism plays a significant role in the stress response, particularly at high strain rates. It is worth mentioning that this relationship has been identified for the cytoplasm of suspended cells (66, 67) but has never been shown on adherent cells. In addition, we showed that the active cytoskeleton remodeling leads to continuous stress relaxation in the network of the cytoskeleton–cell junction (79). Particularly, loads with a higher strain rate result in limited cytoskeleton growth, and thus, higher stress is accumulated within the network. When stress relaxation from the cytoskeleton growth fails to catch the increased stress induced by the continuous increase of the applied strain, a net accumulation of stress occurs. The increase in stress leads to gradual unbinding of cadherin bonds to relax the stress at low strain rates. A robust junction allows a higher capacity for cytoskeleton tension, while a partially ruptured junction reduces this capacity. Although the expected active cytoskeleton remodeling has not been confirmed directly with high-resolution immunofluorescence imaging due to the strong autofluorescence of the printed microstructures on which cells are grown, it has been validated indirectly by both the hysteresis tests and the contractility modulation experiments using cytoskeleton modulation drugs. Furthermore, as cell–cell adhesion is intimately coupled with cell-substrate adhesion (80), we expect that changing the ECM coating may affect the structure of the cell–cell junction and consequently its mechanical strength. However, we do not expect cell–ECM interaction to fundamentally change its strain-rate–dependent mechanical response.

Directly measuring stress dynamics at a single cell–cell junction captures the real-time fracture process of junction cadherins at high strain rate. Specifically, we showed that epithelial cell–cell adhesions are mechanically the weakest linkage in the junction-cytoskeleton system, and they represent the upper limit for the amount of stress that the system can tolerate before complete junction rupture occurs. However, when the cell–ECM adhesion is not sufficiently strong, failure is more likely to occur at focal adhesions. We observed that cells tended to detach from the islands during stretching experiments when a fibronectin concentration lower than 50 µm/mL was used to functionalize the bowtie structure. Moreover, we showed that, at high strain rate, stress accumulation cannot be dissipated fast enough even at low strain levels, and thus, characterization of the critical strain and strain rate at which coordinated stress relaxation and E-Cad clustering can still be sufficient to mitigate stress buildup and to allow for such a remarkable strain tolerance is critical to understand epithelial fracture (45). Further, knockdown of E-Cad changed the strain-rate–dependent behavior of the cell–cell junction, agreeing with previous reports that show E-Cad regulates epithelial viscoelasticity (81). This may also alter the patterns of cell proliferation and migration, which play important roles in disease outcome. This suggests that the mechanical interrogation platform could be used for quantifying disease states and evaluating the effect of treatments.

Conclusion

In the present work, we developed a mechanical testing platform, SCAµTT, that can strain the mutual junction of a single cell pair with precisely defined strain and strain rates while simultaneously recording the junction stress. This platform allows in situ mechanical characterizations of a mature cell–cell junction under physiologically relevant conditions and is sensitive enough to resolve bond rupture events with a resolution of a few bonds. With this innovative platform, we performed strain-rate–controlled mechanical characterization of a single mature cell–cell adhesion junction. We showed that cytoskeleton growth of the cell doublet could relax the stress buildup and prevent junction failure at low strain rates. At high strain rates, a synchronized junction failure occurs at remarkably large strain levels. We expect this platform and our biophysical understanding to form the foundation for the rate-dependent mechanics of cell–cell junctions.

Methods

TPP Fabrication.

To fabricate the structures shown in Fig. 1 and SI Appendix, Figs. S2 and S3, microscale 3D printing based on TPP was used. Computer-aided design (CAD) files in standard tessellation language (STL) format exported from COMSOL 4.2 software were imported into the Describe software (Nanoscribe, GmbH) to compile job files for the Photonic Professional (GT) tool (Nanoscribe, GmbH). The slicing and hatching distances were selected to be 0.4 μm and 0.3 μm, respectively. The vendor-supplied liquid photoresist, IP-S, and a 25× immersion microscope objective were used to print structures in the galvo-scanning mode using the so-called deep-in laser lithography optical arrangement. Glass coverslips with diameters ranging from 11 to 25 mm and thicknesses of ∼160 μm were used as substrates in the present study. Prior to 3D printing, the glass substrates were coated with indium tin oxide (ITO) to achieve optical reflectivity of the IP-S–substrate interface sufficient for autofocusing. The ITO layer had a thickness of ∼50 nm and was deposited using direct current sputtering of an ITO target in an Ar plasma. In our initial tests, we found that the 3D structures printed directly on the ITO-coated glass had insufficient adhesion and would detach from the substrate after prolonged soaking or incubation in aqueous solutions. To address this commonly encountered issue of insufficient adhesion between smooth substrates and 3D structures fabricated using TPP, we used an in-house developed protocol in which an additional layer of porous silicon oxide (PSO) was deposited on top of ITO-coated coverslips. PSO with a thickness of ∼2 μm and a high density of nanopores was found to act as an excellent anchoring layer, eliminating detachment of the 3D printed structures from the substrate during soaking and subsequent experiments in aqueous solutions. For all experiments, arrays of structures (varying from 5 × 4 up to 6 × 6) were fabricated on each coverslip, allowing for increased throughput in testing.

Cell Culture and Transfection.

A431 GFP-tagged E-Cad cells were cultured in a growth medium composed of Dulbecco's modified Eagle's medium and supplemented with 10% fetal bovine serum (Chemie Brunschwig AG) and 1% penicillin-streptomycin (Invitrogen). The experimental medium consisted of CO₂-independent growth medium (Gibco) supplemented with 2 mM L-glutamine (Gibco), 10% fetal bovine serum, and 1% penicillin-streptomycin. All solutions were filtered through 0.22-μm-pore–size filters before use. Shortly before each experiment, the structure is submerged with 2 mL of the experimental medium. All experiments were performed in a temperature-controlled enclosed chamber at 37 °C. Transfection of E-Cad siRNA (SCBT; SC35242) and control siRNA (SCBT; SC37007) were performed using Lipofectamine RNAiMAX Transfection Reagent (Invitrogen), according to the manufacturer’s protocol. The expression of GFP was analyzed by fluorescence microscopy after 48 h. Full-length human E-Cad fused at its C terminus to GFP was constructed by first inserting an E-cadherin complementary DNA (cDNA) into pEGFP-N2 (Clontech, Mountain View, CA) and then inserting the tagged construct into a derivative of the LZRS retroviral expression vector. The final cDNA construct was fully sequenced to ensure no errors were introduced during subcloning.

Structure Preparation for Fluorescence Imaging.

The structures were placed inside of a glass-bottom Petri dish, washed with 70% ethanol, and immediately soaked with PBS for 10 min until all the ethanol dissolved. The substrate was then submerged in 0.3% volume ratio Sudan Black B (Sigma-Aldrich) in 70% ethanol for 1 h to block the autofluorescence of the polymer. To dissolve excessive Sudan Black, the substrate was submerged in 70% ethanol for 1 h and then soaked with PBS for 10 min. The substrate was then coated with fibronectin to enhance the adhesion and growth of the cells on the structures. Fibronectin solution with a concentration of 50 μg/mL in PBS was placed on the substrate and left in the incubator for 2 h. Finally, the fibronectin solution was removed, and the substrate was washed with PBS two times.

Structure Preparation for Mechanical Characterization.

The structures were placed inside of a glass-bottom Petri dish, washed with 70% ethanol, and immediately soaked with PBS for 10 min until all the ethanol dissolved. The substrate was then coated with fibronectin (50 μg/mL in PBS) to enhance the adhesion and growth of the cells on the structures. The fibronectin solution was placed on the substrate and left in the incubator for 2 h. The solution was removed, and the substrate was washed with PBS.

Cell Deposition.

An Eppendorf single-cell isolation setup was used to pick up and position cells on the stretching structure. This setup had a microcapillary (Piezo Drill Tip ICSI, Eppendorf) with a tip inner diameter of 6 μm. The microcapillary was connected to a pressure controller (CellTram 4r Air/Oil, Eppendorf), which could control the inside pressure of the pipette. The micropipette position was controlled with a 3D manipulator (TransferMan 4r, Eppendorf) on an inverted microscope. First, the microcapillary was positioned just above a cell on the substrate and brought into contact with the cell membrane. Then, a negative pressure was applied to suck the cell onto the pipette tip. Finally, the cell was retracted from the surface, positioned on the structure, and detached from the pipette tip by applying positive pressure. The same procedure was performed to pick up and position the second cell (SI Appendix, Fig. S5).

Immunofluorescence and Microscopy.

The A431 cells were E-Cad GFP-tagged to visualize the cell–cell junctions. Alexa Fluor 657 Phalloidin (Invitrogen) was used to stain the actin filaments, and the nuclei were stained with DAPI (Invitrogen). Cells were washed twice with PBS (pH 7.4), fixed using 4% formaldehyde solution in PBS for 15 min at room temperature, and then washed two times with PBS. Subsequently, they were permeabilized with a solution of 0.1% Triton X-100 in PBS for 5 min and then washed twice with PBS. To enhance the quality of the actin fluorescent intensity, 4 drops of Image-iT FX Signal Enhancer (Thermo Fisher) were added and incubated at room temperature with a humid environment for 30 min. After removing the solution and washing with PBS, the phalloidin staining solution with a ratio of 1:100 in PBS was placed on the substrate for 30 min at room temperature and then washed with PBS. Next, the DAPI solution with a ratio of 1:1,000 with PBS was placed on the substrate and incubated for 10 min at room temperature. The solution was removed, and the substrate was washed with PBS. Finally, 3 mL of pure water was added to the Petri dish for imaging. Zyxin staining was performed to visualize the focal adhesion points between cells and the structure. After fixing the cells (see above), the anti-zyxin antibody (Sigma) with a ratio of 1:250 with PBS was added to the sample and refrigerated for 24 h. The solution was then removed, and the sample was washed with PBS. PBS was replaced by goat anti-rabbit IgG (H+L), Superclonal Recombinant Secondary Antibody, Alexa Fluor 647 (Thermo Fisher) and incubated for 1 h at 37 °C. Finally, the sample was washed with PBS, and the actin and nuclei staining protocols were performed. Pharmacological treatments modulating cell contractility included 3 µM Bleb (Sigma-Aldrich) for 2 h and 1 unit/mL Rho Activator I (CN01; Cytoskeleton, Inc., Denver, CO) for 30 min. A Nikon A1-NiE upright confocal system (60× water immersion objective) driven by NIS-Elements Confocal image acquisition and analysis program (Nikon software) was used for immunofluorescent imaging of cells on the structures. All image reconstructions and channel alignments were performed within the Nikon software. Zeiss Axio 7 was used for the stretch test. An AFM setup (Nanosurf AG, Switzerland) was installed on the microscope to apply the displacement to the structures.

Cell Lysis, Gel Electrophoresis, and Immunoblotting.

A431 GFP-tagged E-Cad cells were lysed with radioimmunoprecipitation assay (RIPA) buffer (50 mM Tris-HCl, pH 7.4, 150 mM NaCl, 5 mM ethylenediamine tetraacetic acid (EDTA), 2 mM dithiothreitol, 1 mM phenylmethylsulfonyl fluoride (PMSF) and 1% Triton X-100) containing a protease inhibitor mixture (S8830; Sigma). Whole-cell lysates were incubated on ice for 30 min and then centrifuged at 14,000 × g for 20 min at 4 °C. Proteins were separated by sodium dodecyl (lauryl) sulfate-polyacrylamide gel electrophoresis (SDS-PAGE) using 8% gels and blotted onto polyvinylidene fluoride (PVDF) membranes. The blots were incubated overnight at 4 °C with anti-E-Cad (BD Biosciences; 610181), or anti-β-actin (Santa Cruz Biotechnology; SC-47778). Blots were then washed and incubated with horseradish peroxidase (HRP)-conjugated anti-mouse (Jackson immunoresearch), followed by washing and detection of immunoreactivity with enhanced chemiluminescence (Santa Cruz Biotechnology).

Displacement Tracking Using DIC.

A modified version of MATLAB DIC was used to analyze the frames from the stretch test. The first frame was considered as the reference, and the rest of the frames were compared to the reference frame to calculate the displacement of each island. An ROI with markers within the region was defined for both islands. Then, the MATLAB code calculated the markers’ new coordinates with respect to the first frame, from which the displacement of the islands was calculated. The MATLAB code for calculating the displacement from captured frames is available at https://github.com/YangLabUNL.

Stress–Strain Curve Calculation.

Each stretch test was recorded and analyzed with a customized DIC-based program to calculate each island’s movement. The displacement of each island was obtained by averaging the displacement of markers in the ROI in each frame. Similarly to previous studies on epithelial monolayers (52), the strain was calculated by dividing the difference of the two islands’ displacements by the initial length: ε = (D − δ)/L₀, where D is the Island 2 (actuation) displacement, δ is the Island 1 (sensing) displacement, and L₀ is the initial length. This initial length was defined as the nucleus-to-nucleus distance of the cell pair, which was measured to be 19.18 ± 0.50 µm (SI Appendix, section 13 and Fig. S13). We had assumed that deformation occurred in the region of the cell near to the junction, and the region of the cell behind the nucleus was fully attached to the substrate via cell–ECM adhesion with negligible deformation. This assumption was validated by tracking the movement of marker points inside the nucleus region, and the results showed that, compared with the elongation of the region of the cell near to the junction, the region behind the nucleus remained relatively unmoved (SI Appendix, section 14 and Fig. S14). Understandably, cells adhered to the device via discrete focal adhesion spots at the base of the cell, and these adhesions could actively change during the stretching process. Nevertheless, under large deformation (as the deformation of the cell pair during the stretch can reach several folds of the initial length), the influence of the small variation of the initial length on the calculated stress–strain relationships can be mitigated. Force was calculated using Hooke’s Law, F = kδ, where k is the sensing island stiffness obtained from the AFM experiment. The effective engineering stress was defined by dividing the calculated force by the cross-sectional area of the junctional region, following the same concept adopted by previous studies on epithelial monolayers (52). The cross-sectional area was treated as the junction length multiplied by the thickness of the cell–cell contact region. The measured data showed that the cell–cell junction length varied significantly from one cell pair to another. Thus, the length data obtained from the processing of the cell doublet images in each stretch test were used. The cell–cell contact region was found to be 10.24 µm in thickness with limited variations measured from confocal z-stack imaging (SI Appendix, Fig. S13).

Statistical Analysis.

Curve fittings were performed in MATLAB. All other data analysis was conducted in Origin. For all box plots, the edges of the box represent SD of the data, and the red line marks the mean of the data. A two-tailed Student’s t test was performed for comparison between two data conditions. P < 0.05 was considered statistically significant.

Data Availability.

All study data are included in the article and/or supporting information. The MATLAB code for calculating the displacement from captured frames is available at https://github.com/YangLabUNL.