cola: an R/Bioconductor package for consensus partitioning through a general framework

Abstract

Classification of high-throughput genomic data is a powerful method to assign samples to subgroups with specific molecular profiles. Consensus partitioning is the most widely applied approach to reveal subgroups by summarizing a consensus classification from a list of individual classifications generated by repeatedly executing clustering on random subsets of the data. It is able to evaluate the stability of the classification. We implemented a new R/Bioconductor package, cola, that provides a general framework for consensus partitioning. With cola, various parameters and methods can be user-defined and easily integrated into different steps of an analysis, e.g., feature selection, sample classification or defining signatures. cola provides a new method named ATC (ability to correlate to other rows) to extract features and recommends spherical k-means clustering (skmeans) for subgroup classification. We show that ATC and skmeans have better performance than other commonly used methods by a comprehensive benchmark on public datasets. We also benchmark key parameters in the consensus partitioning procedure, which helps users to select optimal parameter values. Moreover, cola provides rich functionalities to apply multiple partitioning methods in parallel and directly compare their results, as well as rich visualizations. cola can automate the complete analysis and generates a comprehensive HTML report.

INTRODUCTION

Subgroup classification is a basic task in high-throughput genomic data analysis. Based on gene expression (1), DNA methylation (2) or other omics data, samples are separated into distinct groups with specific molecular profiles. Subgroup classification is widely used for subtype identification in cancer studies (3) and cell-type classification in single-cell RNA sequencing (scRNA-Seq) (4). It can also be used to establish relationships between the predicted subgroups and known clinical annotations or to test whether there exist significant batch effects. Mostly, unsupervised clustering methods, e.g., k-means clustering or hierarchical clustering, are applied to predict subgroups without taking any prior sample labelling into account. However, a single run of one clustering algorithm can produce results which lack generality, i.e., which cannot be reproduced with other datasets focusing on the same biological question or subject. Furthermore, single clustering approaches do not reveal which samples are stably classified in the identified structure, and which samples have uncertain class assignments. To solve these issues, consensus clustering or consensus partitioning was proposed (5). It summarizes a consensus classification from a list of individual classifications that are generated by repeatedly executing clustering on randomly sampled subsets of the data. Later, the stability of the consensus partition can be inferred from the individual partitions, e.g., by calculating the probabilities of a sample belonging to every subgroup.

One of the most commonly used R packages for consensus partitioning is ConsensusClusterPlus (6), which partitions samples by hierarchical clustering, k-means clustering or partitioning around medoids. The individual partition list is generated by randomly sampling from the original matrix either by rows or columns. Another package, SC3 (4) was recently developed especially for scRNA-Seq datasets. It runs k-means clustering on matrices obtained by transformation (principal component analysis or graph Laplacian transformation) of the original distance matrix (based on either Euclidean distance, Pearson or Spearman correlation). In SC3, the list of partitions normally contains six individual partitions resulting from the combinations of two transformation methods and three distance methods. diceR (7) applies consensus partitioning by summarizing over partitions from multiple clustering algorithms. Another popular method that can provide consensus partitioning is non-negative matrix factorization (NMF) (8). The NMF package (9) generates individual partitions by randomly selecting seeds for the initialization of an NMF algorithm.

Consensus partitioning can be formalized into a uniform procedure where samples are first classified into k subgroups with trying a list of different k, and then statistical metrics are applied to find the best number of subgroups. To formalize the procedure of consensus partitioning, we developed an R/Bioconductor package, cola, that provides a general framework in which various methods can be user-defined and easily integrated into different steps of the analysis, e.g., for feature selection, sample classification or definition of signatures. cola provides a complete set of tools for comprehensive subgroup analysis, including partitioning, signature analysis, functional enrichment, as well as rich visualizations for interpretation of the results. Moreover, to find the method that best explains a user's dataset, cola allows running multiple methods simultaneously and provides functionalities for a straightforward comparison of results. cola is designed with a clean and simple user interface while still retaining comprehensive access to the analysis. With only a few lines of code, users can trigger the automated execution of a full set of analysis and the generation of a detailed HTML report.

For genomic data with a very large number of features, e.g., genes for expression data or CpG probes for methylation array data, partitioning is normally accompanied with a feature selection step where only the top n features are selected for partitioning (named top-value method in cola). In addition to established top-value methods, cola implements a simple yet powerful method (the ATC method) for selecting features based on the global correlation structure. Additionally, we propose to perform partitioning via spherical k-means clustering (skmeans) (10), based on benchmarks of the performance of various methods with 435 public gene expression datasets. We found that methods in which features are selected by the ATC method or in which samples are partitioned by skmeans tend to generate more subgroups with high stability.

We also assessed the selection of key parameters in consensus partitioning in the framework of comprehensive benchmarks. First, we compared random sampling by rows and columns in the process of generating random subsets of the input data for partitioning. We found that row sampling was in general slightly better than column sampling for generating stable partitions. Second, we benchmarked the number of random samplings for consensus partitioning. The number of random samplings did not affect the consensus partitioning results significantly and increasing the number of samplings only slightly improved the stability of the partition. The difference of consensus partitions between different numbers of samplings was ignorable if the partitions were already stable. Additionally, we applied cola on one methylation array dataset. The results showed that variation-based top-value methods, e.g., standard deviation (SD), were more efficient for selecting features for subgroup detection while correlation-based methods, e.g., ATC, only reveal subgroups based on global methylation differences. We suggest to apply consensus partitioning to CpG probes in different categories separately (e.g., from CpG islands or seas), because they have different methylation profiles to generate different classifications and they might reveal different regulation mechanisms for the investigated biological system.

MATERIALS AND METHODS

Preprocessing the input matrix

cola accepts the input object as a numeric matrix. Frequently, the input matrix contains values of gene expression (e.g., from expression microarray or RNA sequencing) or DNA methylation (e.g., from methylation arrays or whole-genome bisulfite sequencing). More generally, the input object can contain any type of measurements as long as it is represented as a numeric matrix, e.g., a matrix where rows correspond to genomic regions and values are the histone modification intensities that are measured from a chromatin immuno-precipitation sequencing (ChIP-Seq) experiment. For all these types of matrices, cola expects samples to designate columns and this is the dimension in which the subgroups are to be found. Before performing consensus partitioning, an optional but important step is to clean the input matrix. cola provides the function adjust_matrix() to impute missing values, adjust outliers and remove rows with very small variance from the matrix (Figure 1, step 1). It executes the following preprocessing sequentially:

Figure 1.

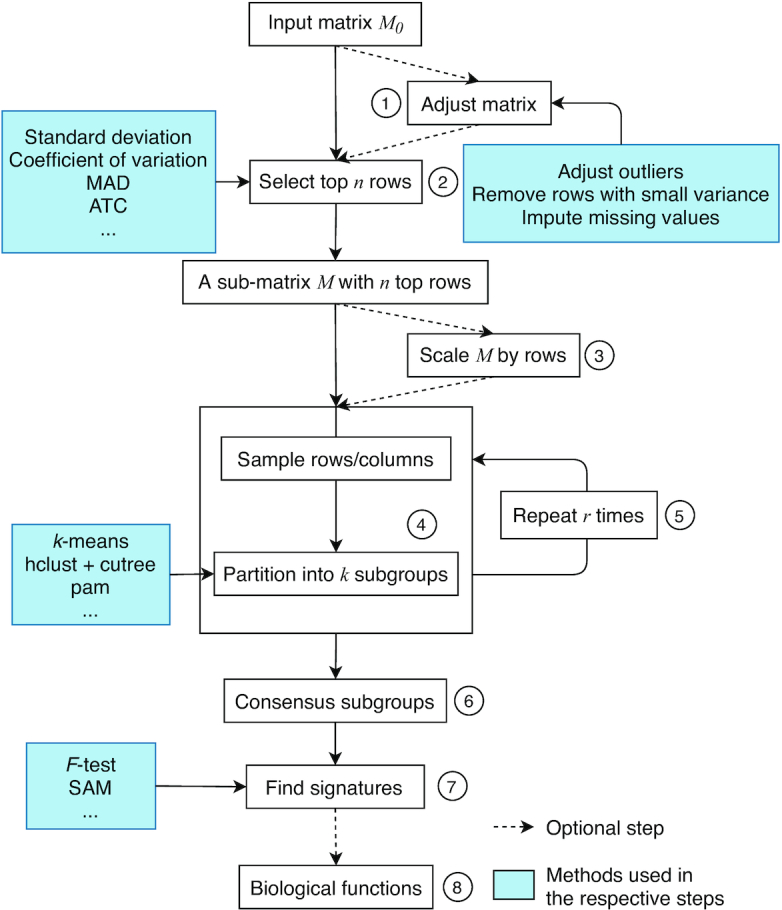
The cola workflow. Steps are as follows: 1. Adjust the input matrix by removing outliers and imputing missing values; 2. Select top n features by a certain method, e.g., standard deviation; 3. Scale the matrix by rows; 4. Randomly sample from the matrix and partition samples by a certain partitioning method; 5. Repeat Step 4 r times to obtain a list of partitions; 6. Construct the consensus partition; 7. Identify features discriminating between subgroups; 8. Apply functional enrichment on signatures if they can be annotated to genes.

1. Rows in which >25% of the samples have missing values are removed;

2. Use impute.knn() from the R package impute (11) to impute missing values if there is any;

3. In every row in the matrix, values larger than the 95^th percentile or less than the 5^th percentile are replaced by corresponding percentiles;

4. Rows with zero variance are removed;

5. Rows with variance less than the 5^th percentile of all row variances are removed.

Top-value methods

Top-value methods are used to assign scores to the rows of a matrix. Later the scores are ordered and only the top n rows with the highest scores are selected for consensus partitioning (Figure 1, step 2). This step is called feature selection (12). cola provides three commonly used methods based on the variability of rows: standard deviation (SD), median absolute deviation (MAD) and coefficient of variation (CV). CV is defined as 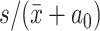where s and 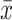are the standard deviation and mean value of row i, and a₀ is a penalty term which is the 10^th percentile from all row means. cola also allows for user-defined top-value methods.

Selecting the top rows from the matrix helps to keep the most informative features for partitioning. In most studies, the top rows are selected based on row variance, however, this choice might deselect rows that are efficient for subgroup classification. When the data contains a high amount of random noise, e.g., in scRNA-Seq data, the most variable genes sometimes are not able to detect any stable subgroups. Conversely, when assuming that stable subgroups for the samples in the data exist, there must be groups of rows showing similar patterns to support the subgrouping. In other words, rows in the same groups should be highly correlated. Thus, if one row correlates or anti-correlates more strongly to a subset of the remaining rows, it has more power to support stable subgroups for the samples. According to this idea, cola implements the ATC (ability to correlate to other rows) method as follows:

For row i in a matrix, denote the variable X as a vector of absolute values of the correlation coefficients to all other rows. Then the ATC score for row i is defined as:

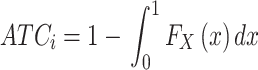where F_X(x) is the cumulative distribution function (CDF) of X. The ATC score corresponds to the area above the CDF curve and the ATC score increases with increasing correlations between row i and other rows. A more detailed explanation of the ATC method with benchmarks on simulated data can be found in Supplementary Material 1. The idea of taking correlation structures into the selection of features is already widely implemented in a variety of available methods (13), however, the ATC method can be very easily integrated into the cola framework and later in the paper we will argue it works effectively in subgroup classifications.

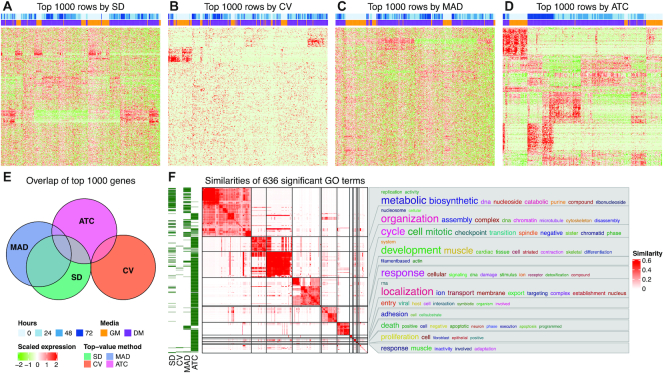
Figure 2A-D compares the top 1000 genes scored by the SD, CV, MAD and ATC methods from the HSMM scRNA-Seq dataset (14). It clearly shows that the genes with the highest ATC scores provide a clean pattern for the subgroup classification. SD and MAD have weaker performance for the segregation of subgroups as objectivated by the heatmaps, and the level of noise is higher. CV performs the worst for this dataset and barely distinguishes any subgroups. More importantly, the top 1000 genes with the highest ATC scores only have a small overlap with the genes selected by the other three methods (686 genes are uniquely selected by the ATC method, Figure 2E), which highlights that the ATC method can uniquely capture informative rows that other methods are not able to catch. Gene Ontology (GO) enrichment analysis on the gene list extracted by the ATC method showed it generated a large number of unique significant GO terms (FDR < 0.01) related to cell cycle, signaling pathways and cell localization, while gene lists extracted by SD and MAD only generated small numbers of significant terms and the gene list extracted by CV generated almost no significant terms (Figure 2F). This implies that the ATC method is able to extract more genes with biological relevance. Supplementary Material 2 compares the four top-value methods for other datasets and they all support that ATC increases discrimination between subgroups as compared to the other top-value methods.

Figure 2.

Comparison of top-value methods. (A) Heatmap of the top 1000 genes extracted by SD, (B) CV, (C) MAD and (D) ATC methods. Expression matrices are row-scaled by z-score transformation. (E) Euler diagram of the overlapping of top 1000 genes extracted by the four top-value methods. (F) Heatmap of the similarities of significant GO terms (FDR < 0.01) from the gene lists generated by the four top-value methods. The green-white row annotation shows for which top-value method the respective GO terms are significant. The word cloud annotation visualizes the summaries of biological functions in each GO cluster. GO enrichment analysis was performed by hypergeometric test with the function functional_enrichment() and GO terms were clustered by the R package simplifyEnrichment. The analysis was done with the HSMM single-cell dataset. Annotations on the heatmaps are: Hours: time points when the primary human skeletal muscle myoblasts (HSMM) cells were captured; Media: the conditions where the cells were expanded (under high mitogen conditions (GM) and low mitogen media (DM)).

Partitioning methods

Partitioning methods are used to classify samples into k distinct subgroups with a given k. cola provides six partitioning methods: hierarchical clustering with cutree (hclust), k-means clustering (kmeans), spherical k-means clustering (skmeans), partitioning around medoids (pam), model-based clustering (mclust) and non-negative matrix factorization (NMF). cola also supports user-defined partitioning methods.

Hierarchical clustering

The clustering is performed by function hclust() with Euclidean distance and ‘complete’ clustering method. Later the dendrogram generated from clustering is cut by function cutree().

Model-based clustering

The function Mclust() from the R package mclust (15) performs partitioning by Gaussian finite mixture models and is applied on the first three principal components of the original matrix.

Spherical k-means clustering

Spherical k-means clustering is a variant of the standard k-means clustering, where cosine similarity is used as the distance measurement. For a matrix with n rows and m columns, to perform spherical k-means clustering on columns, columns are first projected onto the unit hypersphere, then the algorithm follows a similar procedure as k-means clustering, to look for a partition of k sets P = {P₁, P₂, …, P_k} to minimize the following criterion:

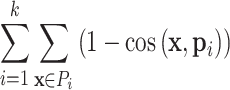where x is a vector in partition P_i and p_i is the centroid of all vectors in P_i. Spherical k-means clustering is performed with the R package skmeans (16). Cosine distance was shown to be efficient for separating groups for high-dimensional datasets and robust to technical noise (17). In later sections of this work, we demonstrate that on a variety of datasets spherical k-means clustering generates more stable partitions compared to other methods.

Non-negative matrix factorization

NMF factorizes a non-negative matrix V into the two matrices W and H, i.e., V ≈ W × H. For a given rank p which corresponds to the number of subgroups, W is an n × p matrix, H is a p × m matrix and V is an n × m matrix. V corresponds to the input matrix for cola analysis and to make V non-negative, ‘min-max’ scaling is applied to matrix rows in advance. The subgroup label is inferred by taking the index of the row of H which has the maximum value for the corresponding sample. NMF is performed with the R package NMF (9).

Row scaling

Before applying partitioning methods, proper scaling should be applied to the matrix rows to remove the difference of absolute levels between rows that might affect the partitioning (Figure 1, step 3). z-score scaling is the most commonly used, while for partitioning methods (e.g., NMF) which do not allow negative values, ‘min-max’ scaling is applied, defined as (x – min)/(max – min). For certain datasets where the absolute levels (e.g., methylation values) should be taken into account for partitioning, row scaling can be omitted.

Finding a consensus partition

Let M denote a sub-matrix of the initial data which contains top rows from the original matrix selected by a certain top-value method. A subset of rows or columns are randomly sampled from M with a probability of p by applying a certain partitioning method, generating a partition P_a (the index a reflects the individual partition). In most cases, we have no prior knowledge of the number of top rows that gives the best results. Therefore, cola tries multiple numbers of top rows of n₁, n₂, …, n_t and integrates all partitions to form a global consensus ensemble. If the random sampling is performed r times, the total number of partitions for a given number of subgroups k is N_P = t × r (Figure 1, steps 4–6).

The consensus subgroup labels are inferred from the N_P partitions by the function cl_consensus() from the R package clue (18) (Figure 1, step 6). Since the labels for individual partitions can be assigned randomly while the partitions are still kept identical, the subgroup labels for one individual partition a are adjusted to the consensus labels by choosing a proper mapping function m_a() for relabelling:

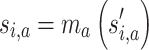to maximize

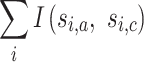where 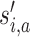is the original label for sample i in partition a, s_i,a is the adjusted label and s_i,c is the consensus subgroup label. I() is the indicator function where I(x = y) = 1 and I(x ≠ y) = 0. The mapping function m_a() is found by solving the linear sum assignment problem, which is by the function solve_LSAP() from the R package clue (18).

The consensus matrix measures how consistently two samples are attributed to the same subgroup. A value c_i,j in the consensus matrix denotes the probability of sample i and sample j to be in the same subgroup in all N_P partitions. It is calculated as:

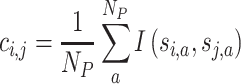where s_i,a and s_j,a are the adjusted subgroup labels for sample i and j in partition a. The consensus matrix is used to evaluate and visualize the stability of the consensus partitioning.

Adjusting partition labels

Moreover, the partition labels can be adjusted between any two sets of partitions. Similarly, the mapping function m() are to be found to maximize

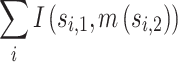where s₁ is the first label set and s₂ is the second label set.

The subgroup label adjustment is frequently used in cola to help the visualization as well as comparisons of partitions between different k and different partitioning methods. It also helps for downstream analysis such as the calculation of a consensus matrix or the concordance scores of the partitions which assume that the subgroup labels are already adjusted. There are several levels of label adjustment, listed as follows (cola adjusts them sequentially):

1. For a specific combination of methods and a specific k, the consensus subgroup labels are ordered according to the average distance in each subgroup, which means that the subgroup with label 1 has the minimal within-group distance.

2. Subgroup labels for individual partitions are adjusted according to the consensus partition labels.

3. The subgroup labels for the consensus partition as well as for individual partitions for k + 1 subgroups are adjusted according to the consensus labels for k subgroups.

4. If multiple methods are applied, for each k, the consensus labels for method i + 1 are adjusted to method i. The individual partition labels are then adjusted to the consensus labels correspondingly.

Selection of the best number of subgroups

For consensus partitioning, the number of subgroups k is a fixed and known parameter. In order to find the optimal value of k, a list of values for k from 2 to a chosen k_max are tested to find the best number of subgroups by applying various metrics. cola provides the following metrics to determine the best k:

Silhouette score

The silhouette score measures how close one sample is to its own subgroup compared to the closest neighbouring subgroup. For sample i, the mean distance to each subgroup is calculated and denoted as d₁, d₂, …, d_k (d_k is the mean Euclidean distance between sample i and every sample in subgroup k). The distance to the subgroup to which sample i belongs is denoted as d_a and the silhouette score s_i is defined as:

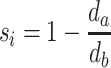where d_b is the minimal distance excluding d_a:

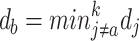The mean silhouette score averaged from all samples is used to select the best k. The higher the mean silhouette score, the better the metric for k.

PAC score

The PAC (the proportion of ambiguous clustering) score measures the proportion of ambiguous subgroup assignments and was originally proposed in (19). If the subgrouping is stable across the N_P partitions, sample i and sample j are in most cases either in the same subgroup or always in different subgroups, and therefore the consensus value c_i,j in the consensus matrix is either close to 1 or to 0. Thus, the proportion of c_i,j being far from 0 or 1 corresponds to the proportion of ambiguous subgroup assignments, defined as F(x₂) - F(x₁), where F() is the CDF of the consensus matrix, and x₁ and x₂ are the cutoffs defining c_i,j to be far from 0 and 1. cola removes the 5% most unstable samples with the lowest silhouette scores before calculating the PAC score. cola uses 1-PAC to determine the best k.

Concordance

This measure quantifies the mean concordance of an individual partition with the consensus partition. It is calculated as follows: for each partition P_a, let c_a be the proportion of overlap with the consensus partition:

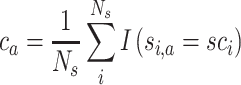where N_s is the number of samples, s_i,a is the subgroup label of sample i in partition a and sc_i is the consensus subgroup label for sample i. Note subgroup labels in single partitions have already been adjusted to the consensus partition labels. The final concordance score is calculated as:

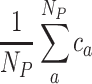where N_P is the total number of partitions. The higher the concordance score, the better the metric for k.

Jaccard index

In some cases, when the number of subgroups increases from k – 1 to k, all metrics imply k is a better choice than k – 1. However, when observing the consensus heatmap, it can be found that a very small set of samples are separated to form a new subgroup (one example can be found in Supplementary Material 3). In this scenario, the subgrouping with k subgroups is highly similar to the one with k – 1 subgroups and hardly provides new information. cola uses the Jaccard index calculated by the function cl_agreement() from the R package clue (18) to measure the similarity of two partitions with k – 1 and k subgroups. For all pairs of samples, denote following symbols:

• a: the number of pairs of samples that are in the same subgroup for k and in the same subgroup for k – 1.

• c: the number of pairs of samples that are in the same subgroup for k and in different subgroups for k – 1.

• d: the number of pairs of samples that are in different subgroups for k and in the same subgroup for k – 1.

The Jaccard index is the ratio of the number of sample pairs that are both in the same subgroup in the partitions at kandk – 1 and the number of sample pairs that are both in the same subgroup in the partitions at kork – 1, calculated as follows:

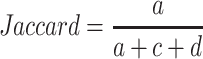Rules to suggest the best k

cola suggests the best number of subgroups based on the following rules:

1. All k with Jaccard index larger than 0.95 are removed because increasing k does not provide enough extra information. If all k are removed, the dataset is marked as no subgroups were detected.

2. For k with 1-PAC score larger than 0.9, the maximal k is taken as the best k. Other k are marked as optional best k.

3. If the second rule is not fulfilled, the k with the majority vote among the highest 1-PAC score, the highest mean silhouette, and the highest concordance is taken as the best k.

Additionally, if 1-PAC score for the best k is larger than 0.9 (<10% ambiguity for the partitioning), cola marks the partition to be stable. It should be noted that it is difficult to find the best k deterministically, especially when k grows larger. We encourage users to compare results for all k and determine a proper one which best explains their studies, i.e., matches prior knowledge.

Identification of signatures

We call signatures those rows which show statistically significant specificity (as defined below) in one or more subgroups. (Figure 1, step 7). We use the term signature genes for gene expression data or signature CpG probes for methylation data. By default, cola removes samples with silhouette scores less than 0.5 from the signature analysis because they are ambiguous. cola provides the following four methods to apply the differential analysis. It also supports user-defined methods to look for signatures.

• F-test. cola uses an F-test to identify rows that are significantly different between subgroups.

• Pairwise t-test. For each row, it looks for the subgroup with the highest mean value, compares it to each of the other subgroups by t-test and takes the maximum P-value from all the t-tests, denoted as p_h. Secondly, it looks for the subgroup with the lowest mean value, compares it to each of the other subgroups again by t-test and takes the maximum P-values, denoted as p_l. The smaller P-value between p_h and p_l is selected as the final P-value for the current row.

• One-versus-others. For each subgroup i in each row, it uses a t-test to compare samples in the current subgroup to all other samples, denoted as p_i. The minimal P-value is assigned for the current row.

• samr or pamr. cola uses the SAM (20) or PAM (21) methods to find rows with significant differences between subgroups.

Signatures can be grouped by patterns among subgroups. In addition to the identification of signatures as described above, cola applies k-means clustering on the signature profiles with automatically selecting the appropriate number of signature groups (an example is in Figure 3I).

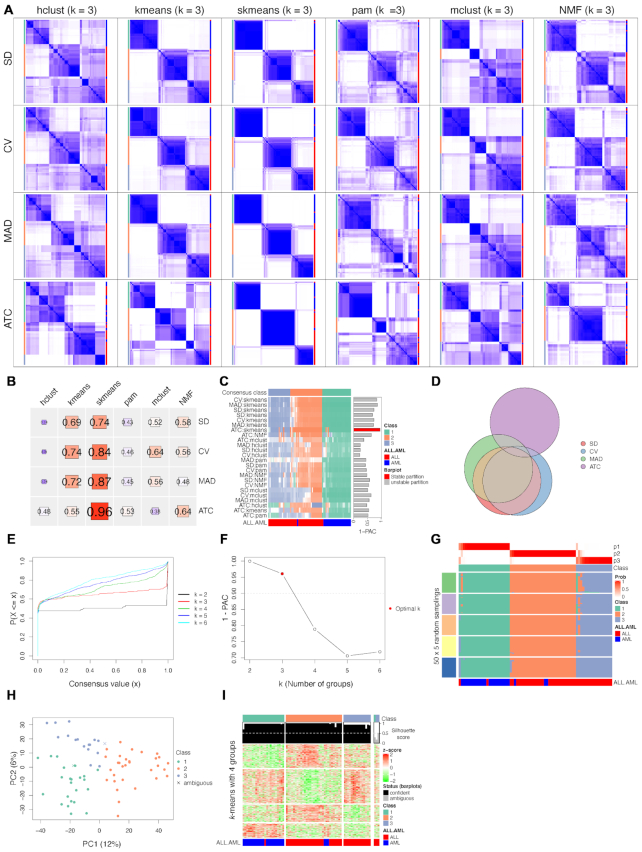
Figure 3.

Visualizations implemented by cola. (A) Parallel consensus heatmaps from four top-value methods and six partitioning methods under three-group classification, generated by the function collect_plot(). (B) Heatmap of 1-PAC scores for the partitions in Figure A, generated by the function collect_stats(). (C) Partitions from 24 combinations of methods generated by the function collect_classes(). Transparency of the heatmap corresponds to the silhouette score for each sample and each method. (D) Euler diagram of top 500 genes extracted by SD, CV, MAD and ATC methods, generated by the function top_row_overlap(). (E) eCDF curve of the consensus matrix from partition by ATC:skmeans, generated by the function plot_ecdf(). (F) 1-PAC scores versus the number of subgroups. The dashed line represents the cutoff for a stable partition. (G) Membership heatmap for the individual partitions, generated by the function membership_heatmap(). (H) PCA plot of samples, generated by the function dimension_reduction(). (I) Heatmap of signature genes under three-group classification, generated by the function get_signatures(). The analysis was done with the Golub leukemia dataset.

Functional enrichment

If the matrix rows correspond to genes (e.g., in the case of a gene expression matrix, or in the case of a methylation array data where CpG sites can be annotated to the transcription start site of genes), cola performs functional enrichment with hypergeometric tests by applying the R packages ClusterProfiler (22), DOSE (23) or ReactomePA (24) (Figure 1, step 8) to the signatures. If signatures are already classified into groups as described in the previous section, functional enrichment is applied to each group of signatures separately.

Implementation of the cola package

The core function consensus_partition() performs consensus partitioning for a single top-value method and a single partitioning method. Both methods can be either selected from the built-in methods or supplied as user-defined functions. consensus_partition() returns a ConsensusPartition object and cola provides rich visualization tools to comprehensively evaluate the consensus partitioning results. The major visualizations are:

• Diagnostic plots with various metrics for determining the best number of subgroups.

• A consensus heatmap that visualizes the consensus matrix.

• A membership heatmap that visualizes the membership of every individual partition generated from random subsets of the original matrix.

• Dimension reduction visualization by UMAP (25), t-SNE (26), PCA or MDS.

• A signature heatmap that visualizes the rows with statistically significant differences between subgroups.

• A heatmap that visualizes how subgroups are divided when the number of subgroups increases.

cola provides a collect_plots() function that can be applied to the ConsensusPartition object and arranges all visualizations for different numbers of subgroups into a single page.

In most cases, it is unclear which top-value method and partitioning method yield the best results for the dataset under analysis. cola provides a helper function run_all_consensus_partition_methods() that provides a convenient way to run multiple top-value methods and partitioning methods simultaneously. run_all_consensus_partition_methods() returns a ConsensusPartitionList object and cola provides tools to compare which combination of methods gives the best prediction of subgroups in an easy way. The functions top_row_overlap() and top_row_heatmap() compare the top n rows from different top-row methods either by Euler diagrams, UpSet plots or heatmaps, which gives direct hints of which top-value method extracts better rows for subgroup classification. The function collect_plots() can also be applied to the ConsensusPartitionList object. In that setting it arranges plots (e.g., consensus heatmaps) from multiple combinations of top-value methods and partitioning methods into a single page, making it straightforward to compare between methods and quickly find out the best combination of methods to use. The function collect_classes() generates a heatmap which lists partitions from every combination of methods, as well as a global consensus partitioning averaged from all methods.

Other useful functions include test_to_known_factors() that performs chi-square test or one-way ANOVA to test the associations between predicted subgroups and known factors, and functional_enrichment() that performs functional enrichment analysis on the signatures if they can be annotated to genes.

cola is implemented as a comprehensive toolbox for consensus partitioning analysis. In addition, it provides an easy user interface to perform the analysis and automatically generates a comprehensive HTML report including all results of the analysis. To perform the complete cola analysis, users only need a minimal set of code of using two functions, such as:

• rl = run_all_consensus_partition_methods (matrix, …)

• cola_report(rl, …)

This design greatly helps researchers with limited knowledge of R programming to perform the analysis. The report also includes code for every individual analysis which is rerunnable and makes the whole analysis reproducible. As consensus partitioning may require substantial computing time, e.g., it takes on average 10.7 hours for NMF or 1.5 hours for skmeans on the recount2 RNA-Seq datasets (27) of approximately 200 samples (180–220 samples where all datasets have 58037 genes) with 1 core (on a 1.2 GHz CPU, Supplementary Material 8: Figure S8.1), cola natively supports multi-core both for computation and report generation.

Pre-preprocessing test datasets

The Golub leukemia dataset is available in the golubEsets Bioconductor package (28,29). Values less than 1 were replaced by NA and later estimated by the function adjust_matrix(). Samples were normalized by quantile normalization. The Ritz ALL dataset is available in the ALL Bioconductor package (30,31). Samples were normalized by quantile normalization. The TCGA GBM dataset was already processed and is available at https://gdc.cancer.gov/about-data/publications/gbm_exp. The HSMM single-cell RNA-Seq dataset is available in the HSMMSingleCell Bioconductor package (14). Expression values were normalized by log₁₀(FPKM + 1) and only the protein-coding genes were used. The MCF10CA single-cell RNA-Seq dataset is available at the EGA database with sample ID SAMEA4666651 and SAMEA4666652 (32). Raw reads were processed by STAR (33) and HTSeq-count (34). Cells with less than 2 million reads were removed and non-protein-coding genes were filtered out. Genes with >5 reads mapped in >50% samples were kept for analysis. Expression values were normalized by log₂(TPM + 1). The GBM 450K methylation dataset is available at the GEO database with ID GSE36278. Probes that are on sex chromosomes and probes that overlap with known SNPs were removed. cola analysis was performed on the complete probe sets and on the probes annotated with CGIs, shores and seas separately.

The recount2 RNA-Seq datasets (27) were downloaded from the recount2 website (https://jhubiostatistics.shinyapps.io/recount/) on November 13, 2018. Datasets with more than 500 samples or less than 50 samples were removed. GTEx and TCGA datasets separated by tissues were also downloaded from recount2 website. Raw counts were normalized by the TPM method. Only the protein-coding genes were used. Genes that have <2 reads in >50% of samples were removed. Expression values of log₂(TPM + 1) were used for cola analysis. The GDS datasets were downloaded from the GEO database by the R package GEOquery (35) on March 12, 2019, with the query ‘Homo sapiens’[porgn] AND 50[n_samples]: 500[n_samples] AND ‘gds’[Filter]. GDS1761 was removed from the analysis due to an error of GEOquery. For each GDS dataset, rows where there are no microarray probe IDs were removed. If the value type for the dataset was not from a two-channel microarray, the distribution of expression values was tested against normal distribution by the Kolmogorov-Smirnov test. If the Kolmogorov-Smirnov statistic was larger than 0.3, we assumed the expression values did not follow a normal distribution and log-transformation was applied. GDS2808 was additionally filtered whereby samples with >25% NA values were removed. Finally, quantile normalization was applied to the samples.

RESULTS

Case studies

We demonstrate the usage of cola by five gene expression datasets which are the Golub leukemia dataset (28), the Ritz ALL dataset (30), the TCGA GBM dataset (1), the HSMM single-cell dataset (14) and the MCF10CA single-cell dataset (32) among which the first three are microarray datasets and the latter two are the RNA-Seq datasets. Four top-value methods (SD, CV, MAD and ATC) and six partitioning methods (hclust, kmeans, skmeans, pam, mclust, and NMF) generating 24 combinations of methods were applied to the datasets. Only results for the Golub leukemia dataset are shown in the main text and the complete reports of the five datasets can be found in Supplementary Material 4. In the following sections of this paper, for simplicity, we refer to a choice of methods for the consensus partitioning by the nomenclature A:B, where A is the top-value method and B is the partitioning method, e.g., SD:hclust.

For two-group classification of the Golub leukemia dataset, cola analysis reveals that ATC:kmeans (1-PAC = 1), ATC:NMF (1-PAC = 0.97) and ATC:skmeans (1-PAC = 1) generate stable partitions. For three subgroups, ATC:skmeans generates a stable partition with 1-PAC score of 0.96 (see cola report on Golub leukemia dataset in Supplementary Material 4). Figure 3 illustrates the typical visualizations for interpreting the results. Figure 3A contains the consensus heatmaps for three-group classification for 24 combinations of four top-value methods and six partitioning methods. It shows that skmeans generates more stable partitions compared to other partitioning methods, especially in combination with ATC. Figure 3B quantitatively visualizes the 1-PAC scores for all 24 consensus matrices, which shows that partitioning by ATC:skmeans generates the highest 1-PAC score (0.96) among all methods. Figure 3C compares the consensus subgroups from all 24 methods where the transparency or shading of a field corresponds to the silhouette score of the respective sample in each partition. 1-PAC scores are visualized as the bar plot annotation on the right of the heatmap and rows are clustered based on the similarity of partitions from different methods. Figure 3C illustrates that for three-group classification, most of the methods generate similar partitions, however, the stability of the partitioning differs. The Euler diagram in Figure 3D visualizes the overlap of the top 500 genes with the highest SD, CV, MAD and ATC scores, where the ATC method generates a very distinct set of genes compared to the other three top-value methods.

After having confirmed that ATC:skmeans generated the most stable partition among all methods for this dataset, we next looked at the diagnostic plots and performed downstream analysis for the partition generated by this specific choice of methods (ATC:skmeans). Figure 3E shows the eCDF curve of the consensus matrix for k = {2, …, 6} by ATC:skmeans. A good k can be selected by aiming at the flatness of the eCDF curve. In this case, that metric suggests that k = 2 or 3 are good choices. Figure 3F visualizes the 1-PAC scores for each k. According to cola’s definition for the rule of selecting the best number of subgroups, k = 3 (1-PAC = 0.96) is selected and k = 2 (1-PAC = 1) is an optional best k. Figure 3G is the membership heatmap which visualizes all the 50 × 5 individual partitions (50 random samplings × 5 top-n values), where the subgroup labels have been adjusted to the consensus subgroup labels. The membership heatmap gives a straightforward way to confirm that the partitions are very stable among all individual partitions, except for very few samples in some individual partitions. Figure 3H shows the dimensionality reduction by PCA on the samples where different colors represent different consensus subgroups and it confirms that the three predicted subgroups are very well separated. The two ambiguous samples with silhouette scores less than 0.5 are indicated in the plot as crosses. Figure 3I visualizes the signature genes that are significantly differentially expressed among the three consensus subgroups (by F-test). Three ambiguous samples with silhouette scores less than 0.5 are separated to the right of the heatmap and marked by grey bar plots. In the signature heatmap, rows are additionally clustered by k-means clustering with automatic selection of a proper number of groups, so that groups of rows with specific expression patterns can be directly inferred from the heatmap.

ATC and skmeans generate more stable partitions

cola can run multiple methods simultaneously, which provides the possibility to benchmark the performance of different methods. We applied cola to 206 GDS microarray datasets and 223 recount2 RNA-Seq datasets (27). For each dataset, consensus partitioning was performed with four different top-value methods (SD, CV, MAD and ATC) and six partitioning methods (hclust, kmeans, skmeans, pam, mclust and NMF), which yielded 24 combinations of methods. For each run, numbers of subgroups were tested from 2 to 6.

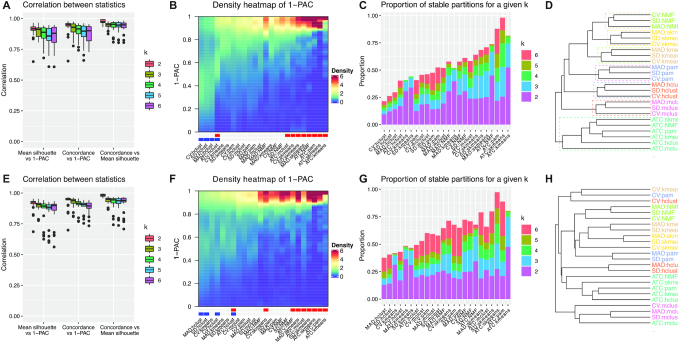
We compared the correlation of three metrics (mean silhouette score, concordance score and 1-PAC score) for determining the best number of subgroups. Generally, for the GDS datasets, the three metrics were highly correlated (overall mean Spearman correlation 0.872 for mean silhouette versus 1-PAC, 0.897 for concordance versus 1-PAC and 0.943 for mean silhouette versus concordance) and the correlation slightly dropped as the number of subgroups increased (Figure 4A). This finding was similar for the recount2 datasets (overall mean Spearman correlation 0.871 for mean silhouette versus 1-PAC, 0.905 for concordance versus 1-PAC and 0.932 for mean silhouette versus concordance, Figure 4E).

Figure 4.

Benchmark of consensus partitioning methods with 203 GDS datasets and 223 recount2 datasets. (A) Pairwise Spearman correlations between mean silhouette scores, concordance scores and 1-PAC scores among partitioning methods. (B) Distribution of 1-PAC scores for the partitions with the predicted optimal number of subgroups. Column annotation below the plot: red: partitions generated by ATC and/or skmeans; blue: partitions generated by hclust. (C) The proportion of partitions with the best number of subgroups that are stable. The order of the methods is the same as in Figure B. (D) General similarity between partitioning methods. Figure A–D were generated from GDS datasets. Figure E–H are analogous to A–D but were generated from recount2 datasets.

Since 1-PAC, mean silhouette and concordance were highly correlated, the 1-PAC score was used as the main metric for measuring the stability of the partitioning in the following sections of the paper. Figure 4B visualizes the distribution of 1-PAC scores for the partitions with the best k in the GDS datasets. The density heatmap shows that methods with ATC and/or skmeans generated partitions with higher 1-PAC scores for the best k (marked in red under the heatmap) while methods with hclust generated low 1-PAC scores (marked in blue under the heatmap). Figure 4C visualizes the proportion of stable partitions (1-PAC > 0.9) for a given best number of subgroups for each method, and as expected, methods with ATC or skmeans gave more stable partitions while methods with hclust gave fewer stable partitions. Interestingly, ATC:NMF and ATC:kmeans gave a high proportion of stable partitions, however, the majority of these stable partitions were only obtained for 2 or 3 subgroups (66.5% and 74.3%). As a comparison, ATC:pam and ATC:skmeans not only gave more stable partitions overall but also revealed more subgroups (48.5% and 45.1% for k ≥ 4). The results were very similar for the recount2 datasets (Figure 4E–G).

Since cola allows performing analysis with multiple methods simultaneously, next we checked the similarity of partitionings obtained by different methods. In Figure 4D, the dendrogram visualizes the similarity of partitions from different methods averaged from individual GDS datasets for k = 4 (Comparisons for other values of k can be found in Supplementary Material 5). Since features extracted by the ATC method were very distinct from those extracted by the other three top-value methods (Supplementary Material 2: Figure S2.18), partitionings performed on ATC features clustered apart from the other methods, while other partitionings clustered by partition methods. These effects were less consistent for the recount2 datasets (Figure 4H).

Comparison of row and column sampling

In consensus partitioning procedures, subsets from the original input matrix are generated by randomly sampling either rows or columns. To benchmark the performance of row and column sampling, we used the five gene expression datasets as test sets. Only two top-value methods (SD and ATC) and two partitioning methods (hclust and skmeans) were tested. Numbers of subgroups were tried from 2 to 6 and cola was run 100 times for each combination of parameters. In Figure 5 we show the results for the TCGA GBM dataset. Results for the other datasets can be found in Supplementary Material 6.

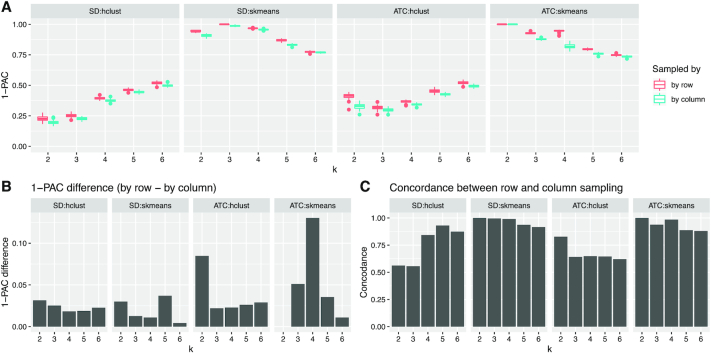
Figure 5.

Comparison of the impact of row and column sampling on consensus partitioning. (A) Boxplots of 1-PAC scores of partitions by SD:hclust, SD:skmeans, ATC:hclust and ATC:skmeans, generated from row and column samplings respectively. (B) Mean 1-PAC differences between row and column samplings. (C) Average concordance of the generated partitions between row and column samplings. The analysis was done with the TCGA GBM dataset.

Figure 5A visualizes the distribution of 1-PAC scores for the row and column sampling. Generally, row sampling generated higher 1-PAC scores than column sampling, but the difference was small. The mean 1-PAC for row sampling was 0.023 higher than for column sampling for SD:hclust, 0.019 higher for SD:skmeans, 0.037 higher for ATC:hclust, and 0.046 higher for ATC:skmeans (Figure 5B).

To test whether row and column sampling generate similar partitionings, we measured the mean concordance of the partitioning from the two types of samplings (Figure 5C). In general, row and column samplings generated very similar partitionings, e.g., for ATC:skmeans with k = 3, partitionings with row and column samplings were both stable with mean concordance 0.939. The concordance dropped as the stability of the partitioning decreased. We also evaluated the mean concordance of partitions for row and column sampling separately (Supplementary Material 6). In general, partitionings from row sampling were more consistent than column sampling, but the difference was very small. The effects described in this paragraph were similar for other gene expression datasets (Supplementary Material 6).

Number of random samplings

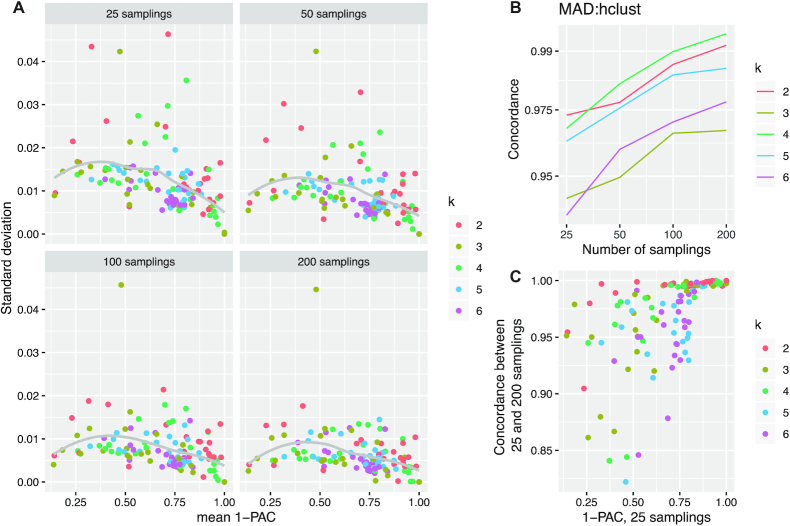
To assess how many random samplings are required to gain stable consensus partitioning, we analyzed the TCGA GBM dataset with the number of random samplings set to 25, 50, 100 and 200, respectively. For each setting, cola was run 100 times to capture the variability of the partitionings. Random samplings were applied on matrix rows.

Partitions became more stable with an increasing number of random samplings (average standard deviation was 0.0077 for 25 samplings, 0.0063 for 50 samplings, 0.0054 for 100 samplings and 0.0050 for 200 samplings, Figure 6A), but this increase in stability was very small. The partition concordance slightly increased with increasing number of random samplings, e.g., for MAD:hclust with k = 2, the mean concordance was 0.973 for 25 samplings and 0.991 for 200 samplings (Figure 6B). We also compared the concordance of the generated partitions between 25 and 200 samplings, and we found that when the partitions were stable, 25 and 200 samplings almost completely agreed. In contrast, when the partitions became unstable, the discordance got higher (Figure 6C). When applying column instead of row sampling we observed very similar results, with an overall slightly higher variance than for row sampling (Supplementary Material 7). Repeating this analysis on the HSMM single-cell dataset confirmed these findings (Supplementary Material 7).

Figure 6.

Benchmark on the number of random samplings. (A) Scatter plots of standard deviations versus mean values of 1-PAC scores of the partitions for every method and every k. The dot for ATC:mclust at k = 2 is removed from the plots because it is an outlier to all other dots and the complete plots including ATC:mclust can be found in Supplementary Material 7. (B) Average concordance of partitions by MAD:hclust with different number of random samplings. Similar plots for the other methods can be found in Supplementary Material 7. (C) The average concordance of partitions between 25 and 200 random samplings versus 1-PAC scores for the partitions with 25 random samplings. The analysis was done with the TCGA GBM dataset.

Application to a methylation dataset

We applied cola to the GBM 450K methylation array dataset (2). Only five partitioning methods, hclust, kmeans, skmeans, pam and mclust, were used while NMF was excluded due to its long runtime. No row-scaling was applied to the methylation matrix because the methylation values were already on a fixed scale (i.e., from 0 to 1). A detailed analysis report on the methylation dataset can be found in Supplementary Material 9.

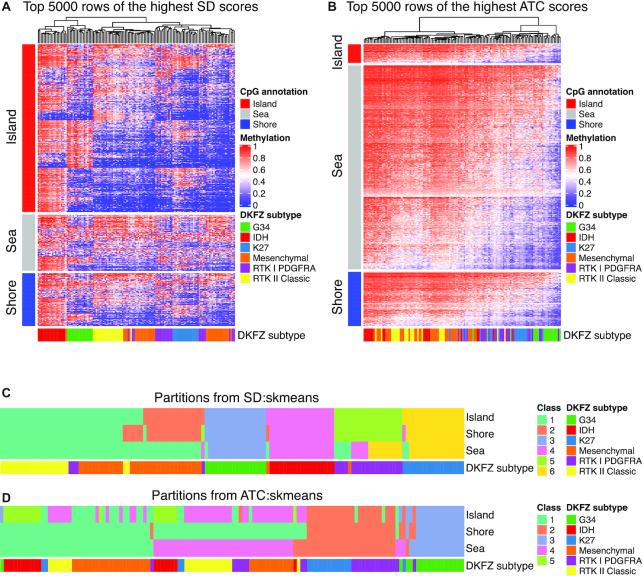
As opposed to gene expression datasets, variation-based methods for feature extraction like SD enabled more stable subgroup classification in the methylation datasets while the ATC method extracted features mainly associated with global methylation changes. Figure 7A shows a clustering of the top 5000 CpG probes with the highest SD scores. As expected, the methylation profiles corresponded well to the classification from the original study (DKFZ subtype) (2) which had also been based on top probes with the highest variance. As a comparison, Figure 7B illustrates the top 5000 CpG probes extracted by ATC, which had a very small overlap with the probes based on SD (1.76%), and also the methylation profiles were completely different from those of the probes extracted by SD.

Figure 7.

Application of cola to the GBM 450K methylation array dataset. (A) Methylation heatmap of the top 5000 CpG probes scored by SD and (B) by the ATC method. Column annotation reflects a classification system from the original publication, encoded as ‘DKFZ subtype’, and row annotation is based on classification of the CpG probes into different categories (island, shore, sea) based on prior knowledge from the annotation of 450K probes. (C) cola classification based on CpG probes separately for each category (island, shore, sea) with method SD:skmeans and (D) with method ATC:skmeans. Column annotation again reflects a classification system from the original publication, encoded as ‘DKFZ subtype’. The DKFZ subtype is the classification from the original study where the subtypes were predicted by top genes with the highest SD scores and by k-means consensus clustering with the R package ConsensusClusterPlus.

Probes can be annotated with different genomic features of the respective CpGs and grouped into categories: CpG islands (CGIs), CGI shores and seas. We found that different top-value methods have different ‘preferences’ on these CpG feature categories. In the top 5000 probes selected by SD, 60.6% were CGI probes while only 30.4% of all probes in the 450K array were in CGIs. In contrast, there were only 6.6% CGI probes in the top 5000 probes selected by ATC, and 72.9% of the probes were in CGI seas (Supplementary Material 9: Figure S9.3). When setting SD as the top-value method, CGI probes gave a very clean image for subgroup classification and distinct groups can be observed from the heatmap (Supplementary Material 9: Figure S9.4A). The profiles for the top CGI probes became noisier from shores to seas (Supplementary Material 9: Figure S9.4B, C). When ATC was set as the top-value method, probes in shores or seas generally separated samples into a high-methylation group and a low-methylation group and they had very small overlap with the probes extracted by SD/CV/MAD (Supplementary Material 9: Figure S9.4–6).

Different CpG feature categories play different biological roles. For example, CGIs are enriched at transcriptional start sites (TSS) and are generally unmethylated for actively expressed genes (36), while CGI seas overlap more with gene bodies or intergenic regions and normally relate to methylation changes in regions with long-range interactions. Accordingly, probes associated with different CpG features exhibited different methylation profiles. Thus, it might be more meaningful to apply consensus partitioning to the probes from different CpG features separately. Figure 7C and D illustrate the cola classification based on probes in the three CpG features using the SD:skmeans and ATC:skmeans methods where all six classifications were stable under the selected number of subgroups. With SD:skmeans, CGIs and shores generated similar classifications and which were highly similar to the originally published classifications, with the exception of a subset of Mesenchymal samples which were classified into the same group as the RTK II Classic subtype. For the classification based on CGI seas, Mesenchymal and RTK II Classic subtypes were merged into one group and some of the RTK I PDGFRA samples were classified into the group of K27 subtype. For comparison, ATC:skmeans generated very different classifications from SD:skmeans. The three different categories of CpG features all identified one separate subgroup corresponding to the G34 subtype, and merged K27 and RTK I PDGFRA subtypes into one subgroup. Partitioning based on CGI probes could still separate the IDH subtype, while it merged Mesenchymal and RTK II Classic into one subtype. Partitioning based on shore probes did not separate IDH, Mesenchymal and RTK II Classic subtypes at all, and partitioning based on Sea probes generated a classification which seems independent of IDH/Mesenchymal/RTK II Classic subtypes.

DISCUSSION

Many analyses of high-throughput genomic data require classification. Samples with specific molecular profiles need to be classified into distinct subgroups based on various omics data. Consensus partitioning solves this task with a special focus on the stability of the classification procedure. In this work, we present cola, an R/Bioconductor package which provides a general framework for this important type of analysis. cola provides comprehensive functionalities and an easy-to-use interface. As a general framework, cola allows various methods to be user-defined and easily integrated into different steps of an analysis. This includes feature selection, sample classification or identification of signatures, i.e., features discriminating between the identified subgroups, and, if the data type permits, functional enrichment. cola provides rich functionalities to directly perform analyses and to compare results from multiple partitioning methods in parallel, as well as rich visualizations, which alleviates the difficulty of choosing methods which best explain a given dataset. In addition to flexibility in the choice of parameters and methods, cola offers standardization of the analysis workflow; it can automate the complete analysis and generates a comprehensive HTML report by a simple piece of code (minimal two lines of code). Furthermore, a new top-value method, i.e., a method to select informative features for the classification procedure, named ATC, is implemented in cola. Beyond the description of the software package cola itself, here we additionally report on extensive benchmarks addressing key parameters in the consensus partitioning procedure using 435 publicly available datasets on gene expression and DNA methylation. This includes whether to perform random sampling by matrix rows or columns, how many random samplings are sufficient for consensus partitioning, and the impact of row scaling on the consensus partitioning. The results can help users to select optimal parameter values for their studies. The HTML reports, as well as the code for cola analyses of these 435 datasets, are all publicly available in a repository on GitHub, which can serve as an online database where researchers can query subgroupings in these datasets.

In addition to established variance-based top-value methods, in cola we have implemented ATC, a top-value method which is correlation-based. The benchmark on publicly available gene expression datasets demonstrates that consensus partitioning with the ATC method generates stable partitions. Among the different combinations of top-value methods and partitioning methods as encoded in the nomenclature A:B, where A is the top-value method and B is the partitioning method, those involving ATC had the highest stability as objectivated by 1-PAC and the highest concordance on gene expression data. When comparing the different partitioning methods, skmeans performed best in a majority of combinations, and ATC:skmeans was the most stable combination in our benchmark. This superiority persisted across different values of k, the number of subgroups. In particular, the combination ATC:skmeans had the highest resolution in the sense that it still yielded stable partitions even for higher numbers of k. Based on the fact that ATC is the only correlation-based top-value method in our benchmark, it extracts a unique set of features with little overlap with the features extracted by other top-value methods (Supplementary Material 2: Figure S2.16). The high stability of the ATC method can be explained by the features or rows selected by this top-value method. By definition, ATC selects features which upon pairwise comparison are highly correlated or anti-correlated and which form clusters of features. When performing several partitions with randomly selected subsets of features, few features of the various clusters may be deselected, but the overall presence of the clusters of features is not altered, which is the basis for stability.

We also compared variance-based and correlation-based top-value methods on a methylation array dataset. The results showed that SD had better performance and the probes it selected clearly separated samples into groups, while the probes selected by ATC only reflected global methylation difference which is of less interest. Since ATC only considers the correlation while ignoring the absolute variation in features, it may prioritize features showing consistent patterns but with very small differences among samples, which is sometimes caused by small batch effects, e.g., a sequencing batch. In those cases, the predicted partition may be statistically meaningful, but it hides the real biological subgroups. A typical example is that in the methylation dataset high ATC scores are more often assigned to features in non-CGI regions, reflecting genome-wide methylation differences. Thus, users need to be careful and a recommendation is to use the function top_row_heatmap() to directly visualize the patterns of the top features.

In the analysis of the methylation dataset, with the SD method, we found that partitionings were more determined by the CGI probes while partitionings generated by the ATC method were dominantly determined by CGI sea probes. We recommend using SD as the top-value method for methylation datasets because the methylation profile for the top probes it selected was efficient for subgroup classification and moreover, the majority of the top probes were located in CGIs and also functionally more related to the changes in gene expression. We found that different CpG features might generate different subgroup classifications, especially for the CGI seas, which is especially important for genome-level methylation profiles (e.g., from whole-genome bisulfite sequencing) because the proportion of CpG sites in seas from the whole genome (85.2% from a WGBS dataset) are much higher than the methylation array (46.2% in 450K methylation array). These different classifications probably reflect different and complementary aspects of the underlying biological system. Thus, it is meaningful to apply consensus partitioning on different CpG features separately.

In addition to an appropriate selection of top-value method and partitioning method, preprocessing also has an impact on the result of a consensus partitioning procedure. In particular, row scaling helps to remove the absolute difference between features while focusing on consistent regulation directions. While in general, applying row scaling on gene expression datasets can be recommended, users need to be cautious. In this work, we chose one dataset, the Golub leukemia dataset, for comparison and performed cola analysis with and without row scaling. This resulted in two different classifications, and both were biologically meaningful.

In the original study of the Golub leukemia dataset, a self-organizing map (SOM) was applied to the entire expression matrix without row scaling. The authors found a two-group classification of the samples with very good agreement with the biological classification of acute myeloid leukemia (AML) and acute lymphoblastic leukemia (ALL) (29). The original analysis only applied SOM once and thus did not consider the stability of the clustering. As shown in Supplementary Material 10, in the cola analysis, when the number of subgroups was set to 2 and rows were scaled, ATC:kmeans, ATC:NMF and ATC:skmeans generated stable partitions. The consensus classification of the three methods had a very high agreement, but a subset of the ALL samples were classified in the same group as AML samples. The top-value methods SD, CV and MAD combined with hclust, kmeans, mclust and NMF separated the samples along with the AML/ALL separation, however, the partitions were not stable. Of note, if rows were not scaled, variance-based methods generated stable partitions, e.g., MAD:skmeans or SD:kmeans, while correlation-based methods lost stability. The two different classifications both separated samples well in the PCA analysis and both had high numbers of signature genes (1810 signature genes in the two-group classification by ATC:skmeans with rows scaled, 1057 signature genes by MAD:kmeans with rows unscaled, with an overlap of 704 genes in the two sets of signature genes, FDR < 0.05). The two sets of signature genes both had a number of enriched biological functions, which implies that both classifications were biologically meaningful.

The Golub leukemia study also classified samples into three groups where ALL samples were additionally classified into two subgroups which corresponded to T-cell and B-cell lineage (29). With three-group classification by cola (Supplementary Material 11), we found that ATC:skmeans with row scaling was the only method that generated a stable partition where ALL samples were separated into two groups. SD:skmeans without row scaling generated the most similar partition as the original Golub classification, however, the partition was highly unstable, especially for the B/T-cell classification. Interestingly, being different from the B/T-cell classification for ALL samples, ATC:skmeans generated a different classification for ALL samples. The signature genes for the two partitions were very different where ATC:skmeans with row scaling selected 1200 signature genes while SD:skmeans without row scaling only selected 228 signature genes. The number of common signature genes was only 17. Functional enrichment analysis showed that ATC:skmeans signature genes enriched many terms in the agreement with prior biological knowledge. Thus, this novel classification might provide a new view on the subgroups of ALL.

Using the same datasets as in the benchmarks above, we also varied other parameters and assessed their influence on stability as well as optimality criteria. In the consensus partitioning process, random samplings can either be performed by rows or columns of the matrix. Through the benchmarks on public datasets, we found that the final partition results were highly consistent between both samplings and partitions from row sampling were slightly more stable than from column sampling. Column sampling ran ∼1.5 times longer than row sampling, which might be an issue for the partitioning methods that need longer runtime, e.g., NMF (Supplementary Material 8). We also evaluated the impact of the number of random samplings on the reproducibility of consensus partitioning. We found that consensus partitioning was well reproducible even for 25 samplings, especially when the partition was already stable. One reason is that the consensus partition is already summarized from a huge amount of single partitionings. cola takes 50 samplings as the default parameter, which is a balance between the stability of the partitionings and runtime.

cola provides a function get_classes() that can be applied to the ConsensusPartitionList object and generates a global classification by averaging consensus partitions from all methods by weighting the mean silhouette score in each method. This process is also visualized by the function collect_classes() and an example can be found in Figure 3C. However, consensus classification across different methods should be applied with care because the assignment of weights to partitions from the various methods is a complex task. Furthermore, as demonstrated with the Golub leukemia dataset, different partition methods can yield complementary and still valid classifications (Supplementary Material 10). Samples having different classification labels between groups will be assigned as ambiguous samples if all methods are merged. In this case, it is worthwhile to look at different classifications separately since they might illustrate different aspects of the data and underlying biological systems.

One popular field to apply partitioning analysis is scRNA-Seq. cola can be applied to scRNA-Seq datasets if the number of cells is intermediate (∼500), however, the runtime and the memory usage might not be acceptable if the number of cells becomes very high, e.g., several thousands. Nevertheless, we can propose the following two strategies to partially solve this problem. (i) A randomly sampled subset of cells which take relatively short runtime (e.g., 100–200 cells) can be first supplied to cola, from which a specific combination of top-value method and partitioning method that gives the best results can be pre-selected. Later the user can then apply only these two specific methods to the complete dataset. This will be much faster than blindly running cola with many methods in sequence. (ii) The selected subset of cells can be treated as a training set to generate a classification. Then, the class labels of the remaining cells can be predicted, e.g., by testing the distance to the centroid of each cell group, without rerunning consensus partitioning. cola implements a function predict_classes() for this purpose. To simplify the use even more, cola implements a function consensus_partition_by_down_sampling() that automatically performs the analysis proposed in the second strategy. Note, since these two strategies are performed by sampling a small subset of cells from the cohort, the cell clusters with small sizes might not be detectable. However, if sufficient annotation is available, the sampling strategy may also be chosen in a semi-supervised way to select representatives of known groups.

cola is a statistical framework for unsupervised partitioning analysis with no assumption on the data types and the biology subjects. Nevertheless, cola provides functions that help to interpret biological implications of the classification. The function functional_enrichment() does this by analyzing the biological functions of the signature genes that best separate subgroups. If more external data is provided, e.g., clinical data such as survival data, the biological interpretation of the classification can be validated. cola provides the function test_to_known_factors() that helps to check the correspondence between cola classification and the known annotation tables by statistical tests.

CONCLUSIONS

We developed cola, an R package that provides a comprehensive analysis for consensus partitioning. We demonstrated the usage of cola and benchmarked the key parameters in the consensus partitioning procedure, which gives valuable hints for users to select proper parameters for their studies. cola is designed with an easy user interface and allows integrating user-defined methods into the partitioning framework. We believe it will be convenient for de novo subgroup identification in studies, as well as for benchmarking new partitioning methods.

DATA AVAILABILITY

The cola package is available on Bioconductor (https://bioconductor.org/packages/cola/). Note that for reproducibility of the analyses presented in this work, the version of cola should be ≥1.3.2. The cola reports for 206 GDS and 223 recount2 datasets, as well as the six public datasets used for demonstration, are publicly available at https://jokergoo.github.io/cola_collection/. The scripts to perform the complete analysis are available at https://github.com/jokergoo/cola_manuscript. The Supplementary Materials are available at https://jokergoo.github.io/cola_supplementary/.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

German Cancer Research Center-Heidelberg Center for Personalized Oncology (DKFZ-HIPO); Molecular Diagnostics Program of the National Center for Tumor Diseases (NCT) Heidelberg. Funding for open access charge: German Cancer Research Center-Heidelberg Center for Personalized Oncology (DKFZ-HIPO); Molecular Diagnostics Program of the National Center for Tumor Diseases (NCT) Heidelberg.

Conflict of interest statement. None declared.