Machine Learning in Arrhythmia and Electrophysiology

Abstract

Machine learning (ML), a branch of artificial intelligence (AI), where machines learn from big data, is at the crest of a technological wave of change sweeping society. Cardiovascular medicine is at the forefront of many ML applications, and there is a significant effort to bring them into mainstream clinical practice. In the field of cardiac electrophysiology, ML applications have also seen a rapid growth and popularity, particularly the use of ML in the automatic interpretation of ECGs, which has been extensively covered in the literature. Much lesser known are the other aspects of ML application in cardiac electrophysiology and arrhythmias, such as those in basic science research on arrhythmia mechanisms, both experimental and computational; in the development of better techniques for mapping of cardiac electrical function; and in translational research related to arrhythmia management. In the current review, we examine comprehensively such ML applications as they match the scope of this journal. The current review is organized in three parts. The first provides an overview of general ML principles and methodologies that will afford readers of the necessary information on the subject, serving as the foundation for inviting further ML applications in arrhythmia research. The basic information we provide can serve as a guide how one might design and conduct a ML study. The second part is a review of arrhythmia and electrophysiology studies in which ML has been utilized, highlighting the broad potential of ML approaches. For each subject, we outline comprehensively the general topics, while reviewing some of the research advances utilizing ML under the subject. Finally, we discuss the main challenges and the perspectives for ML-driven cardiac electrophysiology and arrhythmia research.

1. Introduction

Artificial Intelligence (AI) has become ubiquitous in this day and age. We encounter it on a daily basis – the recognition of faces and objects in our photos, the delivery of verbal commands to Alexa or Siri or to our phones, having our words completed as we type, getting those often-annoying suggestions of what to purchase online. The advancement in the speed of computing, and the development of new algorithms and techniques that mimic the human brain function have led to the widespread implementation of AI-based applications in many fields of science and technology.

AI, and particularly machine learning (ML), a subset of AI, is also becoming a rapidly growing part of medicine, promising a paradigm shift in the way health care providers treat their patients. Modern medicine has seen unprecedented increase in the availability of biological and clinical data that represent information at various levels of biological complexity, such as multiomics, molecular pathways, biomedical imaging data, electronic health records, and data from implantable electronic devices and wearable sensors. ML is envisioned to support medical decision-making and to improve diagnostic and prognostic performance by identifying actionable insights into disease pathophysiology from this data of extraordinary scale, complexity, and rate of acquisition. This requires a close collaboration between computer scientists, engineers, biologists, clinical investigators, and healthcare professionals, so that strengths of ML are properly utilized, and the limitations overcome. The expectation is that as a result, healthcare would become more personalized, more democratic, more efficient, and more effective in ensuring society’s well-being.

Cardiovascular medicine is at the forefront of many ML applications, with a few becoming part of mainstream clinical practice. Several comprehensive reviews^1–3 have been written on the subject, focusing on its main applications, potential impacts and challenges, and attesting to the fact that the number of research articles on the subject has grown at an exponential rate over the last decade. In the field of cardiac electrophysiology, ML applications have also seen a rapid growth and popularity, particularly the use of AI in the interpretation of pulse irregularities and ECGs, the latter being a major diagnostic tool. For instance, the Apple Heart Study⁴ tested the ability of a smartwatch application to identify atrial fibrillation (AF); the ML algorithm was able to identify AF with a positive predictive value of 0.84. Accordingly, a few reviews have been recently published on the application of AI in clinical cardiac electrophysiology^5,6, discussing the expectations for the implementation of these technologies in clinical decision-making and the future of AI in cardiac patient care and precision cardiology.

Several aspects of ML application in cardiac electrophysiology have not been covered in these recent reviews: these include ML utility in basic science research on arrhythmia mechanisms, both experimental and computational; in the development of better techniques for mapping cardiac electrical function; and in translational research related to arrhythmia management. In the current review, we examine comprehensively such ML applications, as they best match the scope of this journal, while touching only very briefly on ECG interpretation. The review is organized in three parts. The first provides an overview of general ML principles and methodologies that will afford readers of this journal the necessary information on the subject, hopefully serving as the foundation for inviting further ML applications in arrhythmia research. The second part is a review of arrhythmia and electrophysiology studies in which ML has been utilized, highlighting the broad potential of ML approaches; in each of these sections we outline comprehensively the general sub-topics and the corresponding references, while reviewing some of the research advances utilizing ML under the specific subject. Finally, we touch upon the main challenges and the perspectives for ML-driven cardiac electrophysiology and arrhythmia research.

2. General Principles of ML

The concept of ML arose as a paradigm shift in the way humans approached AI. Traditional AI required certain input rules (the program) and data to be executed by the program to generate answers. ML turned this concept on its head by eliminating the need for programmers to craft rules, and instead using data and extracting answers from the data to construct the rules. The boom of ML, in great part due to the availability of powerful hardware and large datasets, that began in the 1990s⁷, has solidified ML’s place as one of the most popular subfields of AI. Although closely related to several other fields – such as mathematical statistics, probability, information theory, decision theory – ML tackles problems often involving extremely large and complex data (e.g., millions of images consisting of several thousand pixels), for which traditional statistical techniques may be impractical. Consequently, with the mathematical and theoretical underpinnings of the field still in a nascent state, ML has become a more engineering-oriented approach⁷.

An ML system needs to be explicitly trained to design rules. Once the system is trained, it proceeds to the testing phase in which its ability to generalize – predict answers for never-before-seen data – is evaluated (see Fig.1). This ability to categorize or predict based on data not used in the training phase is the central tenet in ML. To facilitate the training phase and increase the ML system’s (i.e., the model’s) ability to generalize, pre-processing steps are oftentimes needed⁸. For example, in a task of predicting whether given images represent cats or dogs, such pre-processing steps may aim to eliminate the variability among data by cropping all the images to the same size or rescaling the pixel intensities to a fixed range. Applying the same pre-processing methods, called feature extraction, developed on the training set, to the test set improves the ML model generalizability, facilitating classification of new images. Traditionally, the main approach to feature extraction has been feature engineering, in which the researcher uses their experience to condense information from the raw data into values to be used in ML. For example, instead of using raw ECG data as a covariate in a disease prediction ML problem, the researcher may only use the QRS duration. More recently, feature learning has taken the role of feature engineering, shifting the task of uncovering features to the ML model itself by systematically exploring the available training data.

Figure 1. Typical workflow of the machine learning approach.

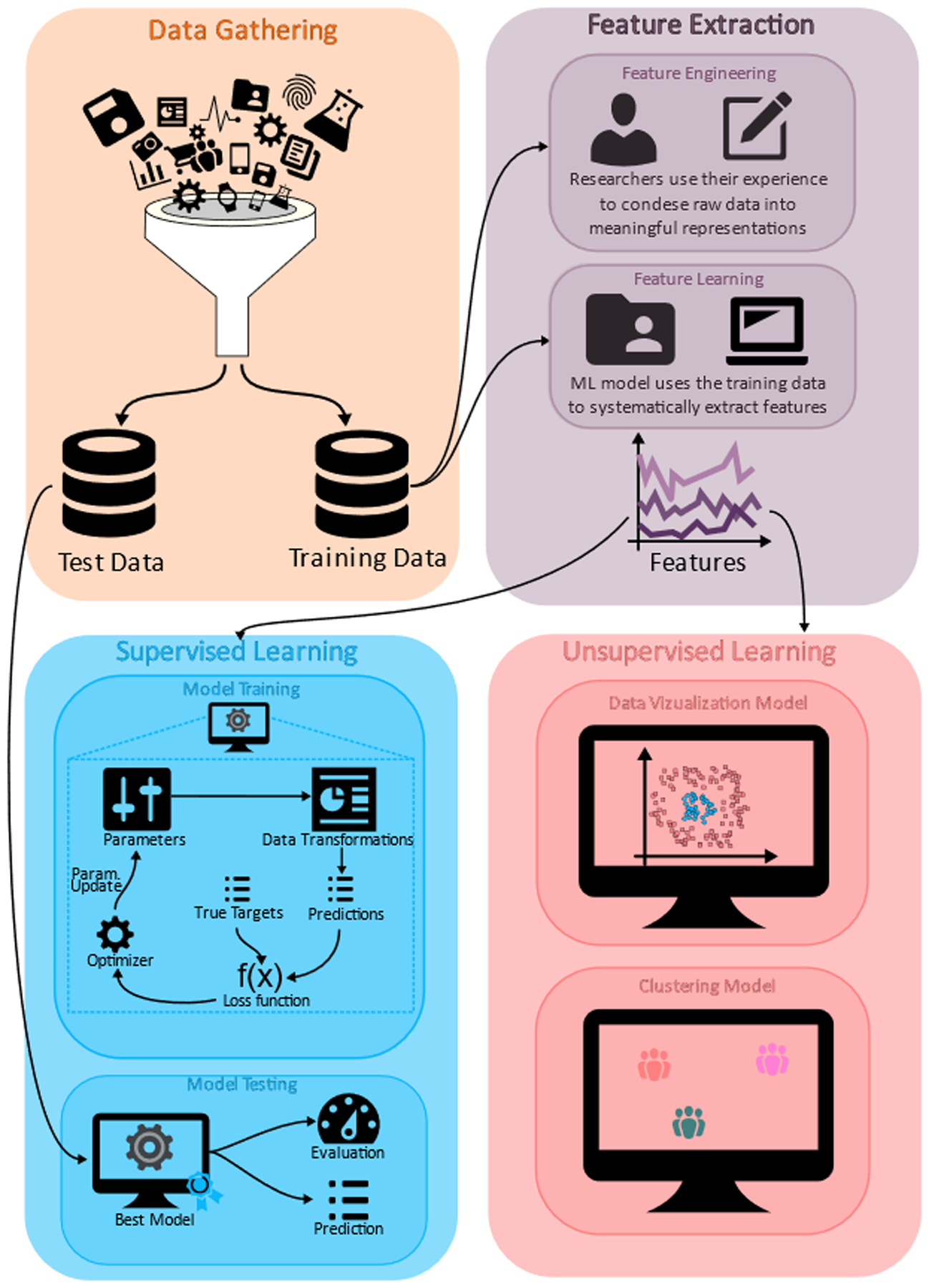
After the data gathering step, data is split into a train set and a test set. Features (useful representations of the data) are then extracted from the training data, either by performing researcher-defined transformations of the data (feature engineering) or using machine learning techniques (feature learning). Depending on the availability of targets (expected answers from the data) and the desired machine learning task, features can be used in either a supervised or unsupervised setting. In the supervised setting, a model is trained by iteratively minimizing a loss function, which adjusts the model’s parameters such that predictions and targets match. The resulting best model is then used on the test data. In the unsupervised setting in which there are no targets available, data can be used for visualization or identifying sub-groups with common characteristics, i.e., clusters.

2.1. ML classification by learning type

ML tasks are typically dichotomized based on whether expected answers (also known as “targets” or “labels”) are available for the training input data. For example, in a risk prediction task, the inputs would be patient characteristics and the targets would be the clinical outcome of whether the patient had/did not have an arrhythmia. If the case where targets are available for the input data and the goal is to predict targets for the unseen data, the learning task is called supervised. For example, most classification tasks would fall under this category, where the ML system’s goal is to learn features of the class (e.g., green eyes in pictures of cats and dogs are indicative of the class “cat”) and apply them when new data is presented. On the other hand, if target data is not available, the task is called unsupervised learning. The aim of such tasks is to find useful representations of the data via various transformations such that data can be better visualized by humans, thereby revealing simpler or reduced structures. Although beyond the scope of this review, there are also hybrid approaches. One such approach is semi-supervised learning, in which labeled training data are only partially available, but the presence of non-labeled data can better guide the supervised task. Finally, reinforcement learning⁹ is a type of ML in which programs go through a process of trial and error to pick actions that maximize rewards. Unlike supervised learning, there is no need to provide labels for this ML learning type, as the system uses its environment and the reward function to guide itself. A particularly noteworthy application of this method is DeepMind’s Alpha Go¹⁰ algorithm, which gained such a deep understanding of the game Go that it would set up counter-intuitive (for humans) strategies in the short term, only to capitalize on them tens of moves later.

2.2. ML classification by task type

Attempting a comprehensive taxonomy of ML algorithms is beyond the scope of this review and is bound to do disservice to many algorithms which have been adapted for multiple tasks. Instead, we discuss four of the most important types of tasks that ML tackles (see Fig.2): classification, regression, clustering, and dimensionality reduction. In the next section, we will give examples of ML algorithms in each category and highlight some of their advantages. Classification tasks typically fall under the supervised learning category and deal with the assigning each input data point to one of a finite number of discrete categories (e.g., “given a raw ECG signal, is it indicative of AF?”). Regression tasks are also supervised and expand on the classification problem by predicting one or more continuous variables (e.g., “Given a stack of cine MRIs, what is the predicted left ventricular ejection fraction?”). The forecasting role that regressions play in ML should be contrasted with that of regressions in applied statistics, which is to establish causal relationships between dependent and independent variables.

Figure 2. Classification of machine learning algorithms by task type.

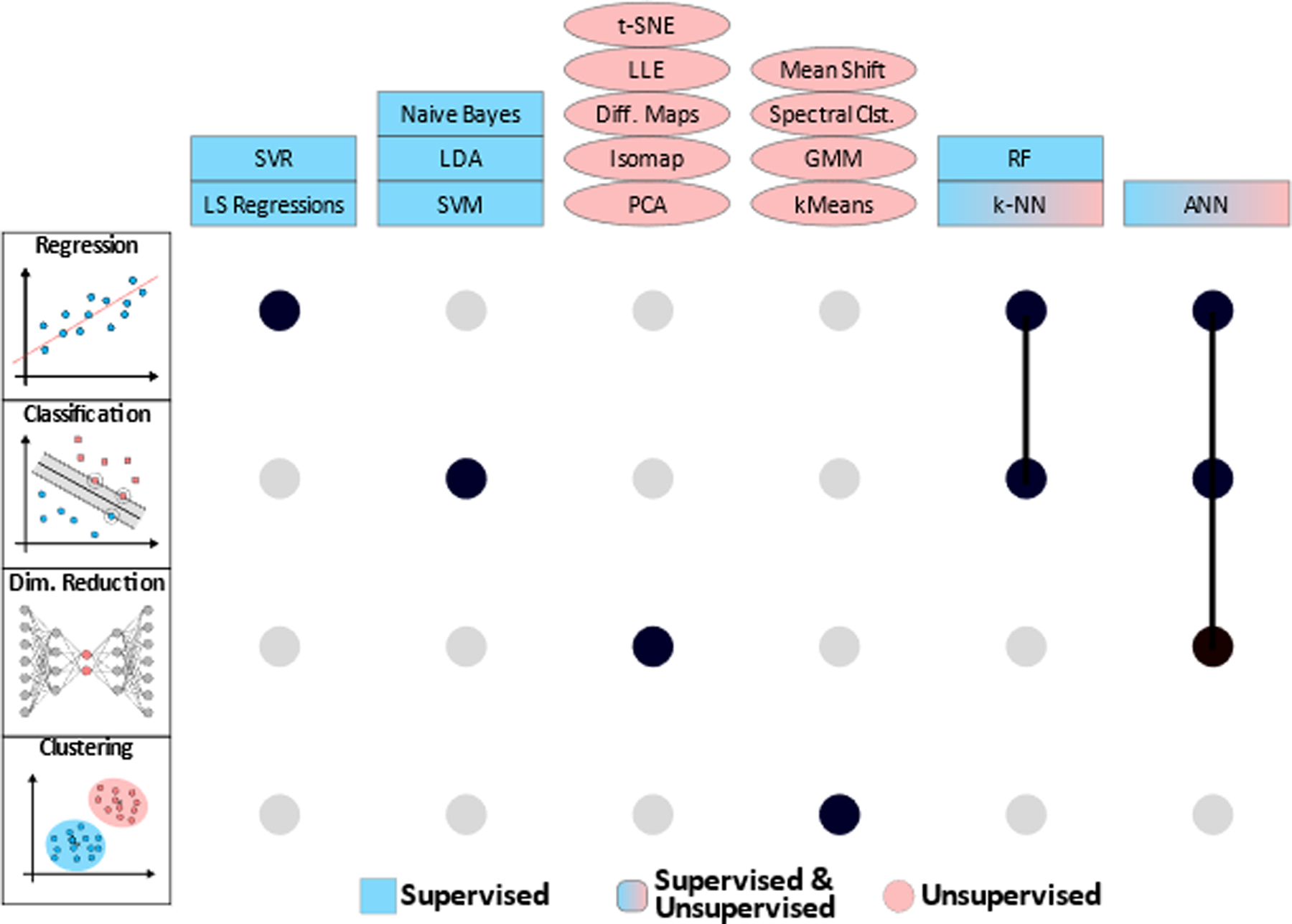
UpSet plot¹⁶⁵ showing algorithms (columns) that can be used for a given task type (rows: regression, classification, dimensionality reduction, and clustering) using black filled-in circles. Gray circles denote algorithms not typically used for the respective task. Connected circles denote algorithms which are used for multiple tasks. Algorithms in blue rectangles are typically supervised, those in red ellipses are typically unsupervised, and algorithms in red and blue can be either supervised or unsupervised.

In certain ML problems, input training data is available without associated labels. The goal here may be identify sub-groups of the data which display some degree of similarity, i.e., clustering. For example, used on a diverse set of patients, clustering may help identify certain sub-cohorts that help clinicians better understand the population. Additionally, one may be interested in reducing the dimension of the data for various purposes, including visualization in 2 or 3 dimensions, or as part of a feature extraction task.

2.3. Most common ML algorithms

We now highlight several widely used ML algorithms, briefly describe them, and provide some of their advantages and disadvantages (for additional algorithms, refer to Table 1).

Table 1.

Common ML algorithms and their advantages and disadvantages

Algorithm	Acronyms/Variations	Description	Advantages	Disadvantages	References
Regressions	LASSO, Ridge, Elastic	Fit a simple function’s parameters to minimize the sum of squared distances to the observed data	Easily interpretable Uncovers causal relationships	Computationally impractical for large, high-dimensional datasets	Tibshirani14, Kennedy13, Zou & Hastie15
Support Vector Machines	SVM, SVR	Use support vectors to identify decision boundaries in the data	Memory efficient Robust, based on the Vapnik Chervonenkis theory	Not suitable for large datasets No probabilistic interpretation of classifiers	Cortes & Vapnik16
k-nearest neighbor	k-NN	Classify new data based on labels of surrounding neighbors	Strong theoretical underpinnings Easily interpretable	Not suitable for large datasets Large memory footprint	Cover & Hart17
k-means clustering	kMeans	Assign each point in the dataset to one of k clusters to minimize within cluster- variance relative to cluster’s centroid	Requires apriori specifying k Good convergence	Not suitable for high dimensional data Sensitive to outliers	Lloyd18
Principal Component Analysis	PCA, POD, SVD, EVD, KLT	Change coordinates to orthonormal basis that maximizes the variance of the data along these new coordinates	Can be used as feature extraction Computationally efficient algorithms available Extensively studied led to many generalizations	Principal components can depend on all input variables. Learned subspace is linear	Bishop8, Wold et al.157
Decision Tree and Random Forest	RF, AdaBoost, XGBoost	Build flowchart-like decision trees for which the questions are learned from data, then ensemble multiple to form random forests	Very easy to interpret, as intermediary decisions can be read directly Performs well on large data sets	Requires manually crafted features Not suitable for perceptual data (e.g., images)	Breiman20
Artificial Neural Networks	(A)NN, CNN, RNN, DNN, GAN	Directed, weighted acyclic graph of neurons arranged in layers, using a propagation function to transmit information	Automatic feature learning Very good performance on imaging data Applicable to a wide range of problems Easy to continue training on additional data	May require large amounts of data Prone to overfitting on small datasets Hard to interpret	Chollet7, Bishop8
Naïve Bayes	N/A	Classification using Bayes’ theorem by assuming independence between features to model class conditional probability	Requires small number of training samples imaging data Easy to interpret	Assumes features are independent Not suitable for high dimensional data	Bishop8
Linear discriminant analysis	LDA, NDA	Find a linear combination of features that that separates input data in classes	Strong performance when assumptions met	Independent variables assumed normal Sensitive to outliers	Duda et al.158
Gaussian Mixture Model	GMM	Assume data follows a linear combination of Gaussian distributions with parameters estimated from data	Fastest algorithm for learning mixture models Simple likelihood-based optimization	Covariance matrix estimation can be difficult Number of components is aproiri specified	Bishop8
Spectral Clustering	N/A	Use eigenvalue decomposition to cluster based on the similarity matrix whose entries Aij express degree of similarity between points i and j	Simple to implement Can be solved efficiently with linear algebra methods	Number of clusters needs to be specified in advance	Ng et al.159
Mean Shift	N/A	A centroid-based clustering method using an iterative approach to search through neighborhood of points and locate modes of density functions	No need to specify number of clusters The bandwidth parameter has physical meaning	Not scalable, as it requires many nearest neighbor searches	Comaniciu & Meer160
Isomap	N/A	Non-linear dimensionality reduction using an isometric mapping (distance-preserving transformation between metric spaces)	High computational efficiency Nonlinear Globally optimal	Sensitive to the parameter governing the connectivity of each point	Tenenbaum et al.161
Local Linear Embedding	LLE, HLLE, MLLE	Non-linear dimensionality reduction by using linear combinations of projected neighborhood points to reconstruct data	Faster than Isomap Can take advantage of sparse matrix algorithms	Sensitive to sampling density (i.e., performs poorly on non-uniform densities)	Roweis & Saul162
Diffusion Maps	N/A	Feature extraction and dimensionality reduction based on a nonlinear approach, in which distances between points are defined in terms of probabilities of diffusion	Nonlinear Computation is insensitive to distribution of the points	Scaling parameter ε requires tuning	Coifman et al.163
t-distributed stochastic neighbor embedding	tSNE	Data visualization tool which defines similarity between two points as the conditional probability one would pick the other as neighbor if neighbors were picked based on Student t probabilities centered at the first point	Constructs 2- or 3-dimensional representations of the data for easy visualization Nonlinear	Highly computationally expensive Due to stochastic nature, sensitive to initial conditions	Roweis & Hinton164

Regressions.

Despite pre-dating the field of ML by almost two centuries^11,12, the general idea is the same – assume the data can be fitted by a given (usually, linear) function, but may deviate due to noise, and find the function’s parameters which minimize the sum of squared distances to the observed data (Fig.3A). However, different regression variants have brought significant enhancements: ridge regression¹³ partially addresses multicollinearity in the data by shifting the diagonal elements of the data matrix; LASSO regression¹⁴ adds a penalty proportional to the absolute value of the regression weights, helping with generalization and variable selection; elastic net regression¹⁵ expands on LASSO with an additional penalty on the sum of squares of the weights for better generalization. One of the main benefits of regressions is their straightforward interpretability, however they lose practicality in the case of large, high dimensional datasets.

Figure 3. Commonly used machine learning algorithms. A. Least square regressions.

For these models, assume the data can be fitted by a given (usually, linear) function (regression line), but may deviate due to noise, and find the function’s parameters which minimize the sum of squared distances (errors) to the observed data. B. Support Vector Machines. Typically using binary classification in a supervised setting, the model aims to locate a decision boundary based on a subset of data points (support vectors) that maximizes the margin, i.e., the perpendicular distance between the decision boundary and the closest of the data points. C. k-nearest neighbors. These are non-parametric models for classification and regression problems, in which the idea is to use a vote (for example, majority) of the k closest neighbors to inform a new point’s predicted value/label. D. K means clustering. The goal of this unsupervised clustering algorithm is to split the available data into k clusters by re-assigning each point to different clusters until some distance (typically, Euclidean) is minimized between all points and the respective cluster’s centroid. E. Random forests. Decision trees are a supervised approach to classification and regression problems in which input data is sequentially classified through a flowchart-like structure, where the features to be learned are questions about the data (e.g., “Is patient’s age less than 40?”). Random forests use many decision trees to construct an ensembled output, offering a more robust learning algorithm. F. Principal component analysis. The goal is to change coordinates for the data to an orthogonal basis (principal components, in red) that maximizes the variance of the data along these new principal component directions. This allows for a truncation after a suitable number of principal components, reducing the dimensions of the data. G. Neural networks. Shown here is a neural network autoencoder which consists of artificial neurons (or nodes, gray and red circles) organized in layers (shaded in gray), sharing weighted, directed connections (thin black lines) amongst themselves, each being responsible for combining inputs via a propagation function and generating outputs to be passed further in the network. The input data is passed through fully connected layers to produce a low dimensional encoding (red circles) during encoding, then decoded using additionally fully-connected layers to produce the reconstructed image (here the image of the number 5).

Support Vector Machines (SVM).

This algorithm originally developed by Vladimir Vapnik and his colleagues at AT&T Bell Lab¹⁶ for binary classification in a supervised setting, has since been expanded to regressions and unsupervised problems. The core idea is to locate a decision boundary based on a subset of data points (support vectors) that maximizes the margin, i.e., the perpendicular distance between the decision boundary and the closest of the data points (Fig.3B). Although effective in high dimensional spaces, this method can lead to severe overfitting (inability to generalize)⁸.

k-Nearest Neighbors (k-NN).

Introduced by Cover and Hart¹⁷, k-NN is a non-parametric model for classification and regression problems, in which the idea is to use a vote (for example, majority) of the k closest neighbors to inform a new point’s predicted value/label (Fig.3C). This is one of the few algorithms for which there is a known bound on the probability of misclassification.

k-Means Clustering (kMeans).

The goal of this unsupervised clustering algorithm is to split the available data into k clusters¹⁸. This is done iteratively by re-assigning each point to different clusters until some distance (typically, Euclidean) is minimized between all points and the respective cluster’s centroid (Fig.3D).

Principal Component Analysis (PCA).

One of the most ubiquitous unsupervised dimensionality reduction techniques, PCA dates back to the early 1900s¹⁹, but has been re-discovered under many names throughout the last century: proper orthogonal decomposition in mechanical engineering, singular value decomposition or eigenvalue decomposition in linear algebra, Karhunen-Loève transform in signal processing, etc. Consequently, there have been many improvements and generalization to the method, but they all share the same idea: given a high-dimensional set of input variables, in which some or all variables are related to one another (multicollinear), decrease the number of input variables while retaining the information contained in them. This is accomplished by changing coordinates for the data to an orthogonal basis (perpendicular axes) that maximizes the variance of the data along these new principal component directions (Fig.3F). Each principal component is an eigenvector of the data matrix; these are ordered according to the amount of explained variance. While there are initially the same number of principal components as input variables, the latter can be truncated by taking the first few principal components which explain most of the variance in the data, thereby reducing the dimensionality of the input.

Decision Trees and Random Forests (RF).

Decision trees are a supervised approach to classification and regression problems in which input data is sequentially classified through a flowchart-like structure, where the features to be learned are questions about the data (e.g., “Is patient age less than 40?”). RFs²⁰ use many decision trees to construct an ensembled output, offering a more robust learning algorithm (Fig.3E). Gradient boosting machine are like RFs as they combine weak classifiers, typically decision trees. They are one of the most successful algorithms today⁷.

Artificial Neural Networks (ANNs or NNs).

Originally proposed as a model for biological neural networks²¹, ANNs consist of artificial neurons (or nodes) organized in layers, sharing weighted, directed connections amongst themselves, each being responsible for combining inputs via a propagation function and generating outputs to be passed further in the network (Fig.3G). Historically, two major breakthroughs renewed interest in NNs: (re)discovery of the backpropagation algorithm in the 1980s that made training them practical; and in 2011, Dan Ciresan’s implementation of a many-layer (deep) neural network (DNN) on graphics processing units (GPUs)⁷. Specialized layers and architectures, such as convolutional NNs (CNNs) for image data, recurrent NNs (RNNs) for time-series data, generative adversarial networks (GANs) for unlabeled data, have propelled NNs to the top of ML algorithms⁷, excelling at supervised and unsupervised tasks in classification, regression and dimensionality reduction problems.

2.4. Training and validation

For most of the algorithms discussed, the process of training, particularly in the case of supervised learning, is based on defining a loss function which will be minimized, typically through an iterative process (e.g., the loss for a simple linear regression is the mean squared error). Some algorithms may have additional degrees of freedom (e.g., number of layers in an ANN), which are chosen by the researcher. These model design parameters – as opposed to parameters resulting from the loss minimization algorithm – are called hyperparameters. Prior to performing any training or optimization, a test set should be identified and sequestered from the training data. Depending on the problem and amount of available data, this could be a percentage (10–30%) of the training data or an entirely separate “external validation” cohort from a different source.

In practical applications, the goal is to use available training data and select a model (algorithm and hyperparameters) that will have the best predictive performance on new data⁸. The performance may be assessed using the loss function or other intuitive metrics chosen by the researcher – e.g., true/false positive/negatives and other measures derived from them. If the training data is plentiful, one easy solution is to carve out a percentage of the training data and use it as a validation set. This will serve as an estimate for the model’s performance on the test set and is often used to optimize hyperparameters of the algorithm by choosing the hyperparameters which maximize performance on the validation set. Unfortunately, there are no rigid rules on what constitutes “enough” data, as this can depend on the difficulty of the learning task, the algorithm used, the desired statistical confidence, etc. In real applications, however, there is usually a scarcity of training and testing data, and more rigorous validation techniques are needed. One staple technique is k-fold cross-validation. This requires the researcher to split the training data in k (typically, 5 or 10) subsets and repeatedly set one subset for validation and train on the remaining k – 1. The performance for this split of the data will be the average across the k different folds, and this process can be further repeated with other random splits, followed by an average across all the runs. One of the downfalls of this approach is that, despite giving more stable performance estimates, the number of times the model needs to be trained can be computationally expensive.

Another popular validation method is the bootstrap²². The main idea behind this method is to sample the training set with replacement, train the model on this bootstrapped set (which may contain duplicates), and estimate the “generalization error” as the discrepancy between performance on the bootstrapped set compared to the whole set, averaged over many repetitions of this process. Although various estimates have been proposed for the bootstrap generalization error, one of the main drawbacks remains that the estimates tend to be overly optimistic, especially in models that are prone to overfit. It is important to note there are no universal validation methods and analysis of these methods remains a very hard problem²³.

Table 1 provides detail on the common ML algorithms and their advantages and disadgvantages.

2.5. Pitfalls

It is undeniable that there has been tremendous optimism for the dawn of ML techniques in the biomedical field in recent years, but periods of unbridled optimism followed by intense skepticism are not new. Symbolic AI in the 1960s and expert systems in 1980s offered promises of “human-level general intelligence”, but failed to deliver, prompting interest to switch away from the field⁷. It may be beneficial to moderate expectations for the short term and avoid the cognitive bias of treating everything like a nail to be tackled with the ML hammer. To apply ML techniques correctly, their limitations need to be understood. As mentioned above, a major concern for ML systems is whether they are truly learning from the training data, or merely memorizing, affecting their ability to generalize to new samples. Similarly, there exists the underlying, often untested, assumption that the new test data will be sampled from the same distribution from which the training data originated. General mathematical theory of advanced ML algorithms is not sufficiently developed, and it can be proven that, for example, for any fixed neural network, there exists a distribution of the data which makes the performance arbitrarily poor²³. Therefore, there exists a constant trade-off between controlling bias (broad enough model to fit the data well) and variance (not too broad that the model overfits). Concerns using ML systems are further amplified when, for example in classification tasks, there is a significant class imbalance – that is, at least one of the classes is disproportionately represented. Unfortunately, this is often the case in biomedical applications and much care is needed to account for this during both training and evaluating.

The existence of limitations should not, however, obscure the vast progress ML algorithms have achieved in the last few years. Tasks such as image classification, speech recognition, handwriting transcriptions, and autonomous driving are performed at near-human-level⁷. In complex strategy games, such as Go, their performance is superhuman. As will be discussed in this review, although only at the beginning of a long path, ML has also reached or even surpassed humans in certain disease-related classification and prediction tasks.

3. Applications of ML in cardiac electrophysiology and arrhythmia research

The exposition in this part of the review presents studies utilizing ML from basic research on ion channels to applications in organ-level electrophysiology research and even touching upon arrhythmia management. For each section, we provided a bulleted list of the research sub-areas where ML has been applied, and then review the main applications.

3.1. Use of ML in ion channels and action potential research

• Predict functional changes in sodium current I_Na from mutations in SCN5A, the gene encoding the cardiac sodium channel²⁴

• Identify structure/function relationships in voltage-gated potassium channels^25,26

• Classify action potentials from stem-cell derived cardiomyocytes^27,28

• Engineer “designer” channelrhodopsin for optogenetics studies²⁹

In biophysical studies of ion channels and cardiac cell electrophysiology aimed at uncovering mechanisms for arrhythmias, ML techniques usage is at its nascent stage. ML has seen early use as a research tool, enabling better classifications and uncovering structure-function relationships. A notable study in this area of research is the paper by Clerx et al,²⁴ which addressed prediction of pathogenicity of variants in SCN5A, the gene encoding the cardiac sodium channel. Predictors of SCN5A variant pathogenicity have typically suffered from poor performance. The study took an intermediate step in improving such prediction, by predicting the functional changes to the sodium current I_Na from known non-synonymous missense mutations in the SCN5A gene; the authors suggested that the I_Na functional changes could later then be used in the final (i.e. two-step) assessment of SCN5A variant pathogenicity. For each SCN5A variant, a set of features was extracted on which a supervised ML algorithm was trained. The substituted residues’ location on the protein correlated with channel function and strongly contributed to predictions, while conservedness and physico-chemical properties did not. The study demonstrated that using this approach, the complexity of SCN5A variant pathogenicity prediction can be reduced, leading to improved predictions.

An example of using ML to identify structure/function relationship is the study of Li and Gallin²⁵ who trained an ML algorithm on available voltage-gated potassium channels amino-acid sequence and electrophysiological data to predict the half-activation voltage of the channel, a central electrophysiological parameter. The optimal model’s predictions were validated by comparison to independently obtained experimental results.

Further, to resolve the uncertainty in classifying the phenotype (ventricular-like, atrial-like, nodal-like, etc.) of human embryonic stem cell-derived cardiomyocytes (hESC-CMs), an unsupervised ML algorithm was employed to cluster (separate) a population of these cardiomyocytes into distinct groups based on the similarity of their action potential shapes, the latter obtained from optical recordings.²⁷ The study found that while there were clusters in the dataset with just one phenotype, majority of cell clusters exhibited multiple phenotypes. The results suggest that hESC-CMs action potentials varied as a continuum from one phenotype to another. These initial results led to a subsequent study²⁸ which conducted a systematic analysis of heterogeneity and phenotypes of populations of hESC-CMs, analyzing 23,000 action potentials. Such analysis could be used in evaluating strategies to improve the quality of human pluripotent stem cell-derived cardiomyocytes (hPSC-CMs) for use in diagnostic and therapeutic applications and in drug screening.

An interesting ML application²⁹ in this research field but in a different direction is the use of ML to guide engineering of light-gated channelrhodopsins (ChRs), which have been extensively used in recent years for optical modulation of cardiac electrical function.^30,31 While a large diversity of ChRs exists, with variants from nature or engineered through recombination and mutagenesis, it is still not possible to predict functional properties of uncharacterized ChR sequences. In the study, an ML algorithm used training data to learn how sequence and structural elements map to ChR function. Once known, that mapping can be used to predict the behavior of untested ChR variants. The trained models were used to engineer 30 ‘designer’ ChR variants with specific combinations of properties, several which have unprecedented photocurrent strength and light sensitivity.

3.2. Use of ML in investigating the effects of drugs on cardiac electrical function:

• Predict (mostly) hERG channel blockade^32–37 and QT prolongation^38–40 liability of compounds

• Evaluate the torsadogenic (causing TdP arrhythmias) potential of drug candidates^41–43 and drug-induced ventricular repolarization dispersion⁴⁴

• Analyze drug effects on stem cell-derived cardiomyocytes^45–48

In drug development, the assessment of the proarrhythmic potential of a compound, and specifically, the risk of torsades de pointes (TdP) arrhythmia occurrence, is an integral part of establishing the drug’s safety profile. QT prolongation is considered the most common risk factor leading to TdP. At the early stages of the drug research and development process, the compound’s blocking potency of the human ether-à-go-go-related gene (hERG) channel is regarded as a surrogate marker of proarrhythmic risk. AI has been used in all these aspects of evaluating a compound’s cardiotoxicity.

There is a large body of research in using ML to predict hERG-related cardiotoxicity; here we point to only a few of the studies. Using training data from a number of international consortia, an ML platform has been developed³³ for rapid prediction of compounds’ maximal inhibitory concentration (IC50) values; the capability of the platform was assessed by comparison to IC50 data from automated patch clamp for a large dataset of hERG blocking and non-blocking drugs, demonstrating superior capabilities. Lee et al³² generated a large experimental dataset of hERG assay results and trained an ANN to predict hERG-related cardiotoxicity, achieving area under the curve (AUC) of 0.764 and accuracy of 90.1%. As structurally diverse molecules bind or inhibit the hERG channel, various molecular features and ML methods have been used to construct prediction models. Studies have attempted to find the pharmacophore pattern of hERG blocking compounds using various conventional ML approaches.^49–51 Cai et al. proposed the first DL-based hERG blocker prediction model,⁵² followed by a DL model with a self-attention approach³⁵ that provides increased interpretability. In their sweeping “from the atom to the rhythm” computational pipeline to predict hERG blocker proarrhythmic risk from the drug chemistry, Yang et al³⁷ applied ML (RFs) to discern the necessary and sufficient parameters that predict arrhythmia vulnerability for two drugs, dofetilide and moxifloxacin.

Assessing the risk of TdP occurrence, Sharifi et al⁴¹ build an ANN-based predictive model for drug-induced torsadogenic and non-torsadogenic drugs based on 55 compounds, and successfully tested the model in 38 external drugs. An interesting two-step approach to TdP risk classification was proposed by Parikh et al⁴³, termed the Multi-channel Blockage at Early After Depolarization, which allowed the authors to isolate the effects of hERG and non-hERG channels in the classification problem. The authors used both direct features (values of drug-induced block of ion channels) as well as derived features (extracted from output of the drug-induced multi-channel blockage simulations in in-silico models). The study also demonstrated that TdP risk for the drugs highly correlates with the likelihood to produce early afterdepolarizations in the computational model. Finally, Cruces et al⁴⁴ used ML to determine potential drug-induced ventricular repolarization dispersion markers that could define proarrhythmic risk. The studies reviewed in this section highlight that, as the compound attrition rate due to cardiotoxicity remains high, there persists an unmet need to develop further ML approaches capable of efficient drug safety testing with high generalizability and interpretability.

The advent of human induced pluripotent stem cell-derived cardiomyocytes (iPSC-CMs) created the possibility of an improved in vitro model of the human myocardium for drug screening. ML techniques have been used in addressing the need to develop a high-throughput, sensitive and non-invasive detection platform for iPSC-CMs. Lee et al⁴⁶ constructed a platform that utilizes optical flow analysis of brightfield images of iPSC-CMs to measure drug effects on cardiomyocyte motion. They paired an optical flow method with SVM algorithm to discern between normal and abnormal cardiomyocyte contractile profiles, detecting changes in a manner that is more sensitive and thus superior to traditional fluorescence methods. Juhola et al⁴⁷ used data from a drug study in catecholaminergic polymorphic ventricular tachycardia-specific iPSC-CMs and trained an ML algorithm for fast recognition of peaks of calcium transient signals, achieving a classification accuracy of 79%. In an earlier study by Lee et al⁴⁸, ML has also been used to analyze functional parameters derived from force readouts of hPSC-CM tissue strips electrically paced at a range of frequencies and exposed to a library of compounds, demonstrating that the model could automatically predict the mechanistic action of an unknown cardioactive drug. Finally, Aghasafari et al⁴⁵ used a long short-term memory NN to predict adult ventricular cardiomyocyte activity from in vitro iPSC-CM activity, thus allowing estimation of drug effects on mature cardiomyocytes without the need of an in vitro drug study. These initial results point to future developments where analysis of iPSC-CM drug effects together with ML could create efficient platforms for drug screening and cardiotoxicity studies, and importantly, platforms for individualizing medication.

3.3. Use of AI in computational research on cardiac electrophysiology and arrhythmia

• Investigate the factors that underlie emergent electrophysiological behaviors and reentrant dynamics in cardiac tissue^53–56

• Classify phenotypes from in-silico electrophysiological activity in cardiac disease^3,57

• Create activation maps from sparse data⁵⁸

• Link AF spatial pattern to re-entrant driver localization⁵⁹

• Personalize cardiac models^60–65

• Localize atrial ectopic beats from simulated body surface P-wave maps⁶⁶ and predict AF ablation outcome⁶⁷

Computational modeling of the heart has been a widely-used research tool in the study of arrhythmia mechanisms, complementary to experimental measurements, and lately has made its first forays into clinical decision-making for arrhythmia prediction and treatment guidance.^68–70 AI approaches have naturally begun to be used on data generated by computational modeling, as such data is noise-less. In this subsection we review studies that have used only in-silico (synthetic) datasets to train algorithms. Hybrid studies utilizing ML, which include both synthetic and experimental or clinical data are reviewed in the respective sections below.

An example of the use of ML in computational research on cardiac electrophysiology and arrhythmia is the utilization of unsupervised algorithms to identify how variability in in-silico cell electrophysiology, particularly in the kinetic properties of ion channel recovery, modulates the dynamics of arrhythmias.⁵³ ML has also been used to detect reentrant activity and its termination in tissue models⁵⁵ and to locate reentrant drivers from electrograms in a model of AF.⁵⁶ In these studies, ML provides means of identifying emergent phenomena at the organ level and highlights how these phenomena can be best interrogated to provide new mechanistic understanding and identification of arrhythmia. An interesting use of ML is the classification of simulated electrophysiological data, such as classifying clinical phenotypes in simulated ECGs for patients with hypertrophic cardiomyopathy^53,56. Physics-informed ANNs accounting for the underlying wave propagation dynamics have also been used to generate full electrical activation maps from sparse synthetic activation data⁵⁸.

Using patient-specific computational models of the atria to analyze how the atrial fibrosis sustains reentrant drivers in AF, Zahid et al⁵⁹ employed ML to determine the characteristics of fibrosis distribution that are most predictive of the locations of reentrant drivers in the atrial substrate. The study found that locations in the atria with a combination of high fibrosis density and high fibrosis entropy were the most likely to sustain reentrant drivers. Such findings have important consequences for clinical decision-making as they indicate how imaging or signal processing of electrical signals can be used to determine the locations of the culprits of arrhythmogenic propensity. The studies reviewed in this section demonstrate how ML can be an integral part in the quest for understanding the causes of human arrhythmias.

Personalization of whole-heart models has been an active avenue of research that utilizes ML approaches^60–65. Personalization entails the incorporation, within a model of cardiac electrical activity, features and characteristics that are extracted from the patient’s clinical records, imaging data, or invasive or non-invasive electrophysiological measurements. By personalizing models of cardiac electrical function, the expectation is that simulations using such models would be able to predict outcome of anti-arrhythmia therapies, or stratify patients for risk of adverse cardiac outcomes. For example, Giffard-Roisin et al⁶⁴ aimed to personalize a set of ventricular electrophysiology modeling parameters for prediction of individual responses to different pacing protocols, in an attempt to assist in decisions regarding the optimal personalized cardiac resynchronization therapy. Synthetic body surface potential maps (BSPMs) resulting from ventricular activation were calculated and features extracted from them, on which a supervised ML algorithm was trained to predict several electrophysiological dysfunction events, among which premature ventricular contractions.

As atrial arrhythmias are the most common human arrhythmias, a large body of simulation research using personalized atrial models has addressed issues ranging from determining the origin of abnormal activations to predicting outcome of AF ablation. The study by Ferrer-Albero et al⁶⁶ localized atrial ectopy from simulated BSPMs. ML was used to spatially cluster and classify ectopic atrial foci into distinct atrial regions by using maps of the integral of the P-wave as a biomarker. The results (Fig.4) demonstrated that ectopic foci with similar integral maps cluster into differentiated atrial regions and that new ectopic activity patterns could be correctly classified into 2 ectopy clusters with an accuracy of 97% and into 4 ectopy clusters with 96% accuracy. In another example, a recent computational study used ML in predicting the outcome of AF ablation. Roney et al⁶⁷ conducted simulations of AF in personalized left arial (LA) models reconstructed from late gadolinium-enhanced cardiac MRI (LGE-MRI) images of 20 paroxysmal AF and 30 persistent AF patients with atrial fibrosis. Model ablation approaches based on clinical standards were tested, but success was limited. To develop an optimal AF ablation approach for each patient, a RF ML algorithm was trained to predict simulated ablation outcome for several input variables that included imaging metrics and well as simulated electrophysiological and lesion metrics. The results demonstrated that achieving optimal outcomes may require employing different AF ablation strategies in different patients.

Figure 4. Clustering and classification of BSPM integrals.

a) Clustering of 57 patterns of BSPM integrals (30 from right and 27 from left atrium) using the K-means algorithm on the torso surface nodes where K is the number of pre-defined ectopy clusters (ECs). For each K, all the foci belonging to the same EC have the same color. b) For each K, left column shows the color and number of each EC resulting from the clustering step (for example blue-k2–0 refers to blue EC, equivalent to class 0, when k=2), while right column shows the classification results identifying the ectopic site that is not well classified with the color of the correct group, to which it really belongs. Reproduced from [⁶⁶].

3.4. Use of ML in assessing cardiac activation from electroanatomical and body-surface-potential mapping

• Reconstruct epicardial maps from endocardial catheter recordings^71,72

• Estimate activation patterns from cardiac cine⁷³ and 3D echocardiographic⁷⁴ images

• Reconstruct surface ECGs from implantable cardioverter-defibrillator (ICD) device intracardiac electrograms⁷⁵

• Reconstruct heart surface potentials from BSPM^76–80

In one of the early ML applications, where electroanatomical maps were used to estimate cardiac activation, ML reconstructed epicardial maps from endocardial catheter recordings in the ventricles^71,72 using experimental data from a dog animal model, in an attempt to localize the onset of focal ventricular activations. AI has also been used to reconstruct ventricular activation maps from images.^73,74 The studies by Prakosa et al⁷³ deduced activation maps from observation of the resulting motion patterns, as electrical activation controls mechanical contraction. To do so, the authors created a patient-specific database of synthetic time series of cardiac cine images using simulations with a personalized cardiac electromechanical model. The database was then used to train an ML algorithm, which estimated the depolarization times of each cardiac segment from global and regional kinematic descriptors based on displacements or strains and their derivatives. The trained algorithm then estimated the patient’s electrical activation times using the acquired clinical images. The approach was first assessed on synthetic sequences and next evaluated on clinical data, showing promising results, with the error between prediction and the invasive intracardiac mapping “ground truth” found to be around 10ms for ischemic patients and 20ms for a nonischemic patient. The approach suggests the possibility of noninvasive activation pattern estimation using cardiac motion imaging. Similar approach was applied to non-invasive activation times estimation using 3D echocardiographic data⁷⁴. Finally, a method was developed to facilitate the remote follow up of patients with ICDs⁷⁵. A time-delay ANN, which uses past values of the input, was trained on simultaneously recorded intracardiac and surface ECG signals from a patient cohort to be able to synthesize the 12-lead surface ECG from device intracardiac electrograms. Inverse electrographic imaging, which involves calculating potentials or activation maps on the heart surfaces from BSPMs, is a promising non-invasive tool to detect abnormal electrical activity on the surfaces of the heart. It has also seen its share of ML applications^76–80 providing data-driven approaches in lieu of inverse problem calculations in determining ventricular surface activations from BSPMs.

3.5. Use of ML in ventricular arrhythmia research and ventricular arrhythmias clinical decision support

• Predict risk of ventricular arrhythmias (VAs) using texture analysis of LGE-MRI^81,82, analysis of electronic health records⁸³, device-measured physical activity,⁸⁴ and ventricular monophasic action potential recordings⁸⁵

• Predict acute hypotension and ventricular fibrillation (VF) from ICU-recorded signals time series⁸⁶

• Locate ventricular tachycardia (VT) exit site or the origin of ventricular activation^87–93

• Learning from images to predict VT ablation targets⁹⁴

Predicting risk of sudden cardiac death due to VAs is a major avenue of research. In patients at high risk for VA, mortality is prevented by the prophylactic deployment of an ICD device.^95–97 However, ICD deployment comes with a significant risk of adverse events (infections, device malfunctions and inappropriate shocks).^98,99 As a result, many patients who undergo implantation of an ICD will never have appropriate ICD therapies, while others, who would benefit from an ICD, do not receive one.^99,100 This necessitates a precise VA risk assessment in patients with heart disease. There is a strong hope in the electrophysiology community that ML would be able to make major contribution to accurate VA risk stratification in patients. Attempts have been already made. As structural remodeling (scar, fibrosis) characterizes a number of heart diseases that result in VA, texture feature analysis of LGE-MRI scans has been used to assess VA risk⁸¹ in hypertrophic cardiomyopathy (HCM); in a small cohort of 64 patients, a number of supervised ML models were tested, achieving diagnostic accuracy ranging from 82.8% to 94.1%. Also assessing structural remodeling as a predictor of VA, Okada et al⁸² used model reduction and ML approaches to construct a patient-specific complexity scores for the LGE-MRI scans of 122 ischemic cardiomyopathy patients (Fig.5). The average complexity score was found to be significantly higher in patients with VA events versus those without. VA risk has been assessed from electronic health records of HCM patients⁸³, where ML identified 10 new variables, in addition to 12 known, as VA risk predictors, and from physical activity time series data of patients with ICDs⁸⁴. In another interesting application⁸⁶, a probabilistic ANN was used to predict, from intensive care unit (ICU) signals (ECGs, non-invasive continuous blood pressure and arterial oxygen saturation) hypotension with an accuracy of 92.5%, and the occurrence of VF 5 min before it occurs with an accuracy of 82.5%. Finally, in a recent study, Rogers et al⁸⁵ used an SVM to predict risk of VT/VF in patients from recordings of ventricular monophasic action potentials acquired during an electrophysiological study; the independent test c-statistic was 0.90.

Figure 5. Substrate spatial complexity analysis.

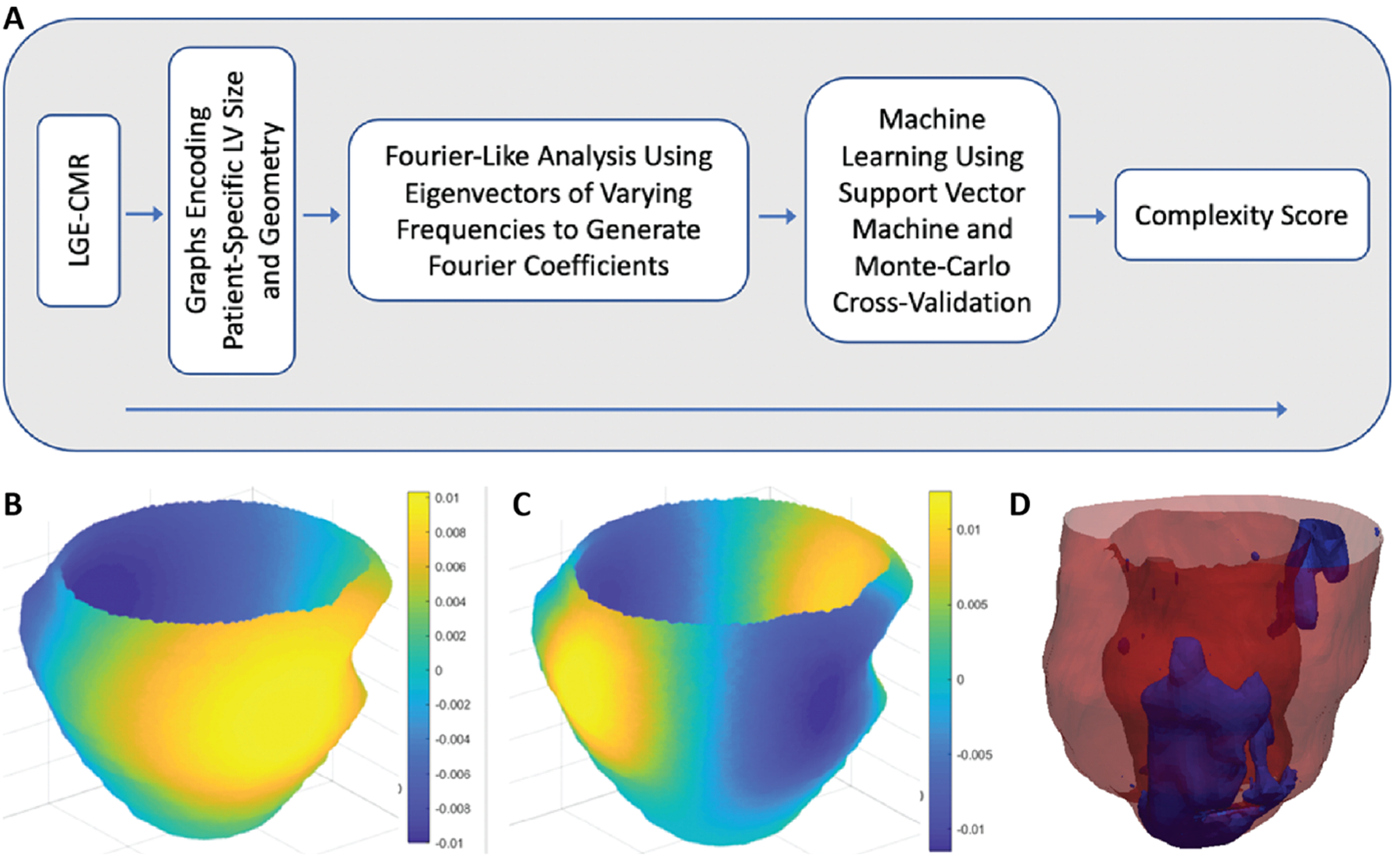
(A) Flowchart of the analysis. Signal intensity patterns from cardiac LGE-MRI were analyzed using a Fourier-like technique for assessment of global irregularity. This analysis generated features that were used in an ML algorithm, which yielded a complexity score ranging from 0 to 1, where 0 represents low arrhythmic risk and 1 represents high arrhythmic risk. (B, C) Eigenvectors (sine-like functions) of varying frequencies oscillating over graphs encoding patient-specific LV size and geometry were compared with signal intensity patterns to generate Fourier coefficients. These coefficients were then used in the ML algorithm. Each panel (B and C) shows a different eigenvector frequency. Colors represent amplitude of the sine-like function. (D) Example of substrate spatial complexity analysis showing LGE-MRI-derived scar pattern from a patient with a low scar burden (12.1 g) but a high complexity score (CS; 0.99) who ultimately had a VA event. Modified from [⁸²].

Catheter-based ablation, which destroys the ability of cardiac tissue to conduct electrical signals, offers the possibility of a permanent cure of VAs, and particularly the life-threatening fast VT, as it disrupts the propagation of abnormal electrical waves sustaining VT. However, eliminating VT with ablation has achieved only modest success, at rates of around 50–88%,^101,102 due to inaccuracies in determining the ablation targets, which are either the VT exit sites, or the origins of abnormal ventricular activation. Recent applications of ML to locate these targets consist of both conventional ML and DL approaches. Yokokawa and co-workers⁸⁷ were the first to demonstrate the feasibility of using ML in localizing the exit site of a scar-related VT from paced 12-lead ECGs during the ablation procedure’s pace-mapping. SVM was trained on the digitized pace-map ECGs combined with the pacing sites, to learn to predict VT exit site location from the clinical VT ECG, so that the location can then be targeted by ablation. However, the algorithm was limited to predicting the exit site in only one of 10 segments on the left ventricular (LV) endocardial surface. Sapp et al. presented two independent methods based on multiple linear regression model to progressively approach the site of origin of early LV activation: the non-invasive population-derived regression methodology and the intra-procedural patient-specific linear regression approach⁸⁸. The population-derived regression approach localized the site of origin of early LV activation onto one of 238 triangular area elements of a generic LV endocardial surface⁸⁸ using a training dataset containing ECGs from pacing at 1012 ventricular sites, achieving a mean localization accuracy of 10mm in a prospective study⁸⁹. The intra-procedural patient-specific linear regression approach^89,90 used 120-ms 3 lead QRS integrals (leads III, V2, and V6) of pace-mapped activations at known pacing sites to predict the site of earliest LV activation from the same 3-lead clinical VT ECG. Extending the latter ML approach to localization of idiopathic VA origin on the patient-specific geometry of LV, RV and neighboring vessels, Zhou et al⁸⁹ achieved, in a recent study, a mean localization accuracy of 3.6 mm.

DL to localize the origin of ventricular activation remain in its infancy. Yang et al. utilized DL to localize the premature ventricular contraction origin onto one of 25 segments of the entire ventricles and to distinguish endocardial from epicardial ventricular activation origin⁸⁹. Gyawali et al⁹¹ trained DL to localize LV activation origin; however, their classification was onto only 10 LV segments that are not used clinically⁹². Another type of ANN, a self-organizing map based on unsupervised competitive learning, was trained on BSPM distributions obtained during ventricular pacing to enable localization of the endocardial VT origin sites⁹³.

3.6. Use of ML in AF research and AF clinical decision support

• Predict which patients will experience AF from electronic health records (EHRs)^103,104 and by using a smartphone camera¹⁰⁵

• Predict stroke risk from a daily AF burden signature¹⁰⁶

• Define AF clinical phenotypes with various treatment patterns and outcomes¹⁰⁷

• Classify intracardiac activation patterns during AF to detect regional rotational activity^108,109

• Predict AF recurrence after catheter ablation from clinical records,^110–112 from atrial shape changes,^113,114 and from the combination of AF simulation results and imaging features¹¹⁵

• Identifying patients who may benefit from AF cardioversion response¹¹⁶

Early detection of AF could lead to significant improvements in outcomes through administering appropriate anticoagulation. It is no surprise that a significant number of ML approaches have been employed in both AF clinical decision support and AF research, and here we review both. For identifying patients at risk of AF, an automated prediction algorithm applied to patient EHR data would be highly desirable. The recent study by Tiwari et al¹⁰⁴ represents a major initial step in this direction. The authors developed and tested an ML model to predict 6-month incidence of AF using EHR data. The time period chosen represented a clinically relevant period of prediction, during which patients could undergo screening tests (ECGs, ICDs and/or wearable monitors) before a clinical decision. The study used EHR data sampled from over 2.2 million individuals and found that a single-layer (shallow) ANN using the 200 most common EHR features provided the optimal classification of AF risk (AUC of 0.8). Hill et al¹⁰³ sought to evaluate novel and conventional statistical and ML models for risk-predication of AF in a cohort study of nearly 3 million adults without a history of AF, identifying time-varying ANNs as the optimal model with an AUC of 0.827; the model’s predictive performance was greater than existing AF risk models and reflected both known and new patient risk factors for AF. These two studies offer hope that ML can be used directly to guide targeted screening of patients at risk of AF. In that vein, an interesting approach for AF screening used an iPhone camera¹⁰⁵ to detect and analyze photoplethysmographic signals from the face and index finger of 217 in-hospital patients by extracting subtle beat‐to‐beat variations of skin color that reflect the cardiac pulsatile signal. The patterns in the photoplethysmographic waveform were classified using a previously trained SVM.

ML classification algorithms have also contributed to better understanding of AF heterogeneity.¹⁰⁷ AF is typically classified on the basis of disease subtype, however, such characterization does not fully capture AF heterogeneity. An ML cluster analysis on 9749 patients with AF revealed different classifications of patients: (1) a cluster with low comorbid burden; (2) a younger/behavioral disorder cluster; (3) a cluster who resembled patients with tachycardia-bradycardia and had ICDs; and (4) a cluster defined by atherosclerotic comorbidities. The authors underscored that the groupings were not driven by conventional classifications and had different risks for adverse clinical outcomes.

AF ablation offers the hope for a permanent cure for AF, however, the success of the therapy remains at 40% to 70% despite advances in AF mechanisms knowledge and ablation technology.¹¹⁷ A potential source of suboptimal procedure performance is the difficulty in interpreting maps of intracardiac activation patterns. An automated method of superior interpretation of AF electrograms could guide ablation therapy. Alhusseini et al¹⁰⁸ trained CNN on regional intracardiac voltage time-series data from basket catheters positioned in left then right atrium to detect regions in the atria containing sites of rotational activity, which can then be targeted for ablation, as shown in Fig.6A. Achieving accuracy of 95.0%, CNNs improved the classification of intracardiac AF maps, while operating with a decision logic similar to rules used by experts, even though these rules were not provided in training. Additionally, in a recent study, Zolotarev et al¹¹⁸ extended the ML usage to intracardiac electrograms for automated AF driver detection, this time using atrial electrogram frequency spectra instead of the actual signals. The approach was tested on recordings from explanted human atria and validated by comparison to subsurface near-infrared optical mapping signals from the same atria, considered the “gold-standard”.

Figure 6.

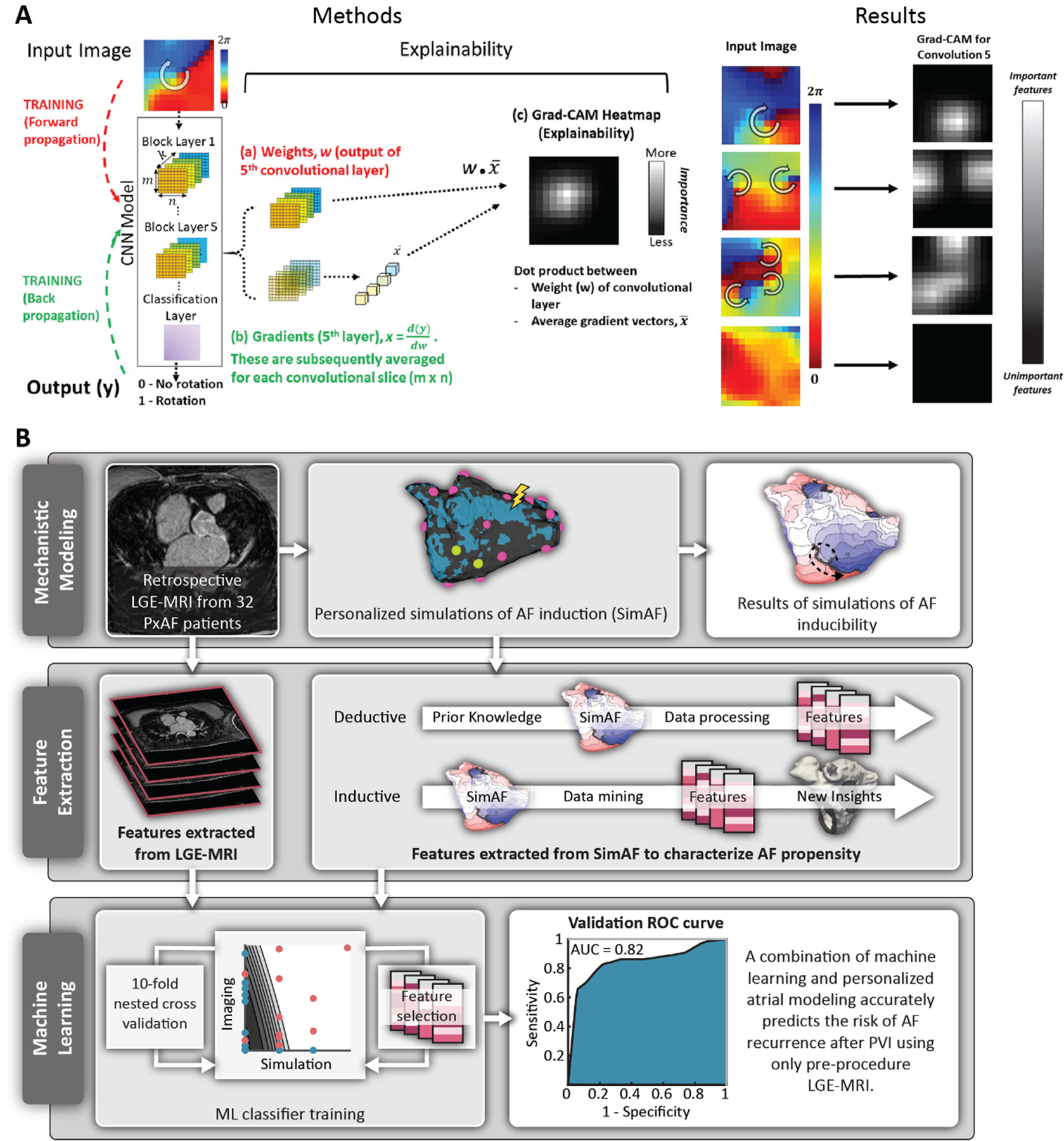
(A) Detecting regions in the atria containing sites of rotational activity. CNN was trained on regional intracardiac voltage time-series data from basket catheters positioned in left then right atrium (left-most column). Explainability analysis (Methods column) to probe how CNN interprets intracardiac AF patterns. In training, ML uses forward propagation of an input tile, creating weights w (red), then backward propagation to update internal weights using gradients x (green). This training process matches each input with its known output label (0,1). Explainability is applied once the CNN is trained. (a) Weights w and (b) gradients x of the output of the fifth convolutional layer are combined by the dot-product operation. (c) Gradient-weighted class activation mapping (Grad-CAM) heatmap plots the importance of each input pixel to the CNN classification. Brighter (higher value) pixels have a greater influence on the CNN. Gradient-weighted class activation mapping (Grad-CAM) heatmaps (Results column) of trained CNN empirically detect AF features identified by experts with domain knowledge. Numbered from top to bottom: 1, Input vector showing site of interest in AF in a 49-year-old female. The heatmap site in Conv 5 coincides with the precise location in the heart coded by experts as a site of rotation. 2, AF in a 63-year-old female with AF, showing 2 concurrent regions of interest. 3, AF in a 64-year-old man, showing 3 regions of interest. 4, AF in 74-year-old-female showing no region of interest. In each case, Grad-CAM heatmaps empirically identified tile regions identified by experts with physiological knowledge, although CNN were not explicitly trained in expert rules. Reproduced and adapted from [¹⁰⁸]. (B) Overview of study by Shade et al in which the researchers predicted recurrence of AF post-PVI by conducting simulations of AF induction in atrial models reconstructed from paroxysmal AF patients with fibrosis on LGE-MRI, and trained an ML classifier on simulated AF episodes and on imaging features to predict, pre-procedurally, the outcome of the clinical procedure. Modified from [¹¹⁵].

A series of research articles focused on using ML to predict risk of AF recurrence after the first catheter ablation procedure^110–115. Identifying patients who are unlikely to remain in sinus rhythm after the ablation is an important pathway towards improving ablation success rates and avoiding ineffective procedures. One approach was to develop an AF relapse risk score post pulmonary vein isolation (PVI) from the patients’ laboratory and clinical parameters using ML^110–112. Another approach was to predict risk of AF recurrence based on the pre-procedure shape of the patient’s atria^113,114, as alterations in atrial chambers have been linked to worse outcomes of AF ablation. The study by Varela et al¹¹⁴ constructed 3D geometrical models from pre-procedural MRI of 144 AF patients and build a statistical atrial shape model. ML, in this case a discriminant analysis, was used to distinguish between patients with and without AF recurrence. The authors proposed a new shape metric, vertical asymmetry, which measures the imbalance of size along the anterior to posterior direction between the superior and inferior left atrial hemispheres. Vertical asymmetry was found, in combination with sphericity, to be the best predictor of post-ablation recurrence at both 12 and 24 months, with AUCs of 0.71 and 0.68, respectively. DNNs were also utilized to estimate AF recurrence from shape descriptors directly from the MRI images with no image pre-processing¹¹³, eliminating the need for expensive pre-processing pipelines and associated manual labor. Finally, the study by Shade et al¹¹⁵ predicted recurrence of AF post-PVI by conducting simulations of AF induction in atrial models reconstructed from paroxysmal AF patients with fibrosis on LGE-MRI, and trained an ML classifier on simulated AF episodes and on imaging features to predict, pre-procedurally, the outcome of the clinical procedure. Fig.6B summarizes the study. This study is important, as if this approach is confirmed to predict failure of PVI pre-procedurally, the patient’s ablation plan could then be adjusted to include targeting of the patient-specific extra-PVI areas of arrhythmogenic driver propensity using the simulation-driven OPTIMA ablation approach⁷⁰.

3.7. Use of ML in arrhythmia management:

• Reduce false arrhythmia alarms in the ICU¹¹⁹ and in ICD therapy^120,121

• Identify which implantable anti-arrhythmia device a patient has¹²²

• Provide kinematic control of robotic flexible ablation catheter¹²³

There are broad applications of ML in patient management. A few studies related to arrhythmia management that do not fit in the other sub-section reviewed above are listed here. In one of them, Howard et al¹²² developed an ML system which identifies the manufacturer and even the model group of a pacemaker or defibrillator from a chest radiograph. The rationale for this study was that medical staff often need to determine the model of an implanted device quickly and accurately. Using radiographic images of 1,676 devices, a CNN classified the images with 99.6% and 96.4% accuracy (manufacturer and model, respectively). This system may help speed up the diagnosis and treatment of patients with heart rhythm devices.

3.8. Use of ML in ECG interpretation and ECG-based diagnosis:

• Classify heart rhythms^124–131 and detect subtle changes in ECG morphology^132,133

• Detect AF^134–137

• Predict VT 1 hour before occurrence¹³⁸

• Predict cardiac resynchronization therapy outcomes^139–142

• Identify (hidden) disease state signatures^{138,143–148}, mortality^149,150, and clinical deterioration¹⁵¹

• Estimate blood pressure¹⁵², and age (“physical age” vs. chronological) and sex¹⁵³

Most of the AI applications in cardiac electrophysiology and arrhythmias are based on the analysis of time-series recordings reflecting cardiac electrical activity, with the signal varying depending on the type of sensor. The most used signal is the ECG. ECG signal recording modalities include standard 12-lead ECG, single or multi-channel Holter recordings, ECG patches, automated external defibrillators, intracardiac leads in pacemakers or defibrillators, and implantable loop recorders. Computerized ECG interpretation has been introduced to clinical settings to aid physician interpretation, and ML has found a firm footing in classifying heart rhythms and detecting rhythm disorders^124–131. Various supervised ML algorithms (including decision trees, Wavelet transformations, Hidden Markov Models, SVM, and ANN) have all been employed in these studies. The early applications of ML resulted in high sensitivity and specificity for detecting normal sinus rhythm, however, in identifying arrhythmia of various types, such approaches had performed worse that the judgement of expert cardiologists, hindered by the presence of noise and poor quality of ECG recordings, as well as by previously untrained rhythm disorders. With the advent of noise reduction techniques and advanced feature extraction, including the use of the unsupervised DNN, arrhythmia detection approaches have achieved much improved performance. For example, the study of Lee et al¹³⁸ was able to predict from the ECG, using ANNs, VT one hour before occurrence.

Particularly fascinating are developments in detecting AF^134–137, including the 2019 landmark study of 0.65 million ECGs by Attia et al¹³⁷ which used CNN for the identification of patients with AF during sinus rhythm. The results demonstrated that AF may be preceded by structural changes in the heart reflected in subtle ECG changes. The success of ML-enabled ECG in identifying patients with undetected AF has important practical implications for management of patients with unexplained stroke. The use of ML in ECG interpretation and rhythm disorder detection has been widely reviewed in the recent literature and we offer here only a brief and incomplete view on this extensive subject; for more in-depth reviews we refer the reader to these publications^3,5,6,154. Efforts to increase the level of interpretability of ML models in ECG interpretation have also been made¹⁴⁸ with notable success.

ML-enabled ECG technology has also been used to predict outcomes of cardiac resynchronization therapy^139–142; advancements in this field are discussed in depth in some of the review publications listed above^5,6. The utilization of unsupervised DNN has led to the ability to identify, from the 12-lead ECG, signatures (often hidden from the human eye) of many diseased states, such as contractile and relaxation dysfunction^143,144,155, PVCs¹⁵⁶, hyperkalemia¹⁴⁵, and nocturnal hypoglycemic events¹⁴⁷, and to estimate blood pressure¹⁵², and “physical age” (vs. chronological) and sex¹⁵³.

4. Challenges and perspectives for ML in electrophysiology and arrhythmia

As this review demonstrates, ML is making rapid inroads in electrophysiology and arrhythmias, from biophysics research at the level of the ionic channel to research on arrhythmias in patient populations. Although there is a palpable exuberance in the research community regarding the potential of ML, it is important to understand the limitations of the various approaches (as described here in section 2.5) and what are the main issues and challenges in ensuring proper application and advancement in the use of ML in our research field. Below we touch on some of these issues.

ML algorithms require significant amounts of data for proper training and validation. Data, with its many aspects, presents challenges to ML adoption in both basic-science and clinical research. Data availability remains a significant roadblock, as data is typically acquired in a particular laboratory or health center and has not been traditionally shared between institutions; democratizing access to data and improving the public’s understanding of ML to dispel fear surrounding use of personal health data is thus of paramount importance. ML algorithms can only learn patterns present in the data on which they are trained, so if data sets do not account for a wide variety of population-based characteristics and regional anomalies, ML algorithms will be more likely to fail when applied on a global scale, which may further contribute to lack of trust in ML. The recent push for data sharing is getting traction, particularly for data from clinical trials, but it requires infrastructure developments to store and analyze big data. Data sharing is also intertwined with the issues of intellectual property and privacy, which remain sizeable barriers to data sharing.

Before training a model, a data analysis step needs to be performed first. The analysis might uncover abnormal samples, outliers, or missing values, which will need to be corrected -- removing the outliers, filling missing values (using median, mean, or estimated values with a sophisticated iterative approach) or simply removing from consideration parameters with missing values. Datasets with poor data organization and/or management, and particularly, with significant inaccuracies affect the performance of ML algorithms. Low-quality data with unbridled noise coupled with insufficient data for training poses one of the critical challenges to ML, overfitting -- we touched upon it in section 2.5 -- where the model learns the noise in training data as (false) relationships, failing to then generalize on another dataset. Finally, if the input data in a study poorly reflects the characteristics of other datasets, the model would not generalize well. By using a non-representative training set, the trained model is not likely to make accurate classifications and predictions. Researchers need to account for that in their study design and adjust expectations accordingly. Furthermore, even a previously “accurate” model may no longer be accurate as more data is collected in the study dataset. This may be particularly important in cases where the system under study changes rapidly and past data no longer fully characterize the processes, resulting in a diminished ML accuracy.

Supervised ML algorithms are often presented with a specific challenge: labels must be available for the input data. Annotation of data with labels is labor-intensive (and often manual). Sometimes data that would best be described with continuous labels might need to be dichotomized, resulting in arbitrariness in the labeling, which could also affect ML performance and generalization. Semi-supervised techniques, which combine a small amount of labeled data and a large amount of unlabeled data to train a model, have attempted to solve this problem. However, they rely on underlying assumptions that do not hold true for all datasets. Even with clean and well-labeled data, class imbalance in the data poses challenges. For instance, when predicting risk of arrhythmia in a population cohort, it might be that only 10% of the training data has a positive label for arrhythmia occurrence. In some instances, datasets could be resampled to be more balanced by removing negative cases and/or replicating positive cases; additional techniques such as augmenting the loss function to more strongly weighting error for the minority class are often employed.

With proper ML application, research in electrophysiology and arrhythmia is poised to gain significantly from the integration of multiple datasets representing processes at different levels of physiological complexity. For instance, models can be trained to learn important characteristics of a particular cardiac disease or condition from disparate data sources, such as genetic biomarkers, cellular imaging, and organ-level optical or electroanatomical mapping data. This will allow to obtain important insights into and interpretations of relationships across the spatial and temporal scales and facilitate optimization of therapy targets. Similarly, various diagnostic data for patients with heart rhythm disorders (e.g. blood tests, MRI, ECG, echocardiography) can be used in an ML model to support clinical decision making and optimize patient treatment.

DL is particularly well-suited for analyzing complex raw data as it does not require manual feature engineering. However, DL algorithms have minimal transparency (i.e. they are “black boxes”) and lack interpretability as it is difficult to identify which aspects of the input influence a DL model’s decision the most. They are also susceptible to adversarial attacks, or inputs designed to trick a classifier into assigning an incorrect label, which are virtually indistinguishable from a true sample. Such attacks are not easily detected due to the uninterpretable nature of most DL models, but adversarial training strategies have evolved to strengthen DL models against them. Further, in recent years, there has been a growing body of research into increasing the explainability of DL by translating the millions of parameters in a neural network into a human-interpretable reason for each decision, such as highlighting a particularly influential region of a medical image or displaying ECG parameters that were most influential in classification. These strategies have potential to overcome many of the research/medical community’s reservations about DL by opening the “black box” and providing much-needed insight into these models.

In this review article, we highlighted the major achievements of ML in electrophysiology and arrhythmias, attesting to the fact that AI is becoming a major research approach in our field. Despite the described above potential pitfalls, there is ample evidence, with many examples reviewed in this article, that the best way to characterize a process or a system on the basis of data is through the application of ML techniques. ML provides unparalleled set of tools in augmenting and extending the effectiveness of cardiac electrophysiology research. Overall, it is poised to enable rapid acceleration in all aspects of biomedical research, from testing hypotheses to translating proof-of-concept studies into real-world technologies. AI is also rapidly promoting a significant paradigm shift in diverse areas of medicine, including clinical cardiac electrophysiology, with its enormous potential to support clinical decision-making and improve diagnostic and prognostic performance. In envisioning the future of both arrhythmia basic research and clinical practice, a close collaboration between basic science biomedical researchers, bioengineers, computer scientists, and clinical investigators will emerge, in the hope that utilization and even deployment of ML approaches would become increasingly seamless.

Of course, in all these advances, it is paramount that we make careful and pragmatic choices. And while we should temper short-term exuberance, the long-term prospects of AI are outstanding, promising to change the world.

Nonstandard Abbreviations and Acronyms:

AF

Atrial fibrillation

ML

Machine learning

AI

Artificial intelligence

DL

Deep Learning

LASSO

Least absolute shrinkage and selection operator

SVM

Support vector machines

k-NN

k nearest neighbors

kMeans

k means clustering

PCA

Principal component analysis

RF

Random forest

(A)NN

(Artificial) neural network

CNN

Convolutional neural network

DNN

Deep neural network

RNN

Recurrent neural network

GAN

Generative adversarial network

hESC-CMs

Human embryonic stem cell-derived cardiomyocytes

hPSC-CMs

Human pluripotent stem cell-derived cardiomyocytes

ChR

Channelrhodopsin

TdP

Torsades de pointes

hERG

Ether-à-go-go-related gene

IC50

maximal inhibitory concentration

AUC

Area under the curve

iPSC-CMs

Human induced pluripotent stem cell-derived cardiomyocytes

AF

Atrial fibrillation

BSPM

Body surface potential maps

MRI

Magnetic Resonance Imaging

LGE-MRI

Late gadolinium-enhanced cardiac MRI

VA

Ventricular arrhythmia

VF

Ventricular fibrillation

VT

Ventricular tachycardia

HCM

Hypertrophic cardiomyopathy

ICU

Intensive care unit

LA

Left atrial

LV

Left ventricular

EHR

Electronic health record

PVI

Pulmonary vein isolation

ICD

Implantable cardioverter-defibrillator