Enhancing Water Sampling of Buried Binding Sites Using Nonequilibrium Candidate Monte Carlo

Abstract

Water molecules can be found interacting with the surface and within cavities in proteins. However, water exchange between bulk and buried hydration sites can be slow compared to simulation timescales, thus leading to the inefficient sampling of the locations of water. This can pose problems for free energy calculations for computer-aided drug design. Here, we apply a hybrid method that combines nonequilibrium candidate Monte Carlo (NCMC) simulations and molecular dynamics (MD) to enhance sampling of water in specific areas of a system, such as the binding site of a protein. Our approach uses NCMC to gradually remove interactions between a selected water molecule and its environment, then translates the water to a new region, before turning the interactions back on. This approach of gradual removal of interactions, followed by a move and then reintroduction of interactions, allows the environment to relax in response to the proposed water translation, improving acceptance of moves and thereby accelerating water exchange and sampling. We validate this approach on several test systems including the ligand-bound MUP-1 and HSP90 proteins with buried crystallographic waters removed. We show that our BLUES (NCMC/MD) method enhances water sampling relative to normal MD when applied to these systems. Thus, this approach provides a strategy to improve water sampling in molecular simulations which may be useful in practical applications in drug discovery and biomolecular design.

1. Introduction

Proteins are found in aqueous environments where water plays a major role in determining their structure, function, and dynamics [6, 26]. Water molecules can also be found in cavities in proteins [18, 30, 38] where they play a variety of roles, such as facilitating receptor-ligand recognition and contributing to the stability of proteins [7, 9, 26, 38, 46].

Classical molecular dynamics (MD) simulations can be used to understand the motions and interactions of biomolecular systems, including how proteins interact with water. However, water exchange between bulk and buried hydration sites can be slow compared to simulation timescales [13, 29, 33]. This leads to the inefficient sampling of the locations of water and water’s role in binding events [15]. Simulations that do not account for these water motions will give an incomplete picture of the binding process and any downstream predictions will thus risk being in error [15, 33].

Several methods may better sample water occupancy and rearrangements in the cavities of proteins. Monte Carlo (MC) methods can substantially accelerate water sampling via large translational water moves around a system, but these MC moves can be difficult to get accepted due to steric clashes in the system. For example, grand canonical Monte Carlo [3, 4], which works by insertion and deletion of water to maintain a specific chemical potential, has been applied to sample water configurations and accelerate occupancy of buried sites [25, 40, 48]. However, this approach has been shown to be inefficient due to steric clashes which results in a high rejection of the proposed moves [31, 41]. Another approach integrates Metropolis MC translational water moves with traditional MD to equilibrate water across steric barriers and into buried hydration sites that are not accessible with pure MD [10].

Here, we seek to enhance the sampling of water rearrangements through extension of our Binding Modes of Ligands Using Enhanced Sampling (BLUES) approach [19], which combines hybrid nonequilibrium candidate Monte Carlo (NCMC) [36] with MD simulations. BLUES has been shown to enhance ligand sampling efficiency by more than two orders of magnitude compared to classical MD when applied to a model test system [19]. In BLUES, NCMC alchemically scales off the electrostatic and steric interactions until a water molecule is no longer interacting with its environment and then translates it to a new location before scaling the interactions back on. This results in a proposed NCMC move which is either accepted or rejected based on the integrated work during this process. After this, the NCMC move is followed by traditional molecular dynamics. By mixing NCMC translational water sampling moves with classical MD simulations, we improve water sampling in a selected region, such as a binding site of a protein, where water motions are known to be challenging or slow to sample and likely to pose problems for calculations of interest, such as free energy calculations [15]. In this work, we use the BLUES framework to exchange waters around a specified region of a system. Here, we focus on testing it in specific contexts where water rearrangements can pose challenges for MD sampling, such as buried binding sites in proteins.

2. Methods

We introduce a method that integrates NCMC translational water moves with classical MD, allowing water molecules to hydrate buried sites. Here, we detail how this approach is implemented and tested.

2.1. Implementation of NCMC/MD in BLUES

BLUES (Binding Modes of Ligands Using Enhanced Sampling), which combines NCMC with classical MD, was originally created to enhance the sampling of ligand binding modes [19], but has begun applying the same techniques to enhance sampling of other degrees of freedom also important in ligand binding, such as sidechain rearrangements [11] and, here, water motions.

A BLUES iteration consists of a NCMC move followed by regular MD. A NCMC move consists of a series of NCMC steps sandwiching a perturbation to the system, such as a translational water move. The NCMC steps are a series of alchemical steps where the electrostatic/steric interactions are gradually turned off and then back on. While the interactions are completely turned off, a perturbation provided by a translational water move occurs.

Some of our key terminology here is as follows:

• BLUES iteration — an NCMC move followed by a series of regular MD steps.

• NCMC move — a series of NCMC steps sandwiching a perturbation to the system.

• NCMC steps — a series of alchemical steps where the electrostatic/steric interactions are gradually turned off and then scaled back on.

• MD steps — a number of steps to advance the MD simulation.

In BLUES, NCMC moves are executed through a switching protocol that is comprised of a series of perturbation and propagation/relaxation steps involving structural and dynamic degrees of freedom [36]. This process helps lower possible steric or electrostatic clashes by allowing the environment surrounding the perturbed region to relax around the proposed state.

NCMC moves are implemented by alchemically “turning off” the interactions between an object in the system and its surrounding environment before the move, followed by turning the interactions back on, as detailed in Figure 1. First, the electrostatic and then the steric interactions are turned off (and then later back on) by scaling λ, a variable that controls the strength of nonbonded interactions, from 1 (fully interacting state) to 0 (noninteracting state) over a user-determined number of n NCMC steps (Figure 1.A–C). At the point where the object is noninteracting (Figure 1.C), the target object’s atoms are repositioned (Figure 1.D) and then the interactions are scaled back on (Figure 1.D–F) until λ=1 in reverse order first sterics and then electrostatics). When the target object’s atoms are repositioned the internal coordinates/conformation remain the same during the move.

Figure 1. Molecular interactions between atoms are turned off and on during a NCMC move to translate a water molecule.

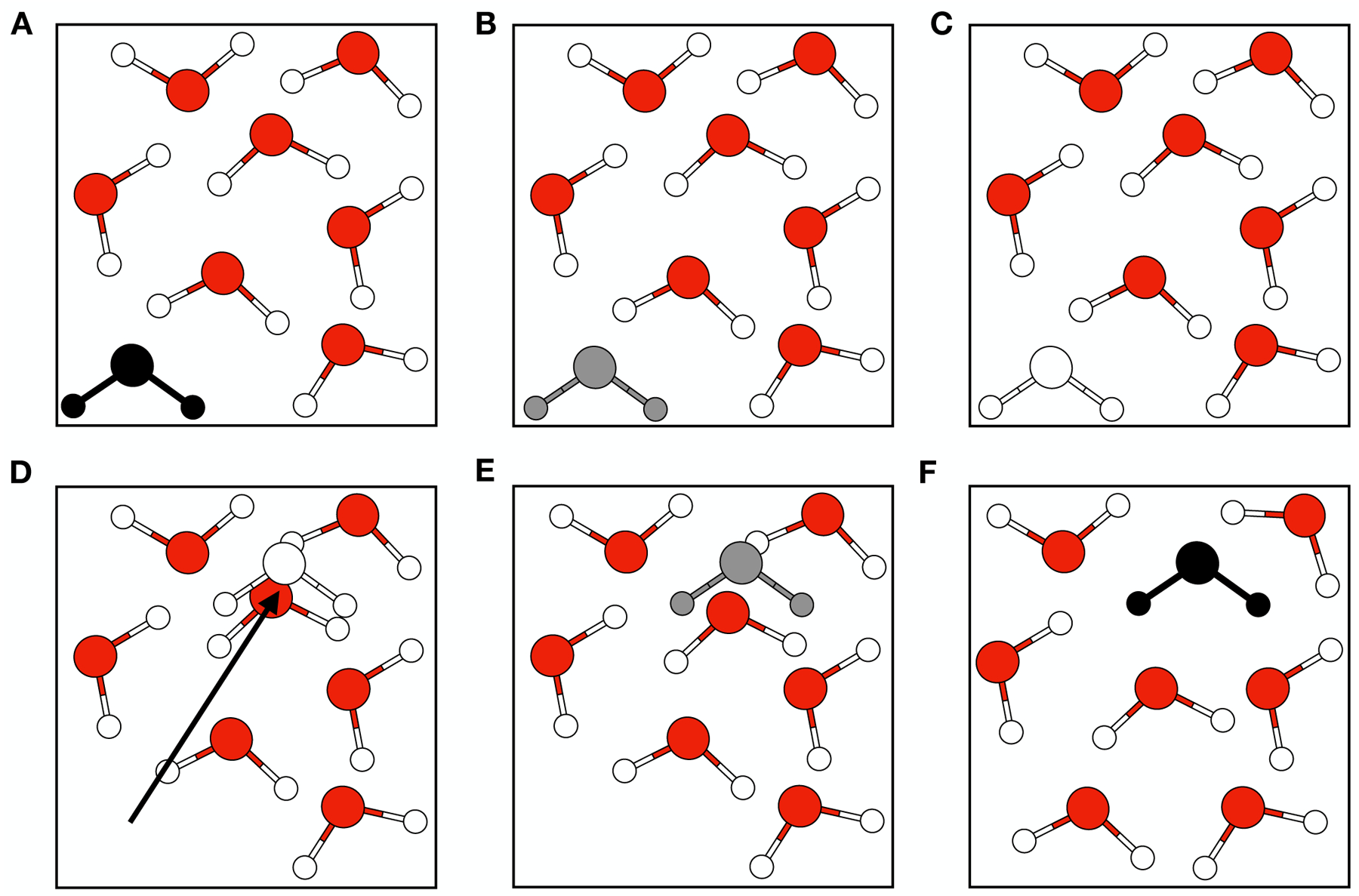
In this cartoon, water molecules are represented here by red and white spheres for the oxygen and hydrogen atoms. The black-filled water represents a fully interacting water molecule that has been selected to be moved. Gray-filled water represents intermediate levels of interaction and white-filled represents the fully non-interacting water molecule. A) The water molecule (in black) is fully interacting with its surrounding environment, and in this case, other water molecules. B) The water’s interactions are partially off, allowing the other water molecules to slightly relax. C) The water’s interactions are fully turned off. D) The water is randomly translated to somewhere else in the system (indicated by a black arrow) with its interactions remaining off. E) The water’s interactions are partially turned on and the propagation steps of NCMC allow relaxation of the translated water and its surroundings to resolve clashes. F) At the end of the NCMC protocol, the water molecule is once again in the fully interacting state and in a new location. This entire process comprises a proposed NCMC move, which is accepted or rejected based on the nonequilibrium work done in this process, and then followed by conventional MD.

The total work done during this process is summed and used to either accept or reject the proposed move (following a modified Metropolis-Hastings acceptance criterion [30] to maintain detailed balance). The NCMC move is then followed by a user-determined number of MD steps. Additional details of BLUES are described in the work of Gill et al. [19].

A proposed NCMC move is either accepted or rejected based on the total work w[X] done during the nonequilibrium process X, estimated as

$$w[X]\equiv \sum _{t=1}^T\left[u_t\left(x_t\right)-u_{t-1}\left(x_t\right)\right]+w_{\text{shadow}}[X]$$ (1)

where x_t is a microstate at a simulation step t and u_t is the reduced potential energy.

The total work includes both “protocol work” and “shadow work” [44]. In the equation above, the first term is the protocol work and the second term is the shadow work which accounts for errors introduced by the use of finite-time-step Langevin integrators [42, 44].

The protocol work is computed every time there is a perturbation to the system, so after changing lambda, we track the potential energy change between the states before and after lambda is changed and add this difference to the protocol work. Accumulation would also happen during translational moves, except that the water is non-interacting and the proposed move is just a rigid body translation move, so the system’s energy does not change and thus no protocol work is accumulated during the translational move. The shadow work can be tracked in a similar fashion, except the total energy differences (potential and kinetic) would be taken into account during the propagation phase. However, use of a BAOAB integrator allows us to neglect the shadow work contribution without introducing large errors (the explanation for this is in the original BLUES paper [20]).

To maintain detailed balance, the acceptance probability A[X] is determined using a modified Metropolis-Hastings criterion [21]

$$A[X]=\text{min}\left\{1,e^{-w_{\text{protocol}}(X)}\right\}$$ (2)

After each accepted or rejected NCMC move, velocities are randomly reassigned based on the Maxwell–Boltzmann distribution in order to maintain detailed balance [20]. The amount of relaxation used does not affect whether this procedure preserves the correct distribution. The NCMC move is followed by a series of conventional MD steps, using a Langevin integrator to relax the entire system. This process of proposing (and accepting or rejecting) a NCMC move then conducting a series of MD steps is then repeated many times. This process of a NCMC move, followed up by traditional MD, is what we refer to as a BLUES iteration.

2.2. Translational water moves with BLUES

Here, we build upon the BLUES framework by incorporating “water hopping” moves where random water molecules can be translated between bulk and within a region via NCMC move proposals. Water hopping moves were created in order to enhance sampling of key hydration sites such as in water bridging locations between a protein and ligand, and particularly in buried cavities inaccessible from bulk water.

To define a region within which the water hops occur, the user selects an atom as the center and defines a radius to generate a sphere which encompasses the area of interest (Figure 2). Additionally, the sampling region can be set to automatically span from the center of mass of a protein or ligand, rather than manually defining a specific atom. This area of interest must be large enough to include some bulk water to allow water exchange. Our algorithm will subsequently use this radius to select a random water molecule and propose moving it to a random new position within this region. During a BLUES iteration, a random water molecule is selected, a random point in this region is generated, then a NCMC move proposal is performed. During the NCMC move proposal the interactions are scaled off between the atoms of the water molecule and its surrounding environment, then the water molecule is translated to the new location defined by the random point, and then the interactions are scaled back on. This the NCMC move proposal process is depicted in Figure 1. The work done during this NCMC move proposal is accumulated and the move is either accepted or rejected using the Metropolis-Hastings acceptance criterion [30]. Afterwards, an interval of regular MD is run. A workflow a BLUES iteration is depicted in Figure 3. Further water hopping implementation details used in this work are available in python scripts deposited in the Supporting Information. More documentation, details, and the full BLUES package are available on GitHub at https://github.com/MobleyLab/blues, in the BLUES documentation (https://mobleylab-blues.readthedocs.io), and detailed in the work of Gill et al. [20].

Figure 2. Example of a user-defined radius that covers a particular area of interest.

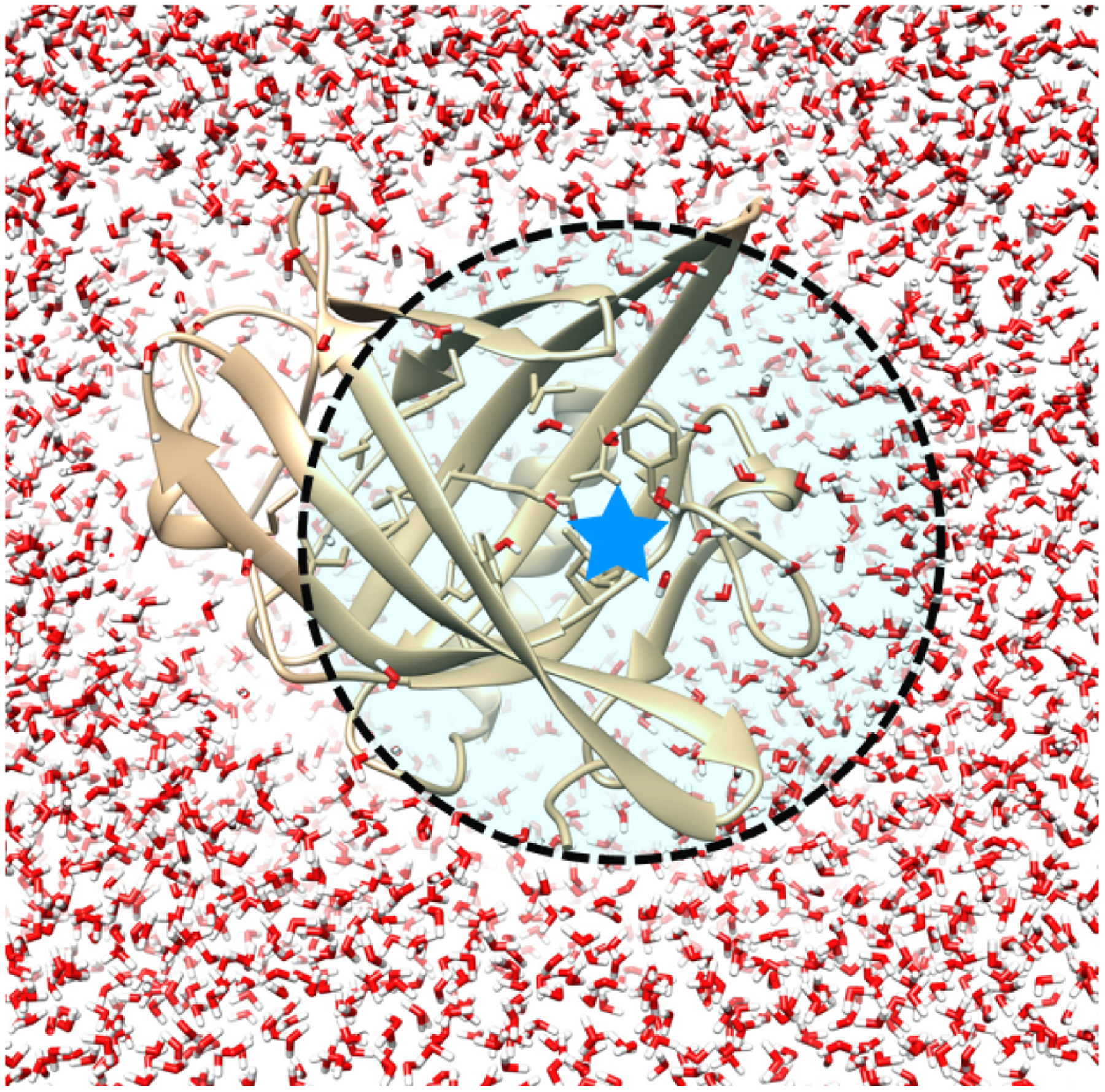
Here, the MUP-1 protein-ligand system is shown. The radius used (indicated by the black dashed line) defines a sphere around a user-selected atom (represented by a blue star) in the system, such as an atom inside the binding site of a protein.

Figure 3. Workflow of a BLUES iteration with translational water hopping move proposals.

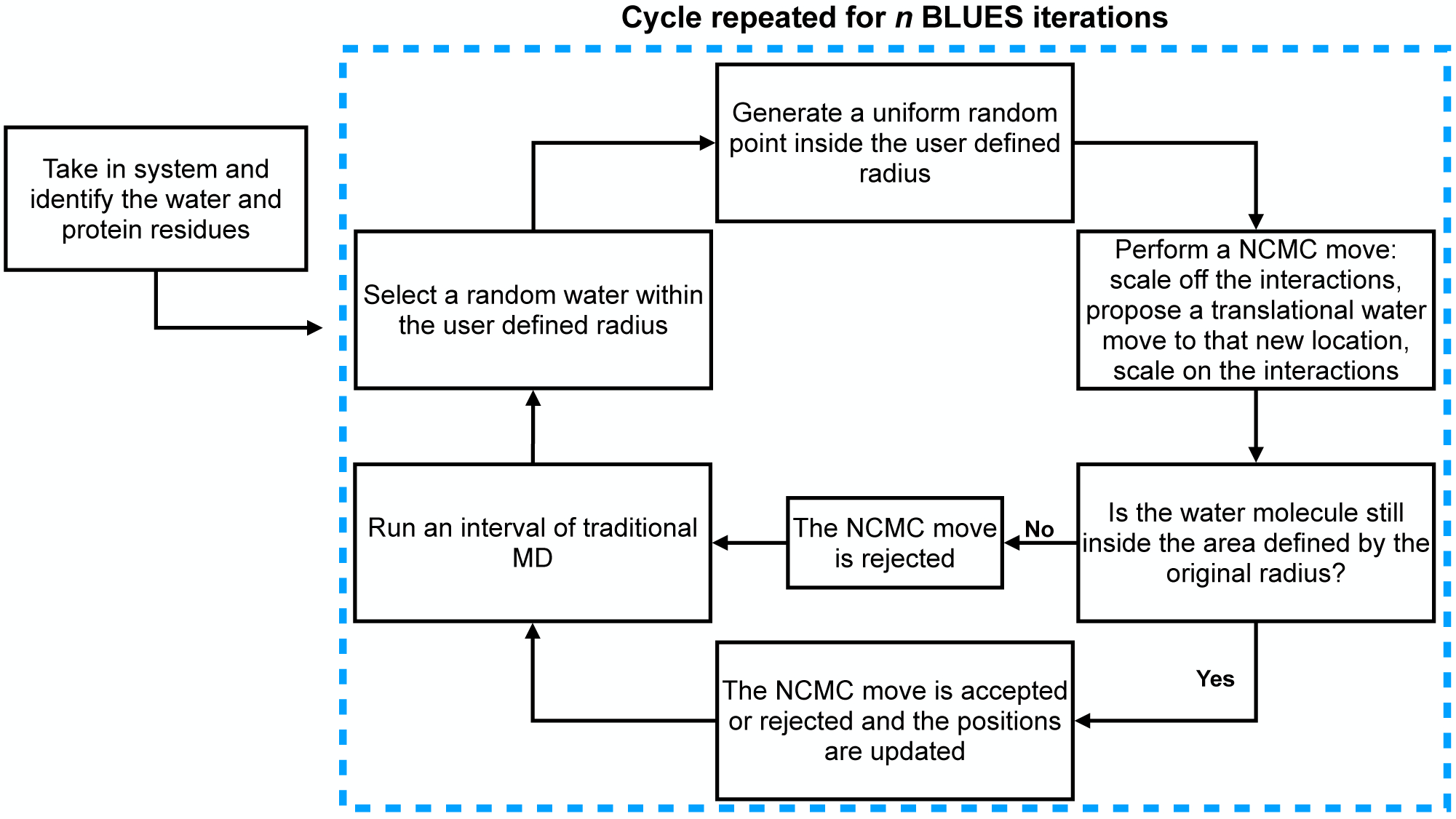
Before any water is translated to a new location, the user first selects an atom and picks a radius defining a sphere encompassing an area of interest around the position of the atom and BLUES identifies all the water and protein residues in the system. Afterward, BLUES goes through a number of BLUES iterations n number of times, where each BLUES iteration is as shown inside the dashed box. A schematic of the NCMC move process is shown in Figure 1.

2.3. Comparing sampling efficiency using the number of force evaluations

BLUES simulations consist of intervals of both classical MD and NCMC moves, so comparing a BLUES simulations to classical MD simulation requires accounting for the cost of the switching protocol that occurs during the NCMC move. We account for the additional cost from NCMC by considering the number of force evaluations rather than the aggregated simulation time in nanoseconds or microseconds.

NCMC carries out a single force evaluation for each perturbation or propagation/relaxation step. The perturbation steps are the instantaneous perturbation of the water molecules coordinates (or for turning off/on the alchemical parameters), and this is combined with propagation steps via Langevin dynamics [19]. In other words, perturbation steps modify the system or its potential, and propagation steps propagate the dynamics. A BLUES simulation consists of NCMC and MD, so a BLUES simulation will have a total cost in force evaluations of:

$$\text{Total force evaluations}=(\mathit{\text{nSteps}}MD+\mathit{\text{nSteps}}\mathit{\text{NCMC}})\times \mathit{\text{nlter}}$$ (3)

where nSteps MD is the number of MD steps per BLUES iteration, nSteps NCMC is the number of NCMC steps per BLUES iteration and nlter is the number of BLUES iterations, which consists of a NCMC move proposal followed by a series of regular MD. The total cost in force evaluations for classical MD is equivalent to the total number of MD steps.

2.4. Test cases and simulation details

We used a C₆₀ buckyball, a water box system with dividing graphene sheets, Major Urinary Protein (MUP-1) and Heat Shock Protein 90 (HSP90) as systems to test the ability of the BLUES (NCMC/MD) water hopping moves to enhance the sampling of water molecules in desired regions. Many of these systems were also used in a similar study to validate Metropolis MC translational water moves with traditional MD [10].

The first system was a C₆₀ buckyball with a water molecule trapped inside (Figure 4.A). This water molecule is unable to interact with bulk water and cannot form any hydrogen bonds with the buckyball’s carbon atoms. Hence, it is in an energetically unfavorable environment, but it is unable to diffuse out. We chose a sampling region that was centered on a carbon atom in the buckyball and extended 12 Å out, such that the region included the entire buckyball and some bulk water. The box size was ~44 × 44 × 44 ų, and had a total of 213 water molecules.

Figure 4. Systems used to test the ability of BLUES (NCMC/MD) water hopping to allow the exchange of water.

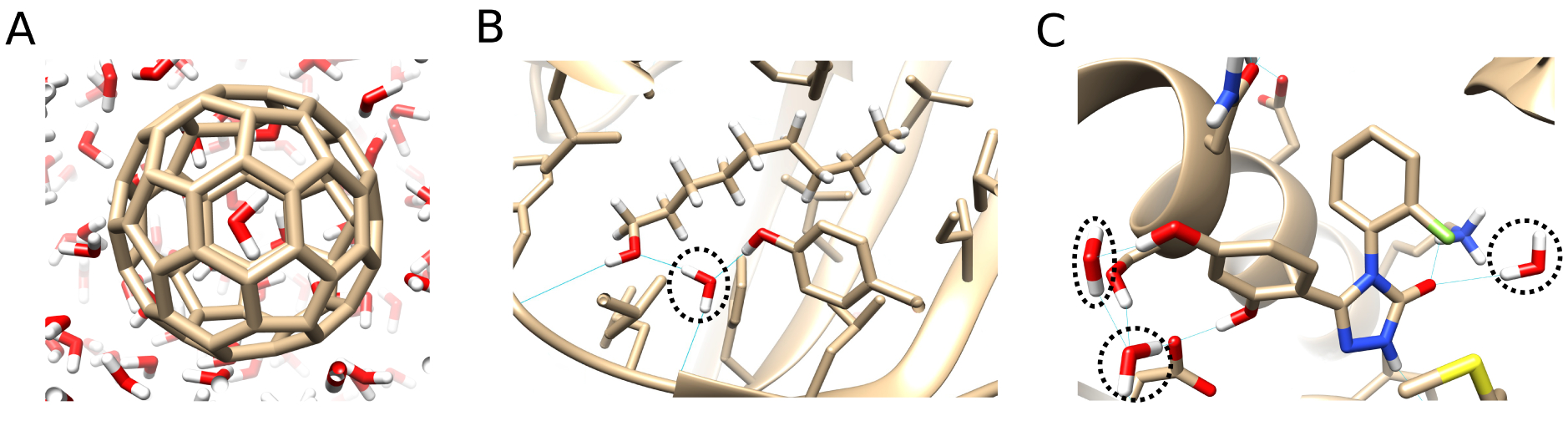
(A) A C₆₀ buckyball with a single trapped water molecule. (B) The buried hydration site of the MUP-1 protein with a bound ligand. (C) The hydration site of the HSP90 protein bound to a ligand. The protein-ligand systems have internal water(s) (indicated by the black dashed line) that do not easily exchange with bulk.

The second system was a rectangular water box divided into two regions by impermeable planar graphene sheets (Figure 5.A). These two regions had initially different water densities where the outer and inner region had densities of about 21.5 water/nm³ and 18.5 water/nm³, respectively. The rectangular box was ~32 × 32 × 85 ų and the system had a total of 1915 water molecules. The initially differing densities between the outer and inner region tested the ability of the BLUES (NCMC/MD) water hopping method to equalize the water densities between the sheets. We chose a sampling region that was centered on a carbon atom in the middle of one of the sheets and extended 15 Å out so that the sampling region covered the same amount of area in the inner and outer regions. This choice was important to ensure that we didn’t make dramatically more move proposals to one region relative to the other. Additionally, we chose our sampling region so that it did not extend outside of the simulation box, thus avoiding issues where we might place waters in the same region more than once due to periodic boundary conditions, leading to artifacts.

Figure 5. Impermeable graphene sheets divide a box into separate regions with initially different densities, testing the ability of water hopping moves to equilibrate the density.

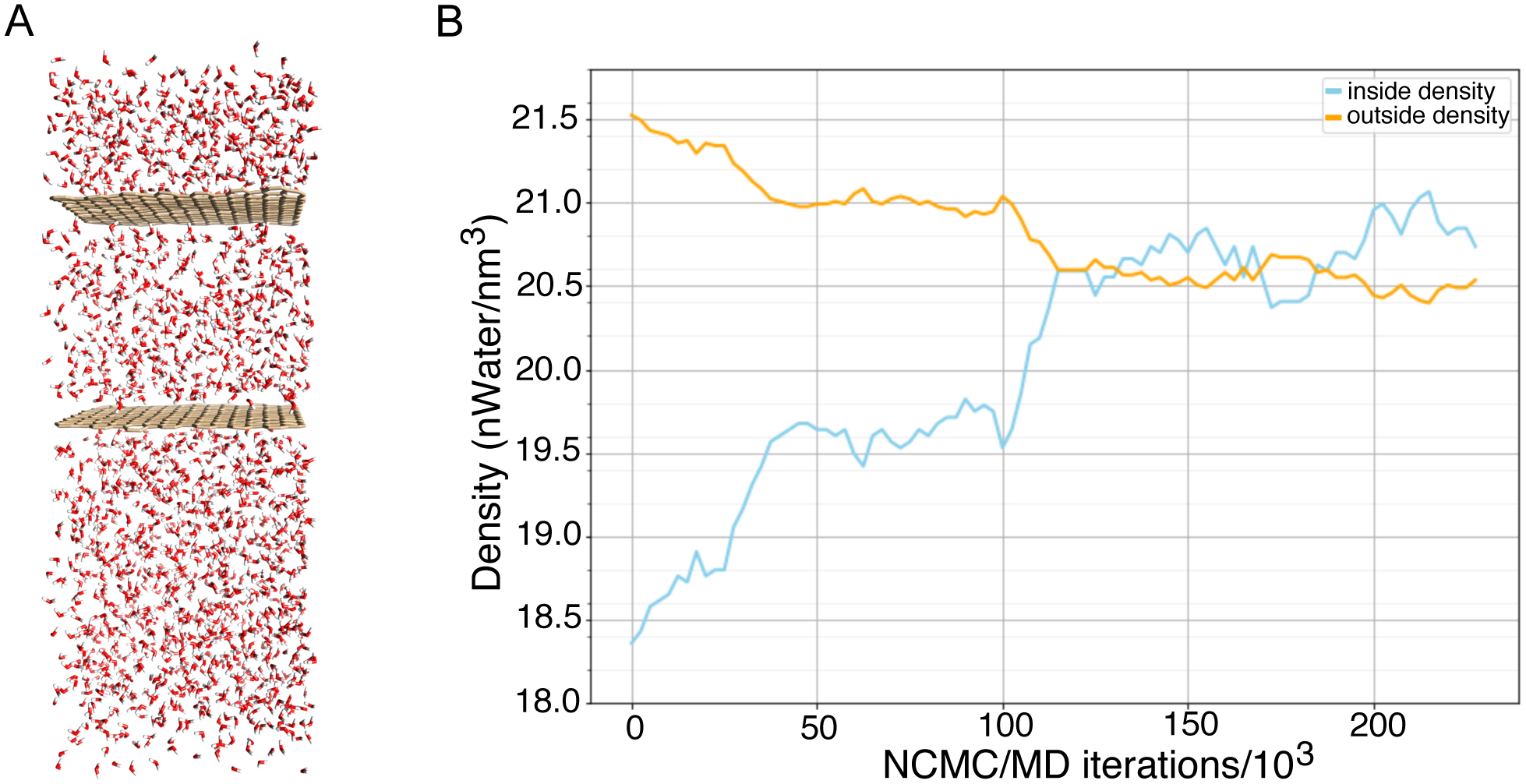
(A) The water box system with dividing graphene sheets. (B) Shown here are the water densities between the two sheets (blue) and outside the sheets (orange). The densities in the two regions reach equilibrium and stabilize with this approach, serving to validate our implementation.

The third and fourth systems tested the method’s ability to exchange water between bulk and buried sites in two proteins. The third system was the MUP-1 protein [45] which contains a buried crystallographic water molecule that bridges between the ligand and the protein (Figure 4.B). The crystallographic water molecule was removed in order to test the ability of our water hopping moves to hydrate the buried cavity and reform the water bridging interaction. We chose a sampling region that was centered on a carbon atom in the ligand and extended 20 Å out to include some bulk water (Figure 2). The box was ~70 × 70 × 70 ų the system had a total of 8,678 water molecules. The fourth system was the HSP90 protein (PDBID:5J64) [5] bound to a ligand which forms interactions with the protein through three bridging water molecules, as shown in Figure 4.C. The box was ~82 × 82 × 82 ų and the system had a total of 13,831 water molecules. We chose a sampling region that was centered on a carbon atom in the ligand, and extended 15 Å out to include some bulk water.

The simulation boxes were built using tleap from AmberTools [12]. All of the systems used, where appropriate, the protein and ligand force field parameters from AMBER ff14SB [23, 28] and GAFF [47], respectively. The water molecules were parameterized using the TIP3P water model [24] in all cases. MD and BLUES simulations were performed using OpenMM (version 7.1.1) [16, 17]. The systems were minimized until forces were below a tolerance of 10 kJ/mol. Long-range electrostatics were calculated using Particle Mesh Ewald [14]. Simulations were run using the hydrogen mass repartitioning scheme with 4 femtosecond timesteps [22].

To focus on water exchange the α-Carbons and ligands in the protein ligand systems were restrained with a force constant of 5 kcal/mol · Ų, thus keeping the protein cavities from quickly collapsing. The carbon atoms in the buckyball and graphene walls in the water box system were also restrained with the same force constant as the protein-ligand systems, which held the buckyball in place and kept the graphene walls from collapsing/folding.

The temperature was set to 300 K in all cases except the water box with graphene sheets, which was set to 500 K so that the water in the system was less dense than liquid water and wouldn’t form water droplets; thus, increasing the NCMC move acceptance rate so that any errors due to the method would be obvious because the density in the two boxes would not reach equilibrium. For the Buckyball system, equilibration consisted of 250 ps of NVT MD and 10 ns of NPT MD of equilibration. For the water box with dividing graphene sheets, equilibration consisted of 5 ns NVT MD. The MUP-1 system was equilibrated for 1 ns of NVT MD and 10ns NPT MD. The MD production run for the water box with dividing graphene sheets and the MUP-1 system was for 40 ns in the NPT ensemble. The HSP90 system was equilibrated for 1 ns of NVT MD and 80 ns NPT MD. The MD production run for HSP90 was for 285 ns in the NPT ensemble.

A BLUES simulation consists of a number of BLUES iterations, where each iteration of BLUES is composed of a NCMC move and traditional MD. Each NCMC move is comprised of a certain number of NCMC perturbation and propagation/relaxation steps (wherein the electrostatic and steric interactions are alchemically scaled off/on, as depicted in Figure 1). Here, we used the same amount of NCMC steps for all of the systems (except MUP-1, detailed below). For the water box system with dividing graphene sheets, BLUES with translational water moves was executed for 240,000 BLUES iterations, with each iteration consisting of 2,500 NCMC steps and 1,000 MD steps. The buckyball system was simulated for a total of 1,000 BLUES iterations, using 2,500 NCMC steps and 1,000 MD steps per iteration. Both of the solvated MUP-1 and HSP90 systems were simulated for a total of 10,000 BLUES iterations. For the MUP-1 system, 1,250, 2,500, 5,000 and 30,000 NCMC steps per iteration were tested to see how the number of NCMC steps affects the rate of water transfer from from bulk to the internal hydration site. The number of MD steps in all cases was 1,000 MD steps per iteration. For the HSP90 system, each BLUES iteration consisted of 2,500 NCMC steps and 1,000 MD steps. Further simulation details are available in scripts deposited in the SI.

3. Results and Discussion

The hybrid BLUES (NCMC/MD) approach described here accelerates water sampling during simulations by incorporating translational water moves during the NCMC component of each BLUES iteration. We refer to these translational water moves in BLUES as “water hopping”. Here, we tested these water hopping moves in a range of systems. Particularly, we use a C₆₀ buckyball, water box system with dividing graphene sheets, MUP-1 and HSP90 protein-ligand systems to validate the water hopping methodology. Across all of the systems tested, we find that BLUES water hopping moves allowed water exchange between regions, while plain MD did not.

The first test system was a C₆₀ buckyball simulated in bulk water, with a single water molecule housed inside (Figure 4.A). For the buckyball, it is very unfavorable to have the water inside the buckyball because the water molecule is in an energetically unstable environment relative to a water molecule in bulk. Having a water molecule inside of the buckyball is a state which should not be sampled (to any significant degree) at equilibrium, and we deliberately started with the water in this state to test if BLUES would allow it to escape relatively efficiently. As expected, we find that water hopping moves can relocate the water molecule from the inside of the buckyball to bulk water. Since the trapped water molecule is unable to interact with bulk water or form hydrogen bonds with the buckyball’s carbon shell, it is thermodynamically favorable for it to escape, but it is unable to do so with conventional MD. We chose a sampling region centered on a carbon atom in the buckyball so that the sampling region encompassed the buckyball and some bulk water. While the water molecule is not able to escape the buckyball with plain MD [10], water hopping allowed the water molecule to escape, returning it to the surrounding bulk water after 2.1×10⁵ force evaluations. The buckyball remains unoccupied after the water molecule leaves. Since we expect unidirectional transitions, we did not explore how the amount of relaxation affects the acceptance rate.

The second test system was a water box system divided into two regions by impermeable graphene sheets (Figure 5.A), with each region having different initial water densities. We find that water hopping successfully equalizes the water between the two regions (Figure 5.B). We chose a sampling region centered on a carbon atom in the middle of one of the graphene sheets, such that the sampling region encompassed equivalent amounts of both the inner and outer regions. The relative densities of each region initially differed, but should become uniform over time if BLUES is allowing waters to hop between the two regions. Standard MD does not allow water to enter the inner region between the graphene sheets because the sheets act as barriers that prevent water from passing through them. However, we find that translational water moves in BLUES allow water molecules to hop across the sheets, causing the densities to gradually equalize in both regions (Figure 5.B). Here we found this took 4.2×10⁸ force evaluations.

Next, we examined a buried hydration site in MUP-1, which has a buried crystallographic water molecule that bridges between the ligand and the protein (Figure 4.B). The crystallographic water molecule was removed from the buried site and water hopping successfully rehydrated it. We chose a sampling region that was centered on an atom in the ligand and extended out to include some bulk water (such as in Figure 2), such that the sampling region encompassed the buried hydration site and had access to bulk. With plain MD the water did not resume its crystallographic bridging position even after 1.5 μs, equivalent to 3.8×10⁸ force evaluations and 120 wallclock hours. However, BLUES was able to recover the crystallographic water. On average (across 11 replicates), it took BLUES 2.6×10⁶ force evaluations and 12 wallclock hours to hydrate the site (using 2,500 NCMC steps and 1,000 MD steps per BLUES iteration, as shown in Table 1), and no BLUES moves were accepted that dehydrated the site. Additionally, we tested how the number of NCMC steps per BLUES iteration affects the rate of water transfer to the hydration site by simulating with 1,250, 2,500, 5,000, and 30,000 NCMC steps per BLUES iteration, and used 1,000 MD steps per BLUES iteration for each. As expected, increasing the number of NCMC steps per BLUES iteration increases the rate of water transfer from bulk to the buried hydration site in MUP-1, as shown in Figure 6. Here, 30,000 NCMC steps is worse than 5,000 NCMC steps because it will take 6x the number of NCMC steps, but the success rate is certainly not 6x higher (it’s only about 2x higher). On the other hand, running 2,500 NCMC steps per BLUES iteration is certainly better than 1,250 NCMC steps. Although it takes 2x the number of NCMC steps, the success rate ends up being more than 2X higher- it’s roughly 4.7X higher. Similarly, running 5,000 NCMC steps per BLUES iteration is better than 2,500 NCMC steps because the success rate is about 4x higher.

Table 1. Increasing the number of NCMC steps generally increases the acceptance rate of all moves in the MUP-1 protein-ligand system.

Here is the average acceptance rate of all BLUES moves, the average number of force evaluations across 10–12 replicates for the buried cavity in the MUP-1 system to become hydrated, and the average wallclock time in hours for BLUES to hydrate MUP-1. Each simulation was run for 10,000 BLUES iterations, where each iteration consisted of a single NCMC move (consisting of n NCMC steps) and 1,000 MD steps.

n NCMC steps	Average acceptance rate of all BLUES moves	Average number of force evaluations to hydrate the MUP-1 cavity	Average wallclock time to hydrate the MUP-1 cavity
1,250	0.1%	7.9×106	50 hours
2,500	0.3%	2.6×106	12 hours
5,000	1.1%	1.1×106	3 hours
30,000	2.8%	2.5×106	4 hours

Figure 6. Increasing the amount of NCMC steps increases the rate of water transfer from bulk to the internal hydration site in MUP-1.

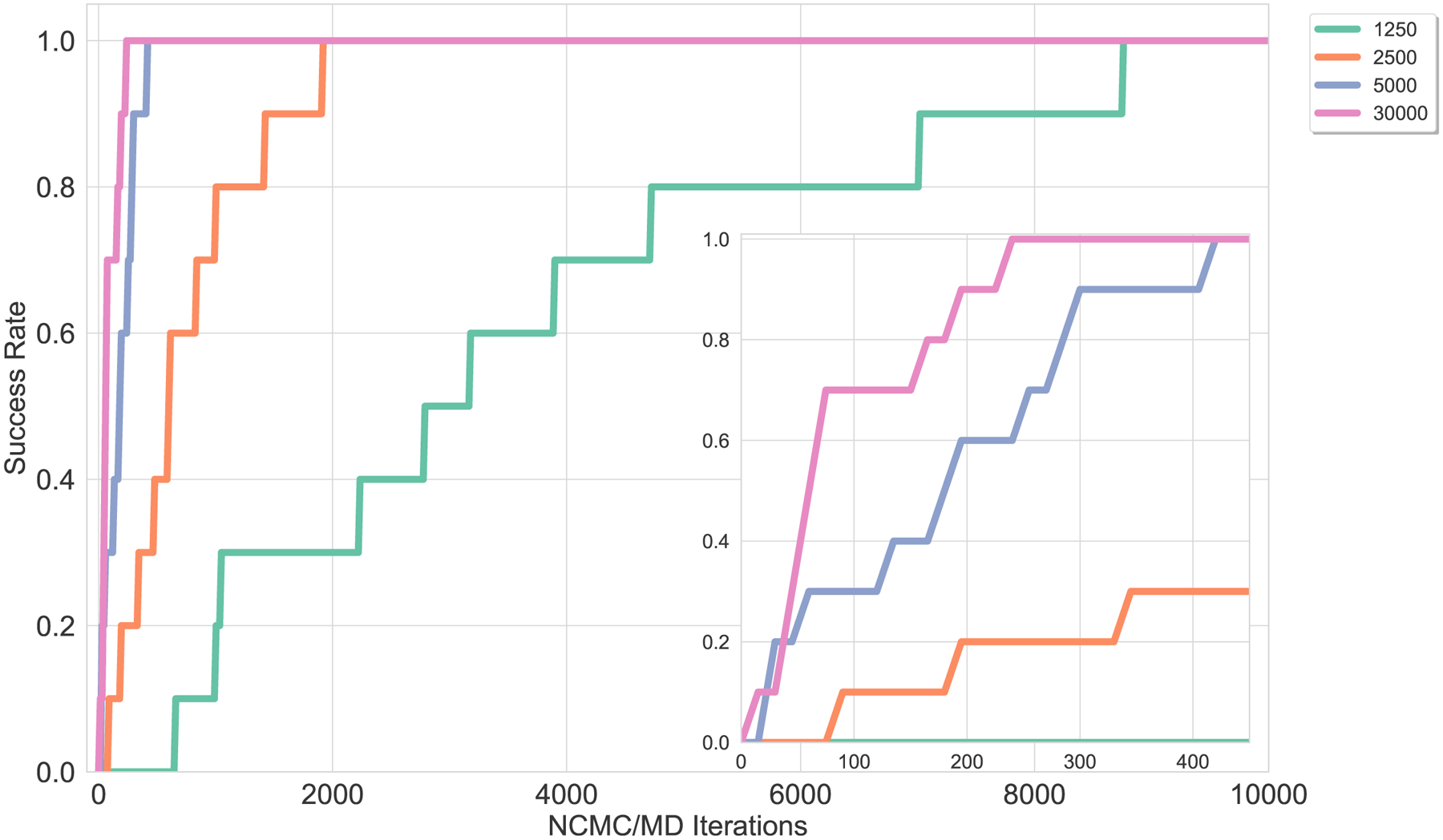
Ten replicate simulations with different random seed numbers were run for each NCMC step value. All of the BLUES simulations were run for 10,000 BLUES iterations, with each iteration consisting of a certain number of steps of NCMC and MD. The different colors indicate various amounts of NCMC steps used. The success rate is equivalent to the ratio of the number of replicate simulations where the MUP-1 site (Figure 4.B) has been hydrated relative to the total number of replicate simulations. (A) shows that using a lower NCMC step amount increases the number of BLUES iterations for the cavity to become hydrated, such as 1,250 (green) and 2,500 (orange) NCMC steps. The inset, (B), zooms in on the success rate at low iteration number and shows that increasing the amount of NCMC steps decreases the number of iterations needed. 5,000 (blue) NCMC steps needed a little more than 400 BLUES iterations to hydrate the cavity and 30,000 (pink) NCMC steps needed no more than 250 BLUES iterations to hydrate the cavity.

Although increasing the number of NCMC steps per BLUES iteration decreases the number of BLUES iterations required for the site to become hydrated, we find that increasing the number of NCMC steps per BLUES iteration can also start to negatively effect the efficiency in terms of force evaluations of the water hopping in hydrating the cavity (Table 1). Eventually, the increase in efficiency from allowing more relaxation is swamped by the associated increase in computational cost. However, relatively small amounts of relaxation have considerable payoff, resulting in a sort of sweet spot in terms of amount of relaxation. To ensure water hopping is as efficient as possible in terms of force evaluations, we recommend keeping the number of NCMC steps in the lower range, such as 1,250, 2,500, or 5,000.

In terms of wallclock time, 5,000 NCMC steps takes roughly the same amount of time to hydrate the cavity as 30,000 NCMC steps. 2,500 NCMC steps requires 4x less wallclock time to hydrate the cavity compared to 1,250 NCMC steps, and using 5,000 NCMC steps takes 4x less wallclock time to hydrate the cavity compared to 2,500 NCMC steps. Based on this, 5,000 NCMC steps seems to be the most efficient in terms of wallclock time.

Lastly, we examined three hydration sites in the binding site region of the HSP90 protein-ligand system (Figure 4.C). All three crystallographic water molecules were removed from the hydration site in the HSP90 system and water hopping successfully rehydrated each hydration site. We chose a sampling region that was centered on a ligand atom and extended out to encompass the buried hydration site, ligand and some bulk water. With plain MD, only one out of the three water molecules were able to resume the crystallographic bridging positions within 285 ns, which is equivalent to 7.1×10⁷ force evaluations. This water molecule moved in from a starting position in bulk water. It took BLUES 5.9×10⁶ force evaluations on average (across 4 replicates) to occupy all three of the hydration sites. After the buried cavity had been hydrated, no NCMC moves were accepted that removed any of the water molecules, indicating that the occupancy of these sites is favorable. We did not explore how the amount of relaxation would affect the acceptance rate as we already explored this in the MUP-1 system and found that, in general, increasing the amount of NCMC increases the acceptance rate of all moves (Table 1). In terms of wallclock time, the 285 ns MD simulation took about 54 hours and was unable to completely fill the cavity. However, BLUES only took 31 hours to completely rehydrate the cavity.

In both of the protein-ligand systems studied, we restrained the proteins and ligands with a force constant of 5 kcal/mol · Ų and artificially removed the crystallographic water, which is highly favorable in its place. Therefore, once the water returned to its crystallographic position, it did not transition out of the binding site again.

The sampling region used for the protein-ligand systems encapsulates the binding pocket and some bulk water. Relative to MD, we find that we can increase efficiency by making the area of interest the focal point of NCMC move attempts. Making the sampling region just large enough to cover a specific ligand-binding site and bulk water allows us to speed up the equilibration of water between these two regions, and this strategy has been successfully used elsewhere [10]. If the sampling region covered a greater amount of bulk water in these cases, the efficiency would decrease because the equilibration of water between regions would be slower as more water moves would move water molecules around in just bulk water. In general, we recommend setting the radius to be as small as possible while ensuring that the particular area of interest and some bulk is covered, thus increasing efficiency. In some cases, a larger sampling region may be more desirable, such as a protein with multiple hydration cavities, and this would simply require defining a larger sampling region which covers all of the cavities. Additionally, the user must be careful when defining the sampling region when using periodic boundary conditions. If the radius is set to encompass any area outside of the box, and periodic boundary conditions are used, there could be overlapping regions in the sampling area and this will result in more water moves being proposed to those areas, creating problems as noted above.

Water hopping could be used to discover important hydration sites in proteins. Crystallography does not always provide an accurate view of water positions and occupancies [37]. Only relatively highly ordered waters can be resolved in crystal structures, which may be a small subset of all waters which are present. Additionally, partial and weak density can obscure determination of where water molecules are present. At the same time, waters can be critical in protein dynamics [43, 50] and for the thermodynamics of ligand binding s [1, 2, 8, 27, 32, 34, 35, 39, 49], meaning that treatment of such waters — even when not obvious from experimental data — can be critical. Our method could explore such feasible hydration sites as well as the orientation of critical water molecules in cases where structural data is ambiguous.

4. Conclusions and Future Work

In this study, we implemented water hopping moves within our BLUES (NCMC+MD) framework to enhance the sampling of water rearrangements relative to traditional MD for systems that have buried hydration sites.

We validated BLUES with translational water moves on a water box with dividing graphene sheets, a buckyball with an energetically unfavorable water trapped inside, and both the MUP-1 and HSP90 proteins bound to a ligand with crystallographic bridging water removed. We then evaluate the efficiency of BLUES in hydrating the sites in the protein-ligand systems, based on the number of force evaluations. Overall, we demonstrate that NCMC enhances sampling relative to normal MD.

This water hopping approach can be used to find areas that are likely to be populated by waters in protein binding sites and sample water rearrangements potentially more efficiently than traditional MD. Water hopping moves could be combined with additional types of BLUES moves such as ligand [19, 42] or sidechain [11] rotational moves for broader applications.

The size of the sampling region is an important parameter in our method, and one we intend to optimize in the future. In the future, additional work could be done to help improve the acceptance of water hopping moves. To improve the acceptance and increase the efficiency of BLUES translational water moves, move proposals could be made to be more selective. In the current work, the move proposals can be made anywhere that is encompassed by the radius. To make the move more efficient, water hopping could be redesigned to help reduce move proposals that only move water molecules around in bulk, thus focusing on move proposals to the interior of the protein using methods like those detailed in the work of Ben-Shalom et al. [10]. Additional work could also include comparisons of BLUES (NCMC/MD) water hopping to MC/MD water hopping, allowing us to test whether or not NCMC enhances sampling relative to MC; here, we compared only with traditional MD.

Previous work from Gill et al. compared the speed of non-equilibrium relaxation and MC for ligand rearrangements and found that NCMC provided benefits over doing large numbers of pure MC attempts [20]. We speculate that the same may be true here. Compared to previous work from Ben-Shalom et al. [10], where MC/MD was run on the same MUP-1 protein-ligand system to hydrate the site, we found that BLUES (NCMC/MD) more efficiently hydrates the crystallographic site. There seems to be a 3–4x increase in efficiency using BLUES (NCMC/MD) based on average number of force evaluations. We believe this increase in efficiency will extend out to other systems, but this needs exploring. Within our current framework, direct comparisons to MC are not feasible (there is a the low acceptance rate and the need to run a large number of trials) because MC evaluations with OpenMM need to be done off-GPU, making the MC move proposals unreasonably slow. This is something that can be explored in future work.

Overall, here, we introduced and validated our new water hopping approach to enhanced sampling of water rearrangements in BLUES, and find it is more efficient than standard MD on a by-force-evaluation basis for the systems considered here.

Abbreviations

BLUES

Binding modes of Ligands Using Enhanced Sampling

MD

Molecular Dynamics

NCMC

Nonequilibrium Candidate Monte Carlo

MUP-1

Major Urinary Protein

HSP90

Heat Shock Protein 90