The rules of cerebellar learning: around the Ito hypothesis

Abstract

As a tribute to Masao Ito, we propose a model of cerebellar learning that incorporates and extends his original model. We suggest four principles that align well with conclusions from multiple cerebellar learning systems. (1) Climbing fiber inputs to the cerebellum drive early, fast, poorly-retained learning in the parallel fiber to Purkinje cell synapse. (2) Learned Purkinje cell outputs drive late, slow, well-retained learning in non-Purkinje cell inputs to neurons in the cerebellar nucleus, transferring learning from the cortex to the nucleus. (3) Recurrent feedback from Purkinje cells to the inferior olive, through interneurons in the cerebellar nucleus, limits the magnitude of fast, early learning in the cerebellar cortex. (4) Functionally different inputs are subjected to plasticity in the cerebellar cortex versus the cerebellar nucleus. A computational neural circuit model that is based on these principles mimics a large amount of neural and behavioral data obtained from the smooth pursuit eye movements of monkeys.

Introduction

The remarkable crystalline circuit architecture of the cerebellum has driven an entire subfield of neuroscience to pursue an understanding of how the circuit works. The driving force behind the research field has been the idea of cerebellar learning, first suggested by Marr (1969) and Albus (1971), and then rendered specific and testable by Masao Ito. Ito (1972) suggested how plasticity in the cerebellar cortex could work within the context of the known circuit for a simple eye movement reflex called the “vestibulo-ocular reflex” or “VOR”. He suggested that the climbing fiber input to the flocculus of the cerebellum provides visual error signals when the VOR is functioning poorly. He proposed that spikes on the climbing fiber cause long-term depression of the parallel fiber to Purkinje cell synapse to alter the simple-spike outputs from Purkinje cells and thereby correct the movement errors.

Remarkably, Ito’s hypothesis from almost 50 years ago is still a significant part of what seems like the truth. The climbing fiber input from the inferior olive to the Purkinje cell does cause synaptic depression in slices and in culture. Extensive data from at least three movement systems – the VOR (e.g. Lisberger, 1994; Blasquez et al., 2004; Rowan et al., 2018; Kimpo et al., 2014), smooth pursuit eye movements (Medina and Lisberger, 2008; Herzfeld, 2020), and classical conditioning of the eyelid response (e.g. Krupa et al., 1993; Heiney et al., 2014; Halverson et al., 2015) – all support the hypothesis in awake, behaving animals. Indeed, the volume of supporting observations is way beyond what can possibly be cited here. Instead, I will focus on my laboratory’s current thinking about the principles of operation of the cerebellar learning circuit and how our view parallels Ito’s original hypothesis.

But first, I reprint a tribute to Ito. In 1999, Ito was invited to deliver the prestigious Bennett Lecture sponsored by the Department of Physiology at UCSF. Because Masao and I were, at the same time, scientific opponents and friends, my colleagues asked me to introduce him at the lecture. Normally, my introductions are “off the cuff’, but I make an exception and write and read them for my students’ thesis defenses and for seminars to be delivered by the most distinguished guests. The tribute below is the introduction that I wrote and read for Masao in December of 1999 at UCSF.

Tribute from December, 1999

It is a tremendous pleasure to introduce Masao Ito, who is, without question, one of the greatest neuroscientists of the 20^th century. Masao has single-handedly created one of the richest and most exciting areas of systems neuroscience research. It would be traditional to introduce Masao by listing his career history, honors, and research areas, but I wish to take a more personal approach and highlight from my own perspective some or Masao’s major contributions.

First, his research in the 1960’s demonstrated that the entire output from the cerebellar cortex, in the form of Purkinje cell axons, was inhibitory. I had the pleasure of reading this series of papers first when I was a graduate student and I recognized then, as I still do now, that this was a remarkable piece of research. One of the hallmarks of a truly great scientist is the ability to see the complex truth out of what seems at first confusing and difficult to fathom. In these experiments, which I need to remind you were conducted in the days when physiologists built their own amplifiers and oscilloscopes and well before the advent of patch electrodes, Masao and his colleagues recorded intracellularly from cells in Deiters nucleus that were targets of Purkinje cell axons. They stimulated cerebellar input and output fibers electrically and devised elegant, creative, and incisive experiments to separate ionic currents caused by Purkinje cell inhibition from shorter latency currents caused by excitatory axon reflexes due to antidromic activation of cerebellar input fibers. The fact of Purkinje cell inhibition is taken for granted now, but it was Masao’s brilliant experiments that proved this point more than 30 years ago when it was stunning and surprising.

Masao’s second, and perhaps greatest accomplishment was the development of the hypothesis of cerebellar learning. He was able to cut to the core of the earlier theoretical papers of Marr, Albus, and Brindley, and suggest an elegant behavioral system in which he proposed that learning in the cerebellar cortex would cause modification of motor output. The brilliance of Masao’s suggestion is just how much of it turned out to be true. In the early 1970’s, he proposed that a part of the cerebellum called the flocculus would be involved in learning in a simple eye movement called the vestibulo-ocular reflex. Subsequent lesion and recording experiments from many labs, including his and mine, showed this to be true. He predicted that the climbing fiber inputs to the cerebellum would convey visual information that could guide learning, a prediction that was soon verified under his mentorship. He predicted that the conjunction of a climbing fiber input with parallel fiber activity would cause “long term depression” (or LTD) of that parallel fiber’s synapses on the Purkinje cell. It is little known that Eccles and Marr tried this experiment in the late 1960’s and failed to demonstrate the mechanism Ito had predicted. However, in Masao’s third great accomplishment, he and his colleagues persevered and eventually understood the conditions necessary to demonstrate “LTD”. In the past 10 years, they have elaborated the mechanism of LTD, giving us a detailed understanding of a mechanism that seems to be really important for learning motor activity. Ito’s research may well have shown us the way to understanding how we learn to walk, talk, hit a tennis ball, catch a fly ball, or play the piano.

In my opinion, one sign of a truly great contribution is the excitement and controversy that surrounds it. In the analysis of the central nervous system, nothing worth learning is simple and uncontroversial. By this standard, Masao’s exposition and experimental defense of the cerebellar learning hypothesis must stand as one of the greatest contributions of the present era. Many laboratories all over the world, including my own, have invested thousands of person years testing, refining, challenging, and eventually largely supporting the original idea of cerebellar learning. I confess that I have been one of the most vociferous challengers of the details of Masao’s proposal. Out of the intensity of our competition has come a body of data that provides as stern a challenge as any hypothesis can stand. Remarkably, the idea of cerebellar learning stands tall. There are still many open questions, and there are theories (including my own and possibly his) that allow for learning in the cerebellar nucleus as well as the cerebellar cortex. Still, Masao’s initial hypothesis stands at the center of all theories. It has stood the test of time.

Before I turn the podium over to Masao Ito, I wish to add one personal note. My interest in the cerebellum, my 23 years of research on learning in the vestibulo-ocular reflex, and my competition with his ideas all stem directly from Ito’s contributions. It was Ito’s book with Eccles and Szentagothai, “The cerebellum as a neuronal machine”, and then his provocative and impressive papers during my graduate career that pushed my interests toward these issues. In 1996, Jennifer Raymond, Mike Mauk, and I published an invited review on cerebellar learning in Science that I envisaged as a tribute to Ito and his book. I wanted to call our paper “The cerebellum as a neuronal learning machine” and the actual title is only subtly different. By this title, I wanted to pay tribute to the man, the idea, and all the subsequent research that have surrounded Masao’s appealing, intuitive, provocative, and seemingly largely-true hypothesis for learning motor activity.

I am not going to try to correct the fact that this introduction has not included the standard listing of academic honors and prizes, nor the outline of positions that Masao has held. I assure you that his CV is as impressive as they come. He has published a ton of papers and has been the mentor without authorship on many more. He has received many prizes including the prestigious Japan Prize in 1996, and has held every position of honor and responsibility that is possible. Today, Professor Ito will deliver the last Bennett lecture of this millenium entitled: “A key to the brain – from studies of the cerebellum”.

Commentary

Forty-eight years have passed, but still there are remarkable similarities between Ito’s first exposition of the proposed neural circuit basis for cerebellar learning based on the vestibulo-ocular reflex (Ito, 1972) and our current thinking based on extensive analysis of learning in smooth pursuit eye movements of monkeys (Herzfeld et al., 2020).

Ito’s proposal in 1972 was based on the emerging anatomical and physiological organization of the vestibulo-ocular reflex (VOR) pathways. The proposal was captured by Figure 1 of Ito’s paper, reproduced here as Figure 1B. In the late ‘60s and early ‘70s, several groups more or less simultaneously discovered that the flocculus of the cerebellum served as one of two parallel pathways that mediate the VOR (Baker et al., 1972; Highstein, 1973). Vestibular inputs project directly into a 3-neuron brainstem reflex arc and to the Purkinje cells in the flocculus, which, in turn, monosynaptically inhibit the interneurons in the 3-neuron brainstem pathway. Ito (1972) postulated, and Maekawa and Simpson (1973) soon discovered, that the climbing fiber pathway to the flocculus was responsive to image motions across the retinal that would signal erroneous performance of the VOR.

Figure 1. Similarity of Ito’s original model of cerebellar learning in the vestibulo-ocular reflex (VOR) and our circuit model based on analysis of direction learning in smooth pursuit eye movements.

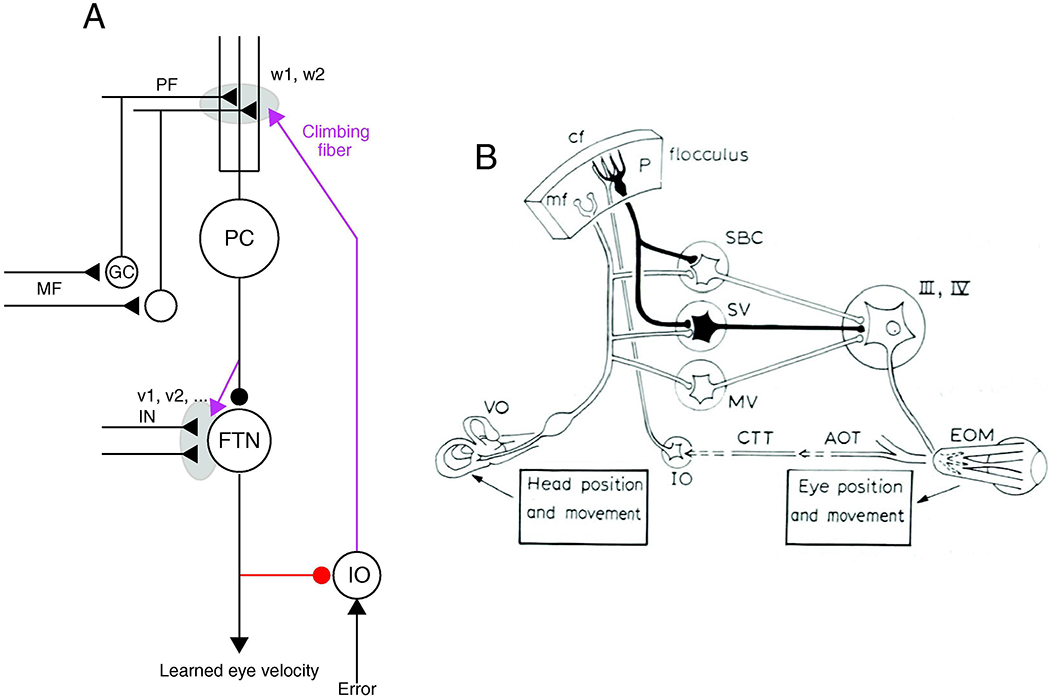
A: Circuit model for pursuit learning. Magenta pathways show teaching signals, gray shading shows sites of plasticity, and red pathway shows recurrent inhibition of inferior olive from Purkinje cells. Abbreviations are: PC, Purkinje cell; PF, parallel fiber; GC, granule cell; MF, mossy fiber; FTN, floccular target neuron; IN, inputs to floccular target neurons, v1, v2, w1, w2, synaptic weights. Reproduced with permission from Herzfeld et al. (2020). B: Circuit model for VOR learning. Abbreviations are: P, Purkinje cell; cf, climbing fiber; mf, mossy fiber; IO, inferior olive; SBC, SV, MV, sub-regions of the vestibular nuclei; III, IV, extraocular motor nuclei; EOM, extraocular muscles; AOT, CTT, pathways in the accessory optic system; VO, vestibular sensory apparatus. Panel A is modified from Herzfeld et al. (2020) and panel B is from Figure 1 of Ito (1972). Both are reproduced with permission.

In keeping with the theory-based proposals of Marr (1969) and Albus (1970), Ito proposed that the movement errors reported by the climbing fiber input would cause depression of the strength of the synapse parallel fibers that carried vestibular signals to Purkinje cells. In the context of the known circuit of the VOR, this would change the balance in the two parallel vestibular pathways, one through the flocculus and one through the brainstem, and alter the size (or “gain”) of the VOR. It took 10 years, but Ito’s group and then many more investigators ultimately demonstrated climbing-fiber driven long-term depression of the parallel fiber to Purkinje cell synapse (Ito and Kano, 1982; Linden et al., 1991; Crepel and Jaillard, 1991; Lev-Ram et al., 1995), validating one of the fundamental premises of Ito’s theory.

Fast forward to 2020. An enormous amount has been learned (recent reviews: Medina, 2019; Wagner and Luo, 2020; Hull, 2020) about the cerebellum in general, the broad and intricate mechanisms of cerebellar plasticity, the complexities of motor learning in the VOR, and cerebellar motor learning in general. Our view of what the cerebellum does, how it does it, and how the cerebellum cooperates with other key brain systems has become at the same time both more specific and broader. Yet, as a field, we have neither proven that Ito’s initial hypothesis is correct nor falsified it. If anything, we have extended and embellished the theory while leaving its fundamental bones intact.

My own laboratory’s studies of learning in smooth pursuit eye movements in monkeys has led to a recently-published model of the circuit basis for cerebellar learning that has remarkable parallels to the original proposal from Ito (1972). Our proposal is captured by Figure 1A, reproduced from Herzfeld et al. (2020). Like Ito’s proposal, ours is based on known neural circuitry. In the monkey, the flocculus cooperates with a part of the ventral paraflocculus to control smooth eye movements (Zee et al., 1981; Rambold et al., 2002) and we call the relevant structure the “floccular complex”. Purkinje cells from the floccular complex inhibit “floccular target neurons” in the vestibular nucleus (Lisberger et al., 1994) that, in turn, project directly to motoneurons (Scudder and Fuchs, 1992). Pursuit eye movements are driven by eye velocity signals, and the inputs to Purkinje cells and floccular target neurons are related to eye velocity rather than vestibular inputs, but otherwise the circuit principles are comparable for the VOR and pursuit. The rest of this review will outline the evidence for our proposal, which postulates four fundamental principles of operation:

• Fast, early neural learning occurs with poor retention at the parallel fiber to Purkinje cell synapse, driven by climbing fiber inputs that report movement errors via visual motion signals.

• Slow, later neural learning with excellent retention occurs at non-Purkinje cell inputs to the FTNs, driven by the learned simple-spike output from Purkinje cells, meaning that the memory is transferred from the cerebellar cortex to the cerebellar nucleus.

• Feedback from the cerebellar cortex through the cerebellar nucleus to the inferior olive regulates the probability and/or duration of climbing fiber inputs and puts limits on the amount of fast, early neural learning in the cerebellar cortex.

• Different input signals are subjected to plasticity at the fast, early versus slow, later sites of learning.

Only the first of these principles was stated explicitly in Ito’s proposal in 1972, but the ideas of multiple sites of neural learning, transfer from the cerebellar cortex to the cerebellar nucleus, and recurrent control of the climbing fiber inputs were included in my discussions with him and some of his writings (Ito, 2013) and have been in the literature for a long time. For example, research on classical conditioning of the eyelid response has demonstrated the relevance of all of these concepts (Mauk et al., 2014). Miles and Lisberger (1981) proposed a second site of neural learning in the cerebellar nucleus based on an understanding of the responses of different neurons in the VOR circuit during learning; they nibbled at the idea of transfer of learning from the cerebellar cortex to the vestibular nucleus. My laboratory’s research on the neural circuit basis for motor learning in the VOR of monkeys supported strongly the existence of multiple sites of neural learning with long-term storage in the vestibular inputs to floccular target neurons (Lisberger, 1994), which are the cerebellar nucleus for the VOR. Indeed, many of the individual components of our four principles of operation have been suggested and/or supported individually by others, and I attempt to give credit in the sections that follow. Our contribution is to stitch all the pieces together with a model based on extensive data from a single behavioral system.

In the next section, I turn to a review of the results from my laboratory that led us to the proposal sketched in Figure 1A. But first, I need to be clear that I know I wear blinders. I am well aware of the huge amount of data in the field of cerebellum and cerebellar learning and I know that much of that data is neglected in a review such as this one. I also know that there is a new literature of cerebellar learning in the VOR of mice (e.g. Rowan et al., 2014; Kimpo et al., 2014; Kodama et al., 2012) that has both supported and extended the model proposed originally from my laboratory’s research on the VOR of monkeys. Plasticity can occur in almost every synapse and neuron in the cerebellum (Hansel et al., 2001; Carey, 2011; Gao et al., 2012), cautioning that behavioral learning is likely caused by a symphony of plasticity mechanisms so that any proposal based on one or two sites and mechanisms of plasticity is doomed to be incomplete. The relative importance of molecular variation across defined cell types (e.g. Sugihara and Shinoda, 2004; White et al., 2014; Rodriques et al., 2019; Kozareva et al., 2020) is at a deeper level of analysis that is ignored (so far) by my focus on the neural circuit mechanisms of behavioral learning. And, perhaps most concerning, our proposal is based on a traditional “error-correcting” form of behavioral learning and on signals that report movement errors at a time in this history of the field when the wide extent of cerebellar inputs and responses related to reward and movement outcome is just becoming apparent (Ohmae et al., 2015; Wagner et al., 2017; Heffley et al., 2018; Heffley and Hull, 2019; Konstadinov et al., 2019; Sendhilnathan et al., 2020).

Yet, I would argue that blinders can be a good thing if they lead to focus. So, I plunge forward with my blinders on in the hope that analyzing cerebellar learning in a very focused way leads to principles of operation that generalize widely across the structure and its many motor and nonmotor functions.

Review

Directional learning in the floccular complex for smooth pursuit eye movements

We study motor learning in smooth pursuit eye movements (Medina et al., 2005) by rewarding monkeys for tracking a strategically-selected sequence of target motions. The motions are designed to instruct the pursuit system that the onset of target motion in one direction predicts that eye movement in a specific orthogonal direction will be required 250 ms later. As illustrated in Figure 2A, the target motion: (1) starts at straight-ahead gaze; (2) moves in an initial direction that we call the “pursuit direction” for 250 ms; (3) adds a component of motion for 400 ms in the orthogonal direction that we call the “learning direction”; and (4) returns to the original direction of motion. We use the term “instruction” to refer to the change in target direction caused by the addition of orthogonal target motion. In the example of Figure 2A and B, the pursuit direction is rightward and the learning direction is downward. The learning paradigm creates the trajectory of target position illustrated by the crooked black arrow between the horizontal and vertical position panels of Figure 2A.

Figure 2. Paradigm for direction learning in smooth pursuit eye movements of monkeys and its neural correlates in the floccular complex of the cerebellum.

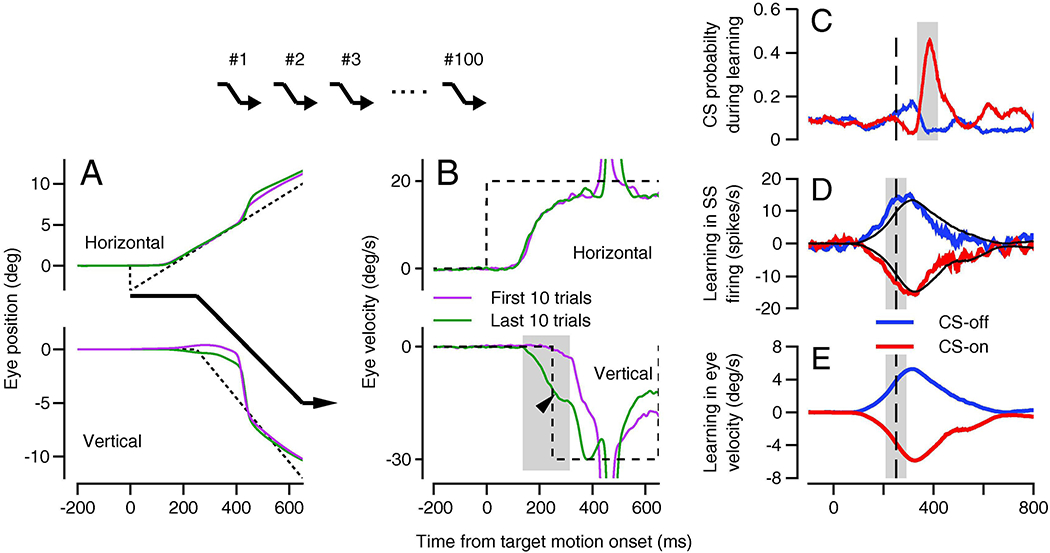
A: Horizontal and vertical position traces with the trajectory of the target motion shown by the black arrows. B: Horizontal and vertical eye velocity traces. In A and B, green and magenta traces show averages across the first and last 10 learning trials in a 100-trial block and the dashed traces show target motion. The arrow head indicates the learned eye velocity and the gray shading indicates the interval used to quantify learning. In A and B, negative values of vertical eye motion indicate the learning direction. The arrows above A and B indicate the sequence of learning trials for this kind of experiment. C: Complex-spike probability for Purkinje cells as a function of time. D, E: Learned simple-spike firing and eye velocity after 100 repetitions of the same learning trial. In C-E, the vertical dashed line shows the time of the instruction and the shaded areas indicate the intervals used to quantify responses. Red and blue traces show data for instructions in the directions that caused increases versus decreases in complex-spike probability. Panels A and B are modified from Yang and Lisberger (2017) and C-E are reproduced from Medina and Lisberger (2008), all with permission.

Vertical eye velocity learns, after 100 repetitions of the learning trial, to predict a substantial fraction of the downward target motion before it actually occurs (Figure 2B, dark green trace). In contrast, in the first few learning trials, the vertical eye velocity is almost entirely reactive to the physical target motion in (Figure 2B, magenta trace), following the change in target direction by a normal visual latency. The difference between the dark green and magenta traces in the vertical eye velocity panel of Figure 2B demonstrates the eye velocity that is learned from 100 learning trials. The visually-driven reaction to the downward target motion also appears in the eye velocity after 100 learning trials with the appropriate 100-ms delay, starting at the end of the gray shading. Thus, the interval indicated by the gray shading shows the time when the learned response can be measured without any influence of the target motion in the learning direction. Importantly, the learned response does not start at the time of the initiation of pursuit. It occurs just before the time of the instructive change in target direction. Learned timing is a prominent feature of pursuit learning (Medina et al., 2005) and eyelid response conditioning (Perrett et al., 1993).

Purkinje cells in the monkey’s floccular complex show responses that are ideal for guidance of pursuit eye movements. Their responses are tuned for the directions of eye and target motion and show simple-spike firing in relation to eye velocity with increases in one direction (typically toward the side of the recording or downward), decreases for eye motion in the opposite direction, and little change in firing for orthogonal directions of target motion. They show climbing fiber responses to the motion of a target across the retina, with direction tuning typically opposite to the simple-spike tuning: increases in climbing fiber responses for the direction of target motion that causes decreases in simple-spike firing rate, and vice versa (Stone and Lisberger, 1990; Medina and Lisberger, 2008).

Floccular Purkinje cells show climbing fiber responses that depend on the direction of the instruction created by the change in target direction (Figure 2C), and large changes in simple-spike responses (Figure 2D) that emerge over 100 learning trials and depend on the climbing fiber responses. Here, upward versus downward instructions drive an increase versus a decrease in the probability of climbing fiber responses with a stereotyped latency of about 100 ms. To characterize neural learning in Purkinje cells during learning more generally, we define their direction tuning as “CS-on” or “CS-off’ according to the directions of the instructive target motion that evoked climbing fiber responses (Herzfeld et al., 2018). The neural learning expressed in simple-spike firing depends on the direction of the instruction. When the instruction causes an increase in climbing fiber probability (CS-on), there is a learned depression of simple-spike firing rate; when the instruction decreases climbing fiber probability (CS-off), there is a learned potentiation of simple-spike firing rate. One hundred repetitions of the same learning trial also cause a learned eye velocity that has the same shape and timing as the learned simple-spike firing rate (Figure 2E and black traces in Figure 2D), but lags the simple-spike firing rate in time by 10-15 milliseconds.

The data in Figure 2 demonstrate that potential neural substrates of both the teaching signal and the behavioral learning exist in the firing of Purkinje cells in the floccular complex. Because floccular Purkinje cells affect the firing of extraocular motoneurons through a disynaptic pathway with a latency of about 10 ms (Lisberger, 1994), we think that the learned changes in simple-spike firing rate drive the learned changes in eye velocity. In our system, the cerebellar nucleus is at least partly in the vestibular nucleus, where floccular target neurons have been identified definitively during behavior in awake monkeys (Lisberger et al., 1994). Because of the possibility that floccular Purkinje cells also affect eye movements via the basal interstitial nucleus of the cerebellum (Langer et al., 1985), we refer to the targets of floccular Purkinje cells as their “cerebellar nucleus”, rather than specifically as the vestibular nucleus. Still, the abundance of knowledge about the relevant circuit and its neurophysiology opens the possibility of using quantitative analysis of pursuit eye movements to delve more deeply into the possible neural circuit mechanisms of cerebellar motor learning.

Climbing fiber inputs as the primary driver of learning

What result would prove that climbing fibers cause plasticity that leads to behavioral learning? The field has proven that climbing fiber inputs can cause plasticity in the parallel fiber to Purkinje cell synapse, in vitro. Behavioral learning is associated in vivo with changes in the simple-spike firing of Purkinje cells that could result from depression of the parallel fiber to Purkinje cell synapse. Even though we have observed large learned changes in simple-spike firing in floccular Purkinje cells (Figure 2D), we cannot be sure that the site of learning for pursuit eye movements is actually in the cerebellar cortex, rather than inherited from cerebellar inputs. Final conclusions must await the results of the challenging experiment of recording from granule cells in the cerebellar input layer throughout a block of learning trials. Even then, proof that the climbing fibers cause plasticity that drives learning may be impossible to achieve without being able to visualize the molecular events of plasticity during learning in behaving animals.

We have come as close to proof as we can in the behaving monkey by demonstrating an “if-and-only-if” link between the occurrence of a single climbing fiber on one behavioral trial and neural learning in simple-spike firing on the subsequent trial. We use the term “single-trial plasticity” to describe the neural phenomenon we discovered, first through analysis of the repeated presentations of the same learning trial that led to the data in Figure 2C–E (Medina and Lisberger, 2008) and then through much more extensive data acquired with a behavioral paradigm that was explicitly designed to study single-trial effects (Yang and Lisberger, 2010). We think of single-trial plasticity as the neural substrate of a fast, early, poorly-retained component of neural learning in pursuit eye movements driven by a short-term form of climbing-fiber driven synaptic depression.

To study single-trial learning and plasticity, we devised the “random-direction paradigm” (Figure 3A), where the pursuit direction always was the same but the direction of the instructive change in target direction was selected randomly from the two orthogonal directions on each trial. The use of random instruction directions allows behavioral learning to occur after each trial, but prevents any long-term behavioral learning. It creates a “stationary” regime where we were able to accumulate many repetitions of the response to each instruction. In Figure 3A, the existence of single-trial learning in eye movements can be appreciated by comparison of the data for the n^th trial (blue traces) with that for the n-1^st trial in a long string of learning trials. The responses in the two trials are almost identical, except for the small, learned bump in eye velocity in the n^th trial that starts just before the time of the instructive change in target direction (vertical eye velocity, blue trace, black arrowhead).

Figure 3: Climbing-fiber linked single-trial plasticity and learning.

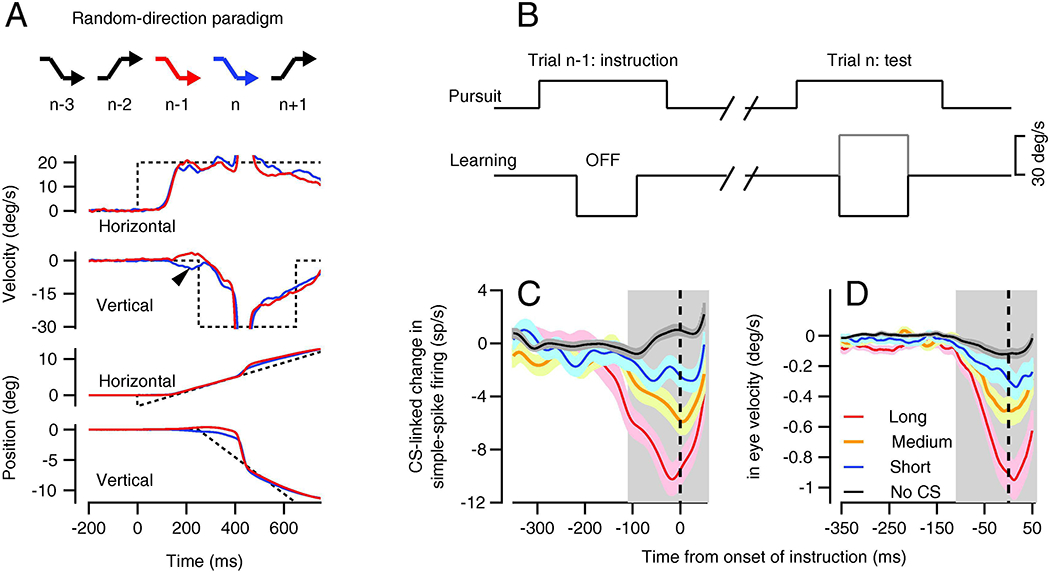
A: The crooked arrows indicate a sequence of target motions during learning trials in the random-direction paradigm. The 4 sets of red and blue traces show the eye velocity and position on the n-1^st and n^th trials, also indicated by the colors of crooked arrows. Dashed traces show target motion and the arrowhead on the vertical eye velocity trace points to single trial learning seen in the n^th trial as a result of the instruction in the n-1^st trial. B: Schematic of the target velocities on the “instruction” and “test” trials. C, D: Trial-over-trial change in simple spike firing (C) and eye velocity (D). Black, blue, orange, and red traces show neural and behavioral learning when there was no complex-spike and when the complex-spike was short, medium, or long in duration. The vertical dashed line shows the time of the instructive change in target direction and the gray shading indicates the interval used for quantitative analysis. Reproduced with permission from Yang and Lisberger (2014).

Recordings from Purkinje cells during the random-direction paradigm revealed an impressive single-trial plasticity of simple-spike firing that was tightly-linked to the occurrence and duration of the complex-spike events caused by climbing-fiber inputs (Medina and Lisberger, 2008; Yang and Lisberger, 2013, 2014). We analyzed the data by dividing the string of learning trials into pairs that we called the “instruction” and “test” trials (Figure 3B). We separated the pairs into two groups according to whether the instruction trial provided a target motion that was in the CS-on versus CS-off direction for the climbing fiber input to the Purkinje cell under study. For pairs that delivered instructions in the CS-on direction, we further divided the trials according to whether or not a climbing fiber response occurred on the instruction trial (it did up to 50% of the time) and according to whether the duration of the resulting complex-spike was in the shorter, middle, or longer third for that Purkinje cell. As illustrated in Figures 3C and D, the trial-over-trial change in both simple-spike firing and eye velocity was related to whether or not a climbing fiber response was present and to the duration of its complex-spike. Trial-over-trial learned changes in eye velocity also were small when the learned simple-spike response was small. Both grew in parallel as a function of the duration of the complex-spike (Yang and Lisberger, 2014). Absent a climbing fiber response (black trace in Figure 3C), trial-over-trial depression of simple-spike firing was absent or might even have changed to a small trial-over-trial potentiation. The small potentiation in the absence of a climbing fiber response (Figure 3C and D) and the fact of a learned increase in simple-spike firing after 100 learning trials in the CS-off direction (Figure 2D) emphasize roles for both synaptic depression and potentiation in pursuit learning, as in VOR learning (Gao et al., 2012). We emphasize depression here because it is so tightly linked to the occurrence of a climbing fiber input.

We draw two conclusions from the analysis of single-trial plasticity and learning. First, we think that the climbing-fiber input on an instruction trial causes the depression of simple-spike firing seen on the subsequent trial. We suggest that the duration of the complex-spike is a proxy for the amount of calcium that enters the Purkinje cells and that more calcium causes larger amounts of plasticity. Second, the fact that single-trial learning in eye velocity tracks the single-trial plasticity recorded from individual Purkinje cells implies that climbing fiber occurrence and complex-spike duration are synchronized across most or all of the Purkinje cells in the relevant population. We recognize that there are other explanations for our data, but these seem like the most likely and plausible ones. They lead us to the conclusion that climbing fibers play a primary, causal role in cerebellar learning and that the trial-over-trial effects in Figure 3 are the neural substrate of a fast, early, poorly-retained component of learning in pursuit eye movements. Our conclusions are in line with the early theories of Marr (1969), Albus (1971), and Ito (1972), with the existence of climbing-fiber induced long-term depression in vitro (e.g. Ito and Kano, 1982), and with in vivo data during motor behaviors, starting as early as Gilbert and Thach (1977) and Dufosse et al., (1978).

Recurrent inhibition of inferior olive limits magnitude of learning

The recurrent projection from Purkinje cells to inhibitory neurons in the cerebellar nucleus to the inferior olive has been known for years (de Zeeuw et al., 1988; Fredette and Mugnaini, 1991). The signs of the synaptic connections imply that depressed simple-spike firing of Purkinje cells should lead to increased inhibition on neurons in the inferior olive, with potential impacts on the electrical excitability of inferior olive neurons and/or the electrical connections among them. Purkinje cells could control the probability of firing on climbing fibers and/or the number of action potentials in a burst on climbing fiber axons (Maruta et al., 2007). Thus, Purkinje cells may regulate their own climbing fiber inputs (Ruigrok and Voogd, 2000; Apps et al., 2018). In support of this conjecture, our recordings revealed a trial-by-trial correlation between the probability of a climbing fiber response to a given instructive change in target direction and the simple-spike firing rate at the time of the instruction. The slope of the relationship was small: a change in probability of 0.2 for each 40 spikes/s of simple-spike firing (Yang and Lisberger, 2013).

Our results (Yang and Lisberger, 2013, 2014) and others’ (Herzfeld et al., 2018; Mauk and Donegan, 1997) support the existence of small, functionally-homogeneous recurrent circuits. The circuits involve very specific climbing fiber inputs to a functionally-equivalent set of Purkinje cells. The data suggest (1) synchronous all-or-none responses within those climbing fibers, (2) unified Purkinje cell outputs to cerebellar nucleus neurons that control movements in the on-CS direction of the climbing fiber inputs, and (3) inhibitory control from the cerebellar nucleus to the inferior olive neurons that give rise to the climbing fibers that signal errors to the Purkinje cells. The very specific recurrent organization of the olivo-cerebellar loop is consistent with known anatomy (Ruigrok and Voogd, 2000; Apps et al., 2018) and is reminiscent of the same proposed organization of loops between the cerebral cortex and the cerebellum (Kelly and Strick, 2003)

For our behavioral learning system, Figure 4 summarizes the evidence that Purkinje cells modulate their own climbing fiber inputs. For a long time, we have been troubled by the fact that pursuit learning reaches an asymptote or at least ceases to increase swiftly long before learning has corrected the error introduced by the instructive change in target direction. For example, in Figure 4A, 100 learning trials with an instruction speed of 5 deg/s lead to a learned eye velocity asymptote at about 1 deg/s. But, the system can acquire a learned eye speed of 5 deg/s within a hundred trials when the instruction speed is 30 deg/s. Why does an instruction speed of 5 deg/s not lead to 5 deg/s of learned eye speed? The shortfall of learning cannot be explained by the reduction in retinal image motion caused by the instruction after 100 learning trials: 20 deg/s of image motion caused by a 20 deg/s instruction is effective in causing learning at the start of a learning block, but not when the same image motion is caused by an instruction at 25 deg/s after 100 learning trials (Figure 4A, green vs. cyan traces). We realized recently that the answer may lie in a causal effect of depression of simple-spike responses on the probability of climbing fiber inputs and the duration of the complex-spikes in Purkinje cells.

Figure 4. Evidence that recurrent feedback to inferior olive limits the magnitude of behavioral learning.

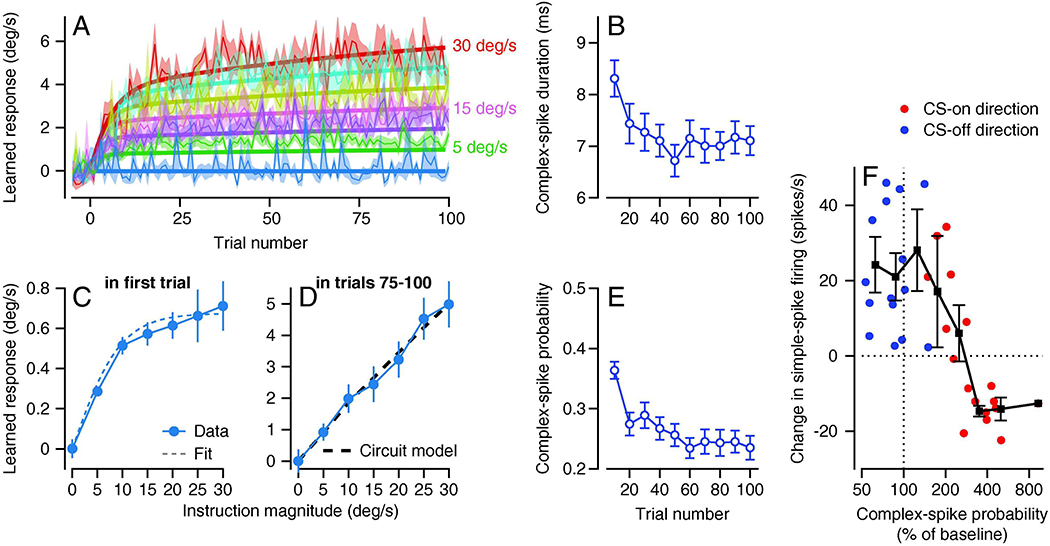
A: Trial course of behavioral learning over 100 trials. Different colors show learning curves for different speeds of instructive target motion, ranging from 0 to 30 deg/s in 5 deg/s steps. Bold curves show predictions of a computational model that includes recurrent feedback. Fine curves show data and ribbons show ±1 SEM. B, E: Duration and probability of complex-spikes decrease over 100 repetitions of the same learning trial. C, D: Learned response as a function of instruction speed in first trial and in last 25 trials of a 100-trial learning block. Dashed line in C shows a fit to the data for single-trial learning that sets parameters in the model with recurrent feedback that produces the prediction shown by the dashed line in D. F: The magnitude of neural learning after 100 learning trials in different Purkinje cells and for on-versus off-directions of instruction, as a function of the probability of complex-spikes. Each red or blue symbol summarizes data from a single Purkinje cell and the connected black symbols show binned means and standard deviations. CS-on and CS-off refer to the directions that caused increases versus decreases in the probability of complex-spikes. Note that the group of red symbols plotted above the horizontal dashed line summarize a group of Purkinje cells that had low probability of complex-spikes for the preferred direction instruction (CS-on) and showed “wrong-way” learning in simple-spike responses. Panels A, C, and D are reproduced from Herzfeld et al. (2020), B and E from Yang and Lisberger (2017) and F from Medina and Lisberger (2008), all with permission.

Several other features of our data agree that neural learning in simple-spikes may reduce the climbing fiber input long before the error caused by the instruction is eliminated.

1. We observe a change in the shape of the relationship between the size of the learned eye velocity and the magnitude of the instruction after 100 trials of behavioral learning (Figure 4D) compared to single-trial learning (Figure 4C). Therefore, the factors that control the magnitude of behavioral learning after 100 trials than are different from those embedded in the “open-loop” stimulus-response relationship for single-trial learning. Computational models (Herzfeld et al., 2020) show that recurrent feedback from Purkinje cells to the inferior olive can be that factor (dashed trace in Figure 4D).

2. Both the probability and duration of complex-spike responses decrease over 100 repetitions of the same learning trial with instructions in the CS-on direction (Figure 4B and E, Medina and Lisberger, 2008; Yang and Lisberger, 2017). Medina and Lisberger (2008) concluded that the probability of a complex-spike needs to be greater than 200% of baseline for depression to outweigh the potentiation that occurs on trials that lack a complex-spike. They did so based on the relationship between the size of the change in simple-spike firing and the probability of complex-spike responses to the instruction across Purkinje cells (Figure 4F). Because complex-spikes occur with a probability of 0.1 in the 100-ms bins used in our analysis, a threshold at 200% of baseline means that depression occurs only if the probability of complex-spikes exceeds 0.2. After 100 consecutive, identical learning trials, the probability of complex-spikes has declined almost to 0.2 (Figure 4E) and therefore may no longer have a net depressive effect on learned simple-spike responses.

3. Computational models depend on the recurrent feedback from Purkinje cells to the inferior olive to reproduce the trial-courses of eye velocity learning for instruction speeds ranging from 5 to 30 deg/s. The excellence performance of the model appears in the agreement between the bold and fine curves in Figure 4A (Herzfeld et al., 2020), and in the ability of the model to simulate the linear relationship in Figure 4D.

We find it confusing that the cerebellum would be designed to constrain the magnitude of learning and prevent motor learning from fully correcting motor errors. We assume that there are good reasons for restricting neural learning, for example to prevent plasticity in the cerebellar cortex from exhausting its full dynamic range. Perhaps the goal is to allow enough time for the brain to validate whether behavioral learning needs to persist, and then to force the pursuit system to distribute neural learning across all nodes in the circuit rather than concentrating it in the cerebellar cortex.

Multiple components and sites of learning

The appeal of the original cerebellar learning theory made it tempting to focus on plasticity at the parallel fiber to Purkinje cell synapse and the role of climbing fibers. Indeed, abundant evidence implies that the cerebellar cortex is necessary for acquisition of behavioral learning and is at least a temporary site of memory storage. However, there always has been evidence for multiple sites of learning in the cerebellar circuit, and possibly outside of it. For classical conditioning of the eyelid response, for example, considerable evidence implies that the conditioned response is stored outside of the cerebellar cortex while learning in the cerebellar cortex adjusts the timing of the eyelid response (Perrett et al., 1993; Krupa et al., 1993; Krupa and Thompson, 1995; Ohyama et al., 2006).

For the VOR, Miles and Lisberger (1981) suggested that learning might reside in the vestibular nucleus, perhaps in addition to the cerebellar cortex. Experimental analyses on monkeys from multiple labs supported an important site of learning at the vestibular inputs to floccular target neurons in the vestibular nucleus. An additional site of learning in the cerebellar cortex, at the synapses from vestibular parallel fibers onto Purkinje cells, has been controversial and contentious (Blasquez et al., 2003). Everyone agrees that plasticity occurs at this site during VOR learning. Yet, there is some evidence that it could cause VOR learning (Nguyen-Vu et al., 2013; Kimpo et al., 2014), and some evidence that plasticity is in the wrong direction to cause VOR learning and instead maintains proper signaling in floccular simple-spike output for a broader set of behaviors (Miles et al., 1980; Lisberger, 1994).

In the VOR of mice, Nguyen-Vu et al. (2013) demonstrated that behavioral learning emerged following coordinated optogenetically-induced firing of Purkinje cell axons and natural vestibular inputs in darkness. Their results establish the plausibility of plasticity in the cerebellar nucleus during learning as well as the idea that Purkinje cell axons could guide plasticity in the cerebellar nucleus and thereby transfer neural learning from Purkinje cells to the cerebellar nucleus. This mechanism would work as follows: (1) learning in the cerebellar cortex would create a simple-spike output to the cerebellar nucleus; (2) the learned signals on Purkinje cell axons would create a conjunction of post-synaptic potentials in cerebellar nucleus neurons with learnable modulation of presynaptic inputs to the same neurons; (3) plasticity mechanisms in the cerebellar nucleus (Zheng and Raman, 2010) would change the weight of the non-Purkinje cell presynaptic inputs, leading to learned changes in the firing of cerebellar nucleus neurons that could drive the learned behavior. Of course, plasticity exists at many, if not all, synapses in the cerebellar cortex (Hansel et al., 2001; Carey, 2011; Gao et al., 2012) so that multiple sites of neural learning may cooperate to cause behavioral learning.

In pursuit eye movements, several lines of evidence support the existence of multiple components of behavioral learning that could reside at different sites in the cerebellar circuit.

1. The trial course of learning is described poorly by a single exponential function and much better by the sum of two exponential functions (Hall et al., 2018). For example, Figure 5A illustrates typical data from one monkey averaged across multiple experiments with more than 1,000 repetitions of the same learning trial. Learned eye velocity shows a rapid rise over the first 20 learning trials followed by an inexorable slow ramp that persists for at least 1,000 trials. A single exponential (dashed curve) fits the trial course poorly, while the sum of two exponentials with fast versus slow time constants (solid curve) fits the trial course nicely. Following the logic of Hodgkin et al. (1952) we take the existence of two disparate time courses as evidence of at least two components of behavioral learning, and we suggest that they have different neural sites.

2. Retention of the learned behavior improves impressively from the first 20 learning trials to after 1,000 learning trials (Herzfeld et al., 2020). We tested retention at different times during a learning block by inserting 10 consecutive “error clamp” trials where the target motion in the learning direction was locked to the eye motion so that there was no stimulus either for learning or unlearning (Figure 5B). We then measured the decay of the learned response over those 10 trials (Figure 5C). When we performed the retention test after 20 learning trials, the learned response decayed fairly rapidly at the rate of about 15% on each trial. When we performed the retention test after 1,000 trials of learning, the learned response decayed more slowly at the rate of less than 4% on each trial. We take the difference in retention early versus late in a learning block as evidence of different mechanisms of learning with different retention properties, possibly at different sites in the pursuit circuit.

3. In our model, the fast, early, poorly-retained component of behavioral learning occurs in the floccular cortex and is transferred via teaching by Purkinje cell outputs to a slow, late, well-retained component of learning in the cerebellar nucleus for the floccular complex, that is, in floccular target neurons. A model based on the transfer concept reproduces the details of a large body of behavioral data (Herzfeld et al., 2020) and also is supported by the studies of Kassardjian et al (2005) on the cat VOR and Shutoh et al. (2006) on the role of the mouse flocculus in learning in a behavior that is closed related to pursuit eye movements, the optokinetic response. Kassardjian et al (2005) showed that reversible inactivation of the flocculus in the cat abolishes 3 hours of adaptation of the VOR, but has little effect on the changes induced by 3 days of adaptation. Shutoh et al. (2006) showed that bilateral reversible inactivation of the flocculus abolished the effects of a day of optokinetic learning but not the effects of a week of optokinetic learning. Further, they showed that ablation of the inferior olive abolished both day-long and week-long learning. Both of these studies imply that learning consolidates to a site outside the cerebellar cortex. The necessity of the climbing fiber input for both short-term and long-term optokinetic learning implies that the learning occurs first in the floccular cortex before it is transferred to the cerebellar nuclei.

Figure 5. Evidence for multiple components and sites of learning.

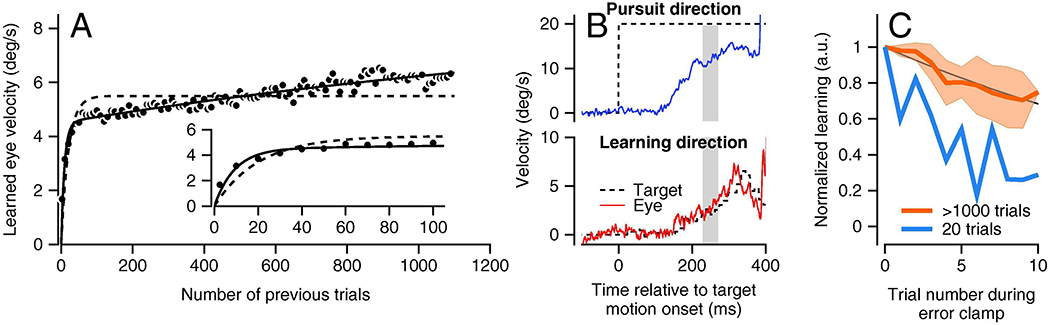
A: Trial course of behavioral learning over >1,000 repetitions of the same learning trial. Symbols show learned eye velocity averaged in bins of 10 trials, dashed and solid curves are fits to the data with single or sum of two exponential functions, respectively. Inset shows first 100 trials in greater detail. B: Eye and target velocity in an “error clamp” trial used to probe retention. Dashed trace shows target velocity and continuous traces show eye velocity. Note that target velocity in the learning direction tracks eye velocity so that retention can be probed without any error. C: Decay of learned eye velocity across 10 error clamp trials. Blue and orange traces show retention after 20 learning trials versus after >1,000 learning trials. Panel A is reproduced from Hall et al. (2018); B and C are reproduced from Herzfeld et al. (2020), all with permission.

Multiple sites of learning and transfer among them seems to be a feature of learning and memory systems. For cerebellar systems, Ito (2013) wrote: “These lines of evidence suggest that the memory of fast OKR adaptation formed in the flocculus may subsequently induce the memory of slow adaptation in vestibular nuclear neurons.” In non-cerebellar systems, different sites of early acquisition versus long-term storage exist for fear memories (Rogan et al., 1997; Do-Monte et al., 2015) and for bird song learning (Bottjer et al., 1984; Nordeen and Nordeen, 1993; Warren et al., 2011). Acquisition of a memory in one structure and long-term storage in separate structures is also a feature of declarative or episodic memory, as evidenced by amnesic subjects, such as HM (Zola-Morgan and Squire, 1990), and many more modern observations (Tonegawa et al., 2018). Perhaps cerebellar learning provides an accessible system for understanding transfer at the level of neural circuits and mechanisms of plasticity.

The neural inputs and signals subjected to plasticity

As a field, we accept that synaptic and intrinsic plasticity are the engines of neural and behavioral learning. But, to understand learning at a circuit level, we need also to (1) understand the nature of the signals that are learned and (2) identify by their functional properties the axons that transmit those signals to sites of plasticity. How are the signals carried by those axons related to the parameters of the sensory and/or motor events that occur during a learning trial? What does that tell us about the nature of the elements whose parallel fiber to Purkinje cell synapses, for example, are subject to depression? The properties of the neural signals that are subjected to plasticity at different sites of neural learning is a fundamental part of the answer to the question of how the brain learns. Even though the analysis is intricate and maybe challenging for the non-specialist, part of my message is that we must perform the analysis and the answer is informative.

The first requirement for neural signals to be subjected to plasticity is that they must be present at or near the time when an instruction is delivered and in the time interval during a movement when behavioral learning is expressed. In our system, this requirement suggests a surprising, but seemingly inescapable conclusion: learning needs to result from plasticity of parallel fiber signals related to eye velocity in the direction orthogonal to the preferred direction for Purkinje cell simple-spike firing. The logic comes from Figure 6A. Here, we are recording from a Purkinje cell that prefers horizontal smooth eye motion. Because we need to study neural learning for pursuit in the cell’s preferred direction, the learning trial starts with target motion in a vertical direction and then adds instructive target motion along the preferred, horizontal axes. In the first learning trial (blue traces), eye motion in the Purkinje cell’s preferred direction (horizontal) deviates little or none from baseline until 100 ms after the instructive change in target direction. But, the learned eye velocity in the Purkinje cell’s preferred direction (red traces) emerges before the instructive change in target direction. Behavioral (and neural) learning is expressed at a time when parallel fibers that prefer eye motion along the preferred directions of Purkinje cells would not modulate their firing rate. Preferred direction inputs simply are not available to undergo plasticity or drive the learning.

Figure 6: Analysis of functional properties of signals that undergo plasticity.

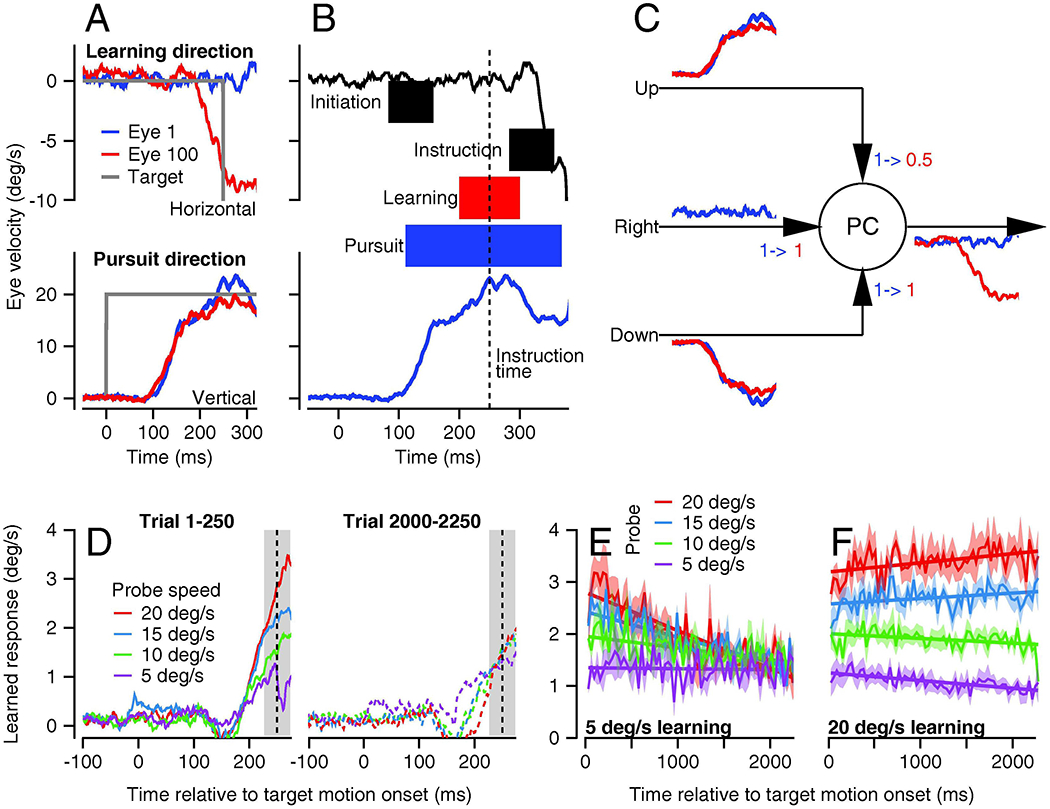
A: Blue and red traces show eye velocities on the 1^st and 100^th repetitions of the same learning trial. Traces in A end before any eye velocity response to the instruction. B: Events on first learning trial from A, expanded in time and extended to include the initial eye velocity response to the instruction. Gray and pale blue shading indicate the time intervals when neural signals related to the visual error or eye velocity in the pursuit direction would be available for plasticity. Pale red shading indicates the interval when learning is expressed. Vertical dashed line shows the time of the instructive change in target direction. C: Cartoon showing the signals available on parallel fiber inputs to PCs on the 1^st and 100^th learning trial, to motivate discussion of which signals are potentially subjected to plasticity. The numbers with arrows (“1->1” and “1->0.5”) indicate changes in the weights of the three parallel fiber inputs to the model Purkinje cell before versus after learning. D: Eye velocity trajectory early versus late in a long learning block. Different colors show expression of learning when the pursuit speed in the probe trial was 5, 10, 15, or 20 deg/s. Pursuit and instruction speeds in all learning trials were 5 and 30 deg/s. E, F: Evolution of generalization of the learned response for pursuit speeds of 5 versus 20 deg/s in the instruction trials. Different colors show learning expression curves for different pursuit speeds in the probe trial. A and B were adapted from Yang and Lisberger (2017). D-F were reproduced from Herzfeld et al. (2020), all with permission.

The requirements for signals that undergo plasticity become more tangible when we expand and annotate the eye velocity traces for the first learning trial (Figure 6B). Learning is expressed strongly in the 100-ms interval (red shading) that surrounds the time of the instruction (vertical dashed line). Visual motion signals from the onset of target motion in the pursuit direction (gray shading labeled “initiation”) are expressed much earlier and will vanish before the interval when learning is expressed. Visual motion signals from the instructive change in target direction (gray shading labeled “instruction”) arrive too late to drive the learned responses. Signals related to eye and target motion in the learning (horizontal) direction (black trace) both are nil before and during the interval when learning is expressed; they become non-zero only after the time of the instruction. Only eye velocity in the pursuit (vertical) direction (blue shading) overlaps with the interval when learning is expressed (red shading). Even then, if signals related to eye motion in the pursuit direction are subjected to plasticity in the cerebellar cortex, the time interval when learning is expressed is smaller than the time interval when pursuit signals are present. There still needs to be a mechanism to specify the timing of the learned response, an issue that has been noted by many authors (e.g. Perrett et al., 1993; Buonomano and Mauk, 1994; Medina et al., 2005; Suvrathan et al., 2016) and remains unresolved in Figure 6.

Figure 6C explains how learning could occur based on eye movement signals orthogonal to the preferred direction of a Purkinje cell. We assume that the model Purkinje cell in Figure 6C prefers rightward eye movement but receives parallel fiber inputs related to upward, downward, and rightward eye movement. Under normal, non-learning conditions, the simple-spike output from the Purkinje cell will show excellent direction tuning because its upward and downward inputs will cancel during pursuit eye movement with a component along the vertical axis. Under the learning conditions illustrated in Figure 6A and B, where upward pursuit leads to a rightward instruction, a climbing fiber response will depress the synapse from the parallel fiber input related to upward eye movement, shown by the numbers “1->0.5” but will not change the strengths of the other parallel fiber inputs, shown by the numbers “1->1”. The upward and downward inputs then are out of balance so that the next upward pursuit will cause decreased firing on this rightward-preferring Purkinje cell and lead to a leftward learned eye movement. The toy model in Figure 6C predicts that Purkinje cells will receive eye movement parallel fiber inputs with very broad tuning. However, it will need additional components to solve the problem of producing a properly-timed learned eye movement. It also could be elaborated to take account of the possibility of “multimodal” parallel fibers that discharge in relation to a combination of horizontal and vertical eye motion, due to Golgi cell feedback (Yamazaki and Tanaka, 2007) or convergence of mossy fibers with different preferred directions (Huang et al., 2013; Ishikawa et al., 2015).

Now, we can go one step further and ask how the signals carried by parallel fibers are related to the kinematics of eye movement in the pursuit direction. We do so by studying generalization of the expression of learning. Our logic is simple. Suppose that the learned response in a Purkinje cell (PC) is PC=gPF, where g is the synaptic weight from a parallel fiber (PF). If the parallel fiber has a firing rate that is linearly related to eye velocity, then the expression of the learned response will scale with the pursuit eye velocity on a test trial. We invert this logic. If the expression of the learned response scales with pursuit eye velocity on a test trial, then the parallel fiber that is subjected to plasticity has a firing rate that is linearly related to eye velocity in the pursuit direction. Thus, the pattern of generalization reveals the functional properties of the signals that are subject to plasticity to cause behavioral learning.

Generalization of the learned response is qualitatively different early versus late in learning. We studied generalization by delivering hundreds of consecutive pairs of trials. The first trial in each pair was an “instruction” trial with (1) a speed of pursuit target motion that was the same throughout the long sequence of trials and (2) a strategically chosen instructive change in target direction. The second trial in each pair was a “probe” trial without an instruction and with the same pursuit direction as the instruction trial, but different pursuit target speeds. Thus, we could test how eye velocity in the pursuit direction affected the expression of learning.

In the first 250 trials of a long block of learning trials, the learned change in eye velocity scaled nicely with the pursuit speed in the probe trial (Figure 6D, left graph). In the last 250 trials, the learned change in eye velocity was independent of the pursuit speed in the probe trial (Figure 6D, right graph). Actually, the situation is still more complicated because the shift in generalization also depends on pursuit speed in the instruction trial. When the pursuit target speed in the instruction trial is 5 deg/s, the transition from linear generalization to no generalization is exactly as described by Figure 6D and occurs gradually over more than 2,000 trials (Figure 6E). When the pursuit target speed in the instruction speed is 20 deg/s, generalization remains linear across the full 2,000 trials (Figure 6F). Thus, generalization after long-term learning is nil when probe speed is higher than pursuit speed in the instruction trial and is linear when probe speed is lower than pursuit speed in the instruction trial. The details are important: they imply that the signals that are subject to plasticity are related linearly to eye velocity for early, fast learning. The transition of generalization across 2,000 learning trials also supports the conclusion of at least two sites of learning with different temporal properties and different input signals subject to plasticity.

The computational model in Figure 7 reproduces these complex data almost perfectly. Generalization in the model (Figures 7F and G) follows the generalization in the data (Figures 7H and I). The relationship between the magnitude of learned eye velocity and the speed of the instruction is similar in the model (Figures 7B and C) and the data (Figures 7D and E), both for single-trial learning (Figures 7B and D) and after 100 trials of learning with the same instruction (Figures 7C and E). The model fits the trial course of learning nicely for the full range of instruction speeds (Figure 4A). The model depends on the assumption that plasticity acts on inputs that are linearly related to pursuit eye velocity in the cerebellar cortex and that are tuned for eye velocity in the cerebellar nucleus of the FTNs. There are precedents for the assumption that Purkinje cells and cerebellar nucleus neurons receive different information (Shinoda et al., 1992; Yamazaki and Tanaka, 2007; Ishikawa et al., 2015), but tuned signals related to eye velocity have not yet been reported (or looked for).

Figure 7. Computational model of the pursuit learning circuit.

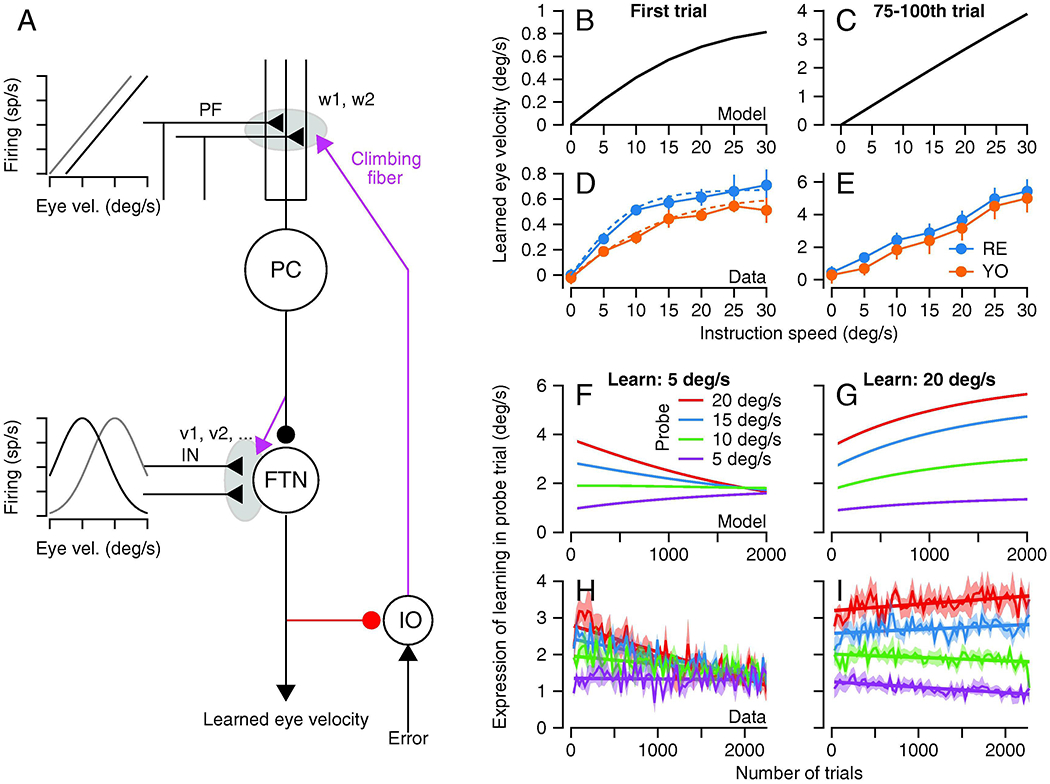
A: The structure of the model and the abbreviations are the same as in Figure 1. The two graphs show the proposed relationship to eye movements of the inputs that are subjected to plasticity in the cerebellar cortex and the cerebellar nucleus of the floccular target neurons. B-E: Relationship between size of learned eye velocity and instruction speed for model (B, C) and data (D, E), for single trial learning (B, D) or after 75-100 trials of learning with the same instruction (C, E). F-I: Generalization of learning measured in probe trials with different pursuit speeds as a function of the number of trials in the learning block. Different graphs show results for the model (F, G) and the data (H, I) when the pursuit speed in the learning trial was 5 deg/s (F, H) or 20 deg/s (G, I). The figure is modified from Herzfeld et al. (2020), with permission.

Concluding thoughts

Even in 1972, Masao Ito understood that his theory of the circuit basis for cerebellar learning was not about the vestibulo-ocular reflex. He knew that the VOR was a model system and that his theory was about the general principles of learning in the cerebellum and elsewhere. We also understand that the main question is not about direction learning in smooth pursuit eye movements, but rather about the general principles of cerebellar learning revealed through study of the easily-controllable system provided by pursuit eye movements. We are gratified that the simple model in Figure 7, when simulated fully, reproduces a large amount of behavioral data on pursuit learning (Herzfeld et al., 2020), and that it has commonalities with models that can explain other simple forms of learning, for example in the vestibulo-ocular reflex, eyelid response conditioning, and the optokinetic response. Our research suggests some general principles that seem to align with the conclusions of others:

• Fast, early, poorly-retained neural and behavioral learning is driven by climbing fiber inputs to the cerebellum and occurs at the parallel fiber to Purkinje cell synapse.

• Neural learning in the cerebellar cortex is transferred to a slow, late, well-retained site in the cerebellar nucleus, guided by the learned responses of Purkinje cells.

• A recurrent circuit from Purkinje cells to the inferior olive limits the magnitude of learning in the cerebellar cortex and forces neural learning to gradually become distributed across the full circuit for a behavior.

• The signals that are subjected to plasticity are different in the cerebellar cortex versus the cerebellar nuclei.

We understand that these principles are based on a fairly rarified behavior and a finite set of experimental observations. But we take pleasure from the fact that they are tightly linked to the original theory of Masao Ito and to the broader view that he espoused, both in his writings and in personal interactions. We recognize the fundamental, seminal contributions of Ito and we honor them, even as we move towards more complex and likely more accurate conclusions about how brain systems work and learn.

• Analysis of smooth pursuit eye movements suggests 4 principles of operation of the cerebellar learning circuit

• Climbing fibers cause fast, early, poorly-retained learning at the parallel fiber to Purkinje cell synapse.

• Learning transfers to a slow, late, well-retained site in the cerebellar nucleus, guided by Purkinje cells.

• A recurrent circuit from Purkinje cells to the inferior olive limits the magnitude of learning in the cerebellar cortex.

• The signals that are subjected to plasticity are different in the cerebellar cortex versus the cerebellar nuclei.