Abstract
Lung cancer is one of the leading causes of cancer-related deaths worldwide and is characterized by hijacking immune system for active growth and aggressive metastasis. Neutrophils, which in their original form should establish immune activities to the tumor as a first line of defense, are undermined by tumor cells to promote tumor invasion in several ways. In this study, we investigate the mutual interactions between the tumor cells and the neutrophils that facilitate tumor invasion by developing a mathematical model that involves taxis-reaction-diffusion equations for the critical components in the interaction. These include the densities of tumor and neutrophils, and the concentrations of signaling molecules and structure such as neutrophil extracellular traps (NETs). We apply the mathematical model to a Boyden invasion assay used in the experiments to demonstrate that the tumor-associated neutrophils can enhance tumor cell invasion by secreting the neutrophil elastase. We show that the model can both reproduce the major experimental observation on NET-mediated cancer invasion and make several important predictions to guide future experiments with the goal of the development of new anti-tumor strategies. Moreover, using this model, we investigate the fundamental mechanism of NET-mediated invasion of cancer cells and the impact of internal and external heterogeneity on the migration patterning of tumour cells and their response to different treatment schedules.
Author summary
When cancer patients are diagnosed with tumours at a primary site, the cancer cells are often found in the blood or already metastasized to the secondary sites in other organs. These metastatic cancer cells are more resistant to major anti-cancer therapies, and lead to the low survival probability. Until recently, the role of neutrophils, specifically tumor-associated neutrophils as a member of complex tumor microenvironment, has been ignored for a long time due to technical difficulties in tumor biology but these neutrophils are emerging as an important player in regulation of tumor invasion and metastasis. The mutual interaction between a tumor and neutrophils from bone marrow or in blood induces the critical transition of the naive form, called the N1 type, to the more aggressive phenotype, called the N2 TANs, which then promotes tumor invasion. In this article, we investigate how stimulated neutrophils with different N1 and N2 landscapes shape the metastatic potential of the lung cancers. Our simulation framework is designed for boyden invasion chamber in experiments and based on a mathematical model that describes how tumor cells interact with neutrophils and N2 TANs can promote tumor cell invasion. We demonstrate that the efficacy of anti-tumor (anti-invasion) drugs depend on this critical communication and N1→N2 landscapes of stimulated neutrophils.
Introduction
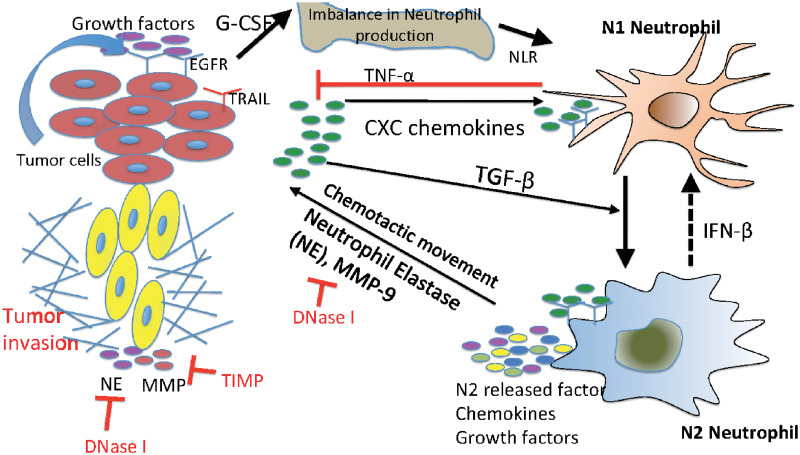
Lung cancer is still the leading cause of cancer-associated deaths worldwide, with 1.8 million deaths in 2018 [1, 2]. Various cell types such as immune cells, fibroblasts, and endothelial cells in a tumor microenvironment (TME) interact with tumor cells via the cytokines and growth factors. Tumor-associated neutrophils (TANs) are of particular interest because experimental studies showed that they can contribute to the tumor growth, critical invasion, epithelial-mesenchymal transition (EMT), and metastasis of cancer cells [3, 4]. Until recently, neutrophils have been considered as merely a bystander in the TME and metastasis [5–7] but they are emerging as an important player due to consistent and continuous evidences of their tumor-promoting roles [3]. It was shown that cancer cells can secrete CXC chemokines, one of four main subfamilies of chemokines, attracting neutrophils to tumor microenvironment [8] and neutrophil invasion is highly correlated with poor clinical outcomes [9, 10]. While the classical form of neutrophils, called N1 TANs, can effectively eliminate tumor cells via lysis [11–13], TNF-α [14], or inducing tumor cell apoptosis [15], another form, called N2 TANs, can support tumor growth, invasion, metastasis [16–20] and ultimately, poor clinical outcomes in many cancers [21]. Metastatic cancer cells were also able to induce neutrophils to form metastasis-promoting NETs without involving infection processes [22].
While the tumor-secreted transforming growth factor (TGF-β) was shown to transform N1 TANs (tumor-suppressive phenotype) to N2 TANs (tumor-promoting phenotype) [23–25], the N2→N1 transition can be mediated by type I IFN [14, 23, 26, 27] (Fig 1). Neutrophil elastase (NE or ELANE) as well as matrix metallopeptidase (MMP) was shown to infiltrate the TME [28] and promote tumor growth and invasion of cancer cells through the PIK3 signaling pathways [8, 29, 30]. More importantly, it was shown that neutrophils can promote the tumor cell invasion in the transwell assay [22, 31] and in vivo experiments [22, 32].
Fig 1. Interaction of the TGF-β, IFN-β, and NE-pathways in the control of tumor cell invasion.
In homeostasis of normal tissue, these pathways are balanced so as to control growth, but in lung cancer, increased secretion of TGF-β by tumor cells induces the N1→N2 transition of the neutrophils and stimulates their secretion of NE and other growth factors. This disrupts the homeostasis and stimulates aggressive tumor invasion.
Mathematical models of tumor microenvironment and tumor-immune system interactions have been developed: fibroblasts-tumor [33–35], macrophages-tumor [36, 37], astrocytes-tumor [38], NK cells-tumor [39–41], neutrophil-tumor [42, 43], tumor-endothelial [44], and immune-tumor [45, 46] interactions. However, the detailed mechanism of tumor invasion and metastasis via communication with TANs is still poorly understood. It would be difficult to build a comprehensive mathematical model of the tumor invasion and metastasis that incorporates all the biochemical and mechanical processes (S1 Text). As a beginning step, we focus on the neutrophil-mediated invasion of tumor cells, for which there are experimental data. Here, we develop a mathematical model based on taxis-reaction-diffusion equations that govern cell-cell signaling and chemotactic cell movement. Our goal is to understand the biochemical factors that are important in regulating the chemotactic movement of tumor cells from the upper chamber to the lower well of the Boyden chamber assay shown in Fig 2. We show that the mathematical model can replicate the major components of experimental findings and we test several anti-invasion intervention strategies with predictions.
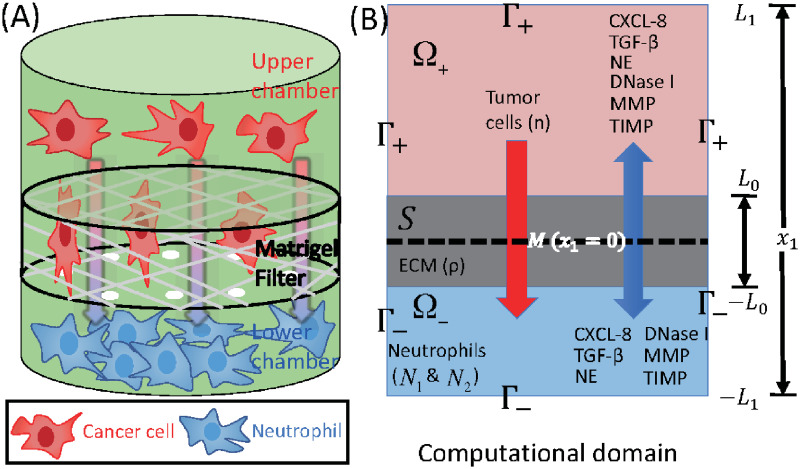
Fig 2. Schematics of an invasion assay system.
(A) Boyden transwell invasion assay. Tumor cells were suspended in the upper chamber, while neutrophils or medium alone (control) were placed in the lower chamber. Semipermeable inserts coated with matrigel (extracellular matrix) were inserted in the filter. In response to NE secreted by N2 neutrophils in the lower chamber, tumor cells degrade the heavy extracellular matrix proteolytically and invade the lower chamber. The number of neutrophils on the lower surface of the permeable insert was counted after 22h in the absence and presence of neutrophils in the lower chamber. (B) TGF-β (G), NE (E), NE inhibitor (D), CXCL8 (C), MMP (P), TIMP (M) and tumor cells (n) can cross the semi-permeable membrane, but neither type of neutrophils (N1, N2) can cross it. Initially, the tumor cells reside in the upper chamber (domain Ω+) while neutrophils are placed in the lower chamber (domain Ω−). An extracellular matrix (ECM) layer (S) surrounds the filter, semi-permeable membrane ().
Materials and methods
We developed a mathematical model of tumor cell invasion in in vitro experiments, a critical step in metastasis [22, 47, 48], based on mutual interactions between tumor cells and neutrophils (Fig 1).
We denote by Ω the 3-dimensional domain
and set
The semi-permeable membrane occupies the planar region
and the ECM occupies a 3-dimensional region
where 0 < L0 < L1. We denote by IA the characteristic function of a set A:
The geometry of the experimental setup of the Boyden invasion chamber is shown in Fig 2A. In the typical transwell migration assay, neutrophils isolated from the bone marrow are plated in the lower chamber, and tumor cells are added on top of Matrigel-coated insert in the upper chamber [22]. In our model, we assume that tumor cells are initially placed on the top of gel-coated area above the membrane with mini-pores in the middle, and invade the lower chamber where neutrophils (or conventional medium for control) reside. The corresponding computational domain is shown in Fig 2B.
We introduce the following variables at space x and time t:
n(x, t) = density of tumor cells,
N1(x, t) = density of N1 neutrophils,
N2(x, t) = density of N2 neutrophils,
ρ(x, t) = concentration of tumor extracellular matrix (ECM),
C(x, t) = concentration of CXCL-8,
G(x, t) = concentration of TGF-β,
E(x, t) = concentration of NET/NE,
D(x, t) = concentration of NET/NE inhibitor,
P(x, t) = concentration of MMPs,
M(x, t) = concentration of MMP inhibitor (TIMP).
The evolution equations for these variables are developed in next sections, but in this work we focus on the Boyden invasion chamber, transwell assay, in one space dimension.
Tumor cell density (= n(x, t))
The mass balance equation for the tumor cell density n(x, t) is
| (1) |
where Jn is the flux and Pn is the net production rate of cancer cells. The flux Jn is comprised of three components, Jrandom, Jchemo, and Jhapto, which are the fluxes due to random motion, chemotaxis, and haptotaxis, respectively [34, 49].
We assume that the tumor extracellular matrix is homogeneous and isotropic in tumor microenvironment, and that the flux due to the random motility is given by
| (2) |
where Dn is the random motility constant of tumor cells.
In lung tissue, tumor cells are strongly attracted to chemotactic attractants [32] such as NE and neutrophils [22, 32] and migrate toward the up-gradient (∇E) of the chemo-attractant, NE, through the process called ‘chemotaxis’ [50]. The chemotactic flux is assumed to be of the form
| (3) |
where χE is the chemotactic sensitivity, δE, σE are scaling parameters, and E is the concentration of NE, whose dynamics will be introduced in Section below. This form reduces to the standard form of the chemotactic flux (Jchemo ≈ C n ∇E; C = constant) under small NE gradients (|∇E| ≪ 1) and saturates (Jchemo ≈ (χE/δE) n u; u = ∇E/|∇E| is the unit vector) under large NE gradients, preventing the blow-up behaviors of solutions [34]. Other forms such as [51] or (C: constant) [52] have been adapted in the literature.
Tumor cell invasiveness is enhanced by proteolytic degradation of the extracellular matrix via MMPs [4, 25, 53] and NEs [29, 54] that are produced by neutrophils. This results in local degradation of tumor ECM [49] and tumor cell movement in the direction of the up-gradient (∇ρ) of ECM via a cellular process called haptotaxis. This process is valid only in the ECM domain S, therefore, we include the characteristic function IS, providing the on-off switch on the ECM membrane. We represent the haptotactic flux in a similar fashion:
| (4) |
where χρ is the haptotactic sensitivity, δρ, σρ are scaling parameters, and ρ is the concentration of tumor ECM, whose dynamics will be introduced in Section below.
The net production of tumor cells is due to active NE-stimulated growth [8, 22] and cell killing by N1 TANs [3, 21, 23], which we represent as follows:
| (5) |
Here r is the proliferation rate of tumor cells in the absence of NE (E), rE is the dimensionless parameter of NE-mediated tumor growth, kE and m are Hill-function coefficients for activation of proliferation in the presence of NE, n0 is the carrying capacity of the tumor in a given TME, and, finally μn is the killing rate of tumor cells by N1 neutrophils (N1) whose dynamics will be described in Section ‘Densities of neutrophils’ below. Here, , .
Combining the several fluxes in Eqs (2)–(4) and growth term in Eq (5) leads to the governing equation for the tumor cell density
| (6) |
Densities of neutrophils: N1 (= N1(x, t)) & N2 (= N2(x, t)) types
We use a similar form of reaction-diffusion-advection equations for the evolution of the densities of neutrophils, based on mass balance as in the previous section. We assume that (i) Neutrophils are chemotactic to the CXCL secreted by tumor cells [55–57], and the chemotactic flux is of the nonlinear form (3), but with different chemotactic sensitivities (χ1, χ2). Since the N2 TANs produce NE and MMPs, the movement of activated neutrophils further enhances tumor invasiveness and growth via the NE-PI3K pathway described earlier. (ii) The anti-tumorigenic (N1) neutrophils transform into the active N2 type at the rate λ12 in the presence of TGF-β, based on experimental evidences [3, 21, 43]. For instance, the N1→N2 transition of TANs with protumour properties was typically observed in a TGF-β-rich tumor microenvironment and the presence of IFN-β or TGF-β inhibitor can mediate the reverse transition (N2→N1) with anti-tumoral properties [3]. Therefore, TGF-β pathway inhibitors are under clinical trials since they were shown to promote the development of N1 TANs [58, 59]. (iii) N1 and N2 phenotypes proliferate at a rate, λ1 and λ2(G), respectively. Then, we have the following evolution equations:
| (7) |
| (8) |
Tumor ECM density (= ρ(x, t))
The tumor ECM provides structural foundation for efficient cell migration [60], but it also needs to be remodeled via proteolysis for tumor cell migration by microenvironmental proteases [55, 61–63]. In this work, we assume that the tumor ECM is degraded by the TAN-secreted NEs [64] and TAN-secreted MMPs [4, 25, 53, 55] as in the invasion experiments [22]. The rate of ECM change can be represented as
| (9) |
Here μρ1, μρ2 are the degradation rates by NEs and MMPs, respectively, which are secreted by N2 neutrophils. Essentially, this equation represents proteolytic degradation of tumor ECM coated on the filter when there is a significant level of tumor ECM present, as is normally the case in a TME.
CXCL8 concentration (= C(x, t))
Tumor cells secrete CXCL in order to recruit the immune cells such as neutrophils [55–57]. CXCLs and corresponding receptors (CXCR) such as CXCL5 and CXCR6 are important prognostic factors, alone or in a combination with the TANs, for shorter overall survival and cumulative risk of recurrence [3, 65, 66]. Thus the governing equation for CXCL8 is
| (10) |
where DC is the diffusion coefficient of CXCL, λC is the secretion rate of CXCL by tumor cells and μC is the decay rate of CXCL.
TGF-β concentration (= G(x, t))
TGF-β is a polypeptide that plays a major role in regulation of many human diseases including cancers [67] due to its capacity of maintaining tissue homeostasis and involving in most of the chronic inflammatory and wounding processes by activating its inactive form in ECM [68]. Tumor cells are the primary source of TGF-β in TME [3, 69]. TGF-β activates proinflammatory and antitumorigenic N1 neutrophils into the aggressive N2 type, which in turn stimulates tumor cell invasion [55, 70]. Thus the governing equation for TGF-β is as follows:
| (11) |
where DG is the diffusion coefficient of TGF-β, λG is the secretion rate of TGF-β by tumor cells, and μG is the decay rate of TGF-β.
Concentrations of NET/NE (= E(x, t)) and its inhibitors (= D(x, t))
NET and NE are highly associated with aggressive invasion, growth, EMT, and metastasis of cancer cells [4, 54, 71]. NE is produced by neutrophils [4, 64, 72] and used for degradation of extracellular matrix and tissue destruction [8, 54, 73]. It was also shown that NE inhibitors such as DNase I block this effect in growth models [8] and invasion assays [22]. In our framework, NET and the associated NEs are merged into one component. Thus, the governing equations for NET/NE and its inhibitors are
| (12) |
| (13) |
where DE, DD are diffusion coefficients of NET/NE and its inhibitors, respectively, λE is the production rate of NET/NE from N2 neutrophils, λD is the injection rate of NET/NE inhibitors at a subdomain ΩI, μE, μD are natural decay rates of NET/NE and its inhibitors, respectively, μED is the consumption rate of NE in response to NE inhibitors with kinetic parameters KD, l (, ).
MMP concentration (= P(x, t))
Matrix metalloproteinases (MMPs) are highly associated with cancer cell invasion and metastasis [48, 74]. Neutrophils, not tumor cells [55, 75], were suggested to the primary source of MMPs [4, 25, 53, 55] including MMP-9 [53] in lung cancer development, showing strikingly predominant presence at the invasive fronts of metastatic cancers [53]. Thus the governing equation for MMPs is
| (14) |
where DP is the diffusion coefficient of MMPs, λP is the MMP production rate by N2 neutrophils, μPM is the degradation of MMPs by its inhibitor, TIMP, with Hill-coefficients KM, m (), μP is the decay rate of MMPs. In general, DP is very small (DP ≪ 1) while the half-life of MMPs is short (μP ≫ 1) [76], leading localized activities at the moving front of invasive cells.
TIMP concentration (= M(x, t))
Tissue inhibitors of metalloproteinases (TIMPs) play an important role in inhibiting tumor invasion and metastasis [77] by regulating major signaling pathways in pericellular proteolysis of various extracellular matrix and cell surface proteins [78]. In the model, TIMPs are injected for inhibition of the proteolytic activities of cancer cell invasion. Note, however, that this action can partially block cancer cell invasion since cancer cells can still execute the NE-mediated invasion. Thus, the governing equation of TIMP is
| (15) |
where DM is the diffusion coefficient, λM is the TIMP supply rate, and μM is the decay rate of TIMP.
Boundary conditions and initial conditions
In the following simulations we prescribe Neumann boundary conditions on the exterior boundary Γ1 (= ∂Ω; see Fig 2B) as follows:
| (16) |
where ν is the unit outer normal vector. The membrane is permeable to all variables (n, N1, N2, C, G, E, D, P, M), but not freely so. We describe the flux at the membrane boundary Γ2 (= ; see Fig 2B) for these variables u = (n, N1, N2, C, G, E, D, P, M) as
| (17) |
where
| (18) |
Here, the parameters γi (γi > 0, i = 1, ⋯, 9) represent the permeability of cells (i = 1, 2, 3) and molecules (i = 4, ⋯, 9). The permeability (γi) is determined by the density and size of the holes on the semi-permeable membrane between upper and lower chambers as well as the size of the moving object relative to the hole size. The holes in the insert are uniformly distributed on the membrane of the Boyden invasion transwell assay [22, 31]. See [79] for the derivation of these Robin-type boundary conditions by the homogenization method. If the size of the circular holes in the membrane is increased (or decreased), the membrane becomes more (or less) permeable, and γi increases (or decreases) [33, 34]. For instance, the diameter of typical cells is in the range of 10-20 μm while the size of growth factors and cytokines such as TGF-β is much smaller [80]. Furthermore, the diffusion coefficient of cells is usually much smaller than that of growth factors and cytokines [81]. While, the typical diffusion coefficient of molecules (CXCL8, EGF, and TGF-β) is in the range of (1.0-2.5) × 10−6 cm2/s [57, 82–86], the random motility coefficient of cells is much smaller ((1.0-10.0) × 10−10 cm2/s). Therefore, the parameter (γi = γc (i = 1, 2, 3)) of the migratory cells is smaller than the permeability parameter (γi = γ (i = 4, ⋯, 9)) of the diffusible molecules due to different physical sizes. In a classical Boyden invasion chamber, a typical, invasive tumor cell in the upper chamber is not able to invade the lower chamber if the diameter of the permeable holes on the membrane is less than 0.4 μm while molecules can diffuse throughout the domain [33]. So, we take the smaller permeability parameter for cells (γc < γ).
Finally, we prescribe initial conditions,
| (19) |
Parameters are given in Tables 1 and 2. Nondimensionalization and parameter estimation of the system (6)–(19) are given in S2 and S3 Text, respectively. This non-dimensional form of governing equations was used for the simulations. Hereafter, the computational domain is restricted to one space dimension, and the computational domain is scaled to unit length.
Table 1. Parameters used in the tumor model.
| Description | Dimensional Value | Refs. | |
|---|---|---|---|
| Diffusion coefficients (cm2 s−1) | |||
| Dn | Tumor cells | 2.5 × 10−8 | [33, 37, 129–131] |
| D1 | N1 Neutrophil | 1.1 × 10−8 | [83] |
| D2 | N2 Neutrophil | 1.1 × 10−8 | [83] |
| DC | CXCL8 (IL-8) chemokines | 2.5 × 10−6 | [57, 82, 83] |
| DG | TGF-β | 1.0 × 10−6 | [84–86] |
| DE | NET/NE | 5.0 × 10−7 | [132–137] |
| DP | MMP | 5.0 × 10−10 | [37, 138, 139] |
| DD | DNase I (NET/NE inhibitor) | 7.374 × 10−6 | [140], estimated |
| DM | TIMP (MMP inhibitor) | 8.33 × 10−7 | estimated |
| DA | TGF-β Anti-body | 8.33 × 10−7 | estimated |
| Production rates | |||
| r | Proliferation rate of tumor cells | 3.3 × 10−4 s−1 | [22, 33], estimated |
| rE | NE-mediated proliferation rate of tumor cells | 7.0 × 10−2 | estimated |
| kE | Hill type coefficient of tumor cell proliferation | 2.15 × 10−9 gcm−3 | [33], estimated |
| m | Hill coefficient of NE-mediated tumor proliferation | 2 | estimated |
| n0 | Tumor cell carrying capacity | 2.5 × 104 cells/cm3 | [33], estimated |
| λ1 | Proliferation rate of N1 neutrophil | 4.38 × 10−6 s−1 | [33, 141], estimated |
| λ12 | Transformation rate from N1 to N2 neutrophils | 4.08 × 103 cm3 g−1 s−1 | [33], estimated |
| λ2 | Proliferation rate of N2 neutrophils | 2.65 × 10−5 s−1 | [33, 141], estimated |
| λC | Production rate of CXC from tumor cells | 4.44 × 10−11 s−1 | [33, 142, 143], estimated |
| λG | Production rate of TGF-β from tumor cells | 4.89 × 10−7 s−1 | [33, 142, 143] |
| λE | Production rate of NET/NEs from Neutrophils | 2.26 × 10−7 s−1 | [144] |
| λP | Production rate of MMPs from Neutrophils | 2.22 × 10−8 s−1 | [144] |
| λD | Production rate of NET/NE inhibitor | 9.0 × 10−13 gcm−3 s−1 | estimated |
| λM | Production rate of TIMP | 1.29 × 10−11 gcm−3 s−1 | estimated |
| λA | Production rate of TGF-β anti-body | 4.78 × 10−5 μMs−1 | estimated |
| Degradation/Decay rates | |||
| μn | tumor cells degradation rate by N1 | 2.78 × 10−1 cm3 g−1 s−1 | estimated |
| μρ1 | ECM degradation rate by NEs | 1.02 × 104 cm3 g−1 s−1 | estimated |
| μρ2 | ECM degradation rate by MMPs | 3.19 × 105 cm3 g−1 s−1 | estimated |
| μC | decay rate of CXCL8 | 6.42 × 10−5 s−1 | [145–147] |
| μG | decay rate of TGF-β | 8.02 × 10−6 s−1 | [33], estimated |
| μE | decay rate of neutrophil elastase | 8.02 × 10−6 s−1 | [148] |
| μP | decay rate of MMP | 5.0 × 10−5 s−1 | [49] |
| μD | decay rate of NE inhibitor | 9.627 × 10−5 s−1 | [149–153] |
| μM | decay rate of TIMP | 4.56 × 10−6 s−1 | [154] |
| μED | degradation rate of NET/NE by its inhibitor | (2.8 × 10−4—2.8 × 10−2) s−1 | estimated |
| μA | decay rate of TGF-β anti-body | 6.42 × 10−5 s−1 | [43, 155] |
| μAG | decay rate of TGF-β by anti-body | 4.8 × 10−3 μM−1 s−1 | [43], estimated |
| KD | Hill coefficient of NET/NE degradation by its inhibitor | 3.2 × 10−9 g/cm3 | [156], estimated |
| l | Hill coefficient of NET/NE degradation by its inhibitor | 2 | [156], estimated |
| μPM | degradation rate of MMPs by TIMP | (2.8 × 10−5—2.8 × 10−4) s−1 | estimated |
Table 2. Parameters used in the tumor model.
Continued from Table 1.: Dimensionless values were marked in *.
| Description | Dimensional Value | Refs. | |
|---|---|---|---|
| Degradation/Decay rates | |||
| KM | Hill coefficient of MMP degradation by TIMP | 4.64 × 10−8 g/cm3 | [156], estimated |
| m | Hill coefficient of MMP degradation by TIMP | 2 | estimated |
| Movement parameters (chemotaxis, haptotaxis) | |||
| χE | Chemotactic sensitivity to NE | 1.117 × 10−9 cm.s−1 | [22, 33, 130, 157] |
| δE | Scaling parameter of NE gradient (|E|) | 6.46 × 10−8 g/cm4 | estimated |
| σE | Scaling parameter of NE gradient (|E|) | 1.0 | estimated |
| χρ | Haptotactic sensitivity | 3.5 × 10−10 cm.s−1 | [22, 158–160], estimated |
| δρ | Scaling parameter of ECM gradient (|ρ|) | 5.0 × 10−3 g/cm4 | estimated |
| σρ | Scaling parameter of ECM gradient (|ρ|) | 1.0 | estimated |
| Chemotactic sensitivity of N1 neutrophils to CXCL8 | 1.1 × 10−9 cm.s−1 | [22, 33, 161], estimated | |
| δ1 | Scaling parameter of CXCL gradient (|C|) | 1.0 × 10−11 g/cm4 | estimated |
| Chemotactic sensitivity of N2 neutrophils to CXCL8 | 1.1 × 10−9 cm.s−1 | [22, 33, 161], estimated | |
| δ2 | Scaling parameter of CXCL gradient (|C|) | 1.0 × 10−11 g/cm4 | estimated |
| σC | Scaling parameter of CXCL8 gradient (|C|) | 1.0* | estimated |
| Membrane parameters | |||
| γc | permeability of cells (Tumor cells, N1 neutrophils, N2 neutrophils) | 0.01-785 (78.5)* | estimated |
| γ | permeability of chemicals (CXCL8, TGF-β, NET/NE, NE inhibitor, MMP, TIMP) | 0.1-7850 (785)* | [33], estimated |
| μ | ECM width | 0.6* | estimated |
All the simulations were performed using a finite volume method (FVM; clawpack (http://www.amath.washington.edu/~claw/)) with fractional step method [87]. A nonlinear solver nksol was used for solving algebraic systems. The Eqs (6)–(19) were solved on a regular uniform grid with grid size 0.01 (hx = 0.01). An initial time step of 0.0001 (or smaller) was used, but adaptive time stepping scheme based on the number of iterations can increase or decrease this step size.
Results
In this section, we investigate the role of NEs in regulation of cancer cell invasion, compare the predictions of our mathematical model with experimental data, and then suggest new therapeutic strategies for blocking invasive tumor cells.
Predictions of the mathematical model
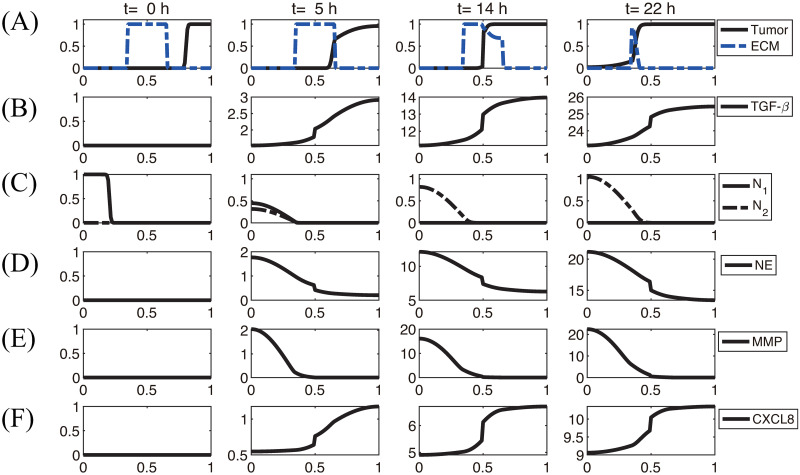
Fig 3 shows the density profiles of all variables (n, N1, N2, ρ, C, G, E, P) at t = 0, 5, 14, 22h in the absence of DNase I and TIMP when neutrophils were added in the lower chamber. In each subframe, the right (or left) half of the computational domain represents the upper (or lower) chamber in the Boyden invasion assay (Fig 2A). By degradation of the tumor ECM on the membrane of the insert, tumor cells in the upper chamber were experimentally shown to have capacity of invading the lower chamber upon stimulus of N1/N2 neutrophils in the lower chamber [22, 31]. Tumor cells in the upper chamber secrete CXCL8 (Fig 3F), which then diffuses and attracts neutrophils in the lower chamber by chemotaxis. On the other hand, tumor cells produce TGF-β (Fig 3B), which diffuses and enhances the N1 → N2 transformation of neutrophils (Fig 3C) in the lower chamber. These activated N2 TANs in the lower chamber then secrete NET/NEs (Fig 3D) and MMPs (Fig 3E) to stimulate chemotactic and haptotactic movement of tumor cells in the upper chamber. Tumor cells break down the ECM component by proteolytic activities with the NE and MMP near the membrane and invade the left chamber (Fig 3A). As they invade, they can sense higher levels of NE, and proliferate at a higher rate (see Eq (6)).
Fig 3. Dynamics of the system.
The time evolution of the density of each variable. (A) tumor cells and ECM (B) TGF-β (C) N1/N2 neutrophils (D) neutrophil elastase (E) MMP (F) CXCL8. Here, ECM = [0.35, 0.65]⊂ Ω = [0, 1]. Note that the initial concentrations of CXCL8, TGF-β, neutrophil elastase and MMPs are uniformly zero, as in experiments. *x-axis = space (the dimensionless length across the invasion chamber), y-axis = the dimensionless density/concentration of the variables.
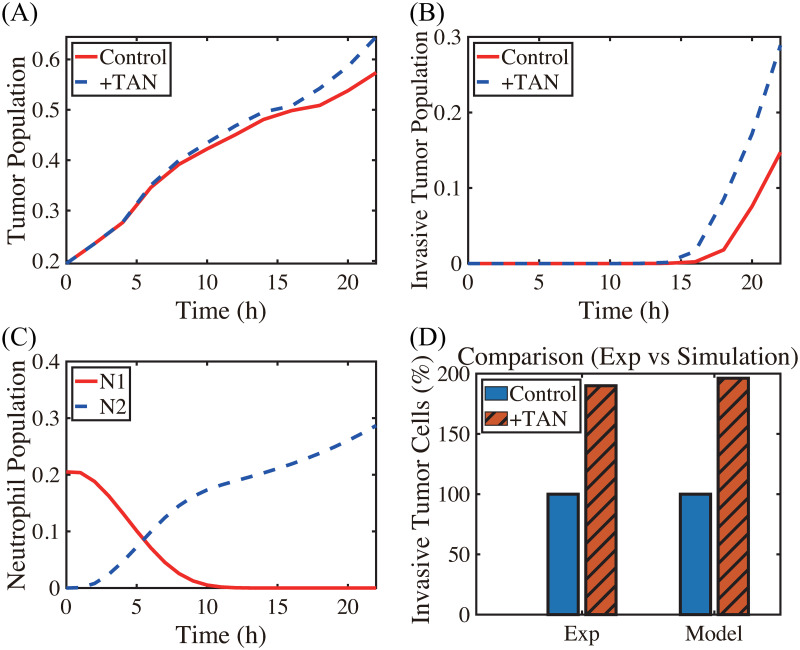
A comparison of computational results from the mathematical model with experimental data [22] is shown in Figs 4 and 5. Hereafter, in order to calculate the population of cells (tumor cells, N1 TANs, N2 TANs) and level of chemical variables (CXCL-8, TGF-β, NET/NE, DNase, MMPs) at various times in the mathematical model, we integrate the density and concentration over the space: density of tumor cells (), N1 TANs (), N2 TANs (), and concentrations of ECM (), CXCL-8 (), TGF-β (), NET/NE (), DNase I (), and MMPs (). In the experiments, Park et al. [22] found that the presence of neutrophils in the lower chamber could enhance tumor cell invasion through NET formation and NE activities, and the DNase treatment abrogated the invasion-promoting effect of neutrophils in the lower chamber. Fig 4A–4C shows time courses of the tumor population, population of invasive tumor cells, and neutrophil population (N1 (red solid), N2 (blue dashed) TANs), respectively, in the absence (control) and presence (+TAN) of neutrophils. In the presence of neutrophils, both total (Fig 4A) and invasive (Fig 4B) tumor cell populations are increased relative to the control case due to neutrophil transition (Fig 4C) and NE activities (Fig 3D) in the system. After 22h the number of 4T1 tumor cells invading the lower chamber almost doubled (∼190%) in the co-culture with neutrophils (red bar (+TAN); left panel in Fig 4D) in the lower chamber as compared to the control (blue bar; left panel in Fig 4D) in experiments [22]. In the model simulations, the number of invading tumor cells increased (∼2-fold) in the presence of neutrophils in the lower chamber (red bar (+TAN); right panel in Fig 4D) relative to the control (absence of neutrophil (blue bar); right panel in Fig 4D). As Park et al. [22] note, several tumor cell lines (4T1, BT-549) invade the lower chamber even in the absence of neutrophils in the lower well, which indicates the intrinsic invasiveness of tumor cells.
Fig 4. TAN-promoted cancer cell invasion (Experiment [22] & simulation).
(A-B) Time courses of populations of total tumor cells (A) and invasive tumor cells (B). (C) Time courses of N1 (red solid) and N2 (blue dashed) neutrophils. (D) Experimental data from the invasion assay in [22] (left column; 4T1 cancer cells) and computational results from mathematical model (right column). The graph shows the (scaled) populations of invasive tumor cells at t = 22 h in the absence (control) or presence (+TAN) of neutrophils. Here and hereafter cell populations are derived from the continuum density.
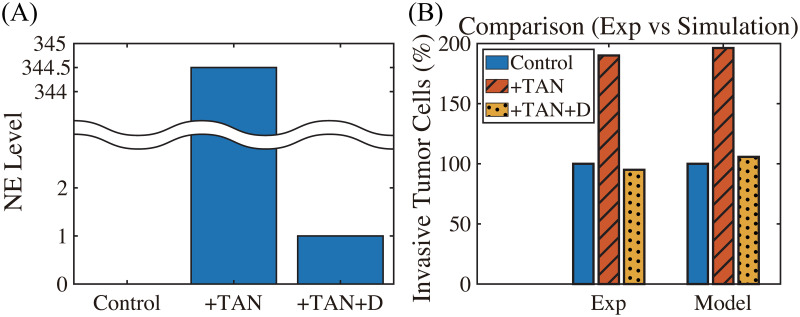
Fig 5. DNase I treatment against NE can abrogate the invasion-boosting effects of neutrophils (Experimental data [22] and simulation results).
(A) NE levels in the system in the absence (control) and presence (+TAN) of neutrophils, and DNase treatment (+TAN+D) cases at t = 22 h. (B) Experimental data from the invasion assay in [22] (left column; 4T1 cancer cells) and computational results from mathematical model (right column). The graph shows the (scaled; %) population of invasive tumor cells at t = 22 h in the absence (control; blue) and presence (+TAN; red shaded) of neutrophils, and DNase treatment (+TAN+D; yellow dotted) cases. Addition of DNase I reduces the number of invading tumor cells by almost 50%.
In Fig 5, we investigate the effect of DNase I against NET/NE on tumor invasion. Our mathematical model predicts that injection of DNase I in the lower chamber of the transwell can inhibit NET/NE activities (Fig 5A) and reduce the TAN-induced invasiveness of tumor cells (right panel in Fig 5B). Park et al. [22] showed that NE inhibition or digestion of the DNA of the NETs by DNase I can effectively abrogated the invasion-promoting effect of TANs in the lower chamber, i.e., the number of invasive 4T1 tumor cells was reduced in the presence of the neutralizing DNase I (+TAN+D) when compared to the TAN case in the absence of the DNase I (+TAN) (left panel in Fig 5B). Thus, simulations are in good agreement with experimental data [22]. By definition, NETs are associated with neutrophil proteases with the extracellular histone-bound DNA [88]. In the experiments [22], pro-invasive effects of NETs were shown to be associated with protease activities of NET-associated protease, NE. Park et al. [22] found that the NE inhibitor reduced the extension of cancer cell-induced NETs and inhibit TAN’s ability to promote the invasion of 4T1 and BT-549 breast cancer cells. They also found that DNase I treatment can also prevent lung metastasis in mice. However, it is worth observing that this DNase I is not enough to completely inhibit the aggressive migration of tumor cells from the upper chamber to the lower chamber, since they are able to invade in the absence of neutrophils.
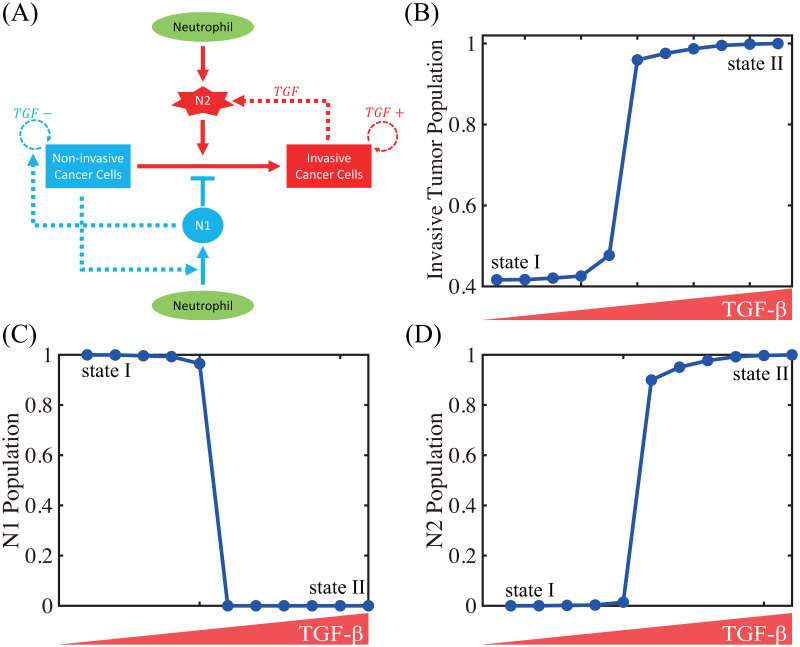
In Fig 6, we illustrate the TGF-β-mediated transition between N1 and N2 neutrophils, thus giving rise to two phenotypic states: (a) state I, dominated by non-invasive cancer cells, and (b) state II, dominated by invasive cancer cells. A conceptual schematic of cancer-immune interplay is shown in Fig 6A. Fig 6B–6D shows the scaled populations of invasive cancer cells and, N1 and N2 neutrophils for various levels of TGF-β (0, 0.0001, 0.001, 0.002, 0.01, 5, 10, 20, 50, 100, 200). When the TGF-β level is low, N1 neutrophils dominate the tumor microenvironment (Fig 6C and 6D), leading to non-invasive states of cancer cells (State I, Fig 6B). As the TGF-β level is increased, the N1-dominant system transits to the N2-dominant state (Fig 6C and 6D), resulting in the invasive state of cancer cells (State II, Fig 6B). These results illustrate that the positive feedback loop between N2 neutrophils and invasive phenotype via up-regulation of TGF-β, chemotaxis through CXCL8 and NET activities essentially determines the phenotypic transition between non-invasive and invasive states.
Fig 6. TGF-β-mediated cancer-TAN interplay can induce two types of phenotypic states: invasive and non-invasive types.
(A) Conceptual interaction network for the mathematical model. (B) Population of invasive tumor cells in the lower chamber as a function of TGF-β. (C,D) Populations of N1 (C) and N2 (D) neutrophils as a function of TGF-β.
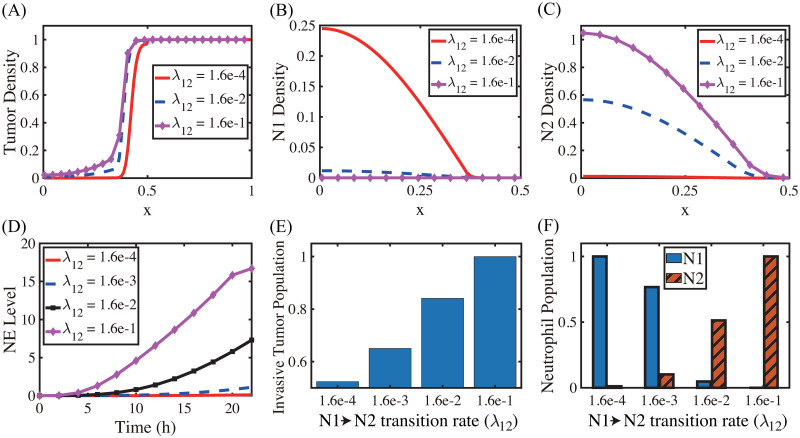
The N1→N2 transition of TANs was shown to play a critical role in promoting tumor growth, angiogenesis, invasion [3, 24, 25, 89], and ultimately metastasis initiation [90, 91]. Fig 7A shows the spatial profiles of the tumor cells for various N1→N2 transition rates (λ12 = 1.6 × 10−4 (red solid), 1.6 × 10−2 (blue dashed), 1.6 × 10−1 (pink with marks)) at the final time (t = 22 h). The N1- and N2-dominant spatial profiles of neutrophils in the lower chamber for the corresponding parameter set are shown in Fig 7B and 7C, respectively. If we increase the rate λ12 (differentiation degree of anti-tumorigenic TANs to tumor-promoting TANs), the N2 population dominates the lower chamber (Fig 7B and 7C) with the higher population ratio N2:N1 of TANs (Fig 7F). Fig 7D shows time courses of NE levels for various values of the differentiation rate (λ12 = 1.6 × 10−4, 1.6 × 10−3, 1.6 × 10−2, 1.6 × 10−1). The corresponding populations of invasive tumor cells and neutrophils (N1,N2) at final time (t = 22 h) are shown in Fig 7E and 7F, respectively. For a larger λ12, more aggressive, tumor-promoting N2 TANs in the lower chamber can interact with tumor cells in the upper chamber (Fig 7A) by secreting more NE (Fig 7D). This leads to an increased tumor population and enhanced tumor cell invasion (Fig 7E). This increased invasiveness of the tumor cells is the result of the mutual interactions between tumor cells in the upper well and the neutrophils in the lower well. For instance, the NET/NE level increases as λ12 increases (Fig 7D). For a large λ12, the most of N1 TANs are converted into the N2 phenotype (4th column (λ12 = 1.6 × 10−1) in Fig 7F), leading to efficient tumor cell migration (Fig 7E). However, when this transition rate is small (λ12 = 1.6 × 10−4), the less effective N1 TANs persist in the lower chamber (Fig 7B) with less population of the N2 phenotype (Fig 7C). This results in the slower (or close to zero) production of NE (Fig 7D) by TANs, and lower secretion of both TGF-β and MMP by tumor cells, which in turn reduces invasiveness of tumor cells by more than 48% (Fig 7E).
Fig 7. Effect of the N1→N2 transformation on tumor invasion and N1/N2 dynamics.
(A) Tumor density profiles on Ω = [0, 1] at the final time (t = 22 h) for various λ12’s (λ12 = 1.6 × 10−4, 1.6 × 10−2, 1.6 × 10−1). (B,C) Density profiles of the N1 and N2 TANs in the lower chamber ([0, 0.5]) for the corresponding λ12’s in (A). (D) Time courses of NE levels for various values of the differentiation rate (λ12 = 1.6 × 10−4, 1.6 × 10−3, 1.6 × 10−2, 1.6 × 10−1). (E,F) Scaled population of invasive tumor cells and neutrophils (N1 and N2) at the final time (t = 22 h) for various λ12’s in (D).
Application of the model
Blocking TGF-β and its receptors was shown to inhibit tumor growth [92, 93] and critical cell invasion [34, 94, 95], decrease tumourigenic potential [92, 96], and reduce metastatic incidence [97] through many different pathways [67, 98]. In order to investigate the effect of TGF-β suppression on tumor cell invasion, we introduce a new variable A(x, t) for the TGF-β anti-body and derive the following equations including the modified equation of TGF-β from Eq (11)
| (20) |
| (21) |
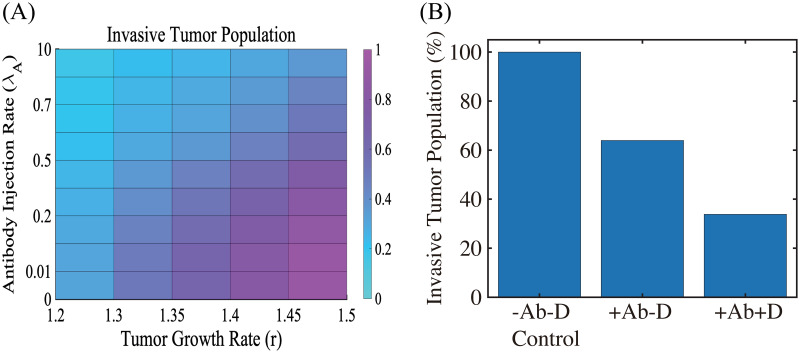
where μAG is the consumption rate of TGF-β due to antibody reaction, DA is the diffusion coefficient of the antibody, λA is the injection rate of the antibody, and, finally, μA is the natural decay rate of the antibody. Fig 8A shows the (scaled) population of invasive tumor cells for various growth rates (r = 1.2, 1.3, 1.35, 1.4, 1.45, 1.5) and injection rates (λA = 0, 1.0 × 10−2, 1.0 × 10−1, 2.0 × 10−1, 3.0 × 10−1, 5.0 × 10−1, 6.0 × 10−1, 7.0 × 10−1, 1.0, 1.0 × 101) of the TGF-β antibody. For a fixed growth rate of tumor cells, the TGF-β inhibitor treatment can effectively reduce the invasiveness of tumor cells. For example, the invasive tumor population with a high dose of antibody (λA = 10) is reduced by 62% compared to the case without the antibody (λA = 0) when r = 1.5. However, the increasing growth rate can abrogate this antibody-induced reduction in tumor cell invasion for a fixed λA (r = 1.2 → 1.3 → ⋯ → 1.5). DNase treatment, the NE inhibitor, was shown to reduce the NE-mediated invasion of tumor cells (4T1 and BT-549) experimentally [22] and theoretically (Fig 5). Thus, another effective therapeutic approach to slowing tumor invasion is to apply DNase I for a combination therapy (TGF-β inhibitor +DNase I) given its pivotal roles in tumorigenesis [4, 8, 22]. We test the efficacy of the combination therapy in Fig 8B. The invasive tumor population is reduced by 36% in response to a high dose of the TGF-β inhibitor (λA = 10; +Ab-D in Fig 8B) compared to control (-Ab-D in Fig 8B). Our simulation shows that blocking NE-mediated proteolytic activity of tumor cells near the membrane by DNase I in the presence of TGF-β inhibitor can further reduce invasiveness of tumor cells (66% reduction) (Fig 8B).
Fig 8. The effect of TGF-β blocking (+Ab) and the combined therapy (+Ab+DNase I) on tumor cell invasion.
(A) The (relative) population of migrating tumor cells for various growth rates (r ∈ [1.2, 1.5]) and injection rates (λA ∈ [0, 10]) of the TGF-β antibody. When TGF-β activity is inhibited by antibody (r = 1.5), fewer cells (62% reduction) invade the lower chamber. (B) Population of migrating tumor cells when the TGF-β antibody was added in the absence (+Ab-D) and presence (+Ab+D) of DNase I relative to the control (-Ab-D). When proteolytic activity of tumor cells near the membrane is blocked by DNase I, fewer cells (66% reduction) invade the lower chamber in the presence of TGF-β inhibitor.
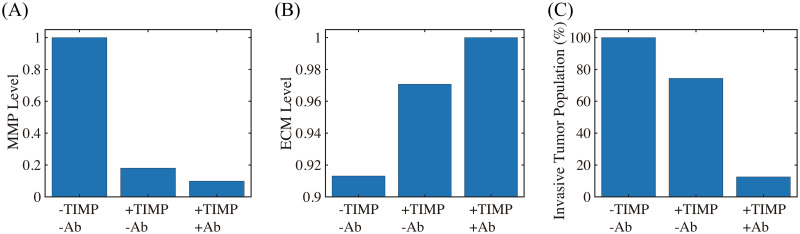
Next, we tested if MMP inhibition by TIMP can effectively reduce the TAN-mediated invasion through the transfilter. It has been shown that TIMP treatment can significantly reduce (> 50%) the number of migratory breast cancer cells through 8-μm pores in a Boyden invasion chamber assay [99]. In the mathematical model, inhibition of MMP is implemented by injecting TIMP (λM > 0) in Eq (15) which abrogates MMP production through a term of degradation of MMPs, , on the right hand side of Eq (14). We also tested if a combination therapy (TIMP+TGF-β inhibitor) can further reduce the invasion potential of tumor cells. Fig 9 shows the (relative) MMP levels, ECM levels, and number of migratory tumor cells at final time (t = 22 h) for control (-TIMP-Ab), TIMP alone (+TIMP-Ab), and combination treatment (+TIMP+Ab). One can see that TIMP treatment can inhibit the tumor cell motility by 26% (+TIMP-Ab in Fig 9C) through the significant reduction in MMP activities (82%; Fig 9A) and relatively intact ECM level (Fig 9B). An introduction of the TGF-β antibody to the system in addition to TIMP (+TIMP+Ab) significantly reduces the tumor cell migration through the filter (> 87%). Blocking tumor-TAN interactions by TGF-β inhibitor effectively lowered MMP levels (Fig 9A) and induced the intact ECM levels on the membrane (Fig 9B) [94, 97], contributing to this anti-invasion effect.
Fig 9. The effect of MMP blocking (+TIMP-Ab) and combined therapy (+TIMP+Ab).
(A,B) Levels of MMPs and ECM when MMP activity was blocked by TIMP in the absence (+TIMP-Ab) and presence (+TIMP+Ab) of the TGF-β antibody relative to the control (-TIMP-Ab). (C) Population of invading tumor cells corresponding to control (-TIMP-Ab), TIMP treatment (+TIMP-Ab), and combined therapy (+TIMP+Ab), respectively.
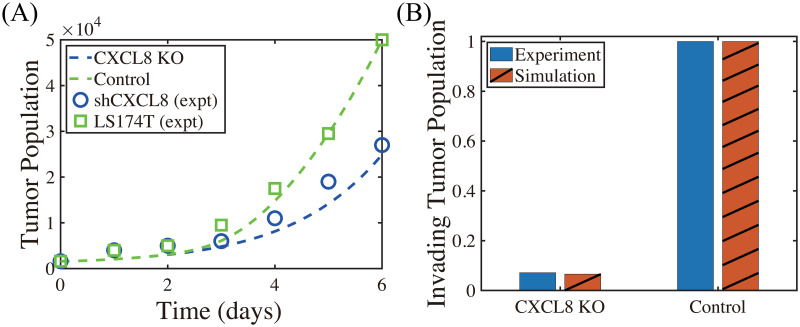
We now investigate the effect of CXCL-8 on tumor growth and invasion in Fig 10. In our model, CXCL-8 knockdown leads to critical reduction of chemotactic movement of the neutrophils, which in turn reduces tumor growth (blue curve; CXCL8 KO, Fig 10A) and invasion (red; CXCL8 KO, Fig 10B) compared to control due to decreased activities of NE (∼40%) and TGF-β (∼50%). These CXCL-KO-mediated reductions in invasive and proliferative potential of tumor cells were consistently observed in experiments. Kumar et al. [100] showed that inhibition of CXCL-8 leads to a drastic decrease (∼14-fold) in proliferation of LS174T cells (shCXCL8 in Fig 10A) and significant abrogation of tumor cell invasion (blue in Fig 10B) relative control.
Fig 10. Inhibition of CXCL8 reduces proliferation, viability and invasion (Experiments vs simulation results).
(A) Time course of cell proliferation shows a drastic decrease in the LS174T cell population with CXCL8 knockdown (shCXCL8; blue) compared to control (LS174T) in in vivo experiments [100]. Model simulation shows a consistent, significant reduction of the tumor cell proliferation in the CXCL knockdown case (CXCL8-KO; blue) compared to control, abrogating tumor growth. (B) CXCL8 knockdown significantly decreases the invasiveness of LS174T cells (blue) [100], as our model simulation illustrates (red).
Discussion
TME plays an important role in regulation of tumor immunogenicity [101], tumor progression, invasion, and metastasis [3, 102]. In particular, the neutrophil-tumor interaction was shown to promote tumor cell invasion, increasing metastatic potential of cancer cells [31]. The invasion and metastasis processes of lung cancer cells may depend on many factors in tumor microenvironment, including immune cells and their cytokines and chemokines [103, 104]. Therefore, targeting players in tumor microenvironment including tumor-associated neutrophils [105] as a therapeutic approach has become more and more important [101, 106]. Experimental [22] and model simulations (Fig 4) suggest that the aggressive tumor invasion through the filter can be promoted by the mutual interaction between tumor cells in the upper chamber and neutrophils in the lower chamber. While the details of the N1→N2 transition of TANs are still poorly understood, our model consistently suggests the pivotal role of TANs in promoting tumor cell invasion in vitro (Figs 6 and 7) through chemotaxis (S4 Text) and haptotaxis (S4 Text). TAN-induced signaling pathways of NET and NE were shown to actively induce tumor invasion and metastasis [71, 107, 108]. On the other hand, the presence of inhibitors of NET/NEs and MMPs was experimentally shown to block tumor invasion [8, 22]. NET was shown to trap the circulating tumor cells (CTCs) in a lung carcinoma model, promoting tumor cell metastasis [19] by up-regulation of β1-integrin on NETs and cancer cells [109]. Thus, blocking this TAN-assisted tumor invasion can be a critical step to decrease the metastatic potential of the tumor cells. For example, DNase I treatment led to the down-regulation of NE and NET activities and reduced the invasive and metastatic potential of tumor cells (Fig 5), which is in good agreement with experimental studies [22]. Interestingly, impeding the formation of NET by DNase I treatment was shown to halt the actuation of dormant cancer cells [110].
The role of MMPs in regulation of cancer cell invasion and metastasis is well-known [48, 74]. MMP2, for instance, can not only induce tumor cell invasion by degrading ECM but promote tumor cell proliferation by enhancing vessel maturation and function in brain tumors [74]. In particular, inhibition of MMP activity can block cancer cell invasion by suppressing cell-ECM tractions and inducing cell softening [48]. In our model, TIMPs were able to partially block tumor cell invasion by heavy degradation of ECM (Fig 9A). However, when we apply combined therapeutic strategies by TIMP and TGF-β antibody, this effectively inhibited the tumor cell invasion through the filter (>87% reduction; Fig 9C). Recently, it was shown that the invasiveness of cancer cells was regulated by MMP catalytic activity via modulation of integrins-FAK signaling network [48]. Recently, TANs are shown to facilitate the metastasis to liver by increased binding activity of CCDC25 to NET DNA [111, 112]. It would be interesting to investigate the detailed mechanism of this signaling.
There are many factors that may change permeability of the narrow intercellular space for cellular infiltration. Even though the permeability parameters are fixed in in vitro experiments, the permeability through the narrow gap for cell invasion varies in the in vivo system and is regulated by cells and their cytokines/chemokines, changing the invasive potential (S4 Text). For example, TANs and NET can mediate cancer cell extravasation through TAN-CTC adhesion and breaking endothelial cell (EC) barriers, leading to active metastasis [113]. The whole process includes an initial strong adhesion process between a CTC and TANs involving selectins/integrins/ICAM1, and a series of signaling networks for CTC-EC adhesion, increased permeability from physical contraction of ECs, and the final extravasation [104, 113, 114]. A multi-scale model [115] may explain the fundamental mechanism behind this complex process in more detail by taking into account specific cell-cell adhesion [116], ECM-cell interaction [117], mechanical stress [81, 93, 95], fluid flow [118], and intracellular signaling of cellular process [38, 93].
Many studies showed that neutrophil to lymphocyte ratio (NLR) in blood can be an important prognostic factor of cancer progression [119–122] including lung cancers [123, 124]. Our simulation results suggest that the presence of a larger portion of TANs in a TME (or high NLR in blood) can effectively stimulate tumor cell invasion and increase the metastatic potential through increased mutual interaction between tumor cells and N2 TANs (S4 Text). TGF-β mediates this critical N1 → N2 transition of TANs and promotes tumor growth and invasion through the filter (Fig 6) by the phenotypic switch from non-invasive status to invasive status. Therefore, the early detection of initial recruitment of TANs to the TME, for example by calculating NLR, may be an important step in decreasing metastatic potential in patients [8, 28, 122, 125]. Further studies on specific downstream pathways of this CCDC25-ILK-β-Parvin signalling [112] would be needed for development of anti-metastatic drugs that target and block the NET-cancer interaction.
Blocking TGF-β and its receptors was suggested to a therapeutic approach due to their ability to inhibit tumor growth [92, 93] and critical cell invasion [34, 94, 95], decrease tumourigenic potential [92, 96], and reduce metastatic dissemination [97] through various different pathways including the SMADs family [67, 98]. We showed that inhibition of TGF-β can effectively decrease migration potential of tumor cells through the transfilter by reducing the critical interaction between neutrophils and tumor cells (Figs 6 and 8). Model simulation and experiments [100] consistently show that CXCL8 knockdown can reduce tumor growth and invasion (Fig 10). These results illustrate the critical role of neutrophils in tumor cell invasion and importance of inhibition of key players such as TGF-β and CXCL8 in suppressing cell infiltration and metastasis potential.
A combined approach with TGF-β inhibitor and DNase I can further reduce the invasiveness of tumor cells through the filter (Fig 8). We note, however, that TGF-β treatment, not TGF-β inhibition, can enhance anti-tumor efficacy through temporal immune suppression in other approaches. For example, Han et al. [126] showed that pretreatment with TGF-β prior to oncolytic virus (OV) therapy effectively inhibited tumor growth by suppressing resident microglia and natural killer (NK) cells in glioblastoma therapy trial. In the same vein, Kim et al. [39] also experimentally and theoretically showed that physical deletion of resident NK cells (−NK) in the TME, unexpectedly, induced better anti-tumor efficacy relative to the control case in the OV-bortezomib combination therapy since residential NK cells, if not removed, also killed infected tumor cells and depletion of NK cells significantly increased OV-mediated tumor killing. It would be interesting to see how this TGF-β-mediated immune suppression affects the tumor invasion and metastasis processes in these combination therapies.
We plan to investigate the role of the continuous spectrum of the N1→N2 transition and the role of TANs in the regulation of NET-mediated metastasis in future work. Signaling between cells is an integral process in controlling invasive and metastatic potential of tumor cells due to unexpected mutations and chromosomal changes. This signaling often involves indirect communications between various immune cells and spatially-separated tumor cells in the TME. For example, the detailed communication between a tumor at a distant site and neutrophils in bone marrow is poorly understood. Intra-tumor heterogeneity from packing density of various cells in TME and large anisotropic transport through the tissue can affect the signaling pathways [127], thus cancer treatment [128], but despite its importance, corresponding experimental data on signaling are insufficient. Interestingly, the aging TME was recently suggested to influence tumor progression including the critical tumor cell invasion [61]. Thus, in silico studies on the effects of these critical interactions on cancer cell invasion, and on the responsiveness of the predictions to physical parameters, can shed insights into guiding experiments aimed at the development of new therapeutic strategies.
Supporting information
(PDF)
(PDF)
(PDF)
(PDF)
Data Availability
All relevant data are within the manuscript and its Supporting information files.
Funding Statement
This paper is supported by the Basic Science Research Program through National Research Foundation of Korea (NRF) funded by Ministry of Science, ICT and Future Planning, www.nrf.re.kr (award number 2018R1A2B6007288) (Y.K.). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Baek S, He Y, Allen BG, Buatti JM, Smith BJ, Tong L, et al. Deep Segmentation Networks Predict Survival of Non-Small Cell Lung Cancer. Sci Rep. 2019;9(1):17286. 10.1038/s41598-019-53461-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Organization WH. Cancer. World Health Organization; 2018.
- 3. Shaul ME, Fridlender ZG. Tumour-associated Neutrophils in Patients With Cancer. Nat Rev Clin Oncol. 2019;16(10):601–620. 10.1038/s41571-019-0222-4 [DOI] [PubMed] [Google Scholar]
- 4. Leach J, Morton JP, Sansom OJ. Neutrophils: Homing in on the myeloid mechanisms of metastasis. Mol Immunol. 2017;pii: S0161-5890(17):30615–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Shaul ME, Fridlender ZG. Neutrophils as Active Regulators of the Immune System in the Tumor Microenvironment. J Leukoc Biol. 2017;102(2):343–349. 10.1189/jlb.5MR1216-508R [DOI] [PubMed] [Google Scholar]
- 6. Piccard H, Muschel RJ, Opdenakker S. On the dual roles and polarized phenotypes of neutrophils in tumor development and progression. Crit Rev Oncol Hematol. 2012;82(3):296–309. 10.1016/j.critrevonc.2011.06.004 [DOI] [PubMed] [Google Scholar]
- 7. Kim J, Bae JS. Tumor-Associated Macrophages and Neutrophils in Tumor Microenvironment. Mediators Inflamm. 2016;2016:6058147. 10.1155/2016/6058147 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Houghton AM, Rzymkiewicz DM, Ji H, Gregory AD, Egea EE, Metz HE, et al. Neutrophil elastase-mediated degradation of IRS-1 accelerates lung tumor growth. Nat Med. 2010;16(2):219–223. 10.1038/nm.2084 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Bellocq A, Antoine M, Flahault A, Philippe C, Crestani B, Bernaudin JF, et al. Neutrophil alveolitis in bronchioloalveolar carcinoma: induction by tumor-derived interleukin-8 and relation to clinical outcome. Am J Pathol. 1998;152(1):83–92. [PMC free article] [PubMed] [Google Scholar]
- 10. Foekens JA, Ries C, Look MP, Gippner-Steppert C, Klijn JG, Jochum M. The prognostic value of polymorphonuclear leukocyte elastase in patients with primary breast cancer. Cancer Res. 2003;63(2):337–41. [PubMed] [Google Scholar]
- 11. Singel KK, Segal BH. Neutrophils in the tumor microenvironment: trying to heal the wound that cannot heal. Immunol Rev. 2016;273(1):329–43. 10.1111/imr.12459 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Lichtenstein A, Kahle J. Anti-tumor effect of inflammatory neutrophils: characteristics of in vivo generation and in vitro tumor cell lysis. Int J Cancer. 1985;35(1):121–7. 10.1002/ijc.2910350119 [DOI] [PubMed] [Google Scholar]
- 13. Otten MA, Rudolph E, Dechant M, Tuk CW, Reijmers RM, Beelen RH, et al. Immature neutrophils mediate tumor cell killing via IgA but not IgG Fc receptors. J Immunol. 2005;174(9):5472–80. 10.4049/jimmunol.174.9.5472 [DOI] [PubMed] [Google Scholar]
- 14. Andzinski L, Kasnitz N, Stahnke S, Wu CF, Gereke M, von Kockritz-Blickwede M, et al. Type I IFNs induce anti-tumor polarization of tumor associated neutrophils in mice and human. Int J Cancer. 2016;138:1982–93. 10.1002/ijc.29945 [DOI] [PubMed] [Google Scholar]
- 15. Tecchio C, Huber V, Scapini P, Clzetti F, Margotto D, Todeschini G, et al. IFNalpha-stimulated neutrophils and monocytes release a soluble form of TNF-related apoptosis-inducing ligand (TRAIL/Apo-2 ligand) displaying apoptotic activity on leukemic cells. Blood. 2004;103(10):3837–44. 10.1182/blood-2003-08-2806 [DOI] [PubMed] [Google Scholar]
- 16. Spiegel A, Brooks MW, Houshyar S, Reinhardt F, Ardolino M, Fessler E, et al. Neutrophils Suppress Intraluminal NK Cell-Mediated Tumor Cell Clearance and Enhance Extravasation of Disseminated Carcinoma Cells. Cancer Discov. 2016;6(6):630–49. 10.1158/2159-8290.CD-15-1157 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Wculek SK, Malanchi I. Neutrophils support lung colonization of metastasis-initiating breast cancer cells. Nature. 2015;528(7582):413–417. 10.1038/nature16140 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Coffelt SB, Kersten K, Doornebal CW, Weiden J, Vrijland K, Hau CS, et al. IL-17-producing γδ T cells and neutrophils conspire to promote breast cancer metastasis. Nature. 2015;522(7556):345–348. 10.1038/nature14282 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Cools-Lartigue J, Spicer J, McDonald B, Gowing S, Chow S, Giannias B, et al. Neutrophil extracellular traps sequester circulating tumor cells and promote metastasis. J Clin Invest. 2013;123(8):3446–3458. 10.1172/JCI67484 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Tazawa H, Okada F, Kobayashi T, Tada M, Mori Y, Une Y, et al. Infiltration of neutrophils is required for acquisition of metastatic phenotype of benign murine fibrosarcoma cells: implication of inflammation-associated carcinogenesis and tumor progression. Am J Pathol. 2003;163(6):2221–32. 10.1016/S0002-9440(10)63580-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Shaul ME, Levy L, Sun J, Mishalian I, Singhal S, Kapoor V, et al. Tumor-associated neutrophils display a distinct N1 profile following TGFbeta modulation: A transcriptomics analysis of pro- vs. antitumor TANs. Oncoimmunology. 2016;5(11). 10.1080/2162402X.2016.1232221 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Park J, Wysocki RW, Amoozgar Z, Maiorino L, Fein MR, Jorns J, et al. Cancer cells induce metastasis-supporting neutrophil extracellular DNA traps. Sci Transl Med. 2016;8(361):361ra138. 10.1126/scitranslmed.aag1711 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Shaul ME, Fridlender ZG. Cancer related circulating and tumor-associated neutrophils—subtypes, sources and function. FEBS J. 2018;Epub ahead of print. 10.1111/febs.14524 [DOI] [PubMed] [Google Scholar]
- 24. Saha S, Biswas SK. Tumor-Associated Neutrophils Show Phenotypic and Functional Divergence in Human Lung Cancer. Cancer Cell. 2016;30(1):11–13. 10.1016/j.ccell.2016.06.016 [DOI] [PubMed] [Google Scholar]
- 25. Fridlender ZG, Sun J, Kim S, Kapoor V, Cheng G, Ling L, et al. Polarization of tumor-associated neutrophil phenotype by TGF-beta: N1 versus N2 TAN. Cancer Cell. 2009;16(3):183–194. 10.1016/j.ccr.2009.06.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Patel MR, Jacobson BA, Ji Y, Drees J, Tang S, Xiong K, et al. Vesicular stomatitis virus expressing interferon-β is oncolytic and promotes antitumor immune responses in a syngeneic murine model of non-small cell lung cancer. Oncotarget. 2015;6(32):33165–77. 10.18632/oncotarget.5320 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Takaoka A, Hayakawa S, Yanai H, Stoiber D, Negishi H, Kikuchi H, et al. Integration of interferon-alpha/beta signalling to p53 responses in tumour suppression and antiviral defence. Nature. 2003;424(6948):516–23. 10.1038/nature01850 [DOI] [PubMed] [Google Scholar]
- 28. Manfroi B, Moreaux J, Righini C, Ghiringhelli F, Sturm N, Huard B. Tumor-associated neutrophils correlate with poor prognosis in diffuse large B-cell lymphoma patients. Blood Cancer J. 2018;8(7):66. 10.1038/s41408-018-0099-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Sun Z, Yang P. Role of imbalance between neutrophil elastase and alpha 1-antitrypsin in cancer development and progression. Lancet Oncol. 2004;5(3):182–90. 10.1016/S1470-2045(04)01414-7 [DOI] [PubMed] [Google Scholar]
- 30. Grecian R, Whyte MKB, Walmsley SR. The role of neutrophils in cancer. Br Med Bull. 2018;xx(xx):xx. 10.1093/bmb/ldy029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Welch DR, Schissel DJ, Howrey RP, Aeed PA. Tumor-elicited polymorphonuclear cells, in contrast to normal circulating polymorphonuclear cells, stimulate invasive and metastatic potentials of rat mammary adenocarcinoma cells. Proc Natl Acad Sci U S A. 1989;86(15):5859–63. 10.1073/pnas.86.15.5859 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Slattery MJ, Dong C. Neutrophils influence melanoma adhesion and migration under flow conditions. Int J Cancer. 2003;106(5):713–722. 10.1002/ijc.11297 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Kim Y, Wallace J, Li F, Ostrowski M, Friedman A. Transformed epithelial cells and fibroblasts/myofibroblasts interaction in breast tumor: a mathematical model and experiments. J Math Biol. 2010;61(3):401–421. 10.1007/s00285-009-0307-2 [DOI] [PubMed] [Google Scholar]
- 34. Kim Y, Friedman A. Interaction of tumor with its microenvironment: A Mathematical Model. Bull Math Biol. 2010;72(5):1029–1068. 10.1007/s11538-009-9481-z [DOI] [PubMed] [Google Scholar]
- 35. Kim Y, Othmer H. Hybrid models of cell and tissue dynamics in tumor growth. Math Bios Eng. 2015;12(6):1141–1156. 10.3934/mbe.2015.12.1141 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Li X, Jolly MK, George JT, Pienta KJ, Levine H. Computational Modeling of the Crosstalk Between Macrophage Polarization and Tumor Cell Plasticity in the Tumor Microenvironment. Front Oncol. 2019;9:10. 10.3389/fonc.2019.00010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Kim Y, Jeon H, Othmer HG. The role of the tumor microenvironment in glioblastoma: A mathematical model. IEEE Trans Biomed Eng. 2017;64(3):519–527. 10.1109/TBME.2016.2637828 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Kim Y, Lee D, Lawler S. Collective invasion of glioma cells through OCT1 signalling and interaction with reactive astrocytes after surgery. Phil Trans R Soc B. 2020;375:20190390. 10.1098/rstb.2019.0390 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Kim Y, Yoo JY, Lee TJ, Liu J, Yu J, Caligiuri MA, et al. Complex role of NK cells in regulation of oncolytic virus-bortezomib therapy. Proc Natl Acad Sci USA. 2018;115(19):4927–4932. 10.1073/pnas.1715295115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Kim Y, Lee J, Lee D, Othmer HG. Synergistic effects of bortezomib-OV therapy and anti-invasive strategies in glioblastoma: a mathematical model. Cancers. 2019;11:215. 10.3390/cancers11020215 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Aspirin AP, de los Reyes V AA, Kim Y. Polytherapeutic strategies with oncolytic virus-bortezomib and adjuvant NK cells in cancer treatment. Journal of the Royal Society Interface. 2020;in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Niu B, Zeng X, Phan TA, Szulzewsky F, Holte S, Holland EC, et al. Mathematical modeling of PDGF-driven glioma reveals the dynamics of immune cells infiltrating into tumors. Neoplasia. 2020;22(9):323–332. 10.1016/j.neo.2020.05.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Kim Y, Lee D, Lee J, Lee S, Lawler S. Role of tumor-associated neutrophils in regulation of tumor growth in lung cancer development: A mathematical model. PLoS One. 2019;14(1):e0211041. 10.1371/journal.pone.0211041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Connor Y, Tekleab Y, Tekleab S, Nandakumar S, Bharat D, Sengupta S. A mathematical model of tumor-endothelial interactions in a 3D co-culture. Sci Rep. 2019;9(1):8429. 10.1038/s41598-019-44713-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Kim PS, Lee PP, Levy D. Dynamics and potential impact of the immune response to chronic myelogenous leukemia. PLoS Comput Biol. 2008;4(6):e1000095. 10.1371/journal.pcbi.1000095 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Frascoli F, Flood E, Kim PS. A model of the effects of cancer cell motility and cellular adhesion properties on tumour-immune dynamics. Math Med Biol. 2017;34(2):215–240. [DOI] [PubMed] [Google Scholar]
- 47. Fares J, Fares MY, Khachfe HH, Salhab HA, Fares Y. Molecular Principles of Metastasis: A Hallmark of Cancer Revisited. Signal Transduct Target Ther. 2020;5(1):28. 10.1038/s41392-020-0134-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Das A, Monteiro M, Barai A, Kumar S, Sen S. MMP Proteolytic Activity Regulates Cancer Invasiveness by Modulating Integrins. Sci Rep. 2017;7(1):14219. 10.1038/s41598-017-14340-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Kim Y, Lawler S, Nowicki MO, Chiocca EA, Friedman A. A mathematical model of Brain tumor: pattern formation of glioma cells outside the tumor spheroid core. J Theo Biol. 2009;260:359–371. 10.1016/j.jtbi.2009.06.025 [DOI] [PubMed] [Google Scholar]
- 50. Roussos ET, Condeelis JS, Patsialou A. Chemotaxis in cancer. Nat Rev Cancer. 2011;11(8):573–587. 10.1038/nrc3078 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Rascle M, Ziti C. Finite time blow up in some models of chemotaxis. 1995;33:388–414. [DOI] [PubMed] [Google Scholar]
- 52. Othmer HG, Stevens A. Aggregation, Blowup, and collapse: The ABC’s of taxis in reinforced random walks. SIAM J APPL MATH. 1997;57(4):1044–1081. 10.1137/S0036139995288976 [DOI] [Google Scholar]
- 53. Benson DD, Meng X, Fullerton DA, Moore EE, Lee JH, Ao L, et al. Activation state of stromal inflammatory cells in murine metastatic pancreatic adenocarcinoma. Am J Physiol Regul Integr Comp Physiol. 2012;302(9):R1067–75. 10.1152/ajpregu.00320.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Kristensen JH, Karsdal MA, Sand JM, Willumsen N, Diefenbach C, Svensson B, et al. Serological assessment of neutrophil elastase activity on elastin during lung ECM remodeling. BMC Pulm Med. 2015;15:53. 10.1186/s12890-015-0048-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Uribe-Querol E, Rosales C. Neutrophils in Cancer: Two Sides of the Same Coin. J Immunol Res. 2015;2015::983698. 10.1155/2015/983698 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Zhu YM, Webster SJ, Flower D, Woll PJ. Interleukin-8/CXCL8 is a growth factor for human lung cancer cells. Br J Cancer. 2004;91(11):1970–6. 10.1038/sj.bjc.6602227 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Jeon NL, Baskaran H, Dertinger SK, Whitesides GM, de Water LV, Toner M. Neutrophil chemotaxis in linear and complex gradients of interleukin-8 formed in a microfabricated device. Nat Biotechnol. 2002;20(8):826–30. 10.1038/nbt712 [DOI] [PubMed] [Google Scholar]
- 58. Terabe M, Robertson FC, Clark K, Ravin ED, Bloom A, Venzon DJ, et al. Blockade of Only TGF-β 1 and 2 Is Sufficient to Enhance the Efficacy of Vaccine and PD-1 Checkpoint Blockade Immunotherapy. Oncoimmunology. 2016;6(5):6058147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Kim S, Buchlis G, Fridlender ZG, Sun J, Kapoor V, Cheng G, et al. Systemic Blockade of Transforming Growth Factor-Beta Signaling Augments the Efficacy of Immunogene Therapy. Cancer Res. 2008;68(24):10247–56. 10.1158/0008-5472.CAN-08-1494 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Lee SW, Kwak HS, Kang MH, Park YY, Jeong GS. Fibroblast-associated tumour microenvironment induces vascular structure-networked tumouroid. Src Rep. 2018;8(1):2365. 10.1038/s41598-018-20886-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Fane M, Weeraratna AT. How the Ageing Microenvironment Influences Tumour Progression. Nat Rev Cancer. 2020;20(2):89–106. 10.1038/s41568-019-0222-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Altorki NK, Markowitz GJ, Gao D, Port JL, Saxena A, Stiles B, et al. The lung microenvironment: an important regulator of tumour growth and metastasis. Nat Rev Cancer. 2019;19(1):9–31. 10.1038/s41568-018-0081-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Bonnans C, Chou J, Werb Z. Remodelling the Extracellular Matrix in Development and Disease. Nat Rev Mol Cell Biol. 2014;15(12):786–801. 10.1038/nrm3904 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Stockley RA. Neutrophils and the pathogenesis of COPD. Chest. 2002;121(5 Suppl):151S–155S. 10.1378/chest.121.5_suppl.151S [DOI] [PubMed] [Google Scholar]
- 65. Zhou SL, Dai Z, Zhou ZJ, Wang XY, Yang GH, Wang Z, et al. Overexpression of CXCL5 Mediates Neutrophil Infiltration and Indicates Poor Prognosis for Hepatocellular Carcinoma. Hepatology. 2012;56(6):2242–54. 10.1002/hep.25907 [DOI] [PubMed] [Google Scholar]
- 66. Gao Q, Zhao YJ, Wang XY, Qiu SJ, Shi YH, Sun J, et al. CXCR6 Upregulation Contributes to a Proinflammatory Tumor Microenvironment That Drives Metastasis and Poor Patient Outcomes in Hepatocellular Carcinoma. Cancer Res. 2012;72(14):3546–56. 10.1158/0008-5472.CAN-11-4032 [DOI] [PubMed] [Google Scholar]
- 67. Bellomo C, Caja L, Moustakas A. Transforming growth factor β as regulator of cancer stemness and metastasis. Br J Cancer. 2016;115(7):761–9. 10.1038/bjc.2016.255 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68. Pickup M, Novitskiy S, Moses HL. The Roles of TGFβ in the Tumour Microenvironment. Nat Rev Cancer. 2013;13(11):788–99. 10.1038/nrc3603 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Mantovani A, Cassatella MA, Costantini C, Jaillon S. Neutrophils in the activation and regulation of innate and adaptive immunity. Nat Rev Immunol. 2011;11(8):519–31. 10.1038/nri3024 [DOI] [PubMed] [Google Scholar]
- 70. Fridlender ZG, Albelda SM. Tumor-associated neutrophils: friend or foe? Carcinogenesis. 2012;33(5):949–55. 10.1093/carcin/bgs123 [DOI] [PubMed] [Google Scholar]
- 71. Moroy G, Alix AJ, Sapi J, Hornebeck W, Bourguet E. Neutrophil elastase as a target in lung cancer. Anticancer Agents Med Chem. 2012;12(6):565–79. 10.2174/187152012800617696 [DOI] [PubMed] [Google Scholar]
- 72. Larco JED, Wuertz BR, Furcht LT. The potential role of neutrophils in promoting the metastatic phenotype of tumors releasing interleukin-8. Clin Cancer Res. 2004;10(15):4895–4900. 10.1158/1078-0432.CCR-03-0760 [DOI] [PubMed] [Google Scholar]
- 73. He J, Turino GM, Lin YY. Characterization of peptide fragments from lung elastin degradation in chronic obstructive pulmonary disease. Exp Lung Res. 2010;36(9):548–57. 10.3109/01902148.2010.489143 [DOI] [PubMed] [Google Scholar]
- 74. Yu CF, Chen FH, Lu MH, Hong JH, Chiang CS. Dual Roles of Tumour Cells-Derived Matrix Metalloproteinase 2 on Brain Tumour Growth and Invasion. Br J Cancer. 2017;117(12):1828–1836. 10.1038/bjc.2017.362 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75. Coussens LM, Tinkle CL, Hanahan D, Werb Z. MMP-9 supplied by bone marrow-derived cells contributes to skin carcinogenesis. Cell. 2000;103(3):481–90. 10.1016/S0092-8674(00)00139-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76. Eisenberg M, Kim Y, Li R, Ackerman WE, Kniss DA, Friedman A. Modeling the effects of myoferlin on tumor cell invasion. Proc Natl Acad Sci USA. 2011;108(50):20078–83. 10.1073/pnas.1116327108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77. Zhang L, Zhao L, Zhao D, Lin G, Guo B, Li Y, et al. Inhibition of Tumor Growth and Induction of Apoptosis in Prostate Cancer Cell Lines by Overexpression of Tissue Inhibitor of Matrix metalloproteinase-3. Cancer Gene Ther. 2010;17(3):171–9. 10.1038/cgt.2009.59 [DOI] [PubMed] [Google Scholar]
- 78. Jackson HW, Defamie V, Waterhouse P, Khokha R. TIMPs: Versatile Extracellular Regulators in Cancer. Nat Rev Cancer. 2017;17(1):38–53. 10.1038/nrc.2016.115 [DOI] [PubMed] [Google Scholar]
- 79. Friedman A, Huang C, Yong J. Effective permeability of the boundary of a domain. Commun In Partial differential equations. 1995;20(1&2):59–102. 10.1080/03605309508821087 [DOI] [Google Scholar]
- 80. Lodish H, Berk A, Zipursky SL, Matsudaira P, Baltimore D, Darnell J. Molecular Cell Biology. 4th ed. New York: W. H. Freeman; 2000. [Google Scholar]
- 81. Stolarska M, Kim Y, Othmer HG. Multiscale Models of Cell and Tissue Dynamics. Phil Trans Roy Soc A. 2009;367:3525–3553. 10.1098/rsta.2009.0095 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82. Liang S, Hoskins M, Khanna P, Kunz RF, Dong C. Effects of the tumor-leukocyte microenvironment on melanoma-neutrophil adhesion to the endothelium in a shear flow. Cell Mol Bioeng. 2008;1(2-3):189–200. 10.1007/s12195-008-0016-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83. Moghe PV, Nelson RD, Tranquillo RT. Cytokine-stimulated chemotaxis of human neutrophils in a 3-D conjoined fibrin gel assay. J Immunol Methods. 1995;180(2):193–211. 10.1016/0022-1759(94)00314-M [DOI] [PubMed] [Google Scholar]
- 84. Brown DR. Dependence of neurones on astrocytes in a coculture system renders neurones sensitive to transforming growth factor beta1-induced glutamate toxicity. J Neurochem. 1999;72(3):943–53. 10.1046/j.1471-4159.1999.0720943.x [DOI] [PubMed] [Google Scholar]
- 85. Koka S, Vance JB, Maze GI. Bone growth factors: potential for use as an osseointegration enhancement technique (OET). J West Soc Periodontol Periodontal Abstr. 1995;43(3):97–104. [PubMed] [Google Scholar]
- 86. Woodcock EA, Land SL, Andrews RK. A low affinity, low molecular weight endothelin-A receptor present in neonatal rat heart. Clin Exp Pharmacol Physiol. 1993;20(5):331–4. 10.1111/j.1440-1681.1993.tb01697.x [DOI] [PubMed] [Google Scholar]
- 87. Tyson R, Stern LG, LeVeque RJ. Fractional step methods applied to a chemotaxis model. J Math Biol. 2000;41(5):455–75. 10.1007/s002850000038 [DOI] [PubMed] [Google Scholar]
- 88. Brinkmann V, Reichard U, Goosmann C, Fauler B, Uhlemann Y, Weiss DS, et al. Neutrophil extracellular traps kill bacteria. Science. 2004;303(5663):1532–1535. 10.1126/science.1092385 [DOI] [PubMed] [Google Scholar]
- 89. Huo X, Li H, Li Z, Yan C, Agrawal I, Mathavan S, et al. Transcriptomic Profiles of Tumor-Associated Neutrophils Reveal Prominent Roles in Enhancing Angiogenesis in Liver Tumorigenesis in Zebrafish. Scientific Reports. 2019;9:1509. 10.1038/s41598-018-36605-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90. Ohshiro K, Bui-Nguyen TM, Natha RSD, Schwartz AM, Levine P, Kumar R. Thrombin Stimulation of Inflammatory Breast Cancer Cells Leads to Aggressiveness via the EGFR-PAR1-Pak1 Pathway. Int J Biol Markers. 2012;27(4):e305–313. 10.5301/JBM.2012.10437 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91. Mitroulis I, Kambas K, Anyfanti P, Doumas M, Ritis K. The Multivalent Activity of the Tissue Factor-Thrombin Pathway in Thrombotic and Non-Thrombotic Disorders as a Target for Therapeutic Intervention. Expert Opin Ther Targets. 2011;15(1):75–89. 10.1517/14728222.2011.532788 [DOI] [PubMed] [Google Scholar]
- 92. Naka K, Hoshii T, Muraguchi T, Tadokoro Y, Ooshio T, Kondo Y, et al. TGF-beta-FOXO Signalling Maintains Leukaemia-Initiating Cells in Chronic Myeloid Leukaemia. Nature. 2010;463(7281):676–680. 10.1038/nature08734 [DOI] [PubMed] [Google Scholar]
- 93. Kim Y, Stolarska M, Othmer HG. The role of the microenvironment in tumor growth and invasion. Prog Biophys Mol Biol. 2011;106:353–379. 10.1016/j.pbiomolbio.2011.06.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94. Serizawa M, Takahashi T, Yamamoto N, Koh Y. Combined treatment with erlotinib and a transforming growth factor-β type I receptor inhibitor effectively suppresses the enhanced motility of erlotinib-resistant non-small-cell lung cancer cells. J Thorac oncol. 2013;8(3):259–69. 10.1097/JTO.0b013e318279e942 [DOI] [PubMed] [Google Scholar]
- 95. Kim Y, Othmer HG. A hybrid model of tumor-stromal interactions in breast cancer. Bull Math Biol. 2013;75:1304–1350. 10.1007/s11538-012-9787-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Kim Y, Lim S. The role of the microenvironment in tumor invasion. 2009 Proceedings of the Fourth SIAM Conference on Mathematics for Industry. 2010; p. 84–92.
- 97. Kudinov AE, Deneka A, Nikonova AS, Beck TN, Ahn YH, Liu X, et al. Musashi-2 (MSI2) Supports TGF-β Signaling and Inhibits Claudins to Promote Non-Small Cell Lung Cancer (NSCLC) Metastasis. Proc Natl Acad Sci U S A. 2016;113(25):6955–6960. 10.1073/pnas.1513616113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98. Wang XG, Meng Q, Qi FM, Yang QF. Blocking TGF-β Inhibits Breast Cancer Cell Invasiveness via ERK/S100A4 Signal. Eur Rev Med Pharmacol Sci. 2014;18(24):3844–3853. [PubMed] [Google Scholar]
- 99. Bemis LT, Schedin P. Reproductive state of rat mammary gland stroma modulates human breast cancer cell migration and invasion. Cancer Res. 2000;60(13):3414–8. [PubMed] [Google Scholar]
- 100. Kumar A, Cherukumilli M, Mahmoudpour SH, Brand K, Bandapalli OR. ShRNA-mediated knock-down of CXCL8 inhibits tumor growth in colorectal liver metastasis. Biochem Biophys Res Commun. 2018;500(3):731–737. 10.1016/j.bbrc.2018.04.144 [DOI] [PubMed] [Google Scholar]
- 101. Murciano-Goroff YR, Warner AB, Wolchok JD. The future of cancer immunotherapy: microenvironment-targeting combinations. Cell Res. 2020;30(6):507–519. 10.1038/s41422-020-0337-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102. Masucci MT, Minopoli M, Carriero MV. Tumor Associated Neutrophils. Their Role in Tumorigenesis, Metastasis, Prognosis and Therapy. Front Oncol. 2019;9:1146. 10.3389/fonc.2019.01146 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103. Mishra DK, Rocha HJ, Miller R, Kim MP. Immune Cells Inhibit the Tumor Metastasis in the 4D Cellular Lung Model by Reducing the Number of Live Circulating Tumor Cells. Sci Rep. 2018;8(1):16569. 10.1038/s41598-018-34983-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104. Granger DN, Senchenkova E. Inflammation and the Microcirculation. San Rafael (CA): Morgan and Claypool Life Sciences; 2010. [PubMed] [Google Scholar]
- 105. Gregory AD, Houghton AM. Tumor-associated neutrophils: new targets for cancer therapy. Cancer Res. 2011;71(7):2411–6. 10.1158/0008-5472.CAN-10-2583 [DOI] [PubMed] [Google Scholar]
- 106. Quail DF, Joyce JA. Microenvironmental regulation of tumor progression and metastasis. Nat Med. 2013;19(11):1423–1437. 10.1038/nm.3394 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107. Brostjan C, Oehler R. The role of neutrophil death in chronic inflammation and cancer. Cell Death Discov. 2020;6(26). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108. Lerman I, de la Luz Garcia-Hernandez M, Rangel-Moreno J, Chiriboga L, Pan C, Nastiuk KL, et al. Infiltrating Myeloid Cells Exert Protumorigenic Actions via Neutrophil Elastase. Mol Cancer Res. 2017;15(9):1138–1152. 10.1158/1541-7786.MCR-17-0003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109. Najmeh S, Cools-Lartigue J, Rayes RF, Gowing S, Vourtzoumis P, Bourdeau F, et al. Neutrophil extracellular traps sequester circulating tumor cells via β1-integrin mediated interactions. Int J Cancer. 2017;140(10):2321–30. 10.1002/ijc.30635 [DOI] [PubMed] [Google Scholar]
- 110. Albrengues J, Shields MA, Ng D, Park CG, Ambrico A, Poindexter ME, et al. Neutrophil extracellular traps produced during inflammation awaken dormant cancer cells in mice. Science. 2018;361 (6409). 10.1126/science.aao4227 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111. Nolan E, Malanchi I. A safety net causes cancer cells to migrate and grow. Nature. 2020;583:33. 10.1038/d41586-020-01672-3 [DOI] [PubMed] [Google Scholar]
- 112. Yang L, Liu Q, Zhang X, Liu X, Zhou B, Chen J, et al. DNA of Neutrophil Extracellular Traps Promotes Cancer Metastasis via CCDC25. Nature. 2020;583:133–138. 10.1038/s41586-020-2394-6 [DOI] [PubMed] [Google Scholar]
- 113. Reymond N, d’Agua BB, Ridley AJ. Crossing the endothelial barrier during metastasis. Nat Rev Cancer. 2013;13(12):858–870. 10.1038/nrc3628 [DOI] [PubMed] [Google Scholar]
- 114. Huh SJ, Liang S, Sharma A, Dong C, Robertson GP. Transiently entrapped circulating tumor cells interact with neutrophils to facilitate lung metastasis development. Cancer Res. 2010;70(14):6071–6082. 10.1158/0008-5472.CAN-09-4442 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115. Kim Y, Stolarska M, Othmer HG. A hybrid model for tumor spheroid growth in vitro I: Theoretical development and early results. Math Models Methods in Appl Scis. 2007;17:1773–1798. 10.1142/S0218202507002479 [DOI] [Google Scholar]
- 116. Kim Y, Kang H, Powathil G, Kim H, Trucu D, Lee W, et al. Role of extracellular matrix and microenvironment in regulation of tumor growth and LAR-mediated invasion in glioblastoma. PLoS One. 2018;13:(10):e0204865. 10.1371/journal.pone.0204865 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117. Kim Y, Powathil G, Kang H, Trucu D, Kim H, Lawler S, et al. Strategies of eradicating glioma cells: A multi-scale mathematical model with miR-451-AMPK-mTOR control. PLoS One. 2015;10(1):e0114370. 10.1371/journal.pone.0114370 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118. Lee W, Lim S, Kim Y. The role of myosin II in glioma invasion: A mathematical model. PLoS One. 2017;12(2):e0171312. 10.1371/journal.pone.0171312 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119. Barker T, Fulde G, Moulton B, Nadauld LD, Rhodes T. An elevated neutrophil-to-lymphocyte ratio associates with weight loss and cachexia in cancer. Sci Rep. 2020;10(1):7535. 10.1038/s41598-020-64282-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120. Chen Y, Yan H, Wang Y, Shi Y, Dai G. Significance of baseline and change in neutrophil-to-lymphocyte ratio in predicting prognosis: a retrospective analysis in advanced pancreatic ductal adenocarcinoma. Sci Rep. 2017;7(1):753. 10.1038/s41598-017-00859-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121. Zeren S, Yaylak F, Ozbay I, Bayhan Z. Relationship Between the Neutrophil to Lymphocyte Ratio and Parathyroid Adenoma Size in Patients With Primary Hyperparathyroidism. Int Surg. 2015;100(7–8):1185–9. 10.9738/INTSURG-D-15-00044.1 [DOI] [PubMed] [Google Scholar]
- 122. Li Z, Hong N, Robertson M, Wang C, Jiang G. Preoperative red cell distribution width and neutrophil-to-lymphocyte ratio predict survival in patients with epithelial ovarian cancer. Sci Rep. 2017;7:43001. 10.1038/srep43001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123. Peng B, Wang YH, Liu YM, Ma LX. Prognostic significance of the neutrophil to lymphocyte ratio in patients with non-small cell lung cancer: a systemic review and meta-analysis. Int J Clin Exp Med. 2015;8(3):3098–106. [PMC free article] [PubMed] [Google Scholar]
- 124. Shimizu K, Okita R, Saisho S, Maeda A, Nojima Y, Nakata M. Preoperative neutrophil/lymphocyte ratio and prognostic nutritional index predict survival in patients with non-small cell lung cancer. World J Surg Oncol. 2015;13:291. 10.1186/s12957-015-0710-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125. Hiramatsu S, Tanaka H, Nishimura J, Sakimura C, Tamura T, Toyokawa T, et al. Neutrophils in primary gastric tumors are correlated with neutrophil infiltration in tumor-draining lymph nodes and the systemic inflammatory response. BMC Immunol. 2018;19(1):13. 10.1186/s12865-018-0251-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126. Han J, Chen X, Chu J, Xu B, Meisen WH, Chen L, et al. TGFβ Treatment Enhances Glioblastoma Virotherapy by Inhibiting the Innate Immune Response. Cancer Res. 2015;75(24):5273–5282. 10.1158/0008-5472.CAN-15-0894 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127. Lawson DA, Kessenbrock K, Davis RT, Pervolarakis N, Werb Z. Tumour heterogeneity and metastasis at single-cell resolution. Nature Cell Biology. 2018;20(12):1349–1360. 10.1038/s41556-018-0236-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128. Sun XX, Yu Q. Intra-tumor Heterogeneity of Cancer Cells and Its Implications for Cancer Treatment. Acta Pharmacol Sin. 2015;36(10):1219–1227. 10.1038/aps.2015.92 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129. Gaffney EA, Pugh K, Maini PK, Arnold F. Investigating a simple model of cutaneous wound healing angiogenesis. J Math Biol. 2002;45(4):337–74. 10.1007/s002850200161 [DOI] [PubMed] [Google Scholar]
- 130. Pettet GJ, Byrne HM, McElwain DLS, Norbury J. A model of wound healing angiogenesis in soft-tissue. Math Bios. 1996;136:35–64. 10.1016/0025-5564(96)00044-2 [DOI] [PubMed] [Google Scholar]
- 131. Bray D. Cell movements. New York: Gerland; 1992. [Google Scholar]
- 132. Aimetti AA, Tibbitt MW, Anseth KS. Human neutrophil elastase responsive delivery from poly(ethylene glycol) hydrogels. Biomacromolecules. 2009;10(6):1484–9. 10.1021/bm9000926 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133. Weber LM, Lopez CG, Anseth KS. Effects of PEG hydrogel crosslinking density on protein diffusion and encapsulated islet survival and function. J Biomed Mater Res A. 2009;90(3):720–9. 10.1002/jbm.a.32134 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134. Campbell EJ, Campbell MA, Boukedes SS, Owen CA. Quantum proteolysis by neutrophils: implications for pulmonary emphysema in alpha 1-antitrypsin deficiency. J Clin Invest. 1999;104(3):337–44. 10.1172/JCI6092 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135. Liou TG, Campbell EJ. Nonisotropic enzyme–inhibitor interactions: a novel nonoxidative mechanism for quantum proteolysis by human neutrophils. Biochemistry. 1995;34(49):16171–7. 10.1021/bi00049a032 [DOI] [PubMed] [Google Scholar]
- 136. Baugh RJ, Travis J. Human leukocyte granule elastase: rapid isolation and characterization. Biochemistry. 1976;15(4):836–41. 10.1021/bi00649a017 [DOI] [PubMed] [Google Scholar]
- 137. Ohlsson K, Olsson I. The neutral proteases of human granulocytes. Isolation and partial characterization of granulocyte elastases. Eur J Biochem. 1974;42(2):519–27. 10.1111/j.1432-1033.1974.tb03367.x [DOI] [PubMed] [Google Scholar]
- 138. Saffarian S, Collier IE, Marmer BL, Elson EL, Goldberg G. Interstitial collagenase is a Brownian ratchet driven by proteolysis of collagen. Science. 2004;306(5693):108–11. 10.1126/science.1099179 [DOI] [PubMed] [Google Scholar]
- 139. Sherratt JA, Murray JD. Models of epidermal wound healing. ProcR SocLond. 1990;B241:29–36. [DOI] [PubMed] [Google Scholar]
- 140. Chitrabamrung S, Bannett JS, Rubin RL, Tan EM. A radial diffusion assay for plasma and serum deoxyribonuclease I. Rheumatol Int. 1981;1(2):49–53. 10.1007/BF00541152 [DOI] [PubMed] [Google Scholar]
- 141. Kunz-Schughart LA, Wenninger S, Neumeier T, Seidl P, Knuechel R. Three-dimensional tissue structure affects sensitivity of fibroblasts to TGF-beta 1. Am J Physiol Cell Physiol. 2003;284(1):C209–19. 10.1152/ajpcell.00557.2001 [DOI] [PubMed] [Google Scholar]
- 142. Wakefield LM, Smith DM, Masui T, Harris CC, Sporn MB. Distribution and modulation of the cellular receptor for transforming growth factor-beta. J Cell Biol. 1987;105(2):965–75. 10.1083/jcb.105.2.965 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 143. Valter MM, Wiestler OD, Pietsch T. Differential control of VEGF synthesis and secretion in human glioma cells by IL-1 and EGF. International Journal of Developmental Neuroscience. 1999;17(5-6):565–577. 10.1016/S0736-5748(99)00048-9 [DOI] [PubMed] [Google Scholar]
- 144. Shiomi T, Okada Y. MT1-MMP and MMP-7 in invasion and metastasis of human cancers. Cancer Metastasis Rev. 2003;22(2-3):145–52. 10.1023/A:1023039230052 [DOI] [PubMed] [Google Scholar]
- 145. Orlikowsky TW, Neunhoeffer F, Goelz R, Eichner M, Henkel C, Zwirner M, et al. Evaluation of IL-8-concentrations in plasma and lysed EDTA-blood in healthy neonates and those with suspected early onset bacterial infection. Pediatr Res. 2004;56(5):804–9. 10.1203/01.PDR.0000141523.68664.4A [DOI] [PubMed] [Google Scholar]
- 146. Redl H, Schlag G, Bahrami S, Schade U, Ceska M, Stutz P. Plasma neutrophil-activating peptide-1/interleukin-8 and neutrophil elastase in a primate bacteremia model. J Infect Dis. 1991;164(2):383–8. 10.1093/infdis/164.2.383 [DOI] [PubMed] [Google Scholar]
- 147. Redl H, Schlag G, Bahrami S, Dinges HP, Schade U, Ceska M. Markers of endotoxin related leukocyte activation and injury mechanisms. Prog Clin Biol Res. 1991;367:83–100. [PubMed] [Google Scholar]
- 148. Yoshimura K, Crystal RG. Transcriptional and posttranscriptional modulation of human neutrophil elastase gene expression. Blood. 1992;79(10):2733–40. 10.1182/blood.V79.10.2733.2733 [DOI] [PubMed] [Google Scholar]
- 149. von Nussbaum F, Li VM. Neutrophil elastase inhibitors for the treatment of (cardio)pulmonary diseases: Into clinical testing with pre-adaptive pharmacophores. Bioorg Med Chem Lett. 2015;25(20):4370–81. 10.1016/j.bmcl.2015.08.049 [DOI] [PubMed] [Google Scholar]
- 150.Gnamm C, Oost T, Peters S. 20140221335 A1. US Patent. 2014.
- 151. Yoshikawa N, Inomata T, Okada Y, Shimbo T, Takahashi M, Akita K, et al. Sivelestat sodium hydrate reduces radiation-induced lung injury in mice by inhibiting neutrophil elastase. Mol Med Rep. 2013;7(4):1091–5. 10.3892/mmr.2013.1318 [DOI] [PubMed] [Google Scholar]
- 152. Nakashima H, Akimoto A, Kitagawa T, et al. General pharmacological studies of sodium N-[2-[4-(2,2-dimethethyl-propionyloxy) phenylsulfonylamino] benzoyl] aminoacetate tetrahydrate (ONO-5046 Na). Pharmacometrics. 1997;54:267–277. [Google Scholar]
- 153. Liao TH, Ho HC, Abe A. Chemical modification of bovine pancreatic deoxyribonuclease with phenylglyoxal–the involvement of Arg-9 and Arg-41 in substrate binding. Biochim Biophys Acta. 1991;1079(3):335–42. 10.1016/0167-4838(91)90078-E [DOI] [PubMed] [Google Scholar]
- 154. Sa Y, Hao J, Samineni D, Clark J, Pyne-Geithman G, Broderick J, et al. Brain Distribution and Elimination of Recombinant Human TIMP-1 After Cerebral Ischemia and Reperfusion in Rats. Neurol Res. 2011;33(4):433–8. 10.1179/1743132810Y.0000000012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 155. Herbertz S, Sawyer JS, Stauber AJ, Gueorguieva I, Driscoll KE, Estrem ST, et al. Clinical development of galunisertib (LY2157299 monohydrate), a small molecule inhibitor of transforming growth factor-beta signaling pathway. Drug Design, Development and Therapy. 2015;9:4479–4499. 10.2147/DDDT.S86621 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 156. Prince WS, Baker DL, Dodge AH, Ahmed AE, Chestnut RW, Sinicropi DV. Pharmacodynamics of recombinant human DNase I in serum. Clin Exp Immunol. 1998;113(2):289–96. 10.1046/j.1365-2249.1998.00647.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 157. Stokes CL, Lauffenburger DA. Analysis of the Roles of Microvessel Endothelial Cell Random Motility and Chemotaxis in Angiogenesis. J theor Biol. 1991;152:377–403. 10.1016/S0022-5193(05)80201-2 [DOI] [PubMed] [Google Scholar]
- 158. Perumpanani AJ, Byrne HM. Extracellular matrix concentration exerts selection pressure on invasive cells. Eur J Cancer. 1999;35(8):1274–80. 10.1016/S0959-8049(99)00125-2 [DOI] [PubMed] [Google Scholar]
- 159. Namy P, Ohayon J, Tracqui P. Critical conditions for pattern formation and in vitro tubulogenesis driven by cellular traction fields. J Theor Biol. 2004;227(1):103–20. 10.1016/j.jtbi.2003.10.015 [DOI] [PubMed] [Google Scholar]
- 160. Dickinson RB, Tranquillo RT. A stochastic model for adhesion-mediated cell random motility and haptotaxis. J Math Biol. 1993;31(6):563–600. 10.1007/BF00161199 [DOI] [PubMed] [Google Scholar]
- 161. Abe R, Donnelly SC, Peng T, Bucala R, Metz CN. Peripheral blood fibrocytes: differentiation pathway and migration to wound sites. J Immunol. 2001;166(12):7556–62. 10.4049/jimmunol.166.12.7556 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(PDF)
(PDF)
(PDF)
(PDF)
Data Availability Statement
All relevant data are within the manuscript and its Supporting information files.