Abstract
Since the start of the pandemic caused by the novel coronavirus, COVID-19, more than 106 million people have been infected and global deaths have surpassed 2.4 million. In Chile, the government restricted the activities and movement of people, organizations, and companies, under the concept of dynamic quarantine across municipalities for a predefined period of time. Chile is an interesting context to study because reports to have a higher quantity of infections per million people as well as a higher number of polymerize chain reaction (PCR) tests per million people. The higher testing rate means that Chile has good measurement of the contagious compared to other countries. Further, the heterogeneity of the social, economic, and demographic variables collected of each Chilean municipality provides a robust set of control data to better explain the contagious rate for each city. In this paper, we propose a framework to determine the effectiveness of the dynamic quarantine policy by analyzing different causal models (meta-learners and causal forest) including a time series pattern related to effective reproductive number. Additionally, we test the ability of the proposed framework to understand and explain the spread over benchmark traditional models and to interpret the Shapley Additive Explanations (SHAP) plots. The conclusions derived from the proposed framework provide important scientific information for government policymakers in disease control strategies, not only to analyze COVID-19 but to have a better model to determine social interventions for future outbreaks.
Keywords: Causality analysis, Meta-learner, Causal forest, Dynamic lockdown policy
1. Introduction
There are some claims in the press that the coronavirus is here to stay, that the world needs to prepare for seasonal outbreaks of a coronavirus as we do for the flu. Assuming that this belief is true, then we need better models to understand the spread of the outbreak so that we may be better prepared to mitigate the effects. The novel coronavirus, COVID-19, is among the largest pandemics in the last century. The Swine Flu (2009–2010) is reported to have killed 200k people; Ebola (2014–2016) killed 11.3k; and, SARS (2002–2003) killed 770k (Discover, 2020). At the time of this writing, COVID-19 is reported to have been the cause of over 2.4-million deaths worldwide. However, the number of deaths is not uniform across the world nor is the response. To try to control and stop the spread of the outbreak world leaders – presidents, congressmen and women, health authorities, health organizations and policy-makers – have taken actions to restrict movement thereby limiting contact of people. For decision-makers, knowing what actions to take is difficult since the choices are not recurrent and there is little previous evidence in the recent past to draw upon about what actions to take during a pandemic to support to their decisions. Hence, there is a need to develop models that are better able to understand the spread and growth of the outbreak to model the impacts that interventions may have.
While some countries have been able to “flatten the curve” with respect to newly reported cases of COVID-19 others have not. Many of the actions that countries have taken to slow the spread have been met with protest and considered draconian. In the U.S., for instance, the number of new unemployment claims have reached all-time highs and the amount of money that the federal government has spent on aid is staggering. The cause of the unemployment and the spend in the U.S. are the result of quarantines that have closed businesses and limited economic activity [1]. In other areas of the world where governments were initially able to curtail the spread, they have witnessed a regrowth or second wave of COVID-19. Many of these countries are regions that were in quarantine or lock-down, and when they reopened the country to commerce and increased individual discretion to move inside the cities the number of new cases quickly grew [2]. Nonetheless, there is hope for optimism as vaccines to prevent COVID-19 are rolling out.
Even though COVID-19 may be controlled by vaccines, the impact will be felt for a long time. This pandemic has demonstrated to the world the fragility of humankind and the impact that new epidemics may have on us as people and on world economies. The propagation and transmission of a virus like COVID-19 in a highly connected world, given the efficiency of transportation and the exchange/mobility of people between countries and regions, is rapid. Therefore, we cannot reject the hypothesis that a new virus may result in a pandemic that propagates even more rapidly across the world in the future. For this reason, we have to be better prepared with models built on prior experience and the efficiency of the models to analyze the social, health, and sanitary decisions made to control future pandemics.
As stated previously, the vast majority of countries have implemented social, health, and sanitary policies to mitigate the spread of the virus. These decisions have had negative economic impacts, resulting in a significant decrease in the GDP of each country. Given the economic and social impacts, it is important to understand how effective the policies have been in actually mitigating the spread of the virus. It is in this context that this paper analyzes different ways of measuring the efficacy of the policies implemented to mitigate the spread. Models used to measure the efficacy of health policies have included the classical conditional mean as well as econometric models such as the difference in difference. Two models that worked well when first developed, the Verhulst and Richards models, have been found to not perform well now despite the fact that they are still commonly used [3]. Earlier logistics models may have performed well in the past for the types of conditions that existed then but are no longer valid under new global conditions. Hence, new models based on machine learning may be better given the increased computational ability and the capacity to take into consideration more features than traditional models. Muñoz Lezcano et al. [4] provide a great review of different machine learning, artificial intelligence and image processing models that are helping to understand the pandemic and to improve the healthcare system tools for pandemic control. These tools can be applied to forecast the pandemic spread, decision making, sanitary policies and disease understanding, among other important topics of any pandemic.
Meta-learning algorithms and causal forest are approaches for causal analysis that may prove to be more accurate to capture the spread of a pandemic, under these new global conditions. Meta-learning algorithms are gaining attention in causal analysis, as they use machine learning algorithms as the basis of the causal analysis. For this, they pose as the link between causality and machine learning, where the framework focuses on a post process of the output of the machine learning model to make the causal analysis. Meta-learners have been used in different domains such as healthcare, datacenters, and marketing to name a few (e.g. [5], [6], [7]). Causal Forest is an algorithm that is modified to make causal inference. While based in Regression Forest (RF), but the splitting criterion and the fitting process are modified to generate an unbiased causal estimator. CF too has been applied to many research fields such as economics, finance, and clinical diagnosis (e.g. [8], [9], [10]).
These machine learning methods, however, are not designed to be able to analyze the effect of time. Nonetheless, time is essential in the context of a pandemic since the number of infected is a time series given contact, incubation, and infectious period which implies that there is a chronological order of the data. Hence, there is a need to both update the types of models that we use and apply time series analyses to the applications. Herein is the motivation for the current work: to develop a model that better assesses the spread of a virus given different health policies through the application of machine learning techniques that takes into consideration the time series.
Time series analysis is, however, widely used in different research areas and techniques learned from these areas may be applied in this context. In particular, an analysis of any outbreak needs to take into account the time effect since the chronological order is fundamental to describing the pandemic behavior. Time can be a proxy to a better understanding of the gravity of a pandemic for the population so that they understand and adopt personal healthcare actions such as the use of a mask, hand washing, non-grouping as well as adjust and get used to new work conditions and lifestyle. Thus, we propose to add a time related feature to be used in a machine learning causality model. This feature allows us to expand the dataset, as each municipality has its own time series together with unique features of the region (e.g. population, density, etc.).
In Chile, the government restricted the activities and movement of people, organizations, and companies, under the concept of dynamic quarantine. The government implemented the dynamic quarantine policy over municipalities for a defined period. Chile, it turns out, is an interesting context because reports have it having a higher quantity of infected people per million as well as a higher number of polymerize chain reaction (PCR) tests per million. The higher testing rate means that Chile has good measurement of the infected compared to other countries. Additionally, the heterogeneity of the social, economic, and demographic variables of each Chilean municipality, allows us to have a robust set of control variables in the model to better explain the infection rate for each city. A good summary and comparative analysis of the Chilean dynamic quarantine measures can be found in [11].
In this paper, we propose a framework to analyze time influence in a causal analysis of the COVID-19 pandemic in Chile with the hypothesis that there is a time series pattern related to the COVID contagious. Additionally, the behavior of the population under lockdown leads us to hypothesize that the effectiveness of the quarantine depends on the weeks since first contagion case. Specifically, we contribute to the literature in two aspects: first, we include a time-related variable, Week Since First Case (WSFC), allowing the analysis of time in the outcome variable, giving richer information as input variable to improve the performance of the models; and, second, with WSFC we can evaluate the influence, relationship, and causal influence of a particular individual through time. This last contribution means that for a particular individual, we have different information for different points of time, but also similar characteristics such as population and sewer, which do not change in the scope of this study. We analyze several different approaches for causal inference based on machine learning, including meta-learners and causal forest. The final causal analysis is made with the best base learner model; the one with the best modeling performance. This is motivated by the econometric view of explanation, where the model that best explains the outcome variable could indicate the correct causal interpretation. Applying the proposed framework, we first find the best model analyzing all the variables possible and then interpret the causality and determine the effectiveness of the dynamic lockdown policy. If the best model is not chosen, all the existing models are not analyzed, or available variables considered, then the conclusions are not valid. Thus, we seek to evaluate the dynamic quarantine approach adopted by the Chilean government for controlling the spread of the pandemic, considering the influence of time and socioeconomic factors. The conclusions provide important scientific information for government policymakers on disease control strategies, not only to analyze COVID-19 but to have better techniques to model social interventions in future outbreaks.
In the next section, we present a brief literature review about the COVID-19 analysis and modeling. In the following section, we describe the classical model to determine efficiency of the sanitary-health policies. Then we present and describe the proposed model as well as the loss function to analyze model improvement. In the fourth section, results are presented and analyzed. Finally, in the fifth section, the main conclusions about the efficacy of the dynamic quarantine policies are presented. We then present the conclusions about the modified model as well as the limitations and future research.
2. Literature review
Over the past several months, there have been many papers that study the pandemic; many of which are not about the medical applications. In fact, a recent (February 02, 2021) search for “COVID-19” resulted in over 97,000.1 Given the breadth of topics and volume of publications, we will not summarize the entire extant of work done but rather highlight a sample of relevant research as it relates to the current work. It is important to note that several studies are interdisciplinary, and from various parts of the world, demonstrating the importance of the topic and the demanding scientific collaboration to improve understanding of the pandemic [12], [13], [14]. Many of the studies that have been conducted are based on China, not surprisingly since the pandemic originated there and therefore has more information availability. The studies of interest here can be classified into three broad categories: modeling of the evolution of the pandemic curve; effects of the health decisions and sanitary policies; and, efficiency analysis of the health and sanitary policies. We will briefly cover each of these areas below.
2.1. Curve prediction
Two commonly used models for describing the dynamics of the COVID-19 pandemic are the Verhulst and Richards models; two types of logistics models. However, Abusam et al. [3] found that these two types of models do not fit the actual results of the curve well. In particular, they suggest that the misfit is likely due to structural problems. To deal with the structural problems, they suggest, may require re-parameterization. Part of the challenge with using the Verhulst and Richards types of models may be based on the fact that the models were developed over 100 years ago. While the approach has worked well in the past, the conditions under which they were developed no longer apply. The speed at which people come into contact with each other across the world driven by airplanes and other rapid modes of transportation has increased significantly. Additionally, the volume of people traveling across boarders has also increased significantly. These structural changes in the way that people exist needs to be accounted for as models are updated.
While logistics models are certainly a traditional approach for modeling the spread of the pandemic, they are not the only way to do it. For instance, Chintalapudi et al. [15], developed a seasonal autoregressive integrated moving average (SARIMA) model to forecast the spread of the virus in Italy. Their findings were able to predict up to 93% accuracy using the SARIMA models. The benefit of the SARIMA is that it captures the time component which was not captured previously.
To take into consideration the spatial effect of a population, Guliyev [16] developed a series of spatial panel models. He looked at the number of confirmed cases in Wuhan which had the largest available dataset at the time. Modeling the spread in Wuhan was an important extension of the literature not only from a methodological perspective but also from a need to understand the propagation given the greater than 11-million people population size. Guliyev first used a standard linear model (SLM) as the basis of comparison and then modeled a spatial autoregression model (SAR), a spatial error model (SEM), and a spatial Durbin model. The intent was to be able to capture endogenous, exogenous, and spillover effects that would otherwise be missed with standard models thereby increasing accuracy. Guliyev found that the best model was a spatially-lagged X model (SLX). However, he noted that while the SLX model outperformed the other models in the study, his results were only modeled on Wuhan and the sample set was not particularly large. One of the recommendations was further work in other contexts with potentially larger datasets.
The use of neural networks to model the spread of COVID-19 have also been developed. For instance, Wieczorek et al. [17] used neural networks to model the global spread of the pandemic. In some cases, their models were able to forecast the spread with 99% accuracy. They did try a recurrent neural network as well but found that the training period took too long and therefore was not an efficient approach. In another study, the authors compare Gompertz, Logistic, and Artificial Neural Network models to forecast the growth of cases [18]. This work is significant because each of the models had similar forecasting capabilities as measured by the R2. However, the total number of cases forecasted for each of the models was significantly different. Hence, the need to continue to develop models which may be better able to accurately forecast the true results. An interesting work is the one of Fong et al. [19], where they applied deep learning with fuzzy rules to enhance a composite Monte-Carlo for a better stochastic understanding of the pandemic. Specifically, they separate the models depending on the characteristic of the data. For highly uncertain data they use a probabilistic approach, and for time series data they use a deterministic approach. Both fits are feed to the MC modeling for better predictions.
There has been an increasing amount of interest in trying to do causal inference with a machine learning approach. Two main approaches seen in the literature include modifying the internal algorithm or adapting the problem to use machine learning as plug-in functions. One of the most known algorithms from the first approach is Causal Forest [20], which modifies the random forest to been able to consider heterogeneity. Causal forest has been used in a variety of studies such as medicine [21], finance [22], and environmental policies [23] among others. It also has been used in studies related to the COVID-19 pandemic, to evaluate treatment [24] and non-pharmaceutical interventions [25]. The second approach consists of training a machine learning algorithm to learn the expected value of one of the groups in a binary treatment setting, and then calculating the treatment effect by difference. This approach has also been applied to several areas including medicine [26], education [27], publication recommendation [28], and others. To our knowledge, there are no peer-reviewed published studies that apply meta-learners to COVID-19 cases.
2.2. Effect of sanitary decisions
One of the most widely used approaches for modeling the pandemic is the Susceptible–Exposed–Infective–Recovered (SEIR) model [29]. Dur-e-Ahmad and Imran [30] use SEIR to determine the basic reproductive number in the most affected countries to date (14 March, 2020). For their data, they managed to make a good pattern prediction of the , considering the novelty of the virus. However, Tang et al. [31] claim that while the SEIR approach is one of the most widely used, it is not the best approach in the current context since it does not take into consideration the interventions taking place. In particular, the SEIR fails to fit the data well because it lacks the ability to model the strength of the interventions like the wide-scale use of the quarantines [31]. Evaluating the effectiveness of the quarantine strategy in China, Tang et al. [31] found that the pandemic is still uncertain and because of this it is necessary to further enhance the quarantine and isolation strategies. Tang et al. [31] stratified their data to include the typical SEIR but added a Susceptible–Quarantined and Quarantined–Suspected components.
Further extending the research beyond just the impacts of quarantine, Hiremath et al. [32] analyzed the impact of lock-down on mental health in India. Their findings suggest that while the lockdowns may have a positive effect on reducing the spread of the virus, it has a negative effect on psychological health in the form of depression, anxiety, and panic disorder. Raveendran and Jayadevan [33] studied the role of reverse quarantine in the control of COVID-19 and concluded that reverse quarantine is a promising public health measure to reduce the morbidity and mortality associated with the disease. In particular, reverse quarantine involves separating those with compromised systems, those most at risk, from the rest of the population in order to minimize their exposure to the virus. While a promising way to minimize their exposure, in light of Hiremath et al. [32], we ought to be aware of the potential psychological effects that this might have on this population.
Gondim and Machado [34] expanded our understanding of quarantines through the development of an age-structured SEIRQ model. In particular, they were able to demonstrate that quarantine length may be relaxed by age. However, it should be noted that their model only included three age groups (young, adult, and elderly). Further refinement might be necessary to get the full scope of the ages and it may be necessary to include an ‘at-risk’ feature to the age dimension to capture those with compromised immune systems. Nabi [35] extended the SEIR modeling even further in the development of an SEIIQHRD which included the hospitalized, recovered, and the dead. His findings suggest that the most important variables are the recovery rate of asymptomatic individuals and quarantining and that the relaxing of social distancing measures too soon my result in spikes.
Annas et al. [36], apply the SEIR model in the context of Indonesia. However, for their model, they add vaccination and isolation factors as model parameters to forecast the impact that these measures have on the mitigation of the spread. Their findings suggest that not only does vaccination and isolation slow the spread but that it might also facilitate healing. They suggest that their finding might be used as an early reference point for when the vaccine is developed.
2.3. Efficiency of sanitary decisions
Cui et al. [37] studied the effects of the quarantine strategies in Wuhan and mainland China, analyzing quarantine magnitudes and quarantine time points. The results show the importance of the quarantine strategies in controlling the spread of the disease, especially at the early period of the disease outbreak. Similar to Tang et al. [31], Cui et al. [37] added the quarantined susceptible and the quarantined exposed variables to the SEIR model. Using ordinary differential equations, they were able to forecast the efficiency of the quarantine magnitudes as well as the timing of them.
Chintalapudi et al. [15] analyzed the importance of the lockdown and self-isolation in Italy in the control of disease transmissibility among the population applying Seasonal ARIMA. The results provide quantitative evaluations of how intervention measures and their timings succeeded, from which lessons can be learned by other countries dealing with future outbreaks. Again, in a study of the efficiency of impact measures in China, Xiao et al. [38] found that when hospitals are established specifically to treat those with COVID-19 the spread declined. In particular, their findings suggest that early detection, reporting, quarantine, and treatment are all necessary to reduce the spread.
Džiugys et al. [39], developed a simplified model using just the Susceptible, Infectious, and Removed (SIR) to quantify the overall effectiveness of the quarantine strategies. They found that their model is effective at evaluating the overall effectiveness of quarantine measures. However, they also identified some significant limitations in their approach. First, they acknowledge that their approach might not work in instances where the country is very large. Second, their approach cannot be applied when the number of daily infected is too small. Therefore, they conclude, more complex models of forecasting need to be developed.
As stated earlier, with over 97,000 articles in peer-reviewed journals, it is not possible to summarize all of the extant literature in the domain. Our goal here was to present some of the work in the stream that typify the types of work ongoing and highlights the development of the field. In the next sections, we present our models, the data, and then the results.
3. Methodology
In this study, we propose a framework that consist of two steps. First, we determine the best base model, which from the outset we assume will explain better the causal interaction presented in the dataset. We test this for different base models of meta-learners and also for causal forest. To determine the best base model, we calculate Mean Square Error (MSE); Mean Absolute Percentage Error (MAPE); and, log-Likelihood (lL). Then, with the best base model, we use it for causal analysis. As one of the contributions of this study, we add a time-related variable (Week Since First Case — WSFC), which allows us to study the time effect of the features through Shapely Additive Explanations (SHAP) dependence plots, together with the classical Conditional Average Treatment Effect (CATE) analysis.
3.1. Causal inference
To conduct the causal inference, we follow the methodology based on the potential outcome theory proposed by Cochran and Chambers [40], Rubin [41], and Splawa-Neyman et al. [42] in which the causal effect is defined as:
| (1) |
In reality, however, this cannot be calculated since just one of the two variables is realized (observed) and the other one is not (counterfactual). This is widely known as the fundamental problem of causal inference [43]. Hence, the level causal effect is unknowable.
In general, the level causal effect is not the quantity of interest, as an overall causal effect over all observations is more appealing for analysis. With observational data as a sample of the overall population, we can establish a conditional average treatment effect (CATE) as:
| (2) |
where represents the output variable value with respect to the treatment status (1 for having received treatment and 0 if not) and is a set of covariates. This is a very standard approach for causal inference but has to assume other restrictions in order to make it possible to calculate.
3.2. Propensity Score Matching approach (PSM)
For the CATE to work with real observational data, we must first define the propensity score (PS) as the probability of receiving treatment in a binary treatment assignment. More formally:
| (3) |
where is the treatment status. This proves to be useful to reduce dimensionality, which is a key problem of observational studies [44]. Dimensionality relates closely to the unconfoundedness condition in causal inference, which can be written as:
| (4) |
Additionally, Rosenbaum and Rubin [45] proves that Eq. (4) can be rewritten as:
| (5) |
if the unconfoundedness condition holds. The implication is that, conditional on propensity score, treatment assignment is as good as random, which is fundamental for obtaining unbiased causal effects in observational studies.
3.3. Meta-learners
Meta-learners (or meta-algorithms) is a framework that focus on estimating the CATE using any regressor estimator (machine learning or classical OLS), which are called base-learners. There are several different approaches, however in this study we focus on the ones discussed in Künzel et al. [46] and Nie and Wager [47], which are S-T-X-learners and r-learners, respectively. To make a proper definition of each approach, let Y be the outcome variable, X the covariates matrix, W a binary treatment assignment, the estimated of the CATE, the estimated propensity score and the estimated outcome variable. Thus, following Künzel et al. (2019), we define the S-T-X-learners as follows.
3.3.1. S-learner
The S-learner approach consist on one step in which the outcome variable is estimated in a naïve way, considering the treatment as another variable for the regressor estimator. Mathematically, we have:
| (6) |
To estimate the CATE via s-learner approach, we have:
| (7) |
3.3.2. T-learner
The T-learner approach consists of two steps. First, a regressor estimates a model for only the treated individuals, and then another regressor estimates a model for the untreated individuals. Finally, the estimated CATE would be the difference between the two. Mathematically, expressed as:
| (8) |
for the untreated and treated, respectively. The t-learner estimation of the CATE then is expressed as:
| (9) |
3.3.3. X-learner
The X-learner is an extension of the T-learner and consists of three steps. First, two regressor estimators are fitted separately into the treated and untreated subsamples. Second, we calculate the imputed treatment effects, which is the difference between the outcome of one group with the estimation of the other group model for the same covariates. Finally, we weight both imputed treatments effect by propensity scores. Mathematically, we first have Eq. (4) for the first step, then we calculate the imputed treatment effects as:
| (10) |
With Eq. (6), we define the local treatment effects as:
| (11) |
Finally, we can calculate the CATE as the weighting average of Eq. (7) using propensity score as the weighting function:
| (12) |
3.3.4. R-learner
The R-learner is based on fitting the regressor estimator by minimizing a special loss function that can capture heterogeneous treatment effects. Following Nie and Wager (2017), first both outcome variable and propensity score are estimated by a regressor, and then the proposed loss function is calculated for performance adjustment (i.e., backpropagation in neural networks). Mathematically, this is expressed as:
| (13) |
The regressor learns (or penalized) following the loss function:
| (14) |
Finally, the CATE is calculated as:
| (15) |
where is a regularization of the complexity of the CATE function.
3.4. Causal Forest (CF)
For the CF analysis, we use the work of Wager and Athey [20], using the ‘GRF’ package created by the same authors in R. This methodology is also based on the potential outcome theory, but it makes use of decision tree theory to ensure heterogeneity in the model. Specifically, following [20], an important aspect for the trees to work is that the data satisfied the unconfoundedness assumption explained above.
This implies, together with the definition in Eq. (2) of propensity scores, that Eq. (1) can be rewritten as an unbiased estimator of the causal effect as:
| (16) |
In order to calculate the CATE in Eq. (8) with decision trees (here on, causal trees, (CT)), they must be honest and achieve heterogeneity in their leaves. The first condition is achieved by a special growing scheme known as double-sample trees. This states that we take a subsample of the data and split it into two groups: one to find the splits of the tree, and the other one the estimation. It is important to note that the split is done without looking at the response variable. The second condition is achieved by changing the loss function. Specifically, the CT are closely related to regression trees in construction, so instead of having a loss function for prediction such as mean square error (MSE), CT must adapt by a loss function that penalizes homogeneity in each split and final leaves. This ensure that not only are the predictions good (which is an important part of causal analysis) but also that each leaf satisfied a matching criterion wherein for each leaf there are similar individuals with different treatment assignment thereby acting as if it were a randomize experiment.
3.5. Proposed methodology
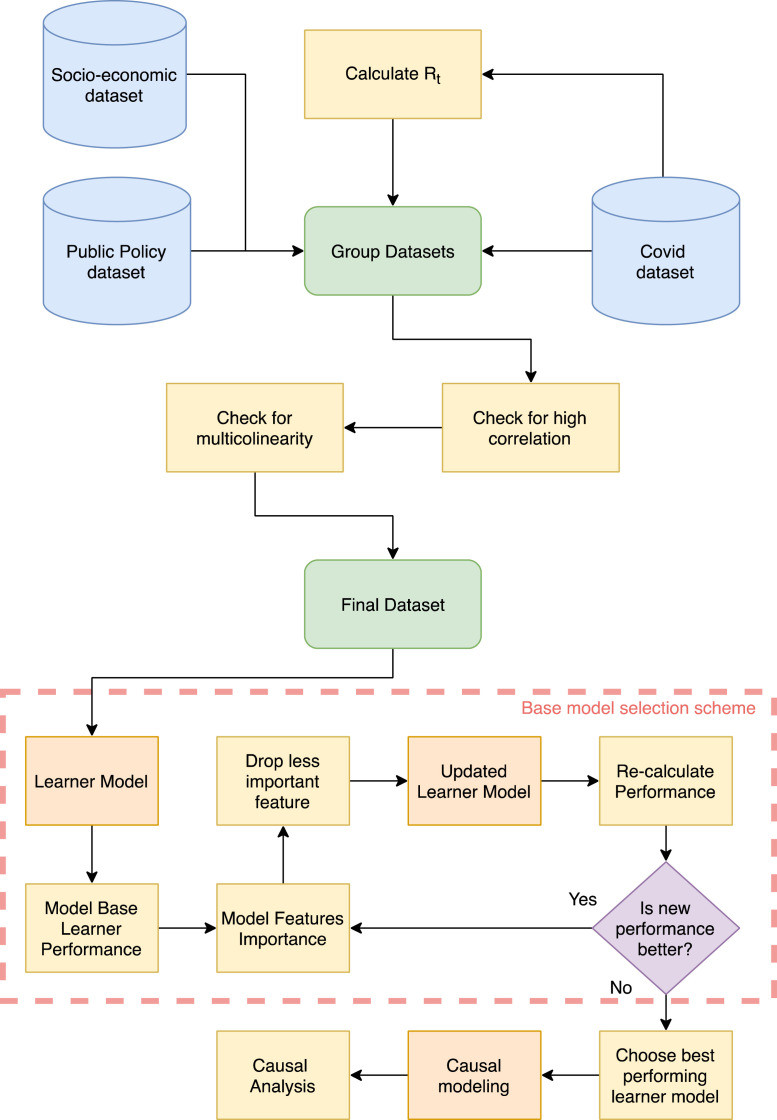
In this study we propose a framework to determine which model to use in a causal inference task. Fig. 3.1 show the steps of the framework.
Fig. 3.1.
Proposed framework to determine causal model for inference.
The first part of the framework consists on aggregating the different datasets that are needed to fit the models. There are three sources of information: first is the data from the Ministry of Health2 (MINSAL) regarding weekly infections, quarantine dates, and daily incidents for . This data is made publicly available to researchers in an effort to promote the development of new knowledge about issues surrounding the pandemic. Information contained on the site include minutes of board meetings and reports published to date. Full descriptions of the data are available on the MINSAL repository. To calculate we use daily data since we use the package “EpiEstim” in R [48]. We use the parametric approach for every municipality separately. Then we average the corresponding weeks to obtain a weekly estimation of for each epidemiological week. Second, the public policy dataset corresponds to the quarantine status of every municipality, updated weekly by the authorities. This information is also available in the MINSAL repository.1 These two datasets are time-dependent and are easy to combine. Finally, the dataset of socio-economic features was obtained from different official sites, all publicly available. Appendix A.1 has all the links and variables available. This dataset is not time-dependent for this study, as the socio-economic characteristic of every municipality remains constant for the analyzed period. To merge this information with the previous datasets, we assume these features to be constant for each municipality across time. Once the three datasets are merged, we check for high correlation and then for multicollinearity that could induce bias/error in the further steps. Table 3.1 shows the final dataset description, in which is the outcome variable, quarantine state (qstatus) is the treatment variable (if the municipality is under quarantine or not for some week), and the rest are the covariates matrix.
Table 3.1.
Variables to use in the causal analysis.
| Variable | Meaning | Unit |
|---|---|---|
| R | Effective reproductive number for municipality i on week j | Real |
| qstatus | If municipality i is on quarantine or not on week j | Binary |
| new_cases | New cases in municipality i on week j | Integer |
| pop | Population of municipality i | Integer |
| IDSE | Social and Economic Development Index for area i | Percent |
| i_percapita | Wage per capita for municipality i | Real |
| poverty | Poverty rate for municipality i | Integer |
| scholarity | Scholarship level for municipality i | Integer |
| sewerage | Sewerage level for municipality i | Percent |
| rural_pop | Total rural population for municipality i | Integer |
| tot_woman | Total woman population for municipality i | Integer |
| rural_housing | Total rural households for municipality i | Integer |
| surface | Total surface area for municipality i | Real |
| density | Density level for municipality i | Integer |
| youth_dep | How many people young ones depend on for municipality i | Integer |
| old_dep | How many people elder ones depend on for municipality i | Integer |
| crit_crowding | Critical overcrowding level for municipality i | Integer |
| WSFC | Weeks since first case for municipality i | Integer |
Variables , qstatus, incident and WSFC relate with time in the following manner. We consider the information of time t as a particular characteristic of the individual in that time, being different than other characteristics at other times. The idea is to add the time series information in the causal analysis, not just of the same time but also of the past as detailed later. This means that a single individual has different characteristics depending on the time that is analyze. The approach is very similar to the time-trend approach adopted in econometrics (e.g. [48], [49], [50], [51]), where time (such as year 2020) is a variable itself in the analysis (i.e., 20 if the analysis started in 2000 and is yearly based). This also implies that we have two kind of variables that characterize each individual: these are variables that differ in time (as mentioned above) and variables that do not change in time, just for each municipality (like population, density and so on). Therefore, the final subjects differ from each other even if the municipality is the same, as their time variables makes them unique and requires a detailed definition of each of these time variables.
WFSC is a direct adaptation of the econometric time-trend approach, with the particularity that each municipality has an individual first time, so that the WFSC is specific for each municipality. Quarantine status can be considered an independent variable across time since we use a weekly analysis of the pandemic, and quarantines are evaluated on a weekly basis as well. Week dates, then, are the same for both quarantine and incidents. By definition, quarantines are analyzed considering several factors, but the fact that the municipality was on quarantine or not does not play a key role in determining the current quarantine status. Here we want to note that in Chile, some quarantines were applied to part of some municipalities but not to the whole. In those cases, we drop those municipalities for those weeks from the analysis, since they do not relate with the research question: does the quarantine help to diminish in the whole municipality?
Incidents and are the same in terms of time consideration. For incidents, we use the weekly data directly from the Science Ministry of Chile. Since both variables are reported weekly but calculated daily, the assumption of independence does not hold. Daily new cases are a random variable by definition. Daily new cases is a separately generated event that does not depend on the number of new cases from the prior day. Since is calculated under the same principle, it is reasonable to think that, weekly, both variables are randomly distributed.
Table 3.1 constituted the final dataset represented as a green box in Fig. 3.1. We train the models described in Sections 3.3, 3.4 with the finalized dataset in the following manner. For the meta-learners, we use the ‘causalml’ library in python [52], using GGXBoost for all four, plus an additional linear regression for the S-learner and multilayer perceptron for the T-learner. For the causal forest, we use the ‘grf’ package in R [53], using generalized regression trees as base models for the outcome and treatment variable. This approach provides a total of 7 possible models to consider for causal analysis.
We propose a selection approach as follows. The first step is to fit the base learner model to analyze and then obtain its performance metrics; this is the regressor used to calculate the outcome variable (according to each individual approach). We consider Mean Square Error, Mean Absolute Error and loglikelihood as sufficient metrics for modeling performance. Then, we get the importance of each features from a causal perspective and drop the least important. With the new covariate matrix, the base learner model is refitted, and performance metrics are recalculated. Finally, if the new metrics are better than the old ones, we repeat the process, else no other feature is dropped, and we end the iterative process. Once every model is optimized by this approach, we compare the final performance of each base learner model (the 7 best base models) and select the model with the best performance. Then, with the best model, we make the final causal analysis, which consists not only in the CATE estimation, but also the importance, SHAP dependence, and SHAP dependence with interaction through time.
3.6. Loss functions
To evaluate which base learner model is able to fit better to the observed data, we calculate three performance metrics: log-likelihood (lL) estimator, Mean Square Error (MSE) and Mean Absolute Error (MAPE). The first one, assuming a normal distribution of the error term in the model, can be calculated as:
| (17) |
where is the estimated outcome variable according to some model with parameters , is the variance of the residuals, and is the mean of the residual of the model.
MSE is calculated as
| (18) |
And MAPE is calculated as
| (19) |
These loss functions are the standard used in most econometric studies. Log-Likelihood measures how well the model can fit the data, where higher values mean a better model. MSE measures how well the model can forecast values after fitting the data. The magnitude of these loss functions depends on the magnitude of the output variable (the independent variable in econometric setting). Contrary to this, MAPE measure, in percentage, the error that the model makes when forecasting a particular data point. The different loss functions allow for a more robust selection of the best model when we compare them. Specifically, we are interested in models with lower MAPE, lower MSE and high lL.
3.7. Shapley values and SHAP plots
For a more comprehensive understanding of the relationship that the covariates have with the outcome variable, we use SHAP plots. These are based on the Shapley values, which are related to the cooperative game theory [54]. They are calculated as the average marginal contribution that a particular covariate has over the average prediction of the outcome variable. In other words, how much a covariate changes the expected value of the outcome variable. With this intuition, Lundberg and Lee [55] create a framework called SHAP (Shapley Additive Explanations) to explain individual prediction instance contribution. Mathematically, SHAP values are obtained as
| (20) |
where D is the simplified features, C is the maximum coalition size, and is the Shapley value. These values represent how much the outcome variable changes for a particular feature (or a set of them). We concentrate the analysis on two SHAP plots: summary and dependence with interaction. The first one is a combination of importance and Shapley values, and each point represents the Shapley value for a particular instance for each feature. The second plot allows for a more comprehensive analysis since it shows the additional combined covariate effect after it isolates the particular covariate effect. Generally, we compare the effects of two covariate. In particular, we compare the combined effect of the covariates with the WSFC variables over the outcome.
4. Results
The data used in this study, as explained in the previous section, comes from three sources. For the socio-economic dataset, we take the information as constant for every municipality across time, selecting the variables that were presented in Table 3.1 in Section 3.6. For the quarantine (public policy dataset) and new cases (COVID dataset), the data was taken from January 15 to August 15 of 2020. We calculate daily for each municipality, and then we average it accordingly to match it to the epidemiological weeks defined by the MINSAL. To have a good representation of the problem, we just take the datapoints in each municipality that have at least 100 accumulated cases. Finally, when the socioeconomic dataset is merged with the other two datasets of the pandemic, we have a matrix of 3149 samples, and variables expressed in Table 3.1 of Section 3.6. It is important to note that some quarantines were applied partially in a municipality; in these cases, we drop the sample since it does not relate with the proposed problem and could induce bias.
We are interested in assessing the impact that the WSFC variable has on model performance and variable interaction, and ultimately if it can produce better causal inference. To see this, we apply the described framework with and without WSFC, and compare the results. Table 4.1, Table 4.2 shows the base model results with and without WSFC, respectively.
Table 4.1.
Best Base model results with WSFC.
| LR | MLP | CF | S-learner | T-learner | X-learner | R-learner | |
|---|---|---|---|---|---|---|---|
| MSE | 1.371 | 1.956 | 0.756 | 0.037 | 0.026 | 0.026 | 0.0329 |
| MAPE | 58.90% | 65.48% | 32.05% | 10.02% | 7.74% | 7.68% | 9.64% |
| LL | −4965.45 | −5524.47 | −4028.54 | 731.65 | 1255.89 | 1293.56 | 909.57 |
Table 4.2.
Best Base model results without WSFC.
| LR | MLP | CF | S-learner | T-learner | X-learner | R-learner | |
|---|---|---|---|---|---|---|---|
| MSE | 1.632 | 1.975 | 1.011 | 0.138 | 0.121 | 0.121 | 0.139 |
| MAPE | 61.80% | 67.26% | 44.01% | 13.58% | 10.66% | 10.66% | 13.79% |
| LL | −5239.43 | −5539.97 | −4484.69 | −1345.42 | −1149.31 | −1149.31 | −1361.55 |
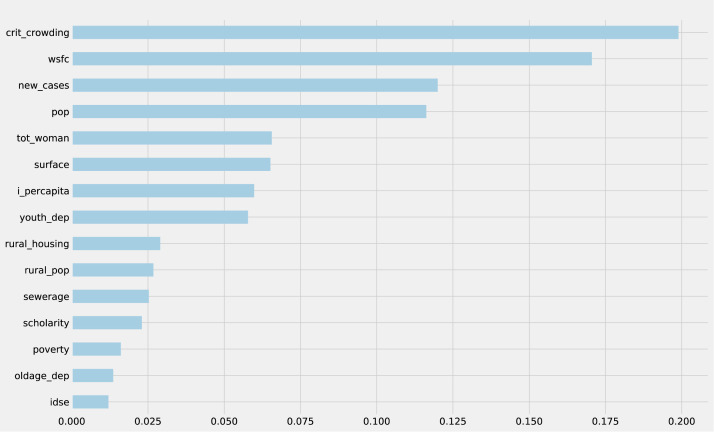
The first interesting result that we see is that in all base learner models, individually, WSFC improves the performance with respect to all three loss functions. Including a time variable in the analysis allows for better understanding of the problem in general and could also imply a better causal model. The second interesting result to note is that the X-learner model has the best performance with and without WSFC, so we select this model to do causal inference over the dataset. It is important to notice that in the case of no WSFC, both T-learner and X-learner achieve the same results. This indicates that, for that particular matrix of covariates, the second step of the X-learner does not change the findings of the first step (which is identical to the T-learner) thus both have the same result. However, when WSFC is added as a covariate, this changes the relationship in the second step, reducing error (and bias) by controlling for imbalance in the sample. With X-learner as the final model, we start by analyzing the importance of each covariate, shown in Fig. 4.1
Fig. 4.1.
X-learner importance.
We can see that the importance distribution is sparse, with 4 variables over 10% of importance as illustrated in Fig. 4.1. These variables are critical crowding, WSFC, new incidents and municipality population. All four of them are very relevant for the control of the pandemic, as they represent key aspect to consider in an air-transmitted disease. Critical crowding is crucial as proximity is an important aspect of COVID-19 transmission. WSFC is the time variable counting weeks passed since the first case appeared in the municipality, which is also important as it is relatively accepted that the pandemic has an asymptotical bell-shaped form, so in the first weeks the virus is strongly present. New cases are related with the previous variable, in the sense that more infected people per week is a clear indicator of the development of a pandemic. Municipality population is also an interesting covariate as the pandemic is related to the amount of people; more people could indicate more cases and a higher contagion rate. There are four more covariates that have just over 5% importance: Total women population, surface of the municipality, income per capita, and youth dependence.
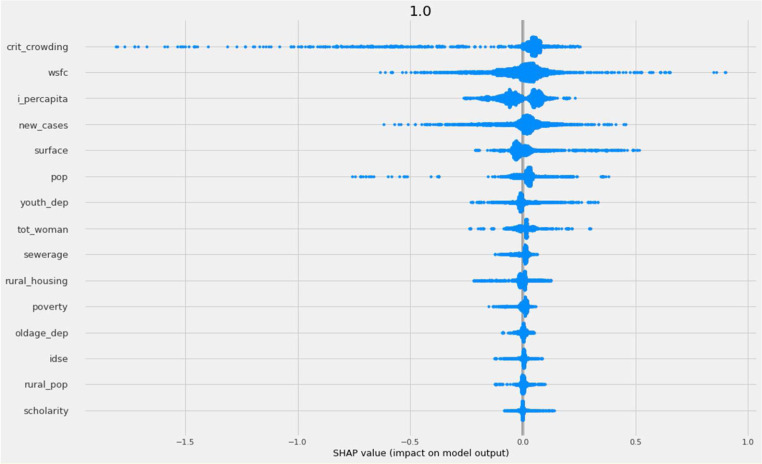
To see the impact of each covariate in the response variable, we make use of a SHAP summary and dependence plot ([55]). Although these are not causally informative, they do illustrate some interesting findings. Fig. 4.2 shows the SHAP summary plot of the X-learner model
Fig. 4.2.
SHAP values for treatment units.
Here we can see that the four most important variables described above, have a relatively positive relationship with . This would imply, for example, that a more crowded municipality has a higher risk of contagion. Second, for the WSFC case, it would imply that when more weeks pass, the pandemic increases. It is also interesting to see that there is an important part of the influence on the negative side, seen in reality when the pandemic passes it peak, where the contagion starts to diminish (in the first wave). New incidents have an interesting interpretation, as it had a slight but almost constant influence over the contagion, which means that the more cases per day there are implies a greater chance of high contagion. Finally, population also has a slight but more clearly positive impact on , meaning that for more populated municipalities, there are more chances of a higher .
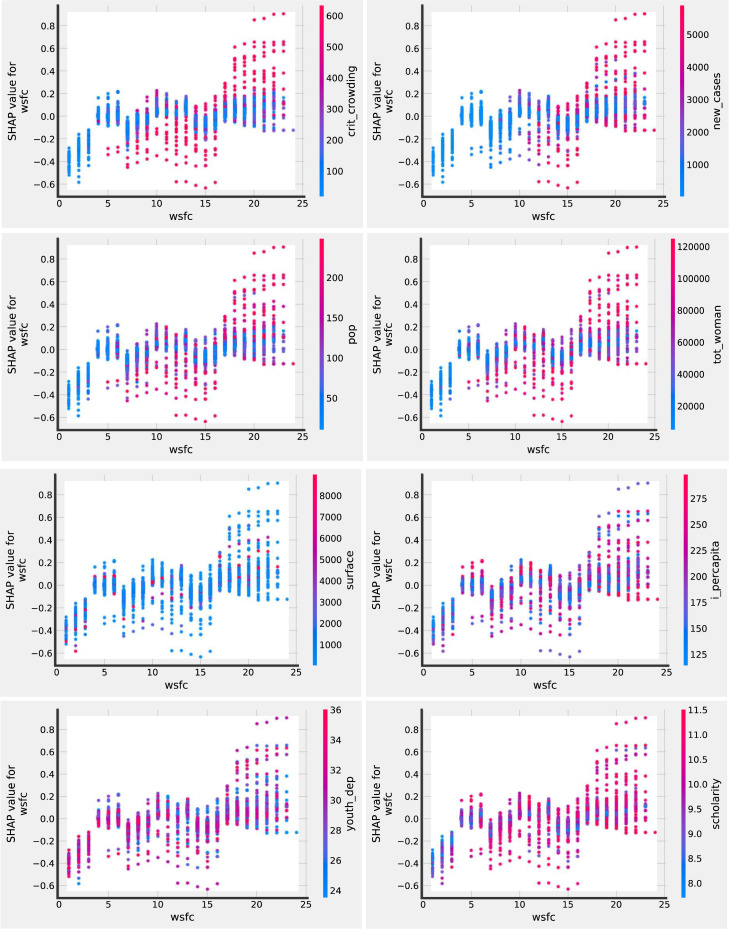
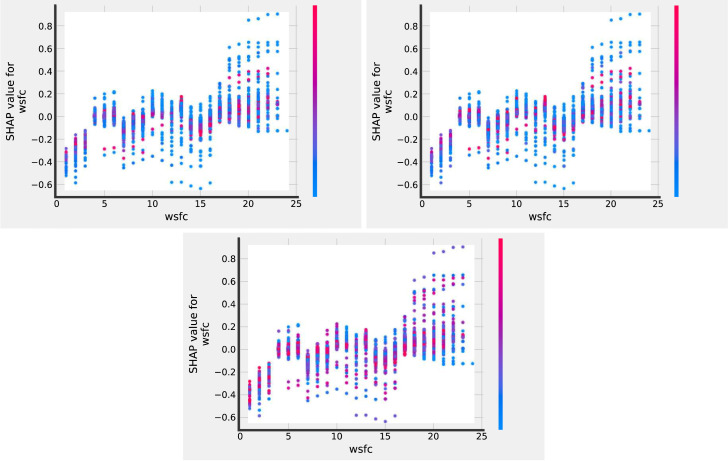
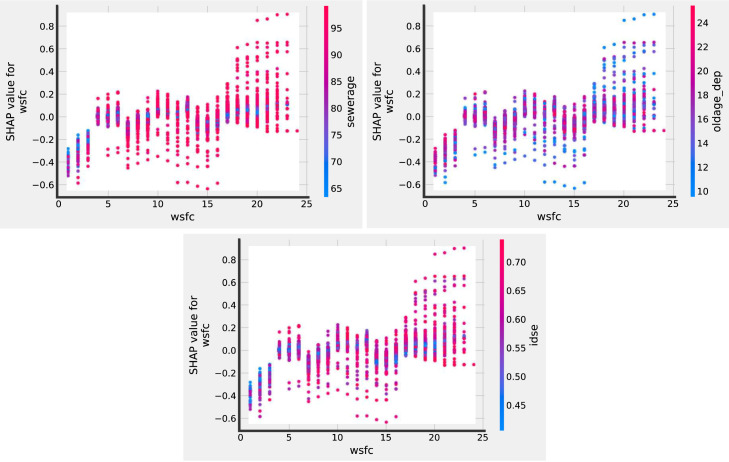
To see more clearly the impact of the WSFC covariate in the analysis, we plot the SHAP dependence interaction of all the other covariates with WSFC. This allows for a time-dependent relationship of these covariates and how they influence the pandemic through time. Fig. 4.3 shows the plots of 8 of the most important covariates. Other covariates are provided in Appendix A.2.
Fig. 4.3.
SHAP dependence interaction plots.
With this we can draw a more comprehensive analysis of the covariates and how they relate to . With the introduction of WSFC, we can observe the influence of each variable over the contagion rate through the time scale and how the value of the variable influences the outcome. In each plot, the blue (red) points are the low (high) values of the studied variable. In general, we can observe that the effectiveness of the lockdown was greater in the first weeks from the first case and in weeks 6 to 16. After week 16, the lockdown policy clearly lost effectiveness.
We can see in the results that critical crowding has a mixed effect through the weeks. We that less dense municipalities were on lockdown in the first three weeks thereafter followed by the more densely populated areas. The higher crowed municipalities were on lockdown after five weeks since the first case. For the low crowed municipalities, the effectiveness of the lockdown is only in the first three weeks after the first COVID case; while for higher crowed municipalities, the effectiveness was from the fifth to sixteenth weeks from the first case. After the sixteenth week, clearly the lockdown policy does not have an effect on the reduction in the contagious. The results suggest that many people did not respect the lockdown and the number of new cases increased.
In the SHAP plot of new cases, it can observed that the number of new cases increased through the weeks since the first cases. The lockdown was effective in the first weeks with the highest number of new cases (red points, weeks 12–16), suggesting that people may have been afraid, but after this period the highest number of new cases does not have a diminishing effect on the contagion. Population and total women have very similar interaction with compared to critical crowding. First the influence is mixed but leaning to negative effects as illustrated in Fig. 4.3, then when around four months have passed the influence on infectious rate is almost strictly positive. This relationship could be related, as the previous covariates, to when the pandemic had some time to spread, the population impacts greatly in the contagion rate.
With respect to surface, the SHAP plot shows that majority of the municipalities that were on lockdown are small (majority of points are blue). In this case, the size of the municipality measured by surface does not have a special behavior through the time scale from the first case.
Income per capita and the youth dependency does not show a clear effect on the contagion rate through the weeks since the first case. In all the weeks, we see that the blue and red points are spread throughout the range of the effect. In the case of the education, we observe that the municipalities that were on lockdown in the first weeks were characterized by lower levels of education.
Up to this point, we have addressed the relationship of the covariates with the and how they vary through time, but no causal effects nor analysis can be drawn. For this, we calculate the Conditional Average Treatment Effect (CATE) for all the models (considering the best base model in every case), which are shown in Table 4.3
Table 4.3.
CATE for all models (best bases model considered).
| LR | MLP | CF | S-learner | T-learner | X-learner | R-learner | |
|---|---|---|---|---|---|---|---|
| With WSFC | −0.289 | −0.730 | −0.579 | −0.220 | −0.650 | −0.331 | −0.322 |
| Without WSFC | −0.507 | −0.821 | −0.597 | −0.307 | −0.722 | −0.355 | −0.346 |
The first thing of note is that when WSFC is added as a covariate, all the CATE values are lowered. This adds to the previous analysis of the relationship of the covariate with . The reduction of the causal effect when the time variable is added could indicate that it was an important cofounder for causal analysis. This is interesting as the WSFC relates strongly with the econometric panel data approach where it is a common practice to consider time as an additional variable for modeling. It also implies that when time is considered, the overall effect of the non-pharmaceutical interventions is less than when it is not considered, which could impact greatly in the evaluation of the public policies.
With this last part, we argue that the dynamic quarantine approach adopted by the MINSAL helped to control the pandemic in Chile, because all the models, with and without the time factor, arrive at a negative CATE. What we find is that the quarantines help to diminish the contagion rate by a considerable amount (−0.331 in the case of the X-learner with WSFC), having several key features controlled (e.g. critical crowding, new weekly cases, etc.). In other words, the results show that non-pharmaceutical intervention, i.e. lockdown, can effectively reduce the spread of the pandemic.
5. Discussion
The results indicate that, at least in Chile, the non-pharmacological intervention of dynamic quarantine helped to slow down the spread of the pandemic. This can be obtained independent of the causal modeling used, and also with and without the WSFC variable. However, it is interesting to see that the effect is lower when time is added to modeling. This could indicate that quarantines are important to control the spread. This is also seen in the literature, where in countries such as Italy [56], China [37], and Canada [57], similar conclusions are drawn. Other studies such as Nussbaumer-Streit et al. [58], Chowdhury et al. [59] also find evidence of the importance of dynamic quarantine.
We compared the impact of the covariates across time using the SHAP dependence plot with interaction. The effectiveness of the lockdown was greater in the first weeks from the first case and in the weeks six to sixteen. After week sixteen, the lockdown policy clearly lost effectiveness. Without the WSFC variable introduction, we would not be able to discriminate the effectiveness of the lockdown through the time scale. It was very important to detect the reducing effect of the lockdown policy to make better decisions in the future in the next wave of COVID-19 or in new pandemic virus.
Although it is accepted that dynamic quarantines are a good measure for (at least) the partial control of the pandemic, it is recommended that it be accompanied with other social measures. In our study, we can see that one of the most important variables is critical crowding. We see that in the SHAP plot, the influence of this features is mainly positive, so more crowded municipalities are more likely to enter in quarantine. However, this could also result in lower quality of life such as confinement (especially in crowded spaces) which could bring negative effect such as poor mental health [60].
The models presented here provide good insights for policy-makers in actions that may be taken to mitigate the spread of a virus during a pandemic. Taken together with the various features of the model, leaders in a municipality such as healthcare providers or human services departments can take sanitary measures that are relevant for their particular makeup. The machine learning applications allow us to more accurately and more quickly take actions that are relevant to the particular locations and circumstances. The result of the improved modeling and action taken may result in better communication and transparency that are not perceived as universal and draconian as mentioned in the introduction to this paper.
6. Conclusions
In this study, we wanted to analyze the causal impact that non-pharmaceutical intervention (lockdown) has on contagion rate () at the municipality level in Chile. For this, we employed various machine learning models that are capable of doing causal inference when the appropriate conditions are met (unconfoundedness, overlap and positivity). For finding the appropriate model for causal inference, we proposed a framework that determines the best base model (this is, the machine learning model for non-causal prediction) following an iterative process where the least important variables are dropped and the model is retrained/fitted. From the best performing models, we selected the top one among them and conducted an influence/relationship analysis through importance and SHAP plots. Finally, we calculated the CATE for causal analysis, and determined the implications of the public policy of dynamic quarantine in Chile.
Before model selection, we found that the time variable(WSFC) improved performance across the board for all seven models analyzed: MSE, MAPE were reduced and lL maximized when we considered the time variable, leading to a better model performance. We find that the best base model was the XGBoost in the X-learner set up, achieving the best performance in all three metrics (MSE, MAPE, lL) and in the two approaches of the study (with and without the time factor). Specifically, we find that both T-learner and X-learner have the best performance in the no-WSFC set up, but since X-learner is an extension of T-learner, we selected the former for further analysis.
With the X-learner model, we analyzed first the performance to see which covariates were affected more in the modeling. We find that there are four covariates that have more than 10% importance: critical crowding; new cases; population; and the time variable (weeks since first case, WSFC). The first interesting thing about these variables is that they are time dependent (new cases and WSFC) and the other two are not (crowding and population). Considering that the most important one is actually one of the two that do not depend on time, we find that time variables improve the modeling capability of machine learning models in tasks that are not of time series. Second, we analyze the contribution to prediction of each variable through SHAP summary plots.
Finally, when causality is analyzed, we see that independent of the models that were use, the dynamic quarantine approach proposed by the MINSAL helped to reduce the contagion rate in Chilean municipalities. Also independent of the model, when WSFC is considered, the causal effect of the lockdown is diminished, which combined with the non-causal analysis, we think is related to a better modeling. With the selected model, we find that the quarantine manages to reduce in about 0.3 points, an important amount if we consider that the mean value of for the dataset is 1.76.
7. Future work
We consider as a future work a more direct approach for causal model discrimination, using indicators or tests that can effectively determine which causal approach is best in a causal setting. Also, the presented framework can easily be extended for other countries, as long as the features are captured and available. Generally, this is the case, but some features like dependence index could be hard to find or simply not measured by the country. In those cases, the framework could be modified accordingly given the flexibility of the approach with respect to features. However, the conclusion cannot be comparable with other countries unless the features are the same. The primary challenge of studies of this type is data availability. On one hand, the COVID-19 data is easy to obtain, either from official international datasets or for local public health offices. However, as briefly mentioned above, the additional features could be difficult to obtain. This could augmented by future work to determine which variables could be added to see if their forecasts influence the impacts the results.
The principal limitation of the study is the unconfoundedness assumption, which implies that we are assuming that, with the additional features considered, the causal impact of quarantine on the effective reproductive number is not mediated by others factor. This is generally assumed but could be interesting to make a causal graph analysis to determine which variables are actually needed to determine the direct causal impact.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgment
We acknowledge financial support from ANID-Chile FONDECYT 1200555.
Footnotes
Appendix.
A.1. Socioeconomic dataset
The socioeconomic dataset was obtained from differentsources. As was mentioned in the Methodology section, some of the variables were dropped due to multi-collinearity or high correlation. From the Urban Observatory (Observatorio Urbano, https://www.observatoriourbano.cl/estadisticas-habitacionales/), we selected the covariates low, normal and critical crowding. From the Public Health Chilean Observatory (Observatorio Chileno de Salud Pública, http://www.ochisap.cl/index.php/nivel-socioeconomico-y-de-salud-de-las-comunas-de-chile) we selected the covariates of IDSE, population, income per capita, poverty, scholarity, construction material level, sewer, survivor hope at birth, human develop index, child mortality. From the National Statistical Instituted (Instituto Nacional de Estadística, http://geoine-ine-chile.opendata.arcgis.com/datasets) we selected the covariates total, youth and old dependence, men and woman population, density, surface, total, rural and urban housing and water accesses.
A.2. SHAP dependence with interaction for the other covariates
See Fig. A.2.1, Fig. A.2.2.
Fig. A.2.1.
SHAP dependence with interaction plots.
Fig. A.2.2.
SHAP dependence with interaction plots.
References
- 1.Bauer L., Broady K.E., Edelberg W., O’Donnell J. The Hamilton Project, Brookings Institute; Washington, D.C.: 2020. Ten Facts About COVID-19 and the U.S. Economy. https://www.brookings.edu/wp-content/uploads/2020/09/FutureShutdowns_Facts_LO_Final.pdf. [Google Scholar]
- 2.Feuere W. CNBC News, Health and Science; 2020. ‘PandEmic Fatigue’ Leads to Resurgence of Coronavirus in Europe where Cases Hit Fresh Records in France and Spain. https://www.cnbc.com/2020/09/18/pandemic-fatigue-leads-to-resurgence-of-coronavirus-in-europe-where-france-and-spain-hit-records.html. [Google Scholar]
- 3.Abusam A., Abusam R., Al-Anzi B. Adequacy of Logistic models for describing the dynamics of COVID-19 pandemic. Infect. Dis. Model. 2020;5:536–542. doi: 10.1016/j.idm.2020.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Muñoz Lezcano S., López Hernández F.C., Corbi Bellot A. Data science techniques for COVID-19 in intensive care units. Int. J. Interact. Multimedia Artif. Intell. 2020;6(Regular Issue):8–17. [Google Scholar]
- 5.Johansson F.D., Shalit U., Kallus N., Sontag D. 2020. Generalization bounds and representation learning for estimation of potential outcomes and causal effects. arXiv preprint arXiv:2001.07426. [Google Scholar]
- 6.Zheng P., Lee B.C. Hound: Causal learning for datacenter-scale straggler diagnosis. Proc. ACM Meas. Anal. Comput. Syst. 2018;2(1):1–36. [Google Scholar]
- 7.Zou W.Y., Du S., Lee J., Pedersen J. 2020. Heterogeneous causal learning for effectiveness optimization in user marketing. arXiv preprint arXiv:2004.09702. [Google Scholar]
- 8.Davis J., Heller S.B. Using causal forests to predict treatment heterogeneity: An application to summer jobs. Amer. Econ. Rev. 2017;107(5):546–550. [Google Scholar]
- 9.Gulen H., Jens C., Page T.B. 2020. An application of causal forest in corporate finance: How does financing affect investment? Available at SSRN. [Google Scholar]
- 10.Wang L., Cao F., Wang S., Sun M., Dong L. Using k-dependence causal forest to mine the most significant dependency relationships among clinical variables for thyroid disease diagnosis. PLoS One. 2017;12(8) doi: 10.1371/journal.pone.0182070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Grebe G., Vélez J.A., Tiutiunnyk A., Aragón-Caqueo A., Fernández-Salinas J., Navarrette M., Laroze D. Dynamic quarantine: A comparative analysis of the Chilean public health response to COVID-19. Epidemiol. Infect. 2020;148 doi: 10.1017/S0950268820002678. 1-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Shamsi A., Mansourzadeh M.J., Ghazbani A., Khalagi K., Fahimfar N., Ostovar A. Contribution of Iran in COVID-19 studies: a bibliometrics analysis. J. Diabetes Metab. Disord. 2020:1–10. doi: 10.1007/s40200-020-00606-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Holmes E.A., O’Connor R.C., Perry V.H., Tracey I., Wessely S., Arseneault L., … D., Bullmore E. Multidisciplinary research priorities for the COVID-19 pandemic: a call for action for mental health science. Lancet Psychiatry. 2020 doi: 10.1016/S2215-0366(20)30168-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chams N., Chams S., Badran R., Shams A., Araji A., Raad M., … D., Hajj Hussein I. COVID-19: a multidisciplinary review. Front. Public Health. 2020;8:383. doi: 10.3389/fpubh.2020.00383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chintalapudi N., Battineni G., Amenta F. COVID-19 virus outbreak forecasting of registered and recovered cases after sixty day lockdown in Italy: A data driven model approach. J. Microbiol. Immunol. Infect. 2020;53:396–403. doi: 10.1016/j.jmii.2020.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Guliyev H. Determining the spatial effects of COVID-19 using the spatial panel data model. Spat. Statist. 2020;38:1–10. doi: 10.1016/j.spasta.2020.100443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wieczorek M., Siłka J., Woźniak M. Neural network powered COVID-19 spread forecasting model. Chaos Solitons Fractals. 2020;140:1–15. doi: 10.1016/j.chaos.2020.110203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Torrealba-Rodriguez O., Conde-Gutiérrez R.A., Hernández-Javier A.L. Modeling and prediction of COVID-19 in Mexison applying mathematical and computational models. Chaos Solitons Fractals. 2020;138 doi: 10.1016/j.chaos.2020.109946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fong S.J., Li G., Dey N., Crespo R.G., Herrera-Viedma E. Composite Monte Carlo decision making under high uncertainty of novel coronavirus epidemic using hybridized deep learning and fuzzy rule induction. Appl. Soft Comput. 2020 doi: 10.1016/j.asoc.2020.106282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wager S., Athey S. Estimation and inference of heterogeneous treatment effects using random forests. J. Amer. Statist. Assoc. 2018;113(523):1228–1242. [Google Scholar]
- 21.B.J. Marafino, A. Schuler, V.X. Liu, G.J. Escobar, M. Baiocchi. 2020. A Causal Machine Learning Framework for Predicting Preventable Hospital Readmissions. arXiv preprint arXiv:2005.14409. [Google Scholar]
- 22.S. Carbo-Valverde, P. Cuadros-Solas, F. Rodríguez-Fernández. A machine learning approach to the digitalization of bank customers: evidence from random and causal forests. Plos one. 2020;15(10):e0240362. doi: 10.1371/journal.pone.0240362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Miller S. Causal forest estimation of heterogeneous and time-varying environmental policy effects. J. Environ. Econ. Manag. 2020;103:102337. [Google Scholar]
- 24.Sbidian E., Josse J., Lemaitre G., Mayer I., Bernaux M., Gramfort A., Garcelon N. 2020. Hydroxychloroquine with or without azithromycin and in-hospital mortality or discharge in patients hospitalized for COVID-19 infection: a cohort study of 4, 642 in-patients in France. MedRxiv. [Google Scholar]
- 25.Zhang Q., Deng H., Zhang C. 2020. The value of early response by surrounding areas of epidemic center hubei during COVID-2019 outbreak in China: A quasi-experiment analysis. Available at SSRN 3548372. [Google Scholar]
- 26.X.S. Zhang, F. Tang, H.H. Dodge, J. Zhou, F. Wang, Metapred: Meta-learning for clinical risk prediction with limited patient electronic health records, in: Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, 2019, pp. 2487–2495. [DOI] [PMC free article] [PubMed]
- 27.Johansson F.D. 2018. Machine learning analysis of heterogeneity in the effect of student mindset interventions. arXiv preprint arXiv:1811.05975. [Google Scholar]
- 28.Sato R., Yamada M., Kashima H. 2020. Poincare: Recommending publication venues via treatment effect estimation. arXiv preprint arXiv:2010.09157. [Google Scholar]
- 29.Godio A., Pace F., Vergnano A. SEIR modeling of the Italian Epidemic of SARS-CoV-2 using computational swarm intelligence. Int. J. Environ. Res. Public Health. 2020;17(10):3535. doi: 10.3390/ijerph17103535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Dur-e-Ahmad M., Imran M. Transmission Dynamics Model of Coronavirus COVID-19 for the outbreak in most affected countries of the world. Int. J. Interact. Multimedia Artif. Intell. 2020;6(Regular Issue):4. [Google Scholar]
- 31.Tang B., Xia F., Tang S., Bragazzi N.L., Li Q., Sun X., Wu J. The effectiveness of quarantine and isolation determine the trend of the COVID-19 epidemics in the final phase of the current outbreak in China. Int. J. Infect. Dis. 2020;95:228–293. doi: 10.1016/j.ijid.2020.03.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hiremath P., Kowshik C.S., Manjunath M., Shettar M. COVID 19: impact of lock-down on mental health and tips to overcome. Asian J. Psychiatry. 2020;51 doi: 10.1016/j.ajp.2020.102088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Raveendran A.V., Jayadevan R. Reverse quarantine and COVID-19. Diabetes Metab. Syndr. Clin. Res. Rev. 2020;14(5):1323–1325. doi: 10.1016/j.dsx.2020.07.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Gondim J.A.M., Machado L. Optimal quarantine strategies for the COVID-19 pandemic in a population with a discrete age structure. Chaor Solitons Fractals. 2020;140 doi: 10.1016/j.chaos.2020.110166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Nabi K.N. Forecasting COVID-19 pandemic: A data-driven analysis. Chaos Solitons Fractals. 2020;139 doi: 10.1016/j.chaos.2020.110046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Annas S., Pratama M.I., Rifandi M., Sanusi W., Side S. Stability analysis and numerical simulation of SEIR model for pandemic COVID-19 spread in Indonesia. Chaos Solitons Fractals. 2020;139 doi: 10.1016/j.chaos.2020.110072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Cui Q., Hu Z., Li Y., Han J., Teng Z., Qian J. Dynamic variations of the COVID-19 disease at different quarantine strategies in Wuhan and mainland China. J. Infect. Public Health. 2020;13:849–855. doi: 10.1016/j.jiph.2020.05.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Xiao Y., Tang B., Wu J., Cheke R.A., Tang S. Linking key intervention timings to rapid decline of the COVID-19 effective reproductive number to quantify lessons from mainland China. Int. J. Infect. Dis. 2020;97:296–298. doi: 10.1016/j.ijid.2020.06.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Džiugys A., Bieliūnas M., Skarbalius G., Misiulis E., Navakas R. Simplified model of COVIF-19 epidemic prognosis under quarantine and estimation of quarantine effectiveness. Chaos Solitons Fractals. 2020;140 doi: 10.1016/j.chaos.2020.110162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Cochran W.G., Chambers S.P. The planning of observational studies of human populations. J. R. Stat. Soc. A. 1965;128(2):234–266. [Google Scholar]
- 41.Rubin D.B. Estimating causal effects of treatments in randomized and nonrandomized studies. J. Educ. Psychol. 1974;66(5):688. [Google Scholar]
- 42.Splawa-Neyman J., Dabrowska D.M., Speed T.P. On the application of probability theory to agricultural experiments. Essay on principles. Section 9. Statist. Sci. 1990:465–472. [Google Scholar]
- 43.Holland P.W. Statistics and causal inference. J. Amer. Statist. Assoc. 1986;81(396):945–960. [Google Scholar]
- 44.Ho D.E., Imai K., King G., Stuart E.A. Matching as nonparametric preprocessing for reducing model dependence in parametric causal inference. Polit. Anal. 2007;15(3):199–236. [Google Scholar]
- 45.Rosenbaum P.R., Rubin D.B. The central role of the propensity score in observational studies for causal effects. Biometrika. 1983;70:41–55. [Google Scholar]
- 46.Künzel S.R., Sekhon J.S., Bickel P.J., Yu B. Metalearners for estimating heterogeneous treatment effects using machine learning. Proc. Nation. Acad. sci. 2019;116(10):4156–4165. doi: 10.1073/pnas.1804597116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Nie X., Wager S. 2017. Quasi-oracle estimation of heterogeneous treatment effects. arXiv preprint arXiv:1712.04912. [Google Scholar]
- 48.Cori A., Ferguson N.M., Fraser C., Cauchemez S. A new framework and software to estimate time-varying reproduction numbers during epidemics. Am. J. Epidemiol. 2013;178(9):1505–1512. doi: 10.1093/aje/kwt133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Arsova A., Örsal D.D.K. Likelihood-based panel cointegration test in the presence of a linear time trend and cross-sectional dependence. Econometric Rev. 2018;37(10):1033–1050. [Google Scholar]
- 50.Barr B., Taylor-Robinson D., Scott-Samuel A., McKee M., Stuckler D. Suicides associated with the 2008-10 economic recession in England: time trend analysis. BMJ. 2012;345 doi: 10.1136/bmj.e5142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Dong C., Linton O. Additive nonparametric models with time variable and both stationary and nonstationary regressors. J. Econometrics. 2018;207(1):212–236. [Google Scholar]
- 52.Chen H., Harinen T., Lee J.Y., Yung M., Zhao Z. 2020. CausalML: Python Package for Causal Machine Learning. arXiv preprint arXiv:2002.11631. [Google Scholar]
- 53.Tibshirani J., Athey S., Friedberg R., Hadad V., Miner L., Wager S., Wright M. 2020. Grf: Generalized random Forests, 2020. URL https://github.com/grf-labs/grf. R package version 1.2.0. [Google Scholar]
- 54.Shapley L.S. A value for n-person games. Contrib. Theory Games. 1953;2(28):307–317. [Google Scholar]
- 55.Lundberg S.M., Lee S.I. Advances in Neural Information Processing Systems. 2017. A unified approach to interpreting model predictions; pp. 4765–4774. [Google Scholar]
- 56.Dickson M.M., Espa G., Giuliani D., Santi F., Savadori L. Assessing the effect of containment measures on the spatio-temporal dynamic of COVID-19 in Italy. Nonlinear Dynam. 2020;101(3):1833–1846. doi: 10.1007/s11071-020-05853-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Tuite A.R., Fisman D.N., Greer A.L. Mathematical modelling of COVID-19 transmission and mitigation strategies in the population of Ontario, Canada. Cmaj. 2020;192(19):E497–E505. doi: 10.1503/cmaj.200476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Nussbaumer-Streit B., Mayr V., Dobrescu A.I., Chapman A., Persad E., Klerings I., … G. Quarantine alone or in combination with other public health measures to control COVID-19: a rapid review. Cochrane Database Syst. Rev. 2020:9. doi: 10.1002/14651858.CD013574.pub2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Chowdhury R., Heng K., Shawon M.S.R., Goh G., Okonofua D., Ochoa-Rosales C., … G., Franco O.H. Dynamic interventions to control COVID-19 pandemic: a multivariate prediction modelling study comparing 16 worldwide countries. Eur. J. Epidemiol. 2020;35(5):389–399. doi: 10.1007/s10654-020-00649-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Guo Y., Cheng C., Zeng Y., Li Y., Zhu M., Yang W., … G., Wu S. Mental health disorders and associated risk factors in Quarantined adults during the COVID-19 outbreak in China: cross-sectional study. J. Med. Internet Res. 2020;22(8) doi: 10.2196/20328. [DOI] [PMC free article] [PubMed] [Google Scholar]