Abstract
Objective:
Adaptive beamformer methods, which have been extensively used for functional brain imaging using EEG/MEG signals, are sensitive to model mismatches. We propose a robust minimum variance beamformer (RMVB) technique, which explicitly incorporates the uncertainty of the lead field matrix into estimation of spatial-filter weights that are subsequently used to perform the imaging.
Methods:
The uncertainty of the lead field is modeled by ellipsoids in the RMVB method; these hyper-ellipsoids (ellipsoids in higher dimensions) define regions of uncertainty for a given nominal lead field vector. These ellipsoids are estimated empirically by sampling lead field vectors surrounding each point of the source space, or more generally by building several forward models for the source space. Once these uncertainty regions (ellipsoids) are estimated, they are used to perform the source-imaging task. Computer simulations are conducted to evaluate the performance of the proposed RMVB technique.
Results:
Our results show that robust beamformers can outperform conventional beamformers in terms of localization error, recovering source dynamics and estimation of the underlying source extents, when uncertainty in the lead field matrix is properly determined and modeled.
Conclusion:
RMVB can substitute conventional beamformers, especially in applications, where source imaging is performed off-line, and computational speed and complexity are not of major concern.
Significance:
A high-quality source imaging can be utilized in various applications such as determining the epileptogenic zone in medically intractable epilepsy patients or estimating the time-course of activity, which is a required step for computing functional connectivity of brain networks.
Keywords: Adaptive beamformer, EEG, Electromagnetic source imaging, Inverse problem, Linearly constrained minimum variance beamformer, MEG, Robust beamformer, Robust minimum variance beamformer
I. Introduction
lectromagnetic source imaging (ESI) [1]–[3] using electroencephalography (EEG) [4], [5] or magnetoencephalography (MEG) [6], [7] measurements is an effective tool for mapping and imaging dynamic brain electrical activities. This functional imaging modality, which is typically non-invasive (see [8]–[10] for ESI using intracranial recordings), has been utilized by many researchers in clinical environments to study the brain function or dysfunction in various physiological or pathological (e.g., in epilepsy patients) conditions. Due to the ill-posed nature of the EEG/MEG source-imaging problem, many techniques have been proposed in the literature to regularize the problem. See [11] for review of ESI techniques. Adaptive beamformers [12], [13], which are the focus of this study, design spatial filters to selectively pass the signals associated with desired locations while suppressing the activities coming from the rest of the brain. The word adaptive corresponds to a feature by which the ultimate model used to solve the inverse problem depends on the measurements as well as the head volume conductor properties. In adaptive beamformers, adaptation is achieved by incorporating the measurements and noise covariance matrices into the problem formulation.
Since first introduced to the brain source imaging community, adaptive beamformers have been more often used for MEG source imaging rather than EEG source imaging [2], [14]. This may in part be due to the fact that sources of uncertainty in the forward modeling of EEG is usually considered to be more extensive compared to MEG. In practice, electrical activities of the brain can be situated anywhere in the brain tissue, while current dipoles are assumed in fixed and pre-discretized locations (in a distributed model). In addition, there are levels of uncertainty in the electrical properties of the head volume conductor, such as the relative conductivity ratios of different tissues (the scalp, the skull and the brain, in boundary element model) and their inhomogeneity profiles. Furthermore, realistic head volume model of the subject may be unavailable in some cases. Unreliable estimation of the covariance matrices because of insufficient or noisy data is another source of error in practice. Consequently, availability of the true lead field is almost impossible in many cases. On the other hand, beamformers are generally sensitive to the errors in the forward models. More specifically, linearly constrained minimum variance (LCMV) beamformer, which is the base of all adaptive beamformers, is known to be highly sensitive even to slight mismatches between the true and estimated models [15], [16]. See e.g., [14] for a detailed beamformer analysis of sensitivity to the forward modeling mismatches.
To deal with these issues, the authors of [17], [18] have applied a technique called diagonal loading (DL) to the MEG source localization problem. DL replaces the covariance matrix of the measurements with a regularized version, by adding a constant factor of the unity matrix to the measurement covariance matrix. Although DL can reduce the sensitivity to some extent, it is understood that such regularizations lead to a trade-off between the output signal-to-noise ratio (SNR) and the spatial resolution of the LCMV [15]. More importantly, it is not clear how to determine the optimal value of the DL factor based on known levels of uncertainty in the lead field matrix [16]. Besides DL, eigenspace beamformer [15], [19] is another technique that can yield robustness against modeling errors as well as measurement noise. We sought to show that the performance of this method may be further improved if the uncertainty in the forward modeling is taken into consideration in the model. While modeling lead field uncertainty has already been investigated in the signal processing community through a technique called robust minimum variance beamformer (RMVB) [16], [20], [21], this study, to the best of our knowledge, is the first to adapt the RMVB to functional brain imaging and source imaging. Besides output SNR, which was originally used to compare the RMVB to its peers, we used three other criteria to investigate the merits and limitations of the RMVB and to compare its accuracy to the conventional adaptive beamformers for the purpose of ESI. To this end, we conducted comprehensive computer simulations to show the merits of a robust modeling.
II. Methods
Brain electrical activities can be modeled by current dipoles [1], [22]. Since Maxwell’s equations are solved in a quasi-static regime, it can be assumed that the relation between these dipoles and the EEG/MEG potentials generated at the sensors is instantaneous and linear [23]. More specifically,
| #(1) |
where is the matrix of EEG/MEG potentials generated /recorded at the sensors at different time points, is the lead field matrix defining the linear relation between the current dipoles and the potentials, is the matrix of current dipoles over time and models the noise at the sensors over time. Assuming sensors, current dipoles and time points, and are the matrices of size is a matrix of size and is a matrix of size , which encompasses the geometrical and electrical properties of the medium through which brain signals propagate to reach to the sensors.
A. Linearly Constrained Minimum Variance (LCMV)
The goal of ESI techniques is to recover the underlying source activity (current dipole matrix J) using a set of electromagnetic recordings (the measurements matrix Φ). Scanning techniques (LCMV, (RAP)-MUSIC, FINES, etc.) [13], [24], [25] use all the measurements to estimate only a single element of the current dipole vector located in a specific voxel, so in order to estimate the full current dipole vector, all predefined source space locations have to be scanned; hence the name scanning. LCMV, which lies in this category, performs the task by designing a spatial filter for each voxel. This spatial filter is a linear operator, which once applied to the measurement matrix Φ, back-projects the activities of a desired voxel from the scalp measurements, while attempting to suppress the activities of all other voxels besides noise. This procedure is repeated until all current dipoles (at every voxel in the source space) are estimated. Speaking more mathematically, LCMV solves the following optimization problem:
| #(2) |
where is the measurements covariance matrix of size (see Practical Considerations section in the Supplementary materials for estimation details), is the column of the lead field matrix corresponding to the current dipole at the voxel and is a vector of size , which yields the estimation of dipole through the following equation:
| #(3) |
Using Lagrange multipliers method, the optimal solution of this optimization problem can be shown to be
| #(4) |
To provide an intuitive interpretation of this procedure, one should notice that the objective function in the optimization problem (2) is in fact the output power of the linear filter (or the variance of the estimated current dipole at voxel ). By minimizing the filter output power (minimum variance (MV)) under the constraint (linearly constrained (LC)), LCMV ensures that to the best of its ability, the filter removes the contribution of all irrelevant activities to the measurements while keeping the desired signal intact.
Based on (4), it is clear that is inversely proportional to the norm of the lead field column associated with the voxel. Since the norm of the lead field vector is generally smaller for the voxels that are located further away from the electrodes, the filter coefficients become larger for deeper locations. This generates some bias towards deeper activities. Additionally, depending on the location and orientation of the dipoles, noise may affect the sources differently. To compensate for the depth and asymmetric spatial distribution of the noise, LCMV is usually followed by a normalization step of the filter coefficients [13], [18], [19], [26]. To this end, the filter coefficients are normalized either by their norm [19] or by a factor, which is a function of noise covariance matrix. This factor can be calculated in different ways [18], for example by finding the power of each voxel, if the filter coefficients are applied to pure noise data. In other words, the filter coefficients can be normalized according to
| #(5) |
where is the noise covariance matrix estimated using baseline (see Practical Considerations section in the Supplementary materials for estimation details). The authors of [13] employed a slightly different strategy; they first customized the filter coefficients by solving the optimization problem (2) for noise-only segments and then followed the same strategy, i.e.,
| #(6) |
where is the solution of the optimization problem (2) with the measurements covariance matrix replaced with noise covariance matrix . This strategy was adopted for normalization throughout this study. It should be mentioned that in some applications such as resting state analysis, the estimation of noise covariance matrix is not straightforward. In such situations, can be replaced with a unity matrix of appropriate size, which is equivalent to assuming pure white and identically distributed noise across all sensors.
Besides the normalization, LCMV can also benefit significantly from a denoising procedure in the end. This method, which is called the eigenspace beamformer, was first introduced by [15], [19] to the source imaging community. The eigenspace beamformer assumes that the number of sources is known a priori. It then exploits this information to separate the signal and noise subspace and project the filter coefficients vector onto the signal subspace as follows:
| #(7) |
where is the truncated covariance matrix of the measurements is calculated by keeping the principal components (associated with dominant singular values) obtained from singular-value decomposition (SVD) of matrix and setting the rest to zero (the small values are assumed to be due to noise). In practice, there are different approaches to determine the number of principal components. The number of components can be estimated by keeping the components that explain a preset level of variation starting from components with higher singular values, or those components that lie above the knee of the curve showing the sorted singular values. In this study, Kaiser’s rule [27] was used to select the number of principal components. More specifically, we kept the components associated with the singular values, which were greater than the average of all singular values.
Based on our simulations, while both the normalization and denoising steps play an important role in the quality of the LCMV solutions, the role of denoising is more crucial. Furthermore, applying both steps in series improves the accuracy of solutions only slightly, compared to the denoising alone. Nonetheless, we decided to implement both steps in this study, since it was quite straightforward to apply the normalization step as well. This method will be referred to as “LCMV-ND-DN” (LCMV-normalized-denoised) in the rest of this paper.
B. Robust Minimum Variance Beamforemer (RMVB)
In order to more explicitly consider the uncertainty in the forward modeling, let be an -dimensional ellipsoid centered at , with matrices and determining its size and shape (). This ellipsoid is assumed to cover all possible values for the lead field column of the voxel, namely the uncertainty region (spanned by and vectors). To consider the uncertainty of the lead field, one idea is to enforce the spatial filter to pass the activities associated with not only , but also all values in the uncertainty region . Hence, the LCMV optimization problem (2) can be reformulated as
| #(8) |
The constraint in (8), which includes infinite number of linear equations, is equivalent to:
| #(9) |
Inequality (9) holds if and only if it holds for that minimizes the term . Cauchy-Schwartz inequality and the constraint lead to [16], [21]. By substituting this value and some manipulations, the optimization problem (8) can be expressed as
| #(10) |
which is a second order cone programming (SOCP) problem [28], [29]. After solving this problem, the solution can be normalized such that . Henceforth, we refer to this problem as the robust minimum variance beamformer (RMVB). While the RMVB does not enjoy a closed-form solution as the conventional LCMV, it can still be solved efficiently using any convex optimization solver such as CVX [30], [31] (See Supplementary materials for more details on convex optimization). Additionally, the normalization and denoising steps can also be applied to the solution of RMVB as before. This will be referred to as the RMVB-ND-DN in the rest of the paper.
C. Uncertainty Region Estimation
Multiple sources of uncertainty have to be considered in order to find the uncertainty region, e.g., uncertainty in the location (due to discretization) and orientation of the current dipoles or uncertainty in the forward model parameters (due to insufficient information about the head volume geometry, conductivities, inhomogeneity, etc.). In any case, it is possible to estimate the uncertainty region empirically by sampling the surrounding source space for each voxel [8] or by using several forward models, for instance, constructed for electrical conductivities in a given range [32]. More specifically, assuming neighbors and forward models, the first and second order statistics of the uncertainty for the voxel can be estimated as
| #(11) |
and
| #(12) |
where is the lead field column of the voxel in the forward model, is the lead field column of the sampled neighbor in the forward model, is the average lead field (of all ) to be used in the inverse problem and is the covariance matrix of the uncertainty. The authors of [8] proposed to apply a projection on each before using them in (12). This projection in a fixed-orientation model, which is the case for this study, translates to flipping the sign of (or equivalently the orientation of dipoles), wherever this reduces the distance between and . This is helpful in avoiding overestimation of the uncertainty region size. , which defines the shape and size of the uncertainty ellipsoid, is indeed an inflated version of . The inflation factor can be found such that the uncertainty region contain all the points [21], which mathematically translates to
| #(13) |
See Practical Considerations section in the Supplementary materials for further details of tuning uncertainty ellipsoids sizes.
D. Computer Simulation Protocol
In order to investigate the performance of robust beamformer and compare its merits and limitations to the conventional beamformer, a series of computer simulations were conducted. To this end, a realistic head volume model was built upon the Montreal Neurological Institute Colin brain [33] consisting of three layers i.e., the scalp, the skull and the brain. To solve the forward problem and to simulate the EEG recordings, a standard -cahnnel BioSemi cap was fitted to the Colin brain, and a boundary element method (BEM) model [4], [34] was then derived to find the lead field matrix, which linearly projects the current dipoles to the electrical potentials at the electrodes.
In order to avoid any form of inverse crime and to evaluate the capabilities of robust beamformer in dealing with model violations, different models were derived for the forward and inverse problems. While cortex was meshed very finely with a grid of mm ( elements on the cortex, in total) in the forward problem, a coarser grid of mm ( elements on the cortex, in total) was used for the inverse problem. In the forward model, the electrical conductivity of the scalp, the skull and the brain ( and ) were set to S/m, S/m and S/m, respectively, while an average model based on what follows was built to solve the inverse problem. For estimation of uncertainty regions only the conductivity and discretization uncertainties were considered. To this end, different models were built. The electrical conductivities of the scalp and the brain were fixed to S/m in all the models, while for the skull it was set such that the conductivity ratio () picked values incrementally with the steps of in the physiological range of [35]–[37]. The brain in each model was meshed with two different choices of grid sizes; a same coarser grid of 5mm for the center of uncertainty regions as in the inverse problem and a very fine grid of mm to estimate the variations for the nearest neighbor in the coarser mesh according to (12). In this setting, each point of the fine mesh was considered as a neighbor of one and only one point in the coarser mesh. Note that different fine meshes were used in the forward problem and estimation of uncertainty regions (grid of mm versus mm); as also in real situations the true source space is unavailable beforehand.
In this study, four different scenarios were simulated. The first scenario consisted of point dipoles placed randomly on the cortex with a fixed orientation normal to the cortex surface. To mimic a realistic inter-ictal spike, each dipole was assigned a time course of activity sampled at the rate of kHz (see Fig. S1 in the Supplementary materials). In order to investigate the effect of number of active nodes on the imaging accuracy, in the second scenario, each configuration had three nodes of activity. The time-courses, in this scenario, were such to yield a minimal correlation between the nodes (see Fig. S2. (A and B) in the Supplementary materials). In the third scenario, the time-courses had high correlation factors to consider the effect of correlation between nodes in 3-node networks (see Fig. S2 (C and D) in the Supplementary materials). Please refer to the Supplementary materials to review the results of this scenario. The last scenario was designed to evaluate the performance of robust and conventional beamformers in situations, where sources are not focal. The general criteria in this scenario remained the same as the second scenario with the exception that each node had an extent with a radius size roughly ranging from mm to mm (randomly selected for each node of the network). In this study, all the voxels within the extent of each node had the same amplitude and the same time-course. After solving the forward problem, the generated potentials at the electrodes were contaminated by additive white Gaussian noise (AWGN) to simulate a more realistic condition. The effect of noise was further assessed by considering two different SNRs (calculated based on power) i.e., and dB representing low and high levels of noise. Finally, a fixed-orientation (normal to the cortex surface) model was used to solve the inverse problem. This choice can be justified by the fact that EEG signals are generated by pyramidal cells, which project their dendrites orthogonally to the cortex surface [38]. The simulation protocol in this study is similar to our previous works [9], [39].
E. Performance Measures
Performance in this study was assessed by different metrics, namely dipole localization error (DLE), signal to noise ratio (SNR), receiver operator characteristics (ROC) curve and Matthew’s correlation coefficient (MCC). The former two metrics were used for focal activity scenarios, while the latter two evaluated the conventional and robust beamformers in the extended source scenario. DLE measures the Euclidean distance between the simulated and recovered source locations, which are determined by estimating the foci of activity employing a PCA-based technique (dominant local maxima of the principal components as the foci of activity) [9], [39]. The SNR characterizes how well the temporal profile of the underlying sources can be recovered by ESI. Noise in this metric is defined as the difference between the simulated and recovered time courses. The power of the simulated signal over the power of noise in logarithmic scale yields the SNR in dB. In order to evaluate the concordance between temporal patterns, both the simulated and recovered signals were normalized by their power before SNR was calculated. The time course of the estimated locations, and not the true source locations, were considered in calculating the SNR. In order to compare the simulated and estimated source distributions in the extended source scenario, ROC curve was used to evaluate the trade-off between sensitivity and specificity of the estimation by plotting the true positive rate (TPR) versus false positive rate (FPR) [40] of the estimation. Any location in the solution beyond a threshold is considered a source and active, while any location with an amplitude below the threshold is inactive and not a source. Thresholds are varied, and the FPR and TPR are calculated accordingly (each point of curve is at a different threshold). Area under the curve (AUC) is the area under the ROC curve; a metric for comparing different ROC curves. The closer the AUC of a ROC curve is to , the more accurate the estimation is [41]. MCC, which in essence measures the correlation between the simulated and estimated distributions, is another metric used in this study to assess the estimation quality [42]. MCC calculates the predictability of an observed and estimated classification, which in this case is the source extent, and is formulated as follows:
| #(14) |
where, TP, TN, FP and FN represent the true positive, true negative, false positive and false negative rates of the estimation, respectively. Since MCC works in a binary mode, it requires a thresholding mechanism to turn the estimated distribution into active and inactive regions. In this study, the threshold was swept and determined in such a way to yield the maximum MCC. We note that MCC takes values from to , from the most disparate case to the most concordant case, respectively.
III. Results
The results presented in this section are to evaluate the effect of normalization and denoising procedures in addition to modeling the lead field uncertainty on the ultimate performance of beamformers. To this end, four types of beamformers namely, LCMV [13], RMVB [16], [21], LCMV-ND-DN [15], [19] and RMVB-ND-DN were tested.
A. Focal Sources
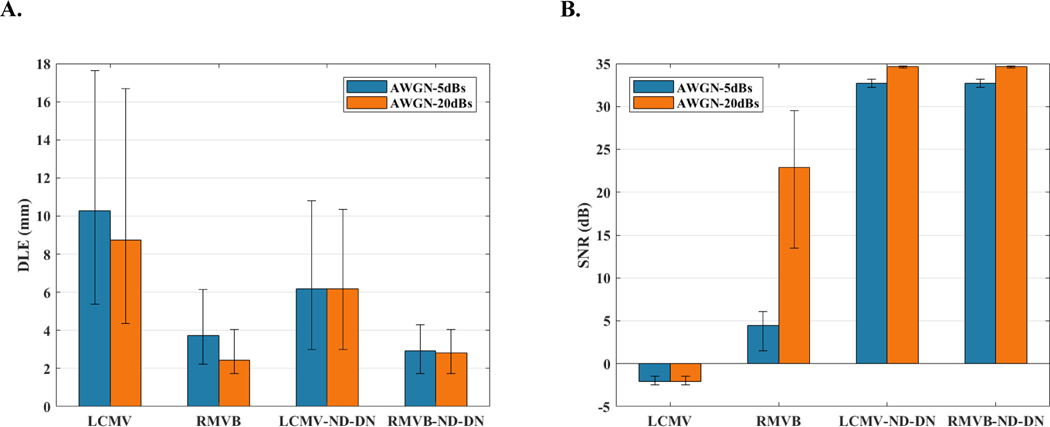
Fig. 1 depicts the performance of the mentioned beamformers in situations, where the underlying source activity can be modeled with a single dominant current dipole. In order to find the effect of noisy measurements on the performance, the simulations were repeated for high and low noise levels associated with the SNRs of dB and dB, respectively. Fig. 1 (A) depicts the median DLE for the dipoles as simulated in the first scenario. To present the uncertainties in the results, the first and third quartiles of data are reported with error bars. These results indicate that the robust adaptive beamformers, i.e., the RMVB and RMVB-ND-DN, outperform their conventional counterparts i.e., the LCMV and LCMV-ND-DN, respectively. Additionally, including the normalization and denoising procedures plays an important role in the quality of the results. Fig. 1 (B) yields the evaluation in terms of output SNR. According to this plot, while both the LCMV-ND-DN and RMVB-ND-DN outperform the LCMV and RMVB, they both perform equally well in recovering the temporal profile of the simulated activity. It can also be observed that including the post-processing steps can considerably decrease the sensitivity to noise levels. In fact, the gap between the RMVB performance in low and high levels of noise compared to the methods with post-processing of the solution, can be justified with regard to its lack of appropriate measures or mechanisms to remove or counteract the effect of noise. Furthermore, since the LCMV does not take into consideration the depth and asymmetric spatial distribution of the noise on one hand and is not designed to be robust against modeling errors on the other hand, its performance is especially poor when estimating output SNRs.
Fig. 1.
The Monte Carlo simulation statistics for the single-node source scenario. (A) The median DLE results for SNRs of 5dB and 20dB and for four types of beamformers namely, LCMV, RMVB, LCMV-ND-DN and RMVB-ND-DN. The error bars mark the first and third quartiles (of DLE distribution). (B) The median output SNR results along with the first and third quartile error bars for the same configuration.
B. The Effect of Number of Active Nodes
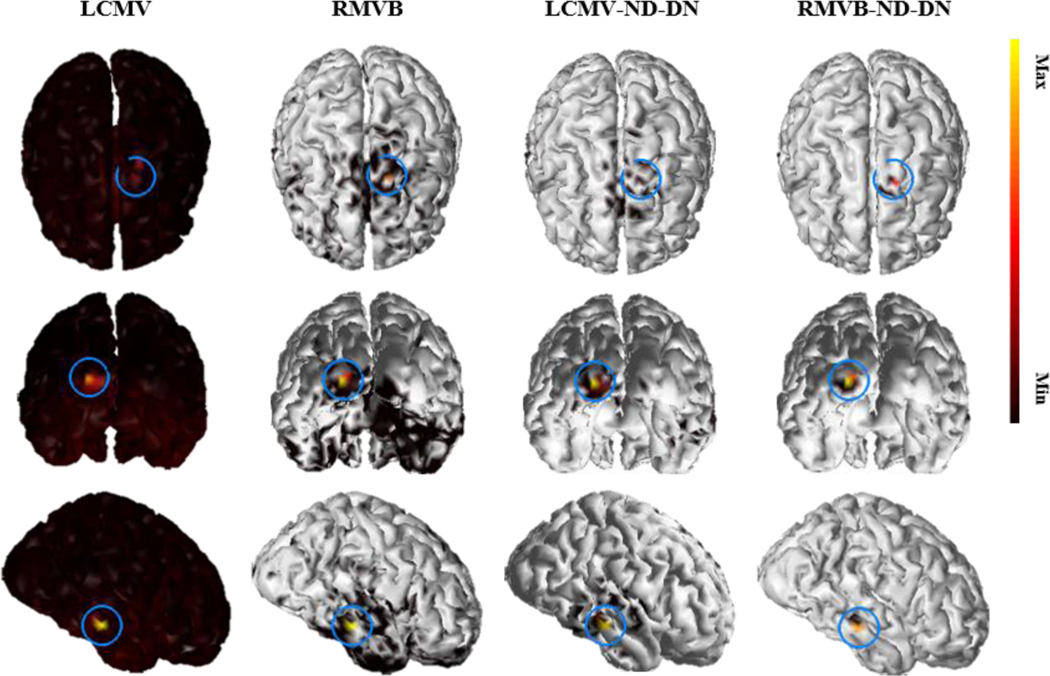
In the second scenario, source configurations each containing three active nodes were considered. Fig. 2 shows an example, where the three simulated current dipoles are placed at the right temporal, left frontal and left occipital lobes, respectively (the center of the blue rings on the plots mark the exact positions). SNR in this example is set to dB. Following the localization procedure discussed in the Computer Simulation Protocol section, it can be found that all versions except the LCMV are able to pinpoint the true location of the simulated dipoles in this example. However, the solution of RMVB-ND-DN is more focal and thus more consistent with the underlying dipole source, while the LCMV yields the smoothest solution, which is not as focal as the RMVB. It should be mentioned that, for display purposes, the threshold was set to % in this figure. This implies that e.g., in the solution of RMVB-ND-DN almost all falsely recovered dipoles are at least times weaker than the strongest activity.
Fig. 2.
An example of a 3-node network with focal activity. The source imaging results for a single 3-node source with focal activity using four types of beamformers namely, LCMV, RMVB, LCMV-ND-DN and RMVB-ND-DN. SNR in this example is set to 20dB and the solution is thresholded with a cut-off value of 0.01. The blue rings of the plots mark the positions of the true source.
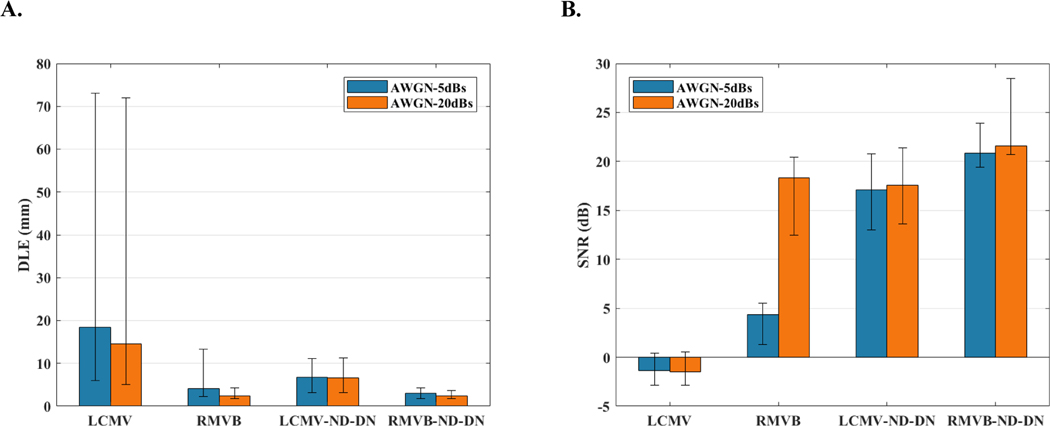
Fig. 3 (A) and Fig. 3 (B) plot the median DLE and SNR along with the corresponding first and third quartile error bars for two noise levels. The LCMV is sensitive to the number of sources in terms of DLE, while the other three techniques show less sensitivity. As in the earlier scenarios, normalization and denoising play a crucial role in the performance of both conventional and robust beamformers. However, robust beamformers are successful in modeling the uncertainty, even without these normalization and denoising steps. When such processing is applied, the results indicate that it is still better to use the robust version instead of the conventional beamformer, if computational resources are available. Furthermore, it can be seen that the RMVB is sensitive to input noise level especially when evaluating the output SNR. Please refer to the Supplementary materials to review the role of normalization in removing the inherent bias of adaptive beamformers toward deeper locations as well as the effect of correlated activities on beamformers performance.
Fig. 3.
The Monte Carlo simulation statistics for the three-node uncorrelated source scenario. (A) The median DLE results for SNRs of 5dB and 20dB and for four types of beamformers namely, LCMV, RMVB, LCMV-ND-DN and RMVB-ND-DN. The error bars mark the first and third quartiles (of DLE distribution). (B) The median output SNR results along with the first and third quartile error bars for the same configuration.
C. Extended Sources
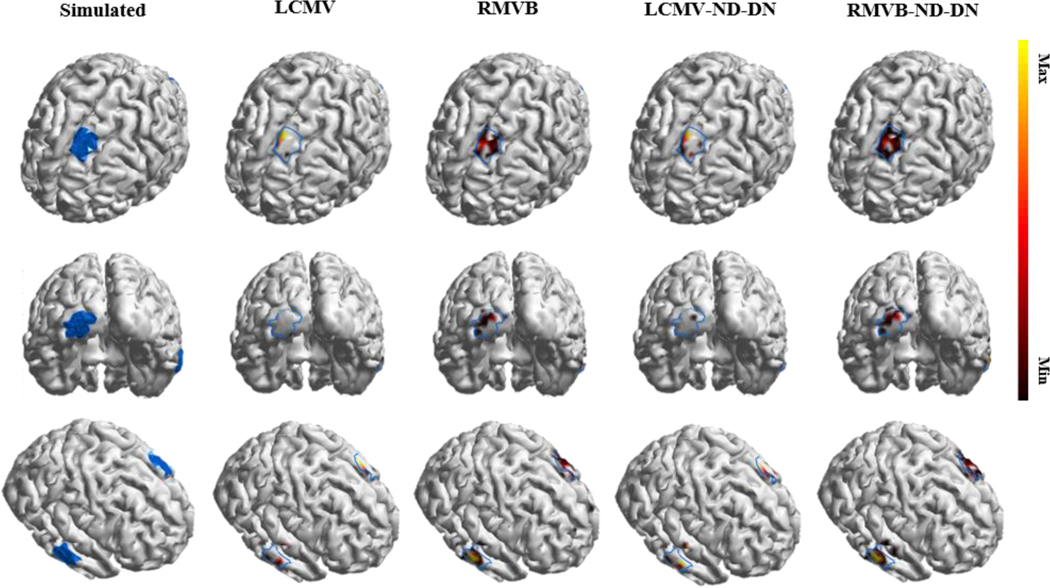
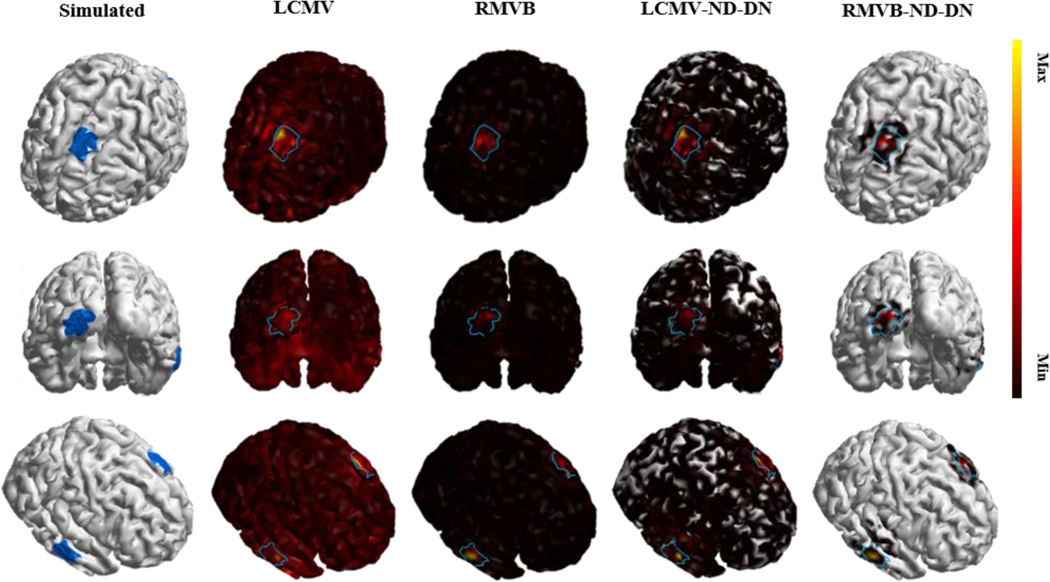
The fourth scenario was designed to evaluate the aforementioned beamformers in determining the distribution and shape of the underlying activities. To this end, Figs. 4 and 5 are to simulate three patches of extended sources rather than point dipoles. The blue boundaries in these plots mark the true source extents. The area of each patch is roughly and again SNR is dB. In Fig. 4, the threshold of display is optimized for each technique separately such that MCC is maximized, while in Fig. 5, it is preset to an arbitrary small value of %. The main observation is that in both cases, the RMVB-ND-DN captures the extent of the underlying activity while keeping number of falsely recovered dipoles small. Whereas, regular beamformers either underestimate the true source extent (Fig. 4) or have high false positive rates (Fig. 5). Since the optimal value of the threshold to detect the source extent is unknown a priori, robustness to threshold is highly valuable in practice.
Fig. 4.
An example of a three-node network with extended activity. The simulated three-node patches of activity as well as the source imaging results using four types of beamformers namely, LCMV, RMVB, LCMV-ND-DN and RMVB-ND-DN. SNR in this example is set to 20dB and the solution of each technique is thresholded separately such that MCC is maximized for that technique. The blue regions and boundaries of the plots mark the true source extents.
Fig. 5.
An example of a three-node network with extended activity. The simulated three-node patches of activity as well as the source imaging results using four types of beamformers namely, LCMV, RMVB, LCMV-ND-DN and RMVB-ND-DN. SNR in this example is set to 20dB and the solution is thresholded with a preset cut-off value of 0.01. The blue regions and boundaries of the plots mark the true source extents.
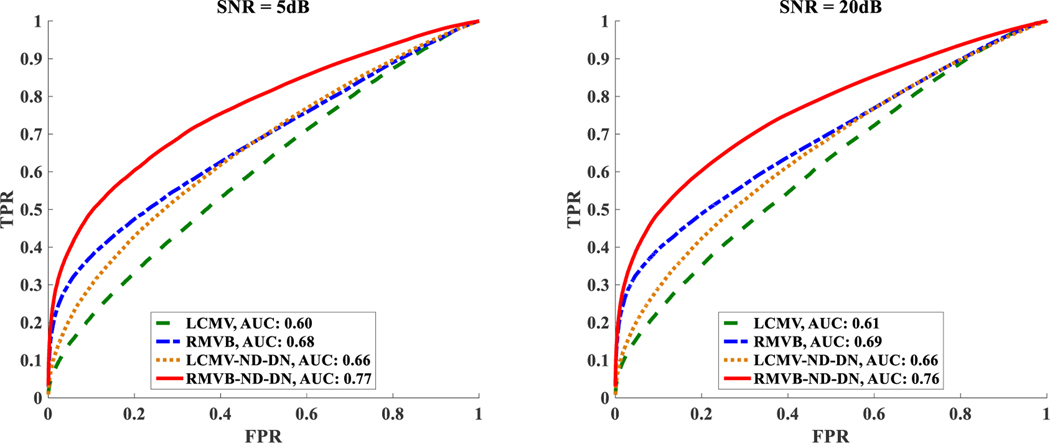
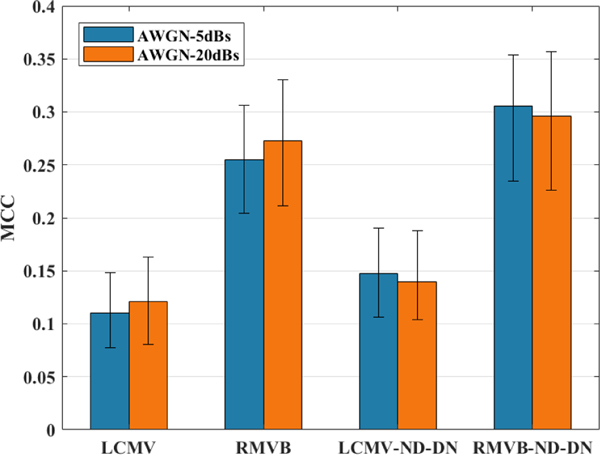
Fig. 6 plots the average ROC curve for source configurations each containing three extended nodes of activity for SNRs of and dB in the left and right panels, respectively. Each point on a ROC curve (TPR versus FPR) is associated with a cut-off threshold, the values below which were set to . The corresponding AUC of all the curves are reported in the legend of this figure. Obviously, the RMVB-ND-DN better estimates the extent of the underlying source compared to other versions of beamformers according to this metric. Moreover, the results of the RMVB and LCMV-ND-DN are close to each other (the RMVB is slightly superior to the LCMV-ND-DN). Fig. 7 reports the median MCC for the same data. The threshold for each source is determined such that MCC is maximized for that specific configuration. As it can be seen, the trend of this figure is the same as Fig. 6, with the RMVB-ND-DN at the top followed by the RMVB, LCMV-ND-DN and LCMV, respectively. It should also be noted that the absolute values of MCC in this figure do not provide much information about the quality of the estimation, and that the goal of this figure is to provide only a benchmark to compare different beamformers’ performance. Finally, interested readers are referred to Fig. S7 and Fig. S8 in Supplementary materials for the results of beamformers with diagonal loading.
Fig. 6.
The Monte Carlo simulation statistics for the extended source scenario. The Average ROC curves for four types of beamformers namely, LCMV, RMVB, LCMV-ND-DN and RMVB-ND-DN and for SNRs of 5 and 20 dB in the left and right panels, respectively. The corresponding AUC of all the curves are reported in the legend.
Fig. 7.
The Monte Carlo simulation statistics for the extended source scenario. The median MCC results along with the first and third quartile error bars for four types of beamformers namely, LCMV, RMVB, LCMV-ND-DN and RMVB-ND-DN and for SNR of 20 dB.
IV. Discussion
In this study, we proposed a new technique named robust minimum variance beamformer (RMVB), which unlike traditional adaptive beamformers, explicitly takes into consideration the uncertainty of the forward models. In order to compare the performance of RMVB with the well-known LCMV adaptive beamformer, we performed Monte Carlo simulations in various scenarios representing different conditions for underlying source activity. We also simulated the modified versions of each technique by applying the post-hoc normalization/denoising step (i.e., LCMV-ND-DN and RMVB-ND-DN techniques). Based on simulation results, RMVB and RMVB-ND-DN can better estimate the underlying source activities compared to LCMV and LCMV-ND-DN respectively; although, LCMV-ND-DN yields favorable results in certain cases as well. As a general observation, both post-processing of the solutions (normalization and/or denoising steps) and modeling the uncertainty (the robust versions) enhance the performance. By combining both procedures in RMVB-ND-DN, our technique outperformed other versions based on all metrics that were used in this study. It was also observed that there is especially a clear benefit in using robust beamformers to estimate extended sources (as depicted in Fig. 6 and Fig. 7).
Although the optimization problem (10) can be solved easily using general-purpose convex solvers such as CVX [30], [31], RMVB can be much slower than the conventional LCMV, since the optimization problem has to be solved for many voxels. While CVX was used in this study, RMVB can be significantly accelerated by employing a specifically tailored algorithm for the optimization module. Fortunately, this algorithm, which is based on Lagrange multipliers method, exists and can solve the problem much more efficiently and faster than the CVX package [21]. Furthermore, parallel computing can also be exploited by virtue of the scanning scheme of the beamformers, yielding further acceleration (by estimating the weights for different voxels in parallel). Overall, it takes about seconds to find the solution of RMVB using parallel computing (in MATLAB and on a server computer with 8×32 GB of RAM and a 2x Intel Xeon E5-2697v2 2.7GHz processor) which is approximately times slower than the conventional LCMV. This amount of time is reasonably short for applications where source imaging is performed off-line. Besides optimization, estimation of uncertainty regions can be computationally demanding as well, since it requires building several forward models depending on the source of uncertainty in the actual problem. However, these regions are computed only once before source imaging is performed. Furthermore, the uncertainty region estimation at each location is independent from other locations. Thus, these can be computed in a parallel fashion (as in solving the optimization problem), resulting in efficient implementations of beamformer approaches. Such reduction in computation times due to parallel computing makes robust beamformer approaches desirable and practically achievable.
Finally, a fixed-orientation model was used to solve the inverse problem in this study. Although this choice can be justified through the anatomical location and orientation of pyramidal neuron cells generating EEG/MEG signals, estimating the orientations through solving the inverse problem rather than assuming the orientation a priori may be beneficial. For instance, segmentation of the cortex may not be accurate enough, and the normal orientations estimated from such segmentation results may be inaccurate, especially if the segmentation is coarse. Estimating the orientation of dipoles while solving the inverse problem may be achieved by considering free orientations for the current dipoles along different axis e.g., and in a Cartesian coordinate. The extension of this work to a vector robust beamformer, which is based on rotational models, will be the topic of a future study.
V. Conclusion
In this work, we have proposed and investigated robust beamformers for the purpose of electromagnetic source imaging. The main advantage of robust beamformers over conventional adaptive beamformers, is that the RMVB and RMVB-ND-DN are more robust to mismatches between the forward and inverse modeling, which are inevitable in practice. The robust beamformers presented in this paper outperformed the conventional beamformers in terms of localization error, recovering source dynamics and estimation of the underlying source extents, when uncertainty in the lead field matrix is properly determined and modeled. This can justify the robust implementation of beamformers for applications, where source imaging is performed to study pathological and normal brain networks.
Supplementary Material
Acknowledgments
This work was supported in part by NIH EB021027, NS096761, MH114233, AT009263, and NSF CAREER CCF-1651825.
Contributor Information
Seyed Amir Hossein Hosseini, University of Minnesota, Minneapolis, MN, USA.
Abbas Sohrabpour, University of Minnesota, Minneapolis, MN, USA.
Mehmet Akçakaya, University of Minnesota, Minneapolis, MN, USA.
Bin He, Carnegie Mellon University, Pittsburgh, PA, USA.
References
- [1].He B. and Ding L, “Electrophysiological mapping and neuroimaging,” in Neural engineering, Springer, 2013, pp. 499–543. [Google Scholar]
- [2].Michel CM, Murray MM, Lantz G, Gonzalez S, Spinelli L, and Grave de Peralta R, “EEG source imaging,” Clin. Neurophysiol, vol. 115, no. 10, pp. 2195–2222, Oct. 2004. [DOI] [PubMed] [Google Scholar]
- [3].Michel CM and He B, “EEG mapping and source imaging,” Niedermeyer’s Electroencephalogr, vol. 6, pp. 1179–1202, 2011. [Google Scholar]
- [4].He B, Musha T, Okamoto Y, Homma S, Nakajima Y, and Sato T, “Electric dipole tracing in the brain by means of the boundary element method and its accuracy,” IEEE Trans. Biomed. Eng, no. 6, pp. 406–414, 1987. [DOI] [PubMed] [Google Scholar]
- [5].Niedermeyer E. and da Silva FL, Electroencephalography: basic principles, clinical applications, and related fields. Lippincott Williams & Wilkins, 2005. [Google Scholar]
- [6].Cohen D, “Magnetoencephalography: detection of the brain’s electrical activity with a superconducting magnetometer,” Science, vol. 175, no. 4022, pp. 664–666, February. 1972. [DOI] [PubMed] [Google Scholar]
- [7].Hämäläinen M, Hari R, Ilmoniemi RJ, Knuutila J, and Lounasmaa OV, “Magnetoencephalography—theory, instrumentation, and applications to noninvasive studies of the working human brain,” Rev. Mod. Phys, vol. 65, no. 2, p. 413, 1993. [Google Scholar]
- [8].Cam SL et al. , “SEEG dipole source localization based on an empirical Bayesian approach taking into account forward model uncertainties,” NeuroImage, vol. 153, pp. 1–15, June. 2017. [DOI] [PubMed] [Google Scholar]
- [9].Hosseini SAH, Sohrabpour A, and He B, “Electromagnetic source imaging using simultaneous scalp EEG and intracranial EEG: An emerging tool for interacting with pathological brain networks,” Clin. Neurophysiol, vol. 129, no. 1, pp. 168–187, January. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Zhang Y, van Drongelen W, Kohrman M, and He B, “Three-dimensional brain current source reconstruction from intra-cranial ECoG recordings,” NeuroImage, vol. 42, no. 2, pp. 683–695, August. 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].He B, Sohrabpour A, Brown E, and Liu Z, “Electrophysiological Source Imaging: A Noninvasive Window to Brain Dynamics,” Annu. Rev. Biomed. Eng, vol. 20, no. 1, p. null, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Spencer ME, Leahy RM, Mosher JC, and Lewis PS, “Adaptive filters for monitoring localized brain activity from surface potential time series,” in [1992] Conference Record of the Twenty-Sixth Asilomar Conference on Signals, Systems Computers, 1992, pp. 156–161 vol.1. [Google Scholar]
- [13].Van Veen BD, Van Drongelen W, Yuchtman M, and Suzuki A, “Localization of brain electrical activity via linearly constrained minimum variance spatial filtering,” IEEE Trans. Biomed. Eng, vol. 44, no. 9, pp. 867–880, 1997. [DOI] [PubMed] [Google Scholar]
- [14].Steinsträter O, Sillekens S, Junghoefer M, Burger M, and Wolters CH, “Sensitivity of beamformer source analysis to deficiencies in forward modeling,” Hum. Brain Mapp, vol. 31, no. 12, pp. 1907–1927, December. 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Sekihara K, Nagarajan SS, Poeppel D, Marantz A, and Miyashita Y, “Application of an MEG eigenspace beamformer to reconstructing spatio-temporal activities of neural sources,” Hum. Brain Mapp, vol. 15, no. 4, pp. 199–215, 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Vorobyov SA, Gershman AB, and Luo Z-Q, “Robust adaptive beamforming using worst-case performance optimization: a solution to the signal mismatch problem,” IEEE Trans. Signal Process, vol. 51, no. 2, pp. 313–324, February. 2003. [Google Scholar]
- [17].Gross J. and Ioannides AA, “Linear transformations of data space in MEG,” Phys. Med. Biol, vol. 44, no. 8, p. 2081, 1999. [DOI] [PubMed] [Google Scholar]
- [18].Robinson SE and Vrba J, “Functional neuroimaging by synthetic aperture magnetometry (SAM),” Yoshimoto T Kotani M Kuriki Karibe H Nakasato N Ed. Recent Adv. Biomagn Tohoku Univ. Press; Sendai Jpn., pp. 302–305, 1999. [Google Scholar]
- [19].Sekihara K, Nagarajan SS, Poeppel D, Marantz A, and Miyashita Y, “Reconstructing spatio-temporal activities of neural sources using an MEG vector beamformer technique,” IEEE Trans. Biomed. Eng, vol. 48, no. 7, pp. 760–771, 2001. [DOI] [PubMed] [Google Scholar]
- [20].Gershman AB, Sidiropoulos ND, Shahbazpanahi S, Bengtsson M, and Ottersten B, “Convex Optimization-Based Beamforming,” IEEE Signal Process. Mag, vol. 27, no. 3, pp. 62–75, May 2010. [Google Scholar]
- [21].Lorenz RG and Boyd SP, “Robust minimum variance beamforming,” IEEE Trans. Signal Process, vol. 53, no. 5, pp. 1684–1696, May 2005. [Google Scholar]
- [22].He B. and Lian J, “Electrophysiological Neuroimaging,” in Neural Engineering, He B, Ed. Springer US, 2005, pp. 221–261. [Google Scholar]
- [23].Malmivuo J. and Plonsey R, Bioelectromagnetism: principles and applications of bioelectric and biomagnetic fields. Oxford University Press, USA, 1995. [Google Scholar]
- [24].Mosher JC and Leahy RM, “Source localization using recursively applied and projected (RAP) MUSIC,” IEEE Trans. Signal Process, vol. 47, no. 2, pp. 332–340, 1999. [DOI] [PubMed] [Google Scholar]
- [25].Xu X-L, Xu B, and He B, “An alternative subspace approach to EEG dipole source localization,” Phys. Med. Biol, vol. 49, no. 2, p. 327, 2004. [DOI] [PubMed] [Google Scholar]
- [26].Huang M-X et al. , “Commonalities and Differences Among Vectorized Beamformers in Electromagnetic Source Imaging,” Brain Topogr, vol. 16, no. 3, pp. 139–158, March. 2004. [DOI] [PubMed] [Google Scholar]
- [27].Kaiser HF, “The application of electronic computers to factor analysis,” Educ. Psychol. Meas, vol. 20, no. 1, pp. 141–151, 1960. [Google Scholar]
- [28].Boyd S. and Vandenberghe L, Convex optimization. Cambridge university press, 2004. [Google Scholar]
- [29].Lobo MS, Vandenberghe L, Boyd S, and Lebret H, “Applications of second-order cone programming,” Linear Algebra Its Appl, vol. 284, no. 1–3, pp. 193–228, 1998. [Google Scholar]
- [30].Grant M. and Boyd S, “Graph implementations for nonsmooth convex programs,” Recent Adv. Learn. Control, pp. 95–110, 2008. [Google Scholar]
- [31].Grant M, Boyd S, and Ye Y, CVX: Matlab software for disciplined convex programming. 2008. [Google Scholar]
- [32].Hansen ST, Hauberg S, and Hansen LK, “Data-driven forward model inference for EEG brain imaging,” NeuroImage, vol. 139, pp. 249–258, 2016. [DOI] [PubMed] [Google Scholar]
- [33].Holmes CJ, Hoge R, Collins L, Woods R, Toga AW, and Evans AC, “Enhancement of MR images using registration for signal averaging,” J. Comput. Assist. Tomogr, vol. 22, no. 2, pp. 324–333, 1998. [DOI] [PubMed] [Google Scholar]
- [34].Hamalainen MS and Sarvas J, “Realistic conductivity geometry model of the human head for interpretation of neuromagnetic data,” IEEE Trans. Biomed. Eng, vol. 36, no. 2, pp. 165–171, 1989. [DOI] [PubMed] [Google Scholar]
- [35].Lai Y. et al. , “Estimation of in vivo human brain-to-skull conductivity ratio from simultaneous extra-and intra-cranial electrical potential recordings,” Clin. Neurophysiol, vol. 116, no. 2, pp. 456–465, 2005. [DOI] [PubMed] [Google Scholar]
- [36].Oostendorp TF, Delbeke J, and Stegeman DF, “The conductivity of the human skull: results of in vivo and in vitro measurements,” IEEE Trans. Biomed. Eng, vol. 47, no. 11, pp. 1487–1492, 2000. [DOI] [PubMed] [Google Scholar]
- [37].Zhang Y, Van Drongelen W, and He B, “Estimation of in vivo brain-to-skull conductivity ratio in humans,” Appl. Phys. Lett, vol. 89, no. 22, p. 223903, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Baillet S, Mosher JC, and Leahy RM, “Electromagnetic brain mapping,” IEEE Signal Process. Mag, vol. 18, no. 6, pp. 14–30, 2001. [Google Scholar]
- [39].Sohrabpour A, Ye S, Worrell GA, Zhang W, and He B, “Noninvasive Electromagnetic Source Imaging and Granger Causality Analysis: An Electrophysiological Connectome (eConnectome) Approach,” IEEE Trans. Biomed. Eng, vol. 63, no. 12, pp. 2474–2487, December. 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Kay SM, Fundamentals of statistical signal processing. Prentice Hall PTR, 1993. [Google Scholar]
- [41].Grova C, Daunizeau J, Lina J-M, Bénar CG, Benali H, and Gotman J, “Evaluation of EEG localization methods using realistic simulations of interictal spikes,” Neuroimage, vol. 29, no. 3, pp. 734–753, 2006. [DOI] [PubMed] [Google Scholar]
- [42].Matthews BW, “Comparison of the predicted and observed secondary structure of T4 phage lysozyme,” Biochim. Biophys. Acta BBA - Protein Struct, vol. 405, no. 2, pp. 442–451, October. 1975. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.