Perspective on musculoskeletal modelling and predictive simulations of human movement to assess the neuromechanics of gait

Abstract

Locomotion results from complex interactions between the central nervous system and the musculoskeletal system with its many degrees of freedom and muscles. Gaining insight into how the properties of each subsystem shape human gait is challenging as experimental methods to manipulate and assess isolated subsystems are limited. Simulations that predict movement patterns based on a mathematical model of the neuro-musculoskeletal system without relying on experimental data can reveal principles of locomotion by elucidating cause–effect relationships. New computational approaches have enabled the use of such predictive simulations with complex neuro-musculoskeletal models. Here, we review recent advances in predictive simulations of human movement and how those simulations have been used to deepen our knowledge about the neuromechanics of gait. In addition, we give a perspective on challenges towards using predictive simulations to gain new fundamental insight into motor control of gait, and to help design personalized treatments in patients with neurological disorders and assistive devices that improve gait performance. Such applications will require more detailed neuro-musculoskeletal models and simulation approaches that take uncertainty into account, tools to efficiently personalize those models, and validation studies to demonstrate the ability of simulations to predict gait in novel circumstances.

1. Introduction

Notwithstanding decades of research, there remain many open questions about the neuromechanics of human locomotion. Our limited fundamental knowledge hinders the development of novel approaches to improve gait performance in both patients and athletes. A better understanding of the principles underlying human locomotion would benefit the design of exoskeletons that reduce metabolic cost or orthopedic treatments that improve gait performance in patients with neuro-muscular disorders. Locomotion results from complex interactions between the central nervous system, the sensory system and the musculoskeletal system with its many degrees of freedom (DoFs) and muscles. Probing the function of each subcomponent is hard, because the invasiveness of available techniques limits direct measurements in humans. In addition, it is hard to experimentally investigate the effect of isolated changes in the neuro-musculoskeletal system on gait performance. Predictive simulations can reveal principles of locomotion by elucidating cause–effect relationships. Such simulations generate novel movements based on a mathematical description, i.e. a model, of the neuro-musculoskeletal system without relying on experimental data (figure 1). They therefore allow studying the influence of isolated neuro-musculoskeletal features by adjusting model parameters. Predictive simulation studies have mostly used conceptual models with few DoFs and without muscles, thereby limiting the questions they could address. Computational roadblocks have long hindered the use of more complex models. However, recent developments in computational approaches have provided powerful tools for simulating movement of complex bodily systems allowing researchers to address long-standing open questions.

Figure 1.

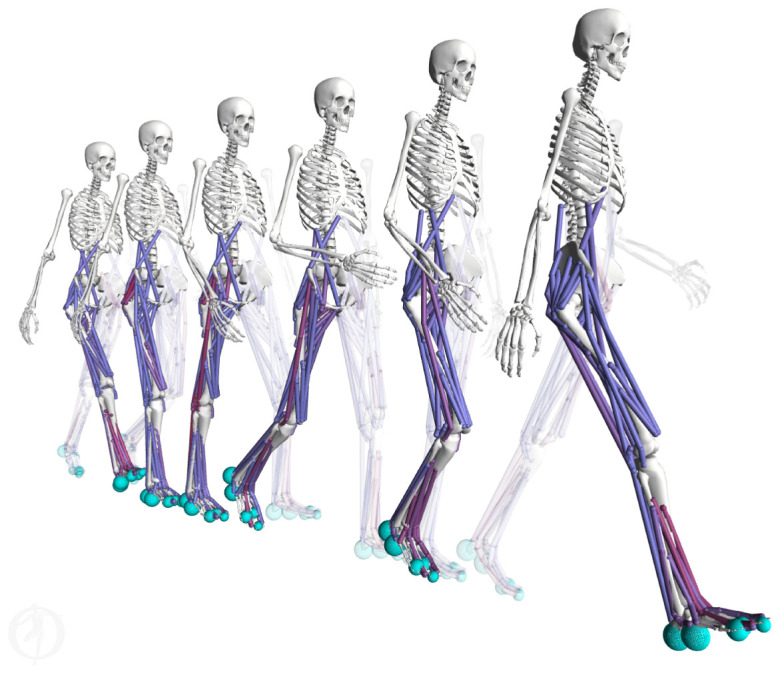
Predictive simulation of human walking. The walking pattern visualized here was generated by trajectory optimization based on a complex OpenSim-based three-dimensional muscle-driven model without relying on experimental data [1,2]. Blue spheres represent contact geometries. Muscles turn red when active. (Online version in colour.)

Conceptual models have advanced our insight into principles of locomotion [3]. Simple models of gait have very few parameters and therefore allow exploring the whole parameter space, which makes them amenable to interpretation [4]. Such conceptual models demonstrated that energy minimization explains many spatio-temporal gait features, for example, the relationship between gait speed and step frequency [5] and the selection of walking and running gaits over other feasible gait patterns [4]. Alternatively, these models describe the importance of leg compliance to explain the salient dynamics of human gait [6]. Conceptual models also revealed principles of gait stability. For example, passive dynamics can stabilize walking in the sagittal plane, whereas lateral stability requires active control [7]. When applied to running, conceptual models revealed that less precise control of leg stiffness and angle of attack is required as running speed increases [8] and that local positive muscle force feedback can control leg stiffness [9]. However, being simple by nature, conceptual models cannot capture how multiple body segments, a redundant set of muscles and the central nervous system interact to achieve gait economy and stability.

Complex models might elucidate how the neuro-musculoskeletal system realizes gait principles identified through conceptual models. Here, we consider a model complex when it represents multiple lower limb segments and joints driven by a redundant set of muscle–tendon actuators with dynamics inspired by muscle physiology. First, taking the complex, three-dimensional, musculoskeletal geometry into account is important to understand both pathological gait and athletic performance. For example, patients with weak hip abductors adopt a Trendelenburg gait pattern with compensations in both the frontal and sagittal planes and sprinters have been shown to have smaller Achilles tendon moment arms and longer toes than non-sprinters [10]. Second, accurately modelling muscle–tendon actuators is important to understand movement economy. Muscle dynamics are closely linked to muscle energetics with muscle force being produced at lower metabolic rates when a muscle works isometrically close to its optimal length [11]. Interactions between muscles and tendons influence muscle efficiency by altering the muscles' operating length and velocity and by allowing for storage and release of energy in the tendons. Third, accurately modelling the musculoskeletal system is crucial to study its interaction with the neural system. The intrinsic mechanical properties of the musculoskeletal system, especially muscles, provide stability against external perturbations, thereby reducing the need for active control (e.g. [12]). Finally, studying how muscles are coordinated by the neural system requires models driven by a redundant set of muscles. Many applications also require such complexity. Using simulations for personalized clinical decision-making requires models that sufficiently describe the musculoskeletal structures and motor control processes that are affected by disease and treatment. For example, children with cerebral palsy often receive orthopedic surgery to correct bony and soft tissue deformities. Integrating predictive simulations in the clinical decision-making process seems promising given the low success rate of such interventions [13] but requires detailed and personalized models. Similarly, using simulations to design exoskeletons that reduce metabolic cost requires models that capture human metabolics, as simply reducing the biological joint torques does not necessarily reduce metabolic cost [14].

Recently, efficient numerical methods and open-source software for predictive simulations based on complex models have become available [2,15–17]. This availability will enable researchers to address questions about the neuromechanics of gait that require complex models and are hard to study solely based on experiments. Here, we review recent advances in predictive simulations of human movement and how those simulations have been used to advance our insight into the neuromechanics of gait. Our review focuses on predictive simulation studies based on complex muscle-driven models. We distinguish predictive simulations, which do not require experimental movement data as input, from tracking simulations, where errors between simulated and experimental kinematics are minimized or constrained. Although we acknowledge that useful insights have been gained from tracking simulations, we believe that the ability to predict de novo movements opens new avenues for research and applications that could not be realized using tracking simulations. We end this perspective with a discussion of open questions and challenges.

2. Simulation approaches

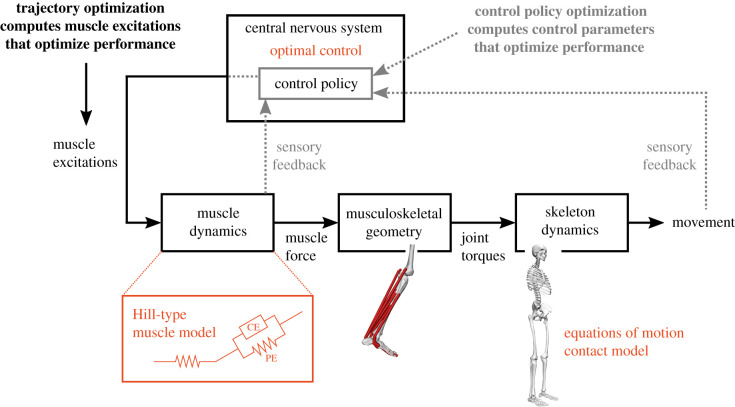
Simulations of movement are typically based on the assumption that the central nervous system optimizes performance, e.g. minimizes the metabolic cost of transport. Under this assumption, predictive simulations can be formulated as optimal control problems. We distinguish approaches that solve for (open-loop) muscle controls, often referred to as trajectory optimization, from approaches that solve for control policies (figure 2). Such control policies describe the dependence of muscle controls on the state of the musculoskeletal system, i.e. feedback control.

Figure 2.

Schematic of predictive simulation approaches using trajectory optimization and control policy optimization. Both approaches are based on a model of the musculoskeletal system. Muscle dynamics describe how muscles transform excitations into forces. Commonly, Hill-type muscle models are used (PE, passive element; CE, contractile element). Musculoskeletal geometry determines how these forces are applied to the skeleton system. Skeleton dynamics describe how the skeleton moves under the influence of joint torques and contact forces with the environment. It is commonly assumed that motor control is optimal in some sense, for example, by minimizing muscle effort, within the constraints imposed by the musculoskeletal system. Trajectory optimization computes open-loop muscle excitations, whereas in control policy optimization the control policy is modelled and control parameters are computed. (Online version in colour.)

Researchers have used trajectory optimization methods with increasing levels of computational efficiency over the last two decades. In 2001, Anderson & Pandy required 10 000 central processing unit (CPU) hours to predict a walking cycle that minimized metabolic energy per distance travelled based on a three-dimensional model with 23 DoFs and 54 muscles [18]. They used a direct shooting approach combined with a simulated annealing algorithm to solve the underlying optimal control problem. The adoption of direct collocation methods, instead of shooting methods, has helped reduce computational time. In shooting methods, the dynamics are integrated over the time horizon of the simulation based on the current guess of the controls to obtain the states required to evaluate the cost function and constraints. In collocation methods, the discretized states and controls are optimization variables and the integration scheme is expressed by a set of constraints that is solved simultaneously with minimizing the cost function. The resulting large-scale nonlinear programming problems (NLP) are sparse and can be efficiently solved using gradient descent algorithms, e.g. IPOPT [19]. Compared to direct shooting, direct collocation reduces the sensitivity of the objective function to the optimization variables by reducing the time horizon of the integration. Hence, collocation methods are especially beneficial to solve problems with unstable dynamics, such as open-loop musculoskeletal dynamics of bipedal locomotion. In 2010, Ackermann & van den Bogert required 35 CPU minutes to predict a walking cycle based on a two-dimensional model with nine DoFs and 16 muscles [20] and in 2018, Lin et al. required between 13 and 17 CPU hours to predict a walking cycle based on a three-dimensional model with 25 DoFs and 80 muscles [21]. Further improvements in computational speed were achieved by combining direct collocation with implicit formulation of the dynamics, which improves the numerical conditioning of the NLP, and algorithmic differentiation [15,22,23]. In 2019, we required on average 35 CPU minutes to simulate a walking cycle based on a three-dimensional model with 29 DoFs and 92 muscles and shared the computational tools we used on open-source platforms [2]. Similar tools have been implemented in OpenSim Moco [16]. Moco frees researchers from implementing direct collocation themselves, which makes it easier to use by non-experts. However, it does not use algorithmic differentiation, and might therefore be less computationally efficient. Overall, predictive simulations of walking using trajectory optimization approaches can now be considered rapid and accessible. However, such approaches do not describe gait control policies and are therefore unsuited to describe how the neuro-musculoskeletal system deals with uncertainty, e.g. sensorimotor noise and external perturbations.

Approaches that solve for gait control policies can capture the robustness of the neuro-musculoskeletal system against noise, yet are often computationally less efficient than trajectory optimization methods. In 2010, Geyer & Herr proposed a reflex-driven control model of gait [24]. They were able to produce stable two-dimensional gait simulations by hand-tuning the control parameters of the model. Since then, their control model has served as a basis for optimization approaches that solve for control parameters by optimizing performance. In their three-dimensional model, Wang et al. combined these reflex-based control laws for the 16 muscles driving the sagittal plane lower limb joints with proportional derivative controllers for the torque actuators driving the remaining 24 DoFs [25]. They used covariance matrix adaptation (CMA) to solve for control parameters [26]. In 2019, Geijtenbeek et al. published SCONE, an open-source software package to generate predictive simulations by computing control policies using CMA [17]. Alternatively, reinforcement learning has been used to solve for control policies. Since 2017, the NeurIPS ‘Learn to move’ competition series has accelerated the adoption of reinforcement learning techniques to simulate human locomotion based on neuro-musculoskeletal models (for detailed reviews, see [27,28]). Overall, approaches that solve for gait control policies were based on simpler neuro-musculoskeletal models than trajectory optimization methods, probably because of computational efficiency. In addition, computational approaches for control policy optimization are typically less suitable for dealing with task constraints, such as periodicity or locomotion speed, than computational approaches for trajectory optimization.

Both trajectory optimization and approaches that solve for gait control policies generated simulations that capture key features of human gait. The realism of simulated movements is typically assessed by comparing simulated and measured joint kinematics, kinetics, ground reaction forces and muscle activities. However, such validation efforts are often qualitative and limited to a single gait pattern. Only few studies went beyond such validation. Song & Geyer solved for gait control policies and validated their simulations against perturbation experiments [29,30]. Their simulations capture the change in muscle activity owing to epidural stimulation of the spinal cord, tendon taps, ankle stretch, slip of the stance leg and trip of the swing leg during walking. Dorn et al. validated whether their optimal reflex-based control policies captured key features of level walking as well as inclined and loaded walking [31]. We validated that our three-dimensional trajectory optimization simulations captured the relationship between gait speed, and, respectively, gait frequency and metabolic cost of transport [2]. Ong et al. performed a similar validation for their reflex-driven two-dimensional simulations [32]. However, we feel that further efforts are needed to validate the underlying motor control assumptions. It is clear that control of gait is neither fully open-loop nor fully reflexive. Yet both models have resulted in realistic mechanics and muscle activities, suggesting an important role of musculoskeletal dynamics in shaping human gait.

Relatively few predictive simulation studies have used three-dimensional models with a redundant set of muscles. However, given that control of movement is realized through a redundant set of muscles and is coupled between planes, such complexity is required to unveil gait control strategies as well as compensation strategies owing to neuro-musculoskeletal deficits. For instance, we observed that we needed to minimize metabolic energy rate squared in addition to muscle activities squared when simulating walking based on a three-dimensional model with a redundant set of muscles to prevent excessive trunk sway in the frontal plane [2], whereas others have obtained realistic sagittal plane gait patterns by minimizing only activations squared based on a two-dimensional model in which agonistic mono- and bi-articular actuators were represented by single muscles [20]. In addition, we showed that weakening the hip muscles of our three-dimensional model produced walking simulations with excessive hip circumduction, a compensation strategy in the frontal plane [2].

3. Key insights from predictive simulation studies

(a). Optimality principles underlying gait control

Predictive simulation studies, mostly based on trajectory optimization, have explored optimality principles underlying human gait. Anderson & Pandy showed that minimizing metabolic energy per unit distance travelled of a three-dimensional muscle-driven model produced a walking pattern that closely matched experimental data [18]. However, they forced their model to walk with a flexed knee during stance by imposing the joint kinematics at the initial state to match experimental data. Ackermann & van den Bogert compared energy-like cost functions, sum of muscle-volume-scaled activations to the power 1–4, and fatigue-like cost functions, sum of activations to the power 2–10 [20]. Fatigue-like cost functions predicted larger and more realistic knee flexion during early stance than energy-like cost functions for a two-dimensional muscle-driven model. Based on these results, they suggest that fatigue minimization may be one of the primary optimality principles driving human gait selection. Miller compared the walking patterns predicted by five different metabolic energy models using a three-dimensional muscle-driven model with trapezoidal excitation controls [33]. Joint kinematics and ground reaction forces varied with the model used, with some models predicting hip circumduction. It is hard to judge how much the simplified control patterns contributed to differences with respect to human walking. We evaluated the influence of various performance criteria on walking patterns predicted using a three-dimensional muscle-driven model [2]. We found that a multi-objective cost function combining metabolic energy, muscle activations and joint accelerations, all terms squared, produced a human-like walking pattern. However, none of the cost functions we tested predicted realistic knee flexion angles and knee extension torques during stance. Our cost function nevertheless captured the walk-to-run transition and clinical gait deficiencies caused by muscle weakness and prosthesis use, suggesting that diverse gaits can emerge from the same optimal control strategy.

Nguyen et al. applied inverse optimal control to identify the cost function underlying a measured walking pattern based on a two-dimensional muscle-driven model [34]. They proposed a cost function with terms related to effort, modelled as activations cubed, stability, modelled as the squared horizontal distance between the middle of the base of support and respectively the head and centre of mass, and smoothness, modelled as the centre of mass jerk squared, and solved for weights that best reproduced experimental data using a bilevel optimization method. Their optimal cost function captures experimental data except for the ankle angle. Note that similar approaches have been applied to two-dimensional torque-driven models (e.g. [35]).

Optimality principles underlying running have also been studied. For example, Miller et al. compared minimizing the metabolic cost of transport, activations squared and total muscle stress based on a two-dimensional muscle-driven model [36]. They found that minimizing activations squared predicted the most realistic joint angles, timing of muscle activity and metabolic cost of transport.

(b). Feasibility of gait control architectures

Simulations have helped elicit the role of control structures, such as reflexes and central pattern generators, in generating stable and versatile walking patterns. By simulating control architectures, often inspired by experimental observations, researchers have tested their ability to generate human-like walking. Taga proposed a control strategy based on a rhythm generator consisting of seven pairs of neural oscillators with sensory inputs supplemented with joint level impedance controllers to drive a two-dimensional model with ideal muscle actuators, i.e. muscle force proportional to input [37]. He fine-tuned the controller parameters through trial and error to generate stable walking. The proposed control architecture was able to generate walking movements at different speeds that were robust against mechanical perturbations. As introduced above, Geyer & Herr proposed a reflex-based control strategy to drive a two-dimensional model with Hill-type muscles [24] and demonstrated that such strategy can generate walking simulations robust against ground disturbances and changes in slope.

Such physiology-inspired control architectures have been combined with performance optimization to test the role of control structures in generating versatile gait. Dzeladini et al. used an optimization approach to demonstrate that a central pattern generator on top of a reflex controller can modulate gait speed based on a two-dimensional muscle-driven model [38]. Song & Geyer extended the reflex-based controller of Geyer & Herr to a three-dimensional version that drives 22 muscles actuating eight DoFs and added a supraspinal layer controlling for foot placement, swing leg length and swing leg selection [29]. They showed that this control architecture is able to produce diverse steady and transitional locomotion behaviours and therefore suggest that spinal reflexes might be functionally more important than central pattern generators in human locomotion. Song & Geyer evaluated whether the reflex-based control policy that minimized metabolic energy of a two-dimensional model during walking captured observed responses to perturbations [30]. The responses of the model were in agreement with experimental observations for local disturbances but were smaller than observed for whole-body perturbations, suggesting that the model should be extended with supraspinal control modulating the reflex gains. Wang et al. modelled the supraspinal control layer with a deep neural network that provides input to the reflex-based controller and that was successfully trained to cope with changing terrains [39].

(c). Effect of musculoskeletal properties and neural impairments on gait mechanics and energetics

Predictive simulations allow assessing of how altered neuro-musculoskeletal properties affect gait performance. Such assessment is hard to perform experimentally because—especially with ageing or neurological pathologies—multiple physiological changes occur simultaneously. Miller et al. found that maximal sprinting speed predicted by trajectory optimization based on a two-dimensional model driven by Hill-type muscles is more sensitive to the force–velocity relationship than to the force–length relationship or tendon elasticity [40,41]. Based on a three-dimensional muscle-driven model, Song & Geyer showed that muscular changes, i.e. loss of muscle strength and mass, contribute more to reduced walking economy and speed in older adults than neural changes, i.e. slower neural conduction speed and sensorimotor noise [42]. We showed that decreasing the strength of the hip muscles in a three-dimensional muscle-driven model produced gaits with excessive hip circumduction, resembling compensated Trendelenburg gait patterns observed in patients with hip muscle weakness, whereas decreasing the strength of the ankle plantarflexors produced calcaneal gaits, which may be observed in children with spastic diplegia who have weak plantarflexors [2]. Ong et al. investigated the differential effect of plantarflexor weakness and contraction, often occurring simultaneously in neurological disorders such as cerebral palsy or stroke, on the gait pattern of a two-dimensional muscle-driven model [32]. Plantarflexor weakness resulted in slower calcaneal gaits with increased per cent time spent in stance, whereas plantarflexor contracture resulted in crouch gait characterized by toe landing and excessive knee and hip flexion. The analyses presented thus far were based on generic models. We also evaluated the differential effects of musculoskeletal and neural impairments on the gait pattern of a child with cerebral palsy using a three-dimensional muscle-driven model with personalized musculoskeletal geometries based on magnetic resonance imaging [43]. We found that altered muscle properties, modelled through personalized Hill-type muscle–tendon parameters, rather than spasticity and reduced neuro-muscular complexity were the primary contributors to the crouch gait pattern of the child, suggesting that they should be the main treatment targets to restore an upright posture.

(d). Gait patterns and joint loading

Predictive simulations have been used to study how alterations in the gait pattern might reduce joint loading. Gait retraining is an attractive rehabilitation strategy in joint disorders such as osteoarthritis. Fregly et al. used simulations based on a three-dimensional torque-driven model to design gait modifications that reduced the knee adduction moment while minimizing deviations from the patient's self-selected kinematics [44]. They found that slightly increasing leg flexion, decreasing pelvic obliquity and increasing pelvic axial rotation decreased the knee adduction moment. Note that knee adduction moment is a proxy for knee joint loading and that a torque-driven model with simple knee geometry, a pin joint in this case, does not capture the effect of muscle coordination and joint geometry. Miller et al. explored gait modifications that reduced axial knee joint loading based on a two-dimensional muscle-driven model [45]. They found that reduced gastrocnemius activity, avoidance of knee flexion during stance and smaller strides reduced knee joint loading. Koelewijn & van den Bogert found that improving moment symmetry in a two-dimensional muscle-driven simulation of transtibial amputee gait resulted in lower hip and knee contact forces in the intact leg at the cost of increased effort and abnormal kinematics [46].

(e). Design of assistive devices

The reflex-based model proposed by Geyer & Herr [24] served as inspiration for the design of assistive device controllers. For example, Markowitz et al. used it for controlling an ankle prosthesis and showed that it resulted in a physiological adaptation of ankle work in response to ground slope variation [47]. Further, Wu et al. used it for controlling hip and knee torques delivered by an assistive lower-limb exoskeleton, and demonstrated its ability to produce near-physiological walking kinematics at near-normative speeds for subjects with spinal cord injury [48].

Alternatively, simulations have been used to explore the effect of prosthesis design on the gait pattern. Handford & Srinivasan used trajectory optimization based on a two-dimensional muscle-driven model to explore the effect of the control strategy on the kinematics and energetics of walking with a transtibial prosthesis [49]. They found that both too little and too much prosthesis work increased the metabolic energy rate, and that metabolic energy rate could be reduced when allowing asymmetric walking patterns. Our simulations using trajectory optimization based on a three-dimensional muscle-driven model captured the ankle plantarflexion torque patterns owing to passive transtibial prosthetic use [2].

(f). Computer graphics applications

Muscle-driven models have been adopted in computer graphics owing to the increased realism of gait patterns predicted with muscle- versus torque-driven models. Mordatch et al. used trajectory optimization to simulate human gaits and other movements based on a three-dimensional muscle-driven model [50]. They minimized dynamic inconsistencies rather than imposing dynamics, reflecting their focus on generating visually plausible movement patterns in a computationally efficient way rather than studying the neuromechanics of human gait. Their simulation produced realistic simulations of steady-state gaits in Earth's and reduced gravity, gait initiation and incline walking.

4. Challenges and future perspectives

Predictive simulations have begun to provide valuable insights into the neuromechanics of gait. Recent computational advances will allow us to further increase the realism of the associated neuro-musculoskeletal models, thereby bridging the gap between how we currently conceptualize principles underlying human locomotion and how they are physiologically realized in the neuro-musculoskeletal system. In addition, the use of models that better reflect an individual's neuro-musculoskeletal properties will advance our understanding of inter-subject differences in gait patterns. Here, we discuss challenges and future perspectives to increase the accuracy of predictive simulations.

(a). Motor control models

Translating available knowledge on motor control into models will be important to improve the realism of simulations. By solving for muscle controls that optimize performance, trajectory optimization makes abstraction of underlying control structures contained in the brain and spinal cord and therefore does not give any insight into how the neural system generates muscle controls. This is an important barrier to study how neurological disorders that affect specific regions in the brain or spinal cord impede gait performance. Approaches that predict human walking by computing optimal control policies have mainly relied on reflex-based controllers. Reflex pathways implemented in popular models are simplifications of the reflex system and only part of the muscle input can probably be attributed to reflexes [51]. Reflex models have been extended by central pattern generators [38] and supraspinal inputs [29], yet none of these simple control models captures the complexity of human motor control. Important sources of sensory information, such as cutaneous receptors and vision, are often not considered and the process of sensory integration is not explicitly modelled. Developing more accurate motor control models is not straightforward as we lack a comprehensive framework and quantitative data, e.g. on the relative contribution of supraspinal and reflex pathways. We might take inspiration from motor control models that have been used to simulate animal locomotion (e.g. [52]).

Translating clinical definitions of neurological symptoms into mathematical models is important to study how these symptoms affect locomotion. For example, spasticity is a common symptom in neurological disorders that is defined as a velocity-dependent increase in tonic stretch reflexes resulting from hyperexcitability of the stretch reflex [53]. This definition has inspired modellers to describe muscle activity owing to hyperactive stretch reflexes as feedback from fibre velocity but such models failed to capture key features of the response to passive stretch in individuals with spasticity. Instead, we took inspiration from in vivo muscle stretch experiments in healthy animals [54] to develop more accurate models of spasticity by describing muscle activity owing to hyperactive stretch reflexes by feedback from history-dependent muscle force [55,56]. Our simulations inspired new experimental studies that confirmed the movement history-dependence of the response to passive stretch in individuals with spastic cerebral palsy [57]. However, studying how spasticity affects whole-body movements will require embedding those reflex models into more complete motor control models that capture task-dependent supraspinal modulation of reflexes.

(b). Optimality principles

There is a need for experiments designed to test potential trade-offs between multiple criteria to advance our understanding of the optimality criteria underlying human movement. Both experiments and simulations suggest that energy minimization shapes human gait [4,58]. While it is likely that other criteria also contribute, it remains challenging to identify them. The search space is vast, i.e. infinite combinations of potential criteria could be tested, and redundant, i.e. different criteria might result in very similar simulated walking patterns. An additional problem is that it is hard to distinguish the effect of optimal control assumptions and musculoskeletal modelling errors on the predicted movement patterns.

While trade-offs between criteria might be subtle for steady-state level-ground walking, they might be more pronounced in other conditions [59]. Predictive simulations could help identify experimental conditions that would allow distinguishing between optimality criteria. For example, simulations could be used to explore the mechanical constraints (e.g. limited joint range of motion or foot-ground contact locations, slopes or stairs, added segment mass or volume) that lead to the largest predicted difference in kinematics when prioritizing minimizing metabolic cost versus muscle activity squared, which might be a measure of fatigue.

Alternatively, inverse optimal control is a useful tool to identify optimality criteria underlying measured movements. Application of inverse optimal control has, nevertheless, been limited to simple two-dimensional models [34,35] probably owing to the high computational cost of performing bilevel optimization. In addition, inverse optimal control can only be expected to be successful when the experimental input data contains sufficient information to distinguish different criteria.

(c). Robust optimal control

Todorov & Jordan demonstrated that it was important to account for uncertainty when optimizing task performance to realistically reproduce upper limb movements [60] but uncertainty, e.g. owing to sensorimotor noise, is often neglected when simulating gait. When using shooting methods to compute control policies, accounting for uncertainty is computationally straightforward because sensorimotor and external noise can be added when evaluating the dynamics. Yet the high computational cost of current computational approaches for control policy optimization might be a barrier to applying stochastic optimal control to complex models. Because robustness against uncertainty requires feedback control, trajectory optimization is by design unsuited for studying stochastic optimal control. Future methodological developments should therefore aim at using the recent computational advances that improved the efficiency of trajectory optimization to stochastic optimal control. For example, Koelewijn & van den Bogert accounted for control noise when simulating walking based on a torque-driven sagittal plane model [61]. They computed open loop controls and gains of reflexive joint controllers by optimizing performance over a set of predefined noise trajectories using direct collocation and gradient-based optimization. Increased control noise resulted in larger foot clearance. We are currently exploring whether the approach suggested by Houska et al. for mechatronic control [62] is applicable to simulate human gait. The main idea is to approximate the stochastic state by its mean and covariance, and to approximate the dynamics of the state covariance using the continuous Lyaponuv equation. The resulting approximate deterministic optimal control problem can then be solved with direct collocation. However, it remains to be seen whether computational efficiency can be improved using such approaches given the large size of the resulting optimal control problems.

(d). Musculoskeletal model complexity

Recent computational advances enable the integration of increasingly complex models of the musculoskeletal system in predictive simulations. Common assumptions in gait simulation studies are to model the feet and the upper body as single rigid segments. Inverse approaches that aim to study joint torques or muscle coordination underlying a measured movement might be less sensitive to such assumptions than predictive simulations. For example, modelling the foot as a two-segment versus single segment system has little influence on the knee torque estimated from motion capture data, i.e. marker trajectories and ground reaction forces, whereas in recent work we found that it has a large effect on the knee torque in predictive simulations (A. Falisse, M. Afschrift, F. De Groote 2021, unpublished data). Model complexity might have important implications for testing optimality principles underlying human gait as well. For example, Song & Geyer found that adaptive feet increased the energetic cost in simulations of walking [63].

Predictive simulations of whole-body movements typically rely on phenomenological Hill-type muscle models that might not accurately capture muscle mechanics and energetics. We think that computational speed is an important limitation to the adoption of more complex and realistic models of muscle dynamics. For example, van Soest & Lemaire needed 10 000 times more CPU time to simulate vertical jumping based on a two-dimensional model driven by six muscles when using a Huxley-type cross bridge model instead of a Hill-type muscle model [64]. In addition, the unavailability of model parameters for the lower limb muscles as well as approaches to scale them to individual subjects might hinder the adoption of alternative models of muscle dynamics.

Insight into how foot-ground contact models influence predicted walking patterns is limited. Elastic foundation and Hunt–Crossley models are popular to describe contacts. Yet they might not accurately capture contact geometries, potentially affecting the predicted movements. Avoidance of inter-limb collisions has also been shown to shape human gaits [65], but inter-limb contacts are typically not modelled. In recent work, we prevented inter-limb collisions by imposing minimum distances between segment origins [2]. Contacts are inherently discontinuous and therefore unsuited for gradient-based optimization. To overcome this issue, researchers have either prescribed the sequence of foot-ground contacts, which is undesirable when the contact sequence is unknown a priori, or used smooth approximations of discontinuous models. Alternative contact descriptions have also been proposed. For example, Mordatch et al. used a contact model that does not impose the dependence of contact forces on deformation [50].

(e). Between subject variation/personalization

Neuro-musculoskeletal models typically represent an average human rather than a specific individual. Methods for image-based modelling of musculoskeletal geometry, i.e. joint definitions and muscle paths, are available (e.g. [66]) but the long time required to build image-based models has limited their use. Similarly, medical imaging can provide information about muscle–tendon properties. However, relating image-based measures and Hill-type model parameters is not always straightforward given the simplified representation of the muscle as a single fibre in series with the tendon in such models. Alternatively, model parameters can be identified based on experimental electromyography (EMG)-torque relationships (e.g. [67,68]). This approach has been successfully applied to estimate properties of the ankle and knee actuators but the inability to collect surface EMG from deep muscles limits its use for the hip actuators. Similarly, dynamic ultrasound-based measures of fibre lengths can be used for parameter identification but such measures are typically limited to very few muscles [69].

Methods for personalized modelling of motor control are scarce. Little is known about how optimality principles underlying gait differ between subjects or within subjects depending on experience and mood. Liu et al. used inverse optimal control to find the optimality criterion underlying three-dimensional torque-driven simulations that best represented an observed movement style [70]. Alternatively, muscle synergies derived from EMG signals measured during walking have been used for personalized modelling of muscle coordination in stroke [71]. The disadvantage of this approach is that experimental data from the movement being studied is needed as input and hence the simulations can no longer be considered predictive.

Available methods for model personalization have in common that they require extensive data collection. Estimation of model parameters based on limited input data is susceptible to overfitting. Predictive simulations could be used to explore the sensitivity of predicted walking patterns to model parameters, thereby enabling targeted selection of model parameters to be personalized and experimental data to be collected.

(f). Personalized treatment selection

Predictive simulations are an attractive tool for personalized treatment selection. Predictive simulations would allow us to test different treatment options in advance of the intervention and to select the treatment option that has the highest potential to improve gait performance. We currently focus on using predictive simulations to predict the effect of single event multi-level surgery in children with cerebral palsy, where treatment outcome is currently unpredictable and variable [72]. However, it is unclear what level of model complexity and personalization is needed to distinguish successful from unsuccessful interventions. Similarly, predictive simulations could accelerate the design of devices aiming to improve gait performance such as running shoes, insoles, prostheses and exoskeletons but it has yet to be convincingly demonstrated that they can predict the effect of such devices on the gait pattern.

(g). Adaptation, learning and experience

The ability to simulate how experience shapes gait mechanics and energetics will be important if we want to predict the effect of gait training or adaptation to devices such as exoskeletons. For example, Sellinger et al. showed that humans change their gait pattern when wearing an exoskeleton such that the energetic cost is minimized and that this process requires exploration away from their non-assisted gait pattern [58]. But even non-gait-specific training might have an influence on gait. Sawers et al. demonstrated that muscle coordination during walking was different in professionally trained ballet dancers as compared to healthy controls [73]. Reinforcement learning might offer a framework to translate experimental observations on adaptation, learning and experience into simulations.

5. Conclusion

We expect the use of predictive simulations for investigating the neuromechanics of human gait to grow in the coming years thanks to recent developments in computational approaches and the availability of open-source software packages. However, challenges remain to further improve the realism of predictive simulations and to validate the simulated outcomes. Addressing these challenges will be important to answer both fundamental questions about the neuromechanics of gait and to use predictive simulations for the design of interventions that improve gait performance.

Data accessibility

This article has no additional data.

Authors' contributions

The two authors contributed equally to this perspective.

Competing interests

We declare we have no competing interests.

Funding

This study was funded by KU Leuven Internal Funds (grant no. C24M/19/064).