Explicit Representation of Cation-π Interactions in Force Fields with 1/r⁴ Non-bonded Terms

Abstract

The binding energies for cation-π complexation are underestimated by traditional fixed-charge force fields owing to their lack of explicit treatment of ion-induced dipole interactions. To address this deficiency, explicit treatment of cation-π interactions has been introduced into the OPLS-AA force field. Following prior work with atomic cations, it is found that cation-π interactions can be handled efficiently by augmenting the usual 12–6 Lennard-Jones potentials with 1/r⁴ terms. Results are provided for prototypical complexes as well as protein-ligand systems of relevance for drug design. Alkali cation, ammonium, guanidinium, and tetramethylammonium were chosen for the representative cations, while benzene and six heteroaromatic molecules were used as the π systems. The required non-bonded parameters were fit to reproduce structures and interactions energies for gas-phase complexes from DFT calculations at the ωB97X-D/6–311++G(d,p) level. The impact of solvent was then examined by computing potentials of mean force (pmfs) in both aqueous and THF solutions using free-energy perturbation (FEP) theory. Further testing was carried out for two cases of strong and one case of weak cation-π interactions between drug-like molecules and their protein hosts, namely, the JH2 domain of JAK2 kinase and macrophage migration inhibitory factor. FEP results reveal greater binding by 1.5 – 4.4 kcal/mol from addition of the explicit cation-π contributions. Thus, in the absence of such treatment of cation- π interactions, errors for computed binding or inhibition constants of 10¹ −10³ are expected.

INTRODUCTION

Cation-π interactions are an important binding element for molecular recognition in synthetic and natural systems. They have been studied for more than 30 years and numerous reviews are available.^1–5 During this time, computational modeling of complex systems in solution has predominantly featured the use of fixed-charge force fields in molecular dynamics or Monte Carlo simulations. However, cation-π interactions are well-known to feature ion-induced dipole interactions,^2–6 which are not explicitly included in such force fields. The consequent errors in computing gas-phase interaction energies increase with the polarizing character of the ion leading to ca. 10 kcal/mol underestimation of gas-phase interaction energies for prototypical cases like K⁺ or NH₄⁺ with benzene.⁶ Approaches to address the deficiencies started in the 1990s, especially in reports by Kollman, Chipot, and co-workers.^6–8 Incorporation of inducible dipoles⁶ on aromatic carbon atoms or addition or Lennard-Jones 12–10 or 12–4 potentials^7,8 all yielded improvements for model complexes in comparison to quantum mechanical results. Our group has also used inducible dipoles for cation-π interactions⁹ and this approach is implemented in the fully polarizable AMOEBA force field.^10,11 A more recent tactic that has been actively pursued is the addition of Drude oscillators to better represent cation-π interactions in polarizable CHARMM force fields.^12–15

At this time, in view of the success of Li et al. in improving interactions with metal ions for an additive force field with addition of a 1/r⁴ term,^16–19 we have undertaken a broader study of the utility of this approach for treating cation-π interactions. Advantages over a fully polarizable model are that it can be readily added to and retains the character of non-additive models, and the effect on execution time is negligible. It also has the correct distance-dependence for ion-induced dipole interactions.^8,19 Simply, a term -κ_iα_j/r_ij⁴ is added to the non-bonded potential energy between site(s) on the cation i and aromatic atoms j, which have associated parameters κ and α to control the strength of the interactions. Thus, the total non-

$$E_{ij}=\frac{q_i{q}_j{e}^2}{r_{ij}}+4{\epsilon }_{ij}\left(\frac{{\sigma }_{ij}^{12}}{r_{ij}{}^{12}}-\frac{{\sigma }_{ij}^6}{r_{ij}{}^6}\right)-\frac{{\kappa }_i{\alpha }_j}{r_{ij}^4}$$ (1)

bonded interaction between such sites i and j is given by a sum of Coulombic, Lennard-Jones 12–6, and 1/r⁴ terms (eq 1). In this study, κ and α parameters have been optimized for alkali, ammonium, tetraalkylammonium, and guanidinium cations interacting with benzene and six aromatic heterocycles that are representative of aromatic amino acids found in proteins and common drug fragments.²⁰ The parameterization was performed in comparison to DFT results for representative complexes in the gas-phase, and testing has included computation of free-energy profiles for the association of cations with benzene and heterocycles in aqueous and THF solution, and computation of the effects of addition of the 1/r⁴ terms on the free energy of binding for three protein-ligand complexes. The resulting improvements are included in the latest version of the OPLS-AA force field, which is termed OPLS/2020.

QUANTUM MECHANICAL RESULTS

In order to obtain reference interaction energies and geometries for ion-molecule complexes, quantum mechanical (QM) calculations were carried out with Gaussian16 including counterpoise corrections for basis set superposition errors (BSSE).^21,22 In deciding on an appropriate level of theory, there have been numerous, systematic studies of the complexes of ammonium and alkali cations with benzene.^4,23–29 CCSD(T), MP2, and ωB97X-D based methods all give high quality results in comparison with experimental data. A previous study by Chai and Head-Gordon³⁰ compared multiple DFT methods and showed that ωB97X-D is the best overall performer based on their thermochemical test sets. As listed in Table S1, we did obtain interaction energies for the benzene-K⁺ complex with MP2 and ωB97X-D using multiple basis sets. MP2 with 6–311G++(2df, 2pd), 6–311G++(3df, 3pd) and aug-cc-pVDZ basis sets and ωB97X-D with 6–311G++(d,p), 6–311G++(2df, 2pd), 6–311G++(3df, 3pd), def2-TZVPPD all gave interaction energies of 18–19 kcal/mol in good accord with the experimental values at 0 K of 18.2 ± 1.4 kcal/mol and 17.5 ±0.9 and.^25,31 As listed in Table S2, good accord is also found between the experimental complexation energies and ωB97X-D/6–311++G(d,p) results for benzene with Li⁺, Na⁺, and NH₄⁺. In addition, as illustrated in Figure 1, the potential energy curves for separation of the benzene-K⁺ complex along the six-fold axis are similar with ωB97X-D/6–311++G(d,p) (solid blue line) and MP2/6–311++G(d,p) (blue dots). For study of additional systems, we chose ωB97X-D/6–311++G(d,p) owing to the combination of accuracy and computational efficiency.

Figure 1.

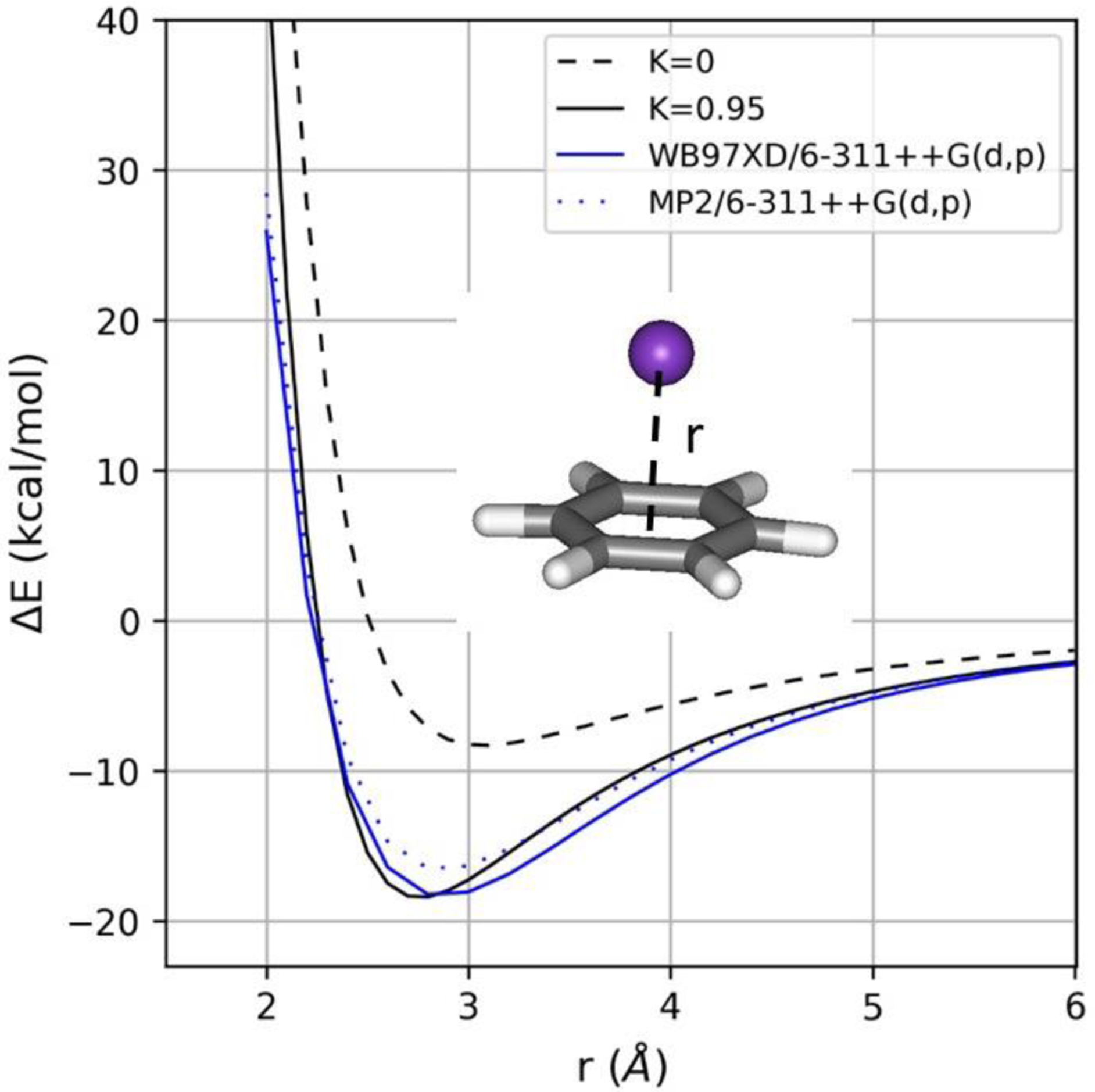
Potential energy curves for separation of the benzene-K⁺ complex from ωB97X-D/6–311++G(d,p) (solid blue line), MP2/6–311++G(d,p) (blue dots), and OPLS-AA with (solid black line) and without (dashed black line) the 1/r⁴ cation-π treatment.

For development of the improved force field with intended application to proteins and protein-ligand binding, we have considered the complexes of ammonium, tetramethylammonium (NMe₄⁺), and guanidinium (Gdm⁺) ions with benzene and indole, as illustrated in Figure 2. For treatment of alternative aromatic molecules, complexes of K⁺ with benzene, pyridine, pyrazine, pyrrole, thiophene, and furan have been included (Figure 3). Energy minima for π-complexes were initially located with B3LYP/6–311++G(d,p) calculations, then rigid potential energy scans²¹ were performed at the ωB97X-D/6–311++G(d,p) level with variation of the distance between the central atom of the ion and the aromatic ring center in 0.1-Å increments. The resultant optimal distances and interaction energies are recorded in Figures 2 and 3, and the results for all complexes are summarized in Table 1. Specific cases receive analysis below.

Figure 2.

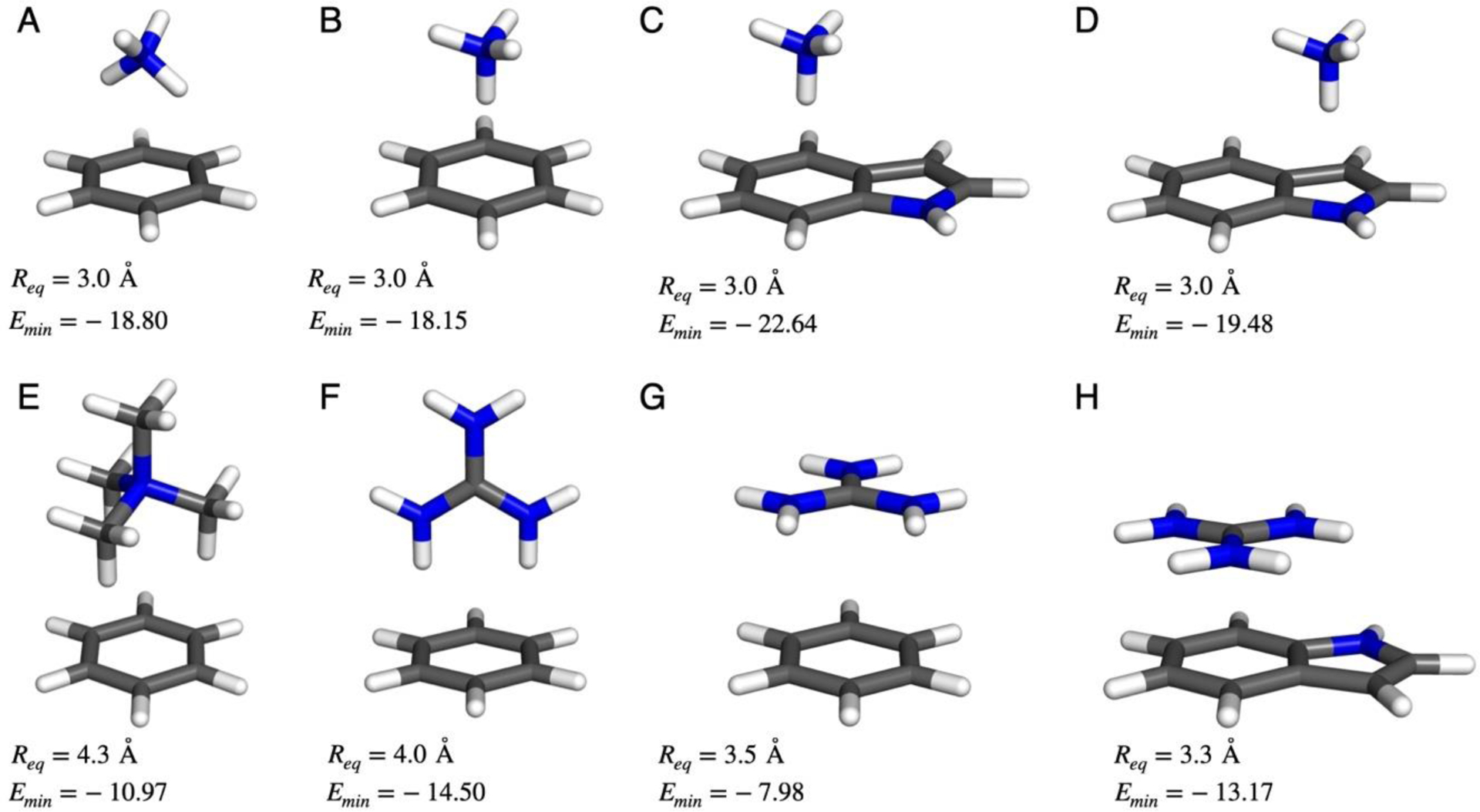
Cation– π complexes for ammonium and guanidinium ions considered here. Optimized distances in Å and interaction energies in kcal/mol from ωB97X-D/6–311++G(d,p) potential energy scans.

Figure 3.

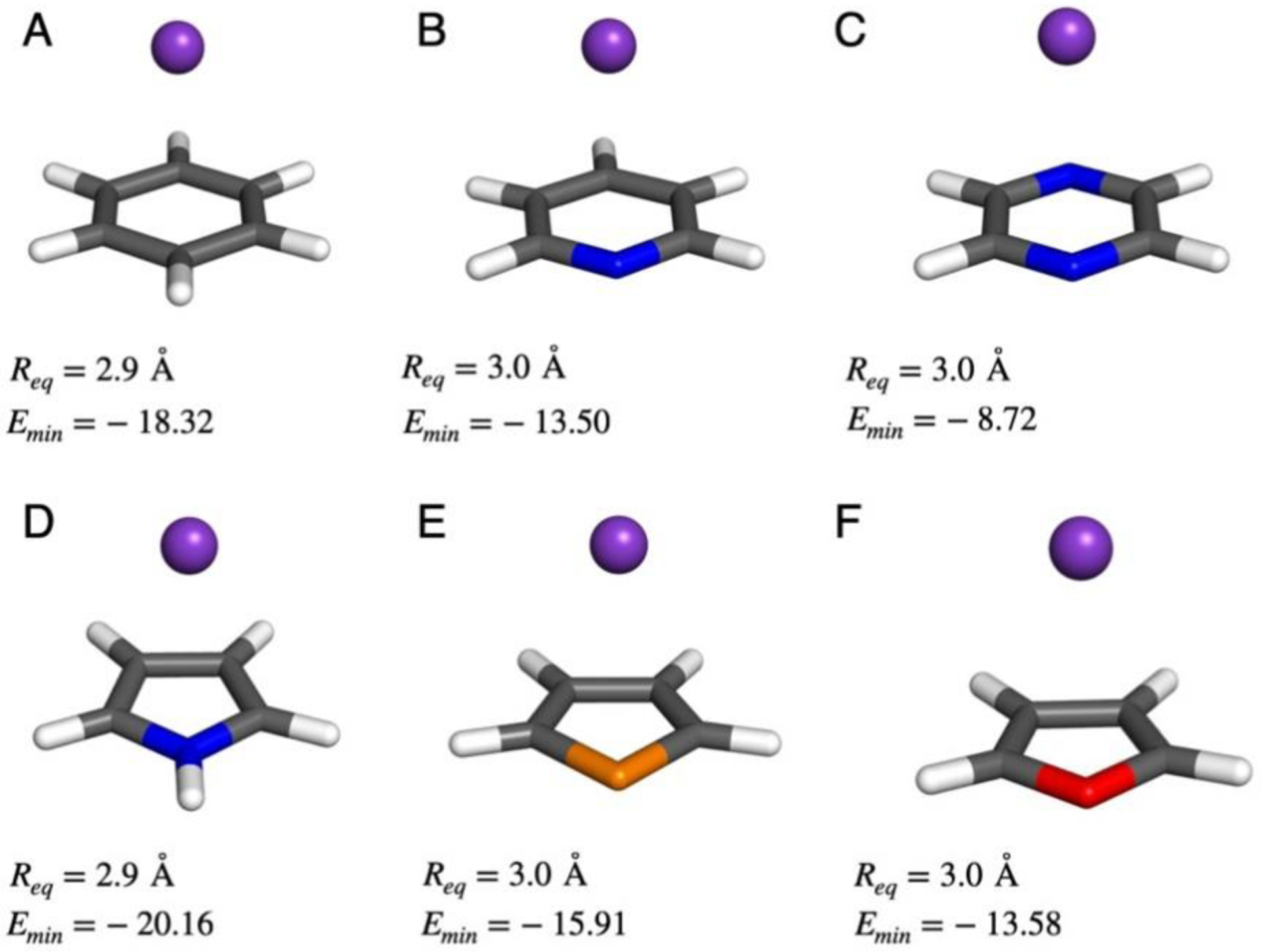
K⁺complexes with aromatic molecules considered here, as in Figure 2.

Table 1.

Interaction Energies and Optimized Distances from ωB97X-D/6–311++G(d,p) Calculations, the OPLS/2020 Force Field, and Non-Polarizable OPLS-AA^a

π	cation	Conf.	ωB97X-D	R	OPLS/2020	R	OPLS-AA	R
benzene	Li+		−38.18	1.9	−39.44	1.7	−19.83	1.9
	Na+		−24.74	2.5	−25.30	2.3	−11.96	2.6
	K+		−18.32	2.9	−18.50	2.8	−8.33	3.1
	Rb+		−13.30	3.2	−13.17	3.0	−7.33	3.3
	Cs+		−11.60	3.4	−11.08	3.3	−6.24	3.5
	NH4+	mono	−18.15	3.0	−19.41	3.0	−10.21	3.2
	NH4+	bi	−18.80	3.0	−18.48	2.9	−10.41	3.0
	NMe4+		−10.97	4.3	−9.47	4.2	−6.71	4.4
furan	K+		−13.58	3.0	−14.39	2.9	−5.79	3.2
pyrrole	K+		−20.16	2.9	−19.55	2.8	−10.52	3.0
thiophene	K+		−15.91	3.0	−15.93	2.8	−8.25	3.1
pyridine	K+		−13.50	3.0	−14.02	2.9	−7.86	3.1
pyrazine	K+		−8.72	3.0	−8.02	2.9	−1.54	3.3
indole	K+	π6	−23.57	2.8	−21.60	2.8	−9.49	3.1
	K+	π5	−21.52	2.9	−18.58	3.2	−7.66	3.2
benzene	Gdm+	stacked	−7.98	3.5	−8.62	3.3	−4.83	3.4
	Gdm+	T-shaped	−14.50	4.0	−14.14	3.7	−10.02	3.8
indole	NH4+	π6	−22.64	3.0	−21.13	2.9	−11.98	3.0
	NH4+	π5	−19.48	3.0	−18.28	3.0	−10.28	3.0
indole	Gdm+	stacked	−13.17	3.3	−13.26	3.3	−7.94	3.4
	Gdm+	T-shaped	−17.71	4.0	−18.79	3.8	−13.65	3.9

^aInteraction energies in kcal/mol and optimized distances R in Å.

For benzene-NH₄⁺, both monodendate and bidendate geometries were studied. In the bidendate form, an interaction energy of −18.8 kcal/mol was obtained; this is in accord with prior results of Ansorg et al.,¹⁰ −18.7 kcal/mol with CCSD(T)/aug-cc-pVTZ and −19.0 kcal/mol with DFT-SAPT. Kim et al.³² reported a similar value of −18.6 kcal/mol at the MP2/aug-cc-pVDZ level with a 2.9-Å equilibrium distance. Another study with a different basis set (CCSD(T)/6–311++G(2d,2p)) by Marshall et al.³³ gave weaker binding, −16.4 kcal/mol at a longer distance, 3.1 Å. However, a CCSD(T)/CBS report yielded stronger binding, −21.4 kcal/mol at a distance of 2.94 Å.³⁴ The experimental enthalpy change for the complexation at 298 K is −19.3 kcal/mol³⁵ and the difference with 0 K is expected to be negligible.²⁵ The monodendate geometry for benzene-NH₄⁺ is 0.65 kcal/mol less favorable than for the bidendate alternative in Figure 2. This result is in accord with a 0.7 kcal/mol difference using CCSD(T)/aug-cc-pVTZ reported by Ansorg et al.¹⁰ at 3.0-Å separation. Overall, the present findings are consistent with a consensus of a ca. −19 kcal/mol interactions energy for benzene-NH₄⁺ and small favoring of the bidendate geometry.

The benzene-NMe₄⁺ complex favors having three methyl groups in contact with the benzene ring.²⁶ The present interaction energy of −11.0 kcal/mol with an N-ring center distance of 4.3 Å is somewhat stronger than the experimental value of −9.4 kcal/mol.³⁶ Other results include −9.5 kcal/mol at the CCSD(T)/CBS level with a separation of 4.28 Å, and −10.5 kcal/mol with MP2/CBS.³⁴

Cation-π interactions for the benzene-Gdm⁺ complex were examined in stacked and T-shaped geometries. In agreement with previous reports, the ωB97X-D/6–311++G(d,p) results confirm that the T-shaped geometry with an interaction energy of −14.5 kcal/mol is preferred over the stacked alternative at −8.0 kcal/mol. Our results are in accord with the studies by Gallivan and Dougherty³⁷ (M06/6–31G(d,p)), which yielded values of −14.9 and −8.6 kcal/mol for the T-shaped and stacked structures. For the stacked one, the present interaction energy, −8.0 kcal/mol, at an interplanar separation of 3.5 Å is also consistent with the value of −7.5 kcal/mol from Kumar et al.⁵ using DLPNO-CCSD(T)/aug-cc-pVTZ at 3.5 Å.

In addition to the complexes in Figure 3, the indole-K⁺ complex was studied in two geometries where the ion is above the pyrrole ring (π5) or the benzene ring (π6) of indole, as for NH₄⁺ in Figure 2. The corresponding interaction energies in Table 1, −21.5 and −23.6 kcal/mol, predict a 2-kcal/mol favoring of complexation with the benzene ring. The larger, more electron rich π-system increases the interaction significantly compared to that for benzene, −18.3 kcal/mol. These results are nicely consistent with a joint experimental and computational study, which yielded an experimental binding energy of −23.9 kcal/mol, and MP2(full)/6–311+G(2d,2p) values of −20.9 and −22.7 kcal/mol for the π5 and π6 alternatives.³⁸ The consensus is that all alkali cations bind preferentially to the benzene ring of indole.^38,39 The π5 and π6 forms are separate energy minima for Li⁺, Na⁺, and K⁺.³⁸ Similarly, we find that ammonium ion binds about 3 kcal/mol more strongly to the benzene rather than pyrrole ring of indole (Figure 2) with interaction energies of −22.6 and −19.5 kcal/mol. For guanidinium ion with indole, a π6 stacked geometry was explored and yielded a significantly enhanced interaction energy of −13.2 kcal/mol compared to the stacked result with benzene, −8.0 kcal/mol.

The interaction of K⁺ with the other π systems shows that indole provides the strongest cation-π binding and the trend in binding strengths is indole > pyrrole > benzene > thiophene > furan ≈ pyridine > pyrazine. The same pattern was found in an early study using HF/6–31G(d,p) calculations for complexes with Na⁺, though thiophene was not included.³⁹ Consideration of basic electrostatics explains well the pattern with azine nitrogens, sulfur and oxygen depleting π-electron density, and aniline or pyrrole-like nitrogen atoms increasing it.³⁹ Another study also found pyrrole to be a stronger π-donor than benzene yielding complexation energies of −18.2 and −16.6 kcal/mol with MP2/aug-cc-pVDZ calculations.³² For interaction with benzene as the π system, the order of cation binding strengths in Table 1 is Li⁺ > Na⁺ > NH₄⁺ ≈ K⁺ > Gdm⁺ > Rb⁺ > Cs⁺ > TMA⁺, which follows the expected trend of increasing charge delocalization. Overall, the ωB97X-D/6–311++G(d,p) results for cation-π interactions are consistent with the best available interaction energies and geometries, and they provide a solid basis for parameterization of a force field.

DETERMINATION OF κ AND α PARAMETERS

Treatment of the 1/r⁴ terms was taken as an add-on to the OPLS-AA force field⁴⁰ and implemented in the BOSS 5.0 and MCPRO 3.3 programs,⁴¹ which were used for gas-phase energy minimizations and potential surface scans, as well as for free-energy perturbation (FEP) calculations in solution. Parametrization of the κ and α parameters in eq 1 focused on reproducing the ωB97X-D/6–311++G(d,p) results for the complexes. The κ for the N of ammonium ions (type N3 in OPLS and AMBER force fields) was set to 1.0, and an initial α for aromatic carbon atoms (type CA) was determined to reproduce well the interaction energy and separation for the benzene-NH₄⁺ complex. This α value could then be used to obtain initial values for the other cations from optimization of their complexes with benzene and the heterocycles. This process was iterated until the κ and α parameters converged to minimize the root-mean-square deviation between the interaction energies calculated with ωB97X-D/6–311++G(d,p) and the modified force field, OPLS/2020.

The resultant parameter values are listed in Table 2, and the results for the 21 complexes are compared in Table 1. The complete non-bonded parameters for the present ions are provided in Table S3. The improved agreement with the QM results is striking with the average error for the interaction energies declining from 8.4 kcal/mol with OPLS-AA to 0.9 kcal/mol with OPLS/2020, while the average error for the computed separations remains at 0.1 Å. The distances for the energy minima are generally 0.1 Å shorter than the QM references with OPLS/2020, while they are ca. 0.1 Å longer with OPLS-AA; the discrepancies were not sufficient to motivate modification of the Lennard-Jones parameters for OPLS-AA with the exception of the σ and ε for ammonium nitrogen atoms, which were changed from 3.25 Å and 0.17 kcal/mol⁴² to 3.48 Å and 0.29 kcal/mol. The partial charges for ammonium and guanidinium ions are the same as published in 1986 and 1993.^42,43 The parameters for the alkali metal cation are from Jensen and Jorgensen.⁴⁴ The OPLS-AA parameters for the cations yield free energies of hydration in good accord with experimental data.^42–44

Table 2.

Optimized κ and α Parameters for OPLS/2020^a

type	atom	κ	type	atom	α
Li	Li+	0.45	CA	benzene, aromatic C	190
Na	Na+	0.70	CW	C2 in furan/thiophene	210
K	K+	0.95	CS	C3 in furan/thiophene	210
Rb	Rb+	0.70	NA	N in pyrrole/indole	150
Cs	Cs+	0.75	NC	N in azine	100
N3	ammonium N	1.00	OA	O in furan	150
N2	guanidinium N	0.25	SA	S in thiophene	50

^aFor use in Eq 1 for gas-phase interactions with r in Å and E in kcal/mol. For condensed-phase systems, scaling the α values by 0.5 is recommended.

For the particularly biologically relevant interactions of ammonium and guanidinium ions as models for lysine and arginine with benzene and indole as models for phenylalanine and tryptophan, underestimates of the cation-π interactions by 5–10 kcal/mol are reduced to differences of ca. 1 kcal/mol in Table 1. The trends for the interactions are also well reproduced with the affinity order for K⁺ being indole > pyrrole > benzene > thiophene > furan ≈ pyridine > pyrazine both from the ωB97X-D/6–311++G(d,p) calculations and OPLS/2020. Furthermore, potential energy scans agreed well, as illustrated in Figure 1; the dissociation curve for the benzene-K⁺ complex from the QM calculations and the OPLS/2020 force field overlap closely, while the curve for unmodified OPLS-AA is shifted up by 10 kcal/mol in the vicinity of the energy minimum and the slope with increasing distance is too small. Addition of the 1/r⁴ terms provides substantial improvement to the interaction profile with correct distance-dependence.

FREE ENERGY PROFILES IN SOLUTION

In order to gauge the influence of solvation, potentials of mean force (pmfs) for separation of the cation-π complexes were computed via Metropolis Monte Carlo (MC) simulations using free-energy perturbation (FEP) theory in water and tetrahydrofuran with the BOSS program.⁴¹ The reaction coordinate (r_c) was taken as the distance from the ring center to the central atom of the cation, as above. 25 windows with double-wide sampling and a 0.1-Å step size were used to cover the range from 2.0 to 7.0 Å.⁴⁵ By that point the pmf curves were flat. Each window consisted of at least 2.5 million configurations of equilibration and 4 million configurations of averaging. All calculations were performed for systems with periodic boundary conditions at 25 C and 1 atm. 740 TIP4P water molecules⁴⁶ or 390 THF molecules⁴⁷ were used with solute-solvent cutoffs of 12 Å and solvent-solvent cutoffs of 10 (water) or 12 Å (THF). Some calculations with 2000 water molecules were also carried out, as noted below.

Computed pmfs for K⁺, NH₄⁺, NMe₄⁺, and guanidinium ion with benzene are shown in Figure 4; additional pmfs are given in Figure S1. The general pattern is that there are no (K⁺) or very shallow minima (ca. −1 kcal/mol) in these free-energy profiles using the non-polarizable OPLS-AA force field; the free energy is roughly unchanged from 7-Å separation to 3–4 Å where the pmfs become sharply repulsive as the cation and π-system come within van der Waal’s contact. In view of the enhanced interactions upon inclusion of the 1/r⁴ terms in the force field, it is not surprising that well-defined minima are introduced in the pmfs near the optimal gas-phase separations with OPLS/2020.

Figure 4.

Computed pmfs for the complexation of benzene with K⁺, NH₄⁺, Gdm⁺, and NMe₄⁺ in TIP4P water at 25 C and 1 atm with (red) and without (black) the explicit treatment of cation-π interactions. r is the distance between the center of the benzene ring and the center atom of the cation.

For benzene-K⁺ in Figure 4, the minimum occurs at 2.9-Å separation with a well-depth of −7.5 kcal/mol. The smoothness of the pmfs suggests good convergence with the present methodology; however, for further testing, two additional independent runs were made for benzene-K⁺ by just changing the number of water molecules from 740 to 742 and 745. The resultant pmfs have well-depths of −8.2 and −7.3 kcal/mol at separations of 2.8 and 2.9 Å. Thus, the statistical uncertainty in the well-depths is 0.5 – 1.0 kcal/mol. The depths are much less negative than the gas-phase interaction energy (−18.5 kcal/mol in Table 1) owing to the dehydration of the ion as it approaches the benzene molecule and to the thermal averaging. Integration of the first peak in the K⁺ – O_w radial distribution function (rdf) to 3.4 Å reveals 7.0 water molecules when r_c is 6.9 Å, which is reduced to 5.0 water molecules at r_c = 2.9 Å. The pmfs for benzene-NH₄⁺ in Figure 4 are similar with a well-depth of −7.6 kcal/mol using the modified force field at an N – ring center distance of 2.9 Å. Near the minimum, one hydrogen atom of the ion is directed towards the benzene ring and there is less dehydration; integration of the N – O_w rdfs to 3.5 Å reveals 6.8 hydrogen-bonded water molecules at r_c = 6.9 Å declining to 5.4 at r_c = 2.9 Å. The benzene-guanidinium ion pmf shows a shallower free-energy minimum, −6.1 kcal/mol at 3.4–3.5 Å separation. The stacked structure is preferred in this distance range in water over the T-shaped one, since it minimizes the loss of hydrogen bonds. Stacked structures are also observed in crystal structures containing arginine-arene contacts.⁵ From the present rdfs and solute-water interaction energies, it is apparent that there are 6 water molecules hydrogen-bonded to the guanidinium ion at all values of r_c, as previously noted.⁴³ For benzene-NMe₄⁺, there is a broad minimum at r_c = 4–5 Å with a well-depth of −3.8 kcal/mol with inclusion of the 1/r⁴ terms with OPLS/2020 vs. −1.2 kcal/mol with OPLS-AA.

Prior results for the well-depths of the contact minima are variable. In the early study by Chipot et al., the pmf obtained for toluene-NH₄⁺ in TIP3P water including the 10–12 cation-π term has a minimum at 3.05 Å with a depth of −5.5 kcal/mol.⁷ Gallivan and Dougherty also obtained a well-depth of −5.5 kcal/mol for the benzene-methylammonium complex using HF/6–31+G(d) calculations and a continuum hydration model.⁴⁸ Car-Parrinello MD has been applied to the benzene-NH₄⁺ system and yielded a pmf with a well-depth of −5.75 kcal/mol at 3.25-Å separation.⁴⁹ With a polarizable model using the Drude approach and SWM4-NDP water model, Orabi and Lamoureux found a minimum for benzene-NH₄⁺ with a depth of only −1.4 kcal/mol at 3.3-Å separation.¹² With the same approach, they subsequently found a deeper well, −3.3 kcal/mol, for a pmf with the ammonium ion constrained to be perpendicular to the face of the benzene ring.⁵⁰ It may be noted that the results in Figure 4 were from unconstrained simulations. In another report using the CHARMM-Drude force field, the computed pmf for toluene-NH₄⁺ has the contact minimum at 2.9 Å with a depth of −2.8 kcal/mol.¹⁴ In a very recent report, Lennard-Jones 12–6 parameters were optimized to reproduce ion-arene pmfs from QM/MM calculations; the resulting well-depth for toluene-NH₄⁺ was ca. −5 kcal/mol.⁵¹

Thus, there is a significant range of results for the free-energy well-depth in water for the fundamental cation-π system, benzene-NH₄⁺, ranging from −1 to the present −7.6 kcal/mol. Some variation stems from differences in the force fields; however, there are also significant differences in the computation of the pmfs, e.g., by FEP or umbrella sampling, length of MD or MC runs, imposition of constraints, number of water molecules, water model, cutoffs, and treatment of long-range interactions. It would seem that the last item should not lead to much variation across the range of r_c (2–7 Å). In the present cases, the cutoff scheme is to include all x-y interactions if any distance between a pair of non-hydrogen atoms in molecules x and y is below the cutoff.⁴¹ The interactions are quadratically smoothed to zero over the last 0.5 Å, and no cutoff corrections are made except for the Lennard-Jones 12–6 interactions in THF. To test the impact of using a much larger system and cutoffs, the benzene-NH₄⁺ and benzene-K⁺ pmfs were also computed using ca. 40 × 40 × 40 Å cubic periodic cells with 2000 water molecules and with both water-water and solute-water cutoffs increased to 15 Å the sampling in each window was lengthened to 6 million configurations of equilibration and 10 M configurations of averaging. For K⁺ the resulting minimum was −7.3 kcal/mol at 2.9 Å, and for NH₄⁺ −8.1 kcal/mol at 3.0 Å. Thus, use of the larger systems and cutoffs gave very similar results as for the smaller ones.

Some additional prior results should be noted. For phenylalanine-Na⁺, Costanzo et al. used modified Lennard-Jones parameters to better represent cation-π interactions and obtained a pmf in SPC water with a well-depth of −4.5 kcal/mol at 2.7 Å,⁵² while with the CHARMM/Drude/SWM4-NDP water model, Orabi and Lamoureux found a shallower minimum for benzene-K⁺ with a depth of only −1.2 kcal/mol at 3.2 Å,¹² while their constrained result for the minimum for benzene-NMe₄⁺ of −3.8 kcal/mol at 4–5 Å is the same as in Figure 4.⁵⁰

For the pmf calculations in THF, the benzene-K⁺ and benzene-NH₄⁺ cases were examined (Figure 5). Without the added 1/r⁴ terms the pmfs are basically flat until r_c = 3.0 Å and then they turn repulsive, while with the explicit cation-π terms contact minima are present with well depths of −6.8 and −6.6 kcal/mol at 2.9 and 3.0 Å for K⁺ and NH₄⁺, respectively. Thus, in both cases the wells are about 1 kcal/mol shallower than for the pmfs in TIP4P water with no significant change to the r_c values. There is again the expected shedding of solvent molecules coordinated to the ions with decreasing separation. For K⁺ integration of the K⁺ – O rdf to 3.7 Å yields 6.3 and 4.7 THF molecules for r_c = 6.9 and 2.9 Å. The corresponding coordination numbers for the NH₄⁺ complex are 6.9 and 5.0 THF molecules. An illustration of the benzene-K⁺ complex at r_c = 2.9 Å is provided in Figure 6.

Figure 5.

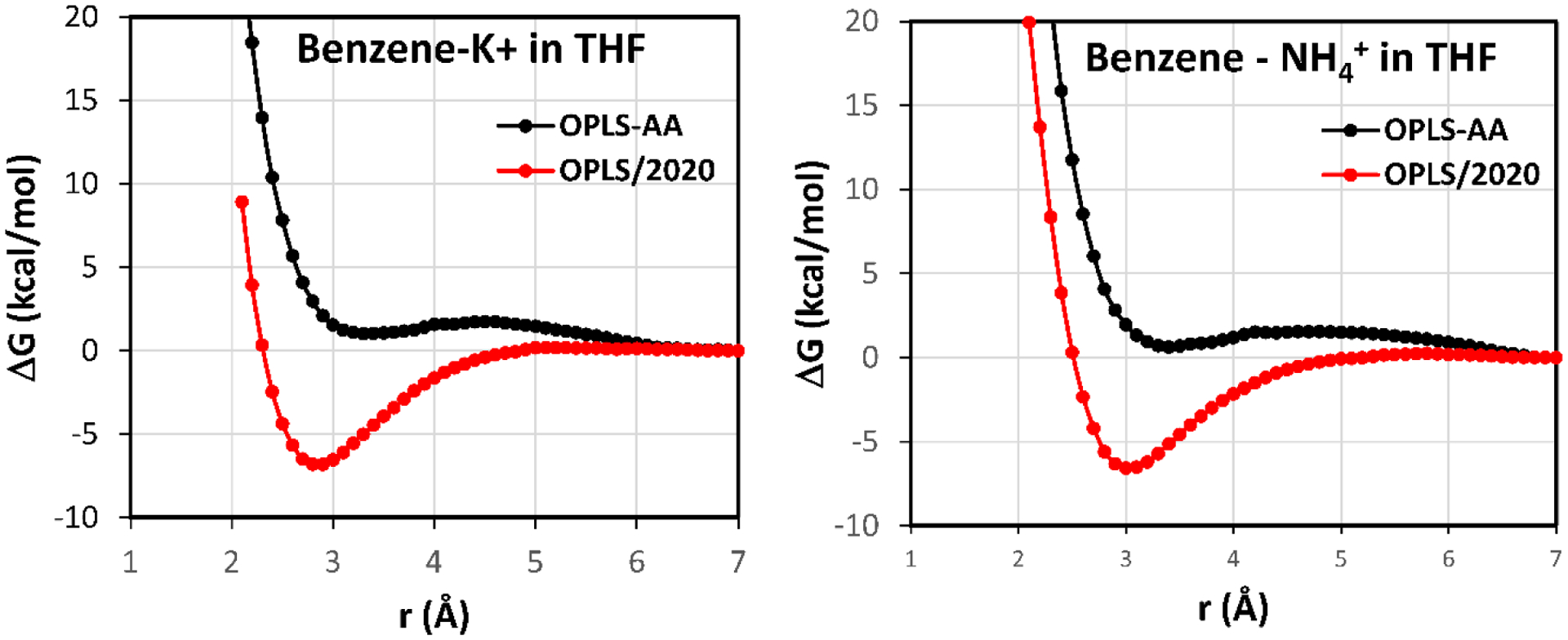
Computed pmfs for the complexation of benzene with K⁺and NH₄⁺ in united atom OPLS THF at 25 C and 1 atm with (red) and without (black) the explicit treatment of cation-π interactions. r is the distance between the center of the benzene ring and the center atom of the cation.

Figure 6.

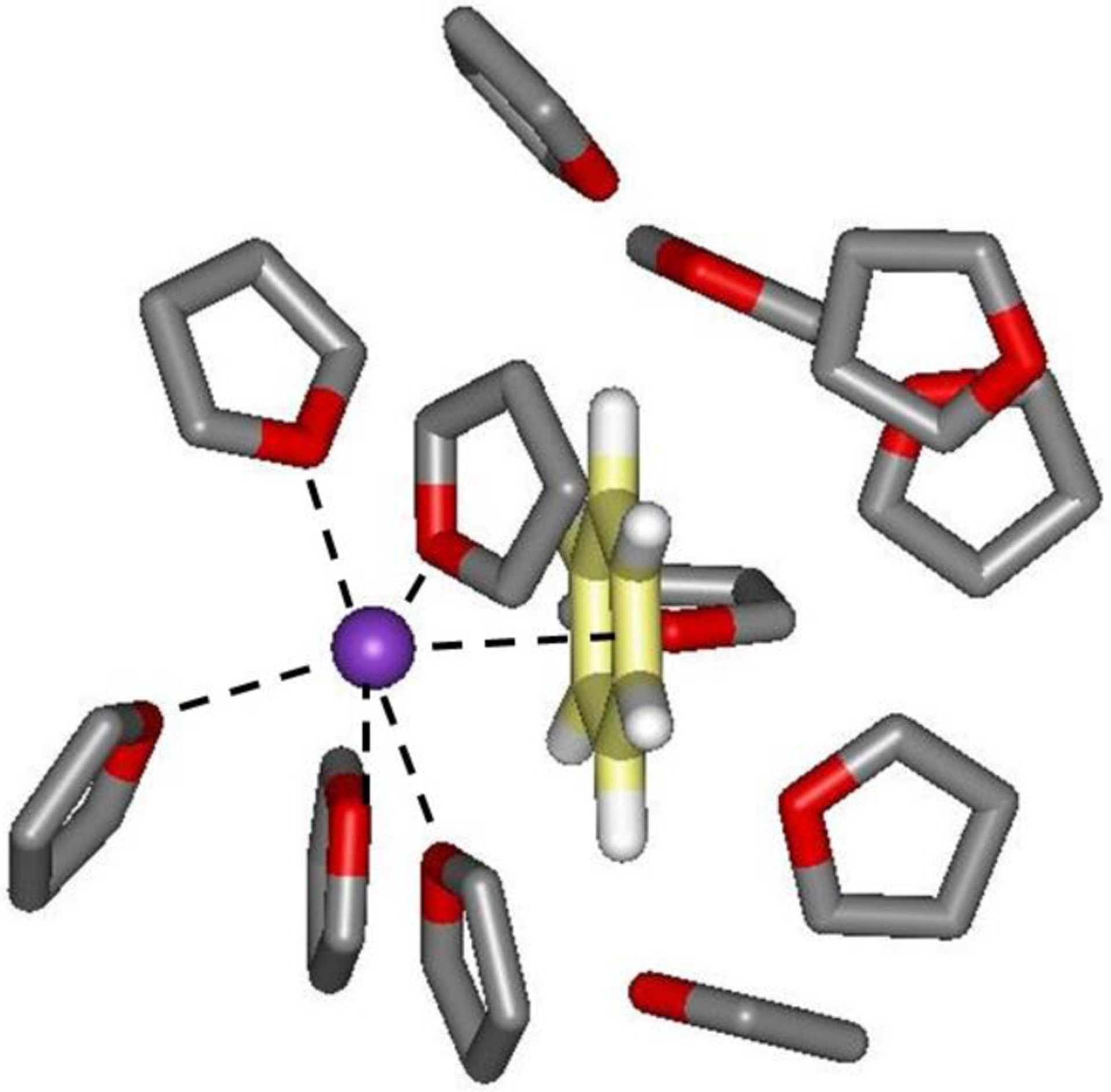
Illustration of the last configuration from the Monte Carlo simulation of the benzene – K⁺ complex in THF at a K⁺ - ring center separation of 2.9 Å. THF molecules with any atom within 4.5 Å of the solute are shown. Five THF molecules are coordinated with K⁺. Carbon atoms of benzene are colored yellow.

FURTHER CONSIDERATION OF THE CONDENSED-PHASE ENVIRONMENT

The present results for the pmfs with alkali cations and NH₄⁺ yield well-depths significantly greater than from recent studies with fully polarizable Drude-based force fields.^12,14,50 A possible contributor is that in the condensed phase the electric field generated by the cation is likely reduced by solvation.^12,51 Specifically, the dipoles of the first-shell solvent molecules would align to oppose the electric field created by the ion, and there would be solvent dipole – arene induced dipole repulsion that is neglected. Thus, the 1/r⁴ treatment that gives correct gas-phase energetics may be too strong in solution. We have explored this notion by comparing results of ωB97X-D/6–311++G(d,p) and force-field optimizations for clusters of one, two, and three water molecules coordinated with the potassium ion in the benzene-K⁺ complex, and also for the complex coordinated with acetate anion (AcO⁻) as illustrated in Figure 7.

Figure 7.

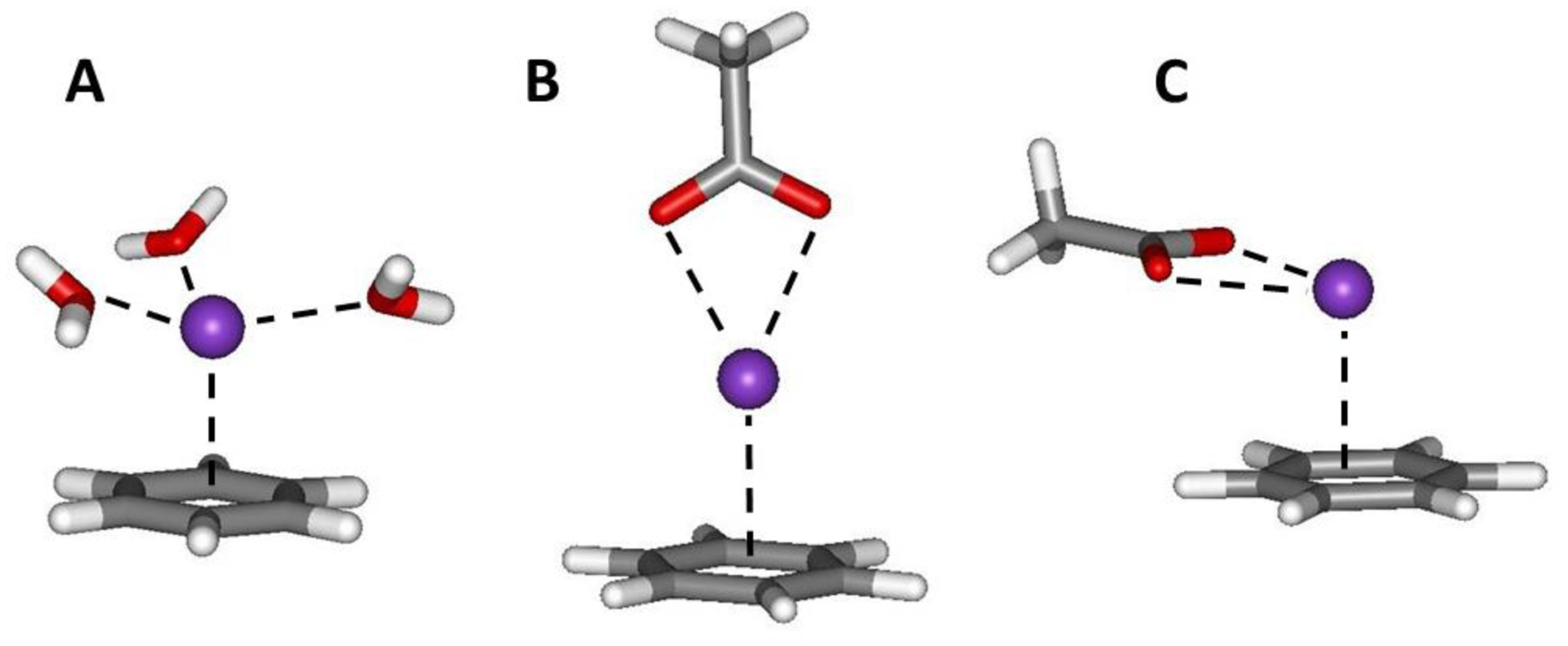
The benzene-K⁺ complex coordinated with three water molecules and two structures for the complex with acetate ion.

The expectation is that the interaction energy between benzene and the K⁺(H₂O)_n cluster should become less favorable with increasing n. Similarly, the interaction energy for benzene with the K⁺AcO⁻ ion pair should be weaker than for benzene-K⁺. As listed in Table 3, the DFT results bear this out with the interaction energies becoming less favorable by about 2.4 kcal/mol for addition of each water molecule such that the interaction energy for benzene-K⁺(H₂O)₃ is raised to −11.2 kcal/mol from the −18.3 kcal/mol with no hydration. However, the force-field results significantly underestimate this effect with the interaction energy for the benzene-K⁺(H₂O)₃ complex only being raised to −16.7 kcal/mol from −18.5 kcal/mol. For the complex of benzene with K⁺AcO⁻, optimization for the linear geometry (Figure 7B) converges to the bent structure in Figure 7C in which the anion and benzene are more parallel. The effects on the interaction energy are somewhat greater in this case with the interaction energy for benzene-K⁺ rising from −18.3 to ca. −9 kcal/mol from the DFT calculations, while the force-field results only weaken the interaction to ca. −16 kcal/mol.

Table 3.

Interaction Energies (kcal/mol) for Benzene-K⁺(H₂O)_n and K⁺AcO^{− a}

Complex	DFTb	FFc	0.5*FFd	OPLS-AA
K+	−18.3	−18.5	−13.0	−8.3
K+(H2O)1	−16.0	−18.1	−12.6	−8.0
K+(H2O)2	−13.6	−17.4	−11.9	−7.4
K+(H2O)3	−11.2	−16.7	−11.3	−6.8
K+AcO− linear	−8.4	−15.9	−10.5	−6.0
K+AcO− bent	−9.5	−16.6	−11.3	−7.0

^aΔE for benzene + K⁺(H₂O)_n or AcO⁻ → benzene + K⁺(H₂O)_n or AcO⁻.

^bωB97X-D/6–311++G(d,p) with counterpoise corrections.

^cUnmodified OPLS/2020 (eq 1).

^dOPLS/2020 with the α values in Table 2 scaled by 0.5.

Thus, the overestimation of the cation-π interactions for the clusters in Figure 7 undoubtedly biases the pmf results with the force field to yield contact energy minima that are too attractive in Figures 4 and 5. In order to correct for this, one might evaluate the electric field at the aromatic atoms and scale the α values accordingly in eq 1. However, this approach would be little different than including inducible dipoles on the aromatic atoms; it would defeat the desire for a simple improvement for cation-π interactions, and it would add complexity for computing derivatives of the energy. As a compromise for condensed-phase modeling, our recommendation is to take a linear-response-like approach^53–55 and reduce the impact of the 1/r⁴ terms by one-half through simply scaling the κ or α values in Table 2 by a factor of 0.5. As with linear-response, the physical notion is that this corrects the interactions with the solute for reorienting solvent molecules. With this approach, the results in the fourth column of Table 3 are obtained. The accord with the DFT interaction energies for the clusters with three water molecules and acetate ion is much improved. As with linear response, this is an average solution that is not perfectly reflective of all condensed-phase environments; however, it is an improvement over not adjusting for the solvent reorientation associated with solvation of the cation. With the 0.5-scaling the computed pmfs for benzene with K⁺ and NH₄⁺ in TIP4P water are shown in Figure 8. The expected reduction of the well-depths is found with depths now of −4.8 and −2.8 kcal/mol, respectively, versus −7 to −8 kcal/mol without the scaling (Figure 4). These provide our best estimates of the pmfs for benzene with K⁺ and NH₄⁺ in water. A similar reduction in the well-depths for the other systems studied here is expected with the 0.5-scaling.

Figure 8.

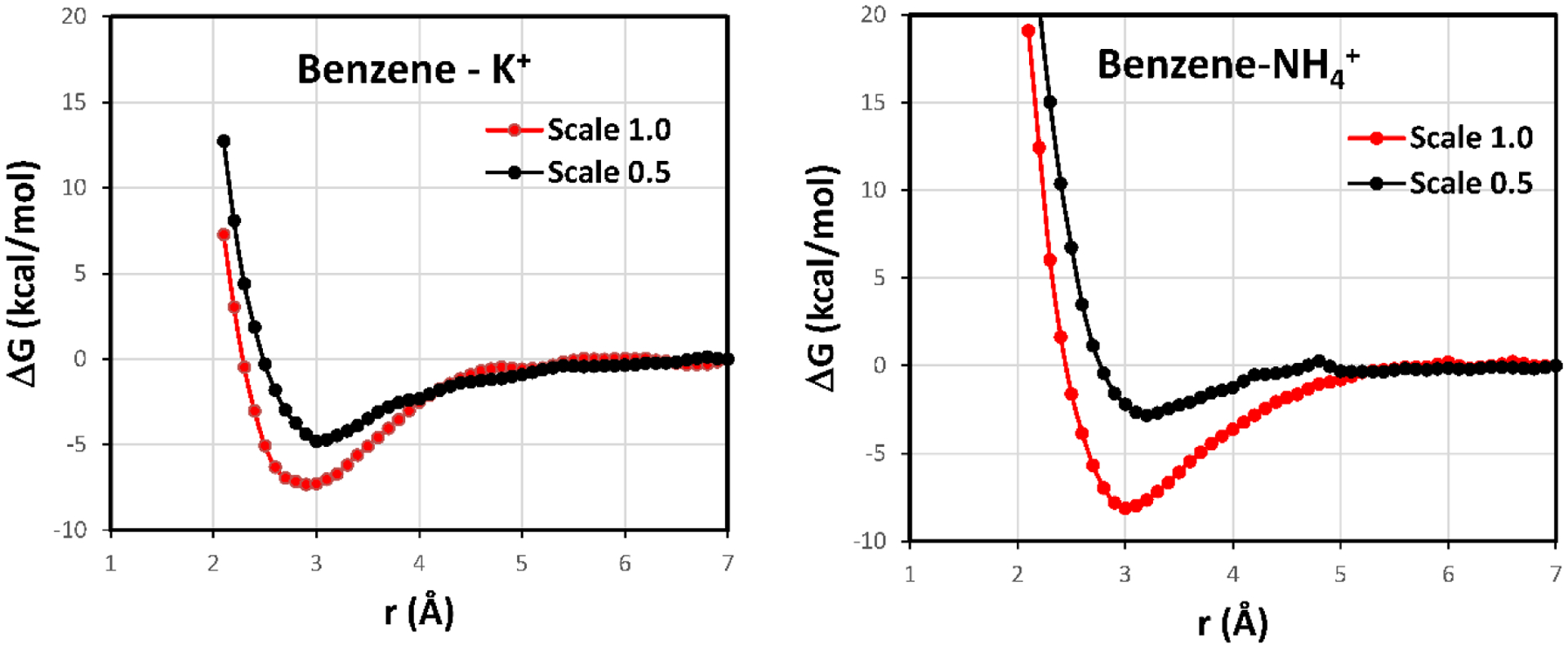
Computed pmfs for the complexation of benzene with K⁺and NH₄⁺ in TIP4P water at 25 C and 1 atm with no scaling (red) and with scaling by 0.5 (black) for the 1/r⁴ treatment of cation-π interactions. r is the distance between the center of the benzene ring and the center atom of the cation. The systems included 2000 water molecules and used 15-Å cutoffs.

A final point from Table 4 is that, as expected, with standard non-polarizable OPLS-AA the interaction energies are uniformly too weak. However, the errors with a non-polarizable force field for cation-π interactions in solution are not as severe as the gas-phase discrepancies suggest. The 10 kcal/mol error for benzene-K⁺ in the gas-phase is reduced to 2.4 – 4.4 kcal/mol when three water molecules or acetate ion are added. Thus, for solution-phase calculations including protein-ligand binding, cation-π interactions are not so poorly described by non-polarizable force fields owing to reduction of the electric field from the cation by solvation.^12,51 Furthermore, any adjustment to a non-polarizable force field by, for example, modifying Lennard-Jones parameters or adding 12-n terms, to reproduce gas-phase ion-π interactions will lead to overestimate of the strength of the interactions in solution.

Table 4.

Results of Energy Minimizations and FEP Calculations for the Protein-Ligand Complexes^a

Complex:	1 with 1/r4	1 with α=0	2 with 1/r4	2 with α=0	3 with 1/r4	3 with α=0
EP-L	−112.2	−109.0	−78.6	−73.4	−57.5	−56.5
EP-L 1/r4	−4.2	−1.1	−5.6	−0.8	−1.3	−0.2
ELys-L	−33.7	−30.5	−12.5	−7.3	−12.9	−11.9
ELys-L 1/r4	−3.1	−0.3	−4.5	−0.2	−1.2	−0.2
ΔGbinding	−2.80±0.01	0	−4.38±0.03	0	−1.47±0.02	0

^aE_P-L is the total protein-ligand interaction energy (kcal/mol) with the 1/r⁴ component on the next row; E_Lys-L is the interaction energy between the key Lys and the ligand; ΔG_binding is the change in free-energy of binding for turning on the 1/r⁴ interaction with the phenyl or indolyl ring atoms.

PROTEIN-LIGAND COMPLEXES

In order to test the impact of including the 1/r⁴ treatment of cation-π interactions for protein-ligand binding, three cases have been considered with both energy-minimizations and FEP calculations in aqueous solution. The first two cases are for compounds 1 and 2 (Figure 9), which bind to the pseudokinase JH2 domain of JAK2 kinase, while compound 3 binds to macrophage migration inhibitory factor. Crystal structures for the three complexes have been determined at resolutions of 1.7, 2.2, and 1.8 Å, respectively.^56–58 As illustrated in Figure 10, the substituted phenyl and indolyl rings in 1 and 2 engage in cation-π interactions with Lys581 in the ATP-binding site of JAK2 JH2; these typify strong cation- π interactions with observed distance of 3–4 Å between ring atoms and the ammonium nitrogen atom of Lys581. In both cases, Lys581 is hydrogen-bonded with Asp699 and at least two other side-chain groups or water molecules. The complex for 3 (Figure 11A) illustrates an expected weak cation-π interaction as the distances are 4.5 – 5.5 Å and Lys32A is at the surface of the protein, well-exposed to the aqueous environment and participating in multiple hydrogen bonds. MIF is a trimer and three copies of 3 are in the crystal structure; there is variation in the tilt of the anisyl ring with rotation of an edge towards Phe113A.

Figure 9.

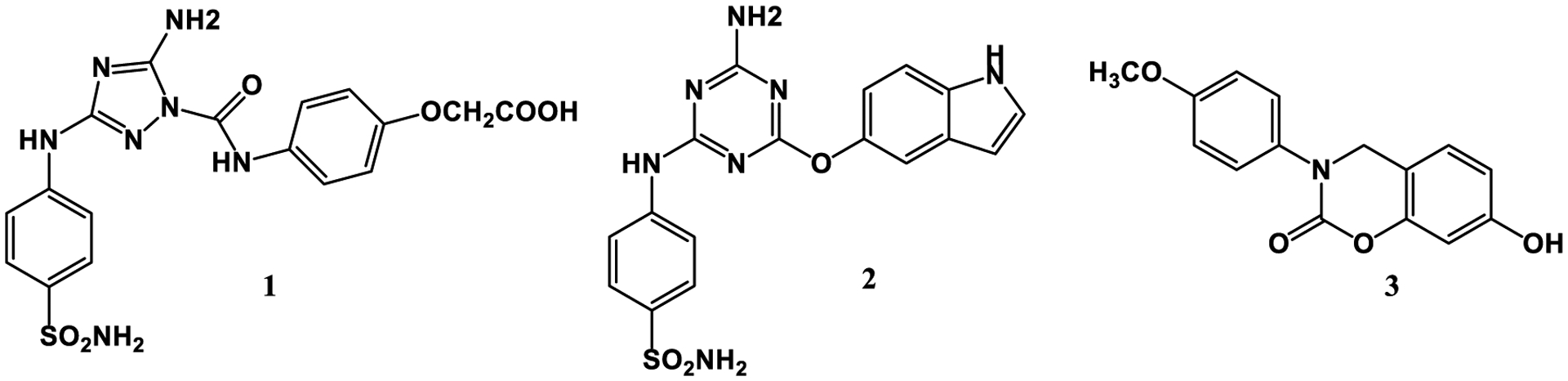
Ligands in the crystal structures illustrating cation-π interactions.

Figure 10.

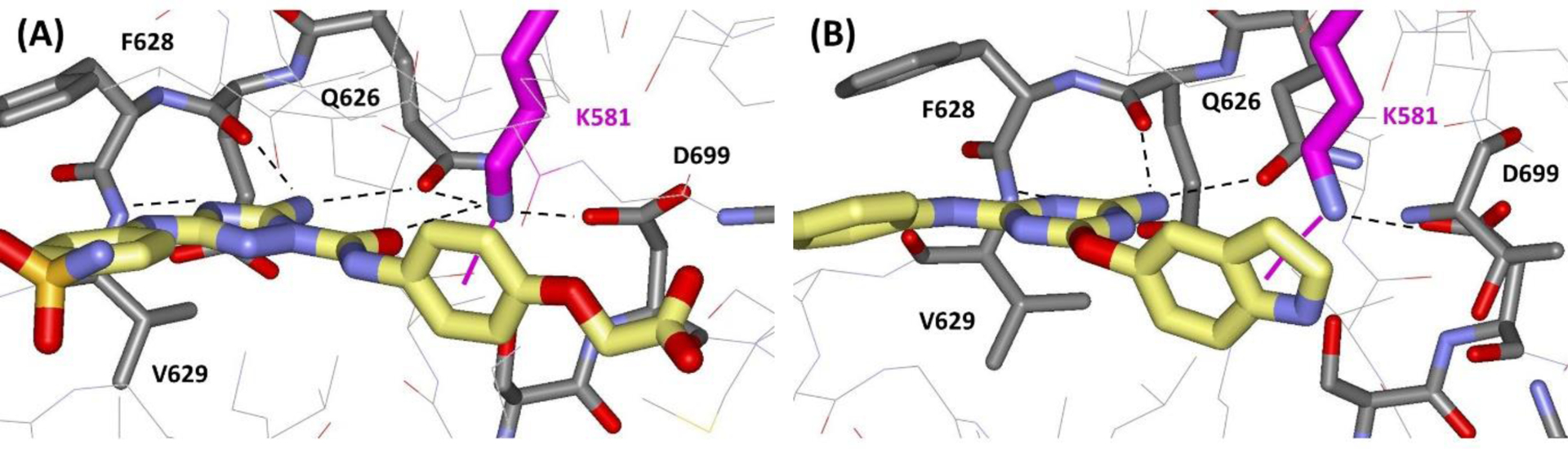
Renderings from the crystal structures for (A) 1 and (B) 2 bound to the JH2 domain of JAK2 kinase (PDB IDs 6OBF and 6XJK). Some hydrogen bonds are noted with dashed lines and the strong cation- π interactions with Lys581 in magenta.

Figure 11.

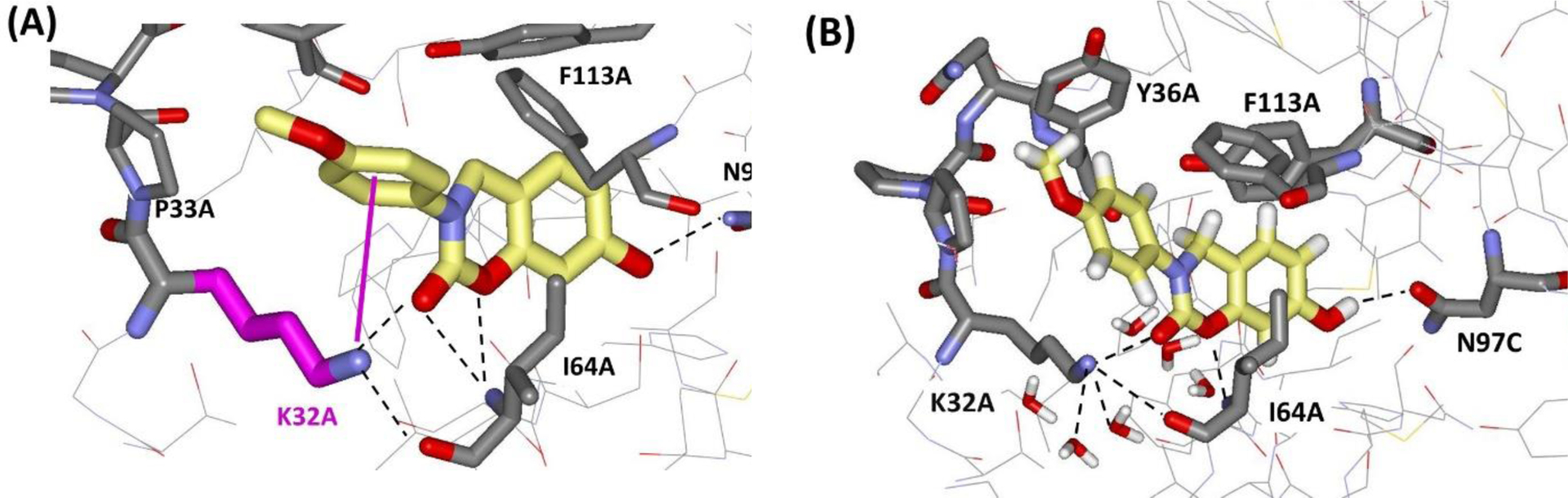
(A) Rendering from the crystal structures for 3 bound to MIF (PDB ID 5HVT) highlighting the weaker cation- π interactions with Lys32A. (B) Snapshot from the end of an MC simulation for the complex in water showing preference for the aryl-aryl interaction with Tyr36A.

To begin, conjugate gradient energy-minimizations were carried out in the gas-phase with the MCPRO program with the code added for the 1/r⁴ terms using the OPLS-AA/M force⁵⁸ field for the protein and OPLS/CM1A for the ligands.^40,41 All protein residues were included with no cutoff. A dielectric constant of 2 was imposed to provide some damping of the Coulombic interactions to mimic a condensed-phase environment. The CM1A partial charges for the ligand atoms were unscaled for 1, which is represented as the carboxylate ion, and scaled by 1.14 for the neutral ligands, as usual.⁴⁰ The calculations were performed including the 1/r⁴ terms with the 0.5-scaling, and then with the α values for the phenyl or indolyl ring atoms set to zero to turn-off the explicit cation-π interaction with the lysine residue.

Key results are summarized in Table 4. For the complex with 1 as the carboxylate ion, the total protein-ligand interaction energy is −112.2 kcal/mol with −4.2 kcal/mol from the 1/r⁴ interactions between all positively-charged residues in the protein and all aromatic atoms in the ligand; the total interaction energy between the ligand and Lys581 is −33.7 kcal/mol with −3.1 kcal/mol coming from the 1/r⁴ terms. When the α values for just the 6 carbon atoms in the benzene ring are set to zero, the third column in Table 4 shows that the protein-ligand interaction becomes less favorable by 3.2 kcal/mol and that this comes almost entirely from loss of the 1/r⁴ boost for the cation-π interaction with Lys581. The structure remains as depicted in Figure 8A; however, when the 1/r⁴ interactions are turned on, the average distance to the lysine decreases by about 0.2 Å for the benzene carbon atoms. The pattern is similar for the complex of 2, but with greater effect owing to the stronger cation-π interaction with an indolyl rather than phenyl ring. The 1/r⁴ contribution is now −5.6 kcal/mol with −4.5 kcal/mol coming from the interaction of Lys581 with the indole ring. The closest contacts are between the ammonium N and the indole C8 (3.1 Å) and N (3.2 Å), as in Figure 10B. Again, the average distance between the Lys581 ammonium nitrogen and the indolyl atoms decreases by 0.2 Å with inclusion of the 1/r⁴ interactions. For 3, the total protein-ligand interaction energy is just −57.5 kcal/mol with only a −1.3 kcal/mol contribution from the 1/r⁴ terms. Thus, this is a significantly weaker cation-π interaction than for 1 and 2, and the distances between Lys32A and the anisyl ring atoms are longer. In fact, on optimization the face-on cation-π geometry in Figure 11A is lost in favor of an edge-to-face aryl-aryl interaction between the anisyl ring and Tyr36A, as reflected in Figure 11B. Thus, for the strong interactions with 1 and 2, the energy-minimizations for the complexes show substantial contributions of 3 – 5 kcal/mol from the specific cation-π terms, which is consistent with the force-field results for the reference complexes. However, the 1/r⁴ contribution can be significantly weaker for less ideal cases such as for 3.

The next question that was addressed was the impact on computed free energies of binding in aqueous solution. For this purpose, FEP calculations were performed with the MCPRO program using standard protocols including addition of ca. 1250 TIP4P water molecules in a spherical cap with 25-Å radius centered on the binding site and with the force fields described above at 298 K.^45,60 The α values for the phenyl or indolyl ring atoms were gradually scaled to zero over 11-windows of simple overlap sampling with 10 million configurations of equilibration and 10 million configurations for averaging in each window. Residue-based cutoffs at 10 Å were invoked and all degrees of freedom were sampled except for restraint of the protein backbone after a short conjugate-gradient energy-minimization. The resultant free-energy changes are reported in Table 4. The present treatment of the highlighted cation-π interactions makes the computed free energies of binding for the complexes of 1, 2, and 3 more favorable by 2.8, 4.4, and 1.5 kcal/mol, respectively. The computed uncertainties are very small since the perturbation is just to scale the α values to zero. Stronger interaction is found for the indole ring in 2 than the phenyl ring in 1, as expected. Water does not intervene for the strong cases of 1 and 2, consistent with the crystal structures (Figure 10). Inclusion of the 1/r⁴ terms has notable effects, and the neglect of explicit treatment of cation-π interactions can be expected to lead to significant errors in predicted binding or inhibition constants, e.g., 10² – 10³ for these cases. For the weaker example of 3, the effects are less but still significant, with ca. a factor of 10 error in the predicted binding constant. For this system there was more variety in the orientation of the π-system with favoring of the aryl-aryl interaction with Tyr36A (Figure 11B). The lysine is now solvent-exposed and several hydrogen-bonded water molecules are present; the hydrogen bonds with the carbonyl group of 3 and Ile64A are also variable.

CONCLUSION

The description of cation-π interactions in force fields used for modeling proteins has been problematic for many years owing to the need to represent ion-induced dipole interactions. Following the success of Li and Merz in treating the related problem of coordination of metal ions,^16–19 we have investigated the utility of including explicit 1/r⁴-dependent terms between alkali, ammonium, and guanidinium ions and aromatic molecules. The required κ and α parameters in eq 1 were obtained by fitting to ωB97X-D/6–311++G(d,p) results for 21 complexes of the cations with benzene and six heterocycles. The average errors in reproducing the gas-phase complexation energies was lowered from 8.4 to 0.9 kcal/mol upon inclusion of the 1/r⁴ terms in the modified force field, which is called OPLS/2020. The distance-dependence of the interactions is also in good accord between the force field and DFT results (Figure 1). The modified force field was then used in computation of potentials of mean force for separation of cation-π complexes in aqueous and THF solution, which yielded the anticipated strengthening of contact free-energy minima (Figures 4, 5). However, consideration of the results and expectations of weakening the electric field from the cations in solution by their coordinating solvent molecules and/or counterions indicated that the 1/r⁴ contribution should be scaled by ca. 0.5, as in a linear-response approach. The analysis also pointed out that the errors from non-polarizable force fields for cation-π interactions in solution are less than might be expected from gas-phase interaction energies. Further testing with the scaled-1/r⁴ model was then carried out for three cases of observed cation-π complexes for the proteins JAK2 JH2 and MIF with drug-like ligands. FEP calculations found predicted enhancements of the free-energies of binding of 2.8 and 4.4 kcal/mol for the two cases of strong cation-π interactions and 1.5 kcal/mol for a weak case on the protein’s surface. Additional study is desirable for computing absolute free energies of binding, and the results could be used to optimize further the scaling for the κ or α parameters. The present approach to treating cation-π interactions is easily implemented in biomolecular modeling programs in comparison to the use of inducible dipoles or Drude particles. Such advances are necessary to improve the accuracy of predictions for protein-ligand and protein-protein interactions, which are central to computer-aided drug design.