A machine-learning approach to map landscape connectivity in Aedes aegypti with genetic and environmental data

Significance

Aedes mosquitoes are projected to continue expanding their ranges, which could expose millions more humans to the diseases they carry. The implementation of vector control methods ranging from traditional (e.g., insecticides) to cutting edge (e.g., genetic modification) could be improved with landscape connectivity maps and increased understanding of the factors that affect mosquito dispersal. Here we present an iterative random forest method for integrating genetic and environmental data to map landscape connectivity. We achieve a correlation of 0.83 between the model’s predicted genetic distance and actual genetic distance. We produce a genetic connectivity map for the southern tier of the United States and discuss important factors to consider in mosquito control, e.g., the release of genetically modified mosquitoes.

Abstract

Mapping landscape connectivity is important for controlling invasive species and disease vectors. Current landscape genetics methods are often constrained by the subjectivity of creating resistance surfaces and the difficulty of working with interacting and correlated environmental variables. To overcome these constraints, we combine the advantages of a machine-learning framework and an iterative optimization process to develop a method for integrating genetic and environmental (e.g., climate, land cover, human infrastructure) data. We validate and demonstrate this method for the Aedes aegypti mosquito, an invasive species and the primary vector of dengue, yellow fever, chikungunya, and Zika. We test two contrasting metrics to approximate genetic distance and find Cavalli-Sforza–Edwards distance (CSE) performs better than linearized F_ST. The correlation (R) between the model’s predicted genetic distance and actual distance is 0.83. We produce a map of genetic connectivity for Ae. aegypti’s range in North America and discuss which environmental and anthropogenic variables are most important for predicting gene flow, especially in the context of vector control.

Landscape genetics—explicitly quantifying the effects of a heterogenous landscape on gene flow—is an important tool for both conservation biology and the control of invasive species and disease vectors including the “yellow fever mosquito” (Aedes aegypti) (1, 2). We demonstrate that current limitations in landscape genetics can be addressed with a machine-learning approach integrated into an iterative optimization process. Isolation by distance (IBD) is a classical model in population genetics that assumes dispersal is limited in proportion to geographic distance, resulting in increasing genetic differentiation with increasing geographic distance between populations (3–5). Although this pattern is commonly seen in nature, factors such as history and dispersal limitations caused by the environment (i.e., “isolation by resistance”) (6) can produce deviations from IBD. Landscape resistance (alias friction) and its inverse, connectivity, determine how organisms move through a landscape (7). Modeling landscape connectivity can be used to identify the environmental variables that affect the organisms’ gene flow and genetic structure; predict how climate and land use change will affect their gene flow and distribution in the future; and inform conservation, vector control, and other management decisions (1, 8–13). Our goals are to use environmental data (the predictors) to build a model of genetic connectivity (the observed data) that improves on IBD and to identify environmental drivers of gene flow patterns.

We implement a machine-learning approach that offers a number of advantages over classical methods in landscape genetics: The machine-learning approach is more objective, it allows the inclusion of correlated variables, and it is able to account for different shapes and magnitudes of correlations between predictor and response variables at different locations in the landscape (14–17). In comparison, a common approach in landscape genetics called resistance surface mapping involves the subjective process of creating resistance surfaces for environmental variables, in which each pixel represents a hypothesized resistance to the organism’s movement often based on expert opinion (6, 18). Effective landscape distances through the resistance surfaces can be found with least cost path or circuit theory analysis (19) and then analyzed for associations with genetic distance (20).

One option to circumvent the subjectivity of creating resistance surfaces is to model genetic connectivity directly from environmental data. Bouyer et al. (7) took this approach and used a maximum-likelihood method to integrate genetic data and environmental data to map landscape resistance in tsetse flies. Additionally, they introduced an iterative optimization approach in which each subsequent iteration used least cost path lines through the previously predicted resistance surface—an improvement over modeling organism movement as straight lines (16, 17). While this presented a major advance, the maximum-likelihood methodology requires exclusion of correlated data, establishing the relationship between environmental variables and genetic distance before building the model, and transforming or discretizing nonlinear relationships. Additionally, this approach assumes one relationship between each environmental variable and the genetic data across the whole landscape. To build on previous advances while overcoming some of their limitations, we combine iterative optimization with a machine-learning method called random forest (RF).

RF is a nonlinear classification and regression tree analysis that can handle many inputs, including redundant or irrelevant variables, as well as continuous and categorical data types (14, 15). RF creates many internal training/testing subdatasets and aggregates the predictors, resulting in stable and consistent results that generally do not overfit the data and can be evaluated through validation processes (14). It is easier to tune and less likely to overfit noisy data than another machine-learning method we considered, gradient boosting (21). Additionally, RF has been successfully incorporated into ecological studies (22) and a small number of landscape genetics studies (16, 17, 23). These studies considered only the environmental predictor values at the genetic collection sites (23) or along straight lines between each pair of sites (16, 17), in contrast to the least cost path analysis we implement here (7).

We demonstrate the efficacy of our method to map landscape connectivity for an important disease vector. Ae. aegypti is highly invasive and the primary vector of yellow fever, Zika, dengue, and chikungunya. Except for yellow fever, there are no reliable, widely used vaccines for these diseases, so vector control is essential. Ae. aegypti originated in Africa and is now found throughout the tropics and increasingly in temperate regions (24–26). The species is temperature constrained, preferring warm, humid areas close to humans (the females’ preferred source for bloodmeals outside their native African range) (27). In the United States, it has a patchy distribution throughout southern states, especially Texas, Florida, and California (28). Although Ae. aegypti can disperse >1 km, its usual lifetime dispersal is only around 200 m (29–32). Passive “hitchhiking” via human transportation networks is responsible for long-distance invasions and worldwide spread of Ae. aegypti and its close relative (33–35). Climate change is also expanding the range of Aedes species, which could expose nearly 1 billion additional people to diseases carried by these mosquitoes for the first time (26).

Although IBD is common in nature and a helpful null model in landscape genetics (20), geographic distance is often an inadequate sole predictor of genetic distance (as in the case of our dataset; SI Appendix, Fig. S1). Therefore, a more complex model is needed to explain and predict genetic distance and corresponding landscape connectivity. In this paper we introduce an iterative machine-learning approach to integrate environmental predictors and genetic observation data and apply it to map landscape connectivity for the Ae. aegypti mosquito in North America. We also find and examine the most important variables for building the connectivity model and provide validation of our proposed method.

Modeling Approach

The input data for the model are genetic distances (response variable: Cavalli-Sforza–Edwards distance (CSE) or linearized F_ST, Table 1) and environmental data (predictor variables: environmental data). To generate genetic data, Ae. aegypti samples from 38 sites (mean sample size = 35.6 individuals) across North America (see Fig. 2 and SI Appendix, Table S1) were genotyped at 12 highly variable microsatellite sites as in Brown et al. (36) (Fig. 1A). For genetic distance, we calculated linearized F_ST (37) and CSE (38, 39), resulting in 703 pairwise genetic distances (Fig. 1C). F_ST is a common measure of population differentiation based on genetic structure, and CSE is a purely geometric measure of genetic differentiation which avoids some of the assumptions of F_ST (7, 40). For environmental data, we used 29 environmental and anthropogenic datasets derived from satellite imagery and freely available to download online (Fig. 1B and SI Appendix, Table S2).

Table 1.

Important terminology and acronyms

Abbreviation	Explanation
IBD	Isolation by distance: the expectation of increased genetic distance with increased geographic distance (3, 4)
CSE	Cavalli-Sforza–Edwards distance (38)
Linearized FST	Measure of genetic distance: FST/(1 − FST)
Full	Complete dataset (38 sites, 703 pairwise genetic distances)
Train	Complete dataset excluding one point and its affiliated pairs (37 sites, 666 pairwise genetic distances)
Test	One point and its affiliated pairs (1 site, 37 pairwise genetic distances)
Rtrain	Pearson correlation between predicted and observed enetic distance for training dataset
Rtest	Pearson correlation between predicted and observed genetic distance for testing dataset
Rfull	Pearson correlation between predicted and observed genetic distance for full dataset
RMSEtrain	Root-mean-square error of model using the training dataset
RMSEtest	Root-mean-square error of model using the testing dataset
RMSEfull	Root-mean-square error of model using the full dataset
RF	Random forest: a nonlinear classification and regression tree analysis
RSQtrain	Pseudo-R-squared (% variance explained by the model) built with the training dataset
RSQfull	Pseudo-R-squared (% variance explained by the model) built with the full dataset

See SI Appendix, Table S3 for more details.

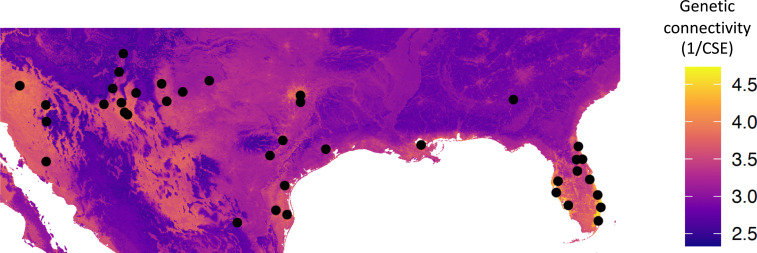
Fig. 2.

Optimized connectivity map using CSE full dataset. The black points show collection sites for Ae. aegypti (the genetic data).

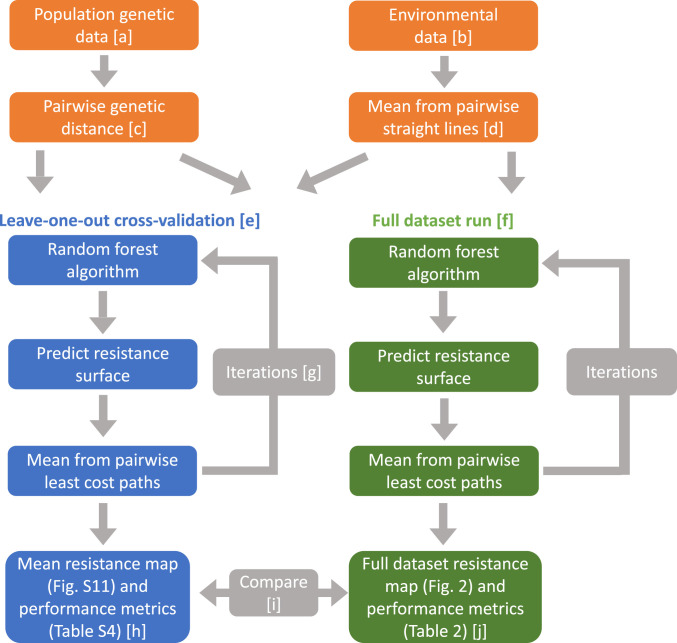
Fig. 1.

Pipeline of model workflow. Left side (leave-one-out cross-validation) ensures internal model accuracy by highlighting potential overfitting; Right side (full dataset run) produces the full dataset model output and overall variable importance.

The model works by finding which predictor variables (environmental data) best predict the observed variable (genetic distance). Initially, straight lines are created connecting each pair of sites, and the extracted mean values along these lines through each environmental raster (Fig. 1D) are used in a RF model to predict genetic distance at the pixel level, resulting in a resistance surface. By taking the inverse of each pixel value, the resistance surface is transformed into a connectivity surface (41). In each iteration, least cost paths through the previous iteration’s connectivity surface are used instead of the straight lines.

A leave-one-out cross-validation was performed, meaning the model was run 38 times, with a different point (and its 37 affiliated pairs) withheld as the testing dataset each time, while the remaining 37 points (and their 666 affiliated pairs) were used as the training dataset (Fig. 1E). Each of the 38-folds was run with 10 iterations (Fig. 1G) since we found this was a sufficient number for performance metrics to be optimized. The iteration with the lowest root-mean-square error using the testing dataset (RMSE_test) was selected as the optimal iteration.

After concluding CSE outperformed linearized F_ST (Results), the full CSE dataset (not withholding any data for the testing dataset, Dataset S1) was used to create a “full dataset model” (Fig. 1F). The results from the full dataset model (specifically RMSE, R, and the connectivity surfaces) were compared to the results from the leave-one-out cross-validation to verify that the full dataset model was an appropriate summary of the cross-validation and that it was not overfitting the data (Fig. 1I).

Results

Genetic Diversity and Population Structure.

Thirty-six of 2,509 (1.4%) locus pairs were in linkage disequilibrium and 12 of 476 (2.5%) locus–population pairs were out of Hardy–Weinberg equilibrium after a Bonferroni correction for multiple comparisons. This is consistent with previous analyses showing the loci can be treated as independent, single-copy neutral markers. Pairwise CSE across the dataset ranges from 0.166 to 0.494, with a mean of 0.336 (38). Pairwise linearized F_ST values range from 0.0124 to 0.254, with a mean of 0.0863. All F_ST values are greater than zero according to a test of significance with 1,000 permutations in Arlequin (P < 0.00001) (37). There is a significant correlation between the log geographic distance and genetic distance across the geographic range using both CSE (Mantel R = 0.493, P < 0.0005) and linearized F_ST (Mantel R = 0.369, P < 0.0005) (SI Appendix, Fig. S1). To compare the null expectation of IBD with the results of our landscape genetics model, we also calculated R (the Pearson correlation) between log geographic distance and genetic distance for CSE (R = 0.493) and linearized F_ST (R = 0.361).

The effects of genetic structure and genetic drift were analyzed to confirm that it was reasonable to include all populations in one model. Principal component analysis and Bayesian clustering analysis do not show clearly defined population groups (SI Appendix, Figs. S2 and S3), consistent with these populations being derived from one relatively old colonization (39, 42–44). Simulations and empirical tests indicate the effect of genetic drift is negligible in our calculations of genetic distance (SI Appendix).

Random Forest Iterative Model.

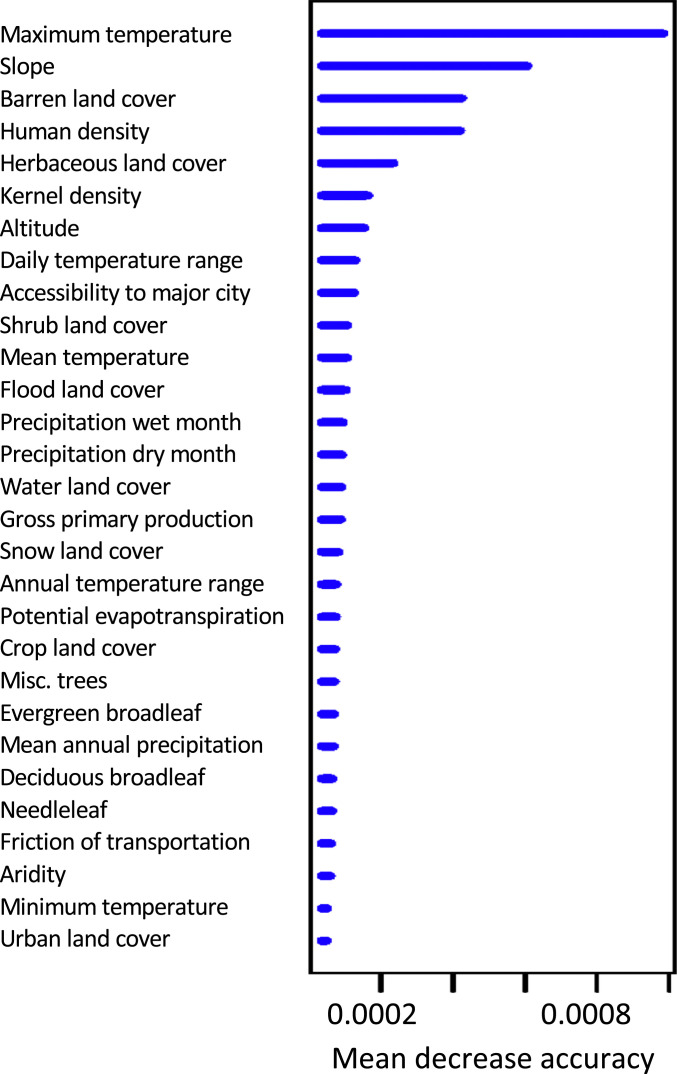
Averaging across the best iterations from each of the 38-folds of the cross-validation using CSE as genetic distance, R_test was $0.771\pm 0.169$ (mean $\pm$ SD) (SI Appendix, Table S4). The RMSE_test of these runs was 0.038 $\pm$ 0.016, and these values were varied across the geographic range showing the model has largely taken spatial autocorrelation into account (SI Appendix, Figs. S4A and S5). The most important variables were maximum temperature, slope, altitude, and mean temperature (SI Appendix, Figs. S6 and S7 and Table S5). Averaging across the cross-validation folds using linearized F_ST as genetic distance, R_test was 0.722 $\pm$ 0.160 (SI Appendix, Table S6). The corresponding RMSE_test of these runs was 0.029 $\pm$ 0.012, and again these values showed variation across the geographic range (SI Appendix, Fig. S4B). The top variables were maximum temperature, accessibility to the nearest major city, slope, and mean temperature (SI Appendix, Figs. S8 and S9 and Table S7). Although there was some variation in most important variables among the 38-folds for both cross-validations, there were consistent general patterns (SI Appendix, Figs. S7 and S9). Additionally, we showed that RMSE is robust to different size testing datasets by performing a leave-two-out cross-validation (SI Appendix).

The iterative optimization improved the results from both cross-validations as shown by significant decreases in the values of RMSE_test between the straight-lines iteration and the optimized iteration for the CSE cross-validation (0.044 to 0.038) and the linearized F_ST cross-validation (0.035 to 0.029) (paired t tests both have P < 10⁻¹⁰). A large improvement occurred between the straight-lines iteration and the first iteration, while the subsequent iterations provided fine-tuning through small changes to the least cost paths (SI Appendix, Fig. S10). Final connectivity surfaces were created by taking the mean of the 38 optimized connectivity surfaces for both measures of genetic distance (SI Appendix, Fig. S11).

In comparing the performance of CSE and linearized F_ST, we found pseudo-R-squared (RSQ) values for the CSE cross-validation model were significantly higher than those for the linearized F_ST model (Student’s t test, P < 10²⁸). R_test values were also higher for the CSE model, although the difference was not significant (Student’s t test, P = 0.20). Although the RMSE_test values for the CSE model were higher than those for the linearized F_ST model, they were smaller in proportion to their respective genetic distance. Specifically, the mean RMSE_test value from the CSE leave-one-out cross-validation model was about 11% of the mean CSE genetic distance value from the full dataset, whereas the mean RMSE_test value was about 33% of the mean linearized F_ST value from the dataset. Together the results suggest CSE performs better in our model than linearized F_ST, although the final connectivity maps appear similar (SI Appendix, Fig. S11).

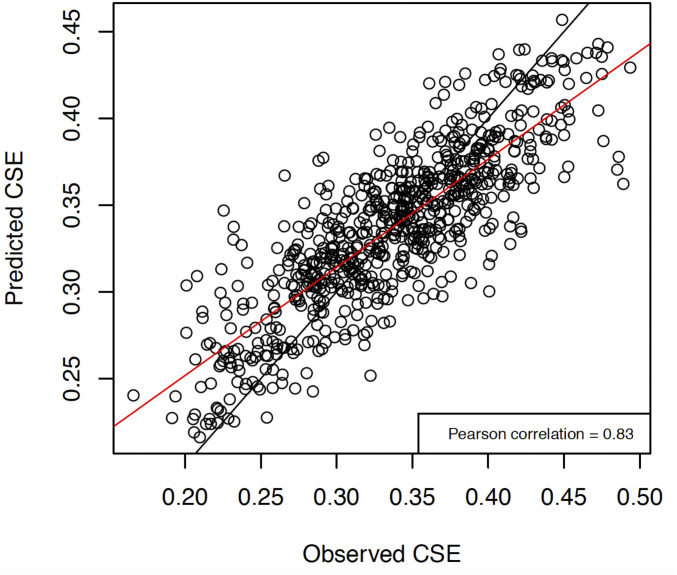
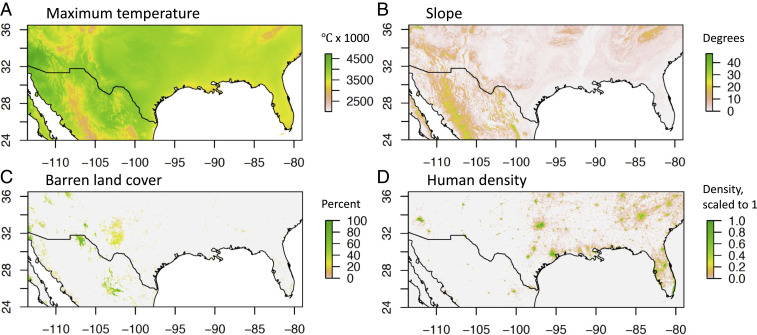
After concluding CSE outperformed linearized F_ST, we ran a full dataset model using CSE as genetic distance. The third iteration had the highest correlation between expected and observed genetic distance (R_full = 0.83) and the lowest root-mean-square error (RMSE_full = 0.035) (Table 2 and see Fig. 5 and SI Appendix, Table S8). The optimized resistance surface is shown in Fig. 2. The most important variables for building the optimized RF model were maximum temperature, slope, barren land cover, and human density (Figs. 3 and 4 and SI Appendix, Fig. S12). The root-mean-square errors of the full dataset model (RMSE_full) and of the CSE cross-validation (mean RMSE_test) were similar (0.035 and 0.038, respectively), indicating that the full dataset model is not overfitting the data. Additionally, the correlation between expected and observed genetic distance for the full dataset model (R_full) was 0.83 (Fig. 5), while the mean correlation between expected and observed genetic distance for the CSE cross-validation (R_test ± SD) was 0.77 ± 0.17. Finally, a Pearson correlation between the final resistance maps shows 77% correlation (SI Appendix, Fig. S13). For the sake of comparison, we showed that replacing RF with a standard linear regression worsens the full dataset model (SI Appendix).

Table 2.

Result from CSE full dataset model

Iteration	Rfull	RMSEfull	RSQfull
Straight	0.786	0.0388	0.606
1	0.825	0.0353	0.674
2	0.824	0.0356	0.669
3	0.832	0.0345	0.688
4	0.820	0.0357	0.667
5	0.830	0.0347	0.685
6	0.817	0.0360	0.661
7	0.817	0.0359	0.662
8	0.821	0.0356	0.669
9	0.818	0.0361	0.658
10	0.828	0.0349	0.680

R_full, Pearson correlation between observed and expected CSE; RMSE_full, root-mean-square error; RSQ_full, percentage of variance explained. Iteration 3 (in bold) has the lowest RMSE_full and is therefore chosen as the optimal iteration.

Fig. 5.

Observed versus predicted genetic distance for CSE full dataset model. The red line is the best-fit linear regression, and the black line is y = x.

Fig. 3.

Variable importance list for the CSE full dataset model. The x axis shows the mean decrease in accuracy of the model when excluding each variable computed from permuting out-of-bag data.

Fig. 4.

Important variables for the CSE full dataset model. (A) Maximum temperature (degrees Celsius × 100). (B) Slope (degree incline). (C) Barren land cover (%). (D) Human density (density of buildings and structures, scaled to a maximum of 1).

We also wanted to know whether spatial autocorrelation was influencing the full dataset model. Geographic distance influences CSE up to 200 km, as shown by increasing semivariance up until this distance in the semivariogram (SI Appendix, Fig. S14A). However, in the full model, a plot of semivariance indicates that geographic distance influences CSE only up until a very short distance (<100 km), meaning that spatial autocorrelation has largely been taken into account (SI Appendix, Fig. S14B).

Discussion

Mapping genetic connectivity and determining how landscape and environmental variables affect gene flow in a species of interest are primary goals in landscape genetics (8, 10). Here we have proposed a modeling framework that uses RF and an iterative optimization process to map landscape connectivity and identify important landscape variables. We test and validate it with data on the Ae. aegypti mosquito in North America.

While the leave-one-out cross-validations using CSE and linearized F_ST both produced strong results that were improved by the iterative optimization, CSE ultimately outperformed linearized F_ST, producing a higher RSQ and a lower RMSE_test in proportion to the genetic distance metric. Therefore, a full dataset model was run with CSE, and it produced similar results to the CSE cross-validation in terms of RMSE, R, and the final resistance surfaces. Therefore, we feel confident it is not overfitting the data and thus is a good summary of the results. The optimized iteration (producing lowest RMSE_test) for the full dataset model was the third iteration (Table 2), and going forward, we will refer to the results from this iteration as the full dataset model or simply our model.

Our model explained genetic distance better than the null expectation of IBD, which predicts that genetic distance increases linearly with the log of geographic distance (5). Specifically, our model’s correlation between observed and expected genetic CSE was 0.83 (Fig. 5), while the correlation between log geographic distance and CSE was only 0.49 (SI Appendix, Fig. S1). Additionally, our model’s performance is on par or higher than results from other landscape genetics papers using RF (16, 17) or other statistical methods (45, 46). Work by Medley et al. (45) is an especially important point of reference, as it deals with Aedes albopictus, a mosquito with many of the same ecological properties as Ae. aegypti, and the studied region overlaps with this study. Using resistance surface modeling, the authors were able to account for 19 uncorrelated land cover types in their analysis, and their most informative model had an R of 0.50 (45). In contrast, we were able to include 29 diverse environmental and anthropogenic variables, including some correlated ones, and our model achieved an R of 0.83. Also important are two landscape genetics studies on amphibians that also used RF but modeled gene flow as straight lines and without the iterative optimization. In these, the most informative model from Murphy et al. had a R of 0.86 (16), and the median R from Hether et al. was 0.69 (17).

We can compare the final connectivity surface from our model (Fig. 2) to the environmental predictors that were most important in building it: maximum temperature, slope, barren land cover, and human density (Fig. 4). This comparison suggests flat regions with high maximum temperature and high human density are generally favorable to Ae. aegpyti gene flow. Barren land cover, which also includes areas of sparse vegetation (47), generally indicates an area of high connectivity, but it is not required for high connectivity. When we ran the model without barren land cover as a spatial variable, accessibility to the nearest major city rose in importance, suggesting the barren variable may capture some information on human accessibility and transportation. Overall, these findings are consistent with the biology of a tropical, anthrophilic mosquito. However, it is important to remember that RF is a nonlinear model which can account for different relationships (e.g., negative/positive correlations) between genetic distance and the environmental variables at different locations.

Different environmental factors are likely to be important for predicting connectivity and predicting habitat suitability, and both are important for understanding a species’ distribution (13). For example, while high habitat suitability increases the likelihood of dense Aedes populations (which could promote gene flow via a stepping-stone model), it also decreases the incentive for individuals to disperse in search of oviposition sites, bloodmeals, or a more hospitable habitat. Indeed, the most important variables in our model (maximum temperature, slope, barren land cover, and human density) are similar but distinct from the most important variables in a recent habitat suitability model conducted at a global scale (absolute humidity, accessibility to the nearest major city, and minimum temperature) (27).

Since Ae. aegypti has a short active natural dispersal on average (29–31) and is well known for “hitchhiking” with humans (33, 48–50), one might expect that all of the most important variables would be related to humans. However, our results suggest that environmental variables are important too, especially temperature and slope. There are several possible (and not mutually exclusive) explanations: 1) Some minimum standard of habitat suitability is required for gene flow, 2) the effects of natural dispersal are not completely outweighed by human-mediated dispersal, and 3) there is some correlation between these environmental features and human activity and transportation that was not captured by our included anthropogenic variables. Our results are also consistent with the finding that both anthropogenic and environmental features affect gene flow in the similar species, Ae. albopictus (45).

Spatial autocorrelation refers to systematic spatial variation in a variable; in other words, proximal observations are more correlated than more distant observations. We implemented several strategies to incorporate spatial autocorrelation into our model. We created a point kernel density surface (51) and used this surface as a predictor variable to represent sampling density and genetic distance. The sampling density was also used to weight the RF bootstrapping (following the methodology described in ref. 52) so that lower-density points were sampled more frequently. Semivariograms show that these strategies effectively accounted for spatial autocorrelation in our model (SI Appendix, Fig. S14). Additionally, the RMSE_test values associated with each fold in the cross-validations show variation across the geographic range (SI Appendix, Figs. S4 and S5). However, the results for sites in areas of low sampling density tend to have higher and more variable values of RMSE_test, indicating results in these areas should be interpreted with some caution.

Our analysis also provides a comparison of two genetic distance metrics: CSE and linearized F_ST. Overall, we find CSE performs better, although the final resistance maps are quite similar (SI Appendix, Fig. S11). Our finding supports a general trend in landscape genetics literature to avoid F_ST-based metrics (7, 17, 40). Although widely used in population genetics, F_ST assumes constant population size and migration rate (40, 53). CSE, a geometric measure of genetic distance, avoids these assumptions and may be more suitable for measuring relative distances between pairs of populations (7, 40).

Landscape connectivity can inform the implementation of vector control, especially the release of mosquitoes that are genetically modified or infected with a bacterium called Wolbachia. Depending on the design of the release program, these interventions are meant to crash the local Ae. aegypti population (32, 54) or replace it with one that does not spread disease (55). How and where such releases are made are crucial to attain the intended goal, and our connectivity map can inform vector control by providing information on the likely movement of both released and wild mosquitoes, assuming the released strain of mosquito will exhibit similar physiology and behavior to the wild strain and therefore respond similarly to geographic barriers. If the goal is to widely spread the modified genes or bacterium, performing releases in areas with high emigration is important. On the other hand, if spatially limited modification is desirable (such as for experiments to test whether modified mosquitoes have unanticipated negative effects), habitats with low emigration should be targeted. Similarly, rates of immigration are important in predicting dilution that would reduce effectiveness of releases.

Specifically, our model provides several regionally specific insights for vector control. Our model shows high connectivity in the southeast, especially Florida, and some high connectivity in Texas generally corresponding to Interstate 35 (Dallas, Ellis, Travis, and Bexar). For example, cities like Houston and Lubbock, which are surrounded with higher resistance landscape, may require fewer releases than the more connected cities along Interstate 35, although the well-connected cities would have an advantage if between-city spread is part of the vector control design. Compared to the southeast, the western portion of the map has more patchy landscape connectivity, consistent with more mountainous, uninhabited areas in this part of the country. This could be an advantage for establishing local-scale release programs or preventing the introduction of new pesticide resistance genes and reintroduction of Ae. aegypti after local eradication.

In future work, additional advances in validation and model development, as well as more explicit links to the mode and range of mosquito dispersal, would be useful pursuits in mosquito landscape genetics. One future advance of interest is applying this approach to Ae. aegypti in other regions, which could provide validation of the method’s ability to predict mosquito movement. Another advance is to incorporate circuit theory (19) into the model, which has the benefit of considering multiple paths across the landscape. Although potentially more realistic to mosquito biology, this advancement would not be applicable to the iterative framework we use in this version of the model. Finally, exploring different machine-learning methods, creating a connectivity surface that shows predicted dispersal distance, and explicit modeling of mosquito movement by human transportation would all be useful pursuits to better understand the role of landscape in mosquito movement, especially as it pertains to vector control.

Materials and Methods

Mosquito Collections and Regions.

We included 38 unique sites across North America in our analyses (Fig. 2 and SI Appendix, Table S1), spanning from Arizona to Florida. All have overwintering populations of Ae. aegypti. Data from 28 of these sites were published previously, and the remainder were genotyped for this study (SI Appendix, Table S1). The number of individuals per site ranged from 8 to 51 (mean = 35.6), and 30 of the sites had more than 30 individuals (SI Appendix, Table S1). The points are nonuniform but closely aligned to where Ae. aegypti can be found, especially in the United State (28). We particularly tried to acquire more samples from the southeast, but local vector control agencies reported they have not been able to find Ae. aegypti in these places (e.g., the Florida panhandle, Alabama, and Mississippi) since Ae. albopictus replaced them in the 1980s. Although Ae. aegypti is present in California and Las Vegas, we did not include these because they are almost certainly the result of recent invasions, and the high genetic distances associated with them are due to recent history and not landscape (56, 57).

Genetic Data and Population Structure.

Genomic DNA was extracted from whole adult mosquitoes using the Qiagen DNeasy Blood and Tissue kit according to manufacturer instructions, including the optional RNase A step. All individuals were genotyped at 12 highly variable microsatellites, as in Brown et al. (36) (Dataset S2). The microsatellite loci are trinucleotide (A1, B2, B3, A9) and dinucleotide repeats (AC2, CT2, AG2, AC4, AC1, AC5, AG1, and AG4) (36, 58). Previous work shows the ability of these loci to distinguish Ae. aegypti populations from around the world, including North America (36, 59).

All microsatellite loci were tested for within-population deviations from Hardy–Weinberg equilibrium and for linkage disequilibrium among loci pairs using 10,000 dememorizations, 1,000 batches, and 10,000 iterations per batch for both tests in the R package Genepop version 1.0.5 (60, 61). To correct for multiple testing, a Bonferroni correction was applied at the 0.05 level of significance.

Including individuals from distinct ancestral groups could confound our landscape genetics model, so we used a number of methods to explore genetic structure in advance. We ran a principal component analysis using the R package Adegenet v. 2.1.1 (39). Additionally, we ran 20 independent runs of STRUCTURE (v. 2.3.4) (43) for K = 1 to 12; we used 600,000 generations, and the first 100,000 were discarded as burn-in. The results were visualized using the program DISTRUCT v.1.1 (62). We used the guidelines from Pritchard et al. (43) and the Delta K method (42, 44) to infer the optimal value of K (number of clusters).

We tested for correlations between the log of geographic distance and genetic distance (CSE and linearized F_ST) using Mantel tests with 9,999 permutations and by calculating the Pearson correlations. F_ST was calculated in Arlequin, and 1,000 permutations were used to test for significance (37). Linearized F_ST was calculated as F_ST/(1 − F_ST). We explored other measures of genetic differentiation including Nei’s distance (calculated in Genodive) (63), Reynold’s distance, and CSE (38) (the last two calculated in Adegenet) (39). We ultimately did not pursue Reynold’s distance and Nei’s distance as they were >95% correlated with F_ST (Pearson correlation). We used CSE as the second measure of genetic distance since it is a purely geometric distance measure with shown success in measuring relative distance between pairs of populations especially in cases of missing data (7, 40), and its correlation with F_ST was only 87% for the North America dataset.

Spatial Data.

Spatial data were downloaded from open-source repositories and were edited and cropped using Geospatial Data Abstraction Library (64) under the Bash environment. Most datasets were available at 1-km resolution, and when not, we resampled the data to a pixel size of 1 km² (see SI Appendix, Table S2 for full list of datasets and sources).

Environmental data.

Mean annual temperature, mean annual precipitation, annual temperature range, daily temperature range, coldest temperature of the coldest month, hottest temperature of the hottest month, precipitation of the wettest month, and precipitation of the driest month were derived from CHELSA (climatologies at high resolution for the earth’s land surface areas) climate data (65). We also included gross primary production, a measure of vegetation photosynthesis (66). Elevation and slope were obtained from MERIT DEM (Multi-Error-Removed Improved-Terrain Digital Terrain Model) (67), and slope was downloaded from the Geomorpho90m dataset (68). To capture humidity, we used the Global Aridity Index and monthly potential evapotranspiration from CGIAR CSI (Consultative Group for International Agricultural Research—Consortium for Spatial Information) (69, 70). To address spatial autocorrelation and geographic distance, we included a kernel density raster (bandwidth 100 km) created using the R package “KernSmooth.” We tried several other bandwidths (50, 150, and 200 km) using one run of the model and linearized F_ST as genetic distance; they all performed similarly, and we selected the bandwidth that was highest in the list of most important variables to include going forward (100 km).

Anthropogenic and land cover data.

University of Oxford Malaria Atlas Project (MAP), Google, the European Union Joint Research Center (JRC), and the University of Twente, The Netherlands collaborated to create a friction map in which each pixel represents the speed of human travel in that area (71). Based on this map, another one was created showing the travel time to the nearest city of 50,000 inhabitants (71). We used the first of these two maps as a measure of human friction and the second as a measure of accessibility. For human population density, we used the Global Human Settlement Layer created by the European Commission (72, 73). Land cover was derived from a global dataset containing 12 land cover metrics (47). For each land cover type, each 1-km² pixel has a value from 0 to 1 representing what percent of the area has the land cover type.

Landscape Genetics: Iterative Random Forest Model.

See Modeling Approach and Fig. 1 for a description of how the model works. We include additional technical details here. To handle the computational demands, the code integrates R (74) (for the modeling part) and Geographic Resources Analysis Support System Geographic Information System (75) (for the least cost path delineation) within a Bash environment and uses sophisticated parallelization. The model uses the “randomforestSRC” package in R, with tuning for the forest average terminal node size (“nodesize”) and the number of variables randomly selected as candidates for splitting a node (“mtry”). RF bootstrapping was weighted by the inverse of the minimum kernel value for each pair of points to ensure points from low-density areas were sampled more often (SI Appendix, Fig. S5).

During the straight-line computation at the beginning of the modeling procedure, values from the ocean are not used to compute the mean values of each predictor since the ocean is masked (labeled as NoData). After the straight-line computation, least cost path lines are drawn on the land surface, and predictors are calculated from those values. We use least cost paths to determine a mean estimate of the environmental conditions that are a reasonable approximation of the landscape between each pair of sampling sites.

As a basis of comparison, we also performed a full model run with CSE in which we used a standard linear regression rather than random forest. Additionally, we performed a leave-two-out cross-validation to ensure that decreasing the training dataset size did not decrease the model’s performance, as evaluated by RMSE_train and RMSE_test.

Data Availability

Code and microsatellite call data have been deposited in GitHub; VectorBase (https://github.com/evlynpless/MOSQLAND/tree/master/ModelingConnectivity) (ID no. VBP0000715) (76). Microsatellite calls are also provided in Dataset S2. All spatial data are freely available online.