The inverse variance–flatness relation in stochastic gradient descent is critical for finding flat minima

Significance

One key ingredient in deep learning is the stochastic gradient descent (SGD) algorithm, which allows neural nets to find generalizable solutions at flat minima of the high-dimensional loss function. However, it is unclear how SGD finds flat minima. Here, by analyzing SGD-based learning dynamics together with the loss function landscape, we discovered a robust inverse relation between weight fluctuation and loss landscape flatness opposite to the fluctuation–dissipation relation in physics. The reason for this inverse relationship is that the SGD noise strength and its correlation time depend inversely on the landscape flatness. Essentially, SGD serves as a landscape-dependent annealing algorithm to search for flat minima. These theoretical insights can lead to more efficient algorithms, e.g., for preventing catastrophic forgetting.

Abstract

Despite tremendous success of the stochastic gradient descent (SGD) algorithm in deep learning, little is known about how SGD finds generalizable solutions at flat minima of the loss function in high-dimensional weight space. Here, we investigate the connection between SGD learning dynamics and the loss function landscape. A principal component analysis (PCA) shows that SGD dynamics follow a low-dimensional drift–diffusion motion in the weight space. Around a solution found by SGD, the loss function landscape can be characterized by its flatness in each PCA direction. Remarkably, our study reveals a robust inverse relation between the weight variance and the landscape flatness in all PCA directions, which is the opposite to the fluctuation–response relation (aka Einstein relation) in equilibrium statistical physics. To understand the inverse variance–flatness relation, we develop a phenomenological theory of SGD based on statistical properties of the ensemble of minibatch loss functions. We find that both the anisotropic SGD noise strength (temperature) and its correlation time depend inversely on the landscape flatness in each PCA direction. Our results suggest that SGD serves as a landscape-dependent annealing algorithm. The effective temperature decreases with the landscape flatness so the system seeks out (prefers) flat minima over sharp ones. Based on these insights, an algorithm with landscape-dependent constraints is developed to mitigate catastrophic forgetting efficiently when learning multiple tasks sequentially. In general, our work provides a theoretical framework to understand learning dynamics, which may eventually lead to better algorithms for different learning tasks.

One key ingredient for the powerful deep neural network (DNN)-based machine-learning paradigm—deep learning (1)—is a relatively simple iterative method called stochastic gradient descent (SGD) (2, 3). However, despite the tremendous successes of deep learning, the reason why SGD is so effective in learning in a high-dimensional nonconvex loss function (energy) landscape remains poorly understood. The random element seems key for SGD, yet makes it harder to understand. Fortunately, many physical systems include such a random element, e.g., Brownian motion, and powerful tools have been developed for understanding collective behaviors in stochastic systems with many degrees of freedom. Here, we use concepts and methods from statistical physics to investigate the SGD dynamics, the loss function landscape, and more importantly their relationship.

We start by introducing the SGD-based learning process as a stochastic dynamical system. A learning system such as a neural network (NN), especially a DNN, has a large number ($N$) of weight parameters $w_i\hspace{0.17em}\left(i=\mathrm{1,2},\dots ,N\right)$. For supervised learning, there is a set of $M$ training samples each with an input ${\overrightarrow{X}}_k$ and a correct output ${\overrightarrow{Z}}_k$ for $k=\mathrm{1,2},\dots ,M$. For each input ${\overrightarrow{X}}_k$, the learning system predicts an output ${\overrightarrow{Y}}_k=G\left({\overrightarrow{X}}_k,\overrightarrow{w}\right)$, where the output function $G$ depends on the architecture of the NN as well as its weights $\overrightarrow{w}$. The goal of learning is to find the weight parameters to minimize the difference between the predicted and correct output characterized by an overall loss function (or energy function)

$$L\left(\overrightarrow{w}\right)=M^{-1}\sum _{k=1}^{M}d\left({\overrightarrow{Y}}_k,{\overrightarrow{Z}}_k\right),$$ [1]

where $d\left({\overrightarrow{Y}}_k,{\overrightarrow{Z}}_k\right)$ is a measure of distance between ${\overrightarrow{Y}}_k$ and ${\overrightarrow{Z}}_k$. In our study, a cross-entropy loss for $d$ is used.

One learning strategy is to update the weights by following the gradient of $L$ directly. However, this batch learning scheme is computationally prohibitive for large datasets and it also has the obvious shortfall of being trapped by local minima. SGD was first introduced to circumvent the large dataset problem by updating the weights according to a subset (minibatch) of samples randomly chosen at each iteration (2). Specifically, the change of weight $w_i\hspace{0.17em}\left(i=\mathrm{1,2},\dots ,N\right)$ for iteration $t$ in SGD is given by

$$\mathrm{\Delta }{w}_i\left(t\right)=-\alpha \frac{\partial L^{\mu \left(t\right)}\left(\overrightarrow{w}\right)}{\partial w_i},$$ [2]

where $\alpha$ is the learning rate and $\mu \left(t\right)$ represents the random minibatch used for iteration $t$. The minibatch loss function (MLF) for minibatch $\mu$ of size $B$ is defined as

$$L^{\mu }\left(\overrightarrow{w}\right)=B^{-1}\sum _{l=1}^{B}d\left({\overrightarrow{Y}}_{{\mu }_l},{\overrightarrow{Z}}_{{\mu }_l}\right),$$ [3]

where ${\mu }_l$ ($l=\mathrm{1,2},..,B$) labels the $B$ randomly chosen samples.

Here, we introduce the key concept of a MLF ensemble $\left\{L^{\mu }\left(\overrightarrow{w}\right)\right\}$, i.e., an ensemble of energy landscapes each from a random minibatch. The overall loss function $L\left(\overrightarrow{w}\right)$ is just the ensemble average of the MLF: $L\equiv {⟨L^{\mu }⟩}_{\mu }$. The SGD noise comes from the variation between a MLF and its ensemble average: $\delta L^{\mu }\equiv L^{\mu }-L$.

By taking the continuous-time approximation and keeping the first-order time derivative term in Eq. 2, we obtain the following stochastic partial differential equation for SGD,

$$\frac{\partial \overrightarrow{w}}{\partial t}=-\alpha \frac{\partial L}{\partial \overrightarrow{w}}+\overrightarrow{\eta }\left(\overrightarrow{w}\right),$$ [4]

where time $t$ and all timescales in this study are measured in the unit of minibatch iteration time $\mathrm{\Delta }t=1$. The continuous-time limit amounts to considering time scales that are much larger than $\mathrm{\Delta }t$; e.g., one epoch time is $M/B\left(\gg 1\right)$. Eq. 4 is analogous to the Langevin equation in statistical physics. The first term $-\alpha \frac{\partial L}{\partial \overrightarrow{w}}$ is the deterministic gradient descent governed by the overall loss function $L$ analogous to the energy function in physics. The second term is the SGD noise term $\overrightarrow{\eta }\equiv -\alpha {\nabla }_{\overrightarrow{w}}\delta L^{\mu }\left(\overrightarrow{w}\right)$ with zero mean $⟨\overrightarrow{\eta }⟩=0$ and equal time correlation $C_{ij}\left(\overrightarrow{w}\right)\equiv ⟨{\eta }_i{\eta }_j⟩={\alpha }^2\times {⟨\frac{\partial \delta L^{\mu }}{\partial w_i}\hspace{0.17em}\frac{\partial \delta L^{\mu }}{\partial w_j}⟩}_{\mu }$, which depends explicitly on $\overrightarrow{w}$.

Recently, there has been increasing evidence in support of the notion that “good” (generalizable) solutions exist at the flat (shallow) minima of the loss function (4–10); however, there is still little understanding of how SGD-based algorithms can find these flat minima in the high-dimensional weight space. The original gradient descent algorithm searches for loss function minima independent of their flatness and it also has the significant disadvantage of being easily trapped by local minima and saddle points in the high-dimensional weight space. Adding isotropic noise to gradient descent (GD) leads to a Langevin equation analogous to those used to describe stochastic dynamics in equilibrium physical systems. However, although the added noise can help GD escape local traps, it does not seem to improve generalization (11). The intuitive reason is that a “useful noise” should depend on the loss landscape. In particular, a useful noise should be larger in directions where the landscape is rougher to help escape from local traps and smaller in directions where the landscape is flatter to find and stay at good solutions. As first pointed out by Chaudhari and Soatto (12), unlike equilibrium physical systems where the noise has a constant strength given by the thermal temperature, the SGD dynamics are highly nonequilibrium as the SGD noise is anisotropic and varies in the weight space. Our working hypothesis is that SGD may serve as an efficient annealing strategy for varying the noise (or effective temperature) “intelligently” according to the loss function landscape to find the shallow (flat) minima. In this paper, we focus on studying the relation between stochastic learning dynamics and the loss landscape by adopting the nonequilibrium stochastic dynamics framework and using key concepts from statistical physics such as the fluctuation–dissipation relation to test this hypothesis.

Learning via Low-Dimensional Drift–Diffusion Dynamics in SGD

In general, SGD-based DNN learning dynamics can be roughly divided into an initial fast learning phase where both the training error and the training loss $L$ decrease rapidly, followed by an “exploration” phase where the training error becomes almost 0 but the loss $L$ still decreases albeit much slower. The weight vectors sampled in the exploration phase can all be considered solutions to the problem given their vanishing training error and small testing error; see SI Appendix for details of the two learning phases in SGD.

The original weights are highly coupled in neural networks, which makes them an inconvenient and unnatural basis for studying the high-dimensional learning dynamics. To circumvent this problem, we first use principal component analysis (PCA) to study weight variations in the exploration phase of SGD (see Methods for details of PCA). We then analyze the learning dynamics in the principal component basis because to the leading order the principal components can be considered as independent collective variables of the system around the minima of its loss function.

Within a large time window $t\in \left[t_0,t_0+T_w\right]$ where $t_0$ is a time in the exploration phase and $T_w$(=10 epochs used here) is a large time window,* the weight dynamics can be decomposed into its variations in different principal components

$$\overrightarrow{w}\left(t\right)={⟨\overrightarrow{w}⟩}_T+\sum _{i=1}^N{\theta }_i\left(t\right){\overrightarrow{p}}_i,$$ [5]

where ${⟨\overrightarrow{w}⟩}_T=T^{-1}{\int }_{t_0}^{t_0+T}\overrightarrow{w}\left(t\right)dt$ is the average weight vector in the time window $T$, and ${\overrightarrow{p}}_i$ is the $i$th principal component base vector with ${\overrightarrow{p}}_i\cdot {\overrightarrow{p}}_j={\delta }_{ij}$. The projection of the weight vector along the PCA direction ${\overrightarrow{p}}_i$ is given by ${\theta }_i\left(t\right)$, which is a linear combination of the individual weights, and $\overrightarrow{\theta }$ is the weight vector in the PCA coordinate.

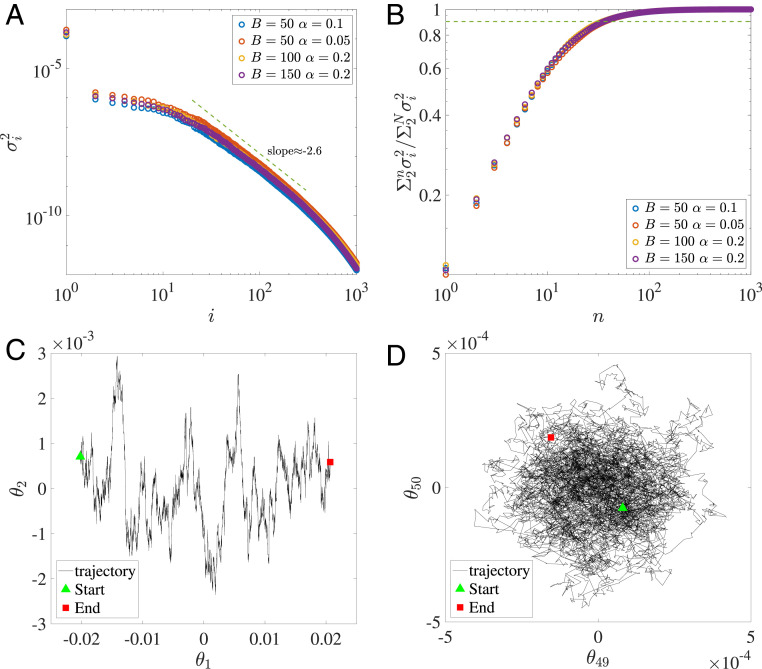
The results reported here are for a simple NN with two hidden layers each with 50 neurons for classification tasks using the Modified National Institute of Standards and Technology (MNIST) database (see Methods for details and other NN architectures used). The PCA was done for the $N=\mathrm{2,500}$ weights between the two hidden layers (results for other NN architectures and databases are included in SI Appendix). In Fig. 1A, we show the PCA spectrum, i.e., the variance ${\sigma }_i^2\equiv T^{-1}{\int }_{t_0}^{t_0+T}{\theta }_i^2\left(t\right)dt$ versus its rank $i$ in descending order $\left({\sigma }_{i+1}<{\sigma }_i\right)$. We found that the variance in the first PCA direction (${\overrightarrow{p}}_1$) is much larger than variances in other directions because the motion along ${\overrightarrow{p}}_1$ has a net drift velocity (see discussion below and Fig. 1C). For other PCA directions, after a small number of leading PCA directions ($2\le i\le 20$), the variance ${\sigma }_i^2$ decays rapidly with its rank: ${\sigma }_i^2\sim i^{-\gamma }$ for $20<i<200$ with a large exponent $\gamma \sim 2.6$ before an even faster decay for higher $i\left(>200\right)$. This means that most of the variations (dynamics) of the weights are concentrated in a relatively small number of PCA directions (dimensions). Quantitatively, as shown in Fig. 1B, even excluding ${\sigma }_1^2$, more than $90\%$ of the total variance occurs in the first 35 PCA modes much smaller than the total number of weights $N=\mathrm{2,500}$, which suggests that the SGD dynamics are embedded in a low-dimensional space (13).

Fig. 1.

The PCA results and the drift–diffusion motion in SGD. (A) The rank-ordered variance ${\sigma }_i^2$ in different principal component (PC) directions $i$. For $i\ge 20$, ${\sigma }_i^2$ decreases with $i$ as a power law $i^{-\gamma }$ with $\gamma \sim 2-3$. (B) The normalized accumulative variance of the top $\left(n-1\right)$ PCs excluding $i=1$. It reaches $\sim 90\%$ at $n=35$ much smaller than the total number of weights $N=\mathrm{2,500}$ between the two hidden layers. (C) The SGD weight trajectory projected onto the $\left({\theta }_1,{\theta }_2\right)$ plane. The persistent drift motion in ${\theta }_1$ and the diffusive random motion in ${\theta }_2$ are clearly shown. (D) The diffusive motion in the $\left({\theta }_i,{\theta }_j\right)$ plane with $j>i\left(\ne \hspace{0.17em}1\right)$ randomly chosen ($i=49$ and $j=50$ shown here). Unless otherwise stated, hyperparameters used are $B=50$, $\alpha =0.1$.

Next, we studied the network dynamics along different PCA directions. We found that along the first PCA direction ${\overrightarrow{p}}_1$, there is a net drift velocity $d{\theta }_1/dt$ with a persistence time much longer than 1 epoch as clearly shown in Fig. 1C where SGD dynamics projected onto the $\left({\theta }_1,{\theta }_2\right)$ space are shown. For all other PCA directions, the dynamics are random walks with a short velocity correlation time (shorter than 1 epoch) as clearly demonstrated in Fig. 2C where the SGD dynamics projected onto a randomly chosen pair of PCA directions $\left({\theta }_{49},{\theta }_{50}\right)$ are shown.

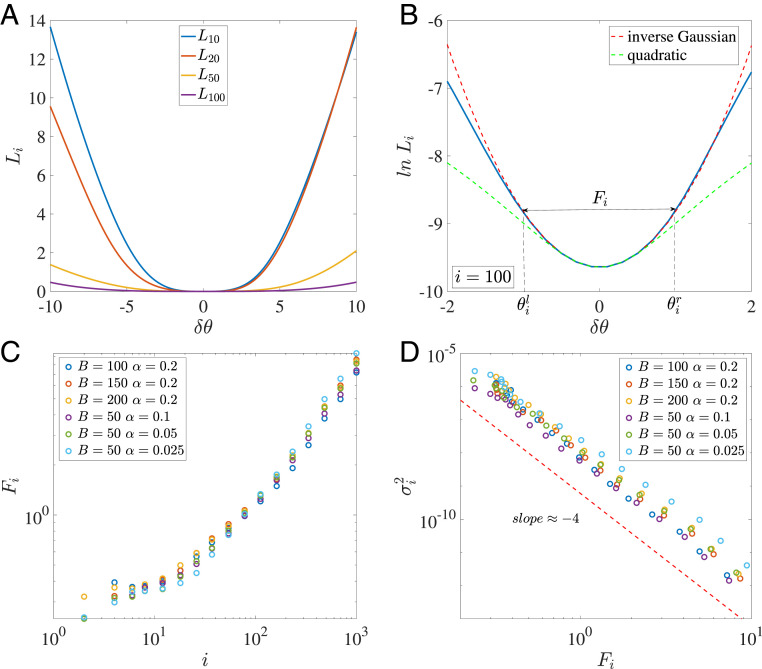
Fig. 2.

The loss function landscape and the inverse variance–flatness relation. (A) The loss function profile $L_i$ along the $i$th PCA direction. (B) The loss landscape (in log-scale). $L_i$ can be fitted better by an inverse Gaussian (the red dashed line) than a quadratic function (the green dashed line). The definition of the flatness $F_i\left(\equiv {\theta }_i^r-{\theta }_i^l\right)$ is also shown (see text for details). (C and D) The flatness $F_i$ for different PCA directions $i$ (C) and the inverse relation between the variance ${\sigma }_i^2$ and the flatness $F_i$ for different choices of minibatch size $B$ and learning rate $\alpha$ (D).

The persistent drift in the first PCA direction ${\overrightarrow{p}}_1$ can be understood by moving a solution ${\overrightarrow{w}}_0$ found by SGD along ${\overrightarrow{p}}_1$ by ${\theta }_1$ to a new weight vector $\overrightarrow{w}={\overrightarrow{w}}_0+{\theta }_1{\overrightarrow{p}}_1$. We find that ${\overrightarrow{p}}_1$ is highly aligned with ${\overrightarrow{w}}_0$. Therefore, moving along ${\overrightarrow{p}}_1$ results roughly in an overall amplification of the weights and the difference between the outputs for the right class and the wrong classes, which leads to a change in the cross-entropy loss function $L\left(\overrightarrow{w}\right)\approx L\left({\overrightarrow{w}}_0\right)\times \exp \left(\beta {\theta }_1\right)$ with $\beta$ a constant parameter. Even though the training error at ${\overrightarrow{w}}_0$ is already 0 (or close to 0), this dependence of $L$ on ${\theta }_1$ leads to the persistent motion along the ${\overrightarrow{p}}_1$ direction with a low speed proportional to $L$ which slowly decreases with time itself (see SI Appendix, section S2 for details). The slow net drift along ${\overrightarrow{p}}_1$ does not improve the training error (it is already zero), but it may improve the robustness of the solution by increasing the margin around the decision boundary and thus enhance generalization. This result is consistent with a previous study (14) in a simpler setting (using gradient descent to find homogeneous linear predictors on linearly separable datasets). Specifically, it was shown in ref. 14 that the predictor converges to the direction of the max-margin solution, which corresponds to the first PCA direction in our study.

In the rest of this paper, we study the majority of the PCA modes ($i\ge 2$), which are diffusive. Our focus is to understand the relation between fluctuations in these diffusive modes and the loss function landscape.

The Loss Function Landscape and the Inverse Variance–Flatness Relation

In the exploration phase, the loss function is small and all of the weight vectors along the SGD trajectory can be considered as valid solutions. However, the solutions found by a SGD trajectory represent only a small subset of valid solutions. To gain insights on the full solution space, we study the loss function landscape around a specific solution ${\overrightarrow{w}}_0$ reached by SGD. Specifically, we compute the loss function profile $L_i$ along the $i$th PCA direction ${\overrightarrow{p}}_i$ determined from PCA of the SGD dynamics:

$$L_i\left(\delta \theta \right)\equiv L\left({\overrightarrow{w}}_0+\delta \theta {\overrightarrow{p}}_i\right).$$ [6]

In Fig. 2A, we show the loss function landscape profiles $L_i\left(\delta \theta \right)$ for several diffusive PCA directions $i=\mathrm{10,20,50,100}$. To characterize the one-dimensional loss function landscape $L_i$ along a given PCA direction $i$ near its minimum, we define a flatness parameter $F_i$ as the width of the region within which $L_i\le e\times L_0$ where $e$ is the Euler’s number (other constant; e.g., 2 can be used without affecting the results) and $L_0\equiv L\left({\overrightarrow{w}}_0\right)$ is the minimum loss at ${\overrightarrow{w}}_0$. As shown in Fig. 2B, we determine $F_i$ by finding the two closest points ${\theta }_i^l<0$ and ${\theta }_i^r>0$ on each side of the minimum that satisfy $L_i\left({\theta }_i^l\right)=L_i\left({\theta }_i^r\right)=e\times L_0$. The flatness parameter is simply defined as their difference:

$$F_i\equiv {\theta }_i^r-{\theta }_i^l.$$ [7]

A larger value of $F_i$ means a flatter landscape in the $i$th PCA direction.

The loss landscape has been studied by computing the Hessian matrix of the loss function (15–17). Even though the flatness parameter $F_i$ defined here is related to the Hessian, they are not the same. $F_i$ is a more robust measure of the landscape flatness as it contains nonlocal information of the landscape in a finite neighborhood of the minimum. In particular, even when the local curvature vanishes or becomes slightly negative, $F_i$ is still well defined (see SI Appendix, section S3 for a detailed comparison). As shown in Fig. 2B, for the MNIST data, $\ln \left(L_i\left(\delta \theta \right)\right)$ can be fitted well by a quadratic function in a finite region near its minimum: $\ln \left(L_i\left(\delta \theta \right)\right)\approx \ln \left(L_0\right)+\frac{4\delta {\theta }^2}{F_i^2}$. Of course, this simple quadratic fit for $\ln \left(L_i\right)$ (or equivalently an inverse Gaussian fit for $L_i$) may not apply to all networks. Nevertheless, the “nonlocal” flatness parameter $F_i$ is well defined regardless of the exact fit and it is used to characterize the loss landscape around its minima in the rest of this paper.

We computed the flatness $F_i$ in each PCA direction $i$ and found that the flatness $F_i$ increases with $i$ as shown in Fig. 2C. Given that the SGD variance ${\sigma }_i^2$ decreases with $i$ as shown in Fig. 1A, this immediately suggests an inverse relationship between the loss function landscape flatness and the SGD variance. Indeed, as shown in Fig. 2D for the MNIST data, the inverse variance–flatness relation follows approximately a power law

$${\sigma }_i^2\sim F_i^{-\psi },$$ [8]

where the exponent $\psi \sim 4$ for different choices of $B$ and $\alpha$. Although the power law dependence may be specific to MNIST, the inverse dependence of ${\sigma }_i^2$ on $F_i$ holds generally true in all other NN architectures and datasets we studied (see SI Appendix, section S6 for details).

The inverse variance–flatness relation is the key finding of our study. Previous work has studied either variations of the weights (13) or the landscape of the loss function (7, 17) but not the strong relation between the two that is discovered here. The inverse variance–flatness relation is highly unusual; it goes against physics intuition. In particular, according to equilibrium statistical physics, the fluctuation of a variable around its equilibrium value is proportional to the change of the variable in response to an external perturbation, which is known as the fluctuation–response (or fluctuation–dissipation) relation aka the Einstein relation (18). A generalized fluctuation–response relation also holds true even for nonequilibrium systems linearized near a fixed point (19). However, for SGD-based learning dynamics, the fluctuation–response relation would imply that the variance of a variable (PCA weight) should be larger for a flatter landscape, which is the opposite to the observed inverse relation shown in Fig. 2D. Therefore, the inverse variance–flatness relation in SGD can also be called the “inverse Einstein relation.”

What is the reason for the inverse Einstein relation in SGD? Unlike generic stochastic systems where the noise strength (e.g., temperature) is a constant, the SGD noise comes from the difference between the gradient of a random MLF and that of the overall (mean) loss function. Therefore, the noise is anisotropic and it varies in the weight space and in time. In the next section, we explain the inverse variance–flatness relation based on the dependence of the SGD noise on statistical properties of the MLF ensemble.

The Random Landscape Theory and Origin of the Inverse Variance–Flatness Relation

The most distinctive feature of SGD is that at any given iteration (time) the learning dynamics are driven by a random minibatch out of an ensemble of minibatches each with its own random MLF. To understand the SGD dynamics, we develop a random landscape theory to describe the statistical properties of the MLF ensemble near a solution ${\overrightarrow{w}}_0$ (we set ${\overrightarrow{w}}_0=0$ for convenience).

As shown in Fig. 3A, $\ln \left(L^{\mu }\right)$ can be approximated by a quadratic function near its minimum or equivalently $L^{\mu }$ can be approximated by an inverse Gaussian function

$$L^{\mu }\left(\overrightarrow{\theta }\right)\approx L_{min}^{\mu }\exp \left[\sum _{i,j=1}^N\frac{M_{ij}^{\mu }}{2}\left({\theta }_i-{\theta }_i^{\mu }\right)\left({\theta }_j-{\theta }_j^{\mu }\right)\right],$$ [9]

where ${\theta }_i=\overrightarrow{\theta }\cdot {\overrightarrow{p}}_i$ is the weight parameter vector projected onto the $i$th PCA direction. The MLF $L^{\mu }$ for minibatch $\mu$ is characterized by its minimum $L_{min}^{\mu }$, its minimum location ${\overrightarrow{\theta }}^{\mu }$, and the symmetric Hessian matrix ${\mathbf{M}}^{\mu }=\left\{M_{ij}^{\mu }\right\}$ for $\ln \left(L^{\mu }\right)$ at the minimum.

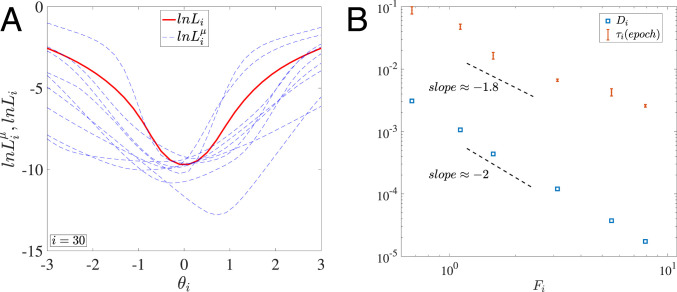
Fig. 3.

Statistical properties of the MLF ensemble. (A) Profiles of the overall loss function $\ln \left(L_i\right)$ (red line) and a set of randomly chosen MLFs $\ln \left(L_i^{\mu }\right)$ (blue dashed lines) in a given PCA direction $i$. (B) The inverse dependence of $D_i$ and ${\tau }_i$ on the flatness $F_i$.

Within the quadratic approximation (Eq. 9), statistical properties of the MLF ensemble are determined by the joint distribution of the parameters $M_{ij}^{\mu }$, $M_{ii}^{\mu }$, ${\theta }_i^{\mu }$, and $L_{min}^{\mu }$. Based on our simulation results and as the first-order approximation, we treat these parameters as independent random variables with normal distributions. By using this mean-field approximation, we can obtain the overall loss function

$$L\equiv {⟨L^{\mu }\left(\overrightarrow{\theta }\right)⟩}_{\mu }\approx L_0\exp \left(\beta {\theta }_1+\sum _{i=1}^N\frac{M_{ii}}{2}{\theta }_i^2\right),$$ [10]

where $L_0\equiv {⟨L_0^{\mu }⟩}_{\mu }$ is the minimum loss with $L_0^{\mu }\equiv L^{\mu }\left(\overrightarrow{\theta }=0\right)=L_{min}^{\mu }\exp \left[{\sum }_{i,j=1}^N{M}_{ij}^{\mu }{\theta }_i^{\mu }{\theta }_j^{\mu }/2\right]$, and $\beta$ and $M_{ii}\left(>0\right)$ are constants that depend on statistical properties of the MLF ensemble. The overall loss function, Eq. 10, has an inverse Gaussian form that is consistent with the empirical results shown in Fig. 2 A and B, and the flatness parameter can be expressed as $F_i\approx {\left(8/M_{ii}\right)}^{1/2}$. Details of derivation of Eq. 10 (including expressions of $\beta$ and $M_{ii}$) and empirical justification of the approximations can be found in SI Appendix, section S4.

From Eq. 9, we can now study the SGD dynamics analytically. By keeping only up to the linear order in ${\theta }_i$, the SGD Langevin equation for ${\theta }_i$ becomes

$$\frac{d{\theta }_i}{dt}=v_i\equiv -\alpha \frac{\partial L^{\mu }}{\partial {\theta }_i}\approx -\alpha L_0^{\mu }\sum _j{M}_{ij}^{\mu }\left({\theta }_j-{\theta }_j^{\mu }\right),$$ [11]

where $v_i\left(t\right)$ is the velocity for ${\theta }_i$ at time $t$. The equation above has an intuitive interpretation: At time $t$, the weight vector $\overrightarrow{\theta }$ is pulled by a random minibatch $\mu \left(t\right)$, whose MLF acts as a spring with a spring tensor ${\mathbf{M}}^{\mu }$ and its force center positioned at ${\overrightarrow{\theta }}^{\mu }$.

For the diffusive PCA directions ($i\ge 2$), dynamics of ${\theta }_i$ are driven by a random velocity with zero mean ${⟨v_i⟩}_{\mu }=0$. The autocorrelation function of $v_i$ can be written as $C_i\left(t\right)\equiv ⟨v_i\left(t+t^{\prime }\right)v_i\left(t^{\prime }\right)⟩=D_i{c}_i\left(t\right),$ where $c_i\left(t\right)=C_i\left(t\right)/D_i$ is the normalized correlation function, and $D_i$ is the velocity variance,

$$D_i=⟨v_i^2⟩\approx A_D{⟨{\left(M_{ii}^{\mu }\right)}^2⟩}_{\mu }{\tilde{\sigma }}_{\theta ,i}^2,$$ [12]

where $A_D={\alpha }^2{⟨{\left(L_0^{\mu }\right)}^2⟩}_{\mu }$ is a constant and ${\tilde{\sigma }}_{\theta ,i}^2\equiv {⟨{\left({\tilde{\theta }}_i^{\mu }\right)}^2⟩}_{\mu }$ is the variance of the minimum location ${\tilde{\theta }}_i^{\mu }$ of MLF $L^{\mu }$ projected onto the $i$th PCA direction.

From the velocity–velocity correlation $C_i\left(t\right)$ and the variance ${\sigma }_i^2$ of the weight variable ${\theta }_i\left(t\right)={\int }_0^t{v}_i\left(t^{\prime }\right)d{t}^{\prime }$ within the PCA time window, we can define a time scale ${\tau }_i$ that characterizes the velocity (or gradient) autocorrelation

$${\tau }_i\equiv {\sigma }_i^2/\left(D_i\mathrm{\Delta }t\right)=T_w^{-1}\mathrm{\Delta }{t}^{-1}{\int }_0^{T_w}\left[{\int }_0^t{\int }_0^t{c}_i\left(t^{\prime }-t^{″}\right)d{t}^{\prime }d{t}^{″}\right]dt,$$ [13]

where $T_w$ is the PCA window size. Note that the minibatch time step $\mathrm{\Delta }t\left(=1\right)$ is included explicitly in the definition above to make ${\tau }_i$ a time scale.

In generic stochastic dynamical systems (19), the noise is independent of the loss landscape. In SGD, however, the noise strength characterized by $D_i$ depends on the landscape flatness. According to Eq. 12, a flatter landscape has a smaller value of $M_{ii}^{\mu }$, which leads to a smaller $D_i$. Both ${⟨{\left(M_{ii}^{\mu }\right)}^2⟩}_{\mu }\propto {\left(M_{ii}^{\left(0\right)}\right)}^2$ and ${\tilde{\sigma }}_{\theta ,i}^2$ can be determined from the MLF ensemble statistics. As shown in SI Appendix, Fig. S7, ${\tilde{\sigma }}_{\theta ,i}\sim F_i$ and $M_{ii}^{\left(0\right)}\sim F_i^{-2}$, and therefore $D_i\sim F_i^{-{\psi }_D}$ with an exponent ${\psi }_D\approx 2$ as shown in Fig. 3B.

The time scale ${\tau }_i$ can be determined by Eq. 13 from the normalized velocity correlation function $c_i\left(t\right)$. In the absence of velocity correlation, i.e., $c_i\left(t\right)=\mathrm{\Delta }t\delta \left(t\right)$, ${\tau }_i=\frac{T_w}{2}$ is a constant (isotropic) time scale determined by the PCA time window. However, we find that there are significant velocity correlations in the SGD dynamics, which leads to a much smaller ${\tau }_i\ll T_w$. Remarkably, the correlation time ${\tau }_i$ also depends inversely on the flatness $F_i$ (see SI Appendix, section S5 for details of calculating ${\tau }_i$). As shown in Fig. 3B, this inverse dependence follows approximately a power law ${\tau }_i\sim F_i^{-{\psi }_{\tau }}$ with the exponent ${\psi }_{\tau }\approx 1.8$. The exact reason for the inverse dependence of ${\tau }_i$ on $F_i$ is not yet clear. However, since ${\tau }_i$ can be interpreted as the number of minibatches needed to estimate the gradient $\frac{\partial L}{\partial {\theta }_i}$, our results indicate that less minibatch subsampling is needed to infer gradients in flatter directions. This result may explain the reason why the Markov chain Monte Carlo (MCMC) method with a relatively small number of updates can be used to accurately estimate the local gradients in algorithms such as stochastic gradient Langevin dynamics in Bayesian learning (20) and entropy-SGD in deep learning (7).

Put all together, the inverse power-law dependence of $D_i$ and ${\tau }_i$ on the landscape flatness $F_i$ leads to the inverse power-law ${\sigma }_i^2=D_i{\tau }_i\sim F_i^{-\psi }$ with an exponent $\psi ={\psi }_D+{\psi }_{\tau }\approx 3.8$, which is in quantitative agreement with the direct simulation result shown in Fig. 2D. Although the power law dependence may not be universal, the inverse dependence of $D_i$, ${\tau }_i$, and ${\sigma }_i^2$ on $F_i$ holds true in general for all NN architectures and datasets we studied (see SI Appendix, section S6 for details).

Preventing Catastrophic Forgetting by Using Landscape-Dependent Constraints

To demonstrate the utility of the theoretical insights gained so far, we tackle a long-lasting challenge in machine learning, i.e., how to prevent catastrophic forgetting (CF) (21, 22). After a DNN learns to perform a particular task, it is trained for another task. Although the DNN can readjust its weights to perform well for the new task, it may forget the previous task and thus fail catastrophically for the previous task. To prevent forgetting, a recent study by Kirkpatrick et al. (23) proposed the elastic weight constraint (EWC) algorithm to train a new task by enforcing constraints on individual weights based on their effects on the performance of the previous task.

Here, by following the same general strategy but using the new insights on the geometry of loss landscape near a solution, we propose a landscape-dependent constraints (LDC) algorithm to train for the new task with constraints applied to the collective PCA coordinates. More specifically, when we find a solution ${\overrightarrow{w}}_1$ in the weight space for the first task (task 1) by SGD, we can characterize the loss function landscape around ${\overrightarrow{w}}_1$ in the PCA coordinate system by the flatness parameter $F_{1i}$ along the $i$th PCA direction ${\overrightarrow{p}}_{1i}$ for task 1. Based on the inverse variance–flatness relationship (Eq. 8), the flatness parameter $F_i$ can be obtained directly (cheaply) from the weight variance instead of computing and diagonalizing the Hessian matrix, which is computationally expensive. When learning the new task, we use a modified loss function for the second task (task 2) by introducing an additional cost term that penalizes the network for going out of the attraction basin of the task-1 solution (${\overrightarrow{w}}_1$) for a small number of PCA directions with the lowest values of flatness:

$${\tilde{L}}_2\left(\overrightarrow{w}\right)=L_2\left(\overrightarrow{w}\right)+\lambda \sum _{i=1}^{N_c}\frac{{\left(\left(\overrightarrow{w}-{\overrightarrow{w}}_1\right)\cdot {\overrightarrow{p}}_{1i}\right)}^2}{F_{1i}^2},$$ [14]

where $L_2$ is the original loss function for task 2, $\lambda$ is the overall strength of the constraints, and $N_c\left(\ll N\right)$ is the number of constrained PCA modes from task 1.

Based on the large attraction basin for a given task as evidenced by the large flatness parameters shown in Fig. 2, we expect that solutions for task 2 exist within the basin of solutions for task 1, so the performance for task 1 should not degrade significantly after learning task 2. We first tested this idea in the simplest case by using the MNIST database with task 1 and task 2 corresponding to classifying two disjoint subsets of digits, e.g., (0,1) for task 1 and (2,3) for task 2 (see Methods for details). To speed up our analysis, we first train the network on all tasks and fix the output layer and input layer; only the hidden layer(s) is initialized and trained for sequential learning with different algorithms. As shown in Fig. 4A in the absence of the constraints ($\lambda =0$), starting with a task-1 solution ${\overrightarrow{w}}_1$, the weights evolve quickly to a solution for task-2 ${\overrightarrow{w}}_2$ with a small task-2 test error ${ϵ}_2$ (red line). However, the performance of task 1 deteriorates quickly with a fast increasing task-1 test error ${ϵ}_1$ (blue line). The reason can be understood in Fig. 4B, where $q_i=\Vert \left({\overrightarrow{w}}_2-{\overrightarrow{w}}_1\right)\cdot {\overrightarrow{p}}_{1i}\Vert$, the projections of the weight displacement vector onto different PCA directions of task 1, are shown. Without constraints, the displacement becomes unbounded for many high-ranking PCA modes (smaller $i$), which leads to the large task-1 test error after learning task 2, i.e., catastrophic forgetting.

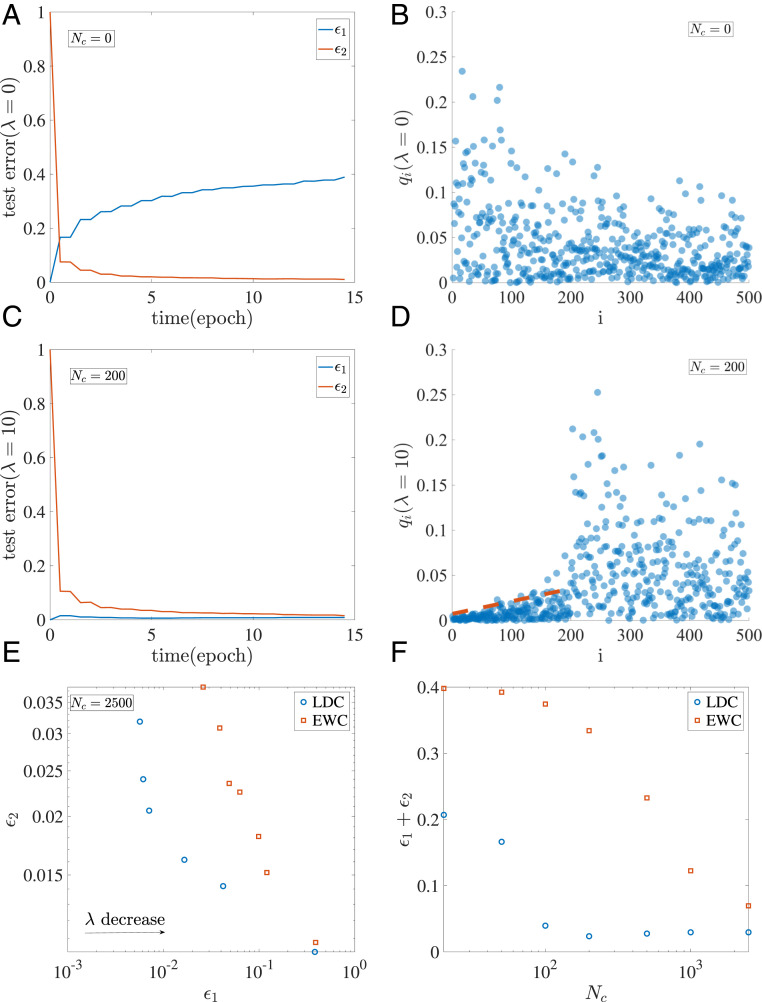
Fig. 4.

The landscape-dependent constraints for avoiding catastrophic forgetting. (A) The test errors for task 1 (${ϵ}_1$) and task 2 (${ϵ}_2$) versus training time for task 2 in the absence of the constraints ($\lambda =0$). (B) The weight displacements $q_i$ in different PCA directions ${\overrightarrow{p}}_{1i}$ from task 1 in the absence of the constraints ($\lambda =0$). C and D are the same as A and B but in the presence of the constraints with $\lambda =10$ and $N_c=200$. The red dashed line in D shows the upper bound $q_i\lesssim 0.008F_{i1}$ for the modes ($i\le N_c$) that are under constraint. (E) The tradeoff between the saturated test errors (${ϵ}_1$ and ${ϵ}_2$) when varying $\lambda$ for LDC (blue circles) and EWC (red squares) algorithms. (F) The overall performance (${ϵ}_1+{ϵ}_2$) versus the number of constrains $N_c$ for LDC (blue circles) and EWC (red squares) algorithms. The two tasks are for classifying two separate digit pairs [$\left(\mathrm{0,1}\right)$ for task 1 and $\left(\mathrm{2,3}\right)$ for task 2] in MNIST.

The performance improves significantly when task 2 is learned with the modified loss function ${\tilde{L}}_2$ given in Eq. 14. As shown in Fig. 4C, with constraints ($\lambda =10$) for the top $N_c=200$ modes, although the learning process for task 2 is slightly slower, the system is able to learn a solution for task 2 with a comparable error ${ϵ}_2$ as before ($\lambda =0$). The significant advantage here is that the performance for task 1 (blue line) remains roughly the same as before; i.e., the system has avoided catastrophic forgetting. As shown in Fig. 4D, $q_i$ now has an upper bound ${\xi }_i$ (dashed red line) for all of the top modes ($i\le N_c$) due to the constraints. The upper bound is found to be proportional to the flatness $F_{1i}$ (${\xi }_i\approx 0.008F_{1i}$), which means that the task-2 solution ${\overrightarrow{w}}_2$ remains within the basin of task-1 solutions.

There is a tradeoff between the two testing errors (${ϵ}_1$, ${ϵ}_2$) when varying $\lambda$. As shown in Fig. 4E, the performance of LDC is better than that of EWC. This is not surprising as LDC uses the full landscape information whereas EWC uses only the diagonal elements of the Fisher information matrix (effectively the Hessian matrix). More interestingly, as shown in Fig. 4F, the overall performance (${ϵ}_1+{ϵ}_2$) of LDC reaches its optimal level when a relatively small number ($N_c^{*}\approx 200$) of the top PCA modes are constrained. For EWC, however, all individual weights contribute to the performance, and thus its optimal performance is reached when all $N=\mathrm{2,500}$ individual weights are constrained. The results from the LDC algorithm suggest that memory of the previous task is encoded in the top $N_c^{*}$ PCA modes and $N_c^{*}$ can be used to estimate the capacity of the network for sequential learning of multiple tasks.

In LDC, the landscape flatness, which is used in the constraints, can be estimated efficiently from the weight variance by using the variance–flatness relationship $F_i\sim {\sigma }_i^{2/\psi }$. To test whether LDC is sensitive to the accuracy of this estimate, we used different values of $\psi =\mathrm{3,4,5}$ to estimate $F_i$. We find that the results do not seem to depend on the exact choice of $\psi$ (see SI Appendix, section S7 for details), which suggests that LDC is robust as long as the constraints are added to the top PCA modes of the previous tasks.

We verified the advantage of the LDC algorithm by considering more complex sequential learning tasks such as more digits (5 instead of 2) in each task from the MNIST dataset and sequential learning of all of the animals and all man-made objects in the Canadian Institute For Advanced Research (CIFAR)10 dataset. The results are consistent with the simple case shown in Fig. 4 and confirm the advantage of using LDC for preventing catastrophic forgetting (see SI Appendix, section S8 for details).

SGD as a Self-Tuned Landscape-Dependent Annealing Strategy for Learning

In the final section of this paper, we go back to evaluate our initial working hypothesis on the learning strategy deployed in SGD. In an equilibrium system with state variables $\overrightarrow{\theta }$ and a free energy function $L\left(\overrightarrow{\theta }\right)$, the statistics of $\overrightarrow{\theta }$ follow the Boltzmann distribution $P\left(\overrightarrow{\theta }\right)=\exp \left[-L\left(\overrightarrow{\theta }\right)/T\right]$ where $T$ is the constant temperature that characterizes the strength of the thermal fluctuations (we set the Boltzmann constant $k_B=1$ here). By expanding the loss function to the second order, $L=L_{min}\left(1+{\sum }_i\frac{4{\left(\overrightarrow{\theta }\cdot {\overrightarrow{p}}_i\right)}^2}{F_i^2}\right)$ around a minimum ${\overrightarrow{w}}_0=0$, it is easy to show that the variance of ${\theta }_i$ would be proportional to the squared flatness $F_i^2$ and temperature $T$: ${\sigma }_i^2\propto T\times F_i^2$, which is a direct consequence of the fluctuation–response (aka fluctuation–dissipation) relation in equilibrium statistical physics.

Remarkably, for the SGD-based learning dynamics, we found an inverse relation between fluctuations of the variables and the flatness of the loss function landscape, Eq. 8, which is the opposite to the fluctuation–response relation in equilibrium systems. We have tested it with different variants of the SGD algorithms such as adaptive moment estimation (Adam) and momentum-based algorithms, different databases (MNIST and CIFAR10), and different DNN architectures (see SI Appendix, Fig. S3 for details). In all cases we studied, the inverse variance–flatness relation holds, suggesting that it is a universal property of the SGD-based learning algorithms.

Unlike thermal noise in equilibrium systems, which represents a passive random driving force with a constant strength (temperature), the SGD “noise” $\overrightarrow{\eta }=\alpha \frac{\partial \delta L^{\mu }}{\partial \overrightarrow{\theta }}$ represents an active learning/searching process that varies in “space” ($\overrightarrow{\theta }$). The intensity of this learning (searching) activity along the $i$th PCA direction ${\overrightarrow{p}}_i$ can be characterized by an active local temperature $T_i\left(\delta \theta ,t\right)$:

$$T_i\left(\delta \theta ,t\right)\equiv \frac{\alpha }{2}{⟨{∥\frac{\partial \delta L^{\mu }\left({\overrightarrow{w}}_0+\delta \theta {\overrightarrow{p}}_i\right)}{\partial \delta \theta }∥}^2⟩}_{\mu },$$ [15]

where $\delta \theta$ is the displacement from ${\overrightarrow{w}}_0$ along the ${\overrightarrow{p}}_i$ direction.

As shown in Fig. 5A, the active temperature $T_i\left(\delta \theta ,t\right)$ has a similar spatial profile to that of the loss function with the active temperature higher away from the minimum. In weight space where the overall loss function is high, the active temperature is also high, which drives the system away from regions in the weight space with high losses. The learning intensity is anisotropic, and it differs in different PCA directions as shown in Fig. 5B. For a flatter direction with a larger value of $F_i$, $T_i$ is lower (Fig. 5 B, Inset) as the basin of solutions is wide and thus no strong active learning is needed. However, for a steeper direction with a smaller value of $F_i$, the solutions exist only in smaller regions and thus more intensive learning (or higher active temperature) is required. Therefore, the MLF ensemble can sense both the local loss and nonlocal flatness of the landscape in different directions and use this information to drive active learning.

Fig. 5.

Profiles and dynamics of the anisotropic active temperature. (A) The active temperature profile $T_i\left(\delta \theta ,t\right)$ in the $i$th PCA direction at $t=200$. (B) The minimum active temperature $T_i\left(0\right)$ in different PCA directions $i$. Inset shows the inverse dependence of $T_i$ on the flatness $F_i$. (C) The active temperature profiles $T_i\left(\delta \theta ,t\right)$ at different times for $i=10$. (D) The active temperature $T_i$ for all directions decreases with time in sync with the loss function (red line) dynamics. The shaded region highlights the transition between the fast-learning phase and the exploration phase. Inset shows the correlation between $T_i$ and $L$.

The active temperature also varies with time. As learning progresses, the active temperature profile decreases with time, as shown in Fig. 5C. In Fig. 5D, dynamics of the active temperature and the overall loss function along a SGD trajectory are shown together. It is clear that the active temperature and the overall loss function are highly correlated as shown directly in Fig. 5 D, Inset, which means that the SGD system cools down as it learns. This reminds us of the well-known simulated annealing algorithm for optimization (24), where temperature is decreased from a high value to zero with some prescribed cooling schedule. However, the SGD algorithm seems to deploy a more intelligent landscape-dependent annealing strategy where the active temperature (learning intensity), driven by the MLF ensemble, is self-tuned according to the local and nonlocal properties of the loss landscape that are sensed by the MLF ensemble. This landscape-dependent annealing strategy drives the system toward the flat minima of the loss function landscape and stays at the flat minima by lowering the active temperature once there.

To verify the effects of landscape-dependent noise for generalization, we studied a simple algorithm where landscape-dependent or “flatness-detecting” noise is introduced to the deterministic GD dynamics. In particular, we have added an anisotropic noise term whose strength depends explicitly on the flatness of the landscape. We find that only with this flatness-detecting noise, the system can enter the exploration phase with flat minima and low generalization error (see SI Appendix, section S9 for details). These results (see also ref. 25 for similar results) support the conclusion that the anisotropic landscape-dependent noise in SGD is responsible for finding generalizable solutions.

Discussion

Modern DNNs often contain more parameters than training samples, which allow it to interpolate (memorize) all of the training samples, even if their labels are replaced by pure noise (26). Remarkably, despite their huge capacity, DNNs can achieve small generalization error on real data. This phenomenon has been formalized in the so-called “double-descent” curve (27). As the model capacity (complexity) increases, the test error follows the usual U-shaped curve at the beginning, first decreasing and then peaking near the interpolation threshold when the model achieves vanishing training error. However, it descends again as model capacity exceeds this interpolation threshold with the test error reaching its (global) minimum in the overparameterization regime where the number of parameters is much larger than the number of samples. Rapid progress has been made to understand this double-descent behavior by using simple models. For example, both optimization and generalization guarantees for overparameterized simple two-layer networks are proved with leaky rectified linear activation function (ReLU) on linearly separable data (28). This result has subsequently been extended to two-layer networks with ReLU activation (29) and two- and three-layer networks with smooth activation functions (30). In a different approach by using the neural tangent kernel (31), which connects large (wide) neural nets to kernel methods, it was shown that the generalization error decreases toward to a plateau value in a power-law fashion as $N_p^{-1/2}$ with $N_p$ the number of parameters in the overparameterized regime (32). In simple synthetic learning models such as the random features model with ridge regression loss function, the double-descent behavior has been shown analytically (33) and this analytical result has been extended to other synthetic learning models (e.g., the random manifold model) and for more general loss functions by using the replica method (34).

However, despite this recent progress, how to characterize the complexity of the solutions in DNNs and how SGD seeks out simple and more generalizable solutions for more realistic learning tasks remain not well understood. The results in this paper shed some light on both of these questions. We found that in the overparameterized regime, starting with different random initializations SGD reaches different solutions with the same statistical properties. Around each solution, the loss landscape is flat in most PCA directions with only a small number of relevant directions where the loss landscape is sharp. The complexity of the solution can thus be characterized by an effective dimension of the solution, which can be defined by the number of sharp directions ($D_s$) in the loss landscape around this solution. In Fig. 6A, the rank-ordered flatness spectra of the loss landscape are shown for solutions found by networks with different sizes. It is clear that as the network size (width $H$) increases, the number of sharp directions (small flatness) does not change, and the landscapes along the additional degrees of freedom are flat with large values of flatness. As shown in Fig. 6B, the effective dimension $D_s$, which is defined with a threshold set by the norm of the solution, is much smaller than the number of parameters $N_p\left(\equiv H^2\right)$. Most importantly, $D_s$ remains roughly a constant as $N_p$ increases. This means that the complexity of the solution found by SGD does not increase with the number of parameters, and the solution remains “simple” with good generalization performance in the overparameterized regime.

Fig. 6.

The flatness spectrum and the effective dimension ($D_s$) of solution. (A) The flatness spectra (rank-ordered flatness) for networks with different width ($H$). (B) The effective dimension of the solution $D_s$, which is defined as the number of directions whose flatness is below a threshold set to be roughly half of the $L_2$ norm of the weights (the dashed line in A), increases weakly as the number of parameters (weights) $N_p\left(\equiv H^2\right)$ increases. The error bars are obtained by using 10 different solutions obtained by 10 random initializations with the same norm for each network size.

Our study also provides evidence on how SGD finds these low-dimensional simple solutions. In particular, we found that the SGD learning activity (temperature) is high only for those directions where the loss landscape is sharp while learning activity along other flat directions becomes quickly frozen during the SGD learning process. An effective learning (searching) dimension $D_l$ can be defined as the number of PCA directions that contain most (e.g., $99\%$ or $99.9\%$) of the total weight variance. Due to the inverse variance–flatness relation, $D_l$ is found to have a similar dependence on the network size to that of $D_s$. Our results show that SGD searches only in a small subspace for solutions after the initial transient and the dimension of the search space $\left(D_l\right)$ has only weak dependence on the network size in the overparameterized regime (see SI Appendix, Fig. S17 for details).

In summary, a careful study of the SGD dynamics and the loss function landscape in this paper reveals a robust inverse relation between fluctuations in SGD and flatness of the loss landscape, which is critical for deciphering the learning strategy in deep learning and for designing more efficient algorithms. Our study demonstrates that ideas and techniques based on statistical physics provide an additional theoretical framework (alternative to the traditional theorem-proving approach) for studying machine learning. It would be interesting to use this framework to address other fundamental questions in machine learning such as generalization (35, 36), relation between task complexity and network architecture, information flow in DNN (37, 38), transfer learning (39), and continuous learning (40–42).

Methods

Neural Network Architecture and Simulations.

Two types of DNNs are studied: 1) Two fully connected neural networks were used for classifying digits in the MNIST database, one with two hidden layers ($784\times 50\times 50\times 10$, main text) and the other with four hidden layers ($784\times 50\times 50\times 50\times 50\times 10$; SI Appendix, Fig. S10A). The response of the hidden layer neurons is ReLU, activation of the output neurons is Softmax, and no bias neuron is used for convenience. We also studied the convolution neural network (CNN). 2) Two convolutional neural networks were used in our experiments. One is trained on the MNIST dataset, which has two convolution layers with size $1\times 3\times 3\times 16$ and $16\times 5\times 5\times 32$ and one fully connected layer with size $\mathrm{1,568}\times 10$. (Here we represent the convolution layer using input neural number $\times$ kernel size $\times$ kernel size $\times$ output neural number.) The stride of convolution is 1 and there is a zero padding to keep the data dimension unchanged. After each convolution layer, there is a $2\times 2$ max pooling layer. Another CNN is trained on the CIFAR10 dataset (SI Appendix, Fig. S10C). It has two convolution layers with size $3\times 5\times 5\times 6$ and $6\times 5\times 5\times 16$ and three fully connected layers with size $400\times 120$, $120\times 84$, $84\times 10$. The stride of convolution is 1 and the size of max pooling is $2\times 2$. We do not use zero padding in this network. All numerical experiments are done on a neural network simulation framework torch.

Principal Component Analysis in Exploration Phase.

For a given time in the exploration phase, we extract the weight matrix between two hidden layers and reshape (flatten) the weight matrix into a weight vector; e.g., a $50\times 50$ weight matrix is flattened to a 2,500-dimensional vector. Then we stack these row vectors from different times horizontally and do PCA on this matrix. The time step is each minibatch and the total window size is $T=10$ epochs. The PCA is applied using the sklearn package provided by Python 3.7.

Multitask Learning.

We divided the MNIST into five groups. Each group contains only two numbers. Here we call each group task 1, task 2, etc. We use the fully connected neural networks with two hidden layers ($784\times 50\times 50\times 10$). The size of the output layer is 10 so it works for all tasks. In the main text, we choose the group containing (0,1) as task 1 and the group containing (2,3) as task 2; see SI Appendix, section S8 for two more complex cases. The LDC learning algorithm follows the following steps: 1) Train the network on task 1; 2) when the learning dynamics for task 1 reach the exploration phase, do PCA to obtain ${\overrightarrow{p}}_{1i}$ and ${\sigma }_i^2$ from which $F_{1i}$ is determined from Eq. 8; 3) train task 2 by using the modified loss function Eq. 14.

Data Availability

There are no data underlying this work.