Toward the Accuracy and Speed of Protein Side-Chain Packing: A Systematic Study on Rotamer Libraries

Abstract

Protein rotamers refer to the conformational isomers taken by the side-chains of amino acids to accommodate specific structural folding environments. Since accurate modeling of atomic interactions is difficult, rotamer information collected from experimentally solved protein structures is often used to guide side-chain packing in protein folding and sequence design studies. Many rotamer libraries have been built in the literature but there is little quantitative guidance on which libraries should be chosen for different structural modeling studies. Here, we performed a comparative study of six widely used rotamer libraries and systematically examined their suitability for protein folding and sequence design in four aspects: (1) side-chain match accuracy, (2) side-chain conformation prediction, (3) de novo protein sequence design, and (4) computational time cost. We demonstrated that, compared to the backbone-dependent rotamer libraries (BBDRLs), the backbone-independent rotamer libraries (BBIRLs) generated conformations that more closely matched the native conformations due to the larger number of rotamers in the local rotamer search spaces. However, more practically, using an optimized physical energy function incorporated into a simulated annealing Monte Carlo searching scheme, we showed that utilization of the BBDRLs could result in higher accuracies in side-chain prediction and higher sequence recapitulation rates in protein design experiments. Detailed data analyses showed that the major advantage of BBDRLs lies in the energy term derived from the rotamer probabilities that are associated with the individual backbone torsion angle subspaces. This term is important for distinguishing between amino acid identities as well as the rotamer conformations of an amino acid. Meanwhile, the backbone torsion angle subspace-specific rotamer search drastically speeds up the searching time, despite the significantly larger number of total rotamers in the BBDRLs. These results should provide important guidance for the development and selection of rotamer libraries for practical protein design and structure prediction studies.

Graphical Abstract

INTRODUCTION

Protein structures and their stabilities are essentially determined by the packing interactions of the side-chains of amino acids along the sequence. Protein side-chain packing (PSCP) is thus of great significance in computational and structural biology, e.g., protein structure prediction,^1,2 structure-based protein and enzyme design,^3–5 and structure refinement.⁶ The three key components of a typical PSCP method are (1) a rotamer library, (2) an energy function, and (3) an optimization algorithm. Solving a PSCP problem involves identifying a sequence of rotamers from a rotamer library that minimizes the folding energy calculated by the energy function using an optimization algorithm. Over the past few decades, many studies have been dedicated to the PSCP problem, but the emphases have been mainly focused on the latter two components,^7–17 with only a handful of studies specifically addressing the rotamer library construction.^18–21 Overemphasis on the energy functions and searching methods has seemingly undervalued the importance of the rotamer libraries. In fact, the quality of a rotamer library significantly affects the PSCP performance.²² Unfortunately, to the best of our knowledge, there is no systematic and quantitative study on how rotamer libraries impact PSCP and which rotamer library is most suitable for this task.

Historically, there have been backbone-independent rotamer libraries (BBIRLs)^20,22,23 and backbone-dependent rotamer libraries (BBDRLs).^18,19,21 Good PSCP performance was achieved using BBIRLs in the earlier years.^7,23 BBDRLs were first proposed by Dunbrack and Karplus¹⁸ and have been more popular and widely used ever since. The latest Dunbrack BBDRL²¹ was released in 2010, and many PSCP programs use this library.^14,15,17 These programs achieve quite similar performance on side-chain torsion angle prediction by correctly predicting 84~86% of the χ₁ dihedral angles and 71~75% of the χ₁₊₂ using a tolerance criterion of 40°. Meanwhile, the overall side-chain root-mean-square-deviation (RMSD) between the predicted and native conformations range from 1.46 to 1.65 Å^14,15,17 Using a very detailed BBIRL consisting of more than 7000 rotamers, Xiang and Honig²² reported that 87% and 74% of χ₁ and χ₁₊₂ angles were predicted to be within a stricter cutoff of 20° to the native angles and the overall predicted RMSD was 1.32 Å. Peterson et al.²⁴ showed that the packing accuracy reached 89% for χ₁ and 78% for χ₁₊₂ using the 40° criterion and an overall RMSD of 1.27 Å by using a BBIRL that had more than 50 000 rotamers. Therefore, from the viewpoint of prediction accuracy, the performance reported for using high-resolution BBIRLs is even more impressive than that reported for using BBDRLs. In a protein–ligand interaction redesign study, Boas and Harbury²⁵ found that the design algorithm could predict protein sequences that bound well with the target ligand only when they used a detailed BBIRL consisting of more than 5449 rotamers. It was also reported that the catalytic geometries of native enzyme active sites could be reproduced only when a BBIRL containing more than 7000 or even 11000 rotamers was used.^26,27 Pupo and Moreno²⁸ performed an extensive statistical comparison of ten rotamer libraries (e.g., including the Dunbrack 2002 BBDRL²⁹ and the detailed Honig BBIRLs²²), excluding the influence of energy functions and searching methods; their results showed that only the Honig BBIRLs were able to correctly reproduce the experimental side-chain conformations for most of the analyzed residues on peptidic ligands using a strict criterion of 20°.²⁸ However, side-chain reproduction rates between the newer Dunbrack 2010 BBDRL²¹ and the detailed Honig BBIRLs on a set of experimental protein structures have not been compared. Moreover, the performance of the two kinds of rotamer libraries on side-chain prediction and protein sequence design has never been quantitatively compared.

In this work, we systematically compared the Dunbrack 2010 BBDRL and two of its derivatives to the Honig BBIRLs in four aspects: (1) capability of reproducing native residue side-chain conformations, which was independent of the energy function and searching method, (2) ability to perform side-chain prediction, (3) native sequence recapitulation performance through de novo protein sequence design, and (4) running time for 2 and 3. To accomplish tasks 2 and 3, we utilized a simulated annealing Monte Carlo (SAMC) based searching method³⁰ and a physics- and knowledge-based energy function (EvoEF2³¹), which was extended from the previously developed EvoEF.³ To compare the quality of sequences designed using different libraries, we used the state-of-the-art protein structure prediction suite, I-TASSER,³² to examine the foldability of the designed sequences.

METHODS

Data Set Construction.

We collected a set of monomeric structures from previous PSCP¹⁴ and protein design studies,^3,26,33 excluding structures with discontinuous chains or missing atoms. To remove redundancy, the protein sequences were clustered using CD-HIT³⁴ with a sequence identity cutoff of 30% and the duplicated sequences in each cluster were removed. A total of 136 structures were retained and this set of proteins was used for side-chain reproduction analysis, side-chain prediction, and de novo sequence design in this work; the proteins in this data set shared <30% sequence identity with every member from the data set used to train EvoEF2.³¹ To check if the data set was biased for side-chain reproduction by a rotamer library, we also collected another larger set of single-chain structures from the Top8000 database,³⁵ where the members shared <70% sequence identity with each other. Proteins with discontinuous chains or missing atoms were discarded and a larger set of 3719 structures was retained for side-chain reproduction analysis.

Definition of Core and Surface Residues.

It has been shown that the side-chain prediction accuracy is quite different for residues located in distinct regions (e.g., core and surface residues) of a protein.^1,15,17,22 In this work, the core and surface residues were defined using criteria similar to that used in refs 36 and 37. Specifically, we defined core residues as those positions that had more than 20 C_β atoms within 10 Å of the C_β atom of the residue of interest, while the surface residues were required to have less than 15 C_β atoms within the same region. C_α atoms were counted for glycine.

Evaluation of Side-Chain Reproduction.

We used two metrics to evaluate the ability of a rotamer library to reproduce the native side-chain conformations. First, we considered that a rotamer library was able to reproduce a given set of side-chain χ angles from a native residue if it contained at least one rotamer that had all of its corresponding χ angles within 20° of the native values. Second, to evaluate the performance of each rotamer library to reproduce the native residue geometries, we generated all of the possible conformations using the rotamer dihedral angles defined in rotamer libraries L1–L6 and calculated the RMSDs between each residue and its corresponding set of rotamers from each library, keeping the lowest RMSD value. The RMSDs were only calculated for side-chain, non-hydrogen atoms, excluding C_β atoms. There are two ways to calculate RMSD among a set of proteins: overall and average RMSD. The overall RMSD is calculated by summing over all of the residues in all of the proteins, while the average RMSD is simply the average value of the sum of RMSDs for each of the proteins from the set. The value of overall RMSD is usually larger than that of average RMSD and was used in this work. The symmetry of residues Asp, Glu, Phe, Arg, and Tyr were considered for RMSD calculation. Alanine and glycine were excluded from analysis, as they are not rotatable.

EvoEF2 Energy Function and Parametrization.

The EvoEF2³¹ energy function was extended from EvoEF, which was first proposed and implemented in our evolutionary profile-based protein design algorithm, EvoDesign.³ EvoEF consists of five energy terms, including van der Waals energy, electrostatic interactions, orientation-dependent hydrogen-bonding interactions, desolvation energy, and the reference energy:

$$\begin{gathered} E_{\mathrm{EvoEF}}=E_{\mathrm{VDW}}+E_{\mathrm{ELEC}}+E_{\mathrm{HB}}+E_{\mathrm{DESOLV}}-E_{\mathrm{REF}} \\ =\sum _{i,j}[w_{\mathrm{vdw}}{E}_{\mathrm{vdw}}(i,j)+w_{\mathrm{elec}}{E}_{\mathrm{elec}}(i,j)+w_{\mathrm{hb}}{E}_{\mathrm{hb}}(i,j) \\ +w_{\mathrm{desolv}}{E}_{\mathrm{desolv}}(i,j)]-\sum _{l=1}^L{E}_{\mathrm{ref}}(a{a}_l) \end{gathered}$$ (1)

Here, E_VDW, E_ELEC, E_HB, E_DESOLV, and E_REF represent the total van der Waals, electrostatic, hydrogen bonding, desolvation, and reference energy terms for a protein system, respectively. The protein reference energy term, E_REF, is used to model the energy of a protein in its unfolded state and is calculated as the sum of amino acid-specific reference energy values. E_vdw(i, j), E_elec(i, j), E_hb(i, j), and E_desolv(i, j) are the pairwise interactions between nonbonded atoms i and j, where w_vdw, w_elec, w_hb, and w_desolv are their relative weights. E_ref(aa_l) is the amino acid-specific reference energy used to model the energy of an amino acid in the unfolded state, where aa_l is the amino acid identity at position l. The detailed mathematical equations for E_vdw(i, j), E_elec(i, j), E_hb(i, j), and E_vdw(i, j) are identical to what was previously described³ and are listed in Text S1 to provide a complete description of the energy function.

In EvoEF2, the above terms were preserved, but the weights and reference energies were optimized using an improved method. Moreover, four new terms were introduced to make EvoEF2 capable of tackling more difficult design cases and to fully utilize the structural information present in a given protein backbone. First, disulfide bonds exist in many proteins, but in EvoEF there is no term to model the possible formation of disulfide bonds. Since the length of a disulfide bond is around 2 Å, which is much less than the sum of the van der Waals radii of two sulfur atoms, possible disulfide-bond configurations in EvoEF may incur large clash penalties. Hence, we consider explicitly modeling disulfide bonds in EvoEF2. Second, the 20 canonical amino acids have different side-chain groups, and for the same amino acid, there may exist different rotamers. The different amino acids and rotamers exhibit distinct propensities and may occur at various frequencies at different protein backbone positions. To model this propensity, we introduced amino acid propensity, Ramachandran, and rotamer probability terms into EvoEF2. The complete EvoEF2 energy function is written as

$$\begin{gathered} E_{\text{EvoEF2}}=E_{\text{VDW}}+E_{\text{ELEC}}+E_{\text{HB}}+E_{\text{DESOLV}}+E_{\text{SS}} \\ +E_{\text{AAPP}}+E_{\text{RAMA}}+E_{\text{ROT}}-E_{\text{REF}} \end{gathered}$$ (2)

Here, E_SS describes the disulfide bonding interactions, which are modeled as follows:

$$E_{\mathit{SS}}=\sum _{i,j}{w}_{\mathit{SS}}[0.8{(1-e^{-10(d_{\mathit{ij}}^{S_{\gamma 1}{S}_{\gamma 2}}-2.03)})}^2+0.005{({\theta }_{\mathit{ij}}^{C_{\beta 1}{S}_{\gamma 1}{S}_{\gamma 2}}-{105}^{°})}^2+0.005{({\theta }_{\mathit{ij}}^{C_{\beta 2}{S}_{\gamma 2}{S}_{\gamma 1}}-{105}^{°})}^2+(\cos (2{\chi }_{\mathit{ij}}^{C_{\beta 1}{S}_{\gamma 1}{S}_{\gamma 2}{C}_{\beta 2}})+1)+1.25\sin ({\chi }_{\mathit{ij}}^{C_{\alpha 1}{C}_{\beta 1}{S}_{\gamma 1}{S}_{\gamma 2}}+{120}^{°})-1.75+1.25\sin ({\chi }_{\mathit{ij}}^{C_{\alpha 2}{C}_{\beta 2}{S}_{\gamma 2}{S}_{\gamma 1}}+{120}^{°})-1.75]$$ (3)

where w_SS is the weight factor, atom pair i and j represent the two S_γ atoms from two different cysteines, $d_{\mathit{ij}}^{S_{\gamma 1}{S}_{\gamma 2}}$ is the distance between them, ${\theta }_{\mathit{ij}}^{C_{\beta 1}{S}_{\gamma 1}{S}_{\gamma 2}}$ is the angle between atoms C_β1, S_γ1, and S_γ2, ${\theta }_{\mathit{ij}}^{C_{\beta 2}{S}_{\gamma 2}{S}_{\gamma 1}}$ is the angle between atoms C_β2, S_γ2, and S_γ1, ${\chi }_{\mathit{ij}}^{C_{\beta 1}{S}_{\gamma 1}{S}_{\gamma 2}{C}_{\beta 2}}$ is the torsion angle between atoms C_β1, S_γ1, S_γ2, and C^β2, ${\chi }_{\mathit{ij}}^{C_{\alpha 1}{C}_{\beta 1}{S}_{\gamma 1}{S}_{\gamma 2}}$ is the torsional angle between atoms C_α1, C_β1, S_γ1, and S_γ2, and ${\chi }_{\mathit{ij}}^{C_{\alpha 2}{C}_{\beta 2}{S}_{\gamma 2}{S}_{\gamma 1}}$ is the torsional angle between atoms C_α2, C_β2, S_γ2, and S_γ1. The distance $d_{\mathit{ij}}^{S_{\gamma 1}{S}_{\gamma 2}}$ must be within [1.95, 2.15] in order to calculate E_SS(i, j), and E_SS(i, j) = 0 if E_SS(i, j) > 0 or $d_{\mathit{ij}}^{S_{\gamma 1}{S}_{\gamma 2}}\notin [1.95,2.15]$.

E_AAPP represents the energy for calculating amino acid propensities at given backbone angles (ϕ/ψ) by

$$E_{\mathrm{AAPP}}=\sum _{1\le l\le L}-w_{\mathrm{aapp}}\ln \frac{P(a{a}_l|{\varphi }_l,{\psi }_l)}{P(a{a}_l)}$$ (4)

where w_aapp is the weight parameter, l is the design position, aa_l and (ϕ_l, ψ_l) are the amino acid type and backbone torsional angles at position l, respectively. P(aa_l|ϕ_l, ψ_l) and P(aa_l) are the probabilities of observing amino acid aa_l at a given (ϕ_l, ψ_l) and any backbone torsional angle, respectively. The statistics were obtained from the Top8000 data set³⁵ using a grid step of 10° for ϕ and ψ. Following a similar strategy to ref 14 for the N-terminal residue and other residues whose ϕ angle cannot be determined by the backbone (due to missing backbone atoms), ϕ is set to −60°, and similarly, for the C-terminal residue and other residues whose ψ angle cannot be determined by the backbone (due to missing backbone atoms), ψ is set to 60°. This is also applicable to the calculation of E_RAMA and E_ROT.

E_RAMA is the Ramachandran term for choosing specific backbone angles (ϕ, ψ) given a particular amino acid:

$$E_{\text{RAMA}}=\sum _{1\le l\le L}-w_{\mathrm{rama}}\ln P({\varphi }_l,{\psi }_l|a{a}_l)$$ (5)

where w_rama is the weight parameter. This term is used to calculate how suitable the backbone (ϕ_l, ψ_l) is given aa_l. The statistics were obtained using the same data set and grid step mentioned above.³⁵

Finally, E_ROT is the energy term for modeling the rotamer probabilities from a Dunbrack BBDRL:

$$E_{\text{ROT}}=\sum _{1\le l\le L}-w_{\mathrm{rot}}\ln P(ro{t}_l|{\varphi }_l,{\psi }_l)$$ (6)

where w_rot is the corresponding weight, l is the design position, (ϕ_l, ψ_l) is the backbone torsional angle at position l. P(rot_l|ϕ_l, ψ_l) is the probability of seeing rotamer rot_l at a given (ϕ_l, ψ_l) for an amino acid type, which is directly taken from the Dunbrack 2010 BBDRL²¹ without further modification. To evaluate E_ROT for a native rotamer (see Results), we calculate its side-chain dihedrals and check if they are reproduced by the rotamer dihedrals taken from the BBDRL. If reproduced, the native rotamer is assigned the probability of the library rotamer. If not, a very low probability of 10⁻⁷ is assigned to the native rotamer, which results in a large positive E_ROT value. E_ROT = 0 for rotamers from the Honig BBIRLs because no rotamer probability information can be obtained from these libraries.

EvoEF was originally optimized and tested on two large sets of thermodynamic mutation data,³ but we found that using this strategy to optimize EvoEF resulted in poor performance on de novo sequence design. We therefore reoptimized EvoEF2 for protein design using a procedure similar to the one-at-a-time approach used by Rosetta.³⁸ Specifically, the weights for each energy term and the 20 reference energies were determined by maximizing the product of e^{−E_min(AA_nat|w)}/∑e^{−E_min(AA_i|w)} across all of the residues positions on a training set of 222 monomers using a gradient descent optimization procedure, where E_min(AA_nat|w) was the energy of the best rotamer for the native amino acid, AA_nat, given the weight set, w, E_min(AA_i|w) was the energy of the best rotamer for amino acid AA_i using the same weight set, w, and the partition function was over all 20 amino acids at each position. The 222 monomers shared <30% sequence identity to any of the 136 test monomers in this work. The rotamers were taken from the Dunbrack 2010 BBDRL L3 (see Results)²¹ or the Honig BBIRL L4 (see Results).²² The energies for the rotamers at each position were calculated in the context of fixed surrounding residues. The determined weights and reference energies were then refined based on the results of complete sequence design for the same training proteins to reduce the deviation of the 20 amino acid distributions between the designed sequences and the native sequences. Similarly, optimization of the weights for interchain interactions was first determined by maximizing the product of e^{−E_min(AA_nat|w)}/∑_i e^{−E_min(AA_i|w)} over the interface residues positions on a training set of 132 dimers, where the weights for the monomeric energy terms and reference energies were fixed. The weights were also refined by complete PPI sequence design simulations for the 132 dimers. The EvoEF2 energy weights and reference energies for the BBDRLs and BBIRLs are listed in Tables S1 and S2, respectively. The source code for EvoEF2 and the SAMC searching method (see below) for side-chain prediction and de novo sequence design, as well as the benchmark data sets are available free of charge at https://zhanglab.ccmb.med.umich.edu/EvoEF/.

Protein Sequence Design and Assessment.

We extended the EvoDesign Monte Carlo (MC) pipeline³ to test the ability of EvoEF2 to perform protein design. Starting from a random sequence, a SAMC³⁰ procedure was used to explore the sequence space for fixed protein backbones, where an MC move consisted of exchanging one rotamer for another at a randomly chosen position. All amino acid types were considered at each design position and their side-chain conformations were taken from any of the rotamer libraries L1–L6. A move was accepted or rejected according to the Metropolis rule, where the acceptance probability for an unfavorable energy increase, ΔE, was e^−ΔE/T. The temperature T was varied from T_high = 5 to T_low = 0.01 with a decrease factor of 0.8, and three SAMC cycles were performed for the sake of convergence. We did not use a protein length-dependent temperature because ΔE did not exhibit strong length dependency. The number of MC moves at each temperature was set to 50 000. Because MC-based methods do not guarantee the global optimum solution, for a given scaffold, we performed five independent simulations starting from different random sequences and selected the lowest energy sequence as the final design and compared it with the native. The SAMC simulation procedure converged well and in almost all cases the sequences obtained from different runs shared >85% sequence identity with similar energies, and the designed sequences in the core regions were nearly identical.

The ability to produce nativelike sequences is an important metric for a protein design algorithm. Therefore, we calculated the sequence identity between each designed sequence and its native counterpart and evaluated the native sequence recapitulation rates for all 20 amino acid types and residues in all, core and surface regions. To further test the design quality, we used I-TASSER³² to examine the foldability of the designed sequences.

Protein Side-Chain Prediction and Assessment.

The protein side-chain prediction procedure was similar to the protein sequence design strategy described above. The major difference between the two is that the amino acid types were held constant and only the side-chain conformations could change at each position for side-chain prediction. Rotamers were taken from libraries L1–L6. We performed five independent side-chain prediction trials and reported the average accuracies and standard deviations.

The accuracy of side-chain prediction is usually assessed in terms of dihedral angle deviations or RMSD values between the predicted and native conformations. Most of the time, the two metrics are not consistent with each other, so both were used in this work. When analyzing dihedral angle deviations, usually only the χ₁ and χ₁₊₂ dihedral angles are considered and a dihedral angle is regarded as being predicted correctly if its value is within 40° of that of the native structure. However, it seems to be relatively easy to achieve a good accuracy (>85% for χ₁ and >70% for χ₁₊₂ with this loose criteria,¹ covering up the difficulty of the side-chain prediction problem. Here, we employed the same criteria used to analyze side-chain reproduction to examine the side-chain prediction accuracy. Specifically, we considered all dihedral angles (χ₁ for Cys, Ser, Thr, and Val, χ₁₊₂ for Asp, Phe, His, Ile, Leu, Asn, Pro, Trp, and Tyr, χ₁₊₂₊₃ for Glu, Met, and Gln, χ_1+2+3+4 for Lys and Arg) and a side-chain was regarded as being predicted correctly if all of its dihedral angle values were within 20° of that of the native structure. The calculation of RMSD between the predicted and native conformations was also identical to that for the side-chain reproduction analysis and the overall RMSDs are reported.

RESULTS

Rotamer Libraries.

The original Dunbrack 2010 BBDRL and two derivatives of it, as well as three detailed Honig BBIRLs were used in this study (Table 1). The libraries are denoted with shorter codes for enhanced clarity (L1–L6). The original Dunbrack 2010 BBDRL (L1) has 726 939 rotamers when considering all 1296 10° × 10° ϕ/ψ bins, with on average 561 rotamers per bin. Two derivatives were created by removing the rotamers whose probabilities were below 1% and 3%, as given in the library, and denoted as L2 and L3, respectively. Here, the strategy of excluding rarely seen rotamers is similar to refs 33 and 36, where it was reported that removal of these rotamers had a negligible effect on protein design accuracy but showed much faster speed. L2 and L3 had 260 500 and 157 190 rotamers in total (on average 201 and 121 per bin), respectively. For the BBDRLs, since each position is indexed into one 10° × 10° bin depending on the ϕ/ψ angles at that position, in a protein design problem, the total number of rotamers for any give position is about 561, 201, or 121 when using L1, L2, or L3, respectively. The three Honig libraries are denoted as L4–L6 and consist of 3222, 7421, and 11 810 rotamers, respectively. It is worth noting that the Honig BBIRLs do not contain rotamer probabilities or deviations of side-chain dihedral angles as the Dunbrack libraries do because the two classes of libraries were constructed using different approaches and the rotamers in the Honig libraries do not always lie at local energy minima.²² In this study, we did not expand rotamer libraries L1–L6 by varying the χ₁ and χ₁₊₂ dihedral angles as reported in some other studies.^39–41

Table 1.

Overview of the Six Rotamer Libraries Used in This Work

rotamer library	number of rotamers	refs
L1: Dunbrack2010BBdep	726939 (561 per bin)	Shapovalov and Dunbrack21
L2: Dunbrack2010BBdep1per	260500 (201 per bin)	Shapovalov and Dunbrack21
L3: Dunbrack2010BBdep3per	157190 (121 per bin)	Shapovalov and Dunbrack21
L4: Honig3222	3222	Xiang and Honig22
L5: Honig7421	7421	Xiang and Honig22
L6: Honig11810	11810	Xiang and Honig22

Native Side-Chain Reproduction.

The native side-chain reproduction accuracy, in terms of dihedral angle deviation and side-chain RMSD for the 136 structures, is shown in Figure 1. The BBDRL L3 and BBIRL L6 showed the lowest and highest reproduction rates for all, core and surface residues, respectively, where L4–L6 reproduced almost all of the side-chains (Figure 1a), which is in agreement with the statistics by Pupo and Moreno.²⁸ The difference between the reproduction rates for the three categories is quite large for libraries L1–L3 but is negligible for L4–L6. For each rotamer library, the highest reproduction rates were observed in the core, while the lowest were observed at the surface, probably because core residues are more constrained and, thus, more easily recapitulated. The original Dunbrack BBDRL, L1, reproduced 88.5%, 93.8%, and 83.8% of all, core, and surface residues, respectively, where the reproduction rates decreased across all three categories when rotamers whose probabilities were <1% (L2) or <3% (L3) were excluded. Using L2, the reproduction rates decreased by 1.6% in the core and 4.4% at the surface, while using L3 caused the rates to decrease by 5.1% and 10.4% in the core and surface, respectively, suggesting that rare rotamers more frequently occur on the surface of proteins. The Honig BBIRLs L4–L6 showed much higher reproduction rates at the expense of considerably increasing the number of rotamers at each position. The largest BBIRL, L6, reproduced 99.4%, 99.8%, and 99.0% of all, core, and surface residues, respectively, in terms of side-chain dihedral angles.

Figure 1.

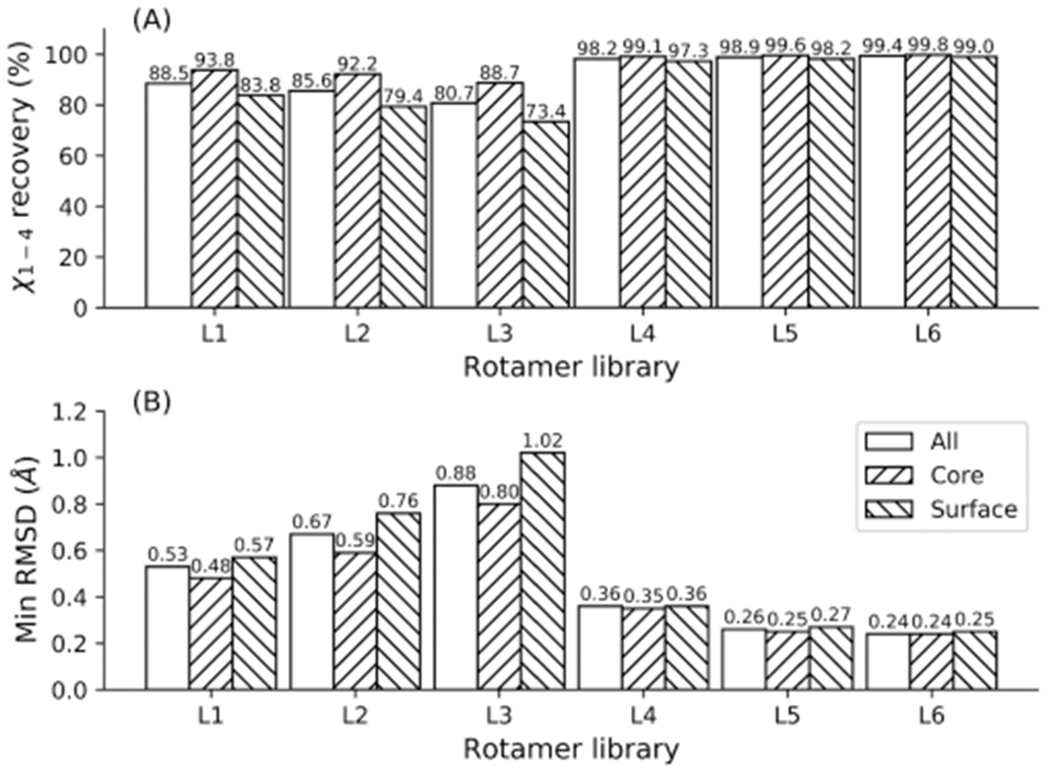
Dihedral angle (χ_1–4) reproduction rates (a) and the minimal side-chain RMSD achievable (b) using rotamer libraries L1—L6 on 136 proteins.

Having significant dihedral angle deviation does not necessarily imply that there are significant differences in spatial geometrical coordinates, since in some cases the individual differences in χ angles may compensate for each other, rendering the overall position of the calculated side-chains close to the native. Therefore, we also measured the minimum overall RMSD that could be achieved between the native geometry and a rotamer from each library. As shown in Figure 1b, the BBIRLs L4-L6 reproduced the side-chain geometrical coordinates much better than BBDRLs L1-L3 with lower RMSDs. For example, the minimum side-chain RMSDs obtained by L6 were less than half those achieved by L1.

To check whether the above statistics were biased due to the relatively small number of structures tested (136 proteins), we tested the side-chain reproduction performance of each library using another larger set of 3719 structures, where the results are presented in Figure S1. Similar results were obtained in terms of both χ angle deviation and RMSD, suggesting the statistics for the 136 proteins are representative. Therefore, we conclude that the selected BBIRLs (L4–L6) are more complete than the BBDRLs (L1–L3) for native side-chain reproduction.

Protein Side-Chain Prediction.

The reproduction rate by a rotamer library can be regarded as the maximum accuracy level achievable by a PSCP algorithm using an identical library, due to the fact that identical criteria is used to evaluate side-chain reproduction and prediction in this work. For instance, the maximum level of dihedral angle recovery should be ≤88.5%, 93.8%, and 83.8% for all, core, and surface residues, respectively, when library L1 is used. Meanwhile, the overall RMSD between the packed structures and native should be ≥0.53, 0.48, and 0.57 Å for all, core, and surface residues, respectively. It is desirable to approach these limits for a side-chain prediction task. To the best of our knowledge, we are the first to use both the strict criterion of 20° and consider the recovery of all side-chain dihedral angles at the same time. To know where our method stands, as a comparison, we performed side-chain prediction using three state-of-the-art programs, SCWRL4,¹⁴ CISRR,¹⁵ and RASP,¹⁷ which were specifically developed for this task; all of them use library L1 for PSCP.

The prediction accuracy in terms of dihedral angle recovery and side-chain RMSD are summarized in Table 2. Overall, the performance of SCWRL4, CISRR, and RASP are comparable; SCWRL4 achieved the highest overall χ angle recovery rate of 62.3%, while in the core CISRR performed the best with a recovery rate of 81.4%. It can be seen that the two metrics are not always consistent as mentioned above (Table 2), i.e., the highest χ angle recovery rate does not always correspond to the lowest RMSD. Among the three programs, CISRR achieved the lowest RMSDs for all, core and surface residues. With a stricter criterion of 20° and all χ angles considered, the overall dihedral angle recovery rates obtained here are much lower than those reported in literature,^14,15,17 where a loose criterion of 40° and only χ₁ and χ₁₊₂ were considered. A huge gap exists between the overall dihedral angle recovery rates (61.1–62.3%) and the maximum achievable reproduction rate (88.5%) using library L1. Similarly, the lowest overall RMSDs obtained by CISRR were much higher than the best reproduced RMSDs by L1 (e.g., 1.68 vs 0.53 Å for all residues, 0.91 vs 0.48 Å for core residues and 2.15 vs 0.57 Å for surface residues). It seems that the difficulty of the side-chain prediction problem has been underestimated using loose criteria for success. The current state-of-the-art PSCP programs are in general good but not perfect.¹

Table 2.

Dihedral Angle Recovery Rates for Side-Chain Prediction on 136 Structures Using Rotamer Libraries L1—L6^a

		χ1–4 recovery rate (%)			overall side-chain RMSD (Å)
method	library	all	core	surface	all	core	surface
CISRR	L1	61.8 ± 0.0	81.4 ± 0.0	46.4 ± 0.0	1.68 ± 0.00	0.91 ± 0.00	2.15 ± 0.00
RASP	L1	61.1 ± 0.0	78.7 ± 0.0	47.2 ± 0.0	1.72 ± 0.00	1.01 ± 0.01	2.16 ± 0.00
SCWRL4	L1	62.3 ± 0.0	81.0 ± 0.0	47.3 ± 0.0	1.70 ± 0.00	0.95 ± 0.00	2.18 ± 0.00
EvoEF2	L1	60.0 ± 0.1	79.1 ± 0.3	44.2 ± 0.3	1.66 ± 0.01	0.97 ± 0.01	2.12 ± 0.01
EvoEF2	L2	59.3 ± 0.1	77.8 ± 0.3	44.0 ± 0.3	1.69 ± 0.01	1.10 ± 0.02	2.13 ± 0.02
EvoEF2	L3	58.5 ± 0.2	75.9 ± 0.2	43.9 ± 0.3	1.76 ± 0.01	1.27 ± 0.01	2.14 ± 0.01
EvoEF2	L4	34.4 ± 0.4	56.0 ± 0.7	18.1 ± 0.4	1.92 ± 0.02	1.14 ± 0.03	2.44 ± 0.01
EvoEF2	L5	37.8 ± 0.3	60.4 ± 0.7	20.2 ± 0.3	1.82 ± 0.01	1.01 ± 0.01	2.37 ± 0.01
EvoEF2	L6	36.7 ± 0.3	59.2 ± 0.8	19.5 ± 0.5	1.84 ± 0.01	1.01 ± 0.02	2.39 ± 0.01

^aThe best performance in each column is shown in bold. Each program was run five times using any of the six rotamer libraries, and the average and standard deviation are reported.

The side-chain prediction performances using libraries L1–L3 were significantly better than those obtained using L4–L6, with much higher dihedral angle recovery rates and lower RMSDs (Table 2), although L4–L6 showed much higher completeness (Figure 1). For example. The worst BBDRL, L3, achieved an overall dihedral angle recovery rate of 58.5% and an RMSD of 1.76 Å, while the best BBIRL, L5, obtained a dihedral angle recovery rate of 37.8% and an RMSD of 1.82 Å. L1 yielded the best performance among the BBDRLs, while L5 performed the best among the BBIRLs, suggesting it is necessary to include the rare rotamers to achieve better accuracy. The best side-chain prediction accuracy for EvoEF2, in terms of dihedral angle recovery rates, was achieved by employing library L1, where 60.0%, 79.1%, and 44.2% of all, core, and surface residue side-chains were recapitulated. These values were quite comparable to those achieved by SCWRL4, CISRR, and RASP (Table 2) and, in fact, EvoEF2 obtained even lower overall side-chain RMSDs than the other three state-of-the-art methods (e.g., EvoEF2: 1.66 Å, CISRR: 1.68 Å, SCWRL4: 1.70 Å, and RASP: 1.72 Å), suggesting that EvoEF2 captures the overall PSCP geometries slightly better than them. It is worth pointing out that EvoEF2 was optimized for sequence design rather than side-chain prediction, as the other programs were, but our results demonstrate that EvoEF2 is generally applicable to side-chain prediction.

Native Sequence Recapitulation.

Native sequence recapitulation is an important metric for evaluating the performance of protein design algorithms.^{33,36,38,40–44} We used EvoEF2 to perform de novo sequence design simulations on the 136 selected proteins using rotamer libraries L1–L6 and compared the sequence design performance for each library. The native sequence recapitulation results are described in Figure 2a. Remarkably, a high percentage (>27%) of all residues were identical to the amino acids in the corresponding positions in the native sequences for libraries L1–L6, which is quite comparable to or even better than the performance achieved by some other programs for de novo sequence design.^36,45–47 However, all of these algorithms use more informative BBDRLs, and to our knowledge, this work is the first to report the ability to recapitulate the native sequences to such a high extent using both BBDRLs and BBIRLs, supporting the accuracy of our energy function and protein design method.

Figure 2.

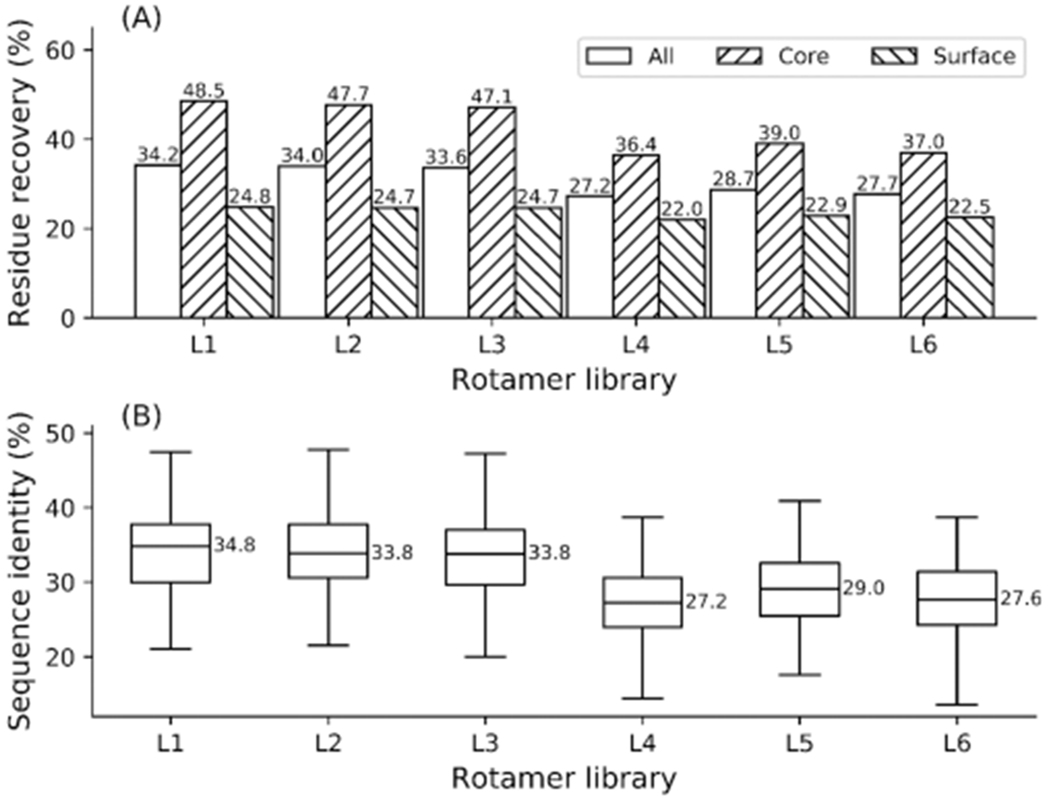
Native sequence recapitulation (a) on 136 proteins and the distribution of sequence identities (b) between the native and designed sequences obtained using rotamer libraries L1—L6.

The BBDRLs outperformed BBIRLs by recapitulating more naturally occurring residues. The highest overall sequence recovery rates were achieved by library L1, followed by L2 and L3 (Figure 2a). Using L1, EvoEF2 recapitulated 34.2%, 48.5%, and 24.8% of all, core, and surface residues, respectively, which is comparable to the state-of-the-art protein design software, Rosetta,⁴⁰ when subrotamers are not included. We also evaluated the sequence identity between the designed and native sequences (Table S3), which is a different metric than the sequence recapitulation rate. The statistical distribution of sequence identities by libraries L1–L6 are illustrated in Figure 2b. The median sequence identity was close to the native sequence recapitulation rate for all residues (e.g., the median sequence identity for L1 was 34.8%), and the distribution of sequence identities by L1–L3 was quite similar. With respect to the BBIRLs, L5 yielded the highest native sequence recapitulation rates by recovering 28.7%, 39.0%, and 22.9% of all, core, and surface residues, respectively, with a median sequence identity of 29.0%.

Foldability Assessment of the Designed Sequences.

Protein design aims to create new protein molecules that adopt specific folds and perform desired biological functions. Therefore, it is important to examine to what extent a designed sequence can fold into the scaffold structure on which the design was performed. High native sequence similarity does not necessarily guarantee the designs are of high quality. To further examine the design quality, we used the state-of-the-art protein structure prediction suite, I-TASSER,³² to test the foldability of the designed sequences and to examine how close the predicted models were to the native scaffolds. The sequences designed using libraries L1–L6 with the lowest EvoEF2 predicted free energies were modeled by I-TASSER in order to assess their foldability. A test protein was defined as foldable if the designed sequence was predicted to fold into a structure with a TM-score⁴⁸ to the native scaffold structure greater than a specified threshold, where a TM-score >0.5 indicates that two structures share a similar fold topology.⁴⁹ Alternatively, RMSD was also used to calculate the similarity between two structures, and generally, two structures share a similar fold when the RMSD is <4 Å.⁴⁷ The TM-scores and RMSDs between the 136 predicted and native proteins for libraries L1–L6 are listed in Tables S4 and S5, respectively. The TM-scores and RMSDs as a function of sequence identity between the designed and native sequences are illustrated in Figures S2 and S3, respectively.

We used three TM-score thresholds, >0.5, >0.7, and >0.9 and three RMSD cutoffs, <4, <2, and <1 Å for the foldability assessment, where the results are summarized in Table 3. Generally, more than 96% of the proteins designed using libraries L1–L6 were predicted to fold into structures with TM-scores >0.5 or, alternatively, RMSDs < 4 Å to their native counterparts, thereby suggesting that all of the tested libraries are reasonably good for sequence design. Nevertheless, on average, higher percentages of proteins designed using BBDRLs were predicted to be foldable, and this became more evident when using stricter RMSD thresholds. For example, when we set the RMSD threshold to <2 Å, which is a reasonable upper bound for regarding protein design as successful,^50,51 94.1%, 93.4%, 94.1%, 86.0%, 90.4%, and 91.9% of the designs using libraries L1–L6 passed this criterion, respectively. Moreover, about 20% less of the designs were predicted to fold into structures within 1 Å of their corresponding native scaffold on which design was performed. According to the I-TASSER assessment results, BBDRLs are better at producing foldable designs than BBIRLs. It is worth noting that different protein structure prediction packages have different search algorithms and energy functions,^52–55 which may lead to discrepancies in terms of foldability assessment. One important reason for using I-TASSER in this study is that the designed sequences shared very high sequence identities to their native counterparts and, therefore, template-based structure modeling from methods such as I-TASSER should be relevant for such assessments.

Table 3.

Percentage of Designed Sequences That Were Predicted to Fold within the Given TM-Score and RMSD Thresholds Using Rotamer Libraries L1—L6^a

	Success Rate (%)
	TM-score			RMSD
library	>0.5	>0.7	>0.9	<4 Å	<2 Å	<1 Å
L1	100.0	98.5	89.7	98.5	94.1	74.3
L2	98.5	98.5	89.0	98.5	93.4	73.5
L3	100.0	98.5	91.1	99.3	94.1	72.8
L4	98.5	95.6	86.0	96.3	86.0	66.9
L5	98.5	97.8	89.0	96.3	90.4	72.1
L6	98.5	97.1	89.0	97.1	91.9	69.1

^aThe best performance in each column is shown in bold.

Computational Time.

The trade-off between accuracy and speed should be considered for PSCP. When not using the native conformer, the best side-chain prediction and de novo sequence design accuracy was obtained by L1 for the BBDRLs and L5 for the BBIRLs. In general, the larger the rotamer library is, the longer time it takes to perform PSCP. The computational time required to perform side-chain prediction and de novo sequence design on the 136 proteins using libraries L1–L6 is presented in Figure 3; each structure was repacked and completely designed using a single 2.50 GHz Intel Xeon CPU on the Extreme Science and Engineering Discovery Environment (XSEDE) cluster.⁵⁶

Figure 3.

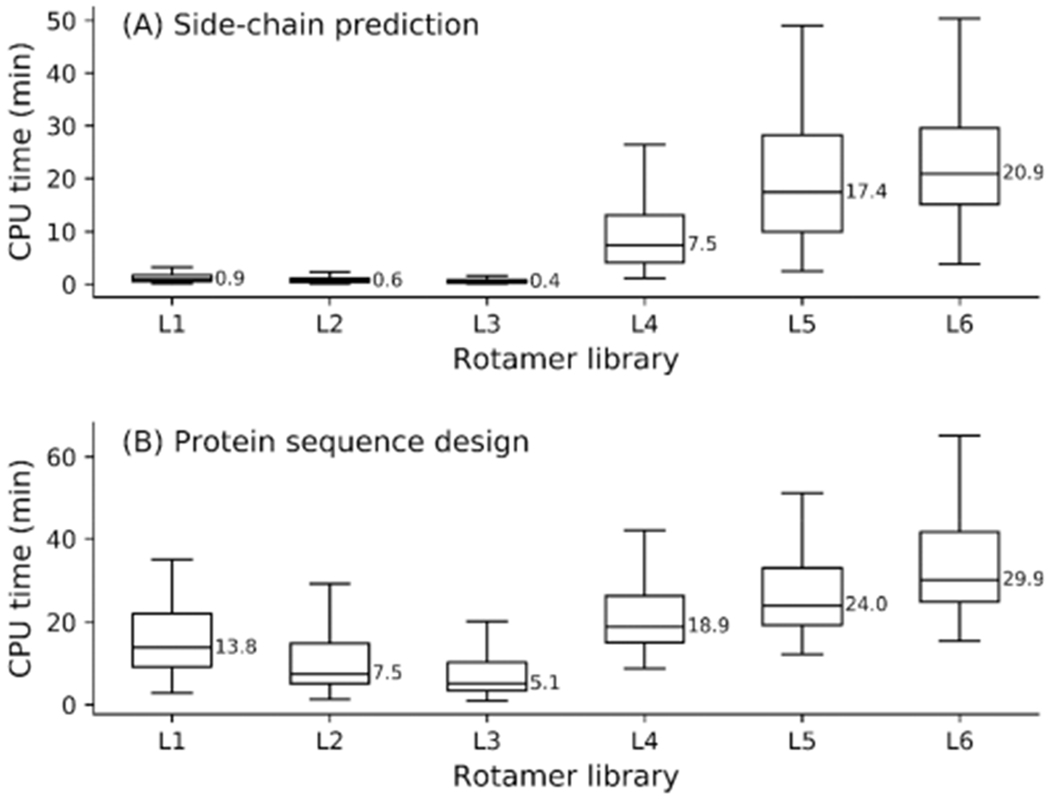
Average CPU time for side-chain prediction (a) and de novo sequence design (b) on 136 proteins.

The median time required for side-chain prediction using L1–L3 were 0.9, 0.6, and 0.4 min, respectively, which were all much shorter than the time consumed by L4–L6 for the same task (Figure 3a). Although it is very efficient for EvoEF2 to repack the residue side-chains of a structure using L1–L3, it is still much slower than SCWRL4, CISRR, and RASP, which were specifically designed for this task. The most efficient method, RASP, can finish repacking each of the 136 structures within one second, while still yielding quite reasonable results. These packing programs use very simple energy functions and efficient heuristic optimization strategies to search for good solutions instead of exhaustively probing the global energy minimum using a global optimization technique like SAMC. With respect to de novo sequence design, the median times used to completely design the 136 structures were 13.8, 7.5, and 5.1 min using BBDRLs L1, L2, and L3, respectively, which were all much shorter than the times required to perform sequence design using BBIRLs L4–L6 (Figure 3b). Additionally, the SAMC optimization method used here is much faster than deterministic searching algorithms (e.g., dead-end elimination⁷ and mixed-integer linear programming²⁶) for protein design. In short, when using EvoEF2, BBDRLs are more advantageous than BBIRLs for efficient and effective side-chain prediction and protein design.

Advantage of Using Rotamer Probabilities from BBDRLs.

From the above results, we can see that the BBDRLs considerably outperformed the BBIRLs in both side-chain prediction and de novo sequence design with shorter computational time following the same computational procedure. We note that a big difference between the BBDRLs and the detailed BBIRLs is that the BBDRLs provide rotamer probabilities as well as the rotamer dihedral angle values. In the side-chain prediction and sequence design experiments with BBDRLs, an energy term (i.e., E_ROT in EvoEF2) derived from rotamer probabilities was utilized and the weight of this term was a nonzero value, suggesting rotamer probabilities are important for these experiments. To check the impact of rotamer probability, we also performed side-chain prediction and sequence design for the 136 structures using libraries L1–L3 by disabling the E_ROT term, and the results are shown in Table 4 and Figure 4, respectively. The sequence identities between the native and designed sequences achieved using L1–L3 with E_ROT disabled are listed in Table S6. For all three BBDRLs L1–L3, the side-chain prediction performance was worse when the rotamer probability term was disabled in terms of both the dihedral angle recovery rate and overall side-chain RMSD (Tables 2 and 4), suggesting that the rotamer probability term is important to identify the correct conformations that are close to native. The impact on prediction performance was greater by removal of E_ROT for a larger library (e.g., L1), partly because a larger rotamer library may result in higher difficulty discriminating correct from incorrect conformations.

Table 4.

Dihedral Angle Recovery Rates and Overall RMSDs for Side-Chain Prediction with the Rotamer Probability Term (E_ROT) Disabled on 136 Structures Using Rotamer Libraries L1—L3^a

	χ1–4 recovery rate (%)			overall side-chain RMSD (Å)
library	all	core	surface	all	core	surface
L1	47.7 ± 0.2	70.3 ± 0.2	29.4 ± 0.4	1.95 ± 0.01	1.08 ± 0.01	2.53 ± 0.01
L2	50.2 ± 0.1	71.3 ± 0.2	32.8 ± 0.4	1.80 ± 0.01	1.16 ± 0.01	2.27 ± 0.01
L3	52.7 ± 0.1	72.3 ± 0.3	36.2 ± 0.2	1.81 ± 0.01	1.28 ± 0.01	2.21 ± 0.01

^aThe best performance in each column is shown in bold. Each program was run five times using each of the three BBDRLs (L1–L3), and the average and standard deviation are reported.

Figure 4.

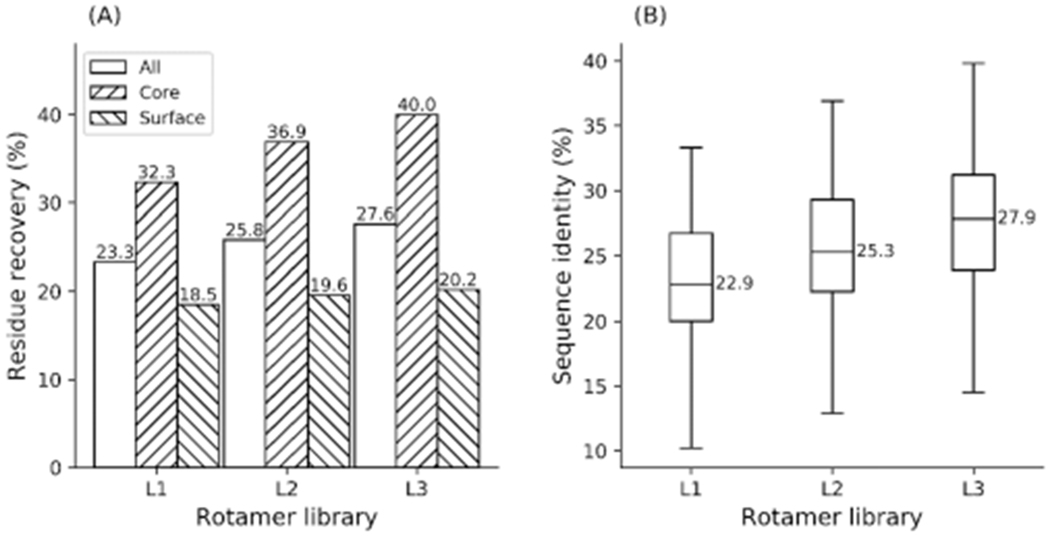
Native sequence recapitulation (a) on 136 proteins and the distribution of sequence identities (b) between the native and designed sequences obtained using rotamer libraries L1—L3 when the rotamer probability term (E_ROT) was disabled.

In terms of dihedral angle recovery rate, L1 performed the worst without E_ROT (Table 4), while it yielded the best performance when this term was considered (Table 2). From Table 4, L1 obtained the lowest RMSD for the core residues but the highest RMSD for the surface residues, while in Table 2, L1 consistently outperformed L2 and L3 by achieving lower RMSDs for residues in all three categories. Bear in mind that libraries L2 and L3 are subsets of L1 with less rotamers, thus all the conformations in L2 and L3 are also included in L1, but L1 has some rare rotamer conformations that are excluded from L2 and L3. Due to the removal of E_ROT, all rotamers in the libraries were considered equally probable, and thus, whether or not a rotamer was chosen at a position was completely determined by the physical interactions between the rotamer and its surrounding context. Since core residues are more constrained and have more contacts with spatially adjacent residues than surface residues, the rotamer conformations of core residues are easier to correctly position based on the physical interactions with one another. In this situation, the library with more abundant rotamers (e.g., L1) yielded lower RMSDs and this explanation can also be partly demonstrated by the side-chain prediction results directly using BBIRLs L4—L6. On the other hand, surface residues, which are more exposed to the bulk solvent, have fewer contacts with other residues and their conformations are not easily determined by the physical energy alone because the solvent molecules are not explicitly modeled in the energy function. In this situation, the near-native conformations were not well identified and usually much higher overall RMSDs were obtained for surface residues whether or not E_ROT was considered (Tables 2 and 4). Another interesting finding is that, compared with libraries L4—L6, the predicted side-chain RMSDs obtained using L1—L3 by removal of E_ROT were quite comparable to those achieved using libraries L4—L6 (Tables 2 and 4).

For protein sequence design, the performance of recapitulating native residues also became much worse using libraries L1—L3 when the rotamer probability term was disabled (Figures 2 and 4). For example, the best performance achieved by L3 with E_ROT disabled, resulted in 27.6%, 40.0%, and 20.2% of all, core, and surface residues being predicted to be identical to the naturally occurring amino acids at the same design positions. But when E_ROT was included, using library L3, the native sequence recapitulation rates for all, core, and surface residues were 33.6%, 47.1%, and 24.7%, respectively. These results emphasize that the energy term derived from rotamer probabilities also plays a significant role in distinguishing amino acid identities for protein sequence design as well as discriminating different rotamer conformations of an amino acid for protein side-chain prediction.

Limitations of Current Rotamer Libraries.

A huge gap exists between the real side-chain prediction performance achieved and the maximum accuracy level attainable. It has been argued that energy functions are the main obstacle to achieving better accuracy.¹ From a different perspective, we show that rotamer libraries have significant influence on the PSCP accuracy (Table 2 and Figure 2). Can we continue improving the PSCP accuracy if we have a better rotamer library? To answer this question, we repeated the side-chain prediction and sequence design experiments using libraries L1—L6 but added the native conformer at each position, where the results are presented in Table 5 and Figure 5, respectively. The sequence identities between the native and designed sequences using experimental rotamers is listed in Table S7.

Table 5.

Dihedral Angle Recovery Rates and Overall RMSDs for Side-Chain Prediction on 136 Structures by Adding Native Conformers to Rotamer Libraries L1–L6^a

	χ1–4 recovery rate (%)			overall side-chain RMSD (Å)
library	all	core	surface	all	core	surface
L1	72.6 ± 0.2	91.0 ± 0.2	55.5 ± 0.3	1.39 ± 0.00	0.62 ± 0.02	1.92 ± 0.01
L2	74.7 ± 0.2	93.0 ± 0.2	57.4 ± 0.2	1.30 ± 0.01	0.48 ± 0.03	1.83 ± 0.02
L3	77.0 ± 0.1	93.9 ± 0.2	60.7 ± 0.1	1.22 ± 0.01	0.43 ± 0.01	1.72 ± 0.02
L4	45.7 ± 0.4	72.3 ± 0.4	24.5 ± 0.4	1.72 ± 0.01	0.78 ± 0.02	2.31 ± 0.01
L5	43.2 ± 0.2	68.5 ± 0.3	23.1 ± 0.2	1.73 ± 0.01	0.83 ± 0.02	2.33 ± 0.01
L6	41.2 ± 0.3	61.1 ± 0.3	21.8 ± 0.5	1.76 ± 0.01	0.86 ± 0.01	2.35 ± 0.01

^aThe best performance in each column is shown in bold. Each program was run five times using any of the six rotamer libraries, and the average and standard deviation are reported.

Figure 5.

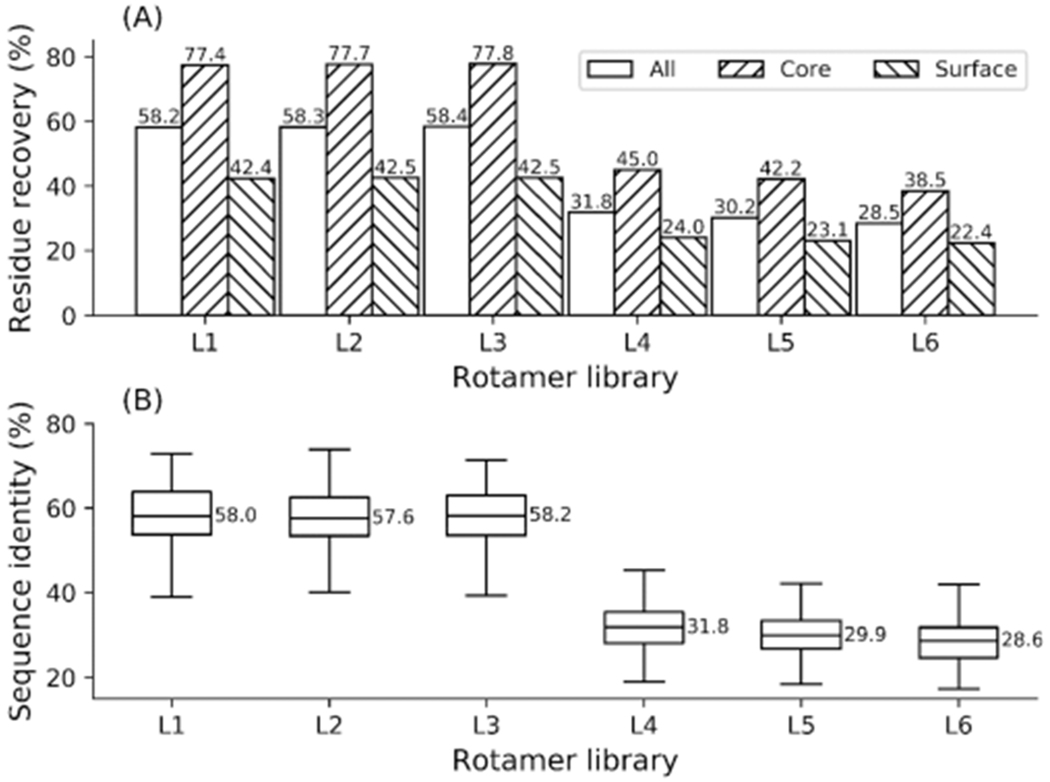
Native sequence recapitulation (a) on 136 proteins and the average sequence identity (b) between the native and designed sequences achieved by adding native conformers to rotamer libraries L1—L6.

Remarkably, the side-chain prediction and native sequence recapitulation performance drastically improved when the native conformers were included. For example, using the BBDRL L1, the dihedral angle recovery rate for side-chain prediction improved from 60.0% to 72.6% for all residues. Similarly, the native sequence recapitulation rate for all residues improved from 34.2% to 58.2%, which is the highest native sequence recapitulation rate reported to date. Similarly, using the BBIRL L4, the dihedral angle recovery rate for side-chain prediction improved from 34.4% to 45.7% for all residues, while the native sequence recapitulation rate for all residues improved from 27.2% to 31.8%.

These results demonstrate that the current rotamer libraries are still limited, as the introduction of native rotamers significantly improved the performance. This can be explained by the fact that non-negligible side-chain deviations were observed between rotamers from libraries and the native conformers (Figure 1). Moreover, in many protein design studies,^33,40 better results were achieved by varying the χ₁ and χ₁₊₂ dihedral angles, suggesting the original rotamer libraries were not perfect. Unlike the experiments without native conformers, where better performance was achieved with larger rotamer libraries (e.g., L1 for the BBDRLs and L5 for the BBIRLs), the best performance was obtained using the smallest libraries (e.g., L3 for the BBDRLs and L4 for the BBIRLs) when the native conformers were added.

DISCUSSION

A rotamer library is one of the three key components of the PSCP problem, which is of great significance in computational and structural biology. Many rotamer libraries have been developed for PSCP applications in protein structure prediction and protein design.^7,18–22 Generally good results have been reported using each of these rotamer libraries.^{3,14,15,17,40,41} This raises the question of which rotamer library yields the best PSCP performance. Additionally, since there is a trade-off between accuracy and speed, which rotamer library should be chosen for effective and efficient PSCP? Although Dunbrack suggested using BBDRLs for protein structure prediction and protein design rather than BBIRLs,²⁹ there was no quantitative support demonstrating that BBDRLs outperform BBIRLs. Moreover, the statistical analysis by Pupo and Moreno²⁸ showed that only the high-resolution Honig BBIRLs could reproduce the experimental geometries for most of the peptidic ligands and the atomic interactions between the peptidic ligands and their receptors. Therefore, up until this point, it seemed that it may be more advantageous to use the detailed BBIRLs.

To answer the above questions, we systematically assessed and compared six rotamer libraries in four aspects. In the side-chain reproduction assessment, we found that the detailed Honig BBIRLs considerably outperformed the Dunbrack 2010 BBDRLs by reproducing higher percentages of side-chain dihedral angles using a strict criterion of 20° and achieving lower side-chain RMSDs, suggesting that the BBIRLs are more complete and show broader coverage. This is probably because the Honig BBIRLs were derived to use a small portion of a complete rotamer library to represent a large fraction of the native side-chain conformations that were observed in a set of proteins;²² the approach of creating these BBIRLs is more relevant to the side-chain reproduction task than the method to build BBDRLs by conformational clustering.¹⁴ In the side-chain prediction and de novo sequence design tests, which are more important for real applications, the BBDRLs considerably outperformed the BBIRLs by recovering more side-chain conformations with better geometries and recapitulating more native residue identities. The independent foldability assessment by I-TASSER³² also suggests that BBDRLs show a better ability to produce proteins that can fold into the same structure as their native counterparts. Moreover, it takes much less time to perform PSCP studies using BBDRLs than BBIRLs. Therefore, it seems that the BBIRLs are only better for side-chain reproduction statistics but not as good as BBDRLs for real side-chain prediction and protein design applications.

This raises the question of why the broader coverage of BBIRLs does not benefit the side-chain prediction and de novo sequence design tasks. A major difference between BBIRLs and BBDRLs is that the rotamer probability information is not considered in BBIRLs because of the different strategies used for library construction and the existence of high-energy rotamers,²² which may be physically unfavorable.²⁹ Moreover, the detailed BBIRLs are very likely to be highly redundant as they include a large number of geometrically similar conformations. The high redundancy and large sizes of BBIRLs can result in great difficulty when it comes to discriminating near-native rotamers from non-native rotamers at a given position, as demonstrated by the decrease in performance when using the larger library L6 as opposed to L5. Therefore, the quality of the BBIRLs may not be as good as the Dunbrack BBDRLs, even though they include more rotamers for any given position in a protein. When the native conformers were added to libraries L1—L6, where all libraries had identical and complete side-chain coverage but different sizes, the performance of each library on side-chain prediction and protein design improved remarkably, where the best performance was achieved using the smallest BBDRL L3 and BBIRL L4. This finding implies that the current libraries tested are limited and confirms that large library sizes can increase the difficulty identifying native conformations and may weaken their performance.

CONCLUSION

Our quantitative benchmark results demonstrate that, for real applications like side-chain prediction and de novo protein sequence design, the Dunbrack 2010 BBDRLs significantly outperform the Honig BBIRLs with better prediction performance as well as faster speed, and specifically, compared with the best BBIRL, the overall side-chain dihedral angle prediction rate and native sequence recapitulation rate improve by more than 20% and 5%, respectively, using the best BBDRL. The advantage of using a BBDRL is largely due to the introduction of an energy term derived from the rotamer probabilities given in the library. Therefore, at present, we suggest using the Dunbrack BBDRL for a PSCP task, and in practice, this library has been found very useful for protein structure modeling. Nevertheless, we also report that the current state-of-the-art Dunbrack 2010 BBDRL is still limited because many native-like conformations are missing from the library and introduction of these conformations can improve the side-chain dihedral angle recovery rate and native sequence recapitulation rate by more than 10% and 20%, respectively. With the rapidly increasing number of experimental protein structures, it may be necessary to build new BBDRLs by clustering the side-chain conformations from a larger set of elaborated structures.

ABBREVIATIONS

PSCP

protein side-chain packing

RMSD

root-mean-square-deviation

BBDRL

backbone-dependent rotamer library

BBIRL

backbone-independent rotamer library

MC

Monte Carlo

SAMC

simulated annealing Monte Carlo