Nonparametric variable importance assessment using machine learning techniques

Abstract

In a regression setting, it is often of interest to quantify the importance of various features in predicting the response. Commonly, the variable importance measure used is determined by the regression technique employed. For this reason, practitioners often only resort to one of a few regression techniques for which a variable importance measure is naturally defined. Unfortunately, these regression techniques are often suboptimal for predicting the response. Additionally, because the variable importance measures native to different regression techniques generally have a different interpretation, comparisons across techniques can be difficult. In this work, we study a variable importance measure that can be used with any regression technique, and whose interpretation is agnostic to the technique used. This measure is a property of the true data-generating mechanism. Specifically, we discuss a generalization of the analysis of variance variable importance measure and discuss how it facilitates the use of machine learning techniques to flexibly estimate the variable importance of a single feature or group of features. The importance of each feature or group of features in the data can then be described individually, using this measure. We describe how to construct an efficient estimator of this measure as well as a valid confidence interval. Through simulations, we show that our proposal has good practical operating characteristics, and we illustrate its use with data from a study of risk factors for cardiovascular disease in South Africa.

1 |. INTRODUCTION

Suppose that we have independent observations Z₁, …, Z_n drawn from an unknown distribution P₀, known only to lie in a potentially rich class of distributions $\mathcal{M}$. We refer to $\mathcal{M}$ as our model. Further, suppose that each observation Z_i consists of (X_i, Y_i), where $X_i≔\left(X_{i1},\dots ,X_{ip}\right)\in {ℝ}^p$ is a covariate vector and $Y_i\in ℝ$ is the outcome of interest. It is often of interest to understand the association between Y and X under P₀. To do this, we generally consider the conditional mean function ${\mu }_0≔{\mu }_{P_0}$, where for each $P\in \mathcal{M}$ we define

$${\mu }_P(x)≔E_P(Y\mid X=x).$$ (1)

Estimation of μ₀ is the canonical “predictive modeling” problem. There are many tools for estimating μ₀: classical parametric techniques (eg, linear regression), and more flexible nonparametric or semiparametric methods, including random forests (Breiman, 2001), generalized additive models (Hastie and Tibshirani, 1990), loess smoothing (Cleveland, 1979), and artificial neural networks (Barron, 1989), among many others. Once a good estimate of μ₀ is obtained, it is often of scientific interest to identify the features that contribute most to the variation in μ₀. For any given set s ⊆ {1, …, p} and distribution $P\in \mathcal{M}$, we may define the reduced conditional mean

$${\mu }_{P,s}(x)≔E_P\left(Y\mid X_{-s}=x_{-s}\right),$$ (2)

where for any vector υ and set r of indices the symbol υ_−r denotes the vector of all components of υ with index not in r. Here, the set s can represent a single element or a group of elements. The importance of the elements in s can be evaluated by comparing μ₀ and ${\mu }_{0,s}≔{\mu }_{P_0,s}$. This strategy will be leveraged in this paper.

The analysis of variance (ANOVA) decomposition is the main classical tool for evaluating variable importance. There, μ₀ is assumed to have a simple parametric form. While this facilitates the task at hand considerably, the conclusions drawn can be misleading in view of the high risk of model misspecification. For this reason, it is increasingly common to use nonparametric or machine learning-based regression methods to estimate μ₀; in such cases, classical ANOVA results do not necessarily apply.

Recent work on evaluating variable importance without relying on overly strong modeling assumptions can generally be categorized as being either (i) intimately tied to a specific estimation technique for the conditional mean function or (ii) agnostic to the estimation technique used. The former category includes, for example, variable importance measures for random forests (Breiman, 2001; Ishwaran, 2007; Strobl et al., 2007; Grömping, 2009) and neural networks (see, eg, Olden et al., 2004), and ANOVA in linear models. Among these, ANOVA alone appears to readily allow valid statistical inference. Additionally, it is generally not possible to directly compare the importance assessment stemming from different methods: they usually measure different quantities and thus have different interpretations. The latter category includes, for example, nonparametric extensions of R² for kernel-based estimators, local polynomial regression, and functional regression (Doksum and Samarov, 1995; Yao et al., 2005; Huang and Chen, 2008); the marginalized mean difference, $E_{P_0}\left\{E_{P_0}\left(Y\mid X=x^1,W\right)-E_{P_0}\left(Y\mid X=x^0,W\right)\right\}$ (van der Laan, 2006; Chambaz et al., 2012; Sapp et al.,2014), where x¹ and x⁰ are two meaningful reference levels of X, and W represent adjustment variables; and the mean difference in absolute deviations, $E_{P_0}\left\{\left|Y-{\mu }_0(X)\right|-\left|Y-{\mu }_{0,s}(X)\right|\right\}$ (Lei et al., 2017). Methods in this latter category allow valid inference and have broad potential applicability. The appropriate measure to use depends on the scientific context.

We are interested in studying a variable importance measure that (i) is entirely agnostic to the estimation technique, (ii) allows valid inference, and (iii) provides a population-level interpretation that is well suited to scientific applications. In this work, we study a variable importance measure that satisfies each of these criteria, adding to the class of technique-agnostic measures referenced above. In particular, we consider the ANOVA-based variable importance measure

$${\psi }_{0,s}≔\frac{\int {\left\{{\mu }_0(x)-{\mu }_{0,s}(x)\right\}}^{2}d{P}_0(x)}{va{r}_{P_0}(Y)}.$$ (3)

For a vector υ and a subset r of indices, we denote by υ_r the vector of all components of υ with index in r. Then, we may interpret (3) as the additional proportion of variability in the outcome explained by including X_s in the conditional mean. This follows from the fact that we can express ψ_0,s as

$$\left[1-\frac{E_{P_0}{\left\{Y-{\mu }_0(X)\right\}}^2}{va{r}_{P_0}(Y)}\right]-\left[1-\frac{E_{P_0}{\left\{Y-{\mu }_{0,s}(X)\right\}}^2}{va{r}_{P_0}(Y)}\right],$$

the difference in the population R² obtained using the full set of covariates as compared to the reduced set of covariates only. Thus, the parameter we focus on is a simple generalization of the classical R² measure of importance to a nonparametric model and is useful in any setting in which the mean squared error is a scientifically relevant population measure of predictiveness. This parameter is a function of P₀ alone, in that it describes a property of the true data-generating mechanism and not of any particular estimation method. In this work, we provide a framework for building a nonparametric efficient estimator of ψ_0,s that permits valid statistical inference.

We emphasize that the purpose of the variable importance measure we study here is not to offer insight into the characteristics of any particular algorithm, but rather to describe the importance of variables in predicting the outcome in the population. This is in contrast to common algorithm-specific measures of variable importance. If a tool for interpreting black-box algorithms is desired, other approaches to variable importance may be preferred, as referenced above.

Care must be taken in building point and interval estimators for ψ_0,s when μ₀ and μ_0,s are not known to belong to simple parametric families. In particular, when μ₀ and μ_0,s are estimated using flexible methods, simply plugging estimates of these regression functions into (3) will not yield a regular and asymptotically linear, let alone efficient, estimator of ψ_0,s. In this paper, we propose a simple method that, given sufficiently accurate estimators of μ₀ and μ_0,s, yields an efficient point estimator for ψ_0,s and a confidence interval with asymptotically correct coverage. We show that this method—based on ideas from semiparametric theory—is equivalent to simply plugging in estimates of μ₀ and μ_0,s into the difference in R² values. In Williamson et al. (2020), we generalize this phenomenon and provide results for plug-in estimators of a large class of variable importance measures.

We note that, while variable importance is related to variable selection, these paradigms may have distinct goals. In variable selection, it is typically of interest to create the best predictive model based on the current data, and this model may include only a subset of the available variables. There are many contributions in both technique-specific (see, eg, Breiman, 2001; Friedman, 2001; Loh, 2002) and nonparametric (see, eg, Doksum et al., 2008) selection. The goal in variable importance is to assess the extent to which (subsets of) features contribute to improving the population-level predictive power of the best possible outcome predictor based on all available features. Of course, variable importance can be used as part of the process of variable selection. To highlight the distinction between importance and selection, it may be useful to consider a scenario in which two perfectly correlated covariates X₁ and X₂ are available. Neither covariate has importance relative to the other, but the variables may be highly important as a pair. A variable importance procedure considering individual and grouped features would identify this, whereas a variable selection procedure would likely choose only one of X₁ or X₂ for use in prediction.

This paper is organized as follows. We present some properties of the parameter we consider and give our proposed estimator in Section 2. In Section 3, we provide empirical evidence that our proposed estimator outperforms both the naive plug-in ANOVA-based estimator and an ordinary least squares-based estimator in settings where the covariate vector is low- or moderate-dimensional and the data-generating mechanism is nonlinear. In Section 4, we apply our method on data from a retrospective study of heart disease in South African men. We provide concluding remarks in Section 5. Technical details and an illustration based on the landmark Boston housing data are provided in the Supporting Information.

2 |. VARIABLE IMPORTANCE IN A NONPARAMETRIC MODEL

2.1 |. Parameter of interest

We work in a nonparametric model $\mathcal{M}$ with only restriction that, under each distribution P in $\mathcal{M}$, the distribution of Y given X = x must have a finite second moment for P-almost every x. For given s ⊆ {1, …, p} and $P\in \mathcal{M}$, based on the conditional means (1) and (2), we define the statistical functional

$${\Psi }_s(P)≔\frac{\int {\left\{{\mu }_P(x)-{\mu }_{P,s}(x)\right\}}^{2}dP(x)}{{\mathit{\text{var}}}_P(Y)}$$ (4)

$$=\left[1-\frac{E_P{\left\{Y-{\mu }_P(X)\right\}}^2}{{\mathit{\text{var}}}_P(Y)}\right]-\left[1-\frac{E_P{\left\{Y-{\mu }_{P,s}(X)\right\}}^2}{{\mathit{\text{var}}}_P(Y)}\right].$$ (5)

This is the nonparametric measure of variable importance we focus on. The value of Ψ_s(P) measures the importance of variables in the set {X_j}_j∈s relative to the entire covariate vector for predicting outcome Y under the data-generating mechanism P. Using observations Z₁, …, Z_n independently drawn from the true, unknown joint distribution $P_0\in \mathcal{M}$, we aim to make efficient inference about the true value ψ_0,s = Ψ_s(P₀).

This parameter is a nonparametric extension of the usual ANOVA-derived measure of variable importance in parametric models. We first note that ψ_0,s ∈ [0, 1]. Furthermore, ψ_0,s = 0 if and only if Y is conditionally uncorrelated with every transformation of X_s given X_−s. In addition, the value of ψ_0,s is invariant to linear transformations of the outcome and to a large class of transformations of the feature vector, as detailed in the Supporting Information. As such, common data normalization steps may be performed without impact on ψ_0,s. Finally, ψ_0,s can be seen as a ratio of the extra sum of squares, averaged over the joint feature distribution, to the total sum of squares. The value of ψ_0,s is thus precisely the improvement in predictive performance, in terms of standardized mean squared error, that can be expected if we build a model using all of X versus only X_−s. If we assume simple linear regression models for μ₀ and μ_0,s, then ψ_0,s is precisely the usual difference in R² between nested models.

We want to reiterate here that, in contrast to simple parametric approaches to variable importance, our functional Ψ_s simply maps any candidate data-generating mechanism to a positive number. This definition does not require a parametric specification of μ₀ or μ_0,s. While this is usual for non- or semiparametric inference problems, it is different from classical approaches to variable importance.

For building an efficient estimator of ψ_0,s, it is critical to consider the differentiability of Ψ_s as a functional. Specifically, we have that (4) is pathwise differentiable with respect to the unrestricted model (see, eg, Bickel et al., 1998). Pathwise differentiable functionals generally admit a convenient functional Taylor expansion that can be used to characterize the asymptotic behavior of plug-in estimators. An analysis of the pathwise derivative allows us to determine the efficient influence function (EIF) of the functional relative to the statistical model (Bickel et al., 1998). The EIF plays a key role in establishing efficiency bounds for regular and asymptotically linear estimators of the true parameter value, and most importantly, in the construction of efficient estimators, as we will highlight below. For convenience, we will denote the numerator of Ψ_s(P) by Θ_s(P) : = ∫{μ_P(x) − μ_P,s(x)}²dP(x). The EIFs of Θ_s and of Ψ_s relative to the nonparametric model $\mathcal{M}$ are provided in the following lemma.

Lemma 1. The parameters Θ_s and Ψ_s are pathwise differentiable at each $P\in \mathcal{M}$ relative to $\mathcal{M}$, with EIFs φ_P,s and ${\phi }_{P,S}^{*}$ relative to $\mathcal{M}$, respectively, given by

$${\phi }_{P,s}^{*}:z\mapsto 2\left\{y-{\mu }_P(x)\right\}\left\{{\mu }_P(x)-{\mu }_{P,s}(x)\right\}+{\left\{{\mu }_P(x)-{\mu }_{P,s}(x)\right\}}^2-{\Theta }_s(P),$$

$${\phi }_{P,s}^{*}:z\mapsto \frac{2\left\{y-{\mu }_P(x)\right\}\left\{{\mu }_P(x)-{\mu }_{P,s}(x)\right\}+{\left\{{\mu }_P(x)-{\mu }_{P,s}(x)\right\}}^2}{{\mathit{\text{var}}}_P(Y)}-{\Theta }_s(P){\left\{\frac{y-E_P(Y)}{{\mathit{\text{var}}}_P(Y)}\right\}}^2.$$

A linearization of the evaluation of Θ_s at $P\in \mathcal{M}$ around P₀ can be expressed as

$${\Theta }_s(P)={\Theta }_s\left(P_0\right)+\int {\phi }_{P,s}(z)d\left(P-P_0\right)(z)+R_s\left(P,P_0\right),$$ (6)

where R_s(P, P₀) is a remainder term from this first-order expansion around P₀. The explicit form of R_s(P, P₀) is provided in Section 2.3 and can be used to algebraically verify this representation. For any given estimator $\widehat{P}\in \mathcal{M}$ of P₀, we can write

$$\begin{gathered} {\Theta }_s(\widehat{P})-{\Theta }_s\left(P_0\right)=\int {\phi }_{\widehat{P},s}(z)d\left(\widehat{P}-P_0\right)(z)+R_s\left(\widehat{P},P_0\right) \\ =\int {\phi }_{\widehat{P},s}(z)d\left({\mathbb{P}}_n-P_0\right)(z)+R_s\left(\widehat{P},P_0\right)-\frac{1}{n}\sum _{i=1}^n{\phi }_{{\widehat{P}}_n,s}\left(Z_i\right) \\ =\frac{1}{n}\sum _{i=1}^n{\phi }_{P_0,s}\left(Z_i\right)+R_s\left(\widehat{P},P_0\right)+H_{s,n}\left(\widehat{P},P_0\right)-\frac{1}{n}\sum _{i=1}^n{\phi }_{\widehat{P},s}\left(Z_i\right), \end{gathered}$$ (7)

where ${\mathbb{P}}_n$ is the empirical distribution based on Z₁, …, Z_n, $H_{s,n}\left(P,P_0\right)≔\int \left\{{\phi }_{P,S}(z)-{\phi }_{P_0,s}(z)\right\}d\left({\mathbb{P}}_n-P_0\right)(z)$ is an empirical process term, and we have made repeated use of the fact that φ_P,s(Z) has mean zero under P for any $P\in \mathcal{M}$. This representation is critical for characterizing the behavior of the plug-in estimator ${\Theta }_s(\widehat{P})$. The four terms on the right-hand side in (7) can be studied separately. The first term is an empirical average of mean-zero transformations of Z₁, …, Z_n. The second term is an empirical process term, and the third term is a remainder term. Both of these second-order terms can be shown to be asymptotically negligible under certain conditions on $\widehat{P}$. The fourth term can be thought of as the bias incurred from flexibly estimating the conditional means (1) and (2) and will generally tend to zero slowly. This bias term motivates our choice of estimator for ψ_0,s in Section 2.2. We will employ one particular bias correction method, and the large-sample properties of our proposed estimator will be determined by the first term in (7).

2.2 |. Estimation procedure

Writing the numerator Θ_s of the parameter of interest as a statistical functional suggests a natural estimation procedure. If we have estimators $\widehat{\mu }$ and ${\widehat{\mu }}_s$ of μ₀ and μ_0,s, respectively—obtained through any method that we choose, including machine learning techniques—a natural plug-in estimator of θ_0,s : = Θ_s(P₀) is given by

$$\begin{gathered} {\widehat{\theta }}_{\text{naive},\text{s}}≔\int {\left\{\widehat{\mu }(x)-{\widehat{\mu }}_s(x)\right\}}^{2}d{\mathbb{P}}_n(x) \\ =\frac{1}{n}\sum _{i=1}^n{\left\{\widehat{\mu }\left(X_i\right)-{\widehat{\mu }}_s\left(X_i\right)\right\}}^2. \end{gathered}$$ (8)

In turn, this suggests using, with ${\overline{Y}}_n$ denoting the empirical mean of Y₁, …, Y_n,

$${\widehat{\psi }}_{\text{naive,}s}≔\frac{{\widehat{\theta }}_{\text{naive,s}}}{{\mathit{\text{var}}}_{{\mathbb{P}}_n}(Y)}=\frac{\frac{1}{n}{\sum }_{i=1}^n{\left\{\widehat{\mu }\left(X_i\right)-{\widehat{\mu }}_s\left(X_i\right)\right\}}^2}{\frac{1}{n}{\sum }_{i=1}^n{\left(Y_i-{\overline{Y}}_n\right)}^2}$$

as a simple estimator of ψ_0,s. We refer to this as the naive estimator. This simple estimator involves hidden trade-offs. On the one hand, it is easy to construct given estimators $\widehat{\mu }$ and ${\widehat{\mu }}_S$. On the other hand, it does not generally enjoy good inferential properties. If a flexible technique is used to estimate μ₀ and μ_0,s, constructing $\widehat{\mu }$ and ${\widehat{\mu }}_S$ usually entails selecting tuning parameter values to achieve an optimal bias-variance trade-off for μ₀ and μ_0,s, respectively. This is generally not the optimal bias-variance trade-off for estimating the parameter of interest ψ_0,s, a key fact from non- and semiparametric theory. The estimator ${\widehat{\psi }}_{\text{naive,s}}$ has a variance decreasing at a parametric rate, with little sensitivity to the tuning of $\widehat{\mu }$ and ${\widehat{\mu }}_S$, because of the involved marginalization over the feature distribution. However, it inherits much of the bias from $\widehat{\mu }$ and ${\widehat{\mu }}_S$. Some form of debiasing is thus needed, as we discuss below. In particular, the estimator ${\widehat{\psi }}_{\text{naive,s}}$ is generally overly biased, in the sense that its bias does not tend to zero sufficiently fast to allow consistency at rate n^−1/2, let alone efficiency. This is problematic, in particular, because it renders the construction of valid confidence intervals difficult, if not impossible.

Instead, we consider the simple one-step correction estimator

$${\widehat{\theta }}_{n,s}≔{\widehat{\theta }}_{\text{naive},\text{s}}+\frac{1}{n}\sum _{i=1}^n{\phi }_{\widehat{P},s}\left(Z_i\right)$$

of θ_0,s, which, in view of (7), is asymptotically efficient under certain regularity conditions. This estimator is obtained by correcting for the excess bias of the naive plug-in estimator ${\widehat{\theta }}_{\text{naive,s}}$ using the empirical average of the estimated EIF as a first-order approximation of (minus) this bias (see, eg, Pfanzagl, 1982). We note that to compute ${\widehat{\theta }}_{n,s}$ it is not necessary to obtain an estimator $\widehat{P}$ of the entire distribution P₀. Instead, estimators $\widehat{\mu }$ and ${\widehat{\mu }}_S$ of μ₀ and μ_0,s suffice. The variance of Y under P₀ may simply be estimated using the empirical variance. It is easy to verify that the resulting estimator of ψ_0,s simplifies to

$$\begin{gathered} {\widehat{\psi }}_{n,s}≔\frac{{\widehat{\theta }}_{n,s}}{{\mathit{\text{var}}}_{{\mathbb{P}}_n}(Y)} \\ ={\widehat{\psi }}_{\text{naive},\text{s}}+\frac{{\sum }_{i=1}^{n}2\left\{Y_i-\widehat{\mu }\left(X_i\right)\right\}\left\{\widehat{\mu }\left(X_i\right)-{\widehat{\mu }}_s\left(X_i\right)\right\}}{{\sum }_{i=1}^n{\left(Y_i-{\overline{Y}}_n\right)}^2}. \end{gathered}$$ (9)

This estimator adjusts for the inadequate bias-variance trade-off performed when flexible estimators $\widehat{\mu }$ and ${\widehat{\mu }}_s$ are tuned to be good estimators of μ₀ and μ_0,s rather than being tuned for the end objective of estimating ψ_0,s. Simple algebraic manipulations yield that ${\widehat{\psi }}_{n,s}$ is equivalent to the plug-in estimator

$$\left[1-\frac{\frac{1}{n}{\sum }_{i=1}^n{\left\{Y_i-\widehat{\mu }\left(X_i\right)\right\}}^2}{{\mathit{\text{var}}}_{{\mathbb{P}}_n}(Y)}\right]-\left[1-\frac{\frac{1}{n}{\sum }_{i=1}^n{\left\{Y_i-{\widehat{\mu }}_s\left(X_i\right)\right\}}^2}{{\mathit{\text{var}}}_{{\mathbb{P}}_n}(Y)}\right]$$ (10)

obtained by viewing ψ_0,s as a difference in population R² values, as in (5). As indicated above, semiparametric theory indicates that plug-in estimators based on flexible regression algorithms typically require bias correction if the latter are not tuned towards the target of inference, as in (9).

Algorithm 1.

Estimating ψ_0,s

1: Choose a technique to estimate the conditional means μ0 and μ0,s, eg, ensemble learning with various predictive modeling algorithms (Wolpert, 1992);

2: $\widehat{\mu }$ ← Regress Y on X using the technique from step (1) to estimate μ0;

3: ${\widehat{\mu }}_s$ ← Regress $\widehat{\mu }(X)$ on X−s using the technique from step (1) to estimate μ0,s;

4: ${\widehat{\psi }}_{n,S}\leftarrow \frac{\frac{1}{n}{\sum }_{i=1}^n{\left\{Y_i-{\widehat{\mu }}_s\left(X_i\right)\right\}}^2-\frac{1}{n}{\sum }_{i=1}^n{\left\{Y_i-\widehat{\mu }\left(X_i\right)\right\}}^2}{\frac{1}{n}{\sum }_{i=1}^n{\left(Y_i-{\overline{Y}}_n\right)}^2}$, as in Equation (10).

Interestingly, as we note from above, this is needed when constructing a plug-in estimator based on the ANOVA representation (4) of ψ_0,s but not based on its difference-in-R² representation (5).

While we are not constrained to any particular estimation method to construct $\widehat{\mu }$ and ${\widehat{\mu }}_s$, we have found one particular strategy to work well in practice. Using any specific predictive modeling technique to regress the outcome Y on the full covariate vector X and then on the reduced covariate vector X_−s does not take into account that the two conditional means are related and will generally result in incompatible estimates. Specifically, we have that ${\mu }_{0,s}(x)=E_{P_0}\left\{{\mu }_0(X)\mid X_{-s}=x_{-s}\right\}$, which we can take advantage of to produce the following sequential regression estimating procedure: (i) regress Y on X to obtain an estimate $\widehat{\mu }$ of μ₀, and then (ii) regress $\widehat{\mu }(X)$ on X_−s to obtain an estimate ${\widehat{\mu }}_s$ of μ_0,s.

The final estimation procedure we recommend for ψ_0,s consists of estimator ${\widehat{\psi }}_{n,s}$, where the conditional means involved are estimated using flexible regression estimators based on the sequential regression approach; see Algorithm 1 for explicit details. This may also be embedded in a split-sample validation scheme, by first creating training and validation sets, then obtaining $\widehat{\mu }$ and ${\widehat{\mu }}_s$ on the training set as outlined above, and finally, obtaining an estimator of ψ_0,s by using the validation data along with predictions from the conditional mean estimators on the validation data. This can be extended to a cross-fitted procedure given in Algorithm 2 and discussed in the Supporting Information.

2.3 |. Asymptotic behavior of the proposed estimator

By studying the remainder term $R_S\left(\widehat{P},P_0\right)$ and the empirical process term $H_{s,n}\left(\widehat{P},P_0\right)$, we can establish appropriate conditions on $\widehat{\mu }$ and ${\widehat{\mu }}_s$ under which the proposed estimator ${\widehat{\psi }}_{n,s}$ is asymptotically efficient. This allows us to determine the asymptotic distribution of the proposed estimator and, therefore, to propose procedures for performing valid

Algorithm 2.

Estimating ψ_0,s using V-fold cross fitting

1: Choose a technique to estimate the conditional means μ0 and μ0,s;

2: Generate a random vector Bn ∈ {1,…, V}n by sampling uniformly from {1,…, V} with replacement, and denote by Dj the subset of observations with index in {i :Bn,i = j} for j = 1,…, V.

3: for υ = 1,…, V do

4: ${\mu }_{\upsilon }$ ← Regress Y on X using the data in ∪j≠υDj using the technique from step (1) to estimate μ0

5: ${\widehat{\mu }}_{s,\upsilon }$ ← Regress ${\widehat{\mu }}_{\upsilon }(X)$ on X−s using the data in ∪j≠υDj to estimate μ0,s;

6: ${\widehat{\psi }}_{n,S}^{\upsilon }\leftarrow \frac{{\sum }_{i\in D_j}{\left\{Y_i-{\widehat{\mu }}_{s,\upsilon }\left(X_i\right)\right\}}^2-{\sum }_{i\in D_j}{\left\{Y_i-{\widehat{\mu }}_{\upsilon }\left(X_i\right)\right\}}^2}{{\sum }_{i\in D_j}{\left(Y_i-{\overline{Y}}_n\right)}^2}$, as in Equation (10);

7: end for

8: ${\widehat{\psi }}_{n,s}^{\text{cv}}\leftarrow \frac{1}{V}{\sum }_{\upsilon =1}^V{\widehat{\psi }}_{n,s}^{\upsilon }$.

inference on ψ_0,s. Below, we will make reference to the following conditions, in which we have defined the conditional outcome variance ${\tau }_0^2:x\mapsto {\mathit{\text{var}}}_{P_0}(Y\mid X=x)$.

• (A1) $\text{max}\left[\int {\left\{{\widehat{\mu }}_s(x)-{\mu }_0(x)\right\}}^{2}d{P}_0\left(x\right),\int {\left\{{\widehat{\mu }}_s(x)-{\mu }_{0,s}(x)\right\}}^2\right]=o_P\left(n^{-1/2}\right)$;

• (A2) there exists a P₀-Donsker class ${\mathcal{G}}_0$ such that $P_0\left({\phi }_{\widehat{P},s}\in {\mathcal{G}}_0\right)\to 1$;

• (A3) there exists a constant K > 0 such that each of μ₀, ${\widehat{\mu }}_0$, ${\widehat{\mu }}_{0,s}$, and ${\tau }_0^2$ has range contained uniformly in (−K, +K) with probability tending to one as sample size tends to +∞.

First, it is straightforward to verify that linearization (6) holds with second-order remainder term R_s(P, P₀) = ∫ {μ_P,s(x) − μ_0,s(x)}²dP₀(x) − ∫ {μ_P(x) − μ₀(x)}²dP₀(x). It follows then that condition (A1) suffices to ensure that $R_S\left(\widehat{P},P_0\right)$ is asymptotically negligible, that is, that $R_S\left(\widehat{P},P_0\right)=o_P\left(n^{-1/2}\right)$. Each of the second-order terms in condition (A1) can feasibly be made negligible, even while using flexible regression techniques, including generalized additive models (Hastie and Tibshirani, 1990), to estimate the conditional mean functions. We thus turn our attention to $H_{s,n}\left(\widehat{P},P_0\right)$. By empirical process theory, we have that $H_{s,n}\left(\widehat{P},P_0\right)=o_P\left(n^{-1/2}\right)$ provided, for example, $\int {\left\{{\phi }_{\widehat{P},S}(z)-{\phi }_{P_0,s}(z)\right\}}^{2}d{P}_0\left(z\right)$ tends to zero in probability and condition (A2) holds (Lemma 19.24 of van der Vaart, 2000). For the former, uniform consistency of $\widehat{\mu }$ and ${\widehat{\mu }}_S$ under L₂(P₀) suffices under condition (A3). We note that if there is a known bound on the outcome support, condition (A3) will readily be satisfied provided the learning algorithms used incorporate this knowledge. For the latter, the set of possible realizations of $\widehat{\mu }$ and ${\widehat{\mu }}_S$ must become sufficiently restricted with probability tending to one as sample size grows. This condition is satisfied if, for example, the uniform sectional variation norm of ${\phi }_{{\widehat{P}}_n,S}$ is bounded with probability tending to one (Gill et al., 1995). When using flexible machine learning-based regression estimators, there may be reason for concern regarding the validity of condition (A2). In such cases, using the cross-fitted estimator ${\widehat{\psi }}_{n,S}^{\text{cv}}$ may circumvent this condition. While this cross-fitted estimator is only slightly more complex, we restrict attention here to studying the simpler estimator and leave study of the cross-fitted estimator to the Supporting Information.

The following theorem describes the asymptotic behavior of the proposed estimator.

Theorem 1. Provided conditions (A1)–(A3) hold, ${\widehat{\psi }}_{n,s}$ is asymptotically linear with influence function ${\phi }_{P_0,s}^{*}$. In particular, this implies that (a) ${\widehat{\psi }}_{n,s}$ tends to ψ_0,s in probability, and if ψ_0,s ∈ (0, 1) (b) $n^{1/2}\left({\widehat{\psi }}_{n,s}-{\psi }_{0,s}\right)$ tends in distribution to a mean-zero Gaussian random variable with variance ${\sigma }_{0,s}^2≔\int {\phi }_{P_0,s}^{*}{(z)}^{2}d{P}_0(z)$.

A natural plug-in estimator of ${\sigma }_{0,S}^2$ is given by ${\widehat{\sigma }}_{n,s}^2≔\frac{1}{n}{\sum }_{i=1}^n{\widehat{\phi }}_{P_0,s}^{*}{\left(Z_i\right)}^2$, where ${\widehat{\phi }}_{P_0,S}^{*}$ is any consistent estimator of ${\phi }_{P_0,s}^{*}$. For example, ${\widehat{\phi }}_{P_0,s}^{*}$ may be taken to be ${\widehat{\phi }}_{P_0,s}^{*}$ with μ₀, μ_0,s, $E_{P_0}(Y)$, ${\mathit{\text{var}}}_{P_0}(Y)$, and θ_0,s replaced by $\widehat{\mu }$, ${\widehat{\mu }}_s$, ${\overline{Y}}_n$, ${\mathit{\text{var}}}_{{\mathbb{P}}_n}(Y)$, and ${\widehat{\theta }}_{n,s}$, respectively. In view of the asymptotic normality of $n^{1/2}\left({\widehat{\psi }}_{n,s}-{\psi }_{0,s}\right)$, an asymptotically valid (1 − α) × 100% Wald-type confidence interval for ψ_0,s ∈ (0, 1) can be obtained as ${\widehat{\psi }}_{n,s}\pm q_{1-\alpha /2}{\widehat{\sigma }}_{n,s}{n}^{-1/2}$, where q_β is the β-quantile of the standard normal distribution.

To underscore the importance of using the proposed debiased procedure, we recall that, in contrast to ${\widehat{\psi }}_{n,s}$, the naive ANOVA-based estimator is generally not asymptotically linear when flexible (eg, machine learning based) estimators of the involved regression are used. It will usually be overly biased, resulting in a rate of convergence slower than n^−1/2. Constructing valid confidence intervals based on the naive estimator can thus be difficult. It may be tempting to consider bootstrap resampling as a remedy. However, this is not advisable since, besides the computational burden of such an approach, there is little theory to justify using the standard nonparametric bootstrap in this context, particularly for the naive ANOVA-based estimator (Shao, 1994).

2.4 |. Behavior under the zero-importance null hypothesis

This work focuses on efficient estimation of a population-level algorithm-agnostic variable importance measure using flexible estimation techniques and on describing how valid inference may be drawn when the set s of features under evaluation does not have degenerate importance. Specifically, we have restricted our attention to cases in which ψ_0,s ∈ (0, 1) strictly and provided confidence intervals valid in such cases. It may be of interest, however, to test the null hypothesis ψ_0,s = 0 of zero importance. Developing valid and powerful tests of this particular null hypothesis is difficult. Because the null hypothesis is on the boundary of the parameter space, ${\phi }_{P_0,s}$ is identically zero under this null, and a higher order expansion may be required to construct and characterize the behavior of an appropriately-regularized estimator of θ_0,s—and thus of ψ_0,s—with good power. However, the parameters Θ_s and Ψ_s are generally not second-order pathwise differentiable in nonparametric models, and so higher order expansions cannot easily be constructed. There may be hope in using approximate second-order gradients, as outlined in Carone et al. (2018), though this remains an open problem. A crude alternative solution based on sample splitting is investigated in Williamson et al. (2020). To highlight the difficulties that arise under this particular null hypothesis, we conducted a simulation study for a setting in which one of the variables has zero importance. The results from this study are provided in the next section.

3 |. EXPERIMENTS ON SIMULATED DATA

We now present empirical results describing the performance of the proposed estimator (9) compared to that of the naive plug-in estimator (8). In all implementations, we use the sequential regression estimating procedure described in Algorithm 1 for each feature or group of interest to compute compatible estimates of the required regression functions, and we compute nominal 95% Wald-type confidence intervals as outlined in Section 2.3.

3.1 |. Low-dimensional vector of features

We consider here data generated according to the following specification:

$$\begin{gathered} X_1,X_2\stackrel{iid}{~}\text{ Uniform }(-1,1)\text{\hspace{0.17em}\hspace{0.17em}and } \\ ϵ~N(0,1)\text{ independent of }\left(X_1,X_2\right) \\ Y=X_1^2\left(X_1+\frac{7}{5}\right)+\frac{25}{9}{X}_2^2+ϵ. \end{gathered}$$

We generated 1000 random datasets of size n ∈ {100, 300, 500, 700, 1000, 2000, …, 8000} and considered in each case the importance of X₁ and of X₂. The true value of the variable importance measures implied by this data-generating mechanism can be shown to be ψ_0,1 ≈ 0.158 and ψ_0,2 ≈ 0.342. This nonlinear setting helps to highlight the drawbacks of relying on a simple parametric model to estimate the conditional means.

To obtain $\widehat{\mu }$, ${\widehat{\mu }}_1$, and ${\widehat{\mu }}_2$, we fit locally constant loess smoothing using the R function loess with tuning selected to minimize a fivefold cross-validated estimate of the empirical risk based on the squared error loss function. Loess smoothing was chosen because it is a data-adaptive algorithm with an efficient implementation, and it satisfies the minimum convergence rate condition outlined in Section 2.3, allowing us to numerically verify our theoretical results. Because we obtained the same trends using locally constant kernel regression, we do not report summaries from these additional simulations here. This fact nevertheless highlights the ease of comparing results from two different estimation techniques.

We computed the naive and proposed estimators and respective confidence intervals for each replication and compared these to a parametric difference in R² based on simple linear regression using ordinary least squares (OLS). Because a simple asymptotic distribution for the naive estimator is unavailable, a percentile bootstrap approach with 1000 bootstrap samples was used in an attempt to obtain approximate confidence intervals based on ${\widehat{\psi }}_{\text{naive,j}}$. For each estimator, we then computed the empirical bias scaled by n^1/2 and the empirical variance scaled by n. Our output for the estimated bias includes confidence intervals for the true bias based on the resulting draws from the bootstrap sampling distribution. Finally, we computed the empirical coverage of the nominal 95% confidence intervals constructed.

Figure 1 displays the results of this simulation. In the left panel, we note that the scaled empirical bias of the proposed estimator decreases towards zero as n tends to infinity, regardless of which feature we remove. Also, we see that both the naive estimator and the OLS estimator have substantial bias that does not tend to zero faster than n^−1/2. This coincides with our expectations: the naive estimator involves an inadequate bias-variance trade-off with respect to the parameter of interest and does not include any debiasing; the OLS estimator is based on a misspecified mean model. Though there is very substantial bias reduction from using the proposed estimator, we see that its scaled bias appears to dip slightly below zero for large n. We expect for larger n to see this scaled bias for the proposed estimator get closer to zero; numerical error in our computations may explain why this does not exactly happen. These results provide empirical evidence that the debiasing step is necessary to account for the slow rates of convergence in estimation of ψ_0,s introduced because μ₀ and μ_0,s are flexibly estimated.

FIGURE 1.

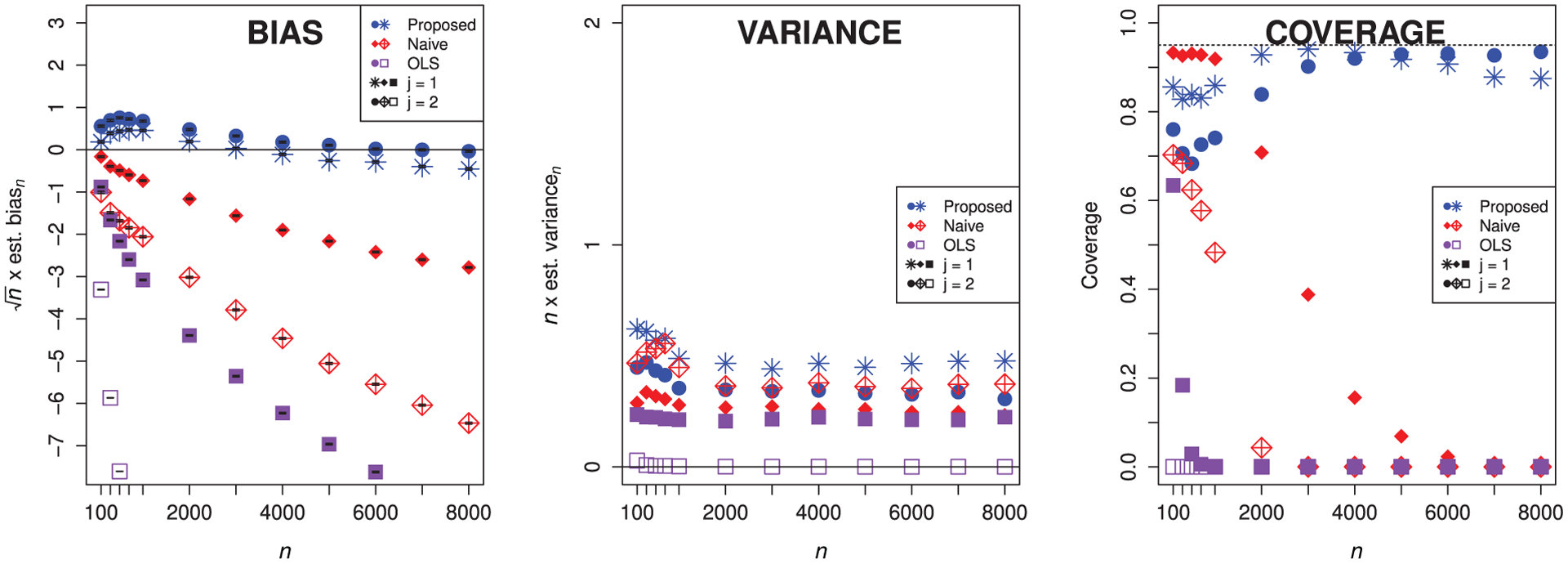
Empirical bias (scaled by n^1/2) with Monte Carlo error bars, empirical variance (scaled by n), and empirical coverage of nominal 95% confidence intervals for the proposed, naive, and OLS estimators for either feature, using loess smoothing with cross-validation tuning (in the case of the proposed and naive estimators). Circles, filled diamonds, and filled squares denote that we have removed X₁; stars, crossed diamonds, and empty squares denote that we have removed X₂.

In the middle panel of Figure 1, we see that the variance of the proposed estimator is close to that of the naive estimator—we have thus not suffered much from removing excess bias in our estimation procedure. The variance of the OLS estimator is the smallest of the three: using a parametric model tends to result in a smaller variance. The ratio of the variance of the naive estimator to that of the proposed estimator is near one for all n considered and ranges between approximately 0.8 and 1.2 in our simulation study. Finally, in the right-hand panel, we see that as sample size grows, coverage increases for the confidence interval based on the proposed estimator and approaches the nominal level. In contrast, the coverage of intervals based on both the naive estimator and the OLS estimator decreases instead and quickly becomes poor.

3.2 |. Testing the zero-importance null hypothesis

We now consider data generated according to the following specification:

$$\begin{gathered} X_1,X_2\stackrel{\text{iid}}{~}\text{ Uniform }(-1,1)\text{ and } \\ ϵ~N(0,1)\text{ independent of }\left(X_1,X_2\right);Y=\frac{25}{9}{X}_1^2+ϵ \end{gathered}$$

We generated 1000 random datasets of size n ∈ {100, 300, 500, 700, 1000, 2000, 3000} and again considered in each case the importance of X₁ and of X₂. The true value of the variable importance measures implied by this data-generating mechanism can be shown to be ψ_0,1 ≈ 0.407 and ψ_0,2 = 0. We estimated the conditional means and summarized the results of this simulation as in the previous simulation.

Figure 2 displays the results of this simulation. In the left-hand panel, we observe that the proposed estimator has smaller scaled bias in magnitude than the naive estimator when we remove the feature with nonzero importance. However, when we remove the feature with zero importance, the proposed estimator has slightly higher bias. While this is somewhat surprising, it likely is due to the additive correction in the one-step construction being slightly too large. The scaled bias of the proposed estimator tends to zero as n increases for both features, which is not true of the naive estimator. In the middle panel, we see that we have not incurred excess variance by using the proposed estimator. In the right-hand panel, we see that both estimators have close to zero coverage for the parameter under the null hypothesis, but that the proposed estimator has higher coverage than the naive estimator for the predictive feature. These results highlight that more work needs to be done for valid testing and estimation under this boundary null hypothesis. While our current proposal yields valid results for the predictive feature, even in the presence of a null feature, ensuring valid inference for null features themselves remains an important challenge.

FIGURE 2.

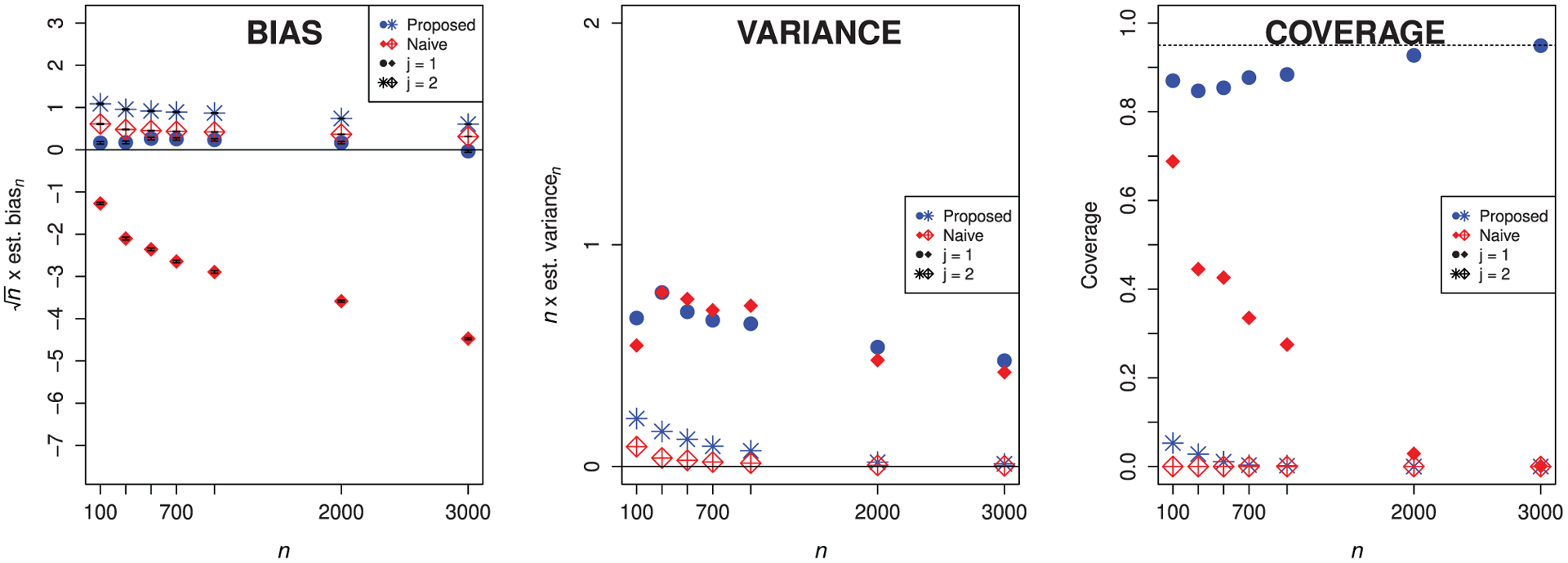
Empirical bias (scaled by n^1/2) with Monte Carlo error bars, empirical variance (scaled by n), and empirical coverage of nominal 95% confidence intervals for the proposed and naive estimators for either feature, using loess smoothing with cross-validation tuning. Circles and filled diamonds denote that we have removed X₁, while stars and crossed diamonds denote that we have removed X₂. We operate under the null hypothesis for X₂, that is, ψ_0,2 = 0.

3.3 |. Moderate-dimensional vector of features

We consider one setting in which the features are independent and a second in which groups of features are correlated. In setting A, we generated data according to the following specification:

$$\begin{gathered} X_1,X_2,\dots ,X_{15}\stackrel{iid}{~}N(0,4)\text{ and } \\ ϵ~N(0,1)\text{ independent of }\left(X_1,X_2,\dots ,X_{15}\right) \\ Y=I_{(-2,+2)}\left(X_1\right)\cdot ⌊X_1⌋+I_{(-\infty ,0]}\left(X_2\right)+I_{(0,+\infty )}\left(X_3\right)+{\left|\frac{X_6}{4}\right|}^3+{\left|\frac{X_7}{4}\right|}^5+\frac{7}{3}\text{cos}\left(\frac{X_{11}}{2}\right)+ϵ. \end{gathered}$$

In setting B, the covariate distribution was modified to include clustering. Specifically, we generated (X₁, X₂, …, X₁₅) ~ MVN₁₅(μ, Σ), where the mean vector is

$$\mu =3\times (0,0,0,0,0,1,1,1,1,1,0,0,0,0,0)-2\times (0,0,0,0,0,0,0,0,0,0,1,1,1,1,1)$$

and the variance–covariance matrix is block-diagonal with blocks

$$\left[\begin{array}{ccc}1& 0.15& 0.15\\ 0.15& 1& 0.15\\ 0.15& 0.15& 1\end{array}\right],\left[\begin{array}{ccc}1& 0.5& 0.5\\ 0.5& 1& 0.5\\ 0.5& 0.5& 1\end{array}\right]\text{ and }\left[\begin{array}{ccc}1& 0.85& 0.85\\ 0.85& 1& 0.85\\ 0.85& 0.85& 1\end{array}\right]$$

and all other off-diagonal entries equal to zero. The random error ϵ and the outcome Y are then generated as in setting A. In both settings, we generated 500 random datasets of size n ∈ {100, 300, 500, 1000} and considered the importance of the feature sets {1, 2, 3, 4, 5}, {6, …, 10}, and {11, …, 15} for each sample size. The true value of the variable importance measures corresponding to each of the considered groups in both settings is given in Table 1. Results for the analysis of additional groupings are provided in the Supporting Information.

TABLE 1.

Approximate values of ψ_0,s for each simulation setting and group considered in the moderate-dimensional simulations in Section 3.3

	Setting
Group	A	B
(X1,X2, … ,X5)	0.295	0.281
(X6,X7, … ,X10)	0.240	0.314
(X11,X12, … ,X15)	0.242	0.179

For each scenario considered, we estimated the conditional mean functions with gradient-boosted trees (Friedman, 2001) fit using GradientBoostingRegressor in the sklearn module in Python. Gradient-boosted trees were used due to their generally favorable prediction performance and large degree of flexibility, with full knowledge that they are not guaranteed to satisfy the minimum rate condition outlined in Section 2.3. We used fivefold cross-validation to select the optimal number of trees with one node as well as the optimal learning rate for the algorithm. We summarized the results of these simulations in the same manner as in the low-dimensional simulations.

The results for setting A are presented in Figure 3. From the top row, we note that as sample size increases, the scaled empirical bias of the proposed estimator approaches zero, whereas that of the naive estimator increases in magnitude across all subsets considered. From the bottom row, we observe that the empirical coverage of intervals based on the proposed estimator increases toward the nominal level as sample size increases and is uniformly higher than the empirical coverage of bootstrap intervals based on the naive estimator.

FIGURE 3.

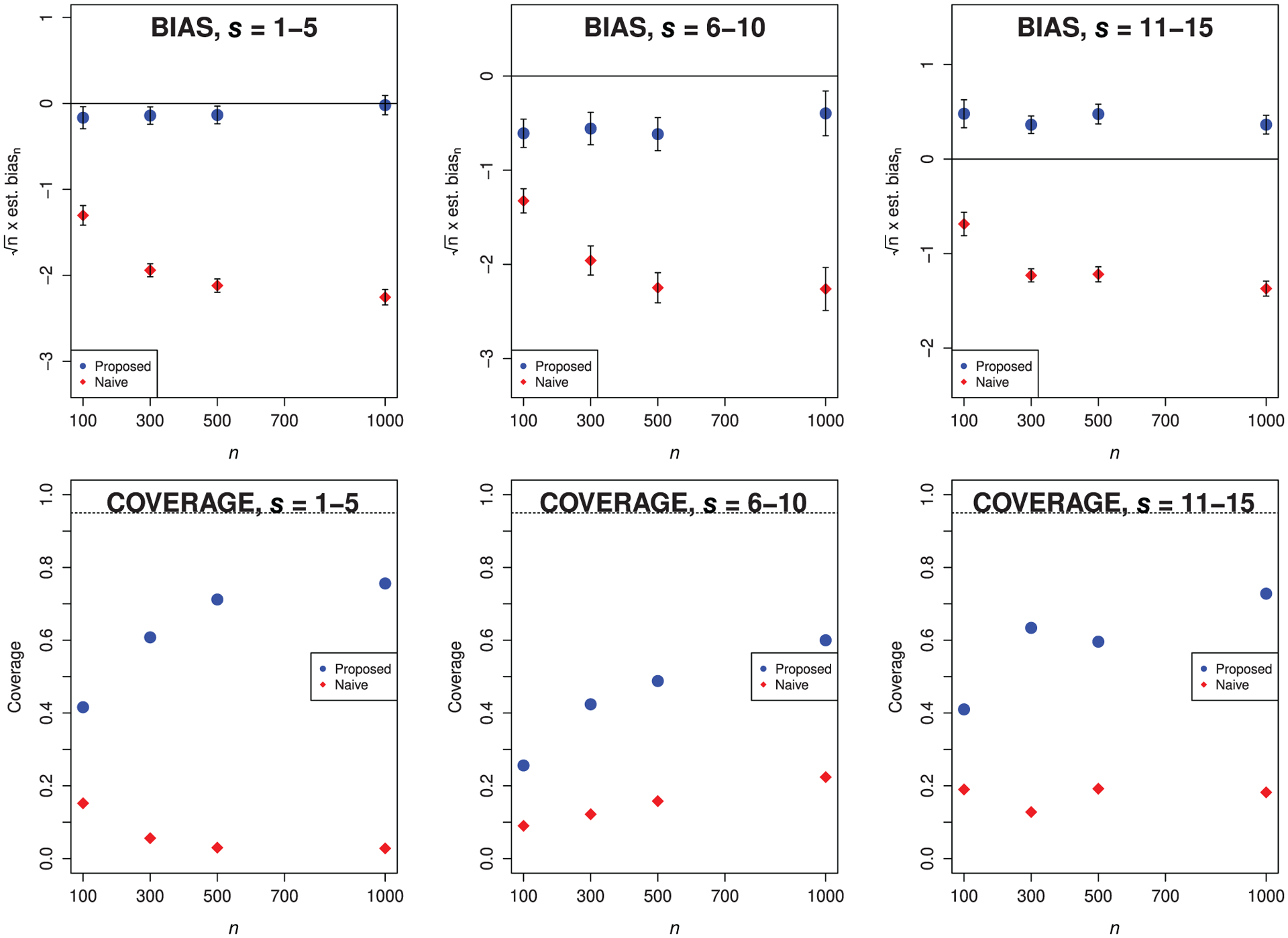
Top row: empirical bias for the proposed and naive estimators scaled by n^1/2 for setting A, based on gradient-boosted trees. Bottom row: empirical coverage of nominal 95% confidence intervals for the proposed and naive estimators for setting A, using gradient-boosted trees. We consider all s combinations from Table 1. Diamonds denote the naive estimator, and circles denote the proposed estimator. Monte Carlo error bars are displayed vertically.

The results for setting B are presented in Figure 4. From the top row, we note some residual bias in the proposed estimator for s = {11, …, 15}. Larger samples may be needed to observe more thorough bias reduction—indeed, this group of features is that with the highest within-group correlation. Nevertheless, the scaled empirical bias of the proposed estimator approaches zero as sample size increases for both s = {1, …, 5} and s = {6, …, 10}. In all cases, the scaled empirical bias of the naive estimator increases in magnitude as sample size increases. In the bottom row, we again see that intervals based on the proposed estimator have uniformly higher coverage than those based on the naive estimator.

FIGURE 4.

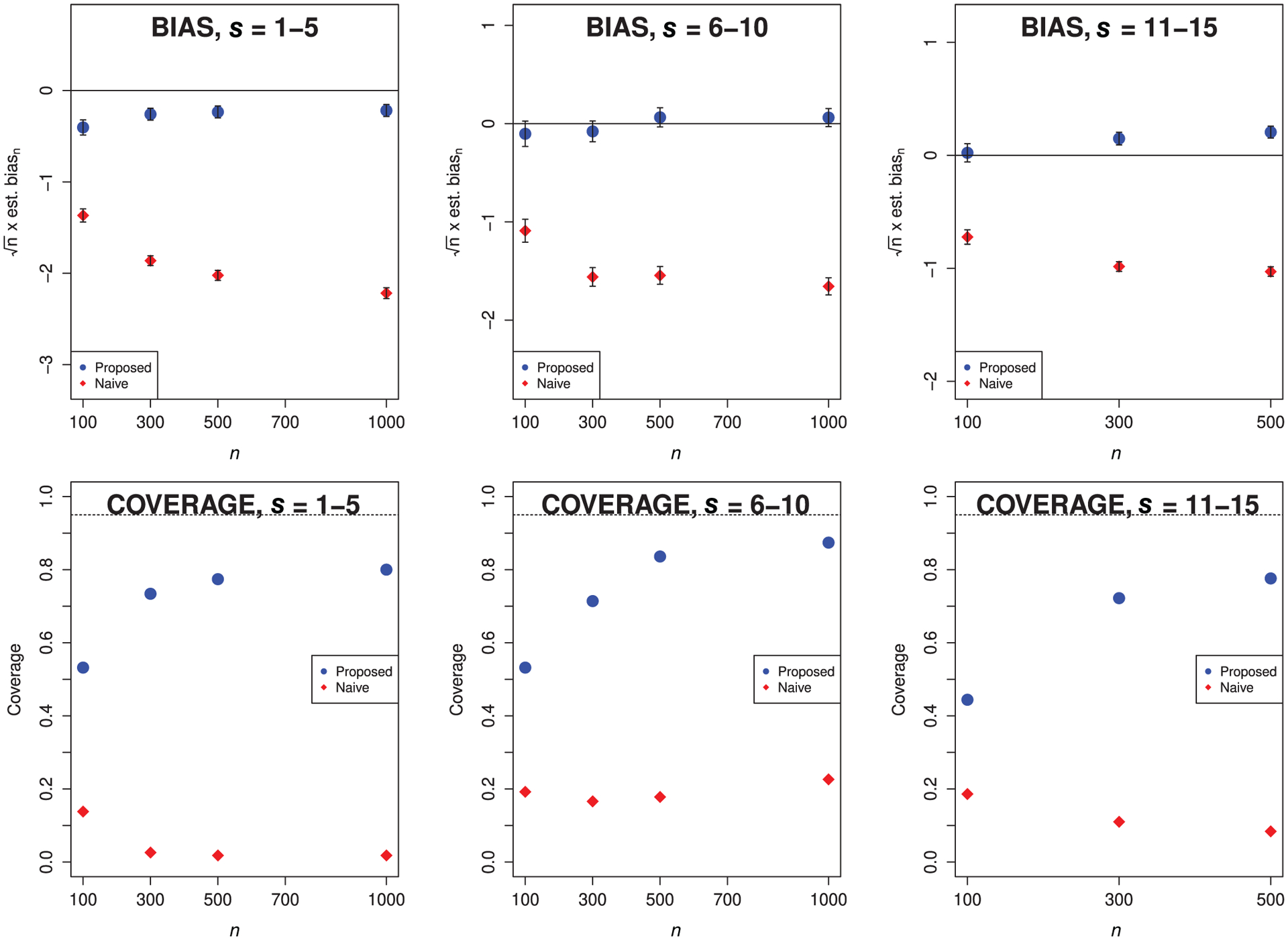
Top row: empirical bias for the proposed and naive estimators scaled by n^1/2 for setting B, using gradient-boosted trees. Bottom row: empirical coverage of nominal 95% confidence intervals for the proposed and naive estimators for setting B, using gradient-boosted trees. We consider all s combinations from Table 1. Diamonds denote the naive estimator, and circles denote the proposed estimator. Monte Carlo error bars are displayed vertically.

The proposed estimator performs substantially better than the naive estimator in these simulations, though higher levels of correlation appear to be associated with relatively poorer point and interval estimator performance. This suggests that it may be wise to consider in practice the importance of entire groups of correlated predictors rather than that of individual features. This is a sensible approach for dealing with correlated features, which necessarily render variable importance assessment challenging. In our simulations, the empirical coverage of proposed intervals for the importance of a group of highly correlated features approaches the nominal level as sample size increases, indicating that the proposed approach does yield good results in such cases.

Use of the proposed estimator results in better point and interval estimation performance than the naive estimator in the presence of null features. This is illustrated, for example, when evaluating the importance of the group (X₁, …, X₅), in which case most other features (ie, X₈, X₉, X₁₀, X₁₂, …, X₁₅) have null importance. However, as before, we expect the behavior of point and interval estimators for the variable importance of null features to be poorer. Additional work on valid estimation and testing under this null hypothesis is necessary.

4 |. RESULTS FROM THE SOUTH AFRICAN HEART DISEASE STUDY DATA

We consider a subset of the data from the Coronary Risk Factor Study (Rosseauw et al., 1983), a retrospective cross-sectional sample of 462 white males aged 15–64 in a region of the Western Cape, South Africa; these data are publicly available in Hastie et al. (2009). The primary aim of this study was to establish the prevalence of ischemic heart disease risk factors in this high-incidence region. For each participant, the presence or absence of myocardial infarction (MI) at the time of the survey is recorded, yielding 160 cases of MI. In addition, measurements on two sets of features are available: behavioral features, including cumulative tobacco consumption, current alcohol consumption, and type A behavior, a behavioral pattern linked to stress (Friedman and Rosenman, 1971); and biological features, including systolic blood pressure, low-density lipoprotein (LDL) cholesterol, adiposity (similar to body mass index), family history of heart disease, obesity, and age.

We considered the importance of each feature separately, as well as that of these two groups of features, when predicting the presence or absence of MI. We estimated the conditional means using the sequential regression estimating procedure outlined in Section 2.2 and using the Super Learner (van der Laan et al., 2007) via the SuperLearner R package. The Super Learner is a particular implementation of stacking (Wolpert, 1992), and the resulting estimator is guaranteed to have the same risk as the oracle estimator, asymptotically, along with finite-sample guarantees (van der Laan et al., 2007). Our library of candidate learners consists of boosted trees, generalized additive models, elastic net, and random forests implemented in the R packages gbm, gam, glmnet, and randomForest, respectively, each with varying tuning parameters. Tenfold cross-validation was used to determine the optimal convex combination of these learners chosen to minimize the cross-validated mean-squared error. This process allowed the Super Learner to determine the optimal tuning parameters for the individual algorithms as part of its optimal combination, and our resulting estimator of the conditional means is the optimal convex combination of the individual algorithms. Finally, we produced confidence intervals based on the proposed estimator alone, since as we have seen earlier, intervals based on the naive estimator are generally invalid.

The results are presented in Figure 5. The ordering is slightly different in the two plots; this is not surprising, since the one-step procedure should eliminate excess bias in the naive estimator introduced by estimating the conditional means using flexible learners. We find that biological factors are more important than behavioral factors. The most important individual feature is family history of heart disease; family history has been found to be a risk factor of MI in previous studies. It appears scientifically sensible that both groups of features are more important than any individual feature besides family history.

FIGURE 5.

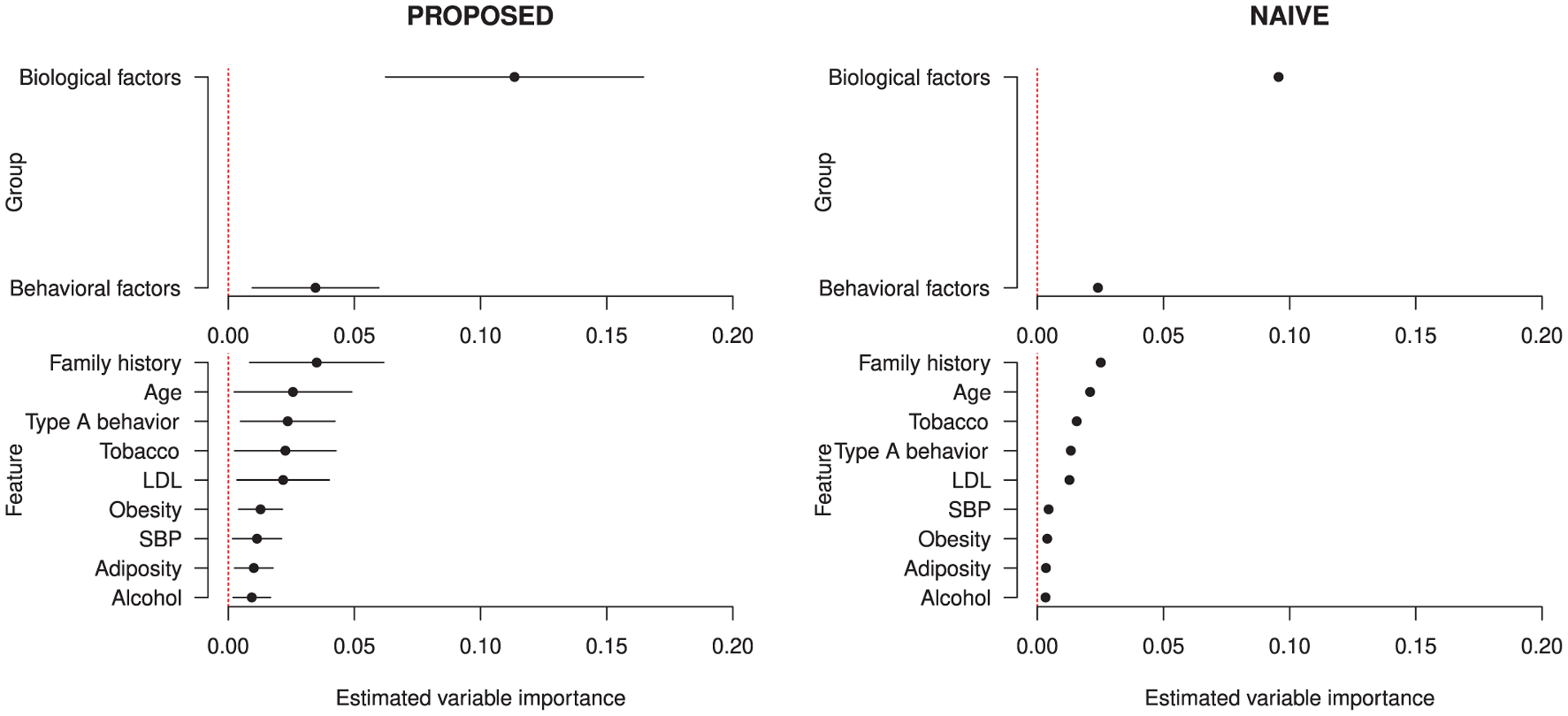
Estimates from the South African heart disease study for the proposed and naive estimators of the variable importance parameter, on left and right, respectively. The Super Learner with library including the elastic net, generalized additive models, gradient boosted trees, and random forests, was used

We compared these results to a logistic regression model fit to these data. Based on the absolute values of z-statistics, logistic regression picks age as most important, followed by family history. This slight difference is captured in our uncertainty estimates (Figure 5): there, we see that the point estimates for age and family history are close, and their confidence intervals largely overlap. We find the same pattern for LDL cholesterol and tobacco consumption, the third- and fourth-ranked variables by logistic regression. While our results match closely with the simplest approach to analyzing variable importance in these data, our proposed method is not dependent on a single estimation technique, such as logistic regression. The use of more flexible learners to estimate ψ_0,s, as we have done in this analysis, renders our findings less likely to be driven by potential model misspecification.

5 |. CONCLUSION

We have obtained novel results for a familiar measure of variable importance, interpreted as the additional proportion of variability in the outcome explained by including a subset of the features in the conditional mean outcome relative to the entire covariate vector. This parameter can be readily seen as a nonparametric extension of the classical R²-based measure, and it provides a description of the true relationship between the outcome and covariates rather than an algorithm-specific measure of association. We have also studied the properties of this parameter and derived its nonparametric EIF. We found that the form of the variable importance measure under consideration can have a dramatic impact on the ease with which efficient estimators may be constructed—for example, debiasing is needed for ANOVA-based plug-in estimators using flexible learners, but not for plug-in estimators based on the difference in R² values. We provide general results describing this phenomenon in Williamson et al. (2020). Leveraging tools from semiparametric theory, we have described the construction of an asymptotically efficient estimator of the true variable importance measure built upon flexible, data-adaptive learners. We have studied the properties of this estimator, notably providing distributional results, and described the construction of asymptotically valid confidence intervals. In simulations, we found the proposed estimator to have good practical performance, particularly as compared to a naive estimator of the proposed variable importance measure. However, we found this performance to depend very much on whether or not the true variable importance measure equals zero. When it does, a limiting distribution is not readily available, and significant theoretical developments seem needed in order to perform valid and powerful inference. However, for those features with true importance, the behavior of point and interval estimates is not influenced by the presence of null features. While the parameter we have studied has broad interpretability, alternative measures of variable importance may also be useful in certain settings (eg, difference in the area under the receiver operating characteristic curve in the context of a binary outcome). We study such measures in Williamson et al. (2020).

For each candidate set of variables, the estimation procedure we proposed requires estimation of two conditional mean functions. To guarantee that our estimator has good properties, these conditional means must be estimated well. For this reason, and as was illustrated in our work, we recommend the use of model stacking with a wide range of candidate learners, ranging from parametric to fully nonparametric algorithms. This flexibility mitigates concerns regarding model misspecification. Additionally, we suggest the use of sequential regressions to minimize any incompatibility between the two conditional means estimated.

A multiple testing issue arises when inference is desired on many feature subsets. Of course, a Bonferroni approach may be easily implemented. Alternatively, we could use a consistent estimator of the variance-covariance matrix for the importance of all subsets of features under study, obtained using the influence functions exhibited in this paper. This alternative multiple-testing adjustment has improved power over a Bonferroni-type approach. Strategies based on this approach are described, for example, in Dudoit and van der Laan (2007).