Abstract
Although the bursting patterns with spike undershoot are involved with the achievement of physiological or cognitive functions of brain with synaptic noise, noise induced-coherence resonance (CR) from resting state or subthreshold oscillations instead of bursting has been widely identified to play positive roles in information process. Instead, in the present paper, CR characterized by the increase firstly and then decease of peak value of power spectrum of spike trains is evoked from a bursting pattern with spike undershoot, which means that the minimal membrane potential within burst is lower than that of the subthreshold oscillations between bursts, while CR cannot be evoked from the bursting pattern without spike undershoot. With bifurcations and fast-slow variable dissection method, the bursting patterns with and without spike undershoot are classified into “Sub-Hopf/Fold” bursting and “Fold/Homoclinic” bursting, respectively. For the bursting with spike undershoot, the trajectory of the subthreshold oscillations is very close to that of the spikes within burst. Therefore, noise can induce more spikes from the subthreshold oscillations and modulate the bursting regularity, which leads to the appearance of CR. For the bursting pattern without spike undershoot, the trajectory of the quiescent state is not close to that of the spikes within burst, and noise cannot induce spikes from the quiescent state between bursts, which is cause for non-CR. The result provides a novel case of CR phenomenon and extends the scopes of CR concept, presents that noise can enhance rather than suppress information of the bursting patterns with spike undershoot, which are helpful for understanding the dynamics and the potential physiological or cognitive functions of the nerve fiber or brain neurons with such bursting patterns.
Keywords: Bursting, Coherence resonance, Spike undershoot, Bifurcation, Fast-slow variable dissection
Introduction
Neural electronic activities contain resting state, subthreshold oscillations, spiking, and bursting, and play important roles in achieving physiological or cognitive functions of the nervous system. Stochastic resonance (SR) or coherence resonance (CR) evoked by noise from resting state or subthreshold oscillations near bifurcation point to spiking or bursting have been widely investigated (Gu et al. 2001, 2002, 2015; Jia and Gu 2012, 2017; Longtin 1997; Pikovsky and Kurths 1997; Wu et al. 2001), which shows that noise plays positive roles in the nervous system (Benzi et al. 1981; Gammaitoni et al. 1998; Lindnera et al. 2004; McDonnell et al. 2015; Simakov and Pérez-Mercader 2013; Sun et al. 2016). SR refers to the phenomenon that an optimized response appears at a moderate noise intensity in nonlinear system driven by both noise and a weak periodic signal (Braun et al. 1994; Douglass et al. 1993; Levin and Miller 1996; Longtin et al. 1991; McDonnell and Abbott 2009), and CR is SR-like phenomenon in system without external signal (Gu et al. 2002, 2015; Pikovsky and Kurths 1997; Wu and Ma 2019). The stochastic firing induced by noise exhibits stochastic transitions between spikes (bursts) and subthreshold oscillations, which resemble the behaviors of some bursting patterns in appearance (Gu et al. 2015; Zhang et al. 2019). Many bursting patterns have been identified in the single neurons of the central nervous system which receives relatively strong synaptic noise, and the burst is suggested to be the unit of information process (Lisman 1997). However, the modulations of noise on bursting patterns have been put much less attention.
In appearance, the behavior of bursting is recurrent transition between burst containing multiple spikes and quiescent state or subthreshold oscillations (Izhikevich 2000a). Some bursting patterns exhibit spike undershoot characteristic, which means that the minimal value of the membrane potential of the spikes within burst is lower than the membrane potential of quiescent state or subthreshold oscillations. The bursting patterns with spike undershoot have been widely observed in the nerve fiber (Del Negro et al. 1998; Guttman and Barnhill 1970; Guttman et al. 1980), in the noncholinergic (putative GABAergic) neurons of medial septum and in many other cell types, including neocortical neurons, mitral cells in the olfactory bulb, magnocellular neuron in hypothalamus, mesencephalic trigeminal neurons, dorsal column nuclei neurons in culture, and hippocampal interneurons in the lacunosum-moleculare layer (Gireesh and Plenz 2008; Serafin et al. 1996; Wang 2002, 2010), which shows that the bursting patterns are involved with the physiological and cognitive functions of the related brain regions. For example, the representatives of such a bursting patten are shown in Fig. 4 of Wang (2010), which are related to in the Theta rhythms and even Gamma rhythm of entorhinal cortex and hippocampus. Therefore, the effects of noise on bursting patterns with spike undershoot are very important for understanding the dynamics and the potential physiological or cognitive function of the related neurons or brain regions. In addition, other bursting patterns do not manifest spike undershoot characteristic, i.e. that the minimal value of the membrane potential of the spikes within burst is higher than the membrane potential of quiescent state or subthreshold oscillations, for example, Fig. 5 in Wang (2010). Considering that more spikes (bursts) evoked from subthreshold oscillations at low or moderate noise intensity is the underling dynamics for the appearance of CR (Gu et al. 2015), we can speculate the effect of noise on bursting behaviors as follows: if noise can induce more bursts (spikes) from the quiescent state or subthreshold oscillations, CR may be evoked; if noise cannot induce more spikes from the the quiescent state or subthreshold oscillations, CR may not be induced. Therefore, the effect of noise on different bursting patterns should be studied to identify the appearance of CR or not. For example, the modulations of noise on bursting patterns with spike undershoot and without spike undershoot should be compared.
Fig. 4.
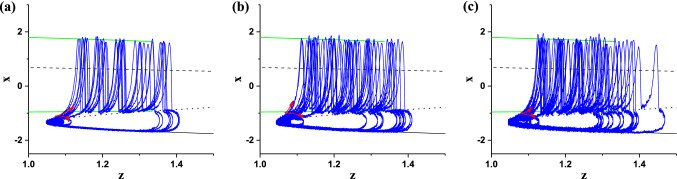
The (z, x) trajectory of the stochastic bursting (blue) at different levels of noise intensity D plotted with the bifurcations of the fast subsystem and the (z, x) projection of the resting state of the HR model when I = 1.25 (same as Fig. 3b). a D = 0.002; b D = 0.005; c D = 0.009. (Color figure online)
Fig. 5.
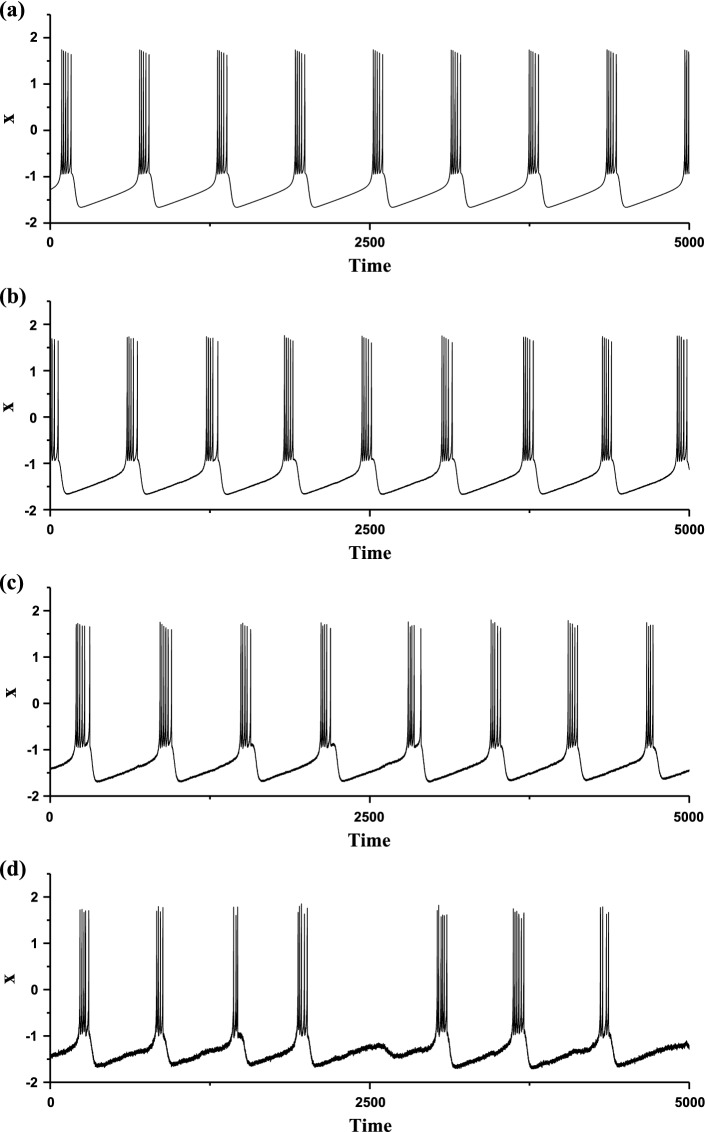
The membrane potentials of the HR model at different levels of noise intensity D when I = 1.3. a Deterministic period-5 bursting when D = 0; b stochastic bursting when D = 0.0002; c stochastic bursting when D = 0.0009; d stochastic bursting when D = 0.005
Theoretically, the bursting appears in the neuron model composed of fast and slow variables, and can be classified into different patterns with bifurcations acquired by fast-slow variable dissection method (Izhikevich 2000a, b, 2007). In recent studies, bifurcation and fast-slow variable dissection are widely used to identify the complex dynamics of bursting behaviors modulated by deterministic or stochastic modulations. For example, abnormal dynamics of bursting patterns modulated by self-feedback (autapse) or electromagnetic induction current (Cao et al. 2018; Jia et al. 2017; Li et al. 2019; Wu et al. 2019; Wu and Gu 2020) are identified with fast-slow variable dissection method, which shows that the firing frequency of bursting patterns increases rather than decreases with increasing inhibitory effect. Especially, the complex stochastic dynamics of bursting patterns modulated by noise are identified with fast-slow variable dissection method and trajectory of bursting patterns in phase plane (Li and Gu 2017). Furthermore, the famous type I bursting is simulated in the Hindmarsh–Rose model and Chay model and observed in the biological experiments on various nervous systems, which exhibits non-spike undershoot characteristic and is classified to be “Fold/Homoclinic” bursting with fast-slow variable dissection method. A kind of type III bursting or sub-Hopf ellitic bursting simulated in the FitzHugh–Rinzel model and observed in the experiment on giant nerve fiber is classified into “Sub-Hopf/Fold” bursting (Del Negro et al. 1998; Guttman and Barnhill 1970; Guttman et al. 1980) and manifests spike undershoot characteristic. Although the “Sub-Hopf/Fold” bursting observed in the experiment resembles stochastic firing (Gu et al. 2015) and noise is inevitable in the real nervous system (Faisal et al. 2008), the modulations of noise on the “Sub-Hopf/Fold” bursting remain unclear.
In the present paper, the effect of noise on the“Sub-Hopf/Fold” bursting with spike undershoot and the “Fold/Homoclinic” bursting without spike undershoot is compared. The “Sub-Hopf/Fold” bursting with spike undershoot exhibits CR, which is characterized by the increase firstly and then decrease of the peak value of power spectrum of stochastic bursting trains, while the “Fold/Homoclinic” bursting dose not. Furthermore, the dynamical mechanism for CR evoked from the “Sub-Hopf/Fold” bursting and for CR not induced from the “Fold/Homoclinic” bursting are identified with the fast-slow variable dissection method. For the “Sub-Hopf/Fold” bursting, the stable node of the fast subsystem, which corresponds to the subthreshold oscillations of the bursting, is within and very close to the stable limit cycle of the fast subsystem, which corresponds to the spikes within burst. Therefore, novel spikes to form burst can be evoked from the quiescent state (stable focus) by noise, which is the underlying mechanism for CR evoked from the “Sub-Hopf/Fold” bursting with spike undershoot. For the “Fold/Homoclinic” bursting, the stable node of the fast subsystem (the quiescent state of the bursting) is outside of and far from the stable limit cycle of the fast subsystem (the spikes within burst). Therefore, no novel spikes can be induced from the quiescent state of the “Fold/Homoclinic” bursting without spike undershoot, which can not induce CR. Such a result presents a novel case of CR that noise can enhance information of bursting and the corresponding bifurcation mechanism, which is different from the previous investigations wherein CR is always evoked from the resting state. Such a result is helpful for identifying the stochastic dynamics and potential physiological or cognitive of nerve fiber or neurons of brain with bursting patterns with spike undershoot.
Theoretical model and methods
Deterministic and stochastic Hindmarsh–Rose models
The Hindmarsh–Rose (HR) model is widely used to describe the deterministic neuronal bursting patterns and stochastic dynamics of resting state near the bursting pattern. For example, CR induced from the resting state near the bifurcation to bursting pattern has been investigated (Longtin 1997). In addition, the HR model can simulate the type I bursting or “Fold/Homoclinic” bursting. In the present paper, the HR model is used and is described as follows:
| 1 |
| 2 |
| 3 |
where x is the membrane potential, y is the recovery variable, and z is the slow adjusting variable. The parameter I is the background current. The parameter values are given as follows: a = 1, b = 3, c = 1, d = 5, s = 4, r = 0.001, = −1.6. The parameter I is taken as the control parameter.
When a Gaussian white noise is introduced into Eqs. (1), (2) and (3) remain unchanged, the stochastic HR model is formed, and the first equation is shown as follows:
| 4 |
The characteristics of are as follows: = 0 and = 2 , where D is the noise intensity, means the average, and is the Dirac -function.
Deterministic and stochastic FitzHugh–Rinzel models
The “Sub-Hopf/Fold” bursting can be simulated in FitzHugh–Rinzel model described as follows (Izhikevich 2000a):
| 5 |
| 6 |
| 7 |
The variables V and w represent the membrane potential and the recovery variable, and y is a slow variable to modulate the slow dynamics of membrane current. The FitzHugh–Rinzel model is dimensionless, and the parameter values are as follows: = 0.3125, = 0.7, = 0.8, = −0.775, = 1, = 0.08, and = 0.0001.
After introducing to the first equation (Eq. (5)) of the deterministic FitzHugh–Rinzel model to form the first equation of the stochastic FitzHugh–Rinzel model, which is shown as follows:
| 8 |
The second and last equations of the stochastic FitzHugh–Rinzel model are the same as those of the deterministic model.
Fast and slow subsystems
For both the HR model and the FitzHugh–Rinzel model, the third equation is the slow subsystem and the the third variable is the slow variable, and the first two equations with the slow variable regarded as bifurcation parameter are the fast subsystem.
Methods
Both the deterministic and stochastic HR model and FitzHugh–Rinzel model are integrated using a Mannella numerical integration method (Mannella and Palleschi 1989) and the integration time step is chosen as 0.001. The bifurcations are acquired with software of XPPAUT (Ermentrout 2002).
Measure to characterize coherence resonance
The power spectrum of bursting trains, which has been widely used to characterize CR (Gu et al. 2015; Pikovsky and Kurths 1997), is used in the present paper. The power spectrum of x(t) for the HR model and V(t) for the FitzHugh–Rinzel model is acquired with the Fast Fourier Transform (FFT). If the peak value of power spectrum increases firstly and then decreases with increasing noise intensity D, CR is evoked.
Results
CR evoked from resting state and bifurcations of the HR model
CR evoked from the resting state
When I = 1.25, the behavior of the deterministic HR model is resting state, as shown in Fig. 1a. When noise is introduced, stochastic bursting with multiple spikes per burst is evoked, and the intervals between two continual bursts are approximately 606.06, as shown in Fig. 1b–d. With increasing noise intensity D, bursts appear more frequently, and the intervals between bursts become more irregular. Therefore, the peak values of the power spectrums of the stochastic bursting patterns exhibit increase firstly and then decrease, as shown in Fig. 2a and b, which shows that CR is evoked from the resting state by noise. The main frequency of stochastic bursting is about 0.00165, which corresponds to the intervals between two continual bursts (about 606.06). Such a result has been reported in Longtin (1997) and is reproduced in the present paper to be compared with the effect of noise on two kinds of deterministic bursting patterns and to be self-contained.
Fig. 1.
The membrane potential of the HR model when I = 1.25 at different levels of noise intensity D. a Resting state when D = 0; b stochastic bursting when D = 0.002; c stochastic bursting when D = 0.005; d stochastic bursting when D = 0.009
Fig. 2.
Characteristics of power spectrum of the stochastic bursting patterns. a Power spectrum of stochastic bursting with different levels of noise intensity D; red (D = 0.002), blue (D = 0.005), and green (D = 0.009); b changes of the peak value of power spectrum with increasing D values. (Color figure online)
Identification of stochastic bursting behaviors with bifurcations
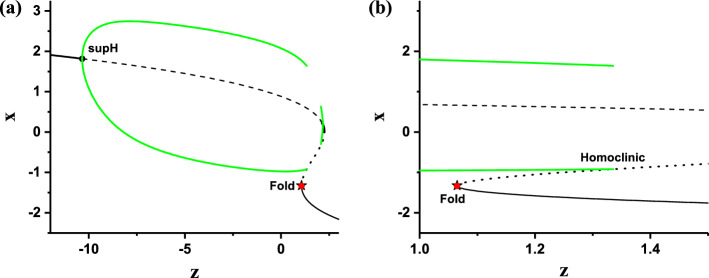
When I = 1.25, the bifurcations of the fast subsystem with respect to z are acquired to investigate the dynamics of the stochastic bursting. The equilibrium point of the fast subsystem of the HR model shows a Z-shaped curve, as shown in Fig. 3a. The middle (dotted line) and lower (black thin solid line) branches are the saddle and stable node, respectively. The intersection point between the middle and lower branches corresponds to a saddle-node bifurcation or fold bifurcation of equilibrium at z 1.08, as shown by “Fold” in Fig. 3. On the upper branch, the fast subsystem exhibits a supercritical Hopf bifurcation (labeled with supH in Fig. 3a) at z 10.30. Via the Hopf bifurcation point, the stable focus (black bold solid line) changes to an unstable focus (dashed line) and meanwhile a stable limit cycle with maximal (upper green) and minimal (lower green) values appears. The stable limit cycle intersects with the saddle on the middle branch to form a homoclinic orbit and terminates at z 1.33, as shown by the “Homoclinic” in Fig. 3b.
Fig. 3.
Fast-slow variable dissection to the resting state. a Bifurcations of the fast subsystem of the HR model with respect to z and the projection (red circle) of the resting state in (z, x) plane; b enlargement of a
The (z, x) projection of the resting state (the stable equilibrium) of the HR model is shown by the red star in Fig. 3a and b, which corresponds to a stable node of the fast subsystem and locates at the left end of the lower branch. Figure 3b is the enlargement of the Fig. 3a.
The (z, x) trajectory of the stochastic bursting (blue), and the bifurcations of the fast subsystem and the (z, x) projection of the resting state (same as Fig. 3b) are plotted in one figure, as shown in Fig. 4. It can be found that noise can evoke burst from the stable node at some time or subthreshold oscillations around the stable node (red point) at other time. The generation of the burst or subthreshold oscillations and running directions of (z, x) trajectory are shown by the arrows. The burst terminates via the Homoclinic bifurcation, and the quiescent state runs along the stable node of the fast subsystem. Therefore, the novel burst containing multiple spikes evoked from the stable node of the fast subsystem is the cause of CR evoked from the resting state of the HR model.
CR not evoked from “Fold/Homoclinic” bursting without spike undershoot and bifurcations of the HR model
Peak of the power spectrum decreases with increasing noise intensity
When I = 1.3, the deterministic HR model (D = 0) exhibits a period-5 bursting pattern, which belongs to “Fold/Homoclinic” bursting without spike undershoot, as shown in Fig. 5a. The bursting without spike undershoot means that the minimal membrane potential within burst is larger than that of the quiescent state, i.e. the levels of membrane potential of the quiescent state is outside of the range of the membrane potential of the burst. This is a most important characteristic of the “Fold/Homoclinic” bursting without spike undershoot. The interburst interval of period-5 bursting is about 606.06.
After introducing noise, the bursting is disturbed by noise, and the stochastic bursting patterns with different levels of noise intensity D are shown in Fig. 5b–d. With increasing D values, no novel bursts are evoked from the quiescent state, and the interburst intervals of the stochastic bursting patterns become irregular. For example, burst with not 5 spikes appears when D = 0.0009, as shown in Fig. 5c, or certain burst is suppressed to form subthreshold oscillation when D = 0.005, as depicted in Fig. 5d. Therefore, with increasing D values, the dominant peak values of the power spectrum of the stochastic bursting decrease, as shown in Fig. 6. The dominant frequency of stochastic bursting is about 0.00165, which approximately corresponds to the interburst interval (606.06). The most obvious characteristics of the stochastic bursting are that the bursts are suppressed, which is very different from the enhancement of stochastic bursting evoked from the resting state.
Fig. 6.
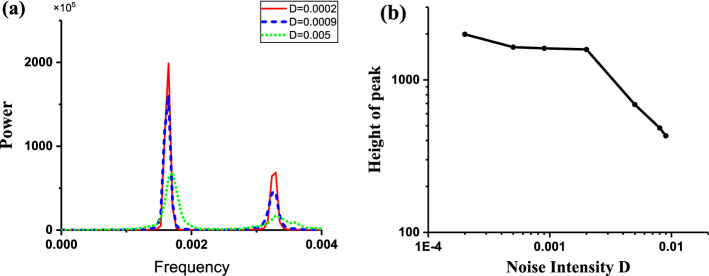
Characteristics of power spectrum of the stochastic bursting patterns of the HR model with I = 1.3. a Power spectrum of stochastic bursting at different levels of noise intensity D; red (D = 0.0002), blue (D = 0.0009), and green (D = 0.005); b changes of peak values of power spectrum with increasing D values. (Color figure online)
Characteristics of the “Fold/Homoclinic” bursting without spike undershoot
When I = 1.3, the bifurcation structures of the fast subsystem of the HR model resemble those of I = 1. 25, as shown in Fig. 7a, except for the small changes of parameter value of bifurcation point. The (z, x) trajectory of the deterministic period-5 bursting (red) is plotted with the bifurcations of the fast subsystem, as shown in Fig. 7b and c. Figure 7c is the enlargement of Fig. 7b. The behavior of burst begins from the Fold bifurcation, runs along the stable limit cycle of the fast subsystem 5 circles from left to right, terminates at the bifurcation of Homoclinic orbit to initiate the behavior of quiescent state, and the quiescent state terminates at the Fold bifurcation. Such a result shows that the period-5 bursting belongs to “Fold/Homoclinic” bursting pattern.
Fig. 7.
Fast-slow variable dissection to bursting of the HR model when I = 1.3. a Bifurcations of the fast subsystem with respect to z; b the (z, x) trajectory (blue) of the period-5 bursting and the bifurcations of the fast subsystem (same as a) are plotted in one figure; c enlargement of b; d the stable node (black star) and the stable limit cycle (green) in (y, x) plane of fast subsystem when z = 1.27. (Color figure online)
As can be found from Fig. 7c, the minimal membrane potential within the burst corresponds to the minimal value (lower green) of the stable limit cycle of the fast subsystem, and the quiescent state of the bursting corresponds to the stable node (black solid) of the fast subsystem. The minimal value (lower green) of the stable limit cycle of the fast subsystem is much higher than the membrane potential of the stable node (black solid). Such a result can be further found from the dynamics in (y, x) plane, as shown in Fig. 7d (z = 1.27). The green cycle represents the stable limit cycle of the fast subsystem and the black star represents the stable node. Except that the membrane potential of the limit cycle is higher than the membrane potential of the stable node, another important characteristic is that the stable node locates outside of the stable limit cycle and is very far from the stable limit cycle. Such characteristics of the “Fold/Homoclinic” bursting without spike undershoot can be used to explain the cause that no spikes evoked from the quiescent state between bursts.
Dynamics of the stochastic bursting
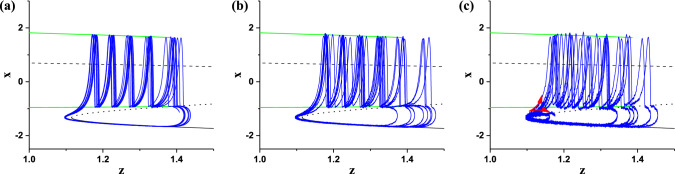
The (z, x) trajectory of the stochastic bursting (blue), and the bifurcations of the fast subsystem are plotted in one figure, as shown in Fig. 8. Figure 8a–c correspond to D = 0.002, 0.005, and 0.009, respectively. When noise intensity D is relative small (D = 0.002 and 0.005), the transition from stable node to limit cycle happens near the Fold point, which resembles the deterministic period-5 bursting. And no other transitions from the stable node to the stable limit cycle appear and advance the Fold point, which is due to the long distance between the stable node and the stable limit cycle of the fast subsystem, i.e. the characteristic of bursting without spike undershoot. On the contrary, when noise intensity is large (D = 0.009), except for the transitions from the stable node to the limit cycle (the upper arrow), some transitions from the quiescent state to the burst are disturbed to form the subthreshold oscillations around the stable node, as depicted by the lower arrow in Fig. 8c. Therefore, the suppression or disappearance of certain bursts is the cause of CR not evoked from the deterministic bursting without spike undershoot.
Fig. 8.
The (z, x) trajectory of the stochastic bursting (blue) at different levels of noise intensity D plotted with the bifurcations of the fast subsystem of HR model when I = 1.3. a D = 0.002; b D = 0.005; c D = 0.009. (Color figure online)
It should be noticed that if noise intensity D is strong enough to induce transitions from the stable node to the limit cycle and prior to the Fold point, complex stochastic bursting patterns may be evoked, which is not investigated in the present paper and will be studied in future.
CR evoked from “Sub-Hopf/Fold” bursting with spike undershoot and bifurcations of the FitzHugh–Rinzel model
CR evoked from bursting with spike undershoot
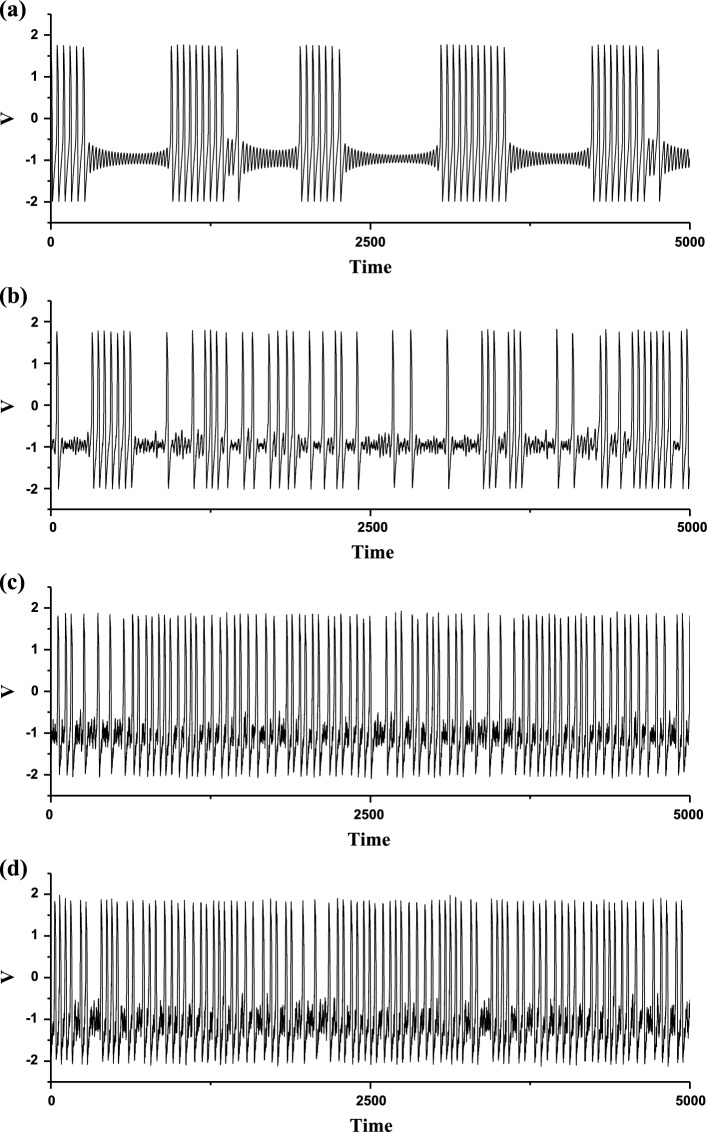
The deterministic FitzHugh–Rinzel model (D = 0) exhibits a “Sub-Hopf/Fold” bursting pattern with spike undershoot, as shown in Fig. 9a. The “Sub-Hopf/Fold” bursting pattern is called sub-Hopf elliptic bursting in Izhikevich (2000a). The bursting exhibits the transitions between subthreshold oscillations and burst and the spike undershoot characteristic, which is different from the “Fold/Homoclinic” bursting without spike undershoot characteristic. Therefore, the membrane potential of the subthreshold oscillations is within the range of the membrane potential of the burst, which is the most important characteristic of the “Sub-Hopf/Fold” bursting with spike undershoot. In addition, there are two other important characteristics of “Sub-Hopf/Fold” bursting. One is that the interspike intervals within the burst is nearly fixed (approximate 52.63), and the other is that some durations of subthreshold oscillations are relatively long.
Fig. 9.
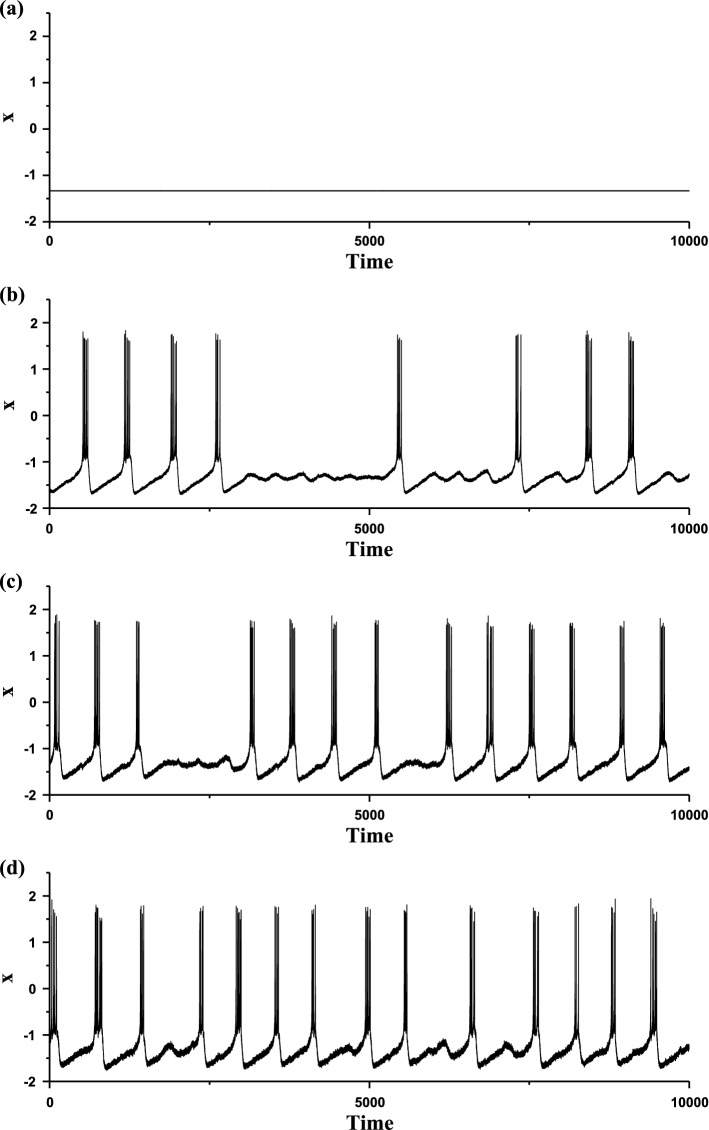
The membrane potentials of the FitzHugh–Rinzel model at different levels of noise intensity D. a Deterministic bursting when D = 0; b stochastic bursting when D = 0.0005; c stochastic bursting when D = 0.006; d stochastic bursting when D = 0.01
The three characteristics of “Sub-Hopf/Fold” bursting determine that noise plays important roles in influencing the bursting behaviors. During the long duration of the subthreshold oscillations, noise can induce novel spikes. The membrane potentials of the stochastic bursting patterns at different levels of noise intensity D are show in Fig. 9b–d. With increasing D values, the spikes become more and more and the durations of subthreshold oscillations become shorter and shorter. For example, as D values increase from 0.0005 (Fig. 9b), to 0.006 (Fig. 9c), and to 0.01 (Fig. 9d), the mean interspike intervals decrease from 96.45, to 61.89, and to 56.59. In addition, as noise intensity D increases to a level such as D = 0.01, the interspike intervals become more irregular, as shown in Fig. 9d. Such results are different from those of the “Fold/Homoclinic” bursting with noise.
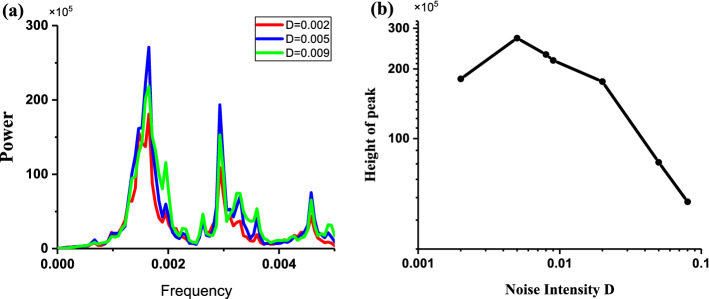
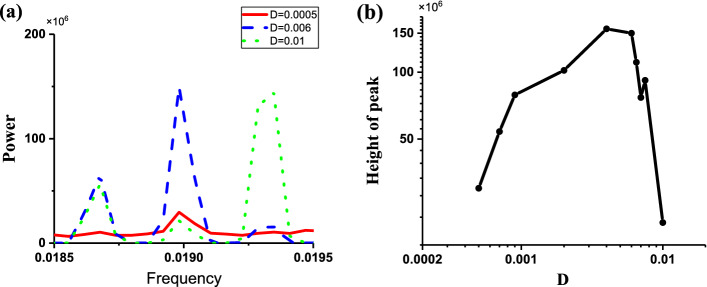
The power spectrums of the stochastic bursting trains at different levels of noise intensity D are depicted in Fig. 10. The frequency is about 0.019, which corresponds to the fixed interspike intervals (about 52.63). The peak value of power spectrum for D = 0.006 (Blue) is larger than those for D = 0.0005 (Red) and D = 0.01 (Green), as shown in Fig. 10a. The peak values of the power spectrum increase firstly and then decrease with increasing D values, as illustrated in Fig. 10b, which shows that CR is evoked from the “Sub-Hopf/Fold” bursting pattern with spike undershoot. The increase and decrease of the peak values is mainly induced by the increase of the spike rate and the decrease of the regularity of the spike trains or interspike intervals, respectively.
Fig. 10.
Characteristics of power spectrum of the stochastic bursting patterns of the FitzHugh–Rinzel model. a Power spectrum of stochastic bursting at different levels of noise intensity D; red (D = 0.0005), blue (D = 0.006), and green (D = 0.01); b changes of peak values of power spectrum with increasing D values. (Color figure online)
It should be pointed out that if the noise intensity D is much stronger, more complex stochastic bursting patterns may be evoked, which will be studied in future.
Dynamics of “Sub-Hopf/Fold” bursting with spike undershoot
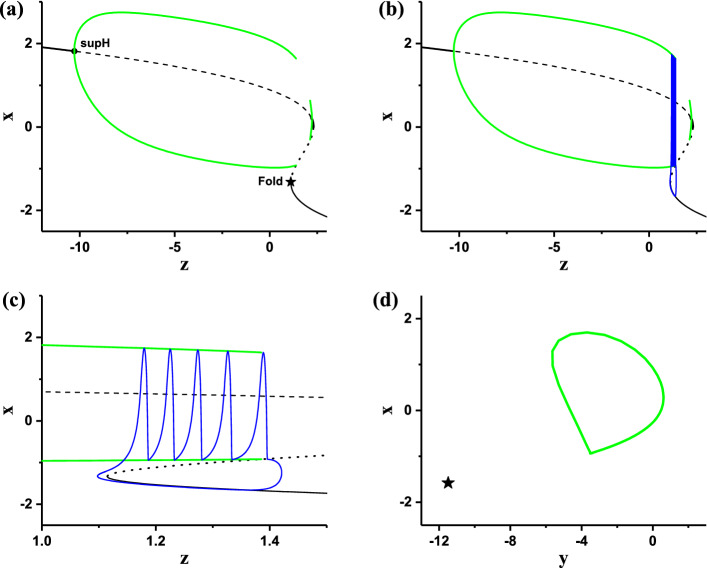
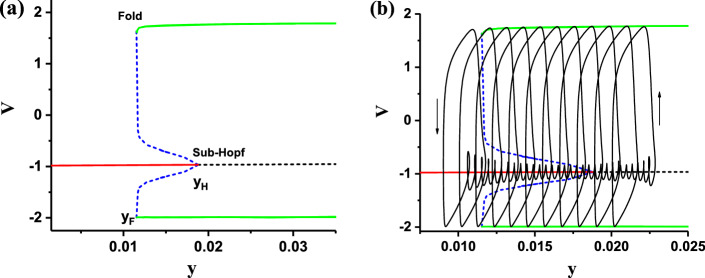
The bifurcations of the fast subsystem of the FitzHugh–Rinzel model with respect to y are shown in Fig. 11a. With increasing y, the stable focus (solid red) changes to unstable focus (black dash) via a subcritical Hopf bifurcation point (labeled with “Sub-Hopf” in Fig. 11a) at 0.01186, meanwhile, an unstable limit cycle appears. The maximal (minimal) value of the unstable limit cycle is represented by the upper (lower) dashed blue curve. The unstable limit cycle collides with a stable limit cycle corresponding to the spike within burst to form a fold or saddle-node bifurcation (labeled with “Fold” in Fig. 11a) of the limit cycle at 0.01152. The maximal (minimal) value of the stable limit cycle is represented by the upper (lower) green curve.
Fig. 11.
The fast-slow variable dissection to the “Sub-Hopf/Fold” bursting of the FitzHugh–Rinzel model. a Bifurcations of fast subsystem with respect to y; b the trajectory of the “Sub-Hopf/Fold” bursting (y, V) and the bifurcations of fast subsystem (same as a) plotted in one figure. (Color figure online)
The (y, v) trajectory of the deterministic “Sub-Hopf/Fold” bursting and the bifurcations of the fast subsystem of the FitzHugh–Rinzel model are plotted in one figure, as depicted in Fig. 11b. The spikes within the burst oscillate between the maximal (upper green) and minimal (lower green) values of the stable limit cycle of the fast subsystem and runs from right to left, which leads to that the burst terminates via the Fold bifurcation of the limit cycle of the fast subsystem. After then, the subthreshold oscillations oscillate around the stable focus firstly and then around the unstable focus via a low passage effect from left to right. The oscillation amplitude decreases before the “Sub-Hopf” point and increases after the “Sub-Hopf” point. As the amplitude of the subthreshold oscillations increases to a value large enough, the subthreshold oscillations will change to spikes to form burst. Therefore, such a bursting belongs to “Sub-Hopf/Fold” bursting. The minimal value of membrane potential of the burst corresponds to the minimal value (lower green) of the stable limit cycle of the fast subsystem, and is lower than the membrane potential of subthreshold oscillations, which shows the spike undershoot characteristic.
Dynamics of the stochastic bursting
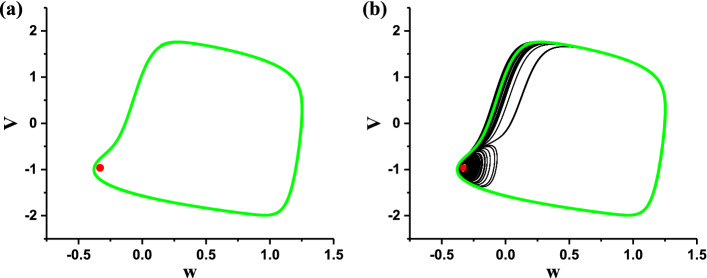
The spike undershoot characteristic of the “Sub-Hopf/Fold” bursting can also be found from dynamics of the fast subsystem in plane (w, V), as shown in Fig. 12a. For example, when y = 0.017, the stable focus (red point) of the fast subsystem locates inside of and is very close to the coexisting stable limit cycle (green) of the fast subsystem. For the deterministic “Sub-Hopf/Fold” bursting, the slow variable modulates the (w, V) trajectory (black) of bursting alternated between the subthreshold oscillations around the focus (red point) and the spikes within burst along the stable limit cycle (green), as shown in Fig. 12b.
Fig. 12.
Dynamics in plane (w, V) of the fast subsystem of the FitzHugh–Rinzel model. The stable focus (red point) locates inside of and is very close to the coexisting stable limit cycle (green); b The (w, V) trajectory of the deterministic “Sub-Hopf/Fold” bursting (blue) and the dynamics of the fast subsystem (same as a) are plotted in one figure. (Color figure online)
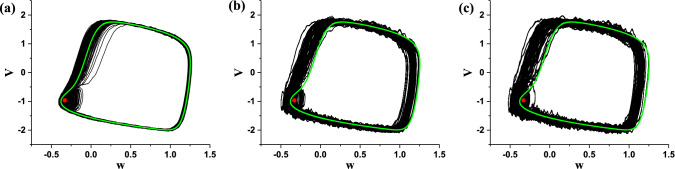
When noise intensity D = 0.0005, 0.006, and 0.01, the (w, V) trajectory (black) of the stochastic bursting, and the stable focus (red point) and stable limit cycle (green) are potted in one figure, as depicted in Fig. 13a–c. With increasing noise intensity (D), the transitions from the subthreshold oscillations to spikes become more frequently, which is due to the very close distance between the stable focus and the coexisting stable limit cycle, and the spikes (or interspike intervals) become more irregular, which is the cause of CR evoked from the deterministic “Sub-Hopf/Fold” bursting with spike undershoot.
Fig. 13.
The (w, V) trajectory (black) of the stochastic bursting with different levels of noise intensity D, and the stable focus (red point) and stable limit cycle (green) are potted in one figure. a D = 0.0005; b D = 0.006; c D = 0.01. (Color figure online)
Discussion and conclusion
For most investigation of single neurons, SR or CR phenomenon is evoked from the resting state near bifurcation (Gu et al. 2001, 2002, 2015; Jia and Gu 2017; Pikovsky and Kurths 1997). In the present paper, CR evoked from a “Sub-Hopf/Fold” bursting with spike undershoot instead of the resting state is simulated. Such a result presents important significance in 3 aspects. Firstly, such a result presents a novel case of CR phenomenon evoked from not resting state but bursting behavior, which extends the scope of the CR concept. Secondly, such a result presents the novel effects of noise on the bursting patterns with spike undershoot, which shows that noise can enhance rather than suppress information of bursting patterns with spike undershoot. Considering that bursting patterns with spike undershoot have been widely observed in the nerve fiber (Del Negro et al. 1998; Guttman and Barnhill 1970; Guttman et al. 1980; Izhikevich 2000a) and many cell types of brain (Gireesh and Plenz 2008; Serafin et al. 1996; Wang 2002, 2010), such a result implies that noise induced-enhancement of information of bursting patterns with spike undershoot is involved with achievement of physiological or cognitive functions in the related nervous systems. Thirdly, the dynamics of bursting pattern with spike undershoot observed in both nerve fiber and brain neurons (Gireesh and Plenz 2008; Serafin et al. 1996; Wang 2002, 2010) are explained. In the present paper, the bursting patterns are suggested to be stochastic firing patterns.
The dynamical mechanism for the CR phenomenon evoked from “Sub-Hopf/Fold” bursting with spike undershoot can be interpreted with bifurcations acquired with fast-slow variable dissection method (Izhikevich 2000a, b, 2007). The behavior of “Sub-Hopf/Fold” bursting is transition between subthreshold oscillations and burst, the durations of most subthreshold oscillations are relatively long, and the spikes within burst exhibit nearly fixed interspike intervals. The subthreshold oscillations correspond to a focus near a subcritical Hopf bifurcation of the fast subsystem of the FitzHugh–Rinzel model, and the spikes within burst is related to the stable limit cycle of the fast subsystem. The focus and stable limit cycle coexist in the fast subsystem, and the stable focus locates inside of and very close to the stable limit cycle. When noise is introduced, noise can induce more spikes from some subthreshold oscillations, which leads to that the spike rate becomes higher (peak values of the power spectrum increase) and the regularity of spikes becomes lower (peak values of the power spectrum decrease) with increasing noise intensity. Therefore, CR phenomenon is evoked from the “Sub-Hopf/Fold” bursting with spike undershoot.
Furthermore, with help of bifurcations, the dynamical mechanism for CR not evoked from the “Fold/Homoclinic” bursting without spike undershoot can be explained. The “Fold/Homoclinic” bursting exhibits transition between quiescent sate and spikes within a burst. For the fast subsystem, a stable node and the coexist stable limit cycle correspond to the quiescent state and spikes within burst, respectively. The stable node is far from and outside of the stable limit cycle. Noise cannot induce spikes from the quiescent state(stable node) but disturb certain bursts. Therefore, CR cannot be evoked from the “Fold/Homoclinic” bursting without spike undershoot. In future, the effect of strong noise on “Fold/Homoclinic” bursting and the effect of noise other bursting patterns mentioned in Izhikevich 2000a will be studied to acquire the comprehensive and deep views on the effect of noise on bursting patterns. In addition, except for the single neuron, CR has been observed in the biological experiment on neuronal network (Kim et al. 2015), which shows that noise play important roles in modulating dynamical behaviors of the network such as phase change of bursting (Cagnan et al. 2019; Kim et al. 2019). In future, the CR for network with bursting behaviors should be studied.
Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grant Nos. 11872276 and 11572225, and 11762001.
Author Contributions
HG conceived the experiments, BC, RW, HG, and YL conducted the experiments, HG, BC, RW, and YL analyzed the results, BC and HG written the paper. All authors reviewed the manuscript.
Compliance with ethical standards
Conflict of interest
The authors declare no competing financial interests.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Benzi R, Sutera A, Vulpiani A. Stochastic resonance in climatic change. J Phys A. 1981;14:L453–L457. doi: 10.1111/j.2153-3490.1982.tb01787.x. [DOI] [Google Scholar]
- Braun HA, Wissing H, Schäfer K, Hirsch MC. Oscillation and noise determine signal transduction in shark multimodal sensory cells. Nature. 1994;367:270–273. doi: 10.1038/367270a0. [DOI] [PubMed] [Google Scholar]
- Cagnan H, Mallet N, Moll CKE, Gulberti A, Holt AB, Westphal M, Gerloff C, Engel AK, Hamel W, Magill PJ, Brown P, Sharott A. Temporal evolution of beta bursts in the parkinsonian cortical and basal ganglia network. Proc Natl Acad Sci USA. 2019;116:16095–16104. doi: 10.1073/pnas.1819975116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao B, Guan LN, Gu HG. Bifurcation mechanism of not increase but decrease of spike numbers within a neural burst induced by excitatory effect. Acta Phys Sin. 2018;67(24):240502. doi: 10.7498/aps.67.20181675. [DOI] [Google Scholar]
- Del Negro CA, Hsiao CF, Chandler SH, Garfinkel A. Evidence for a novel bursting mechanism in rodent trigeminal neurons. Biophys J. 1998;75:174–182. doi: 10.1016/S0006-3495(98)77504-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Douglass JK, Wilkens L, Pantazelou E, Moss F. Noise enhancement of information transfer in crayfish mechanoreceptors by stochastic resonance. Nature. 1993;365:337–340. doi: 10.1038/365337a0. [DOI] [PubMed] [Google Scholar]
- Ermentrout B. Simulating, analyzing, and animating dynamical systems: a guide to XPPAUT for researchers and students. Philadelphia: SIAM; 2002. [Google Scholar]
- Faisal AA, Selen LP, Wolpert DM. Noise in the nervous system. Nat Rev Neurosci. 2008;9(4):292–303. doi: 10.1038/nrn2258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gammaitoni L, Hanggi P, Jung P, Marchesoni F. Stochastic resonance. Rev Mod Phys. 1998;70:223–287. doi: 10.1103/RevModPhys.70.223. [DOI] [Google Scholar]
- Gireesh E, Plenz D. Neuronal avalanches organize as nested theta- and beta/gamma-oscillations during development of cortical layer 2/3. Proc Natl Acad Sci USA. 2008;105:7576–7581. doi: 10.1073/pnas.0800537105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu HG, Ren W, Lu QS, Wu SG, Yang MH, Chen WJ. Integer multiple spiking in neural pacemakers without external periodic stimulation. Phys Lett A. 2001;285:63–68. doi: 10.1016/S0375-9601(01)00278-X. [DOI] [Google Scholar]
- Gu HG, Yang MH, Li L, Liu ZQ, Ren W. Experimental observation of the stochastic bursting caused by coherence resonance in a neural pacemaker. NeuroReport. 2002;13(13):1657–1660. doi: 10.1097/00001756-200209160-00018. [DOI] [PubMed] [Google Scholar]
- Gu HG, Zhao ZG, Jia B, Chen SG. Dynamics of on-off neural firing patterns and stochastic effects near a sub-critical Hopf bifurcation. PloS One. 2015;10(4):e0121028. doi: 10.1371/journal.pone.0121028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guttman R, Barnhill R. Oscillation and repetitive firing in squid axons: comparison of experiments with computations. J Gen Physiol. 1970;55:104–118. doi: 10.1085/jgp.55.1.104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guttman R, Lewis S, Rinzel J. Control of repetitive firing in squid axon membrane as a model for a neuroneoscillator. J Physiol. 1980;305:377–395. doi: 10.1113/jphysiol.1980.sp013370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izhikevich EM. Subcritical elliptic bursting of Bautin type. SIAM J Appl Math. 2000;60(2):503–535. doi: 10.1137/S003613999833263X. [DOI] [Google Scholar]
- Izhikevich EM. Neural excitability, spiking and bursting. Int J Bifurc Chaos. 2000;10(6):1171–1266. doi: 10.1142/S0218127400000840. [DOI] [Google Scholar]
- Izhikevich EM. Dynamical systems in neuroscience: the geometry of excitability and bursting. London: MIT Press; 2007. [Google Scholar]
- Jia B, Gu HG. Identifying type I excitability using dynamics of stochastic neural firing patterns. Cogn Neurodyn. 2012;6(6):485–497. doi: 10.1007/s11571-012-9209-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jia B, Gu HG. Dynamics and physiological roles of stochastic neural firing patterns near bifurcation points. Int J Bifurc Chaos. 2017;27(7):1750113. doi: 10.1142/S0218127417501139. [DOI] [Google Scholar]
- Jia B, Gu HG, Xue L. A basic bifurcation structure from bursting to spiking of the injured nerve fibers in a two-dimensional parameter space. Cogn Neurodyn. 2017;11(2):189–200. doi: 10.1007/s11571-017-9422-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim JH, Lee HJ, Min CH, Lee KJ. Coherence resonance in bursting neural networks. Phys Rev E. 2015;92(4):042701. doi: 10.1103/PhysRevE.92.042701. [DOI] [PubMed] [Google Scholar]
- Kim JH, Lee HJ, Choi W, Lee KJ. Encoding information into autonomously bursting neural network with pairs of time-delayed pulses. Sci Rep. 2019;9:1394. doi: 10.1038/s41598-018-37915-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levin JE, Miller JP. Broadband neural encoding in the cricket cereal sensory system enhanced by stochastic resonance. Nature. 1996;380:165–168. doi: 10.1038/380165a0. [DOI] [PubMed] [Google Scholar]
- Li YY, Gu HG. The distinct stochastic and deterministic dynamics between period-adding and period-doubling bifurcations of neural bursting patterns. Nonlinear Dyn. 2017;87(4):2541–2562. doi: 10.1007/s11071-016-3210-6. [DOI] [Google Scholar]
- Li YY, Gu HG, Ding XL. Bifurcations of enhanced neuronal bursting activities induced by the negative current mediated by inhibitory autapse. Nonlinear Dyn. 2019;97(4):2091–2105. doi: 10.1007/s11071-019-05106-2. [DOI] [Google Scholar]
- Lindnera B, García-Ojalvob J, Neiman A, Schimansky-Geiere L. Effects of noise in excitable systems. Phys Rep. 2004;392:321–424. doi: 10.1016/j.physrep.2003.10.015. [DOI] [Google Scholar]
- Lisman JE. Bursts as a unit of neural information: making unreliable synapses reliable. Trends Neurosci. 1997;20(1):38–43. doi: 10.1016/S0166-2236(96)10070-9. [DOI] [PubMed] [Google Scholar]
- Longtin A. Autonomous stochastic resonance in bursting neurons. Phys Rev E. 1997;55(1):868–876. doi: 10.1103/PhysRevE.55.868. [DOI] [Google Scholar]
- Longtin A, Bulsara A, Moss F. Time-interval sequences in bistable systems and the noise-induced transmission of information by sensory neurons. Phys Rev Lett. 1991;67(5):656–659. doi: 10.1103/PhysRevLett.67.656. [DOI] [PubMed] [Google Scholar]
- Mannella R, Palleschi V. Fast and precise algorithm for compute simulation of stochastic differential equations. Phys Rev A. 1989;40:3381–3386. doi: 10.1103/PhysRevA.40.3381. [DOI] [PubMed] [Google Scholar]
- McDonnell MD, Abbott D. What is stochastic resonance? Definitions, misconceptions, debates, and its relevance to biology. PLoS Comput Biol. 2009;5(5):e1000348. doi: 10.1371/journal.pcbi.1000348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDonnell MD, Iannella N, To MS, Tuckwell HC, Jost J, Gutkin BS, Ward LM. A review of methods for identifying stochastic resonance in simulations of single neuron models. Network. 2015;26(2):35–71. doi: 10.3109/0954898X.2014.990064. [DOI] [PubMed] [Google Scholar]
- Pikovsky AS, Kurths J. Coherence resonance in a noise-driven excitable system. Phys Rev Lett. 1997;78:775–778. doi: 10.1103/PhysRevLett.78.775. [DOI] [Google Scholar]
- Serafin M, Williams S, Khateb A, Fort P, Muhlethaler M. Rhythmic firing of medial septum non-cholinergic neurons. Neuroscience. 1996;75:671–675. doi: 10.1016/0306-4522(96)00349-1. [DOI] [PubMed] [Google Scholar]
- Simakov DS, Pérez-Mercader J. Noise induced oscillations and coherence resonance in a generic model of the nonisothermal chemical oscillator. Sci Rep. 2013;3:2404. doi: 10.1038/srep02404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun GQ, Jusup M, Jin Z, Wang Y, Wang Z. Pattern transitions in spatial epidemics: mechanisms and emergent properties. Phys Life Rev. 2016;19:43–73. doi: 10.1016/j.plrev.2016.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang XJ. Pacemaker neurons for the theta rhythm and their synchronization in the septohippocampal reciprocal loop. J Neurophysiol. 2002;87:889–900. doi: 10.1152/jn.00135.2001. [DOI] [PubMed] [Google Scholar]
- Wang XJ. Neurophysiological and computational principles of cortical rhythms in cognition. Physiol Rev. 2010;90:1195–1268. doi: 10.1152/physrev.00035.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu FQ, Gu HG. Bifurcations of negative responses to positive feedback current mediated by memristor in neuron model with bursting patterns. Int J Bifurc Chaos. 2020;30(4):2030009. doi: 10.1142/S0218127420300098. [DOI] [Google Scholar]
- Wu J, Ma SJ. Coherence resonance of the spiking regularity in a neuron under electromagnetic radiation. Nonlinear Dyn. 2019;96:1895–1908. doi: 10.1007/s11071-019-04892-z. [DOI] [Google Scholar]
- Wu SG, Ren W, He KF, Huang ZQ. Burst and coherence resonance in Rose–Hindmarsh model induced by additive noise. Phys Lett A. 2001;279(5–6):347–354. doi: 10.1016/S0375-9601(01)00020-2. [DOI] [Google Scholar]
- Wu FQ, Gu HG, Li YY. Inhibitory electromagnetic induction current induced enhancement instead of reduction of neural bursting activities. Commun Nonlinear Sci Numer Simul. 2019;79:104924. doi: 10.1016/j.cnsns.2019.104924. [DOI] [Google Scholar]
- Zhang XJ, Gu HG, Guan LN. Stochastic dynamics of conduction failure of action potential along nerve fiber with Hopf bifurcation. Sci China Technol Sci. 2019;62(9):1502–1511. doi: 10.1007/s11431-018-9515-4. [DOI] [Google Scholar]