Sample size requirements for detecting treatment effect heterogeneity in cluster randomized trials

Abstract

Cluster randomized trials (CRTs) refer to experiments with randomization carried out at the cluster or the group level. While numerous statistical methods have been developed for the design and analysis of CRTs, most of the existing methods focused on testing the overall treatment effect across the population characteristics, with few discussions on the differential treatment effect among subpopulations. In addition, the sample size and power requirements for detecting differential treatment effect in CRTs remain unclear, but are helpful for studies planned with such an objective. In this article, we develop a new sample size formula for detecting treatment effect heterogeneity in two-level CRTs for continuous outcomes, continuous or binary covariates measured at cluster or individual level. We also investigate the roles of two intraclass correlation coefficients (ICCs): the adjusted ICC for the outcome of interest and the marginal ICC for the covariate of interest. We further derive a closed-form design effect formula to facilitate the application of the proposed method, and provide extensions to accommodate multiple covariates. Extensive simulations are carried out to validate the proposed formula in finite samples. We find that the empirical power agrees well with the prediction across a range of parameter constellations, when data are analyzed by a linear mixed effects model with a treatment-by-covariate interaction. Finally, we use data from the HF-ACTION study to illustrate the proposed sample size procedure for detecting heterogeneous treatment effects.

1 |. INTRODUCTION

Cluster randomized trials (CRTs), or sometimes called group randomized trials (GRTs), refer to experiments with randomization carried out at the cluster or the group level.¹ CRTs are conducted because the intervention is naturally performed at the group level (e.g., a clinical decision support system delivered to the entire clinic), because the investigators wish to minimize the risk of treatment contamination within the same cluster, or because it is more ethical if the same treatment is applied to individuals in the same geographical unit (e.g., village or county), among others. Such trials are common in epidemiology, social science, and medicine. Over the past decade, CRTs are also adopted for studies embedded in the healthcare delivery systems, where there is a great interest in learning the real-world effectiveness of a system-based intervention.² Numerous statistical methods have been developed for the design and analysis of CRTs; see, for example, the recent methodological reviews by Turneretal.^3,4 However, these previous methods have primarily focused on the overall treatment effect (OTE) averaged over the population characteristics, and little discussion has been offered to address the differential treatment effect among subpopulations. A recent systematic review by Starks et al⁵ also found that only 18 out of 64 health-related CRTs published between 2010 and 2016 examined heterogeneity of treatment effect (HTE) in subgroups. Although not as commonly seen in previous CRTs, the investigation of HTE has received increasing attention because cluster randomized designs are gaining popularity in intervention studies embedded in healthcare systems, where patient-level information is routinely collected and readily available.^6,7 Responding to the lack of guidance on HTE analysis in CRTs,⁵ this article provides a model-based approach to design CRTs that allows investigators to detect HTE for continuous outcomes, with a particular emphasis on sample size and power requirements. Our method applies to two-level CRTs with continuous or binary covariates that are measured at the individual or cluster level.

The concept of HTE refers to potentially variable treatment effects between patient subgroups that can arise due to different reasons, such as different responses to treatment, different vulnerability to certain diseases, and adverse effects.⁸ When HTE is present, the treatment of interest may provide benefit to some patients, but could be neutral or harmful to others.⁸ HTE is usually identified by separate subgroup analysis, or formalized by parametric statistical interaction terms in individually randomized trials. Systematic reviews of individually randomized trials suggest that HTE tends to be overlooked and inadequately reported.^9–11 In particular, the sample size estimates provided in the design stage are usually specific to testing the OTE in the study population, and it is unknown whether the trial has adequate power to detect the HTE. Furthermore, separate subgroup analyses are frequently conducted in an ad hoc fashion and could involve multiple comparisons that are subject to false positive results. Similar concerns translate into the design and analysis of CRTs, with the caveat that CRTs usually require a larger sample size for detecting the OTE due to within-cluster correlations.

Because the unit of randomization is each cluster, another distinguishing feature of CRTs is that the individual-level outcomes are correlated within the same cluster, possibly due to social connections or shared healthcare resources. The intraclass correlation coefficient (ICC) characterizes the similarity of values (e.g., outcomes) for pairs of individuals in the same cluster, and plays an important role in determining the sample size for CRTs. The sample size requirements for testing the OTE in CRTs have been well studied;¹ a typical strategy is to inflate standard sample size estimate obtained under individual randomization by a design effect (also called the variance inflation factor),

$${\theta }_1(m)=1+(m-1){\rho }_y,$$ (1)

where ρ_y is the ICC for individual-level outcomes and m is the cluster size.^12–14 In CRTs, the number of clusters and the cluster size jointly determine the total sample size. Based on this simple expression of design effect, others have also studied the trade-off between increasing cluster sizes vs increasing the number of clusters, and provided insights on optimal design of CRTs to reach the maximum statistical efficiency.^15,16 While these results are particularly powerful in designing CRTs to evaluate the OTE, they do not take into account additional covariates (either cluster-level or patient-level), and so do not apply directly for HTE analysis. On the other hand, the sample size methodology for detecting HTE in individually randomized trials has been formalized either as examining the cross-site difference in treatment effect¹⁷ or as testing the statistical interaction between the treatment and covariates; see, for example, Brookes et al¹⁸ and Shieh¹⁹ for continuous outcomes, Greenland²⁰ and Demidenko²¹ for binary outcomes, and Kang et al²² for censored time-to-event outcomes. We take the latter approach by formalizing the detection of HTE as a test for treatment-by-covariate interaction in a random-effects model that accounts for within-cluster correlations, and aim to clarify the essential ingredients for appropriate sample size planning with HTE analysis in CRTs.

In the educational statistics literature, several authors have previously studied power formulas for HTE analysis in CRTs. For example, Spybrook et al²³ proposed power formulas for detecting treatment-by-covariate interaction effects in CRTs with a binary covariate. They also extended the formula to account for additional adjustment variables which further improve the test power. Dong et al²⁴ extended these formulas to three-level CRTs under both fixed-slope and random-slope models. While these previous results explicitly involve the ICCs of the outcome, the impact of the clustering of the covariate on power has not been explicitly considered. In addition, these previous sample size formulas have not been empirically validated in Monte Carlo simulation studies, and their finite-sample operating characteristics remain to be explored. On the other hand, sample size procedures for testing interaction terms have been discussed in individually randomized studies with repeated measures, namely studies where treatment is randomized to individuals and repeated measurements are then taken for each individual across several time points. In that context, the target parameter that describes the intervention effect is the change in slopes of the individual outcome trajectory, and is parameterized as the statistical interaction between treatment and time (in continuous scale). For continuous outcomes, Heo and Leon²⁵ provided a sample size formula to detect the two-way and three-way slope change over time; their test statistic is based on method of moments and the intraclass correlation for repeated measurements has only been considered in variance estimation. Jung and Ahn²⁶ derived a sample size formula for the slope change based on continuous outcomes analyzed by independence generalized estimating equations.²⁷ Our interaction test for detecting HTE in CRTs is related to and generalizes the results developed for the slope test in longitudinal studies. While the interaction is defined as the product between the treatment and a time variable in longitudinal studies, the interaction term can be defined as the product between the treatment and a general covariate. The general covariate could be either continuous or binary, and could be either measured at the cluster level or individual level, depending on the scientific question. These considerations motivate us to formalize a sample size procedure applicable to the interaction test used to describe HTE in CRTs for continuous outcomes.

The remainder of this article is organized as follows. In Section 2, we introduce the linear mixed effects model with a treatment-by-covariate interaction. In Section 3, we develop a closed-form sample size formula for testing the treatment-by-covariate interaction and provide extensions to multiple covariates. We present numerical evidence in Section 4 to illustrate the proposed sample size formula, and conduct a Monte Carlo simulation study in Section 5 to investigate the accuracy of the proposed power formula. In Section 6, we use data obtained from the HF-ACTION study to illustrate the new sample size formula to detect HTE. Section 7 concludes with a discussion.

2 |. STATISTICAL MODEL

We consider a parallel CRT with n clusters randomly assigned to two arms or conditions. Typically, individuals are recruited in each cluster and the outcomes will be measured for each individual. Let Y_ij be a continuous outcome for the jth individual (j=1, … , m_i) in the ith cluster (i=1, … , n). The linear mixed effects model is commonly used to analyze individual-level outcomes in CRTs, with a random cluster intercept that accounts for the outcome ICC.⁴ When the focus is on the overall intervention effect, a linear mixed effects model with a treatment indicator and a random intercept is written as:

$$Y_{ij}={\alpha }_1+{\alpha }_2{W}_i+{\lambda }_i+{\xi }_{ij},$$ (2)

where α₁ is the grand mean, W_i is the binary treatment indicator (W_i =1 if cluster i is assigned to intervention and W_i =0 otherwise), α₂ is the OTE, ${\lambda }_i~\mathcal{N}\left(0,{\sigma }_{\lambda }^2\right)$ is the random cluster effect, and ${\xi }_{ij}~\mathcal{N}\left(0,{\sigma }_{\xi }^2\right)$ is the residual error, independent of the random cluster effect.

Individual-level covariates are often collected at baseline in CRTs embedded within the healthcare delivery systems.^6,28 In addition to testing for the OTE, investigators may wish to test possible treatment effect heterogeneity with respect to some covariates. In this case, as the power and sample size requirements for the OTE are relatively well known, it would be important to understand the sample size and power requirements with respect to the interaction effect parameter describing treatment effect heterogeneity. Assume that X_ij is a p-dimensional vector of individual-level covariates, such as age, gender, and race among others, we could extend model (2) for the analysis of individual-level outcomes as

$$Y_{ij}={\beta }_1+{\beta }_2{W}_i+{\beta }_3^T{X}_{ij}+{\beta }_4^T{X}_{ij}{W}_i+{\gamma }_i+{ϵ}_{ij},$$ (3)

where X_ij =(X_ij1, … , X_ijp)^T is the set of covariates measured for individual j in cluster i, W_i is defined in model (2), X_ijW_i represents a vector of interactions between treatment and covariates, β₁ is the grand mean, β₂ is the main treatment effect, β₃ = (β₃₁, … , β_3p)^T and β₄ = (β₄₁, … , β_4p)^T are regression coefficients for the covariates and the interaction terms. For example, assuming X_ij is a binary covariate, race, and X_ij =1 denotes black while X_ij =0 white. The parameter β₁ represents the mean response among white patients in the control arm, β₂ represents the treatment effect for white patients, β₁ + β₃ represents the mean response among black patients in the control arm, and β₄ represents the difference in treatment effect among black and white patients, which could be the parameter of interest. Similar to the assumptions in model (2), we assume in model (3) ${\gamma }_i~\mathcal{N}\left(0,{\sigma }_{\gamma }^2\right)$ and ${ϵ}_{ij}~\mathcal{N}\left(0,{\sigma }_{ϵ}^2\right)$, and independence between γ_i and ϵ_ij. This same model has also been discussed in Spybrook et al,²³ where X_ij is binary. Of note, model (3) is a direct extension of those studied in Raudenbush,²⁹ Li et al,³⁰ and Yang et al,³¹ where only main effects of W_i and X_ij are considered. Further extensions of model (3) to allow for random coefficients for X_ij can be found in Jaciw et al³² and Dong et al.²⁴

To proceed, we let $\overline{W}=E\left(W_i\right)$ denote the proportion of clusters that are randomized to the intervention group. When half of clusters are randomized to the intervention arm, $\overline{W}=1/2$, but our results allow $\overline{W}$ to be any value in (0,1). We reparameterize model (3) by subtracting $\overline{W}$ from the treatment variable, and obtain

$$\begin{gathered} Y_{ij}=\left({\beta }_1+{\beta }_2\overline{W}\right)+{\beta }_2\left(W_i-\overline{W}\right)+{\left({\beta }_3+{\beta }_4\overline{W}\right)}^T{X}_{ij}+{\beta }_4^T{X}_{ij}\left(W_i-\overline{W}\right)+{\gamma }_i+{ϵ}_{ij} \\ =b_1+b_2\left(W_i-\overline{W}\right)+b_3^T{X}_{ij}+b_4^T{X}_{ij}\left(W_i-\overline{W}\right)+{\gamma }_i+{ϵ}_{ij}, \end{gathered}$$ (4)

where the coefficients are $b_1={\beta }_1+{\beta }_2\overline{W}$, b₂ = β₂, $b_3={\beta }_3+{\beta }_4\overline{W}$, and b₄ = β₄. From model (4), the total variance of Y_ij adjusting for X_ij is $\text{var}\left(Y_{ij}\mid W_i,X_{ij}\right)={\sigma }_{\gamma }^2+{\sigma }_{ϵ}^2={\sigma }_{y\mid x}^2$, and $\text{cov}\left(Y_{ij},Y_{i^{\prime }{j}^{\prime }}\mid W_i,X_{ij}\right)=\mathcal{I}\left(i=i^{\prime }\right){\sigma }_{\gamma }^2+\mathcal{I}\left(i=i^{\prime },j=j^{\prime }\right){\sigma }_{ϵ}^2$, where $\mathcal{I}$ is the indicator function. The outcome ICC adjusting for X_ij is then defined as²⁹

$${\rho }_{y\mid x}=\frac{{\sigma }_{\gamma }^2}{{\sigma }_{y\mid x}^2}=\frac{{\sigma }_{\gamma }^2}{{\sigma }_{\gamma }^2+{\sigma }_{ϵ}^2}.$$ (5)

Following the terminology in Murray and Blitstein,³³ we define ${\sigma }_{\gamma }^2$, ${\sigma }_{ϵ}^2$ as the adjusted variance components, and ρ_y|x as the adjusted outcome ICC. Furthermore, the joint covariance matrix of within-cluster observations is compound symmetric. In other words, if we define $Y_i={\left(Y_{i1},\dots ,Y_{i{m}_i}\right)}^T$, we can write in matrix notations that $\text{cov}\left(Y_i\mid W_i,X_{ij}\right)={\sigma }_{y\mid x}^2\left[\left(1-{\rho }_{y\mid x}\right)I_{m_i}+{\rho }_{y\mid x}{J}_{m_i}\right]={\sigma }_{y\mid x}^2{R}_i$, where $I_{m_i}$ is the m_i × m_i identity matrix, $J_{m_i}$ is the m_i × m_i matrix of ones, and R_i is the exchangeable correlation matrix.

Define the collection of design points $Z_{ij}={\left(1,\left(W_i-\overline{W}\right),X_{ij}^T,X_{ij}^T\left(W_i-\overline{W}\right)\right)}^T$ and $Z_i={\left(Z_{i1},\dots ,Z_{i{m}_i}\right)}^T$. Given the values of ${\sigma }_{\gamma }^2$ and ${\sigma }_{ϵ}^2$, the covariance matrix and the correlation matrix of Y_i are known. The best linear unbiased estimator (BLUE) of b =(b₁,b₂,b₃,b₄)^T is given by the generalized least squares (GLS)

$$\widehat{b}={\left(\sum _{i=1}^n{Z}_i^T{R}_i^{-1}{Z}_i\right)}^{-1}\left(\sum _{i=1}^n{Z}_i^T{R}_i^{-1}{Y}_i\right).$$ (6)

When n is large, $\widehat{b}$ is approximately normally distributed with mean b and variance matrix

$${\Sigma }_n={\sigma }_{y\mid x}^2{U}_n^{-1},\text{ where }{U}_n=\sum _{i=1}^n{Z}_i^T{R}_i^{-1}{Z}_i.$$ (7)

In practice, both ${\sigma }_{\gamma }^2$ and ${\sigma }_{ϵ}^2$ are unknown, and therefore will be estimated from the data. The restricted maximum likelihood (REML) approach can be used to estimate both b and variance components; additional technical details for estimation can be found in Pinheiro and Bates.³⁴

3 |. SAMPLE SIZE AND POWER CALCULATION

3.1 |. Basic setting with one covariate

We first derive the sample size formula when the treatment effect heterogeneity concerns one covariate. In other words, p =1; this is the case, for example, when the covariate of interest is race (a binary covariate) or age (a continuous covariate). We keep the race variable as a running example through this section. The interaction effect, β₄ is a scalar, and we are interested in testing the null hypothesis H₀ : β₄ = 0 using a two-sided test. In our running example, we would be interested in testing whether the treatment effect differs between two different racial groups. Based on the linear mixed effects model (4), the scaled GLS estimator $\sqrt{n}\left({\widehat{\beta }}_4-{\beta }_4\right)$ is asymptotically normal with mean zero and variance equal to the lower right element of Σ = lim_n→∞nΣ_n, which we denote by ${\sigma }_4^2$. This suggests the use of the z-test statistic, $\sqrt{n}{\widehat{\beta }}_4/{\widehat{\sigma }}_4$, which will be referenced to the standard normal distribution. For a prespecified test size β₄ = Δ, it then follows that the required number of clusters with a nominal test size α and power 1 – λ is given by

$$n=\frac{{\sigma }_4^2{\left(z_{1-\alpha /2}+z_{1-\lambda }\right)}^2}{{\Delta }^2}.$$ (8)

To derive an expression for ${\sigma }_4^2$, we examine the expression for U = lim_n→∞n⁻¹U_n (readers who want to skip the technical intermediate steps can jump to Equation (9) without loss of continuity). Following the conventions in designing CRTs, here we make the simplification assumption that the cluster sizes are equal, namely, m_i = m for all i. With this assumption, the inverse of the exchangeable working correlation structure can be written as³⁵

$$R_i^{-1}=\frac{1}{1-{\rho }_{y\mid x}}{I}_m-\frac{{\rho }_{y\mid x}}{\left(1-{\rho }_{y\mid x}\right)\left\{1+(m-1){\rho }_{y\mid x}\right\}}{J}_m=c{I}_m+d{J}_m,$$

where we define c = 1/(1 – ρ_y|x), and d = −ρ_y|x/[(1 – ρ_y|x){1 + (m − 1)ρ_y|x}]. This allows us to write U_n = cS_n + dT_n, where

$$S_n=\sum _{i=1}^n\sum _{j=1}^m{Z}_{ij}{Z}_{ij}^T=\sum _{i=1}^n\sum _{j=1}^m\left[\begin{array}{cccc}1& W_i-\overline{W}& X_{ij}& \left(W_i-\overline{W}\right)X_{ij}\\ W_i-\overline{W}& {\left(W_i-\overline{W}\right)}^2& \left(W_i-\overline{W}\right)X_{ij}& {\left(W_i-\overline{W}\right)}^2{X}_{ij}\\ X_{ij}& \left(W_i-\overline{W}\right)X_{ij}& X_{ij}^2& \left(W_i-\overline{W}\right)X_{ij}^2\\ \left(W_i-\overline{W}\right)X_{ij}& {\left(W_i-\overline{W}\right)}^2{X}_{ij}& \left(W_i-W\right)X_{ij}^2& {\left(W_i-\overline{W}\right)}^2{X}_{ij}^2\end{array}\right]$$

and

$$T_n=\sum _{i=1}^n\left(\sum _{j=1}^m{Z}_{ij}\right){\left(\sum _{j=1}^m{Z}_{ij}\right)}^T=\sum _{i=1}^n{m}^2\left[\begin{array}{cccc}1& W_i-\overline{W}& {\overline{X}}_i& \left(W_i-\overline{W}\right){\overline{X}}_i\\ W_i-\overline{W}& {\left(W_i-\overline{W}\right)}^2& \left(W_i-\overline{W}\right){\overline{X}}_i& {\left(W_i-\overline{W}\right)}^2{\overline{X}}_i\\ {\overline{X}}_i& \left(W_i-\overline{W}\right){\overline{X}}_i& {\overline{X}}_i^2& \left(W_i-\overline{W}\right){\overline{X}}_i^2\\ \left(W_i-\overline{W}\right){\overline{X}}_i& {\left(W_i-\overline{W}\right)}^2{\overline{X}}_i& \left(W_i-\overline{W}\right){\overline{X}}_i^2& {\left(W_i-\overline{W}\right)}^2{\overline{X}}_i^2\end{array}\right],$$

where ${\overline{X}}_i^l={\left(m^{-1}{\sum }_{j=1}^m{X}_{ij}\right)}^l$ for l =1,2 represent the cluster-specific moment values for the covariate. Next, define ${\mu }_l={\text{lim}}_{n\to \infty }{(nm)}^{-1}{\sum }_{i=1}^n{\sum }_{j=1}^m{X}_{ij}^l$, ${\eta }_2={\text{lim}}_{n\to \infty }{n}^{-1}{\sum }_{i=1}^n{\overline{X}}_i^2$ as the limits of covariate moments and ${\sigma }_w^2=\overline{W}(1-\overline{W})$ as the variation in the treatment assignment, we can obtain the limits

$$S=\underset{n\to \infty }{\text{lim}}{n}^{-1}{S}_n=m\left[\begin{array}{cccc}1& 0& {\mu }_1& 0\\ 0& {\sigma }_w^2& 0& {\mu }_1{\sigma }_w^2\\ {\mu }_1& 0& {\mu }_2& 0\\ 0& {\mu }_1{\sigma }_w^2& 0& {\mu }_2{\sigma }_w^2\end{array}\right]$$

and

$$T=\underset{n\to \infty }{\text{lim}}{n}^{-1}{T}_n=m^2\left[\begin{array}{cccc}1& 0& {\mu }_1& 0\\ 0& {\sigma }_w^2& 0& {\mu }_1{\sigma }_w^2\\ {\mu }_1& 0& {\eta }_2& 0\\ 0& {\mu }_1{\sigma }_w^2& 0& {\eta }_2{\sigma }_w^2\end{array}\right].$$

These calculations allow us to obtain the structure of the limit of the precision matrix in a block form as

Notice that each block in U is actually a diagonal matrix, which permits a simple closed-form derivation of the lower right element of U⁻¹ via block matrix inversion. Specifically, we observe $A={\mu }_1^{-1}C$, and B = C, then the lower right block becomes (D − CA⁻¹B)⁻¹ = (D − CC⁻¹μ₁B)⁻¹ = (D − μ₁B)⁻¹. It follows that the lower-right element of $\Sigma ={\sigma }_{y\mid x}^2{U}^{-1}$ becomes

$${\sigma }_4^2=\frac{{\sigma }_{y\mid x}^2}{m{\sigma }_w^2\left\{c\left({\mu }_2-{\mu }_1^2\right)+dm\left({\eta }_2-{\mu }_1^2\right)\right\}}=\frac{{\sigma }_{y\mid x}^2\left(1-{\rho }_{y\mid x}\right)\left\{1+(m-1){\rho }_{y\mid x}\right\}}{m{\sigma }_w^2\left\{\left(1-{\rho }_{y\mid x}\right)\left({\mu }_2-{\mu }_1^2\right)+m{\rho }_{y\mid x}\left({\mu }_2-{\eta }_2\right)\right\}},$$ (9)

where ${\sigma }_w^2=1/4$ in most CRTs due to balanced allocation of treatment.

Equations (8) and (9) provide a simple approach to calculate the required number of clusters to power the test of treatment effect heterogeneity. Given information on the cluster size m, adjusted ICC of the outcome ρ_y|x, and moment values μ₁, μ₂, and η₂, one could obtain the required number of clusters n by simple calculation. On the other hand, if we have information on the maximum number of clusters n, Equations (8) and (9) imply a quadratic function of the cluster sizes required to achieve the desired level of power, and therefore m can be obtained by the quadratic formula. To get further insights on the sample size formula, it is possible to simplify Equation (9) by introducing a new quantity, ρ_x, which measures the intraclass correlation for the covariate of interest. The concept of covariate ICC has been previously mentioned in Raudenbush,²⁹ and can be viewed as the counterpart of outcome ICC. In our running example, ρ_x measures the degree of similarity between within-cluster individuals in terms of their racial groups. Formally, we define

$${\rho }_x=\frac{E\left(X_{ij}{X}_{ik}\right)-{\mu }_1^2}{{\mu }_2-{\mu }_1^2},$$

where X_ij, X_ik are measured for pairs of individuals in the same cluster. With this quantity, it follows that

$${\eta }_2=\underset{n\to \infty }{\text{lim}}\frac{1}{n{m}^2}\sum _{i=1}^n\left(\sum _{j=1}^m{X}_{ij}^2+\sum _{j\ne k}{X}_{ij}{X}_{ik}\right)=\frac{1}{m}\left[\left\{1+(m-1){\rho }_x\right\}{\mu }_2+(m-1)\left(1-{\rho }_x\right){\mu }_1^2\right].$$

Plugging this expression into (9), and notice that the marginal variance of the covariate X_ij is ${\sigma }_x^2={\mu }_2-{\mu }_1^2$, we have

$${\sigma }_4^2=\frac{{\sigma }_{y\mid x}^2\left(1-{\rho }_{y\mid x}\right)\left\{1+(m-1){\rho }_{y\mid x}\right\}}{m{\sigma }_w^2{\sigma }_x^2\left\{1+(m-2){\rho }_{y\mid x}-(m-1){\rho }_x{\rho }_{y\mid x}\right\}},$$ (10)

and the required total number of individuals in a CRT satisfies

$$nm=\frac{{\left(z_{1-\alpha /2}+z_{1-\lambda }\right)}^2{\sigma }_{y\mid x}^2\left(1-{\rho }_{y\mid x}\right)\left\{1+(m-1){\rho }_{y\mid x}\right\}}{{\Delta }^2{\sigma }_w^2{\sigma }_x^2\left\{1+(m-2){\rho }_{y\mid x}-(m-1){\rho }_x{\rho }_{y\mid x}\right\}}.$$ (11)

Sample size formula (11) depends on the marginal variance of the covariate ${\sigma }_x^2$ and the two ICC parameters ρ_y|x and ρ_x. Compared with the conventional CRT powered to test for the overall treatment effect, we require information of the adjusted outcome ICC, and information of X_ij through two second-order parameters ${\sigma }_x^2$ and ρ_x. The above expression allows us to study the relationship between sample size and distributions of X_ij. Particularly, larger values of marginal variance ${\sigma }_x^2$ reduce the required sample size for fixed outcome ICC, while larger values of covariate ICC ρ_x increase the required sample size for fixed outcome ICC. This is intuitive since larger marginal variability of X_ij and smaller covariate ICC imply more per unit information on estimating the treatment effect heterogeneity and hence improve the efficiency. On the other hand, the relationship between the required number of clusters and the adjusted outcome ICC seems less clear, and we will conduct numerical studies in Section 4.1 to assess such relationships. Another noticeable feature of sample size formula (11) is that it does not depend on the grand mean term or main effect sizes of the treatment and covariate, which suggests that knowledge of the effect size for the interaction term suffices.

The above sample size formula can be inverted to obtain the minimum detectable effect size (MDES) given the available number of clusters n and the cluster size m. In this case, we can easily see that the study would have 1 − λ power to detect an interaction effect size of at least |Δ|, where

$$\text{MDES}=\left|\Delta \right|=\frac{|z_{1-\alpha /2}+z_{1-\lambda }|{\sigma }_{y\mid x}}{{\sigma }_w{\sigma }_x}\sqrt{\frac{\left(1-{\rho }_{y\mid x}\right)\left\{1+(m-1){\rho }_{y\mid x}\right\}}{nm\left\{1+(m-2){\rho }_{y\mid x}-(m-1){\rho }_x{\rho }_{y\mid x}\right\}}}.$$

It is important to notice that sample size formula (11) includes two interesting special cases.

Case 1 (cluster-level covariate). When the covariate of interest is at the cluster-level (e.g., proportion of black patients in each clinic) and hence X_ij = X_i for all j, we naturally have ρ_x = 1 (because the covariate is perfectly correlated with itself in each cluster), and the above formulas reduce to

$${\sigma }_4^2=\frac{{\sigma }_{y\mid x}^2\left\{1+(m-1){\rho }_{y\mid x}\right\}}{m{\sigma }_w^2{\sigma }_x^2},$$ (12)

$$nm=\frac{{\left(z_{1-\alpha /2}+z_{1-\lambda }\right)}^2{\sigma }_{y\mid x}^2\left\{1+(m-1){\rho }_{y\mid x}\right\}}{{\Delta }^2{\sigma }_w^2{\sigma }_x^2},$$ (13)

from which we immediately recognize that the term, 1 + (m − 1)ρ_y|x, corresponds to the usual design effect in a parallel CRT powered for testing OTE, except that the adjusted outcome ICC is used. This is expected because X_iW_i degenerates to a cluster-level covariate, and the variance inflation for X_iW_i due to clustering resembles that for the treatment, which is also a cluster-level covariate. Furthermore, under equal treatment allocation and when X_i is a binary cluster-level covariate with prevalence 1/2, Equation (13) reduces to equation (10) in Spybrook et al.²³ In this regard, formula (13) generalizes equation (10) in Spybrook et al²³ to allow for unequal allocation and an arbitrary cluster-level covariate.

Case 2 (no residual clustering). If there is no residual clustering and that we are interested in testing treatment effect heterogeneity in an individually randomized trial, then we must have ρ_y|x = 0. The variance expression and required sample size can be shown to be

$${\sigma }_4^2=\frac{{\sigma }_{y\mid x}^2}{m{\sigma }_w^2{\sigma }_x^2},$$ (14)

$$N=\frac{{\left(z_{1-\alpha /2}+z_{1-\lambda }\right)}^2{\sigma }_{y\mid x}^2}{{\Delta }^2{\sigma }_w^2{\sigma }_x^2},$$ (15)

where N now represents the total number of individuals, and ${\sigma }_{y\mid x}^2$ is the adjusted total variance. This sample size formula is closely connected with the one provided in Shieh et al,¹⁹ although they did not provide an explicit expression and focused on the t-test statistic.

The forms of Equations (13) and (15) provide the basis for formally defining the design effect due to clustering with respect to testing treatment effect heterogeneity. That is, the design effect for testing treatment heterogeneity with respect to a cluster-level covariate has the same form as that defined for testing OTE,

$${\theta }_1(m)=1+(m-1){\rho }_{y\mid x},$$ (16)

while the design effect for testing treatment effect heterogeneity with respect to an individual-level covariate is implied from Equations (11) and (15),

$${\theta }_2(m)=\frac{\left(1-{\rho }_{y\mid x}\right)\left[1+(m-1){\rho }_{y\mid x}\right]}{1+(m-2){\rho }_{y\mid x}-(m-1){\rho }_x{\rho }_{y\mid x}}.$$ (17)

Unlike θ₁(m), which diverges to infinity as cluster size increases indefinitely, the design effect θ₂(m) converges to a finite constant θ₂(∞) = (1 − ρ_y|x)/(1 − ρ_x). Hence, depending on the relative magnitude of the two ICCs, the limit of the design effect θ₂(∞) may be either greater or smaller than one, which represents a distinguishing feature between θ₁(m) and θ₂(m). In addition, the limit of the design effect θ₂(∞) decreases as ρ_y|x increases and ρ_x decreases, while θ₁(m) is monotone in ρ_y|x. Finally, when the adjusted outcome ICC equals to the covariate ICC, there is no efficiency loss due to clustering in testing the treatment effect heterogeneity, because θ₂(m) = 1 for any m.

3.2 |. Extensions to multiple covariates

Although we mainly focus on the basic scenario, it is possible to extend the above sample size procedure for jointly testing the interactions with multiple covariates. In this case, X_ij =(X_ij1, X_ij2, … , X_ijp)^T is the set of p ≥ 2 covariates, and the interaction parameters of interest are β₄ = (β₄₁, β₄₂, … , β_4p)^T. We are interested in testing the global null hypothesis H₀ : β₄ = 0 based on a Wald test. In the context of the running example, we could have access to p =2 covariates: race and gender, and would be interested in jointly testing whether race and gender modify the treatment effect. From the linear mixed effects model (4), the scaled GLS estimator $\sqrt{n}\left({\widehat{\beta }}_4-{\beta }_4\right)$ is asymptotically normal with mean zero and variance equal to the lower-right p × p block of Σ = lim_n→∞nΣ_n, which we denote by Ω₄. This motivates the Wald test statistics $Q=n{\widehat{\beta }}_4^T{\widehat{\Omega }}_4^{-1}{\widehat{\beta }}_4$, which converges to a Chi-squared distribution χ²(p, ϑ) with p degrees of freedom and the noncentrality parameter $\vartheta =n{\beta }_4^T{\Omega }_4^{-1}{\beta }_4$. For fixed effect size vector β₄, the corresponding power equation of the Wald test is approximated by

$$1-\lambda ={\int }_{{\chi }_{1-\alpha }^2(p)}^{\infty }f(x;p,\vartheta )dx,$$ (18)

where f(x;p,ϑ) is the probability density function of the χ²(p, ϑ) distribution. Fixing n or m, solving Equation (18) for m or n then gives the required sample size.

An explicit sample size equation with multiple covariates now requires the derivation of the variance matrix Ω₄, which determines the noncentrality parameter. We show in Web Appendix A that

$${\Omega }_4=\frac{{\sigma }_{y\mid x}^2\left(1-{\rho }_{y\mid x}\right)\left\{1+(m-1){\rho }_{y\mid x}\right\}}{m{\sigma }_w^2}{\Omega }_x^{-1/2}{\left\{{\Gamma }_x^1+(m-2){\rho }_{y\mid x}{\Gamma }_x^1-(m-1){\rho }_{y\mid x}{\Gamma }_x^0\right\}}^{-1}{\Omega }_x^{-1/2}.$$ (19)

In this expression, information on covariates has been represented by two matrix expressions. The first matrix ${\Gamma }_x^1$ summarizes the marginal correlation between p covariates and is defined as

$${\Gamma }_x^1={\Omega }_x^{-1/2}\left\{E\left(X_{ij}{X}_{ij}^T\right)-h_1{h}_1^T\right\}{\Omega }_x^{-1/2}={\Omega }_x^{-1/2}\left\{H_2-h_1{h}_1^T\right\}{\Omega }_x^{-1/2},$$

where $h_1={\text{lim}}_{n\to \infty }{(nm)}^{-1}{\sum }_{i=1}^n{\sum }_{j=1}^m{X}_{ij}$, $H_2={\text{lim}}_{n\to \infty }{(nm)}^{-1}{\sum }_{i=1}^n{\sum }_{j=1}^m{X}_{ij}{X}_{ij}^T$, ${\Omega }_x=\text{diag}\left(H_2-h_1{h}_1^T\right)$ is the diagonal matrix containing the marginal variances of all covariates. Therefore, the diagonal element of ${\Gamma }_x^1$ is one and the off-diagonal elements represent the marginal correlation between each pair of covariates. The second matrix ${\Gamma }_x^0$ is defined as

$${\Gamma }_x^0={\Omega }_x^{-1/2}\left\{E\left(X_{ij}{X}_{ik}^T\right)-h_1{h}_1^T\right\}{\Omega }_x^{-1/2},$$

which could be regarded as a multivariate extension of the scalar covariate ICC. Specifically, the diagonal element of ${\Gamma }_x^0$ is the ICC of each covariate, while the off-diagonal elements are the intraclass cross-correlations between two different covariates. To further aid the interpretations of the two correlation matrices in Equation (19), we provide in Web Appendix A a simple example where X_ij is generated from a multilevel model, from which we derive explicit forms of ${\Gamma }_x^1$ and ${\Gamma }_x^0$. When p=2 covariates are considered, we additionally derive a more explicit expression of Equation (19) in Web Appendix A, as a function of scalar correlation parameters. Finally, we notice that the variance expression (10) is a special case of (19) when p=1. In that case, ${\Gamma }_x^1=1$, ${\Gamma }_x^0={\rho }_x$, ${\Omega }_x={\sigma }_x^2$ and ${\sigma }_4^2$ is obtained.

Similar to Section 3.1, the expression (19) shed lights on two special cases. For example, when the multiple covariates of interest are all measured at the cluster-level (e.g., proportion of Black patients and proportion of female patients in each clinic), it is easy to verify that ${\Gamma }_x^1={\Gamma }_x^0={\Gamma }_x$, and so the variance expression simplifies to

$${\Omega }_4=\frac{{\sigma }_{y\mid x}^2\left\{1+(m-1){\rho }_{y\mid x}\right\}}{m{\sigma }_w^2}{\Omega }_x^{-1/2}{\Gamma }_x^{-1}{\Omega }_x^{-1/2},$$ (20)

where we again see the expression 1 + (m − 1)ρ_y|x as the design effect due to clustering. Finally, in an individually randomized trial, one could similarly show that the variance becomes

$${\Omega }_4=\left({\sigma }_{y\mid x}^2/{\sigma }_w^2\right){\Omega }_x^{-1/2}{\Gamma }_x^{-1}{\Omega }_x^{-1/2},$$ (21)

which happens to be the expression (19) evaluated at ρ_y|x = 0.

4 |. NUMERICAL ILLUSTRATIONS

In this section, we present some numerical evidence to further illustrate the variance expression (10) in the univariate case. In particular, we aim to study (i) how the power for testing H₀ : β₄ = 0, or equivalently ${\sigma }_4^2$ changes as we vary the two ICC parameters and (ii) the comparisons between the required sample sizes for testing HTE vs those for testing OTE in CRTs.

4.1 |. Roles of the ICC parameters

Because the variance expression ${\sigma }_4^2$ involves two ICC parameters, ρ_y|x for the outcome of interest, and ρ_x for the covariate of interest, it is of particular interest to understand how the values of these two parameters affect the ${\sigma }_4^2$ and hence the power for testing H₀ : β₄ = 0. In Figure 1, we plot values of ${\sigma }_4^2$ over the range of either ρ_x (upper panels) or ρ_y|x (lower panels), with cluster sizes varied from m∈{20,50,100}, and ${\sigma }_{y\mid x}^2={\sigma }_x^2=1$, ${\sigma }_w^2=1/4$. Notice that we allow the largest ρ_x to be 1 and the largest ρ_y|x to be 0.5. The largest value ρ_x = 1 is observed when the covariate is measured at the cluster^| level; this scenario allows us to compare the efficiency between the interaction test with an individual-level covariate and that with a cluster-level covariate. The largest ρ_y|x, however, may be unlikely to be seen in real-world CRT contexts. We include those values merely to illustrate the relationship between ${\sigma }_4^2$ and ρ_y|x. From the upper panels, it is clear that larger values of the covariate ICC ρ_x inflate the variance ${\sigma }_4^2$, and therefore reduce the power of the interaction test, when all other parameters are held fixed. This pattern confirms the analytical result in Section 3.1. When the adjusted outcome ICC is small (ρ_y|x = 0.01), the relationship between ${\sigma }_4^2$ and covariate ICC ρ_x is relatively flat, indicating that the power (which is inversely related to ${\sigma }_4^2$) is not sensitive to ρ_x. But as the adjusted outcome ICC grows larger (ρ_y|x = 0.1), the power of the test becomes increasingly sensitive to changes in ρ_x, especially when ρ_x is larger than 0.5. Because ρ_x = 1 corresponds to the scenario with a cluster-level covariate, it is evident that the power to detect the cluster-level interaction effect could be much smaller than that to detect the individual-level interaction effect, when the adjusted outcome ICC is nontrivial (say, ρ_y|x ≥ 0.05) and the cluster size is not large. From the lower panels, we observe a parabolic relationship between ${\sigma }_4^2$ and ρ_y|x. In general, as the adjusted outcome ICC increases, the variance ${\sigma }_4^2$ first increases to its maximum and then decreases monotonically. In fact, we can use the quadratic formula to show that the value of ρ_y|x that gives the largest variance (stationary or critical point) is

$${\tilde{\rho }}_{y\mid x}=\frac{\sqrt{\left(1-{\rho }_x\right)\left\{1+(m-1){\rho }_x\right\}}-1}{\left(1-{\rho }_x\right)(m-1)-1}\in [0,1),$$ (22)

which clearly depends on both the covariate ICC and cluster size. As the covariate ICC becomes smaller or the cluster sizes become larger, ${\tilde{\rho }}_{y\mid x}$ moves toward zero. This underlies the reason why ${\sigma }_4^2$ is nearly monotonically decreasing in ρ_y|x when ρ_x = 0.05. Web Figure 4 presents the analogous results for m=10 (extremely small cluster sizes) and m=200. Results for m=10 and m =200 are qualitatively similar to those for m=20 and m=100, respectively. Therefore, the patterns seen in Figure 1 extend to smaller and larger cluster sizes.

FIGURE 1.

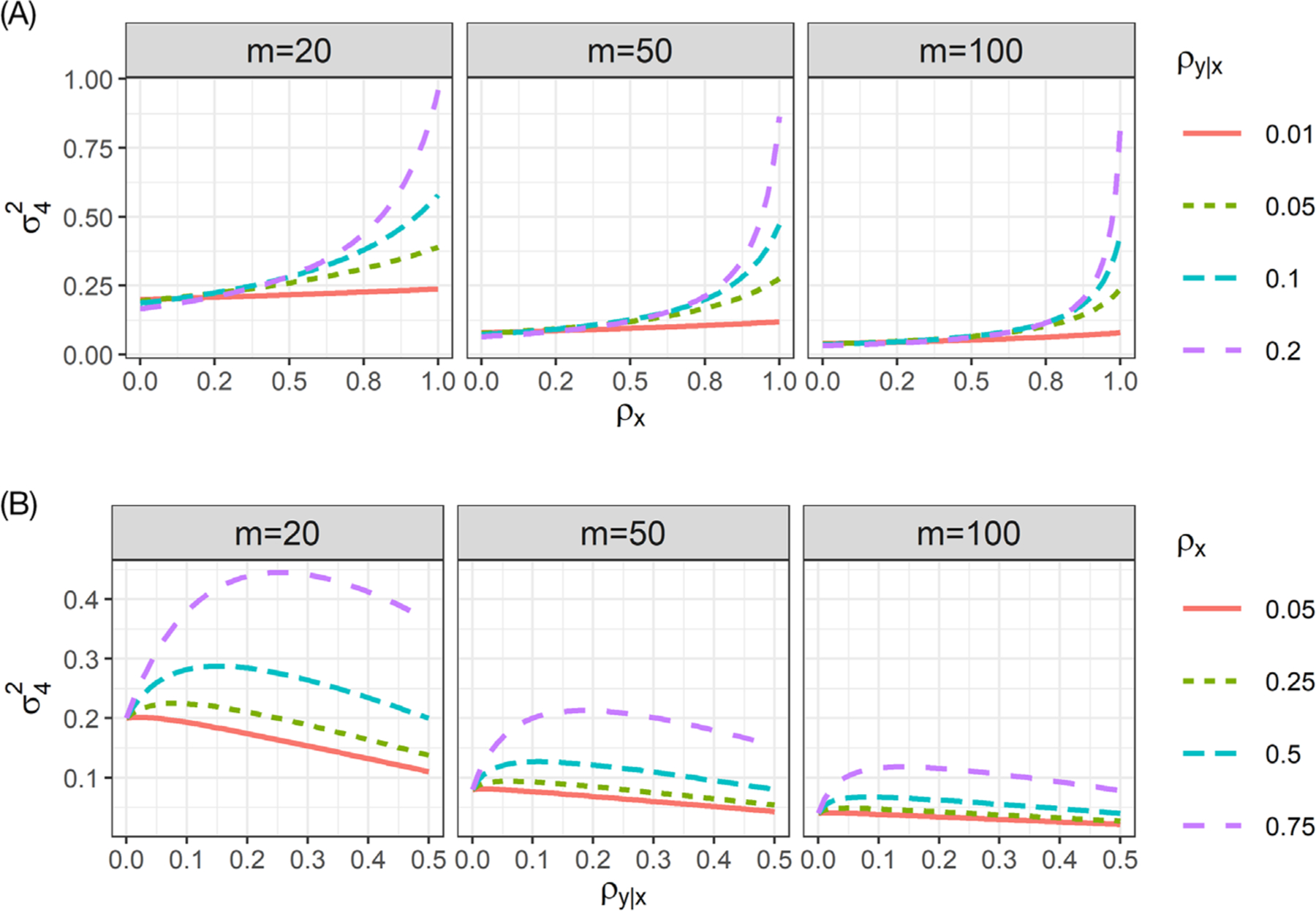
Variance of the GLS estimator for the treatment-by-covariate interaction, ${\sigma }_4^2$, as a function of the, A, covariate ICC ρ_x and, B, adjusted outcome ICC ρ_y|x with cluster sizes m∈{20,50,100}, assuming ${\sigma }_{y\mid x}^2={\sigma }_x^2=1$, and ${\sigma }_w^2=1/4$

4.2 |. Sample size requirements for testing HTE vs testing OTE

Most current CRTs are powered to detect the OTE, parameterized by α₂ in model (2). It is unknown whether such studies have adequate power to detect the treatment-by-covariate interaction, parameterized by β₄ in model (3). In this section, we use a simple example to numerically evaluate how many additional information is required to power the interaction test vs the overall treatment effect test. That is, the sample size difference between testing the null hypothesis H₀ : β₄ = 0 in model (3) vs H₀ : α₂ = 0 in model (2), when the true data generating process follows model (3).

A complication of this evaluation is that when β₄ is nonzero, models (2) and (3) may not hold simultaneously (see Web Appendix B for further details). However, when the true model follows (3), it is possible to approximate the unadjusted model of form (2). To do so, we assume a single continuous covariate generated from a multilevel model such that X_ij = μ + μ_i + τ_ij, where μ is the marginal mean, ${\mu }_i~\mathcal{N}\left(0,{\sigma }_{\mu }^2\right)$, ${\tau }_{ij}~\mathcal{N}\left(0,{\sigma }_{\tau }^2\right)$, and τ_ij is independent of μ_i. We further assume the covariate is mean-centered such that μ = 0. The marginal variance of X_ij is ${\sigma }_x^2={\sigma }_{\mu }^2+{\sigma }_{\tau }^2$, and the covariate ICC is ${\rho }_x={\sigma }_{\mu }^2/\left({\sigma }_{\mu }^2+{\sigma }_{\tau }^2\right)$. We can then rewrite model (3) with this mean-centered covariate as

$$\begin{gathered} Y_{ij}={\beta }_1+{\beta }_2{W}_i+{\beta }_3\left({\mu }_i+{\tau }_{ij}\right)+{\beta }_4\left({\mu }_i+{\tau }_{ij}\right)W_i+{\gamma }_i+{ϵ}_{ij} \\ ={\beta }_1+{\beta }_2{W}_i+\left({\beta }_3{\mu }_i+{\beta }_4{W}_i{\mu }_i+{\gamma }_i\right)+\left({\beta }_3{\tau }_{ij}+{\beta }_4{W}_i{\tau }_{ij}+{ϵ}_{ij}\right) \\ ={\alpha }_1+{\alpha }_2{W}_i+{\lambda }_i+{\xi }_{ij}, \end{gathered}$$

where we treat α₁ = β₁, α₂ = β₂, λ_i = β₃μ_i + β₄W_iμ_i + γ_i, and ξ_ij = β₃τ_ij + β₄W_iτ_ij + ϵ_ij. The approximate model (2) can then be identified once we compute the induced variance components for λ_i and ξ_ij. In Web Appendix B, we show that

$$\begin{gathered} {\sigma }_{\lambda }^2=\text{var}\left({\lambda }_i\right)={\sigma }_{\gamma }^2+B{\sigma }_{\mu }^2 \\ {\sigma }_{\xi }^2=\text{var}\left({\xi }_{ij}\right)={\sigma }_{ϵ}^2+B{\sigma }_{\tau }^2, \end{gathered}$$

and cov(λ_i, ξ_ij) = 0, where $B={\beta }_3^2+{\beta }_4^2\overline{W}+2{\beta }_3{\beta }_4\overline{W}$. Define ${\sigma }_y^2={\sigma }_{\lambda }^2+{\sigma }_{\xi }^2$ and recall that ${\sigma }_{y\mid x}^2={\sigma }_{\gamma }^2+{\sigma }_{ϵ}^2$, the unadjusted outcome ICC can be reasonably approximated by (see Web Appendix B for additional details)

$${\rho }_y=\frac{{\sigma }_{\lambda }^2}{{\sigma }_y^2}=\frac{{\sigma }_{y\mid x}^2}{{\sigma }_{y\mid x}^2+B{\sigma }_x^2}{\rho }_{y\mid x}+\frac{B{\sigma }_x^2}{{\sigma }_{y\mid x}^2+B{\sigma }_x^2}{\rho }_x=\omega {\rho }_{y\mid x}+(1-\omega ){\rho }_x,$$ (23)

which appears as a weighted combination of the adjusted outcome ICC ρ_y|x and covariate ICC ρ_x (with weight ω). Specifically, when all the ICCs are nonnegative, ρ_y ≥ ρ_y|x if and only if ρ_x ≥ ρ_y|x. Furthermore, if the adjusted total variance ${\sigma }_{y\mid x}^2$ is substantially larger than $B{\sigma }_X^2$, then the unadjusted outcome ICC tends to be similar to the adjusted outcome ICC, ρ_y ≈ ρ_y|x.

These derivations allow us to approximate the asymptotic variance of $\sqrt{n}\left({\widehat{\alpha }}_2-{\alpha }_2\right)$, which is given by ${\sigma }_2^2\approx {\sigma }_y^2\left\{1+\left(m-1\right){\rho }_y\right\}/\left(m{\sigma }_w^2\right)$. We further define the ratio of detectable effect size (RDES) as RDES = Δ/Δ_OTE, where Δ is the hypothesized value of β₄, and Δ_OTE is the hypothesized value of α₂ = β₂. Based on expression (8), the ratio of total sample size required for testing HTE vs OTE is given by

$$\begin{gathered} \Theta (m)=\frac{{\sigma }_{y\mid x}^2\left(1-{\rho }_{y\mid x}\right)}{{\sigma }_y^2{\sigma }_x^2\left\{1+(m-2){\rho }_{y\mid x}-(m-1){\rho }_x{\rho }_{y\mid x}\right\}}\times \frac{1+(m-1){\rho }_{y\mid x}}{1+(m-1){\rho }_y}\times \frac{1}{{\text{RDES}}^2} \\ =\frac{{\sigma }_{y\mid x}^2\left(1-{\rho }_{y\mid x}\right)}{{\sigma }_y^2{\sigma }_x^2\left\{1+(m-2){\rho }_{y\mid x}-(m-1){\rho }_x{\rho }_{y\mid x}\right\}}\times \frac{1+(m-1){\rho }_{y\mid x}}{1+(m-1)\omega {\rho }_{y\mid x}+(m-1)(1-\omega ){\rho }_x}\times \frac{1}{{\text{RDES}}^2}, \end{gathered}$$ (24)

where the last equality results from the relationship (23), and ${\sigma }_y^2={\sigma }_{y\mid x}^2+B{\sigma }_x^2$. A more detailed analytical investigation of Θ(m) as a function of covariate ICC can be found in Web Appendix B.

Figure 2 presents the values of Θ(20), Θ(50), and Θ(100), with various values of ρ_x and ρ_y|x, and fixing ${\sigma }_x^2={\sigma }_{y\mid x}^2=1$, β₂ = β₃ = 0.5 and $\overline{W}=1/2$ (equal randomization). This scenario corresponds to a CRT with both main effects as half the magnitude of the total adjusted standard deviation. We vary the RDES ∈{0.1,0.25,0.5,1} to represent scenarios where the interaction effect is one-tenth of, a quarter of, half as and identical to the OTE. Three patterns emerge from the Figure 2. First, Θ(m) appears mostly as a decreasing function of ρ_x, with a few exceptions when ρ_y|x is large. When the adjusted outcome ICC is small (ρ_y|x = 0.01), the variance inflation factor Θ(m) is sensitive to covariate ICC, and decreases sharply as covariate ICC increases. However, as the adjusted outcome ICC increases, the relationship between Θ(m) and covariate ICC ρ_x becomes relatively flat. The total sample size required for the interaction test is more likely to exceed those required for the OTE test when the covariate ICC and outcome ICC are both small. For example, when the interaction effect is one half of the OTE, the total sample size required for testing HTE can be 2.5 times that required for testing the OTE, when the covariate ICC is close to 0, the adjusted outcome ICC is 0.01 and m=20. When the interaction effect is the same as the OTE, however, the total sample size required for testing HTE is smaller than that required for testing the OTE. For individually randomized trials, Brookes et al¹⁸ previously suggested that the sample size should be inflated at least 4- or 16-folds for testing the interaction effect with the same or half magnitude of the OTE with a binary covariate (in their case ${\sigma }_x^2=1/4$). Extrapolating our results to a binary covariate with ${\sigma }_x^2=1/4$, we find that the sample size should be inflated at most 3- and 10-fold for testing the interaction effect with the same or half the magnitude of the OTE in CRTs (these numbers are calculated by four times the numbers in the “worst case scenarios” where the covariate ICC is zero, adjusted outcome ICC is 0.01, $\overline{W}=1/2$, and cluster size is 20). Such indirect comparisons suggest that the sample size inflation for testing an interaction term in CRTs may be no larger than that in individually randomized trials, among the scenarios we considered. Second, Θ(m) becomes smaller as cluster size increases, which indicates that the total sample size required for the two tests are likely to be more comparable when the study involves clusters with more participants. Finally, the determining factor for power of the interaction test is still the RDES. When the RDES is very small (say 0.1), the variation inflation factor Θ(m) can be more than 50 when the cluster size is not large, and any realistic sample sizes used in current CRTs will not be able to power an interaction test with such small effect sizes. Nevertheless, when the interaction effect size is close to OTE (RDES=1), the required sample size for the interaction test is frequently smaller than that for the overall effect test, across the ranges of ICC values we have considered. In the Web Appendix, we have varied the main effect of the covariate β₃ ∈ {0.25,1} and the cluster size m∈{10,200}; the results are presented in Web Figures 5 to 8. Overall, those additional results are similar to Figure 2 and confirm that the patterns observed here extend to small and larger covariate main effect and cluster sizes.

FIGURE 2.

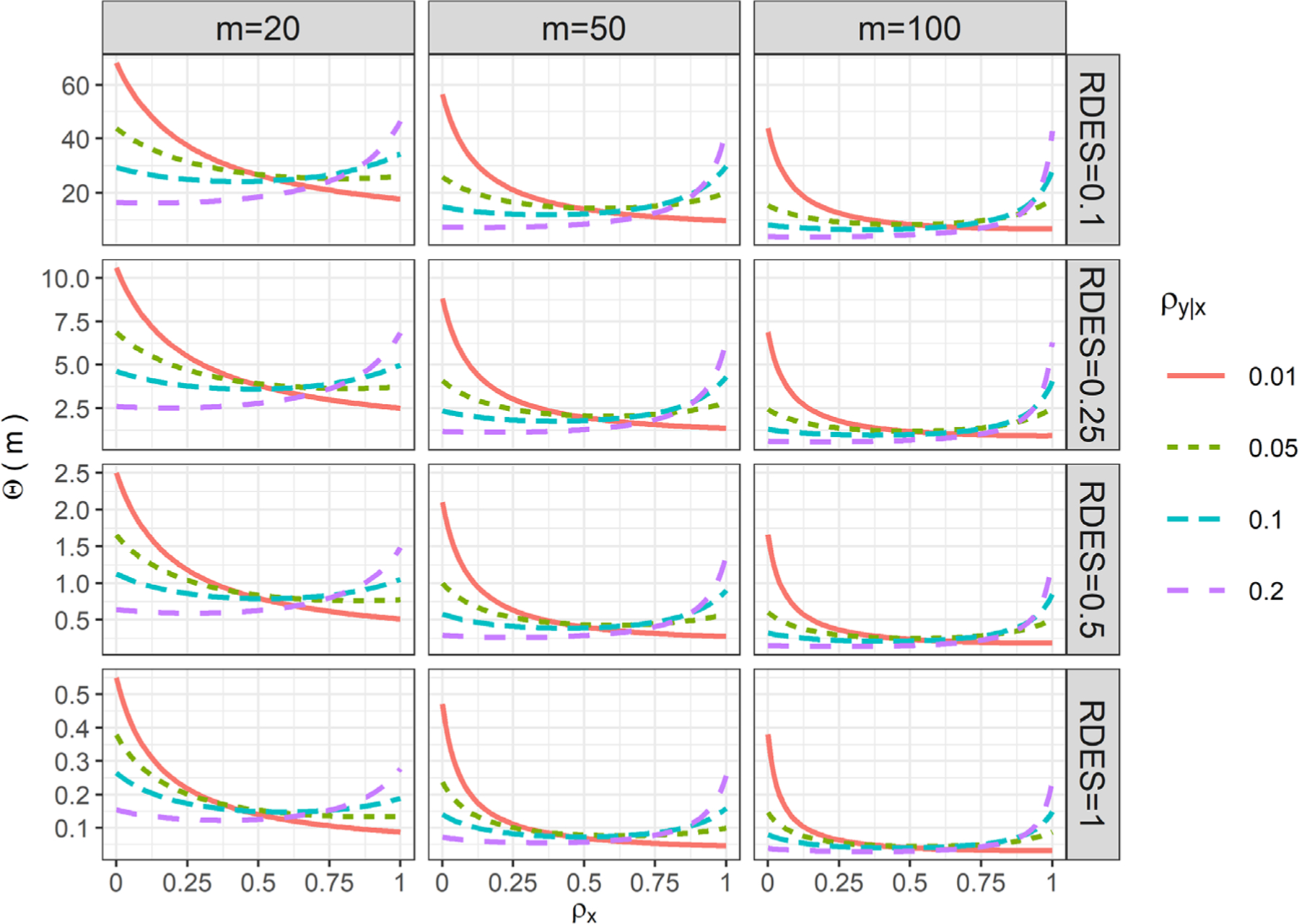
Ratio of total sample size required for testing HTE vs OTE as a function of the cluster size m, covariate ICC ρ_x, adjusted outcome ICC ρ_y|x, and ratio of detectable effect sizes (RDES), assuming ${\sigma }_x^2={\sigma }_{y\mid x}^2=1$, β₂ = β₃ = 0.5, and W = 1/2

5 |. SIMULATIONS

5.1 |. Simulation design

We investigate the performance of the new sample size formula for detecting treatment effect heterogeneity in finite samples via simulations. We focus on a cross-sectional CRT with clusters randomized to two arms in a 1:1 ratio, so that ${\sigma }_w^2=1/4$. For simplicity, we consider a single individual-level covariate X_ij, which could be either continuous or binary. From Equation (11), the total sample size depends on the following parameters: type I error rate, power, the total adjusted variance ${\sigma }_{y\mid x}^2$ and the marginal variance of covariate ${\sigma }_x^2$, adjusted outcome ICC and covariate ICC, cluster size, and the effect size for the treatment-by-covariate interaction. Throughout we fix ${\sigma }_{y\mid x}^2=1$, nominal type I error at 5%, desired level of power at 80%, and vary the remaining parameters in a factorial design. We consider four levels of cluster sizes m∈{10,20,50,100}, representing small to large cluster sizes; three levels of adjusted outcome ICC ρ_y|x ∈ {0.01,0.05,0.1}, representing values commonly reported in the CRT literature;^1,36 three levels of covariate ICC ρ_x ∈ {0.1,0.25,0.5}, mimicking values considered in the illustrative example in Section 6. We fix the interaction effect size at zero to examine the empirical type I error rate, and choose the interaction effect size among {0.10,0.15,0.25} for the continuous covariate scenario and among {0.25,0.35,0.45} for the binary covariate scenario. The differences in the choice of effect size in the continuous and binary covariate scenarios are to offset the differences in the marginal variance ${\sigma }_x^2$ and to obtain comparable sample size estimates. To summarize, for each type of covariate, there are in total 4×3×3×3=108 scenarios. We have also investigated additional scenarios when ρ_x = 0.01 and 0.05, and find similar results. Those results are omitted for brevity.

In the continuous covariate scenario, we fix the marginal variance ${\sigma }_x^2=1$, and generate X_ij from X_ij = 1/2 + μ_i + τ_ij, where ${\mu }_i~\mathcal{N}\left(0,{\rho }_x{\sigma }_x^2\right)$, and ${\tau }_{ij}~\mathcal{N}\left(0,\left(1-{\rho }_x\right){\sigma }_x^2\right)$. In the binary covariate scenario, we simulated X_ij from the beta-binomial model, where the cluster-specific prevalence π_i ~ Beta(q₁, q₂), and X_ij ~ Bernoulli(π_i). The implied marginal prevalence across all clusters from this model is q₁/(q₁ + q₂), and the covariate ICC can be analytically shown as ρ_x = (1 + q₁ + q₂)⁻¹. We choose q₁ and q₂ to ensure the marginal prevalence of X_ij is 30% and to maintain the desired level of covariate ICC. The implied marginal variance is therefore ${\sigma }_x^2=q_1{q}_2/{\left(q_1+q_2\right)}^2$. In each of the above scenario, we use our sample size formula (11) to estimate the required number of clusters, n, rounded to the nearest even integer above. Then given the value of n, we simulate individual-level outcomes Y_ij from model (3), where we choose β₂ = 0.25 and β₃ = 0.1. As we have explained in Section 3.1, these regression parameters are ancillary to sample size determination as they are not part of Equation (11). A total of 5000 data replicates are generated for each scenario, and the linear mixed effects model (3) is fit to each data set using the restricted maximum likelihood estimation (REML). In the null scenario where β₄ = 0, we calculate the empirical type I error rate (ψ₀) as the proportion of false rejections to ensure the test carries a nominal size in finite samples. In the nonnull scenario where β₄ ≠ 0, we calculate the empirical power (ϕ₀) as the proportion of correct rejections and compare with the analytical prediction (ϕ). All analyses are conducted in R (version 3.4.4) using the nlme package.³⁴

5.2 |. Simulation results

Table 1 summarizes the estimated required number of clusters (n), the empirical type I error rate (ψ₀), the empirical power (ϕ₀), and the predicted power (ϕ), when the cluster size m ∈{10,20,50,100}, and three levels of effect sizes Δ for the continuous covariate X_ij. Table 2 parallels Table 1 and summarizes the corresponding results when the covariate X_ij is binary. In the null scenario, the test for HTE maintains the nominal type I error rate across the parameter constellations, indicating that the test is valid. This ensures the validity of the subsequent comparisons between the empirical and predicted power. Across all levels of nonzero effect sizes, the predicted power obtained from our sample size formula is fairly close to the empirical power. Note since the required number of clusters are rounded to the nearest even integer above, the predicted power could be slightly greater than 0.80 in some cases. The mean absolute difference between the empirical and analytical power is 0.007 (IQR=0.008) when X_ij is continuous and 0.01 (IQR=0.011) when X_ij is binary. Overall, our sample size formula performs well since the analytical prediction agrees with empirical power, based on a two-sided test that maintains the nominal type I error rate, even when the number of clusters is as small as 6. It is worth noting that with a small cluster size (eg, m=10), the required number of clusters to power the HTE test could be over 300, which is substantially larger than most current CRTs. However, with a relatively large cluster size (ie, m=50 or m=100), even a small HTE could be detected with enough power when the number of cluster is fewer than 40, which falls into the range of sample size used in most CRTs.

TABLE 1.

Estimated required number of clusters n, empirical type I error Ψ₀, empirical power ϕ₀, and predicted power ϕ obtained from sample size formula, when X_ij is continuous

			Δ = 0.10				Δ = 0.15				Δ = 0.25
	ρx	ρy|x	n	Ψ0	ϕ0	ϕ	n	Ψ0	ϕ0	ϕ	n	Ψ0	ϕ0	ϕ
m = 10	0.10	0.01	318	0.06	0.80	0.80	142	0.05	0.80	0.80	52	0.05	0.81	0.81
		0.05	320	0.05	0.80	0.80	142	0.06	0.79	0.80	52	0.05	0.80	0.81
		0.10	314	0.05	0.80	0.80	140	0.05	0.80	0.80	52	0.05	0.81	0.81
	0.25	0.01	322	0.05	0.80	0.80	144	0.05	0.80	0.80	52	0.05	0.79	0.81
		0.05	336	0.05	0.80	0.80	150	0.05	0.80	0.80	54	0.05	0.79	0.80
		0.10	342	0.05	0.80	0.80	152	0.05	0.80	0.80	56	0.05	0.80	0.81
	0.50	0.01	328	0.05	0.80	0.80	146	0.05	0.79	0.80	54	0.05	0.79	0.81
		0.05	370	0.05	0.80	0.80	164	0.05	0.80	0.80	60	0.06	0.80	0.81
		0.10	398	0.05	0.81	0.80	178	0.05	0.80	0.80	64	0.06	0.80	0.80
m = 20	0.10	0.01	160	0.05	0.80	0.80	72	0.05	0.80	0.81	26	0.05	0.80	0.81
		0.05	162	0.05	0.81	0.80	72	0.06	0.81	0.80	26	0.05	0.79	0.80
		0.10	158	0.05	0.80	0.80	70	0.05	0.81	0.80	26	0.05	0.82	0.81
	0.25	0.01	164	0.05	0.79	0.80	74	0.05	0.80	0.81	28	0.05	0.81	0.83
		0.05	176	0.04	0.80	0.80	78	0.05	0.80	0.80	28	0.06	0.80	0.80
		0.10	178	0.05	0.80	0.80	80	0.06	0.81	0.81	30	0.05	0.81	0.82
	0.50	0.01	172	0.05	0.81	0.80	76	0.05	0.79	0.80	28	0.05	0.78	0.81
		0.05	206	0.05	0.80	0.80	92	0.05	0.80	0.81	34	0.05	0.79	0.82
		0.10	222	0.05	0.80	0.80	100	0.05	0.79	0.81	36	0.05	0.80	0.81
m = 50	0.10	0.01	66	0.05	0.81	0.81	30	0.06	0.81	0.82	12	0.05	0.85	0.85
		0.05	66	0.05	0.80	0.80	30	0.06	0.81	0.81	12	0.06	0.85	0.85
		0.10	64	0.05	0.81	0.81	28	0.05	0.80	0.80	12	0.05	0.86	0.86
	0.25	0.01	70	0.05	0.81	0.81	32	0.06	0.81	0.82	12	0.05	0.82	0.84
		0.05	74	0.04	0.81	0.80	34	0.05	0.81	0.81	12	0.06	0.80	0.81
		0.10	74	0.06	0.80	0.81	34	0.05	0.81	0.82	12	0.05	0.81	0.81
	0.50	0.01	76	0.06	0.80	0.80	34	0.06	0.80	0.81	12	0.06	0.75	0.80
		0.05	96	0.05	0.80	0.81	44	0.06	0.81	0.82	16	0.06	0.80	0.82
		0.10	100	0.05	0.80	0.80	46	0.05	0.81	0.81	16	0.06	0.78	0.80
m = 100	0.10	0.01	34	0.05	0.81	0.81	16	0.05	0.83	0.83	6	0.05	0.84	0.85
		0.05	34	0.05	0.83	0.81	16	0.05	0.84	0.83	6	0.05	0.83	0.85
		0.10	32	0.05	0.81	0.81	14	0.05	0.80	0.80	6	0.04	0.86	0.86
	0.25	0.01	36	0.05	0.80	0.80	16	0.06	0.80	0.80	6	0.06	0.80	0.82
		0.05	40	0.05	0.82	0.82	18	0.05	0.82	0.82	8	0.06	0.88	0.90
		0.10	38	0.05	0.81	0.81	18	0.05	0.83	0.83	6	0.06	0.80	0.80
	0.50	0.01	42	0.06	0.80	0.80	20	0.06	0.80	0.83	8	0.05	0.82	0.87
		0.05	52	0.05	0.80	0.80	24	0.05	0.81	0.82	10	0.05	0.86	0.87
		0.10	54	0.06	0.80	0.81	24	0.05	0.81	0.81	10	0.05	0.86	0.86

Note: Δ is the effect size, ρ_y|x is the adjusted outcome ICC, and ρ_x is the covariate ICC. The results are based on 5000 simulations.

TABLE 2.

Estimated required number of clusters n, empirical type I error Ψ₀, empirical power ϕ₀, and predicted power ϕ obtained from sample size formula, when X_ij is binary

			Δ = 0.10				Δ = 0.15				Δ = 0.25
	ρx	ρy|x	n	Ψ0	ϕ0	ϕ	n	Ψ0	ϕ0	ϕ	n	Ψ0	ϕ0	ϕ
m = 10	0.10	0.01	242	0.05	0.80	0.80	124	0.05	0.80	0.80	76	0.05	0.81	0.81
		0.05	244	0.05	0.80	0.80	126	0.05	0.81	0.81	76	0.05	0.81	0.80
		0.10	240	0.05	0.80	0.80	124	0.05	0.80	0.81	74	0.04	0.80	0.80
	0.25	0.01	246	0.06	0.80	0.80	126	0.05	0.80	0.80	76	0.05	0.80	0.80
		0.05	256	0.05	0.79	0.80	132	0.05	0.79	0.80	80	0.05	0.79	0.80
		0.10	260	0.05	0.80	0.80	134	0.05	0.81	0.80	82	0.05	0.80	0.81
	0.50	0.01	250	0.05	0.80	0.80	128	0.05	0.80	0.80	78	0.05	0.79	0.81
		0.05	282	0.05	0.82	0.80	144	0.05	0.80	0.80	88	0.05	0.80	0.81
		0.10	304	0.05	0.80	0.80	156	0.05	0.80	0.80	94	0.05	0.79	0.80
m = 20	0.10	0.01	122	0.05	0.80	0.80	62	0.05	0.80	0.80	38	0.05	0.80	0.81
		0.05	124	0.05	0.81	0.80	64	0.05	0.80	0.81	38	0.06	0.79	0.80
		0.10	120	0.05	0.80	0.80	62	0.05	0.79	0.81	38	0.06	0.81	0.81
	0.25	0.01	126	0.05	0.81	0.80	64	0.05	0.80	0.80	40	0.05	0.81	0.82
		0.05	134	0.06	0.80	0.80	68	0.05	0.79	0.80	42	0.05	0.79	0.81
		0.10	136	0.06	0.79	0.81	70	0.05	0.81	0.81	42	0.05	0.80	0.81
	0.50	0.01	130	0.05	0.80	0.80	68	0.05	0.79	0.81	42	0.06	0.81	0.82
		0.05	156	0.05	0.80	0.80	80	0.05	0.79	0.80	48	0.06	0.79	0.80
		0.10	170	0.05	0.80	0.80	88	0.05	0.81	0.81	54	0.05	0.80	0.81
m = 50	0.10	0.01	50	0.05	0.80	0.81	26	0.05	0.80	0.81	16	0.06	0.80	0.82
		0.05	50	0.05	0.79	0.80	26	0.05	0.81	0.81	16	0.05	0.80	0.82
		0.10	48	0.05	0.80	0.80	26	0.05	0.83	0.82	16	0.06	0.81	0.83
	0.25	0.01	52	0.05	0.79	0.80	28	0.05	0.81	0.82	18	0.05	0.83	0.84
		0.05	58	0.04	0.81	0.81	30	0.06	0.81	0.82	18	0.05	0.80	0.81
		0.10	56	0.05	0.80	0.80	30	0.05	0.82	0.82	18	0.05	0.81	0.82
	0.50	0.01	58	0.05	0.79	0.81	30	0.06	0.80	0.81	18	0.06	0.76	0.81
		0.05	74	0.05	0.80	0.81	38	0.05	0.81	0.81	24	0.05	0.81	0.83
		0.10	76	0.05	0.79	0.80	40	0.05	0.80	0.81	24	0.05	0.78	0.81
m = 100	0.10	0.01	26	0.05	0.82	0.81	14	0.05	0.83	0.83	8	0.06	0.80	0.81
		0.05	26	0.05	0.81	0.81	14	0.05	0.82	0.84	8	0.05	0.81	0.81
		0.10	24	0.05	0.80	0.80	14	0.05	0.85	0.85	8	0.05	0.83	0.83
	0.25	0.01	28	0.05	0.80	0.81	14	0.06	0.79	0.80	10	0.06	0.84	0.86
		0.05	30	0.05	0.81	0.81	16	0.05	0.81	0.83	10	0.05	0.82	0.84
		0.10	30	0.05	0.81	0.82	16	0.04	0.83	0.84	10	0.05	0.83	0.85
	0.50	0.01	32	0.06	0.79	0.80	18	0.06	0.81	0.84	10	0.04	0.76	0.81
		0.05	40	0.05	0.79	0.81	22	0.06	0.81	0.83	14	0.06	0.81	0.85
		0.10	42	0.05	0.82	0.82	22	0.05	0.81	0.83	14	0.05	0.80	0.85

Note: Δ is the effect size, ρ_y|x is the adjusted outcome ICC, and ρ_x is the covariate ICC. The results are based on 5000 simulations.

The results obtained in Tables 1 and 2 further allow us to evaluate the impact of different design parameters on the estimated required number of clusters n. We fit a multiple linear regression model, where n is the response variable, and cluster size m, covariate ICC ρ_x, adjusted outcome ICC ρ_y|x, and effect size Δ are four covariates (linear term only). Although we know from Equation (11) that their relationship is not necessarily linear, this approach may provide additional insights on the determining factors for sample size calculation for testing HTE in CRTs. We report the unstandardized and standardized regression coefficients and z-score values in Table 3. The standardized regression coefficient, also known as the β-coefficient or β-weight, are obtained from a regression analysis where the variances of the response and independent variables are all scaled to unity, and is therefore invariant to unit of measurement for the original variables. Comparing the standardized coefficients could inform which design parameter has a greater effect on the required sample size. From Table 3, it is evident that both the cluster size m and interaction effect size Δ have a major impact on the required number of clusters. In addition, the impact of covariate ICC ρ_x on sample size n appears larger than that of the adjusted outcome ICC ρ_y|x. The standardized coefficient of ρ_x is two times that of ρ_y|x, highlighting the important role of ρ_x in powering the interaction test in CRTs.

TABLE 3.

Effect of design parameters on the sample size n: results from multiple linear regression analysis

Design parameter	Unstandardized coefficient	Standardized coefficient	Standard error	z-score	P-value
ρx	41.00	0.08	24.39	1.68	.09
ρy|x	85.31	0.04	109.30	0.78	.44
m	−1.39	−0.59	0.11	−12.11	<.001
Δ	−255.26	−0.36	34.41	−7.42	<.001

6 |. THE HF-ACTION DATA EXAMPLE

We illustrate our sample size procedure using data collected from the HF-ACTION study.³⁷ The HF-ACTION study is an individually randomized trial that aimed to test the efficacy and safety of exercise training program among patients with chronic heart failure and reduced ejection fraction. In the study, patients recruited from 82 sites (heart clinics or heart and vascular centers) were randomized to receive either usual care plus aerobic exercise training, or usual care alone. In Yang et al,³¹ we have previously used the outcome and covariate data from the HF-ACTION study to recreate a CRT to assess the bias in estimating the OTE due to baseline imbalance. In this section, we use the same context and baseline covariate data from HF-ACTION to inform the design parameters and exemplify how to estimate the required sample size and power for testing HTE, were the investigators to conduct a CRT using the HF-ACTION population.

Suppose the investigators are interested in conducting a CRT to evaluate the benefit of exercise training program among patients with chronic heart failure and reduced ejection fraction. In this case, each participating site will be randomized to either the aerobic exercise arm or the usual care arm, and ${\sigma }_w^2=1/4$. Suppose the primary outcome of the study is the change of 6-minute walk test distance from baseline to 3 months. From the HF-ACTION baseline data, we estimate the marginal standard deviation of primary outcome to be σ_y ≈ 71 m, and the unadjusted outcome ICC to be ρ_y = 0.04. In the HF-ACTION study, the overall treatment effect size is estimated to be Δ_OTE = 18.85 (P <.001) m. Using the classical sample size calculation based on the design effect (1), and given each site is able to recruit m=27 patients for the study, we found that about n=34 sites are required to ensure 80% power to detect the overall treatment effect size similar to that reported in the HF-ACTION study.

In addition to powering the OTE test, we are also interested in finding out how many more clusters are required to ensure 80% power to detect treatment effect heterogeneity. We use age as an example for the continuous covariate and race as an example for the binary covariate. The considerations for HTE with respect to race is particularly common, as previous studies suggest that black patients respond differently to therapies for heart failure,³⁸ and that there is a statistically significant interaction between black race and exercise training for the 6-minute walk test outcome.³⁹ From the baseline data of HF-ACTION, the mean age is 59.3 years (σ_x = 12.7), and 34.4% are black race (σ_x = 0.48). Figure 3 presents the cluster-specific average age and proportion of black population, and clearly shows substantial variability of both covariates across clusters. We estimate the covariate ICC for age to be ρ_x = 0.08 and that for black race to be ρ_x = 0.22 (the binary ICC was estimated using the ANOVA method⁴⁰). In this case, because σ_y|x ≈ 69 m for both age and race and is substantially larger than σ_x, adjusting for either age or race does not change the outcome ICC so that ρ_{y x} ≈ ρ_y = 0.04. This observation is consistent with the analytical insight provided by Equation (23). Suppose that the effect size for the treatment-by-age interaction is Δ = 0.05Δ_OTE, which implies that one unit change in age (in years) translates into around 1 m difference in 6-minute walk distance. We require about 41 sites to ensure 80% power for the interaction test. Using the race variable as another example, suppose that the treatment-by-black-race interaction effect is the same as that of OTE, which implies a Δ ≈ 19 m difference between the black and white populations. We require 80 sites to ensure 80% power to detect the in a CRT. Equivalently, based on expression (24), we can see that the number of clusters required for the OTE test needs to be increased by a factor of Θ(27) ≈ 1.19 and Θ(27) ≈ 2.36 to obtain the same power for testing differential treatment effect by age and race, respectively. In particular, if the 82 sites included in the HF-ACTION study all agree to participate in a CRT, the study would be adequately powered for both the analysis of overall treatment effect as well as treatment-by-age, treatment-by-race interactions, with respect to the change of 6-minute walk distance outcome.

FIGURE 3.

Distributions of proportion of black population and mean age across 82 sites (clusters) in the HF-ACTION study

7 |. DISCUSSION

Current cluster randomized trials are designed to evaluate the OTE, frequently using a random-effects model that includes only the treatment indicator. In recent years, investigating differential treatment effect among patient subgroups has become increasingly popular, but there has not been extensive discussion on the sample size requirements for testing HTE in CRTs, except in Spybrook et al²³ and Dong et al.²⁴ In this article, we develop a closed-form sample size formula that allows investigators to calculate the required number of clusters or patients to power the interaction test, while accounting for the intraclass correlation coefficients of both the outcome and the covariate. The proposed formula can accommodate an interaction test concerning either individual-level or cluster-level covariates. We realize that many CRTs include the analysis of OTE as their primary analysis, and therefore may not be designed to power the analysis of treatment-by-covariate interaction. In those context, however, our sample size procedure may also be useful in ad hoc power calculation to clarify the sample size requirements in secondary analysis that targets such treatment effect heterogeneity. Although the interaction test may require a larger sample size than the overall test in some scenarios (as in our data example of Section 6), we also demonstrate in Figure 2 that their sample size requirements could be comparable in regions where the adjusted outcome ICC is not too small and the cluster size is large. In any case, the proposed procedure provides a principled approach to identify such scenarios where the sample size requirements are similar for both analyses, and offers an opportunity to enhance the credibility of the analysis of treatment effect heterogeneity in CRTs. Notice that we have adopted a model-based framework and assume the covariate-adjusted linear mixed model (3) holds. However, the results may be somewhat different if one adopts a design-based perspective to the analysis of randomized trials as in Schochet et al^41,42 and Ding et al.⁴³

Although Equation (11) suggests a direct approach to calculate the required sample size for the interaction test, those who are more familiar with the traditional design effect θ₁(m) could use the following three-step approach to obtain the same sample size result. Given the nominal type I error rate and power to detect an overall effect, one could obtain the number of patients (N_ind) required for an individually randomized controlled trial (RCT). This can be done by using the general formula (8), but replacing ${\sigma }_4^2$ with the total variance of the outcome. By assuming the number of patients that would be recruited in each cluster, the second step is to inflate N_ind by the traditional design effect θ₁(m), and obtain N_OTE = N_ind × θ₁(m), which is the number of patients required in a CRT. The required number of clusters for detecting the overall treatment effect is then N_OTE/m, rounded to the nearest integer above. The above two steps are no different from the common practice used in designing CRTs. To calculate the sample size for detecting HTE, one could further inflate (or deflate) N_OTE by a second design effect, Θ(m), defined in Equation (24). This requires knowledge of the relative effect sizes (RDES), the covariate ICC, the adjusted outcome ICC, and the adjusted total variance. The required number of patients to power the test for HTE is given by

$$N_{\text{HTE}}=N_{\text{OTE}}\times \Theta (m)=N_{\text{ind}}\times {\theta }_1(m)\times \Theta (m),$$ (25)

and the required number of clusters would simply be N_HTE/m, rounded to the nearest integer above. Depending on whether Θ(m) is greater than one, we may require more or fewer patients for detecting HTE than for detecting OTE in a CRT.

We have studied how the design parameters influence the sample size determination and power of the interaction test. We have highlighted the roles of the two ICC parameters: ρ_y|x and ρ_x. First, while larger values of the covariate ICC reduce the power of the interaction test, it may reduce the power of the overall treatment effect even more when the outcome ICC is relatively small (see Figure 2 when ρ_y|x=0.01). Second, larger values of the adjusted outcome ICC may not necessarily lead to smaller power in testing the HTE. As a result, the role of the adjusted outcome ICC in testing HTE is strikingly different from the role of unadjusted outcome ICC in testing OTE. We have observed a parabolic relationship between the power of the HTE test and adjusted outcome ICC; the power of the test first reduces and then increases as the adjusted outcome ICC becomes larger. The critical point ${\tilde{\rho }}_{y\mid x}$ that leads to the smallest power is given in Equation (22) and depends on both the covariate ICC and cluster size. In particular, the outcome ICC (either adjusted or unadjusted) commonly reported in the CRT literature only occasionally exceeds 0.1.^33,44 In Figure 1, we observe that when the covariate ICC larger than 0.5 and the cluster size is relatively small (say smaller than 50), the critical point ${\tilde{\rho }}_y$ is usually no smaller than 0.1; in those case, the adjusted outcome ICC still inflates the required sample size for testing HTE. However, as the covariate ICC moves toward zero, the critical point ${\tilde{\rho }}_{y\mid x}$ also moves toward zero, suggesting that larger values of the adjusted outcome ICC may actually increase the power of the HTE test. This is actually the case in our data example of Section 6, because the covariate ICC for either age or race was estimated to be no larger than 0.25 and the anticipated cluster size is only 27. The important role of the covariate ICC has also been highlighted in Table 3, where the multiple linear regression analysis produces a much larger standardized coefficient for ρ_x than for ρ_y|x. Although it is currently recommended to report outcome ICC values in parallel CRTs,^45,46 reporting covariate ICCs has not become standard practice. In scenarios where pilot studies are carried out or baseline information is readily available, the estimation of ICC for covariates can proceed using standard procedures developed for outcome ICC.^3,47 Because the covariate ICC is an essential ingredient of the sample size formula, we advocate future CRTs that examine treatment effect heterogeneity to start reporting ICCs for the covariates of interest. Just like the outcome ICCs, values of covariate ICCs can provide useful information for designing future trials that plan to assess the treatment-by-covariate interaction. In the absence of covariate ICC information, however, our power formula still provides a useful approach for sensitivity analysis, provided a plausible range of ρ_x can be elicited in the design phase.

It is important to notice that the new variance expression derived in this article (Equation (10)) differs from those studied in Spybrook et al²³ and Dong et al.²⁴ Within the same setting of a two-level CRT, the previous work has provided (or indirectly implied) an alternative variance expression for ${\widehat{\beta }}_4$, which depends on both the residual variance of the unadjusted model ${\sigma }_{\xi }^2$ and that of the adjusted model ${\sigma }_{ϵ}^2$. An R-squared parameter $R_{y\mid x}^2=1-{\sigma }_{ϵ}^2/{\sigma }_{\xi }^2$ is further introduced to parameterize the sample size formula and represents the explained variation of the outcome due to covariates. By contrast, our variance expression only assumes knowledge from the adjusted model (3), and does not involve assumptions of the unadjusted model (2). These different assumptions could underlie the different forms of the variance expressions. On the other hand, it remains unclear from previous work whether the covariate ICC ρ_x plays a role in $R_{y\mid x}^2$ and hence the sample size determination. Our approximate derivation in Section 4.2 and Web Appendix B shows that there may be cases where $R_{y\mid x}^2$, as a function of only ${\sigma }_{ϵ}^2$ and ${\sigma }_{\xi }^2$, is invariant to ρ_x, whereas our analytical and simulation results clearly indicate ρ_x plays a major role in determining the required sample size for the interaction test. A keen reviewer also pointed out that the model used in Spybrook et al²³ and Dong et al²⁴ assumed that the covariates were centered around the cluster mean, which may help avoid the complication due to the covariate ICC. From this perspective, an important major contribution of this article is that it facilitates power calculation when the covariates are not centered around the cluster mean. In any case, additional further research is required to formally compare our sample size procedure with the previous procedures via extensive Monte Carlo simulations. These additional comparisons may be able to fully clarify the differences and make recommendations on appropriate use of different sample size formulas in different scenarios.

There are several potential limitations of this article, some of which will be addressed in our future work. Above all, although we provided the extension of the sample size procedure to accommodate multiple covariates, we have mainly focused our discussion and simulation experiments on a single covariate. We recognize that more efforts are required to come up with sensible effect sizes for multiple interaction terms in the design stage, and those values could possibly be informed once more treatment-by-covariate interaction effects are reported in CRTs. Second, we have only considered the interaction test between treatment and covariates in the absence of additional adjustment variables. There are scenarios where additional pretest variables are considered in addition to the treatment-by-covariate interactions to further improve precision; those scenarios have been addressed in Spybrook et al²³ and Dong et al,²⁴ and will be considered in our future work. Third, we have assumed the outcome to be a continuous variable, and therefore the proposed sample size formula could only approximate the required sample size for a binary or count outcome. Additional work is required to develop formal sample size procedures for categorical outcomes, based on the generalized linear mixed model or the generalized estimating equations; section 3 of Li et al⁴⁸ reviews technical details of these models commonly used in CRTs with a binary outcome. Fourth, we have limited our attention to parallel CRTs, while other recent CRTs have considered the crossover⁴⁹ or stepped wedge designs.^35,50,51 It would be interesting to extend the existing sample size procedures developed for these unidirectional designs to similarly accommodate an interaction test. Finally, we have assumed equal cluster sizes to simplify the derivation of the sample size formula. It remains to be explored whether unequal cluster sizes would drastically reduce the efficiency for testing the HTE as it does for testing the OTE in CRTs.¹³ We plan to carry out future work to investigate the impact of variable cluster sizes for testing HTE, and develop a modified sample size formula that adjusts for cluster size variability.