Guiding Cell Network Assembly using Shape-Morphing Hydrogels

Abstract

Forces and relative movement between cells and extracellular matrix (ECM) are crucial to the self-organization of tissues during development. However, the spatial range over which these dynamics can be controlled in engineering approaches is limited, impeding progress toward the construction of large, structurally mature tissues. Herein, shape-morphing materials called “kinomorphs” that rationally control the shape and size of multicellular networks are described. Kinomorphs are sheets of ECM that change their shape, size, and density depending on patterns of cell contractility within them. It is shown that these changes can manipulate structure-forming behaviors of epithelial cells in many spatial locations at once. Kinomorphs are built using a new photolithographic technology to pattern single cells into ECM sheets that are >10× larger than previously described. These patterns are designed to partially mimic the branch geometry of the embryonic kidney epithelial network. Origami-inspired simulations are then used to predict changes in kinomorph shapes. Last, kinomorph dynamics are shown to provide a centimeter-scale program that sets specific spatial locations in which ≈50 μm-diameter epithelial tubules form by cell coalescence and structural maturation. The kinomorphs may significantly advance organ-scale tissue construction by extending the spatial range of cell self-organization in emerging model systems such as organoids.

During tissue morphogenesis, structural features of organisms are built through changes in cell and extracellular matrix (ECM) position, density, and composition over time. Engineers are attempting to mimic these dynamic processes to build more life-like tissues using microfluidic, 3D bioprinting, and organoid technologies.^[1–4] Organoids, 3D tissues grown from stem cells, are an essential approach because of the remarkable cellular diversity and spatial structure that can be achieved through processes of “self-organization,” including spontaneous cell sorting and spatially varied cell differentiation.^[5] However, organoids have largely not addressed longer length-scale (>0.5 mm) tissue developmental processes beyond local self-organization. More prescriptive tissue engineering scaffolds built through 3D bioprinting of cells and ECM, or subtractive hollowing of hydrogels can potentially impose cues for long-range tissue organization.^[6–9] However, such scaffolds do not yet achieve the progressive elaboration of cell and ECM position, density, and composition over time that integrates tissue structure from the cellular to organ scales. The ability to mimic this could bring powerful advances in tissue engineering.^[10]

Forces and relative movement between cells and ECM are particularly important in sculpting tissues during development.^[11–14] Researchers have therefore begun to engineer dynamic interactions between cells and ECM in order to guide multi-cellular structure formation.^[15–24] For example, Davidson et al. found that networks of contractile endothelial cells with different morphologies could be generated by varying the extent to which cells were able to physically reorganize surrounding ECM fibers.^[25] Brownfield et al. also found that mammary epithelial organoids reorganize and align collagen I fibers through cell contractility, and form multi-cellular protrusions that follow preferentially along the axis of ECM alignment.^[26] However, in neither example was the resulting cell network geometry spatially designed or predictable. The ability to spatially control such dynamic cell-ECM interactions is therefore a pressing gap that limits new approaches to cell network engineering in vitro.^[27]

One well-characterized model system that serves as an attractive starting point are MDCK cells—a kidney tubule-derived cell line family. Under certain 3D culture conditions, MDCKs form spheroids or randomly oriented tubules that lumenize (form an internal cavity) by defining distinct apical (lumen-facing) and basal sides.^[28–30] This apicobasal polarization process can be verified by the asymmetric distributions of cell polarity proteins. However, as in many epithelial systems, there is little conceptual framework for orchestrating their structure within 3D ECMs over longer distances and set geometries.

One way to achieve this would be to set the starting composition and geometry of scaffolds within which cell remodeling of ECM is harnessed to create spatial strain patterns (Figure 1A). These strain patterns would increase cell density in programmed sites, causing cells to fuse (coalesce), while also achieving the local ECM fiber recruitment that is thought to promote multi-scale cell network assembly.^[25,26,31] This approach requires a model that would predict the relationship between strain patterns generated by cells in the starting scaffold and its resulting shape change over time.

Figure 1.

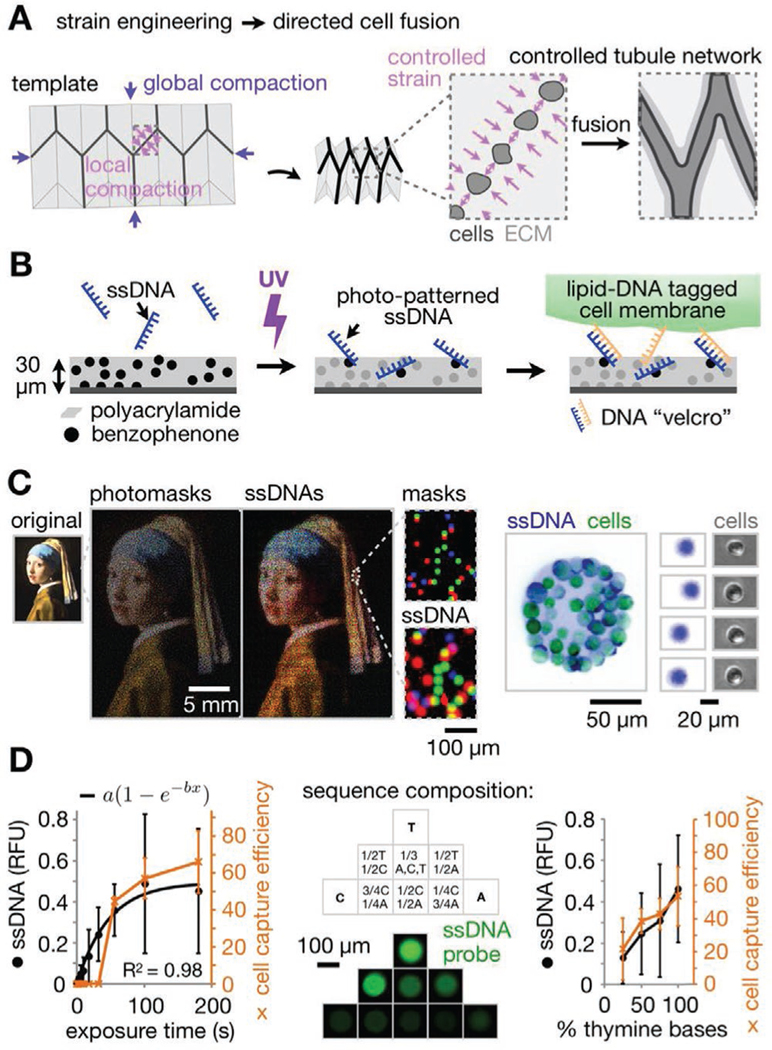
Shape-morphing ECM materials containing photolithographic cell patterns for spatially controlled formation of epithelial networks. A) Strategy for controlling ECM compaction using a mechanical metamaterial design to promote fusion of epithelial spheroids into tubule networks of defined geometry. B) pDPAC workflow showing ssDNA patterning followed by temporary DNA-labeled cell attachment. C) Left: Overlay of red, green, and blue false-colored mask features and DNA spots demonstrating multiple strand patterning across ≈10 μm–25 mm spatial scales (Johannes Vermeer, Girl with a Pearl Earring, c. 1665, Mauritshuis, The Hague, The Netherlands). Right: Fluorescence and phase microscopy images of SYBR Gold-labeled live MDCKs and underlying F DNA spots. Cells were pre-labeled with complementary F′ lipid-DNA and CellTracker dye. D) Left: Amount of 2.5 mm F ssDNA patterned onto pDPAC substrates and capture efficiency of F′ lipid-DNA-labeled MDCK cells versus 254 nm light exposure time (see “Supporting Methods” in the Supporting Information, ±SD, n = 3 experiments from an average of 10 and 5 features per experiment condition respectively). Middle: Fluorescence microscopy images of anti-Y₂₁-FITC probe-labeled 5′-X₂₄-Y₂₁-3′ ssDNA features where X₂₄ is a random 24-mer variable sequence composed of the indicated proportions of bases. Right: Amount of 2.5 mm 5′-T₂₀-X₂₀-3′ ssDNA patterned onto pDPAC gels and capture efficiency of MDCKs for exposure time of 2 min versus the proportion of thymine bases in X₂₀ (see “Supporting Methods” in the Supporting Information, ±SD, n = 3 experiments from an average of 10 and 5 features per experiment condition respectively).

One well-studied approach is origami (a class of mechanical metamaterials), where out-of-plane 3D shape change is determined by strains at crease networks in 2D sheets.^[32–34] In previous work, we found that specific patterns of strain caused by traction forces between cells (especially contractile cell types such as fibroblasts) on the top interface of ECM hydrogel sheets were relieved by the formation of negative curvatures (valleys). However, such strains on the bottom interface led to positive curvatures (mountains).^[35] We found that principal curvature rates and directions could be quantitatively controlled through contractile cell density and spacing, and explored design factors contributing to a high overall robustness of creases to misfolding artifacts in self-folding ECM sheets.^[35] Further, we found that endothelial cells directionally migrated along creases in ECM sheets in response to programmed strains.^[35] These observations set up the possibility of programming ECM reorganization to transform a starting cell pattern into a spatially programmed multicellular network over time.

DNA-patterned assembly of cells (DPAC) is an ideal approach to achieving the necessary geometric control over the starting cell pattern. Cell populations are labeled with lipid-modified single-stranded DNA (ssDNA) oligos that passively insert into cell membranes,^[36,37] and then temporarily adhered by base pairing to spots of a complementary ssDNA patterned onto a glass slide.^[35,38] DPAC has several advantages over other cell patterning methods.^[39,40] First, different cell populations can be independently patterned in the same experiment using orthogonal pairs of oligos. Second, cells can be patterned with spatial resolution of ≈10 μm. Finally, cell patterns can be transferred from the assembly interface into any of a range of hydrogels solidified around them. However, DPAC is significantly limited by the oligo printing speed, and thus the scale at which tissue scaffolds can be built.

In this paper, we seek to 1) vastly increase the scale of cell patterning in ECM sheets using a photolithographic approach to DPAC, so that we can 2) spatially program ECM dynamics that guide the formation of epithelial cell networks at precise locations across cm scales. To do this we build kinomorphs—combining the Greek kinó (propel, drive) and morfí (form, shape)—cell-ECM composite sheets that undergo prescribed changes in ECM strain. These changes specify the locations in which cell networks first form and then undergo structural maturation into tubules, as defined by lumenization and cell polarization. Kinomorphs are a promising approach for achieving geometric control over cell collectives. Such control has several future applications in blending guided cell networks with self-organized cell structures that would extend organoid structure to length-scales that are not currently achievable.

We first asked whether physical ECM remodeling due to cell contractility was sufficient to guide the formation of MDCK cell networks. We began by culturing clusters of MDCKs just below the surface of hydrogel ECM sheets consisting of Matrigel hydrogel impregnated with collagen I fibers. The cell clusters were patterned in regular arrays using DPAC and condensed into spheroids with smooth boundaries (Figure S1, Supporting Information). Subsequent immunostaining of these clusters revealed proper localization of F-actin to apical membranes, and E-cadherin to lateral cell-cell contacts—hallmarks of epithelial polarization.^[41] These spheroids formed in areas where the ECM sheet was adhered to an underlying culture substrate. However, at the edges of the sheet where it lost adhesion to the substrate, spheroids tended to fuse to form tubule-like structures while curling and compacting the gel. Live imaging showed that these dynamics occurred through collective cell movements, remodeling of ECM fibers by cell tractions, and coalescence of spheroids (Video S1, Supporting Information). Similar assembly and structural maturation of mammary epithelial ducts has been observed from cell lines^[31] and primary cells^[24] in compliant, floating ECM contexts, as well as assembly of gut organoids into continuous tubes.^[42] We therefore hypothesized that bringing this property under geometric control could allow us to build cell networks with defined geometries (Figure 1A). In short, since MDCK tubules tended to form at curled and compacted gel regions (creases), we reasoned that building crease networks would guide tubule network formation.

With this emerging strategy, we first sought to make improvements in our cell patterning capabilities in order to reach the scale and speed necessary to build centimeter-scale cell networks. The previous microcantilever-based printing method used to deposit ssDNAs in DPAC is limited in throughput and spatial scale, since individual DNA spots can be printed with a frequency of only ≈1 Hz. We reasoned that we could lift this limitation by shifting to a photolithography approach (“pDPAC”) that would enable millions of DNA features to be printed simultaneously rather than serially.

We first polymerized a 30 μm-thick sheet of 4% polyacrylamide gel containing a photo-reactive benzophenone-methacrylamide co-monomer onto glass slides (Figure 1B).^[43] Applying 254 nm light through photomasks then tethered unmodified ssDNA oligos onto and within the gel in feature sizes down to 10 μm (actual: 11.1 μm ± 5.8% CV, n = 5, Figure 1C). Serial patterning of multiple strands can be performed on the same slide through spatial registration in order to direct the adhesion of different cell populations (Supporting Methods, Supporting Information). ssDNA features were sufficient to temporarily adhere single cells labeled with a complementary lipid-DNA to the polyacrylamide surface with low binding of cells to unpatterned areas (≈4 MDCK cells mm⁻²). We use single-letter nicknames for different patterned DNA/lipid-DNA strand pairs—in this case “F” was patterned onto the pDPAC substrate and cells were labeled with F′, the reverse complement of F (see Supporting Information for full sequences). We found that both the amount of DNA patterned and cell capture efficiency onto pDPAC substrates increased with either the UV dose or the proportion of thymine bases in the patterned DNA (Figure 1D and Figure S2, Supporting Information). We therefore included a T₂₀ tail on DNAs to sensitize them to immobilization during UV exposure. Patterning each DNA strand takes roughly 45 min at scales of at least 5.1 cm × 7.6 cm (or 3.9 × 10⁷ single-cell features); a speed-up of >50× over the previous printing method. Although its performance is comparable to several biomolecule photolithography-based approaches,^[44–47] pDPAC has two advantages specific to kinomorph construction. First, pDPAC enables large-scale cell patterning into ECM sheets, since sheets show little adhesion to the polyacrylamide interface during transfer into culture. Second, neither the glass substrates nor DNAs require expensive chemical modifications.

With a large-scale cell patterning method in place, we sought to encode networks of creases that would promote MDCK tubulogenesis. In short, we needed 1) an apparatus to embed pDPAC cell patterns into ECM sheets, 2) a reference geometry for an epithelial network to serve as a design goal, and 3) a model to predict how candidate crease networks that mimic the reference geometry would emerge from ECM sheets.

For the apparatus: We created a large-format flow cell device that sandwiches two 2” × 3” pDPAC substrates at a distance of ≈250 μm apart (Figure 2A and Video S2, Supporting Information). The flow cell accommodates cell patterning on both the top and bottom polyacrylamide surfaces, from which cells are transferred into collagen I-Matrigel ECM sheets after setting the gel precursor mixture within it. The ECM sheet—which we term a kinomorph—is then dissected and cultured for live imaging. Second, for the reference geometry: We used recently published data to simulate an example ureteric epithelial branching pattern in embryonic day 19 mouse kidney (Figure S3A, Supporting Information).^[48] Finally, for the model: We created a custom origami simulator to enable real-time prototyping of the spatial transformation of candidate crease networks (Figure 2B). The model predicts the position of crease networks in folding 2D sheets based on a given origami design and the target rest angle of creases desired by the user (Supporting Information). We validated the simulator by measuring the “Hausdorff distance”^[49] between 3D meshes created with it to those generated from confocal microscopy images of kinomorphs folded in vitro^[35] (Figure 2B). The Hausdorff distance is computed for each mesh face as the largest of the minimum Euclidean distances of its vertices to any of the vertices defining the other mesh. With distances < 50 μm on average, origami simulator models adequately predicted the approximate mm-tocm-scale shape dynamics of kinomorphs.

Figure 2.

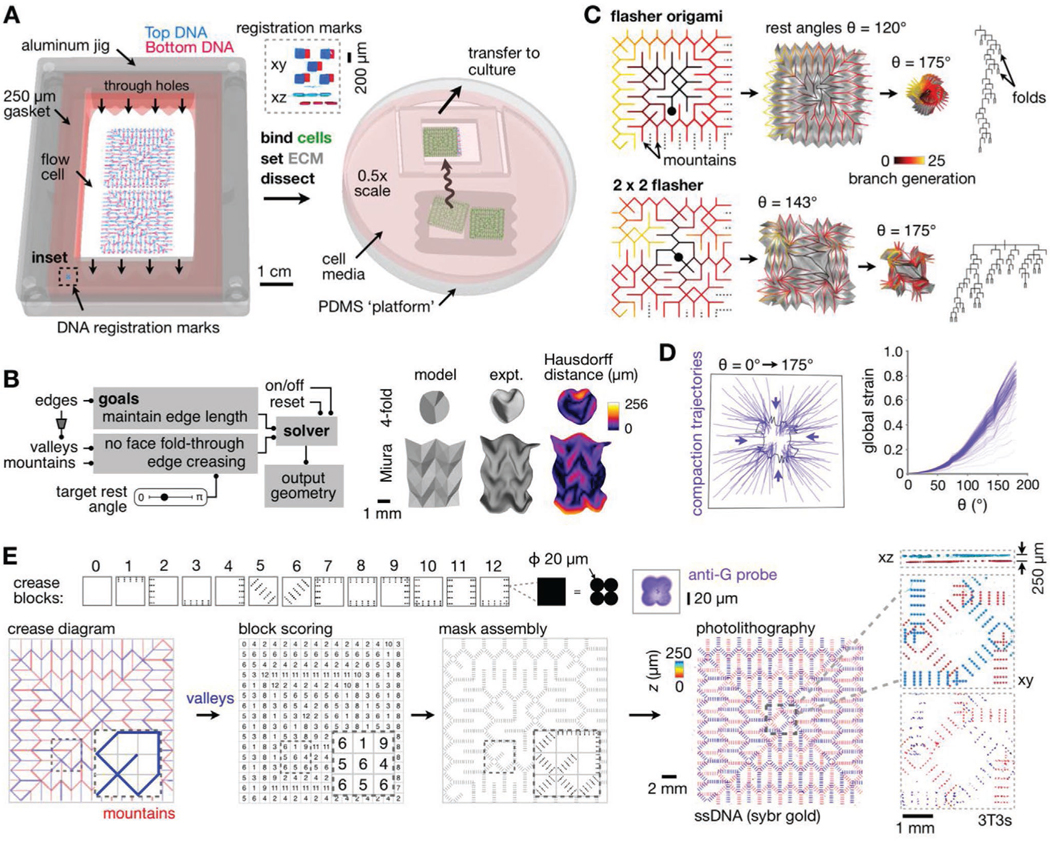
Large-scale model-guided design and production of kinomorphs. A) Schematic of microfluidic flow cell workflow and transfer of kinomorphs to culture. Inset, SYBR Gold-labeled slide registration marks (Supporting Information). B) Left: Flow chart outlining origami simulation of crease networks. Right: Simulated 3D surfaces versus experimentally generated kinomorphs based on classic fourfold and Miura origami crease networks (partly reproduced with permission.^[35] 2018, Cell Press). Experiment kinomorphs are also shown shaded by Hausdorff distance to models. C) Origami simulations for flasher (top) and 2 × 2 tessellated flasher (bottom) crease networks. Left: Crease networks for mountain folds color-coded by number of branch generations from a given crease to center points (black circles). Middle: Simulations at different crease rest angles (θ), including associated sheet surfaces in gray. Right: Branch patterns describing crease networks. D) Left: Trajectories following the movement of several locations on a 2 × 2 flasher model as θ increases from 0° to 175°. Right: Plot of global strain measured for each trajectory. E) Top row: Crease blocks where each black pixel encodes a 2 × 2 grid of 20 μm-diameter circular features. Right: Confocal fluorescence microscopy image of an anti-G-FITC-probed feature associated with one crease block pixel. Bottom row: Flasher origami crease diagram showing valleys (blue) and mountains (red), manual crease scoring to ascribe crease blocks, and block assembly into full mask design. Right: Confocal fluorescence microscopy images of SYBR gold-labeled DNA features on a pair of assembled pDPAC substrates, color-coded by depth. Insets: Detail and xz projection of DNA features and CellTracker dye-labeled 3T3 cells, also color-coded by z depth.

With these three core engineering needs in place, we sought kinomorph crease patterns that approximately matched the reference branching geometry. There are some intrinsic limitations here, because arbitrary crease patterns are not guaranteed to rigidly fold into a target 3D shape.^[32,50] Instead, we searched for existing origami designs having tree-like crease networks with similar branching geometry to the embryonic kidney epithelium, and modeled their folding dynamics. These efforts led us to the “flasher supreme” design that has mountain and valley networks each emanating from a single edge. These networks bifurcate with approximately similar probabilities to those observed over wide ranges in the branching hierarchy of the embryonic mouse ureteric epithelium (Figure 2C and Figure S3, Supporting Information). Flasher supreme creases also collapse together through a rotational dynamic that produces similar “global strains” along any given radial direction as the crease rest angle is increased (Figure 2D). Here we define global strain ε ≈ d/ℓ, where d is the distance traveled along a trajectory by a point on a compacting object and ℓ is the distance from the start of the trajectory to the object’s centroid. Tessellating the original design into 2 × 2 or 3 × 3 versions retains these properties without significant modification (Figure 2C and Figure S3, Supporting Information).

With a candidate crease family selected, we began translating flasher crease networks into cell patterns. We started with patterns of 3T3 fibroblasts, which would actuate strain patterns necessary to promote MDCK tubule formation in later kinomorph designs. We first created “crease blocks”—sets of 20 μm-diameter ssDNA features in anisotropic grid patterns that we previously found to encode creases along specific axes within self-folding ECM sheets.^[35] Each feature represents a mask position at which DNA is deposited on pDPAC substrates, and thus at which cells are patterned (Figure 2E). We then assembled a mosaic of crease blocks into the complete origami design, which we built two at a time for a total of 139 396 DNA features per experiment (equivalent to >38 h of printing time using the original DPAC method, Video S3, Supporting Information). We used pDPAC to create 22.4 × 22.4 × 0.25 mm flasher kinomorphs from this design as ECM sheets with 3T3s patterned in the prospective mountain and valley networks on each side (measured thickness was 229 μm ± 12% CV for n = 7 sites spread across the sheet area). At 5 cm², these kinomorphs were 10.5× larger in area than any self-folding tissue made previously,^[35] enabled primarily by the advantages of pDPAC.

Having built our first kinomorph design, we studied its behavior in culture. An example flasher kinomorph folded into a set of crease networks over 36 h that had 137 of 142 mountain creases in the expected orientation (96%) compared to the corresponding simulated origami (Figure S4 and Video S4, Supporting Information). In origami, a “flat fold” is a crease whose adjacent faces lie flush against each other. Of the properly oriented mountains, 131 (96%) were flat-folded. Proper coordination of crease folding was likely promoted by a minimal influence of external forces such as gravity and stiction to culture plates, since ECM sheets are approximately neutrally buoyant and show little adhesion to culture substrates because of the use of an agarose underlay. Low Reynolds number conditions local to folds additionally prevent inertial momentum from disturbing folding programs.^[51] Based on these observations, we concluded that large self-folding kinomorphs can be successfully programmed with spatial strain patterns that coordinate crease formation over centimeter length-scales.

With these capabilities in place, we sought to add in a kidney epithelial cell population and study its time-dependent behavior. We therefore created a 2 × 2 tessellated flasher kinomorph patterned with clusters of MDCKs (using F/F′ ssDNAs) along gel regions associated with programmed mountain folds, in addition to 3T3s (using an orthogonal strand pair G/G′) (Figure 3A and Figure S5, Supporting Information). Based on our previous observations, we hypothesized that the engineered crease compaction local to these MDCK clusters would direct them to fuse as long-range branched tubule networks. 2 × 2 flashers placed in culture folded steadily within the first 20 h of culture and compacted at similar rates in all radial directions, as observed for the model (Figures 3B,C and 2D; Video S5, Supporting Information). An example kinomorph had all 142 mountain creases (100%) in the programmed orientation and approximately flat-folded. However, kinomorphs did not progress through more radically folded shapes predicted by the origami simulator (Video S6, Supporting Information). This is because even when creases were flat-folded, they became mechanically frustrated due to the thickness of kinomorphs relative to the infinitely thin model sheets. However, we still saw a much greater than expected overall shrinkage (global compaction) in the cross-sectional area of kinomorphs (9.0-fold ± 11% CV, n = 3) relative to the model (1.3-fold) (Figure 3D). Even so, models and experiments could be matched using a uniform (isometric) scaling factor to account for the difference in global compaction. We next quantified kinomorph shrinkage in 3D by segmentation of confocal z-stacks. This analysis showed that global compaction led to a 3.8-fold ± 15% CV reduction in the overall volume of ECM (n = 3). This implies a total ECM protein concentration upward of roughly 25 mg mL⁻¹ on average, neglecting spatial variations and any ECM production or degradation processes induced by cells.

Figure 3.

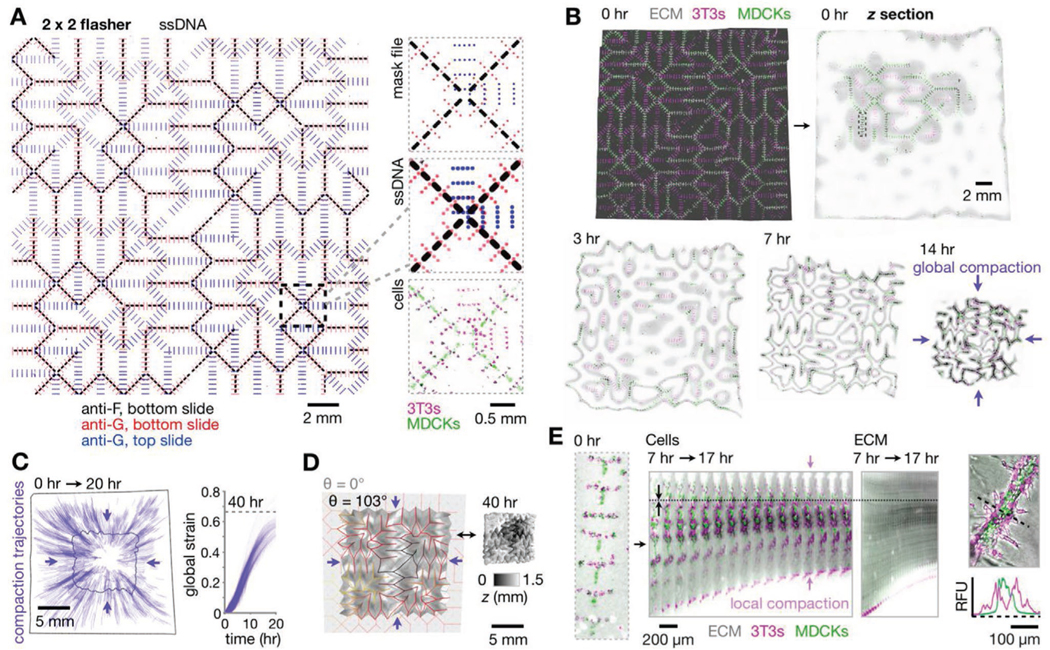
Kinomorphs shepherd cell cluster fusion through controlled local and global compaction. A) Left: Fluorescence microscopy image of assembled pDPAC substrates after patterning with a 2 × 2 flasher design (specifying 3T3 patterning sites using G and MDCK sites using F ssDNAs) and stained with anti-G- and anti-F-FITC probes. Right: Detail of mask design, fluorescence z-projections of corresponding DNA features, and H2B-FP-expressing 3T3/MDCK cells. B) Confocal fluorescence z-projection of the kinomorph imaged immediately after release into media, and mid-plane z sections from a subsequent time-lapse experiment during its compaction in culture. C) Left: Trajectories following the movement of several locations on the kinomorph over 0–20 h. Right: Plot of global strain for each trajectory. D) Left: Output from an origami simulation chosen to match the degree of folding (see Supporting Note 1, Supporting Information) of the kinomorph after 40 h in culture (shown on the right as a 3D rendering shaded by z-height). E) Left: Fluorescence microscopy image of cells patterned at a single crease, kymograph of the crease over a period of 7–17 h after the kinomorph was placed in culture, and kymograph of an ECM region immediately adjacentto cells within the same crease. Note axial compaction of cells and ECM toward a stationary position in the image (dotted line). Right: Relative fluorescence traces across a tubule section show basal 3T3 localization.

In order to better understand the origin of kinomorph global compaction, we next used spatial registration of confocal time-lapse images to track MDCK cell clusters at single creases during the folding process (Video S5, Supporting Information). Individual creases compacted significantly in length during the first ≈20 h of folding (Figure 3E), while neighboring MDCK and 3T3 cell clusters fused into continuous networks. Intriguingly, 3T3 fibroblasts appeared to sort concentrically around (i.e., basally to) MDCKs as cell populations fused (Figure 3E, right). Axial strains of individual creases after 20 h were −59% ± 5.7% and −51% ± 8.2% (s.d., n = 5 creases), measured from the movement of MDCK cells and from the movement of the surrounding ECM, respectively. This shows that traction-based compaction of the ECM by cells rather than migration of cells through ECM was the predominant cause of cell cluster fusion into tubules.

We next asked if axial crease compaction was necessary for these tubule formation phenotypes. In “no 3T3” control kinomorphs that lacked 3T3s, MDCK cell clusters instead condensed into individual spheroids after 24 h (Figure 4A and Figure S6, Supporting Information). In “no folding” control kinomorphs that were adhered to the culture substrate to limit ECM deformation at creases, MDCKs and 3T3s spread to form disorganized 2D sheets. We therefore concluded that programmed ECM compaction during kinomorph folding was necessary for MDCK cluster fusion into continuous 3D tubules along creases.

Figure 4.

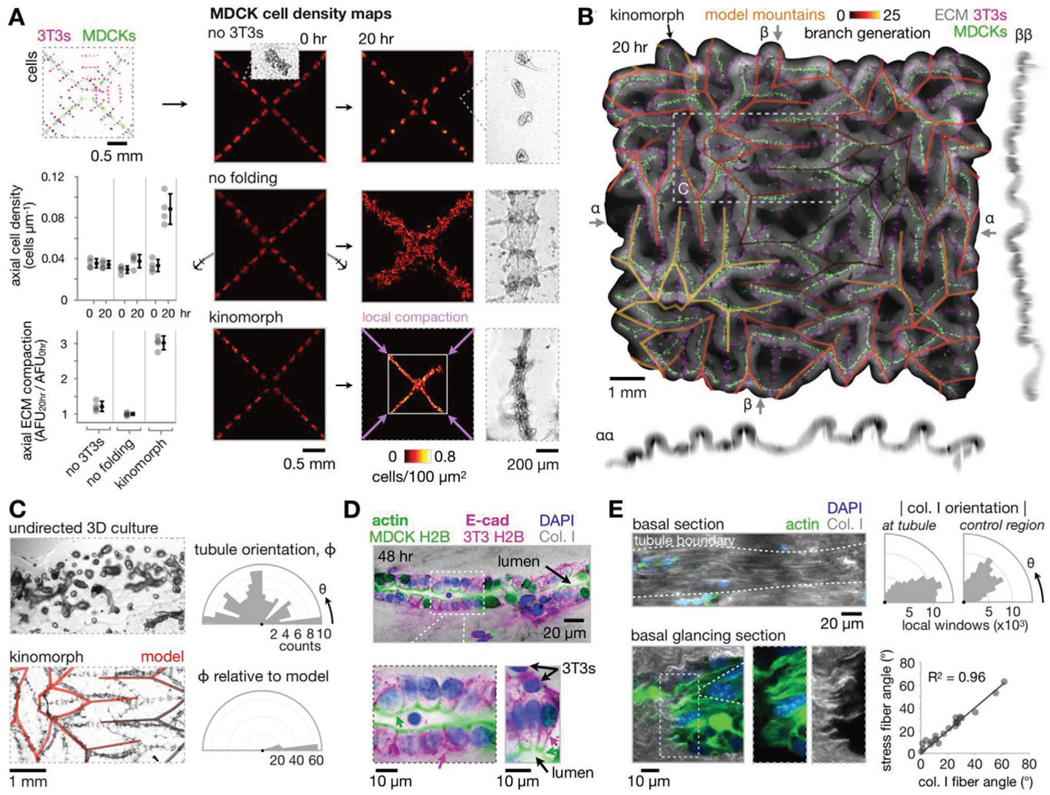
Kinomorphs direct epithelial self-organization and structural maturation at compacted creases. A) Right: MDCK cell density heatmaps at 0 and 20 h for a 2 × 2 flasher kinomorph region and control cases, with phase contrast microscopy images showing collective cell phenotypes. Left: Quantitation of axial cell density and ECM compaction. B) Average z-projection and xz/yz sections of the kinomorph after 20 h in culture. Model predictions of epithelial network edges shown as a transparent overlay. C) Left: 4× phase microscopy images of MDCK cell networks formed from MDCK spheroids in no-3T3 (undirected) kinomorphs versus kinomorphs (model prediction as transparent overlay). Right: Rose plots of tubule orientation in each case. D) 40× immunofluorescence microscopy images of two regions of interest at creases stained for DAPI (nuclei), F-actin (apical membrane, green arrows), and E-cadherin (E-cad, at lateral cell-cell junctions, magenta arrows) after 48 h in culture. Note that the F-actin channel overlaps with MDCK H2B-FP and the E-cad channel overlaps with 3T3 H2B-FP. E) Left: 40× microscopy images of collagen I fiber fluorescence immediately below an example tubule to show fiber alignment. The “glancing section” cuts across the basal interface, showing co-localization of collagen I fibers and intracellular actin stress fibers. Right: Collagen I fiber orientation basal to the tubule relative to a distant control region in the same z-slice. Plot of actin stress fiber angle versus collagen I fiber angle for co-localized fibers.

Since cell clusters fused during kinomorph folding, we next wondered what impact this had on cell and ECM density along areas of kinomorph compaction (Figure 4A). MDCK cells were initially distributed along prospective creases at an axial density of 0.033 cells μm⁻¹ ± 15% CV (n = 12 creases) (i.e., a cell spacing of 31 μm). While no 3T3 and no folding controls showed no significant increase in axial MDCK cell density, kinomorph creases showed a 2.7-fold increase to 0.088 cells μm⁻¹ ± 17% CV (n = 4 creases) at 20 h (an MDCK cell spacing of 12 μm), packing closer to a spacing of 9.0 μm ± 12% CV (n = 10 creases) after 40 h. This spacing is approximately equivalent to the ≈8 μm cell spacing seen in E18 mouse ureteric epithelial tubules.^[52] Axial strain also compacted the surrounding ECM by a factor of 3.0 ± 6.4% CV (n = 4 creases), while little compaction was observed for no 3T3 and no folding controls. Overall, the result of programmed axial crease compaction was a considerable increase in cell and ECM density.

Stepping back to the whole kinomorph scale, cell networks spanned paths through the crease network of up to ≈3 cm (Figure 4B). Further, the origami simulation at a similar “degree of folding” largely mirrored the relative spatial relationships between kinomorph creases (Supporting Note 1, Supporting Information, overlay in Figure 4B). For example, tubule orientation distributions showed a high correspondence between kinomorph and simulation, whereas tubules that formed from MDCK spheroid arrays in “undirected” free-floating ECM sheets did not show any orientation preference (Figure 4C). These data confirmed that kinomorphs successfully specified a prescribed geometry that directed MDCK cell fusion into tubule networks according to a predetermined design.

Having characterized the overall and crease-level behavior of kinomorphs, we sought to test if crease micro-environments were suited to structural maturation of MDCK tubules. We therefore assayed for apico-basal polarization and lumen formation, to determine if tubule cells formed properly localized cell-cell junctions and apical interfaces. ≈50% of the length of MDCK+ creases had columnar MDCK tubules with properly localized F-actin (apical) and E-cadherin (lateral) polarity markers, and 3T3s distributed along the basal-ECM interface (Figure 4D). These tubules were ≈30–60 μm in diameter, similar to E12–16 mouse embryonic kidney epithelial tubule diameters (≈50 μm), as well as adult human renal tubules (≈40 μm), and collecting ducts (40–100 μm).^[53,54]

Remarkably, these tubules formed along engineered kinomorph creases of specified geometry at 5-to-20-fold finer spatial scales than those currently accessible by 3D printing.^[6,7] They were also commonly lumenized with a visible cavity or alternatively, with apical cell surfaces pressed against each other (Figure S7A, Supporting Information). Finally, collagen I fibers were aligned along the basal surface of these tubules and cooriented with actin stress fibers within cells, perhaps implying an intimate connection between ECM cues at compacted areas and epithelial self-organization there (Figure 4E).^[55] We concluded that around half of the length of kinomorph creases were occupied by structurally mature epithelial tubules.

Other crease areas bore tubules with multiple cell layers without clear apicobasal polarity after 48 h, or were associated with open “atria” (non-flat-folded regions lacking tubules) typically at tri-fold junctions where adjacent ECM layers were not fully adhered (Figure S7B, Supporting Information). We hypothesize that the multiple cell layer tubules could be expected to resolve by a lumenization process involving cell death known as cavitation rather than by direct hollowing.^[29] The lack of tubule formation in atria suggests that the flat-folded crease state could stabilize tubule polarity after cell cluster fusion by presenting a basal ECM surface to resident cells in all radial directions within the crease. These atria could perhaps be resolved by embedding folded kinomorphs in a second hydrogel layer. Atria also present an intriguing opportunity as sites to interface kinomorphs with other locally self-organizing tissues, such as kidney organoids, on the ≈200–500 μm length-scale.

Researchers are currently attempting to reconstitute tissue structure up to the organ-scale. Two promising approaches include direct construction (3D bioprinting) and cellular self-organization guided by reconstituted embryonic cues (organoids). Broadly, we are working to bridge these models with a third option, namely, guiding assembly of multi-cellular structures by spatially controlling dynamic interactions between cells and ECM. This approach combines the power of direct construction to impose structural tissue features at larger scales while taking advantage of the intrinsic self-organization capacity of cells at smaller scales.

This new way of building is fully compatible with both organoids and 3D bioprinting. Indeed, researchers are beginning to quantify material responses such as shrinkage and shape change driven by cell behaviors within living bio-inks.^[56,57] To begin taking engineering control over these material dynamics we developed kinomorphs, tissue scaffolds with which particular dynamic mechanical micro-environments can be imposed on cell populations. We began by creating a high-throughput cell patterning technology that allowed us to extend patterning to >10⁷ spatial sites in total fabrication times of ≈2 h and with single-cell resolution. We then used the intrinsic contractility of patterned cells to control the compaction geometry of ECM sheets according to mechanical metamaterial design principles. This created networks of ECM compaction that drove the local assembly and self-organization of epithelial tubules.

Kinomorphs currently have a distinct advantage over most bioprinting approaches in the spatial resolution at which multiple cell populations can be printed. Specifically, kinomorphs achieve printing resolutions of ≈10 μm versus 50–200 μm filaments/layers in 3D printing, and do not require multiple nozzles or cell/polymer blends to accommodate multiple cell types.^[6,7,9,56] Kinomorphs also directly account for changes in spatial structure of cell-ECM composites that occur due to mechanical remodeling by cells, a phenomenon that otherwise contributes to uncontrolled losses in spatial integrity of bioprinted objects.^[56]

Kinomorphs could be extended in a number of ways to achieve more nuanced spatial and compositional structure. First, a broader range of 3D shapes and interfaces could be produced through sequential rather than synchronized folding of kinomorph creases using temporally controlled contractility responses of different cell populations to optical or biochemical cues.^[58–60] The ECM sheet could also be engineered for lower thickness, controlled degradation,^[15] and other types of controlled remodeling by cells,^[61] to enable tissue structures to pack closer together or to activate new instructive cues over time. Indeed, at 48–72 h timepoints, 3T3 fibroblasts in kinomorph creases appeared to infiltrate into the surrounding ECM. Such secondary cell behaviors point toward the potential for further finer-scale colonization of the ECM, which could potentially be sculpted using light- or mechanically-actuated biomolecule release peripheral to tubule locations.^[62,63]

The kinomorph strategy could also be extended to a 3D analogue, for example, by building networks of cell-ECM composite filaments that compact and arrive at a predictable shape, connectivity, and geometry while promoting tissue forming cell behaviors. Organoids could be transferred to kinomorph atria or other geometric features to combine guided cell networks with self-organized cell structures that would lend even finer-scale detail. These efforts would build upon the modest spatial control currently achievable with “assembloid”^[42,64] or cell-material interface^[22] strategies. Kinomorphs could create structurally controlled, biological interfaces between repetitive functional units of organs (e.g., kidney nephrons, lung alveoli, breast epithelial acini, etc.) that emerge in organoid systems but rarely show long-range morphological coordination. Furthermore, the complementary crease networks available on the other side of kinomorph sheets could be a natural host to engineered vascular beds. We therefore imagine future kinomorph versions that spatially scaffold different organoid niches that are dynamically prompted to establish long-range epithelial and vascular communication with each other (Video S7, Supporting Information). More generally, our pDPAC approach should enable co-patterning of different cell types to mimic compositional gradients in native tissues. Finally, kinomorphs could host engineered cell populations that activate synthetic cell-cell signaling circuits to control differentiation or spatial cell sorting.^[65]

In summary, we believe that kinomorphs will serve as a customizable chassis for dynamic tissue engineering efforts. Kinomorphs provide a useful engineering strategy toward gaining control over epithelial organization on length-scales from the single cell to those approaching whole organs.

Experimental Section

Cell Lines and Culture:

NIH 3T3 mouse embryonic fibroblast cells and MDCK cells were tagged with H2B-fluorescent proteins and cultured at 37 °C and 5% CO₂. See Supporting Information for full experimental methods.

Fabrication of Photolithographic DNA-Programmed Assembly of Cells (pDPAC) Substrates:

Glass microscope slides were functionalized with methacrylate groups and used as substrates for polymerization of 30 μm-thick photoactive polyacrylamide gel sheets. See Supporting Information for full experimental methods.

ssDNA Photolithography on pDPAC Substrates:

pDPAC polyacrylamide gels were impregnated with ssDNA oligos and sandwiched against chrome-on-quartz photomasks under nitrogen before exposure with 254 nm light to attach DNAs. See Supporting Information for full experimental methods.

Lipid-ssDNA Labeling of Cells:

Cell lines were incubated with lipid-DNA conjugates to passively label them with adhesive DNA strands. See Supporting Information for full experimental methods.

Assembling pDPAC Substrates and Cell Patterning:

pDPAC substrates were spaced apart with a gasket and assembled as a sandwich in an aluminum jig to form a microfluidic flow cell. Lipid-DNA-labeled cell populations were then introduced and attached to pDPAC substrates within the flow cell, and then embedded in an AlexaFluor 555-labeled collagen I-Matrigel ECM hydrogel prior to releasing them into culture. See Supporting Information for full experimental methods.

Fluorescence Microscopy, Immunofluorescence, and Image Analysis:

pDPAC substrates, attached cells, and kinomorphs were analyzed by live fluorescence microscopy and immunofluorescence microscopy using confocal or widefield microscopes. Image analysis was performed in ImageJ/FIJI software^[66] and Zerene Stacker software (Zerene Systems). See Supporting Information for full experimental methods.

Origami Simulation and Similarity Analysis:

A custom origami simulator was built in Rhino Grasshopper (Robert McNeel & Associates) using Kangaroo2 physics (Daniel Piker). 3D model and kinomorph objects were spatially compared in MeshLab software.^[67] See Supporting Information for full experimental methods.