A General Framework for Integrative Analysis of Incomplete Multi-omics Data

Abstract

There is a tremendous current interest in measuring multiple types of omics features (e.g., DNA sequences, RNA expressions, methylation profiles, metabolic profiles, protein expressions) on a large number of subjects. Although genotypes are typically available for all study subjects, other data types may be measured only on a subset of subjects due to cost or other constraints. In addition, quantitative omics measurements, such as metabolite levels and protein expressions, are subject to detection limits in that the measurements below (or above) certain thresholds are not detectable. In this article, we propose a rigorous and powerful approach to handle missing values and detection limits in integrative analysis of multi-omics data. We relate quantitative omics variables to genetic variants and other variables through linear regression models and relate phenotypes to quantitative omics variables and other variables through generalized linear models. We derive the joint likelihood for the two sets of models by allowing arbitrary patterns of missing values and detection limits for quantitative omics variables. We carry out maximum likelihood estimation through computationally fast and stable algorithms. The resulting estimators are approximately unbiased and statistically efficient. An application to a major study on chronic obstructive lung disease (COPD) yielded new biological insights.

Introduction

Recent technological advances have led to a proliferation of genetics studies involving multiple types of omics data. For example, The Cancer Genome Atlas (TCGA) measured point mutation, copy number aberration, DNA methylation, and mRNA, micro RNA, and protein expressions on tumor tissues and matched normal tissues from >11,000 patients with 33 forms of cancer. As a second example, the Trans-Omics for Precision Medicine (TOPMed) program is generating deep whole-genome sequencing (WGS) and other omics data (e.g., metabolic profiles, protein and RNA expression patterns) on a large number of human subjects with rich phenotypic characterization and environmental exposure data. Such multi-omics studies provide unprecedented opportunities to explore the biological relationships among different types of omics variables, evaluate the direct and indirect effects of genetic variants on complex diseases and traits, and investigate the interplay between omics variables and clinical outcomes [Schadt et al., 2005; Hamid et al., 2009; Vaske et al., 2010; Xiong et al., 2012; Wang et al., 2012; Huang et al., 2014; Zhao et al., 2014; Huang et al., 2016].

A major challenge in integrative analysis of multi-omics data is the problem of missing values. In TCGA, for instance, RNA sequencing and protein expressions are not available for all patients due to cost and lack of tissue samples. In TOPMed, WGS data are currently available for >150,000 subjects, whereas other omics data are collected on much smaller scales due to budget constraints. Another major challenge is that quantitative omics measurements, such as metabolite levels and protein expressions, are subject to detection limits in that measurements below (or above) certain thresholds are not detectable.

There is a large body of statistical literature on missing data [Little and Rubin, 2014]. In the genetics context, single imputation for untyped variants works remarkably well [Marchini et al., 2007; Browning and Browning, 2007; Lin et al., 2008; Li et al., 2010], but the problem of missing data on quantitative omics measurements has received little attention. The prevailing approach to the problem of detection limits is to remove the unknown values or replace them by the detection limit or another value [Yu et al., 2014]. This approach is statistically inefficient and possibly biased [Helsel, 2006; Nie et al., 2010]. Although statistical methods have been developed to handle cases where the variable with a detection limit is either a dependent variable [Epstein et al., 2003; Diao and Lin, 2006] or an independent variable [Cole et al., 2009; Nie et al., 2010], no methods are available to deal with detection limits in joint modeling of multiple data types, where the variable with a detection limit is an independent variable in one model and a dependent variable in another model, or where both the dependent and independent variables are subject to detection limits. In addition, the situation in which a variable is subject to both missingness and detection limit has not been investigated before.

In this article, we propose a valid and efficient approach to handle missing values and detection limits in integrative analysis of multi-omics data. We relate the quantitative omics variable of interest to genetic variants and other variables through a linear regression model, and we relate the phenotype of interest to the quantitative omics variable and other variables through a generalized linear model. Indeed, we consider a very general setting with multi-dimensional quantitative omics variables and multivariate phenotypes by formulating the joint distribution of multi-dimensional quantitative omics variables through a multivariate linear regression model and the joint distribution of multiple phenotypes through a generalized linear mixed model. We derive the joint likelihood for the model parameters by allowing quantitative omics variables to be potentially missing and subject to lower or upper detection limits. We carry out maximum likelihood estimation through efficient expectation-maximization (EM) algorithms [Little and Rubin, 2014]. The resulting estimators are approximately unbiased and statistically efficient with a readily estimated covariance matrix. We demonstrate the advantages of the proposed methods over complete-case analysis and imputation methods through extensive simulation studies. Finally, we provide an application to the SubPopulations and InteRmediate Outcome Measures In COPD Study (SPIROMICS) [Couper et al., 2014], which measured ∼100 blood proteins and >600,000 SNPs on ∼3,000 patients.

Methods

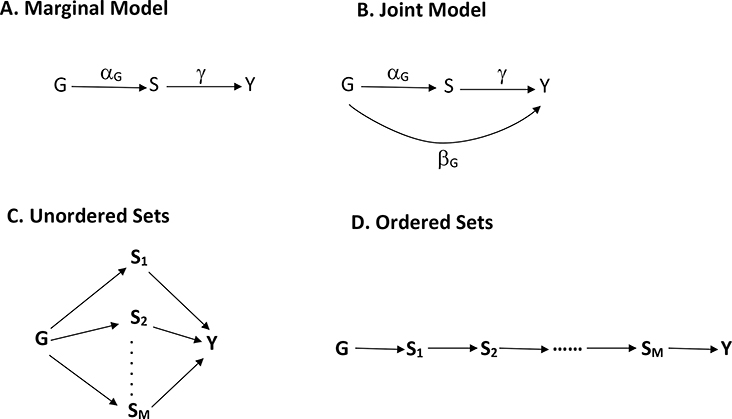
Let Y denote the phenotype of interest, G the genotype of a SNP, and S the quantitative omics variable of interest, which is potentially missing and may have a lower or an upper detection limit. Investigators are typically interested in studying the effects of G on S and S on Y, as shown in Figure 1 (A). They may also be interested in studying the direct and indirect effects of G on Y, as shown in Figure 1 (B). We will refer to these two scenarios as the Marginal Model and the Joint Model, respectively. In either scenario, we may include covariates (e.g., race, gender, age, and principal components for ancestry) in the model.

Figure 1.

Statistical models for integrative analysis of multi-omics data: (A) Marginal Model relating genotypes to quantitative omics variables and relating quantitative omics variables to phenotypes; (B) Joint Model relating genotypes to quantitative omics variables and relating genotypes and quantitative omics variables to phenotypes; (C) unordered relationships among M sets of quantitative omics variables; and (D) ordered relationships among M sets of quantitative omics variables.

We relate S (after an appropriate transformation) to a vector of independent variables X through the linear regression model

$$S={\mathit{\alpha }}^{\text{T}}\mathit{X}+ϵ,$$ (1)

where X typically includes G and covariates, α is a vector of regression parameters, and ϵ is zero-mean normal with variance σ². In addition, we relate Y to S and a vector of independent variables Z through the generalized linear model with density function f(Y|Z,S;η), where Z may overlap with X, and η is a set of unknown parameters. For a quantitative trait, we specify the linear regression model

$$Y={\beta }^{\text{T}}\mathit{Z}+\gamma S+\epsilon ,$$ (2)

where β and γ are regression parameters, and ϵ is zero-mean normal with variance τ², such that η = (β^T,γ,τ²)^T; for a binary trait, we specify the logistic regression model

$$\mathrm{logit}\{\mathrm{Pr}(Y=1)\}={\beta }^{\text{T}}\mathit{Z}+\gamma S,$$ (3)

such that η = (β^T,γ)^T. As mentioned earlier, Z excludes G under the Marginal Model and includes G under the Joint Model. We set the first components in both X and Z to 1, such that the first components of α and β are the intercepts. We denote the components of α and β corresponding to G as α_G and β_G, respectively; see Figure 1 (A) and (B). We are primarily interested in parameter estimation and hypothesis testing on α_G, β_G, and γ.

To provide a general framework for integrative analysis of multi-omics data, we consider multi-SNP genotypes G and multi-dimensional quantitative omics variables S, together with possibly multivariate traits Y. We relate S to X through the (multivariate) density function f(S|X;ξ) indexed by a vector of unknown parameters ξ, where X is a function of G and covariates. It is convenient to specify f(S|X;ξ) through the multivariate linear regression model

$$\mathit{S}={\mathit{\alpha }}^{\text{T}}\mathit{X}+\mathit{ϵ},$$

where α is a matrix of regression parameters, and ϵ is a zero-mean normal random vector with covariance matrix Σ. That is,

$$f(\mathit{S}\mid \mathit{X};\mathit{\xi })={(2\pi )}^{-d/2}|\mathbf{\Sigma }{|}^{-1/2}\exp \{-{\left(\mathit{S}-{\mathit{\alpha }}^{\text{T}}\mathit{X}\right)}^{\text{T}}{\mathbf{\Sigma }}^{-1}\left(\mathit{S}-{\mathit{\alpha }}^{\text{T}}\mathit{X}\right)/2\},$$

where d is the dimension of S, and ξ consists of α and the upper triangle elements of Σ. In addition, we relate Y to S and other independent variables Z through the generalized linear (mixed) model with (multivariate) density function f(Y |Z,S;η), where Z may overlap with X, and η is a vector of unknown parameters. If we know a priori that certain components of S do not directly impact Y, then we set the corresponding regression parameters to zero.

There is considerable flexibility in specifying the relationships among different components of S. Suppose that S consists of S₁,…,S_M, which may pertain to M different types of omics variables or M omics variables of the same type. Figure 1 (C) and (D) show two types of relationships among S₁,…,S_M. In Figure 1 (C), the M sets of omics variables are unordered. In Figure 1 (D), there is a directed pathway from S₁ to S₂, from S₂ to S₃, …, and from S_M−1 to S_M. In the latter case, the density function f(S|X;ξ) can be specified through the sequential linear regression models

$$\begin{array}{c}{\mathit{S}}_1={\mathit{\alpha }}_1^{\text{T}}\mathit{X}+{\mathit{ϵ}}_1,\\ {\mathit{S}}_2={\mathit{\delta }}_1^{\text{T}}{\mathit{S}}_1+{\mathit{\alpha }}_2^{\text{T}}\mathit{X}+{\mathit{ϵ}}_2,\\ ⋮\\ {\mathit{S}}_M={\mathit{\delta }}_{M-1}^{\text{T}}{\mathit{S}}_{M-1}+{\mathit{\alpha }}_M^{\text{T}}\mathit{X}+{\mathit{ϵ}}_M,\end{array}$$

where (α₁,…,α_M) and (δ₁,…,δ_M−1) are regression parameters, and ϵ₁,… ϵ_M are independent zero-mean normal random vectors with covariance matrices Σ₁,…, Σ_M. That is,

$$\begin{gathered} f(\mathit{S}\mid \mathit{X};\mathit{\xi })={(2\pi )}^{-d/2}\prod _{j=1}^M{\left|{\mathrm{\Sigma }}_j\right|}^{-1/2}\exp \{-{({\mathit{S}}_j-{\mathit{\delta }}_{j-1}^{\text{T}}{\mathit{S}}_{j-1}-{\mathit{\alpha }}_j^{\text{T}}\mathit{X})}^{\text{T}} \\ \times {\mathrm{\Sigma }}_j^{-1}({\mathit{S}}_j-{\mathit{\delta }}_{j-1}^{\text{T}}{\mathit{S}}_{j-1}-{\mathit{\alpha }}_j^{\text{T}}\mathit{X})/2\}, \end{gathered}$$

where δ₀ = 0 and S₀ = 0.

Suppose that the study contains n unrelated subjects. For i = 1,…,n, let Y _i, S_i, X_i, and Z_i denote the values of Y, S, X, and Z for the ith subject. In addition, let R_ij indicate, by the values 1 versus 0, whether or not S_ij, the jth quantitative omics variable for the ith subject, is observed. When R_ij = 0, the measurement on S_ij belongs to the interval ${\mathcal{C}}_{ij}$, where ${\mathcal{C}}_{ij}=(-\infty ,L_{ij})$ if S_ij is below the lower detection limit L_ij, ${\mathcal{C}}_{ij}=(U_{ij},\infty )$ if S_ij is above the upper detection limit U_ij, and ${\mathcal{C}}_{ij}=(-\infty ,\infty )$ if S_ij is not measured at all. The observed data consist of $\{{\mathit{Y}}_i,{\mathit{X}}_i,{\mathit{Z}}_i,R_{ij}{S}_{ij}+(1-R_{ij}){\mathcal{C}}_{ij}\}$ (j = 1,…,d;i = 1,…,n).

Under the missing-at-random assumption [Little and Rubin, 2014], the observed-data likelihood for the vector of parameters θ = (η^T,ξ^T)^T is

$$\prod _{i=1}^n\left[{\prod _{j=1}^d\left({\int }_{S_{ij}\in {\mathcal{C}}_{ij}}\right)}^{1-R_{ij}}f({\mathit{Y}}_i\mid {\mathit{Z}}_i,{\mathit{S}}_i;\mathit{\eta })f({\mathit{S}}_i\mid {\mathit{X}}_i;\mathit{\xi })\prod _{j=1}^d{(d{S}_{ij})}^{1-R_{ij}}\right],$$

where the integration is taken over the unknown S_ij. To maximize this likelihood, we adopt the EM algorithm by treating the S_i as potentially missing data. The log-likelihood function with the complete data (Y _i,X_i,Z_i,S_i) (i = 1,…,n) is

$$\sum _{i=1}^n\{\log f({\mathit{Y}}_i\mid {\mathit{Z}}_i,{\mathit{S}}_i;\mathit{\eta })+\log f({\mathit{S}}_i\mid {\mathit{X}}_i;\mathit{\xi })\}.$$

In the M-step of the EM algorithm, we set the conditional expectation of the complete-data score function given the observed data to zero; in the E-step, we calculate the conditional expectation.

To be specific, let g₁(Y _i|Z_i,S_i;η) and g₂(Y _i|Z_i,S_i;η) denote, respectively, the first and second derivatives of log f(Y _i|Z_i,S_i;η) with respect to η, and let h₁(S_i|X_i;ξ) and h₂(S_i|X_i;ξ) denote, respectively, the first and second derivatives of log f(S_i|X_i;ξ) with respect to ξ. In the E-step, we evaluate the conditional expectations of g_k(Y _i|Z_i,S_i;η) and h_k(S_i|X_i;ξ) (k = 1,2) given the observed data and current parameter values, which are denoted by $\widehat{E}\{{\mathit{g}}_k({\mathit{Y}}_i\mid {\mathit{Z}}_i,{\mathit{S}}_i;\mathit{\eta })\}$ and $\widehat{E}\{{\mathit{h}}_k({\mathit{S}}_i\mid {\mathit{X}}_i;\mathit{\xi })\}$ (k = 1,2). For any function g(S_i), the conditional expectation takes the form

$$\widehat{E}\{\mathit{g}({\mathit{S}}_i)\}=\frac{{{\prod }_{j=1}^d\left({\int }_{S_{ij}\in {\mathcal{C}}_{ij}}\right)}^{1-R_{ij}}\mathit{g}({\mathit{S}}_i)f({\mathit{Y}}_i\mid {\mathit{Z}}_i,{\mathit{S}}_i;\mathit{\eta })f({\mathit{S}}_i\mid {\mathit{X}}_i;\mathit{\xi }){\prod }_{j=1}^d{(d{S}_{ij})}^{1-R_{ij}}}{{{\prod }_{j=1}^d\left({\int }_{S_{ij}\in {\mathcal{C}}_{ij}}\right)}^{1-R_{ij}}f({\mathit{Y}}_i\mid {\mathit{Z}}_i,{\mathit{S}}_i;\mathit{\eta })f({\mathit{S}}_i\mid {\mathit{X}}_i;\mathit{\xi }){\prod }_{j=1}^d{(d{S}_{ij})}^{1-R_{ij}}}.$$

Both the numerator and denominator on the right side can be evaluated through numerical integration. In the special case of $R_{i1}=\cdots =R_{ip}=1$, $\widehat{E}\{{\mathit{g}}_k({\mathit{Y}}_i\mid {\mathit{Z}}_i,{\mathit{S}}_i;\mathit{\eta })\}={\mathit{g}}_k({\mathit{Y}}_i\mid {\mathit{Z}}_i,{\mathit{S}}_i;\mathit{\eta })$ and $\widehat{E}\{{\mathit{h}}_k({\mathit{S}}_i\mid {\mathit{X}}_i;\mathit{\xi })\}={\mathit{h}}_k({\mathit{S}}_i\mid {\mathit{X}}_i;\mathit{\xi })$ (k = 1, 2).

In the M-step, we obtain the conditional expectation of the complete-data score equation given the observed data

$$\sum _{i=1}^n\widehat{E}\{{\mathit{g}}_1({\mathit{Y}}_i\mid {\mathit{Z}}_i,{\mathit{S}}_i;\mathit{\eta })\}=0,$$

and

$$\sum _{i=1}^n\widehat{E}\{{\mathit{h}}_1({\mathit{S}}_i\mid {\mathit{X}}_i;\mathit{\xi })\}=0.$$

We update η and ξ through the one-step Newton-Raphson algorithm

$${\mathit{\eta }}^{\text{new}}={\mathit{\eta }}^{\text{old}}-{\left[\sum _{i=1}^n\widehat{E}\{{\mathit{g}}_2({\mathit{Y}}_i\mid {\mathit{Z}}_i,{\mathit{S}}_i;{\mathit{\eta }}^{\text{old}})\}\right]}^{-1}\sum _{i=1}^n\widehat{E}\{{\mathit{g}}_1({\mathit{Y}}_i\mid {\mathit{Z}}_i,{\mathit{S}}_i;{\mathit{\eta }}^{\text{old}})\},$$

and

$${\mathit{\xi }}^{\text{new}}={\mathit{\xi }}^{\text{old}}-{\left[\sum _{i=1}^n\widehat{E}\{{\mathit{h}}_2({\mathit{S}}_i\mid {\mathit{X}}_i;{\mathit{\xi }}^{\text{old}})\}\right]}^{-1}\sum _{i=1}^n\widehat{E}\{{\mathit{h}}_1({\mathit{S}}_i\mid {\mathit{X}}_i;{\mathit{\xi }}^{\text{old}})\}.$$

We iterate between the above E-step and M-step until convergence, i.e., the change of the parameter values at two successive iterations is less than 10⁻⁴. We denote the estimator of θ as $\widehat{\mathit{\theta }}=({\widehat{\mathit{\eta }}}^{\mathrm{T}},{\widehat{\mathit{\xi }}}^{\mathrm{T}}{)}^{\mathrm{T}}$, which is consistent and asymptotically multivariate normal.

We use the Louis-formula [Little and Rubin, 2014] to estimate the covariance matrix of $\widehat{\mathit{\theta }}$. Specifically, we compute the complete-data information matrix

$$Q=-\left[\begin{array}{cc}{\sum }_{i=1}^n\widehat{E}\{{\mathit{g}}_2({\mathit{Y}}_i\mid {\mathit{Z}}_i,{\mathit{S}}_i;\widehat{\mathit{\eta }})\}& 0\\ 0& \sum _{i=1}^n\widehat{E}\{{\mathit{h}}_2({\mathit{S}}_i\mid {\mathit{X}}_i;\widehat{\mathit{\xi }})\}\end{array}\right].$$

We also compute

$${\mathit{U}}_i({\mathit{S}}_i)=\left[\begin{array}{c}{\mathit{g}}_1({\mathit{Y}}_i\mid {\mathit{Z}}_i,{\mathit{S}}_i;\widehat{\mathit{\eta }})\\ {\mathit{h}}_1({\mathit{S}}_i\mid {\mathit{X}}_i;\widehat{\mathit{\xi }})\end{array}\right].$$

In addition, we evaluate $\widehat{E}\{{\mathit{U}}_i({\mathit{S}}_i)\}$ and $\widehat{E}\{{\mathit{U}}_i({\mathit{S}}_i){\mathit{U}}_i{({\mathit{S}}_i)}^{\text{T}}\}$. Finally, we calculate the observed-data information matrix

$$\mathrm{\Omega }=\mathit{Q}-\sum _{i=1}^n\left[\widehat{E}\{{\mathit{U}}_i({\mathit{S}}_i){\mathit{U}}_i{({\mathit{S}}_i)}^{\text{T}}\}-\widehat{E}\{{\mathit{U}}_i({\mathit{S}}_i)\}\widehat{E}{\{{\mathit{U}}_i({\mathit{S}}_i)\}}^{\text{T}}\right].$$

Then the covariance matrix of $\widehat{\mathit{\theta }}$ is estimated by Ω⁻¹.

The above description is very general. Working out the details of the EM algorithm is not a trivial matter. We show how to implement the EM algorithm efficiently for the combination of models (1) and (2) and models (1) and (3) in Appendices A and B, respectively. We also show how to calculate Q, U_i(S_i), $\widehat{E}\{{\mathit{U}}_i(S_i)\}$, and $\widehat{E}\{{\mathit{U}}_i(S_i){\mathit{U}}_i{(S_i)}^{\text{T}}\}$ efficiently in those two situations. The results in the next section are based on the algorithm given in Appendix A.

Results

Simulation Studies

We conducted extensive simulation studies to evaluate the performance of the proposed and existing methods. We generated a quantitative omics variable S from equation (1), in which X consists of five components: X₁ = 1; X₂ = 0, 1, and 2 with probabilities p², 2p(1−p), and (1−p)², respectively; X₃ is standard normal; X₄ is Bernoulli with 0.5 success probability; and X₅ is Uniform(0,1). In this set-up, X₂ represents the genotype of a SNP (i.e., G) with minor allele frequency (MAF) p under the Hardy-Weinberg equilibrium, X₃ represents the first principal component for ancestry, X₄ represents gender, and X₅ represents (normalized) age. To create population stratification, we let $p=e^{0.5X_3}/(1+e^{0.5X_3})$. We generated a quantitative trait Y from equation (2), in which Z is X minus X₂ under the Marginal Model and is the same as X under the Joint Model. We set the two intercepts to 1 and also the two error variances, σ² and τ², to 1. In addition, we set α_G = 0.25, γ = 0.15, and β_G = 0 or 0.2. Finally, we set all other regression parameters to 0.5.

We considered n = 1,000 and set the values of S to be missing (i.e., not measured at all) in a completely random manner for half of the subjects. For the remaining 500 subjects, we varied the lower detection limit from −1 to 1 (with 0.1 increment), such that the proportion of the omics measurements below the detection limit varied from 6.3% to 58.7%, and the number of subjects with detectable values of S (i.e., complete observations) decreased from 468 to 207. We set the nominal significance level at 10⁻³. We simulated 10,000 replicates under the Marginal Model and under the Joint Model with β_G = 0.2, and we simulated 100 million replicates under the Joint Model with β_G = 0.

In addition to the proposed method, we evaluated “complete-case analysis”, which removes subjects with missing or non-detectable values, as well as the imputation approach, which removes subjects with missing values and replaces the measurement below the detection limit by the detection limit L or the mid-point L − log2. We will refer to these two imputation methods as “imputation at limit” and “imputation at mid-point”, respectively. (We have implicitly assumed that S is the log-transformation of the original omics measurement. On the original measurement scale, the detection limit is e^L, such that the mid-point between 0 and the detection limit is e^L/2, which becomes L – log 2 after the log transformation.)

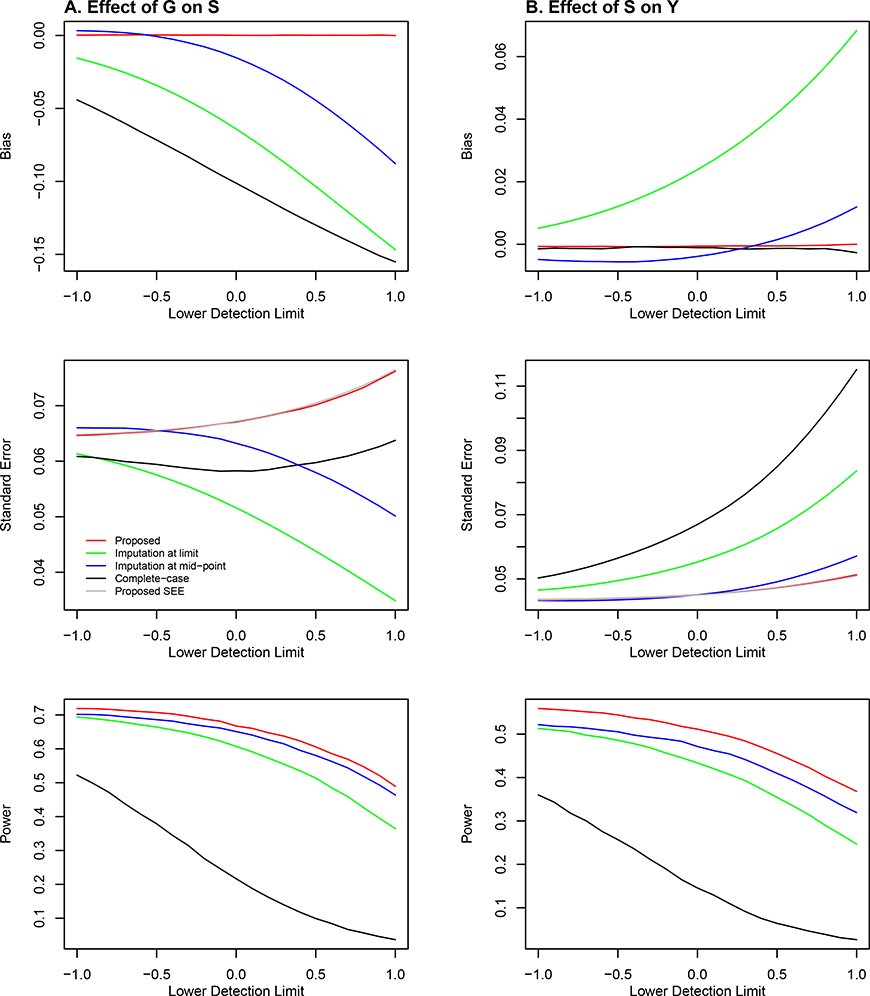
The results under the Marginal Model are shown in Figure 2. The proposed estimators for α_G and γ are virtually unbiased, and the corresponding standard error estimators are accurate. Complete-case analysis yields a severely biased estimator of α_G and much lower power for testing α_G than the proposed method. It yields an approximately unbiased estimator of γ; however, it has a much higher standard error, and thus much lower power for testing γ, than the proposed method. Note that complete-case analysis should yield a biased estimator of α_G and an approximately unbiased estimator of γ because S is the dependent variable under model (1) and an independent variable under model (2). (Complete-case analysis removes not only the subjects with missing values but also those with non-detectable values. Although data are missing completely at random, only the values below the detection limit are non-detectable, such that complete-case analysis is biased when S is the dependent variable in the model.) Imputation at limit yields a negatively biased estimator of α_G and a positively biased estimator of γ, and it is substantially less powerful than the proposed method in testing α_G and γ; the bias and power loss become more severe as the detection limit increases. (The power differences are approximately 0.13 when the detection limit is 1.) Imputation at mid-point also yields seriously biased estimators of α_G and γ, with much lower power than the proposed method, although the bias and power loss are less severe than in the case of imputation at limit.

Figure 2.

Simulation results under the Marginal Model: (A) effect of the SNP genotype on the quantitative omics variable (i.e., α_G); and (B) effect of the quantitative omics variable on the phenotype (i.e., γ). The bias and standard error of the parameter estimator and the power of the association test are plotted against the detection limit of the quantitative omics variable. The red, black, green, and blue curves pertain to the proposed method, complete-case analysis, imputation at limit, and imputation at mid-point, respectively. The silver curve pertains to the mean of the standard error estimator for the proposed method.

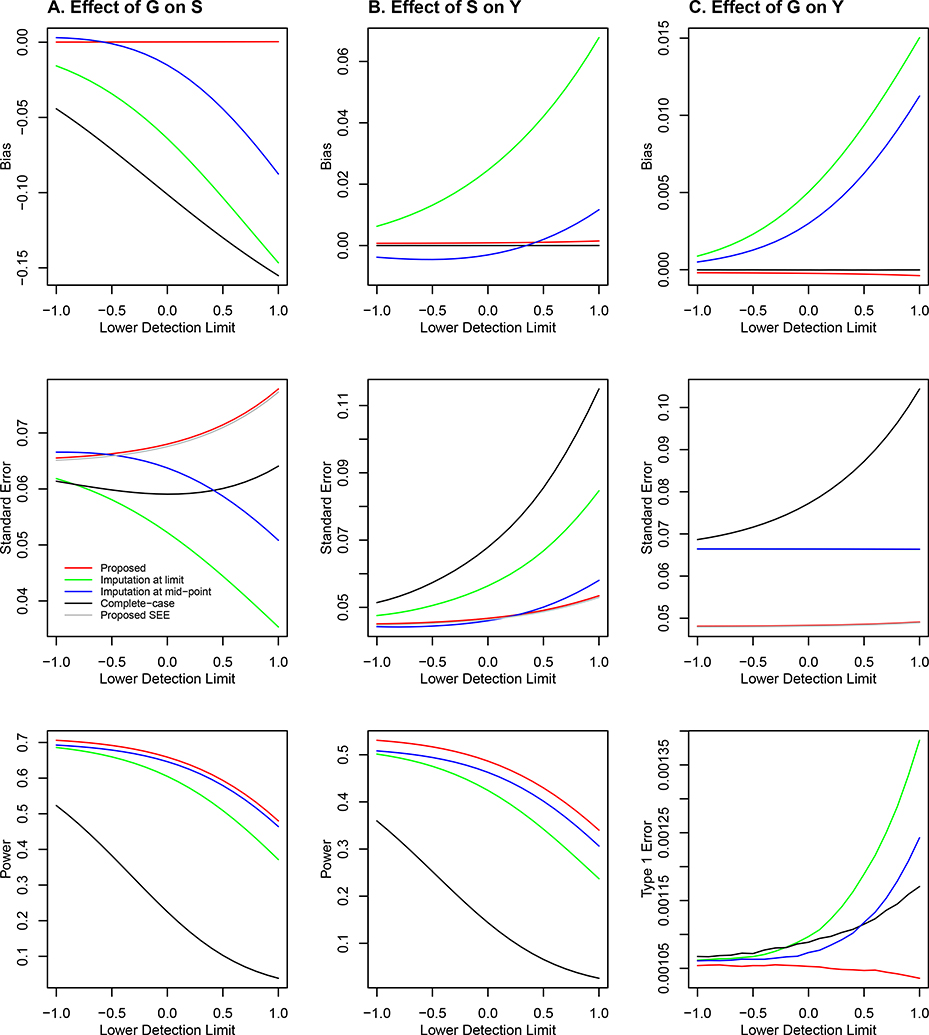
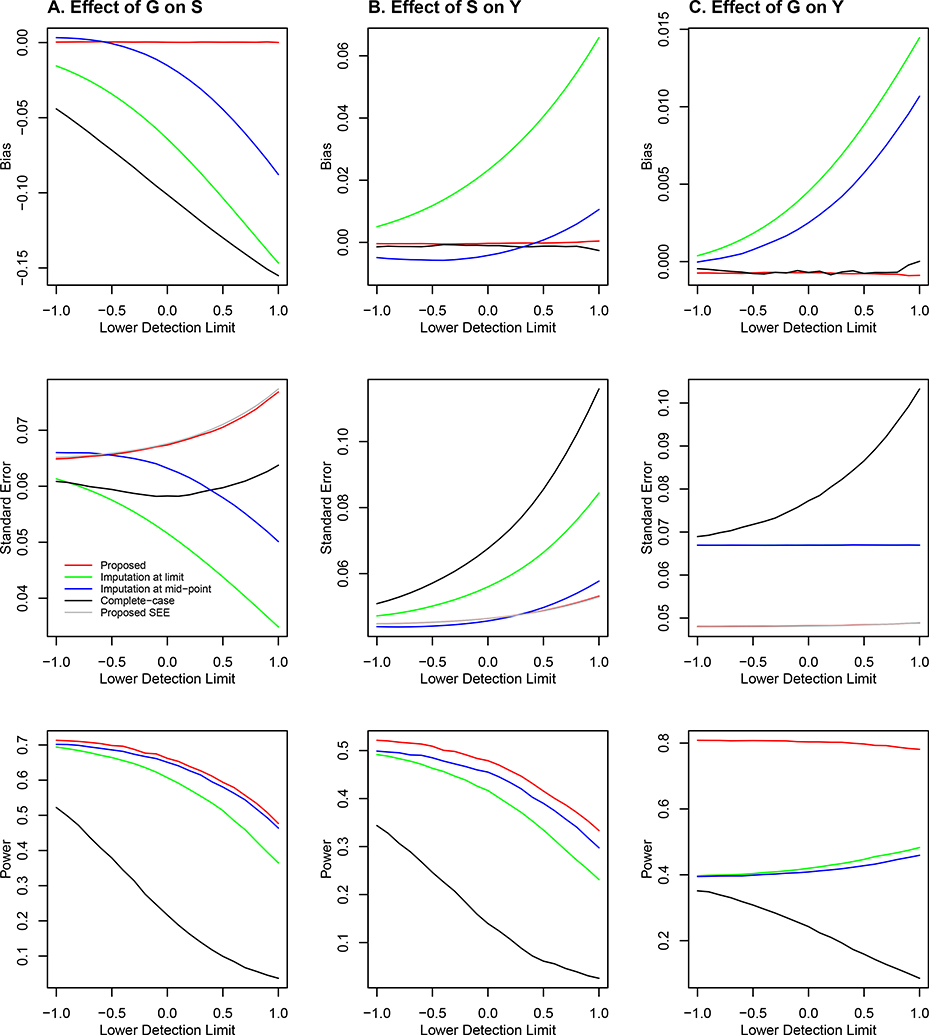
The results for the scenarios of β_G = 0 and 0.2 under the Joint Model are displayed in Figures 3 and 4, respectively. The conclusions regarding the bias and power for α_G and γ are the same as in the case of the Marginal Model. With regard to the inference on β_G, the proposed method yields a virtually unbiased estimator of β_G, an accurate standard error estimator, and correct type I error. Complete-case analysis also yields an approximately unbiased estimator of β_G, but it has a much larger standard error and thus much lower power than the proposed method. The imputation approach, especially imputation at limit, yields severe bias of the parameter estimator for β_G, serious inflation of the type I error (under the null hypothesis), and drastic loss of power (under the alternative hypothesis). The quantile-quantile plots in Figure S1 of the Supplementary Material show the patterns of the type I error inflation for the imputation methods on a broader scale. The poor performance of the imputation approach for making inference about β_G is attributed to the bias in the estimation of γ and the correlation between S and G.

Figure 3.

Simulation results under the Joint Model with β = 0: (A) effect of the SNP genotype on the quantitative omics variable (i.e., α_G); (B) effect of the quantitative omics variable on the phenotype (i.e., γ); and (C) effect of the genotype on the phenotype (i.e., β_G). The bias and standard error of the parameter estimator and the power or type I error of the association test are plotted against the detection limit of the quantitative omics variable. The red, black, green, and blue curves pertain to the proposed method, complete-case analysis, imputation at limit, and imputation at mid-point, respectively. The silver curve pertains to the mean of the standard error estimator for the proposed method.

Figure 4.

Simulation results under the Joint Model with β = 0.2: (A) effect of the SNP genotype on the quantitative omics variable (i.e., α_G); (B) effect of the quantitative omics variable on the phenotype (i.e., γ); and (C) effect of the genotype on the phenotype (i.e., β). The bias and standard error of the parameter estimator and the power of the association test are plotted against the lower detection limit of the quantitative omics variable. The red, black, green, and blue curves pertain to the proposed method, complete-case analysis, imputation at limit, and imputation at mid-point, respectively. The silver curve pertains to the mean of the standard error estimator for the proposed method.

To assess the robustness of the proposed method to the non-normal distributions of quantitative omics measurements, we conducted additional simulation studies under the Joint Model in which the error term of model (1) has a t-distribution with 5 degrees of freedom or is the logarithm of a standard exponential random variable. The rest of the simulation set-up was unchanged. As the lower detection limit varied from −1 to 1, the proportion of the omics measurements below the detection limit decreased from 8.9% to 58.1% for the t-distribution and from 17.8% to 70.8% for the logarithm of the exponential variable. In both situations, we performed the inverse-normal transformation on the observed values of S, such that the values above the detection limit follow approximately a truncated normal distribution. The results on the type I error and power are shown in Figures S2 and S3 of the Supplementary Material. The proposed method continues to have proper type I error and tends to be more powerful than complete-case analysis and imputation methods. We also performed the inverse-normal transformation in the original simulation set-up, where is standard normal. As shown in Figure S4, the use of the inverse-normal transformation does not affect the type I error or power of the proposed method when the omics measurements are normally distributed. Thus, we recommend the use of the inverse-normal transformation on the omics measurements.

In the above simulation studies, 50% of S were missing. We conducted another simulation study by setting only 30% of S to be missing. As shown in Figures S5 and S6, the relative performance of various methods remains the same. Finally, we conducted a simulation study by adding a SNP with MAF of 0.4. As shown in Figure S7, the basic conclusions are unchanged.

SPIROMICS

SPIROMICS is a multi-center observational study of COPD designed to guide future development of therapies by providing robust criteria for classification of COPD patients into groups that are most likely to benefit from a certain therapy and identification of biomarkers that can be used as intermediate outcomes to reliably predict clinical benefits [Couper et al., 2014]. The study enrolled 2,974 subjects in four strata (severe COPD, mild/moderate COPD, smokers without airflow obstruction, and non-smoking controls) between November 2011 and January 2015. Participants underwent a baseline visit that included morphometric measures, spirometry, six-minute walk, inspiratory and expiratory chest computed tomography, and standardized questionnaires. Biospecimens, including plasma, serum, DNA, urine, and induced sputum, were collected and stored.

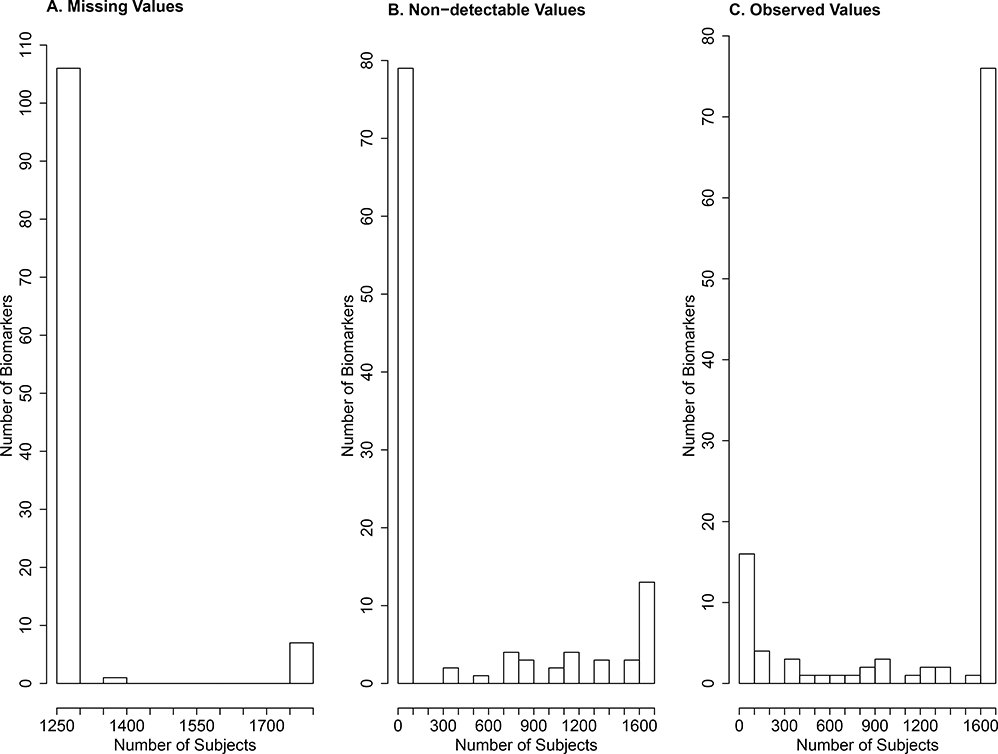
A custom biomarker panel assay was created for 114 blood proteins using 13 Myriad-RBM multiplex assays. The biomarkers were selected on the basis of known or putative links to COPD pathophysiology [O’Neal et al., 2014; Sun et al., 2016]. The assays produced varying levels of missing and non-detectable values among the 114 biomarkers; see Figure 5. For 104 of the biomarkers, 1,280 (43%) subjects have missing values; for the remaining 10 biomarkers, the number of subjects with missing values ranges from 1,281 to 1,763. Out of the 114 biomarkers, 24 have no measurements that are beyond detection limits, 85 have measurements that are below lower detection limits, and 8 have measurements that are above upper detection limits. (Three of the biomarkers have both lower and upper detection limits.) We removed 24 biomarkers with an excessive number of missing or non-detectable values. Each of the remaining 90 biomarkers has over 500 observed values. (Our simulation studies showed that the proposed method is highly reliable with such proportions of observed values.) We performed the inverse-normal transformation on all 90 biomarkers.

Figure 5.

Frequencies of missing values, non-detectable values, and observed values for 114 biomarkers among 2,794 patients in SPIROMICS.

Genotype data on 2,714 participants were derived from Illumina OmniExpress plus Exome GeneChip. There are a total of 673,688 SNPs. After removing those with missing rates > 10% or MAFs < 0.01, we were left with 615,535 autosomal SNPs. Principal component analysis was conducted using common SNPs to identify subjects of divergent ancestry.

We focused on the phenotype emphysema, which is quantified by the percentage of lung voxels ≤ 950 Hounsfield Units on the full inspiratory CT scans. A total of 2,672 subjects have both the phenotype and genotype information. We used the proposed method to handle the missing and non-detectable values in the biomarkers. For comparisons, we also adopted imputation at mid-point (i.e., removing subjects with missing biomarker values and replacing the value below the detection limit by half of the detection limit on the original measurement scale), which was shown in our simulations studies to perform the best among all existing methods. We included age, gender, body mass index, smoking pack years, and current smoking status, together with the top 5 principal components, as covariates in all the models.

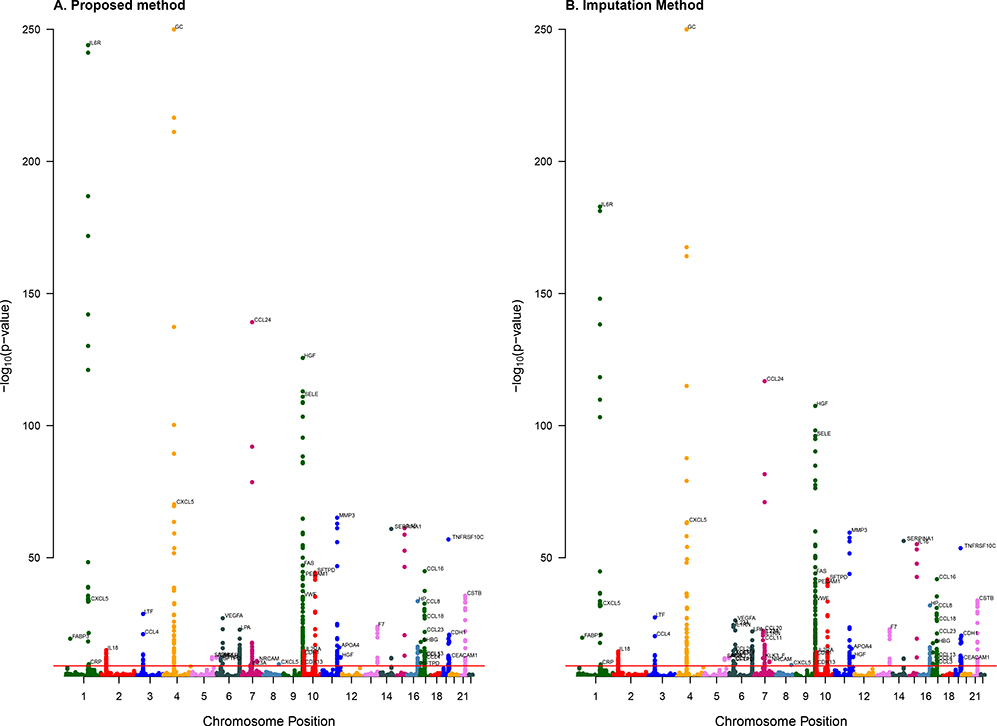
We first fit the Marginal Model; the main results are displayed in Figure 6(A). The quantile-quantile plots (not shown) are well behaved, indicating that the proposed method (with the inverse-normal transformation) is robust to non-normality of biomarker measurements. The combined Manhattan plots in Figure 6(A) show the locations of the SNPs that affect protein variation, which are referred to as protein quantitative trait loci (pQTLs). For the pQTL analysis, the genomewide significance threshold based on the Bonferroni correction for multiple testing of 615,535 SNPs and 90 biomarkers is approximately 9.03 × 10⁻¹⁰. A total of 493 pQTL SNPs in 42 (47%) of the biomarkers achieved the genomewide significance. The most significant pQTL SNPs are rs222047 and rs705120 in GC (vitamin D binding protein) on chromosome 4, with p-values < 10⁻²⁵⁰. The next most significant pQTL SNPs are rs8192284 and rs4129267 in IL6R (interleukin 6 receptor) on chromosome 1, with p-values of 1.02 × 10⁻²⁴⁴ and 6.83 × 10⁻²⁴², respectively.

Figure 6.

Combined Manhattan plots for the associations between SNPs and blood biomarkers in SPIROMICS according to the proposed and imputation methods. The biomarkers with at least one SNP passing the genomewide significance threshold (red line) are marked at the chromosome locations of the top pQTLs. The −log₁₀(p-values) >250 are truncated at 250.

The pQTL analysis results based on the imputation method are displayed in Figure 6(B). The imputation method also identified pQTL SNPs in GC and IL6R, but with less extreme p-values. Indeed, for most of the top pQTL SNPs, the proposed method yielded stronger evidence of association than the imputation method, reflecting the fact that the proposed method makes more efficient use of the data. On the other hand, the imputation method identified pQTL SNPs in CCL11 (chemokin c-c motif ligand 11), CCL20, and KLK3-F (kallikrein 3-F), whereas the proposed method did not. The fact that the same two SNPs are highly significant for three different biomarkers makes the findings of the imputation method dubious. Each of the three biomarkers has a relatively large number of measurements below detection limits (with 881, 1,103, and 895 non-detectable values for CCL11, CCL20, and KLK3-F, respectively).

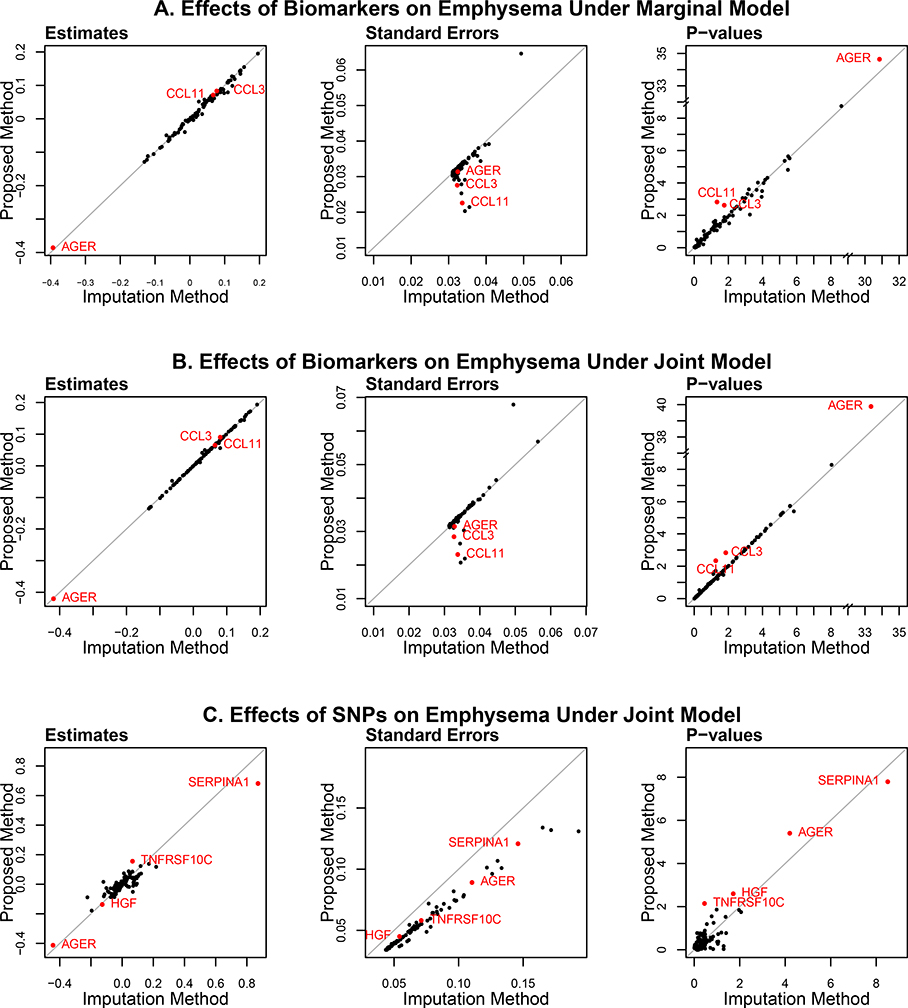
Figure 7 (A) compares the results between the proposed and imputation methods for estimation of the effects of the biomarkers on emphysema under the Marginal Model. For the proposed method, the EM algorithm was applied to the combination of models (1) and (2) for each biomarker, where X contains the genotype of the top pQTL SNP for that biomarker. For the imputation method, standard linear regression was performed on model (2) for each biomarker after mid-point imputation. There are noticeable differences between the effect-size estimates of the two methods. Compared to the imputation method, the proposed method yielded substantially smaller standard errors for the biomarkers with a small number of observed values and more extreme p-values for some of those biomarkers. Specifically, there are 1,351 missing values and 17 non-detectable values for AGER (advanced glycosylation end product-specific receptor); and there are 519 and 881 non-detectable values for CCL3 and CCL11, respectively, along with 1,280 missing values each. For these three biomarkers, the effect size estimates are similar between the two methods, but the proposed method yielded smaller standard errors and thus more extreme p-values.

Figure 7.

Results from the analysis of the SPIROMICS data by the proposed versus imputation methods: (A) effects of biomarkers on emphysema under the Marginal Model; (B) effects of biomarkers on emphysema under the Joint Model; and (C) effects of top pQTL SNPs on emphysema under the Joint Model. Biomarkers with major differences between the proposed and imputation methods are shown in red.

We also fit the Joint Model for each biomarker by adding the top pQTL SNP for that biomarker to equation (2). Figure 7 (B) and (C) compare the results between the proposed and imputation methods: 7 (B) pertains to the effects of the biomarkers on emphysema; 7 (C) pertains to the effects of the corresponding top pQTL SNPs on emphysema. The results for the effects of the biomarkers on emphysema are fairly similar to those of the Marginal Model. For AGER, the difference between the p-values of the proposed and imputation methods is more profound than before.

As shown in Figure 7 (C), the proposed and imputation methods produced appreciably different estimates for the effects of the top pQTL SNPs on emphysema. The proposed method yielded much smaller standard errors for all SNPs and smaller p-values for some SNPs than the imputation method. Specifically, the p-values for the top pQTL SNPs of AGER, HGF (hepatocyte growth factor), and TNFRSF10C (tumor necrosis factor receptor superfamily member 10C) are 3.92 × 10⁻⁶, 0.0025, and 0.0071, respectively, according to the proposed method, whereas the corresponding p-values from the imputation method are 6.3 × 10⁻⁵, 0.019, and 0.35. The pQTL SNPs associated with AGER, HGF, and TNFRSF10C are rs2070600, rs505922, and rs4760, respectively.

As mentioned previously, the top pQTL for AGER is rs2070600, which has an MAF of 3.9%, with G as the reference allele and A as the alternate allele. Under the Joint Model, the proposed method estimated the direct effect of this SNP on emphysema at −0.412, with standard error of 0.089 and 95% confidence interval of (−0.586, −0.238). The effect of this SNP on AGER was estimated at −0.659, with standard error of 0.084, and the effect of AGER on emphysema was estimated at −0.420, with standard error of 0.031, such that the indirect effect of rs2070600 SNP on emphysema was estimated at 0.277, with standard error of 0.041 and 95% confidence interval of (0.197,0.357).

Discussion

There is a worldwide proliferation of multi-omics studies, which provide unparalleled opportunities to understand the biological processes that underlie complex diseases and traits. It is economically impossible to measure all types of omics features on a large number of subjects and technically infeasible to detect quantitative values below (or above) certain thresholds. Thus, incompleteness of data is inevitable in any multi-omics study.

We have presented a very general approach for integrative analysis of multi-omics data with missing values and detection limits and implemented it through computationally efficient algorithms. The novelty of our work lies not only in the creation of the statistical framework but also in the construction of the EM algorithms. We note that genomewide analysis for one biomarker in the SPIROMICS data (containing 615,535 SNPs on 2,672 subjects) took ∼ 16 hours on an IBM Blade HS20 processor. We have posted our code at http://dlin.web.unc.edu/software/iMODA/.

The current approach to analysis of incomplete multi-omics data is to fit each model separately after removing subjects with missing values and imputing values below or above detection limits. This strategy is highly inefficient and potentially biased, and it may yield qualitatively different results than the proposed method, as shown with the SPIROMICS data. Specifically, removing subjects with missing values is inefficient, and it will also bias the analysis if the data are not missing completely at random. The imputation approach biases parameter estimation and reduces statistical power; it can also inflate the type I error. We note that unbiased parameter estimation is of great importance in integrative analysis of multi-omics data, especially when quantifying direct and indirect effects.

Recently, several authors [Cai et al., 2016; Lin et al., 2016; Voillet et al., 2016] proposed imputation methods for incomplete multi-omics data. In general, the imputation approach does not provide unbiased estimation of regression parameters. In addition, the recently proposed imputation methods [Cai et al., 2016; Lin et al., 2016; Voillet et al., 2016] deal with missing data only and do not allow non-detectable values. By contrast, our framework accommodates both missing and non-detectable values.

We have derived the covariance matrix for all model parameters, making it possible to make joint inference on multiple parameters. However, joint inference may require special care. Suppose, for example, that we are interested in estimating the indirect effect of a SNP on a phenotype, i.e., the product of α_G and γ. Although the estimators for α_G and γ are asymptotically normal, the normal approximation to the product of the two estimators is inaccurate unless the sample size is very large. We are currently exploring a resampling approach to construct confidence intervals for indirect effects. We should also note that standard statistical methods cannot be used to test the null hypothesis of no indirect effect, i.e., α_Gγ = 0, because the asymptotic null distribution of ${\widehat{\alpha }}_G\widehat{\gamma }$ depends on whether both α_G and γ are zero or only one of them is zero. We are currently developing proper tests for indirect effects.

Our current framework formulates the conditional distribution of Y given S. Some omics measurements may be influenced by diseases. In that case, the regression parameters in our phenotype models do not have causal interpretations. However, our likelihood approach can be applied to other formulations of the relationships between Y and S.

A previous meta-analysis of the SPIROMICS and COPDGene [Regan et al., 2011] data identified 527 pQTLs in 38 blood proteins [Sun et al., 2016]. Our analysis of the (new) SPIROMICS data confirmed pQTLs in 34 of those 38 blood proteins. In addition, we identified novel pQTLs in 9 blood proteins: A2M (alpha-2-macroglobulin), CCL13, CCL3, CDH13 (Cadherin-13), CEACAM1 (Carcinoembryonic antigen-related cell adhesion molecule 1), CRP (C-reactive protein), FABP3 (fatty acid binding protein 3), IL15, and IL1RN. Most of those biomarkers had relatively large detection limits, such that the proposed method was particularly effective.

In the SPIROMICS data, there was only one type of quantitative omics variables, namely blood proteins, and we considered one protein at a time, such that the analysis was straightforward. Because X and Z can be any vectors, the inclusion of multiple SNPs in the analysis is as easy as the use of a single SNP. Indeed, we considered multiple SNPs in our analysis of the SPIROMICS data, although the results were not shown. Our framework can be applied to multiple types of quantitative omics variables. However, modeling their relationships requires considerable biological expertise.

The TOPMed program has generated WGS data for >150,000 subjects. Other omics data (e.g., methylation profiles, metabolic profiles, RNA expression patterns) are being collected through TOPMed and ancillary studies, but for only a few thousand subjects. We are currently applying the proposed methodology to those data, and the results will be communicated in separate reports.

We have implicitly assumed that multi-omics data are collected from cohort studies and thus used the standard prospective likelihood. If the data are collected from case-control studies and there are missing and non-detectable values, then the retrospective likelihood conditional on the case-control status should be used instead. The corresponding EM algorithms can be constructed by combining the ideas of this article with those of Lin and Zeng [2006].

In microbiome studies, the abundance of the bacteria may be truly zero rather than below a detection limit. Then it is sensible to use a mixture distribution allowing a proportion of measurements to be zero. In addition, the relative microbiomial abundance pertains to compositional data, which require special treatments. It would be worthwhile to extend our framework to incorporate microbiome data.

We have assumed that investigators are interested in analyzing a small subset of multi-omics features at a time, such that the dimension of S is fixed and relatively small. We are currently exploring a penalized-likelhood approach to variable selection with multiple types of potentially missing features. The results will be communicated in due course.