Abstract
Current approaches to single-cell RNA sequencing (RNA-seq) provide only limited information about the dynamics of gene expression. Here we present RNA timestamps, a method for inferring the age of individual RNAs in RNA-seq data by exploiting RNA editing. To introduce timestamps, we tag RNA with a reporter motif consisting of multiple MS2 binding sites that recruit the adenosine deaminase ADAR2 fused to an MS2 capsid protein. ADAR2 binding to tagged RNA causes A-to-I edits to accumulate over time, allowing the age of the RNA to be inferred with hour-scale accuracy. By combining observations of multiple timestamped RNAs driven by the same promoter, we can determine when the promoter was active. We demonstrate that the system can infer the presence and timing of multiple past transcriptional events. Finally, we apply the method to cluster single cells according to the timing of past transcriptional activity. RNA timestamps will allow the incorporation of temporal information into RNA-seq workflows.
Rapid progress in RNA-seq technologies and, in particular, single-cell RNA-seq has enabled detailed molecular characterization of complex tissues. However, because sequencing is a destructive measurement, these approaches provide only an instantaneous snapshot of cellular state, and comparatively little work has been done to examine how cell states arise from complex transcriptional dynamics over timescales of hours. Efforts to add a temporal dimension to RNA-seq through metabolic labeling of newly synthesized RNAs1,2,3,4, or computational inference from the abundance of unspliced transcripts5, provide only the derivative of expression level or information about expression at a single timepoint, so transcriptional histories must still be reconstructed by observations of many cells. To overcome these challenges, we asked whether it might be possible to estimate the age of each individual RNA made by a promoter, eventually allowing us to build up a picture of the transcriptional history of a single cell from the ensemble of RNAs present in the cell.
To that end, we designed a recorder RNA motif, referred to as an RNA timestamp, that reports its age via the gradual accumulation of A-to-I edits caused by an engineered version of the human adenosine deaminase acting on RNA 2 catalytic domain (ADAR2cd; Fig. 1a). This catalytic domain has been shown to be targetable to specific RNAs via fusion to exogenous RNA-binding domains, with minimal off-target activity to untargeted RNAs6,7,8,9,10. We designed the timestamps to be arrays of adenosine-rich sequences that are favored substrates of the ADAR enzyme11,12,13 (Fig. 1b). Edits in this region can subsequently be identified as A-to-G mutations in high-throughput sequencing of the timestamps. ADAR2cd is specifically targeted to MS2 binding sites in the editing region of the timestamps through a fusion with the MS2 capsid protein (MCP)14. We screened multiple RNA and ADAR variants and selected a pair with an editing timescale on the order of hours, a timescale relevant for endogenous transcriptional activity (Supplementary Fig. 1).
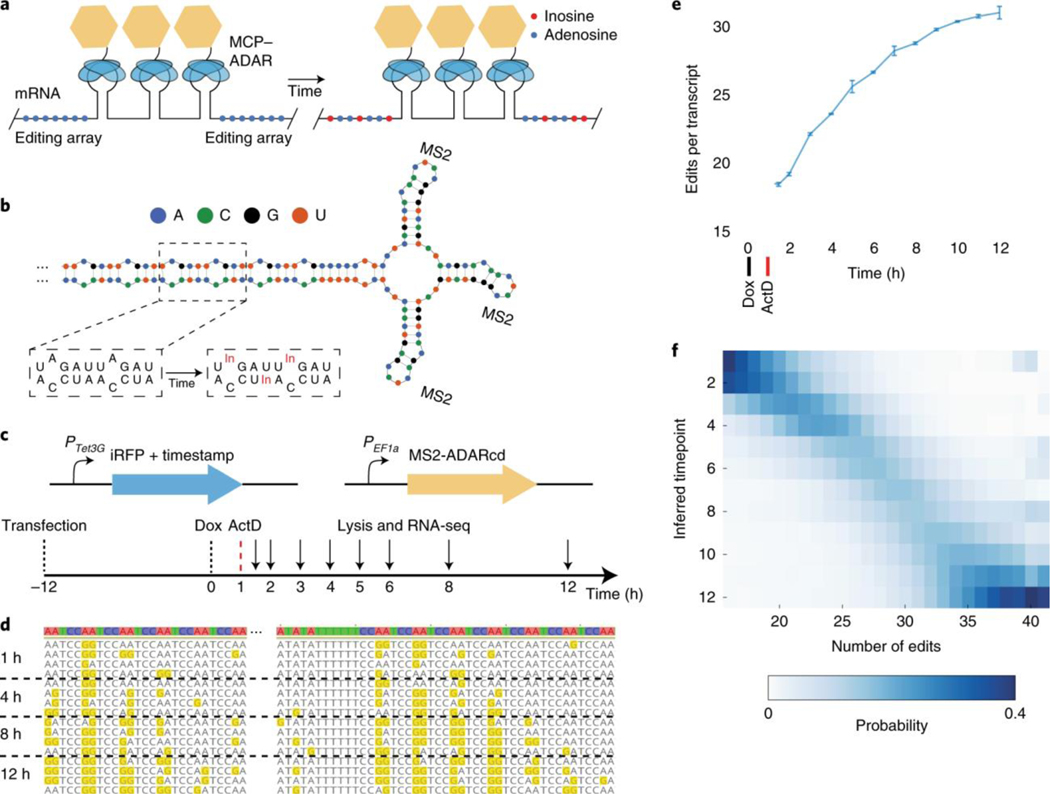
Fig. 1: Encoding of temporal information through RNA edits.
a, Schematic of the timestamps approach, consisting of editing arrays of adenosines (blue dots) and several MS2 step loops in the 3′ UTR of an mRNA. In the presence of an MCP–ADAR fusion (MCP, blue ellipses; ADAR, yellow hexagon), timestamps are edited over time by catalytic conversion of adenosine to inosine (red dots). b, A schematic structure of a portion of one timestamp, showing MS2 stem loops and the repetitive, double-stranded RNA motif that serves as the editing substrate. c, Schematic representation of the Tet-responsive timestamped mRNA system and experimental timeline. d, Examples of timestamps edited for different amounts of time, showing the accumulation of A-to-I edits. e, The mean number of edits per timestamp observed after editing for different amounts of time. Data are represented as mean ± s.d. (n = 3 biological replicates). f, The number of edits per timestamp is shown for different specified ages. Columns are normalized to 1. Each column can be interpreted as a probability distribution of when a timestamped RNA with a given number of edits is likely to have been made.
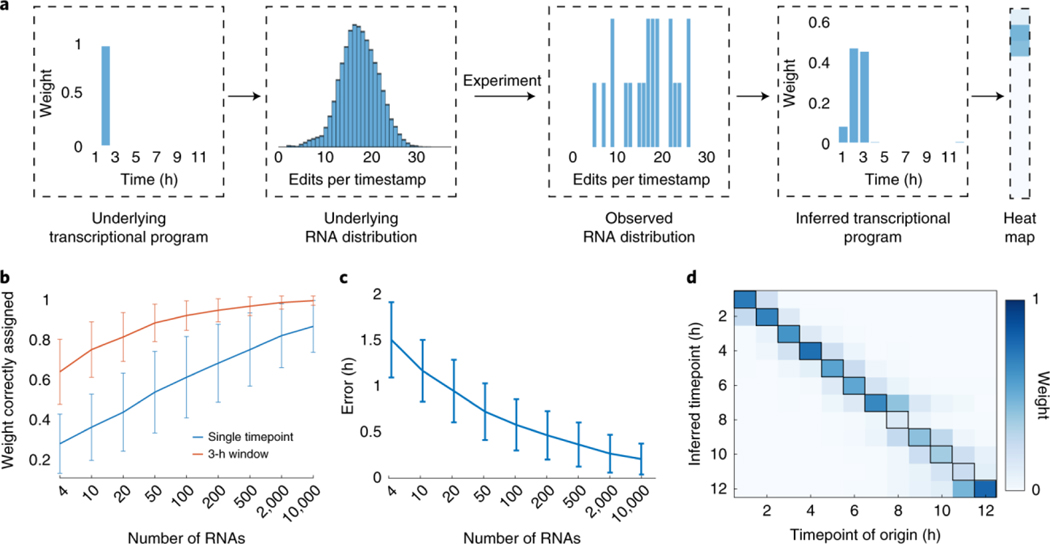
To calibrate our system, we incubated HEK293T cells expressing the ADAR variant and a timestamped RNA under the control of the tetracycline response element (TRE) in medium containing doxycycline for 1 h. The timestamp was placed in the 3′ untranslated region (UTR) of a fluorescent protein-encoding messenger RNA (mRNA)15, which shows minimal degradation over the course of 12 h in mammalian cells (Supplementary Fig. 2). We subsequently added actinomycin D, an RNA transcription inhibitor16, and then lysed the cells after a variable amount of time before sequencing the timestamps (Fig. 1c). Each of these experiments provided us with a population of RNAs with a known age (±30 min), and we observed that the timestamps became progressively more heavily edited over time (Fig. 1d). The mean number of edits per timestamp at any given timepoint was highly reproducible between biological replicates (Fig. 1e), and the accumulation of edits over time could be modeled accurately using a Poisson binomial model (Supplementary Fig. 3). Using the empirical distribution of the number of edits per timestamp, we found that it was possible to estimate the age of a timestamped mRNA transcript purely from the total number of edits on the timestamp with a 95% confidence interval of 2.7 ± 0.4 h (mean ± s.d., n = 26 confidence intervals each derived for timestamps with a different number of edits; Fig. 1f). We, hereafter, refer to the distributions of edits per RNA obtained from these single-hour induction experiments as ‘single-hour editing distributions’. Because cells will often contain many copies of a given RNA transcript, we reasoned that we might be able to infer the underlying transcriptional dynamics of a specific promoter by analyzing the ensemble of timestamped RNAs produced by the promoter. To test this, we built an algorithm that infers, without any assumptions, the transcriptional program that is most consistent with a particular set of timestamps (Methods). By ‘transcriptional program’, we mean the function that describes the number of timestamps generated as a function of time. We represent each transcriptional program in a discretized and normalized form as a set of 12 positive values that sum to 1, with each value representing the fraction of RNAs generated in a different 1-h window. The algorithm infers transcriptional programs by using gradient descent to identify a convex combination of single-hour editing distributions that minimizes the L2 norm between the observed editing distribution and the editing distribution associated with the convex combination (Fig. 2a). The weights that describe the optimal convex combination are, thus, the inferred transcriptional program. We applied the algorithm to sets of timestamped RNAs that were all chosen randomly from the same timepoint and found that it could infer both that the sets came from a single timepoint and which timepoint they came from, with accuracy that increased monotonically with the number of RNAs in the set (Fig. 2b). Consistent with our hypothesis that temporal estimates based on multiple RNAs would be more accurate than temporal estimates based on a single RNA, the temporal error associated with a set of only four RNAs was 1.49 ± 0.42 h (mean ± s.d., n = 12 timepoints; Methods) and declined monotonically with increasing numbers of RNAs (Fig. 2c). For sets of at least 50 RNAs,17,18, the algorithm reproduced weight distributions that clearly resembled the single-hour transcriptional programs from which the RNAs were derived (Fig. 2d).
Fig. 2: Timestamped RNAs can reveal temporal transcription programs.
a, Schematic of the gradient descent algorithm. RNAs are generated by an unknown underlying transcriptional program (for example, a transcriptional event that occurred 2 h before lysis (left)), which corresponds to an underlying distribution of edits per timestamp (middle left)). In any individual experiment, one observes a set of timestamped RNAs sampled from the underlying distribution (middle right). The gradient descent algorithm produces an inferred transcriptional program (right) that best approximates the observed RNA distribution under the L2 norm. Transcriptional programs can then be represented as columns in a heat map (far right). b, For sets of timestamped RNAs drawn from a single timepoint, the fraction assigned by the algorithm to the correct timepoint (blue) or the correct 3-h window (orange) as a function of the number of RNAs in the set (n = 12 timepoints). c, The temporal error associated with the reconstructed transcriptional programs, as a function of the number of RNAs in the set (Methods). d, The average weight assigned by the gradient descent algorithm to each timepoint (y axis) is shown as a function of the timepoint of origin (x axis), for sets of 50 RNAs. Columns sum to 1. Error bars represent mean ± s.d. for b and c.
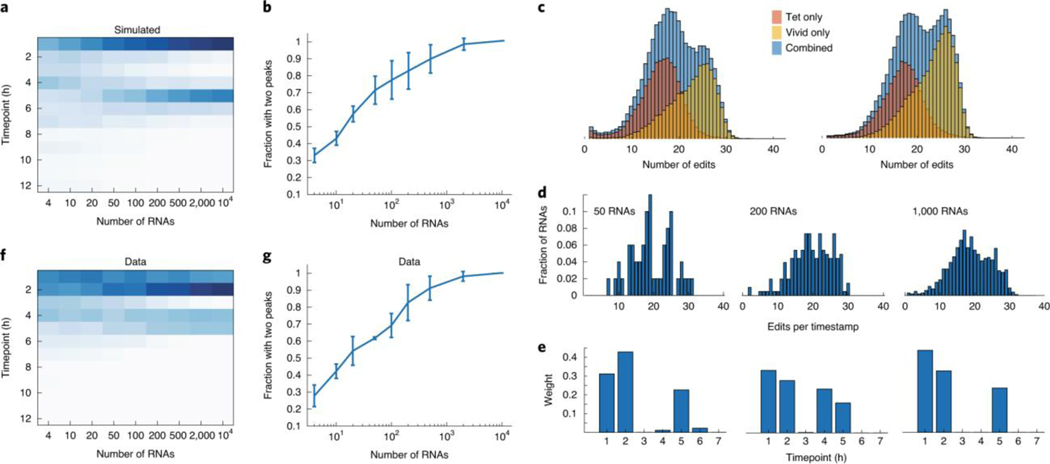
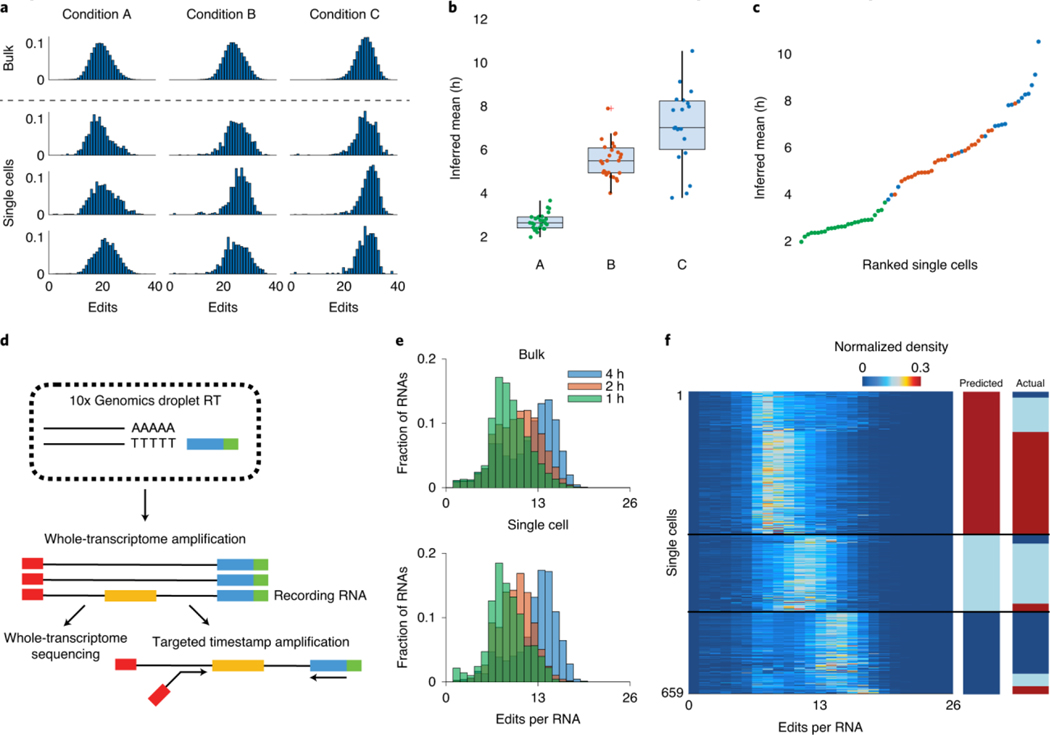
Because each RNA is individually timestamped, we reasoned that the algorithm might be able to identify if a given set of timestamped RNA was produced by multiple, temporally distinct transcriptional pulses. To test this, we computationally generated mixtures of RNAs drawn half from the 1-h timepoint and half from the 5-h timepoint and applied the gradient descent algorithm to infer the transcriptional program most likely to have generated the mixtures (Fig. 3a). Even with only ten RNAs, we were able to identify the presence of two peaks in the transcriptional program 51.3% ± 7.6% of the time, and this increased to 86% ± 13% with 200 RNAs (mean ± s.d., n = 3 biological samples; Fig. 3b and Methods). To validate these predictions experimentally, we transfected cells with barcoded RNAs driven by a doxycycline-sensitive promoter and a light-sensitive transcription factor19. Timestamped RNAs associated with each promoter could be identified by promoter-specific barcodes, allowing for independent reconstruction of light- and doxycycline-induced timestamp editing distributions (Supplementary Fig. 4). Independently stimulating the cells with each promoter at two different times (at 1 h and 5 h) led to an editing distribution with two clear peaks corresponding to the two transcriptional events (Fig. 3c). We then subsampled the timestamped RNAs from this experiment (Fig. 3d) and ran the gradient descent algorithm to generate putative transcriptional programs (Fig. 3e). Even though this was a more challenging task, because the RNAs were not chosen evenly from the two peaks, the results we obtained were very similar to the results obtained in our simulations (Fig. 3f). With ten RNAs, two peaks could be distinguished 44.5% ± 0.7% of the time, and this increased to 90.5% ± 0.7% with 200 RNAs (mean ± s.d., n = 2 biological samples; Fig. 3g). We have also shown that timestamps can be used in primary hippocampal neuron culture to infer the c-fos response from KCl activation of neural activity (Supplementary Fig. 5). The testing context for our technology—that is, a plasmid-based reporter system and a cultured neuron system—had high levels of Fos activity in the absence of KCl stimulation but demonstrates that this technology might enable temporally resolved, sequencing-based readout of neural activity. Given the performance of the timestamp system with relatively few RNAs, we asked whether it could be applied to determine the timing of transcriptional events in individual cells. We transfected cells with timestamped RNAs under the control of TRE, induced with doxycycline, and then induced the cells according to three different single-hour induction protocols (Methods). Individual cells were then sorted into wells of a 96-well plate, and we subsequently performed single-cell timestamp sequencing (Fig. 4a). Analysis of the editing histograms yielded a mean induction time associated with each cell (Methods). The estimation error in the temporal estimate for the single cells in the single-hour induction protocols were 0.2 ± 0.8 h (mean ± s.d., n = 27) for one condition and 0.5 ± 1.0 h (mean ± s.d., n = 19) for the other (Fig. 4b and Methods). Based on these temporal estimates, we were able to order the cells according to the timing of transcriptional events, obtaining only five transpositions out of 72 cells, an accuracy rate of 86% (Fig. 4c).
Fig. 3: Identification of temporally separated transcriptional events.
a, The average weight assigned by the gradient descent algorithm to each timepoint for sets of timestamped RNAs that were drawn randomly (in equal proportion) from the 1- and 5-h timepoints as a function of number of RNAs drawn. Columns sum to 1. b, The percentage of sets of RNA in which two peaks can be identified by the gradient descent algorithm (Methods). Error bars show mean ± s.d., n = 3 data sets from biological replicates. c, Histograms of the number of edits per timestamp are shown for cells that were induced separately with a light-sensitive promoter and a doxycycline-sensitive promoter. Red shows the distribution of edits per RNA for RNAs transcribed off the doxycycline promoter, whereas yellow shows the light-sensitive promoter. Blue shows the combined distribution. Columns show two biological replicates. d, Distributions of edits per timestamp for sets of RNAs chosen randomly from the blue distribution in c. e, The weight distribution inferred by the gradient descent algorithm for the set of RNAs shown in d. f, Same as a but for sets of RNA drawn from the experimental distributions in c. g, Same as b but for sets of RNA drawn from the experimental distributions in c. Error bars show mean ± s.d., n = 2 biological replicates.
Fig. 4: Timestamps can reveal transcriptional programs in single cells.
All editing histograms are normalized to sum to 1. a, Editing histograms for bulk conditions A through C (top) and randomly chosen single cells (bottom). b, Predicted induction times for all single cells in the experiment, calculated as the center of mass of the inferred weight distributions (n = 24 for condition A, n = 27 for condition B and n = 19 for condition C). For the box plot, the middle line is the median, and the lower and upper hinges correspond to the first and third quartiles. Whiskers extend to the largest value no further than 1.5× IQR from the hinge. The lower whisker extends from the hinge to the smallest value at most 1.5× IQR of the hinge, whereas data beyond the end of the whiskers are outlying points that are plotted individually. c, The predicted induction time for each single cell, ranked from least to greatest. Green dots correspond to condition A; red dots correspond to condition B; and blue dots correspond to condition C. d, Schematic of capture and sequencing of timestamps with 10x single-cell sequencing in conjunction with transcriptomic profiling. e, Top, editing histograms for bulk sequencing of 1-h induction events 1, 2 and 4 h before lysis. Bottom, three representative single cells for 1-, 2- and 4-h induction conditions. f, Heat map of distribution of edits per cell for 659 cells. Cells are clustered by k-means according to their editing distribution into three clusters corresponding to predicted induction. ‘Actual’ column shows grouping of cells by condition, determined using a condition barcode on the timestamp reads (red, 1 h; light blue, 2 h; and dark blue, 4 h). IQR, interquartile range.
Recent advances in droplet-based barcoding technologies have enabled the scalable molecular profiling of cells and tissues at the single-cell level20,21. Thus, we asked if we could read out timestamps with 10x single-cell 3′ RNA-seq in combination with paired transcriptomic information. To do so, we developed a molecular biology workflow that enables targeted amplification of timestamps from single-cell barcoded whole-transcriptome amplification products (Methods and Fig. 4d). This allows for both the timestamps and the cell barcode to be read out via paired-end Illumina sequencing. We transfected HEK cells with the barcoded TRE timestamp systems and induced with doxycycline 1, 2 or 4 h before 10x droplet-based sequencing. Single-cell timestamp recordings measured via 10x sequencing is qualitatively similar to bulk sequencing from the same conditions (Fig. 4e). After filtering for high-quality cells, we performed k-means clustering on the timestamps and found three distinct clusters (659 cells, ~85% of cells) corresponding to the 1-, 2- and 4-h inductions (the other 32% corresponded to cells with few edits, potentially without ADAR). Examining these 659 cells, we found that 494 of 659 (~75%) of these cells were assigned to the correct induction condition (Fig. 4f). These results demonstrate that timestamps can be read out in concert with high-throughput single-cell droplet-based methods.
Inferring temporal information from RNA-seq has many distinct advantages: unlike in the case of fluorescent reporter proteins, temporal information can be inferred without direct observation of the cells in situ, and temporal information can be combined with information about cell type through RNA-seq. Several new sequencing technologies have recently added a temporal dimension to RNA-seq—for example, by metabolically labeling newly synthesized RNAs1,2,3,4 or by inferring the instantaneous change in cell state from the abundance of unspliced transcripts. However, these existing tools for inferring temporal information from RNA-seq provide only one-dimensional data: metabolic labeling identifies only RNA made within one specific window, whereas splicing-based techniques identify only the instantaneous derivative of the cell state. In both cases, complex cellular dynamics must, therefore, be inferred from measurements on many cells, and cellular heterogeneity can be lost. On the other hand, several recently published methods have succeeded in recording cell-state information into the sequence of DNA in living cells22,23,24,25,26,27,28,29,30,31,32, but all such methods operate on timescales of days and are, thus, insufficient for recording transcriptional responses to perturbations, which typically take place over hours. RNA timestamps are, thus, the first technology that can record high-dimensional temporal information from individual cells on timescales relevant for understanding complex cellular transcriptional activity.
Here we reported that the continuous enzymatic activity of adenosine deaminases acting on RNA can allow for direct inference of the age of individual RNAs and that statistical methods taking advantage of this phenomenon can reveal the temporal aspect of transcriptional dynamics in individual cells. In general, the inference algorithm that we present can reveal the absolute timing of transcriptional events provided a set of single-hour editing distributions, which serve as a calibration set. However, important caveats remain. For example, simulations suggest that more complex transcriptional programs, such as transcription that slowly ramps up over time, might require thousands of RNAs to decode (Supplementary Fig. 6). Another important practical question is whether a calibration obtained in one system (such as cell culture; see ‘Calibration of editing rate’ in the Methods) can be used to decode distributions obtained in other systems (such as in vivo recordings). Nonetheless, even in the absence of a suitable calibration, algorithms, such as the decoder presented here, can be used to infer the relative timing of transcriptional events, and future work might focus on the development of internal calibration measurements for in vivo experiments.
The concept of RNA timestamps presented here might find widespread utility. For example, the demonstrated ability to order cells by transcriptional response could have great utility for studying the diversity of responses to cellular perturbations33,34. Using the same concept, alternative systems could be designed that record other kinds of signals besides transcription. For example, by using alternative dimerization systems35,36 to link ADAR to constitutively expressed timestamps in a stimulus-specific manner, it might be possible to construct timestamp systems that report on the timing of other kinds of cellular events, such as calcium or other signaling molecules. Moreover, we suspect that timestamps could readily be added to endogenous RNAs or that a similar concept could be used—for example, by observing edits in the poly(A) tail or by examining adenosine-rich parts of the transcript. Together, these observations suggest that RNA timestamps provide a scalable and extensible approach for recording the temporal activity of cells.
Methods
Cloning
All plasmids were constructed using either restriction cloning using restriction enzymes from New England Biolabs and the NEB Quick Ligation kit (M2200L) or the In-Fusion HD cloning enzyme mix (Clontech, 638911). Plasmids were grown in E. cloni 10G Chemically Competent Cells (Lucigen, 60107–1) and were verified by Sanger sequencing (Eton Bioscience). All plasmids (Supplementary Table 1) are deposited on Addgene.
Owing to high repetition present in the RNA editing templates, inserts for plasmids 76, 147, 148, 149 and 187 (Supplementary Table 2) were ordered as sense and antisense ultramer oligonucleotides, which were annealed to each other before cloning. Plasmid 76 was cloned by inserting RNA templates (A_Short, B_Short, C, D and E) into the 3′ UTR of an iRFP transcript expressed under a UbC promoter in a second-generation lentivirus backbone using SphI and ClaI. Subsequently, this plasmid was modified by the addition of a flavivirus xrRNA in the 5′ UTR. Templates A_Short and B_Short were then extended by inserting another pair of annealed ultramers on the 5′ side of A_Short and B_Short using SphI and MluI. The resulting templates are designated A and B. To generate plasmids 147, 148, 149 and 183 (as used in the paper), templates A and B were then moved into different backbones and different promoters by restriction cloning or by Gibson assembly with polymerase chain reaction (PCR) amplification of the timestamp template region. Template A is used throughout the paper; template B is shown in Supplementary Fig. 1 for comparison.
RNA purification, library preparation and sequencing
All cell cultures were lysed with 600 μl of buffer RLT Plus from the Qiagen RNeasy Plus Mini Kit (Qiagen, 74136) and were pipetted up and down vigorously to homogenize. RNA was then purified using the Qiagen RNeasy Plus Mini Kit, following the instructions from the manufacturer. Subsequently, 11 μl of purified RNA was reverse transcribed using SuperScript IV (Thermo Fisher Scientific, 18090050) and a barcoded version of SGR-174 (Supplementary Table 2), following the protocol from the manufacturer. Reverse transcription (RT) reactions were then purified using Agencourt Ampure XP beads at a 1:1 dilution (Beckman Coulter, A63881). Some portion of the eluent, typically 25%, was then analyzed by PCR using P5 and a barcoded version of SGR-176 (Supplementary Table 2) and the Q5 Hot Start High Fidelity 2× Master Mix (NEB, M0492L) with the following settings: 30 s of 98 °C denaturation; then 25–30 cycles of 10-s denaturation at 98 °C; 20 s of annealing at 70 °C; and then 25 s of extension at 72 °C. PCR reactions were then pooled and run on a gel, and a 400-bp band was extracted using the NucleoSpin PCR Cleanup Kit (Macherey-Nagel, 740609.250). The concentration of DNA in the resulting eluent was determined via a Qubit 2 fluorometer (Thermo Fisher Scientific) and was then adjusted to 4 nM for sequencing. The read structure is shown in Supplementary Fig. 7.
Sequencing was performed using NextSeq Mid Output 300 cycle kits (Illumina, FC-404–2004), MiSeq 300 cycle v2 kits (MS-102–2002) or MiSeq 600 cycle v3 kits (MS-102–3003), with at least 80-bp read 1 and 185-bp read 2, with 8-bp index 1 and 15-bp index 2.
HEK and 3T3 cell culture
Except in the case of the single-cell experiments, HEK293FT and 3T3 cells were plated in 24-well plates. Cells were grown in DMEM (Thermo Fisher Scientific, 10566016) and supplemented with penicillin–streptomycin (Thermo Fisher Scientific, 15140122) and 10% certified Tet system-approved FBS (Clontech, 631101). Transfections were performed using the TransIT-X2 system (Mirus, MIR 6000), following the manufacturer’s instructions.
Experiments with the doxycycline promoter
For doxycycline experiments, HEK and 3T3 cells in 24-well plates were transfected with 300 ng of plasmid 147 or 148, 100 ng of pCMV Tet3G from the Tet-on 3G system (Clontech, 631168) and 100 ng of plasmids 116v1, 116v5 or 116v6. In the experiments for Fig. 1 and Supplementary Figs. 1 and 3, they were transfected with both 147 and 148 and received 150 ng of each plasmid. At least 12 h after transfection, cells were stimulated by adding doxycycline to a final concentration of 1 μg ml−1, followed by gentle mixing or swirling of the plate. Subsequently, transcription was halted by adding actinomycin D to a final concentration of 1 μg ml−1 in the same medium. After waiting for the experimental time period, cells were lysed using Buffer RLT Plus, and libraries were prepared as described above.
Experiments with the Vivid promoter
For experiments in Fig. 3c–g and Supplementary Fig. 4, 3T3s were transfected with 300 ng of plasmid 149, 100 ng of plasmid 133 and 100 ng of plasmid 116v5. For conditions in which cells were transfected with both plasmid 147 and plasmid 149, they received 100 ng each of plasmids 149, 147, pCMV Tet3G, 133 and 116v5. Cells were stimulated with a blue LED (Thorlabs, M455L2) with a total power of 200 μW cm−2. The LED was turned on for 1 h and was subsequently turned off. After the LED was turned off, the cells were wrapped in foil to prevent accidental light exposure. Cells were then lysed after the experimental time period.
As shown in Supplementary Fig. 4, cells were stimulated with blue light for 1 h and were then placed in darkness for 7 h. While still in darkness, cells were then stimulated with doxycycline as described above. After 1 h in doxycycline, cells were lysed.
As shown in Fig. 3c–g, cells were stimulated with blue light for 1 h and were then placed in darkness for 4 h. While still in darkness, cells were then stimulated with doxycycline as described above. After 1 h in doxycycline, cells were lysed.
HEK cell doxycycline experiment
For the experiment shown in Fig. 1d–f, cells were stimulated as above and were lysed at the following timepoints: 0 h (that is, immediately before adding doxycycline), 0.5 h after adding doxycycline, 1 h after adding doxycycline (that is, immediately before adding actinomycin D), 2 h after adding doxycycline, 3 h after adding doxycycline, 4 h after adding doxycycline, 5 h after adding doxycycline, 6 h after adding doxycycline, 7 h after adding doxycycline, 8 h after adding doxycycline, 9 h after adding doxycycline, 10 h after adding doxycycline, 11 h after adding doxycycline and 12 h after adding doxycycline. Each timepoint consisted of three replicates. On a separate occasion, we collected three replicates at 2.5 h after adding doxycycline and 4.5 h after adding doxycycline, and these timepoints functioned as our test timepoints in Supplementary Fig. 3. The data from Fig. 1d–f were further used in Figs. 2 and 3a,b.
Single-cell experiments
For all experiments involving single cells, HEK cell cultures were prepared; transfected with 100 ng of pAAV-CAG-GFP (Addgene 37825), 200 ng of plasmid 147, 100 ng of plasmid 116v5 and 100 ng of pCMV Tet3G; stimulated with doxycycline; and then silenced with actinomycin D as described above. The three induction conditions were as follows: cells in condition 1 were left in doxycycline for 1 h before lysis; cells in condition 2 were silenced with actinomycin D after 1 h and then left for 3 h; and cells in condition 3 were silenced with actinomycin D after 1 h and then left for 7 h. Subsequently, cells were treated with trypsin (Life Technologies, 25300054). After trypsinization, cells were centrifuged at 850g, washed in cold PBS and then resuspended in cold PBS. Then, 96-well plates were prepared, with each well containing a solution of 0.2% Triton-X with 2 U μl−1 of RNAse inhibitor. Individual cells were sorted into the wells of this well plate using a MoFlo Astrios EQ flow cytometer. After sorting, the well plate was sealed, centrifuged and then placed at −80 °C overnight.
For the analysis in Fig. 4a–c, cells in condition 2 received plasmid 147B1, whereas cells in condition 3 received plasmid 147B3. The two populations of cells were mixed after trypsinization and sorted together. By contrast, cells in condition 1 received plasmid 147B1 and were sorted separately from the others.
Library preparation for the single cells proceeded as follows. Plates containing single cells were thawed, and 7 μl of nuclease-free water was added to the single cells to bring the total volume up to 11 μl. Subsequently, RT was performed using SuperScript IV and the SGR-174 RT primers, as in the case of the bulk samples, with the following modifications. RT primers were distributed so that each cell at a given timepoint received an RT primer with a different barcode. In addition, for each timepoint, we performed two no-template RT reactions. Finally, after the 50 °C step in the SuperScript IV protocol, we cooled the samples to 37 °C and added 20 U of exonuclease 1 (NEB, M0293S) to the reaction to remove excess primers. Samples then remained at 37 °C for 10 min before proceeding to the 80 °C heat inactivation step. After RT, the RT reactions for all cells and the two no-template controls at a given timepoint were pooled and cleaned with Ampure XP beads at a 1:1 dilution and were then analyzed by PCR using the same protocol as for the bulk samples. Cells were pooled before PCR as a way of reducing the number of cycles necessary to achieve amplification. We excluded cells if they received fewer than 150 reads or if the most common RNA barcode represented fewer than 80% of the total de-duplicated reads, which would indicate index swapping between cells.
For experiments involving 10x single cells, as in Fig. 4d–f, cells in the 1-h condition were induced with doxycycline 1 h before 10x preparation; cells in the 2-h condition were induced with doxycycline 2 h before 10x preparation and silenced with actinomycin D 1 h later and left for 1 h; and cells in the 4-h condition were induced with doxycycline 4 h before 10x preparation, silenced with actinomycin D after 1 h and then left for 3 h. Cells were then treated with trypsin (Life Technologies, 25300054), spun down at 500g, washed in cold PBS and then resuspended in cold PBS with 0.04% wt/vol BSA. Cell concentration was counted, and the appropriate volume of cells was added to a 10x reaction for a targeted cell recovery of 2,000 cells. The reaction was run through a 10x chip according to the 10x Genomics Chromium Single Cell protocol. After the droplet generation step, the reaction was transferred to a PCR strip tube and RT, post-RT cleanup and complementary DNA (cDNA) amplification were completed after the 10x Genomics Chromium Single Cell protocol. After cDNA cleanup, 1–5 μl of the cDNA product was analyzed by PCR with Phusion Hot Start Flex DNA Polymerase (New England Biolabs, M0535S), using a barcoded version of SGR-176 and a version of the 10x Genomics cDNA primer that included a P5 addition, with the following settings: 30 s of 98 °C denaturation; then 15–20 cycles of 10-s denaturation at 98 °C and 20 s of annealing at 63 °C; and then 25 s of extension at 72 °C. The rest of the cDNA product was saved for the remainder of the 10x Genomics Chromium Single Cell protocol. The PCR product was then purified with Ampure beads at a 1:1 dilution and then adjusted to a concentration of 4 nM for sequencing. The libraries were sequenced on a MiSeq with the following read structure: 28 Read 1, 8 Index 1, 8 Index 2 and 200 Read 2. The number of editing sites sequenced per timestamp is fewer, as only Sequencing Read 2 is used for timestamps.
Alignment and edit counting
The alignment and analysis pipeline for sequencing data is summarized in Supplementary Fig. 7. Analysis of sequencing data was performed using custom MATLAB code (MATLAB 2017a). Briefly, in the case of single-cell data, we first performed de-duplication using a 9-bp unique molecular identifier on the RT primer (oligo SGR-174). Other data sets were not de-duplicated. Reads were then filtered to ensure that they had the minimum necessary read length (67 bases on Read 1 and 184 bases on Read 2). Note that Read 1 was on the RT primer, so Read 1 reads the reverse complement of the RNA sequence. Thus, the expected mutation was A to G on Read 2 and T to C on Read 1. Alignment was performed using all bases that were not As on Read 2 or that were not Ts on Read 1. Reads were considered to be aligned to the template if 95% of the non-A (for Read 2) or non-T (for Read 1) bases matched the template. Furthermore, we required 90% of the bases that were expected to be As on Read 2 or Ts on Read 1 to have Q-scores greater than 27 (Supplementary Fig. 7); reads that failed to achieve this threshold were discarded.
Finally, we required that all reads have at least one edit in Read 1 and at least one edit in Read 2 for analysis. We implemented this requirement because it appeared to eliminate several artifacts that we occasionally observed in our data. For example, each well would sometimes have different (large) numbers of RNAs with zero edits or one edit, which would confound attempts to infer timing by gradient descent. As a consequence of this requirement, all of the histograms of edits per RNA presented in this paper appear to show only very few RNAs with fewer than ~12 edits. There are ~12 bases in template A, all of which are on Read 2, that are edited much more quickly than any bases on Read 1. These are of the form UAG and all form bulges in the RNA secondary structure, which are thought to encourage editing by ADAR. Exclusion of RNAs with zero edits on Read 1 or Read 2 predominantly limits the analysis to RNAs that are already fully edited at all 12 of those As, thus causing all RNAs to have at least 12 edits. RNAs with fewer than 12 edits might be useful for inferring transcriptional dynamics on the order of minutes, which we observed in preliminary experiments not presented here.
Calibration of editing rate
When analyzing RNA editing distributions generated in 3T3s using a gradient descent algorithm with basis vectors derived from HEK293 cells (as in Fig. 3), we included a further calibration step before analysis, as follows. First, we generated a timestamp library from 3T3 cells that were transfected with the doxycycline timestamp system, induced with doxycycline for 1 h and then lysed. We then calculated the mean number A of edits per RNA for cells in the 1-h HEK cell induction data set and the mean number B of edits per RNA in the 1-h 3T3 cell induction data set and multiplied the number of edits in subsequent 3T3 data by the ratio A/B. This procedure was done because we observed that the editing rate was uniformly higher in 3T3 data than in the corresponding HEK cell data, for reasons that were not determined.
Exponential model
The exponential model in Supplementary Fig. 3 was implemented using custom code in Python (Python 3.6) as follows. For each editable position i on the template, we assume that the likelihood of base i being edited follows an exponential distribution with parameter λi, to be estimated from the data. Assuming an instantaneous pulse of transcriptional activity at time t = 0, the fraction of edited bases for position i, yi, can be modelled as the cumulative distribution function of the exponential distribution:
To more accurately capture the experimental setup, we model yi as an underlying process, which is exponential, but with start time uniformly distributed in [0, tstop], where t = 0 represents when doxycycline is added to the cells, and tstop is the time at which actinomycin D was added to the cells. Specifically, we fit a function of the form
where tstop was 1 h, and λi was fit to the data using nonlinear least squares. This function was fit for times t ≥ 1.5 h, because the editing distributions for earlier timepoints are strongly affected by populations of RNA present before doxycycline addition. For the analysis in Supplementary Fig. 3, analysis was then performed using only those adenosines for which the R2 of the resulting fit was greater than 0.9. We model the total number of edits to the RNA with a Poisson binomial distribution with n trials where n is the total number of editable positions and success probabilities given by yi(t) for each position i. The probability of having n edits at time t is given by
Here, A is a binary vector with each entry corresponding to a specific adenosine in the timestamp editing region. Ak = 1 if adenosine k has been edited to inosine, and sum(A) counts the total number of edits in A. Time estimates using the exponential model were then made by minimizing the Kullback–Leibler divergence between p(n,t) and the empirical distribution q(n) over t. p(n,t) was calculated in practice via a dynamic programming approach.
For Supplementary Fig. 3, the exponential model was calculated using the data from a single replicate of the HEK doxycycline experiment. The distributions in Supplementary Fig. 3c show the number of edits per RNA calculated across all bases with R2 greater than 0.9 for that replicate, and the Poisson binomial model in Supplementary Fig. 3c likewise included the same bases. By contrast, for Supplementary Fig. 3d, bases were retained only if they had an R2 greater than 0.9 in all three replicates from the HEK doxycycline experiment. For this reason, the apparent numbers of edits per RNA are lower in Supplementary Fig. 3d than in Supplementary Fig. 3c.
Gradient descent
A schematic depicting the gradient descent algorithm is shown in Supplementary Fig. 8. The gradient descent in Figs. 2 and 3 and Supplementary Figs. 6 and 9 was implemented using custom code in MATLAB (MATLAB 2017a). Briefly, the gradient descent algorithm was given an RNA editing distribution (a normalized histogram of edits per RNA), which could be either an experimentally measured distribution (Figs. 2b–d and 3c–g) or a simulated distribution (Fig. 3a,b and Supplementary Figs. 6 and 9). Simulated distributions were generated using data from the experiment in Fig. 1e,f, either by randomly sampling RNAs from a specified timepoint or timepoints from that experiment (as in Fig. 3a,b and Supplementary Fig. 9) or by taking convex combinations of the editing distributions from that experiment (as in Supplementary Fig. 6). The gradient descent algorithm was also given a set of ‘basis vector’ histograms, which were obtained by combining the data at each timepoint from all three replicates from the HEK doxycycline experiment. The gradient descent was then initialized by drawing a set of weights from a Dirichlet distribution with all parameters set to unity. The gradient descent minimized the mean squared error (L2 norm) between the input distribution and the convex combination of the basis vectors given by the weights. For each simulated distribution, we performed the gradient descent 1,000 times and took the solution that minimized the L2 norm.
To avoid overfitting, whenever an input to the gradient descent was simulated, the distributions used as ‘basis’ functions in the gradient descent were averages of all three biological replicates from the experiment in Fig. 1e,f, whereas the simulated distributions were always generated from the data associated with a single replicate.
An exception to this policy was made for Supplementary Fig. 6, where RNAs were randomly chosen from all three replicates, and then the gradient descent was performed using basis functions that were averages of all three replicates. This exception was made to be able to simulate ramp distributions with 10,000 or 30,000 RNAs, which would not have been possible without combining data from all three replicates. For this reason, there is some risk that the accuracy of the decoding in Supplementary Fig. 6 would be lower if different basis vectors were used for the decoding.
An analysis of the performance of the gradient descent algorithm on random simulated transcriptional programs is presented in Supplementary Fig. 9. In general, the gradient descent algorithm succeeded in reproducing the editing histogram with high accuracy (Supplementary Fig. 9a). Additionally, the weight vector found by the gradient descent algorithm was, on average, much closer to the true weight vector than randomly sampled vectors (Supplementary Fig. 9b), although this was not always true (Supplementary Fig. 9c). Because the simulated and approximated editing histograms were generated with different basis distributions, noise present in those basis distributions meant that the true weight vector was not, in general, the optimal solution for the gradient descent (Supplementary Fig. 9d,e).
Analysis of two peaks experiments
In Fig. 3b,g, a weight distribution generated by the gradient descent algorithm was defined to have two peaks if the sum of the weights on the 1- and 2-h timepoints and the sum of the weights on the 4- and 5-h timepoints were both greater than the weight on the 3-h timepoint. When making Fig. 3b,g, we generated several possible definitions for what would constitute ‘two peaks’ and obtained qualitatively similar behavior (monotonically increasing identification of two peaks) for all of them. This definition was chosen for presentation arbitrarily.
Accuracy metrics
In Fig. 2c, temporal estimation error is calculated by multiplying the distance of each timepoint away from the expected timepoint by the weight assigned to that timepoint and summing. Thus, for the 3-h single-induction pulse, if the decoder assigned weights of 0.5 to the 3-h timepoint and 0.5 to the 5-h timepoint, the resulting estimation error would be 0.5*0 + 0.5*2 = 1 h. This metric is not directly comparable to the 95% confidence interval presented in reference to Fig. 1f, but if the procedure used to generate Fig. 2c is repeated for ‘sets’ consisting of a single RNA, the error obtained is 1.9 ± 0.47 h (mean ± s.d., n = 12 timepoints), which is significantly greater than the 1.49 ± 0.42 h obtained for sets of four RNAs (means differ by >3 standard errors), supporting the statement that the error for four RNAs is less than that for a single RNA.
For the arbitrary transcriptional program experiments in Supplementary Fig. 9 and the ramp in Supplementary Fig. 6, we calculated the accuracy as the sum of the absolute values of the differences between the assigned and expected weights, divided by 2 to avoid double counting. Thus, if we expected one timepoint to get 100% of the total weight, and that timepoint, instead, got 80% of the total weight, then the resulting accuracy would be 80%.
In Fig. 4b, the accuracy is calculated as the mean absolute difference between the single-cell estimates and the estimate for the bulk distribution. We calculate the accuracy in this way for the single cells because the underlying transcriptional program is not known. The single cells stay on ice for up to 1 h during processing, and we have not measured the editing kinetics during that time.
Neuron culture preparation and transfection
All procedures involving animals at Massachusetts Institute of Technology were conducted in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals and approved by the Massachusetts Institute of Technology Committee on Animal Care. Primary hippocampal neuron culture was prepared as previously described15. Briefly, neurons were transfected at 6–7 days in vitro (DIV) using a commercial calcium–phosphate kit (Thermo Fisher Scientific, K278001) with 600 ng of pUC19, 200 ng of plasmid 116v5 and 200 ng of plasmid 187. Neurons were then incubated with calcium–phosphate precipitates for 30–60 min, followed by washing with MEM buffer at pH 6.7–6.8 to remove residual precipitates.
Neuron culture stimulation
Neurons were stimulated at 14–15 DIV. Neurons were placed in 1 ml of plating medium (500 ml of MEM, 2.5 g of glucose, 50 mg of transferrin, 1.1 g of HEPES, 5 ml of 200 mM L-glutamine, 12.5 mg of insulin, 50 ml of HI FBS and 10 ml of B27 supplement). To stimulate the neurons, we added 250 μl of 5× depolarization medium and agitated gently. Neurons were then left for 1 h in an incubator. Subsequently, the medium was aspirated, and neurons were washed twice in plating medium. They were then left in plating medium for a variable amount of time before being lysed in 600 μl of buffer RLT Plus.
Plating medium
500 ml of MEM (Thermo Fisher Scientific, 51200–038)
2.5 g of glucose (Sigma-Aldrich, G7528–1KG)
50 mg of transferrin (Sigma-Aldrich, T1283–500 mg)
1.1 g of HEPES (Sigma-Aldrich, H3375–500G)
5 ml of 200 mM L-glutamine (Thermo Fisher Scientific, 25030–081)
12.5 mg of insulin (Millipore, 407709)
50 ml of HI FBS (VWR, 45000–736)
10 ml of B27 Supplement (Thermo Fisher Scientific, 17504–044)
5× depolarization medium
170 mM KCl
10 mM HEPES, pH 7.4
1 mM MgCl2
2 mM CaCl2
Neuron inference experiment
Owing to the limited availability of neuron culture at any given time, the data for Supplementary Fig. 5 were gathered in two separate experiments with different sample replicates per experiment. We collected the following timepoints: before stimulation (that is, immediately before adding depolarization medium); 1 h after stimulation (that is, immediately before washing the neurons in fresh medium); 2 h after stimulation; 3 h after stimulation; 3.5 h after stimulation; 4 h after stimulation; 5 h after stimulation; 5.5 h after stimulation; 6 h after stimulation; and 7 h after stimulation.
The breakdown of the data in Supplementary Fig. 5 by experiment is as follows. In the first experiment, we collected two samples before stimulation, three samples at 1 h, three samples at 2 h, three samples at 3 h, three samples at 4 h and two samples at 5 h. In the second experiment, we collected one sample at 2 h, two samples at 3 h, three samples at 3.5 h, two samples at 4 h, two samples at 5 h, three samples at 5.5 h, two samples at 6 h and two samples at 7 h.
Linear interpolation
In Supplementary Fig. 5, the timepoints associated with the c-fos neural activity were determined by linear interpolation as follows. We first calculated the mean number of edits per RNA for all replicates and determined the mean across replicates for each timepoint (plotted in Supplementary Fig. 5b, designated Mt). Then, to perform the estimate, for each replicate R from timepoint t, we identified the two timepoints, t1 and t2, such that t! = t1,t2 and such that the mean mR of replicate R obeyed Mt1 < mR < Mt2. The time estimate for replicate R is then determined as
Reporting Summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
Raw data were used in all figures that are not described in the captions as schematics. The data sets generated and analyzed during the current study are available on the Zenodo Archive, record 3897464. Raw sequencing data are available at the Sequence Read Archive under PRJNA658989.
Code availability
The code used to produce analysis and figures for the current study is available on the Zenodo Archive, record 3897464.
Supplementary Material
Acknowledgements
We acknowledge N. Jakimo, A. T. Wassie, J. Gootenberg and O. Abuddayeh for helpful discussions. Plasmids containing ADAR2 mutants were generously provided by J. Gootenberg and O. Abuddayeh. Neuron culture was supplied by D. Park. We acknowledge Y. Lin and X. Sun for help with neuron induction experiments. Plasmids deposited on Addgene. F.C. acknowledges funding from 1DP5OD024583, the National Institutes of Health (NIH) Directorʼs Early Independence Award, the Paul G. Allen Frontiers Group, the Burroughs Wellcome Fund and the Schmidt Fellows Program at the Broad Institute. E.S.B. acknowledges funding by John Doerr, the Open Philanthropy Project, NIH 1R01MH114031, the HHMI-Simons Faculty Scholars Program, the U.S. Army Research Laboratory and the U.S. Army Research Office under contract/grant numbers W911NF1510548, NIH 1RM1HG008525, NIH UF1NS107697, NIH 2R01DA029639, NIH 1R01MH103910, UF1NS107697, NIH Director’s Pioneer Award 1DP1NS087724 and the MIT Media Lab. E.S.B. also acknowledges L. Yang as a supporter of his lab. S.G.R. acknowledges funding through the Myhrvold and Havranek Family Charitable Fund Hertz Graduate Fellowship and the National Science Foundation Graduate Research Fellowship Program (award no. 1122374). J.S. acknowledges funding through the Hertz Graduate Fellowship. S.L. acknowledges funding through the Molecular Biophysics Training Grant, NIH/NIGMS T32 GM008313. E.D.Z. acknowledges funding through the National Science Foundation Graduate Research Fellowship Program (award no. 1122374) and through the Computational and Systems Biology training grant, T32 GM087237.
Footnotes
Ethics declarations
Competing interests
All authors are listed as inventors on a patent application for this technology.
Contributor Information
Samuel G. Rodriques, Department of Physics, Massachusetts Institute of Technology, Cambridge, MA, USA Department of Media Arts and Sciences, Massachusetts Institute of Technology, Cambridge, MA, USA; Broad Institute of Harvard and MIT, Cambridge, MA, USA.
Linlin M. Chen, Broad Institute of Harvard and MIT, Cambridge, MA, USA
Sophia Liu, Biophysics Program, Harvard University, Boston, MA, USA; Harvard–MIT Division of Health Sciences and Technology, Massachusetts Institute of Technology, Cambridge, MA, USA.
Ellen D. Zhong, Computational and Systems Biology, Massachusetts Institute of Technology, Cambridge, MA, USA
Joseph R. Scherrer, Department of Physics, Massachusetts Institute of Technology, Cambridge, MA, USA
Edward S. Boyden, Department of Media Arts and Sciences, Massachusetts Institute of Technology, Cambridge, MA, USA Department of Biological Engineering, Massachusetts Institute of Technology, Cambridge, MA, USA; Department of Brain and Cognitive Sciences, Massachusetts Institute of Technology, Cambridge, MA, USA; MIT McGovern Institute, Massachusetts Institute of Technology, Cambridge, MA, USA; Koch Institute, Massachusetts Institute of Technology, Cambridge, MA, USA; Howard Hughes Medical Institute, Cambridge, MA, USA.
Fei Chen, Broad Institute of Harvard and MIT, Cambridge, MA, USA; Department of Stem Cell and Regenerative Biology, Harvard University, Cambridge, MA, USA.
References
- 1.Muhar M, Ameres SL & Zuber J. SLAM-seq defines direct gene-regulatory functions of the BRD4–MYC axis. Science 2793, 1–10 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Herzog VA et al. Thiol-linked alkylation of RNA to assess expression dynamics. Nat. Methods 14, 1198–1204 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Schofield JA, Duffy EE, Kiefer L, Sullivan MC & Simon MD TimeLapse-seq: adding a temporal dimension to RNA sequencing through nucleoside recoding. Nat. Methods 15, 221–225 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Erhard F. et al. scSLAM-seq reveals core features of transcription dynamics in single cells. Nature 571, 419–423 (2019). [DOI] [PubMed] [Google Scholar]
- 5.La Manno G. et al. RNA velocity of single cells. Nature 560, 484–498 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Fukuda M. et al. Construction of a guide-RNA for site-directed RNA mutagenesis utilising intracellular A-To-I RNA editing. Sci. Rep. 7, 41478 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Montiel-Gonzalez MF, Vallecillo-Viejo I, Yudowski GA & Rosenthal JJC Correction of mutations within the cystic fibrosis transmembrane conductance regulator by site-directed RNA editing. Proc. Natl Acad. Sci. USA 110, 18285–18290 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Montiel-González MF, Vallecillo-Viejo IC & Rosenthal JJC An efficient system for selectively altering genetic information within mRNAs. Nucleic Acids Res. 44, e157 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wettengel J, Reautschnig P, Geisler S, Kahle PJ & Stafforst T. Harnessing human ADAR2 for RNA repair - recoding a PINK1 mutation rescues mitophagy. Nucleic Acids Res. 45, 2797–2808 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Cox DBT, Gootenberg JS, Abudayyeh OO, Franklin B. & Kellner MJ RNA editing with CRISPR–Cas13. Science 358, 1019–1027 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Matthews MM et al. Structures of human ADAR2 bound to dsRNA reveal base-flipping mechanism and basis for site selectivity. Nat. Struct. Mol. Biol. 23, 426–433 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kuttan A. & Bass BL Mechanistic insights into editing-site specificity of ADARs. Proc. Natl Acad. Sci. USA 109, 3295–3304 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Eifler T, Pokharel S. & Beal PA RNA-seq analysis identifies a novel set of editing substrates for human ADAR2 present in Saccharomyces cerevisiae. Biochemistry 52, 7857–7869 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bertrand E. et al. Localization of ASH1 mRNA particles in living yeast. Mol. Cell 2, 437–445 (1998). [DOI] [PubMed] [Google Scholar]
- 15.Piatkevich KD et al. A robotic multidimensional directed evolution approach applied to fluorescent voltage reporters. Nat. Chem. Biol. 14, 352–360 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Perry RP & Kelley DE Inhibition of RNA synthesis by actinomycin D: characteristic dose-response of different RNA species. J. Cell. Physiol. 76, 127–139 (1970). [DOI] [PubMed] [Google Scholar]
- 17.Raj A, van den Bogaard P, Rifkin SA, van Oudenaarden A. & Tyagi S. Imaging individual mRNA molecules using multiple singly labeled probes. Nat. Methods 5, 877–879 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Schwanhüusser B. et al. Global quantification of mammalian gene expression control. Nature 473, 337–342 (2011). [DOI] [PubMed] [Google Scholar]
- 19.Wang X, Chen X. & Yang Y. Spatiotemporal control of gene expression by a light-switchable transgene system. Nat. Methods 9, 266–271 (2012). [DOI] [PubMed] [Google Scholar]
- 20.Klein AM et al. Droplet barcoding for single-cell transcriptomics applied to embryonic stem cells. Cell 161, 1187–1201 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Macosko EZ et al. Highly parallel genome-wide expression profiling of individual cells using nanoliter droplets. Cell 161, 1202–1214 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Perli SD et al. Continuous genetic recording with self-targeting CRISPR–Cas in human cells. Science 353, 339–342 (2016). [DOI] [PubMed] [Google Scholar]
- 23.Farzadfard F. et al. Single-Nucleotide-Resolution Computing and Memory in Living Cells. Mol. Cell 75, 769–780.e4 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kalhor R. et al. Rapidly evolving homing CRISPR barcodes. Nat. Methods 14, 195–200 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sheth RU, Yim SS, Wu FL & Wang HH Multiplex recording of cellular events over time on CRISPR biological tape. Science 358, 1457–1461 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Tang W. & Liu DR Rewritable multi-event analog recording in bacterial and mammalian cells. Science 360, eaap8992 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chen H. et al. Efficient, continuous mutagenesis in human cells using a pseudo-random DNA editor. Nat. Biotechnol. 38, 165–168 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Frieda KL et al. Synthetic recording and in situ readout of lineage information in single cells. Nature 541, 107–111 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Shipman SL et al. Molecular recordings by directed CRISPR spacer acquisition. Science 353, aaf1175 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zamft BM et al. Measuring cation dependent DNA polymerase fidelity landscapes by deep sequencing. PLoS ONE 7, e43876 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Schmidt F, Cherepkova MY & Platt RJ Transcriptional recording by CRISPR spacer acquisition from RNA. Nature 562, 380–385 (2018). [DOI] [PubMed] [Google Scholar]
- 32.Farzadfard F. & Lu TK Genomically encoded analog memory with precise in vivo dna writing in living cell populations. Science 346, 1256272 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Tay S. et al. Single-cell NF-kappaB dynamics reveal digital activation and analogue information processing. Nature 466, 267–271 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Nandagopal N. et al. Dynamic ligand discrimination in the notch signaling pathway. Cell 172, 869–880 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Rivera VM et al. A humanized system for pharmacologic control of gene expression. Nat. Med. 2, 1028–1032 (1996). [DOI] [PubMed] [Google Scholar]
- 36.Erhart D. et al. Chemical development of intracellular protein heterodimerizers. Chem. Biol. 20, 549–557 (2013). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Raw data were used in all figures that are not described in the captions as schematics. The data sets generated and analyzed during the current study are available on the Zenodo Archive, record 3897464. Raw sequencing data are available at the Sequence Read Archive under PRJNA658989.