Emergent robustness of bacterial quorum sensing in fluid flow

Significance

Bacteria control multicellular behaviors through a process called quorum sensing (QS). Because QS signaling molecules diffuse between cells, they are susceptible to removal by external fluid flow, which is a ubiquitous feature of bacterial habitats ranging from the lungs, gut, and nasal passage to rivers, lakes, and oceans. It is therefore vital to account for realistic flow conditions when assessing the functional role of QS genetic networks. By systematically connecting cell- and population-level processes, our theory demonstrates and quantifies how positive feedback in QS networks allows bacterial populations to overcome spatiotemporal chemical gradients caused by steady or intermittent external fluid flow and to orchestrate robust collective responses in complex environments.

Abstract

Bacteria use intercellular signaling, or quorum sensing (QS), to share information and respond collectively to aspects of their surroundings. The autoinducers that carry this information are exposed to the external environment; consequently, they are affected by factors such as removal through fluid flow, a ubiquitous feature of bacterial habitats ranging from the gut and lungs to lakes and oceans. To understand how QS genetic architectures in cells promote appropriate population-level phenotypes throughout the bacterial life cycle requires knowledge of how these architectures determine the QS response in realistic spatiotemporally varying flow conditions. Here we develop and apply a general theory that identifies and quantifies the conditions required for QS activation in fluid flow by systematically linking cell- and population-level genetic and physical processes. We predict that when a subset of the population meets these conditions, cell-level positive feedback promotes a robust collective response by overcoming flow-induced autoinducer concentration gradients. By accounting for a dynamic flow in our theory, we predict that positive feedback in cells acts as a low-pass filter at the population level in oscillatory flow, allowing a population to respond only to changes in flow that occur over slow enough timescales. Our theory is readily extendable and provides a framework for assessing the functional roles of diverse QS network architectures in realistic flow conditions.

Bacteria share and respond collectively to information about their surrounding environment through the production, release, and detection of small diffusible molecules called autoinducers (AIs), in a process termed quorum sensing (QS). In QS systems, the individual bacterial expression of genes relevant to the community is promoted when AIs accumulate to a threshold concentration, typically associated with an increasing cell density (1). Population-level behaviors exhibited in QS-activated states include bioluminescence (2, 3), virulence factor production (4), modified mutation rates (5), biofilm and aggregate formation (6, 7), and biofilm dispersal (8). As AIs diffuse between cells, they are often subject to complex and fluctuating features of their environment, such as extracellular matrix components (9, 10), interference by other bacterial species (or the host organism), and external fluid flow. Recent research has started to show how such environmental factors are closely linked to the QS response, building on foundational knowledge gained from studying well-mixed laboratory cultures (11–13). However, improving our understanding of the functional role of QS systems requires understanding how these systems promote appropriate population-level phenotypes in realistic bacterial environments.

Fluid flow is ubiquitous in a diverse range of bacterial habitats from rivers, lakes, and medical devices to the host teeth, gut, lungs, and nasal cavity (14). In addition to its mechanical effects on the structure of cell populations (15–19), external fluid flow has been found to have a strong influence on the transport of relevant chemicals including nutrients (8, 20), antibiotics during host treatment (21, 22), and QS AIs (23–26). Recent experimental (23–27) and numerical (28–34) studies suggest that flow-induced AI transport can affect population-level phenotypes by introducing chemical gradients within populations and, if the flow is strong enough, suppressing QS altogether. These results raise two important questions about QS genetic networks. First, how can QS networks ensure a robust population-level response in order to avoid individual cells committing to a costly multicellular phenotype in isolation, while also avoiding premature population-level QS activation in a spatiotemporally complex environment? Second, how can QS networks enable populations to sense cell density in flow environments that promote high mass transfer (35–38)?

Here we answer these questions by combining simulations and a systematic asymptotic analysis of QS in a cell layer subject to an external flow; we focus on the effect of positive feedback in AI production, a common feature of QS genetic circuits (39). We begin by establishing the conditions required for the emergence of population-level QS activation in steady flow. Our results illustrate how the required conditions for activation depend on the ratio of the timescale of the external flow to the timescale of diffusion through the cell layer. If the required conditions are met in a region of the cell layer, positive feedback causes AIs to flood the population, inducing population-wide QS activation. Interestingly, by accounting for a dynamic flow in our model we find that an ability to avoid premature QS activation is built into systems with positive feedback. We predict that positive feedback acts as a low-pass filter to oscillations in the shear rate; if such oscillations occur over a time period shorter than a critical time that we calculate, the QS system is not activated, even if the required conditions for activation are met during the oscillations. Furthermore, we find that by combining multiple QS signals, a population can infer both cell density and external flow conditions. Overall, our findings suggest that positive feedback allows QS systems to act as spatiotemporally nonlocal sensors of fluid flow.

Results

Population-Level Theory for QS in Flow.

To understand how genetic circuits in individual cells affect population-level bacterial signaling, we investigated an archetypal QS circuit in gram-negative bacteria called a LuxIR system (Fig. 1A and Materials and Methods). In this system, AIs in cells bind to a cognate LuxR protein, and the bound AI–LuxR dimer promotes the transcription of downstream genes. The system exhibits a positive feedback loop through the presence of an AI synthase, LuxI, whose expression is promoted by the bound dimer (12, 39). Thus, to summarize, as the concentration of AIs in a cell increases, there is an increase in the number of bound dimers. Consequently, this promotes the production of LuxI, which further increases the production of AIs.

Fig. 1.

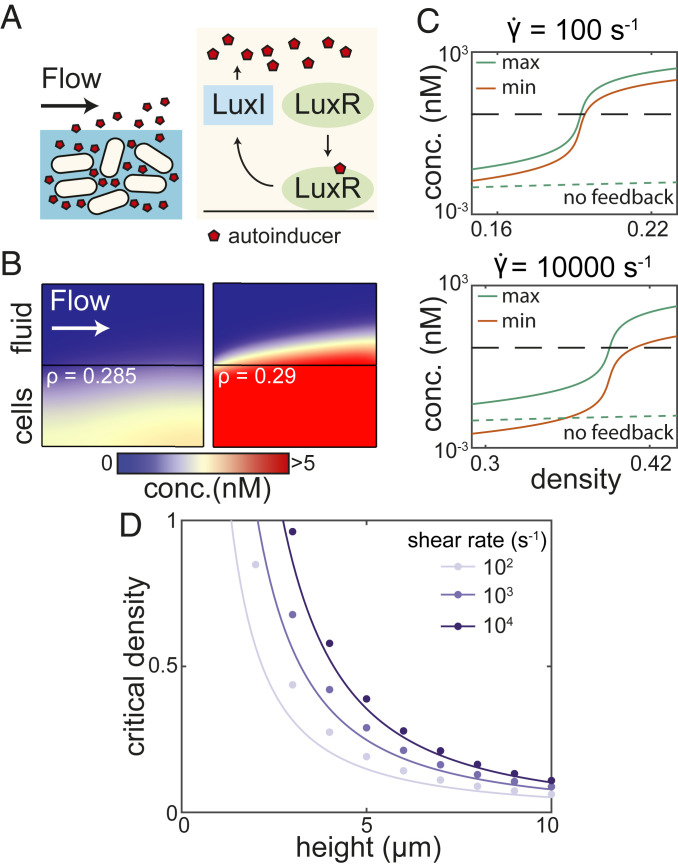
Conditions for the onset of QS activation in a LuxIR-type system in steady flow. (A) We model a population of cells and an external fluid flow above the population (Left). Inside cells, we model a LuxIR-type genetic circuit with positive feedback (12, 39) (Right). (B) AI concentration in steady simulations with an imposed uniform shear flow. If the density is below a critical value, the system remains inactivated (Left). If the density rises just above this critical value, positive feedback causes robust population-level QS activation (Right). (C) The maximum (green line) and minimum (red line) AI concentrations inside a population rise drastically around the critical density in steady simulations (vertical axes scaled logarithmically). Results are shown for shear rates of 100 ${\mathrm{s}}^{-1}$ (Top) and 10,000 ${\mathrm{s}}^{-1}$ (Bottom); the height of the cell layer is taken to be $H=5\hspace{0.17em}\mathrm{\mu }$m. Dashed black lines correspond to the activation threshold, and dashed green lines show the maximum concentration in the cell population when no feedback is present ($\lambda =0$); we note that setting the binding parameters $k_{+}=0$ and $k_{-}=0$ does not have a distinguishable effect in that case. (D) The simulations show that the critical density is larger for a larger shear rate and smaller for a thicker cell layer (dots). Lines show the predicted critical density from Eqs. 6–8. All kinetic parameters in these simulations are given the values listed in SI Appendix, Table S1.

Here, we model the concentration of AIs $\left(A\right)$, LuxR $\left(R\right)$, LuxI $\left(I\right)$, and bound AI–LuxR dimers $\left(C\right)$ in a population of cells through a locally averaged set of governing equations (40, 41). The important cell-scale information is captured through the local volume density of cells $\rho$ (Materials and Methods). We consider the scenario where cells are embedded in an extracellular matrix [matrix generation precedes QS activation in species including Vibrio cholerae (8) and Pseudomonas aeruginosa (25)] over which a fluid flows. As such, the fluid flow imparts a shear stress (which may vary in space and time) to the upper boundary of the cell layer. We neglect growth-induced flows inside the cell layer because their timescales are typically much slower than those of diffusion and external flow (18, 42).

Thus, our problem consists of two coupled domains. To obtain nondimensional equations in each domain, we scale lengths with the height of the cell layer $H$, fluid velocities with $\dot{\gamma }H$, where $\dot{\gamma }$ is a typical shear rate, and times with the diffusion timescale $H^2/D_c$, where $D_c$ is the AI diffusion coefficient in the cell population (Materials and Methods). In the cell population region, a reaction-diffusion equation holds for the AI concentration

$$\frac{\partial A}{\partial t}={\nabla }^{2}A+\rho \left(q+\lambda I-k_{+}AR+k_{-}C\right)-\kappa A,$$ [1]

where ${\nabla }^{2}A$ represents AI diffusion, $q$ is the base production rate of AIs, $\lambda$ is the synthesis rate of AIs by LuxI, $k_{+}$ is the binding rate of AIs and LuxR proteins, $k_{-}$ is the corresponding unbinding rate, and $\kappa$ is the decay rate of AIs. Reaction equations hold for the concentrations of the proteins and dimers inside cells

$$\begin{array}{c}\hfill \frac{\partial I}{\partial t}=\mu C-\alpha I,\\ \hfill \frac{\partial R}{\partial t}=r-k_{+}AR+k_{-}C-\beta R,\\ \hfill \frac{\partial C}{\partial t}=k_{+}AR-k_{-}C-\gamma C,\end{array}$$ [2]

where $\mu$ is the activation rate of LuxI by AI–LuxR complexes; $r$ is the base production rate of LuxR; and $\alpha$, $\beta$, and $\gamma$ are decay rates. We combine the kinetic parameters into two parameter groups,

$$K=\frac{\beta \left(k_{-}+\gamma \right)}{k_{+}\gamma },\hspace{1em}\mathrm{\Lambda }=\frac{\lambda \mu }{\alpha \gamma },$$ [3]

where $K$ represents an effective equilibrium constant for AI–LuxR complex formation and $\mathrm{\Lambda }$ represents the strength of positive feedback in the system. In the external flow region, with flow field $\mathbf{u}$ that satisfies the Navier–Stokes equations, an advection-diffusion equation with decay holds for the AI concentration

$$\begin{array}{c}\hfill \nabla \cdot \mathbf{u}=0,\hspace{1em}\frac{\partial \mathbf{u}}{\partial t}+\mathbf{u}\cdot \nabla \mathbf{u}=-\nabla p+\frac{1}{\text{Re}}{\nabla }^2\mathbf{u},\\ \hfill \frac{\partial A}{\partial t}=\nabla \cdot \left(D\nabla A-\text{Pe}\mathbf{u}A\right)-\kappa A,\end{array}$$ [4]

where $\text{Re}$ is the Reynolds number of the flow and $D$ is the ratio of AI diffusivity in the flow to AI diffusivity in the cell layer. The key control parameter that we use to investigate how external flow affects QS in cell populations is the Péclet number

$$\text{Pe}=\dot{\gamma }{H}^2/D_c,$$ [5]

which quantifies the relative effects of advection in the external flow to diffusion in the cell layer.

QS Activation in Steady Flow.

First, we performed numerical simulations of the governing equations in the finite-element computational software COMSOL Multiphysics for an imposed spatially uniform shear flow, which we assumed to be free of AIs far upstream (see SI Appendix, Fig. S1, for a full description of the numerical procedure). This incorporates a very wide range of laminar flows in simple geometries owing to the large Schmidt number ($\text{Sc}=\nu /D_e>\mathrm{1,000}$, where $\nu$ is the kinematic viscosity and $D_e$ is the diffusion coefficient in the flow) of AIs in water, so that the flow profile can be linearized in the mass-transfer boundary layer. We performed steady simulations to understand the conditions in which it is possible for a population to enter a QS-activated state for typical kinetic and physical parameter values (summarized in SI Appendix, Table S1). The results show that a strong flow can entirely suppress QS activation by removing AIs from the population boundary (Fig. 1B). However, above a critical cell density ${\rho }_c$, the cell population is able to exhibit QS activation through the positive feedback present in the system. At steady state in this regime, the domain becomes flooded with AIs, which increase in concentration by several orders of magnitude throughout the population (Fig. 1B); the large increase does not occur in systems without positive feedback (Fig. 1C). This change occurs over very small changes in cell density (Fig. 1C). In larger cell populations, populations with restricted or reduced AI diffusion, and weaker external flows, the critical density is smaller owing to the reduced mass transfer of AIs out of the population (Fig. 1D and SI Appendix, Fig. S5).

To understand the general principles that guide how the various kinetic, physical, and geometric parameters determine ${\rho }_c$, we analyzed the system of equations for a thin cell layer, where diffusion through the cell layer in the direction of flow is much less important than diffusion in the direction normal to the surface of the cell layer (43). In this systematically reduced model, the entire effect of the external flow region on the AI concentration $A$ within the cell population is reduced to an effective Robin boundary condition on the surface of the cell layer. To derive this condition, we constructed a similarity solution for $A$ in the mass-transfer boundary layer (44) in the external fluid (SI Appendix). This yielded an effective Péclet number, ${\text{Pe}}_{\text{eff}}$, which quantifies the local ratio of advective to diffusive transport at the position $x$ (where the $x$ axis is directed with the flow and $x=0$ corresponds to the upstream edge of the population). Our analysis predicts the effective Péclet number to be

$${\text{Pe}}_{\text{eff}}=\frac{\mathrm{\Gamma }\left(2/3\right){\text{Pe}}^{1/3}{D}^{2/3}}{3^{2/3}{x}^{1/3}}\approx 0.65\frac{{\text{Pe}}^{1/3}{D}^{2/3}}{x^{1/3}},$$ [6]

where $\mathrm{\Gamma }$ is the Gamma function and $D$ is the ratio of the diffusion coefficient in the external flow to the diffusion coefficient in the cell layer (Eq. 16). Our ${\text{Pe}}_{\text{eff}}$ prediction agrees well with simulation results (Fig. 2A) outside a small diffusive boundary layer of thickness O(${\text{Pe}}^{-1/2}$) at the downstream end of the cell population (SI Appendix, Fig. S3).

Fig. 2.

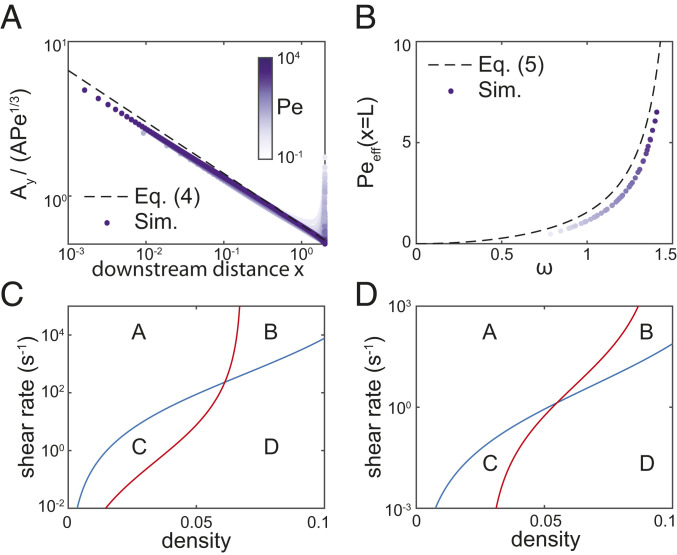
An algebraic relationship links flow, biomass, and kinetics at the onset of QS activation. (A) For the simulations in Fig. 1D, when the calculated effective Péclet number at the cell population boundary, $A_y/A$, is scaled by ${\text{Pe}}^{1/3}$, the simulation data collapse onto the curve $0.65/x^{1/3}$ (dashed line), as predicted in Eq. 6 with $D=1$ (both axes scaled logarithmically). Here $A$ is the AI concentration, $A_y$ is its derivative in the vertical direction (perpendicular to the flow), $x$ is the coordinate parallel to the flow, and $y$ is the coordinate perpendicular to the flow. (B) When plotted against the appropriate nondimensional variables identified in Eqs. 6 and 8, the simulations from Fig. 1D collapse onto the curve defined by Eq. 7 (see also SI Appendix, Fig. S4). (C and D) Illustrative examples of how cells can measure density and flow by measuring activation (Eq. 7) of two different AIs, splitting parameter space into four regions A, B, C, and D (vertical axes scaled logarithmically). (C) Cell population of height 10 $\mathrm{\mu }$m. The first AI has kinetic parameters from SI Appendix, Table S1 (blue line), and the second AI also has a factor of 10 reduction in diffusivity in the cell layer and factor of 5 reduction in LuxR production rate (red line) compared to the first AI. (D) Cell population of height 100 $\mathrm{\mu }$m. The first AI has kinetic parameters from SI Appendix, Table S1, but with factor of 10 increase in LuxI and LuxR decay rates (blue line), and the second AI also has a factor of 500 increase in AI decay rate and factor of 2 increase in LuxR production rate (red line) compared to the first AI.

The steady thin-film governing equations admit a solution for $A$ that satisfies an ordinary differential equation, which we analyze here through the method of matched asymptotic expansions (SI Appendix). Based on the expected orders of magnitude of the parameter values (SI Appendix, Table S1), we exploit the physiologically relevant limits $K\gg 1$ and $\mathrm{\Lambda }\gg 1$, corresponding to a relatively large equilibrium constant for AI–LuxR complex formation and strong positive feedback, respectively (Eq. 3). Our analysis demonstrates that for a fixed ${\text{Pe}}_{\text{eff}}$, the system exhibits an imperfect transcritical bifurcation at a critical density, which marks an orders of magnitude increase in $A$ owing to a drastic increase in positive feedback. We identify this point as the critical density ${\rho }_c$ above which the population exhibits QS activation, which reveals the algebraic relationship

$$\omega \tan \omega ={\text{Pe}}_{\text{eff}}\hspace{1em}\text{at}\rho ={\rho }_c$$ [7]

where

$$\omega \hspace{0.17em}:\hspace{0.17em}=\hspace{0.17em}\sqrt{\frac{\rho r\mathrm{\Lambda }}{K}-\kappa }.$$ [8]

Here $r$ and $\kappa$ represent LuxR production and AI decay, respectively (see Eqs. 1 and 2). In Eq. 7, the effect of flow is captured in ${\text{Pe}}_{\text{eff}}$ and the effect of the kinetic parameters at the population level is captured in the single nondimensional parameter group $\omega$.

To compare the predictions from our systematically reduced model to the simulation results, we note that the onset of QS activation will occur at the lowest effective Péclet number at the boundary of the cell population. Because ${\text{Pe}}_{\text{eff}}$ decreases in $x$ (Eq. 6), we ignore the small downstream boundary layer for simplicity and assume that ${\text{Pe}}_{\text{eff}}$ is minimized at the downstream end of a cell population of length $L$. Therefore, we insert $x=L$ into Eq. 6 to predict ${\text{Pe}}_{\text{eff}}$ for a general population of cells in a uniform shear flow. Plotting our simulation results against the nondimensional parameter groups ${\text{Pe}}_{\text{eff}}$ and $\omega$ (defined in Eqs. 6 and 8, respectively) demonstrates a remarkable collapse onto the predicted curve of Eq. 7 for a wide range of typical kinetic, geometric, and physical parameters (Fig. 2B and SI Appendix, Fig. S4), despite the assumptions in our thin-film reduction. We note that we slightly underestimate ${\text{Pe}}_{\text{eff}}$ (and therefore ${\rho }_c$) due to the thin diffusive region at the downstream end of the population; an improvement would require a full spatial asymptotic analysis of the problem. This collapse onto Eq. 7 can be unwrapped to calculate the critical conditions for activation for a QS network with a given set of kinetic parameters.

For example, we found that by combining two different AI signals, a bacterial population can respond separately to the cell density and the external shear rate, by measuring the activation state of both signals. The key tunable parameters for sensing this difference are the diffusion coefficients of each AI within the cell layer, the decay rates of each AI, and the kinetics of each QS network through the strength of the positive feedback (or, more specifically, the ratio $r\mathrm{\Lambda }/K$ in Eq. 7). We found that two of these parameters must be different between the two AI signals to separate parameter space into four regions that correspond to low and high values of both cell density and shear rate (Fig. 2 C and D). In thin cell layers, where the overall decay of AIs within the cell layer is very small for typical parameters (SI Appendix, Table S1), populations can combine two signals with different diffusion coefficients and different strengths of positive feedback (Fig. 2C). In larger cell layers, populations can also incorporate information from two AIs with different decay rates (Fig. 2D). We note that in very large populations, our model may need to be modified to account for nutrient limitations (SI Appendix, Fig. S10). This ability to measure cell density and shear rate separately is possible because the three tunable parameters affect QS activation conditions in distinct ways: AI diffusivity within the cell layer has a larger effect at larger shear rates, AI decay has a consistent effect across shear rates, and the effect of positive feedback is strongly dependent on the cell density.

QS Activation in Complex Geometries.

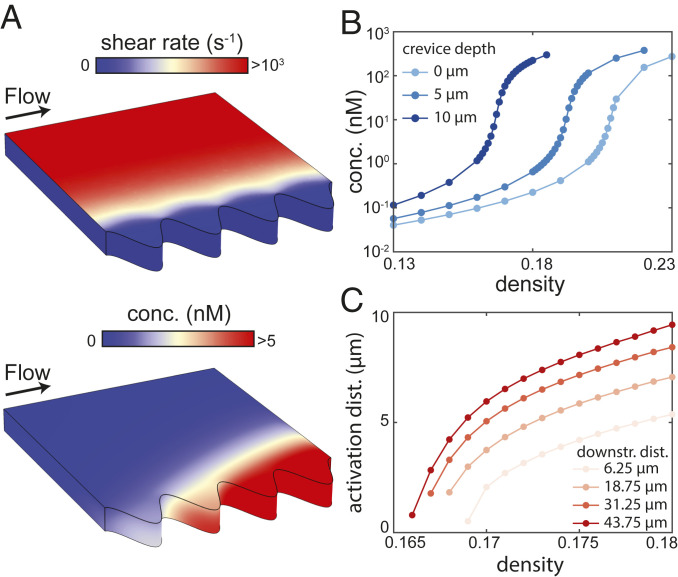
In complex geometries there will be regions of low shear on the cell layer surface, on which the local effective Péclet number (Eq. 6) will be reduced. Eq. 7 predicts that the global ${\rho }_c$ will be lowered in such cell populations, in agreement with a recent experimental study in which QS activation was found to be promoted in crevices or pores (26). To further understand the local and global effects of complex geometries on QS, we performed simulations of the three-dimensional (3D) governing equations in channels which mimic typical host environments such as intestinal crypts and tooth cavities. The channels contain crevices that extend in the horizontal direction transverse to a pressure-induced flow over a cell population that coats the channel floor (Fig. 3A and SI Appendix, Fig. S1). We found that ${\rho }_c$ is reduced in channels with crevices, by an amount that depends on the crevice depth (Fig. 3B) and the number of crevices (SI Appendix, Fig. S6), in agreement with experimental findings (26). Furthermore, we found that once QS is activated in the crevices, diffusion of AIs activates further regions of the cell population outside the crevices, particularly downstream (Fig. 3C). This activation region can extend for lengths far beyond the size of the crevices themselves, even in conditions for which QS activation would be precluded completely in a simple channel (Fig. 3 B and C). This demonstrates that local geometric complexities can have highly nonlocal effects on QS activation through positive feedback.

Fig. 3.

In complex geometries, positive feedback causes robust QS activation based on the region with the lowest effective Péclet number. (A) We simulate steady flow in a channel with crevices in its sidewall; a cell population coats the channel floor. (Top) The shear rate applied by the flow to the top of the cell population is lower in the crevices (no shear is applied to the sides of the cell population). (Bottom) The AI concentration in the cell population is higher in the crevices and downstream. Simulations are performed with $\rho =0.168$ and a crevice depth of $10\hspace{0.17em}\mathrm{\mu }$m, which is twice the height of the population (see SI Appendix, Fig. S1, for further details of the simulation geometry and boundary conditions). (B) Steady simulations show that QS is activated at lower densities in populations in channels with deeper crevices. The maximum AI concentration in the population, which occurs in the most downstream crevice (A), is plotted (vertical axis scaled logarithmically). (C) Steady simulations show that for a larger density, a larger region of the population is activated. The density is plotted against the QS-activated distance along the line transverse to the center of each of the four crevices; the downstream distance of each crevice from the upstream edge of the population is labeled. The QS-activated region is defined as the region for which $A>5$ nM, which we take to be the activation threshold. All kinetic parameters in these simulations are given the values listed in SI Appendix, Table S1.

QS Activation in Unsteady Flow.

To understand the transient process of QS activation in unsteady flows, which are common in bacterial habitats such as the lungs and medical devices, we performed simulations of the dynamic governing equations for spatially uniform flows with a sinusoidally oscillating shear rate. Each oscillating flow is characterized by the time $t_{\text{act}}$ during an oscillation period for which the system is in the QS activation region of parameter space,

$$t_{\text{act}}={\int }_V\mathrm{d}t,$$ [9]

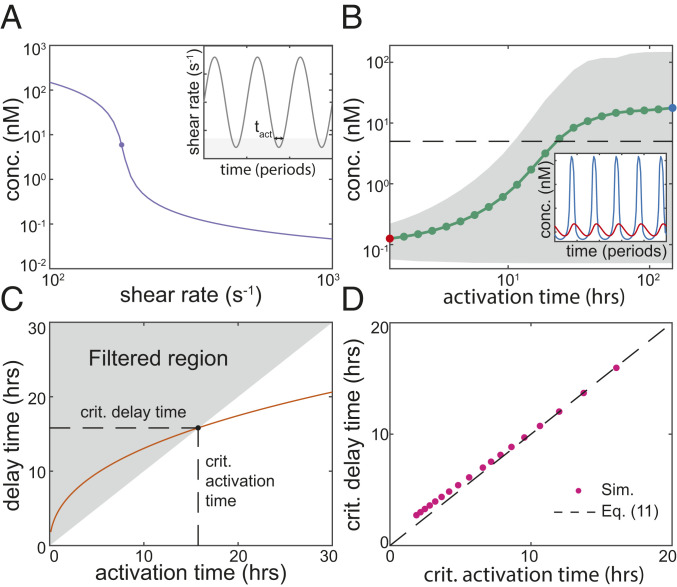
where $V$ is the set of times such that ${\text{Pe}}_{\text{eff}}\left(t\right)<{\text{Pe}}_{\text{eff}}\left(t_c\right)$ over one oscillation and $t_c$ is the time at which the effective Péclet number ${\text{Pe}}_{\text{eff}}$ falls below its critical value identified in Eq. 7 (Fig. 4A, Inset). For the range of shear rates spanned by the oscillations, the steady solution for AI concentration varies over orders of magnitude as the system passes through the critical ${\text{Pe}}_{\text{eff}}$ (Fig. 4A). However, in the dynamic simulations, for a fixed mean and amplitude of oscillation, this range is only achieved for long enough oscillation periods (i.e., larger $t_{\text{act}}$). Surprisingly, for shorter oscillation periods (i.e., smaller $t_{\text{act}}$), the AI concentration remains below the QS-activation threshold; we note that throughout these simulations, $t_{\text{act}}$ remains well above the diffusive timescale. We found that there is a critical oscillation period (i.e., a critical $t_{\text{act}}$) and that as the period increases over this critical value, the mean (and maximum) concentration of AIs increases over several orders of magnitude (Fig. 4B and Movies S1 and S2). We did not observe such a critical oscillation period for a system without feedback ($\lambda =0$), suggesting that this effect is caused by positive feedback (SI Appendix, Fig. S8).

Fig. 4.

Conditions for QS activation in an oscillating flow. (A) In steady simulations with fixed density, the maximum concentration of AIs rises drastically when the shear rate is below its critical value (both axes scaled logarithmically). In the following simulations we oscillate the shear rate across this critical value with a fixed mean and amplitude; the oscillations are defined by the activation time $t_{\text{act}}$ for which the system is in the QS activated region of parameter space (Inset). (B) Simulations are performed with oscillations in the shear rate with mean $\dot{\gamma }=500$ ${\mathrm{s}}^{-1}$ and amplitude $\dot{\gamma }=400$ ${\mathrm{s}}^{-1}$. For oscillation time periods slower than a critical time, corresponding to a critical $t_{\text{act}}$, the mean (green line) and range (gray area) of the maximum AI concentration throughout each oscillation rise drastically (both axes scaled logarithmically; see also SI Appendix, Fig. S7 and Movies S1 and S2). Inset: oscillations in the AI concentration are filtered out for $t<t_{\text{act}}$ (red line), but not for $t>t_{\text{act}}$ (blue line; vertical axis scaled logarithmically). (C) Over a range of oscillation periods, for each oscillation we calculate the activation time using Eq. 9 and the delay time using Eq. 10. Thus, we predict a critical oscillation period by finding the oscillation at which the activation time is equal to the delay time. If the activation time is below the delay time, the oscillation is in the filtered region of parameter space, and the QS system is predicted to remain inactivated. (D) To confirm the validity of our prediction of the critical oscillation period, we perform 1D simulations of the thin-film equations, where the Péclet number is directly controllable. We define the critical oscillation as the one at which the maximum AI concentration first rises above the threshold value of 5 nM; then, we calculate the critical activation time using Eq. 9. We find that when plotted against the predicted critical delay time Eq. 10, this critical activation time collapses onto Eq. 11. All kinetic parameters in these simulations are given the parameter values in SI Appendix, Table S1, and the height of the cell layer is taken to be $H=8\hspace{0.17em}\mathrm{\mu }$m.

To explore how this observation depends on the LuxIR system kinetics and to determine whether it is a general property of the system, we performed a dynamic analysis of the thin-film equations as ${\text{Pe}}_{\text{eff}}$ passes below its critical value at $t=t_c$ and the system enters the QS activation region of parameter space. We found that there is a critical slowing down due to the imperfect transcritical bifurcation which marks the onset of QS activation (SI Appendix); these dynamics are reminiscent of the effects of “ghosts” of saddle-node bifurcations (45–47). This slower timescale introduces a delay time, $t_{\text{delay}}$, which determines the time $t=t_c+t_{\text{delay}}$ at which dynamic QS activation occurs if the effective Péclet number remains below its critical value, i.e., if ${\text{Pe}}_{\text{eff}}\left(t\right)<{\text{Pe}}_{\text{eff}}\left(t_c\right)$ for $t>t_c$. The delay time depends on the system kinetics through two nondimensional parameter groups ${\nu }_1$ and ${\nu }_2$ (defined in Eq. 17; Materials and Methods) and on the imposed external flow through the time-derivative ${\text{Pe}}_{\text{eff}}^{\prime }\left(t_c\right)$ of the effective Péclet number as it passes below its critical value:

$$t_{\text{delay}}={\nu }_1\sqrt{\frac{\log {\nu }_2\left|{\text{Pe}}_{\text{eff}}^{\prime }\left(t_c\right)\right|}{\left|{\text{Pe}}_{\text{eff}}^{\prime }\left(t_c\right)\right|}}.$$ [10]

Thus, the delay time depends on whether the shear rate changes slowly or quickly through the critical value that marks the onset of QS activation.

Interestingly, this result suggests that in a dynamic flow, even if the shear rate falls below its critical value into the QS activation region, the onset of QS activation would not be triggered if the shear rate increases back above its critical value after a time shorter than the delay time of the system. Therefore, for an oscillating flow that enters the QS activation region of parameter space for an activation time $t_{\text{act}}$ during each oscillation, we identify the oscillation period as the critical period if the activation and delay times are equal (Fig. 4C):

$$t_{\text{act}}=t_{\text{delay}}.$$ [11]

Eqs. 10 and 11 predict that for a flow oscillating over a long enough time period, such that $t_{\text{act}}>t_{\text{delay}}$, the QS system passes through cycles of dynamic activation and deactivation. Conversely, for a flow oscillating over a short enough time period, such that $t_{\text{act}}<t_{\text{delay}}$, the system is predicted to remain in the QS-inactivated state. We confirmed the validity of our prediction of the critical oscillation period by performing simulations of the governing thin-film equations, in which the Péclet number and its derivatives are directly controllable. The results show that for a wide range of oscillating Péclet numbers, the calculated properties for the onset of dynamic QS activation collapse onto the curve defined by Eqs. 10 and 11 (Fig. 4D).

In experiments and in our simulations of the governing equations with an imposed flow, it is not possible to control the effective Péclet number and its derivatives directly. However, we can make an order of magnitude estimate of the required conditions for the onset of dynamic QS activation for a sinusoidally oscillating flow with a time period $T_p$ as follows. At onset, ${\text{Pe}}_{\text{eff}}^{\prime }\left(t_c\right)=O\left(1/T_p\right)$ and $t_{\text{act}}=O\left(T_p\right)$. Combining Eqs. 10 and 11 and neglecting the effect of the logarithmic term in Eq. 10 (which we expect to have a lesser effect than the algebraic terms) yields an estimate of $T_p=O\left({\nu }_1^2\right)$ at the onset of dynamic QS activation. For the typical kinetic parameters used in our simulations (SI Appendix, Table S1), this suggests a critical oscillation period of approximately 10 h, which is in agreement with our simulation results for a wide range of oscillating flows (Fig. 4 B and D and SI Appendix, Fig. S7).

Discussion

This study demonstrates how positive feedback in the LuxIR system, an archetypal bacterial QS genetic circuit, promotes a robust population-level response in spatiotemporally varying flow conditions. Because QS systems measure the concentration of passively transported AIs, even simple fluid flows generate concentration gradients which can cause phenotypic gradients within a population. Our results show that positive feedback in QS genetic architectures allows bacteria to overcome flow-induced AI gradients at the population level for a wide range of conditions that represent flows encountered in bacterial habitats such as lakes, rivers, and hosts (Figs. 1 and 3). The key physical determinant of the onset of QS activation in a population is the minimum value of the effective Péclet number ${\text{Pe}}_{\text{eff}}$ (Eq. 6), which quantifies the local advective to diffusive transport at the surface where the population meets the external fluid. Furthermore, a systematic reduction of the governing equations via a thin-film model reveals that for a given ${\text{Pe}}_{\text{eff}}$, the critical population density for the onset of QS activation is determined by a single dimensionless kinetic parameter group $\omega$ (Eq. 8). A compact relationship between these two parameter groups, Eq. 7, links the physical, geometric and kinetic parameters at the onset of QS activation (Fig. 2). Through their transparent dependence on these system parameters, Eqs. 6–8 explain how QS activation is promoted in bacteria with QS architectures with stronger positive feedback or with smaller AI–LuxR dissociation constants (48); in conditions of restricted AI diffusion inside the population, which can be caused by interactions with the extracellular matrix (9) (SI Appendix, Fig. S5); in larger or denser populations; and in populations subject to weaker external flow, in agreement with recent experimental results (25, 26).

The dependence of the critical density on the flow conditions raises the question of whether bacterial QS systems in fluid flow respond to increasing cell density, decreasing mass transfer, or a combination of these factors (37). By calculating the QS activation conditions for AIs with different sets of physical and kinetic parameters using Eqs. 6–8, we suggest that a bacterial population can integrate information from multiple signals to measure cell density and shear rate separately (Fig. 2 C and D). Our results are in qualitative agreement with previous work which considered a well-mixed population subject to spatially uniform AI removal by mass transfer and AI decay (37). However, our results also suggest that in smaller populations subject to external flow, the overall decay of AIs may be too small to separate parameter space into distinct regions; in such populations, physical differences between AI diffusivities [which could be caused by different interactions with surrounding matrix proteins (9)] may provide more information. These results suggest that by combining multiple AI signals with different physical and kinetic properties, bacterial populations in complex environments can add fidelity to measurements of their surrounding conditions and promote the appropriate phenotypic response to these conditions.

An individual bacterium committing to a QS-activated phenotype can incur significant individual costs, such as the generation or abandonment of important extracellular material. It is therefore often beneficial for such a commitment to be shared by the rest of the bacterial population (49). As we have shown, positive feedback promotes a robust, population-scale QS response if appropriate conditions are met in only a local region of a cell population. While this feature of positive feedback is very useful for population-wide commitment, it has the potential downside of triggering premature QS activation in noisy or intermittent flow conditions. However, our analysis of the LuxIR system in dynamic flow conditions suggests that the positive feedback mechanism actually reduces the potential for such a premature response because the feedback itself acts as a low-pass filter at the population level. That is, in a flow oscillating with period smaller than a critical value that we calculate (but still slower than the diffusion timescale), a population responds to the mean effective Péclet number, rather than exhibiting quasi-steady oscillations in QS activation and inactivation (Fig. 4 and SI Appendix, Fig. S11). In such conditions, a growing population’s QS system would be expected to activate eventually through its increasing density (growth is also associated with an activation delay time, but for typical parameters it is of the same order of magnitude as the doubling time; SI Appendix, Fig. S9). The critical time period depends on the nature of the flow oscillation and the system parameters through Eq. 10, which manifests due to a bottleneck induced by an imperfect transcritical bifurcation in the system; such critical slowing down is a universal feature of dynamical systems near critical points (45–47). Overall, this result suggests that population-level low-pass filtering via positive feedback complements other previously identified sources of noise-filtering, or time-averaging (50), in QS systems such as slow AI–LuxR unbinding (51) and diffusional dissipation (52, 53).

Our findings allow us to interpret typical QS network features in a manner that accounts for their expected response to spatiotemporal variations in flow. Our analysis suggests that bacterial species with positive feedback in their QS network, such as P. aeruginosa, use QS as a spatiotemporally nonlocal sensor of flow conditions and cell density. In these systems, positive feedback causes AIs to flood the population if the required conditions are met in a local region, inducing QS activation in a large proportion of the population. Built into this mechanism is an ability to avoid premature population-wide activation in unsteady flow through the delay time that we have identified; the required conditions must persist for long enough for activation to occur. Our predictions of the effects of flow on AI concentration in species in which feedback does not link back to AI production, such as V. cholerae and Vibrio fischeri (39, 54), are shown in Fig. 1C and SI Appendix, Fig. S8. In these systems, AI concentration is much less sensitive to cell density and shear rate, and if the required conditions for QS activation are met in a local region of the population, this does not cause other regions of the population to be activated. Furthermore, in unsteady flows, such systems will exhibit repeated variations in AI concentration, and these variations will occur over diffusive timescales, which are usually faster than timescales of flow variation. Therefore, we expect these species to use QS as a spatiotemporally local sensor of flow conditions and cell density.

To conclude, we have predicted the required conditions for the emergence of robust, population-level QS activation in a spatiotemporally varying fluid flow, for systems that exhibit positive feedback in their QS network architecture. Our results suggest that positive feedback allows cells to avoid an isolated or premature commitment to costly multicellular phenotypes. Furthermore, we have found that populations can integrate multiple signals to sense cell density and flow conditions separately. Our theory demonstrates how QS genetic architectures play a key role in determining the population-level functional response of bacterial intercellular signaling systems in complex environments.

Materials and Methods

Governing Equations.

Inside the cell population, the governing equations are

$$\begin{array}{c}\hfill \frac{\partial Ã}{\partial \tilde{t}}=\tilde{\nabla }\cdot \left({\tilde{D}}_c\tilde{\nabla }Ã\right)+\rho {\tilde{f}}_A\left(Ã,Ĩ,\tilde{R},\tilde{C}\right)-\tilde{\kappa }Ã,\\ \hfill \frac{\partial Ĩ}{\partial \tilde{t}}={\tilde{f}}_I\left(Ĩ,\tilde{C}\right),\hspace{1em}\frac{\partial \tilde{R}}{\partial \tilde{t}}={\tilde{f}}_R\left(Ã,\tilde{R},\tilde{C}\right),\hspace{1em}\frac{\partial \tilde{C}}{\partial \tilde{t}}={\tilde{f}}_C\left(Ã,\tilde{R},\tilde{C}\right),\end{array}$$ [12]

where $\rho$ is the volume fraction of cells, $Ã$ is the concentration of AIs, $Ĩ$ is the concentration of LuxI, $\tilde{R}$ is the concentration of LuxR, and $\tilde{C}$ is the concentration of AI–LuxR dimers. The reaction terms in the system (Fig. 1A) are

$$\begin{array}{c}\hfill {\tilde{f}}_A\left(Ã,Ĩ,\tilde{R},\tilde{C}\right)=\tilde{q}+\tilde{\lambda }Ĩ-{\tilde{k}}_{+}Ã\tilde{R}+{\tilde{k}}_{-}\tilde{C},\\ \hfill {\tilde{f}}_I\left(Ĩ,\tilde{C}\right)=\tilde{\mu }\tilde{C}-\tilde{\alpha }Ĩ,\\ \hfill {\tilde{f}}_R\left(Ã,\tilde{R},\tilde{C}\right)=\tilde{r}-{\tilde{k}}_{+}Ã\tilde{R}+{\tilde{k}}_{-}\tilde{C}-\tilde{\beta }\tilde{R},\\ \hfill {\tilde{f}}_C\left(Ã,\tilde{R},\tilde{C}\right)={\tilde{k}}_{+}Ã\tilde{R}-{\tilde{k}}_{-}\tilde{C}-\tilde{\gamma }\tilde{C}.\end{array}$$ [13]

The meanings and typical orders of magnitude of each dimensional parameter are listed in SI Appendix, Table S1. Here we have assumed that the cells are embedded in extracellular matrix, such that the fluid flow imparts a shear stress to the upper boundary of the cell layer. In our simulations here, this shear stress is below $10\hspace{0.17em}$ Pa, which is expected to be lower than the yield stress of a cell population embedded in matrix (16). For simplicity we have assumed that mRNA concentrations are quasi-steady and have linearized the activation of LuxI by the AI–LuxR dimers (55) (see SI Appendix, Fig. S2, for a discussion of how saturation in promoter occupancy of the transcription factor affects QS activation in flow). We assume that all cells in the population have access to nutrients and are physiologically active, so that base AI production $\tilde{q}$ is uniform throughout the population. This assumption is based on the observation that hemispherical biofilms with radius around 10 $\mathrm{\mu }$m remain uniformly growth-active even in shear rates a hundredfold smaller than the smallest shear rates used here (17) (where a smaller shear rate implies reduced access to nutrients). This assumption may need to be relaxed in nutrient-limited conditions (SI Appendix, Fig. S10). Note also that we do not consider the basal expression of LuxI, which is expected to be small (56), because its only effect is to slightly change the concentration of AIs before activation. Outside the cell population, the governing equations are

$$\tilde{\nabla }\cdot \tilde{\mathbf{u}}=0,\hspace{1em}\frac{\partial \tilde{\mathbf{u}}}{\partial \tilde{t}}+\tilde{\mathbf{u}}\cdot \tilde{\nabla }\tilde{\mathbf{u}}=-\frac{1}{{\rho }_w}\tilde{\nabla }\tilde{p}+\nu {\tilde{\nabla }}^2\tilde{\mathbf{u}},$$ [14]

$$\frac{\partial Ã}{\partial \tilde{t}}=\tilde{\nabla }\cdot \left({\tilde{D}}_e\tilde{\nabla }Ã-\tilde{\mathbf{u}}Ã\right)-\tilde{\kappa }Ã,$$ [15]

where $\tilde{\mathbf{u}}$ is the velocity field of the fluid and ${\rho }_w$ and $\nu$ are the fluid density and kinematic viscosity, respectively, which we take to be those of water. We assume that the flow is free of AIs far upstream and apply continuity of AI concentration and concentration flux at the interface between the cell population and the flow. Full technical details of the boundary conditions, the nondimensionalization of the problem, and the procedures for the asymptotic and numerical solution of the governing equations are given in SI Appendix.

Nondimensional Parameters.

The nondimensional parameters, defined in terms of the dimensional parameters in Eqs. 12 and 13, are

$$\begin{array}{c}\hfill q=\frac{\tilde{q}{\tilde{H}}^2}{{Ã}_0{\tilde{D}}_c},\hspace{1em}r=\frac{\tilde{r}{\tilde{H}}^2}{{Ã}_0{\tilde{D}}_c},\hspace{1em}\lambda =\frac{\tilde{\lambda }{\tilde{H}}^2}{{\tilde{D}}_c},\\ \hfill \mu =\frac{\tilde{\mu }{\tilde{H}}^2}{{\tilde{D}}_c},k_{+}=\frac{{\tilde{k}}_{+}{Ã}_0{\tilde{H}}^2}{{\tilde{D}}_c},\hspace{1em}{k}_{-}=\frac{{\tilde{k}}_{-}{\tilde{H}}^2}{{\tilde{D}}_c},\\ \hfill \alpha =\frac{\tilde{\alpha }{\tilde{H}}^2}{{\tilde{D}}_c},\hspace{1em}\beta =\frac{\tilde{\beta }{\tilde{H}}^2}{{\tilde{D}}_c},\hspace{1em}\gamma =\frac{\tilde{\gamma }{\tilde{H}}^2}{{\tilde{D}}_c},\\ \hfill \kappa =\frac{\tilde{\kappa }{\tilde{H}}^2}{{\tilde{D}}_c},\hspace{1em}\text{Re}=\frac{\dot{\gamma }{H}^2}{\nu },\hspace{1em}D=\frac{{\tilde{D}}_e}{{\tilde{D}}_c}\end{array}$$ [16]

where $\tilde{H}$ is the height of the cell population and ${Ã}_0$ is the threshold concentration of AIs for QS activation. For a compact representation of the time-dependent results, these parameters can be combined into the parameter groups

$$\begin{array}{c}\hfill {\nu }_1=\frac{\sqrt{2I_2\xi }}{\cos \omega },\hspace{1em}{\nu }_2=\frac{I_2\xi K^2{\cos }^2\omega }{{\rho }_c^{2}qr{I}_1{I}_3\mathrm{\Lambda }},\\ \hfill \xi =1+\frac{r{\rho }_c\mathrm{\Lambda }}{K}\left(\frac{1}{\alpha }+\frac{1}{\gamma +k_{-}}\right),\end{array}$$ [17]

where

$$I_1=\frac{\sin \omega }{\omega },\hspace{1em}{I}_2=\frac{1}{2}+\frac{\sin 2\omega }{4\omega },\hspace{1em}{I}_3=\frac{\sin \omega }{\omega }-\frac{{\sin }^3\omega }{3\omega },$$ [18]

and $\omega$ is defined in Eq. 8.

Data Availability

All data related to this paper are within the main text and SI Appendix. All code required to generate the simulation results is available on GitHub at https://github.com/philip-pearce/quorum-flow.