Significance
Engineering at the nanoscale is rich and complex: researchers have designed small-scale structures ranging from smiley faces to intricate sensors. However, designing specific dynamical features within these structures has proven to be significantly harder than designing the structures themselves. Biology, on the other hand, demonstrates fine-tuned kinetic control at nearly all scales: viruses that form too quickly are rarely infectious, and proper embryonic development depends on the relative rate of tissue growth. Clearly, kinetic features are designable and critical for biological function. We demonstrate a method to control kinetic features of complex systems and apply it to two classic self-assembly systems. Studying and optimizing for kinetic features, rather than static structures, opens the door to a different approach to materials design.
Keywords: self-assembly, colloids, inverse design
Abstract
The inverse problem of designing component interactions to target emergent structure is fundamental to numerous applications in biotechnology, materials science, and statistical physics. Equally important is the inverse problem of designing emergent kinetics, but this has received considerably less attention. Using recent advances in automatic differentiation, we show how kinetic pathways can be precisely designed by directly differentiating through statistical physics models, namely free energy calculations and molecular dynamics simulations. We consider two systems that are crucial to our understanding of structural self-assembly: bulk crystallization and small nanoclusters. In each case, we are able to assemble precise dynamical features. Using gradient information, we manipulate interactions among constituent particles to tune the rate at which these systems yield specific structures of interest. Moreover, we use this approach to learn nontrivial features about the high-dimensional design space, allowing us to accurately predict when multiple kinetic features can be simultaneously and independently controlled. These results provide a concrete and generalizable foundation for studying nonstructural self-assembly, including kinetic properties as well as other complex emergent properties, in a vast array of systems.
Kinetic features are a critical component of a wide range of biological and material functions. The complexity seen in biology could not be achieved without control over intricate dynamic features. Viral capsids are rarely infectious if they assemble too quickly (1), protein folding requires deft navigation and control of kinetic traps (2), and crystal growth is largely controlled by the relative rates of different nucleation events (3). However, the design space of kinetic features remains largely unexplored. Self-assembly traditionally focuses on tuning structural properties, and while there have been significant successes in developing complex structural features (4–9), there has been little exploration of dynamical features in the same realm. We demonstrate quantitative control over assembly rates and transition rates in canonical soft matter systems. In doing so, we begin to explore the vast design space of dynamical materials properties.
To intelligently explore the design space of dynamical features, we rely on recent advances in automatic differentiation (AD) (10–14), a technique for efficiently computing exact derivatives of complicated functions automatically, along with advances in efficient and powerful implementations of AD algorithms (15–17) on sophisticated hardware such as GPUs (graphical processing units) and TPUs (tensor processing units). While the development of these software packages is driven by the machine learning community, a distinct, nondata-driven approach is emerging that combines AD with traditional scientific simulations. Rather than training a model using preexisting data, AD connects observables to physical parameters by directly accessing physical models. This enables intelligent navigation of high-dimensional phase spaces. Initial examples utilizing this approach include optimizing the dispersion of photonic crystal waveguides (18), the invention of new coarse-grained algorithms for solving nonlinear partial differential equations (19), the discovery of molecules for drug development (20), and greatly improved predictions of protein structure (21).
Here, we begin to explore a class of complex inverse design problems that traditionally has been hard to access. Using AD to train well-established statistical physics-based models, we design materials for dynamic, rather than structural, features. We also use AD to gain theoretical insights into this design space, allowing us to predict the extent of designability of different properties. AD is an essential component of this approach (22) because we rely on gradients to connect physical parameters to complex emergent behavior. While there are other approaches for obtaining gradient information (e.g., finite difference approximations), AD calculates exact derivatives and more importantly, can efficiently handle large numbers of parameters. Furthermore, the theoretical insights we develop rely on accurate calculations of the Hessian matrix of second derivatives, for which finite difference approaches are insufficient.
We start in Tuning Assembly Rates of Honeycomb Crystals by considering the bulk crystallization of identical particles into both honeycomb and triangular lattices. By differentiating over entire molecular dynamics (MD) trajectories with respect to interaction parameters, we are able to tune their relative crystallization rates. We proceed with a more experimentally relevant example in Tuning Transition Rates in Colloidal Clusters, where we consider small colloidal nanoclusters that can transition between structural states. By optimizing over the transition barriers, we obtain precise control over the transition dynamics. Together, Tuning Assembly Rates of Honeycomb Crystals and Tuning Transition Rates in Colloidal Clusters demonstrate that kinetic features can be designed in classic self-assembly systems while maintaining the constraint of specific structural motifs. The use of AD provides a way to directly access the design space of kinetic features by connecting emergent dynamics with model parameters. This connection reveals insight into the high-dimensional design landscape, enabling us to make accurate predictions in Simultaneous Training of Multiple Transitions regarding when large numbers of kinetic features of the colloidal clusters can be controlled simultaneously. Finally, we conclude in Discussion with an analysis of both the specific and broad impact of these results.
Tuning Assembly Rates of Honeycomb Crystals
We start with the classic self-assembly problem introduced by Rechtsman et al. (23, 24) of assembling a honeycomb lattice out of identical isotropic particles. The honeycomb lattice is a two-dimensional analog of the diamond lattice, which exhibits desirable mechanical and photonic properties, but its low density makes assembling such a crystal a particularly difficult problem. Nevertheless, Rechtsman et al. (23) successfully designed a honeycomb lattice using a potential of the form
| [1] |
They fixed the parameters , , and and optimized , , , and using simulated annealing (23, 24) at zero temperature. We optimize the same set of four free parameters. However, we optimize via AD rather than simulated annealing and work toward a different goal: tuning the rate of assembly at finite temperature while still enforcing the structural constraint that a honeycomb lattice is assembled.
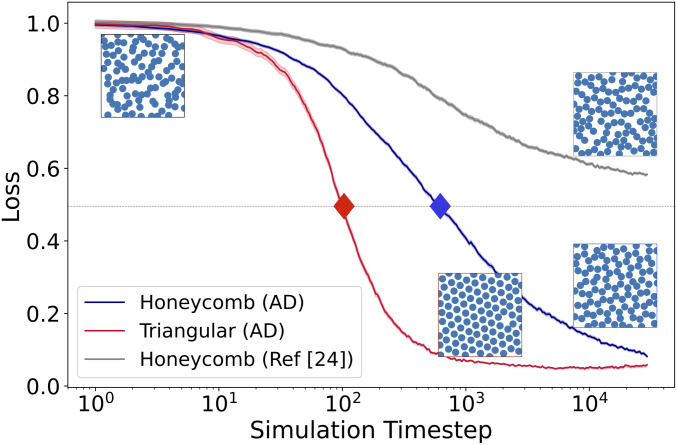
We consider a system of particles that interact via Eq. 1 and evolve under overdamped Langevin dynamics at constant temperature (SI Appendix). The blue curve in Fig. 1 shows the assembly dynamics for a specific set of parameters. Specifically, it shows a “honeycomb loss function,” , that measures the onset of crystallization by identifying the most “honeycomb-like” region, which is a leading indicator of bulk crystallization (SI Appendix). for a randomly arranged system and decreases to for a perfect honeycomb lattice. Going forward, we will define the crystallization rate , where is the time at which drops below 0.5 (indicated by the blue diamond in Fig. 1).
Fig. 1.
Assembly process for honeycomb and triangular lattices. Two different loss functions are pictured: a honeycomb loss and a triangular loss. The honeycomb loss is shown in blue for the parameters found using AD and in gray for the parameters found by Rechtsman et al. (24), whereas the triangular loss is shown in red. The two corresponding potentials are shown in SI Appendix. Each curve is averaged over 200 independent simulations, while the triangular lattice simulations are performed under a higher density than the honeycomb lattice simulations. The three images on the right-hand side are representative examples of the assembled lattice structures. The bottom two images use the same set of parameters as found using AD but have different volume fractions. The image in the upper left shows a sample random initial configuration. In order to extract assembly rates, we note the time at which the lattices are half-assembled, demarcated with a diamond.
The parameters in Fig. 1 were not chosen randomly but are the results of an initial optimization procedure. The starting parameter values input into the optimization procedure match the starting parameters of Rechtsman et al. (23, 24) and do not yield a honeycomb lattice structure on the timescale we consider. To perform the optimization, as explained in SI Appendix, we use AD to calculate the gradient of after 3,300 simulation time steps. With the gradient in hand, we iteratively minimize using a standard optimization procedure. Although not targeting a dynamical rate, these results are our first example of AD-based optimization over an MD simulation. Note that this is slightly different than the aim of Rechtsman et al. (23, 24), who were focused on the zero-temperature ground state, and not surprisingly, their results (gray curve in Fig. 1) are not optimal for finite time, finite temperature assembly.
While the system forms a honeycomb lattice at low-volume fractions, the same system with the same interaction parameters will assemble into a triangular lattice at higher-volume fractions. The “triangular loss function,” , shown in red in Fig. 1 can similarly be used to define a second crystallization rate . These rates are measured relative to intrinsic timescales that are nontrivially coupled to the potential. To regularize the intrinsic timescale, we seek to control relative to .
We use AD over simulations of the assembly process to optimize for our desired assembly dynamics. To understand how we perform this optimization, consider the function
| [2] |
which runs an MD simulation for simulation steps at density , starting from an initial set of positions , and with interactions given by Eq. 1 with parameters . The function returns the final set of positions after simulation time steps. Using this notation, Fig. 1 shows in blue and in red, where are functions that return the respective loss function for a set of positions over time.
The calculation of [or ] is analogous to a simple feed-forward neural network with hidden layers corresponding to each time step and where is applied to the last hidden layer to obtain the output. However, rather than using a set of variable weights and biases to move from one layer to the next, we use the discretized equations of motion to integrate the dynamics. Furthermore, the variables that we train over, , are physical parameters (i.e., that define the interaction potential) rather than the millions of weights and biases that typically comprise a neural network. By using AD to propagate the gradient of, for example, through each simulation step to obtain , we are able to train a stochastic MD simulation in a way similar to standard neural networks. Importantly, however, this is a data-free approach with “baked-in physics” where results are not only interpretable but correspond to physical parameters.
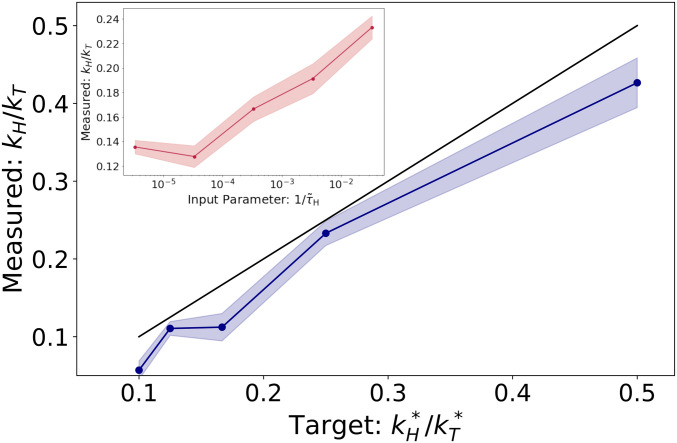
We now seek to find parameters, , such that the rate of assembly of the honeycomb lattice at density is and the rate of assembly of the hexagonal lattice at density is . This is equivalent to minimizing the squared loss, . The gradient , which involves differentiating over two ensembles of MD simulations, is used in conjunction with the RMSProp (25) stochastic optimization algorithm to minimize . Fig. 2 shows the results of this procedure, where we have fixed and varied . While the ratio is not identical to the target ratio, we have obtained nontrivial control over the rates using only four parameters.
Fig. 2.
Ratio of assembly rates as a function of target ratio. Using forward-mode AD, we obtain nontrivial control over assembly rates (black line indicates perfect agreement). Inset shows the results using backward-mode AD (SI Appendix). The backward-mode results are achieved by adjusting a tuning parameter . By changing , we obtain indirect control over the assembly rates by differentiating over only the final 300 simulation steps. Although less precise, this approach is more scalable to systems with many parameters.
These results were generated using “forward-mode” AD, in which memory usage is independent of the length of the simulation but computation time scales with the number of parameters. Forward-mode AD quickly becomes extremely time intensive for more complex systems. A more scalable approach is to use “reverse-mode” AD, where the computation time scales favorably with the number of parameters. In the reverse-mode formulation, however, the entire simulation trajectory must be stored in memory, which severely limits the size and length of the simulation. While techniques such as gradient rematerialization (26) can be used to mitigate this, we have developed an alternative strategy (SI Appendix) where only the last 300 time steps are differentiated over (Fig. 2, Inset). This method provides a more robust solution for large-scale optimization and is similar in spirit to truncated backpropagation used in language modeling (27) and metalearning (28).
Tuning Transition Rates in Colloidal Clusters
We now turn to another ubiquitous dynamical feature in physical and biological systems. Spontaneous transitions between distinct structural configurations are crucially important in many natural processes from protein folding to allosteric regulation and transmembrane transport, and the rates of these transitions are critical for their respective function. While the prediction of transition rates from energy landscapes is well studied (29, 30), there have been few attempts to control transition rates. This is largely because a general understanding of how changes to interactions affect emergent rates is lacking. Such an understanding, as well as the inverse problem of computing energy landscapes for a specific rate, is essential both for understanding biophysical functionality and for exploring feature space in physical systems.
In this section, we focus on a simple system that exhibits such transitions and can be realized experimentally. Clusters of micrometer-scale colloidal particles are ideal model materials both theoretically and in the laboratory. Furthermore, advances in DNA nanotechnology (31–33) have enabled precise control over binding energies between specified particles by coating the colloids with specific DNA strands. As demonstrated by Hormoz and Brenner (34) and Zeravcic et al. (35) and confirmed experimentally by Collins (36), such control over the binding energies allows for high-yield assembly of specific clusters under thermal noise. The assembly of one stable cluster over the others is obtained by choosing the binding energies between particle pairs so that the target structure is the ground state. While there is significant interest in avoiding kinetic traps in order to maximize yield (37), there have been few attempts to control persistent kinetic features of these systems.
We aim to control the rate of transitioning between distinct states. We do this in two ways: first, by simultaneously tuning the energy of the connecting saddle point and the state energies themselves and second, by directly tuning the Kramers approximation for the transition rates, which also takes the curvature of the energy landscape into account. We then consider the question of how many different kinetic features can be tuned simultaneously. To address this, we develop a constraint-based theory analogous to rigidity percolation that predicts when simultaneous control is possible and reveals insight into the nature of the design landscape.
For concreteness going forward, we consider clusters of spheres that interact via a short-ranged Morse potential with binding energy and with dynamics given by the overdamped Langevin equation with friction coefficient (SI Appendix). For positive , Arkus et al. (38) identified all possible stable states up to permutations, each with 15 stabilizing contacts and no internal floppy modes. From these, we pick states that are separated by only a single energy barrier and use the different as adjustable parameters to control the transition kinetics.
The transition rate from state to state is
| [3] |
where is the energy barrier, and with as the Boltzmann constant and as the temperature. is a nontrivial prefactor that we can approximate using Kramers theory (29, 30):
| [4] |
where and are the frequencies of the unstable and stable vibrational modes, respectively, at the saddle point and are the frequencies at state . We will demonstrate control over the transition kinetics in two ways: 1) by controlling the forward and backward energy barriers and and 2) by controlling directly the forward and backward transition rates and using the Kramers approximation.
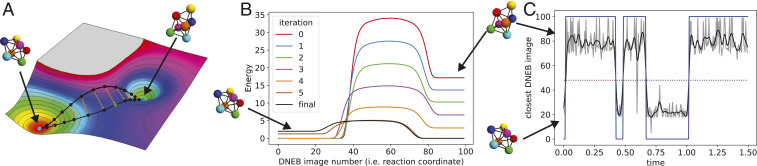
In order to proceed, we first have to find the transition state separating states and . This is done using the doubly nudged elastic band (DNEB) method (39), which is illustrated in Fig. 3A and described in SI Appendix. The transition state, along with the initial and final states, allows us to calculate the energy barriers as well as the vibrational frequencies necessary for Eq. 4.
Fig. 3.
(A) Illustration of the DNEB method (39) for finding the transition state between two local energy minima, which in our case, corresponds to metastable seven-particle clusters. Given such an energy landscape, we construct a series of images that span the two minima and are connected by high-dimensional springs. Keeping the two end points fixed to the minima, the energy of the ensemble is minimized collectively. The resulting images give the steepest descent path from one minimum to the other, traversing the saddle point. Thus, the image with the largest energy approximates the saddle point, or transition state, and we can use the image number as a one-dimensional representation of the steepest descent path, or reaction coordinate. However, note that the spacing between images is not imposed, and so, the image number is not a direct measure of distance. SI Appendix has more details. (B) Energy (in ) along the steepest descent path after successive iterations of the optimization algorithm. For clarity, the minimum energy along the path is subtracted. Note that the regions of constant energy at the beginning and end of the path correspond to global rotations of the cluster. (C) Verification of the transition rates via MD simulation. Periodic snapshots from MD simulations are mapped to the steepest descent path found through the DNEB calculation (gray). Noise is reduced using a Butterworth low-pass filter (black) and then binarized (blue). The dashed line represents the threshold for binarizing the signal and corresponds to the image with the highest energy (i.e., ). Transition rates are calculated from the dwell times of the binarized signal.
With this in hand, we next compute a loss function, . When targeting the energy barriers, we use
| [5] |
where and are the desired energy barriers. When targeting the transition rates directly, we use
| [6] |
where and are the Kramers rates and and are the targets. Finally, we optimize using reverse-mode AD to calculate the 21 derivatives , where are the positions of the particles in the respective states. This gradient is fed into a standard optimization algorithm [RMSProp (25)] to minimize the loss, and is recalculated only as necessary (in practice, every 50 optimization steps [SI Appendix ], which we collectively refer to as a single “iteration”). The entire process (18 iterations) takes roughly 3 minutes on a Tesla P100 GPU.
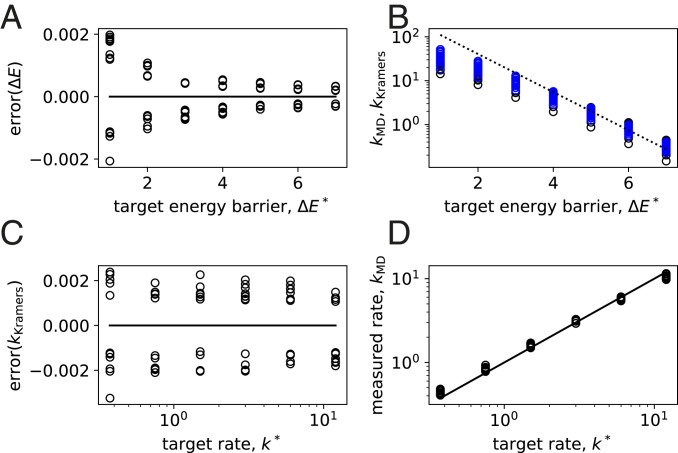
As a first example, we use Eq. 5 to target energy barriers of and between two of the stable particle clusters. Fig. 3B shows the energy along the reaction coordinate (i.e., the steepest descent path that connects the two metastable states via the transition state), after various iterations of the above procedure. The final energy differences of and are both within of their target and can be further refined by continuing the optimization procedure. Fig. 4A shows the results of 49 distinct target combinations and demonstrates that similar accuracy can be obtained over a wide range of energies.
Fig. 4.
Training energy barriers and transition rates. (A) After 18 iterations of our procedure, the energy barrier is trained to within of the target barrier . Shown is the error [] as a function of the target. (B) The transition rates measured via MD simulation (; black data) are not exactly proportional to (the dashed line has a slope of ), indicating that the prefactor in Eq. 3 is not constant. However, this prefactor is captured reasonably well by the Kramers approximation (; blue data). (C) After 18 iterations of training on the Kramers rate , we obtain an accuracy within of the target rate . (D) The rates measured via MD simulation agree very well with the target rate (the solid line corresponds to ). Thus, we are able to accurately and quantitatively design the transition kinetics of the seven-particle clusters we consider.
The connection between the energy barriers and the resulting transition rates is predicted using the Kramers approximation, which is validated via MD simulations where we extract the rates directly (Fig. 3C and SI Appendix). Fig. 4B shows both rates ( and ) as a function of the target energy barrier. While the validation agrees well with the Kramers prediction, the prefactor is not constant, underscoring the difficulty of targeting energy barriers as a proxy for transition rates without a quantitative model for .
An alternative is to target directly, which we do using the rate-based loss function (Eq. 6). As shown in Fig. 4C, we obtain a typical error of after the optimization. As before, , and Fig. 4D shows that the full dynamics of the MD simulations agree extremely well with the target dynamics. Thus, we have succeeded in quantitatively designing the transition kinetics of colloidal-like clusters and can do so accurately over a wide range of rates. By optimizing over experimentally relevant parameters, these results give a direct prediction that can be tested in clusters of DNA-coated colloids.
Simultaneous Training of Multiple Transitions.
In the above results, transition kinetics are designed while simultaneously imposing specific structural constraints. While most self-assembly approaches focus on obtaining a specific structure, we design for both structure and kinetics simultaneously. Indeed, we have designed for two kinetic features, namely the forward energy barrier/rate and the backward energy barrier/rate. Is it possible to take this further and simultaneously specify many kinetic features? Since particles are distinguishable, permutations represent distinct states, and thus, there are many thousands of possible transitions in our seven-particle clusters. What determines which subsets of transitions can be simultaneously and independently controlled?
To address this question, we develop an analogy to network rigidity. Each kinetic feature we would like to impose appears as a constraint in the loss function. If we want to impose kinetic features, then we attempt to minimize a loss function analogous to Eq. 5 with terms of the form .* This constraint satisfaction problem has a strong analogy to network rigidity (40), where physical springs constrain the relative positions of nodes through an interaction proportional to , with as the distance between particles and as the rest length of the spring. When attempting to place a spring, we can look to the eigenvalues of the Hessian matrix of the total energy to determine whether the new constraint can be satisfied. Each “zero mode” (eigenvector of the Hessian with zero eigenvalue) represents a degree of freedom that can be adjusted slightly while maintaining all of the constraints. The relevant question is whether the new constraint can be satisfied with only these free degrees of freedom. If this is the case, then imposing the constraint causes the system to lose a zero mode. However, if the additional constraint cannot be satisfied simultaneously with the other constraints, then the number of zero modes remains the same, and the constraint is called “redundant.” Thus, if the number of nonzero modes equals the number of constraints, than all of the constraints can be satisfied simultaneously.
We employ this same approach in our system to determine if a set of constraints (desired kinetic features) can be simultaneously satisfied by a given set of variables (the 21 binding energies ). To proceed with a given set of desired kinetic features, we start with a random initial set of binding energies and write down a temporary loss function where the targets are equal to the current energy barriers. This is analogous to placing a spring between two nodes such that the spring’s rest length is equal to the separation between the nodes. It also guarantees that the Hessian matrix is positive semidefinite and that the zero modes correspond to unconstrained degrees of freedom. We employ AD to calculate the Hessian matrix, which we then diagonalize and count the number of zero and nonzero modes. If the number of nonzero modes equals the number of constraints, then we predict that the desired set of kinetic features can be simultaneously obtained.
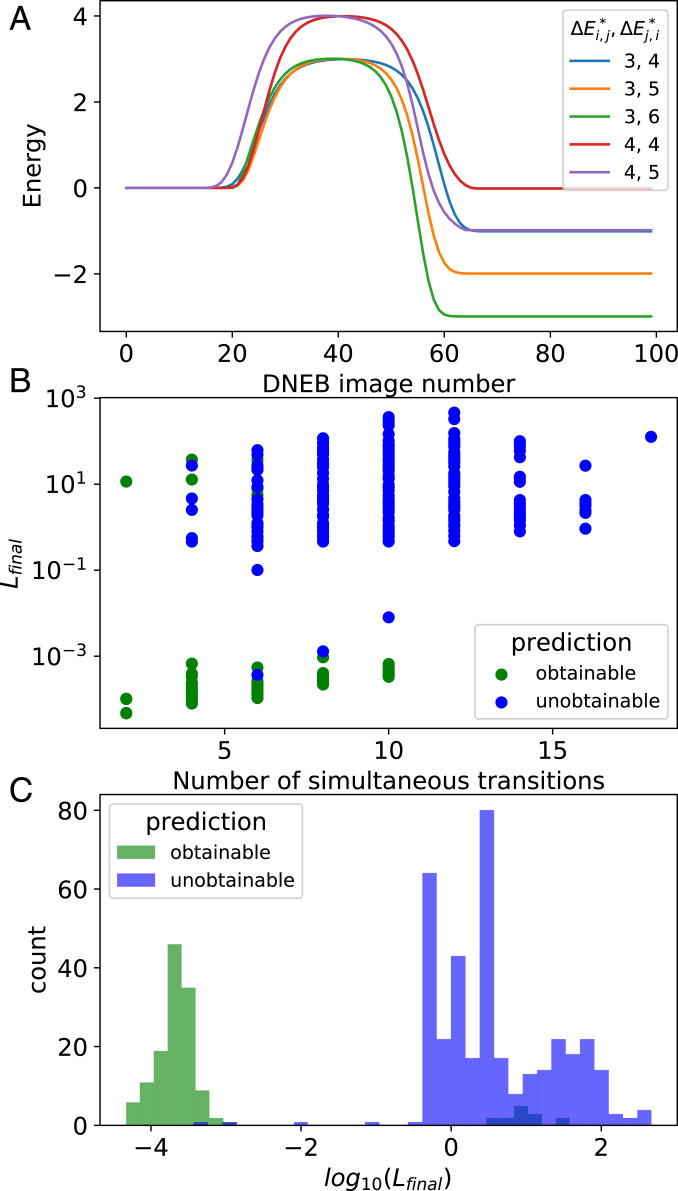
To test this prediction, we have picked an initial structure and nine adjacent structures, with the intention to simultaneously specify the energy barriers of various subsets of the nine forward and nine backward transitions. As a first example, we pick a set of 10 transitions (5 forward and 5 backward) where the Hessian has 10 nonzero modes, meaning our theory predicts that our optimization should be successful. This is confirmed in Fig. 5A, which shows the energy along the five transition pathways after simultaneously optimizing for all 10 barriers. The legend shows the target energy barriers, and , for both the forward and backward transitions, respectively. Each observed barrier is within of the respective target and becomes more accurate with additional training using smaller training rates.
Fig. 5.
(A) Energy (in ) along the steepest descent paths connecting a single starting structure with five adjacent structures, obtained through the DNEB method (Fig. 3 and SI Appendix). These results are after the simultaneous optimization of all 10 energy barriers (target energy barriers [in ] are shown in the legend). The observed energy barriers are within of their targets. (B) The loss function after attempting to simultaneously control the dynamics of multiple transitions, as a function of the number of transitions. Due to the form of the loss function (Eq. 5), simultaneous control is successful when . In practice, when we obtain , this can be further reduced by additional optimization with smaller learning rates, indicating that the transition dynamics can indeed be controlled to a desired precision. The data are colored according to the Hessian-based prediction discussed in the text: green (blue) data correspond to cases where we predicted that simultaneous control could be (could not be) obtained. (C) Histogram of for all data shown in B.
This result is generalized in Fig. 5 Band C, where we show the loss function after optimization for all 511 subsets of the nine transition pathways. Cases where we predict that the kinetic features can be simultaneously obtained (i.e., that ) are shown in green, while cases where we predict that the kinetic features cannot be simultaneously obtained are shown in blue. While our predictions are not perfect, we find that they are correct roughly of the time.
A key difference between our system and network rigidity is that we are trying to predict a highly nonlocal feature of the function space, namely whether or not a loss function can be minimized to zero. Conversely, rigidity in elastic networks is a local property of the energy landscape. We extrapolate from the local curvature to predict highly nonlocal behavior, without proper justification. The fact that this nevertheless works quite well indicates that there is indeed some persistent internal structure in the function space we are considering, despite its considerable complexity. We leave a more in-depth examination of this structure to future studies.
Discussion
Rather than being limited to structural motifs, our results expand the design space of colloids with specific interactions to include complex kinetics. Understanding the connection between interactions and emergent dynamical properties is hugely important in biological physics, materials science, and nonequilibrium statistical mechanics. Moreover, achieving in synthetic materials the same level of complexity and functionality as found in biology requires detailed control over kinetic features.
We demonstrate quantitative control over kinetic features in two self-assembly systems. In the classic problem of assembling a honeycomb lattice using monotonic, spherically symmetric particles, we achieve nontrivial control over lattice assembly rates. Understanding and controlling crystallization kinetics is critical to the design of many real materials and is intimately related to the statistics of defects. Furthermore, since a honeycomb crystal is a diatomic lattice where neighboring particles have different orientational order, assembling a honeycomb lattice out of identical particles is a notoriously difficult problem. Our ability not only to assemble such a lattice but to control its assembly rate relative to a triangular lattice reveals an essential connection between assembly dynamics and particle interactions that we are able to exploit for kinetic design.
Second, by considering small clusters of colloidal-like particles with specific interactions, we discover that transition kinetics are far more designable than was previously thought. Since spherically symmetric particles provide a foundational understanding not only in self-assembly but in fields throughout physics, our results suggest the same potential for designing transition dynamics in numerous other systems.
Moreover, the methodology we present is applicable beyond the study of colloidal kinetics. At its core, this method directly extracts the effect of experimental or model parameters on an emergent property, such as the kinetic rates that we focus on. It does so by measuring the derivative of the emergent property with respect to the underlying parameters. Unlike finite difference approaches to taking derivatives, these calculations are both efficient and exact, enabling, for example, the Hessian calculation that is essential to our analysis in Simultaneous Training of Multiple Transitions. We have shown that despite the stochasticity inherent to the thermal systems we consider, these derivatives are predictive. In other words, the validity of the linear regime accessed by the gradient calculation is not overwhelmed by stochastic noise. Thus, we can cut through the highly complex dependence of emergent dynamical features on model parameters (such as interaction energies, size distributions, temperature and pressure schedules, or even particle shapes) and use this dependence to control behavior.
Thus, we have shown that gradient computations over statistical physics calculations using AD are possible, efficient, and sufficiently well behaved for optimization of kinetic features. This approach is complimentary to other inverse approaches, such as “on-the-fly” optimization methods (41) where iterative simulation results are used to update parameter values at each step in order to suppress competitor structures and promote the desired structure. However, unlike for structural features, it is difficult to intuit the connection between interactions and kinetics. By revealing this connection, the differentiable statistical physics models presented here provide a framework for understanding emergent behavior. Indeed, our work merely scratches the surface of what can be achieved using the principles of kinetic design. This approach scales favorably with the number of input parameters, enabling the design of increasingly complex phenomena. We envision engineering materials with emergent properties, exploring the vast search space of biomimetic function and manipulating entire phase diagrams.
Materials and Methods
MD simulations and AD calculations are performed using a fully differentiable MD package, called JAX MD (22), that has recently been developed by two of us and has hardware acceleration and ensemble vectorization built in. SI Appendix has more information on our methods and procedures.
Data Availability.
All study data are included in the article and/or SI Appendix.
Supplementary Material
Acknowledgments
We thank Agnese Curatolo, Megan Engel, Ofer Kimchi, Seong Ho Pahng, and Roy Frostig for helpful discussions. This material is based on work supported by NSF Graduate Research Fellowship Grant DGE1745303. This research was funded by NSF Grant DMS-1715477, Materials Research Science and Engineering Centers Grant DMR-1420570, and Office of Naval Research Grant N00014-17-1-3029. M.P.B. is an investigator of the Simons Foundation.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
*Or analogous to Eq. 6 with terms of the form . For simplicity going forward, we will focus on imposing kinetic features via energy barriers.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2024083118/-/DCSupplemental.
References
- 1.Perlmutter J. D., Hagan M. F., Mechanisms of virus assembly. Annu. Rev. Phys. Chem. 66, 217–239 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Alexander L. M., Goldman D. H., Wee L. M., Bustamante C., Non-equilibrium dynamics of a nascent polypeptide during translation suppress its misfolding. Nat. Commun. 10, 2709 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Tan P., Xu N., Xu L., Visualizing kinetic pathways of homogeneous nucleation in colloidal crystallization. Nat. Phys. 10, 73–79 (2014). [Google Scholar]
- 4.Dunn K. E., et al. , Guiding the folding pathway of DNA origami. Nature 525, 82–86 (2015). [DOI] [PubMed] [Google Scholar]
- 5.Whitesides G. M., Mathias J. P., Seto C. T., Molecular self-assembly and nanochemistry: A chemical strategy for the synthesis of nanostructures. Science 254, 1312–1319 (1991). [DOI] [PubMed] [Google Scholar]
- 6.Douglas T., Young M., Host–guest encapsulation of materials by assembled virus protein cages. Nature 393, 152–155 (1998). [Google Scholar]
- 7.Stupp S. I., et al. , (1997) Supramolecular materials: Self-organized nanostructures. Science 276, 384–389. [DOI] [PubMed] [Google Scholar]
- 8.Lohmeijer B. G., Schubert U. S., Supramolecular engineering with macromolecules: An alternative concept for block copolymers. Angew. Chem. Int. Ed. 41, 3825–3829 (2002). [DOI] [PubMed] [Google Scholar]
- 9.Hartgerink J. D., Granja J. R., Milligan R. A., Ghadiri M. R., Self-assembling peptide nanotubes. J. Am. Chem. Soc. 118, 43–50 (1996). [Google Scholar]
- 10.Bryson A. E., Denham W. F., A steepest-ascent method for solving optimum programming problems. J. Appl. Mech. 29, 247–257 (1962). [Google Scholar]
- 11.Bryson A., Applied Optimal Control: Optimization, Estimation and Control (Taylor & Francis, 1975). [Google Scholar]
- 12.Linnainmaa S., Taylor expansion of the accumulated rounding error. BIT Numer. Math. 16, 146–160 (1976). [Google Scholar]
- 13.Rumelhart D. E., Hinton G. E., Williams R. J., Learning representations by back-propagating errors. Nature 323, 533–536 (1986). [Google Scholar]
- 14.Baydin A. G., Pearlmutter B. A., Radul A. A., Siskind J. M., Automatic differentiation in machine learning: A survey. J. Mach. Learn. Res. 18, 5595–5637 (2017). [Google Scholar]
- 15.Paszke A., et al. , “Pytorch: An imperative style, high-performance deep learning library” in Advances in Neural Information Processing Systems 32, Wallach H., et al., Eds. (Curran Associates, Inc., 2019), pp. 8024–8035. [Google Scholar]
- 16.Abadi M., et al. , TensorFlow: Large-scale machine learning on heterogeneous systems, Version 2. https://www.tensorflow.org/. Accessed 1 September 2020.
- 17.Bradbury J., et al. , JAX: Composable transformations of Python+NumPy programs, Version 0.2.5 (2018). https://github.com/google/jax#citing-jax. Accessed 22 February 2021.
- 18.Minkov M., et al. , Inverse design of photonic crystals through automatic differentiation. ACS Photonics 7, 1729–1741(2020). [Google Scholar]
- 19.Bar-Sinai Y., Hoyer S., Hickey J., Brenner M. P., Learning data-driven discretizations for partial differential equations. Proc. Natl. Acad. Sci. U.S.A. 116, 15344–15349 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.McCloskey K., et al. , Machine learning on DNA-encoded libraries: A new paradigm for hit-finding. arXiv:2002.02530 (31 January 2020). [DOI] [PubMed]
- 21.Senior A. W., et al. , Improved protein structure prediction using potentials from deep learning. Nature 577, 706–710 (2020). [DOI] [PubMed] [Google Scholar]
- 22.Schoenholz S. S., Cubuk E. D., JAX, M.D.: End-to-end differentiable, hardware accelerated, molecular dynamics in pure python. arXiv:1912.04232v1 (9 December 2019).
- 23.Rechtsman M., Stillinger F., Torquato S., Designed interaction potentials via inverse methods for self-assembly. Phys. Rev. 73, 011406 (2006). [DOI] [PubMed] [Google Scholar]
- 24.Rechtsman M. C., Stillinger F. H., Torquato S., Optimized interactions for targeted self-assembly: Application to a honeycomb lattice. Phys. Rev. Lett. 95, 228301 (2005). [DOI] [PubMed] [Google Scholar]
- 25.Tieleman T., Hinton G., Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude. COURSERA: Neural Networks Mach. Learn. 4, 26–31 (2012). [Google Scholar]
- 26.Griewank A., Walther A., Algorithm 799: Revolve: An implementation of checkpointing for the reverse or adjoint mode of computational differentiation. ACM Trans. Math Software 26, 19–45 (2000). [Google Scholar]
- 27.Mikolov T., Karafiát M., Burget L., Černockáżş J., Khudanpur S., “Recurrent neural network based language model” in Eleventh Annual Conference of the International Speech Communication Association (ISCA [International Speech Communication Association], 2010), pp. 1045–1048. [Google Scholar]
- 28.Al-Shedivat M., et al. , Continuous adaptation via meta-learning in nonstationary and competitive environments. arXiv:1710.03641v1 (10 October 2017).
- 29.Kramers H. A., Brownian motion in a field of force and the diffusion model of chemical reactions. Physica 7, 284–304 (1940). [Google Scholar]
- 30.Hanggi P., Talkner P., Borkovec M., Reaction-rate theory: Fifty years after Kramers. Rev. Mod. Phys. 62, 251–341 (1990). [Google Scholar]
- 31.Mirkin C. A., Letsinger R. L., Mucic R. C., Storhoff J. J., A DNA-based method for rationally assembling nanoparticles into macroscopic materials. Nature 382, 607–609 (1996). [DOI] [PubMed] [Google Scholar]
- 32.Valignat M. P., Theodoly O., Crocker J. C., Russel W. B., Chaikin P. M., Reversible self-assembly and directed assembly of DNA-linked micrometer-sized colloids. Proc. Natl. Acad. Sci. U.S.A. 102, 4225–4229 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Biancaniello P. L., Kim A. J., Crocker J. C., Colloidal interactions and self-assembly using DNA hybridization. Phys. Rev. Lett. 94, 058302 (2005). [DOI] [PubMed] [Google Scholar]
- 34.Hormoz S., Brenner M. P., Design principles for self-assembly with short-range interactions. Proc. Natl. Acad. Sci. U.S.A. 108, 5193–5198 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zeravcic Z., Manoharan V. N., Brenner M. P., Size limits of self-assembled colloidal structures made using specific interactions. Proc. Natl. Acad. Sci. U.S.A. 111, 15918–15923 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Collins J., “Self-assembly of colloidal spheres with specific interactions,” PhD thesis, Harvard University, Cambridge, MA (2014). [Google Scholar]
- 37.Dunn K. E., et al. , Guiding the folding pathway of DNA origami. Nature 525, 82–86 (2015). [DOI] [PubMed] [Google Scholar]
- 38.Arkus N., Manoharan V. N., Brenner M. P., Deriving finite sphere packings. SIAM J. Discrete Math. 25, 1860–1901 (2011). [Google Scholar]
- 39.Trygubenko S. A., Wales D. J., A doubly nudged elastic band method for finding transition states. J. Chem. Phys. 120, 2082–2094 (2004). [DOI] [PubMed] [Google Scholar]
- 40.Jacobs D. J., Thorpe M. F., Generic rigidity percolation: The pebble game. Phys. Rev. Lett. 75, 4051–4054 (1995). [DOI] [PubMed] [Google Scholar]
- 41.Sherman Z. M., Howard M. P., Lindquist B. A., Jadrich R. B., Truskett T. M., Inverse methods for design of soft materials. J. Chem. Phys. 152, 140902 (2020). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in the article and/or SI Appendix.