Computational studies of anaplastic lymphoma kinase mutations reveal common mechanisms of oncogenic activation

Significance

High-risk tumors are genomically heterogeneous, harboring gene amplifications and mutations. The activation status of mutated proteins in cancer can profoundly impact disease progression, patient response, and drug sensitivity. Yet, outside of a few hotspot mutations, functional studies of clinically observed mutations are not commonly pursued. We report a combined experimental profiling and computational analysis of the effects of clinically observed and “test” mutations in the kinase domain of anaplastic lymphoma kinase (ALK), a known oncogenic driver in pediatric neuroblastoma. We find that the activation status of the mutated protein is a good indicator of the transforming ability in NIH 3T3 cells. We also report biophysical as well as data-driven models with predictive power to profile these mutant kinases in silico.

Abstract

Kinases play important roles in diverse cellular processes, including signaling, differentiation, proliferation, and metabolism. They are frequently mutated in cancer and are the targets of a large number of specific inhibitors. Surveys of cancer genome atlases reveal that kinase domains, which consist of 300 amino acids, can harbor numerous (150 to 200) single-point mutations across different patients in the same disease. This preponderance of mutations—some activating, some silent—in a known target protein make clinical decisions for enrolling patients in drug trials challenging since the relevance of the target and its drug sensitivity often depend on the mutational status in a given patient. We show through computational studies using molecular dynamics (MD) as well as enhanced sampling simulations that the experimentally determined activation status of a mutated kinase can be predicted effectively by identifying a hydrogen bonding fingerprint in the activation loop and the αC-helix regions, despite the fact that mutations in cancer patients occur throughout the kinase domain. In our study, we find that the predictive power of MD is superior to a purely data-driven machine learning model involving biochemical features that we implemented, even though MD utilized far fewer features (in fact, just one) in an unsupervised setting. Moreover, the MD results provide key insights into convergent mechanisms of activation, primarily involving differential stabilization of a hydrogen bond network that engages residues of the activation loop and αC-helix in the active-like conformation (in >70% of the mutations studied, regardless of the location of the mutation).

Neuroblastoma (NB) is the third most common cancer in children. Most NBs begin in sympathetic nerve ganglia in the abdomen—about half in the adrenal gland—and children with high-risk NB have a 5-y survival of only around 50%. These high-risk tumors are genomically and genetically heterogeneous, presenting with gene amplifications (mainly of the MYCN gene) and in some cases mutations in other genes—notably ALK (anaplastic lymphoma kinase), which encodes a receptor tyrosine kinase (RTK) (1, 2). Although germline ALK mutations in familial NB were reported first, somatic mutations were subsequently identified in patients, and the majority of all mutations occur in the cytoplasmic tyrosine kinase domain (TKD) of ALK (3). This discovery was important because aberrant kinase activity of the ALK TKD can be inhibited with existing drugs (3–6). Indeed, therapeutic targeting of ALK in other tumors such as non-small cell lung cancer (NSCLC), in which it is activated in an oncogenic fusion protein (7), has been successful. However, as shown for EGFR in NSCLC (8–10) and for ALK in earlier studies in NB, TKD mutations vary in the degree to which they activate the kinase—leading to oncogenesis—and in their effects on sensitivity to inhibition with small molecule inhibitors (5, 11, 12).

We previously identified ALK mutations or amplifications in 14% of 1,600 patients with NB (11). Three hot spots in the ALK TKD (positions 1174, 1245, and 1275) account for 85% of kinase mutations, although mutations at numerous other sites have also been reported (10, 11, 13). These include clearly activating mutations, silent mutations (i.e., those shown not to be activating), and mutations that confer resistance to known ALK kinase inhibitors.

A key challenge is to develop approaches for rapidly identifying which kinase domain mutations in such a list can be classified as cancer drivers (i.e., have an impact on cancer progression or treatment) and which are “passenger” mutations with no clinical consequence (14). Several approaches have been proposed for predicting and/or explaining the effects of mutations on kinase regulation. These include molecular dynamics (MD) simulations, structural bioinformatics methods based on evolutionary analyses, network analysis, and machine learning (ML) (15). The earliest attempts to understand how well sequence changes are tolerated were undertaken not in the context of cancer, but rather as efforts to understand evolutionary distances between sequences. These methods give probabilities of mutation based on phylogenetic trees (16) or sequence alignments (17), but were not designed to predict the effects of mutations on protein function. One of the earliest methods for predicting whether a mutation is deleterious is called Sorts Intolerant From Tolerant (SIFT), which uses sequence conservation to determine “deleteriousness” (18, 19) and remains a benchmark in the field of mutation classification. Several other algorithms have been developed that use sequence conservation or homology to predict the effects of single-nucleotide polymorphisms (SNPs) (20–24). In particular, PolyPhen-2 utilizes several sequence-based and structure-based features for the classification of driver versus passenger mutations arising from SNPs. Another approach (25) uses the mutation rate of noncoding genomic regions as a baseline and tries to identify genes in which there is a statistically significant deviation from this baseline. Several groups have also developed ML techniques to separate driver from passenger mutations. Methods used include random forest (26, 27), entropic methods (28), support vector machines (SVM) (15, 29, 30), graph/network analysis (31), and convolutional neural networks (32). A systematic assessment of the balanced accuracy of these methods is difficult to obtain as the published reports are applied across different datasets. However, a recent review of the predictive power of a subset of the methods outlined here concluded that MD-based and ML-based methods performed better in terms of balanced accuracies (15). MD methods in particular have the additional advantage over other predictive algorithms as they also provide a mechanistic (rather than only correlative) explanation for the results.

Numerous groups have used MD simulations to assess the effects of mutations. MD simulations probe motions on the order of nanoseconds to microseconds, whereas catalysis by protein kinases takes place on the scale of milliseconds to seconds (11, 33–36). Careful analysis of simulation trajectories is therefore needed to gain insight into how mutations affect activity. These analyses can generally be fit into three broad categories (37): 1) analysis of alteration in structure- or energy-based functions, 2) analysis of collective motions, and 3) computation of free energy landscapes. The first category includes methods such as analysis of hydrogen bonds and salt bridges, changes in solvent accessible surface area (SASA), or of hydration dynamics. The second category includes measurements such as root mean squared deviation (RMSD) or fluctuation and calculations based on interatomic covariance matrices such as protein structure networks or principal component analyses. The third category includes a large and growing number of methods for understanding the energetic relationship between different conformational states of a protein. These methods generally rely on some prior knowledge of different conformational states of a protein (e.g., “active” and “inactive” conformations of a kinase) and apply some energetic potential to help the system explore desired states (38–42).

To overcome the limitation of timescales accessible by MD, enhanced sampling methods that allow more rapid exploration of conformational space and determination of energy landscapes have been used on EGFR (43), ABL (44), ALK (45), B-RAF (46), CDK5 (47), insulin receptor kinase (39), c-KIT (48), HCK (49), RET and MET (44), and SRC (50, 51). Changes in hydrogen bonding networks, salt bridges, and hydrophobic interactions, which are easy to compute in MD simulations, have been used as proxies for comparing the stabilities of active and inactive conformations for a given mutated variant (11, 35). We therefore hypothesize that MD simulations can be utilized to classify activating and nonactivating mutations—based on which conformation they favor—balancing both accuracy and interpretability in computational analysis of cancer mutations.

A key limitation of most previous studies is that they have either considered conformational changes only in the wild-type protein or have assessed only a handful of mutated proteins. Where MD has been applied as a predictive tool to classify mutations (11, 15), a key limitation is that any test set of mutations derived from a cancer study is imbalanced in terms of activating mutations (which dominate) and nonactivating mutations. Although upsampling techniques (15) can partially mitigate this issue, the optimal solution is to incorporate a balance between activating and nonactivating mutations in the study design. Here, we investigate the predictive power of MD and ML methods by carefully curating a list of 42 mutations in ALK from clinical data, the Catalogue of Somatic Mutations in Cancer (COSMIC) database (13), and additional “synthetic” test nonactivating mutations that we introduced to improve database balance and/or to address specific mechanistic questions.

Results

Experimental Profiling of Kinase Mutations.

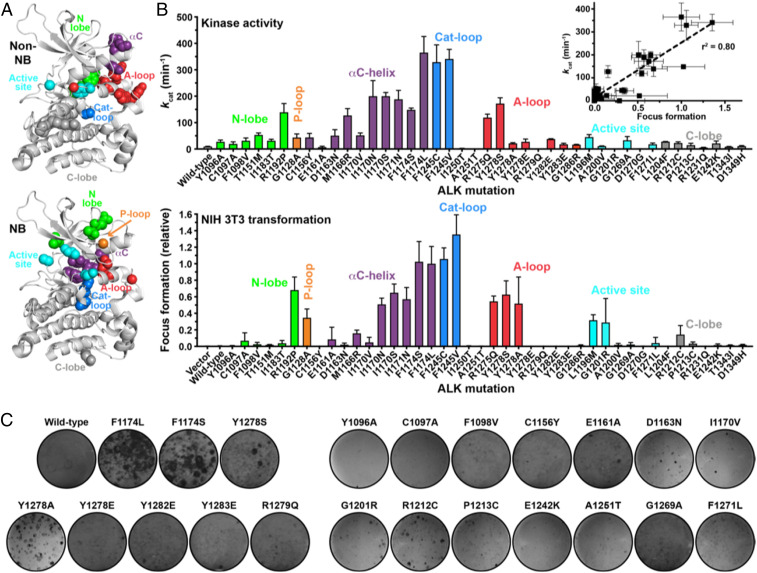
A collection of ALK variants harboring TKD mutations was characterized experimentally by measuring k_cat values for the isolated TKD in peptide phosphorylation assays (5, 11) and assessing oncogenic transformation by the intact mutated receptor in NIH 3T3 cells via focus formation assays (see SI Appendix, section 1 for a description of methods). Importantly, these experimental studies were performed with no prior knowledge of the results of the parallel computational analyses. The mutation collection studied here added 21 substitutions [plus F1174L as known positive control (11)] to the 21 NB mutations analyzed in our previous study (11). Eight of these mutations were reported in the COSMIC database (13) or The Cancer Genome Atlas (TCGA) in NB (F1174S, Y1278S), melanoma (G1201R, E1242K), endometrioid carcinoma (R1212C), gastrointestinal carcinoma (A1251T), or lung cancer (C1156Y, G1269A), with those in lung cancer associated with resistance of ALK fusions to kinase inhibitors (52). Six additional mutations (C1097A, Y1278A/E, R1279Q, Y1282E, and Y1283E) were included to test the ability of our computational approach to recapitulate published studies (53) of how alterations in the ALK TKD YxxxYY motif (in its activation loop) affect activity. It is known that mutating the first tyrosine to serine (in Y1278S) is activating (11), but the Y1278A mutation (or Y1282/Y1283 mutations) is not (53). This presents a good test for our computational approach. The remaining seven mutations studied were selected based on modeling results blind to experiment. Together with our previous studies of NB mutations (11), these data yield a list of 42 well-characterized ALK mutations available for computational analysis. Both k_cat and transformation ability of all 42 variants are presented in Fig. 1, combining the results with our earlier data on NB variants (11).

Fig. 1.

Catalytic activities (k_cat) and transforming potentials of ALK TKD from the collections described in the text. (A) Individual ALK TKD variants are marked in the ALK TKD crystal structure from the PDB (3LCT), with NB mutations in the lower and other ALK mutations in the upper panel. Important structural regions in the TKD are colored as follows: N-lobe, green; P-loop, orange; αC-helix, purple; catalytic loop, blue; A-loop, red; active site, cyan; and C-lobe, gray. (B) Values for k_cat for nonphosphorylated ALK TKD variants with saturating Mg²⁺-ATP (and 2 mM peptide) are shown in the upper plot. Transformation potential from focus formation assays in NIH 3T3 cells is given in the lower plot, relative to the activated F1174L variant (arbitrarily set at a value of 1.0). (C) Representative focus assay plates for the mutations studied here, stained with crystal violet, are shown.

As shown in Fig. 1, the resulting experimental dataset is more balanced with respect to those that are and are not activating, respectively. There is a good correlation between the catalytic activity (k_cat) of the purified (nonphosphorylated) ALK TKD and the ability of the intact ALK variant to transform NIH 3T3 cells (insert in Fig. 1B). Consistent with our previous studies (11), an increase in the k_cat value of >4.5-fold appears to be sufficient for NIH 3T3 cell transformation in most cases—with one exception being Y1278A, which was less active in kinase assays than expected based on NIH 3T3 transformation studies. Similarly, analysis of 22 mutations in BRAF, frequently mutated in melanoma and colorectal cancer, has shown that variants with an elevation in k_cat of approximately three- to fivefold could transform cells in focus formation assays (33, 54, 55). Studies of ErbB2 have also shown that an increase in k_cat of approximately fourfold in assays of the monomeric TKD correlates with transformation in colony formation assays (34, 56). An increase in k_cat by three- to fivefold therefore appears to be a common threshold for cell transformation by these oncogenically activated kinases.

There were a few ALK variants whose catalytic activity could not be analyzed biochemically in kinase assays due to experimental difficulty (or intrinsic nature of the protein). R1279Q and G1201R (as previously reported in ref. 53) did not yield high-quality TKD protein, possibly due to aggregation. The A1251T variant simply showed no activity. G1201R nonetheless exhibited some transforming ability in the context of intact ALK in NIH 3T3 cells, possibly suggesting constitutive signaling from misfolded protein retained in the endoplasmic reticulum as with some other RTK variants (57, 58).

The data in Fig. 1 reveal cases where different substitutions at the same position have different consequences, which provides a good test for our computational approach. For example, the more conservative I1170V substitution appears not to be very activating or transforming, whereas substituting I1170 with N or S activates the kinase >20-fold and promotes strong transformation—consistent with the appearance of these mutations in NB patients (11, 59). In addition, different substitutions of the first activation loop tyrosine, Y1278, have different consequences. Only the Y1278S mutation has been reported in NB (11, 53) with six instances in the COSMIC database (13). Consistent with recent work from Hallberg and colleagues (53), we find that a Y1278A mutation is much less activating (although we did detect NIH 3T3 cell transformation). Moreover, a Y1278E mutation failed to activate the kinase in vitro or to enhance ALK-induced NIH 3T3 cell transformation. We also mutated the other tyrosines in the ALK YxxxYY activation loop motif to glutamates (Y1282E and Y1283E). These variants showed detectably higher catalytic activity than wild-type TKD, with k_cat increasing from 9.3 min⁻¹ (for wild-type) to 37.9 min⁻¹ for Y1282E and 17.7 min⁻¹ for Y1283E, both below the ∼4.5-fold k_cat increase threshold. For comparison, k_cat for Y1278E was 27.5 min⁻¹ but 172 min⁻¹ for Y1278S.

Computational Analysis: The Wild-Type ALK TKD Conformational Change Pathway.

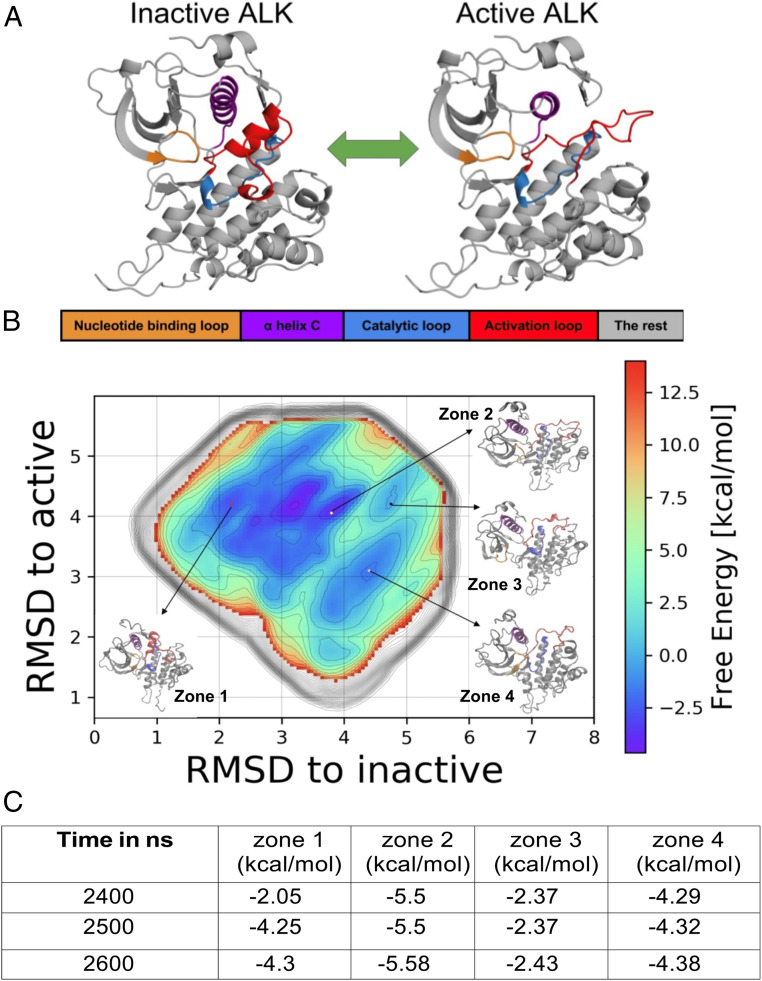
Conformational changes in kinase domains determine their activity status, through well-studied transitions (Fig. 2) between family-specific inactive conformations and common active conformations (60, 61). The ALK TKD has been observed in its inactive conformation in a series of crystal structures (62). We sought to study this conformational change in wild-type ALK TKD using metadynamics simulations (see SI Appendix, section 2 for a description of methods) to observe the complete transition between its inactive and the active conformations. Fig. 2A depicts the reference active and inactive structures of ALK that we employed for this analysis. We chose to consider intermediate structures in the inactive-to-active transition in terms of the RMSD from the reference active and inactive structures of ALK. This choice of collective variables (CVs)—“RMSD from reference active” and “RMSD from reference inactive”—leads to a vast configuration space to be sampled. This is imperative for understanding effects on global changes in the configuration of the ALK TKD, but sampling this space requires a very long biased simulation time. We used well-tempered metadynamics (63) to sample this large conformational space (SI Appendix), resulting in the converged free energy landscape depicted in Fig. 2B. We ensured that the metadynamics simulations converge by verifying that there are identifiable minima in several zones of the free energy landscape (at least four in this case, as labeled in Fig. 2B), corresponding to the various metastable states that intervene between the active-like and the inactive-like ALK TKD configurations (see Fig. 2; the convergence criteria and analyses for the four zones identified are tabulated in panel C and explained further in SI Appendix, section 2C).

Fig. 2.

(A) Snapshots of inactive (from PDB ID: 3LCS) and active configurations (modeled) of ALK. The key regions are color coded: Nucleotide binding P-loop is orange, αC-helix is purple, catalytic loop is blue, and activation loop (A-loop) is red. (B) Free energy landscape constructed from an aggregate 2.6 µs metadynamics simulation, with zones 1 through 4 labeled. (C) Convergence of free energy values F in kilo calories per mole (kcal/mol) in zones 1 through 4. The values reflect the convergence of the free energies in each of the zones to well below 0.6 kcal/mol (1 k_BT) during the course of the 2,600 ns metadynamics simulation. The detailed convergence procedure is described in SI Appendix, section 2C.

The free energy landscape obtained through metadynamics serves to represent the complete transition between the inactive (zone 1) and active states (zone 4) of ALK TKD. The zones are identified based on free energy contour in regions of the free energy landscapes which converged in the aggregate simulation of 2.6 µs. Conformations represented by zones 2 and 3 allow the transition from zone 1 to zone 4 to occur, providing a necessary pathway given that the observed minimum activation energy barrier for a direct transition from zone 1 to zone 4 is 3 kcal/mol. A complete pathway analysis can be performed by considering an ensemble of pathways computed by analyzing the kinetics of transition rates between Markov states (see for examples ref. 64).

The computed free energy difference between zones 1 and 4 is 0.08 kcal/mol. In order to follow changes in structural features of ALK TKD through the transition, we extract structures from each zone as frames, compile them as a trajectory, and then subject them to further analysis of RMSD and hydrogen bond occupancy. Using this approach, we generated 3,056 frames in zone 1, 4,618 frames in zone 2, 28,000 frames in zone 3, and 57,358 frames in zone 4.

Table 1 describes the deviation of structures in the four zones from the reference inactive and active conformations, expressed as the average (±SD) RMSD from the reference structures of the αC-helix and the activation loop. The activation loop shows the largest deviations, with zone 1 displaying a partly helical conformation that is close to the inactive reference state and zone 4 showing an extended loop conformation that is closer to the active reference state (Fig. 2A).

Table 1.

RMSD involving Cα atoms of the αC-helix and the activation loop along the transition pathway, reported as mean ± SD

RMSD (in Å)	Zone 1	Zone 2	Zone 3	Zone 4
αC-helix (ref-active)	0.84	1.28	1.19	0.87
	±0.13	±0.35	±0.41	±0.22
αC-helix (ref-inactive)	0.57	1.18	1.15	0.95
	±0.11	±0.27	±0.33	±0.18
Activation loop (ref-active)	5.76	4.8	4.39	3.29
	±0.32	±1.52	±1.6	±0.47
Activation loop (ref-inactive)	1.95	4.97	5.93	5.98
	±0.58	±1.2	±0.86	±0.49

The terms in parentheses (ref-active and ref-inactive) refer to reference structures for the RMSD calculation.

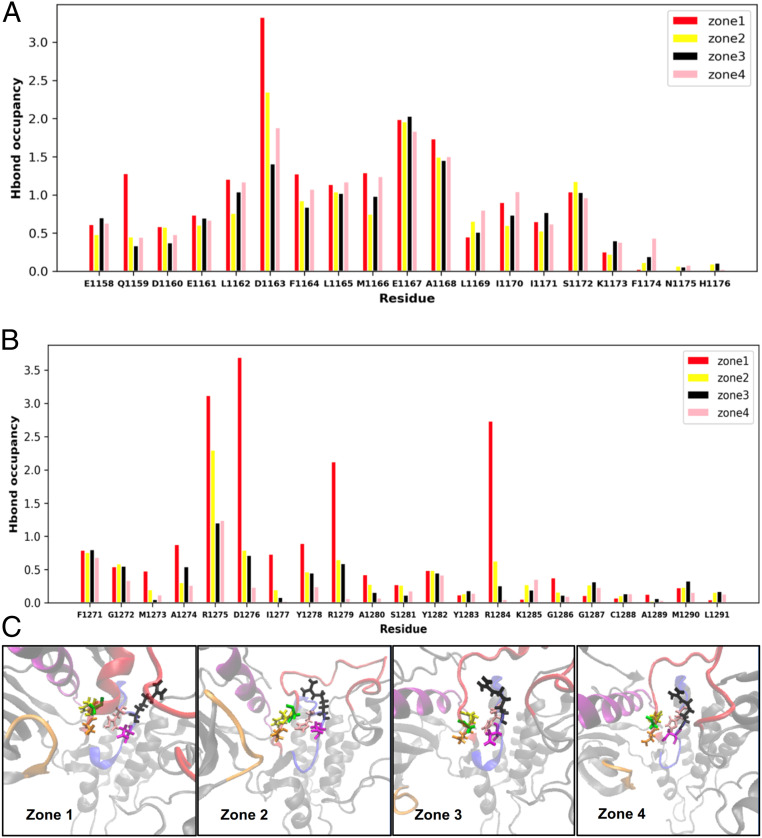
To link the sequence of conformational transitions across zones 1 through 4 (Fig. 2B) to the underlying residue-level interactions in ALK TKD, we computed the hydrogen bond occupancy in each of the four zones. The geometric criteria for a hydrogen bond to be recorded are 1) that the distance between acceptor and the heavy atom connected to the donor hydrogen atom is ≤3.2Å and 2) that the angle subtended by the donor hydrogen acceptor is ≥50°. We computed the hydrogen bond occupancy as the fraction of the compiled trajectory of conformations that meet the criteria in each zone and depicted the results on a per residue basis. The resulting hydrogen bond occupancy fractions for the four zones are reported in Fig. 3, computed for each residue in the αC-helix (Fig. 3A) and the activation loop (Fig. 3B). We only count hydrogen bonds formed between two residues in the αC-helix, between two residues in the activation loop, or that bridge the αC-helix and the activation loop. Values for each residue correspond to the sum of the occupancies of all hydrogen bonds participated in by atoms of that residue, so occupancy can be greater than 1 for residues involved in multiple hydrogen bonds.

Fig. 3.

(A) Hydrogen bond occupancy in the αC-helix residues differs across the four zones, indicating distinct hydrogen bond networks in the active-like and inactive-like configurations. (B) Hydrogen bond occupancy in activation loop residues also differs across the four zones, further indicating altered hydrogen bonding in this region between the active-like and inactive-like configurations. (C) Zoomed in snapshots of the ALK TKD DFG and HRD motifs. The DFG motif is color coded: D, orange; F, yellow; and G, green. The HRD motif is color coded: H, pink; R, black; and D, magenta. Kinase domain regions are color coded as in Figs. 1 and 2.

For activation loop residues, zone 1 (inactive conformation) has the highest hydrogen bond occupancy, and the trend is similar (although changes are more subtle) for αC-helix residues. Our results thus point to a systematic rearrangement of hydrogen bonds involving the αC-helix and activation loop as ALK TKD navigates the four zones and the RMSD transitions from zone 1 to zone 4 (Fig. 2B). We therefore hypothesize that there is a significant correlation between hydrogen bond rearrangement and the shift in RMSD along the transition pathway. We can rationalize the changes in hydrogen bond occupancy by inspecting conformational changes from zone 1 (inactive) to zone 4 (active). The activation loop changes from a partly helical structure to a disordered loop (see snapshots in Fig. 3C), reducing the number of internal hydrogen bonds in the activation loop. Although the αC-helix undergoes an extension, loss of other hydrogen bonds causes an overall reduction in their number. The metadynamics sampling also captures the characteristic αC-helix swing from “out” to “in” depicted in Fig. 2A. Although the αC-helix RMSD values in Table 1 do not show substantial changes across the four zones, the “out” to “in” transition reflects substantial motion of the αC-helix relative to the activation loop. This rearrangement is also reflected in changes to the mean distance between E1167 (in αC) and K1150 (in strand β3): 3.23 Å (zone 1), 3.51 Å (zone 2), 9.55 Å (zone 3), and 3.42 Å (zone 4), indicating that conformations in zones 1 and 4, but not zone 3, are poised to form this salt bridge — which positions the K1150 side chain for interaction with ATP in the active site as seen in the inactive ALK TKD structures seen in the Protein Data Bank (PDB). The DFG (Asp-Phe-Glu) motif is in the “in” (active-like) conformation in all four zones (see snapshots in Fig. 3C). Indeed, a majority of the PDB structures adopt a DFG-in conformation, with around three times more DFG-in structures than DFG-out (65, 66). As evident from the snapshots (and also the data in Table 1), the activation loop undergoes the expected transition from an inactive-like (zone 1) to an active-like (zone 4) configuration. Interestingly, the free energy landscape and the enhanced sampling also succeeds in capturing the rotation in the arginine of the HRD (His-Arg-Asp) motif (see snapshots in Fig. 3C) which provides a link between the catalytic loop, activation loop phosphorylation sites, and the magnesium-binding loop in RD (Arg-Asp)-containing kinases that have this motif (67).

Computational Analysis of ALK Mutants.

To translate these findings for wild-type ALK TKD to mutated systems, we sought to identify scoring functions that can be computed in regular MD trajectories and serve as “proxies” for detecting shifts in RMSD and hydrogen bond occupancy. In addition to hydrogen bond occupancy, we considered the RMSD of A-loop and αC-helix residues (SI Appendix, section 2B) and SASA, which appears to correlate well with ALK activation (11). Time series of hydrogen bond occupancy are shown for inactive and active wild-type ALK TKD in SI Appendix, Fig. S1. These plots reveal how hydrogen bonds involving a few residues (e.g., R1214, R1253, and R1275) are highly dynamic, whereas others are relatively static. Most hydrogen bonds are formed at the start of the simulation and persist for the duration, whereas some (labile) bonds flicker in and out of existence—especially for polar and basic residues. In general, only a few hydrogen bonds show a larger than 30% occupancy difference between the first and second 50 ns of a simulation. Mutations that stabilize or destabilize these labile interactions can impact the overall dynamics and conformational landscape of a protein. In an effort to understand variability in individual hydrogen bonds, we analyzed the lability of individual hydrogen bonds as illustrated in SI Appendix, Fig. S1. Classifying hydrogen bonds with an occupancy change of >30% between the first and second half of any mutant simulation as “labile” bonds, we found that only a small number are labile across all systems (SI Appendix, Table S1). It is worth noting that mapping of the hydrogen bond occupancy differences to the free energy differences will require consideration of all hydrogen bonds, including those between protein and water. However, our goal as described above is to use the hydrogen bond occupancy difference as a measure of RMSD changes and just a proxy for relative stability.

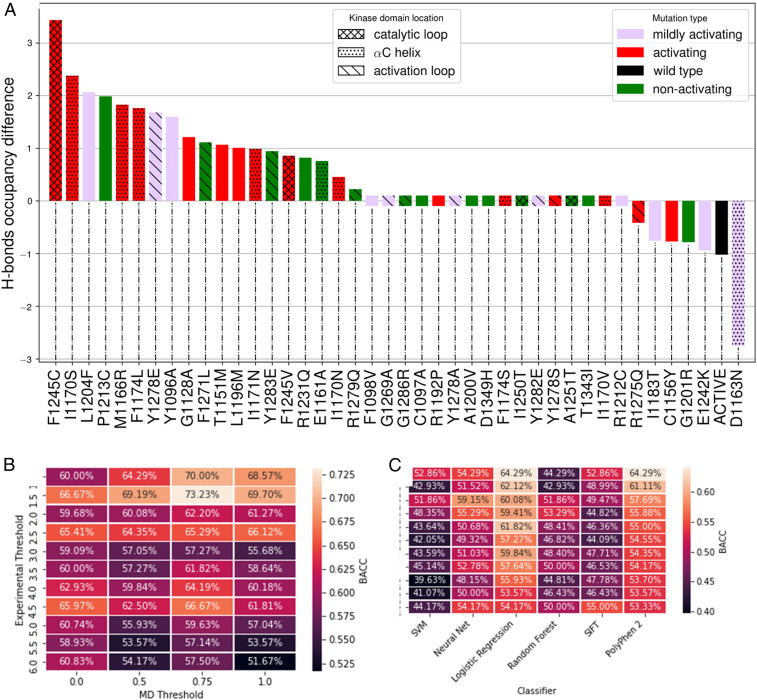
To assess the impact of ALK TKD mutations on hydrogen bond occupancy patterns, we computed the total hydrogen bond occupancy difference, ∆MUT,Total (SI Appendix, section 2B), between a series of inactive conformation simulations for ALK TKD harboring different mutations. After computing the occupancy for each residue i in the inactive wild-type (OWT,i) and residue i in the inactive mutant (OMUT,i), we calculated the occupancy difference for residue i (∆MUT,i) as ∆MUT,i = OMUT,i − OWT,i. We only take into account hydrogen bonds with significant occupancy differences between mutant and wild-type, since small occupancy differences could simply reflect fluctuations around a well-defined minimum. We achieve this by setting a threshold, and if ∆MUT,i > threshold, then ∆MUT,i is added to an accumulator (∆MUT,Total). We set the threshold at 0.75 and consider a mutation to have hydrogen bond occupancy that differs from wild-type only if ∆MUT,Total is nonzero. Any mutant with 0 < ∆MUT,Total < 0.75 must have at least two altered hydrogen bonds, one gained and one lost, since values smaller than 0.75 are not counted in our scheme. The maximum difference in occupancy for one hydrogen bond between two simulations is two, since side chains are considered as a whole, and some residues have two hydrogen bond donors or acceptors. We chose the threshold value of 0.75 by varying this value from 0 to 2 and plotting either the receiver operating characteristic area under the curve (a measure of how well a classifier can distinguish between positive and negative examples) or true positives versus false positives. In both cases, each system had a peak value between 0.7 and 0.8, although in some cases this peak spanned a broader region (data not shown). Results for hydrogen bond occupancy changes for the differently mutated ALK variants are shown in Fig. 4A. We include here all variants represented in the experimental data shown in Fig. 1. Based on our MD analysis, we can score any mutant system as activating if ∆MUT,Total exceeds a MD threshold factor T_MD. Similarly, in the experiments we can score mutants with k_cat/k_cat,wt as activating if this ratio exceeds a threshold factor T_expt. To explore suitable threshold values, we assessed the Balanced ACCuracy (BACC) for the hydrogen bond occupancy–based prediction for a range of T_expt and T_MD values as listed in Fig. 4B. We find that setting T_expt = 1.5 and T_MD = 0.75 gives the highest BACC (73.23%) for MD-based prediction, with T_expt = 4.5 and T_MD = 0.75 yielding the second-best BACC (66.67%). We prefer to adopt the latter of these two regimes, because setting a T_expt = 4.5 also provides maximal agreement between biochemical activation of the kinase and transforming ability in cells measured through focus formation assays. Our predictions for the different mutants using these threshold values (T_expt = 4.5 and T_MD = 0.75) are provided in Table 2 under the column titled “MD.” A similar analysis was also performed with SASA and RMSD for the αC helix and the activation loop (data not shown). The results indicated that utilizing SASA or RMSD, either separately or in conjunction with hydrogen bond occupancy, did not improve the BACC.

Fig. 4.

(A) Hydrogen bond occupancy difference was computed for the mutations, and the mutations for which this is different from that of wild-type were designated as activating under our scheme. The histograms are color coded per experimental results as stated in the legend: k_cat/k_cat,wt < 2, green; k_cat/k_cat,wt > 4.5, red; and k_cat/k_cat,wt =2 to 4.5, purple. (B) Calculated BACC for MD predictions for different values of threshold factors T_expt and T_MD. (C) Calculated BACC for ML predictions.

Table 2.

ALK mutations: Comparison of MD, SVM, Neural Net, Logistic Regression, Random Forest, SIFT, and PolyPhen-2 against experiments

Mutation	MD	SVM	Neural net	Logistic regression	Random forest	SIFT	PolyPhen 2	Experimental	kcat (min−1)	Transformation assay
F1174L	1	0	0	1	0	1	1	1	365	++
F1245V	1	0	0	0	0	1	1	1	341	++
F1245C	1	0	0	0	0	0	1	1	329	++
I1170N	0	0	1	1	0	1	1	1	200	++
I1170S	1	1	1	1	1	1	1	1	200	++
I1171N	1	0	1	1	0	1	1	1	188	++
Y1278S	0	1	1	1	1	1	1	1	172	++
F1174S	0	0	0	1	1	1	1	1	148	++
R1192P	0	0	0	0	0	1	1	1	139	++
M1166R	1	0	0	0	0	0	1	1	127	+/−
R1275Q	0	1	1	1	1	1	1	1	119	++
T1151M	1	0	0	0	0	0	1	1	53.4	—
I1170V	0	0	0	1	0	0	1	1	51.7	—
D1163N	1	0	0	1	0	1	1	1	50.8	—
L1196M	1	1	1	1	1	0	1	1	45.0	+
C1156Y	1	0	0	1	0	1	1	1	43.5	—
G1128A	1	1	1	0	1	1	1	1	43.4	+
Y1282E	0	0	0	1	0	1	1	0	37.9	—
G1269A	0	0	0	0	0	0	1	0	33.2	—
I1183T	0	1	1	1	1	1	1	0	31.5	—
F1098V	0	0	0	1	0	1	1	0	31.4	—
L1204F	1	1	1	0	1	1	1	0	27.7	—
Y1096A	1	1	1	0	1	1	1	0	27.6	—
Y1278E	1	0	0	1	0	0	1	0	27.5	—
R1212C	0	1	1	1	1	1	1	0	22.8	+/−
Y1278A	0	0	1	1	0	1	1	0	21.4	++
E1242K	1	1	0	0	0	1	1	0	21.1	—
C1097A	0	0	0	0	0	1	1	0	19.6	+/−
F1271L	1	0	0	1	0	1	1	0	17.9	—
Y1283E	1	0	0	1	0	1	1	0	17.7	—
G1286R	0	0	0	0	0	0	1	0	16.4	—
P1213C	1	0	0	0	0	1	1	0	15.0	—
A1200V	0	1	0	0	0	1	1	0	11.1	—
D1349H	0	1	1	1	1	1	1	0	11.2	—
Wild type	—	—	—	—	—	—	—	—	9.3	—
T1343I	0	0	0	0	0	1	1	0	8.6	—
E1161A	0	0	0	0	0	1	0	0	7.3	+/−
R1231Q	1	1	1	1	1	0	0	0	5.4	—
I1250T	0	0	0	0	1	1	1	0	2.7	—
D1270G*	0	0	0	0	0	1	1	0	1	—
R1279Q	0	1	1	1	1	0	1	0	†	—
A1251T	0	0	0	0	0	1	1	0	‡	—
G1201R	1	0	0	0	0	1	1	1	†	+
TPR (%)	66.67	27.78	38.89	61.11	33.33	72.22	100.00
FPR (%)	33.33	37.50	33.33	45.83	33.33	79.17	91.67
BACC (%)	66.67	45.14	52.78	57.64	50.00	46.53	54.17

In the table, 1 = activating mutation, 0 = nonactivating mutation; these classifications are based on threshold factors T_expt = 4.5 and T_MD = 0.75.

^*D1270G mutation is considered 0 in MD and ML predictions, since it is a known inactivating mutation of a catalytic residue (D of the DFG motif).

^†Expression problem.

^‡No phosphorylation.

The choice of the threshold in experiments came from independent experiments comparing biochemical activity of kinases and cell transformation activities of mutated ALK variants in focus formation assays (5, 11). Our choice of the threshold in MD was similarly determined by experimental results obtained in other systems such as BRAF and HER2 (ErbB2) (15). Therefore, we would like to emphasize that our predictions are not optimized to the test data, but rather we show the BACC matrix as a sensitivity analysis.

ML Analysis of ALK Mutations.

In addition to the MD studies, we evaluated the ability of ML (SI Appendix, section 2D) and evolutionary algorithms (SIFT and PolyPhen-2) for binary classification of driver (activating) and passenger (nonactivating) mutations in ALK TKD. ML algorithms require a training and test set. The training set is used to train the model and find its optimal hyperparameters. The test set then provides an unbiased evaluation of the final model fit on the training set. We constructed the training dataset by text mining the UniProt database and validated it by cross-referencing a subset of the entire dataset with available literature. For each mutant, a feature vector with 59 elements was thus generated, addressing chemical properties of the wild-type and mutant residues such as the difference in polarity and Kyte–Doolittle hydropathy (68). The final training set used in this study contained 829 total point mutations, with 230 positive (activating) mutations and 599 negative (nonactivating) mutations. The test set consisted of all 41 ALK variants listed in Fig. 4 (D1270G from Fig. 1 is excluded, since it lies in the DFG motif and is involved in Mg²⁺ coordination). The following ML algorithms were evaluated in this study: SVM, Neural Net, Logistic Regression, and Random Forest—alongside SIFT (18) and PolyPhen-2 (24) as commonly used evolutionary algorithms. Performance was compared across all methods using the True Positive Rate (TPR), False Positive Rate (FPR), and BACC metrics (see definitions in SI Appendix, section 2D). Results for the BACC metric are summarized in Fig. 4C and the individual predictions for the mutants are listed in Table 2.

Compared to both MD and the ML algorithms, the evolutionary algorithms SIFT and PolyPhen-2 performed considerably worse. Although both of these algorithms had higher TPRs than the other algorithms (Table 2), SIFT and PolyPhen-2 also had FPRs of 79% and 92%, respectively and lower BACCs compared to MD (but similar to those for ML). This indicates that the evolutionary algorithms predict mutations to be activating most of the time and consequently fail when tasked with determining which mutated systems are not activated. Interestingly, MD outperformed all of the ML algorithms. Although our MD approach had a similar FPR (33%) to some of the ML algorithms, it had a considerably higher TPR (67%) and BACC (67%) compared to the ML algorithms, of which the best performing was Logistic Regression—with TPR and BACC values of 61% and 58%, respectively. This result argues that stabilization of the hydrogen bond network is mechanistically crucial in the transition of ALK TKD from its inactive conformation to its active conformation. As ML considers chemical features more generally, we used a statistical test (F-test: see SI Appendix, Fig. S6) to gain further insight from the suite of ML algorithms and to determine which chemical features are most important. Our analysis indicated that differences in Kyte–Doolittle hydropathy index between the mutant and wild-type amino acid are an important feature. It is clear that there is much potential for the marriage of structural features such as hydrogen bond occupancy and chemical features of the mutated system in the creation of an even more effective algorithm for identifying and classifying driver and passenger mutations. Indeed, although focusing on the hydrogen bonding network for the MD algorithm outperforms the pure ML approaches, it fails in the approach described here to predict activation by a few key mutations such as R1275Q, F1174S, R1192P, and Y1278S. Interestingly, mutations from or to proline are among the most active false negatives (R1192P) and least active false positives (P1213C), suggesting that backbone dynamics might not be adequately accounted for in these cases. Of the remaining “misses” for the hydrogen bond network–based MD approach, 50% involve mutations from or to N/Q/E, suggesting that electrostatic or hydration effects need more attention. A future challenge is to incorporate such considerations to improve precision.

Discussion

The ability to predict which new ALK mutations found in patient genome sequencing studies are activating would provide a valuable guide in the clinic (11). By augmenting the set of patient-derived ALK TKD mutations that we studied previously (11) with a larger set that includes resistance mutations and those introduced to challenge our earlier prediction efforts, we generated a more balanced test set with which to compare prediction algorithms in this study. We profiled kinase kinetics (in peptide phosphorylation assays) and transforming abilities (in focus formation assays) of the additional mutated variants experimentally. With data on a more balanced set of more than 40 ALK TKD variants, we adopted two approaches for computational predictions. One was an unsupervised learning approach using MD and the other a supervised learning approach using a suite of ML classification algorithms—plus SIFT and PolyPhen-2. In the MD approach, intending to make our predictions explainable and interpretable, we rationalized the choice of classifiers used in our predictions by performing enhanced sampling simulations to capture the entire activation pathway/trajectory of the ALK kinase domain. We then analyzed a total of 86 ALK simulations, simulating each mutated system in duplicate and also undertaking two simulations each of the wild-type kinase in active and inactive conformations. We then compared the performance of the MD and ML predictions against our experiments (Table 2).

The predictions from SIFT and PolyPhen-2 have a poor balanced accuracy because both have an FPR of close to 1. ML techniques perform better than SIFT and PolyPhen-2, and F-test results (SI Appendix, Fig. S6) identified the difference in the Kyte−Doolittle hydropathy index between the mutant and wild-type amino acid as an important feature, with no other discernible patterns among the activating (or inactivating) mutations in our dataset. The predictions of MD have the lowest FPR, making it a conservative prediction algorithm but also the best performer when BACC is considered; we note again that both MD and ML predictions were blind to the experimental data. The MD scoring achieves an impressively high BACC based solely on consideration of hydrogen bond occupancy. This suggests that several of the activating mutations perturb hydrogen bond networks in the αC-helix and the activation loop regions to differentially stabilize active conformations—establishing a convergent mechanism for several such activating mutations. Thus, the MD simulations and associated free energy calculations provide us with a mechanistic picture of how changes in kinase structure (or at least its free energy landscape) lead to activation. They also provide a rational basis for scoring mutants with respect to TKD activation status by profiling the hydrogen bond occupancy in the αC-helix and the activation loop.

Our analysis of hydrogen bond occupancy in mutated ALK TKD systems revealed that a small number of labile bonds recur across simulations of different mutants. These labile bonds also account for most of the ∆MUT,Total value determined for the subdomains that contain them. Remarkably, a few labile hydrogen bonds appear capable of capturing most of the predictive power of the MD, as shown by the reported BACC (Table 3). Three of the six labile hydrogen bonds in ALK TKD are in the catalytic loop. Recognizing that oncogenic mutations increase the relative population of the active state relative to the inactive state of the kinase, our results imply that monitoring the hydrogen bonding network in the inactive state can be a proxy for the relative stability of these two states. An exact determination requires the free energy difference between two states which could be obtained through metadynamics of mutant systems. However, such an analysis is computationally demanding, requiring 2 to 10 μs of aggregate metadynamics runs per mutant system, not to mention that the choice of the CVs may also need to be optimized for each system.

Table 3.

Labile hydrogen bonds: Bond occupancy classificatory power by residue(s)

Donors	Acceptors	BACC (%)
R1275, R1279, R1284	D1163, D1276	60.1
R1253, R1275, R1279, R1284	D1249, D1276	59.5
R1275, R1279, R1284	D1276	57.0
—	D1163	55.6
R1275	—	56.5
—	D1276	63.3

We appreciate that other allosteric interactions may also be important for regulation of kinase systems such as ALK, which rely on homo- or heterodimerization for their activation. Alternatively, hydrophobic interactions—which will not be captured by our focus on hydrogen bond occupancy—may dominate. Such effects are likely to play a role for several activating ALK TKD mutations (e.g., at F1245 and F1174—although both are well captured). Another possibility is that the mutation enhances the k_cat directly by stabilizing the transition state of phosphoryl transfer (69). Analysis of cases where these are not well captured (e.g., F1174S, I1170N) will provide valuable insight into how to extend our consideration beyond hydrogen bond occupancy in the αC-helix and the activation loop. For the latter, the inability of SASA analysis of R-spine residues to distinguish activating from nonactivating mutations suggests that more sophisticated scoring functions for hydrophobic analysis based on free energies will need to be invoked (11, 70). Reanalysis of the mutations “missed” by our analysis here will help guide the inclusion of additional dimensions in scoring functions to improve BACC and also shed additional light on activation mechanisms. Another promising future avenue for investigation is the inclusion of hydrogen bond occupancy as a feature in future ML algorithms.

Materials and Methods

Experimental and computational protocols are discussed in detail in SI Appendix, sections 1 and 2; these sections describe the following protocols in detail.

Peptide Phosphorylation and Focus Formation Assays.

In vitro kinase assays measuring ³²P incorporation from γ-[³²P]ATP into a peptide substrate were performed to measure the activities of wild-type and mutant ALK. To assess how biochemical characteristics relate to transforming ability, we measured the ability of intact ALK variants harboring the same kinase domain mutations to induce focus formation in NIH 3T3 cells.

MD and Metadynamics.

MD simulations and analysis were carried out using the BioPhysCode software suite. The initial structure of ALK for the active system was based on the homology model constructed using PDB 1IR3 as template, and for the inactive system, PDB 3LCS was used. Mutations in the wild-type ALK system were introduced using the BioPhysCode Automacs routine.

Well-tempered metadynamics was used to sample the conformational change between the active and the inactive configurations. The biased simulations were performed using PLUMED. The CVs used are RMSD to the active structure of ALK as CV1 and RMSD to the inactive structure of ALK as CV2. Computations were carried out in part on supercomputers available through the Extreme Science and Engineering Discovery Environment (XSEDE) (71, 72).

ML.

Supervised ML techniques were implemented to classify a mutation as activating or not. A pan-kinase mutation dataset was constructed via text mining of the UniProt database using a Perl script. The resulting data set was validated by searching the literature for a subset of the entire dataset to ensure that class assignments were correct. The final set used in this work contained 829 total point mutations, with 230 positive, activating mutations and 599 negative, nonactivating mutations. For each mutation, a feature vector with 59 elements was generated, addressing chemical properties of the wild-type and mutant residues.

Data Availability

All study data are included in the article and/or SI Appendix.