Optical signatures of multifold fermions in the chiral topological semimetal CoSi

Significance

We present a comprehensive combined experimental and theoretical study of optical conductivity in the chiral topological semimetal CoSi based on the development of high-quality crystals. We reveal the presence and the energy range of various exotic multifold quasiparticles in the optical responses and provide experimental evidence for the realization of fourfold spin-3/2 fermions, which were not directly observed previously. Our work is critical to interpreting future optical and transport responses of multifold fermion materials. We believe the methods used in this work will not only stimulate future research in this class of materials but will also provide a strategy for addressing optical signatures of chiral topological fermions in solids.

Abstract

We report the optical conductivity in high-quality crystals of the chiral topological semimetal CoSi, which hosts exotic quasiparticles known as multifold fermions. We find that the optical response is separated into several distinct regions as a function of frequency, each dominated by different types of quasiparticles. The low-frequency intraband response is captured by a narrow Drude peak from a high-mobility electron pocket of double Weyl quasiparticles, and the temperature dependence of the spectral weight is consistent with its Fermi velocity. By subtracting the low-frequency sharp Drude and phonon peaks at low temperatures, we reveal two intermediate quasilinear interband contributions separated by a kink at 0.2 eV. Using Wannier tight-binding models based on first-principle calculations, we link the optical conductivity above and below 0.2 eV to interband transitions near the double Weyl fermion and a threefold fermion, respectively. We analyze and determine the chemical potential relative to the energy of the threefold fermion, revealing the importance of transitions between a linearly dispersing band and a flat band. More strikingly, below 0.1 eV our data are best explained if spin-orbit coupling is included, suggesting that at these energies, the optical response is governed by transitions between a previously unobserved fourfold spin-3/2 node and a Weyl node. Our comprehensive combined experimental and theoretical study provides a way to resolve different types of multifold fermions in CoSi at different energy. More broadly, our results provide the necessary basis to interpret the burgeoning set of optical and transport experiments in chiral topological semimetals.

Topological semimetals are metals defined by topologically protected degeneracies. In the solid state, their simplest realization features two bands that cross at a single node (1–3), known as a Weyl node. Weyl nodes are degeneracies not protected by the crystalline symmetry, and the excitations around them behave as spin-$1/2$ quasiparticles, with a linear relationship between energy and momentum. They are found in a family of noncentrosymmetric transition monopnictides, including TaAs, TaP, NbAs, and NbP (4–11), as well as in the magnetic compounds ${\mathrm{C}\mathrm{o}}_2$MnGa (12) and ${\mathrm{C}\mathrm{o}}_3{\mathrm{S}\mathrm{n}}_2{\mathrm{S}}_2$ (13, 14).

In general, crystal symmetries can protect band crossings with higher degeneracies at high-symmetry points, known as multifold crossings, around which the bands disperse linearly (15, 16). In particular, chiral crystals with nonsymmorphic symmetries that lack inversion and mirror symmetry were predicted to realize a variety of multifold crossings: three-, four-, or sixfold crossings. The dispersion close to each multifold degeneracy is described by a higher-spin quasiparticle, such as a spin-1 fermion in the case of a threefold crossing. Analogous to the case of Weyl nodes, multifold nodes are monopoles of Berry curvature with integer charge. However, the topological charge (i.e., Chern number) of multifold crossings is higher than that of Weyl nodes, which have topological charge $\pm 1$. Remarkably, multifold fermions have been shown to exist in the chiral semimetals CoSi, RhSi, PtAl, and PdGa, all of which crystallize in the chiral space group 198 (17–23). CoSi and RhSi host a threefold spin-1 fermion at the zone center (the $\mathrm{\Gamma }$ point), which is expected to weakly split by the spin-orbit interaction into a fourfold spin-$3/2$ and a twofold spin-$1/2$ Weyl fermion. At the zone boundary (the $R$ point), they host a double spin-1/2 Weyl fermion, which is expected to split into a sixfold spin-1 fermion and a twofold degenerate Kramers pair (17, 18). However, the splitting of the spin 3/2 multifold and the Weyl node was not resolved in the previous photoemission experiments due to the small energy scales that are involved (19–21). The threefold nodes in these materials are fundamentally different from the triply degenerate point in achiral materials such as in MoP (24), which have zero Chern number and occur away from time-reversal invariant momenta (24–28).

The multifold fermions in chiral topological semimetals are responsible for unusual and interesting optical responses such as gyrotropy (29, 30) and the quantized circular photogalvanic effect (17, 31–34). The optical conductivity is a particularly useful tool to probe the multifold node at the zone center since it is expected to dominate the response at low frequencies (35). An accurate measurement of the optical conductivity is also essential to precisely extract nonlinear optical responses such as second harmonic generation (36, 37) and photogalvanic effect precisely (38–44). Clarifying the nonlinear responses in these noncentrosymmetric topological semimetals acts to certify the presence and energy range where topological nodes are active (43, 45, 46). Determining the carrier lifetime and energy range at which topological crossings are activated is the key to observing the quantized circularly photogalvanic effect and to using them in the next generation of efficient topological optoelectronics (31).

Linearly dispersing bands result in a characteristic low-frequency optical conductivity given by ${\sigma }_1\left(\omega \right)\sim {\omega }^{d-2}$, where $d$ is the spatial dimension (47). Although the expected frequency-independent conductivity was observed in graphite (48) and graphene (49), the observation of a linear $\omega$-dependence characteristic of three-dimensional linear bands (50) is often challenging. The latter has been the subject of various experimental studies: for example, in the Dirac semimetals ${\mathrm{C}\mathrm{d}}_3{\mathrm{A}\mathrm{s}}_2$ (51, 52) and ${\mathrm{Z}\mathrm{r}\mathrm{T}\mathrm{e}}_5$ (53–55) and the Weyl semimetal TaAs (56, 57). However, in ${\mathrm{C}\mathrm{d}}_3{\mathrm{A}\mathrm{s}}_2$ the band structure at low energy deviates from linearity, resulting in a sublinear frequency dependence (51). In ${\mathrm{Z}\mathrm{r}\mathrm{T}\mathrm{e}}_5$, the band structure is quite sensitive to the growth method, and the bands can disperse quadratically along one direction, leading to a different frequency dependence of the optical conductivity at low temperature (53–55). In the case of TaAs, coexistence of trivial electron and hole pockets and the small energy difference between two kinds of Weyl nodes complicates the data analysis (56, 57). In RhSi, despite promising initial work (43, 58), good agreement between theory and experiment on the linear scaling of the conductivity, which would signal multifold fermions, has remained elusive. Furthermore, in many materials studied previously, the Lifshitz energy (i.e., the energy below which topological quasiparticles are excited) is so low that it could not be resolved (51–57), a circumstance that makes these systems not ideal for studying linear optical conductivity, in particular the effect of spin-orbit coupling or correlation on the optical conductivity response.

The cubic chiral crystal CoSi is a promising material to reveal the signature of multifold fermions in an optical conductivity experiment. It has a low carrier density and a large Lifshiz energy of $\sim$0.6 eV (18, 19, 21, 59), and the multifold nodes located at the zone center and zone boundary are significantly split by an energy difference $\approx$0.2 eV, with no other bands expected at the Fermi level (19–21). Below 0.2 eV, interband excitations near the nodes at the zone boundary are expected to be Pauli blocked, leaving only the linearly dispersing multifold fermions at the zone center (35, 60). These properties motivate the choice of CoSi as an ideal candidate to display a clean linear relation between the conductivity and frequency and also, to reveal why and how deviations could occur. Optical conductivity on CoSi was first measured more than two decades ago, but an understanding of neither the Drude response nor the interband excitations was provided (61, 62), most likely because it is a weakly correlated semimetal, as evidenced by a normal metallic Sommerfeld constant (63). Most importantly, the topological properties of CoSi and their implications for the optical response were not addressed since the topology of CoSi was not known until very recently (18, 19, 21, 59).

In the present work, we used Fourier-transform infrared (FTIR) spectroscopy to measure the conductivity over a broad range of 40 to 50,000 ${\mathrm{\text{cm}}}^{-1}$, with temperature dependence from 10 to 300 K. Based on improvements of the sample quality, we observed a Drude peak width of 2 meV and low onset energy of interband excitation of 20 meV, which are both around one order of magnitude lower than previous works (61, 62). Due to such improvement, we establish that the optical conductivity in CoSi is determined by the existence of multifold fermions at low frequencies. The temperature-dependent spectral weight of the Drude response is consistent with the Fermi velocity of the electron pocket consisting of the double Weyl quasiparticles. By subtracting a single sharp Drude peak and four narrow phonon peaks from the real part of the conductivity at 10 K, we reveal two approximately linear conductivity regimes separated by a kink at $\approx 0.2$ eV, culminating in a sharp peak at 0.56 eV. Using density functional theory (DFT) and tight-binding calculations, we link the two linear regimes to multifold excitations close to the $\mathrm{\Gamma }$ ($\omega <0.2$ eV) and $R$ ($\omega >0.2$ eV) points and the peak to a saddle point in the band structure at the $M$ point. Crucially, below 0.2 eV our calculations and measurements reveal a slight deviation from a perfect linear conductivity, consistent with a chemical potential that crosses a nearly flat band of a threefold node at the zone center. This observation, combined with the band splitting due to spin-orbit coupling, suggests that the optical transitions below 0.2 eV involve the spin-3/2 and a spin-1/2 Weyl nodes at the zone center. Our work highlights that the location of the chemical potential with respect to the multifold fermion is critical to interpreting future optical and transport responses of multifold fermion materials, due to the presence of a threefold fermion with an approximately flat band at the zone center.

High-quality single crystals of CoSi have been synthesized with a chemical vapor transport (CVT) method (59) and a flux method (64). Since it was found that the Drude response is significantly sharper for unpolished samples (56, 57), all of the reflectivity measurements on CoSi were performed on as-grown flat shiny facets. The data in Figs. 1, 2, and 4 are all measured on the (001) facet of CoSi grown by CVT. Part of the data measured on the flux-grown sample is shown in Fig. 5. (A complete dataset on the flux-grown sample is shown in SI Appendix, section A.) The facet direction is confirmed by X-ray Laue diffraction and second-harmonic generation measurement (36).

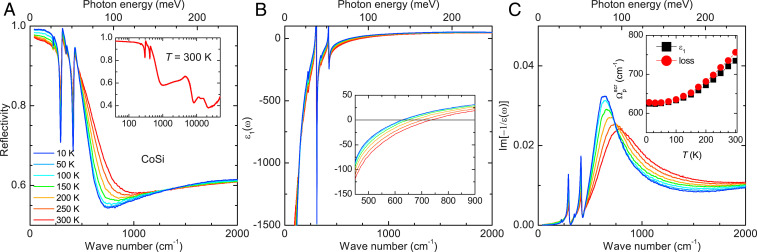
Fig. 1.

(A) Temperature-dependent reflectivity spectra of a (001)-oriented CoSi crystal grown by CVT. Inset shows the reflectivity from 40 to 50,000 ${\mathrm{\text{cm}}}^{-1}$ at room temperature. (B) Temperature dependence of the real part of the dielectric function ${\epsilon }_1\left(\omega \right)$. Inset shows an enlarged view to emphasize the zero crossings of ${\epsilon }_1\left(\omega \right)$, which correspond to screened plasma frequencies at different temperatures. (C) Temperature-dependent loss function. Inset shows the screened plasma frequency of free carriers obtained from the zero crossings of ${\epsilon }_1\left(\omega \right)$ and the peak in the loss function as a function of temperature.

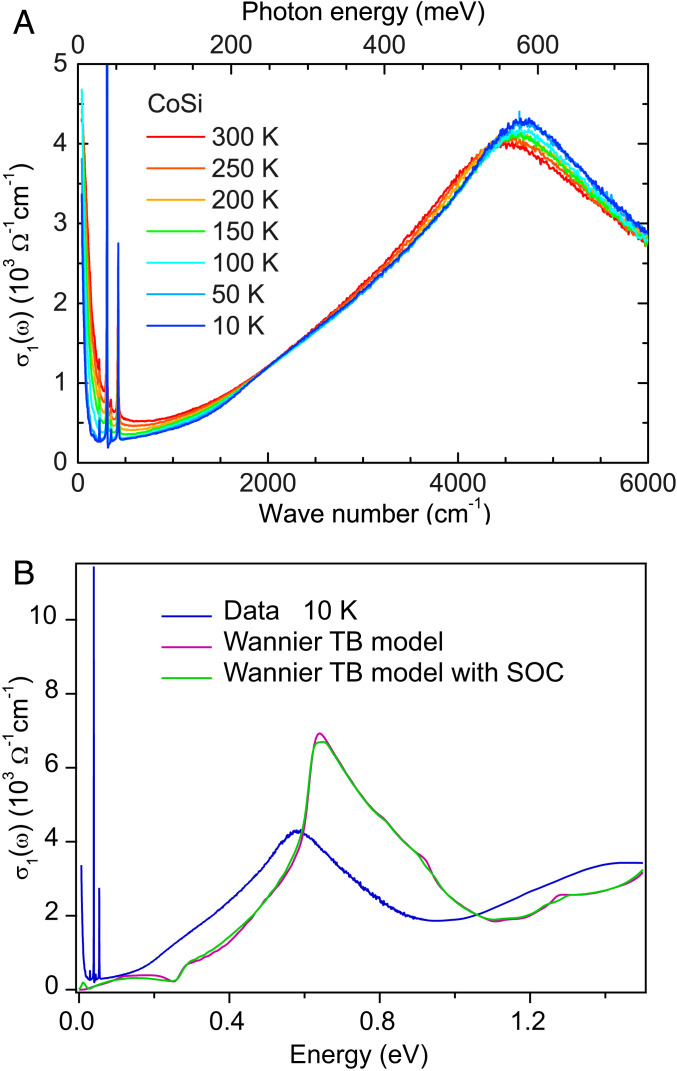
Fig. 2.

(A) Temperature-dependent optical conductivity spectra ${\sigma }_1\left(\omega \right)$ of a CVT-grown CoSi (001) crystal. (B) Measured optical conductivity at 10 K along with the Wannier tight-binding (TB) calculation with and without spin-orbit coupling (SOC) at 10 K.

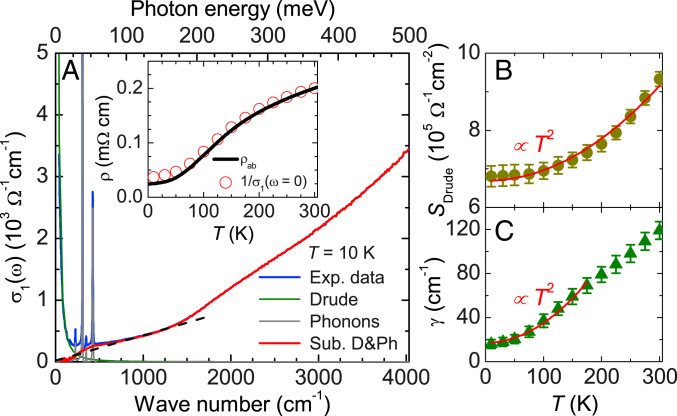
Fig. 4.

(A) Optical conductivity of CoSi at 10 K (blue); thin solid lines represent fit contributions of the Drude term (green) and phonon modes (gray), as well as the remaining interband contribution (subtracting Drude and phonons) to ${\sigma }_1\left(\omega \right)$ (red). The black dashed line indicates the linear conductivity below 0.2 eV. (Inset) Comparison of the dc resistivity, ${\rho }_{ab}$ (solid black line), with the zero-frequency values of the Drude fits to the conductivity data, $1/{\sigma }_1\left(\omega =0\right)$ (red circles). Temperature dependences of (B) the Drude weight and (C) the electronic scattering rate.

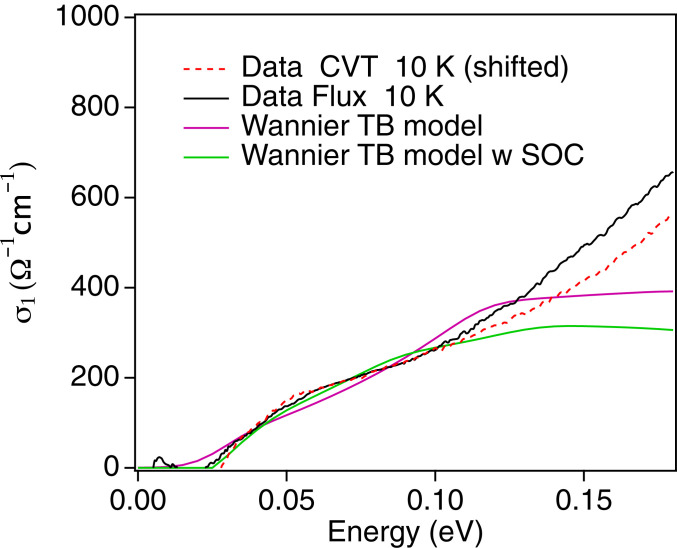
Fig. 5.

Interband optical conductivity in CoSi from measurement in both CVT- and flux-grown samples (red and black curves, respectively) along with Wannier tight-binding (TB) calculations without and with spin-orbit coupling (SOC).

Fig. 1A shows the measured temperature-dependent reflectivity spectra $R\left(\omega \right)$ of CoSi over a wide frequency range. In the low-frequency region ($<\mathrm{1,000}\hspace{0.17em}{\mathrm{\text{cm}}}^{-1}$), $R\left(\omega \right)$ shows a typical metallic response with a rather sharp plasma edge, below which it rapidly approaches unity. The plasma edge exhibits a rather strong temperature dependence. As the temperature decreases, it shifts continuously toward lower frequency and becomes steeper, indicating reductions in both the carrier density and scattering rate. The low value of the plasma edge ($\approx 700\hspace{0.17em}{\mathrm{\text{cm}}}^{-1}$) generally suggests a very small carrier density, consistent with the tiny Fermi surface in this material (19, 21, 64). In addition, we identify four sharper phonon peaks that are located at about 225, 305, 345, and 420 ${\mathrm{\text{cm}}}^{-1}$ and a stronger temperature dependence of the plasma edge than previous works (61, 62).

Fig. 1B shows the real part of the dielectric function ${\epsilon }_1\left(\omega \right)$. At low frequencies, ${\epsilon }_1\left(\omega \right)$ is negative (a defining property of a metal) and can be described by the Drude model $\epsilon \left(\omega \right)={\epsilon }_{\infty }-{\omega }_p^2/\left({\omega }^2+i\omega \gamma \right)$, where ${\epsilon }_{\infty }$ is the high-frequency dielectric constant, ${\omega }_p$ is the Drude plasma frequency, and $\gamma$ is the electronic scattering rate. Fig. 1 B, Inset shows an enlarged view to emphasize the zero crossing of ${\epsilon }_1\left(\omega \right)$ at different temperatures. The zero crossing of ${\epsilon }_1\left(\omega \right)$ corresponds to the screened plasma frequency ${\omega }_p^{\mathrm{s}\mathrm{c}\mathrm{r}}$ of free carriers, which is related to the Drude plasma frequency through ${\omega }_p^{\mathrm{s}\mathrm{c}\mathrm{r}}={\omega }_p/\sqrt{{\epsilon }_{\infty }}$. Fig. 1C shows the temperature-dependent loss function with the peak around 700 ${\mathrm{\text{cm}}}^{-1}$ being the screened plasma frequency. We observe that the temperature dependence of ${\omega }_p^{\mathrm{s}\mathrm{c}\mathrm{r}}$ in the dielectric function and the loss function agree well with the minimum of the plasma edge of $R\left(\omega \right)\approx 700\hspace{0.17em}{\mathrm{\text{cm}}}^{-1}$. As shown in Fig. 1 C, Inset, the screened plasma frequency decreases from about 740 ${\mathrm{\text{cm}}}^{-1}$ at 300 K to 625 ${\mathrm{\text{cm}}}^{-1}$ at 10 K.

Fig. 2A displays the temperature dependence of the real part of the optical conductivity ${\sigma }_1\left(\omega \right)$ in the infrared range. In the low-frequency region, the free carrier contribution to ${\sigma }_1\left(\omega \right)$ is seen as a Drude-like peak centered at zero frequency. Upon cooling, the Drude peak becomes narrower and loses spectral weight, implying that both the quasiparticle scattering rate and carrier density drop with decreasing temperature. This is consistent with the reflectivity analysis shown in Fig. 1. Along with the tail of the Drude peak, the interband optical conductivity increases approximately linearly with $\omega$ (up to about 2,000 ${\mathrm{\text{cm}}}^{-1}$ at 300 K). More interestingly, at low temperatures an upturn kink emerges around 1,600 ${\mathrm{\text{cm}}}^{-1}$ (0.2 eV) in the spectrum of ${\sigma }_1\left(\omega \right)$, resulting in two regions of quasilinear behavior at higher and lower frequencies. The upturn of ${\sigma }_1\left(\omega \right)$ indicates that new interband excitations become allowed above $\approx$0.2 eV. Fig. 2B shows the ${\sigma }_1\left(\omega \right)$ spectrum at 10 K on a larger energy scale up to 1.5 eV. It reveals a sharp peak at 0.56 eV that most likely arises from vertical transitions at the corresponding energy, between bands that disperse nearly parallel in a large region of momentum space.

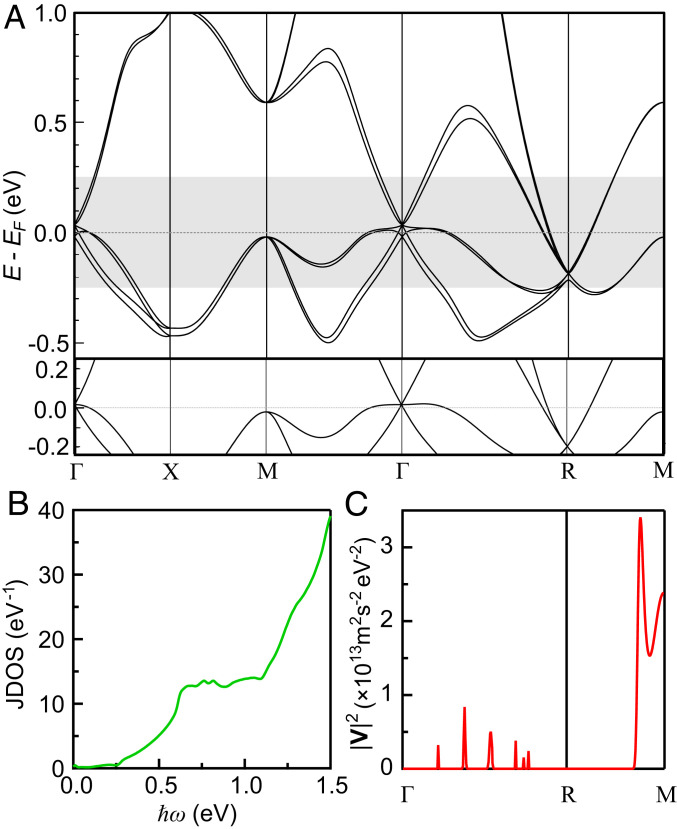
To determine the origin of the observed peak, we performed first-principles DFT band structure calculations (Materials and Methods). We find the relaxed CoSi lattice constant to be $a=4.485$ Å, which matches well with previous theoretical and experimental work (21, 60, 63, 65). The calculated electronic band structure is shown in Fig. 3A and is also in agreement with previous reports (18, 60, 65). Fig. 3 A, Lower shows the electronic bands calculated without spin-orbit coupling. As previously reported (18), in the absence of spin-orbit coupling, CoSi hosts a threefold spin-1 fermion at $\mathrm{\Gamma }$ and a double Weyl fermion at the zone boundary $R$ point, which may be viewed as two degenerate spin-$1/2$ Weyl fermions with equal Chern number. The effect of spin-orbit coupling is to split the threefold node at $\mathrm{\Gamma }$ into a fourfold spin-$3/2$ fermion and a twofold Weyl fermion, as expected from the addition rules for angular momenta (17, 18). At the $R$ point, the double Weyl node splits into a sixfold multifold fermion, which can be viewed as a double spin-1 multifold fermion, and a twofold degenerate Kramers pair. The energetic splitting of the multifold nodes is a measure of the strength of spin-orbit coupling when compared with the bandwidth; at $\mathrm{\Gamma }$, we find a spin-orbit splitting of $\approx 18.1$ meV. Note that the band structure exhibits a saddle point at the $M$ point.

Fig. 3.

(A) Band structure of CoSi with spin-orbit coupling. Lower shows the band structure without spin-orbit coupling in the same shaded energy window of Upper. (B) JDOS as a function of energy. (C) Momentum-resolved matrix element that contributes to the 0.62-eV interband transition along the $\mathrm{\Gamma }-R-M$ direction.

Furthermore, we calculated the maximally localized Wannier functions that represent the DFT valence Bloch states using Wannier90 (66), and we constructed a tight-binding model in this Wannier function basis by fitting to the DFT band structure. We use this model to calculate the interband contribution to the optical conductivity, defined as

$${\sigma }^{ab}\left(\hslash \omega \right)=\pi e^2\hslash \sum _{m\ne n}\int \frac{d^3\mathbf{\text{k}}}{{\left(2\pi \right)}^3}\frac{f_{nm}}{E_{nm}}{v}_{nm}^a{v}_{mn}^b\delta \left(E_{mn}-\hslash \omega \right),$$ [1]

where $f_{nm}\left(\mathbf{\text{k}}\right)=f_n\left(\mathbf{\text{k}}\right)-f_m\left(\mathbf{\text{k}}\right)$ is the occupation difference between Bloch states with band indices $n$ and $m$ at momentum $\mathbf{\text{k}}$, $E_{nm}\left(\mathbf{\text{k}}\right)=E_n\left(\mathbf{\text{k}}\right)-E_m\left(\mathbf{\text{k}}\right)$ is the energy difference between these two bands, and $v_{nm}^a\left(\mathbf{\text{k}}\right)$ is the velocity matrix element along the $a$ direction. With these Wannier orbitals, this model can describe the bands up to 1.5 eV above the Fermi level accurately. As a consequence of cubic symmetry, the conductivity tensor ${\sigma }^{ab}\left(\hslash \omega \right)$ has only one independent component.

The optical conductivity, calculated for the band structure shown in Fig. 3A, is shown in Fig. 2B, in addition to the experimental result at 10 K. For comparison, we present the optical conductivity calculation with and without spin-orbit coupling with a Gaussian broadening of 5 meV, which is close to the Drude peak width at low temperature. (SI Appendix, sections B and C have more details.) The difference between the two calculations is relatively small, as the spin-orbit coupling strength is weak ($\approx$20 meV) in this material. This suggests that a model without spin-orbit coupling is sufficient to describe the coarse features, broader than this energy scale, while spin-orbit coupling is needed to describe finer structure of the response. As mentioned above, the calculation is restricted to the interband contribution to the conductivity, whereas the experimental measurement also shows the (intraband) Drude response, as well as the phonon contribution in the low-energy regime.

Let us first focus on the measured peak around 0.6 eV, which is only due to interband transitions. The calculated optical conductivity shows a peak at $\omega \approx 0.62$ eV, the position of which matches well with the experimentally observed peak. Contributions to the conductivity peak come from all transitions at the peak energy range, which are not Pauli blocked and have nonzero velocity matrix elements.

The joint density of states (JDOS), shown in Fig. 3B for the case of vanishing spin-orbit coupling, is a measure of the number of transitions at a given energy and is thus a significant indicator for the origins of the observed peak. As is clear from Fig. 3B, the JDOS exhibits a shoulder-like feature at $\approx 0.62$ eV, characteristic of a saddle point, which suggests that the interband contributions primarily originate from the $M$ point. The JDOS is a momentum-integrated quantity; therefore, to unambiguously determine which interband transitions give rise to the peak, we plot the (momentum-resolved) integrand of Eq. 1 in Fig. 3C and the momentum-resolved contribution in SI Appendix, section D. In particular, in Fig. 3C we show the quantity $|V\left(\mathbf{\text{k}}\right){|}^2={\sum }_{n\ne m}\frac{f_{nm}\left(\mathbf{\text{k}}\right)}{E_{mn}}|v_{nm}^a\left(\mathbf{\text{k}}\right){|}^2\delta \left(E_{mn}-\hslash \omega \right)$ for fixed energy $\hslash \omega =0.62$ eV along $\mathrm{\Gamma }-R$ and $R-M$, which is a measure of the matrix elements of all allowed transitions at the peak energy. Fig. 3C clearly confirms that the interband transitions giving rise to the peak originate mainly from the vicinity of the $M$ point, which was assigned to a different origin in previous works (43, 58, 60). Note that the calculated peak in Fig. 2B becomes lower and wider with increasing broadening (SI Appendix, section C).

A second feature of the calculated conductivity shown in Fig. 2B is a dip at around 0.25 eV. This is due to the curvature of the middle band in the threefold node at the $\mathrm{\Gamma }$ point. As shown in Fig. 3A, when the energy of the incoming photon is very small, the allowed transitions should occur between the lower band and the middle band at momenta right near $\mathrm{\Gamma }$. Away from $\mathrm{\Gamma }$, the middle band curves downward in energy and becomes occupied, thus blocking transitions from the lower band to the middle band and providing the downward dip in the spectrum. As the energy of the incoming photon increases further, the transitions around the $R$ point become activated, providing the recovery from the dip and the continuation of the spectrum upward. However, this dip is not observed in experiments, probably due to a short lifetime of the hot carriers around 0.25 eV as decreasing the quasiparticle lifetime by broadening the Dirac delta function smears out this dip feature (60) (SI Appendix, section C).

Finally, we focus on the optical conductivity below 0.2 eV. In order to compare the calculation results with experiment below 0.2 eV accurately, we need to extract the interband contribution from the experimental data by subtracting the sharp Drude and phonon responses at low energy. In order to quantify the temperature dependence of the Drude response, in Fig. 4A we fit the low-energy part of ${\sigma }_1\left(\omega \right)$ using the Drude model. Fig. 4 A, Inset shows the dc resistivity $\rho \equiv 1/{\sigma }_1\left(\omega =0\right)$, derived from the fitted zero-frequency value (open red circles), which agrees well with the transport data (solid black curve), indicating that the subtraction of the Drude response is reliable. As shown in SI Appendix, section A, the linear Hall resistivity is dominated by a high-mobility electron channel, which indicates that the narrow Drude response comes from the electron pocket with double Weyl quasiparticles at $R$. The corresponding free carrier weight, $S_{\text{Drude}}=\frac{{\pi }^2}{Z_0}{\omega }_p^2$, where $Z_0$ is the vacuum impedance, and the scattering rate, $\gamma$, are displayed in Fig. 4 B and C, respectively. The free carrier weight shows a $T^2$ temperature dependence as expected for massless Dirac electrons (67). The coefficient before the $T^2$ temperature dependence could be used to extract the Fermi velocity of the Dirac fermions (double Weyl fermions in this case) by the relation ${\omega }_p{\left(T\right)}^2={\omega }_{p0}^2+\frac{2\pi }{9v_F^R}\frac{e^2}{{\hslash }^3}{\left(k_{B}T\right)}^2$ (67, 68). We estimated that $v_F^R$ for the double Weyl fermions is around 1.4 $\times {\mathrm{10}}^5$ m/s, which agrees with the DFT calculation in Fig. 3 A, Lower within 4$\%$. The scattering rate decreases as the temperature is lowered, following a $T^2$ temperature dependence at low temperatures, as shown by the red solid curve through the data points in Fig. 4C. Moreover, the value of $\gamma$ becomes extremely small at low temperatures, which is at least one order of magnitude narrower than the value reported in RhSi (43, 46, 58) and in previous studies of CoSi (61, 62).

The most striking feature of the optical conductivity is its approximately linear behavior up to $\approx 0.2$ eV, obtained after subtracting the single sharp Drude peak and four narrow phonons, as indicated by the black dashed line in Fig. 4A. After Drude subtraction, the optical conductivity derives from vertical interband transitions, and in the case of CoSi we expect that, at low frequencies, these transitions occur between bands associated with the multifold fermions. Below $\approx$0.2 eV, vertical transitions at the $R$ point are Pauli blocked, as is clear from Fig. 3A, except for the tiny 11-meV peak shown in Fig. 2B, which is associated with the interband transitions between spin-orbit split bands along the $R-M$ line (SI Appendix, section E has more discussion). The contribution from these transitions is much smaller, however, than the vertical transitions from the multifold fermions at the $\mathrm{\Gamma }$ point (35). Therefore, the linear conductivity below 0.2 eV is mainly attributed to these interband transitions near the $\mathrm{\Gamma }$ point.

For multifold fermions with linear band dispersion, the optical conductivity at low frequencies (where the linear approximation holds) was shown to have a linear frequency dependence (35), which can be understood qualitatively from dimensional analysis, ${\sigma }_1\left(\omega \right)\sim {\omega }^{d-2}$. In the isotropic limit of the dispersion (i.e., when full rotation symmetry is present), the slope of the conductivity of a single multifold fermion only depends on the Fermi velocity $v_F^{\mathrm{\Gamma }}$ and is inversely proportional to it (35).

To quantitatively understand the linear slope of the observed conductivity and to determine whether it originates from the low-energy multifold fermions, we now analyze the low-frequency regime of the optical conductivity in detail. As a first step, we consider a $k\cdot p$ model for the threefold spin-1 fermion node shown in Fig. 3 A, Lower in the absence of spin-orbit coupling. Interband transitions are allowed from the partially occupied lower linear band to the central flat band but are forbidden between the two linearly dispersing bands due to angular momentum selection rules (35). For this model, the analytic formula for the optical conductivity at $T\to 0$ K is $\frac{e^2\omega }{3\pi \hslash v_F^{\mathrm{\Gamma }}}\theta \left(\hslash \omega -E_0\right)$ (35), where $E_0$ is the energy of the threefold node measured from the Fermi energy. Using a Fermi velocity $v_F^{\mathrm{\Gamma }}$ = 1.9 $\times {\mathrm{10}}^5$ m/s from a fit to the linear band in Fig. 3A (details of the fit are included in SI Appendix, section F), we plot the analytical conductivity in SI Appendix, Fig. S9 (orange curve) in SI Appendix, section F, together with the experimental result. The linear model falls lower than the experimental curves for both samples, failing to capture the shoulder-like features around 50 meV in the data, mainly due to the absence of quadratic corrections to the flat band.

To better understand the origin of the discrepancies, we go beyond the linear model and compare the optical conductivity data with that obtained by the Wannier tight-binding model based on DFT introduced above. The lower-energy regime of optical conductivity in Fig. 2B of the Wannier tight-binding models is shown in Fig. 5. Overall, this analysis establishes that the chemical potential lies below the threefold node at $\mathrm{\Gamma }$ and highlights that deviations from a linear band structure near multifold fermions have an important qualitative impact on the optical conductivity. A simpler four-band tight-binding model for CoSi (17, 32, 35) that captures the symmetries of space group 198 with three parameters that we fit to the first-principles band structure in Fig. 3A reaches the same conclusions (SI Appendix, section G).

Next, we assess the role of spin-orbit coupling at low frequencies. The results of DFT-based Wannier tight-binding model (with spin-orbit coupling) are shown as the green curve in Fig. 5. We subtracted the small peak feature at 11 meV shown in Fig. 2B since it originates from the interband excitations between spin-orbit split bands along the $R-M$ line (SI Appendix, section E). This calculation displays close agreement with the measured conductivity in the flux-grown sample below 0.1 eV. This agreement supports that the low-frequency shoulder below 0.1 eV observed in experiments arises from transitions between the spin-orbit split linear and flat threefold fermion bands, which are composed of a spin-3/2 fourfold node and a spin-1/2 Weyl node.

Finally, we discuss the distinctions between the two crystals studied. Our calculated conductivity agrees well with the interband conductivity data from the flux-grown CoSi sample, while the conductivity data from the CVT-grown sample are higher at low frequencies (by $\approx$80 ${\mathrm{\Omega }}^{-1}\hspace{0.17em}{\mathrm{c}\mathrm{m}}^{-1}$ below 0.1 eV). It turns out that this difference is not due to the observation that the carrier density in the CVT-grown sample is $\approx$10 $\%$ higher than the flux-grown sample by comparing the Drude spectral weight. As shown in SI Appendix, sections G and H, assuming a higher chemical potential does not reach as good agreement as the flux-grown sample. This is an indication that either the additional contribution in the CVT-grown sample is not coming from interband transition (46, 58) or it is related to surface Fermi arcs as (001) (CVT) sample has surface states but (111) (flux) sample does not (69). Nevertheless, the average slopes of both samples and the calculations are comparable after shifting down the experimental result on the CVT sample by $\approx$80 ${\mathrm{\Omega }}^{-1}\hspace{0.17em}{\mathrm{c}\mathrm{m}}^{-1}$ (Fig. 5), suggesting that there is agreement concerning the Fermi velocity (SI Appendix, section H has more discussions).

In summary, we revealed the topological origin of the optical conductivity in CoSi based on the development of high-quality crystals. Our analysis shows that locating the chemical potential accurately with respect to the central flat band is crucial to understanding the optical response. We have shown that both intraband and interband optical conductivities in different frequency regimes are dominated by the existence of different topological multifold fermions, as well as a band structure saddle point. Most notably, we provide evidence of the existence of the fourfold spin-3/2 quasiparticles. Our results not only shed light on the interpretation of circular photogalvanic measurement in this family of materials (17, 31, 43, 45, 46) but also pave the way to study optical signatures in other chiral topological semimetals in the future (16, 34).

Materials and Methods

Millimeter-sized single crystals of CoSi have been synthesized with both a CVT method (59) and a flux method (64). Temperature-dependent infrared reflectance measurements were performed on as-grown flat shiny facets using a Bruker VERTEX 70v FTIR spectrometer with an in situ gold overfilling technique (70) (SI Appendix, section A has details). We performed first-principles DFT band structure calculations with the Quantum Espresso code (71–73). We used norm-conserving pseudopotentials generated with the OPIUM code (74), the Perdew–Burke–Ernzerhof generalized gradient approximation functional (75), and spin-orbit coupling to relax the structure and to calculate the band structures.

Data Availability.

All study data are included in the article and SI Appendix.