Abstract
Motivation
Several methods have been proposed for the paired RNA-seq analysis. However, many of them do not consider the heterogeneity in treatment effect among pairs that can naturally arise in real data. In addition, it has been reported in literature that the false discovery rate (FDR) control of some popular methods has been problematic. In this paper, we present a full hierarchical Bayesian model for the paired RNA-seq count data that accounts for variation of treatment effects among pairs and controls the FDR through the posterior expected FDR.
Results
Our simulation studies show that most competing methods can have highly inflated FDR for small to moderate sample sizes while PairedFB is able to control FDR close to the nominal levels. Furthermore, PairedFB has overall better performance in ranking true differentially expressed genes (DEGs) on the top than others, especially when the sample size gets bigger or when the heterogeneity level of treatment effects is high. In addition, PairedFB can be applied to identify the biologically significant DEGs with controlled FDR. The real data analysis also indicates PairedFB tends to find more biologically relevant genes even when the sample size is small. PairedFB is also shown to be robust with respect to the model misspecification in terms of its relative performance compared to others.
Availability and implementation
Software to implement this method (PairedFB) can be downloaded at: https://sites.google.com/a/udel.edu/qiujing/publication.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
With recent rapid developments in next-generation sequencing (NGS) technologies, high throughput RNA sequencing (RNA-seq) data are available to detect differentially expressed genes (DEGs) by measuring gene expression through counts of mapped short reads. To detect DEGs under certain conditions, a well-designed experiment is usually required to discover causal relationship, where the samples (libraries) of RNA-seq data are taken from each of the experimental units. Among these experiments, the paired-comparison design is a common experimental setting in RNA-seq expression analysis, where the goal is to compare two conditions (e.g. treatment versus control, tumor tissue versus normal tissue, pre- versus post-infection) arranged in the same pair (e.g. subjects, subplots, patients). Paired designs, which are special cases of randomized complete block designs with pairs being the blocks, can increase the precision of comparison by controlling variability within the pair and are therefore widely used in the real application (Chung et al., 2013; Esteve-Codina et al., 2017; Graw et al., 2015; Hardcastle and Kelly, 2013).
Several papers have proposed models applicable to the paired RNA-seq data. The edgeR (McCarthy et al., 2012) and DESeq2 (Love et al., 2014) assumed negative-binomial distribution of data and made the inference based on generalized linear model (GLM) with additive fixed treatment and pair effect. Chung et al. (2013) developed a full Bayesian model through a Poisson-gamma mixture, where the gamma hierarchy was imposed to account for biological variation among pairs while a common fold-change was assumed for the treatment effect across all pairs for the same gene. The ShrinkBayes method (Van De Wiel et al., 2013) provided a more flexible full Bayesian framework for the generalized linear mixed model (GLMM) to analyze paired RNA-seq data. Law et al. (2014) proposed variance stabilizing transformation of the RNA-seq count data and then put the transformed data into the limma pipeline using the same design matrix as edgeR for the paired data to perform the analysis.
Note that the assumption of constant treatment effects across pairs made by the full Bayesian model proposed by Chung et al. (2013) might fail to be true for some data. Although the fold-changes of expression levels might be consistent across pairs for some genes, it has been noted by some authors that the fold-changes of gene expression can vary among biological replicates or pairs in the paired design. For instance, McCarthy et al. (2012) detected over 200 genes with heterogeneous treatment effect across patients (pairs) when analyzing the human cancer data of Tuch et al. (2010) with a paired design. When the treatment effect acts differently among pairs, we say there is interaction between the treatment effect and the pair effect. For such cases, an interaction term between the treatment effect and the pair effect should be included in the model. However, like in any randomized complete block design, even if the interaction between the block and the treatment effect exists, it cannot be included because otherwise there is no degree of freedom to estimate the error variance. Therefore, the recommended analysis for the paired design by edgeR is to include only the pair effect and treatment effect in the model, ignoring the interaction between the pair and the treatment effect (see the edgeR user’s guide, October 11, 2017, page 39). Note that the same problem exists with other GLM or linear model based approaches such as DESeq2 and limma-voom. Another problem for the GLM or linear model based approaches is that they treat the random pair effect as a fixed effect, ignoring the correlation structure inherent in the paired data, which might lead to inflated false positive rates (Cui et al., 2016).
On the other hand, the paired baySeq (Hardcastle and Kelly, 2013) took on a very different approach by modeling the heterogeneous treatment effects directly through a beta-binomial model. Specifically, it assumed a binomial model for the count data of one sample by conditioning on the sum of counts in a pair, and then imposed a beta distribution on the pair-specific binomial proportion to describe the heterogeneity of treatment effect among pairs. Note the binomial proportion is the expected proportion of reads count from one sample out of the pair weighted by the library sizes, where the library size is the total number of read counts for all genes in one sample. By conditioning on the sum of the counts in a pair, this approach preserves the correlation structure of the paired data. The inference of the paired baySeq was performed under the empirical Bayesian framework with quasi-likelihood estimators for dispersion parameters. However, their parameters of interest are not easy to interpret for unequal library sizes (details will be given in Section 2.2). In this paper, we follow the idea of the paired baySeq to model the heterogeneous treatment effects directly with some modification in the parameters of interest and consider statistical inference under a full Bayesian framework.
Another issue with many current packages for the paired RNA-seq data analysis is the false discovery rate (FDR) control. It has been reported by several papers (Cui et al., 2016; Guo et al., 2013; Soneson and Delorenzi, 2013) that some popular methods such as edgeR, paired baySeq and ShrinkBayes though being powerful procedures, suffer from being too liberal in terms of FDR control. It is valuable to develop a powerful procedure that can control FDR at nominal levels.
In this paper, we develop a full Bayesian hierarchical model for the paired RNA-seq data with a modified beta-binomial likelihood to identify DEGs in the presence of heterogeneous treatment effects among pairs. The heterogeneity of treatment effects among pairs is incorporated to the likelihood in a different manner from the paired baySeq so that the parameters of interest in our model have clear interpretation even when the library sizes are different. Specifically, we model the true expression abundance directly and test whether the mean proportion of true expression abundance for one condition out of a pair equals to 1/2. To address the issue of FDR control in a full Bayesian framework, we take the approach of controlling the FDR through the ‘posterior expected FDR’ that was proposed by Newton et al. (2004).
In gene expression analysis, researchers are usually interested in DEGs that are both statistically and biologically significant. Most softwares identify such genes by first identifying genes that are statistically significant and then choosing biologically significant DEGs among them based on their fold-change estimates. Such ad-hoc methods, however, do not take into account of the variation of the fold-change estimates and can lead to many falsely identified biologically significant DEGs. One advantage of our full Bayesian approach is that it can be easily adjusted to identify DEGs that are both statistically and biologically significant with proper FDR control. Interestingly, Liu et al. (2015) proposed a full hierarchical Bayesian model to identify biologically significant DEGs with FDR control for independent RNA-seq data.
The rest of this article is organized as follows. In next section, we present our method by describing the paired data, building the full Bayesian hierarchical model and conducting the posterior inference. In Section 3, the performance of proposed method is examined by simulation studies through two main aspects: the ability of ranking true DEGs on top, and the power and actual FDR at different nominal levels. We further apply our model to a real human cancer dataset in Section 4 and investigate the biological relevance of the results. Finally, we conclude the paper by discussing the advantage, limitation and challenge as well as potential extensions of our method in the discussion section.
2 Method and modeling
2.1 Data structure
For each gene g, the i-th paired RNA-seq data is , where and represent the count data for the treatment and control group, respectively; i denotes the i-th pair (including two libraries); n is the number of pairs or replicates. Therefore, if we have G genes and n pairs, the data set would have in total G rows representing different genes and 2n columns denoting different libraries (or samples).
Here we assume that, given and independently follow Poisson distribution as follows:
| (1) |
where and are the true relative abundance of gene g under pair i for treatment and control group, and are the effective library sizes for the i-th pair. Here the effective library size refers to the product of the original library size and a scaling or normalization factor that adjusts for RNA composition effect and other potential technical effects across replicates. For the real data analysis in this paper, we use the trimmed mean method of Robinson and Oshlack (2010) to calculate the normalization factor.
Therefore, given , the conditional distribution of given the sum will be binomial distribution,
| (2) |
If we denote the proportion of true expression level of one sample out of the pair to be , the likelihood (2) can be rewritten as:
| (3) |
2.2 A full hierarchical Bayesian model
The paired baySeq (Hardcastle and Kelly, 2013) used a beta-binomial structure to model the heterogeneous treatment effects observed in the paired RNA-seq data. They imposed a beta distribution on the proportion in Equation (3) and defined its mean to be , where the parameter pg can only be interpreted as the expected proportion of treatment mean out of the overall pair mean when the effective library sizes for the paired samples are the same (). If the effective library sizes are not equal, it is not clear what the parameter pg refers to. To have a clear interpretation of the parameter of interest, we propose to impose the beta distribution on instead of as follows:
| (4) |
where and . If we denote and , then is the mean of , and is the measure of heterogeneity with larger indicating larger variance. This notation will be adopted from now on in the rest of the paper. It is easy to see that when will follow a degenerated distribution as , which makes the likelihood reduce to the binomial distribution. This corresponds to the case when the treatment effect is assumed to be the same across biological replicates, namely, as in Chung et al. (2013). Here, we allow the treatment effect to vary among biological replicates and the parameter of interest is . We define a gene to be differentially expressed (DE) if the average proportion of treatment mean out of the pair mean is not equal to 0.5, i.e. . The hypotheses we are interested in testing are versus .
To test the hypotheses, we take a full hierarchical Bayesian approach by modeling the parameters πg and through hierarchical prior distributions. This is another major difference of our approach from the paired baySeq, which took an empirical Bayesian approach by estimating the marginal distributions of πg and from the data. To consider a full hierarchical Bayesian model, we rewrite the data model components in (3) and (4) as the likelihood of by integrating out the nuisance parameter :
| (5) |
where B(x, y) is the beta function, and is Gauss’s hypergeometric function (Abramowitz and Stegun, 1964, pp. 558) defined by:
| (6) |
where converges when . In the calculation of the likelihood function, we use a transformation to guarantee its convergence (see Supplementary Discussion Section 1.1 for details). The mean and variance of can be calculated based on the likelihood function (5) (see details in Supplementary Discussion Section 1.2).
Since both the model parameters fall within the range of , we use the following logit transformation to eliminate the range restrictions in prior assignment:
| (7) |
With this new parameterization, a gene is DE if and our testing hypotheses become vs. . Based on the empirical distribution of the method of moment estimators of and from the human cancer dataset by Tuch et al. (2010) (see Supplementary Figs S1 and S2 in the Supplementary Material), we propose a Gaussian hierarchical distribution for and a mixture of 0 and Gaussian distribution for . Specifically,
| (8) |
To consider a mixture of 0 and Gaussian distribution for , we introduce a latent indicator variable γg to indicate whether gene g is DE or not. When , it is a non-DEG with and when , it corresponds to a DEG with . When for a DEG, we assume that follows a Gaussian distribution:
| (9) |
The hierarchical distribution of γg is given by:
| (10) |
and we assign a non-informative prior to the proportion of DEGs p so that
| (11) |
For the hyper parameters , we set , and . Here are fixed and all set to be 0.5 to give non-informative priors. We assume independence among these priors of hyper parameters.
2.3 Posterior inference
The Markov chain Monte Carlo (MCMC) algorithm is performed based on the full hierarchical Bayesian model described in Section 2.2 and the detailed steps are given in Supplementary Discussion Section 1.3. The major statistical inference is based on the posterior probability of the alternative hypothesis for each gene, i.e. , where Y is the count data from all the genes. We estimate this posterior probability by the Rao–Blackwell estimator following Cai and Dunson (2006), i.e. , where b is the number of burn-in samples and I is the total number of iterations in the MCMC.
The standard full Bayesian analysis selects the hypothesis with the maximum posterior as the final decision with no concern to achieve certain nominal FDR levels, as multiplicity correction happens automatically for some Bayesian analyses (Scott and Berger, 2010). In those cases, we simply designate gene g as a DEG if . However, for real applications, when controlling the FDR under certain levels is desired, such decision rule cannot always meet practical needs. Alternatively, we can control FDR through the posterior expected FDR (peFDR) proposed by Newton et al. (2004), where the peFDR is defined as:
| (12) |
Here dg is the indicator of the decision, and γg is the indicator of truth, both of which indicate a DEG at the value of 1. To estimate the peFDR, we first rank all the genes by from the largest values to the smallest. Then the estimated peFDR of the top l genes can be calculated by
| (13) |
It can be shown that the estimated peFDR for the top l genes is monotone non-decreasing with the number l, i.e. (see Supplementary Discussion Section 1.4 for the proof). Thus for a given nominal level α, we can claim the top l genes as DEGs if l is the largest integer such that .
Although the major focus of this paper is to decide whether a gene is statistically significant DE (i.e. ), it is also desirable to decide whether a gene is biologically significant DE. Recall . The larger magnitude of differential expression implies more deviation of πg from and hence larger absolute value of . If we define a DEG to be biologically significant with cutoff, we can estimate the posterior probability of a DEG being biologically significant, i.e. , through the MCMC algorithm. The decision rule for identifying statistically significant DEGs in the previous two paragraphs can easily be adjusted for identifying biologically significant DEGs. All we need to do is to rank all the genes by from the largest values to the smallest and then estimate the peFDR of the top l genes by replacing with in Equation (13). For a given nominal FDR level α, we claim the top l genes as biologically significant DEGs if l is the largest integer such that .
3 Simulation study
3.1 Simulation setting
We set up our simulation scheme based on those described by Hardcastle and Kelly (2013), simulating 1000 genes with n pairs, which gives 2n libraries in total. One hundred simulations are conducted and we report the results based on the average over 100 simulations. To imitate real data as much as possible, we sample parameters from the empirical distributions of the methods of moment estimators based on human tumor dataset of Tuch et al. (2010), which studies the head and neck oral squamous cell carcinoma (OSCC). See Supplementary Discussion Section 1.5 for detailed description of the simulation setting.
3.2 Methods compared
For all simulation settings, we compare the following procedures: the full hierarchical Bayesian model controlling FDR using the peFDR procedure (PairedFB) and the full Bayesian model using the maximum posterior probability as decision rule (maxpost), the paired baySeq using baySeq package (version 2.4.1) in R, edgeR package (version 3.12.0) in R, DESeq2 package (version 1.6.3) in R, the full Bayesian model proposed by Chung et al. (2013) (referred to as Chung method in our comparison), and the limma voom methodology (Law et al., 2014) using limma package (version 3.26.9). We run 10 000 iterations including 2000 burn-in samples for the MCMC algorithm of the PairedFB. The effective sample sizes using R CODA package (Plummer et al., 2006) and the trace plots for MCMC of hyper parameters are randomly checked once under each setting to ensure convergence and adequate iterations. For the paired baySeq, we treat all the pairs as replicates under the same condition as we only aim to detect treatment effect within pairs in the simulation study. For both edgeR and DESeq2, we build additive GLM model treating the pair effect and the treatment effect as fixed effects. For Chung’s full Bayesian model, we set the same number of iterations and burn-in samples in the MCMC algorithm as our proposed Bayesian model. As to the limma voom method, we build the same design matrix as edgeR to fit the linear model for the transformed observations and use the ‘variance modeling at the observational level’ method to incorporate the mean-variance trend. We also try to compare with the ShrinkBayes package proposed by Van De Wiel et al. (2013). However, due to numerous computational problems (see details in Supplementary Discussion Section 1.8), we decided not to include ShrinkBayes in our comparison for the simulation study and real data analysis.
3.3 Simulation results
We have done two sets of simulation studies to compare our method with others. The first set is to do the comparison with the goal of identifying DEGs and the second set is for identifying biological significant DEGs. For both sets of simulation studies, we generate data in the same way but we evaluate the performance of different procedures according to different goals of statistical inference.
3.3.1. Identifying DEGs
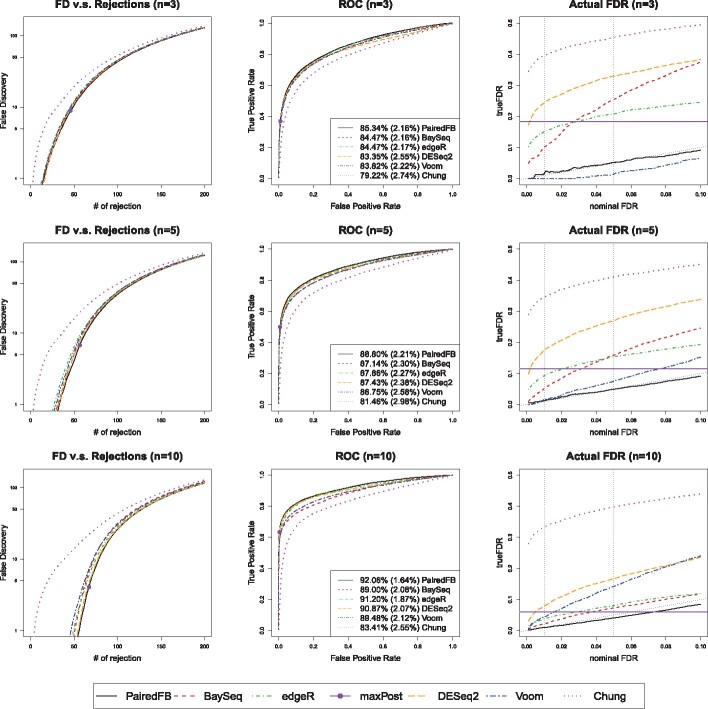
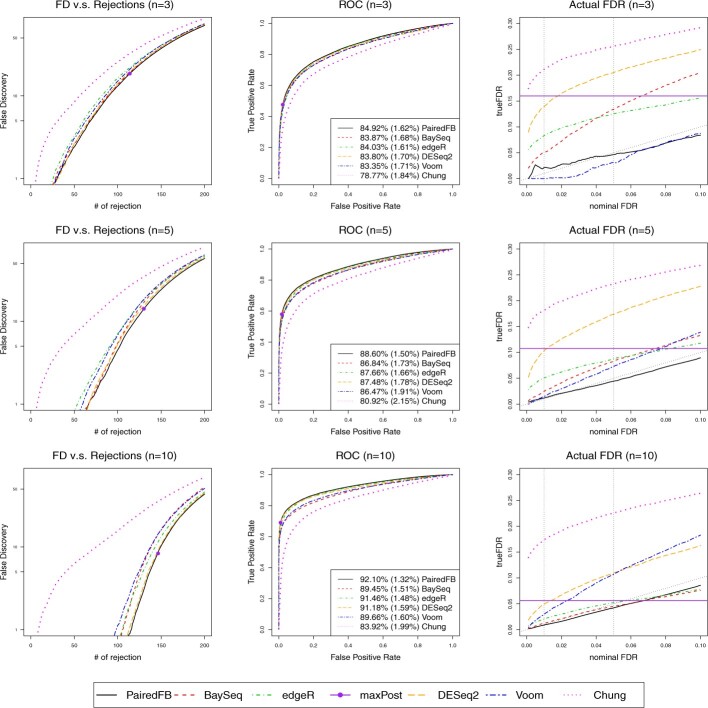
We evaluate the performance of all the procedures according to two criteria: (i) their ability to rank the true DEGs on the top; (ii) their actual FDR performance when the FDR level is controlled at nominal level. The simulation results of Setting SE1 are presented in Figures 1 and 2 with n = 3, 5, 10 and . Please see Supplementary Figures S4–S5, S8–S9, S12–S13 and S16–S17 for results of Settings SE2, E, P1 and P2, respectively. In all of these figures, we present three columns of plots from left to right: the false discovery (FD) plots (Robinson and Smyth, 2007), which draw the numbers of false positives versus the total numbers of top selected genes, the receiver operating characteristic (ROC) curves and the actual FDR curves. Although ROC curves and FD plots are both tools to evaluate the ranking abilities, the former evaluate all genes while the latter highlight top ranked genes. Since the decision rule is fixed for the maxpost procedure, it corresponds to one point in the FD plot and ROC curve of the PairedFB procedure, denoted by a big dot. Similarly, its actual FDR is fixed and will not change with the nominal FDR level. Hence it appears as one horizontal solid line in the FDR plot.
Fig. 1.
False discovery plots (first column), ROC curves (second column) and the actual FDR curves (third column) comparing all methods with different sample sizes (n = 3, 5, 10) under Setting SE1: is drawn from empirical distribution scaled by and is drawn from empirical distribution. Here the DE proportion is . In the third column, the black dotted line indicates the true nominal FDR level and two vertical dotted lines indicates 1 and 5% nominal level
Fig. 2.
False discovery plots (first column), ROC curves (second column) and the actual FDR curves (third column) comparing all methods with different sample sizes (n = 3, 5, 10) under Setting SE1: is drawn from empirical distribution scaled by and is drawn from empirical distribution. Here the DE proportion is . In the third column, the black dotted line indicates the true nominal FDR level and two vertical dotted lines indicates 1 and 5% nominal level
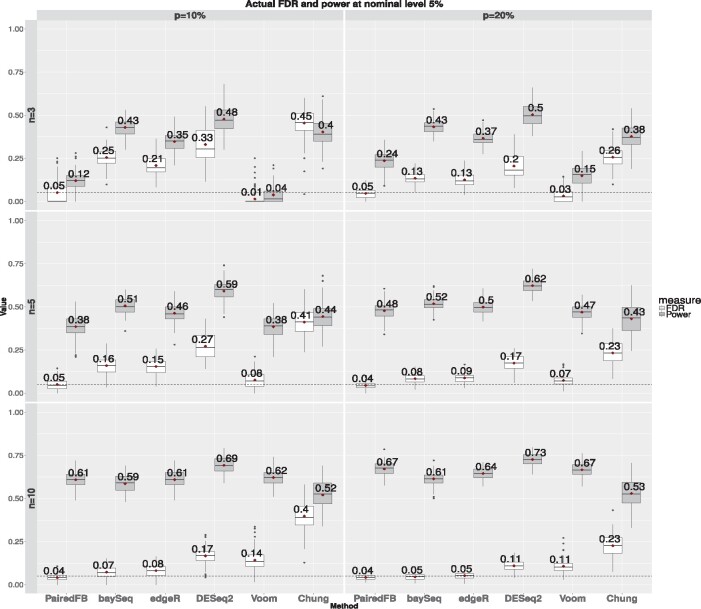
As the actual FDR curves only show average FD proportions at various nominal levels, to check the variation of the results over 100 simulations as well as to compare the powers of different procedures when FDRs are controlled at nominal levels, we provide the box plots of the FD proportions and true detection proportions for each method based on 100 simulations when the nominal levels of FDR are set at 0.05 and 0.1 for various simulation settings (see Fig. 3 and Supplementary Figs S3, S6–S7, S10–S11, S14–S15, S18–S19).
Fig. 3.
The box plots of the actual false discovery proportions (in white boxes) and true detection proportions (in gray boxes) over 100 simulations at nominal level 5% comparing all methods. Subplots in different rows represent different sample sizes (n = 3, 5, 10) and different columns for different DE proportions (). and of DEGs () are sampled under Setting SE1. The numbers besides each box indicate the mean value over 100 simulations. The horizontal black dashed line in each plot outlines the 5% nominal level
Based on all the above-mentioned graphs, we come to our conclusion 1: PairedFB has the best overall performance in terms of ranking the true DEGs on top and is the only procedure that controls the actual FDR at nominal levels for almost all the cases we study. In fact PairedFB has lowest FD plots and highest ROC curves with largest average area under the curve (AUC) with smallest AUC standard error for all cases we consider. Recall the FD plots highlight the performance of top ranked genes while the ROC curves reflect the ranking of true DEGs among all the genes. Therefore, our simulation studies show that the PairedFB has the best ranking ability in terms of both top selected genes and all the genes. In addition to its best ranking ability, the PairedFB has its major advantage of FDR control. The PairedFB almost always controls the actual FDR close to the nominal levels for all cases we consider while other procedures suffer greatly from highly inflated FDR, especially for small sample sizes. Under Setting E with n = 3, the actual FDR of DESeq2, edgeR and paired baySeq can be as high as 0.49, 0.43 and 0.48, respectively, when the nominal level is 0.05 (see top left panel of Supplementary Fig. S10) while the FDR of the PairedFB is controlled at 0.04. In addition, the robustness studies conducted in Supplementary Discussion Section 1.7 also show that PairedFB is robust with respect to model misspecification in terms of its relative performance with existing methods.
The poor FDR control of the competing methods does improve with the sample size n, the proportion of DEGs p and the signal strength reflected by the scalar . When n = 10 and under Setting E, the actual FDRs of DESeq2, edgeR and paired baySeq can drop to 0.13, 0.08 and 0.1, respectively, at nominal level 0.05 (see bottom right panel of Supplementary Fig. S10). Therefore, it is important for researchers to consider large sample sizes for RNA-seq analysis, especially when it comes to noisy human datasets. Here we state our conclusion 2: for many popular packages, a small sample size of 3 can often lead to highly inflated FDR levels. Larger sample sizes are needed if one wants to control FDR at desired nominal levels.
Our simulation studies show that the limma voom procedure tends to have conservative actual FDR and lower power than PairedFB for small sample sizes. However its actual FDR increases with sample size in a very undesirable way: not only it becomes liberal at moderate sample sizes but also the actual FDR deviates even more from the nominal level when sample size increases for all the settings we considered. In addition, when the heterogeneity level of treatment effects increases as in Setting P2, the performance of the limma voom deteriorates significantly and it becomes the second worst procedure in terms of FD plots and ROC curves (see left two columns of Supplementary Figs S16–S17).
We surprisedly find that the hierarchical Bayesian model of Chung et al. (2013) is the worst procedure among all the methods in terms of its ranking ability and FDR control in our study. It has lowest ROC curves, highest FD plots and largest actual FDR curves in all settings considered. Even with 100 000 MCMC iterations and 10 000 burn-in for one simulation setting, their performance is not improved much and remains the worst among all methods considered (see the trace plot and corresponding FD, ROC plots in Supplementary Figs S33 and S34). Therefore, we believe the inferior performance of Chung’s procedure in our simulation studies is due to its failed assumption of constant treatment effects across the pairs while all other methods accommodate the heterogeneous treatment effects either explicitly or implicitly.
As we discussed in the introduction section, the paired baySeq and PairedFB model the heterogeneous treatment effects directly, while DESeq2 and edgeR can accommodate the heterogeneous treatment effects implicitly through the negative-binomial model (see Supplementary Discussion Section 1.9 for details). The limma voom procedure did not address the heterogeneous treatment effects directly. However, based on our simulation studies, it appears that the non-parametric modeling of the relationship between the variance and mean of the read count data in limma voom may accommodate the heterogeneous treatment effects to some extent, but the accommodation is inadequate when the heterogeneity level of treatment effect increases. The surprising result of the inferior performance of Chung’s method and the deteriorating performance of limma voom with sample size and heterogeneity level lead to our conclusion 3: we believe that it is very important to model or accommodate the heterogeneous treatment effects when they exist. Failure to do so may lead to poor ranking ability and highly inflated FDR.
The actual FDR of the maxpost procedure can be over 20% when the sample size n is small under Setting E (see Supplementary Figs S3, S8 and S9). Therefore, we come to our conclusion 4: although the full hierarchical Bayesian model automatically adjusts for multiplicity to some degree, it cannot guarantee the control of FDR at a desired level unless the decision rule targets on the FDR control as done by the PairedFB procedure.
3.3.2. Identifying biologically significant DEGs
As discussed in the introduction and Section 2.3, our Bayesian approach can be easily applied to identify biologically significant DEGs. If we define a DEG to be biologically significant with cutoff, where cutoff is a pre-specified threshold for the parameter of interest, we can use the decision rule proposed in the last paragraph of Section 2.3, which we still refer to as PairedFB. As a comparison, we consider the common practice of identifying biological significant genes by first identifying statistically significant DEGs and then choosing biologically significant DEGs among them based on their fold-change estimates. We expect such ad-hoc procedures can produce many falsely identified biologically significant DEGs because the variation of the fold-change estimates is not accounted for. In this section, we only compare with edgeR because of its good performance among all the other methods based on the simulation studies. We refer to the two-stage ad-hoc method of identifying biologically significant DEGs using edgeR as the two-stage edgeR method.
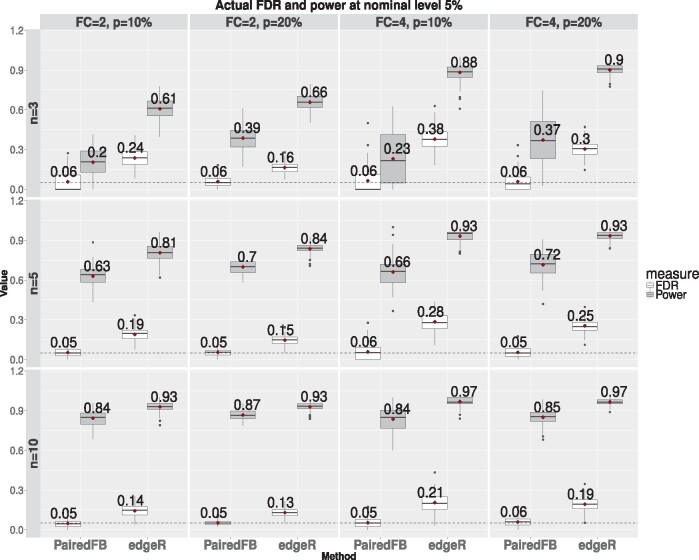
Due to the two-stage feature of the ad-hoc method, we cannot compare the ranking ability of the two-stage edgeR method with PairedFB. Therefore we focus on comparing their actual FDR and power when the FDR is controlled at nominal levels. We consider two empirical settings SE1 and SE2 for generating and , three sample sizes (n = 3, 5, 10), and two DE proportions (). We also consider three different fold-change thresholds to define a biologically significant DEGs: FC= and 4, which correspond to cutoff= and 1.39 in the definition of the biologically significant DEGs. The simulation results based on 100 simulation runs are presented in Figure 4 and Supplementary Figures S20–S24. All the simulation results show that the actual FDR of the PairedFB is under control for all the cases with some fluctuation due to simulation error, while the actual FDR of the two-stage edgeR method is highly inflated in most cases.
Fig. 4.
The box plots of the actual false discovery proportions (in white boxes) and the true detection proportions (in gray boxes) over 100 simulations at nominal level 5% comparing PairedFB and the two-stage edgeR procedure. Subplots in different rows represent different sample sizes (n = 3, 5, 10) and different columns for different DE proportions () and fold-change thresholds for biological significance (FC and 4). and of DEGs () are sampled under Setting SE1. The numbers besides each box indicate the mean value over 100 simulations. The horizontal black dashed line in each plot outlines the 5% nominal level
When n = 3, the actual FDR of the two-stage edgeR procedure can be as high as 0.24 and 0.38 at nominal level of 0.05 when FC or 4 under Setting SE1 with (see top panel 1 and 3 from the left in Fig. 4). Although the actual FDR of the two-stage edgeR decreases with n, p and , it increases with FC. Therefore, even when n = 10, the FDR of the two-stage edgeR method can still be as high as 0.19 or 0.21 when FC under Setting SE1 (see bottom right two panels of Fig. 4). Such highly inflated FDR level at a large sample size is likely due to the ad-hoc nature of the two-stage method by using the fold-change estimates to determine the biological significance of a gene. Supplementary Figures S20–S23 also show an undesirable property of the two-stage edgeR procedure: the actual FDR curve is very flat as a function of the nominal level for the cases when the fold-change threshold is large (see right panels of Supplementary Figs S20–S23). This means that the actual FDR level of the two-stage edgeR procedure doesn’t depend on the nominal level. When FC, we see the actual FDR is almost always at least 20% under Setting SE1 no matter what the nominal level is. In other words, we cannot control the FDR level at desired levels as long as the nominal level is smaller than 0.2.
On the contrary, the PairedFB procedure always produces the desired FDR levels no matter what the nominal levels and the sample sizes are and what fold-change thresholds one choose to define the biological significance. Although the power of the PairedFB can be low for small sample sizes, it increases quickly with the sample sizes. For instance, when n = 3, its power ranges from 20 to 65% depending on the settings. But it becomes 63–82% when n = 5 and ranges from 84 to 94% when n = 10 (see Fig. 4 and Supplementary Fig. S24). Therefore, we conclude that the PairedFB procedure is the preferred method for identifying biologically significant DEGs.
4 Real data analysis
4.1 Pre-processing data
In this section, we analyze the paired RNA-seq data from the study of OSCC in Tuch et al. (2010), which was examined by both paired baySeq (Hardcastle and Kelly, 2013) and edgeR (McCarthy et al., 2012). OSCC is one type of head and neck squamous cell carcinoma (HNSCC), which is the sixth most commonly observed cancers worldwide (Tuch et al., 2010). In this study, samples of tumor and matched normal tissue were taken from three patients, constructing the biological replicates here. We follow the same data pre-processing steps as was conducted by the paired baySeq: first mapping the RefSeq identifiers included in the dataset to gene symbols through Entrez Gene IDs using the human genome wide annotation package org.Hs.eg.db (version 3.0.0) in R, then discarding data associated with RefSeq identifiers that are no longer in current NCBI annotation, and finally keeping observations with the greatest number of exons for those duplicated gene symbols. We end up with 10 522 genes after data pre-processing. Before the data analysis, we apply the trimmed mean of M-value normalization method (Robinson and Oshlack, 2010) to adjust for the library sizes and RNA composition effect. It takes about one and half hours to run 25 000 iterations of the MCMC algorithm for PairedFB, and 15 000 posterior samples are used after 10 000 burn-in samples. We limit our comparison of the real data analysis to the paired baySeq, edgeR and voom, which have shown overall better performances in their actual FDRs and ranking abilities when n = 3 based on our simulation studies.
4.2 Results
4.2.1. Posterior summaries for the data analysis
The trace plots are checked for all the hyper parameters to ensure the convergence of the chain (Supplementary Fig. S35), and the effective sample sizes of these chains are checked to be adequate using R CODA package. The posterior mean of the proportion of DEGs (i.e. ) is estimated to be 33.42%. Our simulation studies show that this number tends to be smaller than the true parameter p (see Table 1.) We also provide the 95% credible intervals of πg for the top 20 genes ranked by our proposed method (Supplementary Fig. S37), and the histogram of posterior mean of πg for the 1190 DEGs identified by our method at 5% FDR level (Supplementary Fig. S38).
Table 1.
The average of the posterior mean estimators of the proportion of DE, p, over 100 simulations for various simulation settings
| Setting | True p (%) | p = 3 | p = 5 | p = 10 |
|---|---|---|---|---|
| E | 10 | 4.92 (0.415) | 6.29 (0.288) | 7.42 (0.163) |
| 20 | 13.89 (0.603) | 14.64 (0.352) | 16.12 (0.213) | |
| SE1 | 10 | 8.45 (0.236) | 8.88 (0.145) | 9.25 (0.106) |
| 20 | 17.04 (0.261) | 18.01 (0.192) | 18.81 (0.134) | |
| SE2 | 10 | 8.99 (0.169) | 9.32 (0.115) | 9.51 (0.085) |
| 20 | 18.02 (0.202) | 18.6 (0.166) | 19.27 (0.111) |
Note: The numbers in the parenthesis are the standard errors of the estimator.
4.2.2. Comparing with competing methods at various nominal FDR levels
The numbers of DEGs identified by different methods at various nominal FDR levels are shown in Table 2. As expected from the simulation studies for n = 3, voom is the most conservative method and gives the shortest DEG list at the same nominal FDR levels. The paired baySeq and edgeR detects more DEGs than the PairedFB, but likely at the cost of inflated FDR levels according to the simulation results. At the nominal level 5%, PairedFB, edgeR, baySeq and voom detect 1190, 1269, 1528 and 638 DEGs, respectively (see Venn diagram of the DEGs at nominal level 5% for all the methods in Supplementary Fig. S39). Please find the top 20 DEGs detected by our method in Supplementary Table S1. Note that there are minor differences between our analyses using edgeR and baySeq and those obtained by the original papers of McCarthy et al. (2012) and Hardcastle and Kelly (2013). Please see Supplementary Discussion Section 1.10 for detailed explanations.
Table 2.
Number of DEGs identified by different methods at various nominal FDR levels for the carcinoma data by Tuch et al. (2010)
| Nomimnal level (%) | PairedFB | edgeR | baySeq | voom | maxpost |
|---|---|---|---|---|---|
| 1 | 641 | 840 | 786 | 79 | 2310 |
| 2 | 833 | 971 | 1062 | 266 | 2310 |
| 3 | 976 | 1090 | 1260 | 389 | 2310 |
| 4 | 1090 | 1161 | 1408 | 522 | 2310 |
| 5 | 1190 | 1269 | 1528 | 638 | 2310 |
| 10 | 1604 | 1546 | 1971 | 1134 | 2310 |
Note: Here ‘maxpost’ represents our Bayesian model using maximum posterior probability as the decision rule.
Since the posterior mean of the proportion of DEGs is estimated to be 33.43% and it tends to underestimate the true proportion, there are likely more than DEGs for this data. However, Table 2 shows the maximum number of DEGs declared by different methods with FDR control is 1528 and 1971 by baySeq at a nominal FDR level of 0.05 and 0.1, respectively. Based on our simulation studies, the baySeq tends to have highly inflated FDR for n = 3 and therefore, the percentage of true DEGs that are detected by various methods is pretty low for this data. Larger sample size is needed to detect a larger percentage of true signals.
From Table 2, we can see that the result of voom is too conservative with the length of DEG list over 50% less than those detected by other methods at the nominal level 5%. Also based on the Venn Diagram of the DEG lists of all the methods at 5% nominal level in Supplementary Figure S39, we find that over 98% of DEGs detected by voom are also identified by PairedFB. Since voom detects considerably fewer DEGS than other methods and the majority of its detected DEGs are also identified by PairedFB, we end up focusing on comparing the results of PairedFB with edgeR and baySeq only.
We provide the performance comparison of edgeR, baySeq and PairedFB at a comparable FDR level. Comparable FDR level means that the resulting actual FDR levels are comparable. Since our simulation studies show that the ranking abilities of the three methods are similar when n = 3, the actual FDR of the three methods would be comparable when their powers are comparable. We thus compare the performance of PairedFB at 5% nominal level with paired baySeq at 3% and edgeR at 4% such that they detect similar amount of DEGs (as highlighted in bold in Table 2). One purpose of doing such a comparison is to remind readers that one can trust the nominal FDR level of PairedFB, while they need to be cautious about interpreting the nominal FDR level of the edgeR or paired baySeq method. The detailed results are reported in Supplementary Discussion Section 1.11. The gene sets enrichment analysis there indicates that genes uniquely identified by PairedFB are more related to HNSCC.
4.2.3. Comparing our list of candidate genes at 5% FDR level with existing biological discoveries
We follow the practice of McCarthy et al. (2012) and Hardcastle and Kelly (2013) by comparing the DEG list by our method at 5% nominal level with some existing biological discoveries. Among the 1190 DEGs detected by PairedFB at nominal level 5%, 15 genes are in the list of 25 important HNSCC genes reported by Yu et al. (2008) (see Table S2). The genes IL8 and MMP3 in their list are detected as DEGs at nominal level 10% by our method. One advantage of the full Bayesian model is that we can evaluate the biological significance of the identified DEGs through their posterior probabilities of the mean fold-change exceeding 2 or 4 (we denote them as ‘pp_2FC’ or ‘pp_4FC’ in our results). Among the 15 genes declared as significant by PairedFB in Table S2, the top 10 genes are very likely to have fold-change larger than 2 (pp_2FC >0.96) and six of them are very likely to have fold-change larger than 4 (pp_4FC >0.90). Note that by checking the posterior probability of fold-change exceeding a certain threshold, we can have an idea of differential expression level of the DEGs. For example, genes PLAU and POSTN among important genes reported by Yu et al. (2008) (top 12 and 14 in Table S2) have large pp_2FC while very small pp_4FC, which would indicate that these genes may have moderate level of differential expression <4-fold-change, although they both show strong statistical significance at 5% FDR level. The PairedFB does not declare 10 bottom genes as statistical significant at nominal FDR level 0.05 because these genes either have large variation or only show differential pattern for one of the three pairs. For instance, the raw count data for the gene ‘KRT5’ is 10 445 versus 7358 and 9335 versus 5948 for the first two patients and 4091 versus 10 548 for the third patient. Therefore, the three patients show inconsistent pattern in the differential expression for this gene. For sample sizes as small as three, the PairedFB cannot declare these genes as DEGs. More sample size is needed.
In addition, our method detects six of the nine genes of biological interest that were discussed by Tuch et al. (2010) at FDR level <1% (See Supplementary Table S3). Based on the posterior probability of biological significance, these top six genes are very likely to have fold-change larger than 2 (pp_2FC >0.886) and the top one gene CASQ1 is very likely to have fold-change larger than 4 (pp_4FC).
These results are comparable to what was reported by edgeR in McCarthy et al. (2012), where they found 17 of the 25 genes of Yu et al. (2008), and 6 of the 9 genes in Tuch et al. (2010). Since the data analysis conducted in Hardcastle and Kelly (2013) addressed different testing hypotheses (see Supplementary Discussion Section 1.10 for details), we cannot compare their bioinformatics analysis to ours here.
Gene ontology analysis reveals GO terms for the 1190 DEGs identified by PairedFB method tend to be associated with biological processes like cell structure, differentiation that relate to tumor development (see top 50 GO terms for the significant DEGs identified by PairedFB method at nominal level 5% in Supplementary Table S4).
4.2.4. Comparing with competing methods without FDR control
Sometimes, biologists may choose to look at a fixed number of top genes instead of controlling FDR. Here we compare the PairedFB with the two competing methods by focusing on their top DEGs without controlling FDR. Supplementary Table S6 displays the number of overlapping genes among the three methods when focusing on the top 100, 200 and 500 genes. We see the percentage of overlapping between any two methods is increasing with the number of selected genes. When top 100 genes are considered, PairedFB has 57 and 50% overlapping DEGs with paired baySeq and edgeR, respectively. The overlapping rates increase to 70.5 and 75% when top 200 genes are considered. For the top 500 gene list, the rates become 86.8% when comparing both methods. We focus on the top 500 genes since the overlapping rate is high and we can use the overlapping genes as benchmark to evaluate the uniquely identified genes.
To understand how the three methods differ in their uniquely identified genes, we conduct gene sets enrichment analysis as in McCarthy et al. (2012) and Hardcastle and Kelly (2013) by using the Fisher’s exact test to check the association between the detected gene list of each method and the curated gene sets (C2 category) from the MSigDB database (Subramanian et al., 2005). We emphasize the comparison of the uniquely identified DEGs by either method with those detected by both methods through their biological relevance. We show the Venn diagrams of the top 20 enriched gene sets based on DEGs detected by both PairedFB and edgeR (or baySeq), by PairedFB only, and by edgeR (or baySeq) in Supplementary Figure S42. We also report the detailed top 20 enriched gene sets based on the overlapping DEG list between PairedFB and edgeR (or baySeq), the list of uniquely identified genes by the PairedFB, and edgeR only (or baySeq only) in Table S7a and b, respectively. Note that the first columns of the two tables show that the top 20 enriched gene sets based on overlapping DEGs list of PairedFB and edgeR (or baySeq) are mostly cancer-related (highlighted in bold). The ‘RICKMAN HEAD AND NECK CANCER F’ gene set is ranked on top 1, which implies strong relationship to the biological target. This enhances the role of the overlapping genes as the benchmark for comparing the ‘PairedFB only’ and the ‘edgeR only’ (or ‘baySeq only’). When compared with edgeR, genes identified by ‘PairedFB only’ have seven top enriched gene sets in common with those from overlapping list, most of which are top ranked enriched gene sets based on the common DEG list, while genes identified by ‘edgeR only’ have three top enriched genes sets in common with the overlapping list (Supplementary Fig. S42). Furthermore, the PairedFB contains a unique gene set related to the HNSCC, called ‘RICKMAN TUMOR DIFFERENTIATED WELL VS MODERATELY UP’, at top 6. Similar conclusion can be made when compared with baySeq. In summary, although the simulation studies do not indicate much advantage of our method in terms of FD among a fixed number of top selected genes when the sample size is three, the gene sets enrichment analysis demonstrates our top-ranking list is biologically more relevant than the other competing methods.
4.2.5. Results of biologically significant genes at FDR level 5%
We apply the PairedFB to identify biologically significant genes with mean fold-change above 4 at nominal FDR level of 0.05 and compared with the results from the two-stage edgeR procedure. As expected based on the simulation studies, the two-stage edgeR procedure detects more genes with fold-change above 4 than the Paired FB with 634 genes (by two-stage edgeR) versus 180 genes (by PairedFB). However, it is very likely that the two-stage edgeR detected a larger number of large fold-change DEGs at the cost of much higher FDR according to our simulation studies (see Fig. 4 and Supplementary Figs S16–S20).
We conduct gene sets enrichment analysis for the biologically significant genes identified by PairedFB and the two-stage edgeR procedure, respectively. Supplementary Tables S8 and S9 present the top 20 enriched gene sets of the gene list with mean fold-change above 4 for PairedFB and edgeR, respectively. In Supplementary Table S8, we can see that among the top 20 gene sets enriched by 180 genes detected by PairedFB, three gene sets are directly related to OSCC or HNSCC (top 1 ‘RICKMAN HEAD AND NECK CANCER F’, top 11 ‘RICKMAN HEAD AND NECK CANCER E’, top 15 ‘CROMER TUMORIGENESIS DN’), and other enriched gene sets are related to lung cancer, skin and muscle fiber development. Based on 634 genes detected by edgeR using fold-change cutoff 4, we find less gene sets that are directly related HNSCC in Supplementary Table S9 with only top 1 ‘RICKMAN HEAD AND NECK CANCER F’ and many other gene sets are related to breast, uterous or prostate cancer.
5 Conclusion and discussion
We have presented a hierarchical full Bayesian model to analyze the paired RNA-seq gene expression data allowing the treatment effect to vary among pairs. To incorporate the heterogeneity of treatment effect among pairs, we impose beta distribution on the expected proportion of treatment mean out of the overall pair mean. Through comprehensive simulation studies and real data analysis, we demonstrate at least three major advantages of our model: (i) compared with existing popular methods for analyzing the paired RNA-seq data, the proposed PairedFB procedure has overall better performance in ranking the true DEGs on the top, especially for large sample sizes and large level of heterogeneity in treatment effects across the pairs. (ii) The PairedFB controls the FDR at desired levels for all the cases considered, while competing methods have highly inflated FDR levels for small to moderate sample sizes. (iii) Our method can be applied to identify biologically significant DEGs with controlled FDR, while the common two-step procedure can have highly inflated FDR even for large sample sizes. In addition, our procedure is robust to model misspecification in terms of its relative performance compared to competing methods with better ranking ability and lowest actual FDR.
Our comprehensive simulation studies also lead us to make the following conclusions: (i) we believe it is very important to model or accommodate the heterogeneous treatment effects when they exist. Failure to do so may lead to poor ranking ability and highly inflated FDR; (ii) when the sample size is small, all the procedures considered in the paper suffer either in terms of highly inflated FDR or low power based on our simulation studies. We thus highly recommend that one should consider designing a paired RNA-seq experiment with sample sizes larger than 3 (preferably larger than 5).
As is the case for most full Bayesian analysis using MCMC algorithm, the computation time for our model is more intense than frequentist method or empirical Bayesian method. By optimizing the program through Rcpp package (Eddelbuettel and François, 2011), we are able to run 25 000 iterations of MCMC algorithm in about one and half hours for over 10 000 genes. Besides, in order to have clear interpretation of parameter of interest, we include special function in the likelihood, which brings instability of our computation especially when the gene expression data is large, we overcome the problem by using the equivalent transformation of Gauss’s hypergeometric function and successfully implement it through the GNU Scientific Library for C++ (Gough, 2009). However, the complexity and intense computation of our model are not sacrificed without any benefits. Our method is able to directly interpret the biological significance of each gene by providing the posterior probabilities of the fold-change exceeding certain range, which is beyond merely claiming statistical significance for each gene. In addition, these posterior probabilities can be easily applied to the ‘posterior expected FDR’ decision rule in order to claim statistical significance for different magnitude of biological significance.
In this paper, we have considered a single normal prior distribution for of DEGs. In some cases, with both up- and down-regulated genes, a two-component mixture of normal might work better for the DEGs. This can be investigated in our future work. Note that our full hierarchical Bayesian model can also be extended to the paired design for comparison under multiple K conditions. The choices should be made among possible models for each gene instead of 2, where each model represents a combination of indicators to indicate whether the gene is DE under certain condition. We could include condition-specific mean proportion of treatment mean out of the overall pair mean in the likelihood and find the maximum posterior under certain condition by using model averaging or to develop condition- or model-specific FDR decision rule. Another future direction can be generalizing the PairedFB to randomized complete block design by imposing a Dirichilet-Multinomial model when one considers the conditional distribution of the several counts given the total sum of the counts in each block.
Supplementary Material
Acknowledgements
We sincerely thank three anonymous reviewers for critically reading the manuscript and suggesting substantial improvements.
Funding
This work is partially done with the use of the BIOMIX compute cluster at University of Delaware, which was made possible through funding from Delaware INBRE (NIGMS P20GM103446), the State of Delaware and the Delaware Biotechnology Institute. Jianlin Chen is partially supported by National Science Foundation grant (NO. IOS1545780).
Conflict of Interest: none declared.
Contributor Information
Yuanyuan Bian, Department of Statistics, University of Missouri, Columbia, MO, USA.
Chong He, Department of Statistics, University of Missouri, Columbia, MO, USA.
Jie Hou, Department of Electrical Engineering and Computer Science, University of Missouri, Columbia, MO, USA.
Jianlin Cheng, Department of Electrical Engineering and Computer Science, University of Missouri, Columbia, MO, USA.
Jing Qiu, Department of Applied Economics and Statistics, University of Delaware, Newark, DE, USA.
References
- Abramowitz M., Stegun I.A. (1964) Hypergeometric functions. In: Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. Vol. 55. Courier Corporation, Chelmsford, MA, pp. 555–566. [Google Scholar]
- Cai B., Dunson D.B. (2006) Bayesian covariance selection in generalized linear mixed models. Biometrics, 62, 446–457. [DOI] [PubMed] [Google Scholar]
- Chung L.M. et al. (2013) Differential expression analysis for paired RNA-seq data. BMC Bioinformatics, 14, 110.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cui S. et al. (2016) What if we ignore the random effects when analyzing RNA-seq data in a multifactor experiment. Stat. Appl. Genet. Mol. Biol., 15, 87–105. [DOI] [PubMed] [Google Scholar]
- Eddelbuettel D., François R. (2011) Rcpp: seamless R and C++ integration. J. Stat. Softw., 40, 1–18. [Google Scholar]
- Esteve-Codina A. et al. (2017) A comparison of RNA-seq results from paired formalin-fixed paraffin-embedded and fresh-frozen glioblastoma tissue samples. PLoS One, 12, e0170632.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gough B. (2009) GNU Scientific Library Reference Manual. Network Theory Ltd, Godalming, Surrey, UK. [Google Scholar]
- Graw S. et al. (2015) Robust gene expression and mutation analyses of RNA-sequencing of formalin-fixed diagnostic tumor samples. Sci. Rep., 5, 12335.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo Y. et al. (2013) Evaluation of read count based RNAseq analysis methods. BMC Genomics, 14, S2.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hardcastle T.J., Kelly K.A. (2013) Empirical Bayesian analysis of paired high-throughput sequencing data with a beta-binomial distribution. BMC Bioinformatics, 14, 135.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Law C.W. et al. (2014) Voom: precision weights unlock linear model analysis tools for RNA-seq read counts. Genome Biol., 15, R29.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu F. et al. (2015) A semi-parametric Bayesian approach for differential expression analysis of RNA-seq data. J. Agric. Biol. Environ. Stat., 20, 555–576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Love M.I. et al. (2014) Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol., 15, 550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCarthy D.J. et al. (2012) Differential expression analysis of multifactor RNA-seq experiments with respect to biological variation. Nucleic Acids Res., 40, 4288–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newton M.A. et al. (2004) Detecting differential gene expression with a semiparametric hierarchical mixture method. Biostatistics, 5, 155–176. [DOI] [PubMed] [Google Scholar]
- Plummer M. et al. (2006) CODA: convergence diagnosis and output analysis for mcmc. R News, 6, 7–11. [Google Scholar]
- Robinson M.D., Oshlack A. (2010) A scaling normalization method for differential expression analysis of RNA-seq data. Genome Biol., 11, R25.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson M.D., Smyth G.K. (2007) Moderated statistical tests for assessing differences in tag abundance. Bioinformatics, 23, 2881–2887. [DOI] [PubMed] [Google Scholar]
- Scott J.G., Berger J.O. (2010) Bayes and empirical-bayes multiplicity adjustment in the variable-selection problem. Ann. Stat., 38, 2587–2619. [Google Scholar]
- Soneson C., Delorenzi M. (2013) A comparison of methods for differential expression analysis of RNA-seq data. BMC Bioinformatics, 14, 91.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Subramanian A. et al. (2005) Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc. Natl. Acad. Sci., 102, 15545–15550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuch B.B. et al. (2010) Tumor transcriptome sequencing reveals allelic expression imbalances associated with copy number alterations. PLoS One, 5, e9317.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van De Wiel M.A. et al. (2013) Bayesian analysis of RNA sequencing data by estimating multiple shrinkage priors. Biostatistics, 14, 113–128. [DOI] [PubMed] [Google Scholar]
- Yu Y.-H. et al. (2008) The evolving transcriptome of head and neck squamous cell carcinoma: a systematic review. PLoS One, 3, e3215.. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.