SArKS: de novo discovery of gene expression regulatory motif sites and domains by suffix array kernel smoothing

Abstract

Motivation

We set out to develop an algorithm that can mine differential gene expression data to identify candidate cell type-specific DNA regulatory sequences. Differential expression is usually quantified as a continuous score—fold-change, test-statistic, P-value—comparing biological classes. Unlike existing approaches, our de novo strategy, termed SArKS, applies non-parametric kernel smoothing to uncover promoter motif sites that correlate with elevated differential expression scores. SArKS detects motif k-mers by smoothing sequence scores over sequence similarity. A second round of smoothing over spatial proximity reveals multi-motif domains (MMDs). Discovered motif sites can then be merged or extended based on adjacency within MMDs. False positive rates are estimated and controlled by permutation testing.

Results

We applied SArKS to published gene expression data representing distinct neocortical neuron classes in Mus musculus and interneuron developmental states in Homo sapiens. When benchmarked against several existing algorithms using a cross-validation procedure, SArKS identified larger motif sets that formed the basis for regression models with higher correlative power.

Availability and implementation

https://github.com/denniscwylie/sarks.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Discrete sequences—of tones, of symbols or of molecular building blocks—can provide clues to other characteristics of the entities from which they are derived: a phrase in a bird’s song can reveal which species it belongs to, the use of an idiomatic expression can pinpoint a speaker’s geographic origin and a specific short string of nucleotide residues can illuminate the function of a DNA domain. In these examples, insights are gleaned from the occurrence of informative motifs—short subsequences that match some frequently recurring discernible pattern.

Of particular interest are DNA regions modulating differential gene expression. The regions contain motifs that produce defined patterns of gene expression, however, the details of how and which motifs are needed for expression specificity remain poorly understood.

We present a broadly applicable algorithm for identifying DNA regulatory regions that support differential gene expression. Our strategy is predicated on the following suppositions: (i) gene expression regulatory regimes involve the binding of transcription factors (TFs) to sites on non-coding DNA in the vicinity of a transcription start site (TSS) (Maston et al., 2006; Nguyen and D’haeseleer, 2006); (ii) TFs act combinatorially to attract and repel transcription machinery (Walhout, 2006); (iii) the same TF-binding site may appear multiple times within a stretch of DNA, interspersed with other binding sites (Gotea et al., 2010); and (iv) there is more than one solution: different genes, even those co-expressed within a single cell, may rely on different regulatory mechanisms (Badis et al., 2009). In accord with these suppositions, we aim to identify TF-binding sites associated with enriched transcripts and scrutinize their arrangement for significant patterns that can then be evaluated experimentally.

Many motif identification methods have been described. Consensus-based methods such as Weeder (Pavesi et al., 2001, 2004) focus on fixed-length motifs that repeatedly occur (with few mismatches) in sequences of interest, and can be efficiently implemented using suffix trees (Marsan and Sagot, 2000; Pavesi et al., 2001; Sagot, 1998). Alternately, profile-based methods such as MEME (Bailey and Elkan, 1995; Bailey et al., 2006, 2009) build a probabilistic motif profile to be compared with a background model in order to classify subsequences as either matching the motif or not.

In contrast, discriminative methods (Sinha, 2003) identify motifs that differentiate one set of sequences (e.g. promoter regions for genes with a given expression pattern) from another (e.g. reference promoter regions). Many approaches have been applied to this differentiation problem (e.g. Fauteux et al., 2008; Huggins et al., 2011; Redhead and Bailey, 2007; Segal and Sharan, 2005; Segal et al., 2002; Valen et al., 2009; Yao et al., 2014). One popular example, DREME (Bailey, 2011), employs Fisher’s exact test to compare counts of motif matches in the target/positive sequences with counts in the background/negative sequences. HOMER (Heinz et al., 2010) uses similar hypergeometric enrichment calculations, but couples them to a zero-or-one-occurrence-per-sequence (ZOOPS) scoring approach. The recent motif finder STEME (Reid and Wernisch, 2014) extends a suffix tree-based approximate expectation-maximization approach (Reid and Wernisch, 2011) into a practical tool capable of discriminative motif discovery.

When discriminative methods are applied to differential gene expression, they impose a binary representation (such as elevated or not elevated expression). However, differential gene expression is generally described using a continuous measure (t-statistics, f-statistics, etc.), with some genes more affected than others by a difference in state. It is more useful, therefore, to use ‘correlative motif discovery,’ which seeks motifs whose presence signals a trend toward higher or lower values of the continuous measure. A few such correlative algorithms have been described, including MOTIF REGRESSOR (Conlon et al., 2003), which first applies the (non-correlative) MDScan (Liu et al., 2002) algorithm to identify motifs in a subset of high-scoring sequences, then filters the motif set based on the predictive value of regression models based on the selected motifs. Another correlative algorithm, FIRE (Elemento et al., 2007), iteratively optimizes the mutual information between sequence scores and occurrences of candidate motifs, starting from a set of most informative ‘seed’ motifs. Both of these algorithms may be seen as applying correlational information (regression or mutual information, respectively) as a filter to select and refine a set of candidate motifs generated in a non-correlative manner.

The generation of a seed motif set paves the way for sequence ranking by counting occurrences of the uncovered motifs within each sequence w_b. However, as the number of possible motifs of length k grows exponentially with k, given a fixed set of sequences $\left\{w_b\right\}$ and a suitably large k, only a fraction of possible length-k motifs will be observed in any sequence w_b. For example, in 1000 sequences $w_1,\dots ,w_{1000}$ each of length $\left|w_b\right|=1000$, at most one million k-mers of any length k can be found.

In contrast, we aimed to develop SArKS as an algorithm for discovery and localization of correlative motifs that does not require seed motifs to minimize the possibility of missing informative motifs due to suboptimal seeding. Our solution was to focus on observed substrings of the sequences w_b, not all possible k-mer patterns that could be present in the w_b.

Specifically, SArKS relies on suffixes of w_b—substrings formed by deleting the beginning of a string. As there are only $\left|w_b\right|$ non-empty suffixes of w_b, SArKS is able to process all suffixes of its input sequences even when when they are long and/or numerous. SArKS then assesses suffix similarity by lexicographic sorting: just as words sharing a common prefix are found close together in a dictionary, suffixes starting with a shared k-mer are assigned similar numeric positions in the sorted list of all suffixes (Fig. 1). By correlating sorted suffix position with suffix sequence score using kernel smoothing, SArKS develops this idea into an algorithm for de novo discovery of motif sites, with a natural extension for identification of longer multi-motif domains (MMDs) spanning tens to hundreds of bases (Section 2).

Fig. 1.

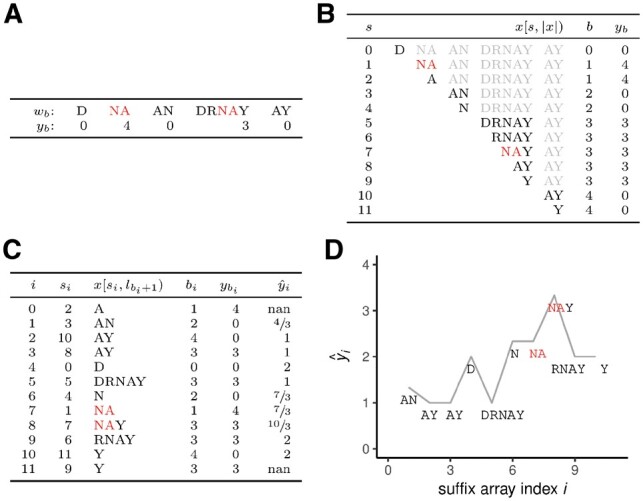
Overview of SArKS method. (A) Concatenation of sequences w_b (end-of-sequence character indicated by white space instead of $ for visual clarity) to form string $x=\mathrm{D}\$\text{NA}\$\text{AN}\$\text{DRNAY}\$\text{AY}\$$. (B) Table of all suffixes of x (part of each suffix following first end-of-sequence character shown in light gray), along with index b of input sequence w_b each suffix derived from and score y_b associated with w_b. (C) Sorted suffix table indicating suffix array index i, suffix array value s_i, suffix (sequence following first end-of-sequence character has been removed), sequence of origin b_i, associated score $y_{b_i}$, and smoothed score ${\widehat{y}}_i$ generated using smoothing window of size 3 (kernel half-width κ  =  1). (D) Smoothed scores ${\widehat{y}}_i$ plotted against suffix array index i, indicating peak at i = 8 corresponding to suffix NAY of input sequence DRNAY. Note that prefix NA of this suffix is longest substring common to the two input sequences w₁ and w₃ with scores $y_b>0$

We applied SArKS to two RNA-seq datasets using non-parametric permutation testing to compute significance thresholds and to estimate false positive rates. We demonstrate that SArKS outperforms existing algorithms at identifying correlative motifs in cross-validation testing scenarios. The top motif patterns and MMDs identified by SArKS include known regulatory elements (Elbarbary et al., 2016; Mathelier et al., 2015). Thus, the correlational approach used by SArKS takes full advantage of differential expression RNA-seq data to illuminate prospective sequence-dependent mechanisms of gene expression regulation.

2 Materials and Methods

Symbolic notation is described both when introduced and systematically in Section S2.1.

Given n sequences w_b (also referred to as words) with associated scores y_b, the essential steps of the algorithm (illustrated in Fig. 1 and described in Section 2.1) consist of:

1. concatenating all the sequences w_b into one supersequence x;

2. constructing the suffix array $[s_i]$ of this supersequence (Equation 2), where i indexes all suffixes of x sorted into lexicographic order;

3. mapping suffix positions i back to the sequences $w_{b_i}$ from which the beginnings of the associated suffixes are derived (Equation 3); and

4. for each i, applying kernel smoothing to locally regress the sequence scores $y_{b_j}$ on suffix positions j lexically near i (Equation 4).

We thus encode the motif pattern corresponding to the first few characters of the suffix of x beginning at character s_i with the numerical suffix array index value i. Because i gives the position of a suffix in the lexicographically sorted list of suffixes of the concatenated supersequence x, multiple occurrences of a highly conserved motif—even if they derive from different sequences w_b—will be consolidated into a run i, i + 1, …, j of consecutive index values. Averaging together runs of j − i consecutive scores by kernel smoothing using a kernel of width j − i thus offers a way to compare the scores $y_{b_i},\hspace{0.17em}{y}_{b_{i+1}}$, …, $y_{b_j}$ to the overall score distribution (1).

2.1 Motif selection

Concatenate all words w_b (each assumed to end in the line-terminator character $ lexically prior to all other characters) to form word

$$x=w_0*w_1*\dots *w_{n-1}$$ (1)

of length $l_n=\left|x\right|=\sum _b\left|w_b\right|$. Define also $l_b=\sum _{b\prime <b}\left|w_{b\prime }\right|$. Then $x[l_b,l_{b+1})=w_b$; that is, the substring of the concatenated string starting at position l_b (inclusive) and ending immediately before position $l_{b+1}$ (exclusive) is the sequence w_b (we denote the first character of a string w by $w[0]$, the second $w[1]$, etc.).

Lexically sort suffixes $x_s=x[s,|x|)$ into ordered set

$$S=\{x_{s_0},x_{s_1},\dots ,x_{s_{l_n-1}}\}$$ (2)

thereby defining suffix array $[s_i]$ mapping index i of suffix in S to suffix position s in x [in our software, we rely on the Skew algorithm (Kärkkäinen and Sanders, 2003) modified to use a difference cover of 7 and implemented in SeqAn (Döring et al., 2008) to efficiently compute the suffix array].

Define block array $[b_i]$ by

$$b_i=\text{max\hspace{0.17em}}\mathit{\{}{\mathit{\text{b|l}}}_b\le {\mathit{\text{s}}}_{\mathit{\text{i}}}\}$$ (3)

mapping index i of suffix in S to block b containing suffix position s_i. The block array then tells us that the character $x[s_i]$ at position s_i in the concatenated string x is derived from $w_{b_i}[s_i-l_{b_i}]$ in the sequence $w_{b_i}$.

Calculate smoothed scores as locally weighted averages

$${\widehat{y}}_i=\frac{{\displaystyle \sum _j{K}_{ij}}{y}_{b_j}}{{\displaystyle \sum _j{K}_{ij}}}$$ (4)

where the kernel K_ij acts as a weighting factor for the contribution of the score $y_{b_j}$ to the smoothing window centered at sorted suffix index i. K_ij is used to measure how similar (the beginning of) the suffix $x[s_j,|x|)$ is to be considered to (the beginning of) the suffix $x[s_i,|x|)$ in the calculation of a representative score ${\widehat{y}}_i$ averaged over suffixes similar to $x[s_i,|x|)$. As the suffixes have been sorted into lexicographic order, the magnitude of the difference i − j reflects this similarity: the key idea of the kernel smoothing approach described here is that Equation (4) with K_ij defined to be a function of $|i-j|$ may therefore offer a computationally tractable approach for identifying similar substrings which tend to occur preferentially in high-scoring words w_b.

In this work, we use a uniform kernel

$$K_{\mathit{ij}}^{(\kappa )}=\{\begin{array}{cc}1\hfill & \text{if}\hspace{0.17em}|i-j|\le \kappa \hfill \\ 0\hfill & \text{otherwise}\hspace{0.17em}\hfill \end{array}$$ (5)

which allows Equation (4) to be computed in terms of cumulative sums:

$$\frac{\sum _j{K}_{\mathit{ij}}^{(\kappa )}{y}_{b_j}}{\sum _j{K}_{\mathit{ij}}^{(\kappa )}}=\frac{1}{2\kappa +1}\sum _{j=i-\kappa }^{i+\kappa }{y}_{b_j}=\frac{1}{2\kappa +1}\left(\sum _{j=1}^{i+\kappa }{y}_{b_j}-\sum _{j=1}^{i-\kappa -1}{y}_{b_j}\right)$$ (6)

The kernel half-width κ appearing in Equation (5) is an important adjustable parameter controlling the degree of smoothing. Increasing κ smooths over more diverse suffixes, potentially increasing statistical power at the expense of the resolution of the detected motifs (i.e. length of k-mer prefix common to suffixes in the smoothing window). We recommend investigating a range of values of this parameter as is illustrated in Section 3.

Set length ${\widehat{k}}_i$ for k-mer associated with suffix array index i by averaging locally the length of suffix sequence identity:

$${\widehat{k}}_i=\frac{{\displaystyle \sum _{j\ne i}{K}_{ij}}\text{max\hspace{0.17em}}\{\mathit{\text{k}}\le {\mathit{\text{k}}}_{\text{max}}\mathit{\text{|x}}[{\mathit{\text{s}}}_j,{\mathit{\text{s}}}_j\mathit{\text{+k}})\mathit{\text{=x}}[{\mathit{\text{s}}}_i,{\mathit{\text{s}}}_i\mathit{\text{+k}})\}}{{\displaystyle \sum _{j\ne i}{K}_{ij}}}$$ (7)

where $k_{\text{max}}$ functions both to increase computational efficiency and to make ${\widehat{k}}_i$ more robust in the presence of a small number of long identical substrings. All results presented here based on $k_{\text{max}}=12$: This value was selected as $k_{\text{max}}\approx {\hspace{0.17em}\text{log}\hspace{0.17em}}_4\left|x\right|$ where x is the longest concatenated sequence string considered in Section 3.2.1, so that for $k>k_{\text{max}}$ there are more distinct k-mers than there are positions for such k-mers to occur in all of the sequences w_b composing x.

Equation (7) is similar to Equation (4) except that: (i) Equation (7) smooths the length of the longest prefix on which the suffixes $x[s_i,|x|)$ and $x[s_j,|x|)$ agree instead of smoothing the score $y_{b_j}$ as in Equation (4); and (ii) Equation (7) omits the central term i = j as it trivially compares the suffix beginning at s_i to itself and is thus uninformative.

A straightforward approach to identifying correlative motifs using SArKS would then be to set a score threshold θ and take motifs to be k-mers prefixing the suffixes starting at the positions s_i in the concatenated string x. This is the essence of our method, though below we add two filters designed to pinpoint the optimal locations s_i at which to initiate motifs and, in Section S2.2, to remove likely false positive positions.

Defining the negative spatial shift operator $\eta (i)$ which yields the unique suffix array index corresponding to the spatial position immediately prior to s_i, so that $s_{\eta (i)}=s_i-1$, as well as the positive shift operator $\rho (i)$ similarly defined by the condition $s_{\rho (i)}=s_i+1$, we start with a preliminary filtered suffix array index set I consisting of those i for which (i) the smoothed score ${\widehat{y}}_i\ge \theta$ and (ii) ${\widehat{y}}_i$ is not less than the smoothed scores of the spatial positions in x immediately adjacent to s_i (i.e. s_i must be the loci of a peak in plot of ${\widehat{y}}_i$ versus spatial position s_i):

$$I=\left\{i|\left({\widehat{y}}_i\ge \theta \right)\wedge \left({\widehat{y}}_{\eta (i)}\le {\widehat{y}}_i\ge {\widehat{y}}_{\rho (i)}\right)\right\}$$ (8)

from which we obtain the associated set M of k-mers beginning at the positions s_i in x by

$$M=\left\{x[s_i,s_i+\lfloor {\widehat{k}}_i\rceil )|i\in I\right\}$$ (9)

where $\lfloor {\widehat{k}}_i\rceil$ is the nearest integer to ${\widehat{k}}_i$. Strategies for setting the filtering threshold θ based on the permutation testing method are described in Section S2.5. In the next section, we recommend one additional filter—designed to limit the impact of intra-sequence tandem repeats on reported motifs—to be incorporated into the definition of the index set I, replacing Equation (8) by Equation (10), for use in Equation (9).

The k-mers composing the set M (Equation 9) constitute the SArKS motif set when spatial smoothing is not employed. When spatial smoothing is employed to detect MMDs (Sections 2.3 and S2.4), a modified procedure for merging spatially contiguous motif sites within such domains leads to Equation (S9) for the final k-mer motif set $M_{\text{spatial}}$.

2.2 Limiting the impact of intra-sequence repeats

The frequent occurrence of short tandem repeats in the genome (Ellegren, 2004) can cause smoothing windows to be skewed toward a relatively small number of distinct sequences (discussed in Section S2.2). As a result, the smoothed scores ${\widehat{y}}_i$ may reflect fewer input sequences, reducing precision and increasing false positive rates among the high-scoring k-mers. To filter out such false positives, Section S2.2 introduces the Gini impurity score g_i measuring the ‘effective sequence count’ contributing to the smoothing window centered at i, while Section S2.5 demonstrates that g_i predicts the variance of the smoothed score for suffix array index i under the null hypothesis of independence between sequence and score. We can thus modify Equation (8) to remove potential false positive i values characterized by low Gini impurities g_i:

$$I=\left\{i|({\widehat{y}}_i\ge \theta )\wedge \left({\widehat{y}}_{\eta (i)}\le {\widehat{y}}_i\ge {\widehat{y}}_{\rho (i)}\right)\wedge (g_i\ge g_{\text{min}})\right\}$$ (10)

screening out positions i for which the repeated occurrence of a few high-scoring words in the window centered at i leads to ${\widehat{y}}_i\ge \theta$.

2.3 Spatial smoothing to identify MMDs

Existing motif discovery approaches recognize the tendency of regulatory motifs to cluster into domains (Wasserman and Sandelin, 2004). Our algorithm exploits this feature, identifying candidate regulatory regions through the application of a second round of kernel smoothing over suffix positions s_i within words:

$${\widehat{\widehat{y}}}_{s_i}=\frac{{\displaystyle \sum _j{L}_{s_i{t}_j}}{\widehat{y}}_j}{{\displaystyle \sum _t{L}_{s_{i}t}}}$$ (11)

where we use uniform kernels of the form

$$L_{s_i{t}_j}^{(\lambda )}=\{\begin{array}{ll}1\hfill & \text{if }\left(0\le (t_j-s_i)<\lambda \right)\wedge \left(b_i=b_j\right)\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (12)

(generally with width $\lambda \ne \kappa$) to search for regions of length λ with elevated densities of high-scoring motif sites. Note that ${\widehat{\widehat{y}}}_{s_i}$ defined by Equation (11) is indexed not by suffix array index i but by suffix array value s_i giving the spatial position s_i in the concatenated word x.

Spatial smoothing requires a threshold ${\theta }_{\text{spatial}}\ne \theta$, as the doubly smoothed scores ${\widehat{\widehat{y}}}_{s_i}$ tend to be less dispersed compared with the singly smoothed ${\widehat{y}}_i$. The threshold ${\theta }_{\text{spatial}}$ can be used to define an index set $I_{\text{spatial}}$ in a manner similar to how I is defined by Equation (10). This procedure is detailed in Section S2.4, which additionally defines the set $J_{\text{spatial}}$ of suffix array indices i corresponding to the starting positions of MMDs. It then details the procedure adopted by SArKS to merge spatially contiguous motif sites within the same MMD, yielding the set $I_{\text{spatial}}$ of suffix array indices i and merged motif lengths ${\widehat{\widehat{k}}}_{s_i}$ required to obtain the merged motif set $M_{\text{spatial}}$ analogous to Equation (9).

2.4 Permutation testing to establish significance of motif set

The significance of the correlation between the occurrences of motifs uncovered by SArKS and the sequence scores y_b can be evaluated by examining results obtained when the sequences w_b and the scores y_b are independent of each other. To this end, the word scores y_b are subjected to permutation π to define $y_b^{(\pi )}=y_{\pi (b)}$. If the permutation π is randomly selected independently of both the sequences w_b and the scores y_b, any true relationships between sequences and scores will be disrupted. Sections S2.5–S2.6 develop the strategy used by SArKS to set thresholds θ (and/or ${\theta }_{\text{spatial}}$) for each combination of parameters $\kappa ,\lambda ,g_{\text{min}}$ to control the overall false positive rate.

3 Results and discussion

3.1 Illustration of SArKS using simulated data

To illustrate SArKS, we first applied it to a simple simulated toy dataset in which 30 random sequences w_b were generated with each letter $w_b[s]$ drawn independently from a $\text{Unif}\left\{\mathrm{A},\mathrm{C},\mathrm{G},\mathrm{T}\right\}$ distribution. We then embedded the k-mer motif CATACTGAGA (k = 10) in the last 10 sequences (i.e. those w_b with $b\ge 20$) by choosing a position s_b independently for each sequence w_b from $\text{Unif}\left\{0,\dots ,\left|w_b\right|-k\right\}$ and replacing $w_b[s_b,s_b+k)$ with the motif. Scores were assigned to the sequences according to whether the motif had been embedded: y_b = 0 if $b\in [0,20)$, y_b = 1 if $b\ge 20$.

The kernel half-width κ = 4 was used to obtain smoothing windows of size similar to the number of motif-positive sequences, $2\kappa +1\approx \left|\right\{b|y_b=1\}|$. As this number cannot be known in advance when applying SArKS to real data, in practice we recommend testing a range of κ-values as done in Section 3.2.1 below.

Figure 2 plots ${\widehat{y}}_i$ as obtained from Equation (4) applying the method of Section 2.1 to search for motifs. The highest peaks in the plot correspond to the positions of various substrings of the embedded motif, and correspond to the set M of k-mers defined by the $x[s_i,s_i+\lfloor {\widehat{k}}_i\rceil )$ column of Table 1.

Fig. 2.

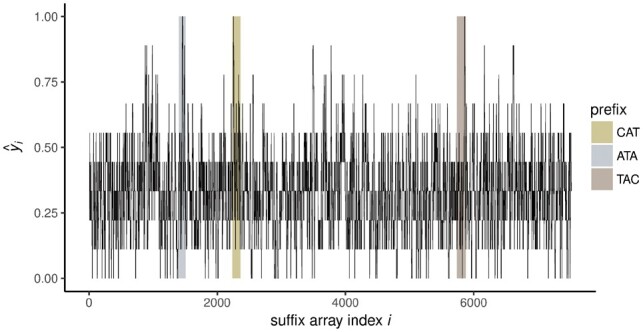
Locating peaks in kernel-smoothed scores ${\widehat{y}}_i$. Kernel-smoothed scores ${\widehat{y}}_i$ [Equation (4), using kernel half-width κ = 4] are plotted against suffix array index i for simulated dataset. Gold, silver and bronze bars indicate positions in lexicographically sorted table of suffixes beginning with prefixes CAT, ATA and TAC, which correspond to the first five characters of embedded motif CATACTGAGA. Detailed information on the peak locations at which the smoothed score ${\widehat{y}}_i=1$ is presented in Table 1 below

Table 1.

Suffix array peak positions with ${\widehat{y}}_i\ge \theta$

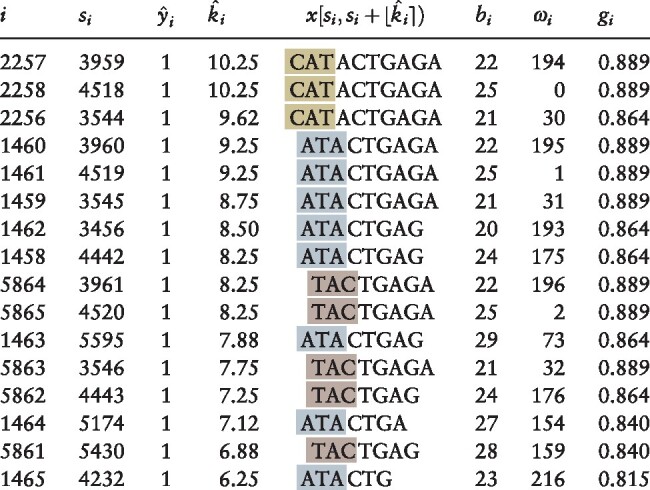
Note: Illustration of motif selection process (Section 2.1) applied to simulated data (using kernel half-width κ = 4). All positions for which sequence smoothed score ${\widehat{y}}_i\ge \theta =1$ are shown; table is sorted in descending order of the estimated motif length ${\widehat{k}}_i$. Columns indicate values of key variables for the suffix associated with the corresponding peak: (i) suffix array index i giving position of suffix in lexicographically sorted list of all suffixes; (s_i) suffix array value s_i giving spatial position of suffix in concatenated sequence x; (${\widehat{y}}_i$) kernel-smoothed score ${\widehat{y}}_i$ (Equation 4); (${\widehat{k}}_i$) estimated length ${\widehat{k}}_i$ (Equation 7) of conserved $\lfloor {\widehat{k}}_i\rceil$-mer prefix of suffixes within smoothing window centered on suffix array index i; ($x[s_i,s_i+\lfloor {\widehat{k}}_i\rceil )$) the corresponding conserved $\lfloor {\widehat{k}}_i\rceil$-mer $x[s_i,s_i+\lfloor {\widehat{k}}_i\rceil )$ (Equation 9); (b_i) the input sequence b_i (Equation 3) from which the suffix is derived; (ω_i) the spatial position ω_i at which the suffix is found within sequence b_i; and (g_i) the Gini impurity g_i (Equation S4) for the smoothing window centered at i. Note that each of these peaks corresponds to a suffix derived from a position within the first three characters of an instance of the embedded motif CATACTGAGA. Gold highlighting indicates peaks starting from the first character of the embedded motif, silver the second and bronze the third.

Removing nested k-mers from Table 1 as described in Section S2.3, Equation (S7) leaves only the rows for $i\in \{2257, 2258, 2256, 1462, 1458, 1463\}$. Applying Equation (S8) then extends the 8-mer ATACTGAG of the rows $i\in \{1462, 1458, 1463\}$ to the full 10-mer, so that, following Equation (S9), the final k-mer set $M\prime =\left\{\text{CATACTGAGA}\right\}$ is recovered (Table 1).

Section S2.5 illustrates the utility of setting a minimum Gini impurity $g_{\text{min}}$ during motif selection to reduce the false positive rate: 190 out of 1000 random permutations generated at least one position $i^{(\pi )}$ for which ${\widehat{y}}_{i^{(\pi )}}^{(\pi )}=1\ge \theta$ (for this toy model θ was taken to have the maximum possible value of 1), but only 20 of these permutations yield any results if $g_{\text{min}}=0.8506$ [following Equation (S5) with $\gamma =0.1$] is applied. Based on these results, we can derive a 95% confidence interval of (1.2%, 3.1%) for the family-wise error rate (FWER, a type of false positive rate; see Section S2.6).

3.2 Uncovering promoter motifs associated with differential gene expression

We set out to analyze two published RNA-seq datasets (Close et al., 2017; Mo et al., 2015) using SArKS. The first study presented transcriptome data for adult mouse neurons sorted according to cell class (Mo et al., 2015). In particular, this study was among the first to profile parvalbumin (PV)-expressing interneurons, a major inhibitory subclass in the mammalian neocortex. PV basket and chandelier neurons are intimately involved in the microcircuitry of sensory processing, memory formation and critical period plasticity (Cobb et al., 1995; Klausberger and Somogyi, 2008). Dysfunction of PV interneurons has been linked to autism and schizophrenia (Lewis et al., 2005), and the ability to access these neurons using a cell type-specific promoter has been a priority for brain scientists. The second study examined transcriptomes of differentiating interneurons at several developmental time points (Close et al., 2017). In the sections below, we describe the parameters and results of SArKS analyses for both datasets. In Section S3.2.2, we inspect the SArKS-elicited motifs associated with PV neurons and demonstrate how to extend the application of SArKS to identify promoter MMDs.

3.2.1 Dataset 1: cell class-specific transcriptome analysis

We analyzed RNA-seq gene expression data from mouse neocortical neurons pooled based on genetically defined cell classes (Mo et al., 2015) to identify regulatory motifs associated with PV neuron-specific gene expression.

After accounting for differential expression and chromatin accessibility (Section S2.7.1), we examined two sets of sequences for 6326 unique transcripts. The first set covered upstream regions −3000 base pairs (bp) to the TSS, the second set extended from the TSS to +1000 bp.

We tested a range of half-window sizes $\kappa \in \{250, 500, 1000, 2500\}$ with the maximum value of 2500 selected to produce a smoothed window of size $2\kappa +1=5001$ similar to the number of input sequences (6326). Note that smaller windows are less likely to contain sample multiple suffixes from the same promoter sequence: in particular, windows of width greater than the number of distinct sequences must contain multiple suffixes from at least one promoter sequence.

For each half-window size κ, we applied two minimum Gini impurity values $g_{\text{min}}$ set according to Equation (S5) with first $\gamma =0.1$ and then $\gamma =0.2$. Also for each value of κ, we examined three separate spatial window sizes $\lambda \in \{0, 10, 100\}$. These values were selected to investigate the performance of SArKS using no spatial smoothing (λ = 0), using a window λ = 10 of the typical length scale of eukaryotic TF-binding sites (Stewart et al., 2012), and using a window λ = 100 to target the low end of the enhancer length distribution (Loots, 2008). Thresholds θ (for analyses with no spatial smoothing) or ${\theta }_{\text{spatial}}$ (for analyses with $\lambda \in \{10, 100\}$) were set according to the permutation testing strategy detailed in Section S2.5 using R = 100 permutations.

3.2.2 Dataset 2: differentiating interneuron transcriptome analysis

We examined RNA-seq data for differentiating human interneurons (Close et al., 2017), applying SArKS to identify promoter motifs associated with elevated gene expression in doublecortin-positive (DCX+) GABAergic neurons compared with DCX− cells. Differential expression was assessed for 6939 genes as detailed in Section S2.7.2 and we analyzed upstream sequences (from −3000 bp to the TSS) and downstream sequences (from the TSS to +1000 bp) as described in Section 3.2.1.

SArKS analysis was conducted using all combinations of half-window size $\kappa \in \{250, 500, 1000, 2500\}$ and spatial smoothing window $\lambda \in \{0, 10, 100\}$ for the reasons described in Section 3.2.1. However, for this dataset, the minimum Gini impurity thresholds were computed using only $\gamma =0.1$—we had seen little benefit from including the higher value $\gamma =0.2$ in our experience with the Mo (2015) dataset (see Section 3.2.4). Thresholds θ or ${\theta }_{\text{spatial}}$ were set according to the permutation testing strategy detailed in Section S2.5 using R = 100 permutations.

3.2.3 Benchmark comparisons for correlative motif discovery

We conducted a cross-validation benchmarking study to compare SArKS correlative motif discovery performance to that of five motif search algorithms. Two of these methods, FIRE (Elemento et al., 2007) and MOTIF REGRESSOR (Conlon et al., 2003), were chosen because they rely on alternative approaches to correlative motif discovery. The remaining algorithms, DREME (Bailey, 2011), HOMER (Heinz et al., 2010) and STEME (Reid and Wernisch, 2014) are popular discriminative methods, which we have run by discretizing our score data with promoter sequences b considered ‘positive’ sequences if the score $y_b\ge 2$, ‘negative’ otherwise. While there is a definite loss of information in this discretization—the avoidance of which is one of the primary motivations for the introduction of SArKS, as well as other correlative motif algorithms—we were interested in direct comparison of correlative and discriminative algorithms to assess the degree to which correlative algorithms actually benefit from avoiding discretization.

We note also that most of the algorithms compared here (DREME, HOMER, MOTIF REGRESSOR and STEME) use a position-weight matrix representation of sequence motifs, while FIRE opts for a simpler regular expression representation. In contrast, SArKS takes the more granular approach of directly returning a list of k-mers, with degenerate motif patterns represented as multiple similar-yet-distinct k-mers. These k-mers can be clustered into higher-order motif structures—one method for doing so is offered in our software implementation of SArKS (https://github.com/denniscwylie/sarks)—but, as this step is essentially independent of the SArKS algorithm itself, we do not consider such k-mer clustering further in this article.

We split the 6326 transcripts selected from the Mo (2015) dataset into five disjoint subsets $V_1,V_2,\dots ,V_5$ (the name V_f intended to suggest the $f\text{th}$ validation set) of approximately equal size ($\left|V_1\right|=1266$, while $\left|V_f\right|=1265$ for f > 1). The set of 6939 genes selected from the Close (2017) dataset was similarly partitioned into disjoint cross-validation folds.

For both datasets, for both promoter sequence ranges investigated, and for each of the algorithms evaluated, five separate motif identification analyses were conducted corresponding to the five cross-validation folds V_f. For each analysis $f\in \{1,\dots ,5\}$, motif discovery was performed using the sequences and scores from all folds except V_f: the genes assigned to V_f were instead held out for validation of the discovered motif (so that the set of genes used to learn the motif sets was in each case disjoint from the set of genes used for validation). Existing algorithms were run at their default parameter settings where possible; exact specifications are given in Section S2.8, while SArKS parameters were set as described in Sections 3.2.1 to 3.2.2.

We used tomtom (Gupta et al., 2007) to compare the pooled motif sets identified by each algorithm. Supplementary Figure S3 shows the resulting overlap between motifs sets by algorithm: for each of the benchmarked algorithms, the majority of identified motifs had a SArKS-identified counterpart. SArKS also identified many additional motifs.

The Pearson correlation between the count of occurrences of a given motif in sequence w_b with the score y_b across the sequence-score pairs (w_b, y_b) provides a natural metric for assessing correlative motif discovery performance. Figure 3 plots the estimated Pearson correlation values for each motif identified (by each algorithm) evaluated using the held-out validation set $\{(w_b,y_b)|b\in V_f\}$ appropriate for the fold f in which the motif was discovered (with Figure 3A and B presenting results for the Mo (2015) and Close (2017) datasets, respectively).

Fig. 3.

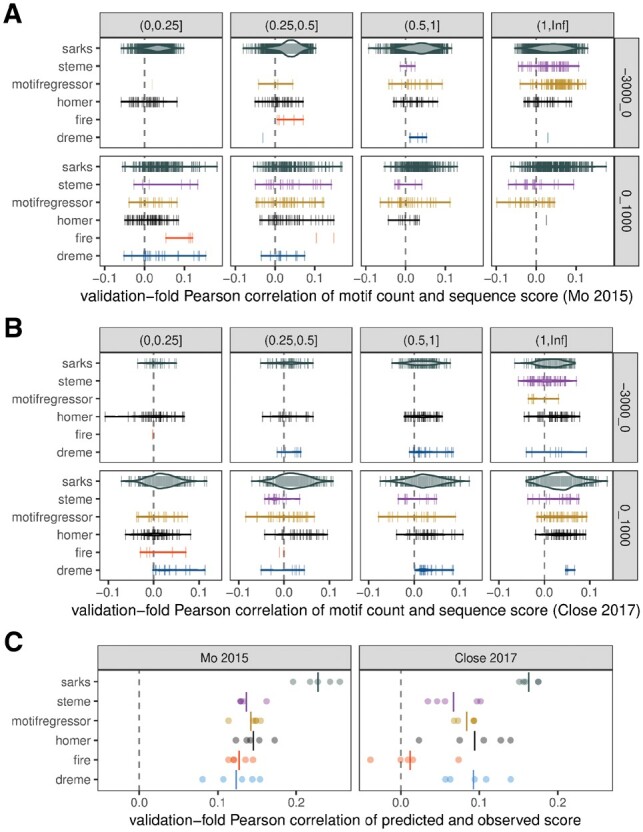
Benchmark comparisons of correlations between motif counts and gene specificity scores in held-out validation subsamples. (A) Each vertical line represents a motif identified by the indicated algorithm in one of the five cross-validation folds for the Mo (2015) dataset (Mo et al. 2015). The horizontal position of the line encodes the Pearson correlation coefficient of the motif count with the associated sequence score (calculated using only the genes in the held-out validation set for the cross-validation fold in which the motif was identified). The count for a given motif in sequence w_b was assessed using fimo (Grant et al. 2011) for DREME, HOMER, MOTIF REGRESSOR and STEME—all of which represent motifs as position-weight matrices—and using a simple regular expression search for FIRE (which returns regular expression representations of motifs) and for SArKS k-mers. In all cases, motif counts were based on motif occurrences on either the forward or reverse strand. Row: sequence region for motif counts, either 3 kb upstream or 1 kb downstream of TSS; column: interval containing average number of occurrences of motif within sequence region across all analyzed genes. Widths of violins represent motif density and are scaled consistently across all panels. (B) Same as (A), except applied to Close (2017) dataset (Close et al. 2017). (C) Motif regression model predictions correlate with gene specificity scores in held-out cross-validation subsamples. Each of five cross-validation folds is plotted as separate point for each algorithm. Each regression model was built using feature vector constructed by concatenating counts of upstream motifs in upstream regions with counts of downstream motifs in downstream regions. Left panel: results of modeling applied to Mo (2015) dataset; right panel: same for Close (2017) dataset. Vertical lines indicate mean Pearson correlation across all folds

As Figure 3A and B and Supplementary Figure S3 demonstrate, the number of motifs identified by different algorithms can be highly variable: DREME, FIRE $\ll$HOMER, MOTIF REGRESSOR < SArKS (the motif count for STEME is a fixed input parameter). The interpretation of the number of motifs is, however, complicated by two factors: (i) the occurrence rate of individual motifs in the relevant biological sequences (promoters, etc.) may differ substantially (e.g. longer motifs may occur less frequently, while motifs allowing for substantial variation at some positions may occur more frequently) and (ii) some motifs may be very similar in sequence.

The first of these complications is illustrated in Figure 3A and B by faceting horizontally on motif occurrence rate (count per sequence): one visible trend here is that the DREME-, FIRE- and HOMER-identified motifs tend to occur less frequently than do the MOTIF REGRESSOR and STEME motifs, indicating that DREME, FIRE and HOMER tend to define motifs more granularly than do MOTIF REGRESSOR or STEME. SArKS-identified motifs are spread across a wide range of per-sequence occurrence rates in this plot, as SArKS identifies both more and less granular motifs as the size of the smoothing window κ is varied through the ranges specified in Sections 3.2.1 to 3.2.2.

The second complication—the similarities among identified motifs—may be addressed by noting that correlative motif discovery can also be viewed as a form of feature extraction. In this vein, we can assess the performance of such algorithms by using the selected motifs as predictors to build regression models for associated sequence score y_b based on the motif counts in the sequence w_b. Figure 3C plots validation set-estimated Pearson correlations of the predictions made by building a linear ridge regression model [using generalized cross-validation (Golub et al., 1979) to select the L2 regularization parameter] with the sequence scores for each cross-validation fold by algorithm. Motifs were counted only within the sequence range in which they were identified, with these counts then merged into a single feature vector per gene to allow the regression models to consider both upstream and downstream motifs simultaneously. This approach collapses the variation in quantity and quality of individual motifs down to variation of a single quantity—the regression model predictions—thereby facilitating a head-to-head comparison of motif discovery algorithms bypassing both of the complications discussed above. As the similarity of some identified motifs manifests as collinearity of regression predictors, regularization is a key component of this modeling approach.

SArKS yields better results than the other algorithms for both validation datasets (Fig. 3C); aside from SArKS, the other two correlational motif discovery algorithms (FIRE and MOTIF REGRESSOR) do not appear to show a consistent advantage in performance relative to the discriminative algorithms.

If, instead of using the merged motif feature set, the regression models are built using only upstream or downstream motif counts, the results shown in Supplementary Figure S2 are obtained, making clear that all six algorithms generally perform better when searching the downstream regions (for which SArKS shows a particularly strong advantage in both datasets).

Considering the downstream motif results, we noted that for every algorithm applied to the Mo (2015) dataset, the motif with the highest Pearson correlation coefficient between occurrence count and PV specificity score in the held-out cross-validation fold exhibited significant tomtom similarity ($q\le 0.1$) to the ESRRA/ESRRB/ESRRG trio of TF-binding motifs documented in the JASPAR database (Mathelier et al., 2015). Looking at the Close (2017) downstream motif results, we observed that the most highly cross-validation-correlated motifs for three of the algorithms—FIRE, HOMER and SArKS—were significantly similar to all of the JASPAR motifs TGIF1/TGIF2/MEIS2/MEIS3/PKNOX1/PKNOX2.

In contrast, the top upstream motif results showed no such convergence on common JASPAR profiles: applied to the Mo (2015) dataset, only one pairwise combination of two algorithms—FIRE and STEME—produced top upstream motifs (ranked by cross-validated Pearson correlation) that showed significant tomtom similarity ($q\le 0.1$) to a common JASPAR profile (NR5A2, whose binding motif closely resembles the ESRRA/ESRRB/ESRRG pattern mentioned above). Applied to the Close (2017) dataset, no two algorithms produce motifs similar to the same JASPAR profile.

We see that in those cases where all of the algorithms performed better in the cross-validation testing (downstream), the top motifs were more likely to converge on known TF-binding motifs. Interestingly, SArKS outperformed the other algorithms to a greater degree in the analyses of downstream regions than of upstream regions.

Comparison of all of the motifs discovered by the various algorithms with known TF-binding motifs is further explored in Section S3.2.

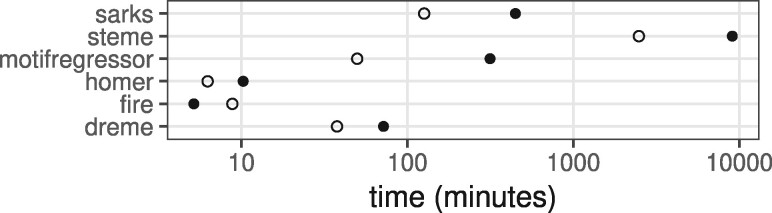
Finally, we compared the average run times for each of the benchmarked algorithms applied to the upstream and downstream cross-validation analyses. As is shown in Figure 4, SArKS took longer than most of the other algorithms with the exception of STEME; FIRE and HOMER are quite fast relative to the others. Further discussion of the computational complexity of SArKS is provided in Section S3.3.

Fig. 4.

Benchmarked algorithm run times. Average run times per cross-validation fold for each motif discovery algorithm applied to either upstream (solid circles) or downstream (open circles) regions for selected genes from Close (2017) dataset (for which all analyses were run on the same computer system)

3.2.4 Permutational analysis of SArKS results

The permutation testing procedure used to set SArKS score thresholds can be used for directly assessing the statistical significance of the motif set SArKS reports as well. This is done by (i) following the procedure laid out in Sections S2.5 and S2.6 using a set of R randomly drawn permutations of the input sequence scores to determine threshold values for motif selection and (ii) independently drawing a second set of R₂ permutations from which the false positive rate corresponding to these thresholds can be estimated according to Equation (S26).

To demonstrate this procedure, we re-applied SArKS to both the Mo (2015) and Close (2017) datasets here including all 6326 or 6939 selected genes (respectively) without cross-validation subsetting. We again investigated all combinations $(\kappa ,\lambda )\in \{250, 500, 1000, 2500\}\times \{0, 10, 100\}$ for the smoothing half-width κ and spatial length λ, computing $g_{\text{min}}$ for each value of κ following Equation (S5) using the γ values indicated in Sections 3.2.1 to 3.2.2, and determining significance thresholds using R = 100 randomly generated permutations.

For the Mo (2015) dataset, the analyses performed using the stricter $g_{\text{min}}$ values obtained using $\gamma =0.1$ yielded larger k-mer motif sets: 3393 total distinct k-mers versus only 1232 using $\gamma =0.2$ for the upstream sequence set; 380 distinct k-mers using $\gamma =0.1$ versus just 180 using $\gamma =0.2$ for the downstream sequence set. More than 98% of the k-mers discovered using $\gamma =0.2$ were also identified using $\gamma =0.1$ (for both sequence ranges: 1208 of the 1232 upstream; 179 of the 180 downstream). Based on these results for the Mo (2015) analysis, we focused exclusively on $\gamma =0.1$ for the Close (2017) analysis, as described in Section 3.2.2.

The results above demonstrate that restrictive values of γ can yield larger motif sets that include almost all of the motifs obtained using more permissive γ values. This highlights the importance of the Gini impurity filter in focusing SArKS on potential motifs that appear within sufficiently many distinct sequences w_b to achieve reasonable statistical confidence.

We assessed the statistical significance of these SArKS results following the method of Section S2.6 with thresholds θ and ${\theta }_{\text{spatial}}$ set by Equation (S24) and Equation (S25) using z = 4. Upstream sequence analysis of the Mo (2015) set considering $R_2=250$ independent random permutations resulted in 12 (4.8%) for which any of the parameter sets $\left(\kappa ,g_{\text{min}},\lambda \right)$ yielded a non-empty set of identified motifs; for the Close (2017) set, the same procedure resulted in 8 (3.2%) non-empty motif sets. These upstream sequence results correspond to a 95% family-wise error rate confidence interval (FWER CI) of (2.5%, 8.2%) in the Mo (2015) analysis and (1.4%, 6.2%) in the Close (2017) analysis.

For the downstream sequence analysis, $R_2=250$ independent permutations yielded 8 (3.2%) instances of non-empty motif sets for Mo (2015) and 1 (0.4%) non-empty motif set for Close (2017), from which we estimate 95% FWER CIs of (1.4%, 6.2%) for Mo (2015) and (0.01%, 2.2%) for Close (2017).

The role of the parameter z in Equations (S24 and S25) in balancing FWER against sensitivity can be seen in the analyses presented here by considering the consequence of increasing z: at z = 5 for the same 250 permutations, the permutation analysis using upstream regions resulted in non-empty motif sets in only two permutations for Mo (2015) or one permutation for Close (2017). Similarly, for the downstream regions, permutation analysis with z = 5 resulted in 4 or 1 permutation(s), respectively. The cost of these decreased false positive rates to sensitivity is apparent in that at most half of the motif k-mers identified using z = 4 were still discovered using z = 5 in each of the analyses; for the Close (2017) upstream analysis conducted with z = 5, SArKS returned no significant motif results at all. Here we were willing to accept the FWER values associated with z = 4 (point estimates ranging from 0.4% to 4.8% in these analyses) in order to maintain a higher sensitivity.

Selection of the parameter z to appropriately balance sensitivity against false positive rate will generally depend on the range of κ, λ, and $g_{\text{min}}$ values investigated. When SArKS analyses are conducted for many combinations of these parameters there will be correspondingly more possible opportunities for false positives, requiring a higher value of z to maintain confidence in the results. In cases where the size of the returned motif set may be large, there is an additional factor to consider: the smaller motif sets associated larger values of z benefit not only from greater statistical confidence but also from a reduction in the computational effort required to refine and process the motif set (Section S3.3).

4 Conclusions

We introduce SArKS as a method for de novo discovery of the sites and domains of correlative motifs. SArKS avoids the dichotomization—and consequent loss of information (Fedorov et al., 2009)—of sequence scores into discrete groups as required by discriminative motif discovery algorithms. SArKS does not require specification of parametric background sequence models, instead using non-parametric permutation methods (Ernst, 2004) to set thresholds for motif identification and to estimate false positive rates. SArKS smooths over spatial motif location to identify MMDs, which can in turn help refine the identified motifs. We have benchmarked SArKS against several existing discriminative and correlative algorithms using previously published RNA-seq data: SArKS uncovered particularly rich motif sets and SArKS motif sets functioned as more predictive feature sets in a cross-validated regression modeling approach than did motif sets generated by existing algorithms. SArKS thus offers an approach to the discovery and localization of motifs capable of fulling exploit differential gene expression data.