N ⁶-Methyladenosines in mRNAs reduce the accuracy of codon reading by transfer RNAs and peptide release factors

Abstract

We used quench flow to study how N⁶-methylated adenosines (m⁶A) affect the accuracy ratio between k_cat/K_m (i.e. association rate constant (k_a) times probability (P_p) of product formation after enzyme-substrate complex formation) for cognate and near-cognate substrate for mRNA reading by tRNAs and peptide release factors 1 and 2 (RFs) during translation with purified Escherichia coli components. We estimated k_cat/K_m for Glu-tRNA^Glu, EF-Tu and GTP forming ternary complex (T₃) reading cognate (GAA and Gm⁶AA) or near-cognate (GAU and Gm⁶AU) codons. k_a decreased 10-fold by m⁶A introduction in cognate and near-cognate cases alike, while P_p for peptidyl transfer remained unaltered in cognate but increased 10-fold in near-cognate case leading to 10-fold amino acid substitution error increase. We estimated k_cat/K_m for ester bond hydrolysis of P-site bound peptidyl-tRNA by RF2 reading cognate (UAA and Um⁶AA) and near-cognate (UAG and Um⁶AG) stop codons to decrease 6-fold or 3-fold by m⁶A introduction, respectively. This 6-fold effect on UAA reading was also observed in a single-molecule termination assay. Thus, m⁶A reduces both sense and stop codon reading accuracy by decreasing cognate significantly more than near-cognate k_cat/K_m, in contrast to most error inducing agents and mutations, which increase near-cognate at unaltered cognate k_cat/K_m.

INTRODUCTION

N ⁶-methylation of adenosines yields N⁶-methyladenosine (m⁶A) in untranslated regions (UTRs) and open reading frames (ORFs) of mRNAs and is ubiquitous throughout the three domains of life. m⁶As have been ascribed roles as ‘fine tuners’ of gene expression (1), and have been proposed to modulate the elongation rate of translating ribosomes (2–4). More recently, it was shown with single-molecule spectroscopy with fluorescence detection and ensemble kinetics measurements with quench-flow techniques that introduction of N⁶-methylation of adenosines in first and second codon nucleotide position greatly slows down GTP hydrolysis on ternary complex (T₃) in response to cognate codon in ribosomal A site (5). Although excess hydrolysis of GTP on EF-Tu compared to peptide bond formation during native, cognate codon reading is negligible, in the presence of m⁶A in first codon nucleotide position there is 50% excess hydrolysis of GTP per cognate peptidyl transfer event. To be sure, by ‘cognate’ we mean in this context of tRNA reading of mRNAs the highly efficient codon translation associated either with codon–anticodon interactions with three Watson–Crick pairs or two pairs complemented with a wobble pair. Furthermore, successively changing the experimental conditions from high, invivo-like accuracy to low, suboptimal accuracy by increasing Mg²⁺ concentration reduces the kinetic difference between native and modified codons (5). From those experiments, it appears that N⁶-methylation of adenosine in first codon nucleotide position leads to a hyper accurate ribosomal phenotype, like that emerging from certain alterations in ribosomal protein S12 with streptomycin resistance, pseudo-dependence or dependence (6).

In the present work we focus on the effects of N⁶-methylation on the middle adenosine in sense and stop codons on the accuracy of codon translation by tRNAs and class-1 release factors, respectively. Here, we probe the effects of N⁶-methylation of adenosines in the second codon position rather than in the first as previously studied (5). Significantly different effects of m⁶A introduction on first and middle base positions could provide keys to the understanding of basal kinetic aspects of N⁶-methylation on codon reading. We were, in particular, interested in putative differences regarding the effects on rate of ternary complex binding and subsequent codon-anticodon complex formation, on initial selection of codons before GTP hydrolysis and on accuracy amplification by proofreading of tRNAs after GTP hydrolysis. A particular concern, given the ubiquity of N⁶-methylation in all organisms including humans, has been whether middle position modifications greatly increase the frequency of errors in codon translation, perhaps with medical consequences. Another question to answer was if N⁶-methylation similarly affects sense codon reading by tRNAs and stop-codon reading by class-1 release factors, which could suggest a previously unknown mechanistic mimicry between tRNA based and release factor based codon reading.

Interestingly, we found that N⁶-methylation of middle position adenosines greatly decreases, rather than increases, the accuracy of both sense and stop codon reading. Defining UAA and UAG or UAA or UGA as cognate stop codons for RF1 or RF2, respectively, our findings show that the accuracy decrease is due to selective reduction of the efficiency (k_cat/K_m) of cognate codon reading at less altered efficiency of near-cognate codon reading. We also found striking similarities of the functional effects of m⁶A introduction in sense codons, read by tRNAs, and stop codons, read by class-1 RFs. Intriguingly, the present and previous (5) results indicate that the different kinetic effects of N⁶-methylation of adenosines in different codon nucleotide positions may, in fact, be used to create an intricate signaling network for peptide elongation and termination.

MATERIALS AND METHODS

Codon reading by ternary complex

Reagents and buffers

We used an Escherichia coli system for cell-free protein synthesis with purified components and invivo-like kinetic properties (7,8). 70S ribosomes from the E. coli strain MRE600, unmodified messenger RNAs, initiation factors, elongation factors and f[³H]Met-tRNA^fMet were prepared according to (7) and references therein. Native E. coli tRNA^Glu was from Chemical Block, [³H]Met and [³H]GTP were from Perkin Elmer, and all other chemicals were from Merck or Sigma-Aldrich. N⁶-methylated mRNAs were from GE Healthcare. Polymix buffer (9) contained 5 mM Mg(OAc)₂, 95 mM KCl, 5 mM NH₄Cl, 0.5 mM CaCl₂, 8 mM putrescine, 1 mM spermidine, 5 mM potassium phosphate pH 7.5, 1 mM dithioerythritol. The energy supply system of the buffer contained 1 mM ATP and 1 mM GTP (2 mM ATP and very low GTP concentration in the ternary complex mixture for GTP hydrolysis measurements) along with 10 mM phosphoenolpyruvate (PEP), 1 μg/ml pyruvate kinase and 0.1 μg/ml myokinase. All kinetic experiments were performed in polymix buffer with free Mg²⁺ concentration ranging from 2.3 to 25 mM (extra addition to polymix buffer from 2 to 30 mM Mg²⁺). The calculation connecting free and total Mg²⁺ uses that PEP chelates Mg²⁺ with a K_d-value of 6 mM at 37°C (10) and that one ATP or GTP molecule chelates one Mg²⁺. All experiments described below were performed at 37°C.

Kinetics measurements

GTP hydrolysis for cognate and near-cognate reactions, and measurement of dipeptide formation for cognate reactions were performed in a temperature controlled quench-flow instrument (RQF-3; KinTek Corp.). Measurements of near-cognate dipeptide formation were performed manually. Ribosome and ternary complex mixtures of equal volumes were mixed and quenched with 17% (final concentration) formic acid at different incubation times. In sections below, the final concentrations of components after mixing were as specified.

GTP hydrolysis on ribosome bound ternary complex

Ribosome mixtures, containing ribosomes programmed with mRNA displaying A-site codon specified in each experiment (GAA, GAU, Gm⁶AA or Gm⁶AU), were prepared by incubating 70S ribosomes (0.3–1 μM), f[³H]Met-tRNA^fMet (1.2× ribosomes), mRNA (2× ribosomes), IF1 (1.5× ribosomes), IF2 (0.5× ribosomes), IF3 (1.5× ribosomes) in polymix buffer with energy supply and extra Mg(OAc)₂ (varying concentrations) at 37°C for 15 min. Ternary complex mixtures were prepared by incubating tRNA^Glu (2 μM), EF-Tu (varying concentrations from 0.2 to 0.5 μM and always less than half of ribosomes), [³H]GTP (same as EF-Tu concentrations), amino acid (0.2 mM) and Glu-tRNA^Glu synthetase (1.5 units/μl) in polymix buffer with energy supply (with 2 mM ATP and lack of GTP) and extra Mg(OAc)₂ (varying concentrations) at 37°C for 15 min. For measurements with aminoglycoside, 10 μM of paromomycin or 10 μM of neomycin was added in both ribosome and ternary complex mixtures. Measurements were done in a quench-flow instrument.

Near-cognate dipeptide formation

Ribosome mixtures were prepared by incubating 70S ribosomes (0.3 μM), f[³H]Met-tRNA^fMet (0.36 μM), mRNA (0.6 μM), IF1 (0.45 μM), IF2 (0.15 μM) and IF3 (0.45 μM) in polymix buffer with energy supply at 2.3 mM free Mg(OAc)₂ at 37°C for 15 min. Ternary complex mixtures were prepared by incubating the tRNA^Glu (0.7 or 1.4 μM), EF-Tu (5 μM), EF-Ts (1.5 μM), amino acid (0.2 mM), and Glu-tRNA^Glu synthetase (1.5 units/μl) in polymix with energy supply at 2.3 mM free Mg(OAc)₂ at 37°C for 15 min. Ribosome and ternary complex mixtures were mixed manually and quenched by KOH (0.33 M final) after different incubation times.

Chase of H84A mutant ternary complex by wild type ternary complex

Mixtures with GAA and Gm⁶AA programmed ribosomes were prepared by incubating 70S ribosomes (0.5 μM), f[³H]Met-tRNA^fMet (0.6 μM), mRNA (1 μM), IF1 (0.75 μM), IF2 (0.25 μM), IF3 (0.75 μM) in polymix buffer at 2.3 mM free Mg(OAc)₂ at 37°C for 15 min. Ternary complex mixtures were prepared by incubating the tRNA^Glu (10 μM), wild type EF-Tu, (T₃, 2 μM), H84A EF-Tu mutant, (T_3(H84A), 6 μM), EF-Ts (1.5 μM), amino acid (0.2 mM) and Glu-tRNA^Glu synthetase (1.5 units/μl) in polymix with energy supply and addition of 2.3 mM free Mg(OAc)₂ at 37°C for 15 min.

Dipeptide formation experiments were performed in a quench-flow instrument with ternary complexes in excess over ribosomes. Independent experiments were performed for ribosomes with GAA and Gm⁶AA A-site codons with the same ternary complex mixture. Kinetics displayed biphasic behavior. There was a fast phase with overall rate constant k_fast and amplitude A_fast, reflecting direct binding of T₃ to the ribosome followed by GTP hydrolysis and peptide bond formation and a slow phase with overall rate constant k_slow and amplitude A_slow, reflecting first binding of T_3(H84A), eventually followed by T₃ binding to the ribosome. T₃ with wild type EF-Tu had 3-fold higher efficiency for GTP hydrolysis than T_3(H84A). Therefore the concentration ratio [T_3(H84A)]/[T₃] was adjusted to a value of three (11) so that the fast and slow phases in the chase reaction had similar amplitudes. Under these conditions the rate constant for dissociation of GTPase deficient ternary complex from the ribosome, k_diss, is related to k_slow as described in main text.

Sample treatment

For all GTP hydrolysis and cognate dipeptide formation measurements reaction quenching by 17% (final concentration) formic acid was followed by 15 min centrifugation at 20 000 g and 4°C. The extents of [³H]GTP in the supernatants and [³H]dipeptide in the pellets were quantified by ion-exchange (MonoQ) and C18 reversed-phase HPLC, respectively, equipped with a β-RAM model 3 radioactivity detector (IN/US Systems) (12). For near-cognate dipeptide formation measurements, reactions were quenched by 0.33 M KOH (final concentration) followed by 30 min incubation at 37°C. 17% of formic acid was then added to each sample and centrifuged for 15 min at 4°C. The extent of [³H]dipeptide in the supernatants was quantified on RP-HPLC. Origin 7.5 (OriginLab Corp.) was used for data analysis.

k_cat/K_m for GTP hydrolysis

To measure k_cat/K_m for GTP hydrolysis we used ribosomes in excess over ternary complex. k_GTP was estimated by fitting the data to a single exponential model. Control experiment with double ribosome concentration displayed doubled k_GTP-value, showing that k_cat/K_m could be estimated as k_GTP divided by the ribosome concentration.

k_cat/K_m for near-cognate dipeptide formation

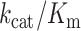-values were estimated from experiments in which ternary complex was titrated from 0.7 to 1.4 μM, always in excess over the 70S ribosome (0.3 μM), so that the rate of dipeptide formation (k_dip^nc) was mainly determined by ternary complex concentration. k_dip^nc was estimated by fitting the data into a single exponential model, where dip(t) was the time evolution of near-cognate dipeptide formed, and the plateau [Rib] was the active ribosome concentration in the reaction. k_dip^nc-values doubled with doubled ternary complex concentration, showing the measurements to be in the k_cat/K_m range, so that k_cat/K_m-values could be estimated as k_dip^nc divided by ternary complex concentration.

Accuracy parameters for initial selection and proofreading

Initial selection (I) was calculated as the ratio of k_cat/K_m values for cognate and near-cognate GTP hydrolysis reactions. The total accuracy (A) was calculated as the ratio of k_cat/K_m values for cognate and near-cognate dipeptide formation reactions.

Codon reading by class-1 release factor

Buffers and reaction components

Buffers and all E. coli components for cell-free protein synthesis were prepared essentially as described above for elongation studies. Reaction buffer was polymix with free Mg²⁺ concentration reduced to 2.5 mM by adding 2.5 mM Mg²⁺-chelating UTP. The mRNAs were leaderless with sequence GAUGUUCUAC[stop]AAAAAAAAAAAA (ORF underlined).

Ribosomal termination complexes (RT) contained tritium (³H) labeled [³H]fMet-Phe-Tyr-tRNA^Tyr in the P site and unmodified (UAA, UGA) or N⁶-methylated in the second position (Um⁶AA, Um⁶AG) codon in the A site. RTs were prepared as described (13) except (i) the reaction buffer and sucrose cushions contained 5 mM potassium phosphate pH 7.5, no HEPES and no additional Mg(OAc)₂, (ii) the final mRNA concentration was increased to 10 μM and (iii) 150 μM E. coli bulk tRNA (Roche) was used as tRNA source. Around 70% of RTs contained [³H]fMet-Phe-Tyr peptide and the rest contained [³H]fMet-Phe or [³H]fMet. Peptide composition was determined by reversed-phase HPLC (Waters) equipped with a β-RAM model 4 radioactivity detector (IN/US Systems) in a buffer containing 39% methanol and 0.1% trifluoretic acid.

RF2 containing Ala in position 246 was overexpressed in E. coli, with mainly unmethylated glutamine (Q) in the GGQ motif (13). The concentration of RF2 active in peptide release was determined by titrating with RF2 when RTs were in excess and determining the amount of released peptide by scintillation counting, as described below for peptide release experiments.

Peptide release reactions

RTs at final concentrations of 0.05 or 0.02 μM (for UAA) were reacted with indicated amounts of RF2 at 37°C in a quench-flow instrument or manually, and the reactions were stopped at different time points by quenching with 17% (final concentration) formic acid. Precipitated [³H]fMet-Phe-Tyr-tRNA^Tyr was separated from soluble [³H]fMet-Phe-Tyr peptide by 15 min centrifugation at 20 000 g and 4°C. The pellets of precipitated [³H]fMet-Phe-Tyr-tRNA^Tyr were dissolved in 0.5 M KOH by incubating for 15 min at 37°C. The amounts of tRNA-bound and released peptides were quantified by scintillation counting of the ³H radiation in Quicksafe Flow 2 scintillation liquid in a Beckman Coulter LS 6500 counter.

Small amounts of shorter peptides, present in RT preparations, had no effect on the rate constant of peptide release (k_rel). 0.3 μM RTs with UAG in the A site were reacted to 3.3 μM RF2, after quenching each sample was divided into two parts and the released peptide quantified either by scintillation counting or by HPLC, as described above. The k_rel of total peptide release determined by scintillation counting was the same as k_rel of only [³H]fMet-Phe-Tyr release determined by HPLC (Supplementary Figure S2).

Data analysis

The k_rel values at different RF2 concentrations were estimated by fitting the data of peptide release over time to a single exponential model. Kinetic parameters k_cat and k_cat/K_m were obtained from k_rel plotted versus RF2 concentration and fitted to Michaelis-Menten equation with Origin 8 software (OriginLab Corp.) Error bars represent standard deviation calculated as weighted averages from at least two independent experiments.

Single-molecule termination assay

Reagents and buffer

Mutant E. coli 30S and 50S ribosomal subunits containing hairpin loop extensions in 16S rRNA helix 44 and 23S rRNA helix 101 were constructed and purified as described before (14,15). IF2, EF-Tu, EF-G, EF-Ts, RRF and ribosomal protein S1 from E. coli were purified from overexpressing strains as previously described (15,16). fMet-tRNA^fMet and Phe-tRNA^Phe were charged and purified according to published protocols (17,18). The MF-UAA mRNA, which was chemically synthesized by Dharmacon, contains a 5′-biotin followed by a 5′-UTR and Shine–Dalgarno sequence derived from gene 32 of the T4 phage upstream of the AUG start codon. There are four spacer Phe codons downstream of the UAA stop codon. Cy5.5-labeled RF1 and RF2 were generated from single-cysteine variants of the proteins which were purified with previously described protocol (16). The purified proteins were incubated with 30-fold excess of the Cy5.5-maleimide dye (Lumiprobe) for 24 h at 4°C. Removal of free dye and storage was done as previously described (16).

All single-molecule experiments were conducted in a Tris-based polymix buffer consisting of 50 mM Tris-acetate (pH 7.5), 100 mM potassium chloride, 5 mM ammonium acetate, 0.5 mM calcium acetate, 5 mM magnesium acetate, 0.5 mM EDTA, 5 mM putrescine–HCl and 1 mM spermidine. Prior to the single-molecule experiments, the purified 30S and 50S ribosomal subunits (final concentration 1 μM) were mixed in 1:1 ratio with the fluorescent dye-labeled DNA oligonucleotides complementary to the mutant ribosome hairpin extensions (14,15) at 37°C for 10 min and then at 30°C for 20 min in the Tris-based polymix buffer system. The 30S subunit was labeled with 5′-Cy3B-labeled DNA and 50S subunit was labeled with 3′-BHQ-2-labeled DNA.

ZMW-based single-molecule fluorescence assay on PacBio RSII

The 30S pre-initiation complexes (PICs) were formed as described by incubating the following at 37°C for 10 min: 0.25 μM Cy3B–30S, pre-incubated with stoichiometric S1, 1 μM IF2, 1 μM fMet-tRNA^fMet, 1 μM mRNA and 4 mM GTP to form 30S PICs in the polymix buffer. Before use, we pre-incubate a SMRT Cell v3 from Pacific Biosciences (Menlo Park, CA, USA), a ZMW chip, with 0.2% (w/w) Tween 20 in 50 mM Tris-acetate pH 7.5 and 50 mM KCl at room temperature for 10 min. After washing the chip in cell-washing buffer (50 mM Tris-acetate pH 7.5, 100 mM potassium chloride, 5 mM ammonium acetate, 0.5 mM calcium acetate, 5 mM magnesium acetate and 0.5 mM EDTA), the chip was incubated with a 1 mg/ml Neutravidin solution in 50 mM Tris-acetate pH 7.5 and 50 mM KCl at room temperature for 5 min. The cell is then washed with cell-washing buffer again. The formed 30S PICs were diluted with our Tris- based polymix buffer containing 4 mM GTP down to 10 nM PIC concentration. The diluted PICs were then loaded into the SMRT cell at room temperature for 3 min to immobilize the 30S PICs into the ZMW wells. Any excessive unbound material was washed away with our Tris-based polymix buffer containing 4 mM GTP. The immobilized 30S PICs were immersed with 20 μl of our Tris-based polymix buffer containing 4 mM GTP, 5 mg/ml BSA, 1 μM blocking dsDNA oligonucleotide, 2.5 mM Trolox, and a PCA/PCD oxygen scavenging system (2.5 mM 3,4-dihydroxybenzoic acid and 250 nM protocatechuate deoxygenase (19).

Ternary complexes (T₃) were formed between charged Phe-tRNA^PheE. coli tRNAs and EF-Tu(GTP) by incubating in bulk the tRNA, EF-Tu, EF-Ts, GTP and energy regeneration system (phosphoenolpyruvate and pyruvate kinase). The T₃ were added to the delivery mix at final concentration of 200 nM along with 200 nM BHQ-2–50S, 200nM EF-G, 4 – 40 nM Cy5.5-RF1 or RF2, 40 μM RRF, 4 mM GTP, 5 mg/ml BSA, 1 μM blocking dsDNA oligo, 2.5 mM Trolox and the oxygen scavenging system (PCA and PCD) in polymix buffer. Before starting an experiment, the SMRT Cell is loaded into a modified PacBio RSII sequencer. At the start of the experiment, the instrument illuminates the SMRT cell with a green laser and then transfers 20 μl of a delivery mixture onto the cell surface at t = 10 s. All experiments were performed at 20°C, and data were collected for 8 min. Since the SMRT Cell contains 30S PICS immersed in 20 μl of polymix mixture, the final concentration of all the components during the experiment was 100 nM BHQ-2–50S, 100 nM T₃, 100 nM EF-G, 2–20 nM Cy5.5-RF1 or RF2, 20 μM RRF, 4 mM GTP, 5 mg/ml BSA, 1 μM blocking dsDNA oligo, 2.5 mM Trolox, 2.5 mM PCA and 250 nM PCD.

RSII-instrumentation and data analysis

Single-molecule intersubunit FRET and factor occupancy experiments were conducted using a commercial PacBio RSII sequencer that was modified to allow the collection of single-molecule fluorescence intensities from individual ZMW wells about 130 nm in diameter in four different dye channels corresponding to Cy3, Cy3.5, Cy5 and Cy5.5 fluorescence. The RSII sequencer has two lasers for dye excitation at 532 nm and 632 nm. In all the Cy5-RF1 and Cy5-RF2 experiments, data was collected at 10 frames per second (100 ms exposure time) for 6 min using energy flux settings of the green laser at 0.72 mW/mm² and red laser at 0.10 mW/mm².

Data analyses for all experiments were conducted with MATLAB (MathWorks) scripts written in-house (20). Briefly, traces from either the ZMW were automatically selected based on fluorescence intensity, fluorescence lifetime and the changes in intensity. Filtered traces exhibiting intersubunit FRET or single-molecule binding signals were then manually curated for further data analysis. The FRET states were assigned as previously described (21) based on a hidden Markov model based approach and visually corrected. All lifetimes were plotted as cumulative distributions and fitted to single-step and two-step exponential fits using curve-fitting tool on MATLAB.

k_a, q_dis, and k_cat/K_m for RF1/RF2 termination

Association rate constants (k_a) for RF1 and RF2 were calculated by fitting the cumulative distribution (f) of measured RF arrival times as a function of time (t) to single exponential function:

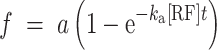The cumulative distribution of RF2 arrival kinetics to UAA codon produced a biphasic behavior, thus for this we fit it to a double exponential function:

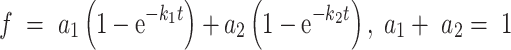From this fit, the rate constant with the larger contribution (a₁ = 0.75) was used for calculating the bimolecular association rate constant for RF2. Dissociation rate constants (q_dis) for RF1 and RF2 were calculated by fitting the cumulative distribution of measured RF occupancy times to single exponential function. k_cat/K_m was calculated using the following equation:

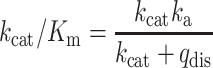using k_a and q_dis measured from single-molecule assay and k_cat (3s⁻¹) from the quench-flow peptide release assay.

RESULTS

Impact of m⁶A modification on initial cognate and near-cognate codon reading

We first used ensemble kinetics techniques (quench flow) (7,22) to characterize the effects of N⁶-methylated adenosines (m⁶As) in middle codon nucleotide position in open reading frames (ORFs) of mRNA on maximal rate (k_cat) and efficiency (k_cat/K_m) of cognate (sense) and near-cognate (missense) initial codon reading by aminoacyl–tRNA in ternary complex (T₃), in an experimental system described by the cartoon in Figure 1A. For initial codon reading k_cat/K_m is the rate constant for T₃ binding to the ribosome (k_a) multiplied by the probability that the binding event leads to GTP hydrolysis and k_cat is the inverse of the time from T₃·ribosome complex (RC₁) formation (Figure 1A) to GTP hydrolysis (22). Michaelis–Menten constants k_cat and k_cat/K_m, normally estimated from multiple turnover experiments under steady state conditions, can equally well be precisely estimated from transient single turnover experiments. Indeed, as shown by mean time analysis, the key to the power of the transient method is that it not only provides all information available from Michaelis–Menten interpretation of steady state experiments (9–11), but also confers additional, more detailed data of studied reactions (22).

Figure 1.

Kinetic scheme for efficiency and accuracy of codon reading by tRNA (A) and release factors (B). (A) Ribosome complex RC₀ has peptidyl-tRNA in P site and A site programmed with native (GAA) or modified (Gm⁶AA) Glu codon, native (GAU) or modified (Gm⁶AU) Asp codon. Glu-tRNA^Glu, with cognate codon GAA, initially is in free ternary complex (T₃) with EF-Tu and GTP. T₃ binds into A/T site of RC₀, leading to ribosome complex RC₁, where the anticodon of T₃ lacks codon contact. Codon-anticodon contact is formed by conformational change of tRNA in T₃ leading to complex RC₂. Subsequent hydrolysis of GTP in EF-Tu induces conformational change of EF-Tu and leads to complex RC₃. Then EF-Tu in the GDP form rapidly dissociates from RC₃, leading to complex RC₄. In RC₄ tRNA may be accommodated into A site and receive a nascent peptide from P-site tRNA, leading to complex RC₅. Alternatively, tRNA is discarded from the ribosome in a proofreading reaction, which brings RC₄ back to complex RC₀. The efficiencies (k_cat/K_m) for GTP hydrolysis on ribosome bound T₃ for peptide bond formation in response to GAA, Gm⁶AA, GAU and Gm⁶AU codons in A site are in M&M defined in terms of rate constants in Figure 1A (Materials and Methods). (B) Ribosomal termination complex RT₀ has peptidyl-tRNA in P site and A site programmed with native (UAA) or modified (Um⁶AA) stop codon in cognate reactions and with UAG or Um⁶AG in near-cognate reactions. Release factor 1 (RF1) or 2 (RF2) binds to RT₀ forming RT₁. Either release factor (RF) undergoes a conformational change and forms complex RT₂ via transition state RT₁₂* or dissociates from the ribosome. We suggest that the modest selectivity of ground state RT₁ is enhanced in the transition state RT₁₂* (37). Hydrolysis of ester bond in peptidyl-tRNA leads to ribosomal complex RT₃ followed by peptide release and, eventually, RF-release. The efficiency (k_cat/K_m) and maximal rate (k_cat) for ester bond hydrolysis on ribosome bound RF in response to UAA, Um⁶AA, UAG and Um⁶AG codons are defined in terms of rate constants in Figure 1B (Materials and Methods).

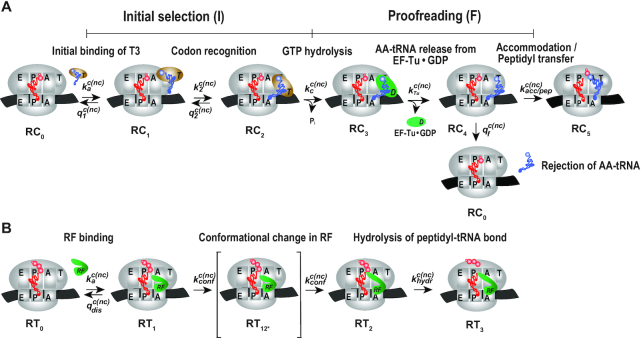
Here, we have performed single turnover experiments at 37°C in polymix buffer (9) at varying concentrations of free Mg²⁺ (22) in the absence or presence of aminoglycoside antibiotics (paromomycin, neomycin) (11,23). We studied initial codon reading by Glu-tRNA^Glu in T₃-complex with EF-Tu and ³H-GTP on pre-translocation 70S ribosomes with initiator tRNA (fMet-tRNA^fMet) in P site. The ribosomal A site was programmed with cognate native (GAA) or modified (Gm⁶AA) Glu codon or with near-cognate native (GAU) or modified (Gm⁶AU) Asp codon. The same T₃ solution was rapidly mixed with either one of the four 70S ribosome solutions in a quench-flow instrument. Each reaction was quenched by formic acid at different reaction times, as described (7). The extent of GTP hydrolysis was estimated by HPLC-separation of ³H-GDP from ³H-GTP, on-line digital monitoring of the ³H-GDP and ³H-GTP beta-emissions and computation of the absolute amount of GTP hydrolysis from the [³H-GDP]/([³H-GDP] + [³H-GTP]) fractions and the total guanine nucleotide concentration. For illustration of method, we show the time-dependency of [³H-GDP]/([³H-GDP] + [³H-GTP]) fractions from experiments performed at low (2.3 mM) (Figure 2A, B) and much higher Mg²⁺ concentration (Supplementary Figure S1) in the absence (Figure 2A and Supplementary Figure S1A) and presence (Figure 2B and Supplementary Figure S1B) of m⁶A within the programming mRNA. From these and similar data we computed k_cat/K_m-values for cognate and near-cognate initial codon reading. [Mg²⁺] was varied in the presence or absence of aminoglycoside for unmodified (Figure 2C) and modified (Figure 2D) codons, as summarized in Table 1. In line with previous data (11), in the absence of m⁶A the cognate k_cat/K_m increased 3-fold from about 60 to 200 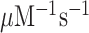when free [Mg²⁺] increased from 2.3 to 25 mM. Also in the presence of m⁶A the cognate k_cat/K_m increased 3-fold here from about 6 to 20 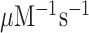when [Mg²⁺] increased from 2.3 to 16 mM. These results imply that the relative increase of the cognate kinetic efficiency with increasing [Mg²⁺] was virtually identical in the absence and presence of N⁶-methylation, although the absolute k_cat/K_m-values were an order of magnitude smaller in the modified cases. We further note that addition of aminoglycosides left cognate efficiency unaltered in response to [Mg²⁺] variation in the absence of (Figure 2C), as seen before (11), as well as in the presence of N⁶-methylation of the middle adenosine (Figure 2D). The near-cognate codon reading efficiency increased greatly with increasing [Mg²⁺] without (Figure 2C) and with (Figure 2D) N⁶-methylation of adenosine. At high [Mg²⁺], therefore, near-cognate efficiencies had become more similar to their cognate counter parts. This convergence of cognate and near-cognate efficiencies was even stronger in the presence than in the absence of m⁶A or aminoglycoside (Table 1). In the next section we report on the kinetic impact of N⁶-methylation of adenosine in middle codon nucleotide position on the decoding of mRNA.

Figure 2.

How m⁶A modification affects the impact of [Mg²⁺] variation and aminoglycoside addition on the efficiency of codon reading by T₃. Fractions of GTPs hydrolyzed on T₃ (y-axis) at different free [Mg²⁺] values and reaction times (x-axis, log₁₀ display) for T₃ reading of unmodified (A) GAA (closed black squares), GAA + paromomycin (Par) (open black squares), GAU (closed red circles), GAU + Par (open red circles) and modified. (B) Gm⁶AA (closed black squares), Gm⁶AA + Par (open black squares), Gm⁶AU (closed red circles), Gm⁶AU+Par (open red circles). k_cat/K_m-values for GTP hydrolysis on T₃ (y-axis) at different free [Mg²⁺] values for T₃ of unmodified. (C) GAA (closed black squares), GAA+Par (open black squares), GAU (closed red circles), GAU+Par (open red circles), GAU+Neo (open green circle) and modified. (D) Gm⁶AA (closed black squares), Gm⁶AA+Par (open black squares), Gm⁶AU (closed red circles), Gm⁶AU+Par (open red circles). All k_cat/K_m-data are summarized in Table 1. (A) and (B) were performed at 2.3 mM Free Mg^2+.

Table 1.

Magnesium and aminoglycoside effects on GTP hydrolysis for tRNA^Glu reading unmodified and m⁶A-modified codons. Related to Figure 2A, B and Supplementary Figure S1. Par, paromomycin; Neo, neomycin

		(kcat/Km)GTP (μM−1s−1) at varying Mg2+ concentration
Codon	Aminoglycoside	2.3 mM	5.3 mM	9.8 mM	16 mM	25 mM
GAA	No	59 ± 7	150 ± 19	193 ± 26	210 ± 22	200 ± 32
GAU	No	0.98 ± 0.11	5.9 ± 0.9	9.1 ± 1.3	20 ± 0.8	20 ± 1.5
GAA	10 μM Par	68 ± 6.7	158 ± 18	207 ± 15	186 ± 10	212 ± 24
GAU	10 μM Par	9.3 ± 0.92	29 ± 2.8	37 ± 4.6	48 ± 4.7	53 ± 6.3
GAU	10 μM Neo	–	–	–	–	79 ± 7.6
Gm6AA	No	5.6 ± 0.55	13 ± 1.8	18 ± 1.7	20 ± 1.1	–
Gm6AU	No	0.38 ± 0.02	2.7 ± 0.24	8.2 ± 1.1	11 ± 0.7	–
Gm6AA	10 μM Par	7.02 ± 0.9	15 ± 1.5	14 ± 1.1	20 ± 0.8	–
Gm6AU	10 μM Par	3.2 ± 0.34	11 ± 1.2	13 ± 1.4	21 ± 1.4	–

Impact of m⁶A on the ‘effective selectivity’ of initial codon reading by ternary complex

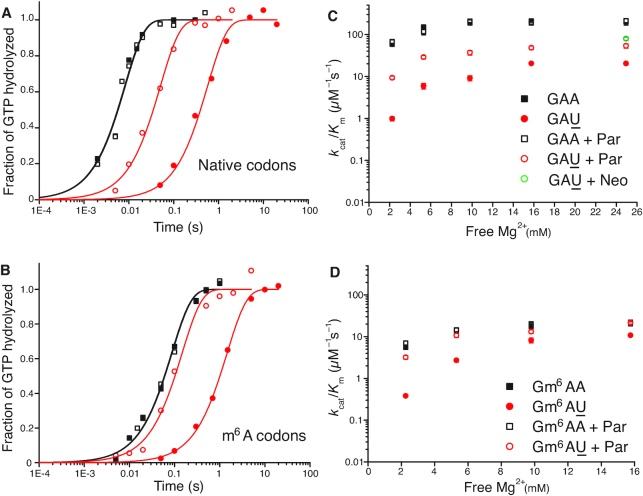
We used the data in Table 1 to construct linear efficiency-accuracy trade-off plots (Figure 3) (22). For this we plotted initial codon reading efficiency, i.e. k_cat/K_m for ribosome dependent GTP hydrolysis in T₃, for cognate initial codon reading efficiency, y =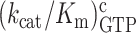, as a function of the initial codon reading accuracy, I, which is the ratio between cognate and near-cognate initial codon reading efficiency, 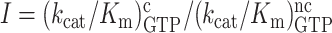, at different values of [Mg²⁺]. The ‘effective selectivity’ of initial codon reading by ternary complex, d_e, is the value of the accuracy I in the limit where ternary complex-bound ribosome state RC₁ is in chemical equilibrium with free ternary complex and free ribosome state RC₀ in Figure 1A (23). This high accuracy limit is approached when free [Mg²⁺] is titrated from high to low values, and is estimated by the x-value of the straight line in the zero kinetic efficiency limit (y = 0) (22). The high efficiency limit where the cognate efficiency equals the rate constant for ternary complex association (y = ) is approached at high [Mg²⁺] and is estimated by the y-value of the straight line in the maximal kinetic efficiency limit (x = 1) axis. Such plots, constructed from the data in Table 1, are shown in Figure 3, and the accuracy parameter estimates are summarized in Supplementary Table S1.

Figure 3.

m⁶A effects on efficiency-accuracy trade-off in absence and presence of paromomycin. Cognate k_cat/K_m-values for GTP hydrolysis on T₃ (y-axes) versus ratios (accuracy of initial selection; I) of pairs of cognate to near-cognate k_cat/K_m-values at different free [Mg²⁺] values (x-axes) for native mRNA (black and red squares; main figure) with cognate GAA and near-cognate GAU codon and modified mRNA (blue and magenta squares; insert) with cognate Gm⁶AA and near-cognate Gm⁶AU codon in the absence and presence of paromomycin. Intercepts with x = 1 axes display cognate association rate constants and intercepts with x-axes display effective d-values, d_e (23) as summarized in Supplementary Table S1.

In the case of native mRNA d_e is 80 in the absence and 11 in the presence of the aminoglycoside paromomycin (Supplementary Table S1), in line with previous data (11,23). In the case of m⁶A-containing mRNA d_e is 20 in the absence and 2.8 in the presence of paromomycin (Supplementary Table S1), meaning that there is 4-fold d_e-reduction by the mRNA modification both in absence and presence of the m⁶A modification. These data show that the cognate rate constant for T₃ association with the ribosome (k_a) is reduced from 239 to about 20 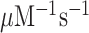in response to N⁶-methylation of the middle adenosine. Since the first ribosomal complex formed with T₃ lacks codon anti-codon specificity (Figure 1A) (11,24), we contend that cognate and near-cognate rate constants for T₃ association are the same: , where k_a is reduced about 10-fold by the N⁶-methylation of the adenosine at middle codon nucleotide position. So far, we have found two distinct effects of N⁶-methylation of adenosine. The first is a 10-fold reduction of both cognate and near-cognate association rate constants, which remains virtually unaltered in response to [Mg²⁺] alteration or aminoglycoside addition. The second distinct effect is a 4-fold decrease in effective selectivity (d_e), akin to the effects of aminoglycosides (11,23), other error inducing drugs (25,26) and error inducing mutations (27). In the next section we describe the compounded effects of N⁶-methylation of adenosine on efficiency and accuracy of peptide bond formation for cognate and near-cognate codon reading (7). The results reveal how introduction of m⁶A affects the proofreading (28,29) of aa-tRNA, a mechanism driven by dissipation of free energy provided by excess hydrolysis of GTP on EF-Tu (30,31).

Impact of m⁶A modification on the efficiency of cognate and near-cognate peptide bond formation

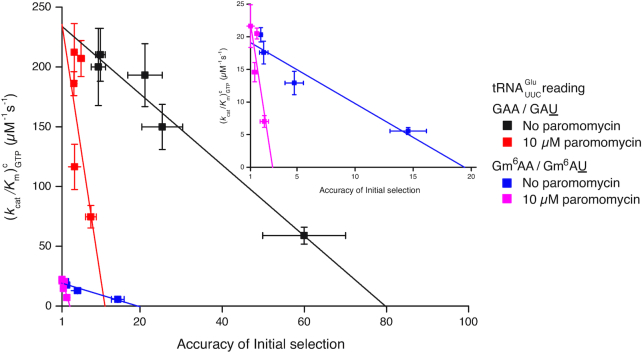
We determined the kinetics of peptide bond formation on the path from free ribosome and free ternary complex up to and including peptidyl transfer (Figure 1A; (32)). In codon reading leading to peptidyl transfer k_cat/K_m is the rate constant for ternary complex association with the ribosome, i.e. the same as in initial codon reading, multiplied by the probability P_p that the first binding event leads to peptide bond formation. In these experiments, the efficiencies of peptide bond formation in cognate and near-cognate cases also reflect how m⁶A affects the proofreading of aa-tRNA (28,29). Proofreading occurs after GTP hydrolysis on T₃ in one or several steps where near-cognate aa-tRNA is preferentially discarded from the ribosome while cognate aa-tRNA is preferentially kept ribosome-bound until peptidyl transfer occurs. Accordingly, proofreading brings the total accuracy A of amino acid selection for amino acid insertion into the nascent peptide chain to a much higher level than is provided by the accuracy I of initial ternary complex selection before GTP hydrolysis, by multiplying I with a proofreading factor, F, which is much larger than one (30,31): A = IF. The parameter F is equal to the ratio, f_nc/f_c, between the mean number of GTPs hydrolyzed on EF-Tu in the near-cognate (f_nc) and cognate (f_c) reaction. By definition, F corresponds to the ratio between the probability (1/f_c) that a cognate aminoacyl-tRNA participates in peptidyl transfer after GTP hydrolysis on EF-Tu and the corresponding probability (1/f_nc) for a near-cognate aminoacyl-tRNA. The biological relevance of our biochemical data is ascertained by the tuning of the free Mg²⁺concentration in our ‘physiological’ polymix buffer to 2.3 mM leading to in vivo-like codon reading speed and accuracy (33,34). From this correspondence between intracellular and biochemical data, we suggest that initial selection of ternary complex before and proofreading selection of aminoacyl-tRNA after GTP hydrolysis on EF-Tu, which can only be distinguished in the test tube, are at work also in the living cell. Under those in vivo-like conditions N⁶-methylation of adenosine reduces the cognate efficiency of GTP hydrolysis, 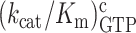, from 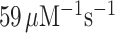for native A to for m⁶A in middle codon nucleotide position (Figure 4A, Supplementary Table S2). From the very same cognate experiment we estimated the time dependence of the extent of peptide bond formation with native and modified mRNAs (Figure 4B). From this we obtained overall average times (1/k_dip) for all steps leading from free ternary complex and ribosome into state RC₁ and then all the way to Glu-tRNA^Glu accommodation and fMet-Glu-tRNA^Glu formation in state RC₅ for cognate, native GAA and modified, Gm⁶AA codons (Figure 1A, Supplementary Table S2). We estimated 1/k_dip as 20 ms for GAA and 50 ms for Gm⁶AA. The average time for GTP hydrolysis, 1/k_GTP, was estimated as 8.3 ms for GAA and 83 ms for Gm⁶AA. Subsequently the time,1/k_pep, from completed GTP hydrolysis to peptidyl transfer, was estimated by the formula 1/k_pep= 1/k_dip – 1/k_GTP (22), as 12 ms for GAA and 17 ms for Gm⁶AA. This means that the N⁶-methylation of adenosine in middle codon nucleotide position did not significantly affect the peptidyl transfer time, 1/k_pep. Instead, the modification affected earlier steps in codon recognition, in line with previous observations from a different cognate codon reading case (5). The plateau value for the extent of dipeptide formation is the same for native and modified mRNA (Figure 4B), meaning that the presence of m⁶A did not alter the average number of GTPs hydrolyzed per cognate peptidyl transfer reaction: this ratio was close to one in both modified (Figure 4B) and unmodified (8) cases. The 1:1 stoichiometry between cognate GTP hydrolysis and peptide bond formation means that cognate k_cat/K_m-values for GTP hydrolysis (Figure 4A), and peptide bond formation (Figure 4B), are the same, so that a 10-fold decrease in one (Table 1) corresponds to a 10-fold decrease also in the other (Table 1). This follows since 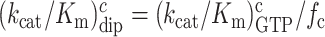, where 1:1 stoichiometry means that the number f_c of GTPs hydrolyzed per cognate peptide bond is equal to one. Thus, for the experiments in Figure 4A and B the equality 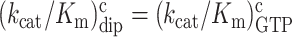is valid. This also means that the accuracy amplifying proofreading factor F = f_nc/f_c was here equal to just the number f_nc of GTPs hydrolyzed per near-cognate peptide bond formation (35), and that . We studied near-cognate dipeptide formation for unmodified GAU (Figure 4C) and for Gm⁶AU (Figure 4D) under conditions when the reaction mean time is proportional to 1/[T₃] and, hence, 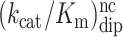was estimated as the mean reaction time normalized to [T₃]. We found that 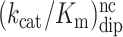= 3.4 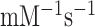and 4.1 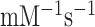in the unmodified and modified cases, respectively (Supplementary Table S3). This means that the N⁶-methylation led to a modest (20%) increase in near-cognate efficiency of peptide bond formation (Figure 4C, D; Supplementary Table S3). Although the k_a-values for T₃ binding to the ribosome decreased by the same factor of ten in response to m⁶A introduction in cognate and near-cognate cases (Supplementary Table S1), in the near-cognate case the k_a-decrease was compensated for by a 4-fold increase in the probability that T₃ binding leads to GTP hydrolysis (Initial selection values in Supplementary Table S1) rather than to T₃ dissociation and a 3-fold increase in the probability that GTP hydrolysis leads to peptidyl transfer (proofreading values in Supplementary Table S1), rather than to aminoacyl tRNA discarding in proofreading. Accordingly, there was virtually no net-effect of m⁶A on the overall efficiency of peptide bond formation in the near-cognate case (Supplementary Table S3) although there was a 10-fold efficiency decrease in the cognate case corresponding to a 10-fold increase in missense error. (Supplementary Table S1; see Discussion).

Figure 4.

m⁶A modification and overall accuracy of peptide bond formation. All experiments in Figure 4 are carried out in polymix buffer at 2.3 mM free Mg²⁺ concentration, where the accuracy level of peptide bond formation is calibrated to that in the living bacterial cell, as described (34). Fractions of GTPs hydrolyzed (A, y-axis) or fMet-Glu dipeptides formed (B, y-axis) are plotted at different reaction times (x-axis, log₁₀ display) from a single experiment, where cognate T₃ reads unmodified GAA (closed squares), and modified Gm⁶AA (open circles) codons. Fractions of fMet-Glu dipeptides formed from near-cognate T₃ at 0.7 μM (open squares) or 1.4 μM (closed squares) concentration reading (C) GAU or (D) Gm⁶AU codon. Compounded rate constants for dipeptide formation are doubled in response to double T₃ concentration so that each compounded rate constant divided by T₃ concentration estimates the k_cat/K_m-value of the reaction (main text).

Impact of N⁶-methylation of adenosine on the mean time for ternary complex dissociation from the ribosome

To clarify further the cause of initial accuracy reduction by N⁶-methylation of the adenosine we estimated the mean-time, 1/k_diss, for dissociation of GTPase deficient T₃ (T_3(H84A)), containing Glu-tRNA^Glu, His84Ala mutated EF-Tu (36) and GTP, from ribosomes programmed with native (GAA) or modified (Gm⁶AA) Glu codon (Figure 5). For this we rapidly mixed in a quench-flow instrument one solution containing both wild type T₃ and GTPase deficient T_3(H84A) with another solution containing ribosomes with initiator tRNA (fMet-tRNA^fMet) in the AUG programmed P site and the A site programmed either with GAA or Gm⁶AA. Each ternary complex was present in large excess over the ribosome complex. After mixing, ribosomes that were first hit by a native T₃ complex formed fMet-Glu dipeptides in a ‘fast phase’ of amplitude A_fast and mean reaction time 1/k_fast (Figure 5). Ribosomes first hit by a modified T_3(H84A) complex formed fMet-Glu dipeptides in a ‘slow phase’ of amplitude A_slow and mean reaction time 1/k_slow determined by the mean time 1/k_diss for T_3(H84A) dissociation and the inverse of the probability that T_3(H84A) dissociation is followed by rebinding of T₃ rather than T_3(H84A) (28):

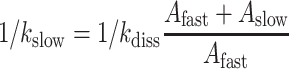Figure 5.

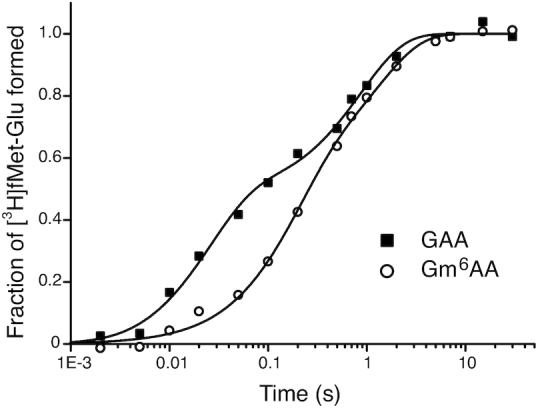
Competition between GTPase deficient and wild type T₃ for native and m⁶A modified A-site codon. Fraction of fMet-Glu formed (y-axis) at different reaction times (x-axis, log₁₀ display) in experiments where free T₃ with wild type EF-Tu competes with GTPase deficient H84A-mutated EF-Tu for ribosomes with GAA (closed squares) and Gm⁶AA (open circles) codons. Both types of ternary complex are rapidly added to ribosomal complex RC₂ (Figure 1) leading to rapid peptide bond formation upon initial native T₃ binding and slow peptide bond formation upon initial GTPase deficient T₃ binding and its eventual exchange for native T₃. Note that peptide bond formation is much slower at Gm⁶AA than GAA codons due to m⁶A-dependent reduction of the rate constant for binding of T₃ to A site (see main text).

The above relation can be understood when it is recognized that its right-hand side is the mean dissociation time, 1/k_diss, for T_3(H84A) multiplied by the mean number of dissociation events that precede peptide bond formation. The reaction was quenched with formic acid at different reaction times and the extent of ³H-fMet-Glu formed was monitored by HPLC with on-line radiation detection (Materials and Methods). From experiments in Figure 5 we estimate k_diss as 2.4 s⁻¹ and 1.4 s⁻¹ for GAA and Gm⁶A codons, respectively (Supplementary Table S4). This means, in other words, that there was a 1.7-fold reduction of k_diss by the m⁶A introduction (see Discussion).

Impact of m⁶A modification on accuracy of stop codon reading by release factor 2

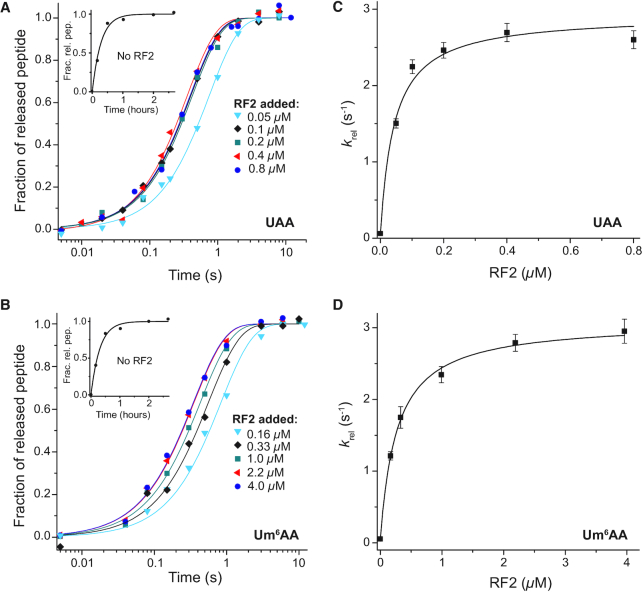
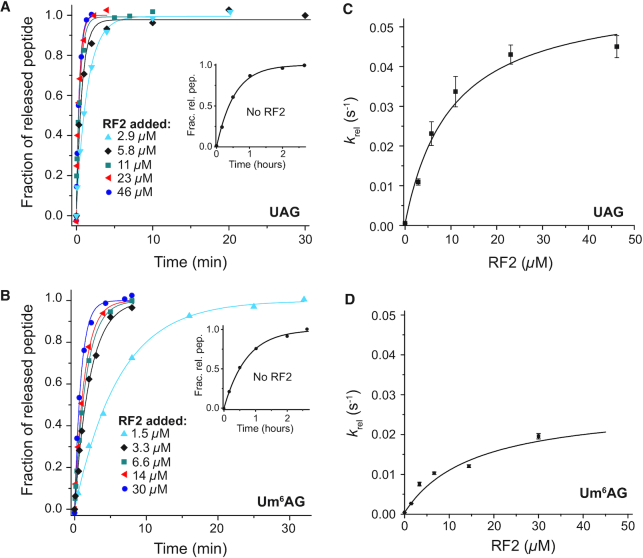
We also used quench-flow techniques to characterize the effects of m⁶A on the Michaelis–Menten parameters k_cat and k_cat/K_m for cognate and near-cognate stop codon reading by ribosomal termination factor RF2. Two different types of solutions were prepared. One with release factor 2 (RF2) and the other with ribosomal termination complex RT₀, the latter containing f[³H]Met-Phe-Tyr-tRNA^Tyr in the P site (Figure 1B) and the A site programmed with UAA or Um⁶AA stop codons, cognate to RF2 and release factor 1 (RF1), or with UAG or Um⁶AG stop codons, near-cognate to RF2 but cognate to RF1. Ribosome and RF2 solutions were rapidly mixed in a quench-flow instrument or by hand with RF2 always in excess over RT₀ and the reactions were quenched after different incubation times. The fractions of released f[³H]Met-Phe-Tyr peptides for all RF2 concentrations and incubation times are shown for the cognate native UAA and modified Um⁶AA codon in Figure 6A and B, respectively. Corresponding rate parameters k_rel, estimated as inverted mean times, are displayed in Figure 6C and D, respectively. Cognate k_cat and k_cat/K_m parameters are summarized in Table 2. Modification of UAA to Um⁶AA leaves the cognate k_cat-value unaltered but decreases the cognate k_cat/K_m-value 6-fold. Time curves for the fractions of released tripeptides for all RF2 concentrations are shown for the near-cognate codons UAG and Um⁶AG in Figure 7A for UAG and 7B for Um⁶AG, and the corresponding k_rel-values are displayed in Figure 7C and D, respectively. All data are summarized in Table 2, from which it is seen that the near-cognate k_cat/K_m-value decreased 3-fold by N⁶-methylation of the middle adenosine so that the error increased 2-fold (6.4/3.5). Furthermore, the efficiency of termination was about 12 000 times larger at the cognate UAA than at the near-cognate UAG codon (70/0.006), an accuracy difference an order of magnitude larger than a previous estimate (37).

Figure 6.

How m⁶A modification of cognate stop codon UAA to Um⁶AA affects RF2-dependent termination. Ribosomal termination complex RT₀ (Figure 1B), at concentration 0.02 μM with native UAA codon (A) or 0.05 μM with modified Um⁶AA codon (B) in A site and with ³H-labeled fMet-Phe-Tyr-tRNA^Tyr in P site were reacted with RF2 at indicated concentrations. The fractional extents (y-axis) of terminated ribosomes, RT₃ (Figure 1B), are shown as functions of time (x-axis, log₁₀ display). Inserts: spontaneous termination without RF2. From these curves average reaction times for peptide release were estimated and their inverses, the generalized rate constants for peptide release, k_rel, are displayed in (C) for UAA and in (D) for Um⁶AA codons. The maximal rates (k_cat) and efficiencies (k_cat/K_m) for these termination reactions are summarized in Table 2.

Table 2.

Kinetic parameters of peptide release by RF2 on m⁶A-modified and unmodified codons. Accuracy (A) is the ratio of efficiencies (k_cat/K_m) on respective codons

	Rate constants of peptide release			Accuracy (A)
Codon	k cat (s−1)	k cat/Km (μM−1 s−1)	K m (μM)	Codon pair	Accuracy
UAA	2.8 ± 0.18	70 ± 13	0.04 ± 0.008	UAA / UAG	12000 ± 3000
Um6AA	3.0 ± 0.06	11 ± 0.5	0.27 ± 0.014	Um6AA / Um6AG	6500 ± 500
UAG	0.06 ± 0.006	0.006 ± 0.001	10 ± 2	UAA / Um6AA	6.4 ± 1.2
Um6AG	0.027 ± 0.007	0.0017 ± 0.0001	16 ± 1	UAG / Um6AG	3.5 ± 0.8

Figure 7.

How m⁶A modification affects RF2-dependent termination at near-cognate for RF2 UAG codon. Ribosomal termination complex RT₀ (Figure 1B), at concentration 0.05 μM with native UAG (A) or modified Um⁶AG (B) codon in A site and with ³H-labelled fMet-Phe-Tyr-tRNA^Tyr in P site were reacted with RF2 at indicated concentrations. The fractional extents (y-axis) of terminated ribosomes, RT₃ (Figure 1B), are shown as functions of time (x-axis) Inserts: spontaneous termination without RF2. From these curves average reaction times for peptide release were estimated and their inverses, the generalized rate constants for peptide release, k_rel, are displayed in (C) for UAG and (D) for Um⁶AG. The maximal rates (k_cat) and efficiencies (k_cat/K_m) for these termination reactions are summarized in Table 2.

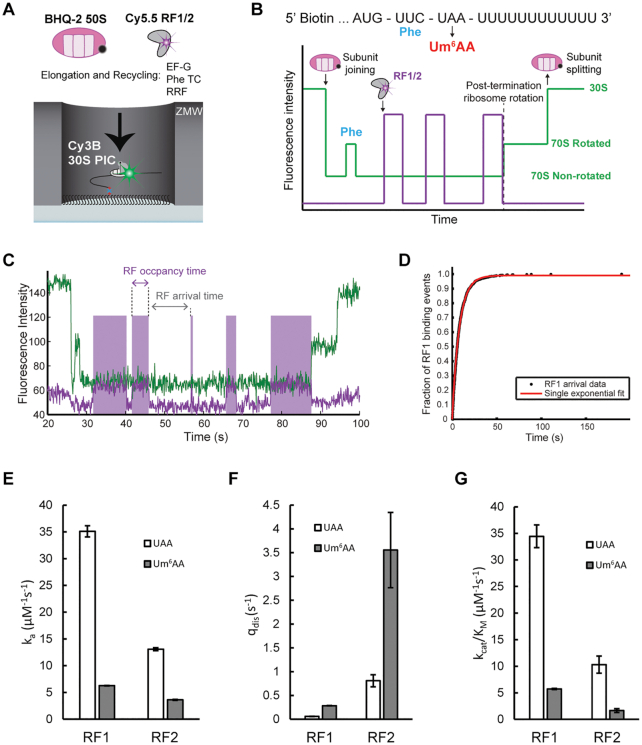
We note that the 6-fold smaller cognate k_cat/K_m for RF2 termination that we observed for the modified Um⁶AA compared to the native UAA codon agrees with the release factor association and dissociation rates estimated from single-molecule fluorescence experiments. In a previously-established zero-mode waveguide (ZMW)-based setup (16), 30S pre-initiation complex consisting of Cy3B-labeled 30S subunit, fMet-tRNA^fMet, IF2, and 5′-biotinylated mRNA encoding fMet-Phe dipeptide followed by a UAA stop codon (MF-UAA); was immobilized to the surface and BHQ-2 labeled 50S subunit, ternary complex, EF-G, RRF, and Cy5.5-labeled RF1 or RF2 were delivered to the immobilized system (Figure 8A). This allows real-time monitoring of subunit joining and one cycle of elongation from inter subunit Förster resonance energy transfer (FRET) between Cy3B and BHQ-2. During the elongation cycle the UAA stop codon is translocated into the A site and subsequent binding and dissociation of Cy5.5-RF was tracked (Figure 8B). The dwell times during Cy5.5-RF binding were defined as RF occupancy and RF arrival times, as shown in Figure 8C. Cumulative distribution of these measured dwell times (Figure 8D) were used to determine the association rate constant (k_a), dissociation rate constant (q_dis), and k_cat/K_m. These measurements showed that replacing UAA with Um⁶AA leads to an about 6-fold (Supplementary Figure S3A) or 4-fold (Figure 8E) lower association rate of RF1and RF2, respectively, to the ribosomal termination complex. This modification also accelerates the dissociation rates of RF1 (Supplementary Figure S3B) and RF2 (Supplementary Figure S3D) by 5-fold and 4-fold, respectively (Figure 8F). These effects on RF binding kinetics result in overall 6-fold reduction of k_cat/K_m in both RF1 and RF2 (Figure 8G).

Figure 8.

How m⁶A modification of cognate stop codon UAA to Um⁶AA affects RF1 and RF2 association and dissociation rates. (A) In all single-molecule experiments, 30S preinitiation complexes (PIC) containing Cy3B-30S, fMet-tRNA^fMet, and IF2 is immobilized on the surface of the ZMW wells through biotinylated mRNAs. The reaction is started by delivery of BHQ-2–50S, T₃, EF-G, RRF, and Cy5.5-labeled RF1 or RF2. (B) Expected sequence of fluorescence signals starting with quenching of Cy3B (green) that signals 50S subunit joining, one cycle of changes in Cy3B intensity that signals intersubunit rotations in one elongation cycle, Cy5.5 (purple) intensity increase/decrease signaling class I RF binding/dissociation, Cy3B eventual intensity increase signaling post-termination ribosome rotation, and complete dequenching of Cy3B signaling subunit splitting during ribosome recycling. (C) Representative trace of Cy5.5-RF1 terminating on Um⁶AA stop codon, with RF occupancy time defined as the time interval between binding and dissociation of Cy5.5-RF and RF arrival time defined as the time interval between dissociation and next binding of Cy5.5-RF. (D) Cumulative distribution of Cy5.5-RF1 arrival times on UAA stop codon, fit to single-step exponential function. (E) RF1/RF2 association rate constant (k_a) on UAA and Um⁶AA codons. Error bars are defined as 95% CI. (F) RF1/RF2 dissociation rate constant (q_dis) on UAA and Um⁶AA codons. Error bars are defined as 95% CI. (G) k_cat/K_m of RF1 and RF2 on UAA and Um⁶AA codons calculated using k_a and q_dis from single-molecule measurements and k_cat (3 s⁻¹) from bulk kinetics measurements (Table 2). Error bars are defined as propagated error from k_a and q_dis.

DISCUSSION

N ⁶-methylated adenosines are ubiquitous in open reading frames and untranslated regions of mRNAs in all organisms. How these modifications affect rate and accuracy of ribosomal sense and stop-codon reading by the messenger RNA-encoded ribosome could therefore be of vital concern for living cells. Increased error levels in genetic code translation will be costly for organisms (38) but could also diversify gene expression and codon interpretation (39). Here, we used classical quench-flow techniques to study how m⁶A in middle positions of mRNA codons tunes the efficiency by which ternary complex with aa-tRNA and EF-TuGTP is activated for ribosome-dependent GTP hydrolysis (Table 1) and affects proofreading of aminoacyl-tRNAs with cognate or near-cognate codon-anticodon interactions (Supplementary Table S1). For comparison, we used the same rapid kinetics techniques to study how N⁶-methylation of adenosines in middle codon nucleotide position introduction affects the efficiency of cognate and near-cognate stop-codon reading by the RF2 protein (37). The efficiency (k_cat/K_m) of cognate peptide bond formation from ternary complex and free post-translocation ribosomes was reduced by more than an order of magnitude by N⁶-methylation of adenosine in middle position of the A-site codon. Surprisingly, the efficiency of near-cognate peptide bond formation was virtually unaltered by this modification, corresponding to a mis-sense error increase by an order of magnitude by the N⁶-methylation. This contrasts the action of most known error inducing agents like, for instance, the antibiotic drugs streptomycin (25), aminoglycosides (11) and viomycin (26), as well as error inducing mutations in ribosomal proteins S4, S12 and S5 (27). All those alterations greatly increase near-cognate but have small effects on cognate codon reading efficiencies and thus greatly increase codon translation errors by increasing near-cognate codon reading efficiency.

Through detailed studies of the kinetics of GTP hydrolysis in ternary complex and its dependence on free Mg²⁺ concentration (Figure 2, Supplementary Figure S1, and Table 1) we found N⁶-methylation of middle codon adenosine to (i) reduce by 10-fold the second order rate constant (k_a) for ternary complex binding to ribosomes programmed with cognate and near-cognate sense codons alike; (ii) increase by 4-fold the low probability that an already bound ternary complex proceeds to GTP hydrolysis in near-cognate codon reading; (iii) leave the near 100% probability for GTP hydrolysis after ternary complex binding unaltered in cognate codon reading; (iv) reduce by 3-fold the high probability of near-cognate aa-tRNA discarding in proofreading; (v) leave the near zero probability of cognate aa-tRNA discarding apparently unaltered. This means, in summary, that the same m⁶A dependent 10-fold reduction of the rate constant for ternary complex binding to cognate and near-cognate ribosomes is neutralized by a 10-fold increase in the probability that near-cognate ternary complex binding results in peptidyl transfer rather than aa-tRNA dissociation. No such compensation is possible in the cognate case where the probability that ternary complex binding results in peptidyl transfer is close to one already for native codons.

The large N⁶-methylation caused decrease in association rate constant for cognate and near-cognate ternary complex alike corresponds to a large increase in activation free energy for ternary complex binding into a ribosome state lacking codon-anticodon interaction. We note that if m⁶A introduction were to reduce a putative barrier for complex formation, then a corresponding 10-fold reduction in the rate constant for ternary complex dissociation would be expected. There is, in contrast, only a 1.7-fold m⁶A-dependent decrease in the rate constant for cognate ternary complex dissociation (Supplementary Table S4). From this we suggest that the bound states of ternary complex are all shifted to a higher standard free energy by m⁶A introduction. It also seems that the 4-fold error increase in initial selection of ternary complex (Supplementary Table S1) is too large to be accounted for by a uniform, 1.7-fold, reduction in rate constant for ternary complex dissociation in cognate and near-cognate reactions alike, as in the case of aminoglycosides (23). It is therefore possible that the intrinsic discrimination, the ‘d-value’ (23) is corrupted by the presence of N⁶-methyladenosine in the middle codon position.

The present study has also revealed that m⁶A in middle codon position has strikingly similar effects on codon reading by ternary complex and RF2. We found that the efficiency of cognate termination at UAA codons by RF2 decreased 6-fold when UAA was replaced by Um⁶AA, while the efficiency of near-cognate termination at UAG stop codon by RF2 was reduced less upon UAG replacement with Um⁶AG. Here, again, we see that it is a more impaired cognate reaction efficiency and not a greatly boosted near-cognate reaction efficiency that increases codon reading errors. By analogy with the ternary complex case, we propose, firstly, that m⁶A introduction in middle codon position greatly reduces the rate constant for class-1 release factor binding to the ribosomal termination complex in cognate and near-cognate reactions alike and, secondly, that the efficiency of the near-cognate reaction is partially rescued by m⁶A-enhanced probability that an already ribosome-bound release factor promotes ester bond hydrolysis. Single-molecule termination assay results support this hypothesis by showing that m⁶A in middle codon position of UAA both decreases the association rate constant and increases the dissociation rate constants of RF1 and RF2, resulting in 6-fold reduction of k_cat/K_m for both factors.

The present findings regarding N⁶-methylation of adenosine in second codon position have similarities with but also intriguing deviations from previous data on m⁶A introduction in first codon position (5). There it was found that first base modification of Lys AAA to m⁶AAA reduces the efficiency of initial AAA reading by a factor of twenty under high-accuracy, in vivo-like conditions (33,34). This result is apparently in line with present data on cognate reading of Glu-codon by tRNA^Glu containing ternary complex, where m⁶A replacing middle codon position A leads to a 10-fold reduction of cognate GTP hydrolysis efficiency (Table 1). However, the previous observation that increasing Mg²⁺ concentration strongly increases the efficiency of cognate m⁶AAA reading by Lys-tRNA^Lys leading to converging efficiencies for AAA and m⁶AAA reading above 10 mM Mg²⁺ concentration was not seen here. Furthermore, the previous observation that one GTP is hydrolyzed per peptide bond for native, cognate codon reading, and that there is 50% excess GTP hydrolysis for cognate reading of an N⁶-methylated adenosine in first codon position under high-accuracy in vivo-like condition (5) is not seen here with the modification in second codon position. Here we always observe 1:1 stoichiometry between GTP hydrolysis and peptide bond formation for cognate codon reading by ternary complex. From these data we tentatively suggest that m⁶A introduction in middle and first codon nucleotide position are fundamentally different. In the former case, the modification induced error increase depends on a selective reduction of cognate peptide bond formation efficiency. In the latter case (5) error induction is similar to that induced by antibiotic drugs like aminoglycosides (11,23) and mutations in ribosomal proteins (6) and depends on enhanced near-cognate codon reading efficiency at virtually unchanged cognate codon reading efficiency. By such scenarios there would be a great potential for diverse tuning of codon reading efficiency by m⁶A introduction in different codon nucleotide positions.

Modified nucleotides in mRNA thus represent an extra layer of potential regulation in gene expression, modulating mRNA stability, protein binding and as shown above, the rates and fidelity of protein synthesis and its termination. How the networks of diverse modifications evolve temporally across the transcriptome, and how they control biological processes remains a compelling yet unanswered question. To answer will require further quantitative measurements like those described here.

DATA AVAILABILITY

Data available upon request.

Notes

Present address: Gabriele Indrisiunaite, Department of Biology, University of Copenhagen, Ole Maaløes Vej 5, DK-2200 Copenhagen N, Denmark.

Present address: Arjun Prabhakar, Pacific Biosciences, Inc., Menlo Park, CA 94025, USA.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Swedish Research Council [VR 2018-0404, VR 2016-0624 to M.E.]; Knut and Alice Wallenberg Foundation (to M.E.); NIH grant [GM51266 to J.D.P.]; Swedish Research Council[VR 2016-06824 to K.-W.I.]; Selma Anderson and Tullberg scholarships (Uppsala University) (to G.I.); NIH Molecular Biophysics Training grant [T32-GM008294]; Stanford Interdisciplinary Graduate Fellowship (to A.P.). Funding for open access charge: Swedish Research Council; Knut and Alice Wallenberg Foundation.

Conflict of interest statement. None declared.